- 1Jülich Centre for Neutron Science JCNS, Forschungszentrum Jülich GmbH, Outstation at Institut Laue-Langevin, Grenoble, France
- 2Institut für Kristallographie der RWTH Aachen University, Aachen, Germany
- 3Forschungsneutronenquelle Heinz Maier-Leibnitz FRM-II, Technische Universität München, Garching bei München, Germany
- 4Institut Laue-Langevin, Grenoble, France
- 5SPSMS, UMR-E 9001, CEA-INAC/UJF-Grenoble 1, MDN, Grenoble, France
- 6European Synchrotron Radiation Facility, Grenoble, France
- 7Peter Grünberg Institut PGI and JARA-FIT, Forschungszentrum Jülich GmbH, Jülich, Germany
- 8Jülich Centre for Neutron Science JCNS and Peter Grünberg Institut PGI, JARA-FIT, Forschungszentrum Jülich GmbH, Jülich, Germany
The Néel temperature of the new frustrated family of SrRE2O4 (RE = rare earth) compounds is yet limited to ~0.9 K, which more or less hampers a complete understanding of the relevant magnetic frustrations and spin interactions and an exploration of potential interesting properties. Here we report on a new frustrated member to the family, SrTb2O4 with a record TN = 4.28(2) K, and an experimental study of the magnetic interacting and frustrating mechanisms by polarized and unpolarized neutron scattering. The compound SrTb2O4 displays an incommensurate antiferromagnetic (AFM) order with a transverse wave vector Q0.5 KAFM = (0.5924(1), 0.0059(1), 0) albeit with partially-ordered moments, 1.92(6) μB at 0.5 K, stemming from only one of the two inequivalent Tb sites mainly by virtue of their different octahedral distortions. The localized moments are confined to the bc plane, 11.9(66)° away from the b axis probably by single-ion anisotropy. We reveal that this AFM order is dominated mainly by dipole-dipole interactions and disclose that the octahedral distortion, nearest-neighbour (NN) ferromagnetic (FM) arrangement, different next NN FM and AFM configurations, and in-plane anisotropic spin correlations are vital to the magnetic structure and associated multiple frustrations. The discovery of the thus far highest AFM transition temperature renders SrTb2O4 a new friendly frustrated platform in the family for studying the nature of magnetic interactions and frustrations and exploring potential macroscopic functionalities and new quantum states.
1. Introduction
Revealing the magnetic coupling mechanism is often a critical step toward understanding the role of magnetism in intriguing phenomena such as colossal magnetoresistance (CMR), high TC superconductivity, multiferroicity or frustration in correlated electron materials [1–5]. By way of example, the indirect double- and super-exchange interactions were successfully elaborated in qualitatively explaining the CMR effect and associated magnetic orders based only on the spin and charge degrees of freedom [1]. In 4f-based insulators, the indirect oscillating interaction [4–7] between pairs of localized 4f moments via the intermediary of valence electrons is blocked. Therefore, possible super-, dipole-dipole and multipolar, and Dzyaloshinsky-Moriya (DM) exchange interactions are primarily responsible for potential magnetic ordering [4]. Without detailed knowledge of the structural and magnetic parameters, it is hard to uniquely determine which interaction acts as the major exchange mechanism [8]. In this case, the origins of the related incommensurable spin structures become elusive [4]. In addition, the competition between spin-orbital coupling and crystal electric field (CEF) at low temperatures largely affects the highly-degenerate Hund's rule ground state, and besides the anisotropic dipolar and DM interactions, determine the magnitude of the magnetic anisotropy [9, 10]. This anisotropy strongly influences the degree of magnetic frustration. Sometimes, it may disorder or even quench potential magnetic moments, leading to a virtually nonmagnetic ground state [11].
Magnetic frustration can lead to novel quantum states such as spin liquid, spin ice, cooperative paramagnetism or the magnetic Coulomb phase based on magnetic monopole excitations, providing an excellent testing ground for theories [4, 12–25]. A Monte Carlo simulation indicates that the observed diffuse scattering in SrEr2O4 originates from a ladder of Er triangles [26]. A computation of the crystal-field levels demonstrates site-dependent anisotropic single-ion magnetism in the compounds of SrHo2O4 and SrDy2O4 [27]. Lanthanide-based magnetic compounds, e.g., edge-sharing tetrahedra, corner-sharing spinels, or triangular Kagomé and pyrochlore lattices, often show anomalous magnetic properties due to geometric frustration [28–31]. The family of SrRE2O4 (RE = Y, Gd, Ho, Yb) compounds was first synthesized in 1967 [32]. Recently, a study on polycrystalline SrRE2O4 (RE = Gd, Dy, Ho, Er, Tm, Yb) samples demonstrates that they adopt the orthorhombic structure [33] with a geometric frustration for the magnetic ions revealed by the existence of magnetic short-range orders down to ~1.5 K [34]. Subsequently, single crystals of SrRE2O4 (RE = Y, Lu, Dy, Ho, Er) were successfully grown [35]. Single-crystal neutron-scattering studies on SrRE2O4 (RE = Ho, Er, Yb) compounds with respective antiferromagnetic (AFM) transition temperatures at 0.62, 0.73, and 0.9 K were reported [36–40], generally confirming that there exists a coexistence of long- and short-range magnetic orders. It is pointed out that for the case of SrHo2O4, Young et al. [41] observed only a short-range spin order inconsistent with other reports [36, 37, 40]. Further experimental tests would be necessary to address this discrepancy. Since the adopted orthorhombic structure accommodates two RE sites (RE1 and RE2), it is hard to derive the crystallographic origins of the two types of spin ordering. In addition, single-crystal SrDy2O4 displays only weak diffuse magnetic scattering which persists down to ~20 mK [42]. The low transition temperatures of the magnetic orders, to some extent, prevent a complete understanding of the nature of magnetic interactions and frustrations in the family. To overcome these problems and address the relevant interesting physics necessitate a search in the SrRE2O4 (RE = rare earth) family for a new compound that displays a higher Néel temperature, thus permitting a technically easier study of the two coupling mechanisms.
In this study, we report on a new frustrated member to the family of SrRE2O4, namely SrTb2O4, which has not been studied yet by neutron scattering. The single-crystal SrTb2O4 displays a long-range magnetic order relative to the underlying lattice. The noncollinear incommensurate AFM structure forms at TN = 4.28(2) K upon cooling. The synthesis of SrTb2O4 with the highest Néel temperature in the family opens up an easier route to elucidate the magnetic coupling and frustrating mechanisms. By polarized and unpolarized neutron scattering we uniquely determine the detailed structural and magnetic parameters to understand the magnetism in SrTb2O4.
2. Materials and Methods
Polycrystalline samples of SrTb2O4 were synthesized from stoichiometric mixtures of SrCO3 (99.99%) and Tb4O7 (99.99%) compounds by standard solid-state reaction [43]. Both raw materials were preheated at 800° for 12 h and weighted at ~200°. The mixed and milled raw materials were calcined twice at 1473 and 1573 K for 48 h each in air in order to perform decarbonization and prereaction. The resulting powder was pressed into cylindrical rods with an isostatical pressure of ~78 MPa. The rods were sintered two times at 1573 and 1673 K for 48 h at each temperature in air. After each round of the isostatic pressing and subsequent firing, the product was reground and ball-remilled, which results in a dense and homogenous sample and ensures a complete chemical reaction. The single crystal of SrTb2O4 was grown by optical floating-zone method with an atmosphere of ~98% Ar and ~2% O2. The growing speed is ~4 mm/h with rotations of the feed and seed rods at +32 and −28 rpm, respectively. The phase purity of the polycrystalline and single-crystalline samples was checked by in-house X-ray powder diffraction. The electrical resistivity of a bar-shaped single crystal by standard dc four-probe technique was measured on a commercial physical property measurement system.
High-resolution neutron powder diffraction (NPD) patterns were collected with a pulverized SrTb2O4 single crystal (~5 g) mounted in a 3He insert on the structure powder diffractometer (SPODI) [44] with constant wavelength λ = 2.54008(2) Å at the FRM-II research reactor in Garching, Germany.
The SrTb2O4 single crystal (~2.2 g) for the neutron-scattering studies was oriented in the (H, K, 0) scattering plane with the neutron Laue diffractometer OrientExpress [45] and the IN3 thermal triple-axis spectrometer at the Institut Laue-Langevin (ILL), Grenoble, France. The mosaic of this single crystal is 0.494(5)o full width at half maximum (FWHM) for the nuclear (2, 0, 0) Bragg reflection at 1.5 K. Longitudinal XYZ neutron polarization analysis [46] was carried out on the D7 (ILL) diffractometer with a dilution fridge and λ = 4.8 Å. Unpolarized elastic neutron-scattering studies were performed at the two-axis D23 diffractometer (ILL) with incident wavelength 1.277 Å and the IN12 (ILL) cold triple-axis spectrometer with fixed final energy of 5.3 meV and the beam collimation set as open-40′-sample-60′-open.
Here the wave vector Q(HKL) (Å−1) = (QH, QK, QL) is defined through (H, K, L) = quoted in units of r.l.u., where a, b, and c are relevant lattice constants referring to the orthorhombic [33] unit cell.
3. Results
Figure 1 shows the neutron polarization analysis in the spin-flip (SF, i.e., Z-flipper on) and non-spin-flip (NSF, i.e., Z-flipper off) channels. Compared with the maps at 300 K (Figure 1A), it is clear that extra fourfold Bragg peaks around (±1.6, ±1, 0) appear symmetrically in both SF and NSF reciprocal space maps at 50 mK (Figure 1B) due to a long-range magnetic transition. Polarized neutron magnetic scattering depends on the direction of the neutron polarization with respect to the scattering vector , and also the direction of the ordered-moments . In our case, (Z-component) ‖ c-axis [46], and the magnetic Bragg reflections are observed in the (H, K, 0) plane, i.e., . In this case, the neutron-scattering cross sections of the NSF and SF channels are
respectively. The first and the second terms in each equation refer to the magnetic and spin-incoherent scatterings, respectively. The third term in Eq. (1) denotes nuclear and isotope incoherent contributions [46]. The presence of the incommensurable AFM Bragg peaks in the NSF channel (Figure 1B) indicates that one component of is parallel to the c axis, while their appearances in the SF channel imply a component lying in the ab plane.
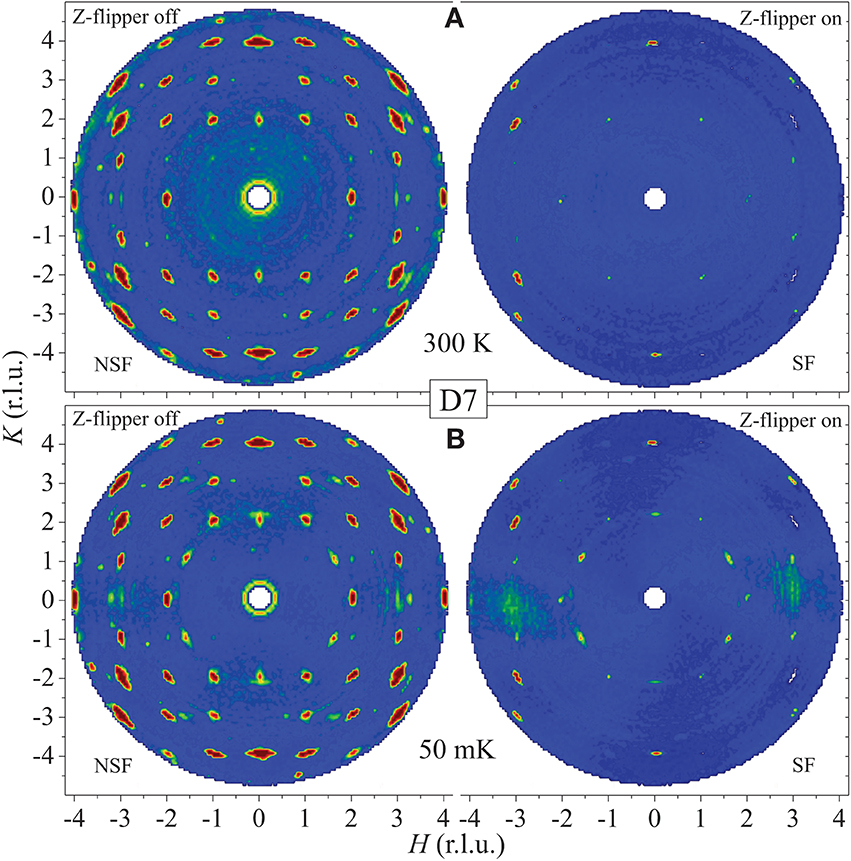
Figure 1. Polarization analysis data measured using D7 (ILL). (A) At 300 K. (B) At 50 mK. The NSF (i.e., Z-flipper off, left panel) and SF (i.e., Z-flipper on, right panel) channels are shown with the same color code for intensity. The non-perfect polarization involuntarily leads to the presence of some nuclear Bragg peaks, e.g., (0, ±4, 0), in the SF channel at both temperatures. The horizontal bar-shaped neutron-scattering intensities around (0, ±2.15, 0) and the extremely-broad diffuse scattering around (±3, 0, 0) in (B) may correspond to some short-range magnetic components. It is pointed out that similar diffuse magnetic scattering also appears in the SrHo2O4 and SrEr2O4 single crystals [36–38].
We observe the magnetic Bragg peak only at 0.5 K in our NPD study (Figure 2). We thereby refine the AFM wave vector exactly as QAFM = (0.5924(1), 0.0059(1), 0) by the profile-matching mode [47] and a total moment || = 1.92(6) μB at the maximum amplitude for the Tb1 ions only with the b- and c-components equalling to +1.88(8) and +0.40(23) μB (Table 1), respectively. The moment size of the Tb2 site is negligible. Figure 3 schematically shows the resulting crystal and magnetic structures as well as the structural parameters for the bent Tb6 honeycombs. The temperature dependence of the AFM (1.6, 1, 0) Bragg peak is shown in Figure 4. The extracted integrated intensity (I) was fit to a power law , which produces a Néel temperature TN = 4.28(2) K, and a critical exponent β = 0.55(2) probably indicative of a second-order type phase transition and possible three-dimensional Heisenberg-like spin interactions [48].
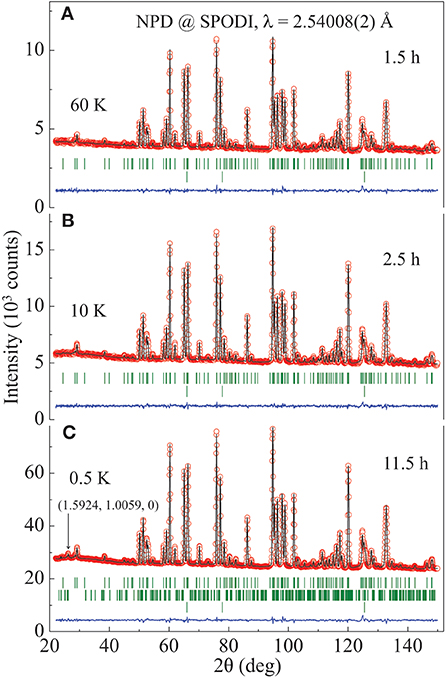
Figure 2. Observed (circles) and calculated (solid lines) NPD patterns from the study using SPODI (FRM-II). (A) At 60 K with counting time ~1.5 h. (B) At 10 K with counting time ~2.5 h. (C) At 0.5 K with counting time ~11.5 h. The vertical bars mark the positions of nuclear and magnetic Bragg reflections of SrTb2O4 as well as the Al nuclear Bragg peaks (from sample environment), respectively. The lower curves represent the difference between observed and calculated patterns. No obvious diffuse magnetic scattering appears as observed in polycrystalline SrRE2O4 (RE = Ho, Er, Dy) compounds in Ref. [34].
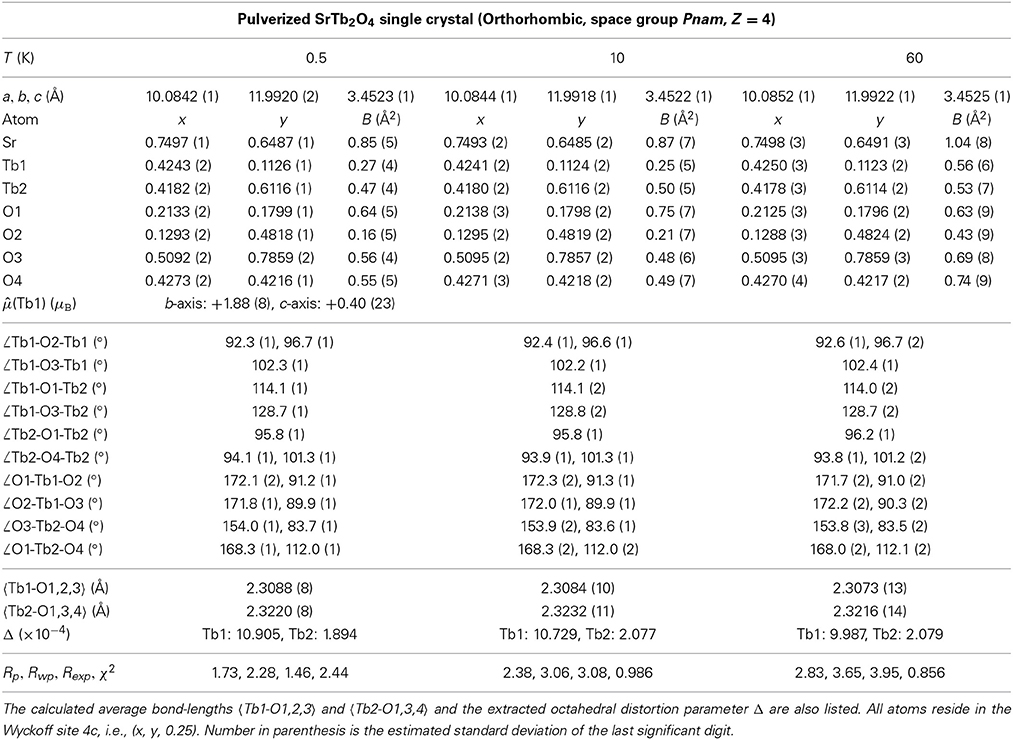
Table 1. Refined structural parameters (lattice constants, atomic positions, Debye-Waller factor B, bond angles and bond lengths), magnetic moment , and the corresponding goodness of refinement by the Fullprof Suite [47] from the NPD data measured at 0.5, 10, and 60 K using SPODI (FRM-II).
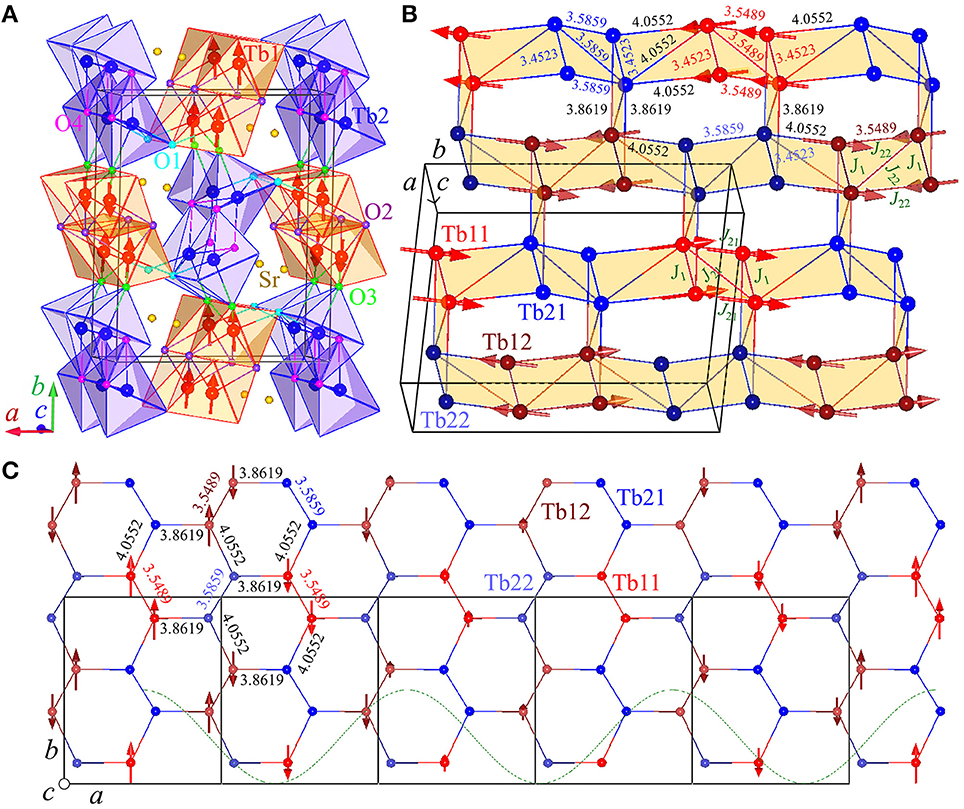
Figure 3. Crystal and magnetic structures of SrTb2O4. (A) As refined with the SPODI (FRM-II) data measured at 0.5 K. (B) Detailed Tb-Tb bond lengths within the bent Tb6 honeycombs. J1 and J21/J22 represent the nearest-neighbor (NN) and next-NN (NNN) magnetic couplings. (C) Projection of the bent Tb6 honeycombs to the ab plane. The cosine-curve (dashed line) beginning from the center of the first unit-cell in left schematically shows the incommensurable spin modulation along the a axis. In (A–C), the arrows drawn through the Tb1 ions represent the Tb1 partially-ordered moments, and the connected lines represent the crystallographic unit cell(s). To clearly show the magnetic frustration, Tb1 and Tb2 sites in (A) are transferred into Tb11 and Tb12 as well as Tb21 and Tb22 sites, respectively, as shown in (B,C) by the irreducible representation analysis to the P-1 symmetry [47].
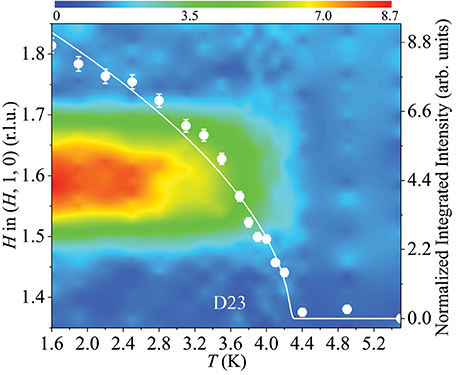
Figure 4. Temperature-dependent ordering parameter of the AFM transition. Temperature dependent H-scans around the AFM (1.6, 1, 0) Bragg peak (left ordinate) performed at D23 (ILL) and the corresponding integrated intensities (circles) (right ordinate). The solid line is the fit with a power law as described in the text. The error bars are statistical errors.
We record a reciprocal space map (Figure 5A) around the AFM (1.6, 1, 0) Bragg peak at 1.7 K using D23, and the central scans along the qH and qK directions (Figure 5B) were measured at IN12. In both figures, the FWHM of the magnetic Bragg peak along the qH and qK directions is sharply different. Both magnetic Bragg peaks are broader than the nuclear Bragg (2, 0, 0) reflection in the reciprocal space as shown in Figure 5B, which indicates that the observed magnetic Bragg peaks are beyond the instrument resolution. Therefore, Figure 5B shows a real in-plane magnetic anisotropy.
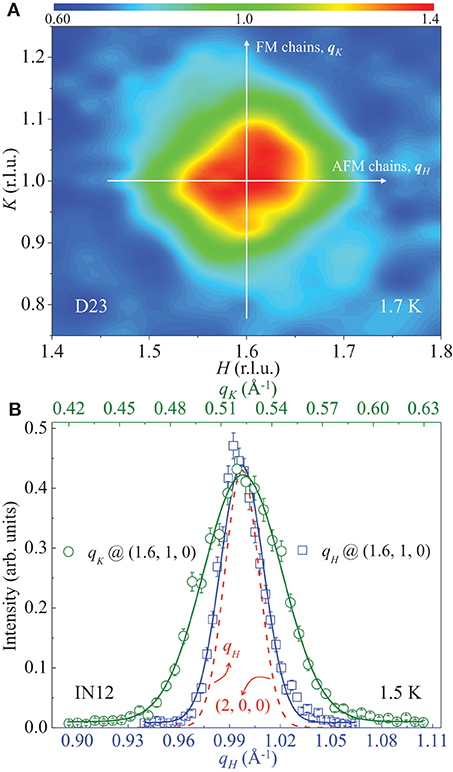
Figure 5. Anisotropic in-plane spin correlations of SrTb2O4. (A) Unpolarized neutron data around the AFM (1.6, 1, 0) Bragg reflection measured at 1.7 K using D23 (ILL). The two perpendicular arrows point out the directions of qH (i.e., the in-plane AFM chains) and qK (i.e., the in-plane FM chains), respectively. (B) Unpolarized neutron data around the (1.6, 1, 0) (void symbols) and the (2, 0, 0) (dashed line) Bragg peaks measured at 1.5 K using IN12 (ILL). For comparison, the qH values around the nuclear (2, 0, 0) Bragg peak are reduced by 0.2547 Å−1. The solid lines are Gaussian fits to the magnetic data convoluted with the nuclear correlation length as expected Q-resolution.
4. Discussion
To quantitatively estimate the in-plane anisotropy, we take the FWHM of the nuclear Bragg (2, 0, 0) peak as the detecting accuracy which is convoluted in fitting the magnetic peaks by a Gaussian function shown as the solid lines in Figure 5B. This results in FWHM = 0.0183(1) and 0.0492(2) Å−1 along the qH and qK directions, respectively, implying highly anisotropic in-plane spin correlations consistent with the observation that strong magnetic frustration exists in SrTb2O4. We roughly estimate the spin-correlation length (ξ) by , i.e., ξH = 343.7(22) Å and ξK = 127.6(4) Å. Therefore, . Similar in-plane anisotropic magnetic correlations were also observed in the iron-based superconductors [49–53] that are highly frustrated, too, where its microscopic origin, from the ellipticity of the electron pockets or the competing exchange interactions associated with the local-moment picture, is still highly debated [54–57]. It is undoubted that the observed in-plane magnetic anisotropy in SrTb2O4 indicates an appearance of the competing spin exchanges and is certainly associated with a description of the purely-localized magnetism of ionic Tb3+ ions. A deeper understanding of the insulating state necessitates theoretical band structure calculations. We tentatively estimate the compatibility between ordered magnetic and nuclear crystalline domains based on the non-deconvoluted FWHM (κ) of the Bragg (1.6, 1, 0) (κm = 0.0300(7) Å−1) and (2, 0, 0) (κn = 0.0238(2) Å−1) peaks, i.e., κn/κm = 79(2)%, which implies that the incommensurate AFM structure orders in a long-range fashion relative to the underlying lattice of the single crystal.
We further analyze the spin-correlation length with our NPD data (Figure 2C). Firstly, it is pointed out that the positive and negative momenta cannot technically be differentiated in a NPD study. As shown in Figure 6A, taking into account the corresponding SPODI instrument resolution (dashed line) [46], a Gaussian fit (solid line) to the AFM Bragg (1.5924, 1.0059, 0) peak (squares) results in an average ξAFM = 864(36) Å in real space. This indicates that the AFM ordering observed in SrTb2O4 is indeed of long range in character in comparison with the reported extremely-broad magnetic diffuse scattering which was attributed to the presence of short-ranged magnetic ordering in polycrystalline SrRE2O4 (RE = Ho, Er, Dy) samples in the study of Ref. [34]. With the same method utilized in Figure 6A, we also analyze the NPD peak of the nuclear Bragg (2, 0, 0) reflection as shown in Figure 6B and extract that ξ(200) = 1304(34) Å. This indicates that ξAFM/ξ(200) = 66(3)% basically in accord with the compatibility between ordered magnetic and nuclear crystalline domains extracted with our single-crystal neutron-scattering data. Since our NPD data were collected from a pulverized SrTb2O4 single crystal, that ξAFM is ~2.5 times larger than ξH may indicate that there have strong magnetic and crystalline domain effects in single-crystal SrTb2O4, or a large part of spins are blocked probably due to a pining effect by strains accumulated during single crystal growth. In any case, this difference between single-crystalline and polycrystalline samples in turn supports the fact that there is a strong magnetic frustration in single-crystal SrTb2O4. Further studies with high pressures would be of great interest.
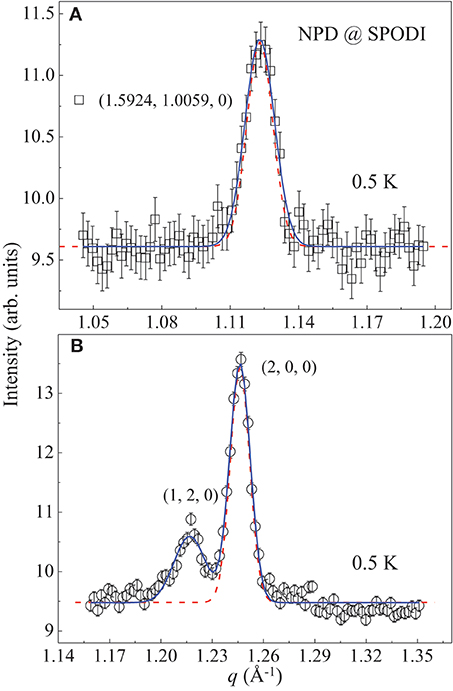
Figure 6. NPD peaks of the incommensurate AFM (1.5924, 1.0059, 0) and the nuclear Bragg (2, 0, 0) reflections. The data were measured at 0.5 K using SPODI (FRM-II) and extracted from Figure 2C. (A) NPD data of the incommensurate AFM (1.5924, 1.0059, 0) Bragg reflection (squares), and (B) of the nuclear Bragg (1, 2, 0) and (2, 0, 0) reflections (circles). The solid lines are Gaussian fits convoluted with the corresponding Q-resolutions (dashed lines) [46].
In most cases, the strength of the indirect magnetic interactions such as conventional double- or super-exchange [1] can be influenced more or less by the value of the revelent bond angle [58–61], e.g., the ∠Tb-O-Tb bond angles in SrTb2O4 as listed in Table 1 (see also Figure 7). However, the respective values of ∠Tb-O-Tb display no appreciable difference within accuracy between 0.5 and 10 K (Table 1), below and above the TN, respectively, which may indicate an invalidity of the two conventional magnetic coupling mechanisms (double- or super-exchange) in SrTb2O4. This is consistent with the study of SrTm2O4 [11] and in excellent agreement with our transport study, where any attempts to measure possible resistivity in SrTb2O4 from 2 to 300 K were fruitless. We estimate that the resistance of the single crystal measured is beyond at least 106 ohm. We thus conclude that SrTb2O4 is a robust insulator, and the electrons responsible for the incommensurable antiferromagnetism are mainly from the localized 4f8 shell of the ionic Tb3+ ions. In this localized picture, the interionic exchange interactions dominate for the formation of the magnetic structure [4, 6]. The nearest Tb neighbors are stacked linearly along the c axis (Figure 3B). The shortest Tb1-Tb1 and Tb2-Tb2 have the same bond length. However, the NN Tb1 ions have a ferromagnetic (FM) arrangement. By contrast, the interaction between the NN Tb2 ions is blocked unexpectedly (Figure 3B). There is no appreciable difference in the NN Tb-Tb bond length, i.e., the c lattice constant, between 0.5 and 10 K (Table 1), which probably rules out the potential direct exchange interaction consistent with the fact that unpaired 4f electrons are deeply embedded under the 5s2p6 shells and also indicates that the prevalent dipole-dipole interaction is subjected to some condition, i.e., the octahedral distortion as discussed below, in agreement with the study of SrTm2O4 [11].
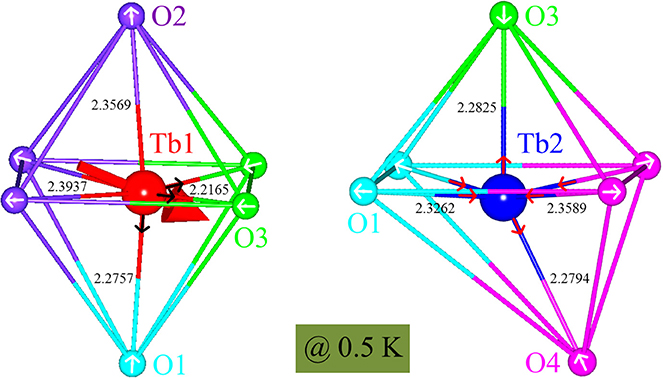
Figure 7. Local octahedral environment of the two Tb sites. The detailed Tb-O bond lengths within the TbO6 octahedra as refined from the SPODI (FRM-II) data collected at 0.5 K. The big arrow drawn through the Tb1 ion represents the Tb1 moment. The small arrows sitting on the O ions or the Tb-O bonds schematically show the deduced octahedral distortion modes as displayed.
As a non-Kramers ion, Tb3+ (S = 3, L = 3, J = 6, gJ = 1.5) in principle keeps the time reversal symmetry and doesn't show any energy degeneracy in the presence of the purely-localized electric field. However, we refine two kinds of octahedra as shown in Figure 7: Tb1O6 and Tb2O6, corresponding to the partially-ordered and totally-frozen Tb1 and Tb2 ions, respectively. The average octahedral distortion [58, 59] can be quantitatively measured by the parameter Δ defined as: , where dn and 〈d〉 are the six Tb-O bond lengths along the six crossed directions (Figure 7) and the mean Tb-O bond length (Table 1), respectively. It is noteworthy that the Δ values of the Tb1 and Tb2 ions are in the same magnitudes as those of the Mn3+ Kramers and Mn4+ non-Kramers ions, respectively, in the Jahn-Teller (JT) distorted regime of single-crystal LaSrMnO3 [60]. This sharp contrast implies that the Tb1 ions are strongly distorted, while the Tb2 ions behave normally within the non-Kramers scheme. Therefore, the Δ magnitude that reflects the ion local symmetry and thus the strength of the surrounding CEF directly determines the existence of the magnetic ordering, which is supported by the observation that below TN the respective Δ values of the Tb1 and Tb2 ions change oppositely with temperature (Figure 8). We therefore infer that one possible reason for the formation of the incommensurable magnetic structure is the modulated distribution of the 4f16s2 valence electrons which modify the surrounding environment experienced by the localized unpaired 4f electrons. The corresponding modulation of the local symmetry may plausibly be attributed to the spatial zigzag-type Tb arrangements along the a and b axes in the process of forming the crystallographic domains. This is supported by the fact that the honeycomb columns run straightly along the c axis, and there is no spin modulation at all in that direction.
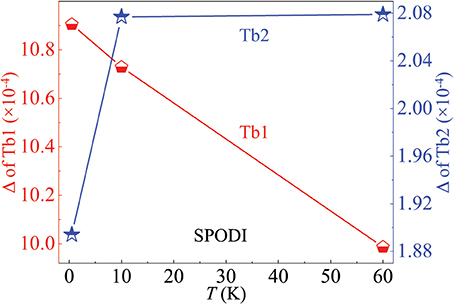
Figure 8. Octahedral distortions of the Tb1 and Tb2 sites. Octahedral distortion parameter Δ of the Tb1 (left ordinate) and Tb2 (right ordinate) sites as refined from the SPODI (FRM-II) data.
Based on the refined Tb-O bond lengths, we deduce two distortion modes for the Tb1O6 and Tb2O6 octahedra (Figure 7), respectively. The possible product of the Tb1 subjected stress-vectors (small arrows) should point qualitatively to the direction of the Tb1 moment, implying a strong single-ion anisotropy. This JT-like distortion mode leads to the large Δ value of the Tb1 ions, and possibly lifts further the degenerate multiplets. By contrast, the Tb2 ions are subjected to opposing stresses in all the three pair-directions. In this case, the octahedral distortion strongly depends on their competing strengths. This mode makes the small Δ value of the Tb2 ions and their potential total magnetic moments quenched vitally.
The maximum Tb1 moment size is mere 1.92(6) μB, 21.3(7)% of the theoretical saturation value (gJ J = 9 μB). It is of particular interest to explore the frustrating mechanism. The virtual non-Kramers state of the Tb2 site reduces the total moment size per molar formula by 50%. The Tb1 moment fluctuates like a wave defined as , where Rx is a spin coordinate along the a axis, and ϕ is a phase parameter. The existence of the strong single-ion anisotropy indicates a large CEF effect which should be comparable to the energy scale of the magnetic interactions. We have shown the clear evidence for a large magnetic exchange anisotropy (Figure 5), which is ascribed to the anisotropic dipole-dipole interaction. The NN magnetic arrangement is FM (Figure 3B), implying no possibility for a magnetic frustration. The NNN magnetic configurations display a dual character, i.e., FM and AFM for the equivalent Tb11 and Tb12 sites, respectively. This sharp difference may frustrate the Heisenberg-exchange coupled NNN spins.
5. Conclusions and Outlook
To summarize, we have synthesized large enough SrTb2O4 single crystals suitable for neutron scattering and revealed a modulated spin structure in SrTb2O4 with the highest AFM transition temperature at TN = 4.28(2) K in the SrRE2O4 family, which provides a technically friendly platform to explore the related magnetic coupling and frustrating mechanisms. Our studies show that the localized Tb1 moments lie in the bc plane with the FM chains along both the b and c directions and the AFM modulation mainly along the a axis. We have found two distinct octahedra for the non-Kramers Tb3+ ions: Tb1O6 being strongly distorted, corresponding to the partially-ordered moments; Tb2O6 being frustrated entirely in the non-Kramers state. Therefore, the octahedral distortion has a decisive influence on the Hund's rule magnetic ground state (7F6) and the related frustrations. The magnetocrystalline anisotropy is crucial in determining the direction of the ordered moments. The direct NN interaction results in a FM arrangement for the Tb1 ions along the c axis, and the different NNN Tb configurations (FM and AFM) further lift the magnetic frustration. The present results make SrTb2O4 a particularly significant compound in the family for theoretical and further experimental studies. Inelastic neutron-scattering studies to determine the detailed crystal-field and magnetic-interaction parameters would be of great interest. The factors that influence the value of the AFM transition temperature would be further explored in combination with theoretical calculations.
Author Contributions
Cong Zhang, Paul Meuffels, and Hai-Feng Li prepared the polycrystals and grew the single crystals. Anatoliy Senyshyn and Hai-Feng Li performed the SPODI experiments and analyzed the data. Martin Boehm, Binyang Hou, and Hai-Feng Li performed the IN3 experiments. Andrew Wildes and Hai-Feng Li performed the D7 experiments and analyzed the data. Karin Schmalzl, Wolfgang Schmidt, and Hai-Feng Li performed the IN12 experiments and analyzed the data. Wolfgang Schmidt, Karin Schmalzl, Eric Ressouche, and Hai-Feng Li performed the D23 experiments. Hai-Feng Li, Cong Zhang, Anatoliy Senyshyn, Andrew Wildes, Karin Schmalzl, Wolfgang Schmidt, Martin Boehm, Eric Ressouche, Binyang Hou, Paul Meuffels, Georg Roth, and Thomas Brückel discussed and analyzed the results. Hai-Feng Li wrote the main manuscript text. Cong Zhang, Anatoliy Senyshyn, Andrew Wildes, Karin Schmalzl, Binyang Hou, Georg Roth, and Thomas Brückel commented on the manuscript and all authors reviewed the paper. Hai-Feng Li conceived and directed the project.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work at RWTH Aachen University and Jülich Centre for Neutron Science JCNS Outstation at ILL was funded by the BMBF under contract No. 05K10PA3. Hai-Feng Li thanks the sample environment teams at ILL and FRM-II for expert technical assistances.
References
1. Santen, JHV, and Jonker, GH. Electrical conductivity of ferromagnetic compounds of manganese with perovskite structure. Physica (1950) 16:599–2. doi: 10.1016/0031-8914(50)90104-2
2. Bednorz, JG, and Müller, KA. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z Phys B (1986) 64:189–5. doi: 10.1007/BF01303701
3. Fiebig, M, Lottermoser, Th, Fröhlich, D, Goltsev, AV, and Pisarev, RV. Observation of coupled magnetic electric domains. Nature (2002) 419:818–3. doi: 10.1038/nature01077
5. Lacroix, C, Mendels, P, and Mila, F. Introduction to Frustrated Magnetism. Springer Series in Solid-State Sciences, Vol. 164. New York, NY: Springer (2011).
6. Li, HF, Xiao, Y, Schmitz, B, Persson, J, Schmidt, W, Meuffels, P, et al. Possible magnetic-polaron-switched positive negative magnetoresistance in the GdSi single crystals. Sci Rep. (2012) 2:750–6. doi: 10.1038/srep00750
7. Feng, YJ, Wang, JY, Silevitchb, DM, Mihailac, B, Kima, JW, Yan, JQ, et al. Incommensurate antiferromagnetism in a pure spin system via cooperative organization of local itinerant moments. Proc Natl Acad Sci USA. (2013) 110:3287–92. doi: 10.1073/pnas.1217292110
8. Xiao, Y, Su, Y, Li, HF, Kumar, CMN, Mittal, R, Persson, J, et al. Neutron diffraction investigation of the crystal magnetic structures in KCrF3 perovskite. Phys Rev B (2010) 82:094437–5. doi: 10.1103/PhysRevB.82.094437
9. Tian, W, Li, JY, Li, HF, Lynn, JW, Zarestky, JL, and Vaknin, D. Neutron Scattering Studies of LiCoPO4 & LiMnPO4. J Phys Conf Ser. (2010) 251:012005–5. doi: 10.1088/1742-6596/251/1/012005
10. Li, HF. A second-order spin-flop transition in collinear two-sublattice antiferromagnets. (2014) arXiv:1404.3914.
11. Li, HF, Hou, B, Wildes, A, Senyshyn, A, Schmalzl, K, Schmidt, W, et al. The absence of magnetic ordering in the ground state of single-crystal SrTm2O4: a polarized and unpolarized neutron-scattering study. (2014) arXiv:1404.0044.
12. Morris, DJP, Tennant, DA, Grigera, SA, Klemke, B, Castelnovo, C, Moessner, R, et al. Dirac strings magnetic monopoles in the spin ice Dy2Ti2O7. Science (2009) 326:411–4. doi: 10.1126/science.1178868
13. Gardner, JS, Dunsiger, SR, Gaulin, BD, Gingras, MJP, Greedan, JE, Kiefl, RF, et al. Cooperative Paramagnetism in the Geometrically Frustrated Pyrochlore Antiferromagnet Tb2Ti2O7. Phys Rev Lett. (1999) 82:1012–4. doi: 10.1103/PhysRevLett.82.1012
14. Lake, B, Tennant, DA, and Nagler, SE. Novel Longitudinal Mode in the Coupled Quantum Chain Compound KCuF3. Phys Rev Lett. (2000) 85:832–4. doi: 10.1103/PhysRevLett.85.832
15. Braun, HB, Kulda, J, Roessli, B, Visser, D, Krmäer, KW, Güdel, HU, et al. Emergence of soliton chirality in a quantum antiferromagnet. Nat Phys. (2005) 1:159–163. doi: 10.1038/nphys152
16. Harris, MJ, Bramwell, ST, McMorrow, DF, Zeiske, T, and Godfrey, KW. Geometrical frustration in the ferromagnetic pyrochlore Ho2Ti2O7. Phys Rev Lett. (1997) 79:2554–7. doi: 10.1103/PhysRevLett.79.2554
17. Bramwell, ST, and Gingras, MJP. Spin ice state in frustrated magnetic pyrochlore materials. Science (2001) 294:1495–7. doi: 10.1126/science.1064761
18. Lee, SH, Broholm, C, Ratcliff, W, Gasparovic, G, Huang, Q, Kim, TH, et al. Emergent excitations in a geometrically frustrated magnet. Nature (2002) 418:856–8. doi: 10.1038/nature00964
20. Moessner, R, and Ramirez, AP. Geometrical frustration. Phys Today (2006) 59:24–6. doi: 10.1063/1.2186278
21. Han, YL, Shokef, Y, Alsayed, AM, Yunker, P, Lubensky, TC, and Yodh, AG. Geometric frustration in buckled colloidal monolayers. Nature (2008) 456:898–903. doi: 10.1038/nature07595
22. Gingras, MJP. Observing monopoles in a magnetic analog of ice. Science (2009) 326:375–6. doi: 10.1126/science.1181510
23. Tsymbal, EY, and Dowben, PA. Grand challenges in condensed matter physics: from knowledge to innovation. Front Phys. (2013) 1:32–4. doi: 10.3389/fphy.2013.00032
24. Picozzi, S. Ferroelectric Rashba semiconductors as a novel class of multifunctional materials. Front Phys. (2014) 2:10. doi: 10.3389/fphy.2014.00010
25. Morgan, JP, Bellew, A, Stein, A, Langridge, S, and Marrows, CH. Linear field demagnetization of artificial magnetic square ice. Front Phys. (2013) 1:28. doi: 10.3389/fphy.2013.00028
26. Hayes, TJ, Balakrishnan, G, Deen, PP, Manuel, P, Chapon, LC, and Petrenko, OA. Coexistence of the long-range and short-range magnetic order components in SrEr2O4. Phys Rev B (2011) 81:024708–6. doi: 10.1103/PhysRevB.84.174435
27. Fennell, A, Pomjakushin, VY, Uldry, A, Delley, B, Prévost, B, Désilets-Benoit, A, et al. Evidence for SrHo2O4 SrDy2O4 as model J1−J2 zigzag chain materials. Phys Rev B (2014) 89:224511–5. doi: 10.1103/PhysRevB.89.224511
28. Kawamura, H. Universality of phase transitions of frustrated antiferromagnets. J Phys Condens Matter (1998) 10:4707–48. doi: 10.1088/0953-8984/10/22/004
29. Ramirez, AP, Espinosa, GP, and Cooper, AS. Strong frustration and dilution-enhanced order in a quasi-2D spin glass. Phys Rev Lett. (1990) 64:2070–4. doi: 10.1103/PhysRevLett.64.2070
30. Binder, K. Ordering of the face-centered-cubic lattice with nearest-neighbor interaction. Phys Rev Lett. (1980) 45:811–4. doi: 10.1103/PhysRevLett.45.811
31. Petrenko, OA. Low-temperature magnetism in the honeycomb systems SrLn2O4 (Review Article). Low Temp Phys. (2014) 40:106–7. doi: 10.1063/1.4865556
32. Barry, TL, and Roy, R. New rare earth-alkaline earth oxide compounds predicted compound formation and new families found. J Inorg Nucl Chem. (1967) 29:1243–6. doi: 10.1016/0022-1902(67)80365-8
33. Pepin, JG. Crystal data for SrRE2O4 (RE = rare earth + Y, In). J Appl Cryst. (1981) 14:70–2. doi: 10.1107/S0021889881008753
34. Karunadasa, H, Huang, Q, Ueland, BG, Lynn, JW, Schiffer, P, Regan, KA, et al. Honeycombs of triangles magnetic frustration in SrL2O4 (L=Gd, Dy, Ho, Er, Tm, and Yb). Phys Rev B (2005) 71:144414–8. doi: 10.1103/PhysRevB.71.144414
35. Balakrishnan, G, Hayes, TJ, Petrenko, OA, and McK, DP. High quality single crystals of the SrR2O4 family of frustrated magnets. J Phys Condens Matter (2009) 21:012202–3. doi: 10.1088/0953-8984/21/1/012202
36. Ghosh, S, Zhou, HD, Balicas, L, Hill, S, Gardner, JS, Qiu, Y, et al. Short range ordering in the modified honeycomb lattice compound SrHo2O4. J Phys Condens Matter (2011) 23:164203–5. doi: 10.1088/0953-8984/23/16/164203
37. Wen, JJ, Koohpayeh, S, McQueen, T, Tian, W, Li, HF, and Yan, JQ. Magneticordering in SrHo2O4. APS March Meeting (2014) 59:Y4.00008. Available online at: http://meetings.aps.org/link/BAPS.2014.MAR.Y4.8
38. Petrenko, OA, Balakrishnan, G, Wilson, NR, de Brion, S, Suard, E, and Chapon, LC. Low-temperature magnetic ordering in SrEr2O4. Phys Rev B (2008) 78:184410–6. doi: 10.1103/PhysRevB.78.184410
39. Quintero-Castro, DL, Lake, B, Reehuis, M, Niazi, A, Ryll, H, Islam, ATMN, et al. Coexistence of long- short-range magnetic order in the frustrated magnet SrYb2O4. Phys Rev B (2012) 86:064203–10. doi: 10.1103/PhysRevB.86.064203
40. Hayes, TJ, Young, O, Balakrishnan, G, and Petrenko, OA. Magnetisation studies of geometrically frustrated antiferromagnets SrLn2O4, with Ln = Er, Dy and Ho. J Phys Soc Jpn. (2012) 81:024708–6. doi: 10.1143/JPSJ.81.024708
41. Young, O, Wildes, AR, Manuel, P, Ouladdiaf, B, Khalyavin, DD, Balakrishnan, G, et al. Highly frustrated magnetism in SrHo2O4: coexistence of two types of short-range order. Phys Rev B (2013) 88:024411–8. doi: 10.1103/PhysRevB.88.024411
42. Cheffings, TH, Lees, MR, Balakrishnan, G, and Petrenko, OA. Magnetic field-induced ordering in SrDy2O4. J Phys Condens Matter (2013) 25:256001–6. doi: 10.1088/0953-8984/25/25/256001
43. Li, HF. Synthesis of CMR Manganites Ordering Phenomena in Complex Transition Metal Oxides. Jülich: Forschungszentrum Jülich GmbH Press (2008).
44. Hoelzel, M, Senyshyn, A, Juenke, N, Boysen, H, Schmahl, W, and Fuess, H. High-resolution neutron powder diffractometer SPODI at research reactor FRM II. Nucl Instr Methods Phys Res Sec A (2012) 667:32–6. doi: 10.1016/j.nima.2011.11.070
45. Ouladdiaf, B, Archer, J, McIntyre, GJ, Hewat, AW, Brau, D, and York, S. OrientExpress: a new system for Laue neutron diffraction. Physica B (2006) 385–386:1052–3. doi: 10.1016/j.physb.2006.05.337
46. Stewart, JR, Deen, PP, Andersen, KH, Schober, H, Barthélémy, JF, Hillier, JM, et al. Disordered materials studied using neutron polarization analysis on the multi-detector spectrometer, D7. J Appl Cryst. (2009) 42:69–84. doi: 10.1107/S0021889808039162
47. Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Physica B (1993) 192:55–69. doi: 10.1016/0921-4526(93)90108-I
49. Li, HF, Tian, W, Yan, JQ, Zarestky, JL, McCallum, RW, Lograsso, TA, et al. Phase transitions iron-ordered moment form factor in LaFeAsO. Phys Rev B (2010) 82:064409–6. doi: 10.1103/PhysRevB.82.064409
50. Li, HF, Broholm, C, Vaknin, D, Fernandes, RM, Abernathy, DL, Stone, MB, et al. Anisotropic quasipropagating spin excitations in superconducting Ba(Fe0.926Co0.074)2As2. Phys Rev B (2010) 82:140503–5. doi: 10.1103/PhysRevB.82.140503
51. Prokeš, K, Hiess, A, Bao, W, Wheeler, E, Landsgesell, S, and Argyriou, DN. Anisotropy of the (π, π) dynamic susceptibility in magnetically ordered (x = 0.05) and superconducting (x = 0.40) Fe1.02Te1-xSex. Phys Rev B (2012) 86:064503–5. doi: 10.1103/PhysRevB.86.064503
52. Li, HF, Yan, JQ, Kim, JW, McCallum, RW, Lograsso, TA, and Vaknin, D. Anisotropic magnetoelastic coupling in single-crystalline CeFeAsO as seen via high-resolution x-ray diffraction. Phys Rev B (2011) 84:220501–5. doi: 10.1103/PhysRevB.84.220501
53. Xiao, Y, Nandi, S, Su, Y, Price, S, Li, HF, Fu, Z, et al. Magnetic anisotropic energy gap low-energy spin wave excitation in the antiferromagnetic block phase of K2Fe4Se5. Phys Rev B (2013) 87:140408–6. doi: 10.1103/PhysRevB.87.140408
54. Zhao, J, Adroja, DT, Yao, DX, Bewley, R, Li, SL, Wang, XF, et al. Spin waves magnetic exchange interactions in CaFe2As2. Nat Phys. (2009) 5:555–6. doi: 10.1038/nphys1336
55. Diallo, SO, Pratt, DK, Fernandes, RM, Tian, W, Zarestky, JL, Lumsden, M, et al. Paramagnetic spin correlations in CaFe2As2 single crystals. Phys Rev B (2010) 81:214407–10. doi: 10.1103/PhysRevB.81.214407
56. Fisher, IR, Degiorgi, L, and Shen, ZX. In-plane electronic anisotropy of underdoped ‘122’ Fe-arsenide superconductors revealed by measurements of detwinned single crystals. Rep Prog Phys. (2011) 74:124506–21. doi: 10.1088/0034-4885/74/12/124506
57. Wang, C, Zhang, R, Wang, F, Luo, HQ, Regnault, LP, Dai, PC, et al. Longitudinal Spin excitations magnetic anisotropy in antiferromagnetically ordered BaFe2As2. Phys Rev X (2013) 3:041036–6. doi: 10.1103/PhysRevX.3.041036
58. Li, HF, Su, Y, Persson, J, Meuffels, P, Walter, JM, Skowronek, R, et al. Correlation between structural magnetic properties of La7/8Sr1/8Mn1-γO3+δ with controlled nonstoichiometry. J Phys Condens Matter (2007) 19:016003–12. doi: 10.1088/0953-8984/19/1/016003
59. Li, HF, Su, Y, Persson, J, Meuffels, P, Walter, JM, Skowronek, R, et al. Neutron-diffraction study of structural transition magnetic order in orthorhombic and rhombohedral La7/8Sr1/8Mn1-γO3+δ. J Phys Condens Matter (2007) 19:176226–12. doi: 10.1088/0953-8984/19/17/176226
60. Li, HF, Su, Y, Xiao, Y, Persson, J, Meuffels, P, and Brückel, Th. Crystal and magnetic structure of single-crystal La1-xSrxMnO3 (x ≈ 1/8). Eur Phys J B (2009) 67:149–9. doi: 10.1140/epjb/e2009-00019-5
Keywords: new frustrated compound, highest transition temperature, single crystal, antiferromagnetism, octahedral distortion, single-ion anisotropy
Citation: Li H-F, Zhang C, Senyshyn A, Wildes A, Schmalzl K, Schmidt W, Boehm M, Ressouche E, Hou B, Meuffels P, Roth G and Brückel T (2014) Incommensurate antiferromagnetic order in the manifoldly-frustrated SrTb2O4 with transition temperature up to 4.28 K. Front. Phys. 2:42. doi: 10.3389/fphy.2014.00042
Received: 16 May 2014; Accepted: 18 June 2014;
Published online: 21 July 2014.
Edited by:
Olga Kazakova, National Physical Laboratory, UKReviewed by:
Sean Langridge, Science and Technology Facilities Council, UKIrina Yakimenko, Linköping University, Sweden
Jasper Altman Drisko, University of Maryland, College Park, USA
Copyright © 2014 Li, Zhang, Senyshyn, Wildes, Schmalzl, Schmidt, Boehm, Ressouche, Hou, Meuffels, Roth and Brückel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hai-Feng Li, Jülich Centre for Neutron Science JCNS, Forschungszentrum Jülich GmbH, Outstation at Institut Laue-Langevin, 71 Avenue des Martyrs, BP 156, F-38042 Grenoble Cedex 9, France; Institut für Kristallographie der RWTH Aachen University, Jaegerstrasse 17-19, D-52056 Aachen, Germany e-mail:aGZsaUBpbGwuZnI=;
Thomas Brückel, Jülich Centre for Neutron Science JCNS and Peter Grünberg Institut PGI, JARA-FIT, Forschungszentrum Jülich GmbH, Leo-Brandt-Straße, D-52425 Jülich, Germany e-mail:dC5icnVlY2tlbEBmei1qdWVsaWNoLmRl
 Hai-Feng Li
Hai-Feng Li Cong Zhang
Cong Zhang Anatoliy Senyshyn3
Anatoliy Senyshyn3 Binyang Hou
Binyang Hou