Quantum features of a charged particle in ionized plasma controlled by a time-dependent magnetic field

1. Introduction

On account of the importance of plasma and plasma physics on materials science and nuclear fusion, the dynamical characteristics of plasma have been increasingly studied until now. Not only plasma reveal diverse properties during their process but also the features taken place in the plasma are so complex that it is very hard to control their behaviors and reactions. In a static magnetic field, charged particles go round in circles when their velocity vector is perpendicular to magnetic field lines. They however go round in helix in case they have a velocity component parallel to the lines of B-field as well as perpendicular. If the external magnetic field varies in time or in space, the motion of ionized particles becomes more random and both its treatment and analytical analysis require high technology.

The influence of magnetic fields on the motion of a charged particle involves the essential properties of acceleration and the transport of highly ionized particles. The analysis of classical and quantum behaviors of charged particles is important in connection with a well known application of the confinement of magnetized plasma. Charged particles are accelerated and decelerated as they cross a magnetic lens in a magneto optical trapping of ionized plasma. Although the charged particles are trapped both in the high-field region and low-field region, the plasma profile does not follow the naive magnetic field lines. More precisely, the radius of circling particle in the high-field region is smaller than the one that would be obtained by simply tracking the field line from the low-field radial edge toward the high field region [1]. Another application of the external magnetic field in ionized plasma is the use of it in reducing the effect of splash in pulsed laser deposition technique in plasma surface science [2, 3].

Exact theoretical description for quantum and classical properties of plasma may play a pivotal role for understanding the physics of plasma. Lewins studied the motion of a charged particle in a time-dependent magnetic field considering the conservation of magnetic moment about the circling center [4]. Stimulated by this work, we study in this paper quantum features of a charged particle moving under a time-dependent magnetic field in plasma. As magnetic field varies with time, the new electric potential would be created according to the Maxwell's equation. Hence, the motion of charged particle is more complex in the situation characterized by a varying magnetic field than by a static one.

The exact Hamiltonian for the motion of charged particle will be constructed considering the time dependence of the magnetic field. The complete quantum solutions of the system will be derived with the help of a quadratic invariant operator that is a potential tool for treating quantum systems that have time-dependent parameters. The introduction of the invariant operator is the main idea that enables us to overcome the difficulty in quantizing the system that is somewhat complicated. According to reports of Lewis and Riesenfeld [5, 6], a Schrödinger solution ψ(r, t) of a system that has time-dependent parameters is given in terms of an eigenstate ϕ(r, t) of the invariant operator. In fact, we can obtain ψ(r, t) by multiplying ϕ(r, t) by an appropriate phase factor. The Schrödinger solution ψ(r, t) plays a major role in investigating the quantum characteristics of the system. Quantized energy of the particle will be evaluated in this work using ψ(r, t) and its time behavior will be analyzed in detail in some situations that the time dependence of the magnetic field is chosen differently.

2. Hamiltonian Dynamics

Let us consider non-relativistic motion of a charged particle in ionized plasma controlled by a magnetic field. The magnetic force acting on a particle that has charge q under the static magnetic field is given by F = qv × B, where v = dr/dt is the velocity of the particle. However, if the magnetic field varies with time, it produces a new electric field according to the Maxwell's equation:

$\begin{array}{cc}\nabla \times E_{\text{produced}}(t)=-\frac{\partial B(t)}{\partial t}.& (1)\end{array}$

Then, the overall force exerting on the charged particle is

$\begin{array}{cc}F=q[E_{\text{produced}}(t)+v\times B(t)].& (2)\end{array}$

This gives the following Newtonian equation of motion for the particle

$\begin{array}{cc}\frac{d^{2}r}{d{t}^2}=\frac{q}{m}\left[\frac{1}{2}r\times \frac{dB(t)}{dt}+\frac{dr}{dt}\times B(t)\right],& (3)\end{array}$

where m is the mass of the particle. Lewins showed that the radial part of the above equation in cylindrical coordinate described by a set of variables (r, θ, z) becomes [see Equation (22) of Lewins 4]

$\begin{array}{cc}\frac{d^{2}r}{d{t}^2}+{\omega }^2(t)r=\frac{r_0^4{K}^2}{r^3},& (4)\end{array}$

where r₀ = r(0), ω(t) is a time-dependent frequency of the form

$\begin{array}{cc}\omega (t)=\left|q\right||B(t)|/(2m).& (5)\end{array}$

and K is a constant expressed as $K=\frac{d\theta }{dt}{|}_{t=0}-\omega (0)$. We can see that angular momentum of the particle is conserved in variable magnetic fields as well as in the static limit [7]. Several interesting phenomena that take place by the presence of magnetic field in an ionized plasma include plume confinement, particle acceleration and deceleration, dissipation of kinetic energy into thermal energy, Debris mitigation, and instability of plasma [8–10].

The difficulty in the study of the quantum motion of charged particles in a “time-dependent” magnetic field is insisted many times in the literature [4, 11–13] because of the production of electric field. We, in this work, may need to deal the problem of a time-dependent Hamiltonian system (TDHS) which is not easy to handle. There are several mathematical techniques available for rigorous quantum treatment of TDHSs, such as invariant operator method [5, 6], reduction method [14], propagator method [15], and canonical transformation method [16]. Among them, we will use invariant operator method as mentioned in the introductory part.

The Hamiltonian that yields the equation of motion given in Equation (4) can be written as

$\begin{array}{cc}\widehat{H}(\widehat{r},\widehat{p},t)={\widehat{H}}_{\text{HO}}(\widehat{r},\widehat{p},t)+\frac{1}{2}m{r}_0^4{K}^2\frac{1}{{\widehat{r}}^2},& (6)\end{array}$

where $\widehat{p}$ = −iℏ∂/∂r and Ĥ_HO is the Hamiltonian of the harmonic oscillator with the time-dependent frequency ω(t), that is represented as

$\begin{array}{cc}{\widehat{H}}_{\text{HO}}(\widehat{r},\widehat{p},t)=\frac{{\widehat{p}}^2}{2m}+\frac{1}{2}m{\omega }^2(t){\widehat{r}}^2.& (7)\end{array}$

Even if a general harmonic oscillator in one dimension is defined through entire region for r, (−∞, ∞), Equation (7) is meaningful only in the positive r. In the next section, we will solve Schrödinger equation of the system that is described by the Hamiltonian (6) and quantum features of the system will be studied.

3. Theory and Results

3.1. Invariant Operator and Quantum Solutions

The Hamiltonian given in the last section is explicitly dependent on time as the magnetic field varies. Hence the system is a kind of TDHSs that have attracted wide interest in the physical society [5, 6, 17–26]. To derive quantum solutions of a TDHS, it is convenient to introduce an invariant operator [5, 6] because the quantum properties of such system can be investigated via the eigenstates of the invariant operator. From the Liouville-von Neumann equation dÎ/dt = ∂Î/∂t + [Î, Ĥ]/(iℏ) = 0, it is possible to derive a quadratic invariant operator Î. Thus, considering Equation (6), we have the invariant operator as

$\begin{array}{cc}\widehat{I}={\widehat{I}}_{\text{HO}}+m{K}^2{r}_0^4\chi (t){\chi }^{\ast }(t)\frac{1}{{\widehat{r}}^2},& (8)\end{array}$

where χ(t) is a complex classical solution of the following differential equation

$\begin{array}{cc}\ddot{\chi }(t)+{\omega }^2(t)\chi (t)=0,& (9)\end{array}$

and Î_HO is the invariant operator of the system described by Ĥ_HO [24]:

$\begin{array}{cc}\begin{array}{l}{\widehat{I}}_{\text{HO}}=\frac{{\chi }^{\ast }(t)\chi (t)}{m}{\widehat{p}}^2-{\dot{\chi }}^{\ast }(t)\chi (t)\widehat{r}\widehat{p}\\ -{\chi }^{\ast }(t)\dot{\chi }(t)\widehat{p}\widehat{r}+m{\dot{\chi }}^{\ast }(t)\dot{\chi }(t){\widehat{r}}^2.\end{array}& (10)\end{array}$

One can check, by direct differentiation of Equation (8) with respect to time, that Î does not vary with time.

Since the eigenstates of the invariant operator play a crucial role in the development of the quantum theory of TDHS, it is necessary to compute them from fundamental relations. Let us write the eigenvalue equation of the invariant operator as

$\begin{array}{cc}\widehat{I}\varphi (r,t)=\lambda \varphi (r,t).& (11)\end{array}$

We will derive the eigenstates ϕ(r, t) by evaluating this equation. The substitution of Equation (8) with Equation (10) into the above equation yields

$\begin{array}{cc}\begin{array}{l}[\frac{{\partial }^2}{\partial r^2}+\frac{m\beta (t)}{i\hslash }r\frac{\partial }{\partial r}-\frac{m^2{\dot{\chi }}^{\ast }\dot{\chi }}{{\chi }^{\ast }\chi {\hslash }^2}{r}^2\\ -\frac{m^2{K}^2{r}_0^4}{{\hslash }^2}\frac{1}{r^2}+\Pi (t)]\varphi =0,\end{array}& (12)\end{array}$

where β(t) and Π(t) are time functions of the form

$\begin{array}{cc}\beta (t)=\frac{{\dot{\chi }}^{\ast }(t)}{{\chi }^{\ast }(t)}+\frac{\dot{\chi }(t)}{\chi (t)},& (13)\end{array}$

$\begin{array}{cc}\Pi (t)=\frac{m\lambda }{{\chi }^{*}(t)\chi (t){\hslash }^2}+\frac{m\dot{\chi }(t)}{i\chi (t)\hslash }.& (14)\end{array}$

Notice that β(t) is always real. In case of χ(t) = c(t)e^iy(t) where c(t) and y(t) are time-dependent real values, we have β(t) = 2ċ(t)/c(t). On the other hand, for χ(t) = c₁e^iy(t) + c₂e^−iy(t) where c₁ and c₂ are real constants, β(t) becomes

$\begin{array}{cc}\beta (t)=-\frac{4c_1{c}_2\dot{y}(t)\sin [2y(t)]}{c_1^2+c_2^2+2c_1{c}_2\cos [2y(t)]},& (15)\end{array}$

which is a more complicated expression. By putting r = $\sqrt{\rho }$ from Equation (12), we can rewrite the eigenvalue equation in the form

$\begin{array}{cc}\begin{array}{l}\frac{{\partial }^2\varphi (\rho ,t)}{\partial {\rho }^2}+\frac{1}{2}(\frac{m\beta }{i\hslash }+\frac{1}{\rho })\frac{\partial \varphi (\rho ,t)}{\partial \rho }\\ +(\frac{\Pi }{4}\frac{1}{\rho }-\frac{m^2{K}^2{r}_0^4}{4{\hslash }^2}\frac{1}{{\rho }^2}-\frac{m^2{\dot{\chi }}^{\ast }\dot{\chi }}{4{\chi }^{\ast }\chi {\hslash }^2})\varphi (\rho ,t)=0.\end{array}& (16)\end{array}$

Now we let

$\begin{array}{cc}\varphi (\rho ,t)={\rho }^s{e}^{-\gamma (t)\rho }F(\rho ,t),& (17)\end{array}$

where a constant s and a time function γ(t) is given by

$\begin{array}{cc}s=\frac{1}{4}[1+{(1+\frac{4m^2{K}^2{r}_0^4}{{\hslash }^2})}^{1/2}],& (18)\end{array}$

$\begin{array}{cc}\gamma (t)=\frac{m}{2\hslash }\left[\frac{\beta (t)}{2i}+{(\frac{{\dot{\chi }}^{\ast }(t)\dot{\chi }(t)}{{\chi }^{\ast }(t)\chi (t)}-\frac{{\beta }^2(t)}{4})}^{1/2}\right].& (19)\end{array}$

Then, the substitution of Equation (17) in Equation (16) leads to

$\begin{array}{cc}\begin{array}{l}\rho \frac{{\partial }^{2}F(\rho ,t)}{\partial {\rho }^2}+[2s+\frac{1}{2}+(\frac{m\beta }{2i\hslash }-2\gamma )\rho ]\frac{\partial F(\rho ,t)}{\partial \rho }\\ +(\frac{m\beta s}{2i\hslash }-2\gamma s-\frac{\gamma }{2}+\frac{\Pi }{4})F(\rho ,t)=0.\end{array}& (20)\end{array}$

We easily derive the solution of this equation to be

$\begin{array}{cc}\begin{array}{l}F(\rho ,t){=}_1{F}_1(s-(\frac{\Pi (t)}{4}-\frac{\gamma (t)}{2}){(2\gamma (t)-\frac{m\beta (t)}{2i\hslash })}^{-1},\\ 2s+\frac{1}{2};(2\gamma (t)-\frac{m\beta (t)}{2i\hslash })\rho ),\end{array}& (21)\end{array}$

where ₁F₁ is the hypergeometric series. Thus, we completely identified the solution ϕ(r, t) in Equation (12). After some rearrangements, the full expression of the normalized eigenstates becomes

$\begin{array}{cc}\begin{array}{l}{\varphi }_n(r,t)={[\frac{2\Gamma (n+1)}{\Gamma (n+\nu +1)}{(\frac{m\Omega }{2\hslash \chi (t){\chi }^{\ast }(t)})}^{\nu +1}]}^{1/2}{r}^{\nu +1/2}\\ \times \exp {(\frac{im\dot{\chi }(t)}{2\hslash \chi (t)}{r}^2)}_1{F}_1(-n,\nu +1;\frac{m\Omega }{2\hslash \chi (t){\chi }^{\ast }(t)}{r}^2),\end{array}& (22)\end{array}$

where

$\begin{array}{cc}n=\frac{\lambda }{2\hslash \Omega }-\frac{\nu }{2}-\frac{1}{4},& (23)\end{array}$

$\begin{array}{cc}\nu =\frac{1}{2}{(1+\frac{4m^2{K}^2{r}_0^4}{{\hslash }^2})}^{1/2},& (24)\end{array}$

$\begin{array}{cc}\Omega =i[\chi (t){\dot{\chi }}^{\ast }(t)-{\chi }^{*}(t)\dot{\chi }(t)].& (25)\end{array}$

Here, it can be easily shown that n should be quantized numbers (n = 0, 1, 2, …) from the condition that the physically allowed eigenstates cannot be divergent as r grows [27]. While it is manifest that ν is independent of time, we can easily verify that the Wronskian Ω is also a time-constant real value. For convenience, we choose χ(t) in a way that Ω to be positive. This can be always done without loss of generality.

We see from Equation (23) that the eigenvalues are given by

$\begin{array}{cc}{\lambda }_n=\hslash \Omega (2n+\nu +1/2).& (26)\end{array}$

According to the invariant operator theory of Lewis-Riesenfeld [5, 6], the wave functions ψ_n(r, t) that satisfy Schrödinger equation are represented in terms of the eigenstates of the invariant operator. Hence, we can write the Schrödinger solutions in the form

$\begin{array}{cc}{\psi }_n(r,t)={\varphi }_n(r,t)\exp [i{\phi }_n(t)],& (27)\end{array}$

where φ_n(t) are some time-dependent phases. By inserting the above equation together with Equation (6) into Schrödinger equation, we obtain the analytical forms of φ_n(t) such that

$\begin{array}{cc}{\phi }_n(t)=-(2n+\nu +1)\frac{\Omega }{2}{\displaystyle {\int }_0^t\frac{d{t}^{\prime }}{\chi (t^{\prime }){\chi }^{\ast }(t^{\prime })}}+{\phi }_n(0).& (28)\end{array}$

Thus, the complete radial wave functions of the system are identified. These wave functions are very useful for investigating quantum characteristics of the system. Recall that the expectation values of quantum observables are obtained via the use of wave functions.

3.2. Spectrum of Quantized Energy

We apply the quantization scheme developed previously to particular cases for better understanding of quantum features of the system. As an appropriate quantum observable that is worth to be investigated here, let us consider the radial part of the quantum energy. As is well known, the expectation values of the quantum energy are obtained from

$\begin{array}{cc}{E}_n=\langle {\psi }_n(t)|\widehat{H}(\widehat{r},\widehat{p},t)|{\psi }_n(t)\rangle .& (29)\end{array}$

With the use of Equation (6) and the wave functions in Equation (27), we readily have

$\begin{array}{cc}\begin{array}{l}{E}_n=\frac{1}{4}\hslash (\frac{\Omega }{\chi (t){\chi }^{\ast }(t)}+\frac{\chi (t){\chi }^{\ast }(t)}{\Omega }[{\beta }^2(t)+4{\omega }^2(t)])\\ \times (2n+\nu +1).\end{array}& (30)\end{array}$

This is the general expression of nth order quantum energy. The time evolution of quantum energy is determined by the type of B(t).

As an example, we choose a magnetic field that decreases with time in a fashion that

$\begin{array}{cc}B(t)=B_0\frac{1}{{(1+kt)}^2},& (31)\end{array}$

where B₀ is the initial field and k is a positive constant which is relatively small (0 < k « 1). If we put χ(t) as χ(t) = χ₀(1 + kt)z(t) where χ₀ is a real constant, we can confirm via the use of Equations (5), (9), and (31) that the differential equation that z(t) should obey is given by

$\begin{array}{cc}\frac{d^{2}z(t)}{d{t}^2}+\frac{2k}{1+kt}\frac{dz(t)}{dt}+\frac{q^2{B}_0^2}{4m^2{(1+kt)}^4}z(t)=0.& (32)\end{array}$

From a direct evaluation, we see that the solution for z(t) is an exponential function of the form z(t) = e^{−iqB₀/[2mk(1+kt)]}. Hence, a complex solution of Equation (9) is given by

$\begin{array}{cc}\chi (t)={\chi }_0(1+kt)\exp (-i\frac{q{B}_0}{2mk}\frac{1}{1+kt}).& (33)\end{array}$

In this case, Equation (30) becomes

$\begin{array}{cc}{E}_n=\hslash [\frac{m{k}^2}{q{B}_0}+\frac{q{B}_0}{2m{(1+kt)}^2}](2n+\nu +1).& (34)\end{array}$

While the first term is constant, the second term decreases with time. We see from the above equation that quantum energy is independent of χ₀. In general, the choice of any value for χ₀ does not affect to the time behavior of a quantum system [15]. The time evolution of E_n for this case is plotted in Figure 1 with various values of k. As the magnetic field gradually disappears with time according to Equation (31), E_n also decay. Figure 1 shows that E_n decrease more rapidly for large k. If we consider the fact that k determines the rate of the decrease of applied magnetic field, this consequence is natural and corresponds to the classical analysis.

FIGURE 1

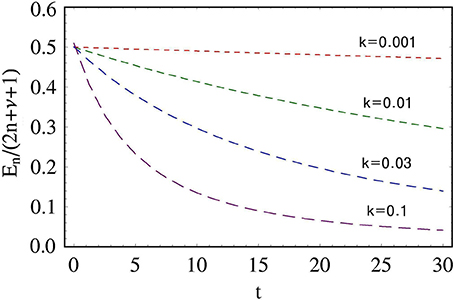
Figure 1. Time evolution of the radial energy expectation values divided by (2n + ν + 1) with the choice of B(t) as Equation (31). The values we used are ℏ = 1, m = 1, q = 1, and B₀ = 1. All these values are taken to be dimensionless for convenience.

Now, as an another example, let us see the case that the time dependence of the external magnetic field is given by

$\begin{array}{cc}B(t)=B_0{e}^{kt}.& (35)\end{array}$

In this case, the magnetic field (exponentially) increases with time whereas the field in the previous case decreases. It is easy to show from a little evaluation that Equation (9) has the form

$\begin{array}{cc}{\tau }^2\frac{d^2\chi (t)}{d{\tau }^2}+\tau \frac{d\chi (t)}{d\tau }+{\tau }^2\chi (t)=0,& (36)\end{array}$

where τ = qB₀e^kt/(2mk). A complex solution for this equation is given by

$\begin{array}{cc}\chi (t)={\chi }_0[J_0(\frac{q{B}_0{e}^{kt}}{2mk})+i{N}_0(\frac{q{B}_0{e}^{kt}}{2mk})],& (37)\end{array}$

where J₀ and N₀ are zeroth order Bessel functions. We see from Figure 2 that the corresponding energy increases with time due to the amplification of the field, as expected. The ratio of energy increase becomes large with time due to the exponential increment of the field.

FIGURE 2

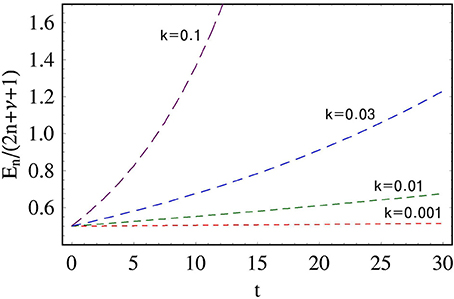
Figure 2. Time evolution of the radial energy expectation values divided by (2n + ν + 1) with the choice of B(t) as Equation (35). The values we used are ℏ = 1, m = 1, q = 1, and B₀ = 1. All these values are taken to be dimensionless for convenience.

4. Conclusion

Quantum motion of a charged particle in an ionized plasma controlled by a time-dependent external magnetic field is studied using the invariant operator method that is available for TDHSs. If we consider that the time-varying magnetic field produces an electric field that plays the role of an another source of force acting on the moving particle that has some charge, the problem becomes more or less complicated. The radial part of equation of motion for the particle is represented in terms of a time-dependent angular frequency ω(t) as shown in Equation (4). Hence, the corresponding Hamiltonian given in Equation (6) with Equation (7) is a kind of TDHSs.

To see quantum features of the system, the invariant operator is constructed through the method of Lewis-Riesenfeld [see Equation (8)]. This enabled us to manage the system in more or less simple way by avoiding the direct consideration of the time-dependent problem by means of a constant of motion that is a quadratic form. The normalized radial wave functions derived from the use of the invariant operator are represented as Equation (27) with Equations (22) and (28). An interesting mathematical feature in this case is that the quantum solutions are expressed in terms of the complex classical solutions of Equation (9).

Considering the expression of the phases given in Equation (28), we can also define another invariant operator in the form 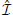= Î + ℏΩ/2 which seems a little improved than Î. It is easy to show that the eigenvalue equation of 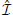results in 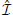ϕ(r, t) = Λ_nϕ(r, t) with

$\begin{array}{cc}{\Lambda }_n={\lambda }_n+\frac{1}{2}\hslash \Omega =\hslash \Omega (2n+\nu +1).& (38)\end{array}$

Although we have used Î in order to study quantum features of the system, 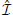may be more consistent invariant operator since its eigenvalues are represented in terms of (2n + ν + 1) which appear in the phases of the wave functions [Equation (28)]. In what follows, it is possible to derive exact quantum states by using either Î or .

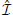The nth order expectation value of the Hamiltonian is computed by taking advantage of the wave function, as represented in Equation (30). This is the radial part of quantized energy for the particle. To promote the understanding of our development, we considered particular cases characterized by time-dependent magnetic fields appeared in Equations (31) and (35). We confirm from Figure 1 that E_n for the first example decrease with time as the magnetic field gradually vanishes, whereas, from Figure 2, the energy for the second example increases with time as the field grows. These consequences are consistent with the corresponding classical analyses.

All of the results in this work are obtained by treating electromagnetic field as classical backgrounds without incorporating the full quantized Yang-Mill theory. We believe that our theory is valid with high precision so long as we are interested in only the phenomenological quantum behavior of the charged particle, provided that the complex classical solutions χ and χ* of Equation (9) are found for given types of the time dependence of B(t).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (Grant No.: NRF-2013R1A1A2062907) and was supported by the International Research and Development Program of the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology(MEST) of Korea (Grant No.: 2011-0030864).

References

1. Tatematsu Y, Saito T, Kiwamoto Y, Ito K, Abe H, Ishikawa M, et al. Cyclotron emission spectra from collisionless electrons resonantly heated by cyclotron waves in a magnetic mirror. Fusion Eng Design (2001) 53:229–36. doi: 10.1016/S0920-3796(00)00489-0

CrossRef Full Text

2. García T, de Posada E, Villagrán M, Ll JLS, Bartolo-Pérez P, Peña JL. Effects of an external magnetic field in pulsed laser deposition. Appl Surf Sci. (2008) 255:2200–4. doi: 10.1016/j.apsusc.2008.07.061

CrossRef Full Text

3. Jordan R, Cole D, and Lunney JG. Pulsed laser deposition of particulate-free thin films using a curved magnetic filter. Appl Surf Sci. (1997) 109–110:403–7. doi: 10.1016/S0169-4332(96)00760-X

CrossRef Full Text

4. Lewins JD. On the motion of charged particles in a varying magnetic field. Int J Eng Sci. (1995) 33:1491–505. doi: 10.1016/0020-7225(94)00124-3

CrossRef Full Text

5. Lewis HR Jr. Classical and quantum systems with time-dependent harmonic-oscillator-type Hamiltonians. Phys Rev Lett. (1967) 18:510–2. doi: 10.1103/PhysRevLett.18.510

CrossRef Full Text

6. Lewis HR Jr, Riesenfeld WB. An exact quantum theory of the time-dependent harmonic oscillator and of a charged particle in a time-dependent electromagnetic field. J Math Phys. (1969) 10:1458–73. doi: 10.1063/1.1664991

CrossRef Full Text

7. Lewins JD. Conservation of angular momentum in a varying magnetic field. Fusion Tech. (1998) 34:241–53.

8. Joshi HC, Kumar A, Singh RK, Prahlad V. Effect of a transverse magnetic field on the plume emission in laser-produced plasma: an atomic analysis. Spect Acta B Atom Spect. (2010) 65:415–9. doi: 10.1016/j.sab.2010.04.018

CrossRef Full Text

9. Harilal SS, O'Shay B, Tillack MS. Debris mitigation in a laser-produced tin plume using a magnetic field. J Appl Phys. (2005) 98:036102. doi: 10.1063/1.1999851

CrossRef Full Text

10. Harilal SS. Confinement and dynamics of laser-produced plasma expanding across a transverse magnetic field. Phys Rev E (2004) 69:026413. doi: 10.1103/PhysRevE.69.026413

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

11. Laroze D, Rivera R. An exact solution for electrons in a time-dependent magnetic field. Phys Lett A (2006) 355:348–51. doi: 10.1016/j.physleta.2006.03.002

CrossRef Full Text

12. Abdalla MS, Choi JR. Propagator for the time-dependent charged oscillator via linear and quadratic invariants. Ann Phys. (2007) 322:2795–810. doi: 10.1016/j.aop.2007.01.006

CrossRef Full Text

13. Vatansever E, Akinci U, Polat H. Time dependent magnetic field effects on the ±J Ising model. J Magn Magn Mater. (2013) 344:89–95. doi: 10.1016/j.jmmm.2013.05.025

CrossRef Full Text

14. Degli Esposti Boschi C, Ferrari L, Lewis HR. Reduction method for the linear quantum or classical oscillator with time-dependent frequency, damping, and driving. Phys Rev A (1999) 61:010101(R). doi: 10.1103/PhysRevA.61.010101

CrossRef Full Text

15. Gweon JH, Choi JR. Propagator and geometric phase of a general time-dependent harmonic oscillator. J Korean Phys Soc. (2003) 42:325–30. doi: 10.3938/jkps.42.325

CrossRef Full Text

16. Park TJ. Canonical transformations for time-dependent harmonic oscillators. Bull Korean Chem Soc. (2004) 25:285-8. doi: 10.5012/bkcs.2004.25.2.285

CrossRef Full Text

17. Dekker H. Classical and quantum mechanics of the damped harmonic oscillator. Phys Rep. (1981) 80:1–110. doi: 10.1016/0370-1573(81)90033-8

CrossRef Full Text

18. Lohe MA. Exact time dependence of solutions to the time-dependent Schrödinger equation. J Phys A Math Theor. (2009) 42:035307. doi: 10.1088/1751-8113/42/3/035307

CrossRef Full Text

19. Choi JR. Nonclassical properties of superpositions of coherent and squeezed states for electromagnetic fields in time-varying media. In: Lyagushyn S, editor. Quantum Optics and Laser Experiments. Rijeka: InTech. (2012). p. 25–48.

20. Choi JR. (ed.). Quantum unitary transformation approach for the evolution of dark energy. In: Dark Energy-Current Advances and Ideas, Kerala: Research SignPost (2009). p. 117–134.

21. Maamache M, Bekkar H. Evolution of Gaussian wave packet and nonadiabatic geometrical phase for the time-dependent singular oscillator. J Phys A Math Gen. (2003) 36:L359–64. doi: 10.1088/0305-4470/36/23/105

CrossRef Full Text

22. Choi JR, Gweon BH. Operator method for a nonconservative harmonic oscillator with and without singular perturbation. Int J Mod Phys B (2002) 16:4733-42. doi: 10.1142/S0217979202014723

CrossRef Full Text

23. Choi JR. Exact quantum state and relation between Berry's phase and Hannay's angle for general time-dependent harmonic oscillator perturbed by a singularity. Int Math J. (2003) 4:209–27.

24. Malkin IA, Man'ko VI, Trifovov DA. Coherent states and transition probabilities in a time-dependent electromagnetic field. Phys Rev D (1970) 2:1371–85. doi: 10.1103/PhysRevD.2.1371

CrossRef Full Text

25. Dodonov VV, Malkin IA, Man'ko VI. Even and odd coherent states and excitations of a singular oscillator. Physica (1974) 72:597–615. doi: 10.1016/0031-8914(74)90215-8

CrossRef Full Text

26. Trifonov DA. Exact solutions for the general nonstationary oscillator with a singular perturbation. J Phys A Math Gen. (1999) 32:3649–61. doi: 10.1088/0305-4470/32/19/314

CrossRef Full Text

27. Ikhdair SM, Sever R. Exact polynomial eigensolutions of the Schrödinger equation for the pseudoharmonic potential. J Mol Struct. (2008) 855:13–7. doi: 10.1016/j.theochem.2007.12.044

CrossRef Full Text