The effect of time-dependent macromolecular crowding on the kinetics of protein aggregation: a simple model for the onset of age-related neurodegenerative disease

Introduction

Several neurodegenerative diseases, most prominent among them Alzheimer's Dementia and Parkinsonism, are extremely rare in individuals under the age of about sixty, but the incidence rises sharply above that age, reaching 10–25% at the age of eighty [1, 2]. The root cause of age-related incidence has been the subject of much conjecture (Google “aging and neurodegeneration”) but no solid consensus has been formed. The purpose of this communication is to suggest a common mechanism underlying the age-related onset of a variety of neurodegenerative diseases based upon the effect of excluded volume on the kinetics of protein aggregation.

The model to be developed here is based upon the notion that most if not all proteins are subject to a gradual process of degradation leading to a loss of solubility and consequent biological function. Under laboratory conditions thought to reflect physiological conditions, degradation may be imperceptibly slow on the time scale of an ordinary experiment. However, it is a common experience that proteins in purified solutions left at room temperature for extended periods will begin to precipitate, and that addition of small amounts of destabilizing agents can significantly accelerate the loss of function or formation of various types of aggregates.

It was shown long ago that the addition of a moderately high concentration of functionally unrelated polymers or proteins can significantly reduce the solubility of a variety of trace proteins [3–5], and quantitative models based upon the concept of excluded volume were shown to account semi-quantitatively for the observed dependence of solubility on the concentration of added polymer or protein were introduced [3, 4, 6, 7].

More recently, studies carried out in several laboratories [8–12] revealed that the addition of significant concentrations of functionally unrelated polymers or proteins can greatly accelerate the formation of fibrillar protein aggregates. A simple model based upon excluded volume theory was shown to quantitatively account for the dependence of the kinetics of amyloid fiber formation upon the concentration of added polymer [10].

At the same time, gerontological studies have revealed a gradual reduction in the water content of aging tissue, including brain tissue [13–16], which is equivalent to an increase in the total macromolecular concentration in the aqueous compartments of these tissues.

In the following section we review simple models for the effect of excluded volume (“crowding”) upon the kinetics of solubility loss and fiber formation. Next we introduce a time-dependent increase in the concentration of an additional inert volume-excluding substance (termed “crowder”), and show that this leads to a highly cooperative appearance of aggregate. The models developed here provide a possible explanation of why aggregates of different proteins with widely disparate intrinsic stabilities may accumulate on a comparable time scale in aging individuals.

Models

The models to be summarized below are based upon highly simplified hard particle representations of molecular size and shape, which have been found useful for semi-quantitative estimation of the effect of crowding upon the free energies, equilibrium, and rate-constants of reactions in crowded solutions [17–19]. A complementary description of the crowding effect termed “depletion attraction” has been presented [20] but so far has not been utilized to quantify the effect of crowding on chemical equilibria and kinetics.

Condensation

The reaction to be modeled is P (solution) ⇄ P (aggregate). P in solution is assumed to be monomeric, and the aggregate is assumed to be thermodynamically equivalent to a condensed phase. The thermodynamic solubility constant is given by

$\begin{array}{cc}{K}_s^0=\frac{1}{a_s}=\frac{1}{{\gamma }_s{c}_s}& (1)\end{array}$

where a_s, γ_s, and c_s respectively denote the thermodynamic activity, activity coefficient, and concentration of soluble protein in equilibrium with the condensed phase. We then define the effective solubility constant [21]

$\begin{array}{cc}{K}_s\equiv \frac{1}{c_s}=K_s^0{\gamma }_s& (2)\end{array}$

For transition-state rate limited (i.e., slow) association reactions, crowding affects primarily the association rate constant [21], so we may write

$\begin{array}{cc}\ln \left(k_a/k_a^0\right)\cong \ln \left(K_s/K_s^0\right)=\ln {\gamma }_s& (3)\end{array}$

where k⁰_a denotes the value of the association rate constant in dilute (ideal) solution. We represent the soluble protein as an equivalent hard sphere with radius r_s and the background environment as a fluid containing a volume fraction ϕ of uniform hard spheres (“crowders”) with radius r_c. Scaled particle theory [22] then yields the approximate expression

$\begin{array}{cc}\ln {\gamma }_s=\ln \left(1-\varphi \right)+A_{1}z+A_2{z}^2+A_3{z}^3& (4)\end{array}$

where

$\begin{array}{cc}{A}_1=R^3+3R^2+3R& (5\text{a})\end{array}$

$\begin{array}{cc}{A}_2=3R^3+4.5R^2& (5\text{b})\end{array}$

$\begin{array}{cc}{A}_3=3R^3& (5\text{c})\end{array}$

$\begin{array}{cc}z=\frac{\varphi }{1-\varphi }& (6)\end{array}$

and R ≡ r_s/r_c.

We assume that the condensed phase (aggregate) is essentially insoluble, and that the rate of dissolution may be neglected. The kinetics of aggregation are then described by the following first-order rate equation:

$\begin{array}{cc}\frac{d{f}_s}{dt}=-k_a{f}_s& (7)\end{array}$

where f_s denotes the mass fraction of soluble protein, and the fraction of aggregated protein is just 1 − f_s.

Fibrillation

The association reaction to be modeled is the addition of monomer to the end(s) of a growing fibrillar aggregate: P₁ + P_n ⇄ P_{n + 1}. The thermodynamic equilibrium constant is given by

$\begin{array}{cc}{K}_n^0=\frac{a_{n+1}}{a_1{a}_n}=\frac{{\gamma }_{n+1}{c}_{n+1}}{{\gamma }_1{c}_1{\gamma }_n{c}_n}& (8)\end{array}$

and the effective equilibrium defined in terms of concentrations is then given by

$\begin{array}{cc}{K}_n\equiv \frac{c_{n+1}}{c_1{c}_n}=K_n^0\frac{{\gamma }_1{\gamma }_n}{{\gamma }_{n+1}}& (9)\end{array}$

As before, the monomer is modeled as an equivalent hard sphere of radius r₁, and its activity coefficient calculated according to Equations (4–6), with R = R₁ ≡ r₁/r_c. The oligomeric fibrils P_n and P_{n + 1} are modeled as hard spherocylinders (cylinders capped with hemispheres on each end) with radius r_sc and the ratios of cylindrical length to diameter L_n and L_{n + 1} respectively. The activity coefficient of an isolated spherocylinder in a fluid containing volume fraction ϕ of uniform hard spheres of radius r_c is estimated using Equations (4,6), with

$\begin{array}{cc}{A}_1=R^3+3R^2+3R+1.5L\left(R^2+2R+1\right)& (10\text{a})\end{array}$

$\begin{array}{cc}{A}_2=3R^3+4.5R^2+4.5L\left(R^2+R\right)& (10\text{b})\end{array}$

$\begin{array}{cc}{A}_3=3R^3+4.5L{R}^2& (10\text{c})\end{array}$

where R = R_sc ≡ r_sc/r_c [23].

As in the case of condensation, it is assumed that crowding affects primarily the association rate constant, so that

$\begin{array}{cc}\ln \left(k_a/k_a^0\right)\cong \ln \left(K_n/K_n^0\right)=\ln {\gamma }_1+\ln {\gamma }_n-\ln {\gamma }_{n+1}& (11)\end{array}$

We may write

$\begin{array}{cc}\ln {\gamma }_{n+1}=\ln {\gamma }_n+\frac{d\ln \gamma }{dn}=\ln {\gamma }_n+\frac{d\ln \gamma }{dL}\frac{dL}{dn}& (12)\end{array}$

It follows from equations [10a–c] that

$\begin{array}{cc}\begin{array}{l}\frac{d\ln {\gamma }_{sc}}{dL}=1.5\left(R_{sc}^2+2R_{sc}+1\right)z\hfill \\ +4.5\left(R_{sc}^2+R_{sc}\right)z^2+4.5R_{sc}^2{z}^3\hfill \end{array}& (13)\end{array}$

Assuming conservation of volume upon association, we obtain

$\begin{array}{cc}\frac{dL}{dn}=\frac{2}{3}{\left(\frac{r_1}{r_{sc}}\right)}^3& (14)\end{array}$

Inspection of Equations (12–14) reveals that lnγ_{n + 1} − ln γ_n, equal to the excess free energy of adding a monomer to an oligomer, is independent of the size of the oligomer. This result agrees with our intuition, since fiber growth only occurs at the ends of the oligomer. Then Equation (11) may be rewritten as

$\begin{array}{cc}\ln \left(k_a/k_a^0\right)=\ln {\gamma }_1-\frac{d\ln {\gamma }_{sc}}{dL}\frac{dL}{dn}& (15)\end{array}$

where ln γ₁ is calculated using Equations (4–6) with R = R₁, and dln γ_sc/dL and dL/dn are calculated using Equations (13, 14) respectively.

As in the case of the condensation model, we shall assume that the linear fibrils are essentially insoluble, so that the dissociation rate may be neglected relative to the association rate. Then the rate of addition of monomer to oligomer will be given by the first order rate expression

$\begin{array}{cc}\frac{d{f}_1}{dt}=-k_a{f}_1& (16)\end{array}$

where f₁ denotes the mass fraction of monomer, and the mass fraction of fibril is just 1 − f₁.

Time-Dependence of Crowding

The concentration of soluble protein in various regions of human brain has been reported to increase roughly linearly with age [13], in some regions doubling over a lifespan of 80 years. We therefore model the total volume fraction of “crowder” as a linear function of time:

$\begin{array}{cc}\varphi ={\varphi }_0+\beta t& (17)\end{array}$

Parameswaran et al. [16] measured the fraction of volume excluded to albumin in rat mesenteric tissue as a function of the age of the rat, and reported that this fraction increased from 20 to 40% over the lifetime of the rat (650 days). We shall use the results cited above as a qualitative basis for positing a possible linear increase in volume fraction of crowder from 0.2 to 0.4 over the 80 year lifespan of a human, i.e., ϕ₀ = 0.2 and β = 0.0025yr⁻¹. Simulations were carried out varying each of these parameters about the values cited.

Calculation of the mass fraction of aggregated protein according to the solubility model was performed by numerical integration of Equation (7) with a time-dependent value of k_a calculated according to Equations (3–5, 17), using the differential equation solver ODE15s in MATLAB v. 2013b (Mathworks, Natick, MA). The corresponding calculation carried out according to the fibrillation model was performed by numerical integration of Equation (16) with a time-dependent value of k_a calculated according to Equations (13, 14, 15).

Results and Discussion

The dependence of the mass fraction of polymer on elapsed time, calculated using the condensation and fibrillation models with various parameter sets shown in the figure caption, are plotted in Figures 1A,B. The dashed reference curve in panel A represents the classical decaying exponential solution to the first-order rate Equation (7) with k_a equal to a constant value of 0.1. Results obtained from both models are qualitatively similar. Each curve representing the calculated dependence of f_p on elapsed time may be characterized by two parameters: t₅₀, the time at which half of the protein is aggregated, and a kinetic cooperativity parameter, α, a measure of the steepness of the curve at t₅₀, defined according to Hall and Mnton [24]

$\begin{array}{cc}\alpha =\frac{{\left(d\ln f_p/d\ln t\right)}_{t=t_{50}}}{\ln 2}& (18)\end{array}$

FIGURE 1

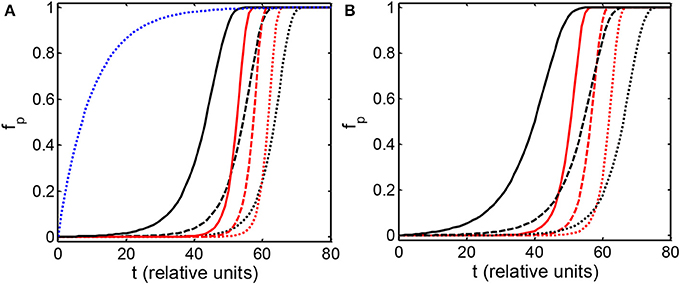
Figure 1. Dependence of the mass fraction of polymer upon elapsed time, calculated according to the condensation model (A) and the fibrillation model (B) as described in the text. Parameters associated with each simulation are presented in Table 1. The blue dotted curve in (A) is the solution to the first order rate Equation (7) with a constant value of log k_a = −1.

TABLE 1

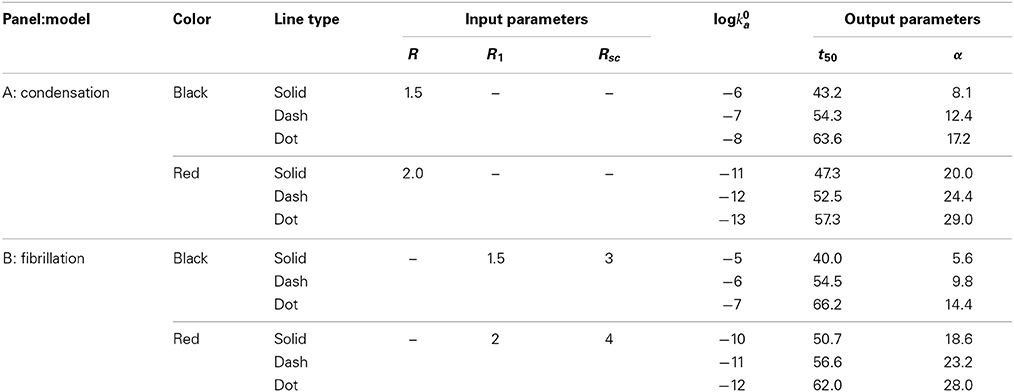
Table 1. Input and output parameters characterizing each simulation plotted in Figures 1A,B.

The value of α so defined is identically equal to 1 for the time dependence of f_p obtained from solution of Equation (7) with a constant (time-independent) value of k_a (for example, the reference curve plotted in Figure 1A), and increases with the steepness of the dependence of f_p on t. General properties of the model may be easily deduced upon inspection of correlations between the various input parameters and the output parameters t₅₀ and α. It follows from Equations (16, 18) that

$\begin{array}{cc}\frac{\alpha }{t_{50}}=\frac{k_{a,50}}{\ln 2}& (19)\end{array}$

where k_a,50 is the value of k_a at t = t₅₀.

In Figure 2A the dependence of f_p on elapsed time is plotted for three simulations carried out with the condensation model with the parameters indicated in the Figure caption. These parameters were selected to provide significantly different rates of increase of k_a with time, as shown in Figure 2B, but similar values of t₅₀. The results of comparable simulations carried out using the fibrillation model are qualitatively similar and are therefore not shown. It is evident that the delay time preceding the onset of the appearance of significant quantitities of polymer, and the rapidity of significant accumulation of polymer, as reflected in the value of α, are both strongly correlated with the rate of increase of k_a, and thus the rate of increase of volume occupancy by crowder [cf. Equations (3–5)]. It should also be noted that simulations yielding a relatively abrupt onset of the appearance of polymer (i.e., a high value of α), with very similar values of t₅₀ (e.g., curves b and c of Figure 2A) may be obtained for values of k⁰_a differing by several orders of magnitude.

FIGURE 2

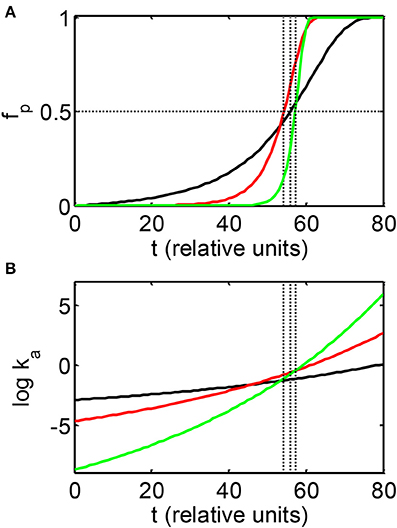
Figure 2. Dependence of the mass fraction of polymer (A) and the logarithm of the association rate constant (B), calculated according to the condensation model as described in the text. Parameters associated with each simulation are presented in Table 2. Vertical dotted lines indicate the values of t₅₀ associated with each simulation.

TABLE 2

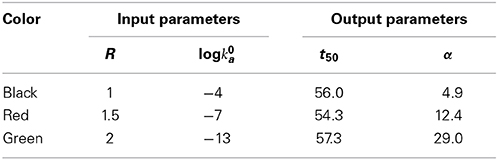
Table 2. Input and output parameters characterizing each simulation, calculated using the condensation model, plotted in Figures 2A,B.

We therefore conclude that, independent of the particular model or details of the simulation, the apparently sudden accumulation of significant amounts of aggregate following a long delay is a consequence of a rate constant for polymer growth that is initially undetectably small, but increases at least exponentially with time. These conditions are met in a wide variety of simulations reflecting broad variation in initial rates of polymer growth, polymer geometry and size, and postulated temporal gradients of volume occupancy by an inert crowder.

The model for fibrillation presented here does not take into account the potential fragmentation of growing fibrils [25]. The rate of fragmentation would be expected to increase with the average size of growing fibrils and hence an increase in the number of growth sites with time, leading to a potentially cooperative accumulation of fibrillated protein with time [26]. An increasingly crowding-accelerated rate of addition of monomer to an increasing number of growth sites would enhance the cooperative appearance of fibril exhibited by the model presented here, thus strengthening the qualitative conclusions derived from this model.

While the models proposed above are highly speculative, we believe that they may have physiological relevance for the following reasons. The appearance of neurodegenerative diseases is relatively abrupt and occurs at an advanced age, except in the case of unstable mutant proteins. There have been many hypotheses proposed relating the aggregation of a protein or peptide associated with a particular disease to the ensuing neuronal damage and death [27, 28], including loss of essential native protein function and toxicity of oligomers or large aggregates. The models proposed here suggest that if neurons are particularly susceptible to water loss and the concomitant increase in intracellular crowding with aging, then many neuronal proteins, independent of their intrinsic stability, would at some point abruptly appear to lose solubility as their respective rates of condensation or fiber formation begin to rapidly accelerate. Which protein first becomes substantially insoluble, and thus identified as the cause of a particular infirmity, depends upon the time-dependent macromolecular composition of a particular cell or tissue type, and is therefore subject to variation between individuals.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author thanks Drs. Peter McPhie and Travis Hoppe (NIH) for helpful comments on an early draft of this report. This work was supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases

References

1. Hebert LE, Scherr PA, Beckett LA, Albert MS, Pilgrim DM, Chown MJ, et al. Age-specific incidence of Alzheimer's Disease in a community population. J Am Med Assoc. (1995) 273:1354–9. doi: 10.1001/jama.1995.03520410048025

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

2. Gurland BJ, Wilder DE, Lantigua R, Stern Y, Chen J, Killeffer EH, et al. Rates of dementia in three ethnoracial groups. Int J Geriatric Psychiatry (1999) 14:481–93.

Pubmed Abstract | Pubmed Full Text

3. Laurent TC. The interaction between polysaccharides and other macromolecules VI. Further studies on the solubility of proteins in dextran solutions. Acta Chem Scand. (1963a) 17:2664–8. doi: 10.3891/acta.chem.scand.17-2664

CrossRef Full Text

4. Laurent TC. The interaction between polysaccharides and other macromolecules. The solubility of proteins in the presence of dextran. Biochem J. (1963b) 89:253–7.

Pubmed Abstract | Pubmed Full Text

5. Atha DH, Ingham KC. Mechanism of precipitation of proteins by polyethylene glycols. Analysis in terms of excluded volume. J Biol Chem. (1981) 256:12108–117.

Pubmed Abstract | Pubmed Full Text

6. Laurent TC, Ogston AG. The interaction between polysaccharides and other macromolecules. 4. The osmotic pressure of mixtures of serum albumin and hyaluronic acid. Biochem J. (1963) 89:249–53.

Pubmed Abstract | Pubmed Full Text

7. Ogston AG. On interaction of solute molecules with porous networks. J Phys Chem. (1970) 74:668–9. doi: 10.1021/j100698a032

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

8. Wilf J, Gladner JA, Minton AP. Acceleration of fibrin gel formation by unrelated proteins. Thromb. Res. (1985) 37:681–8. doi: 10.1016/0049-3848(85)90197-5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

9. Drenckhahn D, Pollard TD. Elongation of actin filaments is a diffusion-limited reaction at the barbed end and is accelerated by inert macromolecules. J Biol Chem. (1986) 261:12754–8.

Pubmed Abstract | Pubmed Full Text

10. Hatters DM, Minton AP, Howlett GJ. Macromolecular crowding accelerates amyloid formation by human apolipoprotein C-II. J Biol Chem. (2002) 277:7824–30. doi: 10.1074/jbc.M110429200

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

11. Shtilerman MD, Ding TT, Lansbury PT, Jr. Molecular crowding accelerates fibrillization of alpha-synuclein: could an increase in the cytoplasmic protein concentration induce Parkinson's disease? Biochemistry (2002) 41:3855–60. doi: 10.1021/bi0120906

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

12. Uversky VN, Cooper EM, Bower KS, Li J, Fink AL. Accelerated alpha-synuclein fibrillation in crowded milieu. FEBS Lett. (2002) 515:99–103. doi: 10.1016/S0014-5793(02)02446-8

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

13. Naber D, Korte U, Krack K. Content of water-soluble and total proteins in the aging human brain. Exp Geront. (1979) 14:59–63. doi: 10.1016/0531-5565(79)90010-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

14. Nagy I, Nagy K, Nagy V, Kalmar A, Nagy E. Alterations in total content and solubility characteristics of proteins in rat brain and liver during aging and centrophenoxine treatment. Exp Geront. (1981) 16:229–40. doi: 10.1016/0531-5565(81)90018-8

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

15. Nagy IZ, Nagy K, Lustyik G. Protein and water contents of aging brain. Exp Brain Res. Suppl. (1982) 5:118–22. doi: 10.1007/978-3-642-68507-1_15

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

16. Parameswaran S, Barber BJ, Babbitt RA, Dutta S. Age-related changes in albumin-excluded volume fraction. Microvasc Res. (1995) 50:373–80. doi: 10.1006/mvre.1995.1065

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

17. Hall D, Minton AP. Macromolecular crowding: qualitative and semiquantitative successes, quantitative challenges. Biochim Biophys Acta (2003) 1649:127–39. doi: 10.1016/S1570-9639(03)00167-5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

18. Minton AP. The effective hard particle model provides a simple, robust, and broadly applicable description of nonideal behavior in concentrated solutions of bovine serum albumin and other nonassociating proteins. J Pharm Sci. (2007) 96:3466–9. doi: 10.1002/jps.20964

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

19. Zhou HX, Rivas G, Minton AP. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Ann Rev Biophys. (2008) 37:375–97. doi: 10.1146/annurev.biophys.37.032807.125817

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

20. Marenduzzo D, Finan K, Cook PR. The depletion attraction: an underappreciated force driving cellular organization. J Cell Biol. (2006) 175:681–6. doi: 10.1083/jcb.200609066

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

21. Minton AP. The effect of volume occupancy upon the thermodynamic activity of proteins: some biochemical consequences. Mol Cell Biochem. (1983) 55:119–40. doi: 10.1007/BF00673707

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

22. Lebowitz JL, Helfand E, Praestgaard E. Scaled particle theory of fluid mixtures. J Chem Phys. (1965) 43:774–9. doi: 10.1063/1.1696842

CrossRef Full Text

23. Cotter MA. Hard spherocylinders in an anisotropic mean field: a simple model for a nematic liquid crystal. J Chem Phys. (1977) 66:1098–106. doi: 10.1063/1.434044

CrossRef Full Text

24. Hall D, Mnton AP. Effects of inert volume-excluding macromolecules on protein fiber formation. II. Kinetic models for nucleated fiber growth. Biophys Chem. (2004) 107:299–316. doi: 10.1016/j.bpc.2003.09.016

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

25. Hall D, Edskes H. A model of amyloid's role in disease based upon fibril fracture. Biophys Chem. (2009) 145:17–28. doi: 10.1016/j.bpc.2009.08.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

26. Knowles TPJ, Waudby CA, Devlin GL, Cohen IA, Aguzzi A, Vendruscolo M, et al. An analytical solution to the kinetics of breakable filament assembly. Science (2009) 326:1533–7. doi: 10.1126/science.1178250

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

27. Glabe CG. Common mechanisms of amyloid oligomer pathogenesis in degenerative disease. Neurobiol Aging (2006) 27:570–5. doi: 10.1016/j.neurobiolaging.2005.04.017

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

28. Marshall KE, Marchante R, Xue WF, Serpell LC. The relationship between amyloid structure and toxicity. Prion (2014) 8:1–5.

Pubmed Abstract | Pubmed Full Text