The effect of macromolecular crowding on mobility of biomolecules, association kinetics, and gene expression in living cells

We discuss a quantitative influence of macromolecular crowding on biological processes: motion, bimolecular reactions, and gene expression in prokaryotic and eukaryotic cells. We present scaling laws relating diffusion coefficient of an object moving in a cytoplasm of cells to a size of this object and degree of crowding. Such description leads to the notion of the length scale dependent viscosity characteristic for all living cells. We present an application of the length-scale dependent viscosity model to the description of motion in the cytoplasm of both eukaryotic and prokaryotic living cells. We compare the model with all recent data on diffusion of nanoscopic objects in HeLa, and E. coli cells. Additionally a description of the mobility of molecules in cell nucleus is presented. Finally we discuss the influence of crowding on the bimolecular association rates and gene expression in living cells.

1. Introduction

The milieu of cytoplasm is commonly considered as a highly crowded and concentrated environment that impacts the kinetics and thermodynamics of biochemical reactions [1–11]. The effect of macromolecular crowding on reaction rates and equilibrium constants may arise from: (i) change of reactants' mobility [12–15], (ii) depletion interaction (excluded volume effect) that results in attraction between reactants [1, 8, 16–18], and (iii) non-specific chemical interaction with crowders [9, 10, 19, 20]. Over three decades of studies of crowded systems, both at the theoretical and experimental level, contributed significantly to our understanding of these effects. However, the quantitative impact of every component seems to be still elusive in living cells. In this review, we describe recent in vivo studies of biomolecules' mobilities and their interactions. We focus mostly on differences between diffusion constants in cytoplasms of prokaryotic and eukaryotic cells and their nuclei as well as on kinetics of bimolecular protein-protein and protein-DNA interactions, with gene expression in particular. We refer to theoretical models or in vitro systems only in the introductory parts and when necessary to make this review self-supported. Therefore, at the beginning of the review, we give a short introduction to our own contribution to this field of research i.e., motion of probes in synthetic complex liquids. The material presented in this paper does not overlap significantly with many informative reviews written in the last few years that concern theoretical and in vitro experimental contributions to protein mobility [21–24], protein folding [8, 10, 23], and protein-protein interactions [10, 11, 24].

2. Current Status of Research

2.1. Motion in Synthetic Crowded Environment

Complex liquids, in particular polymer solutions, are often considered as systems mimicking crowded environment of the cellular interior. Until recently however there has not been a single model of diffusion in synthetic complex liquids that could be applied to living systems. We have proposed [14] the phenomenological description of the diffusion in the complex fluid, either synthetic or biological, as well as the viscosity of those complex systems. The model is primarily applied to polymers [14, 25], to micellar systems [14] and recently to colloidal systems [26]. In this model the viscosity is defined via the fluctuation dissipation theorem:

$\begin{array}{ll}\frac{D_0}{D}=f=\frac{{\eta }_{\text{eff}}}{{\eta }_0}.\hfill & \left(1\right)\hfill \end{array}$

Here D₀ is the diffusion coefficient in a pure solvent of viscosity η₀ and D is the diffusion coefficient in a crowded environment. η_eff denotes the viscosity that is effectively “felt” by the particle diffusing in the crowded environment. Here f is the hydrodynamic drag in a crowded environment divided by the drag in water. f is a function of the length scales R_eff and ξ, characterizing the whole system (the probe and the environment), given by the Equation 2:

$\begin{array}{ll}f\left(R_{\text{eff}},\xi \right)=\exp \left[b{\left(\frac{R_{\text{eff}}}{\xi }\right)}^a\right],\hfill & \left(2\right)\hfill \end{array}$

where R_eff and ξ are defined as:

$\begin{array}{ll}\begin{array}{cc}{R}_{\text{eff}}^{-2}=r_{\text{p}}^{-2}+R_{\text{h}}^{-2},& \xi =R_{\text{g}}{\left(\frac{c}{c^{\ast }}\right)}^{-\beta }.\end{array}\hfill & \left(3\right)\hfill \end{array}$

In Equation 3, r_p and R_h are the hydrodynamic radii of the probe particle and of the polymer, respectively. ξ is the correlation length (a mean distance between entanglement points in polymer matrix) and R_g denotes gyration radius of the polymer coil. c and c* are polymer concentration and the overlap concentration, respectively. β is the exponent related to the Flory's exponent ν: β = ν/(3ν − 1). Exponent a (cf. Equation 2) is a constant of the order of 1, and b is temperature dependent parameter [27].

In Figure 1 we show the plot of the diffusion coefficient of a hypothetical, globular, and inert probe in a polyethylene glycol solution as a function of r_p, calculated according to Equation 2 for a constant concentration (20%), molecular weight of the polymer (10.94 kg/mol) and temperature (25°C). The diffusion coefficient takes value given by the Stokes-Sutherland-Einstein formula:

$\begin{array}{ll}D=\frac{kT}{6\pi {\eta }_{\text{eff}}{r}_{\text{p}}},\hfill & \left(4\right)\hfill \end{array}$

where k denotes Boltzmann constant and T is the absolute temperature. In considered polymer matrix, probes of r_p < R_h experience effective viscosity that is much lower than the macroscopic viscosity η_m. On the contrary, probes with r_p ≫ R_h experience a viscosity equal to η_m. It is noteworthy that the value of the diffusion coefficient D = D₀ is never reached for the physically meaningful range of probe sizes. For example, the diffusion coefficient of the fluorescent dye of r_p = 0.58 nm is around 14 times smaller than that in a pure solvent (Figure 1).

FIGURE 1

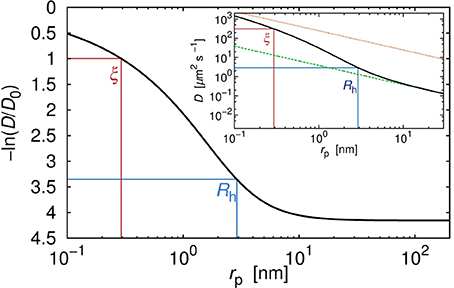
Figure 1. Relative diffusion coefficient (diffusion coefficient divided by its value in pure water) as a function of the hydrodynamic radius r_p of the hypothetical probe diffusing in the polyethylene glycol solution. Number averaged molecular weight of the polymer M_n = 10944 g/cm³. Concentration of the polymer was 20% by weight. Two characteristic length scales, ξ and R_h determined the viscosity experienced by the probe. For probes whose r_p was far smaller than ξ the probe diffused like in the solvent. For probes whose r_p was longer than R_h, the experienced viscosity reached the same values as the macroscopic viscosity of the solution. In the inset we showed absolute values of the diffusion coefficient for the same probes in the same polymer solution. The upper dotted line corresponded to the diffusion coefficient calculated according to the SSE equation (Equation 4) with η equal to the viscosity of the solvent η₀. Bottom dashed line corresponded to the diffusion coefficient calculated according to the SSE equation (Equation 4) with η = η_m (where η_m denoted the macroscopic viscosity). For probes whose hydrodynamic radius was few times larger than R_h, assumption that in Equation (4) η = η_m seemed reasonable. For probes whose r_p ≲ R_h, assumption that η = η_m failed in the same manner as the assumption that η = η₀.

Diffusion coefficient of the probe particles strongly depends on the structure of the fluid. In Figure 2 we compare diffusion coefficient of hypothetical probes in polymer (same as for Figure 1) and in solutions of elongated and rigid micelles of non-ionic surfactant C₁₂E₆. The ratio c/c* for both systems is equal to 14.7 and corresponds to concentration of 14% for C₁₂E₆ and 37.5% for polymer. We calculate the diffusion coefficients using Equation 2 as described in Kalwarczyk et al. [14]. Parameters a and b, differing between systems, are taken from Kalwarczyk et al. [14]. Calculated diffusion coefficient of probes in surfactant systems are from 2 to 50 times higher than diffusion coefficients for polymer solutions proving that the network composed of rigid micelles is more permeable for moving probes than dense polymer matrix.

FIGURE 2

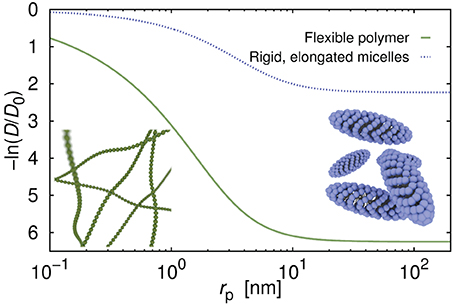
Figure 2. Diffusion coefficient as a function of the probe's hydrodynamic radius, r_p, in aqueous solution of the flexible polymer polyethylene glycol, and of the micelles formed of non-ionic surfactant C₁₂E₆. The c/c* ratio (concentration divided by the overlap concentration) for both systems was set the same and equal to 14.67, and corresponded to the concentrations of 14 and 37.5% for surfactant and for polymer, respectively. Curves were generated using Equation (2) with parameters: a = 0.62, b = 2.42 for polymer solutions, and a = 0.87, b = 0.9 for surfactant solutions; for details see [14].

2.2. Motion in the Cytoplasm of Eukaryotes

Although the synthetic systems may not be good experimental models to monitor biological processes, the physics governing the motion is the same for synthetic (in vitro) as well as for biological (in vivo) systems. Therefore, polymer systems, can be used as models mimicking the viscous response of the biological system to the probe's diffusion, despite the fact that the cytoplasm of living cell is sometimes described as a poroelastic material [28, 29].

Kalwarczyk et al. [14] used the concept of the length-scale dependent viscosity, represented by Equation 2, to study the viscosity of the cytoplasm of mammalian cells and diffusion therein. In synthetic systems, control over the diffusion rate of probes could be achieved by changes of concentration, c and of size, R_h of objects crowding the given system (see also Equations 2 and 3). In living organisms this was not the case as concentration of the crowding objects and their size were constant (at given growth conditions). In cells Equation 2 had to be rewritten as a function of r_p only. The Equation 2, therefore, took the following form:

$\begin{array}{ll}f\left(r_{\text{p}}\right)=A\exp \left[{\left(\frac{{\xi }^2}{R_{\text{h}}^2}+\frac{{\xi }^2}{r_{\text{p}}^2}\right)}^{-a/2}\right]\hfill & \left(5\right)\hfill \end{array}$

with ξ and R_h as free parameters. A was a pre-exponential factor of the order of one. Kalwarczyk et al. [14] used Equation 5 to describe the effective viscosity experienced by probes during their motion in the cytoplasm of Swiss 3T3 and of HeLa cells. Dependence of the effective viscosity experienced by probes on their hydrodynamic radii is depicted in Figure 3. The length scale corresponding to the biggest crowding agents, R_h was comparable to the hydrodynamic radius of the actin filaments in the cytoplasm of HeLa cells. In Swiss 3T3 cells ξ = 7 ± 2 nm while in HeLa ξ ≈ 5 [14].

FIGURE 3

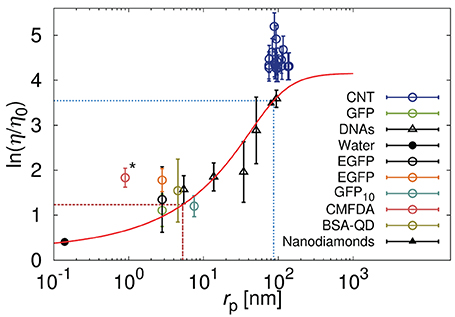
Figure 3. Relative viscosity (η/η₀) that is equivalent to the reciprocal of the diffusion coefficient (D₀/D) for various probes diffusing in the cytoplasm of HeLa cells. Black points correspond to the data [149–152] discussed in Kalwarczyk et al. [14] and the red solid line represent the best fit (Equation 5) to those data with: ξ ≈ 5 nm and R_h ≈ 86 nm marked as red dashed and blue dotted lines, respectively, [for details please see [14]]. Reproduced with permission from reference 14. Copyright 2011 American Chemical Society. Colored points represent data published recently for carbon nanotubes (CNT) [32], green fluorescent protein (GFP) [33], enhanced green fluorescent protein (EGFP) [34], oligomer of ten GFP proteins (GFP₁₀) [29], fluorescent dye – 5-chloromethylfluorescein diacetate (CMFDA) [29], and quantum dots stabilized with bovine serum albumin protein (BSA-QD) [31]. The carbon nanotubes, having huge aspect ratio, during the motion experience the hydrodynamic friction resulting not only from translational but also from the rotational motion. Increased effective friction is responsible for the increase of the effective viscosity experienced by the nanotubes with respect to the model represented by Equation (5). We expect that the globular object of r_p corresponding to r_p of the nanotubes will experience the viscosity predicted by the Equation (5). The CMFDA dye (the point marked by asterisk) in the cytoplasm can react with an intracellular thiols [36] leading to underestimation of the size of the probe and apparent deviations from the predictions.

Although the physical meaning of ξ for living cells remains unclear its value correlates with the radius of the cytoplasmic water pores in the Swiss 3T3 cells that is equal to 7 nm Luby-Phelps et al. [30]. The same value for the radius of the water pores is reported by Moeendarbary et al. [29]. Indeed such interpretation is in agreement with the interpretation of ξ for the synthetic systems (polymer solutions) as a distance between entanglement points that is proportional to the size of a water channel in the polymer network.

As the value of ξ in mammalian cells is around 7 nm, proteins with typical radius of 4 nm, experience the viscosity comparable to the viscosity of water. In that sense for most proteins, the cytoplasm can not be regarded as the crowded environment. Larger probes with radius exceeding ξ, e.g., ribosomes or protein aggregates, experience the effective viscosity η_eff (Equations 1–5) that results from the crowding.

Very recent data on diffusion in HeLa cells [29, 31–34] appear to confirm, to some extent, Kalwarczyk's predictions (cf. Figure 3). Deviations from the predictions, are observed for small fluorescent dye 5-chloromethylfluorescein diacetate (CMFDA) [29]. This dye, inside the cell, is enzymatically cleaved and become fluorescent [35]. On the other hand the chloromethyl group of the CMFDA dye can react with intracellular thiols in a reaction mediated by glutathione S-transferase [36], whose hydrodynamic radius is roughly around 2.6 nm. The CMFDA dye, therefore, can not be regarded as freely diffusive in the cellular interior and its intracellular size is probably underestimated and lead to deviations shown in Figure 3. Another deviation toward the higher values of viscosity is observed for carbon nanotubes diffusing in the cytoplasm of HeLa cells [32]. Equations 2 and 5 are valid only for probes of globular shape, so that the rotational diffusion of those object, occurring at much shorter time-scale, do not influence the translational motion of the probes. In D ∝ F⁻¹, where F is an effective friction given by the sum of translational, F_t, and rotational F_r friction. In case of globular objects F_t ≫ F_r and F ≈ F_t. Nanotubes are characterized by huge aspect ratio and their rotational diffusion in the cytoplasm is strongly hindered and affects translational motion. In general F_r is not negligible with respect to F_t and the effective friction F experienced by the nanotubes is increased by the rotational friction felt by the nanotubes.

2.3. Motion in the Cell Nucleus

Genetic material of the cell is separated from the cytoplasm in a dedicated cellular compartment called nucleus. Huge amount of genetic material (around 6 × 10⁹ base pairs) in a form of long DNA molecules (46 in human somatic cells) is packed in the nucleus with diameter of around 10 microns. Squeezing of 46 long molecules in a small volume, requires highly efficient compaction [37]. It is achieved with the help of nucleosomes leading to higher order chromatin structure which fits into the nucleus. Before any gene can be transcribed from the compact chromatin it needs to be untangled. The structure of the chromatin in the nucleus is highly complex, with parts of accessible and inaccessible chromatin, named euchromatin (open), and heterochromatin (closed), respectively. The distribution of chromatin is highly regulated with active genes located at the borders of physical domains of chromosomes [38, 39]. There are many proteins involved in the maintenance of DNA molecules and they need to reach their specific locations in the nucleus to perform their function.

One of the first measurements of diffusion in a nucleus was done by Seksek et al. [40] who determined the diffusion coefficients of inert probes such as dextrans, in the cytoplasm and nucleus of MDCK epithelial and 3T3 fibroblast cells. They found that the diffusion coefficient decreased around 4 fold in comparison to D₀ for all studied probe sizes (r_p = 4–30 nm), with D/D₀ = 0.25 ± 0.02 (MDCK) and 0.27 ± 0.03 (3T3). In the experiments performed with oligonucleotides [43 base pairs Oligo(dA), M_W ~13 kDa]), a slight drop from D₀ = 5.7 ± 0.2 × 10⁻⁷ cm²/s (in water) to D = 5.05 ± 0.52 × 10⁻⁷ cm²/s (in the nucleus) was observed (D/D₀ = 0.886), showing that for inert probes with the radius of several nm diffusion in the nucleus was unhindered. At the same time, the diffusion of the probe Oligo(dT) similar in size but capable of interaction with polyadenylated RNA, was slowed down 6 times, from 5.0 ± 0.2 × 10⁻⁷ cm²/s to 0.87 ± 0.02 × 10⁻⁷ cm²/s (D/D₀ = 0.174). Even slower diffusion was observed for the range of endogenous polyadenylated RNA (with the sizes in the range of several thousands base pairs) where the diffusion coefficient was equal to 0.06 ± 0.01 × 10⁻⁷ cm²/s [41]. The movement of polyadenylated RNA was diffusive and the space available for diffusing molecules was restricted to the regions free from chromatin. For the range of synthetic DNA molecules of sizes ranging from 21 to 6000 base pairs (bp) an empirical formula was found [42], describing diffusion coefficients, D₀, of the DNA fragments in water. D₀ was related empirically to DNA size with the following formula: D₀ = 4.9 × 10⁻⁶ cm²/s ×[bp size]^−0.72. Thus, in this size range D₀ decreased with increasing size from 53 × 10⁻⁸ to 0.81 × 10⁻⁸ cm²/s. When introduced into the nucleus, these fragments were found almost immobile, likely because of the extensive binding to almost immobile obstacles (e.g., chromatin). Inert probes such as dextrans (of M_w. up to 580 kDa) with the size similar to DNA fragments diffused freely in the nucleus with D/D₀ of around 0.16 (6× slower than in water). Interestingly, dextran of molecular weight of 2000 kDa was found immobile to the same degree as studied DNA fragments, with the D/D₀ smaller than 0.01, however no exact value of diffusion coefficient was reported.

Unhindered diffusion for inert probes in wide range of sizes r_p indicated that water channel in the nucleus are larger than 30 nm. Similar behavior is observed in lamellar phases of ionic surfactant with water channels >150 nm [43]. Probably water channels are most filled with proteins at the volume fractions ϕ = 0.1–0.2 (suggested by 2–8 fold decrease of the mobility for most proteins).

The mobility measured for several nuclear proteins tagged with GFP [44] reveal their highly dynamic nature. It became apparent that many nuclear complexes undergo constant exchange with the kinetics of the order of seconds [45–48], which has a substantial effect on their diffusional mobility. For three studied proteins, HMG-17, SF2/ASF, and fibrillarin, the diffusion coefficients values are 0.45 × 10⁻⁸ cm²/s, 0.24 × 10⁻⁸ cm²/s, and 0.53 × 10⁻⁸ cm²/s, respectively. Molecular weight of these proteins is only about 2 times higher than that of GFP which diffuses in the nucleus with D = 9.8(±1.6) × 10⁻⁸ cm²/s [49]. Thus, D-values for HMG-17, SF2/ASF, and fibrillarin are about 20–40 times lower than values reported for free solutes in the nucleus or for GFP alone indicating that interactions of these proteins with nuclear components slow down the diffusion. Similar results are observed for Src peptides [50], where interactions with DNA reduced significantly the diffusion coefficients measured in vivo (from D₀ = 2 ± 1 × 10⁻⁷ cm²/s to D_nucleus = 4 ± 2 × 10⁻⁹ cm²/s).

Some studies interpret the results on diffusion in the nucleus with the help of anomalous diffusion, where mean square displacement does not change linearly with time, and is described by anomaly index, α, according to the formula 〈r²(t)〉 ~ t^α. There are several microscopic models which can give rise to an anomalous diffusion behavior but physical origins of these phenomenon are still discussed [51, 52].

In the study by Wachsmuth et al. [49] measurements performed with fluorescent proteins revealed that the diffusion of GFP was slowed down around 5 times (in AT-1 and COS-7 cells). The results could be analyzed using two models of diffusion: normal diffusion with two components (fast and slow) and anomalous diffusion (one diffusion time and anomaly index) [49, 53]. The obtained translational diffusion times for the fast component were similar for both models, indicating a 5 fold decrease in diffusion coefficient relative to diffusion in water. The absolute value of the diffusion coefficient in cytoplasm was D = 12.5(±1.3) × 10⁻⁸ cm²/s, while the two components in the nucleus moved with diffusion coefficients of D₁ = 9.8(±1.6) × 10⁻⁸ cm²/s, and D₂ = 1.0(±0.6) × 10⁻⁸ cm²/s. For the anomalous diffusion model, we have D₁ = 8.7(±1.0) × 10⁻⁸ cm²/s, and α = 0.87. Here D₁ is given as a time dependent diffusion coefficient taken at time τ₁ being the diffusion time through the focal volume of size ω; D₁ = D(τ₁) = ω²/4τ₁, where 〈r²(t)〉 = 6D(t)t = 6D₁ (t/τ₁)^α. In the same study the diffusion coefficient measured for protein EGFP-b-galactosidase (M_W ~ 80 kDa) was lower than the one for GFP (M_W 27 kDa) by a factor of 1.4. Such difference could be explained by the mere difference in size of the two proteins, confirming previous observations, that the relative viscosity in the nucleus was rather size independent (at least up to M_w of around 2000 kDa). The ratio of cytoplasmic to nuclear diffusion coefficients of GFP was 1.28(= 12.5/9.8), similar to the value of 1.22 measured for another protein TIF-IA [54] indicating that diffusion of a given protein was often slower in the nucleus than in the cytoplasm with slightly higher degree of crowding in the nucleus, however some studies report similar degree of molecular crowding in both compartments [55].

Generally the diffusion of the molecules that do not bind to chromatin is slowed down 2–8 times [40, 41, 44, 49, 56–58], whereas more hindered diffusion is observed for protein that interact with chromatin. Some studies report the diffusion in the nucleus to be size independent and interpret results within the model of the fractal geometry of chromatin [57], whereas other results indicate some dependence of nuclear diffusion on the size of the diffusing object [42, 56].

Interesting data were reported for the different regions of chromatin revealing differences between euchromatin and heterochromatin. Less compact euchromatin was shown to have higher fractal dimension than heterochromatin. The diffusion in the euchromatin region was slowed down around 3 times (relative to diffusion in water), whereas in heterochromatin region slowing down was almost 6 fold for the tracer molecule consisting of GFP multimers. The chromatin architecture was described as fractal-like on the length scales smaller than ~100 nm, giving rise to size-independence of the relative diffusion coefficient since most proteins or protein complexes were smaller than 100 nm. Another interpretation of diffusive motion of GFP in the nucleus was given by Hinde et al. [59], who used a normal diffusion model with two components in the pair correlation function analysis to image diffusional barriers and passages. For the region of low DNA density (euchromatin) they obtained two different mobilities with diffusion coefficient D₁ = 22.8 × 10⁻⁸ cm²/s and D₂ = 0.3 × 10⁻⁸ cm²/s. In the high DNA density (heterochromatin) regions, obtained values were D₁ = 23 × 10⁻⁸ cm²/s and D₂ = 0.48 × 10⁻⁸ cm²/s. Thus, the diffusion characteristics of EGFP in the nucleus was rather constant and did not depend on DNA density, however relative contribution of slow component was higher in the heterochromatin region. Yet slightly different results were found in the study by Capoulade et al. [60], where a diffusional mapping in 3T3 cells was performed with the use of selective plane illumination microscope. They measured the diffusion coefficients for the heterochromatin protein 1 (HP1α-EGFP) in the nucleus of 3T3 fibroblasts. Results indicated the differences between euchromatin and heterochromatin with respect to the fast (D₁) and slow (D₂) components of the diffusive pool of HP1α. Different slow diffusion coefficients were obtained for euchromatin (D₂ = 0.33 ± 0.16 × 10⁻⁸ cm²/s) and for heterochromatin (D₂ = 0.16 ± 0.07 × 10⁻⁸ cm²/s), whereas fast diffusion coefficient D₁ = 8.1 × 10⁻⁸ cm²/s was similar for both chromatin regions. Slow diffusion component (D₂) was taken as a measure of interaction of HP1α-EGFP with chromatin. Weaker interaction of HP1α-EGFP with euchromatin was indicated by 2 fold higher mobility in this region.

In Figure 4 we plotted the data for the effective viscosity experienced by the probes during the diffusion across the nucleus for several types of probes. The effective viscosity was calculated as the reciprocal of the relative diffusion coefficient provided in Seksek et al. [40], Lukacs et al. [42], Phair and Misteli [44], and Hinde et al. [59]. Hydrodynamic radius of the DNA fragments was calculated from the relation taken from the work of Kalwarczyk et al. [15]: r_p = 0.024M^0.57_w; where M_w corresponded to molecular weight of the DNA. Hydrodynamic radius of dextran polymers was calculated from the relation obtained on the basis of experiments of Ioan et al. [61]: r_p = 0.072M^0.45_w.

FIGURE 4

Figure 4. Effective viscosity experienced by the probes diffusing in the cell nucleus [40, 42, 44, 59, 60]. Data for DNA fragments diffusing in the nucleus of the HeLa cell [42], are represented as the dashed line and corresponds to the average value calculated for the fragments of hydrodynamic radii in the range of 5–135 nm. Data for dextran polymers as probes are represented as black squares (nucleus of the Madin-Darby Canine Kidney Epithelial Cells – MDCK) and green squares (nucleus of Swiss 3T3 cells – 3T3), respectively, [40]. Data for proteins fused with GFP and moving in the nucleus of the HeLa and of the Baby Hamster Kidney (BHK) cells are marked by yellow squares [44]. The plot shows also data for the EGFP in the nucleus of Chinese Hamster Ovary (CHO) cells [59]. The data for EGFP reveal the heterogeneous structure of the nucleus. Hinde et al. [59] measure the diffusion in high-density DNA (hdDNA) and low-density DNA (ldDNA) regions. In both cases they obtain two diffusion coefficients, fast and slow (D₁, D₂) that differ by two orders of magnitude. On the plot we show the effective viscosity corresponding to the D₁ in ldDNA, D₁ in hdDNA, D₂ in ldDNA, and D₂ in hdDNA. The heterogeneous structure of the nucleus is also represented by the data for HP1-GFP diffusing in the nucleus of 3T3 cells [60]. Both the slow and the fast component are comparable with results of Hinde et al. [59]. The top panel shows a cartoon representation of the nucleus as a heterogeneous environment consisting of densely and loosely packed DNA regions. Errorbars not shown to keep the clarity of the figure. Most of errorbars does not exceed an order of magnitude.

Some speculations about the mechanisms leading to the discrepancies in the nuclear diffusion of small molecules are presented below. The structure of the nucleus is heterogenous and constitutes of the regions poor and rich in DNA. In both regions the DNA may be densely packed (heterochromatin) forming a fibrinal structure, or loosely packed (eurchromatin). In the DNA poor region, the motion of small probe is not hindered and the probe diffuses in soup of proteins and other small (macro)molecules. When the same probe gets into the region rich in a loosely packed DNA, (eurchromatin) its motion is drastically hindered due to the hindering effect of the DNA strands. A similar but not the same situation occurs in regions rich in highly packed DNA (heterochromatin). Due to the highly packed structure of the DNA the probe may diffuse inside the fibers forming the heterochromatin as is partially suggested by Hinde et al. [59].

Nucleus is involved in multiple functions in the living cells, ranging from most important gene expression to regulation of cell cycle and mechanotransduction. The dynamic structure of the nucleus is a subject of intense studies and significant insight has been achieved in past decades of research [62–64]. Diffusion has been shown to be a major mechanism of protein transport in the nucleus and further studies are needed to understand and quantitatively describe the dynamic structure of this organelle. We expect that the model of length-scale dependent viscosity valid in the cytoplasm of living cells can be also applied for cell nucleus. Currently available data, however do not allow for any quantitative conclusions. In the nucleus, ξ length scale is expected to be 30 nm and so the studies with bigger probes are required to confirm this prediction.

2.4. Motion in the Cytoplasm of Prokaryotes

Size of the water channel ξ in the cytoplasm of eukaryotes is of the order of several nanometers. Prokaryotes, however, are usually about ten times smaller than eukaryotic cells and their cytoplasm is roughly 3 times more crowded. Concentration of macromolecules is of the order of 10% (by volume) for eukaryotes and 30% for prokaryotes. An increase in the concentration of macromolecules is reflected by much lower ξ value for prokaryotes than for eukaryotes.

Kalwarczyk et al. [15] observed almost 10 fold decrease of ξ in E. coli with respect to HeLa and Swiss 3T3 cells. They collected literature data [12, 13, 65–77] of diffusion coefficients in the cytoplasm of E. coli and used Equation 5 to fit the data. From this fit they determined ξ of around 0.5 nm and R_h ≈ 42 nm [15]. It was found to correspond to the radius of the DNA loops. In Figure 5 we added the recent data [78] on diffusion in the cytoplasm of E. coli which confirmed the model predictions [15].

FIGURE 5

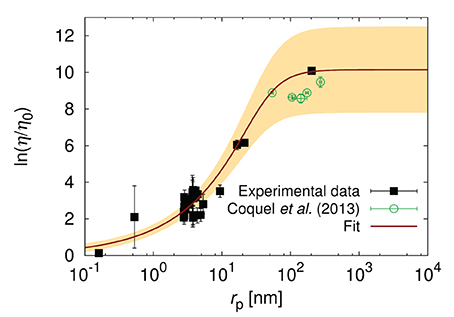
Figure 5. The logarithm of the effective relative viscosity (η/η₀ = D₀/D) experienced by the probe particles in the cytoplasm o E. coli. Plot shows the literature data for the reciprocal of diffusion coefficients [12, 13, 65–71, 73–77] (black pints), the fit of Equation (5) to the data, and the data of Coquel et al. [78]. The yellow shaded area corresponds to the maximal error of fitting. The plot is adopted from Kalwarczyk et al. [15] with a permission granted under the Creative Common license v3.0. The new data points obtained by Coquel et al. [78] are marked in green. D₀ is the diffusion coefficient in water of viscosity η₀.

Diffusion in the cytoplasm of E. coli is very sensitive to the size of the particle. The probes whose radii lie between ξ and R_h, experience the viscosity that increases exponentially with the particle size r_p. Therefore, even small proteins (i.e., GFP whose r_p = 2.8 nm) experience viscosity of around 12 times higher than the viscosity of water leading to 12 times slower diffusion. The protein with twice larger r_p diffuse 35 times slower than in water. Finally the ribosome whose r_p ≈ 16.5 nm experience viscosity that is 450 times the viscosity of water. From the point of view of proteins the ribosome is almost immobile as its diffusion time τ_D (the time needed to diffuse over the distance of one diameter) is nearly 10⁴ times longer than for GFP (τ_D = 4 ms vs. τ_D = 0.5 μs). Such strong dependence on the size of the particle undergoing self-diffusion can be used for determination of the unknown size of protein aggregates or the interactions of probe particle with the environment. The length-scale dependent viscosity can be used to determine the diffusion coefficient of probes of known size in any cell. This has been done to predict in-cellular diffusion coefficients of all known proteins synthesized from the genome of E. coli Kalwarczyk et al. [15]. There is not enough data for diffusion collected for the same growth conditions of cells. Therefore the data used in Kalwarczyk et al. [15] and presented in Figure 5 refer to diffusion in cells treated with different stimuli (various osmotic conditions and antibiotic treatment). Mika et al. [13] shows that cell treatment and growth conditions may have a significant impact on the diffusion processes in living cells.

The results for large macromolecular complexes such as RNA-protein [79], chromosomal loci [80, 81], and protein-protein aggregates or plasmids [82], show that these objects may move subdiffusively through cytoplasm of E. coli. The movement seems metabolism-dependent [81, 82] because ATP synthesis inhibition causes significant quantitative change in the mobility of these complexes. The anomaly index, α, is 0.7 ± 0.1 for RNA-protein complexes [79] and 0.39 ± 0.04 for chromosomal loci [80]. The chromosomal loci are confined by virtue of their connection with chromosome and movement of the specific locus depends on motion of its neighbors. Weber et al. [80] apply the model of a polymer in viscoelastic environment and show that the confinement is not solely responsible for anomality from the normal diffusion [83]. Parry et al. [82] demonstrate for protein-protein aggregates (fusion of avian reovirus protein μNS with GFP), that the value of the anomaly index, α, decreases with increasing particle size above 40 nm. Below that size the diffusion is normal. Additionally, they observe very strong probes confinement in ATP-depleted cells (treated with 2,4-dinitrophenol, DNP) with much stronger decrease in the anomaly index and the diffusion constant of the aggregates than in untreated cells. The same confinement is observed in a stationary phase of growth and under carbon starvation of cells. Parry et al. [82] interpret these results as emerging from cytoplasm properties that are characteristic of glass-forming liquids. They suggest that high macromolecular crowding in E. coli, cell confinement, and macromolecule interactions are responsible for glassy dynamics. All the observed deviation of particle diffusion from normality is only for macromolecules of sizes above 40 nm. On the contrary, other studies of protein aggregates [78] and large plasmids [75] show that diffusion of these macromolecules does not deviate from normal diffusion (we include them in Figure 5). The source of these discrepancies is currently unknown and more quantitative measurements for the same conditions are needed [82].

2.5. Association Kinetics in Living Cells

Mobility of proteins affects kinetics of reactions. Measurements of bimolecular reaction kinetics for hybridization of short DNA strands [84] and protein-protein association [85] in living HeLa cells show that intracellular crowding changes reaction rates up to several-fold as compared with reactions in buffer. Here we discuss quantitatively these rates.

Schoen et al. [84] studied kinetics of hybridization of short DNA chains at two different lengths 12- and 16-bp. The sequences of DNA were chosen to minimize specific interactions with other nucleic acids in cells and dsDNAs were delivered into cells by lipofection. The kinetics of opening/closing of DNA due to temperature oscillations driven by laser were measured by Förster resonance energy transfer (FRET) method. Non-monotonic change of association kinetics was determined in vivo, i.e., acceleration of association of the 16-mers when compared to in vitro data (2.9 × 10⁷M⁻¹s⁻¹ vs. 4.2 × 10⁶M⁻¹s⁻¹) but decelerated binding kinetics for 12-mers (5.5 × 10⁶M⁻¹s⁻¹ vs. 2.7 × 10⁷M⁻¹s⁻¹).

In vitro data point to non-diffusion limited hybridization of these DNA fragments studied by Schoen et al. [84]. Moreover, the kinetics of associations is slightly enhanced in vitro with crowding agents such as Ficoll-70 and dextrans [84] pointing that these agents cause depletion interactions and speed-up the binding. In the light of in vivo data it is clear that the reactions are modulated by specific interactions with nucleic acid binding molecules and the resulting effect depends on the length of DNA probes. The explanation proposed by authors states that likely acceleration of association of 16-mers in vivo is an effect of presence of magnesium cations or recombination mediator proteins, but deceleration rate of 12-mers is due to buffering by ssDNA- or dsDNA-binding proteins. The viscosity reference curve determined for HeLa cells (Figure 3) point that intracellular macromolecular crowding does not change the mobility of the short DNA strains. The change of hybridization kinetics, as argued by Schoen et al. [84], is only due to specific interactions inside cells.

The protein-protein association kinetics was studied by Phillip et al. [85] using FRET method and microinjection. The usage of prokaryotic proteins TEM1-β-lactamase and its protein inhibitor BLIP, foreign to the HeLa cells, possibly diminished the proteins interactions with cytoplasmic constituents. Observed reaction rate constants for wild type proteins in living cells and cell extracts were only slightly decelerated when compared to in vitro values (1.9 × 10⁵M⁻¹s⁻¹, 2.3 × 10⁵M⁻¹s⁻¹ and 3.0 × 10⁵M⁻¹s⁻¹, respectively). The association rate constants were however 4-orders of magnitude smaller than predicted for diffusion limited protein-protein binding.

Recently, we have computed [86] in vivo protein-protein binding rate constants determined by Phillip et al. [85] taking only into account changes in reactant mobilities. In our approach, we have combined the length scale-dependent viscosity model of HeLa cytoplasm [14] to predict translational diffusion constants for reacting proteins and Zhou's model [87] for kinetics of binding of two spheres with small reactive patches. The model requires also knowledge of rotational diffusion constants for proteins. The best agreement with experiment is obtained under assumption that the viscosity of HeLa cytoplasm experienced by rotating proteins is equal to water viscosity. Theoretical and experimental studies [88–91] show also that rotations of probes of protein sizes are slightly affected in cellular-like complex liquids. On the contrary, probes with hydrodynamic radii surpassing the sizes of largest crowders in HeLa cytoplasm experience during rotations macroscopic viscosity [32] as described in previous sections.

The same reaction was investigated in a buffer with PEG or dextran as crowders [85]. The measured reaction rate constants were also similar to diluted case. This apparent lack of change of reaction rate was attributed to the combination of two opposing effects: reduction in translational mobility of the proteins and attraction between them due to depletion effect. The combination of both effects results in the identical association rate constants as in pure water in the absence of both effects. However, the quantitative impact of depletion interactions on protein-protein association rate in vivo is hard to calculate because the interactions strongly depend on the shape of molecules under study and also on solvent involvement in the model [17]. The matter is complicated further by presence of weak, non-specific interactions [10, 20, 92].

It is worth noting that studies of interaction between molecules in PEG solutions should be carried with caution since this crowder is not inert and may induce unexpected system behavior. For example Hou et al. [93] performed in vitro studies of the cleavage process taking part in a bacteria's self-defense against viruses system. Authors performed the DNA cleavage using HindIII restriction enzyme. They monitored the result of the cleavage process 1 h after the reaction started for 24 h. Next they compared results of cleavage in buffer solution with those obtained in the samples containing low molecular weight polyethylene glycol (lmwPEG; M_n = 3461 g/mol) and high molecular weight polyethylene glycol (hmwPEG; M_n = 854096 g/mol). Authors observed that the cleavage process was stopped (no cleavage occurred) when the concentration of the lmwPEG exceeded 7% by weight. On the other hand in solutions of hmwPEG the process of cleavage proceeded without any changes.

Comparison of the viscosity experienced by the HindIII enzyme suggests that the stopping of the cleavage process is not governed by the hindering effect of the crowded environment. The possible explanation of the hindering effect of the lmwPEG solutions, as suggested by Hou et al. [93], are depletion interactions leading in surfactant solutions to the phase separation [94–97] or in solution of DNA leading to the condensation of DNA [93, 98]. From above we deduce that the solutions of the flexible, polyethylene glycol like polymers may not be preferable as in vitro models to study the influence of cellular crowding on the in-cell processes.

Study of the folding stability of the protein chymotropsin inhibitor 2 in the lyophilized E. coli cytosol [20] showed that crowder molecules interact with the protein destabilizing it. This is opposite to expected stabilizing entropic effect due to the fact that folded protein occupies less space than denaturated one. Also the cytoplasm of E. coli is highly crowded environment that should significantly reduce reaction rate constants between proteins [86] as predicted by the model in which only protein mobilities are taken into consideration.

2.6. Gene Expression in Living Cells

Gene expression is a process consisting of many reactions driven either by diffusion (regulation of initiation rate of gene expression by transcription factors [99–101]) or powered by hydrolysis of ATP or GTP molecules (RNA polymerase and ribosome movement or histone displacement). The studies of the crowding effects on particular steps of gene expression are concentrated on in vitro systems [102, 103] with crowding agents and comparison with dilute solutions. There is a growing number of experimental studies concerning transcription factor kinetics in bacteria [104–106] and eukaryotes [45, 46, 50, 107].

Morelli et al. [108] studied theoretically the impact of macromolecular crowding on gene expression and its regulation. The authors parametrized the model on the basis of changes of activity coefficients for hemoglobin at different concentrations [1, 109]. The crowding affects both equilibrium binding constants and diffusion of proteins. The reactions were assumed to be diffusion-limited. The effect of crowding was mainly caused by a shift of the equilibrium rather than reduction of protein diffusion i.e., the crowding increased probability of RNAP binding to the promoter that enhanced transcription rate. Similar behavior was observed in the synthetic systems for long dextran polymers [103]. The crowding effects on gene transcription was also studied by Brownian dynamics and Monte Carlo simulations [110]. This study revealed that for crowding at volume fractions being close to physiological values transcript abundances reached maximum levels, in accordance with in vitro studies for various crowders [102, 103, 111]. Ge et al. [102] used three crowding agents PEG-8000, Ficol-70, and Ficol-400 to study expression of Renilla luciferase driven by T7 promoter. They observed maximal enhancement of transcription for intermediate concentration of crowders [with maximum ~4 fold for Ficol-70 at concentration 20% (w/v)], as compared with diluted solutions, but translation was inhibited by each crowder. The authors suggested that the inhibition is due to protein precipitation for PEG solutions and non-specific interaction of Ficoll molecules with translational machinery proteins. The effects of crowding by dextran polymers of 6 kDa and 2 MDa on gene expression was studied in synthetic cellular nano-systems [103]. This study revealed enhancement of the binding rate and decrease of dissociation rate of T7 RNA polymerase for long dextran solutions. Also significant increase of total gene expression rate was observed for long dextran polymers at concentration of 10% (w/v). The crowded systems exhibited higher robustness of gene expression, i.e., less susceptibility to solution composition and concentration of ions. This buffering as an effect of macromolecular crowding was proposed as one of the main factors facilitating response of the cells to osmotic stress [112, 113]. Also increased gene expression efficiency driven by T7 RNAP at intermediate level of crowders was noticed in clay hydrogel [111].

In vivo rate of binding of transcription factor (lac repressor) to the specific site was measured [104, 105] in E. coli. Combination of methods such as single-particle tracking of the fluorescently-labeled repressor, in vivo FCS, and detection by localization [104] revealed that single lac repressor localized its target on the nucleoid in ~6 min, being absorbed with non-specific DNA sites 87% of the search time (diffusion constant of the protein was 0.4 μm²s⁻¹ in cells and was enhanced by the protein without DNA-binding domains to 3.0 μm²s⁻¹). Subsequent studies with double specific sites determined the scale of the correlated motion of the repressor [105]. The results showed that the repressor when bound to DNA scanned 36 base pairs of the nucleoid DNA. In fact, crucial parameters of the facilitated diffusion model of the lac repressor in living prokaryotic cells were determined in these studies.

On the basis of these experiments we calculated the impact of macromolecular crowding [15] inside E. coli cell on transcription factor binding rates to specific sites [114]. We considered multilevel impact of in vivo crowding on association rates to specific sites in the facilitated diffusion model: (1) reduction of the nucleoid volume due to the presence of nucleoid-associated proteins that modify persistence length of DNA and cross-link DNA chains, (2) reduction of transcription factor three- and one-dimensional diffusion constants [15], (3) obstruction of transcription factor binding to non-specific DNA and its sliding due to presence of nucleoid-associated proteins [115–119]. The model predicted the similar binding rate to experimentally observed for cells in the exponential phase of growth. The lac repressor was nearly optimized for binding with respect to association and dissociation rates to/from non-specific DNA. We extrapolated data from lac repressor to all annotated transcription factors in E. coli assuming the same equilibrium binding constants but different diffusivities. The assumption of equal affinities in vivo resulted from the observation of similar values of binding constants to DNA for various transcription factors [104, 120, 121]. Similarity of in vivo equilibrium constants to these determined in dilute solutions [100, 122, 123] additionally poses a question about the effect of excluded volume interactions inside living prokaryotic cells [112]. From the model, we also obtain that the in vivo number of nucleoid-associated proteins affecting nucleoid volume is enough to shrink it to experimentally observed values.

Intracellular macromolecular crowding is also expected to shrink solely the nucleoid to the observed in vivo volume due to purely entropic effects [124, 125]. Indeed, the fast real-time compaction of chromosomes to native volumes [126] is observed in systems crowded by polymers. Our predictions are obtained for exponential phase of growth of E. coli, for which nucleoid is in an expanded state. We look forward to models in which more dense chromosome structures are taken into consideration. One could, for example, consider detailed models of nucleoid compaction [127, 128] and apply them in the studies of transcription factor kinetics. It would be interesting to know how the kinetics changes during the transition to the stationary phase, for which DNA crowding affects transcription factor distribution [129]. The parametrization of the model can be carried out in vivo by the proposed method of extracting diffusion and transition rates from single-molecule experiments [130]. Moreover, in-cell distributions of RNA polymerases and ribosomes are not uniform and there is a strong tendency for occupation of different regions of cell by these complexes [77].

The mechanism of gene regulation in eukaryotes involves many protein factors interacting in concert with active repositioning of nucleosomes [131–133]. Only recently, the kinetics of transcription factors have been studied in eukaryotes [45, 46, 50, 107] revealing basic features of the facilitated diffusion of transcription factors in nuclei. The striking feature, as compared with prokaryotes, is a proportion of the time spent in 3D translocation and in interaction with non-specific DNA during the search process. DNA-bound fraction of glucocorticoid receptor, in MCF-7 breast cancer cell line, is 12% and enhanced to 37% after induction with dexamethasone [45]. Transcription factors Sox2 and Oct4, in mouse embryonic stem cells, spend 18 and 21% of the time [46] being bound with non-specific DNA, respectively. These numbers show that the target search time is dominated by 3D diffusion in mammalian cells. Moreover, the localization time of the single specific site by a single Sox2 protein in the genome, as estimated by Chen et al. [46], is ~31 days. The time is ~7000 times slower than in case of lac repressor in E. coli cell [104]. Taking determined rate constants for Gal4 regulatory protein in Saccharomyces cerevisiae [107] and volume of the nucleus [134] we calculate that the value of the single target localization time is ~14 days. Nuclear environment is markedly distinct and more complex than prokaryotic nucleoid. There is a lack of detailed kinetic models of transcription factor facilitated diffusion in eukaryotes at present. It would be of great interest to establish the impact of the crowding and chromosome structure in nucleus on the transcription factor kinetics.

Many effects are expected to be induced due to decreasing molecule mobility by macromolecular crowding. For example, diffusion of transcription factors is predicted to enhance gene expression noise [135]. The kinetics of translation has been recently studied theoretically in E. coli [136]. The results show that slow diffusion of the tRNA in the crowded milieu of cytoplasm limits translation and consequently growth rate of cells [136]. Intriguingly, the diffusion of macromolecules is predicted to be responsible for prokaryotic and eukaryotic cell sizes [137]; as such, the sizes minimize the times of migration of macromolecules throughout the cells.

3. Conclusions and Future Perspectives

The macromolecular crowding plays important role in key processes in living cells starting from life emergence [111, 138] up to regulation of cell sizes [137]. We have pointed to three different phenomena emerging as a consequence of crowding: the length-scale dependent viscosity, depletion interactions, and non-specific binding.

Quantitative description of interactions inside living cells is currently based on the analysis of free diffusion inside cells. Therefore in our review we emphasize effects of in vivo macromolecular crowding on mobility of the macromolecules and kinetics of interactions between them. We review, according to our knowledge, all studies concerning mobility of molecules in prokaryotic (E. coli) and eukaryotic (HeLa) cells. We show that the cytoplasm has transport property described by the length scale-dependent viscosity. It means that the effective viscosity experienced by moving probes depends on their size [14, 25]. Inside a cell nucleus we expect weakly crowded large water channels (of sizes >30 nm), because most studies show that in a wide range of sizes (4–30 nm) the viscosity is constant in a cell nucleus, only slightly larger than the water viscosity. In lamellar phases of ionic surfactants similar lack of size dependence of viscosity is observed (up to sizes >150 nm) [43]. More experimental studies with larger probes are required to give clear answer about transport properties of proteins in the cell nucleus.

There is a significant difference in the diffusion of proteins between prokaryotic and eukaryotic cells. In eukaryotic cells proteins diffuse as in water, while in prokaryotic cells because of much higher crowding the diffusion coefficient of proteins is much smaller. This property has consequences for the kinetics of protein-protein interactions in prokaryotic cells [86] i.e., none of such reactions would have the same reaction rate as in vitro (buffer) conditions. On the contrary in the cytoplasm of eukaryotic cells we expect that the reaction rates for protein-protein association should be similar to those measured in water.

Our review also shows the importance of non-specific interactions with cytoplasm constituents for the interpretation of the impact of macromolecular crowding on biochemical reactions [20, 84]. Non-monotonic changes of reaction rates of DNA hybridization [84] and destabilization of the protein [20] can be explained only by direct interactions with cytoplasm components. Non-specific interactions of transcription factors with DNA affect the search process for operators [99]. Without those interactions LacI repressor should find its target (one base pair, since TF shift in position by one base pair results in distinct DNA binding sequence [99, 116]) in a volume of E. coli in 7 s. In vivo and in the model including binding of LacI to non-specific sequences of DNA this time is 400 s. Thus, identification of strong non-specific interactions is important in the study of the influence of crowding environment on biological processes. Mobility data including the length-scale dependent viscosity are helpful in such identification e.g., by comparison of the motion of inert probe to the motion of the probe of interest of similar size. Any differences in their motion would be a signature of interactions with cellular components.

Lot of attention was devoted to depletion interactions in crowded solutions [1, 8, 16–18]. Two similar objects, immersed in solutions of solutes different in size and shape from them, attract each other. Such interaction is called the depletion interaction. The strength of the depletion interactions is calculated from the osmotic pressure of the solutions multiplied by the excluded volume between the object and the solute particle. For proteins in flexible polymer solutions this non-specific interaction is particularly strong. For 12% of PEG (M_w = 6 kg/mol) solution the osmotic pressure is of the order of 10⁵ Pa and the excluded volume in the range of tens of nm³. Thus, typical free energy change upon binding of two colloidal particles in the polymer solution is several kJ/mol. The depletion interactions strongly depend on the shape of studied molecules, change of excluded volume upon binding and incorporation of solvent to the models [17]. For protein solutions the effect is probably small because all molecules have similar shape. Therefore, we do not expect in the cytoplasm strong depletion interactions. However denaturated proteins could in principle exert stronger depletion effect in protein solutions.

Interpretation of in vivo protein-protein kinetic studies requires understanding of in-cytoplasm rotational diffusion (inversely proportional to rotational viscosity) of proteins [11, 85, 86]. Proteins upon binding have to be oriented properly with respect to each other. Typical time for proper alignment of reactive patches on proteins necessary for complex formation depends on rotations of proteins. The impact of crowding on protein rotation and rotational viscosity is expected to be significant in prokaryotic cells for which ξ is an order of magnitude smaller than the typical size of proteins. The Brownian dynamics studies [89] of the model cytoplasm of E. coli crowded only by proteins show that the rotational viscosity does not change much with the increase of protein molecular weight. On average this viscosity is 10 times larger than the viscosity of water, but smaller than the length scale dependent viscosity characterizing translational motion. This difference between rotational and translational viscosity is not unphysical and arises as a consequence of depletion. The rotational viscosity is always smaller than the translational viscosity because in a crowded environment the excluded volume effects and depletion are ubiquitous. The depletion layer i.e., a layer around a particle depleted from other particles (e.g., observed for colloids in polymer solutions) leads to non-uniform viscosity around the particle [139–146]. The viscosity changes from the solvent viscosity close to the surface of an object to the solution viscosity in a bulk solution over a short distance of the depletion layer (usually of the order of 0.1 to few nm). Roughly speaking the rotations of molecule experience the local solvent or almost solvent viscosity while translations the one of the solution. What remains to be investigated is how hydrodynamic long-range interactions affect the rotations of macromolecules [90, 91, 147]. Certainly, the most urgent are experimental studies of the rotational diffusion constants as a function of protein shapes and sizes in cytoplasm of living cells or cell extracts [148].

Kinetics of gene expression and its regulation in living cells has been studied only within last decade. The detailed picture of the regulation kinetics is available only for lac repressor in E. coli [104–106]. The existing models, taking intracellular crowding into account and all existing experimental data show that this transcription factor is nearly optimized for its function [105, 114, 116]. We look forward to studies of gene regulation kinetics of other transcription factors to check generalization of the predictions in prokaryotes and detailed models of facilitated diffusion in eukaryotes.

Author Contributions

All authors contribute in manuscript writing, Marcin Tabaka and Tomasz Kalwarczyk contribute equally.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported from the sources of the National Science Centre according to the decision number DEC-2013/08/W/NZ1/00687 (SYMFONIA grant). Sen Hou and Robert Holyst acknowledge the collaboration with the State Key Laboratory of Medicinal Chemical Biology, Nankai University, Tianjin, China within the Grant No. 20130301.

References

1. Minton AP. The effect of volume occupancy upon the thermodynamic activity of proteins: some biochemical consequences. Mol Cell Bioch. (1983) 55:119–40. doi: 10.1007/BF00673707

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

2. Zimmerman SB, Minton AP. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu Rev Bioph Biom. (1993) 22:27–65. doi: 10.1146/annurev.bb.22.060193.000331

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

3. Minton AP. Implications of macromolecular crowding for protein assembly. Curr Opin Struct Biol. (2000) 10:34–9. doi: 10.1016/S0959-440X(99)00045-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

4. Minton AP. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J Biol Chem. (2001) 276:10577–80. doi: 10.1074/jbc.R100005200

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

5. Ellis RJ. Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr Opin Sruc Biol. (2001) 11:114–9. doi: 10.1016/S0959-440X(00)00172-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

6. Ellis RJ. Macromolecular crowding: obvious but underappreciated. Trends Biochem Sci. (2001) 26:597–604. doi: 10.1016/S0968-0004(01)01938-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

7. Minton AP. Influence of macromolecular crowding upon the stability and state of association of proteins: predictions and observations. J Pharm Sci. (2005) 94:1668–75. doi: 10.1002/jps.20417

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

8. Zhou HX, Rivas G, Minton AP. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Ann Rev Biophys. (2008) 37:375–97. doi: 10.1146/annurev.biophys.37.032807.125817

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

9. Minton AP. Quantitative assessment of the relative contributions of steric repulsion and chemical interactions to macromolecular crowding. Biopolymers (2013) 99:239–44. doi: 10.1002/bip.22163

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

10. Zhou HX. Influence of crowded cellular environments on protein folding, binding, and oligomerization: biological consequences and potentials of atomistic modeling. FEBS Lett. (2013) 587:1053–61. doi: 10.1016/j.febslet.2013.01.064

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

11. Phillip Y, Schreiber G. Formation of protein complexes in crowded environments–from in vitro to in vivo. FEBS Lett. (2013) 587:1046–52. doi: 10.1016/j.febslet.2013.01.007

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

12. Elowitz M, Surette M, Wolf P, Stock J, Leibler S. Protein mobility in the cytoplasm of Escherichia coli. J Bacteriol. (1999) 181:197–203.

Pubmed Abstract | Pubmed Full Text

13. Mika JT, van den Bogaart G, Veenhoff L, Krasnikov V, Poolman B. Molecular sieving properties of the cytoplasm of Escherichia coli and consequences of osmotic stress. Mol Microbiol. (2010) 77:200–7. doi: 10.1111/j.1365-2958.2010.07201.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

14. Kalwarczyk T, Ziebacz N, Bielejewska A, Zaboklicka E, Koynov K, Szymanski J, et al. Comparative analysis of viscosity of complex liquids and cytoplasm of mammalian cells at the nanoscale. Nano Lett. (2011) 11:2157–63. doi: 10.1021/nl2008218

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

15. Kalwarczyk T, Tabaka M, Holyst R. Biologistics-Diffusion Coefficients For Complete Proteome Of Escherichia coli [Article]. Bioinformatics (2012) 28:2971–8. doi: 10.1093/bioinformatics/bts537

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

16. Asakura S, Oosawa F. On interaction between 2 bodies immersed in a solution of macromolecules. J Chem Phys. (1954) 22:1255–6. doi: 10.1063/1.1740347

CrossRef Full Text

17. Berg OG. The influence of macromolecular crowding on thermodynamic activity: solubility and dimerization constants for spherical and dumbbell-shaped molecules in a hard-sphere mixture. Biopolymers (1990) 30:1027–37. doi: 10.1002/bip.360301104

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

18. Marenduzzo D, Finan K, Cook PR. The depletion attraction: an underappreciated force driving cellular organization. J Cell Biol. (2006) 175:681–6. doi: 10.1083/jcb.200609066

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

19. Sarkar M, Li C, Pielak GJ. Soft interactions and crowding. Biophys Rev. (2013) 5:187–94. doi: 10.1007/s12551-013-0104-4

CrossRef Full Text

20. Sarkar M, Smith AE, Pielak GJ. Impact of reconstituted cytosol on protein stability. Proc Natl Acad Sci USA. (2013) 110:19342–7. doi: 10.1073/pnas.1312678110

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

21. Mika JT, Poolman B. Macromolecule diffusion and confinement in prokaryotic cells. Curr Opin Biotechnol. (2011) 22:117–26. doi: 10.1016/j.copbio.2010.09.009

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

22. Elcock AH. Models of macromolecular crowding effects and the need for quantitative comparisons with experiment. Curr Opin Struct Biol. (2010) 20:196–206. doi: 10.1016/j.sbi.2010.01.008

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

23. Frembgen-Kesner T, Elcock AH. Computer simulations of the bacterial cytoplasm. Biophys Rev. (2013) 5:109–19. doi: 10.1007/s12551-013-0110-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

24. Theillet FX, Binolfi A, Frembgen-Kesner T, Hingorani K, Sarkar M, Kyne C, et al. Physicochemical properties of cells and their effects on Intrinsically Disordered Proteins (IDPs). Chem Rev. (2014) 114:6661–714. doi: 10.1021/cr400695p

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

25. Holyst R, Bielejewska A, Szymański J, Wilk A, Patkowski A, Gapiński J, et al. Scaling form of viscosity at all length-scales in poly (ethylene glycol) solutions studied by fluorescence correlation spectroscopy and capillary electrophoresis. Phys Chem Chem Phys. (2009) 11:9025–32. doi: 10.1039/b908386c

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

26. Kalwarczyk T, Sozanski K, Jakiela S, Wisniewska A, Kalwarczyk E, Kryszczuk K, et al. Length-scale dependent transport properties of colloidal and protein solutions for prediction of crystal nucleation rates. Nanoscale (2014) 6:10340–6. doi: 10.1039/C4NR00647J

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

27. Sozanski K, Wisniewska A, Kalwarczyk T, Holyst R. Activation energy for mobility of dyes and proteins in polymer solutions: from diffusion of single particles to macroscale flow. Phys Rev Lett. (2013) 111:228301. doi: 10.1103/PhysRevLett.111.228301

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

28. Zhou EH, Martinez FD, Fredberg JJ. Cell rheology: mush rather than machine. Nat Mater. (2013) 12:184–5. doi: 10.1038/nmat3574

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

29. Moeendarbary E, Valon L, Fritzsche M, Harris AR, Moulding DA, Thrasher AJ, et al. The cytoplasm of living cells behaves as a poroelastic material. Nat Mater. (2013) 12:253–61. doi: 10.1038/nmat3517

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

30. Luby-Phelps K, Castle P, Taylor D, Lanni F. Hindered diffusion of inert tracer particles in the cytoplasm of mouse 3T3 cells. Proc Natl Acad Sci USA. (1987) 84:4910–3. doi: 10.1073/pnas.84.14.4910

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

31. Nakane Y, Sasaki A, Kinjo M, Jin T. Bovine serum albumin-coated quantum dots as a cytoplasmic viscosity probe in a single living cell. Anal Methods (2012) 4:1903–5. doi: 10.1039/c2ay25318f

CrossRef Full Text

32. Reuel NF, Dupont A, Thouvenin O, Lamb DC, Strano MS. Three-dimensional tracking of carbon nanotubes within living cells. ACS Nano (2012) 6:5420–8. doi: 10.1021/nn301298e

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

33. Daddysman MK, Fecko CJ. Revisiting point FRAP to quantitatively characterize anomalous diffusion in live cells. J Phys Chem B (2013) 117:1241–51. doi: 10.1021/jp310348s

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

34. Kloster-Landsberg M, Tyndall D, Wang I, Walker R, Richardson J, Henderson R, et al. Note: multi-confocal fluorescence correlation spectroscopy in living cells using a complementary metal oxide semiconductor-single photon avalanche diode array. Rev Sci Instrum. (2013) 84:076105. doi: 10.1063/1.4816156

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

35. Poot M, Kavanagh TJ, Kang HC, Haugland RP, Rabinovitch PS. Flow cytometric analysis of cell cycle-dependent changes in cell thiol level by combining a new laser dye with hoechst 33342. Cytometry (1991) 12:184–7. doi: 10.1002/cyto.990120214

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

36. Zhang YZ, Olson N, Mao F, Roth B, Haugland RP. New fluorescent probes for long-term tracing of living cells. FASEB J. (1992) 6:A1835.

Pubmed Abstract | Pubmed Full Text

37. Kornberg RD. Chromatin structure: a repeating unit of histones and DNA. Science (1974) 184:868–71. doi: 10.1126/science.184.4139.868

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

38. Cremer T, Cremer C. Chromosome territories, nuclear architecture and gene regulation in mammalian cells. Nat Rev Genet. (2001) 2:292–301. doi: 10.1038/35066075

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

39. Hou C, Li L, Qin ZS, Corces VG. Gene density, transcription, and insulators contribute to the partition of the drosophila genome into physical domains. Mol Cell (2012) 48:471–84. doi: 10.1016/j.molcel.2012.08.031

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

40. Seksek O, Biwersi J, Verkman A. Translational diffusion of macromolecule-sized solutes in cytoplasm and nucleus. J Cell Biol. (1997) 138:131–42. doi: 10.1083/jcb.138.1.131

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

41. Politz JC, Tuft RA, Pederson T, Singer RH. Movement of nuclear poly(A) RNA throughout the interchromatin space in living cells. Curr Biol. (1999) 9:285–91. doi: 10.1016/S0960-9822(99)80136-5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

42. Lukacs G, Haggie P, Seksek O, Lechardeur D, Freedman N, Verkman A. Size-dependent DNA mobility in cytoplasm and nucleus. J Biol Chem. (2000) 275:1625–9. doi: 10.1074/jbc.275.3.1625

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

43. Szymański J, Wilk A, Hołyst R, Roberts G, Sinclair K, Kowalski A. Micro-and macro-shear viscosity in dispersed lamellar phases. J Non-Newton Fluid. (2008) 148:134–40. doi: 10.1016/j.jnnfm.2007.04.008

CrossRef Full Text

44. Phair RD, Misteli T. High mobility of proteins in the mammalian cell nucleus. Nature (2000) 404:604–9. doi: 10.1038/35007077

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

45. Gebhardt JCM, Suter DM, Roy R, Zhao ZW, Chapman AR, Basu S, et al. Single-molecule imaging of transcription factor binding to DNA in live mammalian cells. Nat Methods (2013) 10:421–6. doi: 10.1038/nmeth.2411

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

46. Chen J, Zhang Z, Li L, Chen BC, Revyakin A, Hajj B, et al. Single-molecule dynamics of enhanceosome assembly in embryonic stem cells. Cell (2014) 156:1274–85. doi: 10.1016/j.cell.2014.01.062

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

47. Speil J, Baumgart E, Siebrasse JP, Veith R, Vinkemeier U, Kubitscheck U. Activated STAT1 transcription factors conduct distinct saltatory movements in the cell nucleus. Biophys J. (2011) 101:2592–600. doi: 10.1016/j.bpj.2011.10.006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

48. Mazza D, Abernathy A, Golob N, Morisaki T, McNally JG. A benchmark for chromatin binding measurements in live cells. Nucl Acids Res. (2012) 40:e119. doi: 10.1093/nar/gks701

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

49. Wachsmuth M, Waldeck W, Langowski J. Anomalous diffusion of fluorescent probes inside living cell nuclei investigated by spatially-resolved fluorescence correlation spectroscopy. J Mol Biol. (2000) 298:677–89. doi: 10.1006/jmbi.2000.3692

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

50. Vukojević V, Papadopoulos DK, Terenius L, Gehring WJ, Rigler R. Quantitative study of synthetic Hox transcription factor–DNA interactions in live cells. Proc Natl Acad Sci USA. (2010) 107:4093–8. doi: 10.1073/pnas.0914612107

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

51. Szymanski J, Weiss M. Elucidating the origin of anomalous diffusion in crowded fluids. Phys Rev Lett. (2009) 103:038102. doi: 10.1103/PhysRevLett.103.038102

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

52. Ernst D, Köhler J, Weiss M. Probing the type of anomalous diffusion with single-particle tracking. Phys Chem Chem Phys. (2014) 16:7686–91. doi: 10.1039/c4cp00292j

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

53. Szymanski J, Patkowski A, Gapinski J, Wilk A, Holyst R. Movement of proteins in an environment crowded by surfactant micelles: anomalous versus normal diffusion. J Phys Chem B (2006) 110:7367–73. doi: 10.1021/jp055626w

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

54. Szymanski J, Mayer C, Hoffmann-Rohrer U, Kalla C, Grummt I, Weiss M. Dynamic subcellular partitioning of the nucleolar transcription factor TIF-IA under ribotoxic stress. BBA-Mol Cell Res. (2009) 1793:1191–8. doi: 10.1016/j.bbamcr.2009.05.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

55. Guigas G, Kalla C, Weiss M. The degree of macromolecular crowding in the cytoplasm and nucleoplasm of mammalian cells is conserved. FEBS Lett. (2007) 581:5094–8. doi: 10.1016/j.febslet.2007.09.054

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

56. Dross N, Spriet C, Zwerger M, Müller G, Waldeck W, Langowski J. Mapping eGFP oligomer mobility in living cell nuclei. PLoS ONE (2009) 4:e5041. doi: 10.1371/journal.pone.0005041

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

57. Bancaud A, Huet S, Daigle N, Mozziconacci J, Beaudouin J, Ellenberg J. Molecular crowding affects diffusion and binding of nuclear proteins in heterochromatin and reveals the fractal organization of chromatin. EMBO J. (2009) 28:3785–98. doi: 10.1038/emboj.2009.340

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

58. Politz JC, Browne ES, Wolf DE, Pederson T. Intranuclear diffusion and hybridization state of oligonucleotides measured by fluorescence correlation spectroscopy in living cells. Proc Natl Acad Sci USA. (1998) 95:6043–8. doi: 10.1073/pnas.95.11.6043

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

59. Hinde E, Cardarelli F, Digman MA, Gratton E. In vivo pair correlation analysis of EGFP intranuclear diffusion reveals DNA-dependent molecular flow. Proc Natl Acad Sci USA. (2010) 107:16560–5. doi: 10.1073/pnas.1006731107

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

60. Capoulade J, Wachsmuth M, Hufnagel L, Knop M. Quantitative fluorescence imaging of protein diffusion and interaction in living cells. Nat Biotechnol. (2011) 29:835–9. doi: 10.1038/nbt.1928

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

61. Ioan C, Aberle T, Burchard W. Structure properties of dextran. 2. Dilute solution. Macromolecules (2000) 33:5730–9. doi: 10.1021/ma000282n

CrossRef Full Text

62. Hancock R, Jeon KW. New Models of the Cell Nucleus: Crowding, Entropic Forces, Phase Separation, and Fractals. San Diego: Academic Press (2013).

63. Schuldt A. The dynamic nucleus. Nat Rev Mol Cell Biol. (2010) 11:678–9. doi: 10.1038/nrm2983

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

64. Gorski SA, Dundr M, Misteli T. The road much traveled: trafficking in the cell nucleus. Curr Opin Cell Biol. (2006) 18:284–90. doi: 10.1016/j.ceb.2006.03.002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

65. Kumar M, Mommer MS, Sourjik V. Mobility of cytoplasmic, membrane, and DNA-binding proteins in Escherichia coli. Biophys J. (2010) 98:552–9. doi: 10.1016/j.bpj.2009.11.002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

66. Cluzel P, Surette M, Leibler S. An ultrasensitive bacterial motor revealed by monitoring signaling proteins in single cells. Science (2000) 287:1652–5. doi: 10.1126/science.287.5458.1652

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

67. Mullineaux C, Nenninger A, Ray N, Robinson C. Diffusion of green fluorescent protein in three cell environments in Escherichia coli. J Bacteriol. (2006) 188:3442–8. doi: 10.1128/JB.188.10.3442-3448.2006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

68. van den Bogaart G, Hermans N, Krasnikov V, Poolman B. Protein mobility and diffusive barriers in Escherichia coli: consequences of osmotic stress. Mol. Microbiol. (2007) 64:858–71. doi: 10.1111/j.1365-2958.2007.05705.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

69. Slade KM, Steele BL, Pielak GJ, Thompson NL. Quantifying green fluorescent protein diffusion in Escherichia coli by using continuous photobleaching with evanescent illumination. J Phys Chem B (2009) 113:4837–45. doi: 10.1021/jp810642d

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

70. Nenninger A, Mastroianni G, Mullineaux CW. Size dependence of protein diffusion in the cytoplasm of Escherichia coli. J Bacteriol. (2010) 192:4535–40. doi: 10.1128/JB.00284-10

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

71. Konopka MC, Shkel IA, Cayley S, Record MT, Weisshaar JC. Crowding and confinement effects on protein diffusion in vivo. J Bacteriol. (2006) 188:6115–23. doi: 10.1128/JB.01982-05

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

72. Derman AI, Lim-Fong G, Pogliano J. Intracellular mobility of plasmid DNA is limited by the ParA family of partitioning systems. Mol Microbiol. (2008) 67:935–46. doi: 10.1111/j.1365-2958.2007.06066.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

73. Jasnin M, Moulin M, Haertlein M, Zaccai G, Tehei M. Down to atomic-scale intracellular water dynamics. EMBO Rep. (2008) 9:543–7. doi: 10.1038/embor.2008.50

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

74. Golding I, Cox EC. RNA dynamics in live Escherichia coli cells. Proc Natl Acad Sci USA (2004) 101:11310–5. doi: 10.1073/pnas.0404443101

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

75. Campbell CS, Mullins RD. In vivo visualization of type II plasmid segregation: bacterial actin filaments pushing plasmids. J Cell Biol. (2007) 179:1059–66. doi: 10.1083/jcb.200708206

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

76. English BP, Hauryliuk V, Sanamrad A, Tankov S, Dekker NH, Elf J. Single-molecule investigations of the stringent response machinery in living bacterial cells. Proc Natl Acad Sci USA (2011) 108:E365–73. doi: 10.1073/pnas.1102255108

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

77. Bakshi S, Siryaporn A, Goulian M, Weisshaar JC. Superresolution imaging of ribosomes and RNA polymerase in live Escherichia coli cells. Mol Microbiol. (2012) 85:21–38. doi: 10.1111/j.1365-2958.2012.08081.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

78. Coquel AS, Jacob JP, Primet M, Demarez A, Dimiccoli M, Julou T, et al. Localization of protein aggregation in Escherichia coli is governed by diffusion and nucleoid macromolecular crowding effect. PLoS Comput Biol. (2013) 9:e1003038. doi: 10.1371/journal.pcbi.1003038

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

79. Golding I, Cox E. Physical nature of bacterial cytoplasm. Phys Rev Lett. (2006) 96:098102. doi: 10.1103/PhysRevLett.96.098102

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

80. Weber SC, Spakowitz AJ, Theriot JA. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Phys Rev Lett. (2010) 104:238102. doi: 10.1103/PhysRevLett.104.238102

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

81. Weber SC, Spakowitz AJ, Theriot JA. Nonthermal ATP-dependent fluctuations contribute to the in vivo motion of chromosomal loci. Proc Natl Acad Sci USA (2012) 109:7338–43. doi: 10.1073/pnas.1119505109

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

82. Parry BR, Surovtsev IV, Cabeen MT, O'Hern CS, Dufresne ER, Jacobs-Wagner C. The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity. Cell (2014) 156:183–94. doi: 10.1016/j.cell.2013.11.028

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

83. Weber SC, Theriot JA, Spakowitz AJ. Subdiffusive motion of a polymer composed of subdiffusive monomers. Phys Rev E (2010) 82:011913. doi: 10.1103/PhysRevE.82.011913

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

84. Schoen I, Krammer H, Braun D. Hybridization kinetics is different inside cells. Proc Nat Acad Sci USA (2009) 106:21649–54. doi: 10.1073/pnas.0901313106

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

85. Phillip Y, Kiss V, Schreiber G. Protein-binding dynamics imaged in a living cell. Proc Natl Acad Sci USA (2012) 109:1461–6. doi: 10.1073/pnas.1112171109

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

86. Tabaka M, Sun L, Kalwarczyk T, Holyst R. Implications of macromolecular crowding for protein–protein association kinetics in the cytoplasm of living cells. Soft Matt. (2013) 9:4386–9. doi: 10.1039/c3sm00013c

CrossRef Full Text

87. Zhou HX. Brownian dynamics study of the influences of electrostatic interaction and diffusion on protein-protein association kinetics. Biophys J. (1993) 64:1711–26. doi: 10.1016/S0006-3495(93)81543-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

88. Swaminathan R, Hoang C, Verkman A. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys J. (1997) 72:1900–7. doi: 10.1016/S0006-3495(97)78835-0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

89. McGuffee SR, Elcock AH. Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput Biol. (2010) 6:e1000694. doi: 10.1371/journal.pcbi.1000694

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

90. Mereghetti P, Wade RC. Atomic detail brownian dynamics simulations of concentrated protein solutions with a mean field treatment of hydrodynamic interactions. J Phys Chem B (2012) 116:8523–33. doi: 10.1021/jp212532h

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

91. Dlugosz M, Antosiewicz JM. Evaluation of proteins' rotational diffusion coefficients from simulations of their free Brownian motion in volume-occupied environments. J Chem Theor Comput. (2014) 10:481–91. doi: 10.1021/ct4008519

CrossRef Full Text

92. Zhou HX. Polymer crowders and protein crowders act similarly on protein folding stability. FEBS Lett. (2013) 587:394–7. doi: 10.1016/j.febslet.2013.01.030

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

93. Hou S, Ziebacz N, Kalwarczyk T, Kaminski TS, Wieczorek SA, Holyst R. Influence of nano-viscosity and depletion interactions on cleavage of DNA by enzymes in glycerol and poly(ethylene glycol) solutions: qualitative analysis. Soft Matter. (2011) 7:3092–9. doi: 10.1039/c0sm00899k

CrossRef Full Text

94. Demyanchuk I, Staniszewski K, Holyst R. Coalescence-induced coalescence and dimensional crossover during the phase separation in ternary surfactant/polymer/water mixtures. J Phys Chem B (2005) 109:4419–24. doi: 10.1021/jp0455834

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

95. Kalwarczyk T, Ziebacz N, Fialkowski M, Holyst R. Late stage of the phase-separation process: coalescence-induced coalescence, gravitational sedimentation, and collective evaporation mechanisms. Langmuir (2008) 24:6433–40. doi: 10.1021/la704003q

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

96. Hołyst R. Some features of soft matter systems. Soft Matter. (2005) 1:329–33. doi: 10.1039/b509105e

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

97. Holyst R, Staniszewski K, Demyanchuk I. Ordering in surfactant mixtures induced by polymers. J Phys Chem B (2005) 109:4881–6. doi: 10.1021/jp045226t

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

98. Lis JT, Schleif R. Size fractionation of double-stranded DNA by precipitation with polyethylene glycol. Nucl Acids Res. (1975) 2:383–90. doi: 10.1093/nar/2.3.383

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

99. Berg OG, Winter RB, von Hippel PH. Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory. Biochemistry (1981) 20:6929–48. doi: 10.1021/bi00527a028

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

100. Winter RB, Berg OG, von Hippel PH. Diffusion-driven mechanisms of protein translocation on nucleic acids. 3. The Escherichia coli lac repressor–operator interaction: kinetic measurements and conclusions. Biochemistry (1981) 20:6961–77. doi: 10.1021/bi00527a030

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

101. von Hippel PH, Berg OG. Facilitated target location in biological systems. J Biol Chem. (1989) 264:675–8.

Pubmed Abstract | Pubmed Full Text

102. Ge X, Luo D, Xu J. Cell-free protein expression under macromolecular crowding conditions. PLoS ONE (2011) 6:e28707. doi: 10.1371/journal.pone.0028707

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

103. Tan C, Saurabh S, Bruchez MP, Schwartz R, Leduc P. Molecular crowding shapes gene expression in synthetic cellular nanosystems. Nat Nanotechnol. (2013) 8:602–8. doi: 10.1038/nnano.2013.132

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

104. Elf J, Li GW, Xie XS. Probing transcription factor dynamics at the single-molecule level in a living cell. Science (2007) 316:1191–4. doi: 10.1126/science.1141967

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

105. Hammar P, Leroy P, Mahmutovic A, Marklund EG, Berg OG, Elf J. The lac repressor displays facilitated diffusion in living cells. Science (2012) 336:1595–8. doi: 10.1126/science.1221648

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

106. Hammar P, Walldén M, Fange D, Persson F, Baltekin Ö, Ullman G, et al. Direct measurement of transcription factor dissociation excludes a simple operator occupancy model for gene regulation. Nat Genet. (2014) 46:405–8. doi: 10.1038/ng.2905

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

107. Poorey K, Viswanathan R, Carver MN, Karpova TS, Cirimotich SM, McNally JG, et al. Measuring chromatin interaction dynamics on the second time scale at single-copy genes. Science (2013) 342:369–72. doi: 10.1126/science.1242369

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

108. Morelli MJ, Allen RJ, Wolde PR. Effects of macromolecular crowding on genetic networks. Biophys J. (2011) 101:2882–91. doi: 10.1016/j.bpj.2011.10.053

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

109. Adair G. A theory of partial osmotic pressures and membrane equilibria, with special reference to the application of Dalton's law to haemoglobin solutions in the presence of salts. Proc R Soc Lond A (1928) 120:573–603. doi: 10.1098/rspa.1928.0167

CrossRef Full Text

110. Matsuda H, Putzel GG, Backman V, Szleifer I. Macromolecular Crowding as a Regulator of Gene Transcription. Biophys J. (2014) 106:1801–10. doi: 10.1016/j.bpj.2014.02.019

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

111. Yang D, Peng S, Hartman MR, Gupton-Campolongo T, Rice EJ, Chang AK, et al. Enhanced transcription and translation in clay hydrogel and implications for early life evolution. Sci Rep. (2013) 3:3165. doi: 10.1038/srep03165

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

112. Zimmerman SB, Trach SO. Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli. J Mol Biol. (1991) 222:599–620. doi: 10.1016/0022-2836(91)90499-V

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

113. Record MT Jr., Courtenay ES, Cayley S, Guttman HJ. Biophysical compensation mechanisms buffering E. coli protein–nucleic acid interactions against changing environments. Trends Biochem Sci. (1998) 23:190–94. doi: 10.1016/S0968-0004(98)01207-9

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

114. Tabaka M, Kalwarczyk T, Hołyst R. Quantitative influence of macromolecular crowding on gene regulation kinetics. Nucleic Acids Res. (2014) 42:727–38. doi: 10.1093/nar/gkt907

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

115. Flyvbjerg H, Keatch SA, Dryden DTF. Strong physical constraints on sequence-specific target location by proteins on DNA molecules. Nucleic Acids Res. (2006) 34:2550–7. doi: 10.1093/nar/gkl271

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

116. Li GW, Berg OG, Elf J. Effects of macromolecular crowding and DNA looping on gene regulation kinetics. Nat Phys. (2009) 5:294–7. doi: 10.1038/nphys1222

CrossRef Full Text

117. Murugan R. Theory of site-specific interactions of the combinatorial transcription factors with DNA. J Phys A (2010) 43:195003. doi: 10.1088/1751-8113/43/19/195003

CrossRef Full Text

118. Zabet NR, Adryan B. The effects of transcription factor competition on gene regulation. Front Genet. (2013) 4:197. doi: 10.3389/fgene.2013.00197

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

119. Marcovitz A, Levy Y. Obstacles may facilitate and direct DNA search by proteins. Biophys J. (2013) 104:2042–50. doi: 10.1016/j.bpj.2013.03.030

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

120. Kao-Huang Y, Revzin A, Butler AP, O'Conner P, Noble DW, Von Hippel PH. Nonspecific DNA binding of genome-regulating proteins as a biological control mechanism: measurement of DNA-bound Escherichia coli lac repressor in vivo. Proc Natl Acad Sci USA (1977) 74:4228–32. doi: 10.1073/pnas.74.10.4228

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

121. Bakk A, Metzler R. In vivo non-specific binding of lambda CI and Cro repressors is significant. FEBS Lett. (2004) 563:66–8. doi: 10.1016/S0014-5793(04)00249-2

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

122. DeHaseth PL, Lohman TM, Burgess RR, Record MT Jr. Nonspecific interactions of Escherichia coli RNA polymerase with native and denatured DNA: differences in the binding behavior of core and holoenzyme. Biochemistry (1978) 17:1612–22. doi: 10.1021/bi00602a006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

123. Kalodimos CG, Biris N, Bonvin AM, Levandoski MM, Guennuegues M, Boelens R, et al. Structure and flexibility adaptation in nonspecific and specific protein-DNA complexes. Science (2004) 305:386–9. doi: 10.1126/science.1097064

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

124. Zimmerman SB, Murphy LD. Macromolecular crowding and the mandatory condensation of DNA in bacteria. FEBS Lett. (1996) 390:245–8. doi: 10.1016/0014-5793(96)00725-9

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

125. Jun S, Wright A. Entropy as the driver of chromosome segregation. Nat Rev Microbiol. (2010) 8:600–7. doi: 10.1038/nrmicro2391

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

126. Pelletier J, Halvorsen K, Ha BY, Paparcone R, Sandler SJ, Woldringh CL, et al. Physical manipulation of the Escherichia coli chromosome reveals its soft nature. Proc Natl Acad Sci USA (2012) 109:E2649–56. doi: 10.1073/pnas.1208689109

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

127. Wiggins PA, Cheveralls KC, Martin JS, Lintner R, Kondev J. Strong intranucleoid interactions organize the Escherichia coli chromosome into a nucleoid filament. Proc Natl Acad Sci USA (2010) 107:4991–5. doi: 10.1073/pnas.0912062107

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

128. Fritsche M, Li S, Heermann DW, Wiggins PA. A model for Escherichia coli chromosome packaging supports transcription factor-induced DNA domain formation. Nucleic Acids Res (2012) 40:972–80. doi: 10.1093/nar/gkr779

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

129. Kuhlman TE, Cox EC. Gene location and DNA density determine transcription factor distributions in Escherichia coli. Mol Syst Biol. (2012) 8:610. doi: 10.1038/msb.2012.42

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

130. Persson F, Lindén M, Unoson C, Elf J. Extracting intracellular diffusive states and transition rates from single-molecule tracking data. Nat Methods (2013) 10:265–9. doi: 10.1038/nmeth.2367

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

131. Kaplan N, Moore I, Fondufe-Mittendorf Y, Gossett AJ, Tillo D, Field Y, et al. Nucleosome sequence preferences influence in vivo nucleosome organization. Nat Struct Mol Biol. (2010) 17:918–20. doi: 10.1038/nsmb0810-918

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

132. Struhl K, Segal E. Determinants of nucleosome positioning. Nat Struct Mol Biol. (2013) 20:267–73. doi: 10.1038/nsmb.2506

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

133. Weingarten-Gabbay S, Segal E. The grammar of transcriptional regulation. Hum Genet. (2014) 133:701–11. doi: 10.1007/s00439-013-1413-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

134. Jorgensen P, Edgington NP, Schneider BL, Rupeš I, Tyers M, Futcher B. The size of the nucleus increases as yeast cells grow. Mol Biol Cell (2007) 18:3523–32. doi: 10.1091/mbc.E06-10-0973

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

135. van Zon JS, Morelli MJ, Tanase-Nicola S, ten Wolde PR. Diffusion of transcription factors can drastically enhance the noise in gene expression. Biophys J. (2006) 91:4350–67. doi: 10.1529/biophysj.106.086157

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

136. Klumpp S, Scott M, Pedersen S, Hwa T. Molecular crowding limits translation and cell growth. Proc Natl Acad Sci USA (2013) 110:16754–9. doi: 10.1073/pnas.1310377110

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

137. Soh S, Banaszak M, Kandere-Grzybowska K, Grzybowski BA. Why cells are microscopic: a transport-time perspective. J Phys Chem Lett. (2013) 4:861–5. doi: 10.1021/jz3019379

CrossRef Full Text

138. Spitzer J, Poolman B. The role of biomacromolecular crowding, ionic strength, and physicochemical gradients in the complexities of life's emergence. Microbiol Mol Biol R (2009) 73:371–88. doi: 10.1128/MMBR.00010-09

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

139. Fleer G, Skvortsov A, Tuinier R. Mean-field equation for the depletion thickness. Macromolecules (2003) 36:7857–72. doi: 10.1021/ma0345145

CrossRef Full Text

140. Kuttner YY, Kozer N, Segal E, Schreiber G, Haran G. Separating the contribution of translational and rotational diffusion to protein association. J Am Chem Soc. (2005) 127:15138–44. doi: 10.1021/ja053681c

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

141. Tuinier R, Dhont J, Fan TH. How depletion affects sphere motion through solutions containing macromolecules. Europhys Lett. (2006) 75:929. doi: 10.1209/epl/i2006-10200-0

CrossRef Full Text

142. Fan TH, Dhont JKG, Tuinier R. Motion of a sphere through a polymer solution. Phys Rev E (2007) 75:(1 Pt 1). doi: 10.1103/PhysRevE.75.011803

CrossRef Full Text

143. Tuinier R, Fan TH. Scaling of nanoparticle retardation in semi-dilute polymer solutions. Soft Matter. (2008) 4:254–7. doi: 10.1039/b711902j

CrossRef Full Text

144. Lekkerkerker HN, Tuinier R. Colloids and the Depletion Interaction. Dordrecht: Springer (2011) 833:233. doi: 10.1007/978-94-007-1223-2

CrossRef Full Text

145. Ochab-Marcinek A, Holyst R. Scale-dependent diffusion of spheres in solutions of flexible and rigid polymers: mean square displacement and autocorrelation function for FCS and DLS measurements. Soft Matter. (2011) 7:7366–74. doi: 10.1039/c1sm05217a

CrossRef Full Text

146. Ochab-Marcinek A, Wieczorek SA, Ziebacz N, Holyst R. The effect of depletion layer on diffusion of nanoparticles in solutions of flexible and polydisperse polymers. Soft Matter. (2012) 8:11173–9. doi: 10.1039/c2sm25925g

CrossRef Full Text

147. Ando T, Skolnick J. Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc Natl Acad Sci USA (2010) 107:18457–62. doi: 10.1073/pnas.1011354107

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

148. Kuimova MK, Botchway SW, Parker AW, Balaz M, Collins HA, Anderson HL, et al. Imaging intracellular viscosity of a single cell during photoinduced cell death. Nat Chem. (2009) 1:69–73. doi: 10.1038/nchem.120

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

149. Zhao L, Sukstanskii AL, Kroenke CD, Song J, Piwnica-Worms D, Ackerman JJH, et al. Intracellular water specific MR of microbead-adherent cells: HeLa cell intracellular water diffusion. Magn Reson Med. (2008) 59:79–84. doi: 10.1002/mrm.21440

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

150. Ruan Q, Chen Y, Gratton E, Glaser M, Mantulin W. Cellular characterization of adenylate kinase and its isoform: two-photon excitation fluorescence imaging and fluorescence correlation spectroscopy. Biophys J. (2002) 83:3177–87. doi: 10.1016/S0006-3495(02)75320-4

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

151. Hui YY, Zhang B, Chang YC, Chang CC, Chang HC, Hsu JH, et al. Two-photon fluorescence correlation spectroscopy of lipid-encapsulated fluorescent nanodiamonds in living cells. Opt Exp. (2010) 18:5896–905. doi: 10.1364/OE.18.005896

CrossRef Full Text

152. Dauty E, Verkman A. Actin cytoskeleton as the principal determinant of size-dependent DNA mobility in cytoplasm. J Biol Chem. (2005) 280:7823–8. doi: 10.1074/jbc.M412374200

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text