- Department of Physics and Earth Sciences, Faculty of Science, University of the Ryukyus, Okinawa, Japan
We determined many functional representations of interparticle interactions between water molecules, all of which reproduce the experimentally measured density-temperature relation at 1 bar with an accuracy better than obtained by previous models. Numerous similar descriptions of pair interactions will be discovered increasingly in the coming years, which will help us to understand why solid water has polymorphic structures and why liquid water has a large number of anomalies. We used a self-consistent Ornstein-Zernike approximation (SCOZA) with a potential given by multi-Yukawa terms. Because any smooth potential function can be fitted by multi-Yukawa terms, the method can be applied to various types of fluids. We also present a new simple fitting technique that makes the application of the SCOZA to any type of liquid much easier compared to a conventional Yukawa fit. Our new SCOZA fitting technique is among the most useful methods for determining the pair interaction between molecules of any liquid, and the potential will be helpful in improving realistic models.
1. Introduction
The thermodynamic properties of liquid water can be derived by using thermodynamics and statistical mechanics if the interparticle interactions between water molecules are understood. However, the precise shape of the potential function is unknown. To estimate the interparticle interactions, we first consider the interaction between two water molecules. A water molecule is composed of one oxygen atom and two hydrogen atoms. The oxygen atom is made up of one positively-charged oxygen nucleus and eight negatively-charged electrons. A hydrogen atom is composed of one positively-charged hydrogen nucleus and one negatively charged electron. Therefore, one water molecule is made of 13 particles. Thus, we would be able to determine the interaction potential between two water molecules from the quantum mechanical wave function that describes this 26-particle system, which is not an easy task. Furthermore, in real water, a large number of molecules exist around the molecules under consideration. The surrounding molecules will affect the wave function. That is to say, many more particles than those of the system of two water molecules must be taken into account to obtain the interaction potential between water molecules in real water. Therefore, it would be impossible to describe the interaction realistically from the basic equations of quantum mechanics or some other physics.
Presently there are two methods that are often used to approximate the interparticle interactions between water molecules. In the first method, the positive and negative charges in a water molecule are treated as point charges and are located at fixed places near the oxygen atom. The oxygen atoms interact with each other through the Van der Waals force, and each charged particle interacts with those of different molecules through the electrostatic Coulomb force. The thermodynamic properties of a system composed of such molecules can be estimated by using molecular dynamics simulations or Monte Carlo methods [1–8]. A large number of models of this type have been put forward, and their predicted thermodynamic properties have been compared with experimentally measured data. Among them, the simple m-Water model [8] is known to reproduce experimental data most accurately. Although it is well known that the m-Water model produces a tetrahedral network, its reproduction of the experimental density anomaly is not so good. We explain below that it is not necessarily the same thing to produce a tetrahedral network and to reproduce the density anomaly. Furthermore, it does not seem to be so easy to elucidate the physics underlying the anomalous behaviors of liquid water. This is because a realistic model includes a great number of miscellaneous effects, even if it is highly precise and is able to reproduce experimentally measured data. In other words, all of the miscellaneous properties together would not induce the density anomaly, and therefore it is thought to be almost impossible to identify the direct causes of the density anomaly from them. In fact, none of the realistic models tells us anything about how and why the tetrahedral structure induces positive expansion at temperatures above 4°C, but negative expansion below that temperature.
The second method was proposed to elucidate which shape characteristics of the interaction potential cause the density anomaly by assuming that the potential is given by a spherically symmetric function (simplified or core-softened model). A number of simplified (core-softened) potentials have been presented by different authors. These can be divided into two groups: one composed of a hard-core (HC) plus a purely repulsive tail, and the other composed of a HC plus a soft repulsion and an attraction. Models from both groups have presented us with many fruitful results about the anomalous behaviors of liquids. Although the shapes of the potential tails of both groups are quite different, both exhibit water-like anomalous behaviors (e.g., [9–21] and references quoted therein). However, the simplified potential models presented so far have not been shown to reproduce quantitatively the experimental behaviors of liquid water with sufficient accuracy. This prevents the formation of conclusive explanations of the density anomaly because the thermodynamic properties of liquids depend strongly on the interparticle interactions. Here we present a simplified potential model that reproduces quantitatively the density anomaly of liquid water much better than the models proposed so far. Moreover, the model decisively explains the anomalies. A sophisticated model that reproduces experimental data with high accuracy can bring great progress to the solution of this problem.
We concentrate our study on the thermal properties of water in liquid phases. Our study is blind to freezing and, more generally, to the solid phases of the system (see e.g., [22]), but it will give significant insight into the thermodynamic properties of water in these phases.
Here we report on our study of the thermodynamic properties of liquid water on the basis of statistical mechanics and thermodynamics by using the thermodynamically self-consistent Ornstein-Zernike approximation (SCOZA). The SCOZA is known to describe the overall thermodynamics of liquids very well and provide a remarkably accurate critical point and coexistence curve. This scheme is entirely self-contained, which means that no supplementary thermodynamic or other input is necessary. So far, the SCOZA has been applied to the Yukawa, Sogami-Ise, square-well, triangle-well, and screened-power series potentials, and many useful results have been obtained (see [23–28] and references quoted therein). Here we apply the SCOZA to our core-softened models with a hard-core (HC) repulsion plus a tail. The tail is composed of a soft repulsion and an attraction. We will show that a number of tails can reproduce the experimentally measured density-temperature relation at 1 bar with sufficient accuracy. This will help us to understand the reasons why solid water has polymorphic structures and why liquid water has many anomalies.
In the next section, we present the SCOZA in a general form. Any smooth potential tails can be approximated with sufficient accuracy by multi-Yukawa terms. The SCOZA for a hard-core-multi-Yukawa fluid is described in Section 3. We next apply the scheme to some potential models in Section 4. In Section 5, we present a new simple fitting technique for any smooth function by multi-Yukawa terms, which makes the SCOZA much easier to apply to liquids with any smooth tail than the SCOZA with a conventional Yukawa fit. Section 6 presents the summary and discussion. We will elucidate the thermodynamic mechanism that induces the density anomaly in a following paper.
2. SCOZA for a Fluid
We consider a fluid of spherical particles with a pair potential given by an HC repulsion and some tail ϕ(r). The thermodynamic properties of the fluid can be obtained from the pair distribution function g(r) or the total correlation function h(r) = g(r) − 1. The Ornstein-Zernike (OZ) relation defines the direct correlation function c(r) in terms of the total correlation function
where ρ is a number density. Under a thermodynamically self-consistent Ornstein-Zernike approximation (SCOZA), the closure relation is written as
where β = 1/kT, in which k is the Boltzmann constant and T is temperature. Equation (2) reflects the impenetrability of the hard cores, and the hard-sphere diameter σu is used as a unit of length. The direct correction function cHS(r) of the hard-sphere (HS) fluid is given by
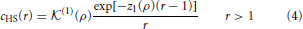
where  (1)(ρ) and z1(ρ) are known functions of the density ρ. The function R(ρ, β) of the thermodynamic state of the system is introduced to satisfy the thermodynamic consistency condition between the reduced compressibility χred and the excess internal energy u per unit volume. The condition is expressed as (see [23] and references cited therein)
(1)(ρ) and z1(ρ) are known functions of the density ρ. The function R(ρ, β) of the thermodynamic state of the system is introduced to satisfy the thermodynamic consistency condition between the reduced compressibility χred and the excess internal energy u per unit volume. The condition is expressed as (see [23] and references cited therein)
The reduced compressibility χred is given by
where (k) is the Fourier transform of the direct correlation function. The excess internal energy u per unit volume is given by the integral of the interaction weighted by the radial distribution function:
The equations to be solved are the OZ relation (1) with the thermodynamic consistency relation (5) supplemented with the closure relations (2) and (3).
Here we apply the SCOZA to a fluid of spherical particles with a pair potential given by an HC repulsion and multi-Yukawa tails expressed as
where N is an arbitrary integer, and zn and an are arbitrary constants. Here, the depth of the tail εu is used as a unit of energy.
3. SCOZA for an HC-Multi-Yukawa Fluid
Following Baxter's factorization method it can be shown that under certain conditions the OZ relation (1) is equivalent to the equations
where the factor function Q(r) has been introduced.
To solve the Baxter equations with the SCOZA closure relations (2) and (3) for the multi-Yukawa tails (8), we can take advantage of the known analytic properties of the solution under the mean-spherical approximation [29, 30]. The factor function Q(r) has the form
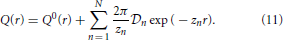
The function Q0(r) in (11) is written as
for 0 < r < 1, where
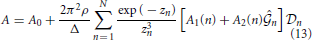
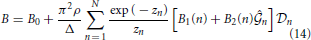
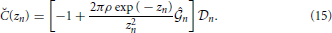
Here,
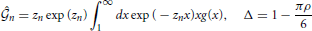
and coefficients A0, B0, A1(n), B1(n), A2(n) and B2(n) are shown in the Appendix.
The set of unknowns (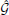 n,
n, 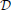 n) is obtained by solving the following system of 2N Equations (16)-(19) via a Newton-Raphson technique:
n) is obtained by solving the following system of 2N Equations (16)-(19) via a Newton-Raphson technique:
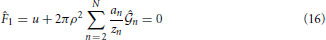
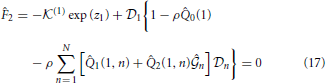
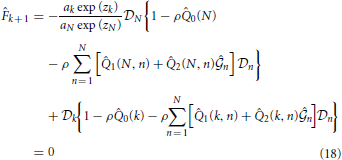
for (k = 2, 3, ···, N − 1),
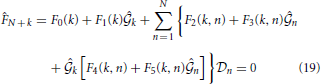
for k = 1, 2, ···, N. Here, coefficients 0(k), 1(k, n), 2(k, n), F0(k), F1(k), F2(k, n), F3(k, n), F4(k, n) and F5(k, n) are shown in the Appendix.
Equation (5) is rewritten as
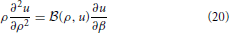
where
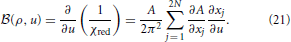
Here, xj =  j and xN + j =
j and xN + j =  j (j = 1, 2, ···, N). Unknowns ∂xj/∂u are obtained by solving the following linear equations:
j (j = 1, 2, ···, N). Unknowns ∂xj/∂u are obtained by solving the following linear equations:
Equation (20) has been solved numerically by an implicit finite-difference algorithm [31] described in detail in Pini et al. [24] in the region (β, ρ) ∈ [0, βf] × [0, ρ0]. The integration with respect to β starts at β = 0 and goes down to lower temperatures. At each temperature, the set of non-linear Equations (16)–(19) is solved, yielding ( n,
n,  n). To ensure rapid convergence, the values of (
n). To ensure rapid convergence, the values of (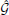 n,
n, 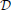 n) obtained at the previous temperature step are taken as an initial guess for the solution of the system of non-linear equations. In the next step, A(ρ, β), ∂A/∂xj, and ∂xj/∂u are determined to calculate the coefficient
n) obtained at the previous temperature step are taken as an initial guess for the solution of the system of non-linear equations. In the next step, A(ρ, β), ∂A/∂xj, and ∂xj/∂u are determined to calculate the coefficient 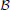 (ρ, u).
(ρ, u).
The boundary conditions are the same as in Pini et al. [23]; for ρ = 0 one obtains from (7)
If we make use of the so-called high-temperature approximation [32] at ρ = ρ0 one obtains for reduced compressibility
The initial condition u(ρ, β = 0) can be determined by taking into account that for β = 0; the direct correlation function c(r) coincides with that of the HS gas. Thus, R(ρ, β = 0)an exp (zn)/kT = 0, yielding 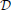 n = 0 for n > 1. The set of unknowns (
n = 0 for n > 1. The set of unknowns (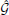 1,
1, 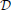 1) is obtained by solving the following set of equations:
1) is obtained by solving the following set of equations:
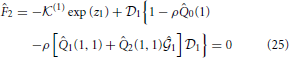
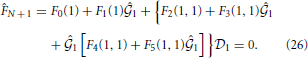
The unknown 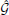 k is obtained by solving the following equation:
k is obtained by solving the following equation:
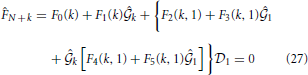
for k = 2, 3, ···, N and thus
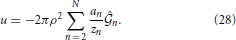
The unphysical region inside the spinodal curve is determined by checking the sign of A(ρ, β) given in (13); in the forbidden region, A(ρ, β) becomes negative. The boundary conditions on the spinodal used here are the same as those in Pini et al. [23]
where ρSi (i = 1, 2) are approximations of the spinodal densities on the discrete density grid at a given temperature. Their values are determined by locating the change of sign of A(ρ, β). uS(ρ) is the value of the excess internal energy per unit volume where χred−1 = 0. This value is determined by solving the following set of equations
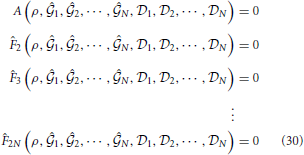
with respect to 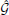 1,
1, 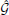 2, ···,
2, ···, 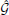 N,
N,  1,
1, 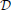 2, ···,
2, ···, 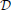 N. Inserting the solutions
N. Inserting the solutions 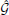 2,
2, 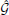 3, ···,
3, ···, 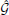 N into (28) yields uS(ρ).
N into (28) yields uS(ρ).
Once u(ρ, β) has been determined by solving (20), the pressure P and the chemical potential μ are obtained by integrating (∂βP/∂β) and (∂βμ/∂β) with respect to β from
where at β = 0, we have taken as integration constants the Carnahan Starling values for βP and βμ
where η = πρ/6.
Alternatively, βP and βμ can be obtained by integrating, respectively, χred−1 and (ρχred)−1 with respect to the density from
In a manner similar to that described for the energy route, we have taken the Carnahan Starling values above as integration constants at β = 0. At ρ = ρls on the liquid side spinodal, however, we have taken the values of βP(ρls, β) and βμ(ρls, β) obtained from the energy route as integration constants. We have confirmed that both paths lead to the same thermodynamics with remarkable accuracy because of the thermodynamic consistency enforced by (5).
4. Models of the Potential between Water Molecules
The thermodynamic properties of liquid water are obtained from the excess internal energy u given by Equation (7). The equation shows that there will be many different combinations of interparticle interaction ϕ(r) and distribution function g(r) that will yield the same internal energy u and isobaric density-temperature relation. In this section we present a selection of such potential tails.
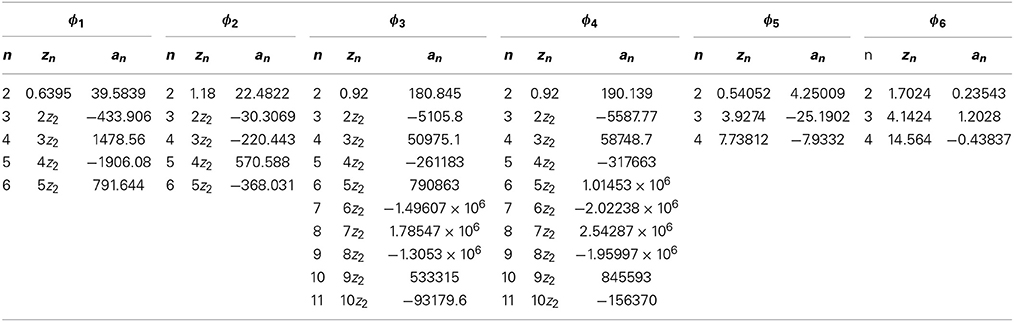
Table 1 lists the parameters that determine the shape of the potential tails of six cases of ϕ1(r) − ϕ6(r). We refer hereafter to a liquid model with tail ϕi(r) simply as “Model i” (i = 1 − 6). The tails are shown in Supplementary Figure 1 by blue, red, orange, purple, black, and dashed lines, respectively, and are all found to have much different shapes.
Numerical solution of (20) for a model with the initial condition and the boundary conditions have been determined on a density grid Δρ for ρ ≤ ρ0 and a temperature grid Δβ for β ≤ βf. To accurately locate the critical point, Δβ is decreased when approaching the critical point and then increased back to the initial value. The critical point (ρc, βc) is located by the vanishing of the inverse compressibility χred−1. Henceforth we express physical quantities at the critical point by the subscript c. At subcritical temperatures the region enclosed by the spinodal is excluded. In the present paper, we focus our study on the thermodynamic properties of water in liquid phases. The parameters used in the numerical computations are listed in Table 2.
Supplementary Figure 2 shows the density-temperature relations at 1 bar obtained by using Models 1−5 (blue, red, orange, purple, and black full circles, respectively). It is found that Models 1, 2, 4, and 5 produce nearly the same density-temperature relation, which reproduces the experimentally measured data at 1 bar (open circles [33]) in the wide temperature range of −20 < T(°C) < 100 much better than previous models (e.g., Figure 4 in [8]). In contrast, the density-temperature curve for Model 3 shown by the full orange circles reproduces relatively well the experimental data at lower temperatures, although it is worse for higher temperatures. Those results will help us to obtain a more optimum potential between water molecules that reproduces the experimental density at any temperature.
We expect that much more potential functions with shapes different from those presented here will be found in upcoming years that will reproduce the same thermodynamic properties as liquid water. These will help us to understand the reasons why solid water has polymorphic structures and liquid water has many anomalous properties.
5. A New Simple Technique of Fitting by Multi-Yukawa Terms
In the present paper, we have used the SCOZA to estimate the interparticle interactions between water molecules. We can take advantage of the known analytic properties of the solution of the OZ equation for the case in which the potential tail is given by multi-Yukawa terms [29, 30] or a screened power series (SPS) [28] under the mean spherical approximation (MSA). The SCOZA is applicable to fluids with a large variety of smooth potential functions because they may be fitted with high accuracy by multi-Yukawa terms or SPS.
The fitting accuracy can be improved by increasing the Yukawa terms or the number of z in the case of multi-Yukawa terms, but the computation time will increase drastically. It would take a few days, a few months, or a few years to mimic any smooth potential by five, six, or seven Yukawa terms, respectively. On the contrary, an SPS fit can greatly reduce the computation time it takes to attain the same accuracy as that by a conventional Yukawa fit [28]. However, the computer program required for the SCOZA with SPS tails is much more complicated than with multi-Yukawa tails. Here we present a new simple fitting technique that makes the SCOZA much easier to operate than by using a conventional Yukawa fit.
In the case of Model 5, we have used a Lennard-Jones-like function given by
where n = 4.3, m = 4, γ = 1.537, and = 37.595 as a helpful lead to finding a model that quantitatively reproduces sufficiently well the density anomaly of liquid water. The function ϕ5(σur) is fitted to a high accuracy by three Yukawa terms by using the fitting technique described in Yasutomi [28]. The parameters an and zn are listed in Table 1. The computer time is about 30 min.
We present here a new simple fitting technique by multi-Yukawa terms. First, we determine the shape of the potential tail so that it is expected to reproduce the experimental density anomaly of liquid water. The tail is divided into parts in the radial direction, and each part is expressed by a polynomial or other function. Each approximate tail ϕi(r) is fitted by the following multi-Yukawa terms:
where zn = (n − 1)z2 for n > 2. We can easily obtain the optimum z2 by using the method described in Yasutomi [28]. In this way, we can obtain a tail given by multi-Yukawa terms in a few minutes of computer time almost independently of N, and it makes the application of the SCOZA to any liquid much easier than a conventional Yukawa fit.
6. Summary and Discussion
We have determined several pair interactions between water molecules. All of them reproduce the experimental density anomaly at 1 bar with better accuracy than other models available in the literature. There will be numerous other such pair interactions discovered in the near future. These will help us to understand the reasons why solid water has polymorphic structures and why liquid water has a number of anomalies.
We have considered a liquid of spherical particles with a pair potential given by a hard-core repulsion and a tail. The tail is composed of a soft repulsion and an attraction and is given by multi-Yukawa terms. We have presented a new simple fitting method to any smooth function by multi-Yukawa terms. The new scheme makes the application of the SCOZA to any type of liquid much easier compared to a conventional Yukawa fit. This new SCOZA technique is one of the most useful methods for determining the pair interaction between molecules of any liquid, and the potential will help to improve realistic models.
We have assumed here that the interparticle interaction is independent of density and temperature, but the effect by the surrounding water molecules on the relative positions and physical states of the oxygen nucleus, two hydrogen nuclei, and ten electrons constituting a water molecule depends on the density and temperature. Therefore, such effects should be taken into consideration to optimize the interparticle interactions between molecules.
Finally we discuss what thermodynamic mechanism induces the density anomaly, which has been long studied by different authors with numerous ideas put forward [34–47]. However, it has also been long pointed out that these ideas tell us nothing about what causes the negative thermal expansion at temperatures below 4°C. For example, one claim is that the tetrahedral structure of ice causes the density anomaly, but there is no evidence for this. As a counter analogy, consider a folding umbrella. To open or close it, one pushes or pulls the base of the frame with hand power. The frame itself has no power to open or close itself without human intervention. In the case of the umbrella, the direct cause of its expansion and contraction is human hand power and not the frame itself. To clarify the thermodynamic mechanism that causes the density anomaly, it is necessary to find the power that acts as an attractive force to condense water at temperatures above 4°C, but acts as a repulsive force to expand water below 4°C with reducing temperature. Such a force (hereafter referred to for simplicity as the “anomaly force”) is the immediate cause of the density anomaly of liquid water. It is difficult to imagine how the tetrahedral structure could have an “anomaly force” analogous with the case of the folding umbrella.
Another suggestion is that hydrogen bonding causes the density anomaly. However, hydrogen bonding is attractive at any temperature and has the tendency to reduce the distance between molecules in thermodynamic equilibrium to condense liquid water. Therefore, it is difficult to consider how hydrogen bonding could turn into a repulsive force below 4°C to cause negative thermal expansion.
Regarding the network or clathrate models [8–12], even though it may be plausible that isolated water molecules go into cavities as the temperature lowers to cause liquid water to condense, the models tell us nothing about what makes isolated water molecules leave the filled cavities at temperatures below 4°C with reducing temperature to induce negative expansion.
Lactic acid was long believed to be the substance that causes muscle fatigue because it increases with fatigue, but lactic acid was recently found to be a substance that assists in recovery from fatigue. It is now known that active oxygen is the substance responsible for fatigue. Similarly, it cannot be claimed that the density anomaly is caused by some phenomenon just because it accompanies the density anomaly. We can apply this principle to almost every idea put forward until now.
A large number of numerical simulations using realistic models have been performed by many different authors with the goal of understanding the physics underlying the density anomaly of liquid water. However, these studies tell us little about what induces the anomaly because it is impossible to extract the essential effects that induce the anomaly from the numerous miscellaneous effects included in the models. We believe that we have succeeded in constructing a model that includes only the essential effects that cause the density anomaly and in finding the “anomaly force”. Our next paper is in preparation.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fphy.2014.00064/abstract
References
1. Beveridge DL, Mezei M, Mehrotra PK, Marchese FT, Ravi-Shankar G, Vasu T, et al. Molecular-based study of fluids. In: Haile JM, Mansoori GA, editors. Advances in Chemistry, Vol. 204. Washington, DC: American Chemical Society (1983). p. 297–351.
2. Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. (1983) 79:926–35. doi: 10.1063/1.445869
3. Jorgensen WL, Madura JD. Temperature and size dependence for Monte Carlo simulations of TIP4P water. Mol Phys. (1985) 56:1381–92. doi: 10.1080/00268978500103111
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
4. Mahoney MW, Jorgensen WL. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J Chem Phys. (2000) 112:8910–22. doi: 10.1063/1.481505
5. Berendsen HJC, Postma JPM, van Gunsteren WF, Hermans J. Interaction models for water in relation to protein hydration. In: Pullman B, editor. Intermolecular Forces, Volume 14 of The Jerusalem Symposia on Quantum Chemistry and Biochemistry. Springer Netherlands (1981). p. 331–42. doi: 10.1007/978-94-015-7658-1-21
6. Berendsen HJC, Grigera JR, Straatsma TP. The missing term in effective pair potentials. J Phys Chem. (1987) 91:6269–71. doi: 10.1021/j100308a038
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
7. Stanley HE, Buldyrev SV, Giovambattista N, Nave EL, Mossa S, Scala A, et al. Application of statistical physics to understand static and dynamic anomallies in liquid water. J Stat Phys. (2003) 110:1039–54. doi: 10.1023/A:1022188608924
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
8. Molinero V, Moore EB. Water modeled as an intermediate element between carbon and silicon. J Phys Chem B (2009) 113:4008–16. doi: 10.1021/jp805227c
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
9. Oliveira ABD, Netz PA, Barbosa MC. An ubiquitous mechanism for water-like anomalies. EPL (2009) 85:36001. doi: 10.1209/0295-5075/85/36001
10. Gribova NV, Fomin YD, Frenkel D, Ryzhov VN. Waterlike thermodynamic anomalies in a repulsive-shoulder potential system. Phys Rev E (2009) 79:051202. doi: 10.1103/PhysRevE.79.051202
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
11. Fomin YD, Tsiok EN, Ryzhov VN. Inversion of sequence of diffusion and density anomalies in core-softened systems. J Chem Phys. (2011) 135:234502. doi: 10.1063/1.3668313
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
12. Sadr-Lahijany MR, Scala A, Buldyrev SV, Stanley HE. Liquid-state anomalies and the stell-hemmer core-softened potential. Phys Rev Lett. (1998) 81:4895–8. doi: 10.1103/PhysRevLett.81.4895
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
13. Wilding NB, Magee JE. Phase behavior and thermodynamic anomalies of core-softened fluids. Phys Rev E (2002) 66:031509. doi: 10.1103/PhysRevE.66.031509
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
14. Gibson HM, Wilding NB. Metastable liquid-liquid coexistence and density anomalies in a core-softened fluid. Phys Rev E (2006) 73:061507. doi: 10.1103/PhysRevE.73.061507
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
15. Caballero JB, Puertas AM. Density anomaly and liquid-liquid transition from perturbation theories. Phys Rev E (2006) 74:051506. doi: 10.1103/PhysRevE.74.051506
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
16. Lomba E, Almarza NG, Martin C, McBridge C. Phase behavior of attractive and repulsive ramp fluids: Integral equation and computer simulation studies. J Chem Phys. (2007) 126:244510. doi: 10.1063/1.2748043
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
17. Jagla EA. Low-temperature behavior of core-softened models: water and silica behavior. Phys Rev E (2001) 63:061509. doi: 10.1103/PhysRevE.63.061509
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
18. Yan Z, Buldyrev SV, Giovambattista N, Stanley HE. Structural order for one-scale and two-scale potentials. PRL (2005) 95:130604. doi: 10.1103/PhysRevLett.95.130604
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
19. Yan Z, Buldyrev SV, Kumar P, Giovambattista N, Stanley HE. Correspondence between phase diagrams of the TIP5P water model and a spherically symmetric repulsive ramp potential with two characteristic length scales. Phys Rev E (2008) 77:042201. doi: 10.1103/PhysRevE.77.042201
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
20. Prestipino S, Saija F, Malescio G. Anomalous phase behavior in a model fluid with only one type of local structure. J Chem Phys. (2010) 133:144504. doi: 10.1063/1.3499830
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
21. Malescio G, Prestipino S, Saija F. Anomalous melting and solid polymorphism of a modified inverse-power potential. Mol Phys. (2011) 109:2837–44. doi: 10.1080/00268976.2011.609146
22. Prestipino S. On the accuracy of the melting curves drawn from modelling a solid as an elastic medium. J Phys Condens Matt. (2012) 24:035102. doi: 10.1088/0953-8984/24/3/035102
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
23. Pini D, Stell G, Wilding NB. A liquid-state theory that remains successful in the critical region. Mol Phys. (1998) 95:483–94. doi: 10.1080/00268979809483183
24. Pini D, Stell G, Dickman R. Thermodynamically self-consistent theory of structure for three-dimensional lattice gases. Phys Rev E (1998) 57:2862–71. doi: 10.1103/PhysRevE.57.2862
25. Schöll-Paschinger E. Self-consistent ornstein-zernike approximation for the Sogami-Ise fluid. J Chem Phys. (2004) 120:11698–711. doi: 10.1063/1.1755192
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
26. Schöll-Paschinger E. Vapor-liquid equilibrium and critical behavior of the square-well fluid of variable range: a theoretical study. J Chem Phys. (2005) 123:234513. doi: 10.1063/1.2137713
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
27. Betancourt-Cárdenas FF, Galicia-Luna LA, Benavides AL, Ramirez JA, Schöll-Paschinger E. Thermodynamics of a long-range triangle-well fluid. Mol Phys. (2008) 106:113–26. doi: 10.1080/00268970701832397
28. Yasutomi M. A self-consistent Ornstein-Zernike approximation for a fluid with a screened power series interaction. J Chem Phys. (2010) 133:154115. doi: 10.1063/1.3503590
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
29. Yasutomi M. Analytical solution of the Ornstein-Zernike equation for a multicomponent fluid with a screened Coulomb plus power series interaction. J Phys Condens Matt. (2001) 13:L255–60. doi: 10.1088/0953-8984/13/11/106
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
30. Yasutomi M. Mean spherical approximation algorithm for multicomponent fluid mixtures with multi-screened Coulomb plus power series interactions. J Phys Condens Matt. (2003) 15:8213-33. doi: 10.1088/0953-8984/15/49/002
31. Ames WF. Numerical Methods for Partial Differential Equations. New York, NY: Academic Press. (1977).
32. Hansen JP, McDonald IR. Theory of Simple Liquids, 2nd Edn. New York, NY: Academic Press. (1986).
34. Röntgen WC. Ueber die Constitution des flüssigen Wassers. Ann Phys. (1892) 281:91–7. doi: 10.1002/andp.18922810108
35. Bernal JD, Fowler RH. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J Chem Phys. (1933) 1:515–48. doi: 10.1063/1.1749327
36. Pople JA. Molecular association in liquids. II. A theory of the structure of water. Proc R Soc Lond A (1951) 205:163–78. doi: 10.1098/rspa.1951.0024
37. Bernal JD. The bakerian Lecture, 1962. The structure of liquids. Proc R Soc Lond A (1964) 280:299–322. doi: 10.1098/rspa.1964.0147
38. Sceats MG, Rice SA. The water-water pair potential near the hydrogen bonded equilibrium configuration. J Chem Phys. (1980) 72:3236–47. doi: 10.1063/1.439560
39. Sceats MG, Rice SA. A random network model calculation of the free energy of liquid water. J Chem Phys. (1980) 72:6183–91. doi: 10.1063/1.439077
40. Rice SA, Sceats MG. A random network model for water. J Chem Phys. (1981) 85:1108–19. doi: 10.1021/j150609a009
41. Samoilov OY. A new approach to the study of hydrogen of ions in aqueous solutions. Discuss Faraday Soc. (1957) 24:141–6. doi: 10.1039/df9572400141
42. Pauling L. The structure of water. In: Hadzi D, Thompson HW, editors, Hydrogen Bonding, London: Pergamon Press Ltd. (1959). p. 1–6. doi: 10.1016/B978-0-08-009140-2.50004-X
43. Némety G, Scheraga HA. Structure of water and hydrophobic bonding in proteins. I. A model for the thermodynamic properties of liquid water. J Chem Phys. (1962) 36:3382–400. doi: 10.1063/1.1732472
44. Stanley HE. A polychromatic correlated-site percolation problem with possible relevance to the unusual behaviour of supercooled H2O and D2O. J Phys A Math Gen. (1979) 12:L329. doi: 10.1088/0305-4470/12/12/003
45. Malenkov G. Liquid water and ices: understanding the structure and physical properties. J Phys Condens Matt. (2009) 21:283101. doi: 10.1088/0953-8984/21/28/283101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
46. Poole PH, Sciortino R, Essmann U, Stanley HE. Phase behaviour of metastable water. Nature (1992) 360:324–8. doi: 10.1038/360324a0
47. Chatterjee S, Debenedetti PG, Stillinger FH, Lynden-Bell RM. A computational investigation of thermodynamics, structure, dynamics and solvation behavior in modified water models. J Chem Phys. (2008) 128:124511. doi: 10.1063/1.2841127
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: liquid water, interparticle interactions, polymorphic structures, solid water, SCOZA, a new simple fitting technique, multi-Yukawa terms, density anomaly
Citation: Yasutomi M (2014) Interparticle interactions between water molecules. Front. Phys. 2:64. doi: 10.3389/fphy.2014.00064
Received: 19 June 2014; Accepted: 27 October 2014;
Published online: 18 November 2014.
Edited by:
Gang Zhang, Institute of High Performance Computing, SingaporeCopyright © 2014 Yasutomi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Makoto Yasutomi, Department of Physics and Earth Sciences, Faculty of Science, University of the Ryukyus, Senbara 1, Nishihara-Cho, Okinawa 903-0213, Japan e-mail:ZzgwMDAwMkBsYWIudS1yeXVreXUuYWMuanA=
 Makoto Yasutomi
Makoto Yasutomi