The impressive experimental realization of weakly interacting Bose-Einstein condensation (BEC) in dilute alkali gases [1–3] has renewed the theoretical and experimental interest in studies of Bose systems. The BEC of alkali gases were identified by the existence of a sharp peak in the momentum distribution below a certain critical temperature. Unlike the intensively studied strongly interacting liquid 4He system, the momentum distribution of cold atomic systems is easily accessible due to the inhomogeneity of the trapped atoms. While, the focus of the first generation of cold gas experiments has been on BEC of weakly interacting bosons, the center of research has now shifted toward the study of both normal and superfluid phases in strongly interacting bosons. The main advances in this direction have been archived by increasing the interaction through controlling the two-body scattering length (a) or exposing the atoms to optical lattices [4, 5].
Impressive theoretical efforts are currently devoted to study the effect of interactions on Bose-Einstein condensation [6–8]. Until recently, there was no consensus on the sign of the shift of critical temperature in the presence of strong interactions. Now it is believed that the shift can be described as ΔTc = 1.3an1/3T0c, where n is the density and T0c is the critical temperature of an ideal Bose gas [9, 10]. Further, it has been shown that none of the mean field theories correctly predict the expected second-order BEC-normal phase transition [11]. These mean field theories include, Hartree-Fock (HF) [8, 12], Popov [13], Yukalov-Yukalova (YY) [14], and t-matrix approximations [15, 16]. Recently, a self-consistent mean field theory was proposed as the sole mean-field theory that explains the correct second-order transition [17]. All theories mentioned above have been applied to study either the properties of the BEC phase or the phase transition. Little attention has been paid to the normal phase.
One of the most popular and intensively applied theories in literature was proposed by Bijlsma and Stoof [16] and Shi and Griffin [15]. This t-matrix approximation (TM) was developed based on Popov theory. The authors in [15] and [16] however, go beyond the contact interaction and include the many-body effects by taking into account higher order scattering. Then neglecting the momentum dependence on the t-matrix, these authors have derived a simple analytical expression for density in both normal and superfluid phases. The expected advantage of TM theory is that it is applicable for both superfluid BEC and normal phases. In this opinion article, we show that this t-matrix approximation based theory breaks down in the normal phase and the expected advantage and simplicity of the theory is no longer valid.
TM theory: First we summarize the TM approach for the normal phase of bosons, following the reference [15]. The density of the normal bosons is n = g3/2[βΔ]/λ3, where λ = [2πℏ2/(mkBT)]1/2 is the thermal deBroglie wavelength and gn(x) is the well known Bose integral. The parameter Δ is related to the density n, chemical potential μ, many-body t-matrix T = U/(1 + αU), and an additional parameter α through the expression μ = Δ + (2nU)/(1 + αU), where
Here U = 4πℏ2a/m is the free-space scattering amplitude, ℏ is the plank constant, kB is the Boltzmann constant, β = 1/(kBT) is the inverse temperature, and m is the mass of a boson. The quasi particle energy is given by Ek = ϵk − Δ with ϵk = ℏ2k2/2m. At the normal-BEC transition, Δ → 0, while α → ∞ yielding a chemical potential μc = 0 as in the case of an ideal Bose gas. In order to demonstrate the problematic behavior of the theory, we solve these set of equations for the density profile of a harmonically trapped Bose gas. Using local density approximation, replacing μ → μ0 − mω2r2/2, the density profile of the trapped gas is shown in Figure 1 as a function of spatial coordinate r. Here μ0 is the chemical potential at the center of the trap and ω is the trapping frequency. The density profile is shown at the onset of the BEC. In other words, the trap center r = 0 is set to be at the BEC where we set central chemical potential to be μ0 = μc.
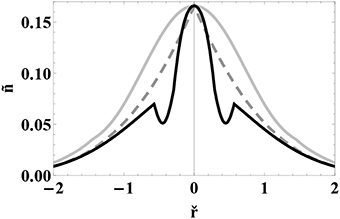
Figure 1. The scaled density profiles of a harmonically trapped Bose gas at the onset of BEC. While the center of the trap (ř = 0) is set to be at BEC transition, the entire tail of the density profile is in normal state. The interaction strength and temperature are fixed to be U = ℏω and kBT = ℏω. The dashed-line represents a non-interacting Bose gas, the black and gray lines represent t-matrix and Hartree-Fock theories respectively. The density = nl3 and the radial coordinate ř = r/l are scaled with the oscillator length l = .
HF theory: As a comparison, we show HF density profile for the same parameters in gray color in Figure 1. HF approach is a self-consistent approach that simplifies the N-particle interacting states into effectively one-particle non-interacting states whose energy spectrum depends self-consistently on both density and the interaction. The HF normal density is given by n = g3/2[β(μ − 2nU)]/λ3. At the BEC transition, the chemical potential is μc = 2Ug3/2[0]/λ3. It is worth pointing out that each of the mean field theories, HF, Popov, and YY are equivalent in the normal phase but they differ in the BEC phase. Notice that the critical density at the transition is the same as that of the TM approach and the non-interacting Bose gases, but the critical chemical potential is different. The non-interacting density profile at the onset of BEC is also shown as a dashed line.
The homogenous density in the normal phase is expected to be a monotonic function of chemical potential. Likewise, the density profile in a trap is expected to be a monotonically decreasing function of the spatial coordinate r. However, as opposed to the HF theory, the TM approach gives non-monotonic density variation. The density at the vicinity of BEC (density of the gas at the trap center is at criticality) however, agrees within the two approaches. The results are shown for representative values of interaction and temperature. The qualitative behavior is very similar for all finite interactions and temperatures. Even though this TM approach is widely used in literature, this problematic behavior has not been previously reported. This may be due to the fact that most studies focus on the BEC phase (where the density is monotonic as expected), but not on the normal phase. Though we use the local density approximation to a harmonically trapped boson system to demonstrate this ill behavior, the same behavior exists as a function of chemical potential. In other words, the density is not a monotonically increasing function of chemical potential. Therefore, it is not the local density approximation, but the approximation made to the t-matrix approach that must be responsible for this problematic behavior.
In conclusion, we have revisited the normal state bosons using a momentum independent t-matrix approach and discovered that the expected validity of the theory breaks down in the normal phase. Although this theory has been applied in numerous previous studies, this ill behavior has not been previously reported as to the best of our knowledge. We anticipate that the theory can be recovered by the inclusion of momentum dependence on the t-matrix. This will be a non trivial task due to the infrared divergences and including these will destroy the simplicity of the theory.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Joseph Newton for critical comments on the manuscript.
References
1. Anderson MH, Ensher JR, Matthews MR, Wieman CE, Cornell EA. Observation of bose-einstein condensation in a dilute atomic vapor. Science (1995) 269:198. doi: 10.1126/science.269.5221.198
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
2. Davis KB, Mewes M-O, Andrews MR, van Druten NJ, Durfee DS, Kurn DM, et al. Bose-einstein condensation in a gas of sodium atoms. Phys Rev Lett. (1995) 75:3969. doi: 10.1103/PhysRevLett.75.3969
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
3. Bradley CC, Sackett CA, Tollett JJ, Hulet RG. Evidence of bose-einstein condensation in an atomic gas with attractive interactions. Phys Rev Lett (1995) 75:1687. doi: 10.1103/PhysRevLett.75.1687
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
4. Navon N, Piatecki S, Gunter K, Rem B, Nguyen TC, Chevy F, et al. Dynamics and thermodynamics of the low-temperature strongly interacting bose gas. Phys Rev Lett. (2011) 107:135301. doi: 10.1103/PhysRevLett.107.135301
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
5. Papp SB, Pino JM, Wild RJ, Ronen S, Wieman CE, Jin DS, et al. Bragg spectroscopy of a strongly interacting 85Rb bose-einstein condensate. Phys Rev Lett. (2008) 101:135301. doi: 10.1103/PhysRevLett.101.135301
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
6. Lee TD, Yang CN. Many-body problem in quantum mechanics and quantum statistical mechanics. Phys Rev. (1957) 105:1119. doi: 10.1103/PhysRev.105.1119
7. Huang K and Yang CN. Quantum-mechanical many-body problem with hard-sphere interaction. Phys Rev. (1957) 105:767. doi: 10.1103/PhysRev.105.767
8. Griffin A, Snoke DW, Stringari S. Bose-Einstein Condensation. (1995). Cambridge: Cambridge University press.
9. Kashurnikov VA, Prokofév NV, Svistunov BV. Critical temperature shift in weakly interacting bose gas. Phys Rev Lett. (2001) 87:120402. doi: 10.1103/PhysRevLett.87.120402
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
10. Arnold P, Moore G. BEC transition temperature of a dilute homogeneous imperfect bose gas. Phys Rev Lett. (2001) 87:120401. doi: 10.1103/PhysRevLett.87.120401
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
11. Olivares-Quiroz L, Romero-Rochin V. On the order of BEC transition in weakly interacting gases predicted by mean-field theory. J Phys B At Mol Opt Phys. (2010) 43:205302. doi: 10.1088/0953-4075/43/20/205302
12. Pethic CJ, Smith H. Bose-Einstein Condensation in Dilute Gases. (2008). Cambridge: Cambridge University press.
14. Yukalov VI, Yukalova EP. Condensate and superfluid fractions for varying interactions and temperature. Phys Rev A. (2007) 76:013602. doi: 10.1103/PhysRevA.76.013602
15. Shi H, Griffin A. Finite-temperature excitations in a dilute Bose-condensed gas. Phys Rep. (1998) 304. doi: 10.1016/S0370-1573(98)00015-5
16. Bijlsma M, Stoof HTC. Variational approach to the dilute Bose gas. Phys Rev A. (1997) 55:498. doi: 10.1103/PhysRevA.55.498
Keywords: bose-einstein condensation, t-matrix approximation, normal state bosons, HF theory, failure of t-matrix
Citation: De Silva TN (2014) Evidence for the breakdown of momentum independent many-body t-matrix approximation in the normal phase of bosons. Front. Phys. 2:78. doi: 10.3389/fphy.2014.00078
Received: 17 September 2014; Accepted: 01 December 2014;
Published online: 22 December 2014.
Edited by:
James Avery Sauls, Northwestern University, USACopyright © 2014 De Silva. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence:dGRlc2lsdmFAZ3J1LmVkdQ==
 Theja N. De Silva
Theja N. De Silva