Perspective on completing natural inflation

1. Introduction

After the recent report by the BICEP2 group on a large tensor-to-scalar ratio r [1], natural inflation [2] and the method of completing it [3] have attracted a great deal of attention [4–9, 11]. Completing natural inflation employs at least two grand unification(GUT) scale non-Abelian gauge groups, which can be called 2−, 3−, …, N−flation models. In this paper, we present a perspective on completing natural inflation.

Cosmic inflation is a paradigm for a solution of the homogeneity and flatness problems [12–14]. For a sufficient inflation with the e-fold number e > (50−60), one needs small inflation-parameters, $ϵ(\equiv \frac{1}{2}{M}_{\text{P}}^2{(V^{\prime }/V)}^2)$ and η ( ≡ M²_PV″/V) [15, 16]. Single bubble inflation were proposed with the initial condition near the origin in the Coleman-Weinberg type logarithmically-flat hilltop potential [17], or at a large field value for a chaotic type potential [18]. With the slow-roll conditions satisfied, the local non-Gaussianities |f^local_NL| are much smaller than 1 for a single field inflation [19], which was reported by the Planck 2013 group [20]. In addition, if the BICEP2 result with a large r is confirmed, the hybrid inflation predicting n_s > 1 (arising from the hilltop inflation) [21] and the λϕ⁴ chaotic inflation are disfavored from the data [20]. Even though the size of dust contribution is still an ongoing issue [22], here we assume a large r of order 0.1.

The negligible non-Gaussianity pins down the inflation models to the single field m²ϕ² chaotic inflation [4–9, 11] or the multi-field hilltop inflation [21]. The m² ϕ² chaotic inflation needs a fine-tuning of order m² ≈ 10⁻¹⁰ in units of the reduced Planck mass, M_P ≃ 2.44 × 10¹⁸ GeV. For the predictability of the Einstein equation, we need that the potential V during inflation must be much smaller than M⁴_P. In fact, this can be easily realized in natural inflation where there exists a GUT scale heavy axion coupling to a GUT scale confining force [2]. With the heavy axion potential at the GUT scale (≈ Λ_GUT ≈M_GUT), the explicit breaking potential of the Peccei-Quinn (PQ) symmetry is given by $\propto \frac{1}{2}{\Lambda }_{\text{GUT}}^4(1-\cos (a/f))$, where a and f denote the axion and its decay constant, respectively; thus the potential energy is bounded by Λ⁴_GUT.

The m²ϕ² chaotic inflation has a problem, “Why does one keep only the quadratic term?” It is known that a large trans-Planckian field value is needed in the m²ϕ² chaotic inflation for a large tensor-to-scalar ratio r, which is known as the Lyth bound 〈ϕ〉 > 15 M_P [23]. In particular, with the large trans-Planckian field value higher order terms might be more important [21]. To reconcile the trans-Planckian field value with the natural inflation idea, Kim, Nilles, and Peloso (KNP) introduced two axions and two confining forces at the GUT scale. It has been generalized to N-flation [24]. An ultra-violet completed theory, in particular the heterotic string theory, may not allow a large number of non-Abelian gauge groups. We scrutinize the inflaton path, arising from the limited rank of the total gauge group, and present an argument that 2-flation (possibly 3-flation also), i.e., the KNP type, is an easily realizable one.

In Section 2, we briefly review the KNP scenario and its N-flation extension. In Section 3, we discuss the maximum rank of the heterotic string, which is argued for a limitation of the number of GUT scale confining gauge groups. Section 4 is a conclusion.

2. The 2-Flation

A large vacuum expectation value (VEV) of a scalar field is possible with a small mass parameter if a very small coupling constant λ is assumed,

$\begin{array}{cc}V=\frac{1}{4}\lambda {\left(|\varphi {|}^2-f^2\right)}^2.& \left(1\right)\end{array}$

The mass parameter in this theory is m² = λf². With a GUT scale m, f can be trans-Planckian of order > 10M_P for λ < 10⁻⁶. However, the potential (1) with the small λ describes inflation starting from near the convex hilltop point (due to the high temperature effect before inflation) and hence it is not favored by the BICEP2 data [21]. This has led to the recent surge of studies on concave potentials near the origin of the field space in case of single field inflations [4–9, 11]. The concave potentials give positive η's.

The simplest concave potential is the m²ϕ² chaotic potential. Since this potential is not bounded from above, the natural inflation with a GUT scale confining force has been introduced so that the potential is bounded from above [2] where the GUT scale axion is the inflaton and the inflaton potential is

$\begin{array}{cc}V={\Lambda }_{GUT}^4\left(1-\cos \frac{a_N}{f_N}\right).& \left(2\right)\end{array}$

With O(1) parameters at the GUT scale, f_N is O(M_GUT). This potential arises from $V=-\frac{1}{2}({\Lambda }_{GUT}^4+A)e^{ia/f}+\text{h}.\text{c}.$ where A is a function of a real scalar field ρ. So, the potential (2) mainly depends on the axion field a, and f_N is not determined by Equation (2) but by the potential breaking the PQ symmetry spontaneously, i.e., by Equation (1). For the radial direction to roll down quickly, we need λ ≫ 10⁻⁶ and f_N is of order M_GUT.

Since we need a trans-Planckian value for the decay constant of the GUT axion, the KNP model has been proposed with two axions a₁ and a₂ and two GUT scale (Λ₁ and Λ₂) confining forces, resulting in the following minus-cosine potential

$\begin{array}{cc}\begin{array}{l}V={\Lambda }_1^4\left(1-\cos \left[\alpha \frac{a_1}{f_1}+\beta \frac{a_2}{f_2}\right]\right)\hfill \\ +{\Lambda }_2^4\left(1-\cos \left[\gamma \frac{a_1}{f_1}+\delta \frac{a_2}{f_2}\right]\right),\hfill \end{array}& \left(3\right)\hfill \end{array}$

where α, β, γ, and δ are determined by two U(1) quantum numbers. Of course, f₁ and f₂ are O(M_GUT). Let us comment on a few issues related to the above potential.

If there is only one confining force at the GUT scale, we can set Λ₂ = 0 in Equation (3). In this case, there exists a flat Goldstone boson direction as shown with the red valley in Figure 1A. The blue bullet field point of Figure 1A quickly rolls along the blue path down to the red line vacuum. This flat red line direction cannot work as an inflation direction, but it corresponds to an axion potential with an infinite axion decay constant. Thus, with two axions and two nonvanishing axion potentials of Equation (3), there is a possibility of obtaining a trans-Planckian decay constant.

FIGURE 1

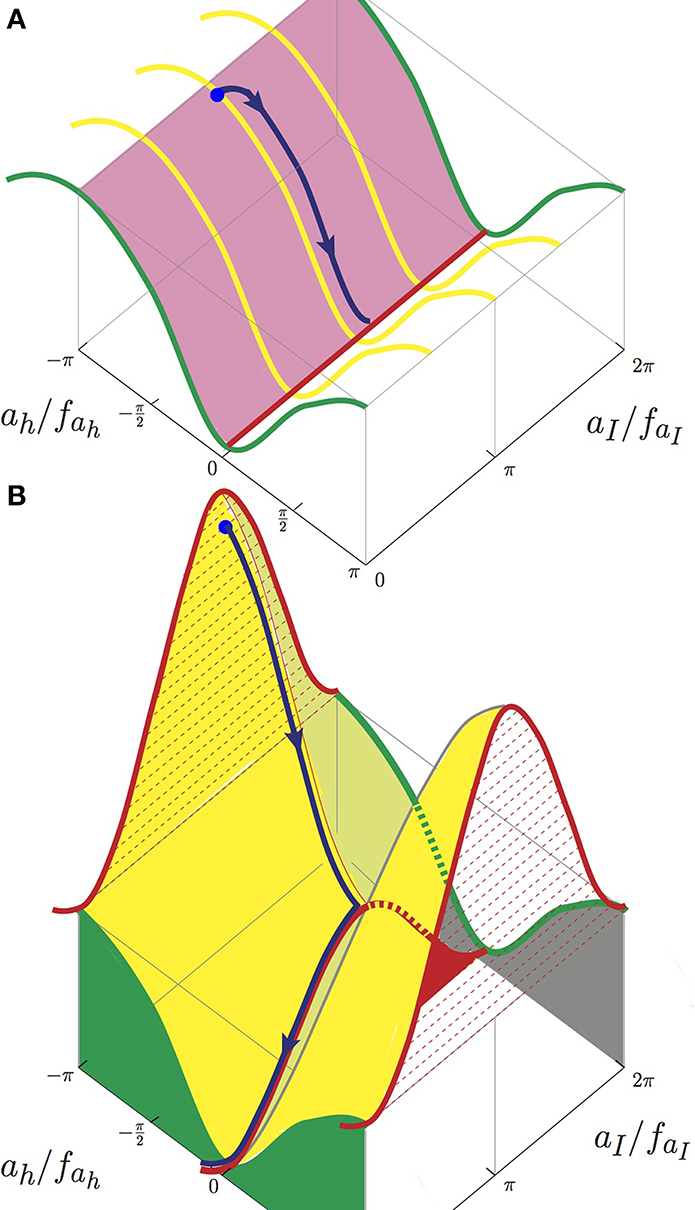
Figure 1. Two-flation. (A) The flat valley with one confining force is shown as the red line. We present yellow lines to show the curvature in the heavy axion direction. Even if the initial move of the vacuum is into an arbitrary direction, it quickly follows the heavy axion direction down to the flat valley, which is shown as the blue arrowed-curve. (B) In the KNP model, two confining forces generate two mass eigenvalues, those of the heavy axion a_h and the inflaton a_I. The flat valley of (a) rises to the red valley and f_aI can be much larger than f_ah. An inflation direction is shown as the blue arrowed-curve.

If there are two confining forces with nonvanishing Λ⁴₁ and Λ⁴₂, the situation is shown in Figure 1B [3], with no Goldstone boson direction. The red line direction of Figure 1A is lifted. To mimic the large f limit of Figure 1A, we choose a direction such that the PQ quantum numbers are aligned, and some people use the terminology ‘aligned inflation’ instead of natural inflation. The condition for the alignment is αδ ≈ βγ. This is because two axion masses, the heavy axion a_h and the light axion a_I, are

$\begin{array}{cc}{m}_{a_h}^2=\frac{1}{2}(A+B),& \left(4\right)\end{array}$

$\begin{array}{cc}{m}_{a_I}^2=\frac{1}{2}(A-B),& \left(5\right)\end{array}$

where

$\begin{array}{cc}A=\frac{{\alpha }^2{\Lambda }_1^4+{\gamma }^2{\Lambda }_2^4}{f_1^2}+\frac{{\beta }^2{\Lambda }_1^4+{\delta }^2{\Lambda }_2^4}{f_2^2},& \left(6\right)\end{array}$

$\begin{array}{cc}B=\sqrt{A^2-4{(\alpha \delta -\beta \gamma )}^2\frac{{\Lambda }_1^4{\Lambda }_2^4}{f_1^2{f}_2^2}}.& \left(7\right)\end{array}$

Let the approximation, αδ ≈ βγ, is described by a small number Δ, i.e., αδ = βγ + Δ. Then, the heavy axion and inflaton masses are

$\begin{array}{cc}\begin{array}{l}{m}_{a_h}^2\simeq \frac{{\alpha }^2{\Lambda }_1^4+{\gamma }^2{\Lambda }_2^4}{f_1^2}+\frac{{\beta }^2{\Lambda }_1^4+{\delta }^2{\Lambda }_2^4}{f_2^2},\hfill \\ m_{a_I}^2\simeq \frac{{\Delta }^2{\Lambda }_1^4{\Lambda }_2^4}{D}\hfill \end{array}& \left(8\right)\hfill \end{array}$

where D = f²₂(α²Λ⁴₁ + γ²Λ⁴₂) + f²₁(β²Λ⁴₁ + δ²Λ⁴₂). For simplicity of discussion, we will set Λ₁ = Λ₂ = Λ and f₁ = f₂ ≡ f. Then, the heavy and light masses are

$\begin{array}{cc}{m}_{a_h}^2\simeq ({\alpha }^2+{\beta }^2+{\gamma }^2+{\delta }^2)\frac{{\Lambda }^4}{f^2},& \left(9\right)\end{array}$

$\begin{array}{cc}{m}_{a_I}^2\simeq \frac{{\Lambda }^4}{({\alpha }^2+{\beta }^2+{\gamma }^2+{\delta }^2)f^2/{\Delta }^2},& \left(10\right)\end{array}$

from which we obtain

$\begin{array}{cc}{f}_{a_I}=\frac{\sqrt{{\alpha }^2+{\beta }^2+{\gamma }^2+{\delta }^2}f}{|\Delta |}.& \left(11\right)\end{array}$

With the same order of α, β, γ, and δ, the small number Δ can be O(1) to realize f_aI ≈ 100f if α, β, γ, δ = O(50). Thus, the probability for Δ ≈ 1 to be realized is 1 out of 50 × 50, i.e., the large f_aI ≈ 100f_ah is possible in 0.04% of random PQ quantum numbers α, β, γ, and δ of O(50). However, note that α, β, γ, and δ are integer PQ quantum numbers. So, realizing the needed 2–flation is assigning α, β, γ, and δ such that they are O(50). They are not random numbers but quantum numbers of singlet scalar fields. The question is how one can assign these large PQ quantum numbers. It belongs to a question on discrete symmetries [25]. If it is difficult to obtain such discrete symmetries, then one can say that the probability is small. If we do N-flation with a large N, then the PQ quantum numbers of O(2–10) are needed as briefly commented below, which may be easier to construct with discrete symmetries. However, the main perspective here is not on the PQ quantum numbers but are on the feasibility of obtaining a large numbers of non-Abelian gauge groups.

Suppose that we have a Z₁₂₀ discrete symmetry. Then, singlet scalar fields can have quantum numbers of 0, 1, …, 119. If this discrete symmetry is embedded in the U(1) PQ symmetry, the PQ domain wall number α, β, γ, and δ can be 0, 1, …, 119. If the singlets having the PQ quantum numbers of 0, 1, …, 49 and 71, …, 119 are not allowed to obtain VEVs, then α, β, γ, and δ can be 50, …, 70. In this way, we obtain a desirable quantum numbers such that αδ − βγ = O(1). This is not an issue of fine tuning but an issue on the VEVs of scalar fields.

We commented above that the flat valley of Figure 1A rises to the red valley of Figure 1B and f_aI can be ≈ 100f_ah in a small region of the PQ quantum number space and the inflaton is the blue curve on top of the red valley.

3. Number and Sizes of Non-Abelian Gauge Groups

The KNP 2-flation model has been generalized to N-flation models [24]. The N-flation has adopted two merits of 2-flation, one that the decay constant is ≈ $\sqrt{2}$ times larger and the other that the maximum height of the potential is ≈ 2 times larger, as depicted in Figure 1B. Namely, in the N-flation we expect that the decay constant can be ≈ $\sqrt{N}$ times larger and the maximum height of the potential is ≈ N times larger. Then, from the highest point of the potential the denominators in the ϵ and η calculation become N times larger, making ϵ and η N times smaller, and the decay constant is about $\sqrt{N}$ times larger. These merits are gradually diminished as the heavy axion paths shift directions as they roll down the hill¹.

In addition, in the N-flation the PQ quantum numbers are not tuned to large values of O(50). However, an N-flation with a large N suffers from the theoretical requirement of introducing N (≫ 2) GUT scale non-Abelian gauge groups. In obtaining N, we must satisfy the SM phenomenology also. After realizing the weak mixing angle, θ_W should be sin² ${\theta }_W=\frac{3}{8}$ at the GUT scale [27], non-prime orbifold compactification became popular since 2004 [28, 29], and sin² ${\theta }_W=\frac{3}{8}$ is possible in many non-prime orbifold GUTs. In general, sin² ${\theta }_W=\frac{3}{8}$ was not easy to be realized in earlier orbifold models [30–33]. Successful SM construction have been obtained in the Z_12−I [34–36] and Z_6−II orbifold compactifications [37–39]. However, heterotic string models have not provided a useful moduli stabilization program, even though there exist some suggestions on stabilization of some moduli [40–42]². Dynamical supersymmetry breaking [45] would also be another issue in a 2-flation model with a rank 16 gauge group. In the heterotic string theory with level 1 construction, the sum of the ranks of gauge groups is 16 [or 22 in the Narain compactification [46]³]. Out of rank 16, the SM uses 4 and rank 12 is left for the GUT scale confining gauge groups. If we use SU(4)'s for the N-flation, the maximal N is 4. This is not a case that the N-flation, motivated to have a large N, is aiming at. For N = 3, the sum of the ranks of the GUT gauge groups is barely acceptable, taking into account another non-Abelian group for breaking supersymmetry. As commented before, cases of N ≥ 3 reduce the PQ quantum number condition of the N = 2 case. For example, to obtain f_aI ≈ 100f, we need an approximate 10 × 10 × 10 PQ quantum numbers (as we obtained Equation (11) for the N = 2 case). Thus, the probability to obtain f_aI ≈ 100f is about 0.1%. But note that this is the PQ quantum numbers which are not really random priors. It is the problem of vacuum expectation values of singlet scalars with an appropriate discrete symmetry.

In the D-brane construction of string theory, Ramond-Ramond (RR) charges of D-branes should be canceled with proper orientifold p-planes (O_p-planes), which can be regarded as the fixed planes under a Z₂ symmetry: anti-D branes can also compensate the RR charge of D-branes, but they hardly break SUSY, making the system unstable. The RR charge of an O_p-plane (p = 0, 1, 2, …, 9), Q_Op is given by Q_Op = −2 · 2^p−5 × Q_Dp, where Q_Dp denotes the RR charge of a Dp brane⁴. [The maximum Q_Op is −32 Q_Dp.] It can be canceled by a stack of N_c Dp branes (the maximum number is 32 Q_Dp) parallel to an Op-plane, which yield a rank N_c/2 (the maximum number is 16) gauge group. Therefore, even in the D-brane construction, it is quite hard to obtain a gauge group whose rank is larger than 16.

4. Conclusion

The idea of natural inflation, using a GUT scale axion, has been extended to include 2, 3, …, N axions. For the 2-flation, the PQ quantum numbers are almost degenerate, e.g. differing 1 out of 50. This almost degeneracy of the PQ quantum numbers can be relaxed by increasing N. In addition, the slow-roll parameters ϵ and η can be reduced by a factor 1/N. Models along this line can be constructed at field theory level.

However, in string compactification the number of non-Abelian gauge groups are restricted, which makes the realization of N-flation very difficult. Most SM constructions from string compactification used the level 1 construction in which case the rank is 16. Even if higher levels are assumed, the rank is 22. In any case, the rank cannot be of order 100. Because of this difficulty of obtaining a large number of non-Abelian GUT scale gauge groups, the easiest realization of the trans-Planckian decay constant is the 2– and 3–flation. Nevertheless, it will be interesting to find out N ≥ 4 non-Abelian GUT scale gauge groups from string compactification with the features satisfying the low energy SM phenomenology.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Ki-Young Choi is supported by the National Research Foundation (NRF) grant funded by the Korean Government (MEST) (No. 2011-0011083), Jihn E. Kim is supported in part by the NRF grant (No. 2005-0093841) and by the IBS(IBS CA1310), and Bumseok Kyae is supported in part by the NRF grant (No. 2013R1A1A2006904).

Footnotes

1. ^See, for example McDonald [26].

2. ^For moduli stabilization in other frameworks, see e.g., Kachru et al. [43], Goldberger et al. [44].

3. ^For level greater than 1, it is possible to go beyond rank 16. We are aware of one example of construction at level 3 [47], containing the SM gauge group (with suitable Higgs fields for breaking the gauge group) with three families of quarks and leptons. In principle, other string theories dual to the heterotic one with higher levels would also allow gauge groups whose rank is larger than 16. For instance, see [48].

4. ^See, for example, Equation (15) of Giveon and Kutasov [49].

References

1. Ade PAR, Aikin RW, Barkats D, Benton SJ, Bischoff CA, Bock JJ et al. BICEP2 I: Detection Of B-mode Polarization at Degree Angular Scales. Phys Rev Lett. (2014) 112: 241101. doi: 10.1103/PhysRevLett.112.241101

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

2. Freese K, Frieman JA, Orlinto AV. Natural inflation with pseudo Nambu.Goldstone bosons. Phys Rev Lett. (1990) 65: 3233–36. doi: 10.1103/PhysRevLett.65.3233

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

3. Kim JE, Nilles HP, Peloso M. Completing Natural Inflation. JCAP (2005) 0501: 005. doi: 10.1088/1475-7516/2005/01/005

CrossRef Full Text | Google Scholar

4. Freese K, Kinney WH. Natural inflation: consistency with cosmic microwave background observations of planck and BICEP2. arXiv:1403.5277 [astro-ph. CO]

5. Kappl R, Krippendorf S, Nilles HP. Aligned Natural Inflation:Monodromies of two Axions. Phys Lett B (2014) 737: 124–8. doi: 10.1016/j.physletb.2014.08.045

CrossRef Full Text | Google Scholar

6. Choi K, Kim H, Yun S. Natural inflation with multiple sub-Planckian axions. Phys RevD (2014) 90: 023545. doi: 10.1103/PhysRevD.90.023545

CrossRef Full Text | Google Scholar

7. Dayan IB, Pedro FG, Westphal A, Wrase T. Towards natural inflation in string theory. arXiv:1407.2562 [hep-th]

8. Harigaya K, Ibe M, Yanagida TT. R-symmetric Axion/Natural Inflation in supergravity via deformed moduli dynamics. arXiv: 1409.0330[hep-ph]

9. Das K, Dutta K. N-flation in Supergravity. arXiv: 1408.6376[hep-ph]

10. Kim JE, Semertzidis YK, Tsujikawa S. Bosonic coherent motions in the Universe. Front Phys. (2014) 2: 60. doi: 10.3389/fphys.2014.00060

CrossRef Full Text | Google Scholar

11. Li T, Li Z, Nanopoulos DV. Helical Phase Inflation. arXiv: 1409.3267[hep-ph]

12. Guth A. The inflationary universe: a possible solution to the Horizon and flatness problems. Phys RevD (1981) 23: 347–56. doi: 10.1103/PhysRevD.23.347

CrossRef Full Text | Google Scholar

13. Linde AD. A new inflationary universe scenario: a possible solution of the Horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys Lett B (1982) 108: 389–93. doi: 10.1016/0370-2693(82)91219-9

CrossRef Full Text | Google Scholar

14. Albrecht A, Steinhardt PJ. Cosmology for grand unified theories with radiatively induced symmetry breaking. Phys Rev Lett. (1982) 48: 1220–3. doi: 10.1103/PhysRevLett.48.1220

CrossRef Full Text | Google Scholar

15. Mukhanov V. Physical Foundations of Cosmology, Cambridge: Cambridge University Press.

16. Lyth DH, Riotto A. Particle physics models of inflation and the cosmological density perturbation. Phys Rep. (1999) 314: 1–146. doi: 10.1016/S0370-1573(98)00128-8

CrossRef Full Text | Google Scholar

17. Coleman SR, Weinberg EJ. Radiative corrections as the origin of spontaneous symmetry breaking. Phys RevD (1973) 7: 1888–910. doi: 10.1103/PhysRevD.7.1888

CrossRef Full Text | Google Scholar

18. Linde AD. Chaotic inflation. Phys Lett B (1983) 129: 177–81. doi: 10.1016/0370-2693(83)90837-7

CrossRef Full Text | Google Scholar

19. Tsujikawa S, Ohashi J, Kuroyanagi S, De Felice A. Planck constraints on single-field inflation. Phys RevD (2013) 88: 023529. doi: 10.1103/PhysRevD.88.023529

CrossRef Full Text | Google Scholar

20. Ade PAR, Aghanim N, Armitage-Caplan C, Arnaud M, Ashdown M, Atrio-Barandela F et al. [Planck Collaboration]. Planck 2013 results. XXII. Constraints on inflation. [arXiv:1303.5082 [astro-ph.CO]].

21. Kim JE. The inflation point in U(1)_de hilltop potential assisted by chaoton, BICEP2 data, and trans-Planckian decay constant. Phys Lett B (2014) 737: 1–5. doi: 10.1016/j.physletb.2014.08.025

CrossRef Full Text | Google Scholar

22. Ade PAR, Aghanim N, Arnaud M, Aumond J, Baccigalupi C, Banday AJ et al. [Planck Collaboration]. Planck intermediate results. XXX. The angular power spectrum of polarized dust emission at intermediate and high Galactic latitudes. arXiv: 1409.5738 [astro-ph.CO].

23. Lyth DH. What would we learn by detecting a gravitational wave signal in the cosmic microwave background anisotropy?. Phys Rev Lett. (1997) 78: 1861–3. doi: 10.1103/PhysRevLett.78.1861

CrossRef Full Text | Google Scholar

24. Dimopoulos S, Kachru S, McGreevy J, Wacker JG. N-flation. JCAP (2008) 0808: 003. doi: 10.1088/1475-7516/2008/08/003

CrossRef Full Text | Google Scholar

25. Kim JE. Abelian discrete symmentries Z_N and Z_nR from string orbifolds. Phys Lett B (2013) 726: 450–5. doi: 10.1016/j.physletb.2013.08.039

CrossRef Full Text | Google Scholar

26. McDonald J. A minimal sub-planckian axion inflation model with large tensor-to-scalar ratio. arXiv:1407.7471 [hep-ph]

27. Kim JE. Z₃ orbifold construction of SU(3)³ GUT with sin² ${\theta }_W=\frac{3}{8}$. Phys Lett B (2003) 564: 35–41. doi: 10.1016/S0370-2693(03)00567-7

CrossRef Full Text

28. Choi K-S, Kim JE. Quarks and Leptons from Orbifolded Superstring. Lect Notes Phys. 696: 1–406. doi: 10.1007/b11681670

CrossRef Full Text

29. Kobayashi T, Raby S, Zhang R. Searching for realistic 4d string models with a Pati-Salam symmetry: Orbifold grand unified theories from heterotic string compactification on a Z₆ orbifold. Nucl Phys B (2004) 704: 3–55. doi: 10.1016/j.nuclphysb.2004.10.035

CrossRef Full Text | Google Scholar

30. Ibañez LE, Kim JE, Nilles HP, Quevedo F. Orbifold Compactifications with Three Families of SU(3)×SU(2)×U(1)ⁿ. Phys Lett B (1987) 191: 282–6 doi: 10.1016/0370-2693(87)90255-3

CrossRef Full Text | Google Scholar

31. Casas A, Munoz C. Three Generation SU(3)×SU(2)×U(1)_Y Models from Orbifolds. Phys Lett B (1988) 209: 214–20 doi: 10.1016/0370-2693(88)90452-2

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

32. Ibañez LE. Computing the weak mixing angle from anomaly cancellation. Phys Lett B (1993) 303: 55–62. doi: 10.1016/0370-2693(93)90043-H

CrossRef Full Text | Google Scholar

33. Ibañez LE. The Weak mixing angle in string theory and the Green-Schwarz mechanism. In: 23rd EloisatronWorkshop on Properties of SUSY particles, Erice, 1992: 54–64. arXiv: hep-ph/9303244

34. Kim JE, Kyae B. Flipped SU(5) from Z_12-I orbifold with Wilson line. Nucl Phys B (2006) 770: 47–82. doi: 10.1016/j.nuclphysb.2007.02.008

CrossRef Full Text

35. Kim JE, Kim J-H, Kyae B. Superstring standard model from Z_12-I orbifold compactification with and without exotics, and effective R-parity. JHEP (2007) 0706: 034. doi: 10.1088/1126-6708/2007/06/034

CrossRef Full Text | Google Scholar

36. Huh J-H, Kim JE, Kyae B. SU(5)flip x SU(5)′ from Z_12-I. Phys RevD (2009) 80: 115012. doi: 10.1103/PhysRevD.80.115012

CrossRef Full Text | Google Scholar

37. Lebedev O, Nilles HP, Raby S, Ramos-Sanchez S, Ratz M, Vaudrevange PKS et al. A Mini-landscape of exact MSSM spectra in heterotic orbifolds. Phys Lett B (2007) 645: 88–94. doi: 10.1016/j.physletb.2006.12.012

CrossRef Full Text | Google Scholar

38. Lebedev O, Nilles HP, Raby S, Ramos-Sanchez S, Ratz M, Vaudrevange PKS et al. The Heterotic Road to the MSSM with R parity. Phys RevD (2008) 77: 046013. doi: 10.1103/PhysRevD.77.046013

CrossRef Full Text | Google Scholar

39. Nilles HP, Ramo-Sanchez S, Ratz M, Vaudrevange PKS. From strings to the MSSM. Euro Phys J C (2009) 59: 249–67. doi: 10.1140/epjc/s10052-008-0740-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

40. Veneziano G, Yankielowitz S. An Effective Lagrangian for the Pure N = 1 Supersymmetric Yang-Mills Theory. Phys Lett B (1982) 113: 231–36. doi: 10.1016/0370-2693(82)90828-0

CrossRef Full Text | Google Scholar

41. Dixon L, Kaplunovsky V, Louis J, Peskin M. (1990). L. Dixon, talk presented at the A. P. S. D. P. F.Meeting at Houston; V. Kaplunovsky, talk presented at “Strings 90” workshop at College Station. Unpublished.

42. Casas JA, Lalak Z, Munoz C, Ross GG. Hierarchical Supersymmetry Breaking and Dynamical Determination of Compactification Parameters by Nonperturbative Effects. Nucl Phys B (1990) 347: 243–69. doi: 10.1016/0550-3213(90)90559-V

CrossRef Full Text | Google Scholar

43. Kachru S, Schulz MB, Trivedi S. Moduli stabilization from fluxes in a simple IIB orientifold. JHEP (2003) 0310: 007. doi: 10.1088/1126-6708/2003/10/007

CrossRef Full Text | Google Scholar

44. Goldberger WD, Wise MB. Modulus stabilization with bulk fields. Phys Rev Lett. (1999) 83: 4922–5. doi: 10.1103/PhysRevLett.83.4922

CrossRef Full Text | Google Scholar

45. Nilles HP. Dynamically Broken Supergravity and the Hierarchy Problem. Phys Lett B (1982) 115: 193. doi: 10.1016/0370-2693(82)90642-6

CrossRef Full Text | Google Scholar

46. Narain KS. New heterotic string theories in uncompactified dimensions < 10. Phys Lett B (1986) 169: 41–6. doi: 10.1016/0370-2693(86)90682-9

CrossRef Full Text | Google Scholar

47. Kakushadze Z, Tye H. Three family SO(10) grand unification in string theory. Phys Rev Lett. (1996) 77: 2612–5. doi: 10.1103/PhysRevLett.77.2612

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

48. DeWolfe O, Hauer T, Iqbal A, Zwiebach B. Uncovering infinite symmetries on [p, q] 7-branes: Kac-Moody algebras and beyond. Adv TheorMath Phys. (1999) 3: 1835–91. arXiv: hep-th/9812209

49. Giveon A, Kutasov D. Brane dynamics and gauge theory. RevMod Phys. (1998) 71: 983–1084. doi: 10.1103/RevModPhys.71.983

CrossRef Full Text | Google Scholar