Macromolecular crowding studies of amino acids using NMR diffusion measurements and molecular dynamics simulations

Introduction

Macromolecular crowding effects have traditionally been overlooked in many biophysical studies with discussion based on concentration instead of activity, but in the last 20 years there has been resurgence of interest in this important but less understood effect [1–7]. It is well known that in biological systems there are many compartments where macromolecular crowding occurs. The cytoplasm, for example, is a crowded mixture of components such as proteins/soluble macromolecules, small molecules and membranes. Cell membranes also constitute crowded environments with carbohydrates and proteins being “dissolved” in the membrane lipid “solvent.” Similarly polysaccharides and collagen influence crowding effects, particularly in the extracellular matrix of tissues [8, 9]. Minton and Zimmerman [6, 10] showed that the concentration of proteins inside Escherichia coli is in the range 200–300 mg/ml, whereas that of RNA is in the range 75–150 mg/ml. Therefore, the total cytoplasmic concentration of protein and RNA molecules is in the range of 300–400 mg/ml and they occupy of 20–30% of the total cellular volume. In contrast, red blood cells contain about 350 mg/ml of hemoglobin while blood plasma contains 80 mg/ml of protein. In general, the macromolecules occupy between 20 and 30% of the total cell volume and hence this volume is unavailable to other molecules in the system [6, 10].

In many cases the macromolecular components in the cellular systems exist as “background molecules” and do not directly interact with the reactants or products of particular reactions [11]. However, the net effect of all the inert background macromolecules on a particular process may be quite significant, especially in a crowded environment. In this situation, the excluded volume stimulates the macromolecules to bind with each other [2, 11–13]. Crowding is responsible for macromolecular association (protein association or self-association) and conformational changes (rate of folding or refolding, stability of proteins) [5, 14–17]. As the number of macromolecules (or small molecules) increase, the placement of molecules is less likely to be random as compared to an ideal uncrowded solution. This results in a decrease in configurational entropy and increases in both the free energy and the chemical potential of each macromolecule (dilute as well as concentrated macromolecules) present in the system [12, 18]. Consequently, equilibria in the system are affected and this favors the reactants or products that exclude the least volume. Zhou et al. [1] have considered a number of biological systems which demonstrate the effects of volume exclusion on conformational effects and free energy of macromolecules in crowded and confined systems.

Since volume exclusion and obstruction are intimately related, macromolecular crowding also affects thermodynamics and diffusion processes in the cellular system [13, 19]. Diffusion is a natural method to study the effects of crowded solutions [19–21]. A number of diffusion studies have been used to characterize aggregation in amino acids [22–25]. The diffusion coefficient of both small and large molecules inside a cell has been found to be smaller compared to their infinite dilution diffusion coefficient due to crowding effects [17, 19, 21, 26, 27]. The rate of diffusion limited reaction in biochemical solutions inside cells decreases, irrespective of the size of molecules involved in the reaction [1, 19]. The activity coefficient of hemoglobin has been found to vary non-linearly with increasing hemoglobin concentration [13]. Schnell and Turner [18] have explained the major difference between cytoplasmic and test tube biochemical kinetics using the law of mass action, power-law approximation and fractal-like kinetics under in vivo conditions. Crowding also affects the diffusion processes of solutes by increasing the solution viscosity [28, 29]. At high concentrations of macromolecules, in addition to solvent interactions, the motion of particles also reflects interaction with macromolecules. At time scales much smaller than the collision time, the inter particle interactions do not significantly disturb the diffusive path. However, at long time scales, such interactions are significant leading to lengthened diffusive paths [20, 30]. The diffusion coefficient (D) is related to the mean squared displacement (MSD) via the Einstein relationship [31–33]:

$\begin{array}{cc}D(t)=\frac{\text{MSD}(t)}{nt},& (1)\end{array}$

where n = 2, 4, or 6 for one, two or three dimensions, respectively.

Nuclear magnetic resonance (NMR) based measurement of self-diffusion (i.e., NMR diffusometry) is a powerful tool for studying associating biomolecular systems including ligand binding and protein self-association [17, 27]. Amino acids, being simpler than proteins, are a logical stepping stone toward understanding crowded biological systems. The clustering of amino acids such as glycine has been studied using NMR diffusion experiments and molecular dynamics (MD) simulations as a function of concentration, pH and temperature [22–24, 34–38]. Hughes et al. [23] used a multidisciplinary approach (i.e., NMR diffusion, MD simulations and small-angle neutron scattering) to investigate the crystallization of glycine in aqueous solutions. Hamad et al. [34] have attempted to explain the size of glycine clusters using radial distribution functions (RDFs) and hydrogen bonding. Campo et al. [35] used MD simulations to study the modifications of the glycine structure with changes in solution pH, and observed changes in the diffusion coefficient of glycine solutions. Ma et al. [24] investigated the diffusion coefficients of valine, isoleucine, serine, threonine and arginine in aqueous solutions at 298 K using a holographic technique. However, despite the significance of crowding on solution thermodynamics, the molecular level mechanism of crowding including how it influences diffusion remains to be clarified [19, 36–38]. The major hindrance to understanding crowding is the lack of a direct comparison of experimental data with theoretical data for the same system [39].

In this work, the diffusion of four amino acids (glycine, alanine, valine and phenylalanine) was investigated up to their solubility limit in water using NMR. The solubility of glycine, alanine, valine and phenylalanine in water at 298 K is about 249.9, 166.5, 88.5, and 29.65 mg/ml, respectively [40]. The experimental data was then analyzed using various aggregation and obstruction models. MD simulations of the amino acids were also performed to enable comparison with the experimental diffusion results to give a clearer understanding of the molecular level solution interactions in crowded systems. This work is organized as follows: In the theoretical background section, the analysis of NMR diffusion data of associated systems using aggregation distribution and obstruction models are discussed. In the Materials and Methods section, the experimental and simulations details are provided. In the Results and Discussion section, NMR diffusion results of amino acids with aggregation and obstruction models are discussed. This section also includes MD simulation results analyzed using radial distribution functions, hydrogen bonding and diffusion coefficients in different force fields. Concluding remarks are presented in the final section.

Theoretical Background

Diffusion Measurements of Associating Systems

Polydisperse systems are formed with increasing concentration in associating systems and at least in principle the diffusion data obtained by experimentation can be used to calculate the degree of polydispersity. However, in reality, the size of the different molecules and calculated degree of polydispersity in these complicated systems are difficult to separate from diffusion measurements [41–43]. The infinite dilution diffusion coefficient of a molecule is related to its molecular weight through its effective hydrodynamic radius via the Stokes-Einstein-Sutherland equation [33, 44–46]:

$\begin{array}{cc}{D}_0=\frac{kT}{f},& (2)\end{array}$

where k is the Boltzmann constant, T (K) is temperature and f (kg s⁻¹) is the friction coefficient of the diffusing molecule. In the case of a spherical particle with an effective hydrodynamic radius r_S (m) in a solvent of viscosity η (Pa s), f = cπηr_S where the constant c characterizes the interaction between the solute and the solvent with c = 4 or 6 denoting the “slip” and “stick” conditions respectively. However, the Stokes-Einstein-Sutherland equation (Equation 2) [33, 44–46] is derived under many assumptions related to the size, shape and concentration of the solute and solvent molecules [31, 47]. The Stokes-Einstein-Sutherland equation (Equation 2) is only valid at infinite dilution such that interactions between solute particles can be ignored. It is further assumed that the solute is much larger than the solvent molecules so that the solute sees the solvent as a continuum. These assumptions reduce the system to a one body problem [48]. Correspondingly, when large particle interactions are significant (e.g., in highly concentrated solutions) and cannot be ignored (e.g., in cell cytoplasm), this corresponds to a complicated many body problem [31]. In this situation, the diffusive path of smaller molecules (e.g., water, glucose) increases as they have to diffuse around the larger and generally irregularly shaped and tumbling “obstructing” molecules (e.g., macromolecular components of cell cytoplasm) [6, 20, 49].

Magnetic field gradient based NMR diffusion measurements [e.g., the pulsed gradient spin-echo method (PGSE)] are non-invasive in nature and do not disturb the thermodynamics of the system [17, 27, 50–53]. In this method, magnetic gradients and rf (radio-frequency) pulses are applied to nuclei (usually ¹H) in a pulse sequence to measure the attenuation of the spin-echo signal due to self-diffusion. A detailed description of the technique can be found elsewhere [31, 51, 53–55]. The NMR echo signal of a single freely diffusing species attenuates according to [55, 56]:

$\begin{array}{cc}\begin{array}{l}E(g,\Delta )=\exp \text{}(\text{}-{\gamma }^2{g}^{2}D{\delta }^2(\Delta -\delta /3)),\hfill \\ \text{=}\text{exp}(\text{}-bD)\hfill \end{array}& (3)\end{array}$

where b = −γ²g²δ²(Δ − δ/3), γ is the gyromagnetic ratio (rad s⁻¹ T⁻¹), g is the magnitude of the magnetic gradient pulse (T m⁻¹), δ is the duration of the gradient pulse (s), and Δ is the diffusion time (s).

Concomitant with the improved technical abilities of modern NMR spectrometers to measure diffusion, there has been increased awareness of the experimental limitations and the need for more realistic models for analyzing diffusion data from associating systems [43, 50, 57]. The NMR visibility of the various oligomeric species present changes with aggregation state in an NMR diffusion measurement. As aggregation increases, higher oligomers become partially or completely NMR invisible due to relaxation weighting thereby leaving only the small oligomers visible in the spectrum (Figure 1). In solutions containing highly aggregated species, the visible NMR species will diffuse faster (more free path to move) due to less obstruction from other particles. In a polydisperse sample formed from a single monomer species, the magnetization of the ith species is directly proportional to MW_in_i, where MW_i is the molar mass of the ith aggregate species, and n_i is the number of such aggregates present. The resultant echo signal amplitude of N freely diffusing species with individual diffusion coefficient D_i, and spin-spin relaxation time, T_2i, is given by [17, 51]:

$\begin{array}{cc}S(g,\Delta )\text{}=\text{}{\displaystyle \sum _i^{N}M}{W}_i{n}_i\exp \text{}\left(\text{}\text{}\frac{-2\tau }{T_{2i}}\text{}\text{}\right)\exp \text{}(\text{}\text{}-{\gamma }^2{g}^2{\delta }^2(\Delta -\delta /3)D_i),& (4)\end{array}$

where 2τ is the length of the pulse sequence.

FIGURE 1

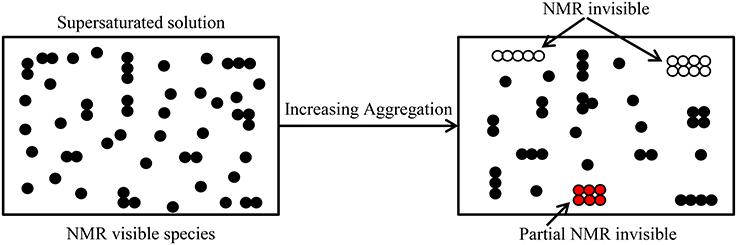
Figure 1. Depiction of molecules in a supersaturated solution with increasing aggregation and their visibility in an NMR diffusion measurement. Dimers and higher oligomers (some have complex shapes) form with increasing concentration. As the oligomeric size increases the T₂ value becomes shorter, consequently according to Equation (4) the oligomer becomes increasingly NMR invisible.

Normalization with the g = 0 case removes the effects of relaxation from the analysis. The normalized spin-echo attenuation [i.e., E(g,Δ)] of a polydisperse species undergoing diffusion is [31, 58]:

$\begin{array}{cc}\begin{array}{l}E(g,\Delta )=\frac{S(g,\Delta )}{S(0,\Delta )}\hfill \\ =\frac{{\displaystyle {\sum }_i^{N}M}{W}_i{n}_i\exp \text{}\left(\frac{-2\tau }{T_{2i}}\right)\exp (-{\gamma }^2{g}^2{\delta }^2(\Delta -\delta /3)D_i)}{{\displaystyle {\sum }_i^{N}M}{W}_i{n}_i\exp \text{}\left(\frac{-2\tau }{T_{2i}}\right)}\hfill \end{array}& (5)\end{array}$

In the simplest case when the signals from the different species are distinct, the diffusion coefficients determined from each NMR signal can be used to differentiate between different species which can be used to resolve the spectra of such a mixture of solutes [59–61]. However, in most real systems (e.g., aggregating proteins and other polymers) the signals of different sized species are overlapped thereby complicating the analysis [41–43]; thus, the echo signal attenuation from a polydisperse system (i.e., Equation 5) will be multiexponential. Since, for many associating systems the experimentally observed attenuation is usually single exponential (i.e., “linear” when plotted on a log scale). It can be assumed that there is a process which results in ensemble averaging of the diffusion coefficients of the aggregated systems (e.g., [17, 41, 58]). An example of a non-linear attenuation plot on log scale for overlapped signals for two species is shown in Figure 2.

FIGURE 2

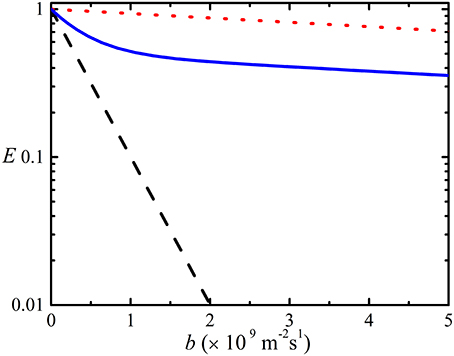
Figure 2. Simulated ¹H echo attenuation plots for a fast diffusing species () such as water (2.3 × 10⁻⁹ m²s⁻¹) in hemoglobin solution, a slowly diffusing species () with a diffusion coefficient of (6.8 × 10⁻¹¹ m²s⁻¹) [62]. Also shown is the sum of the attenuation values of the two species () if the signals of fast and slow diffusion species are overlapped and in equal concentration. The simulation was performed with γ = 2.67 × 10⁸ rad s⁻¹T⁻¹, Δ = 200 ms and δ = 6 ms and g ranging from 0 to 0.20 T m⁻¹.

Ignoring the relaxation terms (i.e., assuming that any difference in relaxation properties of different sized aggregates is negligible), Equation (5) gives the combined diffusion averaging effects for the different oligomers. The averaging effect is approximated by taking the cumulant expansion of Equation (5) to second order [31, 58]:

$\begin{array}{cc}\text{1n}(E)=-b{\langle D\rangle }_w+\frac{b^2}{2}\left({\langle D\rangle }_w^2-{\langle D^2\rangle }_w-{\langle D^2\rangle }_w\right)\text{},& (6)\end{array}$

where〈D〉_w, is the weight-averaged diffusion coefficient:

$\begin{array}{cc}{\langle D\rangle }_w=\frac{{\displaystyle {\sum }_i^{N}M}{W}_i{n}_i{D}_i}{{\displaystyle {\sum }_i^{N}M}{W}_i{n}_i}.& (7)\end{array}$

If the quadratic terms are ignored in Equation (6), the experimentally determined diffusion will then give an apparent diffusion coefficient which also includes the effect of obstruction. The resulting NMR signal attenuation is defined by [17, 31, 50, 58]:

$\begin{array}{cc}E(g,\Delta )=\exp \text{}(\text{}-b{\langle D\rangle }_W^C),& (8)\end{array}$

where the superscript C denotes the effects of obstruction (i.e., obstruction from crowding). Thus, the measured diffusion coefficient inherently contains the effects of polydispersity and obstruction.

Aggregate Distribution

In a given aggregation model, the exact populations of the aggregates in a distribution of different sized oligomers can be derived. Many models exist for calculating the distribution of the different sized oligomers [63]. In an attenuated K model, the addition of a molecule to an oligomer has been proposed to occur with constant enthalpy. However, successive additions become less probable and hence less favored entropy, and decreasing equilibrium constant [63]. The attenuated K model requires iterative solutions making it more difficult to use in practice. On the other hand, an isodesmic model is a simpler and more general approach for assigning the equilibrium constant for the self-association of proteins. In an isodesmic model aggregation leads to equal free energy and equilibrium constant [63]. Here we consider an isodesmic model [63, 64] for analysing experimental diffusion data (Figure 3). This distribution model has been used in characterizing protein association [17, 51]. The aggregate propagates by addition of a monomer unit, M₁, as described by [17, 64]:

$\begin{array}{cc}{M}_{i-1}+M_1\stackrel{K_e}{\leftrightarrow }{M}_{i}i=2\dots \infty ,& (9)\end{array}$

where K_e (= K₂ = K₃ = · · · = K_i) is the equilibrium constant (M⁻¹). The total concentration of aggregates in the system (in units of monomers) is given by [17, 64]:

$\begin{array}{cc}C={\displaystyle \sum _{i=1}^{\infty }{c}_i}i,& (10)\end{array}$

where c_i is the concentration of the ith oligomer state. Hence, the mole fraction of oligomer is given by [17, 64]:

$\begin{array}{cc}{\alpha }_i=i{(K_{e}C)}^{i-1}\left(\frac{2K_{e}C+1-\sqrt{1+4K_{e}C}}{2{(K_{e}C)}^2}\right){\text{}}^i.& (11)\end{array}$

FIGURE 3

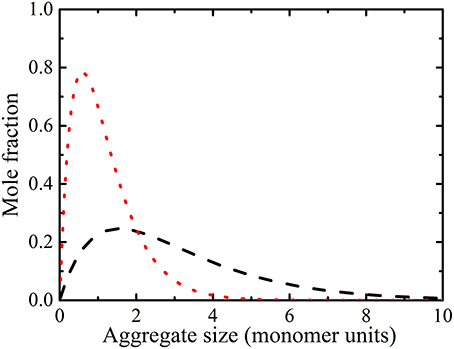
Figure 3. Mole fraction plots of alanine aggregate species in 0.2 () and 1.669 M () solutions calculated from the isodesmic model (i.e., Equation 11) with K_e = 1.39 (equilibrium constant from Table 1). The simulations reveal that large oligomers are present at high concentrations.

The apparent diffusion coefficient of the oligomeric system including the effects of aggregation and obstruction can be defined by [17, 51]:

$\begin{array}{cc}{\langle D\rangle }_W^C=O_D(C)D_1^0{\displaystyle \sum _{i=1}^N{\alpha }_i}{i}^{-1/3},& (12)\end{array}$

where D⁰₁ is the infinite dilution diffusion coefficient of the monomer and O_D represents a suitable expression for self-obstruction as a function of concentration. The effects of obstruction or volume exclusion are present even in the absence of aggregation [17, 27]. Therefore, when measuring diffusion in solutions with increasing concentration it is necessary to be able to differentiate between the effects of association and obstruction in order to accurately model and account for changes in the diffusive behavior.

Obstruction

Obstruction can be quantified by introducing an obstruction factor which is defined as the ratio, D(t)/D₀, of the observed diffusion coefficient and the local diffusion coefficient D₀ (bulk diffusion coefficient). The obstruction factor depends on the shape, volume fraction, and spatial and orientation distribution of the obstructing molecules [48, 65–67]. The simple obstruction models derived to date assumed that all of the obstructing particles have the same size and shape (generally taken to be spheres) and are only valid at very low concentrations [48, 65–71]. Furthermore, these obstruction models do not account for the effects from electrostatic interactions. In reality, the shapes of diffusing particles are much more complex than spheres or ellipsoids and the effects of hydration, charge and rugosity of their surfaces also need to be considered [17, 31]. Additionally, none of these models account for the presence of aggregation which is important since even with the same total concentration (expression as monomers), the degree of obstruction will change with the degree of polydispersity. A number of different obstruction models are used to simulate obstruction in glycine solution as a function of concentration in Figure 4. Jönsson et al. [65] derived the obstruction factor for a system containing evenly spaced monodisperse spherical particles in a cell including the binding effects from solvent molecules [72]. Lekkerkerker and Dhont [71], on the other hand, provided the obstruction factor using the MSD of interacting Brownian particles. Han and Herzfeld [48] derived a relationship for a hard sphere diffusing among hard spherocylinders while Tokuyama and Oppenheim (T and O) [70, 73] used the Navier-Stokes equation to develop a model for the dynamics of concentrated hard-sphere suspensions of interacting Brownian particles with both hydrodynamic and direct interactions.

FIGURE 4

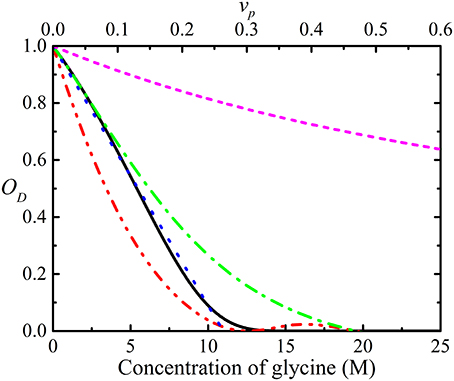
Figure 4. Simulations of the obstruction factor, O_D, as a function of the concentration of glycine in water, using the models of Jönsson et al. () [65], Han and Herzfeld () [48], Lekkerkerker and Dhont () [71], T and O short () and long () range hydrodynamic interactions [70, 73]. Note: while glycine is only soluble up to ~5 M under standard conditions, the graph depicts obstruction up to much higher concentration. The equivalent volume fractions (v_p) are shown in the secondary x-axis.

NMR diffusion measurements are usually carried out with solutes or macromolecules present in the millimolar range or above, yet most of the theory used to analyse the diffusion data has been derived on the assumption that diffusion is occurring at infinite dilution. Clearly, cellular milieu are never at infinite dilution and they are almost always crowded systems. Thus, diffusion measurements of biological systems can be reporting on true self-diffusion, obstruction and molecular association simultaneously. Without cogent models it is extremely difficult to separate these effects. Yet, the ability to separate them would provide a huge increase in the amount of information that can be available. Mathematically it is very difficult to develop analytical models for such systems without numerous simplifying assumptions. For example, obstruction is a many-body problem and in general a numerical solution of the obstruction factor is the only practicable approach. MD simulations for these systems can provide valuable information on the solute-solute, solvent-solvent and solute-solvent interactions at the atomic level [37, 38, 74–76].

MD Simulations

In MD simulations, the force field is a sum of different forces responsible for bonded and non-bonded interactions between molecules in a solution. A number of force fields have been developed to study a variety of different systems or properties by computer simulation [77–80]. These force fields have the same interaction sites of molecules but differ in the Lennard-Jones and Coulombic terms, which give significant differences in calculated properties for the molecules of interest [37, 81]. Hence, the choice of force fields plays a crucial role in determining different interactions between molecules for a particular system. Elcock et al. [37] investigated the performance of different force fields on highly crowded amino acid solutions. Note that the effect of different force fields on the simulated diffusion coefficients of water and amino acids also needs to be compared with experimental results. Accurate values for the diffusion coefficients of complex molecules are very difficult to obtain using MD simulations [35, 82]. However, MD simulations have continuously been improved to study the dynamics and structure properties of complex systems [83–85]. There are two methods to calculate diffusion coefficients from MD simulations: (i) using the velocity auto-correlation function and (ii) from determination of the MSD. All diffusion coefficients in this study were determined using MSD analysis.

The diffusion coefficient of water simulated using different water models [i.e., SPC (simple point charge), SPC/E (extended simple point charge), TIP3P (transferable intermolecular potential 3P)] with different velocity rescaling methods and other simulation parameters has been examined at 298 K [81, 86, 87]. In this work, three different force field and water model combinations were used in the MD simulations: GROMOS 53A6 [79] with the SPC/E water model [88], OPLS-AA/L [80] with the TIP3P water model [89], and AMBER ff99SB-ILDN [77, 78] with the TIP3P water model [89].

Materials and Methods

Materials

The following amino acid solutions at various concentrations were prepared in D₂O (99.9%, Cambridge Isotope Laboratories): Glycine (99.0%, Sigma) from 0.01 to 3.72 M, alanine (99.0%, Fluka) from 0.006 to 1.69 M, valine (99.5%, Sigma) from 0.018 to 0.43 M and phenylalanine (99.0%, Sigma) from 0.02 to 0.17 M. No visible precipitation of the amino acids was observed in the NMR tubes (5 mm, Wilmad Lab Glass) during any of the experiments.

NMR Experiments

¹H NMR diffusion experiments were performed at 298 K on a Bruker Avance 400 MHz NMR spectrometer with a 5 mm broadband BBO probe equipped with a z-axis magnetic field gradient. The z-axis gradient strength was calibrated by measuring the known diffusion coefficient of residual water (1.9 × 10⁻⁹ m²s⁻¹) [90] in D₂O at 298 K. The maximum gradient strength was found to be 0.55 T m⁻¹. The PGSTE sequence [55] with rectangular gradients was used for all translational diffusion measurements. Typical acquisition parameters were gradient pulse duration δ = 1.5 ms, diffusion measurement timescale Δ = 0.2 s with g varied from 0.005 to 0.253 T m⁻¹ in increments of 0.017 T m⁻¹ to give 16 data points for each attenuation curve. The values δ, g, and Δ were selected so that the echo signal was attenuated by at least 80% with the largest value of g. In all cases the spectral width was 5.58 kHz and a total of 22 k data points were acquired. Each spectrum was averaged at least over 8 scans depending on the signal-to-noise ratio. Recycle delays were chosen to achieve five times spin-lattice relaxation time between scans. The NMR diffusion data were analyzed by non-linear least squares regression of the appropriate attenuation expression using OriginPro 9 (OriginLab) software. The error estimates given in the figures are those from the data fitting. The true error will be typically of the order of 1% or more [91].

MD Simulation Details

All MD simulations were performed using GROMACS software version 4.6.3 [92, 93]. The systems studied in the simulation consisted of glycine, alanine, valine and phenylalanine zwitterions immersed in a cubic box of water with periodic conditions. Simulations were performed at solute concentrations of 50, 100, 200, and 300 mg/ml. The solutions were modeled by cubic simulation cells (with lengths between 31.35 and 32.86 Å for glycine, 31.38 and 33.09 Å for alanine, 31.43 and 33.22 Å for valine and 31.50 and 33.34 Å for phenylalanine depending on concentration) in which the 1000 water molecules were kept constant. The box dimensions were fixed by the corresponding densities at 298 K and 1 atm. All systems were first minimized using steepest decent minimization for 1000 steps. The temperature was then equilibrated using an NVT ensemble with temperature at 298 K using the v-rescale thermostat at 0.1 ps. The NVT ensemble was carried out for 400 ps. After temperature equilibration, the pressure was equilibrated using an NPT ensemble at 1 atm using the Parrinello-Rahman barostat [94] at 0.1 ps. The NPT ensemble was carried out for 1 ns. During the simulations, the Lennard-Jones forces were cut off at 12 Å and electrostatic forces were treated by the particle mesh Ewald (PME) method [95]. The equations of motion were integrated using the Leapfrog algorithm with a 1 fs time step for 10 ns and the covalent bonds were restored using the LINCS algorithm [96]. The coordinates and energy values were saved at 5 ps intervals. MSD plots of water models were used to confirm the stability of the simulations.

Results and Discussion

NMR Diffusion Measurements

It was observed that the diffusion coefficient of the residual protonated water (i.e., HOD) in the amino acid solutions was lower than that of neat water [90] (i.e., 1.9 × 10⁻⁹ m²s⁻¹) (Figure 5). In crowded solutions, the available volume for solvent molecules will be restricted leading to excluded volume effects, thus, the solvent diffusion coefficient should decrease with amino acid concentration.

FIGURE 5

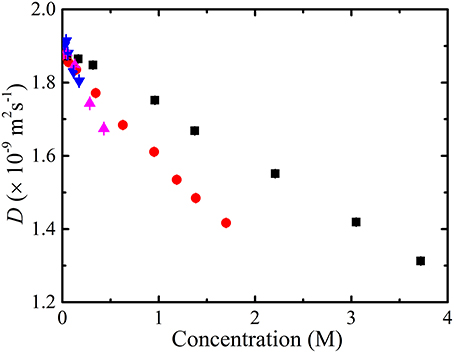
Figure 5. Experimentally measured (i.e., NMR) derived diffusion coefficients of the residual water molecules in D₂O as a function of the concentration of glycine (), alanine (), valine () and phenylalanine (). The error bars for the measurements are also included; however, the errors are much smaller than the drawn symbols.

The results of the diffusion measurements performed on glycine, alanine, valine and phenylalanine in D₂O are summarized in Figure 6. The diffusion coefficients of the amino acids were concentration dependent and decreased with amino acid concentration. Extrapolation of the measured diffusion coefficients using a linear function gave the diffusion coefficient of each amino acid at infinite dilution. The diffusion coefficient of the smallest amino acid (glycine) was the largest and phenylalanine the slowest amongst the amino acids at the same concentration. The extrapolated infinite diffusion coefficients of alanine and phenylalanine were in agreement with previous NMR diffusion studies [22].

FIGURE 6

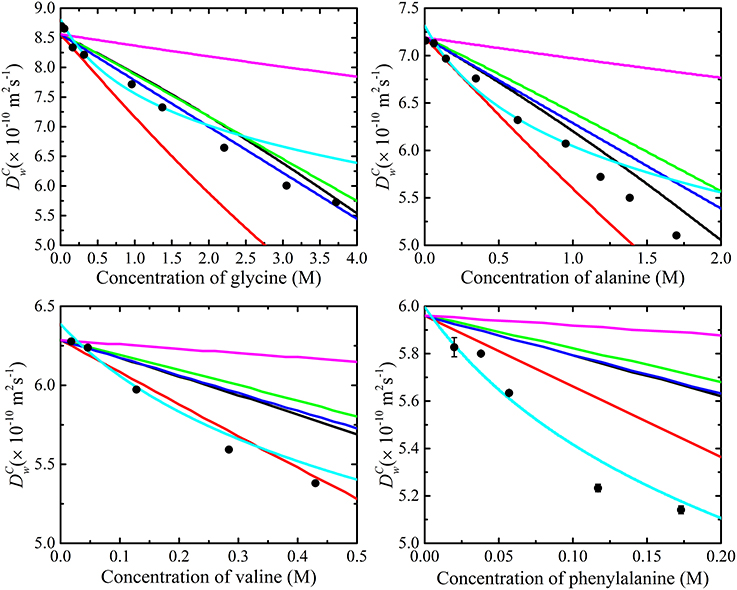
Figure 6. The measured diffusion coefficients (•) of glycine, alanine, valine, and phenylalanine in D₂O at 298 K as a function of amino acid concentration modeled using obstruction and aggregation models separately (i.e., Equation 12 with N = 1). Clearly, none of the current obstruction models [i.e., Lekkerkerker and Dhont () [72], Han and Herzfeld () [49], T and O's short interactions model (), T and O's long interactions model () [71], and Jönsson et al. () [66], fit to the experimental data well. Also shown is the fitting of the isodesmic (i.e., Equation 11) aggregation model () [65] to the experimental data. The measured diffusion coefficients are lower than those predicted by the obstruction models which imply that an additional process such as aggregation is likely to be present. The isodesmic association model doesn't fit or provide cogent information if obstruction is unaccounted for. On the basis of the poor fit of the T and O long range interaction model, one may conclude that aggregation is not occurring. However, in this model the diffusion coefficient is reduced due to the presence of non-local hydrodynamic interactions and the absence of direct interactions-meaning that aggregation might still be occurring. The error bars for the measurements are also included; however, the errors are typically much smaller than the symbols.

The decrease in the obtained amino acid diffusion coefficients can be explained by analyzing the data using aggregation and obstruction models. The extrapolated infinite dilution diffusion coefficients of the amino acids were used to predict the obstruction factors of the amino acids. Equation (12) with N set to 1 (i.e., assuming no aggregation and all amino acids present in monomer form) was fitted to the experimental data and the values of the fitted parameters are given in Table 1. The results presented in Figure 6 clearly show that none of the obstruction models (i.e., Figure 4) were able to accurately describe the decrease with concentration of the experimental amino acid diffusion data. Similarly, the isodesmic association model (i.e., Figure 3) also poorly described the experimental amino acid diffusion data. The poor fitting from both aggregation and obstruction models to the experimental amino acid diffusion data indicates that amino acids are undergoing self-aggregation in the presence of obstruction from other amino acid molecules. Hence, both aggregation and obstruction models need to be taken into account to explain the decreased amino acid diffusion coefficients.

TABLE 1

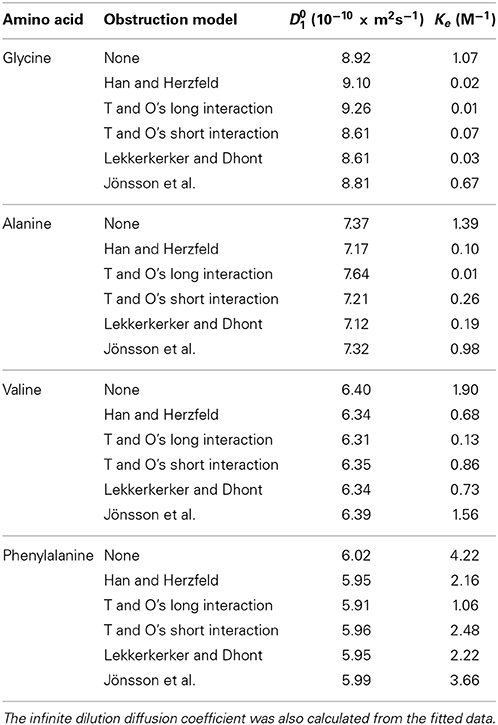
Table 1. Summary of the fitting results from regressing Equation (12) including the isodesmic association model and various obstruction models [48, 65, 70, 71, 73] on to the experimental glycine, alanine, and valine and phenylalanine diffusion data.

The experimentally determined amino acid diffusion coefficients were then analyzed by fitting aggregation and obstruction models (i.e., Equation 12). The maximum oligomeric state of the amino acids was limited to a pentamer. The fitting results are summarized in Figure 7 and Table 1. Comparison of Figures 6, 7 reveals that the amino acids are likely subject to both association and obstruction in solution. The best fit to the experimental data was obtained with Lekkerkerker and Dhont's, T and O's short interactions, and Han and Herzfeld's model together with the isodesmic association model. The fitting of the obstruction model of Jönsson et al. to the diffusion data in highly concentrated solutions was reasonable as it includes the solvation effects from the solvent molecules. On the other hand, that T and O's long range interaction model gave a poor fit to the experimental data implies the absence of direct interactions between small amino acid molecules.

FIGURE 7

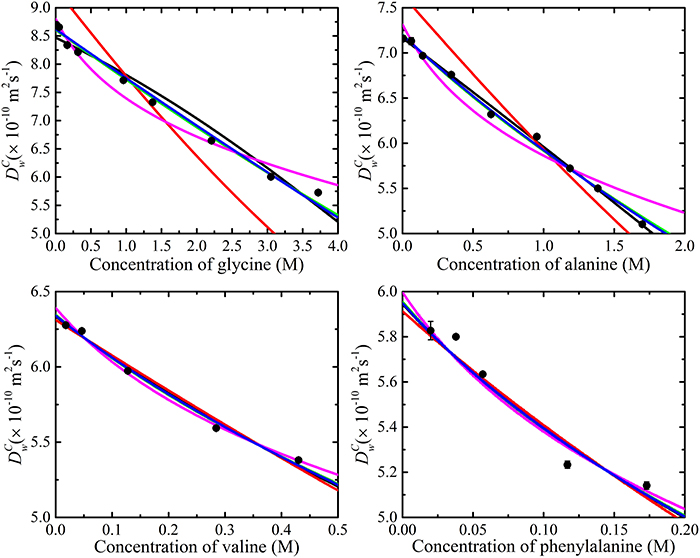
Figure 7. The various obstruction models fitted to the experimental data with the isodesmic model using Equation (12). Lekkerkerker and Dhont's (), Han and Herzfeld's () and T and O's short interactions model () best fit to experimental data. Also shown are Jönsson et al. () and T and O's long interactions model (). The error bars for the measurements are also included; however, the errors are much smaller than symbols.

It is important to note that amino acids also exist as zwitterions and that these obstruction models do not account for the effects of electrostatic interactions between molecules. It would be interesting therefore to perform a similar study of amino acid solutions at different pH values using MD simulations and to experimentally observe the effects of electrostatic interactions on the diffusion coefficient.

Radial Distribution Function Analysis

RDFs are used to understand the size and shape of different clusters formed by association of amino acid molecules. The RDF between different amino acid molecules is defined by [92]:

$\begin{array}{cc}\begin{array}{l}{g}_{AB}(r)=\frac{\langle {\rho }_B(r)\rangle }{{\langle {\rho }_B\rangle }_{local}},\hfill \\ \text{=}\frac{1}{{\langle {\rho }_B\rangle }_{local}}\frac{1}{N_A}{\displaystyle \sum _{i=A}^{N_A}{\displaystyle \sum _{j=B}^{N_B}\frac{\delta (r_{ij}-r)}{4\pi r^2}}},\hfill \end{array}& (13)\end{array}$

where 〈ρ_B(r)〉 is the particle density of type B at a distance r around particles A and 〈ρ_B〉_local the particle density of type B averaged over all spheres around particles A with radius r_max.

The value of g (r) was calculated for each amino acid at different concentrations by splitting each amino acid into a number of groups. The carboxylate oxygen and the amine nitrogen of each amino acid were used to obtain information about changes in salt bridge interactions with solute concentration. RDF plots were obtained for all solutions but, as examples, glycine and alanine solutions with GROMOS 53A6, and valine and phenylalanine solutions with OPLS-AA/L and AMBER ff99SB-ILDN are shown in Figure 8. The RDF plots clearly show that peak heights are affected by increasing solute concentration resulting in different strengths of salt bridge interactions. The RDF peak heights increase with molecular size but are the same for different force fields. It was evident from all force fields that salt bridge interactions do not affect the separation distance between molecules with concentration and are independent of molecular size. This suggests that salt-bridge interactions are independent of Lennard-Jones parameters from different force fields. The results presented here are in agreement with previous simulated results [37] excluding the variation in the GROMOS 53A6 salt bridge interactions. Elcock et al. [37] found that GROMOS 53A6 salt bridge interactions are of marginal stability compared to other force fields. However, present results indicate that salt bridge interactions are not affected by the force fields. The only difference between the two simulations is the use of different water models. It has previously been shown that the salt bridge interactions can be affected by the choice of different water models with force field [97].

FIGURE 8

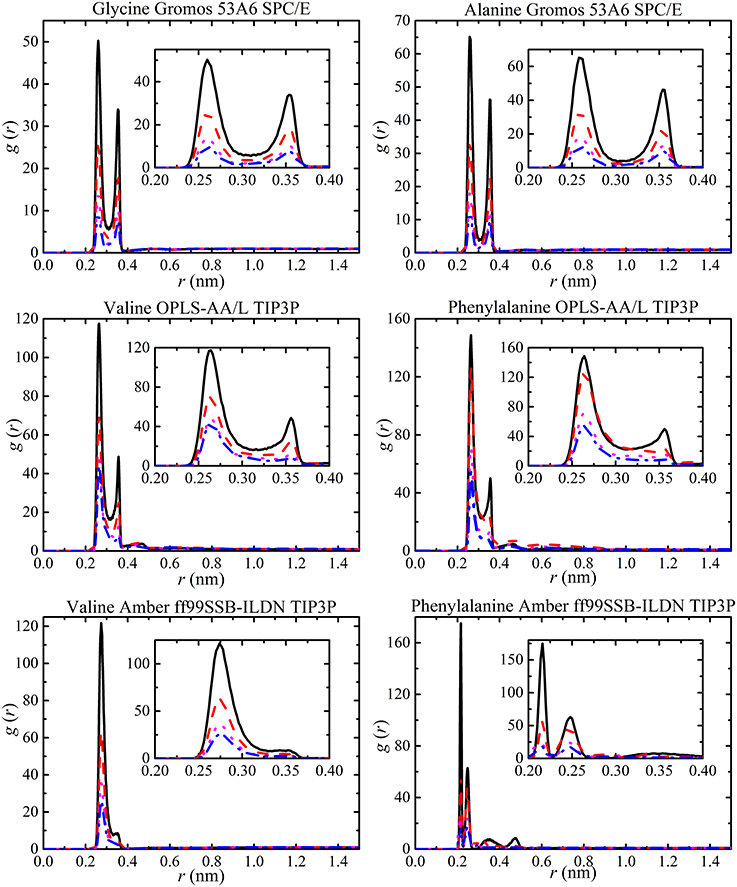
Figure 8. RDFs of the carboxylate oxygen and amine nitrogen of each amino acid at different amino acid concentrations [i.e., 50 (), 100 (), 200 (), and 300 mg/ml ()] and different force fields at 298 K.

In previous studies, the results from small-angle X-ray studies and simulations have been used to explain the RDF peaks in terms of the polydispersity of amino acids [34, 98, 99]. The different RDF peaks provide information about hydrogen bonded oligomers. The RDF peaks for all aggregates (monomers, dimers, trimers, etc.) forming in the simulations are shown in Figure 9. The largest peak corresponds to monomers at 0.10 nm, dimers at 0.115 nm, and trimers at 0.15 nm and followed by high oligomers. The separation distance between molecules was not affected by solute concentration but the probability of finding a molecule increased with concentration. The analysis of hydrogen bonded oligomers from RDF peaks becomes very complex due to the single large peak for monomers. Hence, the hydrogen bonding was analyzed to obtain aggregate distribution of amino acids at different concentrations.

FIGURE 9

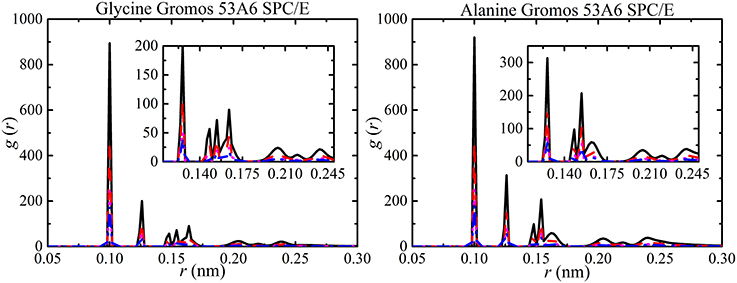
Figure 9. RDFs of amino acid aggregates at different amino acid concentrations [i.e., 50 (), 100 (), 200 (), and 300 mg/ml ()] and different force fields at 298 K.

Hydrogen Bonding

The amino acid clusters formed in the MD simulations were analyzed by examination of hydrogen bonding interactions. The numbers of aggregates in different amino acid simulations were classified on the basis of the hydrogen bonds between two molecules. All amino acid molecules that form hydrogen bonds less than 0.35 nm were considered to be in contact with each other. The percentage of amino acid molecules that exist as monomers (i.e., no hydrogen bond to any other molecule), dimers (i.e., one hydrogen bond between a pair of molecules) and other higher oligomers were calculated from the simulations for each concentration. The results obtained from the MD simulations for glycine and alanine solutions with GROMOS 53A6 and AMBER ff99SB-ILDN force fields, valine and phenylalanine solutions with OPLS-AA/L force field are shown in Figure 10.

FIGURE 10

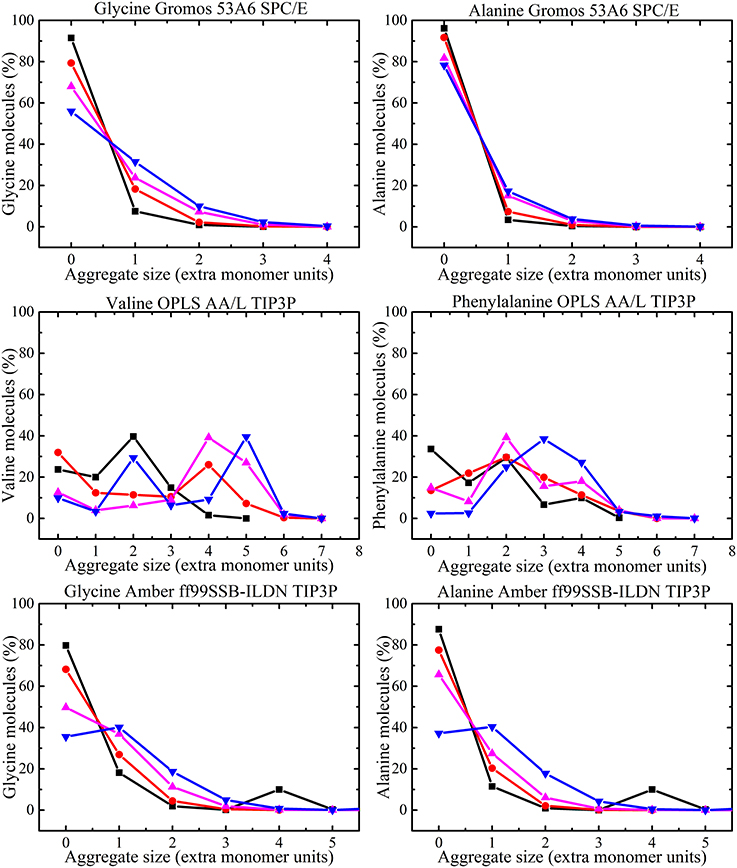
Figure 10. Aggregate size distribution for each amino acid as a function of concentration [i.e., 50 (), 100 (), 200 (), and 300 mg/ml ()] determined using different force fields at 298 K.

Using GROMOS 53A6 force field, monomers are found to be the dominant species at the amino acid concentrations studied. However, the number of higher oligomers also increases with concentration. The numbers of monomers decreases with molecular size predicting that large hydrogen bonded oligomers are formed for large molecules. For the AMBER ff99SB-ILDN force field, monomers were dominant at low concentrations followed by higher oligomers. In simulations using the OPLS-AA/L force field, higher oligomers with much greater size were predicted than when other force fields were used. In fact for 300 mg/ml phenylalanine solutions most of the aggregates were trimers or larger. Similar results from OPLS-AA/L have been noted in the literature [37]. The aggregate size at each concentration was found to be limited by the total number of amino acid molecules added to the solution, but none of the simulations reached that limit of aggregation (i.e., the maximum aggregate size in 50 mg/ml phenylalanine solution is a hexamer).

MD Simulated Diffusion Coefficients

The stability of the MD simulation was confirmed by the linearity of the MSD plots of different water models as a function of amino acids concentration (see Figure 11).

FIGURE 11

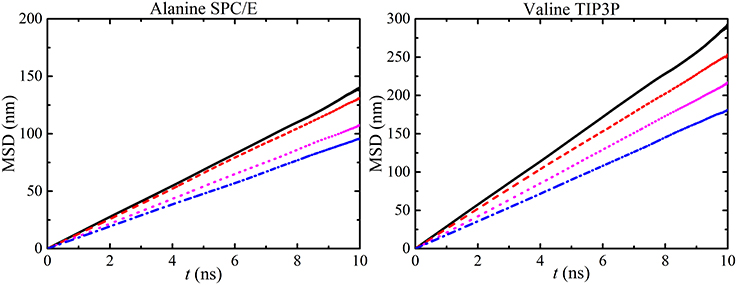
Figure 11. MSD vs. time calculated from water molecules in different alanine and valine concentrations [i.e., 50 (), 100 (), 200 (), and 300 mg/ml ()] with SPC/E and TIP3P models respectively. The linearity of MSD plots decrease with concentration and similar graphs were also obtained for other amino acid solutions.

The MD simulations were performed in normal water whereas the NMR experiments were performed in D₂O. From Equation (2) the diffusion coefficient varies according to the inverse of the viscosities, hence using the known viscosities of H₂O and D₂O [100], the diffusion is expected to be faster in the MD simulations. Crowding effects on water can be seen by comparing the change in the water diffusion coefficient with amino acid concentration in both the experimental and simulation studies. The diffusion coefficients of water and amino acids in different force fields as a function of amino acid concentration are shown in Figure 12. For all force fields, the water diffusion coefficient decreases as a function of concentration (as seen experimentally in Figure 5). In our simulations, at low concentration (50 mg/ml, alanine) there were 100 water molecules per alanine molecule and at high concentration (300 mg/ml, alanine) there were 16 water molecules per alanine molecule. So, crowding effects from amino acids on water molecules were not expected at low amino acid concentrations. The diffusion coefficient of water from the GROMOS 53A6 force field at low amino acid low concentration (50 mg/ml) was close to the experimental value of 2.3 × 10⁻⁹ m²s⁻¹ of pure water [81, 101]. For the TIP3P water model, the diffusion coefficient was also in agreement with simulated literature values of pure water [81].

FIGURE 12

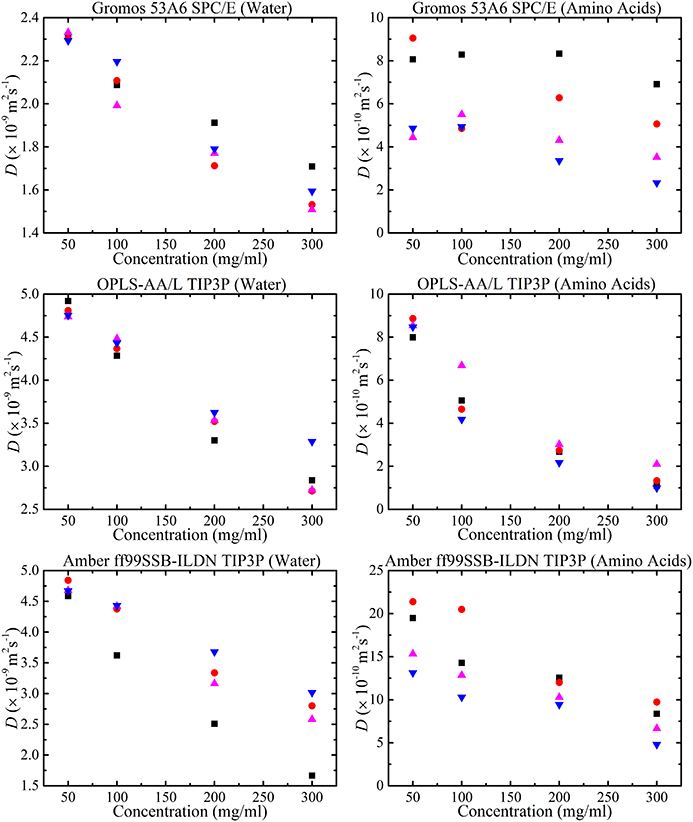
Figure 12. Amino acid concentration dependence of water (left column) and amino acid (right column) diffusion coefficients using GROMOS 53A6 and the SPC/E water model, OPLS-AA/L and the TIP3P water model and AMBER ff99SB-ILDN and the TIP3P water model obtained from the MD simulations with concentration of glycine (), alanine (), valine (), and phenylalanine () molecules at 298 K.

The variation of the water diffusion coefficient using different models from different velocity scaling methods was expected to be around 2–7% [81]. Each simulation run was repeated to check the stability of the diffusion coefficients. Using the same water model (TIP3P), the diffusion coefficient of water changed depending on the force field. The diffusion coefficient of water in amino acid solution was dependent on its interaction with the amino acids. As the Lennard-Jones parameters were different for each force field this led to a deviation in the diffusion coefficient of water in different force fields.

It can be argued that the change in diffusion coefficient of the amino acids with concentration from different force fields is linked to the number of oligomers formed in the simulation. Interestingly, the diffusion coefficient of the amino acids calculated with GROMOS 53A6 and SPC/E didn't decrease significantly with concentration. Previous simulation results for glycine molecules using GROMOS 53A6 force field by Campo et al. [35] were much higher than the present results. However, the results of Campo et al. [35] were more focused on the incorporation of ions into the solution. It is worth stressing that crowding effects from different force fields are dependent on the strength of the interactions (i.e., Lennard-Jones parameters) between molecules. But, results from GROMOS 53A6 have revealed large differences in salt-bridge interactions and the presence of oligomers with concentration indicating a stable force field. The fluctuating behavior of diffusion coefficients in amino acid solutions calculated with the GROMOS 53A66 force field might be linked to the water model used with the force field. Hence, it would be very interesting to compare diffusion coefficients using different water models with GROMOS 53A66. On the other hand, AMBER ff99SB-ILDN overestimated the amino acid diffusion coefficients. Hamad et al. [34] have also calculated diffusion coefficients of glycine using the AMBER force field and our results for glycine molecules were higher than theirs. Diffusion coefficients were highly dependent on the fluctuations in MSD with time and diffusion coefficients reported by Hamad et al. cannot be considered as accurate as their MSD curves appear to fluctuate greatly [34, 82].

There was strong evidence in experimental data to suggest that the diffusive path of amino acids changed with the formation of higher oligomers. Similarly, simulations using the OPLS-AA/L force field showed greater formation of higher oligomers as compared to AMBER ff99SB-ILDN or GROMOS 53A6 (Figure 10). Therefore, a change in diffusion coefficient with concentration in OPLS-AA/L could be linked to the presence of higher oligomers in amino acid solutions. In addition, the diffusion coefficient results from OPLS-AA/L fit best to the experimental data. OPLS-AA/L optimization simulations with different water models did not result in change in the diffusion coefficient [102]. Hence, it seems that OPLS-AA/L is the best current force field for predicting changes in diffusive behavior in crowded solutions.

Conclusions

From the experimental and simulated results presented here of amino acids in water, it can be concluded that diffusion studies can be used to differentiate between the effects of aggregation and obstruction. There was strong evidence to suggest that the diffusive path of water molecules in these systems was obstructed by the presence of amino acids. The experimental amino acid diffusion coefficients showed the presence of aggregation and obstruction at all amino acid concentrations. The analysis of the NMR diffusion data was strongly dependent on the aggregation and obstruction model used. The relative contribution of obstruction and aggregation for different amino acids at different concentrations can be seen by comparing Figures 6, 7. Figure 6 shows the change in diffusion coefficient due only to obstruction, whereas Figure 7 shows the change in diffusion coefficient due to aggregation and obstruction.

On the other hand, MD simulations showed a considerable difference in salt bridge interactions with different concentrations with all three force fields and indicated that the interactions are dependent on the choice of water models used. The stability of the MD simulations in various force fields was verified by comparison with previous experimental and simulation studies. The diffusion coefficients of the amino acids calculated with different force fields are not in agreement with each other but all force fields have shown the presence of aggregation and obstruction. The simulation results showed different polydispersity profiles for all amino acid solutions but all force fields predicted a decrease in the water diffusion coefficient with increasing amino acid concentration. The decrease in water diffusion coefficient was found to be different for each amino acid and each force field. It is clear that current force fields need to be balanced between the different interaction sites present for different species in the solution. In summary, the simulations and experimental diffusive studies of the amino acids presented here provided a clearer understanding of the changes in molecular dynamics due to crowding in amino acid solutions.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgment

The authors acknowledge the facilities, and the scientific and technical assistance of the National Imaging Facility, University of Western Sydney Node.

References

1. Zhou HX, Rivas G, Minton AP. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu Rev Biophys. (2008) 37:375–97. doi: 10.1146/annurev.biophys.37.032807.125817

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

2. Minton AP. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J Biol Chem. (2001) 276:10577–80. doi: 10.1074/jbc.R100005200

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

3. Laurent TC. An early look at macromolecular crowding. Biophys Chem. (1995) 57:7–14. doi: 10.1016/0301-4622(95)00048-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

4. Minton AP. Influence of excluded volume upon macromolecular structure and associations in “crowded” media. Curr Opin Biotechnol. (1997) 8:65–9.

Pubmed Abstract | Pubmed Full Text | Google Scholar

5. van den Berg B, Ellis RJ, Dobson CM. Effects of macromolecular crowding on protein folding and aggregation. EMBO J. (1999) 18:6927–33. doi: 10.1093/emboj/18.24.6927

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

6. Zimmerman SB, Minton AP. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu Rev Biophys Biomol Struct. (1993) 22:27–65. doi: 10.1146/annurev.bb.22.060193.000331

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

7. Ralston GB. Effects of “crowding” in protein solutions. J Chem Educ. (1990) 67:857–60. doi: 10.1021/ed067p857

CrossRef Full Text | Google Scholar

8. Brooks DE. Can cytoplasm exist without undergoing phase separation? In: Harry Walter DEB, Paul AS, editors. International Review of Cytology. Knoxville, TN: Academic Press (1999), Vol. 192, pp. 321–30.

Pubmed Abstract | Pubmed Full Text

9. Goodsell DS. Inside a living cell. Trends Biochem Sci. (1991) 16:203–6. doi: 10.1016/0968-0004(91)90083-8

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

10. Zimmerman SB, Trach SO. Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli. J Mol Biol. (1991) 222:599–620. doi: 10.1016/0022-2836(91)90499-V

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

11. Minton AP. Implications of macromolecular crowding for protein assembly. Curr Opin Struct Biol. (2000) 10:34–9. doi: 10.1016/S0959-440X(99)00045-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

12. Ellis RJ. Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr Opin Struct Biol. (2001) 11:114–9. doi: 10.1016/S0959-440X(00)00172-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

13. Minton AP. The effect of volume occupancy upon the thermodynamic activity of proteins: some biochemical consequences. Mol Cell Biochem. (1983) 55:119–40. doi: 10.1007/BF00673707

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

14. Muramatsu N, Minton AP. Tracer diffusion of globular proteins in concentrated protein solutions. Proc Natl Acad Sci USA. (1988) 85:2984–8. doi: 10.1073/pnas.85.9.2984

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

15. Richter K, Nessling M, Lichter P. Macromolecular crowding and its potential impact on nuclear function. Biochim Biophys Acta (2008) 1783:2100–7. doi: 10.1016/j.bbamcr.2008.07.017

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

16. Luby-Phelps K, Castle PE, Taylor DL, Lanni F. Hindered diffusion of inert tracer particles in the cytoplasm of mouse 3T3 cells. Proc Natl Acad Sci USA. (1987) 84:4910–3. doi: 10.1073/pnas.84.14.4910

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

17. Price WS, Tsuchiya F, Arata Y. Lysozyme aggregation and solution properties studied using PGSE NMR diffusion measurements. J Am Chem Soc. (1999) 121:11503–12. doi: 10.1021/ja992265n

CrossRef Full Text | Google Scholar

18. Schnell S, Turner TE. Reaction kinetics in intracellular environments with macromolecular crowding: simulations and rate laws. Prog Biophys Mol Biol. (2004) 85:235–60. doi: 10.1016/j.pbiomolbio.2004.01.012

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

19. Banks DS, Fradin C. Anomalous diffusion of proteins due to molecular crowding. Biophys J. (2005) 89:2960–71. doi: 10.1529/biophysj.104.051078

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

20. Bernadó P, dela Torre JG, Pons M. Macromolecular crowding in biological systems: hydrodynamics and NMR methods. J Mol Recognit. (2004) 17:397–407. doi: 10.1002/jmr.694

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

21. Dix JA, Verkman AS. Crowding effects on diffusion in solutions and cells. Annu Rev Biophys. (2008) 37:247–63. doi: 10.1146/annurev.biophys.37.032807.125824

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

22. Germann MW, Turner T, Allison SA. Translational diffusion constants of the amino acids: measurement by NMR and their use in modeling the transport of peptides. J Phys Chem A (2007) 111:1452–5. doi: 10.1021/jp068217o

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

23. Hughes CE, Hamad S, Harris KDM, Catlow CRA, Griffiths PC. A multi-technique approach for probing the evolution of structural properties during crystallization of organic materials from solution. Faraday Discuss. (2007) 136:71–89. doi: 10.1039/b616611c

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

24. Youguang M, Chunying Z, Peisheng M, Yu KT. Studies on the diffusion coefficients of amino acids in aqueous solutions. J Chem Eng Data (2005) 50:1192–6. doi: 10.1021/je049582g

CrossRef Full Text | Google Scholar

25. Myerson AS, Lo PY. Cluster formation and diffusion in supersaturated binary and ternary amino acid solutions. J Cryst Growth (1991) 110:26–33. doi: 10.1016/0022-0248(91)90862-Y

CrossRef Full Text | Google Scholar

26. Verkman AS. Solute and macromolecule diffusion in cellular aqueous compartments. Trends Biochem Sci. (2002) 27:27–33. doi: 10.1016/S0968-0004(01)02003-5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

27. Price WS, Tsuchiya F, Arata Y. Time dependence of aggregation in crystallizing lysozyme solutions probed using nmr self-diffusion measurements. Biophys J. (2001) 80:1585–90. doi: 10.1016/S0006-3495(01)76131-0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

28. Garcia-Pérez AI, López-Beltrán EA, Klüner P, Luque J, Ballesteros P, Cerdán S. Molecular crowding and viscosity as determinants of translational diffusion of metabolites in subcellular organelles. Arch Biochem Biophys. (1999) 362:329–38. doi: 10.1006/abbi.1998.1051

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

29. Banipal TS, Singh G. Thermodynamic study of solvation of some amino acids, diglycine and lysozyme in aqueous and mixed aqueous solutions. Thermochim Acta (2004) 412:63–83. doi: 10.1016/j.tca.2003.08.026

CrossRef Full Text | Google Scholar

30. García De la Torre J, Huertas M, Carrasco B. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys J. (2000) 78:719–30. doi: 10.1016/S0006-3495(00)76630-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

31. Price WS. NMR Studies of Translational Motion: Principles and Applications. Cambridge: Cambridge Univ Press (2009). doi: 10.1017/CBO9780511770487

CrossRef Full Text | Google Scholar

32. Woessner DE. NMR spin-echo self-diffusion measurements on fluids undergoing restricted diffusion. J Phys Chem. (1963) 67:1365–7. doi: 10.1021/j100800a509

CrossRef Full Text | Google Scholar

33. Einstein A. Investigations on the theory of the brownian movement. Fürth R, Editor. Cowper AD, Translator. New York, NY: Dover Publications, Inc. (1956).

Pubmed Abstract | Pubmed Full Text

34. Hamad S, Hughes CE, Catlow CRA, Harris KDM. Clustering of glycine molecules in aqueous solution studied by molecular dynamics simulation. J Phys Chem B (2008) 112:7280–8. doi: 10.1021/jp711271z

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

35. Campo MG. Molecular dynamics simulation of glycine zwitterion in aqueous solution. J Chem Phys. (2006) 125:114511–9. doi: 10.1063/1.2352756

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

36. Lu C, Prada-Gracia D, Rao F. Structure and dynamics of water in crowded environments slows down peptide conformational changes. J Chem Phys. (2014) 141:045101–7. doi: 10.1063/1.4891465

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

37. Andrews CT, Elcock AH. Molecular dynamics simulations of highly crowded amino acid solutions: comparisons of eight different force field combinations with experiment and with each other. J Chem Theory Comput. (2013) 9:4585–602. doi: 10.1021/ct400371h

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

38. Cino EA, Karttunen M, Choy W-Y. Effects of molecular crowding on the dynamics of intrinsically disordered proteins. PLoS ONE (2012) 7:e49876. doi: 10.1371/journal.pone.0049876

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

39. Elcock AH. Models of macromolecular crowding effects and the need for quantitative comparisons with experiment. Curr Opin Struct Biol. (2010) 20:196–206. doi: 10.1016/j.sbi.2010.01.008

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

40. Dunn MS, Ross FJ, Read LS. The solubility of the amino acids in water. J Biol Chem. (1933) 103:579–95.

Google Scholar

41. Willis SA, Dennis GR, Zheng G, Price WS. Averaging effects in PGSE NMR attenuations observed in bimodal molecular weight PMMA solutions. Macromolecules (2010) 43:7351–6. doi: 10.1021/ma1017007

CrossRef Full Text | Google Scholar

42. Willis SA, Price WS, Eriksson-Scott IK, Zheng G, Dennis GR. Influence of polymer architecture on the averaging effects in PGSE NMR attenuations for bimodal solutions of linear and star poly(vinyl acetates). J Mol Liq. (2012) 167:110–4. doi: 10.1016/j.molliq.2012.01.006

CrossRef Full Text | Google Scholar

43. Stait-Gardner T, Willis SA, Yadav NN, Zheng G, Price WS. NMR diffusion measurements of complex systems. Diffusion Fundam. (2009) 11:Special Issue “Diffusion Fundamentals III,” 1–22.

Google Scholar

44. Stokes GG. On the effect of internal friction of fluids on the motion of pendulums. Trans Camb Phil Soc. (1856) 9:8–106.

Google Scholar

45. Sutherland W. XVIII. Ionization, ionic velocities, and atomic sizes. Philos Mag 6 (1902) 3:161–77.

46. Sutherland W. A dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin. Philos Mag 6 (1905) 9:781–5.

Google Scholar

47. Edward JT. Molecular volumes and the Stokes-Einstein equation. J Chem Educ. (1970) 47:261–70. doi: 10.1021/ed047p261

CrossRef Full Text | Google Scholar

48. Han J, Herzfeld J. Macromolecular diffusion in crowded solutions. Biophys J. (1993) 65:1155–61. doi: 10.1016/S0006-3495(93)81145-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

49. Nilsson PG, Lindman B. Water self-diffusion in nonionic surfactant solutions. hydration and obstruction effects. J Phys Chem. (1983) 87:4756–61. doi: 10.1021/j100246a041

CrossRef Full Text | Google Scholar

50. Price WS. Protein association studied by NMR diffusometry. Curr Opin Colloid Interface Sci. (2006) 11:19–23. doi: 10.1016/j.cocis.2005.10.005

CrossRef Full Text | Google Scholar

51. Price WS. 2 NMR gradient methods in the study of proteins. Annu Rep Prog Chem Sect C Phys Chem. (2000) 96:3–53. doi: 10.1039/B000773K

Google Scholar | CrossRef Full Text

52. Nesmelova IV, Fedotov VD. Self-diffusion and self-association of lysozyme molecules in solution. Biochim Biophy Acta (1998) 1383:311–6. doi: 10.1016/S0167-4838(97)00224-0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

53. Price WS. Pulsed-field gradient nuclear magnetic resonance as a tool for studying translational diffusion: part 1. basic theory. Concepts Magn Reson. (1997) 9:299–335.

Google Scholar

54. Hahn EL. Spin echoes. Phys Rev. (1950) 80:580–94. doi: 10.1103/PhysRev.80.580

CrossRef Full Text | Google Scholar

55. Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. (1965) 42:288–92. doi: 10.1063/1.1695690

CrossRef Full Text | Google Scholar

56. Hahn E, Maxwell D. Spin echo measurements of nuclear spin coupling in molecules. Phys Rev. (1952) 88:1070–84. doi: 10.1103/PhysRev.88.1070

CrossRef Full Text | Google Scholar

57. Marqusee JA, Deutch JM. Concentration dependence of the self-diffusion coefficient. J Chem Phys. (1980) 73:5396–7. doi: 10.1063/1.439936

CrossRef Full Text | Google Scholar

58. Callaghan PT, Pinder DN. Influence of polydispersity on polymer self-diffusion measurements by pulsed field gradient nuclear magnetic resonance. Macromolecules (1985) 18:373–9. doi: 10.1021/ma00145a013

CrossRef Full Text | Google Scholar

59. Stilbs P. Molecular self-diffusion coefficients in fourier transform nuclear magnetic resonance spectrometric analysis of complex mixtures. Anal Chem. (1981) 53:2135–7. doi: 10.1021/ac00236a044

CrossRef Full Text | Google Scholar

60. Nicolay K, Braun KPJ, Graaf RAD, Dijkhuizen RM, Kruiskamp MJ. Diffusion NMR spectroscopy. NMR Biomed. (2001) 14:94–111. doi: 10.1002/nbm.686

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

61. Van Zijl PC, Moonen CT, Faustino P, Pekar J, Kaplan O, Cohen JS. Complete separation of intracellular and extracellular information in NMR spectra of perfused cells by diffusion-weighted spectroscopy. Proc Natl Acad Sci USA. (1991) 88:3228–32. doi: 10.1073/pnas.88.8.3228

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

62. Everhart CH, Johnson CS, Jr. The determination of tracer diffusion coefficients for proteins by means of pulsed field gradient NMR with applications to hemoglobin. J Magn Reson. (1982) 48:466–74.

63. Martin RB. Comparisons of indefinite self-association models. Chem Rev. (1996) 96:3043–64. doi: 10.1021/cr960037v

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

64. Li M, Nadarajah A, Pusey ML. Modeling the growth rates of tetragonal lysozyme crystals. J Cryst Growth (1995) 156:121–32. doi: 10.1016/0022-0248(95)00262-6

CrossRef Full Text | Google Scholar

65. Jönsson B, Wennerström H, Nilsson PG, Linse P. Self-diffusion of small molecules in colloidal systems. Colloid Polym Sci. (1986) 264:77–88. doi: 10.1007/BF01410310

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

66. Tokuyama M, Cukier RI. Dynamics of diffusion-controlled reactions among stationary sinks: scaling expansion approach. J Chem Phys. (1982) 76:6202–14. doi: 10.1063/1.443023

CrossRef Full Text | Google Scholar

67. Wang JH. Theory of the self-diffusion of water in protein solutions. A new method for studying the hydration and shape of protein molecules. J Am Chem Soc. (1954) 76:4755–63. doi: 10.1021/ja01648a001

CrossRef Full Text | Google Scholar

68. Clark M, Burnell E, Chapman N, Hinke J. Water in barnacle muscle. Iv. factors contributing to reduced self-diffusion. Biophys J. (1982) 39:289–99. doi: 10.1016/S0006-3495(82)84519-0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

69. Jóhannesson H, Halle B. Solvent diffusion in ordered macrofluids: a stochastic simulation study of the obstruction effect. J Chem Phys. (1996) 104:6807–17. doi: 10.1063/1.471347

CrossRef Full Text | Google Scholar

70. Tokuyama M, Oppenheim I. Dynamics of hard-sphere suspensions. Phys Rev E (1994) 50:16–9. doi: 10.1103/PhysRevE.50.R16

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

71. Lekkerkerker HNW, Dhont JKG. On the calculation of the self-diffusion coefficient of interacting brownian particles. J Chem Phys. (1984) 80:5790–2. doi: 10.1063/1.446602

CrossRef Full Text | Google Scholar

72. Parks P. A. M. Lyapunov's stability theory-100 years on. IMA J Math Control Inform. (1992) 9:275–303. doi: 10.1093/imamci/9.4.275

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

73. Tokuyama M, Cukier R. Dynamics of diffusion controlled reactions among stationary sinks: scaling expansion approach. J Chem Phys. (1982) 76:6202–14. doi: 10.1063/1.443023

CrossRef Full Text | Google Scholar

74. Gupta P, Hall CK, Voegler A. Computer simulation of the competition between protein folding and aggregation. Fluid Phase Equilib. (1999) 158–60:87–93. doi: 10.1016/S0378-3812(99)00119-3

CrossRef Full Text | Google Scholar

75. McGuffee SR, Elcock AH. Atomically detailed simulations of concentrated protein solutions: the effects of salt, pH, point mutations, and protein concentration in simulations of 1000-molecule systems. J Am Chem Soc. (2006) 128:12098–110. doi: 10.1021/ja0614058

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

76. Uchida H, Matsuoka M. Molecular dynamics simulation of solution structure and dynamics of aqueous sodium chloride solutions from dilute to supersaturated concentration. Fluid Phase Equilib. (2004) 219:49–54. doi: 10.1016/j.fluid.2004.01.013

CrossRef Full Text | Google Scholar

77. Lindorff-Larsen K, Piana S, Palmo K, Maragakis P, Klepeis JL, Dror RO, et al. Improved side-chain torsion potentials for the AMBER FF99SB protein force field. Proteins (2010) 78:1950–8. doi: 10.1002/prot.22711

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

78. Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, et al. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J Am Chem Soc. (1995) 117:5179–97. doi: 10.1021/ja00124a002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

79. Oostenbrink C, Villa A, Mark AE, van Gunsteren WF. A biomolecular force field based on the free enthalpy of hydration and solvation: the gromos force-field parameter sets 53A5 and 53A6. J Comput Chem. (2004) 25:1656–76. doi: 10.1002/jcc.20090

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

80. Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J Phys Chem B (2001) 105:6474–87. doi: 10.1021/jp003919d

CrossRef Full Text | Google Scholar

81. Mark P, Nilsson L. Structure and dynamics of the TIP3P, SPC, and SPC/E water models at 298 K. J Phys Chem A (2001) 105:9954–60. doi: 10.1021/jp003020w

CrossRef Full Text | Google Scholar

82. Chitra R, Yashonath S. Estimation of error in the diffusion coefficient from molecular dynamics simulations. J Phys Chem B (1997) 101:5437–45. doi: 10.1021/jp9703059

CrossRef Full Text | Google Scholar

83. Vishnyakov A, Lyubartsev AP, Laaksonen A. Molecular dynamics simulations of dimethyl sulfoxide and dimethyl sulfoxide-water mixture. J Phys Chem A (2001) 105:1702–10. doi: 10.1021/jp0007336

CrossRef Full Text | Google Scholar

84. Wensink EJW, Hoffmann AC, Van Maaren PJ, Van der Spoel D. Dynamic properties of water/alcohol mixtures studied by computer simulation. J Chem Phys. (2003) 119:7308–17. doi: 10.1063/1.1607918

CrossRef Full Text | Google Scholar

85. Zhang C, Yang X. Molecular dynamics simulation of ethanol/water mixtures for structure and diffusion properties. Fluid Phase Equilib. (2005) 231:1–10. doi: 10.1016/j.fluid.2005.03.018

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

86. Yeh IC, Hummer G. System-size dependence of diffusion coefficients and viscosities from molecular dynamics simulations with periodic boundary conditions. J Phys Chem B (2004) 108:15873–9. doi: 10.1021/jp0477147

CrossRef Full Text | Google Scholar

87. Shirts MR, Pande VS. Solvation free energies of amino acid side chain analogs for common molecular mechanics water models. J Chem Phys. (2005) 122:134508–21. doi: 10.1063/1.1877132

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

88. Berendsen HJC, Grigera JR, Straatsma TP. The missing term in effective pair potentials. J Phys Chem. (1987) 91:6269–71. doi: 10.1021/j100308a038

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

89. Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. (1983) 79:926–35. doi: 10.1063/1.445869

CrossRef Full Text | Google Scholar

90. Mills R. Self-diffusion in normal and heavy water in the range 1-45°C. J Phys Chem. (1973) 77:685–8. doi: 10.1021/j100624a025

CrossRef Full Text | Google Scholar

91. Furó I, Jóhannesson H. Accurate anisotropic water-diffusion measurements in liquid crystals. J Magn Reson A (1996) 119:15–21.

Google Scholar

92. Van Der Spoel D, Lindahl E, Hess B, Groenhof G, Mark AE, Berendsen HJC. Gromacs: fast, flexible, and free. J Comput Chem. (2005) 26:1701–8. doi: 10.1002/jcc.20291

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

93. Hess B, Kutzner C, van der Spoel D, Lindahl E. Gromacs 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J Chem Theory Comput. (2008) 4:435–47. doi: 10.1021/ct700301q

CrossRef Full Text | Google Scholar

94. Parrinello M, Rahman A. Polymorphic transitions in single crystals: a new molecular dynamics method. J Appl Phys. (1981) 52:7182–90. doi: 10.1063/1.328693

CrossRef Full Text | Google Scholar

95. Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh ewald method. J Chem Phys. (1995) 103:8577–93. doi: 10.1063/1.470117

CrossRef Full Text | Google Scholar

96. Hess B. P-lincs: a parallel linear constraint solver for molecular simulation. J Chem Theory Comput. (2007) 4:116–22. doi: 10.1021/ct700200b

CrossRef Full Text | Google Scholar

97. Debiec KT, Gronenborn AM, Chong LT. Evaluating the strength of salt bridges: a comparison of current biomolecular force fields. J Phys Chem B (2014) 118:6561–9. doi: 10.1021/jp500958r

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

98. Erdemir D, Chattopadhyay S, Guo L, Ilavsky J, Amenitsch H, Segre CU, et al. Relationship between self-association of glycine molecules in supersaturated solutions and solid state outcome. Phys Rev Lett. (2007) 99:115702–6. doi: 10.1103/PhysRevLett.99.115702

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

99. Chattopadhyay S, Erdemir D, Evans JMB, Ilavsky J, Amenitsch H, Segre CU, et al. SAXS study of the nucleation of glycine crystals from a supersaturated solution. Cryst Growth Des. (2005) 5:523–7. doi: 10.1021/cg0497344

CrossRef Full Text | Google Scholar

100. Hardy RC, Cottington RL. Viscosity of deuterium oxide and water from 5° to 125°C. J Chem Phys. (1949) 17:509–10. doi: 10.1063/1.1747310

CrossRef Full Text | Google Scholar

101. Price WS, Ide H, Arata Y. Self-diffusion of supercooled water to 238 K using PGSE NMR diffusion measurements. J Phys Chem A (1999) 103:448–50. doi: 10.1021/jp9839044

CrossRef Full Text | Google Scholar

102. Siu SWI, Pluhackova K, Böckmann RA. Optimization of the OPLS-AA force field for long hydrocarbons. J Chem Theory Comput. (2012) 8:1459–70. doi: 10.1021/ct200908r

CrossRef Full Text | Google Scholar