- 1Edward S. Rogers Sr. Department of Electrical and Computer Engineering, University of Toronto, Toronto, ON, Canada
- 2Princess Margaret Cancer Centre, Toronto, ON, Canada
Monte Carlo (MC) simulation is recognized as the “gold standard” for biophotonic simulation, capturing all relevant physics and material properties at the perceived cost of high computing demands. Tetrahedral-mesh-based MC simulations particularly are attractive due to the ability to refine the mesh at will to conform to complicated geometries or user-defined resolution requirements. Since the chosen MC method does not inherently require approximations on the materials, it is applicable to the broadest set of biophotonic simulation problems. MC methods also have other implementation features including inherent parallelism, and permit a continuously-variable quality-runtime tradeoff. We demonstrate here a complete MC-based prospective fluence dose evaluation system for interstitial PDT to generate dose-volume histograms on a tetrahedral mesh geometry description. To our knowledge, this is the first such system for general interstitial photodynamic therapy employing MC methods and is therefore applicable to a very broad cross-section of anatomy and material properties. We demonstrate that evaluation of dose-volume histograms is an effective variance-reduction scheme in its own right which greatly reduces the number of packets required and hence runtime required to achieve acceptable result confidence. We conclude that MC methods are feasible for general PDT treatment evaluation and planning, and considerably less costly than widely believed.
1. Introduction
Photodynamic Therapy (PDT) is an emerging treatment modality for cancerous lesions in a variety of indications. It is widely used for indications which are superficial in terms of both the method of light application and the lesion depth, so currently mostly actinic keratosis [1] and skin cancer [2]. For more difficult interstitial applications, it shows both great promise [3] and ongoing challenges with inconsistent outcomes [4, 5].
Photodynamic cell killing mechanisms depend on cell physiology (response to radical production), and require the overlap of photosensitizer, tissue oxygen, and photon fluence. Selectivity is achieved through influencing these factors by methods including: designing photosensitizer biochemistry for preferential uptake by the tumor; exploiting pharmacokinetic differences between diseased and healthy tissue; controlling oxygen delivery dynamics; artificially inducing or using naturally-occurring differential sensitivity between tumor and nearby tissue; and by controlling the shape of the light fluence field to achieve spatially selective photosensitizer activation. We focus here on control of the light fluence field, as it is largely independent of the other factors and all else being equal an improvement in light targeting always improves the outcome. The ability to simulate the light fluence field is also critical to understanding optical measurements made (including for implicit or explicit dosimetry parameters), and for optimal placement of monitoring probes to detect optical properties in vivo.
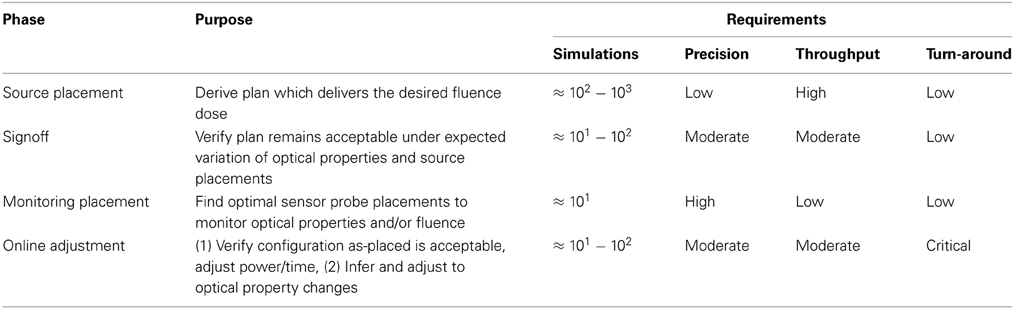
MC is also the standard of care for ionizing radiation therapy (IRT), where the coefficients of absorption and scattering are lower resulting in significantly fewer interaction events per photon and hence much lower compute requirements. Ionizing radiation therapy (IRT) has become a main-line treatment for cancers, with well-developed workflows, numerical optimization based on Monte Carlo simulation, and rigorous quality-assurance procedures. Such practices are still emerging for PDT treatment planning and monitoring, with some challenges due to the unique characteristics of PDT. Compared to IRT, the red or near-infrared photons used for PDT have significantly higher coefficients of interaction with the target tissue. The greater propensity to scatter leads to light confinement within much smaller volumes around the implanted light source which facilitates treatment targeting. Such selectivity comes at a cost, though; since each photon undergoes a very large number of scattering events prior to absorption (and hence causing cell damage), the cost of computational modeling is correspondingly increased. A complete PDT treatment plan covers a large range of parameters, some under control of the treating physician and some outside as summarized in Table 1, yielding a difficult optimization problem. Given the large number of degrees of freedom and the often-long compute times to simulate the fluence field, one of the challenges in successfully delivering PDT is numerical optimization of the treatment plan.
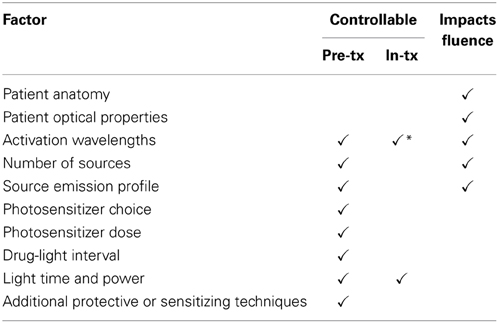
Table 1. Controllable and non-controllable factors in PDT treatment planning, showing which parameters will alter the fluence field and hence require separate optical simulations (* denotes limited range).
Based on simulations of the fluence field, we derive dose-volume histograms (DVH) and related metrics which are extremely widely used in radiation therapy planning. Operating within a defined planning volume, the dose-volume histogram displays the percentage of each organ within the planning volume receiving a dose (vertical axis) which exceeds a given dose level (independent, horizontal axis). The DVH permits the ability to query what fraction of an organ receives a dose exceeding ΦJ/cm2, or conversely to find the minimum dose received by the v% most heavily-treated portion of an organ. Where used, simulation-based PDT treatment planning often expresses tumor exposure goals in terms of D90, the minimum dose received by at least 90% of the tumor. When the dose is scaled to deliver sufficient energy to meet the D90 objective, the DVH permits inspection of the dose distribution received by other organs at risk to assess the likelihood of complications. Under the photodynamic threshold model [6], those portions of the organs at risk receiving more than their threshold fluence dose are not expected to survive.
One advantage of IRT over PDT is that the imaging (CT) and treatment use similar photon energies and hence the imaging modality used to build the geometric model directly provides measurements of the necessary propagation properties. On the other hand, the patient properties relevant to PDT (coefficients of absorption μa and scattering μs) are considerably more variable [4] both intra-patient (day-to-day and treatment-induced changes), and inter-patient (population variance). Successful PDT delivery will need to account for these variations through a variety of techniques including implicit and explicit dosimetry monitoring, online plan adjustment, and a planning process which is robust with respect to the anticipated range of optical properties. All of these require the ability to calculate and optimize the fluence field within the treatment volume. Robust treatment planning will also require validating a given source geometry against a range of perturbations in optical properties and source placement errors. Adequate exploration of the large space of variation and possible plans will require the ability to conduct many simulations quickly, as well as good optimization algorithms.
Figure 1 illustrates our proposed PDT treatment planning workflow, analogous to current standards of care in radiotherapy [7]. It comprises several distinct phases, each with differing computational requirements. The areas impacted by the present article are highlighted to place them in context of the full treatment flow, and approximate computation requirements are listed in Table 2.
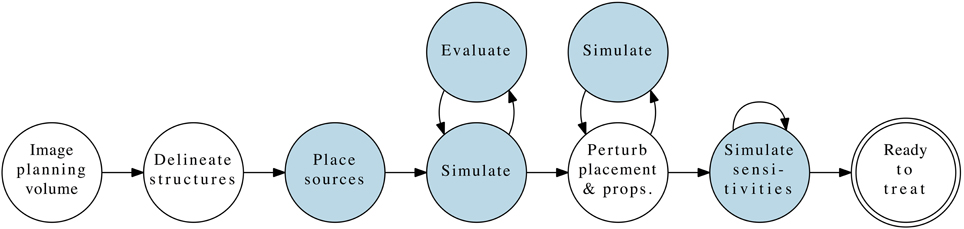
Figure 1. Complete PDT pre-treatment planning workflow, with the phases contributed by this article highlighted.
From this workflow, we can derive a set of requirements for a simulation environment which could be applied to any indication for which PDT is suitable:
1. Gives valid results in low-scattering areas
2. Able to accommodate curved surfaces
3. Refinable geometry model to provide high detail where needed
4. Able to model varied light emitters and probes, including customized extended sources
5. Predictable, quantifiable result uncertainty
6. Modest run-time requirements to support iterative optimization
7. Broad range of quality-effort tradeoffs, capable of high precision when needed
We demonstrate below a software implementation “FullMonte” which meets all these criteria using a tetrahedral mesh description of the planning volume, and a Monte Carlo simulation to solve for the light distribution. We also show that the use of dose-volume histograms for assessing a proposed treatment geometry acts as a variance reduction scheme which greatly reduces the computational cost of Monte Carlo simulations. Taken together with our work on hardware acceleration, we conclude that MC-based prospective PDT treatment evaluation, planning, and online monitoring are both feasible and desirable.
2. Background
Of the workflow illustrated in Figure 1, we focus on the first loop: simulation and evaluation, in which the simulator calculates the light fluence within the planning volume resulting from the specified treatment geometry (patient anatomy, optical properties, source(s) with positions and emission patterns). Based on those simulations of the fluence field, the second component generates measures of the resulting plan's quality using the prescribed target characteristics. We choose to focus on the dose-volume histogram as our primary evaluation tool, given its prevalence in IRT planning and use by many clinicians. The discussion below provides background on prior work in both of these areas. Given a simulation-evaluation loop of sufficient quality and performance, a scalar merit objective function to maximize, and a set of constraints, the next natural step is to perform automatic iterative algorithmic optimization using those building blocks.
2.1. Biophotonic Simulations
Simulation of light propagation through living tissue is complicated by the very high scattering coefficients within the optical window generally used for photosensitizer activation. Physically, a photon will scatter many times before absorption, with the expected number of interactions depending on the material's albedo. Tissue has a higher albedo for interactions with optical photons than x-rays, meaning that considerably more scattering must be modeled for PDT compared to IRT. The Radiative Transfer Equation (RTE, or sometimes ERT) expresses the conservation relationship which must hold for light transport in a scattering medium. Solution techniques can be classified into three groups: analytic and finite-element numerical solutions using the diffusion approximation (the simplest and least accurate method); other numerical methods to solve the RTE directly; and Monte Carlo methods.
2.1.1. Diffusion approximation (DA)
The Diffusion Approximation (DA) [8] yields analytic solutions for simple problem geometries and can be formulated for non-trivial geometries using the finite-element method to achieve relatively fast run-times at the expense of approximations in both the materials (isotropic, highly scattering) and physics (neglecting reflection/refraction) of the problem. NIRFAST [9] is an example of a widely-used open-source package generally used for fluorescence and bioluminescence studies which includes a diffusion solver. Similar techniques are also employed for propagation modeling in PDT treatment as discussed below. For certain anatomical regions, particularly homogeneous organs of solid highly-scattering tissue, the DA holds reasonably for points several mean free paths away from a source or material boundary.
However, there are several conditions which would invalidate the diffusion approximation in a large fraction of the treatment volume:
1. Use of extended sources where an appreciable volume of tissue is located near (within a few mean free paths of) a light source (Jacques and Pogue [8], particularly Figures 1, 4, 7 therein)
2. Heterogeneous structures with a large number of material interfaces (see previous point)
3. Presence of air-tissue interfaces with reflection and refraction (e.g., sinuses, esophagus in head and neck; see Figures 1, 7 in Jacques [10])
4. Presence of low-scattering voids (e.g., cerebral-spinal fluid in brain/spine; bladder) or high-absorbing regions (discussed with references in Boas et al. [11])
For many indications, one or more of these conditions will be violated, yielding incorrect simulation results which would jeopardize the safety and efficacy of the treatment.
2.1.2. Numerical solutions to the RTE
Other solution methods with less onerous approximations have been applied to the RTE. Klose and Larsen, for instance, have shown an SP3 solution [12] which relaxes the requirement for the radiance to be isotropic, a model refinement shown to offer better accuracy in bioluminescence applications [13] that could likely translate to PDT as well. In exchange for increased result precision, such methods require longer run times (2.5x longer than to diffusion) to formulate and solve the problem. For SP3 methods, some error remains near material boundaries and sources, which may be problematic in PDT. Many cases will also involve extended sources and highly heterogeneous anatomy, placing a significant proportion of tissue within a small number of transport mean free paths of a source or boundary.
2.1.3. Monte Carlo methods
Monte Carlo methods are generally acknowledged as the “gold standard” for biophotonic simulations, covering the widest set of problem descriptions with accuracy which can be arbitrarily refined, at the perceived cost of long run times required to produce sufficient result confidence. Particularly for air-tissue interfaces (e.g., head-and-neck cancers) and volumes with low-scattering voids (e.g., bladder cancers), the approximations required for other solution techniques are likely to invalidate the results, while MC methods remain able to deliver a quality solution.
A diversity of prior work exists using Monte Carlo methods to solve biophotonic problems with a variety of geometry descriptions. The basic concept started in the early 1980's with Wilson and Adam [14]. Wang and Jacques' MCML [15] remains a widely-used open-source package for layered media (e.g., skin) with normally-incident light beams, running packets of photons through the popular “hop, drop, spin” pipeline. Variations on that technique for scoring different output quantities and geometries exist, including time-resolved calculations for semi-infinite media [16], and hardware accelerated calculations in layered media [17, 18].
Diffuse imaging applications [11] often make use of a voxelized approach in which a general 3D treatment volume is divided into a cubic grid with each cube being assigned optical properties. Unlike the diffusion approximation, this permits simulation of anisotropy and low-scattering regions but it does not provide correct normals for curved surfaces. While very successfully applied for imaging applications (e.g., brain) where the refractive indices are matched, the lack of normals are a known problem [19] for reflection and refraction. Hardware-accelerated implementations using this voxelized approach also exist (e.g., MCX [20]) which achieve considerable runtime speedup, albeit subject to the same restrictions on the problem domain.
To address refractive interfaces correctly, several 3D tetrahedral-mesh-based simulators have been created [21] including our own FullMonte [22] which is the fastest such open-source software at the time of publishing this report to our knowledge. Such simulators are able to model very general structures to an arbitrary degree of precision through selection of an appropriate mesh size and number of packets. A finer mesh requires more memory and computing time but offers a closer geometric approximation.
Offsetting the many benefits of Monte Carlo simulation are the perceived computational costs. Despite a high amount of effort expended on software optimization, required run times for high-quality simulations of complex geometries remain long. Shen and Wang's TIM-OS made efficient use of multi-core processors and Intel's automatic vectorization capabilities for double-precision floating point arithmetic. We improved further on those results when writing FullMonte by moving to single precision floating-point (including validating that there was no loss of quality), and using hand-tuned SIMD instructions for further performance gains. We have also demonstrated a pre-existing but previously-unknown quality-runtime tradeoff (the wmin roulette parameter) which permits result quality to be varied across the dynamic range such that the results in areas with very low fluence (i.e., significantly below PDT threshold, and therefore not clinically of interest) can be coarsened to provide a speed boost on the order of 25%. Further advancing the state of the art, we created an FPGA implementation of the FullMonte pipeline for limited mesh sizes [23] using custom digital logic to run 4x faster and 67x more power-efficiently than a highly-tuned CPU implementation. Work currently in progress should increase that performance to ≈16x while maintaining compelling cost and power-efficiency advantages.
2.2. PDT Treatment Geometry Evaluation
For superficial applications, PDT treatment planning generally consists of illuminating the surface with a set energy per unit area, after giving a standard photosensitizer dose in mg/kg. For deeper-seated lesions optical diffusers may be used to increase the penetration depth of the light [3]. When delivering interstitial PDT, the simplified treatment planning approach is clearly deficient since the fluence distribution within the tissue is highly dependent on optical properties [10] and geometry. Work on interstitial PDT has thus far been focused on the prostate because it is a large, relatively homogeneous structure which is easily accessed for placement of light sources. Working with more difficult areas will require more involved simulation, treatment planning, and dosimetry.
Some of the first algorithmic PDT planning was demonstrated by Altschuler et al. [24] using the Cimmino algorithm for prostate PDT planning. The forward model used was a simple evaluation of the diffusion-theory equation for a point source in an infinite homogeneous medium, convolved with the light source positions and strengths. They then evaluated dose-volume histograms for a given configuration, and optimized the configuration to minimize dose to organs at risk while maintaining a specified target dose.
Researchers at Lund University and SpectraCure AB [25] have run clinical trials for prostate cancer using the SpectraCure IDOSE platform, which uses multiple treatment fibers and real-time monitoring. Their planning system uses a diffusion-based solver to calculate light fluence, aiming to deliver a minimum threshold dose to the entire prostate gland while minimizing exposure to nearby organs [26]. The fluence dose was evaluated by dose-volume histogram and dose maps to evaluate the delivery of light throughout the target volume. Conservative dose targets and tissue heterogeneities were proposed to explain some observed under-treatment in the trials.
A series of clinical trials vascular-targeted photodynamic therapy of prostate cancer using Tookad at the Ontario Cancer Institute [4] also used dose-volume histograms to express treatment criteria. Their software used a finite-element method solver similar to the Lund group, with treatment geometries specified manually and then evaluated by dose-volume histograms and observation of isofluence contours representing damage thresholds for both tumor and the urethra/rectal wall. The biopsy results were interpreted according to D90, the minimum light dose received by at least 90% of the target volume. In vivo measurements demonstrated the ability of the simulation engine to predict the location of isofluence contours to within ±2 mm. The time to create a mesh description of the geometry and calculate a light dose were reported to be between 10 and 20 min, with a total 2–5 h required to create a plan. While the exact ratio is difficult to predict, a single-digit factor of speed improvement is likely on a current computer compared to the one used in the study 6 years ago.
While a few works have used MC methods, for instance calculating the dose received at the surface of a cylindrical area around a light source in the prostate [27], these have generally used simple geometry models. To our knowledge, no work has yet gone so far as to use 3D MC simulations for treatment planning.
3. Methods
We divide the treatment evaluation process into three stages discussed individually below. First, the problem description consisting of patient geometry, optical properties, target volume, and light sources must be defined. Next, the description is given to the Monte Carlo simulator to run a user-specified number of photon packets. Finally, the results are interpreted in terms of dose-volume histograms and fluence field visualizations.
Future work would naturally use a numerical optimization method coupled with the plan evaluation methods shown here to iteratively refine the source descriptions toward user-prescribed goals. Given sufficient computing resources, different wavelengths may also be contemplated in the optimization by assigning wavelength-appropriate optical properties to each tissue type.
Variability of optical properties is one of the most important factors in safe and effective delivery of PDT. Computationally, our method can address this by evaluating multiple plans spanning the anticipated range of optical properties, an approach made more feasible by our short run times. A thorough study of the effect of such variability on PDT planning and delivery would be an important future contribution outside the scope of the present discussion, but enabled by the methods presented here. Given such an understanding, we would use these plan evaluation tools to develop treatment planning methods which are robust to the major sources of PDT variability.
3.1. Problem Description
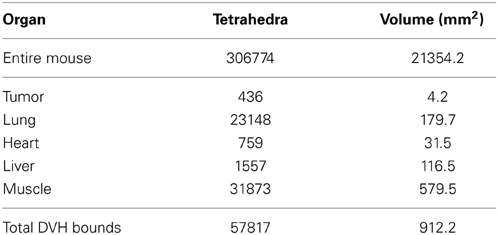
The planning system accepts as input a tetrahedral mesh in which each mesh element is assigned a tissue type. Generally this would be done by a radiologist using CT or MRI information, followed by software generation of a volumetric mesh from the provided curves. Pending creation of such infrastructure, we demonstrate our capability using Digimouse [28] since it is widely available and a common model for imaging experiments. We placed a hypothetical tumor in the abdomen near the lung, and then placed a single line source interactively using software (depicted in Figure 2). For dose-volume histogram generation, we defined (again interactively) a bounding box to exclude tissue outside the region of interest (x, y, z) : x ∈ [7, 17], y ∈ [35.5, 45.5], z ∈ [6.5, 16.5]. The bounding box is needed to exclude the large portions of the mesh which receive no fluence and would otherwise dominate the dose-volume histogram for organs at risk. The mesh statistics for the entire mouse, tumor, and organs at risk are given in Table 3. We note that the DVH volume does not sum to 1000 mm3 because of the inclusion of some air space, and because of the exclusion of border elements which are not completely contained within the box. Trade-offs involved in mesh generation and refinement are discussed in the results section.
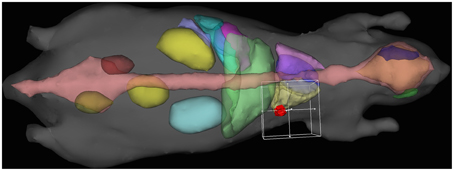
Figure 2. Interactive treatment plan input using Digimouse [28] mesh showing tumor (red), heart (purple), liver (green), lungs (yellow/light purple), and skeleton (pink), with the 10 mm DVH bounding cube.
3.2. Simulation
Monte Carlo simulation was carried out using our FullMonte software, which uses a tetrahedral mesh geometry description and sums the total energy Ei absorbed within each mesh element i of volume Vi during the simulation. Conversion to fluence for each absorbing element of uniform absorption coefficient takes place by . The roulette parameters were set to wmin = 10−5 and as is standard practice in TIM-OS and MCML, though up to 30% speedup could be realized at minimal quality cost by increasing wmin as discussed in our paper introducing the FullMonte software [22].
FullMonte is able to handle arbitrary combinations of a number of clinically relevant light sources: isotropic points, cut-end fibers (cone beam emitted from a disc of finite extent), volume sources (the interior of a tetrahedral element), face sources (a triangular face of a tetrahedral element), line sources, and pencil beams. For this instance, we used a single cylindrical diffusing fiber which emits isotropically in the plane normal to the fiber axis. Extension to sources with a tailored emission profile [29] or to a point source tracing out a path (e.g., as used in mesothelioma treatments at the University of Pennsylvania [30]) is trivial.
3.3. Dose-Volume Histogram Generation
For each tetrahedral element which lies entirely within the bounding box, the fluence is calculated from the energy absorbed within the volume Ei. The elements are divided according to the organ (or tumor) to which it is assigned, and the DVH is calculated in the usual manner [31]. For illustration purposes, we have scaled the output for each individual run such that D90 = 100%, i.e., 90% of the tumor receives the target dose. Naturally, the x (fluence dose) axis may be scaled arbitrarily by increasing or decreasing power and/or duration; the shape and relative positions of the curves are what determine how specifically the plan is targeting the intended treatment volume.
3.4. Fluence Field Visualization
Finally, the fluence field is visualized as both a set of isofluence contours to evaluate the spatial distribution. In this case, the source is close enough to the surface that the isofluence contours are truncated at the skin since fluence is not scored beyond the outer limit of the geometry. When using MC simulations for planning, we aim to use many low-quality runs to quickly eliminate poor candidates using the DVH variance reduction scheme, and produce a short list of several good plans for consideration. Having narrowed the list, we can spend more time on those few plans to produce high-quality results for visualization and sign-off.
4. Results and Discussion
4.1. Geometry Setup
Two treatment plans were tested to illustrate the method: a subjectively “good” plan, in which the line source was positioned along the long axis of the tumor [(11.4, 42.4, 10.4) − (11.7, 41.6, 11.0)], and a “bad” plan in which the source extended beyond the edges of the tumor into both lung and liver tissue [(11.5, 40.0, 10.4) − (12.5, 45.1, 12.1)]. The organs at risk which had significant volumes within the bounding box and received meaningful doses were the tumor, lung, liver, and surrounding muscle (the default material in Digimouse where no organ is assigned). The optical properties used in these simulations are listed in Table 4.
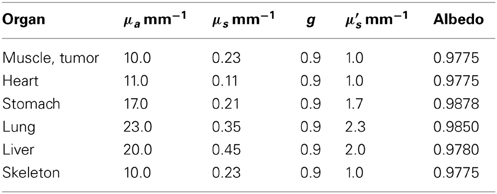
Table 4. Selected simulation optical properties, as provided in Shen and Wang [21].
The dose-volume histogram (DVH, as described in the introduction) results of one simulation run with one million packets for each of the plans (good/bad) is shown in Figure 3. In the present situation, the resolution of the dependent variable (% of volume) is determined by the volumes of the tetrahedral elements comprising the region, while the horizontal position is the fluence output from the simulator. The statistical uncertainty in the horizontal positions arising from Monte Carlo fluence simulation is dealt with below.
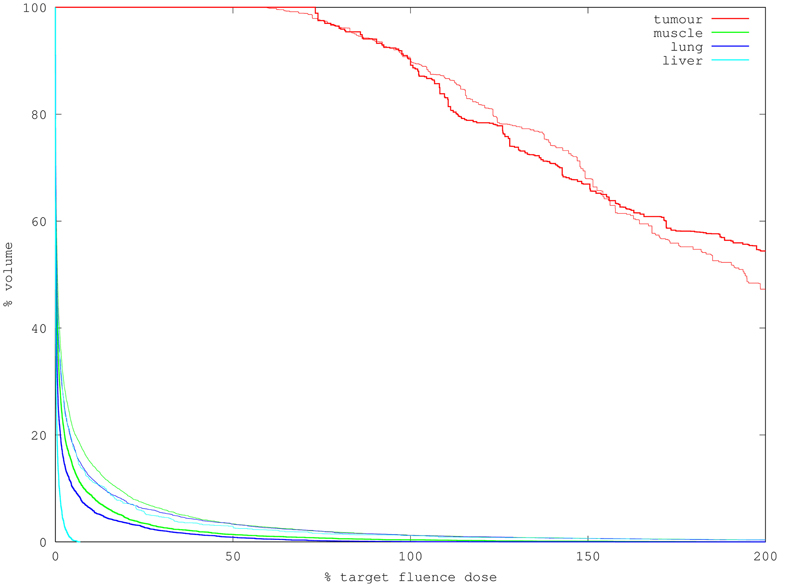
Figure 3. DVH for two treatment plans using 10M packets to simulate (2 min runtime each). Bold lines indicate the “good” plan in which the source is contained within the tumor; faint lines of matching color indicate the corresponding organ in the “bad” plan. Note the good plan treats more of the tumor to doses exceeding 90% of targe while delivering much less dose to the organs at risk.
4.2. Result Variance
As a statistical numerical method, Monte Carlo simulation shows variability in its output results, with the standard deviation scaling proportional to where N is the number of trials conducted (here photon packets launched). To establish the variance in output for the example scenario shown, we ran 100 simulations with differing seeds for the random-number generator, and calculated the mean μi and variance σ2i for the energy absorbed in element i across the set of simulation runs. Mirroring the physical process which it models, the MC simulation shows Poisson-like behavior where the variance of absorbed energy in an element is approximately proportional to its mean value. We say approximately here because the simulator saves computational effort by propagating photon packets which are proportionally absorbed through multiple interaction events, rather than discrete photons which undergo either scattering or absorption. The relative uncertainty, measured by coefficient of variation (), therefore scales inversely with the square of the energy absorbed in an element
The absorbed energy integrated over volume is not directly useful for calculating photodynamic dose because it does not separate photosensitizer absorption from other chromophores; that requires knowledge of photosensitizer concentration (outside the scope of the optical simulator), absorption cross-section (a material property), and fluence (derived from optical simulation). Conversion of absorbed energy into fluence requires simply multiplication by a constant () if we assume homogeneous fluence and absorption coefficient over the volume element in Equation (1). That multiplication changes the values of mean (kμ) and variance (k2σ2) but not the coefficient of variation due to algebraic cancelation. We can conclude therefore that the relative uncertainty in the fluence value for an element is the same as the relative uncertainty in the absorbed energy, which is inversely proportional to both its absorption coefficient and its volume.
The variance of an individual element in isolation is of greatest interest when looking at fluence maps, or calculating the value that would be measured by a very small isotropic point probe. For evaluating the merits of a specific treatment plan, though, examining and extracting values from the dose-volume histogram (DVH) is the customary method. The DVH is built from a set of simulated fluence values through sorting. We can expect, and indeed find, significant reduction in the variance of the order statistics represented by the DVH compared to the variance of its individual constituents. This is shown graphically in Figure 4, where the DVH from each of the 100 different runs are overlaid to indicate the range of variation in output. Based on that set of runs, the standard deviation of D90 extracted from a very quick and coarse 100k-packet run is just 1.2%, which is well below the currently-permitted calibration error of 5% when measuring optical power for PDT. Visually, it appears that for most of the curve DVH generation achieves a reduction in standard deviation of the D90 value of at least 2–4x compared to its constituent elements. Figure 5 shows a simulation using 10x as many packets (1M) and the corresponding decrease in uncertainty.
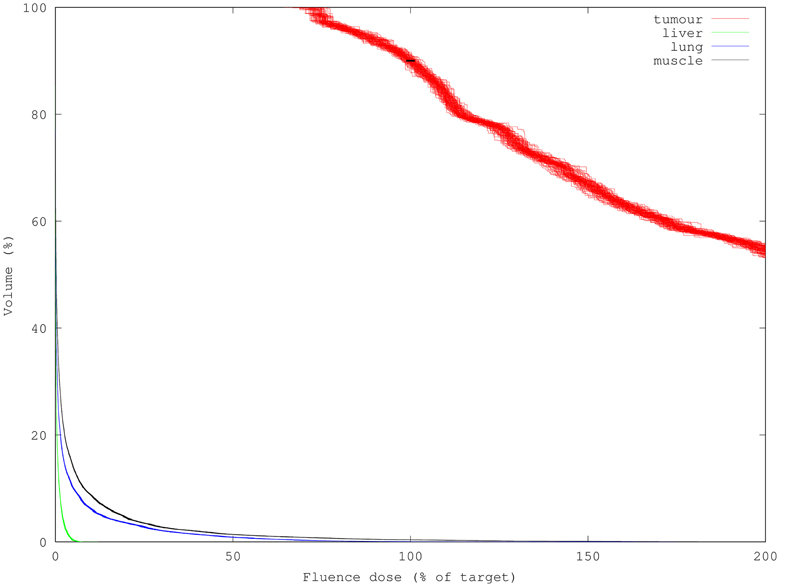
Figure 4. 100 DVHs (100k packets each) overlaid to show result variance; note organs at risk have much lower DVH variance than the target tumor despite having lower fluence. Standard deviation of the D90 derived from these DVHs is only 1.2% (black bar overlay) despite being composed of high-variance individual results.
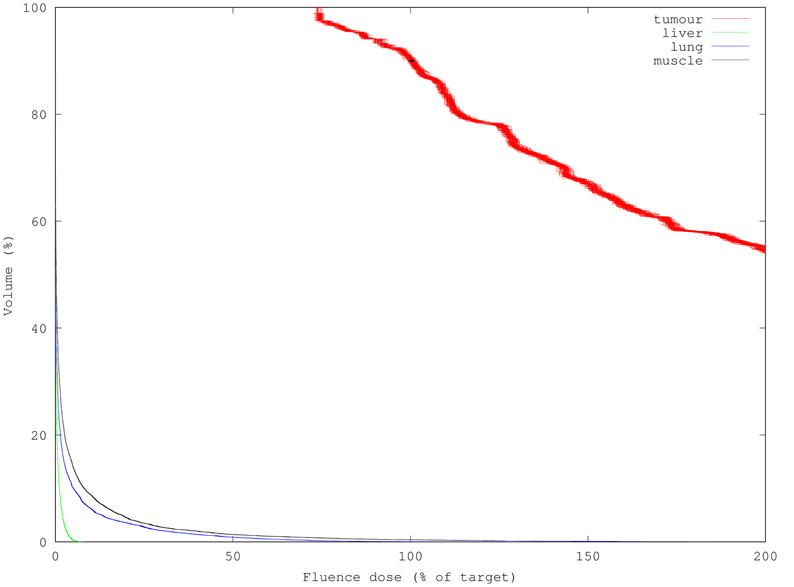
Figure 5. 100 DVHs (1M packets each) overlaid to show result variance reduction relative with increasing simulation packet count. Each simulation used 10x more packets than Figure 4, requiring 10x longer (12 s) to compute but yielding 3.3x smaller uncertainty per mesh element. D90 standard deviation was reduced to 0.6%.
The same effect is noticeable when trying to determine Vx, the volume of an organ which receives a dose greater than x% of the target, whereby x is defined by the safety require for a particular indication. Details of the dose-volume histogram for muscle tissue at risk are shown in Figure 6, which depicts the region around 100% of target dose, which is critical in determining the extent of probable damage to organs at risk. The red bars show a range of ±σ on each individual fluence element comprising the DVH; note that of 100 runs, one would expect 5% of results to lie outside the larger zone of ±2σ based on individual variance. In fact, we do not see that in the plot because the DVH is more stable than its constituent elements, permitting us to calculate to within 1–5% relative uncertainty (black overlay bars, ± 1σ) the Vx values for the organs at risk despite creating the DVH from noisy elements. Again this is integer factors better than would be expected and most importantly the runtime decrease for a given increase in acceptable per-element standard deviation is quadratic because σ ∝ . The variance reduction from DVH generation is therefore comparable to the quality improvement resulting from at least a 4–16x decrease in runtime.
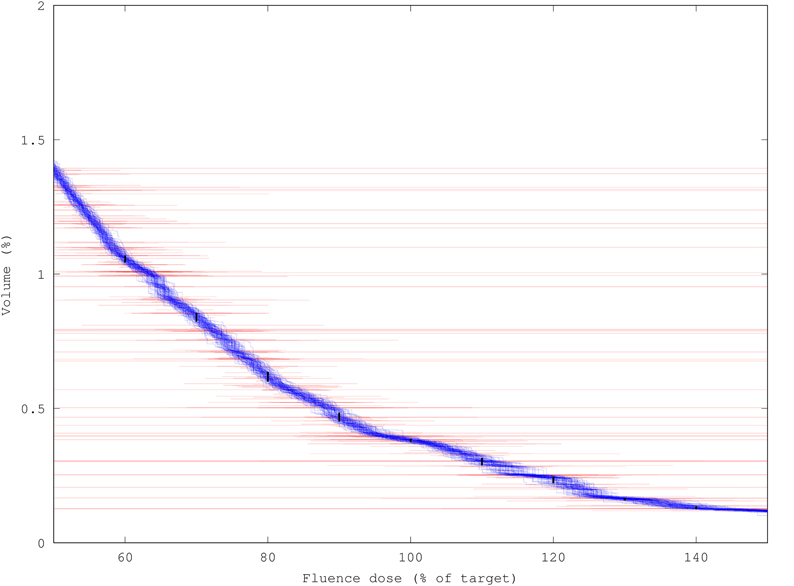
Figure 6. Variance-reduction effect of DVH generation demonstrated by overlaying 100 DVHs for muscle tissue at risk, each created from a run of 100k packets (1.3 s runtime each), on top of ±σ bars (red) for each individual fluence component. Black bars show ± 1σ uncertainty in determining the volume of tissue Vp receiving more than p% of target dose (p = 60, 70, … 140); uncertainties range from 1–5% of Vp tissue volume.
One interesting point is that the organs at risk (OAR), which have much lower fluence, and one would therefore expect to yield higher relative uncertainty, actually show lower variation in the DVH traces. This is due in part to the much larger number of elements captured in the OAR traces; though each element has high uncertainty, we are sorting a large list of such variables so that the order statistics (DVH) become relatively stable.
We posit that increasing the spatial resolution of the mesh may sometimes paradoxically decrease the variance in the DVH. The increased mesh resolution may modestly increase the compute time per packet, but a reduction in DVH variance will require the simulation of fewer packets to achieve an acceptable result. It may therefore be possible to reduce the required compute time by working with a finer mesh, increasing spatial resolution and the confidence in the DVH despite increasing the variance of the individual constituent elements. Figure 7 shows the resulting isofluence lines for one simulation. The impact of differing optical properties in the tissues is clear from the contours' lobed appearance, particularly around the lung and liver, both of which have lower albedo due to higher scattering (≈2x) and even higher absorption (≈3 – 4x) coefficients compared to the surrounding muscle tissue. This simulation used ten million packets, requiring 2 min of run time to create a smoother isofluence surface.
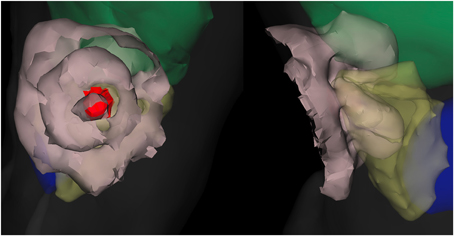
Figure 7. Fluence field for “good” plan depicted as isofluence contours (beige surfaces, spaced in factors of 10). The organs visible are liver (green), lung (yellow), and heart (blue) along with the outer surface (faint gray). Both views show the same case from different perspectives. The tumor is the interior red surface, with the embedded line source shown in a darker red. The impact of optical-property differences between the organs is visible from the lobed appearance of the outer contour particularly.
4.3. Run Times
One advantage of the Monte Carlo method for biophotonic simulations is that it allows a continuously-variable tradeoff of run time and result variance. Due to statistical averaging in the output, the uncertainty (standard deviation) for the fluence in any individual output element is inversely proportional to where N is the number of photon packets simulated. Considering the simulation result for a single mesh element, the variance is influenced by the number of absorption events during the simulation which is itself determined by several factors: wmin roulette parameter [22], mesh element volume, material albedo, and element fluence (which depends on the surrounding geometry and sources). Of these, only the number of packets run, wmin, and mesh element volume are under control of the user with the rest dictated by the problem being simulated. A refinement of the mesh will give finer spatial resolution to the output fluence, at the cost of increased result variability due to the reduced number of absorption events within each smaller mesh volume.
Simulations were conducted on a high-performance laptop (MacBook Pro 15″, mid-2014 model) with a latest-generation Intel Haswell processor, 2.8 GHz (Turbo to 3.6 GHz) quad-core with hyper threading supporting 8 simultaneous threads. Previous comparisons have shown that the required compute time scales inversely with increasing numbers of cores and clock speed, and linearly with the number of packets requested. To conduct a coarse but indicative simulation of 100k packets (Figure 4), the average time required was just 1.34 s. The required time scaled up linearly in the number of packets, with 200k packets taking 2.32 s and 1M packets running in 12.1 s. These runtime figures show some minor deviations from a linear fit, likely due to other processes and/or clock speed changes due to thermal management.
Desired result quality and problem geometry are the primary factors affecting required run time. As discussed in the DVH section above, for evaluation of treatment plans, several factors come into play to determine the required precision for individual elements to yield an acceptable measure of plan merit. Given the American Association of Physicists in Medicine (AAPM) absolute calibration standards of optical power meters for PDT to within 5% [32], we suggest that a DVH dose confidence level of 1% is more than adequate to render the impact of simulation error on outcome negligible. Appropriate understanding of the confidence level in the output can therefore reduce run time considerably by shifting the user's perception of the number of simulated packets required to achieve their desired outcome.
When conducting PDT treatment planning, a large number of candidate plans will be examined to determine which is the best under a given measure of plan merit. Comparing two plans will thus have some probability of yielding an incorrect result based on the confidence bounds of each of the solutions, and thus mis-directing the optimizer. One can and should try to use optimization techniques that are robust to noisy inputs. Ideally, though, we would like to run simulations which are “good enough” with respect to the degree of confidence in the output without incurring excessive computational cost (run time or financial cost of hardware).
A different degree of confidence may be required depending on the end goal of a simulation run. As described below, the generation of dose-volume histograms gives a variance reduction effect. If, on the other hand, the user is looking for the sensitivity of fluence within a single element to a small change of input parameters, for instance in looking to place a small fluence-rate monitoring probe, a much greater number of packets may be required to reduce the variance to an acceptable level. For such smaller regions, the options for variance reduction are more limited but spatial averaging remains a viable option. When designing a complete workflow one can achieve significant savings by customizing the level of effort to the level of quality needed, for instance running a large number of plans quickly to rapidly explore the space before running more refined calculations. It should also be feasible to separate source planning and monitor plan execution as discussed in the introduction such that many candidate placements can be examined at low packet counts, prior to running fewer high-resolution simulations for deriving a monitoring plan.
5. Conclusions and Future Work
5.1. Conclusions
We have shown that Monte Carlo methods are computationally tractable for PDT treatment evaluation, permit continuously-variable quality-runtime tradeoffs, and are amenable to hardware acceleration. Additionally, the computation of dose-volume histograms (DVHs) from MC simulations functions as a significant variance-reduction scheme which greatly reduces the runtime required to achieve a given level of output confidence. Current run times can be sufficiently low, even on a laptop computer, that tetrahedral-mesh MC is a viable option for evaluating PDT treatment plans. Higher-precision simulations with a larger number of packets which will permit accurate sensitivities (e.g., to probe placements or to personalized optical properties) can also be calculated. For iterative treatment planning and algorithmic optimization, accelerated hardware enables a very large volume of simulations to be run quickly. In short, given an appropriate understanding of the requirements for acceptable output quality, and of the effects of DVH generation, Monte Carlo simulations for PDT treatment planning may be considerably (integer factors) less expensive than is generally perceived.
5.2. Optical Property Variability
This work demonstrates the capability and low computational cost of using Monte Carlo methods to evaluate the dose delivered by a given light source configuration into a specified tissue geometry with known optical properties. In the practice of interstitial PDT delivery, however, patient optical properties vary widely [33, 34]. Development of treatment plans which are robust to a range of optical properties, as well as techniques for in-vivo detection and compensation for such variability (building on prior efforts in the prostate [4, 25]), would be important contributions to PDT practice. The first part involving assessment of variability is enabled in a straightforward way by the present work, requiring only simulation of clinically-derived meshes over a range of properties with analysis of the results. Development of robust optimization techniques and optical property detection/compensation methods are more difficult questions; this work provides an important prerequisite, namely a fast and accurate plan evaluation engine.
5.3. Algorithmic Treatment Planning Flow
Using the infrastructure developed, we aim to create an automated numerical optimization system which works toward user-defined treatment plan goals (minimum dose for tumor, maximum dose to organs at risk, and a penalty function for deviations). It will need to be robust to misdirection due to the output variance, though to what degree remains to be determined. One may contemplate a highly robust algorithm (e.g., simulated annealing) which works on very short, low-quality/high-variance simulation runs; or, one may choose to employ an algorithm which is less demanding in the number of sample plans to evaluate but requires higher-quality input.
5.4. Hardware Acceleration
In previous work, we have also demonstrated the capability to perform identical Monte Carlo simulations using Field-Programmable Gate Arrays (FPGA) custom digital logic [23], running 4x faster and 67x more power-efficiently than a high-end quad-core Intel processor for mesh sizes up to 48k elements. Such simulations can replace the software kernel used herein to generate results considerably more quickly and cheaply than the general-purpose CPU used. We aim to use this specialized platform to enable algorithmic optimization of PDT treatment plans.
5.5. Dose Concept Refinement
While the present work focuses entirely on delivering a evaluating the light fluence delivered, definitions of photodynamic dose encompassing more factors exist [5, 6]. Given the existing simulator's output of fluence within the tissue, additional explicit dosimetric information regarding oxygenation, photosensitizer concentration, and tissue sensitivity can be incorporated to produce a DVH of photodynamic dose which should more closely predict the clinical outcome. Such additional factors would need to be modeled separately and integrated with the fluence information from the optical simulator, for computation of photodynamic dose-volume histogram rather than (or in addition to) simple light fluence dose.
5.6. Impact of Mesh Refinement
The connection between mesh size and DVH variance needs further investigation. As discussed in the results section, there are contrary pressures when mesh element size decreases: individual element variance would tend to increase because of a smaller number of arrivals to be summed; DVH variance would however tend downwards due to the variance-reduction properties of sorting the fluence elements. Mesh refinement also adds a mild computational burden, which may or may not be offset by the decreased number of packets which will be required to achieve an acceptable level of confidence in the DVH.
Funding
This work was supported by the Canadian Institutes of Health Research, the Canadian Natural Sciences and Engineering Research Council, Altera Corporation, and the Ontario Ministry of Health and Long-Term Care.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
We thank Dr. Robert Weersink of the Princess Margaret Cancer Centre for helpful discussions regarding treatment planning practices in radiotherapy. The authors are also grateful to KitWare Inc for creating and maintaining the Visualization Toolkit (VTK) which was used to create the interactive planning and visualization software.
References
1. Tarstedt M, Rosdahl I, Berne B, Svanberg K, Wennberg AM. A randomized multicenter study to compare two treatment regimens of topical methyl aminolevulinate (Metvix)-PDT in actinic keratosis of the face and scalp. Acta Derm Venereol. (2005) 85:424–8. doi: 10.1080/00015550510032887
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
2. Fien SM, Oseroff AR. Photodynamic therapy for non-melanoma skin cancer. J. Natl Compr Cancer Netw. (2007) 5:531–40.
3. Biel MA. Photodynamic Therapy. Methods Mol. Biol. (2010) 635:281–93. doi: 10.1007/978-1-60761-697-9/18
4. Davidson SRH, Weersink RA, Haider MA, Gertner MR, Bogaards A, Giewercer D, et al. Treatment planning and dose analysis for interstitial photodynamic therapy of prostate cancer. Phys Med Bio. (2009) 54:2293–313. doi: 10.1088/0031-9155/54/8/003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
5. Zhu TC, Finlay JC. Prostate PDT Dosimetry. Photodiagnosis Photodyn Ther. (2006) 3:234–6. doi: 10.1016/j.pdpdt.2006.08.002
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
6. Patterson MS, Wilson BC, Graff R. In vivo tests of the concept of photodynamic threshold dose in normal rat liver photosensitized by aluminum chlorosulfonated phthalocyanine. Photochem Photobiol. (1990) 51:343–9. doi: 10.1111/j.1751-1097.1990.tb01720.x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
7. Fraass B, Doppke K, Hunt M, Kutcher G, Starkschall G, Stern R, et al. American association of physicists in medicine radiation therapy committee task group 53: quality assurance for clinical radiotherapy treatment planning. Med Phys. (1998) 25:1773–829. doi: 10.1118/1.598373
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
8. Jacques SL, Pogue BW. Tutorial on diffuse light transport. J Biomed Opt. (2008) 13:041302. doi: 10.1117/1.2967535
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
9. Dehghani H, Eames ME, Yalavarthy PK, Davis SC, Srinivasan S, Carpenter CM, et al. Near infrared optical tomography using NIRFAST : algorithm for numerical model and image reconstruction. Commun Numer Methods Eng. (2008) 25:711–32. doi: 10.1002/cnm.1162
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
10. Jacques SL. How tissue optics affect dosimetry of photodynamic therapy. J Biomed Opti. (2010) 15:051608. doi: 10.1117/1.3494561
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
11. Boas D, Culver J, Stott J, Dunn A. Three dimensional monte carlo code for photon migration through complex heterogeneous media including the adult human head. Opt Express. (2002) 10:159–70. doi: 10.1364/OE.10.000159
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
12. Klose AD, Larsen EW. Light transport in biological tissue based on the simplified spherical harmonics equations. J Comput Phys. (2006) 220:441–70. doi: 10.1016/j.jcp.2006.07.007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
13. Lu Y, Machado HB, Bao Q, Stout D, Herschman H, Chatziioannou AF. In vivo mouse bioluminescence tomography with radionuclide-based imaging validation. Mol Imaging Biol. (2011) 13:53–8. doi: 10.1007/s11307-010-0332-y
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
14. Wilson B, Adam G. A Monte Carlo model for the absorption and flux distributions of light in tissue. Med Phys. (1983) 10:824–30. doi: 10.1118/1.595361
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
15. Wang L, Jacques SL, Zheng L. MCML - Monte Carlo modeling of light transport in multi-layered tissues. Comput Methods Programs Biomed. (1995) 47:131–46. doi: 10.1016/0169-2607(95)01640-F
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
16. Alerstam E, Svensson T, Andersson-Engels S. Parallel computing with graphics processing units for high-speed Monte Carlo simulation of photon migration. J Biomed Opt. (2012) 13:060504. doi: 10.1117/1.3041496
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
17. Alerstam E, Lo WCY, Han TD, Rose J, Andersson-Engels S, Lilge L. Next-generation acceleration and code optimization for light transport in turbid media using GPUs. Biomed Opt Express. (2010) 1:658–75. doi: 10.1364/BOE.1.000658
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
18. Lo WCY, Redmond K, Luu J, Chow P, Rose J, Lilge L. Hardware acceleration of a Monte Carlo simulation for photodynamic therapy treatment planning. J Biomed Opt. (2009) 14:014019. doi: 10.1117/1.3080134
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
19. Binzoni T, Leung TS, Giust R, Rüfenacht D, Gandjbakhche AH. Light transport in tissue by 3D Monte Carlo: influence of boundary voxelization. Comput. Methods Programs Biomed. (2008) 89:14–23. doi: 10.1016/j.cmpb.2007.10.008
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
20. Fang Q, Boas Da. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Opt Express. (2009) 17:20178–90. doi: 10.1364/OE.17.020178
21. Shen H, Wang G. A study on tetrahedron-based inhomogeneous Monte Carlo optical simulation. Biomed Opt Express. (2010) 2:44–57. doi: 10.1364/BOE.2.000044
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
22. Cassidy J, Lilge L, Betz V. FullMonte: a framework for high-performance Monte Carlo simulation of light through turbid media with complex geometry. In: Proc SPIE BiOS. Vol. 8592. San Francisco, CA: SPIE (2013). p. 85920H–14.
23. Cassidy J, Lilge L, Betz V. Fast, power-efficient biophotonic simulations for cancer treatment using FPGAs. In: International Symposium on Field-Configurable Custom Computing Machines. Boston, MA: IEEE (2014).
24. Altschuler MD, Zhu TC, Li J, Hahn SM. Optimized interstitial PDT prostate treatment planning with the Cimmino feasibility algorithm. Med Phys. (2005) 32:3524–35. doi: 10.1118/1.2107047
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
25. Swartling J, Axelsson J, Ahlgren G, Kälkner KM, Nilsson S, Svanberg S, et al. System for interstitial photodynamic therapy with online dosimetry: first clinical experiences of prostate cancer. J Biomed Opt. (2010) 15:058003. doi: 10.1117/1.3495720
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
26. Johansson A, Axelsson J, Andersson-Engels S, Swartling J. Realtime light dosimetry software tools for interstitial photodynamic therapy of the human prostate. Med Phys. (2007) 34:4309. doi: 10.1118/1.2790585
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
27. Zaak D, Sroka R, Höppner M, Khoder W, Reich O, Tritschler S, et al. Photodynamic therapy by means of 5-ALA induced PPIX in human prostate cancer - preliminary results. Med Laser Appl. (2003) 18:91–5. doi: 10.1078/1615-1615-00092
28. Dogdas B, Stout D, Chatziioannou AF, Leahy RM. Digimouse: a 3D whole body mouse atlas from CT and cryosection data. Phys Med Biol. (2007) 52:577–87. doi: 10.1088/0031-9155/52/3/003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
29. Rendon A, Beck JC, Lilge L. Treatment planning using tailored and standard cylindrical light diffusers for photodynamic therapy of the prostate. Phys Med Biol. (2008) 53:1131–49. doi: 10.1088/0031-9155/53/4/021
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
30. Friedberg JS, Culligan MJ, Mick R, Stevenson J, Hahn SM, Sterman D, et al. Radical pleurectomy and intraoperative photodynamic therapy for malignant pleural mesothelioma. Ann Thorac Surg. (2012) 93:1658–65. discussion:1665–7. doi: 10.1016/j.athoracsur.2012.02.009
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
31. Drzymala R, Mohan R, Brewster L, Chu J, Goitein M, Harms W, et al. Dose-volume histograms. Int J Rad Oncol. (1991) 21:71–8. doi: 10.1016/0360-3016(91)90168-4
32. Zhu TC, Bonnerup C, Colussi VC, Dowell ML, Finlay JC, Lilge L, et al. Absolute calibration of optical power for PDT: report of AAPM TG140. Med Phys. (2013) 40:081501. doi: 10.1118/1.4813897
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
33. Svensson T, Andersson-Engels S, Einarsdóttír M, Svanberg K. In vivo optical characterization of human prostate tissue using near-infrared time-resolved spectroscopy. J Biomed Opt. (2007) 12:014022. doi: 10.1117/1.2435175
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
34. Jacques SL. Optical properties of biological tissues: a review. Phys Med Biol. (2013) 58:5007–8. doi: 10.1088/0031-9155/58/14/5007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: Monte Carlo, photodynamic, dosimetry, tetrahedral, dose-volume histogram
Citation: Cassidy J, Betz V and Lilge L (2015) Treatment plan evaluation for interstitial photodynamic therapy in a mouse model by Monte Carlo simulation with FullMonte. Front. Phys. 3:6. doi: 10.3389/fphy.2015.00006
Received: 01 November 2014; Accepted: 28 January 2015;
Published online: 24 February 2015.
Edited by:
Ulas Sunar, University at Buffalo, USAReviewed by:
Adam Thomas Eggebrecht, Washington University School of Medicine, USARongxiao Zhang, Dartmouth College, USA
Copyright © 2015 Cassidy, Betz and Lilge. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jeffrey Cassidy, Edward S. Rogers Sr., Department of Electrical and Computer Engineering, University of Toronto, 10 King's College Road, Toronto, ON M5S 3G4, Canada e-mail:amVmZnJleS5jYXNzaWR5QG1haWwudXRvcm9udG8uY2E=
 Jeffrey Cassidy
Jeffrey Cassidy Vaughn Betz
Vaughn Betz Lothar Lilge
Lothar Lilge