- National Centre for Nuclear Research, Warsaw, Poland
The frequent occurrence of extremist views in many social contexts, often growing from small minorities to almost total majority, poses a significant challenge for democratic societies. The phenomenon can be described within the sociophysical paradigm. We present a modified version of the continuous bounded confidence opinion model, including a simple description of the influence of emotions on tolerances, and eventually on the evolution of opinions. Allowing for psychologically based correlation between the extreme opinions, high emotions and low tolerance for other people's views leads to quick dominance of the extreme views within the studied model, without introducing a special class of agents, as has been done in previous works. This dominance occurs even if the initial numbers of people with extreme opinions is very small. Possible suggestions related to mitigation of the process are briefly discussed.
1. Introduction
Modeling of opinion dynamics is one of the core domains of sociophysics, rising in popularity since the early 1990's. The use of an analogy of opinions with spins and exchanges of information during social contacts with spin-spin interactions has allowed an effective use of the considerable range of tools developed for magnetic systems. In particular, the early models of opinion formation focused on the processes leading to consensus—corresponding to a fully magnetized state, e.g., [1–8]. Despite significant simplifications, quite a few interesting regularities were discovered, corresponding, in a general way, to observed behaviors in social systems. Unfortunately, a quantitative description of the actual societies and the psycho-social phenomena remains a rather elusive goal.
At the same time, the observation that a complete consensus is quite unusual in the real social situations has led to creation of models focused on the coexistence of several opinions in the same society, often in an open conflict. Many of these works were based on the same conceptual foundations and technical methods as the “consensus” studies, but have introduced a particular type of modification, namely the introduction of inflexible agents, designed to lead to a long lasting state of disagreement. Examples include the bounded confidence approach [9, 10]; the discrete opinion model of Galam [11]; the binary Naming Game approach [12–14]; the voter model [15, 16]; the Sznajd model [17, 18] and the approaches based on the notion of stubbornness [19, 20]. Despite the differences in many basic properties of these models: the available opinion space (binary opinions, multiple discrete values or continuous spectrum); the social network (fully connected, geometrical, small-world or scale free network); the specific method of describing the interactions between agents—all these works point out that the presence of even a small group of agents with fixed opinions may sway a large part of the community or even the whole of it. These special agents get labeled in various ways: zealots, inflexibles, independents or extremists. The diversity of the models is due to different kinds of simplifications of social systems they use, focusing on separate aspects of individual characteristics. At the same time, the similarity of the model outcomes documents, in author's opinion, the robustness and importance of the result of sociophysical modeling, especially in the context of group behavior and its driving mechanisms. The universality of the relationship between presence of inflexible extremists and evolution of opinions deserves much broader recognition and interdisciplinary approach.
One of the reasons for the difficulties in constructing sociophysical models of opinion change quantitatively describing some actual societies, is the fact that the changes of individual views on many issues depend not only on the current opinion state of the person and the perceived opinions of others (as assumed in most models), but also on the person's own emotions and the emotions of others (see for example, [21–27]). The individual dynamical processes of opinion change may be complex functions of many variables, internal and external, much more difficult to describe than the spin-spin interactions. The interpersonal contacts involve not only transmission of information and argumentation, but also mutual influences changing the emotional states. The same applies to the ways in which media or propaganda influence opinions. Social studies recognize the significant role of emotions in the increasing polarization of opinions, observed in many social systems, from politics to scientific issues [28–35], and the recent sociophysical studies begin to cover this aspect of the process. Based on these ideas, a model that combines opinions and emotions has already been proposed by the author. It is based on a discrete version of the cusp catastrophe description of an individual opinion change resulting from a pairwise communication process. The model has been coupled with a realistic social communication network, and has been used successfully to quantitatively describe the behavior of the users of a political discussion forum [36–38]. One of the results of this work was that even without the introduction of a special class of inflexibles, the emotions due to a conflict of opinions may “harden” the behavior of individuals and groups, leading to a stable, conflicted social state. The model presented in the current paper has a much simpler background. Using the well known bounded confidence framework, in which opinions may take any value from a continuous spectrum, we introduce a correlation between the extreme opinions and low flexibility, mediated via a persons emotion. The model does not aim at a quantitative description of any social environment. Its goal is to show that the shift to extreme and intolerant views in many social situations may be modeled without resorting to a special class of agents.
2. Materials and Methods
2.1. Bounded Confidence and Relative Agreement Opinion Change Models
The bounded confidence approach forms a special class of opinion change models, characterized by continuous distribution of possible opinions within a given range and a simple, intuitive mechanism for individual opinion changes. The original formulation proposed by Deffuant et al. [4] stems from the following observations: to be mutually influenced, the two communicating agents must have initially opinions that are close enough. If the difference of opinions is too big, the communication process is impossible, and there is no change in the respective opinions as the effect of the interaction. On the other hand, the model postulates that if the initial opinions are close enough, the interaction between the agents brings them even closer. If we denote individual opinion of agent i at given time t as oi(t), and consider the outcome of the interaction between agents i and j, then the opinions at time t + 1 are governed by the following equations:
if |oi(t)−oj(t)| ≤ d. Otherwise oi(t + 1)= oi(t) and oj(t + 1)= oj(t). The value of d, called tolerance threshold, was initially considered to be the same for all agents in the system. The constant μ is assumed to lie between 0 and 0.5, and determines the speed of convergence of the opinions.
The basic model described above leads to an aggregation of the opinions into a few narrowly defined bands, distributed approximately regularly in the available opinion domain. The number of these final opinions depends on the relationship between the tolerance threshold d and the width of the available opinion space D, and may be approximated by D/2d.
The Deffuant model is one of the most studied in sociophysics. It has been used in various communication topologies, starting from fully connected network, where any agent may communicate with any other; grid models with limited range of interactions and complex social networks [39]. Sousa [40] has studied the bounded confidence model on a growing scale free network, in which the new agents adjust their opinions to the ones who have already communicated (and who may have attuned their opinions previously). Other modifications include substituting the step-like form of the effects of the tolerance by some continuous function [41]. An important modification is the “relative agreement model” [42], in which the agents are characterized by individual opinions and uncertainties, which both may evolve as the outcome of the communication between agents. Another interesting modification is the introduction of the effects of rejection, if the two agents' opinions differ too much [43].
Most of these works have assumed an initially random distribution of opinions and other agent characteristics, which may not be a realistic approach and in some cases lead to theoretically interesting, but non-applicable results. For this reason, Carro et al. [44] devoted part of their study to the role played by nonuniform initial conditions, a topic that we shall also examine in this work. In general, the Deffuant model, despite its conceptual simplicity, provides a fertile ground for creative extensions and model variants (recent interesting works include [45–47]).
An important example of such modification was the introduction of a small number of agents with extreme views and very small tolerances, and study of how such admixture may influence the behavior of the majority [41, 42]. These works have shown that even a small number of the inflexible agents may shift the opinions of the large part of the community toward the extreme values. The justification for the introduction of the special class of the extremists, given in [41] was “often people who have extreme opinions tend to be more convinced. On the contrary, people who have moderate initial opinion express the lack of knowledge (and uncertainty).” Our present effort is to use—within the same philosophy—a basic connection between emotions associated with extreme views and accompanying low tolerances, and to show that a corresponding modification of the model can lead to a qualitative explanation of the polarization phenomena and shifts to extreme opinions found in many social situations, without introducing any special class of agents, allowing that anyone may become an extremist.
2.2. Deffuant Model with Emotions
In our work we consider a variation of the Deffuant, Amblard and Weisbuch model, where extreme opinions are connected with high emotions and low tolerances. Thus, changing the opinion of any agent changes its emotions and tolerance as well. For example, if the available spectrum of opinions is given by the interval between 0 and 1, we assume that opinions close to 1 (defined as the extreme view) are associated with strong emotions while those with values close to 0 (moderates) have low levels of emotions. Such choice of the opinion space is natural for the case of the emergence of extreme opinions with respect to some issues, for example in the case the moderates do not consider the issue important and do not have a fixed opinion, while others think the issue is very important, have a definite opinion and approach it with high levels of emotions (the extremists). This follows directly from the justification quoted above. It is very interesting that the psychological research [48] confirms that people with extreme political views are more resistant to externally generated anchors, supporting the hypothesis that the extremists have very high confidence in their opinions.
The basic equations governing the bounded confidence opinion dynamics which we shall use follow the modifications introduced many years ago by Weisbuch et al. [49], who substituted the single single universal d in Equations (1) and (2) by individual tolerances of the agents di:
As before, there is no change of opinion of the agent i if the difference of the opinions of the two agents exceeds the tolerance di.
We propose that for an agent with opinion oi, the emotional involvement of the agent would be proportional to oi and due to this increasing involvement, the tolerance threshold of that agent would be some decreasing function of the individual opinion di = F(oi).
These considerations may be generalized simply into the cases of two opposing opinions, located at the extreme ends of the opinion space (for example taking the −1 and +1 values). In such case, the individual tolerance threshold can be written as decreasing function of the absolute value of the opinion, di = F(|oi|). In such case, we would call agents with opinion close to 0 the “moderates,” while the name “extremists” would apply to agents with opinions close to 1 or to −1.
We chose a very simple relationship between the opinion and the tolerance of an agent, namely
where dmax is the tolerance for the moderates and dmin is the tolerance for the agents with the extreme opinions; while L is the exponent determining the rate of decrease of the tolerance with increasing opinion value. In this work we assume dmin to be very small (0.0001) while dmax is one of the parameters of the simulations. We shall study the system behavior for L = 1, 2, and 3. The larger values of L correspond to a slower decrease of di with the increasing value of the opinion oi, and a more tolerant behavior of the agents with intermediate opinions (Figure 1).
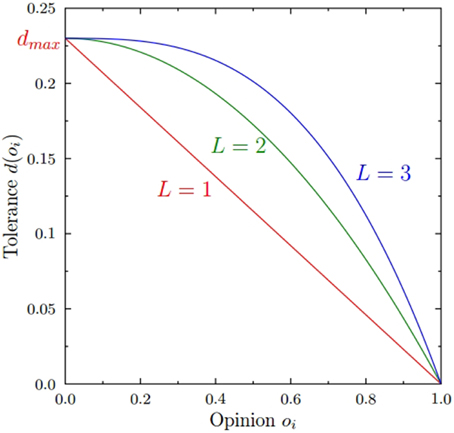
Figure 1. Graphical example of the postulated form of the dependence of the tolerance di on the current opinion oi, for L = 1, 2, 3 and dmax = 0.23 and dmin = 0.0001.
Due to the assumed form of dependence of di on oi, the outcome of the communication between two agents becomes an asymmetric function of the agents' opinions. Suppose that oi > oj so that di < dj. It is possible to encounter a situation when agent j would find agent i within its radius of tolerance and therefore adjust its opinion, while agent i would perceive j to be beyond its tolerance threshold and remain unchanged. As the result of the asymmetry, the moderates are more likely to change their opinions to more extreme values, while the extremists have less chances to moderate their views. The evolution of the system is driven largely by this asymmetry.
3. Results
3.1. Results for Uniform Distribution of Initial Opinions
We shall start our discussion of the results with the simulations using a uniform, random distribution of the initial opinions within the [0:1] domain. This is a typical assumption used in many opinion dynamics models, which provides particularly easy implementation. In our simulations we have used a “society” of NA = 20,000 agents, communicating in a simple, fully connected, any-to-any topology, in a random sequence. The time is measured in steps, each of which corresponds to NA single communication events, that is one event per agent. We note here that on the average there would be two communications per agent in each step (one “initiated” by the agent, and one in which it is a “target”). Each presented simulation covers a total time of 500 steps, which is, for most of situations, enough to reach stable final configuration. The random differences in the initial opinion distribution and in history of communication between single simulation runs lead to slightly different final distributions. For this reason, we have run the simulations for the same parameter values 200 times, and the figures show averaged aggregates of such repeated simulations.
The simulation results are presented in Figures 2–4, for L = 1, 2, and 3, respectively. For small values of the moderate agents' tolerance threshold dmax, in all three cases the system very quickly evolves into a stable state. This state is characterized by the presence of a few discrete opinion values, around which the final agent opinions cluster. Such behavior is the hallmark of the Deffuant model. The difference from the original simulations is that the separation between these peaks in the final opinion distribution gets smaller with increasing opinions. This is simply due to the decrease of the local tolerances. In the of L = 1 and L = 2 (Figures 2A, 3A), for small enough dmax the peak structure becomes washed out around oi ≈ 1.
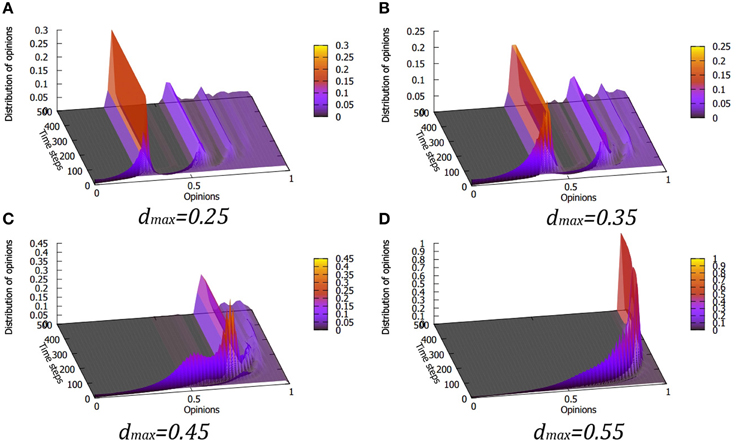
Figure 2. Cumulative distribution of opinion evolution gathered from 200 simulation runs at various values of the maximum tolerance dmax for the linear form of the Equation (5), i.e., L = 1. For small enough values of dmax (A) the results resemble the traditional deffuant model, with locally rescaled distances between opinion maxima. Increasing dmax shifts the position of the peaks and causes some rearrangement at the high end of the opinion spectrum (B,C). Above certain value of the tolerance of the open-minded agents (D) we observe fast transition to a single, extremist opinion. Note the differences in the vertical scales in the figure panels. The small oscillations visible especially in the early evolution in (C,D) are artifacts of the visualization.
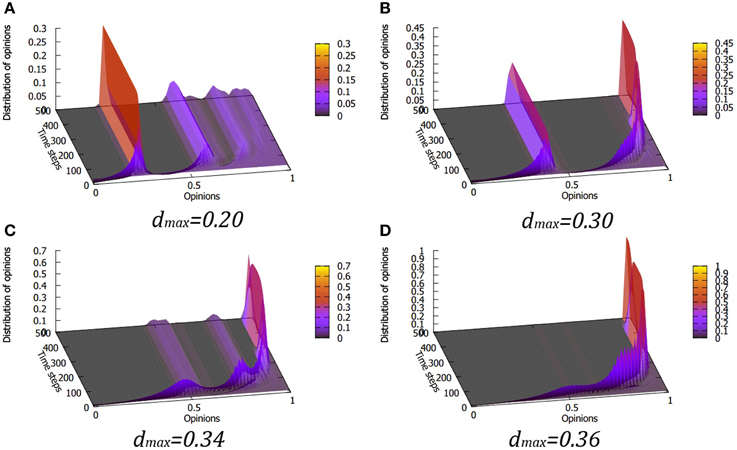
Figure 3. Cumulative distribution of opinion evolution gathered from 200 simulation runs at various values of the maximum tolerance dmax for the quadratic form of the Equation (5), i.e., L = 2. As in the linear case, for small values of dmax we observe stable maxima of opinions with decreasing separation as opinion increases (A). However, in the quadratic dependence of tolerance on opinion, the transition to a single, extremist opinion happens for much smaller values of dmax and the dependence of the system behavior on dmax is much more rapid [cf. the transition from a two-peak form (B) for dmax = 0.30, via an intermediate state (C) to a single maximum (D) at dmax = 0.36].
When the value of dmax is increased, the final pattern of opinion distribution peaks shifts progressively to larger values of opinions (Figures 2A,B, 3A,B 4A,B). This is exactly what one would expect from the results of the original bounded confidence models.
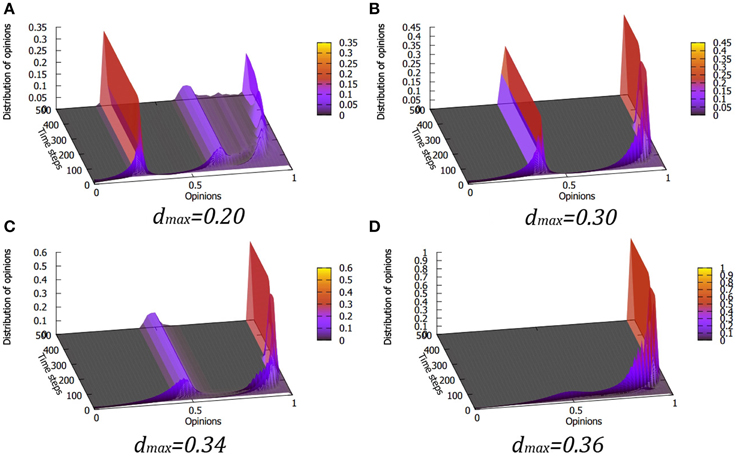
Figure 4. Evolution of opinion distributions for various values of the maximum tolerance dmax for L = 3. The results are very similar to the case of L = 2. Panels (A–D) correspond to dmax values of 0.20, 0.30, 0.34 and 0.36, respectively.
What is perhaps more interesting is the appearance, for large enough values of dmax, at the early stages of the system evolution (t < 200), of a “traveling maximum” in the opinion distribution, shifting to higher values of opinions as the time progresses. For L = 1 this transition state appears at quite large value of dmax ≈ 0.45, while for for L = 2 and 3 it occurs at much smaller values (around dmax ≈ 0.35). The traveling peak gathers most of the moderate agents in a single group with similar opinions, which shift toward more extreme values, eventually leading to a single state, in which the whole society is unified in the extreme opinion (Figures 2D, 3D, 4D).
The rapidness of the transition between the “classical” state of several opinion peaks and the state with a single extremist consensus, as a function of changing dmax depends on the exponent L. For L = 1 the transition is gradual, while for L = 2 and L = 3 it is very steep. We note here that while the results for L = 1 (with linear dependence of the tolerance threshold) are quite different from those obtained for L = 2 and L = 3, the latter two lead to a very similar behavior, which can be seen comparing Figures 3, 4.
We note here that using values of L smaller than 1 leads to a “less interesting” behavior: even for quite large values of dmax the system remains in a state similar to the one depicted in Figures 2A,B i.e., a series of peaks in the density of final states corresponding to groups with separated opinion, no longer capable to interact between each other. This is due to much faster drop of the agents' tolerance with the increasing value of their opinion.
The origin of the above results may be described in plain language. For small enough dmax, the initial process of grouping of opinions quickly leads to a situation, where the local maxima in opinion distribution become separated by distances greater than the local tolerances, leading to a stable multi-peak structure. On the other hand, for large values of dmax, the local tolerances are greater than the separation between the peaks, which allows agent transfer between the groups. Such transfer is, as we have noted, asymmetric: the moderate agents are more likely to become convinced by the more extremist ones, and are unable to “defend” their views.
3.2. Effects of Decreased Tolerance due to Contact with Different Opinions
Another psychologically based modification of the bounded confidence model is the consideration of the emotional effects of communication with people whose opinions differ by more than the tolerance threshold. Examples of such modifications include the repulsion effects such as the ones studied by Huet, Deffuant and Jager [50] or partial antagonism considered by Kurmyshev et al. [51].
In our case, the main dynamic equations governing the opinion evolution remain unchanged. However, we postulate that the tolerance of any agent who met someone whose opinion was beyond the tolerance threshold may be temporarily decreased. This is due to the immediate negative emotional reaction caused by confronting “intolerable” views. The effective individual tolerance threshold shall be defined as follows: di(t) = mi(t)·di(t), with mi(t) ≤ 1. The factor mi(t) may be called the “mood” of the agent i. If the latest interaction of the agent i was with an agent within the tolerance limits, then the mood is “good” and mi(t) = 1. On the other hand, if the latest interaction was with an agent whose opinion was beyond the tolerance threshold, the mood becomes “bad,” and the mood factor becomes mi(t) = m < 1. In the current work we have used m = 0.5. The mood is applied only once per turn to any agent, so there are no cumulative effects.
The substitution of the effective tolerance di(t) in place of di(t) leads to significant changes of the behavior of the system (Figures 5, 6). The trend toward extremist consensus appears at lower values of dmax. Moreover, the “traveling peak” becomes visible even when there are still well defined “classical” maxima in the opinion distribution function. In general, the introduction of the mood factor broadens the range of conditions under which the system evolves into the uniform extremist state.
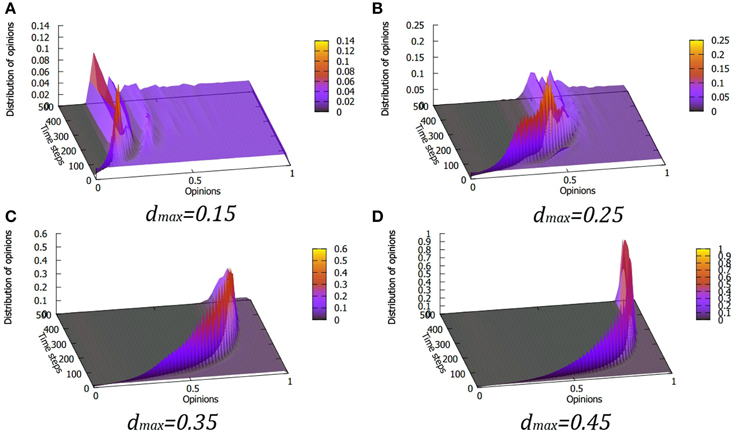
Figure 5. Evolution of opinion distribution for various values of the maximum tolerance dmax for the linear form of the Equation (5), i.e., L = 1, for the mood factor m = 0.5. Panels (A–D) correspond to dmax values of 0.15, 0.25, 0.35 and 0.45, respectively.
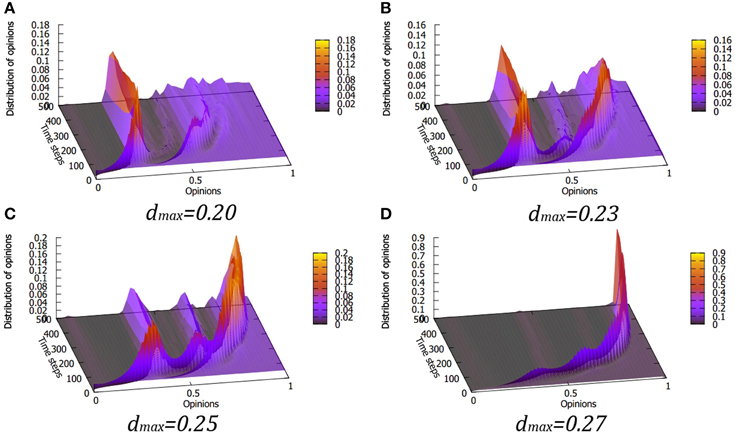
Figure 6. Evolution of opinion distribution for various values of the maximum tolerance dmax for the quadratic form of the Equation (5), i.e., L = 2 and the mood factor m = 0.5. Panels (A–D) correspond to dmax values of 0.20, 0.23, 0.25 and 0.27, respectively.
The explanation for this phenomenon is the increase of the asymmetry between moderates and extremists caused by the presence of the mood factor. If we consider, as before, the pair of agents i and j, with oi > oj then if di is small enough that agent i fails to tolerate agent j, its effective tolerance di would diminish further. At the same time, the more tolerant moderate agent j would not decrease its effective tolerance dj. As the result, the less tolerant agents are, in general, becoming even less tolerant, and less likely to adjust their opinions.
When the mood is taken into account, the system evolution becomes more complex, especially within the transition range of dmax (Figures 5B,C, 6B,C). The key observation, that for large enough values of the initial tolerance of the moderates the system eventually reaches the extremist consensus, remains unchanged. Including the mood modification leads, however, to a significant lowering of the value of dmax at which such transition occurs.
3.3. Effects of Nonuniform Initial Conditions
As we have noted, most simulations of opinion dynamics start with the uniform random distribution of the agents' characteristics. This corresponds to high temperature limit in statistical physics, but may be quite inappropriate to the study of real social systems, where uniform randomness is quite unusual. The results shown in the previous sections were obtained with such starting conditions. In this section we shall consider the effects of a nonuniform distribution of the initial opinions.
From the point of view of the social sciences one of the most interesting initial distributions is the one in which the number of the people with the extreme opinions is initially rather small. This corresponds to the question: would such small admixture of extreme opinions lead to eventual adoption of these views by the majority, and if yes, under which conditions?
To check this possibility, we have simulated the behavior of our system starting from an exponential initial distribution of opinions, described by p(oi) ~ exp(−aoi), with a = 5. Relatively large value of a ensures that initially the majority of agents have opinions close to zero [the initial ration of the number of agents with opinions close to 1 (extreme views) and those with opinion close to 0 (moderates) is less than 0.0067].
Figure 7 shows the averages of evolving distributions of opinions with the exponential initial conditions and with other simulation parameters corresponding to the system in shown in Figure 3. There is no modification due to mood factor (i.e., m = 1) and L = 2.
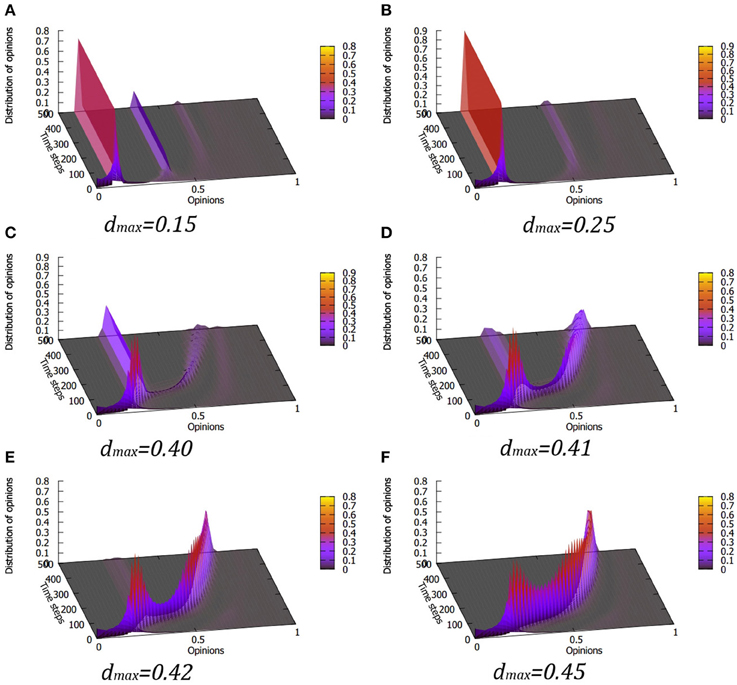
Figure 7. Opinion evolution for various values of the maximum tolerance dmax for the exponential distribution of the initial opinions. Quadratic form of the Equation (5), i.e., L = 2 is used; there is no mood modification. Despite initially dominant position of the moderate agents, above dmax = 0.42 the system evolves toward the extreme consensus. The evolution is, however, much slower than in the case of the uniform initial opinion distribution. Still, even a small number of zealots can convince the whole society eventually to their views. Panels (A–F) correspond to dmax values of 0.15, 0.25, 0.40, 0.41, 0.42 and 0.45, respectively.
For low values of dmax (Figures 7A,B) the familiar pattern of multiple, separated peaks is seen, with very small contribution of the agents with large values of opinions. When dmax becomes greater than a certain threshold, we observe that a single traveling peak forms in the distribution, which moves to ever higher values of opinion as time passes (Figures 7D–F). Especially interesting is the situation for dmax ≈ 0.41 (Figure 7D), where the final situation includes two separate groups: one, for which the opinion remains stable and relatively moderate and the second, which gradually shifts to more and more extreme views. Above dmax = 0.42 this second group “gathers” the majority of the agents. This shows that if the tolerance of the moderate agents is large enough, even a very small fraction of extreme opinions can cause the whole society to gradually shift their views to the extreme position.
3.4. Competition between Two Opinions
The results presented so far were for a simple moderate↔extremist opinion range [0:1], that is for the case when the “competition” is between no opinion and a definite opinion. However, our model may be easily extended to a conflicted, binary opinion case. Then, depending on the initial conditions, we could also have the eventual dominance of the extreme views, but this time located at both extreme ends of the spectrum [−1:+1]. Such an evolution, squeezing out the moderates and effectively inhibiting any communication between the conflicted camps not only corresponds to many actual social systems, but also could provide an alternative introduction to the discrete models of opinion change, resulting from the continuous one, such as the Deffuant model.
Figure 8 presents an example of the system behavior close to the transition point for starting conditions that favor moderate opinions: the initial distribution is a symmetrical, exponentially vanishing one (corresponding to the one used in the previous section). The averaged distribution of evolving opinions shows quite rapid transition from the central moderate opinion to two separate populations as the value of dmax is increased. Above a certain value of the moderates' tolerance, despite their initial dominant position, the system quickly evolves into a dual-extremist society, with the two groups being separated beyond their respective tolerances, effectively unable to communicate. Because the initial distribution of opinions was symmetrical, the evolution averaged over multiple simulation runs is also symmetrical. We remind, however, that due to the randomness present in the simulation process, the results for single runs may not be symmetrical, sometimes with significant differences between the numbers of supporters of positive and negative opinions and even an occasional dominance of one group over the other. If one assumes an asymmetrical initial distribution of opinions, or a presence of some sort of a bias favoring the positive or negative opinions (e.g., due to propaganda), the model may lead to a stable polarized society, with an adjustable average ratio of majority/minority community sizes.
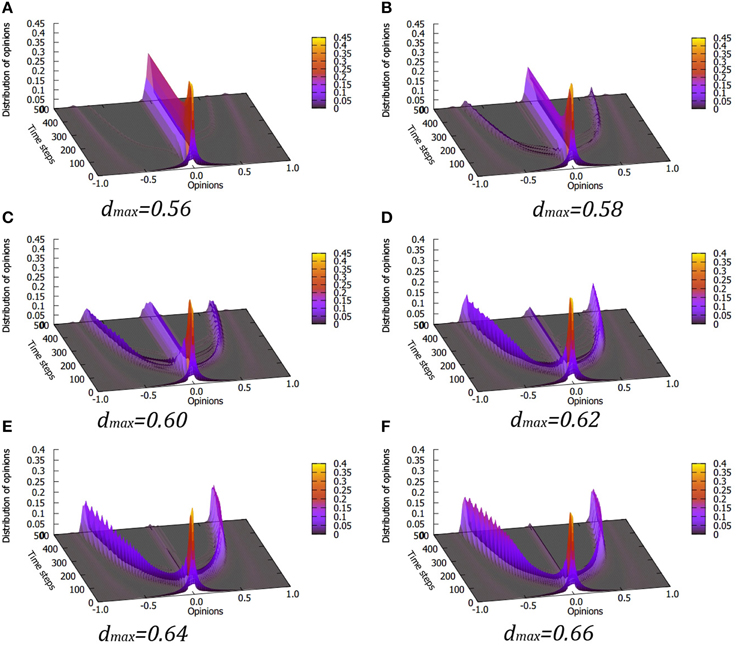
Figure 8. Case of two competing opinions, with opinion scale from −1 to +1. A symmetric, exponentially decaying distribution of the initial opinions is used. As in Figure 2, L = 2 is used, there is no mood modification. Results are shown for values of dmax at which the transition from a single moderate majority peak to two separate, opposite opinion groups occurs. Note much larger values of the tolerance dmax, for which the transition from moderate final state to extremism occurs, than in the previous simulations. However, this should be compared to the fact that available opinion space is twice as large. Panels (A–F) correspond to dmax values of 0.56, 0.58, 0.60, 0.62, 0.64 and 0.66, respectively.
4. Discussion
The proposed modification of the continuous bounded confidence models does not change the agent-to-agent dynamics, but examines simply the results of the correlations of opinions and tolerances, linking the extreme opinions with high emotional involvement and low tolerances. As such, it may be considered a relatively minor change—yet the results seem to be quite profound.
The basic outcome of our model may be simply summarized as follows: in situation when extreme opinions are associated with high emotions and small tolerance, the more tolerant are the initial non-extremists, the more extreme becomes the final society. This result is obtained without the adjustment of the core dynamics of the opinions (Equations 3 and 4). For the tested values of small (1000 agents) and medium size (20,000) communities we observed no difference (other than a larger “noise” between the individual simulation runs for small system sizes) in the resulting distributions. There was only a small change of the time scale of reaching the final configurations. It is possible that for very large communities (1M or more), the fact that only a small “sampling rate” of all possible connections (with the time tick defined as communication events equal to the number of agents and the number of connections proportional to the square of the number of the agents) is actually used in the process may lead to a more diverse simulation results. Perhaps one should then scale the time ticks in quadratic relation to the number of the agents. On the other hand, in our opinion, the any-to-any topology is in any case a model one, oversimplifying the real social systems. Our modest goal was to show an indicative behavior. The future work should focus on the effects due to more realistic social network topologies, including dynamic networks (in which a possible reaction to meeting an agent outside the tolerance limit results in cutting the communications). In such networks the average number of links per agent does not grow linearly with the number of agents, but may remain fixed.
The decreasing tolerance associated with extreme opinions, leads to a disappearance of the moderate agents who are tolerant enough to “listen” to the extremists. This observation extends the statement by Weisbuch et al [49], that “in the long run the behavior depends on “open-minded” (high threshold) agents, in the short run on the low threshold ones.” If open-mindedness is correlated with one opinion and low tolerance with the other, the model predicts that the closed-minded part of the community would gain the upper hand. The casual observation of many social phenomena in recent years indicates that such reasoning might be close to reality.
The model of extremism propagation created by Deffuant, Amblard and Weisbuch [41, 42] has shown that a small fraction of artificially introduced inflexible fanatics (agents with very low tolerances) can, indeed, influence a much larger society. The two approaches share the same pessimistic final conclusion: not only the final state is dominated by the extreme opinions, but also their tolerances are very small (Figures 7, 8 of reference [42]). This offers little hope for a possible reversal of the situation, by propaganda or by the introduction of “counter-extremist” agents—because after reaching the extreme opinion, the majority of the agents becomes close-minded. One of the ways the opinion/tolerance correlation, used in our work, may form is through emotions, especially the negative ones: fear, hatred, anger, rejection… The analysis of the political discussion fora confirms this reasoning [38, 52, 53]. Even in the situations where proponents of the opposing opinions actively seek out contact with each other, the chances of influencing the opinion of the opponents are practically zero. Moreover, if we look at the actual tactics of many extremist movements (in politics and in other domains), we note the conscious and quite effective use of he negative emotions in the group consolidation and establishing orthodoxy. The proposed model offers some suggestions on combating the shift toward the extreme opinions. The obvious method for the initial stages (when the majority of the population is still moderate) is to decrease the tolerance of the majority. This can be done via propaganda that builds up the negative emotions regardless of the opinions held (effectively decreasing dmax). It can be done, for example, by media which would portray the situation as dangerous; by instilling fear of change or invoking special orthodoxy status to certain (moderate) opinions. Such tactics may be recognized in many social situations. The system would then remain in the state with significant presence of the moderates, but there is an associated social cost to such tactics. While the opinions of the agents would remain moderate, their tolerances would be low and the social communication would be weak. This cost must be weighted against the possible danger of harboring and encouraging the shift to extreme opinions (and the associated social and political decisions).
A much more difficult task is reversing the transition to the extremist consensus in the latter stages of the system evolution. Here, the only hope is in a combination of increase of the tolerance of the extremists (increasing dmin) and in the presence of inflexible moderate agents or appropriate propaganda leading away from the extreme opinions. Attempts to change opinions without increasing the tolerances of the extremists, for example by calm and rational arguments—tactics often tried in the real world—are bound to fail. Perhaps one of the ways of increasing the tolerances by promoting the sense of security, calm, even by assuring the positive feeling of achievement in the members of the newly formed majority, opening the way for opinion change. Otherwise, the final state is not only extremist, but also effectively frozen in that state. It is not surprising, that the leaders of the extremist groups, after they achieve a relative dominance, continue the efforts of keeping the tolerance of their supporters very low, for example by stressing the presence of “enemies” and the dangers of “heresy.”
A recent analysis of many social systems by Ramos et al. [19] has shown an universal, nonlinear behavior of the fraction of people holding extreme views on many issues when compared to the overall support (both moderate and extreme) for the issue in question. This nonlinearity has been observed in many domains, including religious views, political interests, economic situation evaluation, book and movie reviews. In most cases, for low values of the overall support of a given opinion (denoted in Ramos et al. [19] by f), the fraction of extremists (denoted by fe) is much smaller. On the other hand, when f becomes close to 1, fe becomes comparable to f, i.e., most supporters adopt extreme position.
These findings were accompanied by a dynamical model of individual opinion changes, in which the averaged opinion of neighbors was modified via a parameter describing an individual stubbornness. The model proposed by Ramos et al. has shown a similar kind of nonlinearity between f and fe.
Despite the simplicity of the modified Deffuant model presented in this paper, it produces results that are qualitatively similar to those of Ramos et al. Figures 2–7 show that for low enough dmax, the final ratio of the number of extremist views fe (defined by opinions greater than, for example, 0.7) to the total number of supporters f (defined by opinions greater than 0.3) is less than 1. On the other hand, for large enough values of dmax, most or all agents supporting an issue have extreme views and fe/f ≈ 1. An example of the time evolution of these numbers is shown in Figure 9, which compares the fractions of agents with opinions greater than 0.3, 0.5 and 0.7, for dmax values just below and just above the transition to the extremist consensus (corresponding to Figures 7C,E). Depending on the value of dmax the ratio fe/f evolves in a nonlinear fashion in time, qualitatively corresponding to the analyses of actual opinions provided by Ramos et al. [19].
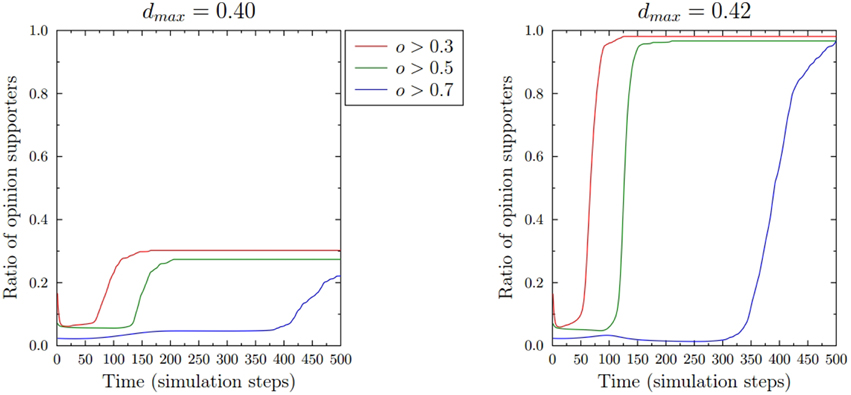
Figure 9. Time dependence of the ratio of agents with opinions greater than 0.3, 0.5, and 0.7, respectively, in the case of L = 2 and exponential initial conditions. If one defines the general support for the issue as having an opinion greater than 0.3 and the extreme views as those greater than 0.7, then the ratio between the two varies nonlinearly with time starting from values much smaller than 1 and approaching 1 after longer periods of time. The absolute values of the support depend on the initial tolerance of the moderates dmax.
5. Conclusions
The persistence and increasing strength of extremist views poses a grave threat to democratic societies. Recent years have shown many examples of rather quick transition from moderate societies to ones dominated by intolerance, zealotry and prejudices. Understanding the mechanisms leading to such changes is, therefore, quite important.
This paper claims no special, unique or directly applicable explanation of the real world phenomena. It belongs, in our opinion, to a broad and diverse group of models that focus on the general conditions leading to extremism formation. Despite the significant differences between these models—for example present in descriptions of the individual behaviors and of the social interactions—they have indicated that even a small group of inflexible proponents of extremist views often leads to the eventual dominance of the extremism.
In this work, as in our earlier discrete approaches [36, 37], we have connected the degree of tolerance and capacity for changing one's own opinion with the emotional state, recognizing (in a rough way) the complexity of human psychology. In our approach anyone can become an extremist, anyone can become an inflexible zealot, so there is no need to introduce a special class of agents. The suggestion coming from the current model is that to fight extremism it is not sufficient to present counterarguments (which would not appeal to the narrow-minded extremists), but to strive to lower the emotional commitment and therefore to promote open-mindedness, as necessary condition for any social discussion. Conversely, in the presence of the small minority groups threatening the moderate majority, the best defensive tactics is to lower the tolerance of the moderates—for example by emotional appeals. In a recent paper [54], Sznajd-Weron, Szwabinski and Weron have analyzed, in similar spirit of basic models, the differences between the opinion changes due to personal and situational influence. In the first case, the dominant role is played by fixed personal traits (for example a certain fraction of agents are inflexibles, while others change their opinions easily). In the situational model, all agents share the same probability of opinion change. The parameters of the two models can be chosen in such a way that the frequency of opinion changes is the same—but it turns out that the results of the two approaches in certain conditions are very different, and the approach based on fixed personal traits may lead to less realistic simulation results. In the light of this analysis, our approach, which correlates certain characteristics of the agents, without assigning special status to any of them, may be described as situational. At the same time, the final configurations resulting from the simulations may include agents with individually distinct behavior (flexible or inflexible). The induced agent characteristics of low tolerance in a certain social issue may “spill over” to other issues, where it would be seen as a personal trait. In this aspect, the task of distinguishing the two types of behavior becomes even more difficult to model.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author wishes to thank Guilliaume Deffuant for the discussions regarding the model, and the organizers of the CODYM Spring Workshop 2014 in Wroclaw for a very stimulating event.
References
1. Nowak A, Szamrej J, Latané B. From private attitude to public opinion: a dynamic theory of social impact. Psychol Rev. (1990) 97:362–76. doi: 10.1037/0033-295X.97.3.362
2. Kacperski K, Holyst JA. Opinion formation model with strong leader and external impact: a mean field approach. Phys A. (1999) 269:511–26. doi: 10.1016/S0378-4371(99)00174-0
3. Sznajd-Weron K, Sznajd J. Opinion evolution in closed community. Int J Mod Phys C. (2000) 11:1157–66. doi: 10.1142/S0129183100000936
4. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Adv Complex Syst. (2000) 3:87–98. doi: 10.1142/S0219525900000078
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
5. Holyst JA, Kacperski K, Schweitzer F. Social impact models of opinion dynamics. Annu Rev Comput Phys. (2001) 9:253–273. doi: 10.1142/9789812811578_0005
6. Hegselmann R, Krause U. Opinion dynamics and bounded confidence models, analysis, and simulation. J Artif Soc Soc Simul (2002) 5. Available online at: jasss.soc.surrey.ac.uk/5/3/2.html
7. Stauffer D, de Oliveira PMC. Persistence of opinion in the Sznajd consensus model: computer simulation. Eur Phys J B Condens Matter. (2002) 30:587–92. doi: 10.1140/epjb/e2002-00418-0
8. Fortunato S. Universality of the threshold for complete consensus for the opinion dynamics of Deffuant et al. Int J Mod Phys C. (2005) 16:259–70. doi: 10.1142/S0129183105007078
9. Deffuant G. Comparing extremism propagation patterns in continuous opinion models. J Artif Soc Soc Simul. (2006) 9:1–24. Available online at: jasss.soc.surrey.ac.uk/9/3/8.html
10. Franks DW, Noble J, Kaufmann P, Stagl S. Extremism propagation in social networks with hubs. Adapt Behav. (2008) 16:264. doi: 10.1177/1059712308090536
11. Galam S, Jacobs F. The role of inflexible minorities in the breaking of democratic opinion dynamics. Phys A Stat Mech Appl. (2007) 381:366–76. doi: 10.1016/j.physa.2007.03.034
12. Xie J, Sreenivasan S, Korniss G, Zhang W, Lim C, Szymanski BK. Social consensus through the influence of committed minorities. Phys Rev E. (2011) 84:011130. doi: 10.1103/PhysRevE.84.011130
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
13. Xie J, Emenheiser J, Kirby M, Sreenivasan S, Szymanski BK, Korniss G. Evolution of opinions on social networks in the presence of competing committed groups. PloS ONE (2012) 7:e33215. doi: 10.1371/journal.pone.0033215
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
14. Verma G, Swami A, Chan K. The impact of competing zealots on opinion dynamics. Phys A Stat Mech Appl. (2014) 395:310–31. doi: 10.1016/j.physa.2013.09.045
15. Mobilia M. Does a single zealot affect an infinite group of voters? Phys Rev Lett. (2003) 91:028701. doi: 10.1103/PhysRevLett.91.028701
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
16. Mobilia M, Petersen A, Redner S. On the role of zealotry in the voter model. J Stat Mech Theory Exp. (2007) 2007:P08029. doi: 10.1088/1742-5468/2007/08/P08029
17. Sznajd-Weron K, Tabiszewski M, Timpanaro AM. Phase transition in the Sznajd model with independence. Europhys Lett. (2011) 96:48002. doi: 10.1209/0295-5075/96/48002
18. Nyczka P, Sznajd-Weron K. Anticonformity or independence? – Insights from statistical physics. J Stat Phys. (2013) 151:174–202. doi: 10.1007/s10955-013-0701-4
19. Ramos M, Shao J, Reis SDS, Anteneodo C, Andrade JS Jr, Havlin S, et al. How does public opinion become extreme? arXiv:1412.4718v1 (2014).
20. Burghardt K, Rand W, Girvan M. Competing opinions and stubborness: connecting models to data. arXiv:1411.7415v1 (2014).
21. Simon HA. Making management decisions: the role of intuition and emotion. Acad Manag Exec. (1987) 1:57–64. doi: 10.5465/AME.1987.4275905
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
23. Petty RE, and Wegener DT. Attitude change: multiple roles for persuasion variables. Handb Soc Psychol. (1998) 1:323–90.
24. Allen CT, Machleit KA, Kleine SS, Notani AS. A place for emotion in attitude models. J Bus Res. (2005) 58:494–9. doi: 10.1016/S0148-2963(03)00139-5
25. Clore GL, Huntsinger JR. How emotions inform judgment and regulate thought. Trends Cogn Sci. (2007) 11:393. doi: 10.1016/j.tics.2007.08.005
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
26. Nielek R, Wawer A, Wierzbicki A. Spiral of hatred: social effects in Internet auctions. Between informativity and emotion. Electron Commer Res. (2010) 10:313–30. doi: 10.1007/s10660-010-9058-9
27. Walla P, Brenner G, Koller M. Objective measures of emotion related to brand attitude: a new way to quantify emotion-related aspects relevant to marketing. PLoS ONE (2011) 6:e26782. doi: 10.1371/journal.pone.0026782
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
28. Fisher DR, Waggle J, Leifeld P. Where does political polarization come from? Locating polarization within the US climate change debate. Am Behav Sci. (2013) 57:70–92. doi: 10.1177/0002764212463360
29. Stroud NJ. Polarization and partisan selective exposure. J Commun. (2010) 60:556–76. doi: 10.1111/j.1460-2466.2010.01497.x
30. Campante FR, Hojman DA. Media and Polarization. Harvard University, John F. Kennedy School of Government, Cambridge, MA (2010).
31. Baldassarri D, Bearman P. Dynamics of political polarization. Am Sociol Rev. (2007) 72:784. doi: 10.1177/000312240707200507
32. Prior M. Media and political polarization. Annu Rev Polit Sci. (2012) 16:101–27. doi: 10.1146/annurev-polisci-100711-135242
33. Conover MD, Ratkiewicz J, Francisco M, Goncalves B, Flammini A, Menczer F. Political polarization on Twitter. In: Proc. 5th Intl. Conference on Weblogs and Social Media. Barcelona (2011).
34. Galam S. Heterogeneous beliefs, segregation, and extremism in the making of public opinions. Phys Rev E. (2002) 71:046123. doi: 10.1103/PhysRevE.71.046123
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
35. Wood AJ, Ackland GJ. Evolving the selfish herd: emergence of distinct aggregating strategies in an individual-based model. Proc R Soc B Biol Sci. (2007) 274:1637–42.
36. Sobkowicz P. Discrete model of opinion changes using knowledge and emotions as control variables. PLoS ONE (2012) 7:e44489. doi: 10.1371/journal.pone.0044489
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
37. Sobkowicz P. Minority persistence in agent based model using information and emotional arousal as control variables. Eur Phys J B. (2013) 86:1–11. doi: 10.1140/epjb/e2013-40029-0
38. Sobkowicz P. Quantitative agent based model of user behavior in an internet discussion forum. PLoS ONE (2013) 8:e80524. doi: 10.1371/journal.pone.0080524
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
39. Amblard F, Deffuant G. The role of network topology on extremism propagation with the relative agreement opinion dynamics. Phys A Stat Mech Appl. (2004) 343:725–38. doi: 10.1016/j.physa.2004.06.102
40. Sousa AO. Consensus formation on a triad scale-free network. Phys A Stat Mech Appl. (2005) 348:701–10. doi: 10.1016/j.physa.2004.09.027
41. Deffuant G, Amblard F, Weisbuch G. Modelling group opinion shift to extreme: the smooth bounded confidence model. In: 2nd European Social Simulation Association (ESSA) Conference. Valladolid (2004).
42. Deffuant G, Amblard F, Weisbuch G, Faure T. How can extremism prevail? A study based on the relative agreement interaction model. J Artif Soc Soc Simul. (2002) 5. Available online at: jasss.soc.surrey.ac.uk/5/4/1.html
43. Huet S, Deffuant G. Bounded confidence with rejection: clusters or scattered opinions? In: 5th European Social Simulation Association (ESSA) Conference, Vol. 12. Brescia (2008).
44. Carro A, Toral R, San Miguel M. The role of noise and initial conditions in the asymptotic solution of a bounded confidence, continuous-opinion model. J Stat Phys. (2013) 151:131–49. doi: 10.1007/s10955-012-0635-2
45. Mäs M, Flache A. Differentiation without distancing. Explaining bi-polarization of opinions without negative influence. PLoS ONE (2013) 8:e74516. doi: 10.1371/journal.pone.0074516
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
46. Chau HF, Wong CY, Chow FK, Fung CHF. Social judgment theory based model on opinion formation, polarization and evolution. Physica A: Statistical Mechanics and its Applications, 415:133–40. doi: 10.1016/j.physa.2014.07.082
47. I~niguez G, Török J, Yasseri T, Kaski K, Kertész J. Modeling social dynamics in a collaborative environment. EPJ Data Sci. 3:1–20. doi: 10.1140/epjds/s13688-014-0007-z
48. Brandt MJ, Evans AM, Crawford JT. The unthinking or confident extremist? Political extremists are more likely than moderates to reject experimenter-generated anchors. Psychol Sci. (2014) 26:189–202. doi: 10.1177/0956797614559730
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
49. Weisbuch G, Deffuant G, Amblard F, Nadal JP. Interacting agents and continuous opinions dynamics. In: Cowan R, Jonard N, editors. Heterogenous Agents, Interactions and Economic Performance, Vol. 521, of Lecture Notes in Economics and Mathematical Systems. Berlin; Heidelberg: Springer (2003). p. 225–42.
50. Huet S, Deffuant G, Jager W. A rejection mechanism in 2D bounded confidence provides more conformity. Adv Complex Syst. (2008) 11:529–49. doi: 10.1142/S0219525908001799
51. Kurmyshev E, Juárez HA, González-Silva RA. Dynamics of bounded confidence opinion in heterogeneous social networks: concord against partial antagonism. Phys A Stat Mech Appl. (2011) 390:2945–55. doi: 10.1016/j.physa.2011.03.037
52. Sobkowicz P, Sobkowicz A. Dynamics of hate based internet user networks. Eur Phys J B. (2010) 73:633–43. doi: 10.1140/epjb/e2010-00039-0
53. Sobkowicz P, Sobkowicz A. Properties of social network in an internet political discussion forum. Adv Complex Syst. (2012) 15:1250062. doi: 10.1142/S0219525912500622
54. Sznajd-Weron K, Szwabinski J, Weron R. Is the person-situation debate important for agent-based modeling and vice-versa? PLoS ONE (2014) 9:e112203. doi: 10.1371/journal.pone.0112203
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Keywords: opinion dynamics, extremism, agent based modeling, bounded confidence model, sociophysics
Citation: Sobkowicz P (2015) Extremism without extremists: Deffuant model with emotions. Front. Phys. 3:17. doi: 10.3389/fphy.2015.00017
Received: 30 December 2014; Paper pending published: 05 February 2015;
Accepted: 08 March 2015; Published: 24 March 2015.
Edited by:
Andre C. R. Martins, Universidade de São Paulo, BrazilReviewed by:
Francisco Welington Lima, Universidade Federal do Piauí, BrazilYougui Wang, Beijing Normal University, China
Danny Eric Paul Vanpoucke, Ghent University, Belgium
Copyright © 2015 Sobkowicz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pawel Sobkowicz, National Centre for Nuclear Research, A. Soltana 7, 05-400 Otwock, Warsaw, PolandcGF3ZWxzb2Jrb0BnbWFpbC5jb20=
 Pawel Sobkowicz
Pawel Sobkowicz