- 1State Key Laboratory of Nuclear Physics and Technology, School of Physics, Peking University, Beijing, China
- 2WCI Center for Fusion Theory, National Fusion Research Institute, Daejeon, South Korea
We report a phase transition model for the onset of fast magnetic reconnection. By investigating the joint dynamics of streaming instability (i.e., current driven ion acoustic in this paper) and current gradient driven whistler wave prior to the onset of fast reconnection, we show that the nonlinear evolution of current sheet (CS) can be described by a Landau-Ginzburg equation. The phase transition from slow reconnection to fast reconnection occurs at a critical thickness, , where vthe is electron thermal velocity and vc is the velocity threshold of the streaming instability. For current driven ion acoustic, Δc is ≤ 10de. If the thickness of the CS is narrower than Δc, the CS subcritically bifurcates into a rough state, which facilitates breakage of the CS, and consequently initiates fast reconnection.
1. Introduction
Critical behavior is ubiquitous in magnetic reconnection related phenomena, e.g., Ôflux transfer event at magnetopause [1, 2], solar flare, etc. A universal property in these phenomena is that there is always a long development or slow reconnection phase before its transition into fast reconnection phase [3]. It is found that the formation of microscopic current sheets (CSs) is a necessary condition for the transition from slow collisional reconnection to fast collisionless reconnection [3–5]. The idea that (whistler) wave can catalyze fast reconnection has been explored both theoretically [6–8] and experimentally [9]. It has been found by Drake et al. [6] that a thin CS can be broken into small scale vortices by whistler wave turbulence and hence facilitate the fast reconnection. They also showed that prior to breakup of the CS, the critical thickness of the CS is smaller than the electron skin depth. Generation of fractal CS structure is also thought to be a way that links the microscopic and macroscopic scales in reconnection [10]. One approach to induce a fractal CS is via a series of macroscopic MHD instabilities, such as secondary tearing mode, Rayleigh-Taylor instability [11], etc. It is a “top-down” process, cascading from macro-scales to micro-scales. Another approach is a “bottom-up” process, i.e., formation of the fractal CS is initiated via microscopic instabilities. This process is plausible when the thickness of the CS shrinks into a very thin level (e.g., a hybrid width of ion skin depth and electron skin depth). By then, microscopic instabilities (e.g., streaming instability, whistler wave, etc.) tends to be excited. In this paper, we study the precursor of the fast reconnection, where the nonlinearity is weak and hence a perturbation analysis is applicable. By investigating the dynamics of the CS prior to the fast reconnection, we give an estimation of a possible process of the interaction of electron- and ion-beam-driven instabilities during their passage through a CS.
The onset of fast reconnection usually happens in a violent way, which is quite analogous to critical-phase-transition phenomena. In general critical phenomena, the state of the system is measured by its order parameter. As the system approaches to its critical point of phase transition, the order parameter undergoes a sudden increase, so that the system evolves into a new state. For the evolution of a CS, the amplitude of the current density disturbance is a natural order parameter. In laminar reconnection scenario, the amplitude of the disturbance is small. Once the phase transition occurs, the order parameter will acquire a finite amplitude transiently. So that the CS becomes rough, which tends to facilitate the formation of fractal CS structure, and hence the fast reconnection is induced. The normal formalism, describing critical-phase-transition/subcritical bifurcation, is Landau-Ginsburg theory [12]. For a narrow CS, the two typical microscopic modes are streaming instability and and whistler mode, which are driven by the strength of current intensity and the gradient of current density, respectively. An caveat: for “narrow,” we mean a CS with a thickness between ion skin depth and electron skin depth, thus both the ions' and electrons' dynamics should be incorporated. As a paradigmatic model, we choose current-driven-ion-acoustic (CDIA) as the representative of the streaming mode. The CDIA is an electrostatic mode, and it occurs when electron temperature is much higher than ion temperature [13]. The current gradient driven whistler wave (CGDW) is an electromagnetic mode and has been observed experimentally in the electron diffusion regime [14, 15]. We find that, under the joint interactions of CDIA and CGDW, the CS evolution is governed by a Landau-Ginsburg type equation. Once the CS is narrower than a critical thickness, the order parameter of the CS will acquire a finite value via subcritical bifurcation, and then the CS evolve into a rough state (but keep its topology). The roughened CS can be easily broken up by various instabilities, e.g., micro-tearing mode, KH mode [6], and hence accelerate the corresponding magnetic reconnection. We also make an estimation of the critical thickness of the CS, which is about 10de and is larger than that in Drake et al. [6]. The physics picture discussed in this paper is consistent with the results given by other approaches [6, 16].
The rest of the paper is organized as follows. In Section 2, the linear dynamics of CDIA and CGDW is analyzed. Section 3 gives a heuristic discussion of the nonlinear dynamics of CDIA and CGDW. Combining the conclusions in Sections 2 and 3, a Landau-Ginsburg evolution equation for the current density disturbance is obtained, and its bifurcation property is discussed in Section 4. Section 5 is a summary.
2. Linear Dynamics of CDIA and CGDW
Since electrons are the primary carriers of the current density, for simplicity, we assume the CS being purely composed of electrons, and hence all the free energy of the CS is stored in the electrons current sheet. The evolution of the electron distribution function is
where the collision effect in neglected. Integrating Equation (1) over e, ⊥(⊥ means perpendicular to the guide field in ) yields a drift-kinetic equation
where and . In Equation (2), the parallel and perpendicular kinetic of Fe are linearly coupled, so evolution of Fe can be decomposed into the following two processes
and
For the parallel kinetics, the evolution of the CS is driven by the free energy stored in the strength of the current intensity. A simplest, nontrivial choice for the relevant mode is CDIA, which transfers the momentum of electrons to that of ions [17]. The perpendicular kinetics is determined by the evolution of the perpendicular collective velocity Ve, ⊥, which is in turn determined by the EMHD equation. Therefore, the relevant mode to perpendicular dynamics of the CS is CGDW, which is driven by the free energy stored in the spatial gradient of the CS and is a whistler-like instability and is related to electron momentum transport [18, 19]. A consistent and complete treatment of the CS dynamics must deal with these two modes, simultaneously. Under the driving of inflow, the CS shrinks to a thin layer, and both the strength and the inhomogeneity of the current density tends to increase, so that both CDIA and CGDW modes may appear. An caveat: the realistic motions of particles inside a CS are extreme complex [16] and could invalid the use of drift-kinetic equation. However, the full kinetic 3D simulations indeed observed efficient particle acceleration inside a reconnecting CS and hence streaming instabilities (e.g., two electron beam instability) tend to occur inside a CS [16]. In the purpose of having a general view (not going the details of full kinetics of particles) of interaction between particle beams, we employ the drift-kinetic equation.
Since the CDIA and CGDW have been extensive studied in literatures [18–21], we provide a brief and heuristic discussion of the linear and nonlinear features of the CDIA and the CGDW modes, and focus on the evolution of the CS under the physics consequence of the joint interactions of these two modes.
2.1. Linear Instability of CDIA
CDIA belongs to a kind of electron streaming mode, which serves to generate anomalous resistivity. The CDIA occurs when the electron temperature, Te, significantly exceeds the ion temperature, Ti, e.g., in flare environment [20, 22]. Or else, it will be strongly suppressed by the ion Landau damping. Nevertheless, if Te ≃ Ti, a different streaming instability, Buneman instability, might occur, which has a higher velocity threshold in the order of electron thermal velocity, vthe. CDIA and Buneman instabilities only differ in details, and they share the common physical basis of a streaming instability triggered by electron streaming velocity that exceed critical values [13]. In fact, it leads to a similar conclusion if we replace the CDIA with Buneman instability.
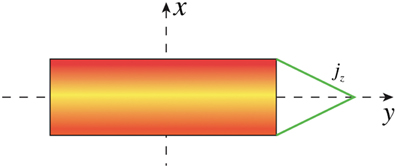
The initial current sheet is assumed in a laminar state. The maximum of current density is at the mid-plane (x = 0) of the CS, and decays to zero at the edge in a linear way (Figure 1). (x, y) is the reconnection plane with ± the direction of outflows. A strong guide field is in the out-of-plane direction, so the lower hybrid drift instability is excluded in the present paper [23]. We choose this profile for simplicity and a more realistic CS configuration can be chosen, but it is expected that the qualitative conclusion will not change. CDIA is well studied in literatures [17, 21, 24], so we directly write its dispersion relation as follows
where ωCDIAk is the real frequency and γCDIAk is the linear growth rate of the CDIA. kz is the wavenumber in z direction, 〈ve〉 is the mean electron streaming velocity in , and vc is the threshold velocity. Neglecting the effect of a mean electric field, which is small in the precursor of fast reconnection, vc is just the ion acoustic speed. Though a mean electric field may slightly shift the value of the threshold velocity [21], the structures of the dispersion relations, Equations (5) and (6), will not change. In the Appendix, we present a derivation of γCDIAk in the existence of a weak mean electric field, and show that only is the threshold velocity slightly shifted. As an illustration, we use the results of Bychenkov et al. [21]:
where cs = (Ti + Te/mi)1/2 is the ion acoustic speed, mi is the ion mass, and a = 2.14. The equilibrium distribution function of electrons is
Without losing of generality, the electron streaming velocity at the center of the CS is taken to be marginal, i.e., 〈ve〉(x = 0) = vc. We also assume 〈ve〉(x) varying linearly, 〈ve〉(x) = vc + 〈ve〉′x, with current shear 〈ve〉′ < 0 (here we take x > 0). Then the general form of γCDIAk(x) for a inhomogeneous CS follows as
where . γCDIAk has been assumed to be marginal in the middle plane of the CS, it becomes more and more negative as approaching the edge.
2.2. Linear Instability of CGDW
CGDW is an electromagnetic mode and can be described by EMHD equation [25]
where de is the electron skin depth, je = −eneve = ∇ × B is the electron current density, and B is the total magnetic field with a strong guide component in . The linear growth rate of the CGDW is proportional to the gradient of the CS. By extracting the free energy terms in linearizing Equation (9), one has
where the terms with higher spatial derivatives(〈ve〉,″ 〈ve〉‴…) are ignored. Employing the transformations of ∂t → γCGDWk, ∇ → ik yields
γCGDWk is solved as
In the above derivation, we have assumed that the current density shear is caused by electron drift velocity, other than density inhomogeneity [26, 27].
Though CGDW is driven by gradient of current density, it is not electron Kelvin-Helmholtz (KH) mode. The real frequency of CGDW is in the order of the whistler frequency, while the electron KH mode is a purely growing mode. CGDW is driven predominantly by the gradient in the out-of-plane current density, while electron KH mode is driven by shears of the in-plane electron flows [9, 28, 29]. Therefore, CGDW and electron KH modes are two different types of instabilities. Whistler wave has been confirmed in laboratory experiments and satellite observations, and is considered to be important in initiating fast reconnection [6, 14, 15]. In simulations, a current gradient driven mode with similar features has also been observed [30].
3. Nonlinear Dynamics of CDIA and CGDW Modes
Prior to the onset of fast reconnection, the nonlinearities of the parallel and perpendicular dynamics are weak, so that a perturbation analysis of the nonlinear dynamics of the CS is applicable.
3.1. Nonlinear Instability of CDIA
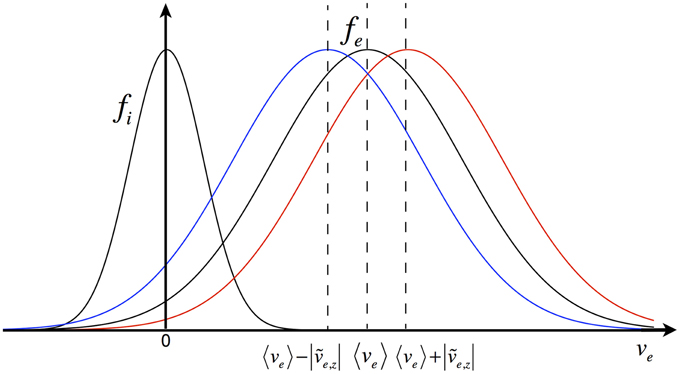
To the first order, fe is adiabatically shifted [31] by a finite perturbation of electron drift velocity in (See Figure 2), e, z, i.e.,
Depending on the sign of e, z, the nonlinear change of the free energy in the intensity of the current density is positive (e > 0, the red one in Figure 2) or negative (e, z < 0, the blue one in Figure 2). For the positive change, the CDIA is nonlinearly unstable, or else it is nonlinearly stable. Substituting Equation (13) into Equation (6), the nonlinear growth rate is readily derived as
where .
Combining Equations (8) and (14), the evolution of |e, z| driven by CDIA is (i.e., Equation 3)
where and . is used in deriving Equation (15), because the spectrum width of CDIA modes is narrow in the initial nonlinear stage. For a positive perturbation (the case of interest), the CS is nonlinearly unstable and hence, to reach a saturated state, one needs consider higher order nonlinear interaction. For acoustic turbulence [32], three-wave coupling is lacked, and the next-to-order nonlinear interaction scales as O(|e, z|3). Therefore, for the nonlinear dynamics of CDIA, only the lowest nonlinear interaction needs to be included.
3.2. Nonlinear Dynamics of CGDW
It has been demonstrated that a sharpening CS can be flattened via a (nonlinear)hyper-diffusion [33, 34], which corresponds to the electron momentum transport perpendicular to the CS. There are also accumulated numerical evidence that point to the plausibility of a hyper-diffusion process in broadening the CS [18]. Here we focus on the general structure of the current density evolution equation in the impact of the CGDW turbulence. The nonlinearity of Equation (9) comes from the two terms on the RHS of Equation (9). Since both e and are functions of , the strength of the nonlinear interaction of Equation (9) is ~ j2. Keeping minimal algebras, we write the nonlinear evolution of a “test” mode (z, k) as
where C(k, k′) is the nonlinear coupling coefficient given by Equation (9). The three components of k are related with each other via Equation (9) and incompressibility condition, ∇ · = 0. So, the nonlinear coupling on the RHS of Equation (16) can be expressed in the form of self-coupling of z, k. With direct interaction approximation [35], the nonlinear coupling in Equation (16) is approximated as z, −k′z, k′ + k ≃ z, −k′(2)z, k′ + k, and the coherent response (2)z, k′ + k is given by Equations (9) and (16):
where the response function Rωk′ + k, k′ + k takes the form of
Here ωwhistler is the whistler frequency, and (kz + kz′)〈ve〉 is the effect of Doppler shift. In the resonance condition ωk′ + k − ωhistler − (kz + kz′)〈ve〉 = 0), Rωk′ + k, k′ + k is simplified as
Combining Equations (17) and (19), Equation (16) yields
Since the spectrum of z, k is narrow, one has z, k′ ≃ z, k. Equation (20) is further approximated as
where
The “test” mode z, k is stabilized by the nonlinear term in Equation (21), so βk should be a positive coupling coefficient [36]. Combining Equations (12) and (21), one obtains the evolution of |e, z| driven by CGDW (i.e., Equation 4)
where and with .
4. Subcritical Bifurcation of the CS
Combining Equations (15) and (22) yields the full evolution equation of |e, z|
where the total linear growth rate γL is
and its marginally stable position is
Since the edge of the CS is relatively the most stable point, we take it as an indicator of the global state of the CS. In other words, if phase transition occurs at the edge, the whole CS will transit into the new state, too. The bifurcation property of Equation (23) is determined by the sign of e, z. For a positive perturbation, e, z > 0, the CS is subcritical bifurcation, or else it is supercritical bifurcation. In the supercritical bifurcation case, both the nonlinear terms tend to stabilize the linear term, so that the amplitude of the order parameter is constrained to a relative small value. While in the subcritical bifurcation case, the first nonlinear interaction on the RHS of Equation (23) is nonlinearly unstable, so that e, z can acquire an finite value after the phase transition. Therefore, the subcritical bifurcation is more relevant to the onset of fast magnetic reconnection, and it is the case of interest in the present paper.
In the subcritical bifurcation scenario, e, z = |e, z| and Equation (23) becomes
which is a real Landau-Ginzburg equation [12]. The corresponding free energy is
In the steady state, one has δF/δ|e, z| = 0. |e, z| is solved as
Figure 3 provides a schematic illustration of the three types of solutions and their stabilities.
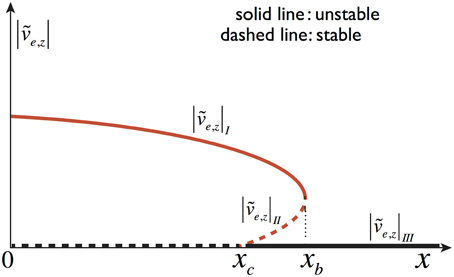
Figure 3. Bifurcation diagram: solid lines represent unstable points, and dashed lines represent stable points. The red lines represents the solutions, |e, z|I and |e, z|II, and black line represents the solution, |e, z|III.
The most remarkable feature of these solutions is their subcritical bifurcation. At the beginning, the nonlinearity (the 2nd term on the RHS of Equation 26) of the CDIA starts to drive the current density perturbation (i.e., e, z) to grow in an explosive way. Transiently, the hyper-diffusion induced by the nonlinearity (the 3rd term on the RHS of Equation 26) of the CGDW comes into effect and saturates the explosive growth. Via the above process, the order parameter acquires a finite value instantly and the CS evolves into a rough state.
The subcritical bifurcation occurs at
with . The 2nd term on the RHS of Equation (31) scales as ~ me/mi)1/2de. Compared with xc(~ (mi/me)1/2de), it is negligible. For isotropic turbulence, substituting Equation (7) into Equation (25) yields the critical thickness of the CS,
where Te ≫ Ti is used and de < |k−1| < di. Equation (32) indicates that the mass ratio of ion and electron plays an important role in determining the critical thickness [37]. The above crude estimation is also comparable with experimental observations [37, 38]. As is pointed out earlier, the specific value of the critical thickness is very sensitive to the type of streaming instability. For example, if the streaming instability is Buneman instability, which has a much higher threshold velocity in the order of electron thermal velocity [13], putting vc ≃ vthe into Equation (25), the corresponding critical thickness is approximately Δc ~ de. It should be pointed out that the proceeded calculation can only give a simple estimation. For more precise and complete description of the CS dynamics, first principle 3D simulations are needed [16].
The phase transition of the CS proceeds in an explosive way. We can see this by observing the temporal behavior of |e, z|. In the early nonlinear stage, the 1st and 3rd terms on the RHS of Equation (26) are ignorable, and one has
Thus, |e, z| scales as |e, z| ~ (t0 − t)−1 and time t0 is determined by initial conditions. Near the phase transition point, the CS grows so fast that other instabilities (e.g., tearing mode) have no time to make a significant impact on the transition process. Under the driving of the inflow, the CS shrinks along the stable line (state |e, z|III, solid, black line in Figure 3) to a thickness equaling to Δc, and then it subcritically bifurcates into the state, |e, z|I, where the order parameter |e, z| acquires a finite value, instantly. Consequently, the CS is deformed and becomes rough, but its topology is not changed. The newly induced rough structures will facilitate the occurrence of micro-instabilities, e.g., micro-tearing mode, and hence induce fast reconnection. Figure 4 provides a diagrammatic sketch of this process.
5. Summary
In this paper, we study the nonlinear dynamics of a CS prior to the onset of fat reconnection. We show that under the joint interactions of the CDIA and CGDW, the CS can transmit into a rough state from a laminar state via subcritical bifurcation. The thickness of the CS is a “controller” of the phase transition. The phase transition occurs once it is narrower than a critical value. The rough CS can facilitate the formation of a fractal CS, and hence induce fast reconnection. Through the critical thickness is predicted as Δc ~ 10de/(1 + k2d2e), the model proposed here is only paradigmatic. As we stressed in the paper, the type of streaming instability is very important in giving a quantitative prediction of Δc. Also, in this work we focus on the CS dynamics below the ion skin depth, and the kinetic effect [e.g., kinetic Alfvén wave (KAW)] of ions is ignored [39, 40]. In the KAW dominant regime (characteristic scale of fluctuations is order of ion's skin depth/Lamor radius), the nonlinear dynamics of the CS will be determined by the joint interactions of streaming instability and KAW instability. However, since the dispersion relation of whistler wave and KAW are similar, it can expect that the CS will also undergo subcritical bifurcation process at some other critical width. The qualitative physics picture proposed in this paper is testable in numerical studies dedicated to the onset of fast reconnection [41].
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the Ministry of Science and Technology of China under Grant Nos. 2013GB111001, and 2013GB112002. ZG was also supported by the WCI Program of the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology of Korea [WCI 2009-001].
References
1. Walsh AP, Fazakerley AN, Lahiff AD, Volwerk M, Grocott A, Dunlop MW, et al. Cluster and double star multipoint observations of a plasma bubble. Ann Geophys. (2009) 27:725–43. doi: 10.5194/angeo-27-725-2009
2. Owen CJ, Marchaudon A, Dunlop MW, Fazakerley AN, Bosqued JM, Dewhurst JP, et al. Cluster observations of crater flux transfer events at the dayside high-latitude magnetopause. J Geophys Res. (2008) 113:A07504. doi: 10.1029/2007JA012701
3. Cassak P, Shay M. Magnetic reconnection for coronal conditions: reconnection rates, secondary islands and onset. Space Sci Rev. (2012) 172:283–302. doi: 10.1007/s11214-011-9755-2
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
4. Daughton W, Scudder J, Karimabadi H. Fully kinetic simulations of undriven magnetic reconnection with open boundary conditions. Phys Plasmas. (2006) 13:072101. doi: 10.1063/1.2218817
5. Daughton W, Roytershteyn V. Emerging parameter space map of magnetic reconnection in collisional and kinetic regimes. Space Sci Rev. (2011) 172:271. doi: 10.1007/s11214-011-9766-z
6. Drake JF, Biskamp D, Zeiler A. Breakup of the electron current layer during 3-D collisionless magnetic reconnection. Geophys Res Lett. (1997) 24: 2921–4. doi: 10.1029/97GL52961
7. Shay MA, Drake JF, Denton RE, and, Biskamp D. Structure of the dissipation region during collisionless magnetic reconnection. J Geophys Res Space Phys. (1998) 103:9165–76. doi: 10.1029/97JA03528
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
8. Shay MA, Drake JF, Rogers BN, and Denton RE. The scaling of collisionless, magnetic reconnection for large systems. Geophys Res Lett. (1999) 26: 2163–6. doi: 10.1029/1999GL900481
9. Deng XH, Matsumoto H. Rapid magnetic reconnection in the Earth's magnetosphere mediated by whistler waves. Nature (2001) 410:557–60. doi: 10.1038/35069018
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
11. Isobe H, Shibata K. Reconnection in solar flares: outstanding questions. J Astrophys Astr. (2009) 30:79–85. doi: 10.1007/s12036-009-0007-8
12. Crawford JD. Introduction to bifurcation theory. Rev Mod Phys. (1991) 63:991. doi: 10.1103/RevModPhys.63.991
13. Roussev I, Galsgaard K, Judge PG. Physical consequences of the inclusion of anomalous resistivity in the dynamics of 2D magnetic reconnection. Astron Astrophys. (2002) 382:639–49. doi: 10.1051/0004-6361:20011645
14. Ji H, Terry S, Yamada M, Kulsrud R, Kuritsyn A, Ren Y. Electromagnetic fluctuations during fast reconnection in a laboratory plasma. Phys Rev Lett. (2004) 92:115001. doi: 10.1103/PhysRevLett.92.115001
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
15. Singh N. Whistler mode based explanation for the fast reconnection rate measured in the MIT versatile toroidal facility. Phys Rev Lett. (2011) 107:245003. doi: 10.1103/PhysRevLett.107.245003
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
16. Siversky TV, Zharkova VV. Particle acceleration in a reconnecting current sheet: PIC simulation. J Plasma Phys. (2009) 75:619–36. doi: 10.1017/S0022377809008009
17. Sagdeev RZ. On Ohms law resulting from instability. Proc Symp Appl Math. (1967) 18:281. doi: 10.1090/psapm/018/9919
18. Drake JF, Kleva RG, Mandt ME. Structure of thin current layers: implications for magnetic reconnection. Phys Rev Lett. (1994) 73:1251. doi: 10.1103/PhysRevLett.73.1251
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
19. Che H, Drake JF, Swisdak M. A current filamentation mechanism for breaking magnetic field lines during reconnection. Nature (2011) 474:184–7. doi: 10.1038/nature10091
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
20. Uzdensky DA. Petschek-like reconnection with current-driven anomalous resistivity and its application to solar flares. Astrophys J. (2003) 587:450–7. doi: 10.1086/368075
21. Bychenkov VY, Silin VP, Uryupin SA. Ion-acoustic turbulence and anomalous transport. Phys Rep. (1988) 164:119–215. doi: 10.1016/0370-1573(90)90122-I
22. Rosner R, Golub L, Coppi B, Vaiana GS. Heating of coronal plasma by anomalous current dissipation. Astrophys J. (1978) 222:317. doi: 10.1086/156145
23. Davidson RC, Gladd NT, Wu CS, Huba JD. Effects of finite plasma beta on the lower-hybrid-drift instability. Phys Fluids. (1977) 20:301. doi: 10.1063/1.861867
24. Diamond PH, Itoh S-I, Itoh K. Modern Plasma Physics: Physical Kinetics of Turbulent Plasmas, Vol. 1. Cambridge, UK: Cambridge University Press (2010).
25. Priest E, Forbes T. Magnetic Reconnection: MHD Theory and Applications. Cambridge, UK: Cambridge University Press (2007).
26. Asano Y, Nakamura R, Baumjohann W, Runov A, Vörös Z, Volwerk M, et al. How typical are atypical current sheets? Geophys Res Lett. (2005) 32:108. doi: 10.1029/2004GL021834
27. Zelenyi LM, Malova HV, Artemyev AV, Popovc VY, Petrukovich AA. Thin current sheets in collisionless plasma: equilibrium structure, plasma instabilities, and particle acceleration. Plasma Phys Rep. (2011) 37: 118–60. doi: 10.1134/S1063780X1102005X
28. Ferraro, NM Rogers BN. Turbulence in low-beta reconnection. Phys Plasmas. (2004) 11:4382. doi: 10.1063/1.1776565
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
29. Loureiro NF, Schekochihin AA, Uzdensky DA. Plasmoid and kelvin-helmholtz instabilities in sweet-parker current sheets. Phys Rev E. (2013) 87:013102. doi: 10.1103/PhysRevE.87.013102
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
30. Fujimoto K, Sydora RD. Plasmoid-induced turbulence in collisionless magnetic reconnection. Phys Rev Lett. (2012) 109:265004. doi: 10.1103/PhysRevLett.109.265004
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
31. Rosenbluth MN, Dagazian RY, Rutherford PH. Nonlinear properties of the internal m= 1 kink instability in the cylindrical tokamak. Phys Fluids. (1973) 16:1894–902. doi: 10.1063/1.1694231
33. Boozer AH. Ohm's law for mean magnetic fields. J Plasma Phys. (1986) 35:133. doi: 10.1017/S0022377800011181
34. Bhattacharjee A, Hameiri E. Self-consistent dynamolike activity in turbulent plasmas. Phys Rev Lett. (1986) 57:206. doi: 10.1103/PhysRevLett.57.206
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
36. Guo ZB, Diamond PH, Wang XG. Magnetic reconnection, helicity dynamics, and hyper-diffusion. Astrophys J. (2012) 757:173. doi: 10.1088/0004-637X/757/2/173
37. Ren Y, Yamada M, Ji H, Gerhardt SP, Kulsrud R. Identification of the electron-diffusion region during magnetic reconnection in a laboratory plasma. Phys Rev Lett. (2008) 101:085003. doi: 10.1103/PhysRevLett.101.085003
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
38. Zhong JY, Li YT, Wang XG, Wang JQ, Dong QL, Xiao CJ, et al. Modeling loop-top X-ray source and reconnection outflows in solar flares with intense lasers. Nat Phys (2010) 6:984–7. doi: 10.1038/nphys1790
39. Rogers BN, Denton RE, Drake JF, and Shay MA. Role of dispersive waves in collisionless magnetic reconnection. Phys Rev Lett. (2001) 87:195004. doi: 10.1103/PhysRevLett.87.195004
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
40. Boldyrev S, Horaites K, Xia Q, Perez JC. Toward a theory of astrophysical plasma turbulence at subproton scales Astrophys J. (2013) 777:41. doi: 10.1088/0004-637X/777/1/41
41. Singh N. Evolution of an electron current layer prior to reconnection onset. Phys Rev Lett. (2012) 109:145001. doi: 10.1088/0004-637X/777/1/41
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Appendix
Linear CDIA Instability with a Weak Mean Electric Field
Constitutive equations for CDIA with a mean electric field are
Equation (A1) is the 1D kinetic equation for electron. Equations (A2) and (A3) are ion's continuity and momentum equation, separately. In deriving the dispersion relation, we write all quantities into a mean piece and a fluctuation piece, i.e., and E = 〈E〉 + .
e is composed by a adiabatic part, , and a non-adiabatic, g. Thus, putting into Equation (A1) yields the evolution equation for g
The characteristic equations of Equation (A4) are
And their solutions are
where x(0) = x and v(0) = v. Then the Green function of Equation (A4) is obtained as
The RHS of Equation (A9) can be seen as Laplace transformation of , i.e., 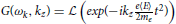 .
.
Using the formula,
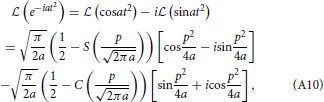
where , and S(p), C(p) are Fresnel functions, one obtains G(ωk, k) in the weak mean field limit, ,
By Equations (A4) and (A11), the Fourier component of g is
If the weak mean electric field tens to zero, , the conventional non-adiabatic response is recovered [17, 24]. Then the total response of electron is
The response of ions' density is obtained from Equations (A2) and (A3)
Using the quasi-neutrality condition, growth rate γCDIAk of the CDIA is obtained as
where the critical point(γCDIAk = 0) is slightly shifted by the mean electric field, but the basic structure of γCDIAk is not changed.
Keywords: magnetic reconnections, fast reconnection, current sheets, bifurcation analysis, plasma waves
Citation: Guo Z and Wang X (2015) Onset of fast magnetic reconnection via subcritical bifurcation. Front. Phys. 3:18. doi: 10.3389/fphy.2015.00018
Received: 14 September 2014; Accepted: 12 March 2015;
Published: 01 April 2015.
Edited by:
Valery M. Nakariakov, University of Warwick, UKReviewed by:
David Tsiklauri, Queen Mary University of London, UKValentina Zharkova, Northumbria University, UK
Copyright © 2015 Guo and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhibin Guo, WCI Center for Fusion Theory, National Fusion Research Institute, Seoul National University, Room#A304, BK International House, Building 946, Gwanak-ro 1, Gwanak-gu, Seoul 151-851, South KoreaZ3VvemhpcGt1QGdtYWlsLmNvbQ==
 Zhibin Guo
Zhibin Guo Xiaogang Wang1
Xiaogang Wang1