- 1Department of Geophysics Environmental Sciences, Munich University, Munich, Germany
- 2Department of Space Physics, International Space Science Institute, Bern, Switzerland
- 3Space Research Institute, Space Physics Branch, Austrian Academy of Sciences, Graz, Austria
A kinetic approach to the notion of information is proposed, based on Liouville kinetic theory. The general kinetic equation for the evolution of the N-particle information 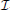 N in a Hamiltonian system of large particle number N ≫ 1 is obtained. It is shown that the N-particle information is strictly conserved. Defining reduced particle number information densities in phase space should be possible to obtain a kinetic equation for the ordinary one-particle information
N in a Hamiltonian system of large particle number N ≫ 1 is obtained. It is shown that the N-particle information is strictly conserved. Defining reduced particle number information densities in phase space should be possible to obtain a kinetic equation for the ordinary one-particle information 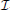 1 ≡
1 ≡ 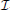 following the Bogoliubov prescription. The kinetic equation for
following the Bogoliubov prescription. The kinetic equation for 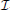 is a kind of generalized Boltzmann equation with interaction term depending on the hierarchy of reduced informations. This term in its general form is the most general expression for the Kolmogorov entropy rate of evolution of the information.
is a kind of generalized Boltzmann equation with interaction term depending on the hierarchy of reduced informations. This term in its general form is the most general expression for the Kolmogorov entropy rate of evolution of the information.
1. Introduction
The internal information content of a physical system is its entropy S which, in classical Hamiltonian systems with one-particle (index 1) Hamiltonian H1(q, p) = ∑i(p2i/2m) + ∑j≠i U(qj), is a function of the particle coordinate vectors p, q in Boltzmann's 6-dimensional (3 time dependent momentum vector p(t) and 3 space vector q(t) coordinates, with t time) one-particle μ-phase space, mass m and potential energy U(qj), respectively, with i, j particle number. It depends on the complete dynamics of all indistinguishable particles on the kinetic level under the action of the interparticle forces (accounted for in the potential U) which contribute to H1 and are defined by the Hamilton equations of motion 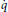 = ∂H1/∂p, ṗ = −∂H1/∂q. This internal information is, according to Boltzmann and Shannon, given as the product of the μ-phase space density F1(p, q, t), the one-particle distribution function, and its logarithm log F1, with F1 satisfying the Boltzmann equation ∂tF1 + [H1, F1] =
= ∂H1/∂p, ṗ = −∂H1/∂q. This internal information is, according to Boltzmann and Shannon, given as the product of the μ-phase space density F1(p, q, t), the one-particle distribution function, and its logarithm log F1, with F1 satisfying the Boltzmann equation ∂tF1 + [H1, F1] =  B, with […, …] ≡ (∂pH1)(∂qF1) − (∂qH1)(∂pF1) the one particle Poisson bracket, and
B, with […, …] ≡ (∂pH1)(∂qF1) − (∂qH1)(∂pF1) the one particle Poisson bracket, and  B Boltzmann's collision integral.
B Boltzmann's collision integral.
In any realistic classical physical system composed of N subsystems (particles) of very large number N ≫ 1, the Boltzmann equation is replaced by the Liouville equation
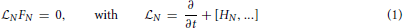
which holds in the 6N-dimensional Gibbs' Γ-phase space (for a general reference cf., e.g., 1, including a discussion of quantum systems). The operator  N is the N-particle Liouville operator. It contains the N-particle Hamiltonian HN(pN, qN), which in classical theory is not an operator. Here the brackets […, …] are N-particle Poisson's brackets.
N is the N-particle Liouville operator. It contains the N-particle Hamiltonian HN(pN, qN), which in classical theory is not an operator. Here the brackets […, …] are N-particle Poisson's brackets.
This Liouville equation, unlike the Boltzmann equation, is exact. It acts on the exact phase space density, which for classical point particles is defined as
All dynamics is contained in the time-dependent phase space coordinates of the N particles (subsystems) qi(t), pi(t) via Hamilton's equations. FN, being a phase space (probability) density, must be normalized accordingly. In this sense, Liouville's and Hamilton's equations are tautologies. However, the former offers the advantage of a probabilistic approach which avoids the necessity of solving for all N fully dynamical Hamilton equations 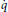 N = ∂HN/∂pN, ṗN = −∂HN/∂qN.
N = ∂HN/∂pN, ṗN = −∂HN/∂qN.
The Liouville equation describes the flow of the N particles through N-particle phase-space under the action of the N-particle Hamiltonian, explicitly exhibiting the conservation of particles. Its (formally known) solution FN though exact is rather impractical. It requires knowledge of all N exact particle orbits at all times t. The Liouville equation can, however, be reduced to a one-particle Boltzmann-like equation holding in one-particle phase space (with all particles identical distinguished only by mass, charge, and energy) following a complicated procedure of reductive integration known as the BBGKY hierarchy (after N. N. Bogoliubov, M. Born, H. S. Green, J. G. Kirkwood, and J. Yvonne) [for reference cf., e.g., 2, 3]. We will refer to an equivalent of this approach below in Section 3.
The question which interests us here concerns the nature of entropy/information on the N-particle level in N-particle Gibbs' Γ-phase space. Answering this question should provide an evolution theory for the information of a physical system. In other words, one may hope obtaining a Boltzmann-like one-particle μ-phase space kinetic equation for the information.
This question is not purely academic. Interest in the physics of information arose primarily with the advent of chaos theory in the early sixties [for a collection of different approaches in different fields the reader is referred to the Santa Fe proceedings volume 4]. Indeed, information is one of the central quantities not only in physics but also in several other fields like communication, biology etc. all referring in one or the other sense to information theory. Information theory makes use of a physical definition of information that is exploited for instance in maximum entropy methods of data analysis as also in various applications to the determination of probability measures, chaotic behavior, as well as quite practical problems like weather prediction in meteorology, climate research, prediction theory in the evolution of time series, in space physics in general and space weather in particular (in the latter respect see e.g., the comprehensive review in Balasis et al. 5 and references therein) where low-dimensional chaotic approaches have found wide application. Thermodynamics predicts that information cannot be lost. Under stationary conditions it enters thermodynamics respectively statistical mechanics being the central quantity in the first and second thermodynamic laws where it relates directly to internal energy and external work done on the system. Under non-stationary conditions its evolution is barely known while being of utmost importance. Since thermodynamics is rooted in kinetic theory it is reasonable to ask whether information cannot be subject to kinetic theory as well.
So far, chaos theory of low-dimensional systems provides tools already to infer about generation of information and its effects on the system. However, most physical systems are composed of very many subsystems the interaction of which should be taken into account when considering information, inferring about its evolution, production and accumulation. Such a theory should be rooted in first physical principles, i.e., for systems consisting of many subsystems and having large numbers of degrees of freedom it should be based on Liouville theory in order to make information accessible to well known physical methods, technical treatment and providing a deeper understanding of its evolution and distribution throughout the system and sharing by the various subsystems. Since information, once generated, cannot be lost, such distribution processes are of importance in particular in view of processes which, like information spread in societies, so far are not subject to any treatment in physics. In such systems apparently very small amounts of energy are involved causing large effects by information transfer. In the following we briefly sketch how a time-dependent physical information theory could be developed.
2. N-particle Information
Let us define an equivalent N-particle phase-space information density 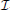 N following the Boltzmann-Shannon prescription
N following the Boltzmann-Shannon prescription

assuming that it is also normalized (for instance to Boltzmann's constant kB). Via the phase space density FN it depends on the complete phase space dynamics of the system contained in the Hamiltonian and Hamilton's equations. The question is then, which equation does the exact N-particle information satisfy?
In order to answer this question we tentatively apply the above Liouville operator  N to
N to 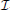 N keeping in mind that it applies strictly only to the N-particle phase space distribution function FN. Before doing this we rewrite
N keeping in mind that it applies strictly only to the N-particle phase space distribution function FN. Before doing this we rewrite 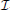 N using the definition of the exact phase space density Equation (2)
N using the definition of the exact phase space density Equation (2)
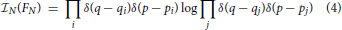
the logarithm of the product becomes a sum ∑jlogδ(q−qj)δ(p−pj). Mathematically the logarithm of a distribution—the delta function—must be taken with care; this is a weakness in the Shannon definition on the microscopic level. Hence the expression is to be considered as a formal representation only. Formally, however, the delta functions take care for that all mixed products vanish. Hence one finds the obvious result that
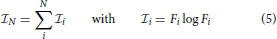
is the sum of all single particle informations. In other words, the N-particle information is additive (extensive). This is a consequence of the logarithmic dependence imposed by the Shannon prescription to which we restrict here. Other definitions as, for instance, the generalisations available in the literature [for instance 6–8] or that given recently in Treumann and Baumjohann [9] may destroy the extensivity already on the Liouville level by adding correlations in the last expression.
If we apply the Liouville operator to Equations (3) and (5), it is easy to demonstrate for any conservative system that
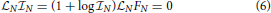
which holds for any physically reasonable 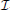 N ≠ − 1 and because of Equation (1). For this reason the exact N-particle information satisfies the exact N-particle Liouville equation
N ≠ − 1 and because of Equation (1). For this reason the exact N-particle information satisfies the exact N-particle Liouville equation

The N-particle information thus follows Liouville dynamics in phase space with the dynamic equations prescribed by the N-particle Hamiltonian function. We may note here that this is a classical and no quantum theory. Generalisation to quantum theory is by no means obvious. The nonlinear nature of the information inhibits the simple replacement of Poisson's brackets with commutators/anti-commutators.
Within Shannon theory we therefore find an exact kinetic equation for the exact classical N-particle Shannon information 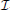 N, and that this equation is the Liouville Equation (7) acting on the full N-particle phase space. In principle, this is an expected result.
N, and that this equation is the Liouville Equation (7) acting on the full N-particle phase space. In principle, this is an expected result.
However, like in the case of exact kinetic particle theory, this equation is an identity and not yet an equation with that one could operate. It just says that in the exact N-particle phase space the N-particle information is conserved and behaves like a phase space information density which corresponds to an information flow through phase space. In fact this is not such a surprise. Since no averaging has been done when following the exact orbits of all particles, no overall disorder of the phase space is produced. The total information content which has been there in the total phase space volume at the beginning is still there; it is simply conserved. Information could not have gone anywhere from the total volume.
It is again noteworthy that this conclusion is strictly valid only for the N-particle Shannon information. Other definitions might not reproduce Liouville's equation in its known form with vanishing right hand side. In the general case one expects that an N-particle diffusion term occurs on the right in this case being responsible for the dispersion of the generalised information in N-particle phase space and violating the extensivity of the N-particle information expressed in Equation (7). If this is the case, there must be some physical reason imposed from the outside for the definition of information at variance. Non-conservation of information then means that loss or gain of total information is attributed to this reason. One may, for instance, think of interaction with some external field which, on the global level, extracts information from the system or adds information to it. We will not consider this case here.
3. Hierarchy
Physical reality as experienced in practice does, however, not take place on the microscopic level of N-particle phase space. The path to a practical kinetic theory of (Shannon) information is in principle prescribed by the analogy to kinetic theory. There a hierarchy of average n = (N − j)-particle distributions Fn, with j ∈ N, j ≤ N − 1 is prescribed as the suitably normalized integral over the phase space coordinates of all particles j. This procedure, known as BBGKY hierarchy, ultimately reduces the phase space to the one-particle μ-phase space of the now undistinguishable N particles. It in this case produces the average one-particle phase space distribution function f(q, p) ≡ F1 and, from Liouville's equation, the ultimate one-particle kinetic equation describing the evolution of f(q, p) under the action of the reduced one-particle Hamiltonian H1(q, p). This final one-particle Boltzmann-like kinetic equation contains a non-vanishing right-hand side which collects all correlations between the particles and their mutual interaction fields [cf., e.g., 1, 10, 11, for their explicit classical and quantum forms]. In case of merely hard-core binary collisions, this term reduces further to Boltzmann's μ-space equation which, in the total absence of any collisions and just for purely classical field interactions, becomes the zero-right hand side Vlasov equation [12, Ch. 3] or, including quasilinear interactions with self-excited field fluctuations in the one-particle kinetic equation, the Fokker-Planck equation [for a rigorous and lucid derivation of the Fokker-Planck equations cf., e.g., 10].
A similar procedure should go along the lines of an analogous definition of phase-space-averaged “reduced” informations 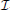 n forming a descending in n chain. The philosophy behind this approach is that the Shannon information is understood as the average of the logarithm of the distribution function itself. Thus, any reduced information is given as
n forming a descending in n chain. The philosophy behind this approach is that the Shannon information is understood as the average of the logarithm of the distribution function itself. Thus, any reduced information is given as
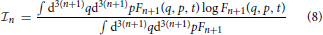
The problem consists in finding the kinetic equation that governs the evolution of 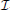 n with n → 1 from the exact Liouville equation for
n with n → 1 from the exact Liouville equation for 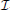 N. This step is substantially more complex and less transparent than in the case of the BBGKY hierarchy of the n-particle distribution function which results in the Boltzmann equation. There the nonlinearity is provided by the Hamiltonian, while in the case of the information the n-particle information itself is intrinsically nonlinear, and care must be taken in each step when applying the reduced Hamiltonians.
N. This step is substantially more complex and less transparent than in the case of the BBGKY hierarchy of the n-particle distribution function which results in the Boltzmann equation. There the nonlinearity is provided by the Hamiltonian, while in the case of the information the n-particle information itself is intrinsically nonlinear, and care must be taken in each step when applying the reduced Hamiltonians.
Carrying through this program is a formidable task though being quite straightforward. In every step of the reduction procedure one has to take care of the reduced Liouville operator, the hierarchy equation of the former step for the reduced distribution function. Already in the BBGKY hierarchy a non-vanishing and rather complicated term on the right-hand side of the reduced kinetic equation is produced to which each reduction step adds further terms. This will also happen in the case of the reduction of the Liouville Equation (7) for the information. In this note we refrain from performing all these steps leaving it to someone else who can explicit it. The present paper is just a perspective paper that intends to present the basic idea of constructing a viable physical theory of the dynamics of information. However, some simple arguments can be given what the reduction procedure, the information hierarchy, will lead us to.
In the case of the BBGKY hierarchy the form of the Liouville equation on the left hand side of the equation reproduces in each step with descending subsystem (particle) number n from n = N down to n = 1, the wanted final form of the kinetic equation. All correlations and subsystem (particle) interactions become relegated to form an ever more complicated interaction term on the right hand side of these equations. Because the structure of the N-subsystem Liouville equation for the N-subsystem information 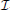 N is identical to that of the N-particle Liouville equation for FN, we expect that this behavior will reproduce also in the case of the information hierarchy. We conjecture that the final one-subsystem (particle) kinetic equation for the information will be of the form
N is identical to that of the N-particle Liouville equation for FN, we expect that this behavior will reproduce also in the case of the information hierarchy. We conjecture that the final one-subsystem (particle) kinetic equation for the information will be of the form
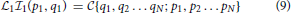
where  1 ≡
1 ≡  = ∂t + [H1(p, q),…], with p ≡ p1, q ≡ q1 and H1(p, q) the one-particle Hamiltonian, is the one-particle Liouville operator, and
= ∂t + [H1(p, q),…], with p ≡ p1, q ≡ q1 and H1(p, q) the one-particle Hamiltonian, is the one-particle Liouville operator, and  , as indicated by the braces {…}, functionally contains all coordinates and correlations. It results in the reductive procedure leading from the N- to the one-subsystem kinetic equation. All the dynamics that causes the evolution of the information in the interaction between the particles is contained in
, as indicated by the braces {…}, functionally contains all coordinates and correlations. It results in the reductive procedure leading from the N- to the one-subsystem kinetic equation. All the dynamics that causes the evolution of the information in the interaction between the particles is contained in  . Since the Hamiltonian also contains collisionless interactions with external and self-consistent fields, such interactions are taken care on the left-hand side of the above kinetic equation. It is, however, questionable whether neglect of the right-hand side can be justified in the case of information as is done in Vlasov and Klimontovich [12] theory. Presumably, since information (entropy) cannot be erased but can only grow, no comparably simple argument can be found for dropping
. Since the Hamiltonian also contains collisionless interactions with external and self-consistent fields, such interactions are taken care on the left-hand side of the above kinetic equation. It is, however, questionable whether neglect of the right-hand side can be justified in the case of information as is done in Vlasov and Klimontovich [12] theory. Presumably, since information (entropy) cannot be erased but can only grow, no comparably simple argument can be found for dropping  in the case of information unless the system is in thermodynamic equilibrium when its dynamics and evolution is obsolete.
in the case of information unless the system is in thermodynamic equilibrium when its dynamics and evolution is obsolete.
4. Discussion
Presumably, the dynamical theory of Boltzmann-Shannon information will result in a Boltzmann-like kinetic equation for the one-subsystem information 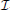 1 with, however, very complicated non-vanishing correlation term on its right. It is clear that this is particular only to the Boltzmann-Shannon information. Other definitions of entropy-information found in the literature might not lead to similar kind of reductions. Having conjectured the form of the one-subsystem kinetic equation for the one-subsystem information and determined the implicit functional form of the correlation term on the right of the above equation, will provide a full kinetic theory of the evolution of information in an N-subsystem configuration. This is most interesting for a number of obvious reasons and may apply not only to physics but also to other sciences and engineering where information generation and evolution plays an important role. Here we have restricted ourselves to physics alone.
1 with, however, very complicated non-vanishing correlation term on its right. It is clear that this is particular only to the Boltzmann-Shannon information. Other definitions of entropy-information found in the literature might not lead to similar kind of reductions. Having conjectured the form of the one-subsystem kinetic equation for the one-subsystem information and determined the implicit functional form of the correlation term on the right of the above equation, will provide a full kinetic theory of the evolution of information in an N-subsystem configuration. This is most interesting for a number of obvious reasons and may apply not only to physics but also to other sciences and engineering where information generation and evolution plays an important role. Here we have restricted ourselves to physics alone.
To close this perspective article we point out that the above conjectured kinetic equation for the one-subsystem information can also be understood differently. The reduced (one-subsystem) Liouville operator on the left can be written as the total time derivative in the one-subsystem phase space. The kinetic equation then reads
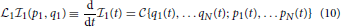
The formal solution of this version is
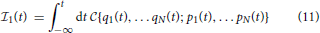
which yields the time evolution of the one-subsystem information. The difficulty here lies not only in the necessity to know the explicit functional form of  which follows from the hierarchy approach, it is relegated in addition to the knowledge of time dependence of the one-, two-, … subsystem trajectories in phase space, which strictly spoken implies the knowledge of the full particle dynamics in phase space which are not known a priori. Thus, the above formal solution is a tautology, and one has to apply some kind of approximation like perturbation methods to treat the perturbation of an initial state. This resembles the situation encountered in kinetic theory. Nevertheless, though this is not completely satisfactory, the above form shows that the total time derivative of the one-subsystem information is determined by the functional
which follows from the hierarchy approach, it is relegated in addition to the knowledge of time dependence of the one-, two-, … subsystem trajectories in phase space, which strictly spoken implies the knowledge of the full particle dynamics in phase space which are not known a priori. Thus, the above formal solution is a tautology, and one has to apply some kind of approximation like perturbation methods to treat the perturbation of an initial state. This resembles the situation encountered in kinetic theory. Nevertheless, though this is not completely satisfactory, the above form shows that the total time derivative of the one-subsystem information is determined by the functional  . Conventionally, in the theory of chaotic interactions of a small number of particles this is taken to be the so-called Kolmogorov entropy rate K [13, 14] which originally appeared as a metric entropy rate in Kolmogorov-Arnold-Moser (KAM) theory of chaotic processes [for reference cf., e.g., 15]. Hence, performing the derivation of the hierarchy leads in a straight way to the physical definition of the Kolmogorov K entropy rate for an N-subsystem configuration as
. Conventionally, in the theory of chaotic interactions of a small number of particles this is taken to be the so-called Kolmogorov entropy rate K [13, 14] which originally appeared as a metric entropy rate in Kolmogorov-Arnold-Moser (KAM) theory of chaotic processes [for reference cf., e.g., 15]. Hence, performing the derivation of the hierarchy leads in a straight way to the physical definition of the Kolmogorov K entropy rate for an N-subsystem configuration as
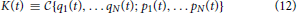
as an implicit function of time and the number of subsystems (particles). For any non-stationary system  ≠ 0 for the simple reason that entropy/information can only grow. Since
≠ 0 for the simple reason that entropy/information can only grow. Since  itself depends implicitly on the higher order informations, the Kolmogorov entropy rate is also a functional of information. Moreover, t =
itself depends implicitly on the higher order informations, the Kolmogorov entropy rate is also a functional of information. Moreover, t = 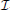 −1 is the (properly normalized) inverse functional of the information. One thus writes
−1 is the (properly normalized) inverse functional of the information. One thus writes

where, for simplicity, we dropped the index 1. From here we obtain the interesting expression

with its formal solution
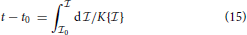
yielding the time elapsed during the evolution of the information from state 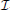 0 to
0 to 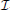 . This solution suggests that for K =
. This solution suggests that for K =  = 0 the elapsed time is infinite, which is nothing else but another expression for that the information does not change but is conserved. Otherwise, for K → ∞ the system seems to evolve at a diverging rate. However, inspection of the second last equation reveals that dt = 0 in this case, and the entire expression becomes obsolete. This case corresponds to complete stochasticity with no production nor evolution of information at all, the final thermodynamic equilibrium state of maximum information.
= 0 the elapsed time is infinite, which is nothing else but another expression for that the information does not change but is conserved. Otherwise, for K → ∞ the system seems to evolve at a diverging rate. However, inspection of the second last equation reveals that dt = 0 in this case, and the entire expression becomes obsolete. This case corresponds to complete stochasticity with no production nor evolution of information at all, the final thermodynamic equilibrium state of maximum information.
The important case is the intermediate one where K is finite, corresponding to a state of nonlinear non-stochastic (chaotic) interactions. They cause the information to evolve in finite time. Speculatively, this expression can be taken as an equation for the “production of time.” In such an interpretation, time is “generated” under circumstances when information is produced—a physically not unreasonable assertion. In this interpretation there is more room left for speculation. The case K = 0 corresponds to stationarity with no time evolution of information. Information can only be redistributed convectively then. K = ∞ means complete stochasticity. Hence, stochastic systems do, in this interpretation, not produce any time at all. Time, again in this interpretation, is attributed to the nonlinear, non-stochastic action that generates information in a complex system.
Though these remarks are intriguing, the sound physical result is contained in the one-subsystem (particle) kinetic equation of information which forms the basic equation for the evolution of information in an N-particle system with N ≫ 1. We have not given an explicit derivation of its right hand side, the correlation functional  = K, the Kolmogorov entropy rate. This is left as an exercise for future research until the hierarchy equations have been constructed. Rigorous construction of the hierarchy equations is inhibited in this communication by restriction of space. We have also neither invested effort into any quantum mechanical nor field theoretical formulation which both are of utmost interest in applications, nor have we envisaged investigation of any different more general definition of information than the classical Boltzmann-Shannon information.
= K, the Kolmogorov entropy rate. This is left as an exercise for future research until the hierarchy equations have been constructed. Rigorous construction of the hierarchy equations is inhibited in this communication by restriction of space. We have also neither invested effort into any quantum mechanical nor field theoretical formulation which both are of utmost interest in applications, nor have we envisaged investigation of any different more general definition of information than the classical Boltzmann-Shannon information.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the three reviewers for their intriguing and extraordinarily helpful remarks on the importance of information and some other more formal questions.
References
1. Balescu R. Statistical Dynamics. Matter Out of Equilibrium. London: Imperial College Press (2000).
2. Bogoliubov NN. Problems of a dynamical theory in statistical physics. In: De Boer J, Uhlenbeck GE editors. Studies in Statistical Mechanics, Vol. 1. Amsterdam: North-Holland (1962). p. 1.
4. Zurek WH (Ed.). Complexity, Entropy and the Physics of Information. Santa Fe Inst. Studies, Vol. VIII. Redwood, CA: Addison-Wesley (1990).
5. Balasis G, Donner RV, Potirakis SM, Runge J, Papadimitriou C, Daglis IA, et al. Statistical mechanics and information-theoretic perspectives on complexity in the Earth system. Entropy (2013) 15:4844–88. doi: 10.3390/e15114844
7. Wehrl A. General properties of entropy. Rev Mod Phys. (1978) 50:221. doi: 10.1103/RevModPhys.50.221
8. Tsallis K. Possible generalization of Boltzmann-Gibbs statistics. J Stat Phys. (1988) 52:479. doi: 10.1007/BF01016429
9. Treumann RA, Baumjohann W. Beyond Gibbs-Boltzmann-Shannon: general entropies - the Gibbs-Lorentzian example. Front Phys. (2014) 2:49. doi: 10.3389/fphy.2014.00049
12. Klimontovich YL. The Statistical Theory of Non-Equilibrium Processes in a Plasma. Cambridge, MA: The M.I.T. Press (1967).
13. Kolmogorov AN. General theory of dynamical systems and classical mechanics. In: Proceedings International Congress of Mathematicians 1:315. Amsterdam: North-Holland Publisher (1958).
14. Kolmogorov AN. Entropy per unit time as a metric invariant of automorphism. Dokl Russ Acad Sci. (1959) 124:754–5.
Keywords: information, liouville theory, kinetic theory, dynamics of information, kolmogorov entropy
PACS: 45.70.−n, 51.30.+i, 95.30.Tg, 52.25.Kn
Citation: Treumann RA and Baumjohann W (2015) Kinetic theory of information—the dynamics of information. Front. Phys. 3:19. doi: 10.3389/fphy.2015.00019
Received: 14 January 2015; Paper pending published: 01 March 2015;
Accepted: 13 March 2015; Published: 30 March 2015.
Edited by:
Ioannis A. Daglis, National and Kapodistrian University of Athens, GreeceReviewed by:
Giuseppe Consolini, Istituto Nazionale di Astrofisica, Istituto di Astrofisica e Planetologia Spaziali, ItalyGeorgios Balasis, National Observatory of Athens, Greece
Yannis Kominis, National Technical University of Athens, Greece
Copyright © 2015 Treumann and Baumjohann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rudolf A. Treumann, Department of Space Physics, International Space Science Institute, Hallerstr. 6, 3012 Bern, SwitzerlandcnVkb2xmLnRyZXVtYW5uQGdlb3BoeXNpay51bmktbXVlbmNoZW4uZGU=
 Rudolf A. Treumann
Rudolf A. Treumann Wolfgang Baumjohann
Wolfgang Baumjohann