Ideal MHD turbulence: the inertial range spectrum with collisionless dissipation

1. Introduction

Collisionless turbulence [for reviews cf., e.g., 1–3] is abundant in space, from stellar winds (with solar wind the only accessible paradigm) to interstellar and intergalactic matter. Its collisionless nature poses a problem on the relevant dissipation mechanism. Anomalous collision frequencies in plasma have never ever been confirmed to assume the required theoretically predicted magnitudes. How then does the turbulent energy injected at large scales and forming large-scale eddies in ideal MHD dissipate?

In MHD turbulence the large-scale magnetic field B is frozen to the plasma. Turbulent stirring causes Alfvénic eddies. Their average field reassures their approximate two-dimensionality (first realized in Iroshnikov 4; Kraichnan 5; Kraichnan 6). It also causes anisotropy of the turbulence (confirmed e.g., in Alexandrova et al. 7; Chen et al. 8; Narita et al. 9; Sahraoui et al. 10; Wicks et al. 11). Cascading to smaller scales forms narrower current layers until reaching scales of thermal ion gyroradii ${\rho }_i=v_i/{\omega }_{ci}=\sqrt{2m_i{T}_{i\perp }}/eB\equiv {\lambda }_i/\sqrt{{\beta }_i}$ (with ${\omega }_{ci}=eB/m_i,{\omega }_i=e\sqrt{N/{ϵ}_0{m}_i},{\beta }_i=2{\mu }_{0}N{T}_i/B^2$ ion cyclotron and plasma frequencies, v_i, T_i, m_i ion thermal speed, temperature, mass, respectively) where ions decouple from magnetic field, ion dynamics is determined by inertia, and the character of turbulence changes, with electrons being responsible for current flow, including Hall currents, but interact with ions via charge coupling [cf., e.g., 12, for a review]. Depending on ${\beta }_i\equiv v_i^2/v_A^2\begin{array}{c}>\\ <\end{array}1$ there is a subtlety on whether or not ion inertia effects come into play earlier at the ion-inertial scale λ_i = c/ω_i. Either ρ_i or λ_i can be taken serving as dissipative scale for large-scale eddies in the MHD cascade. Further dissipationless cascading toward electron gyro ${\rho }_e=v_e/{\omega }_{ce}\equiv {\lambda }_e/\sqrt{{\beta }_e}$ and inertial scales λ_e = c/ω_e spans the length interval λ_i ≳ ℓ ≳ λ_e, roughly ~2 orders of magnitude in a proton-electron plasma. When the cascade approaches its small-scale end ℓ ≲ λ_e the narrow filamentary current eddies enter the range of collisionless reconnection [for reviews of reconnection observations and theory see 13, 14] undergoing violent destruction and dissipation of the turbulent energy (in various forms predicted in Leamon et al. 15; Schekochihin et al. 12; Karimabadi et al. 16). Collisionless particle-in-cell (pic) simulations [cf., 17] established reconnection being based on demagnetised electron, electron inertia and generation of local non-diagonality in the electron pressure tensor (predicted in Hesse and Winske 18; Hesse et al. 19) due to thermal electron meandering in the current layer resulting in large electron-shear viscosity. This was simulationally confirmed [20] yielding the lower-hybrid frequency ω_lh [21] as robust absolute upper limit on the dissipation rate for the magnetic energy that is fed into formation of small-scale currents [cf., 22, for astrophysical application]. We remark here that dissipation in the narrow current layers is not caused by a simple instability leading to anomalous collisions. Its mechanism is complex involving electron inertia, meandering electron orbits and deformation of the electron pressure tensor P_e = P_e⊥ I + (P_e|| − P_e⊥)BB/B² which is anisotropic but diagonal in the frame of the local magnetic field B but assumes all nine components when transformed into the locally plane current frame, with non-diagonal terms playing the role of electron volume and shear viscosities.

2. Inertial Range Spectrum

With this philosophy in mind [for our purposes ignoring the effects of anisotropy, cf., e.g., 8, 10, 11, 24, 25] we determine which shape collisionless MHD turbulence spectra assume under conditions where the energy is injected at scale λ_i ≪ ℓ_in ≪ L much exceeding the ion inertial length though still shorter than the macroscale L of the plasma. We assume the turbulence is of the Iroshnikov-Kraichnan (IK) type (though the observations [cf., e.g., 7, 26, and others; see Figure 1] sometimes indicate substantially flatter than IK-turbulent large-scale spectra, in addition to other differences) which does not change much on what follows. On such scales, in a weakly magnetized plasma with β > 1, initial eddy scales are typically Alfvénic ℓ_A ~ v_A/τ_A, with $v_A=B/\sqrt{{\mu }_0{m}_{i}N}$ the Alfvén speed, τ_A an Alfvén transition time across the eddy. At the shorter scales ℓ ≲ λ_i eddies might become kinetic Alfvén waves [as argued in Leamon et al. 15], possibly contributing to dissipation. The IK-like inertial-range scales as

$\begin{array}{cc}{E}_{k,\text{IK}}\simeq A_{\text{IK}}{ϵ}^{\frac{1}{2}}{k}^{-\frac{3}{2}},k_{in}\lesssim k\lesssim k_i& \left(1\right)\end{array}$

with proportionality factor $A_{\text{IK}}=C_{\text{IK}}\sqrt{v_A}$, where C_IK is the IK-coefficient. Here k_in = 2π/ℓ_in and k_i = 2π/λ_i (or = 2π/ρ_i for ρ_i < λ_i) with λ_i (or ρ_i) playing the role of dissipation length terminating the IK-range spectrum. Further up to larger wave numbers, the spectrum follows the Kolmogorov (K) scaling

$\begin{array}{cc}{E}_{k,\text{K}}\simeq C_{\text{K}}{ϵ}^{\frac{2}{3}}{k}^{-\frac{5}{3}},k_i\lesssim k\lesssim k_e& \left(2\right)\end{array}$

with C_K ~ 1.6 − 1.7 Kolmogorov's constant, and k_e = 2π/λ_e the electron inertial wave number, playing the role of a K-dissipation scale entering the collisionless (kinetic) reconnection regime at ℓ ≲ λ_e.

FIGURE 1

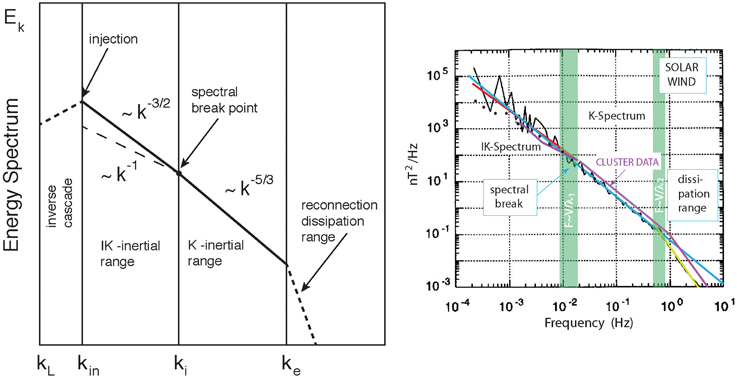
Figure 1. Power spectra in collisionless magnetohydrodynamic turbulence. Left: Proposed structure of the inertial range spectrum in collisionless MHD turbulence evolving in a system of scale L, when energy is injected at a rate ϵ into large-scale Alfvénic eddies of wave numbers k_in = 2π/ℓ_in ≫ k_L = 2π/L. Cascading to smaller scale eddies, still in the Alfvénic range, is two-dimensional and determined by the Alfvénic interaction time τ_A = ℓ_A/v_A, causing the inertial range IK-spectrum of shape k^−3/2. When the eddy scale reaches the ion inertial scale k_i = 2π/λ_i, eddy formation enters the three-dimensional Kolmogorov range with spectral shape k^−5/3. Finally, when the current eddy width approaches the electron scale k_e = 2π/λ_e, dissipation in reconnecting current sheets sets on. Here the injection of energy at the large initial scale k_in becomes dissipated. Right: Turbulent magnetic power spectral density (nT²/Hz) measured in the solar wind by the Mariner 10 spacecraft (March 20, 1974) [data adapted from Goldstein et al. 23: courtesy of AGU]. Though the scatter of data is large in particular at low frequencies, one may distinguish two different regimes of turbulence. The red line indicates the IK spectral decay at low frequencies which is followed at higher frequencies by a K spectrum (which had already been identified in the original work). At frequencies close to ~ 1 Hz the dissipation range is entered. The K range extends just over roughly ~1.5 orders of magnitude in excellent agreement with the assumption that it covers not more than a scale interval of the ratio of ion- to electron-inertial lengths. The pink lines are recent CLUSTER data [adapted from Alexandrova et al. 7] fitting precisely the older observations though, for the different solar wind conditions, are slightly shifted to higher frequencies. Here the spectral break is more clearly expressed with low-frequency slope closer to IK [noted in Alexandrova et al. 7]. The black dots are lower frequency solar wind power spectra data taken from Horbury et al. [24]. At the low frequencies there is no difference between transverse and parallel power spectra. Under the Taylor assumption of convective transport of eddies [applied in Goldstein et al. 23, where the spectrum was interpreted as a complete K spectrum], the transition to K and dissipation ranges is indicated by the green vertical bars. Assuming these scales being the ion- and electron-inertial scales leads to failure when taking reasonable values for the solar wind speed V. The inferred solar wind densities N become far to low. This poses a sensitive problem to our assumptions in application to the solar wind and raises the question why the extension of the K range fits the above ratio in both observations shown and what would cause collisionless dissipation of turbulence already on ion scales if reconnection does not come up for it. In the dissipation range (yellow line) the frequency spectrum decays as ~ f⁻³ indicating that the ultimate exponential decay is superseded here by some other process (cf. the Discussion Section). The CLUSTER data exhibit the same dissipative power law decay which, above 10 Hz [not shown, cf. Alexandrova et al. 7], merges into the expected exponential dissipation law.

The composed spectrum is shown in Figure 1. Matching the spectra at k = k_i gives for

$\begin{array}{cc}{C}_{\text{IK}}\approx C_{\text{K}}{v}_A^{-\frac{1}{2}}{ϵ}^{\frac{1}{6}}{k}_i^{-\frac{1}{6}}& \left(3\right)\end{array}$

[Any general large-scale spectrum $E_{k<k_i}\simeq A_{\alpha }(ϵ,v_A)k^{-\alpha },\alpha <\frac{3}{2}$, yields of course $A_{\alpha }\approx C_{\text{K}}{ϵ}^{\frac{2}{3}}{k}_i^{-\frac{3}{2}+\alpha }$.] Identification of the dissipation scales permits expressing the viscosities ν in terms of the large scale stationary energy injection rate ϵ and plasma quantities. From Kraichnan theory [6] follows that

$\begin{array}{cc}{\lambda }_i\approx {({\nu }_i^2{v}_A/ϵ)}^{\frac{1}{3}}\text{or}{\nu }_i\approx {({\lambda }_i^3ϵ/v_A)}^{\frac{1}{2}}& \left(4\right)\end{array}$

The viscosity, defined as ν_i = λ²_i ν_{i, an}, yields the equivalent anomalous collision rate

$\begin{array}{cc}{\nu }_{i,an}\approx {(ϵ/v_A{\lambda }_i)}^{\frac{1}{2}}& \left(5\right)\end{array}$

in IK-turbulence, the frequency at which energy disappears from the IK- into the K-range. Though this is not a real dissipation rate, it stands as the equivalent of it. Replacing λ_i with ρ_i yields ${\nu }_{i,an}\approx {(ϵ{\omega }_{ic}/v_A^2)}^{\frac{1}{2}}$ instead.

Applied to the K-dissipation scale ${\lambda }_e={({\nu }_e^3/ϵ)}^{\frac{1}{4}}$, where reconnection sets on, the same reasoning yields the electron viscosity

$\begin{array}{cc}{\nu }_e\approx {ϵ}^{\frac{1}{3}}{\lambda }_e^{\frac{4}{3}}& \left(6\right)\end{array}$

With ν_e = λ²_e ν_{e, an} the equivalent collision frequency for collisionless dissipation of the turbulent energy injected at the large eddy scale ℓ_in becomes

$\begin{array}{cc}{\nu }_{e,an}\approx {(ϵ/{\lambda }_e^2)}^{\frac{1}{3}}& \left(7\right)\end{array}$

This “anomalous” (equivalent) quasi-stationary collision rate in collisionless MHD turbulence holds when the injected turbulent energy ultimately dissipates in reconnection of current filaments on the electron-inertial scale, an assumption supported by all recent collisionless simulation studies of reconnection in high temperature plasmas. It allows relating the energy injection rate (per unit mass) to the reconnection rate. Using the the local lower hybrid frequency ${\omega }_{lh}~\sqrt{m_e/m_i}{\omega }_{ce}$ as the robust upper limit [21] based on numerical simulations, we obtain

$\begin{array}{cc}ϵ\approx {(m_i/m_e)}^{\frac{1}{2}}{\omega }_{ci}{v}_A^2& \left(8\right)\end{array}$

with ω_ci = eB/m_i the ion cyclotron frequency. Hence, in stationary ideal MHD turbulence dissipation of turbulent energy by reconnection adjusts itself in such a way that the energy injection rate is at the lower-hybrid frequency. Temporarily higher rates causes the large eddies that control energy injection and distribution to provide a strong enough magnetic field to settle stationarily into a state where the above condition is satisfied. Larger injection rates that cannot be handled by generating sufficiently large electron viscosities on the electron inertial scale, should cause the spectrum to develop along an inverse cascade in the direction of the largest available macro-scale L of the plasma. Once this scale is ultimately reached, stationarity should break down, and the inertial range will become modified. Under such extreme conditions reconnection below the electron inertial scale changes to the state of strongly driven reconnection when other processes than electron viscosity generation take over.

3. Conclusions

Figure 1 (Left), obtained by the Mariner 10 spacecraft in 1974 [23], shows an early solar wind magnetic turbulence spectrum with slightly different slopes of the two inertial-range spectra merging at the spectral break point. Spectral breaks have been detected in recent years only in solar wind turbulence with availability of high resolution instrumentation and sophisticated analysis methods [cf., e.g., 7, 9, 26–31, and references therein]. For example, CLUSTER [7], Figure 1 (Right, pink line), MESSENGER and Ulysses observations closer to the Sun [26] confirming the Mariner 10 measurements, exhibit the break at about the expected position in the spectrum. The K-inertial range has been identified in all these observations in complete agreement to span an interval of at most two orders of magnitude in frequency. Temporal spectra have been transformed into wave number spectra assuming Taylor's convective transport hypothesis (most recently in Alexandrova et al. 7; Alexandrova et al. 30; Perri et al. 26; Perri et al. 31; Sahraoui et al. 27; Narita et al. 29). The IK-like range is mapped less clearly with varying slopes ranging from extremely flat ~ k⁻¹ up to IK as, for instance, indicated in the CLUSTER observation in Figure 1 of Alexandrova et al. [7], Horbury et al. [24] and more pronounced in the MESSENGER/Ulysses observations [26] where the slope found was ~ −$\frac{5}{4}$. At the high frequency end the spectrum enters a dissipation range, at 0.5 Hz <f<0.8 Hz in Figure 1, still power law though from case to case exhibiting varying slopes ≲ −3 [e.g., 26, 32], sometimes even much steeper. It was found from CLUSTER [7, 32] that at frequencies f > 10 Hz (corresponding to electron gyro- or inertial scales) the spectral decay becomes exponential indicating takeover of pure dissipation. Originally, dissipation was attributed to ion-cyclotron damping (e.g., in Goldstein and Roberts 23; Zhou et al. 3) of magnetized ions, implying the magnetized-ion range extending in frequency substantially beyond the observed dissipation range in Figure 1. Kinetic Alfvén wave damping, in particular when resulting from nonlinear evolution, would be another option [15], in addition to causing anisotropy. Other suggestions favorise whistler wave damping [30] which, however, should be too weak for dissipating the input of mechanical turbulent energy.

The solar wind is neither homogeneous, nor isotropic, nor stationary; it is thus not the ideal place to check our hypothesis. Its turbulence source is the solar corona from where expanding convection transports it radially outward, distributing it over large angular ranges. Cascading takes place in the corona and underway, when the stream becomes ever more dilute with distance. Additional sources of turbulence are instabilities and internal interactions in the flow, generating spectral anisotropy and modifying eddies and clusters of turbulent waves. One does not expect that observations of solar wind turbulence yield any ideal spectra of stationary homogeneous turbulence when applying the Taylor hypothesis that all the eddies in the flow are simply convected downstream (see discussion in Sahraoui et al. [32]).

The temporal K-range extension (roughly a factor ~50) is almost precisely the order of the proton-inertial range ${\lambda }_i/{\lambda }_e\approx \sqrt{m_i/m_e}$ between ion and electron inertial lengths (or gyro lengths, at constant temperature ratio 5 ≲ T_e/T_i ≲ 10), not put in question by any of the more recent observations (using gyroradii introduces a factor $2\lesssim \sqrt{T_e/T_i}\lesssim 3$ in K-range extension). The corresponding transition frequencies in Figure 1 are f₁ ~ (V_sw/c) ω_i/2 π ≈ 0.015 Hz and f₂ ~ (V_sw/c) ω_e ≈ 0.6 Hz, with V_sw the (constant) average solar wind velocity. With nominal solar wind speed V_sw ~ 300 km/s, using f₂ ≈ f(λ_e) in estimating the solar wind density N_sw, however, yields an unrealistically low solar wind density (at the location of Mariner 10) of N_sw ≲ 10⁻³ cm⁻³. When referring to gyroradii instead of inertial lengths, the above temperature ratio is reproduced, indicating that the scales of demagnetization of ions and electrons cause the dominant effect. On shorter scales than ρ_i, ion inertia takes over control of further evolution. Currents become purely electronic and form narrow filaments including Hall currents. When electrons demagnetize on ℓ ≲ ρ_e and the current width scale drops to ℓ ≲ λ_e, such current filaments are subject to violent collisionless reconnection.

Two recent CLUSTER observations in the magnetosheath [33] and solar wind [34] suggest that turbulence indeed consists of large numbers of narrow electric current filaments on demagnetized electron scales ℓ ~ ρ_e. In addition, in the magnetosheath current filaments inference of plasma heating suggested ongoing reconnection [33]. Where does the reconnection dissipation set on?

Indications for exponential spectral decays have been found in solar wind [7] and Earth's foreshock [32] as inferred from CLUSTER magnetic fields at high frequencies f ≳ f_exp ≫ f₂ at f_exp ~ 10² Hz, roughly two orders of magnitude above f₂. Identifying f_exp ≈ f(λ_e), the inferred solar wind density N_sw ~ f²_λe ≈ 10 cm⁻³ agrees conveniently with measured average densities. In both cases the observed exponential decay is modified by other effects, such as related to shocks [in the case of e.g., 32, the exponential multiplied a power law], and to the validity of the Taylor hypothesis. Solar wind spectra [7] decay ~ exp(−α$\sqrt{f}$), most probably indicating a frequency dependent damping rate ν ∝ 1/$\sqrt{f}$. Here, the flow was quasi-perpendicular to the mean magnetic field implying turbulent wave vectors k along V_sw for rendering Taylor's hypothesis applicable to the magnetically parallel magnetic power spectrum S_||(k_⊥) (magnetically perpendicular power spectra S_⊥(k_||) with magnetic field parallel to streaming and wave number parallel to the mean field are unaffected because for them k · V_sw = 0 in this case). One may note here that inspection of spectral anisotropies [11, 24] suggests that power spectra S_||(k_⊥) follow the K-inertial slope. Strictly spoken, Taylor's hypothesis applies to V = V_sw + v_gr, with v_gr the eddy group velocity. Any v_gr > 0 shifts the frequency spectrum up into the dissipation range, causing modification of the spectrum to the observed power law (see Figure 1] and the foreshock spectrum [32]. For instance, the power law ~ f⁻³ could result from shifting the K-range up by a turbulent flow-parallel velocity spectrum $|\langle v_{gr}^2\rangle {|}^{\frac{1}{2}}~k^{-\frac{7}{4}}$ [for discussion of steeper slopes cf., 32].

Any v_gr < 0 partially cancels the streaming effect. Referring to MHD turbulence (the IK model), v_gr ~ v_A is of the order of the Alféen velocity. In the solar wind the average ratio of the Alfvén-to-solar wind speed is 0.1 ≲ v_A/V_sw ≲ 0.3 with minor effect on the spectrum only. Once narrow current layers form, this field is locally stronger concentrating in small-scale filaments. For a line current, the local Alfvén speed increases like B ~ r⁻¹ (unless locally $B_{loc}/\sqrt{N_{loc}}$ remains constant) which implies a locally reduced Mach number M_{A, loc} ≡ V_sw/v_{A, loc}. Turbulence with v_gr < 0 thus seems composed of “shocklet-like” or “solitary-like” structures, i.e., current filaments of spatial scales in the range λ_e ≲ ℓ ≲ min(λ_i, ρ_i) propagating at enhanced v_{A, loc} (Alfvén speeds on scales ℓ < ρ_i are dominated by electrons and become large). Propagating all at about same phase velocity v_gr ~ v_{A, loc}, they behave like simple waves, grow nonlinearly on the collisionless plasma stream and localise at large amplitude. Their dispersive steeping contributes to the cascade of current filaments. At electron gyro- and—ultimately inertial—scales the cascade enters the reconnection range where the turbulent energy is transferred into heat and particle acceleration. The spectrum of turbulent eddies with v_gr > 0 obscures the dissipative spectral range superseding its exponential decay in the interval between f₂ and f_λe. In this range other processes like whistler damping and kinetic Alfvén wave effects may contribute to dissipation.

We finally note that after acceptance of this Perspective we became aware of a recent submission of a new extended 3d pic simulation [35] which very clearly demonstrates that dissipation in MHD turbulence indeed takes place when the filamentary current sheet structure reaches into the electron inertial scale range not only in the relatively ambiguous observations but also in simulations. In that most recent paper, no identification is given, unfortunately, of the physical dissipation mechanism nor reference to reconnection.

4. Summary

Ideal MHD turbulence ultimately dissipates its (motional) energy via collisionless magnetic reconnection (first implicited in Karimabadi et al. 16) after cascading down in two steps from large scales to electron scales [cf., 7, 27, 32, for electron gyroscales] forming narrow current filaments (recently inferred in Retinó et al. 33; Perri et al. 34, 37 from Cluster observations in Earth's magnetosheath and solar wind). The large-scale ~2d-turbulence, following some variant of an inertial IK-like process, “dissipates” at ion-gyro and inertial scales in transition to inertial K-turbulence. Dissipation by collisionless reconnection starts when the K-range matches the electron inertial scale ℓ ≲ λ_e. The low-frequency (large-scale) spectra depend on factors which we ignored here. More recent investigations suggest, in addition to anisotropy, a variety of power laws for the low-frequency range, reaching from powers close to one up to IK. The spectral extension of the K range is independent of the realisation of an IK spectrum or some equivalent, as observations agree.

This picture of ideal MHD turbulence is free of assumptions on generation of anomalous collisions on ion scales. Processes like ion damping etc. are not inhibited but probably cause weak effects only, resulting in some modulation of the spectral slope at spatial scales longer than electron gyroradii. Ultimate dissipation of the turbulent energy is presumably not provided by any linear plasma instability but attributed to collisionless reconnection, a violent, well established [17, 20, 36] plasma process driven by electron inertia, meandering motion and the generation of electron viscosity [18, 19, 21] within many electron inertial-scale turbulent current filaments.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the two referees for their very constructive comments on the original version of this paper. In particular the demand to include more recent data (in this case from the Messenger and Cluster spacecraft) and to refer to the observational constraints on reconnection were very useful indeed.

References

1. Biskamp D. Magnetohydrodynamic Turbulence. Cambridge, UK: Cambridge University Press (2003).

Google Scholar

2. Davidson PA. Turbulence. An Introduction for Scientists and Engineers. Oxford, UK: Oxford University Press (2004).

Google Scholar

3. Zhou Y, Matthaeus WH, Dmitruk P. Colloquium: magnetohydrodynamic turbulence and time scales in astrophysical and space plasmas. Rev Mod Phys. (2004) 76:1015–35. doi: 10.1103/RevModPhys.76.1015

CrossRef Full Text | Google Scholar

4. Iroshnikov PS. Turbulence of a conducting fluid in a strong magnetic field. Astron Zhurn. (1963) 40:742.

Google Scholar

5. Kraichnan RH. Kolmogorov's hypotheses and eulerian turbulence theory. Phys Fluids. (1964) 7:1723–34. doi: 10.1063/1.2746572

CrossRef Full Text | Google Scholar

6. Kraichnan RH. Inertial-range spectrum of hydromagnetic turbulence. Phys Fluids. (1965) 8:1385–7. doi: 10.1063/1.1761412

CrossRef Full Text | Google Scholar

7. Alexandrova O, Saur J, Lacombe C, Mangeney A, Mitchell J, Schwartz SJ, et al. Universality of solar-wind turbulent spectrum from MHD to electron scales. Phys Rev Lett. (2009) 103:165003. doi: 10.1103/PhysRevLett.103.165003

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

8. Chen CHK, Mallet A, Schekochihin AA, Horbury TS, Wicks RT, Bale SD. Three-dimensional structure of solar wind turbulence. Astrophys J. (2012) 758:120–24. doi: 10.1088/0004-637X/758/2/120

CrossRef Full Text | Google Scholar

9. Narita Y, Glassmeier K-H, Sahraoui F, Goldstein ML. Wave-vector dependence of magnetic-turbulence spectra in the solar wind. Phys Rev Lett. (2010) 104:171101. doi: 10.1103/PhysRevLett.104.171101

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

10. Sahraoui F, Goldstein ML, Belmont G, Canu P, Rezeau L. Three dimensional anisotropic k spectra of turbulence at subproton scales in the solar wind. Phys Rev Lett. (2010). 105:131101. doi: 10.1103/PhysRevLett.105.131101

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

11. Wicks RT, Forman MA, Horbury TS, Oughton S. Power anisotropy in the magnetic field power spectral tensor of solar wind turbulence. Astrophys J. (2012) 746:103–26. doi: 10.1088/0004-637X/746/1/103

CrossRef Full Text | Google Scholar

12. Schekochihin AA, Cowley SC, Dorland W, Hammett GW, Howes GG, Quataert E, et al. Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys J Suppl. (2009) 182:310–77. doi: 10.1088/0067-0049/182/1/310

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

13. Paschmann G, Øieroset M, Phan T. In-situ observations of reconnection in space. Space Sci Rev. (2013) 178:385–417.

Google Scholar

14. Treumann RA, Baumjohann W. Collisionless magnetic reconnection in space plasmas. Front. Phys. (2013) 1:31. doi: 10.3389/fphys.2013.00031

CrossRef Full Text | Google Scholar

15. Leamon RJ, Smith CW, Ness NF, Wong HK. Dissipation range dynamics: kinetic Alfvén waves and the importance of β_e. J Geophys Res. (1999) 104:22331–44.

Google Scholar

16. Karimabadi H, Roytershteyn V, Daughton W, Liu Y-H. Recent evolution in the theory of magnetic reconnection and its connection with turbulence. Space Sci Rev. (2013) 178, 307–23. doi: 10.1007/s11214-013-0021-7

CrossRef Full Text | Google Scholar

17. Pritchett P. Onset and saturation of guide-field magnetic reconnection. Phys. Plasmas (2005) 12:062301. doi: 10.1063/1.1914309

CrossRef Full Text | Google Scholar

18. Hesse M, Winske D. Electron dissipation in collisionless magnetic reconnection. J Geophys Res. (1998) 103:26479–86. doi: 10.1029/98JA01570

CrossRef Full Text | Google Scholar

19. Hesse M, Schindler K, Birn J, Kuznetsova M. The diffusion region in collisionless magnetic reconnection. Phys Plasmas. (1999) 6:1781–95. doi: 10.1063/1.873436

CrossRef Full Text | Google Scholar

20. Hesse M, Aunai N, Sibeck D, Birn J. On the electron diffusion region in planar, axisymmetric, systems. Geophys Res Lett. (2014) 41:8673–80. doi: 10.1002/2014GL061586

CrossRef Full Text | Google Scholar

21. Treumann RA, Baumjohann W. Superdiffusion revisited in view of collisionless reconnection. Ann Geophys. (2014) 32:643–50. doi: 10.5194/angeo-32-643-2014

CrossRef Full Text | Google Scholar

22. Karimabadi H, Lazarian A. Magnetic reconnection in the presence of externally driven and self-generated turbulence. Phys Plasmas (2013) 20:112102. doi: 10.1063/1.4828395

CrossRef Full Text | Google Scholar

23. Goldstein ML, Roberts DA, Matthaeus WH. Magnetohydrodynamic turbulence in the solar wind. Ann Rev Astron Astrophys. (1995) 33:283–326. doi: 10.1146/annurev.aa.33.090195.001435

CrossRef Full Text | Google Scholar

24. Horbury TS, Wicks RT, Chen CHK. Anisotropy in space plasma turbulence: solar wind observations. Space Sci Rev. (2012) 172:325–42. doi: 10.1007/s11214-011-9821-9

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

25. Galtier S. Kolmogorov vectorial law for solar wind turbulence. Astrophys J. (2012) 746:184–7. doi: 10.1088/0004-637X/746/2/184

CrossRef Full Text | Google Scholar

26. Perri S, Carbone V, Veltri P. Where does fluid-like turbulence break down in the solar wind? Astrophys J Lett. (2010) 725:L52–5. doi: 10.1088/2041-82057725/1/L52

CrossRef Full Text | Google Scholar

27. Sahraoui F, Goldstein ML, Robert P, Khotyaintsev YV. Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys Rev Lett. (2009) 102:231102. doi: 10.1103/PhysRevLett.102.231102

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

28. Narita Y, Glassmeier K-H, Treumann RA. Wave-number spectra and intermittency in the terrestrial foreshock region. Phys Rev Lett. (2006) 97:191101. doi: 10.1103/PhysRevLett.97.191101

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

29. Narita Y, Glassmeier K-H, Gary SP, Goldstein ML, Treumann RA. Wave number spectra in the solar wind, the foreshock, and the magnetosheath. In: Laakso H, Taylor MGTT, and Escoubet CP editors. The Cluster Active Archive. Studying the Earth's Space Plasma Environment. Berlin: Springer (2010). p. 363–8.

Google Scholar

30. Alexandrova O, Chen CHK, Sorriso-Valvo L, Horbury T, Bale SD. Solar wind turbulence and the role of ion instabilities. Space Sci Rev. (2014) 47:25–63. doi: 10.1007/978-1-4899-7413-6-3

CrossRef Full Text | Google Scholar

31. Perri S, Carbone V, Yordanova E, Bruno R, Balogh A. Scaling law of the reduced magnetic helicity in fast streams. Planet Space Sci. (2011) 59:575–9. doi: 10.1016/j.pss.2010.04.017

CrossRef Full Text | Google Scholar

32. Sahraoui F, Huang SY, Belmont G, Goldstein ML, Retinó A, Robert P, et al. Scaling of the electron dissipation range of solar wind turbulence. Astrophys J. (2013) 777:15. doi: 10.1088/0004-637X/777/1/15

CrossRef Full Text | Google Scholar

33. Retinó A, Sundkvist D, Vaivads A, Mozer F, André M, Owen CJ. In situ evidence of magnetic reconnection in turbulent plasma. Nat Phys. (2007) 3:236–8. doi: 10.1038/nphys574

CrossRef Full Text | Google Scholar

34. Perri S, Goldstein ML, Dorelli J, Sahraoui F, Gurgiolo CA, Karimabadi H et al. Observation of Thin Current Sheets in the Solar Wind and Their Role in Magnetic Energy Dissipation. San Francisco, CA: AGU, Fall Meeting, abstract # SH51B-2099 (2013).

Google Scholar

35. Wan M, Matthaeus WH, Roytershteyn V, Karimabadi H, Parashar T, Wu P, et al. Intermittent dissipation and heating in 3D kinetic plasma turbulence. Phys Rev Lett. (in press) 114.

36. Hesse M, Neukirch T, Schindler K, Kuznetsova M, Zenitani S. The diffusion region in collisionless magnetic reconnection. Space Sci Rev. (2011) 160:3–23. doi: 10.1007/s11214-010-9740-1

CrossRef Full Text | Google Scholar

37. Gogoberidze G, Perri S, Carbone V. The Yaglom law in the expanding solar wind. Astrophys J. (2013) 769:111–5. doi: 10.1088/0004-637X/769/2/111

CrossRef Full Text | Google Scholar