- Department of Physics, Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA, USA
Quantum gravity is often expected to solve both the singularity problem and the information-loss problem of black holes. This article presents an example from loop quantum gravity in which the singularity problem is solved in such a way that the information-loss problem is made worse. Quantum effects in this scenario, in contrast to previous non-singular models, do not eliminate the event horizon and introduce a new Cauchy horizon where determinism breaks down. Although infinities are avoided, for all practical purposes the core of the black hole plays the role of a naked singularity. Recent developments in loop quantum gravity indicate that this aggravated information loss problem is likely to be the generic outcome, putting strong conceptual pressure on the theory.
1. Introduction
There is a widespread expectation that quantum gravity, once it is fully developed and understood, will resolve several important conceptual problems in our current grasp of the universe. Among the most popular ones of these problems are the singularity problem and the problem of information loss. Several proposals have been made to address these questions within the existing approaches to quantum gravity, but it is difficult to see a general scenario emerge. Given such a variety of possible but incomplete solution attempts, commonly celebrated as successes by the followers of the particular theory employed, it is difficult to use these models in order to discriminate between the approaches. In this situation it may be more fruitful to discuss properties of a given approach that stand in the way of resolving one or more of the big conceptual questions. Here, we provide an example regarding the information loss problem as seen in loop quantum gravity.
Loop quantum gravity [1–3] is a proposal for a canonical quantization of space-time geometry. It remains incomplete because it is not clear that it can give rise to a consistent quantum space-time picture (owing to the so-called anomaly problem of canonical quantum gravity). Nevertheless, the framework is promising because it has several technical advantages compared to other canonical approaches, in particular in that it provides a well-defined and tractable mathematical formulation for quantum states of spatial geometry. The dynamics remains difficult to define and to deal with, but there are indications that a consistent version may be possible, one that does not violate (but perhaps deforms) the important classical symmetry of general covariance. These indications, found in a variety of models, lead to the most-detailed scenarios by which one can explore large-curvature regimes in the setting of loop quantum gravity.
The word “loop” in this context refers to the importance attached to closed spatial curves in the construction of Hilbert spaces for geometry according to loop quantum gravity [4]. More precisely, one postulates as basic operators not the usual curvature components on which classical formulations of general relativity are based, but “holonomies” which describe how curvature distorts the notion of parallel transport in space-time. If we pick a vector at one point of a closed loop in curved space and move it along the loop so that each infinitesimal shift keeps it parallel to itself, it will end up rotated compared to the initial vector once we complete the loop. The initial and final vectors differ from each other by a rotation with an angle depending on the curvature in the region enclosed by the loop. Loop quantum gravity extends this construction to space-time and quantizes it: It turns the rotation matrices into operators on the Hilbert space it provides. An important consequence is the fact that (unbounded) curvature components are expressed by bounded matrix elements of rotations. Most of the postulated loop resolutions of the singularity problem [5–11] rely on this replacement.
Classical gravity, in canonical terms, can be described by a Hamiltonian H that depends on the curvature. If H is to be turned into an operator for loop quantum gravity, one must replace the curvature components by matrix elements of holonomies along suitable loops, because only the latter ones have operator analogs in this framework. One has to modify the classical Hamiltonian by a new form of quantum corrections. The classical limit can be preserved because for small curvature, the rotations expressed by holonomies differ from the identity by a term linear in standard curvature components [12, 13]. At low curvature, the classical Hamiltonian can therefore be obtained. At high curvature, however, strong quantum-geometry effects result which, by virtue of using bounded holonomies instead of unbounded curvature, can be beneficial for resolutions of the singularity problem.
Given the boundedness, it is in fact easy to produce singularity-free models. But one of the outstanding problems of this framework is to show that the strong modification of the classical Hamiltonian can be consistent with space-time covariance. This question is not just one of broken classical symmetries (which might be interesting quantum effects). Covariance is implemented by a set of gauge transformations which eliminate unphysical degrees of freedom given by the possibility of choosing arbitrary coordinates on space-time. When these transformations are broken by quantum effects, the resulting theory is meaningless because its predictions would depend on which coordinates one used to compute them. Showing that there are no broken gauge transformations (or gauge anomalies) is therefore a crucial task regarding the consistency of the theory. The problem remains unresolved in general, but several models exist in which one can see how it is possible to achieve anomaly-freedom, constructed using operator methods [14–18] or with effective methods [19–23].
2. A Model of Deformed Canonical Symmetries
As a simple, yet representative, example, we consider a model with one field-theoretic degree of freedom ϕ(x) and momentum p(x). There is no room for gauge degrees of freedom in this model, and therefore we use it only to consider the form of symmetries of gravity, not the way in which spurious degrees of freedom are removed.
2.1. Algebra of Transformations
For the example, we postulate a class of Hamiltonians
with a function f to be specified, and with the prime denoting a derivative by the one spatial coordinate x. As in general relativity, the Hamiltonian depends on a free function N(x) because there is no absolute time. The freedom of choosing N corresponds to choosing different time lapses and directions along which H[N] would generate translations. Also the dependence of H[N] on the canonical fields is modeled on gravity, where f(p) would be a quadratic function (p standing for extrinsic curvature), and the derivative terms of ϕ present a simple version of spatial curvature (a function quadratic in first-order and linear in second-order derivatives of the metric). The main formal features of gravitational Hamiltonians are therefore captured by this model. One can indeed check that the general results of [19–23] follow from the structure of derivatives in Equation (1) in combination with a function f(p) which modifies the classical momentum dependence. (Compare with Equation (A4) in Appendix A).
The Hamiltonian, as a generator of local time translations, is accompanied by a second generator of local spatial translations, the form of which is more strictly determined: It is given by D[w] = ∫dxwϕp′ with another free function w(x). It generates canonical transformations given by
as they would result from an infinitesimal spatial shift by −w(x):
(The transformation of ϕ is slightly different owing to a formal density weight).
Of special importance is the algebra of symmetries, which can be computed by Poisson brackets (as a classical version of commutators). We obtain
Two local time translations have a commutator given by a spatial shift. (The numerical coefficients chosen in Equation (1) ensure that the bracket (Equation 3) is closed). Although our model is simplified, the result (Equation 3) matches well with calculations in models of loop quantum gravity, constructed for spherical symmetry [18, 20, 23] and for cosmological perturbations [21, 22]. (See Equation (A4) in Appendix A). The same type of algebra has also been obtained for H-operators in 2+1-dimensional models [14]. Since our choice (Equation 1) extracts the main dynamical features of loop models, it serves to underline the genericness of deformed symmetry algebras when f(p) is no longer quadratic.
2.2. Geometry
For the classical case in which f(p) = p2 is a quadratic function of p, half the second derivative in Equation (3) is a constant equal to one and the spatial shift is simply N′M − NM′. This relation agrees with the result obtained in general relativity (except that in the latter case one would have to use the spatial metric to turn the 1-form N′M − NM′ into a vector). It has an interesting interpretation if we use linear functions of the form cΔt+ (v/c)x for N and M (with the speed of light c). The constant Δt amounts to a rigid shift in time. The linear term can be understood if one thinks of Minkowski diagrams in special relativity: a Lorentz boost tilts the x-axis into a new position by an angle given by the boost velocity v. (The new x-axis is the set of points where the new time coordinate
is constant). The commutator of Lorentz boosts and time translations can be derived from Equation (3) with linear N and M: For N = cΔt + (v/c)x and M = −(v/c)x (undoing the boost after time Δt), we have N′M − NM′ = vΔt. The commutator simply amounts to a spatial shift
as expected. (It may not be possible to have globally linear functions N and w on a general manifold, but local Poincaré transformations, with N and w linear in some neighborhood, can always be realized).
Holonomy effects of loop quantum gravity can be modeled by using a bounded function f(p) instead of a quadratic one. (A popular choice in the field is f(p) = p20sin2(p/p0) with some constant p0, such as Planck-sized curvature). The number of classical symmetries remains intact because the relation (Equation 3) is still a closed commutator. But the structure of space-time changes: we can no longer think in terms of local Minkowski geometry because the spatial shift in Equation (3) with d2f/dp2 ≠ 1 violates the relation Δx = vΔt found classically in Equation (4). The deviation from classical space-time is especially dramatic at high curvature, near any maximum of the holonomy function f(p): Around a maximum, the second derivative is negative, d2f/dp2 < 0. For the popular choice of f(p) = p20sin2(p/p0), we have d2f/dp2 = cos(2p/p0) which is equal to −1 at the maximum of f(p). The counter-intuitive relation Δx = −vΔt can be interpreted in more familiar terms: the change of sign means that the classical Lorentz boost is replaced by an ordinary rotation. (An infinitesimal rotation by an angle θ in the (x, y)-plane and a spatial shift by Δy commute to Δx = −θΔy). At high curvature, holonomy-modified models of general relativity replace space-time with pure and timeless higher-dimensional space, a phenomenon called signature change [24–26].
2.3. Field Equations
At the level of equations of motion, signature change means that hyperbolic wave equations become elliptic partial differential equations (in all four dimensions, or two in the model). Indeed, if one computes equations of motion from the Hamiltonian Equation (1), one obtains
where d2f(p)/dp2 is a function of via = Ndf(p)/dp. This partial differential equation, which is hyperbolic for d2f(p)/dp2 > 0, becomes elliptic for d2f(p)/dp2 < 0.
In the latter case, the equation requires boundary values for solutions to be specified; it is not consistent with the familiar evolution picture implemented by an initial-value problem. Instead of specifying our field and its first time derivative at one instant of time, once curvature (or in the model) becomes large enough to trigger signature change we must specify the field on a boundary enclosing a 4-dimensional region of interest—including a “future” boundary in the former time direction. We can no longer determine the whole universe from initial data given at one time1.
Although our specific model is simplified, the main conclusion about signature change agrees with the more detailed versions cited above, which latter directly come from reduced models of loop quantum gravity combined with canonical effective techniques. (See Appendix A for an example with spherical symmetry). Our model presented here shows that the main reason for signature change is the modified dependence of gravitational Hamiltonians on curvature components when holonomies are used to express them, together with the general structure of curvature terms. (Especially the presence of spatial derivatives seems crucial for derivatives of the modification function to show up in the symmetry algebra after integrating by parts). The rest of our discussions does not rely on the specific model but rather on the general consequence of signature change.
2.4. General Aspects of Signature Change
As shown in Bojowald and Brahma [27], the structure of constraint algebras or gauge transformations, of which Equation (3) provides a model, is much less sensitive to details of regularization effects or quantum corrections than the precise dynamics implied. Even if there may be additional quantum corrections in Equation (5) in a fully quantized model, structure functions of the algebra, such as d2f/dp2 in Equation (3), provide reliable effects of a general nature. For details, the reader is referred to the above citation or Appendix B, but the crucial ingredient in this observation is the definition of effective constraints CI = 〈ĈI〉 as expectation values of constraint operators ĈI (or symmetry generators H and D in the model here), and their brackets as {CI, CJ} = 〈[ĈI, ĈJ]〉/iħ. A regularization of a constraint operator ĈI leads to corresponding modifications of the effective constraint 〈ĈI〉. For any consistent operator algebra, the bracket of effective constraints mimics the commutator of constraint operators. Even if 〈ĈI〉, computed to some order in quantum corrections, may give a poor approximation to the quantum dynamics, the consistent forms of effective constraint algebras restrict the possible versions of quantum commutators. If effective constraints of a certain form, such as those obtained with holonomy modifications, always lead to a change of sign of structure functions, the same must be true for operator algebras.
As the preceding discussion has made clear, there are no assumptions in this effective method other than the form of modifications of constraints and that the theory can be consistent at all. In particular, the phase space or symplectic structure is not assumed but derived from quantum commutators. The method therefore provides reliable evaluations of loop models which otherwise could be analyzed only with difficulties, or in very special circumstances that provide solvability. Certain proponents of loop quantum gravity often refer to a ready-made argument in their defense of the theory. If the effective method shows that there is signature change and corresponding indeterminacy, they say, then there must be something wrong with this method [28]. It is therefore important to realize that the effective method is merely used to evaluate loop models. It does make assumptions, but only of general type: it assumes that it is possible to have some anomaly-free realization of constraint algebras, and that sufficiently general semiclassical states exist which allow one to derive mode equations with quantum corrections. (The latter assumption is necessary in background-independent theories, but not only for their effective analysis). It is also important that the effective method is the only one so far that has provided results on the off-shell constraint algebra of loop quantum gravity. The constructions by Henderson et al. [15], Henderson et al. [16], Tomlin and Varadarajan [17] are only partially off-shell at isolated points, in such a way that they do not show deformations of the constraint algebra by holonomy corrections, which are responsible for signature change. The constraint analysis of black-hole models by Gambini and Pullin [11] makes use of a simple Abelianization which is available only in this specific situation, and only for the classical constraints. Although these models implement holonomy modifications after the classical constraints have been Abelianized, they do not allow conclusions about quantum space-time as given by holonomy-modified constraints.
As noted also in Mielczarek [25], Barrau et al. [29], equations of the form Equation (5) sometimes appear for matter systems with instabilities, in cosmology but also in other areas such as transonic flow. An instability would normally not be interpreted as signature change as long as a standard Lorentzian metric structure remains realized, as is the case in all the known matter examples. The present context, however, is different, because the instability affects the geometry of space-time itself, and not just matter propagating in space-time. (In models of loop quantum gravity, ϕ in Equation 5 stands for metric inhomogeneities). Such an instability is more severe, and at the same time more inclusive because it affects all excitations—matter and geometry—in the same way. Indeed, the most fundamental structure where it appears is not the equation of motion Equation (5) but the symmetry algebra Equation (3). If matter is present, its Hamiltonian would be added to the gravitational one, the resulting sum satisfying a closed algebra of the form (Equation 3). (If adding matter terms would break the algebra, there would be anomalies making the theory inconsistent). Matter and geometry are then subject to the same modified symmetries, and correspondingly to a modified evolution picture with a boundary rather than initial-value problem at high density.
Solutions might exist for elliptic partial differential equations with an initial-value problem. However, such solutions are unstable and depend sensitively on the initial values; therefore, initial-value problems for elliptic partial differential equations are not well-posed. Sometimes, a physical model of this form may just signal a growing mode which is increasing rapidly in actual time. In quantum gravity and cosmology, however, instabilities from signature change in Equation (3) or Equation (5) are much more debilitating. In this context, one does not perform controlled laboratory experiments in which one can prepare or directly observe the initial values. When signature change is relevant, it happens in strong quantum-gravity regimes where the analogs of f(p) differ much from the classical behavior. Not only initial values but also the precise dynamical equations (subject to quantization ambiguities) are so uncertain that an initial-value formulation can give no predictivity. (In cosmological parlance, instabilities from signature change present severe versions of trans-Planckian and fine-tuning problems. For more information on the dynamics of affected modes see [30]). In contrast to some matter systems in which elliptic field equations may appear, quantum-gravity theories do not allow initial-value formulations in such regimes but rather require 4-dimensional boundary-value problems.
Evolution in these models is no longer fully deterministic. In the remainder of this article, we apply this conclusion to black holes and show that even low-curvature regions, where observers have no reason to expect strong quantum-gravity effects, will be affected by indeterminism. In this context, consequences of signature change are therefore much more severe than their analogs in cosmological models.
3. Black Holes
Black holes in general relativity have singularities where space-time curvature diverges. Loop quantum gravity has given rise to models in which curvature is bounded, apparently resolving the singularity problem [31]. As in some other approaches [32–35], there is then no event horizon but only an apparent horizon which encloses large curvature but eventually shrinks and disappears. If there is no singularity and information can travel freely through high-curvature regions, there is no information loss, so this important problem seems to be resolved too. However, previous black-hole models of this type in loop quantum gravity did not consider the anomaly problem. In an anomaly-free version, curvature may still be bounded, but when it is large (Planckian, or near the upper bound provided by the models), there can be signature change, preventing information from travelling freely through this regime. It is no longer obvious that the information-loss problem can be resolved in singularity-free models of black holes.
If the singularity is resolved, there are two scenarios for Hawking-evaporating black holes: The black-hole region enclosed by an apparent horizon could reconnect with the former exterior at the future end of high curvature, or it could split off into a causally disconnected baby universe. The latter case does not solve the information-loss problem because information that falls into the black hole is sealed off in the baby universe. The former case resolves the information-loss problem only if information can travel through high curvature. (In this article, we leave aside other problems of such remnant scenarios, as discussed for instance in Giddings [36], and focus on issues that originate from the same mechanism that is used to remove singularities). If signature change happens, nothing travels through the high-curvature region and the fate of information must be reconsidered.
The elliptic nature of field equations in the high-curvature core of black holes requires one to specify fields at the future boundary, which would evolve into the future space-time after black-hole evaporation. (The signature-change models analyzed here may also arise as effective versions of wave-function collapse models proposed in [37, 38]. Free boundary data around the high-curvature core would then correspond to the undetermined wave function obtained by quantum collapse). In Figure 1, boundary values on the bottom line surrounding the hashed high-curvature region would be determined by evolving past initial values forward in time, but boundary data on the top line around the region would have to be specified, unrestricted by any field equations. Their values are not predicted by the theory, and yet they are essential for determining the future space-time. Once the high-curvature region is passed by an outside observer, space-time is no longer predictable. The black-hole's event horizon 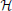 extends into a Cauchy horizon
extends into a Cauchy horizon  : The region above
: The region above  is affected by undetermined boundary data. Even if there are no infinities, the classical black-hole singularity is, for practical purposes, replaced by a naked singularity, a place out of which unpredictable fields can emerge.
is affected by undetermined boundary data. Even if there are no infinities, the classical black-hole singularity is, for practical purposes, replaced by a naked singularity, a place out of which unpredictable fields can emerge.
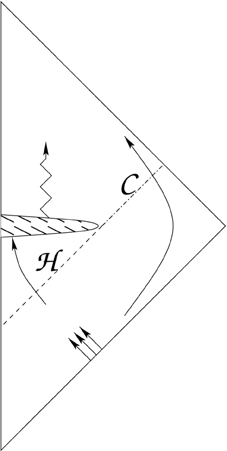
Figure 1. Acausality: Penrose diagram of a black hole with signature change at high curvature (hashed region). In contrast to traditional non-singular models, there is an event horizon (dashed line 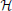 , the boundary of the region that is determined by backward evolution from future infinity) and a Chauchy horizon (dash-dotted line
, the boundary of the region that is determined by backward evolution from future infinity) and a Chauchy horizon (dash-dotted line 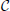 , the boundary of the region obtained by forward evolution of the high-curvature region). After an observer crosses the Cauchy horizon, space-time depends on the data chosen on the top boundary of the high-curvature region and is no longer determined completely by data at past infinity. Information that falls through
, the boundary of the region obtained by forward evolution of the high-curvature region). After an observer crosses the Cauchy horizon, space-time depends on the data chosen on the top boundary of the high-curvature region and is no longer determined completely by data at past infinity. Information that falls through 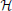 affects field values in the hashed region, but not on the top boundary or its future; it is therefore lost for an outside observer. Unrestricted boundary values at the top part of the hashed region influence the future universe even at low curvature (zigzag arrow), a violation of deterministic behavior.
affects field values in the hashed region, but not on the top boundary or its future; it is therefore lost for an outside observer. Unrestricted boundary values at the top part of the hashed region influence the future universe even at low curvature (zigzag arrow), a violation of deterministic behavior.
In terms of information loss, whatever infalling matter hits the high-curvature core of the black hole determines some part of the boundary conditions required for the elliptic region, and thereby influences part of the solution in the core. But it does not restrict our choice for the future boundary data, or anything that evolves out of it at lower curvature. Infalling information is therefore lost even if there is no black-hole singularity in the sense of infinite curvature. Similar conclusions apply to the alternative of a baby universe: Infalling information cannot be retrieved in the old exterior, and it cannot be passed on to the baby universe.
4. Conclusions: A No-Heir Theorem?
We have presented here a mechanism which appears to be generic in loop quantum gravity and helps to resolve curvature divergence, but makes the information loss problem of black holes worse. (Interestingly, models of string theory have occasionally resulted in similar effects of signature change or related phenomena [39, 40]). Black-hole singularities can turn into naked singularities in this framework, which implies an end to predictivity. In classical general relativity, there is strong evidence that cosmic censorship applies: given generic initial data, singularities may form but are enclosed by black-hole horizons; no naked singularities appear that would affect observations made from far away. In loop quantum gravity, a stronger version of cosmic censorship would be required if signature change is confirmed to be generic. Naked singularities (Cauchy horizons) could be avoided only if black-hole interiors split off into baby universes. But even then, information could not be passed on to the baby universe. From the point of view of observers in this new universe, the former black-hole singularity would appear as a true beginning, just as the big bang appears to us in our universe.
The information-loss problem has turned into a more-severe problem of indeterminism. Two options remain for loop quantum gravity to provide a consistent deterministic theory without Cauchy horizons. First, one might be able to show that signature change does not happen under general conditions in the full theory or that non-perturbative effects in ħ somehow allow for deterministic propagation, a question which requires an understanding of the off-shell constraint algebra and the thorny anomaly problem, together with the equally difficult problem of non-perturbative physical observables. All current indications, however, point in the opposite direction and suggest that signature change is generic. With signature change, Cauchy horizons can be avoided only if the high-curvature regions of black holes always remain causally disconnected from the universe in which they formed, that is if black holes open up into new baby universes. In this scenario, information that falls in a black hole is still lost even for the baby universe, but at least the more-severe problem of a Cauchy horizon can be avoided. In either case, a detailed analysis of possible consistent versions of the constraint algebra of loop quantum gravity could lead to a “no-heir theorem” if deterministic evolution through the high-density regime of black holes turns out to be impossible under all circumstances. Black holes would have no heirs since everything possessed by a collapsing star, including the information carried along, would be lost even if space-time did not end in a curvature singularity.
So far, loop quantum gravity is not understood sufficiently well for a clear model of black holes to emerge from it, but the mechanism analyzed here shows that, at the very least, scenarios obtained from generalizations of simple homogeneous models, such as the one postulated in Ashtekar and Bojowald [31], are likely to be misleading. Inhomogeneity can change the picture drastically, not just because there may be back-reaction on a homogeneous background but also, and often more surprisingly, because the non-trivial nature of symmetry algebras such as Equation (3) or Equation (A4) is much more restrictive for inhomogeneous models. (The right-hand side would just be identically zero with homogeneity, hiding the crucial coefficient and its sign which indicates signature change). Our considerations of black-hole models provide a concrete physical setting in which loop quantum gravity and its abstract anomaly problem can be put to a clear conceptual test.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported in part by NSF grant PHY-1307408. The author thanks Steve Giddings, Karl-Georg Schlesinger and Daniel Sudarsky for interesting suggestions about related work.
Footnotes
1. ^A region of signature change can be seen as a barrier to propagation and might resemble tunneling in some respects. However, there is a crucial difference between these two phenomena: In the barrier of a tunneling problem in quantum mechanics, there is a change of sign of a term in the relevant partial differential equation, given by the potential minus the total energy. This term plays the role of a source term in the partial differential equation and does not affect the highest derivative orders. In a region of signature change, by contrast, the coefficients of highest derivative orders are affected as for instance in Equation (5). Therefore, signature change has important implications for well-posed initial/boundary data and causal structures, which are absent in standard tunneling problems. Our discussion in the next section relies on these new features.
References
1. Thiemann T. Introduction to Modern Canonical Quantum General Relativity. Cambridge, UK: Cambridge University Press (2007).
3. Ashtekar A, Lewandowski J. Background independent quantum gravity: a status report. Class Quant Grav. (2004) 21:R53–152. doi: 10.1088/0264-9381/21/15/R01
4. Rovelli C, Smolin L. Loop space representation of quantum general relativity. Nucl Phys B (1990) 331:80–152. doi: 10.1016/0550-3213(90)90019-A
5. Bojowald M. Absence of a singularity in loop quantum cosmology. Phys Rev Lett. (2001) 86:5227–30. doi: 10.1103/PhysRevLett.86.5227
6. Date G, Hossain GM. Genericity of big bounce in isotropic loop quantum cosmology. Phys Rev Lett. (2005) 94:011302. doi: 10.1103/PhysRevLett.94.011302
7. Ashtekar A. Pawlowski T. Singh P. Quantum nature of the big bang. Phys Rev Lett. (2006) 96:141301. doi: 10.1103/PhysRevLett.96.141301
8. Ashtekar A, Bojowald M. Quantum geometry and the schwarzschild singularity. Class Quant Grav. (2006) 23:391–411. doi: 10.1088/0264-9381/23/2/008
9. Modesto L. Loop quantum black hole. Class Quant Grav. (2006) 23:5587–601. doi: 10.1088/0264-9381/23/18/006
10. Gambini R. Pullin J. Black holes in loop quantum gravity: the complete space-time. Phys Rev Lett. (2008) 101:161301. doi: 10.1103/PhysRevLett.101.161301
11. Gambini R. Pullin J. Loop quantization of the schwarzschild black hole. Phys Rev Lett. (2013) 110:211301. doi: 10.1103/PhysRevLett.110.211301
12. Rovelli C. Smolin L. The physical hamiltonian in nonperturbative quantum gravity. Phys Rev Lett. (1994) 72:446–9. doi: 10.1103/PhysRevLett.72.446
13. Thiemann T. Quantum spin dynamics (QSD). Class Quant Grav. (1998) 15:839–73. doi: 10.1088/0264-9381/15/4/011
14. Perez A, Pranzetti D. On the regularization of the constraints algebra of quantum gravity in 2 + 1 dimensions with non-vanishing cosmological constant. Class Quant Grav. (2010) 27:145009. doi: 10.1088/0264-9381/27/14/145009
15. Henderson A, Laddha A, Tomlin C. Constraint algebra in LQG reloaded : toy model of a U(1)3 gauge theory I. Phys Rev D (2013) 88:044028. doi: 10.1103/PhysRevD.88.044028
16. Henderson A, Laddha A, Tomlin C. Constraint algebra in LQG reloaded : toy model of an Abelian gauge theory - II spatial diffeomorphisms. Phys Rev D (2013) 88:044029. doi: 10.1103/PhysRevD.88.044029
17. Tomlin C, Varadarajan M. Towards an anomaly-free quantum dynamics for a weak coupling limit of euclidean gravity. Phys Rev D (2013) 87:044039. doi: 10.1103/PhysRevD.87.044039
19. Bojowald M, Hossain G, Kagan M, Shankaranarayanan S. Anomaly freedom in perturbative loop quantum gravity. Phys Rev D (2008) 78:063547. doi: 10.1103/PhysRevD.78.063547
20. Reyes JD. Spherically Symmetric Loop Quantum Gravity: Connections to 2-Dimensional Models and Applications to Gravitational Collapse. Ph.D. thesis, The Pennsylvania State University (2009).
21. Cailleteau T, Mielczarek J, Barrau A, Grain J. Anomaly-free scalar perturbations with holonomy corrections in loop quantum cosmology. Class Quant Grav. (2012) 29:095010. doi: 10.1088/0264-9381/29/9/095010
22. Cailleteau T, Linsefors L, Barrau A. Anomaly-free perturbations with inverse-volume and holonomy corrections in loop quantum cosmology. Class Quant Grav. (2014) 31:125011. doi: 10.1088/0264-9381/31/12/125011
23. Bojowald M, Paily GM, Reyes JD. Discreteness corrections and higher spatial derivatives in effective canonical quantum gravity. Phys Rev D (2014) 90:025025. doi: 10.1103/PhysRevD.90.025025
24. Bojowald M, Paily GM. Deformed general relativity and effective actions from loop quantum gravity. Phys Rev D (2012) 86:104018. doi: 10.1103/PhysRevD.86.104018
25. Mielczarek J. Signature change in loop quantum cosmology. Springer Proc Phys. (2014) 157:555. doi: 10.1007/978-3-319-06761-2/77
26. Bojowald M. Back to the beginning of quantum spacetime. Phys Today (2013) 66:35. doi: 10.1063/PT.3.1916
29. Barrau A, Bojowald M, Calcagni G, Grain J, Kagan M. Anomaly-free cosmological perturbations in effective canonical quantum gravity. arXiv:1404.1018.
30. Bojowald M. Fluctuation energies in quantum cosmology. Phys Rev D (2014) 89:124031. doi: 10.1103/PhysRevD.89.124031
31. Ashtekar A, Bojowald M. Black hole evaporation: a paradigm. Class Quant Grav. (2005) 22:3349–62. doi: 10.1088/0264-9381/22/16/014
32. Frolov VP, Vilkovisky GA. Spherically symmetric collapse in quantum gravity. Phys Lett B (1981) 106:307–13. doi: 10.1016/0370-2693(81)90542-6
33. Roman TA, Bergmann PG. Stellar collapse without singularities? Phys Rev D (1983) 28:1265–77. doi: 10.1103/PhysRevD.28.1265
34. Hayward SA. Formation and evaporation of non-singular black holes. Phys Rev Lett. (2006) 96:031103. doi: 10.1103/PhysRevLett.96.031103
35. Page DN. Information loss problem and a ‘black hole’ model with a closed apparent horizon. arXiv:1402.5446.
36. Giddings SB. Constraints on black hole remnants. Phys Rev D (1994) 49:947. doi: 10.1103/PhysRevD.49.947
37. Modak SK, Ortíz L, Peña I, Sudarsky D. Black holes: information loss but no paradox. arXiv:1406.4898.
38. Modak SK, Ortíz L, Peña I, Sudarsky D. Non-paradoxical loss of information in black hole evaporation. arXiv:1408.3062.
39. Perry MJ, Teo E. Nonsingularity of the exact two-dimensional string black hole. Phys Rev Lett. (1993) 70:2669–72. doi: 10.1103/PhysRevLett.70.2669
41. Bojowald M. Spherically symmetric quantum geometry: states and basic operators. Class Quant Grav. (2004) 21:3733–53. doi: 10.1088/0264-9381/21/15/008
42. Bojowald M, Reyes JD, Tibrewala R. Non-marginal LTB-like models with inverse triad corrections from loop quantum gravity. Phys Rev D (2009) 80:084002. doi: 10.1103/PhysRevD.80.084002
43. Bojowald M, Skirzewski A. Effective equations of motion for quantum systems. Rev Math Phys. (2006) 18:713–45. doi: 10.1142/S0129055X06002772
44. Bojowald M, Sandhöfer B, Skirzewski A, Tsobanjan A. Effective constraints for quantum systems. Rev. Math. Phys. (2009) 21:111–54. doi: 10.1142/S0129055X09003591
45. Bojowald M, Tsobanjan A. Effective constraints for relativistic quantum systems. Phys Rev D (2009) 80:125008. doi: 10.1103/PhysRevD.80.125008
Appendix A
Anomaly-free Constraint Algebras in Spherically Symmetric Models
This appendix recalls further details of anomaly-free constraints derived for spherically symmetric models of gravity. The details of variables and constraints are more contrived than in the toy model of Section 2, but the same key features are realized.
Spherically symmetric triad variables and their momenta can be parameterized by two pairs of fields (Kx, Ex) and (Kϕ, Eϕ) depending on a radial coordinate x, with Ex and Eϕ components of a densitized triad and Kx and Kϕ parameters for extrinsic curvature [41]. The Hamiltonian constraint with potential modifications from holonomy effects of loop quantum gravity can be parameterized as [20, 23, 42]
with the spin-connection component Γϕ = −(Ex)'/2Eϕ and two functions f1 and f2 of extrinsic curvature (or possibly the triad as well).
Classically, f1 = K2ϕ and f2 = KxKϕ, but this is not the only possibility of anomaly-free constraint algebras, together with the diffeomorphism constraint
It remains unknown how the linear dependence on Kx of the classical constraint can be modified in an anomaly-free way (which, as shown in Bojowald et al. [23], would likely involve higher spatial derivatives). But the dependence on Kϕ is not uniquely determined by anomaly-freedom alone. As shown by Reyes [20], if f2 = KxF2(Kϕ, Ex, Eϕ) with F2 related to the free function f1 by
there is a closed algebra
with
a function of the canonical variables. In the simple case in which F2 does not depend on Ex, we have
of the form (Equation 3).
The same relations of modification functions and deformed algebras can be derived at the operator level [18]. Therefore, consequences such as signature change are not restricted to effective derivations, but they are much easier to see in this way based on the mode equations implied. (More generally, signature change and other properties of quantum space-time structure are reflected abstractly in the structure functions of hypersurface-deformation algebras such as Equation (A4). Similar results have been derived for linear perturbations in cosmological models [22]; see [29] for a detailed comparison with spherically symmetric models.
Field equations generated by a modified constraint Equation (A1) (with Equation A2) could be used to find explicit solutions for the model pictured in Figure 1. However, details of solutions depend on a large set of quantization ambiguities summarized here in the free function f1(Kϕ). They would also be sensitive to additional corrections from quantum back-reaction of fluctuations and higher moments. The qualitative model of Figure 1, on the other hand, is robust: for any bounded f1(Kϕ), as implied by holonomy modifications, β is negative near a local maximum of curvature according to Equation (A6). Moreover, as shown in Bojowald and Brahma [27] and Appendix B, β is not subject to quantum back-reaction from moments.
Appendix B
Canonical Effective Theory and Constraints
Canonical effective methods [43] evaluate dynamical equations for expectation values and moments of a state based on algebraic properties of quantum operators. No specific Hilbert-space representation is assumed, implying key advantages especially for constrained systems where physical Hilbert spaces are often difficult to derive.
Starting with a *-algebra 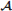 generated by some basic operators Âi, i = 1, …, n, a state is a positive linear functional 〈·〉:
generated by some basic operators Âi, i = 1, …, n, a state is a positive linear functional 〈·〉:  → ℂ. That is, 〈Â*Â〉 ≥ 0 for all  ∈
→ ℂ. That is, 〈Â*Â〉 ≥ 0 for all  ∈  . (The *-relation is abstractly defined, here for simplicity assuming Â*i = Âi for self-adjoint generators. In a Hilbert-space representation, the *-relation would be given by taking adjoint operators).
. (The *-relation is abstractly defined, here for simplicity assuming Â*i = Âi for self-adjoint generators. In a Hilbert-space representation, the *-relation would be given by taking adjoint operators).
Instead of working with entire states, we can paramaterize them by an infinite set of numbers given by the expectation values 〈Âi〉 of basic operators and the moments
with products taken in totally symmetric ordering so as to remove redundancies. (For a1 + ··· + an = 2, the resulting moments are fluctuations and covariances).
The set of basic expectation values and moments is turned into a quantum phase space by introducing a Poisson bracket by
for expectation values and extending it to products as in Equation (A7) using the Leibniz rule.
The expectation value of a combination of the basic operators (in totally symmetric ordering), such as a constraint ĈI = CI(Âi), can be written as a function on the quantum phase space by a formal Taylor expansion
(For polynomial CI, the sum is finite and an exact representation of the left-hand side).
Seen as functions of basic expectation values and moments as per Equation (A9), the condition that 〈ĈI〉 = 0 in a physical state (ĈIψ = 0 in a Hilbert-space representation) provides a constraint function on the quantum phase space [44, 45]. Moreover, any expression of the form 〈ĈI〉 = 0 must vanish in a physical state but generically provides a constraint independent of 〈ĈI〉 = 0 if p ≠ 1. Every constraint operator ĈI〉 generates an infinite set of independent constraints on the quantum phase space, which can be organized by the polynomial degree of restricted to polynomials in basic operators Âi. (One can easily see that an infinite set of constraints is necessary in order to restrict not just the basic expectation value Âi but also all the Ai-moments if the classical Ai is totally constrained by CI).
By definition of the Poisson bracket (Equation A8) on the quantum phase space, the quantum commutators of constraints ĈI, and therefore the whole constraint algebra, are faithfully mapped to corresponding Poisson-bracket relations of effective constraints obtained by applying Equation (A9). It is usually easier to compute Poisson brackets than commutators, especially in the presence of ordering and other ambiguities. Moreover, if one truncates Equation (A9) to finite orders of moments up to some maximum order, one can obtain order-by-order information on the constraint algebra in a semiclassical expansion. (For a semiclassical state, a moment of order a1 + ··· + an behaves as O(ħ(a1+···+an)/2), as can be checked explicitly for a Gaussian). Some key properties of constraint algebras are independent of the order, and therefore provide information suitable for strong quantum regimes. In this paper, the main result of Bojowald and Brahma [27] is important, which states that structure functions in constraint algebras of the form {CI, CJ} = fKIJ(Ai)CK with phase-space dependent fKIJ (such as the inverse metric hab in Equation A4) do not receive quantum corrections by moments.
As a brief justification of this result, one may note that the effective algebra reads
if KIJ quantize the classical structure functions. One could expect moment-dependent corrections of the structure functions if the right-hand side could be written with a factor of 〈KIJ〉 and f is non-linear in Ai. However, expanding as in Equation (A9) in such a way that all resulting terms are proportional to effective constraints 〈ĈI〉 (but not CI(〈Âi〉) which need not vanish for physical states), we have
with higher-order constraints 〈ÂjĈK〉 and so on, but no moment corrections in the coefficients fKIJ(〈Âi〉) of 〈ĈK〉. Also the higher-order constraints which appear due to the additional quantum degrees of freedom have coefficients such as ∂fKIJ(〈Âi〉)/∂〈Âj〉 independent of moments. In other words, quantum back-reaction is realized in effective constraint algebras not by moment corrections in structure functions, but by an extension of the algebra to quantum degrees of freedom. In spherically symmetric models, β in Equation (A6) is not modified by quantum back-reaction and holds to all orders in an ħ-expansion. Effects which depend only on the general form of constraint algebras as opposed to specific corrections of individual constraints are therefore reliable even in strong quantum regimes where moments may be large. Signature change and possible consequences presented in this paper are the main example.
Keywords: signature change, loop quantum gravity, black holes, information loss, effective theory
Citation: Bojowald M (2015) Information loss, made worse by quantum gravity? Front. Phys. 3:33. doi: 10.3389/fphy.2015.00033
Received: 25 January 2015; Accepted: 01 May 2015;
Published: 20 May 2015.
Edited by:
Martin Anthony Hendry, University of Glasgow, UKReviewed by:
Davood Momeni, L.N. Gumilyov Eurasian National University, KazakhstanJerzy Lewandowski, Uniwersytet Warszawswski, Poland
Copyright © 2015 Bojowald. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Martin Bojowald, Department of Physics, Institute for Gravitation and the Cosmos, The Pennsylvania State University, 104 Davey Lab, PMB 256, University Park, PA 16802, USA,Ym9qb3dhbGRAZ3Jhdml0eS5wc3UuZWR1
 Martin Bojowald
Martin Bojowald