- 1Department of Geophysics and Environmental Sciences, Munich University, Munich, Germany
- 2International Space Science Institute, Bern, Switzerland
- 3Space Research Institute, Austrian Academy of Sciences, Graz, Austria
We present an operator formalism for the recently developed kinetic information theory, construct Poisson brackets between the Liouville 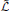 and information
and information 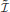 operators in μ space, proposing its quantum version. Making use of the universal quantum of time, the Planck time τp, a pseudo-energy-time uncertainty relation is constructed. It suggests that tiny amounts of information production may cause large variations in energy. The Hubble time τH sets an upper bound on information in the universe.
operators in μ space, proposing its quantum version. Making use of the universal quantum of time, the Planck time τp, a pseudo-energy-time uncertainty relation is constructed. It suggests that tiny amounts of information production may cause large variations in energy. The Hubble time τH sets an upper bound on information in the universe.
In Treumann and Baumjohann [1] we have put forward the principles of a physical kinetic theory of information starting from the idea that information is based in the dynamics of many particle N ≫ 1 systems encountered in physics as well as in other domains of nature and society. The basic equation governing the N-particle (Boltzmann-Shannon-) information  N(FN) = FN log FN turned out to be the exact N-particle Liouville equation in Gibbs' 6N-dimensional Γ phase space
N(FN) = FN log FN turned out to be the exact N-particle Liouville equation in Gibbs' 6N-dimensional Γ phase space
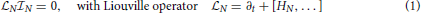
and HN the N-particle classical Hamiltonian. (In Equation 6 of that work a typo occurred: log N should be replaced with log FN, and the sentence following it can be dropped.) We also conjectured that it can be reduced by the methods of the BBGKY hierarchy construction to a one-particle N = 1 kinetic equation in Boltzmann's 6-dimensional (no index) μ phase space
N should be replaced with log FN, and the sentence following it can be dropped.) We also conjectured that it can be reduced by the methods of the BBGKY hierarchy construction to a one-particle N = 1 kinetic equation in Boltzmann's 6-dimensional (no index) μ phase space
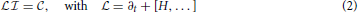
Its non-vanishing right-hand side 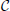 ≠ 0, an information-production term, we related to the Kolmogorov [2] entropy rate
≠ 0, an information-production term, we related to the Kolmogorov [2] entropy rate 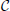 = K(
= K( ), with
), with  ≡
≡  1.
1.
Effectively, the classical Liouville operator 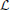 = d/dt ≡ { ˙ } is a total, not a partial time derivative in μ-space yielding
= d/dt ≡ { ˙ } is a total, not a partial time derivative in μ-space yielding

Preference for use of the total time derivative is justified by the equivalence to kinetic theory. For small information production rates, one has K( ) ≈ K0
) ≈ K0 , and the μ-space Liouville equation yields the exponentially growing solution
, and the μ-space Liouville equation yields the exponentially growing solution  (t) ≈
(t) ≈  (0) exp[K0t], where 0 < K0 = ∑iλi is the total sum of all positive Lyapunov exponents λi ≥ 0 of the parts of which the system is constituted. Generally, any exponential growth of
(0) exp[K0t], where 0 < K0 = ∑iλi is the total sum of all positive Lyapunov exponents λi ≥ 0 of the parts of which the system is constituted. Generally, any exponential growth of  (t) with time t, as inferred in low-dimensional systems, holds only for this linear dependence of K on information. Saturation of information at a value
(t) with time t, as inferred in low-dimensional systems, holds only for this linear dependence of K on information. Saturation of information at a value  sat ≈ −2K0/K(2) > 0 becomes possible for negative second derivative K(2) = d2K/d
sat ≈ −2K0/K(2) > 0 becomes possible for negative second derivative K(2) = d2K/d 2 < 0, when including the quadratic term in the expansion of K(
2 < 0, when including the quadratic term in the expansion of K( ) ≈ K0
) ≈ K0 + K(2)
+ K(2) 2 + ….
2 + ….
We tentatively interpret 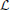 and
and  as operators
as operators 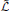 ,
, 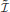 acting to the right on some phase space density function F(p, q). Formally applying the commutator [
acting to the right on some phase space density function F(p, q). Formally applying the commutator [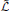 ,
, 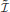 ] to the phase space density function, keeping in mind that we are dealing with a total time derivative, yields
] to the phase space density function, keeping in mind that we are dealing with a total time derivative, yields
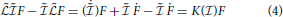
and hence

with the right-hand side as usual understood as multiplied by a unit operator. The Kolmogorov entropy rate appears as the commutator of the Liouville and information operators in μ-phase space, thus describing the kinetic evolution of the Boltzmann-Shannon information operator together with the phase space density.
Applying the same argument to the N-particle Gibbs' Γ-phase space, we have 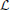 N
N N = 0. Hence, in Γ space the commutator of the Liouville and information operators vanishes identically:
N = 0. Hence, in Γ space the commutator of the Liouville and information operators vanishes identically:

due to conservation of Shannon information in Γ-space. Other definitions of information than Shannon's, introducing a non-vanishing right hand side in Γ-space, a N-particle Kolmogorov entropy rate KN, will result in non-vanishing commutators.
There is an important difference between the Liouville and information operators. The former is a differential operator. The latter, instead, refers to the sum over all states of the system; it is thus a (properly normalised) integral operator
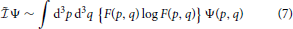
acting on any function Ψ(p, q) that depends on the μ-phase space coordinates.
Wishfully the above commutator should serve as starting point of a quantum theory of information. However, K( ) is not a fixed constant; it is a variable that depends upon the information itself and thus upon the full dynamics in μ space. One way of generalisation to a quantum version may be via defining
) is not a fixed constant; it is a variable that depends upon the information itself and thus upon the full dynamics in μ space. One way of generalisation to a quantum version may be via defining

where, with 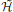 q the quantum Hamiltonian, we introduced von Neumann's quantum Liouville operator
q the quantum Hamiltonian, we introduced von Neumann's quantum Liouville operator 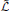 q = ħ ∂t + i[
q = ħ ∂t + i[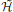 q, …] which acts on the phase-space density matrix . Here
q, …] which acts on the phase-space density matrix . Here 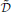 ≡
≡ 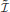 K−1, obtained by multiplication with the inverse scalar K−1 from the right, plays the role of a “duration operator” (or time operator), with time not the life-time of a particle, however, as in ordinary quantum mechanics. This expression applies to the quantum evolution of information or, otherwise, duration, the “dynamics of time.” Since information cannot be erased, duration cannot be erased either. It can only accumulate increasing time elapsed. K(
K−1, obtained by multiplication with the inverse scalar K−1 from the right, plays the role of a “duration operator” (or time operator), with time not the life-time of a particle, however, as in ordinary quantum mechanics. This expression applies to the quantum evolution of information or, otherwise, duration, the “dynamics of time.” Since information cannot be erased, duration cannot be erased either. It can only accumulate increasing time elapsed. K( ) ≡ K(p, q) is a function of (p, q); thus the operator
) ≡ K(p, q) is a function of (p, q); thus the operator 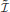 in the duration operator
in the duration operator 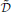 =
= 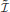 K−1 acts on the product K−1. The above commutator equation should give rise to an integro-differential equation instead of a partial differential equation.
K−1 acts on the product K−1. The above commutator equation should give rise to an integro-differential equation instead of a partial differential equation.
Returning to 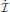 = K(
= K( ), again referring to
), again referring to 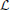 as a total time derivative and writing it as Δ
as a total time derivative and writing it as Δ = KΔt, with Δt = 2π/Δω = 2πħ/Δϵ, yields Δ
= KΔt, with Δt = 2π/Δω = 2πħ/Δϵ, yields Δ · K−1Δϵ = 2πħ. The meaning of energy ϵ in this expression remains unclear thus preventing calling it an energy-information uncertainty relation. On the other hand, (arbitrarily) introducing the universal quantum of time, the Planck time τP = as the shortest (physically motivated) time element, yields
· K−1Δϵ = 2πħ. The meaning of energy ϵ in this expression remains unclear thus preventing calling it an energy-information uncertainty relation. On the other hand, (arbitrarily) introducing the universal quantum of time, the Planck time τP = as the shortest (physically motivated) time element, yields
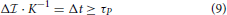
Re-introducing energy, this expression can be written as
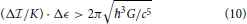
which, formally, is an information-energy uncertainty relation with right hand side a universal constant though again undefined meaning of energy. Physical motivation for the use of the Planck time is based on τP being the natural limit of validity of quantum electrodynamics where it merges into quantum gravity. So far the above commutator does not contain any gravity. The appearance of the gravitational constant G in the last expression thus suggests that a proper quantum theory of information (respectively time/duration) cannot be expected prior to a consistent formulation of quantum gravity.
The Planck time, in our choice, imposes an absolute lower bound on the ratio of information change and Kolmogorov entropy rate. In this interpretation, “physical time in information production” can be “generated at the smallest” in τP quanta only. We repeat [1] that K = 0 implies Δ = 0, no production of information (nor time, in this interpretation), while K → ∞ is non-physical.
= 0, no production of information (nor time, in this interpretation), while K → ∞ is non-physical.
In order to give the above assertion another twist, one may square the second last expression to obtain
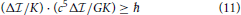
Here, with explicit expression for the energy differential Δϵ = (c5/G)(Δ /K) and Δt = Δ
/K) and Δt = Δ /K, the energy-time uncertainty relation ΔϵΔt ≥ ħ is formally reproduced. However, since both its terms on the left contain the ratio Δ
/K, the energy-time uncertainty relation ΔϵΔt ≥ ħ is formally reproduced. However, since both its terms on the left contain the ratio Δ /K as the sole variable, this is not a genuine uncertainty relation. This version of the former relation suggests that, due to the huge factor c5/G ≈ 1052 J s−1 in the energy factor Δϵ, small information changes Δ
/K as the sole variable, this is not a genuine uncertainty relation. This version of the former relation suggests that, due to the huge factor c5/G ≈ 1052 J s−1 in the energy factor Δϵ, small information changes Δ /K may imply large energy variations—an interesting notion in view of the enormous practical effects any dispersion of information is observed to cause.
/K may imply large energy variations—an interesting notion in view of the enormous practical effects any dispersion of information is observed to cause.
Duration is also strictly bound from above by the Hubble time τH ≥ Δ /K(
/K( ), which in the universe with accelerated expansion is itself a function of time. For fixed (average universal) production rate KU(
), which in the universe with accelerated expansion is itself a function of time. For fixed (average universal) production rate KU( ) this bound limits the total amount of information production in the visible universe. Knowledge of the total universal entropy Δ
) this bound limits the total amount of information production in the visible universe. Knowledge of the total universal entropy Δ U provides an estimate of the (average) universal entropy/information production rate (assuming that no information is lost to higher dimensional space—by generation of Klein-Kaluza particles in the bulk of D-brane cosmologies, for instance). Assuming, in particular, exponential growth of the universal entropy throughout its entire evolution (implying KU ~ KU0
U provides an estimate of the (average) universal entropy/information production rate (assuming that no information is lost to higher dimensional space—by generation of Klein-Kaluza particles in the bulk of D-brane cosmologies, for instance). Assuming, in particular, exponential growth of the universal entropy throughout its entire evolution (implying KU ~ KU0 U) yields that KU0 ≳ τ−1Hlog{
U) yields that KU0 ≳ τ−1Hlog{ U(τH)/
U(τH)/ U0}, with index 0 referring to the beginning.
U0}, with index 0 referring to the beginning.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Keywords: information, Liouville theory, Kinetic theory, dynamics of information, Kolmogorov entropy PACS: 45.70.−n, 51.30.+i, 95.30.Tg, 52.25.Kn
Citation: Treumann RA and Baumjohann W (2015) Information kinetics—an extension. Front. Phys. 3:34. doi: 10.3389/fphy.2015.00034
Received: 29 March 2015; Accepted: 01 May 2015;
Published: 19 May 2015.
Edited by:
Ioannis A. Daglis, National and Kapodistrian University of Athens, GreeceReviewed by:
Dimitris Vassiliadis, West Virginia University, USAAnastasios Anastasiadis, National Observatory of Athens, Greece
Copyright © 2015 Treumann and Baumjohann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rudolf A. Treumann, International Space Science Institute, Bern, Switzerland,cnVkb2xmLnRyZXVtYW5uQGdlb3BoeXNpay51bmktbXVlbmNoZW4uZGU=
 Rudolf A. Treumann
Rudolf A. Treumann Wolfgang Baumjohann
Wolfgang Baumjohann