- 1Department of Physics and Astronomy, Northwestern University, Evanston, IL, USA
- 2Department of Physics and Astronomy, Center for Correlated Electron Systems, Institute for Basic Science, Seoul National University, Seoul, Korea
Recent theories of Sr2RuO4 based on the interplay of strong interactions, spin-orbit coupling and multi-band anisotropy predict chiral or helical ground states with strong anisotropy of the pairing states, with deep minima in the excitation gap, as well as strong phase anisotropy for the chiral ground state. We develop time-dependent mean field theory to calculate the Bosonic spectrum for the class of 2D chiral superconductors spanning 3He-A to chiral superconductors with strong anisotropy. Chiral superconductors support a pair of massive Bosonic excitations of the time-reversed pairs labeled by their parity under charge conjugation. These modes are degenerate for 2D 3He-A. Crystal field anisotropy lifts the degeneracy. Strong anisotropy also leads to low-lying Fermions, and thus to channels for the decay of the Bosonic modes. Selection rules and phase space considerations lead to large asymmetries in the lifetimes and hybridization of the Bosonic modes with the continuum of un-bound Fermion pairs. We also highlight results for the excitation of the Bosonic modes by microwave radiation that provide clear signatures of the Bosonic modes of an anisotropic chiral ground state.
Introduction
Superfluid 3He and unconventional superconductors share a common and fundamental property that the ground state breaks one or more symmetries of the normal Fermionic vacuum in conjunction with the usual U(1) gauge symmetry associated with BCS condensation. In the case of Sr2RuO4 the connection with superfluid 3He may be stronger. The theoretical proposal for a spin-triplet, p-wave ground state in Sr2RuO4 was motivated by similarities between Sr2RuO4 and liquid 3He, particularly the existence of exchange enhanced paramagnetism in a strongly correlated Fermi liquid [1]. In liquid 3He long-lived ferromagnetic spin fluctuations (“paramagnons”) are believed to be the mechanism responsible for the BCS pairing instability to a spin-triplet, p-wave ground state [2, 3]. The Balian-Werthamer (BW) state [4], identified as the B-phase, with total angular momentum J = 0 fully gaps the 3D Fermi surface, and as a result minimizes the free energy in the weak-coupling limit. The BW state is time-reversal invariant, but spontaneously breaks relative spin-orbit rotation symmetry. However, spin-triplet correlations, which differentiate between the Anderson-Morel (AM) state and BW states, feedback to modify the spin-fluctuation exchange interaction, leading to stabilization of the AM state at high pressures [5, 6]. This is the chiral A-phase which breaks time-reversal (T) symmetry and reflection symmetry in any plane containing the chiral axis (P2), but preserves T × P2 (chiral symmetry).
Similarly, Rice and Sigrist argued that for Sr2RuO4, which is a layered perovskite belonging to the D4h, point group, the likely pairing state, in analogy with 3He, would be the planar state, the 2D analog of the BW state. In weak-coupling theory, and neglecting spin-orbit coupling, the planar state, which belongs to the one-dimensional A1u representation of D4h, is degenerate with the 2D chiral AM state, which belongs to the 2D E1u representation. Thus, if spin-fluctuation exchange is also the mechanism for pairing in Sr2RuO4, we expect the strong-coupling feedback effect will stabilize the chiral AM state. However, in addition to the near two-dimensionality of the Fermi surface of Sr2RuO4, incommensurate spin-density-wave (SDW) fluctuations connected with the quasi-one-dimensional α and β bands co-exist with ferromagnetic fluctuations at lower temperatures [7]. Spin-orbit coupling, and the possibility of pairing on multiple Fermi surface sheets likely play important roles in determining the pairing symmetry class, ground state order parameter [8–12] as well as the Bosonic excitation spectrum in Sr2RuO4.
In what follows we develop a field theory for the Bosonic modes based on the Ginzburg-Landau theory (TDGL) for spin-triplet, odd-parity pairing that allows one to compare predictions for 3He and Sr2RuO4, and to examine the roles of crystalline anisotropy and strong correlation effects on the Bosonic modes. The Bosonic modes are excitations of a condensate of Cooper pairs for which the parent state is the Fermionic vacuum. Thus, although the TDGL field theory provides insight into the Bosonic excitation spectrum, it misses key features of a more complete theory of the low-lying excitations of the BCS pair condensate. Notably, (i) polarization effects of the underlying Fermionic vacuum on the excitation energies (masses and dispersion) of the Bosonic modes, (ii) finite lifetimes of the Bosonic excitations due to coupling to the Fermionic continuum and (iii) selection rules and matrix elements for the coupling of the Bosonic modes to the electromagnetic (EM) field. Key predictions of a microscopic theory of interacting Fermionic and Bosonics modes are summarized, including microwave spectroscopic signatures of the Bosonic excitation spectrum.
Order Parameter
The mean-field order parameter for spin-triplet Cooper pairs, Δαβ(p) = dμ(p)(iσμσy)αβ, where α, β label the projections of fermion spins of the Cooper pair, {iσμσy | μ = x′, y′, z′} is the spin-triplet basis of 2 × 2 matrices, is expressed as
where dμ(p) is a vector under rotations in spin space, and is a function of the vector basis of p-wave orbital basis functions, (x, y, z), for bulk 3He. Thus, the amplitudes Aμi provide a bi-vector representation of SO(3)S × SO(3)L. For quasi-two-dimensional Sr2RuO4, the orbital basis, (Yx(p), Yy(p)), provides a 2D vector representation in which Yx,y(p) transforms as px,y under the point group D4h. These basis functions reflect anisotropic pairing on the Fermi surface.
The chiral AM state is the stable equilibrium phase in a narrow temperature window TAB ≤ T < Tc of bulk 3He at pressures P ≥ Pc = 21 bar. However, if we confine 3He as a thin film or within a thin cavity of thickness D ≤ Dc ≈ 1 μm the quasi-2D A-phase with is the ground state for all pressures and temperatures [13]. We refer to this order parameter as the “Anderson-Morel (AM) state,” the “chiral state” or the “A-phase order parameter.”
However, in the weak-coupling limit the chiral AM phase is degenerate with the 2D planar phase, . In the context of Sr2RuO4 the 2D planar state is referred to as the “helical state” [11]. The degeneracy between the chiral and helical ground states is lifted by strong-coupling corrections to weak-coupling theory, or spin-orbit coupling. For 3He strong-coupling effects dominate the nuclear spin-orbit coupling, with the spin-triplet feedback effect on the ferromagnetic spin-fluctuation exchange interaction favoring the chiral AM state over the helical state. Recent NMR experiments on 3He confined in thin slabs imply that the chiral AM state is stable relative to the helical state down to P ≈ 0 bar [14]. If superconductivity in Sr2RuO4 is also driven by ferromagnetic spin-fluctuations then we expect the chiral phase to be favored. However, recent theoretical calculations based on RG analysis that includes spin-orbit coupling within a multi-band pairing model also find both helical and chiral phases, depending upon the interaction parameters defining the lattice pairing Hamiltonian [11]. For the chiral state the pairing gap, |Δ(p)| ≡ |(p)|, is found to be strongly anisotropic on all three bands with deep gap minima over a wide range of material parameters [11]. Thus, the main observations are: (i) there are competing low energy scales that determine the ground state for Sr2RuO4, (ii) it is not currently settled whether or not Sr2RuO4 is a chiral superconductor [15], or even if the order parameter for Sr2RuO4 belongs to a two-dimensional representation [16], and (iii) whatever the ground state—e.g., chiral or helical—low-energy Bosonic excitations may provide unique signatures of the ground state based on their symmetry and selection rules.
Ginzburg-Landau Theory
Consider the Ginzburg-Landau theory for the class of equal-spin pairing (ESP) states of confined superfluid 3He in 2D. A simple generalization also describes spin-triplet superconductivity on a 2D cylindrical Fermi surface, i.e., pairing on the γ band in Sr2RuO4 within the E1u representation of D4h. The general form of the order parameter is then given by
where {Yi(p)|i = x, y} are basis functions for the 2D irreducible representation, E1u, of D4h, and A = Ax + Ayŷ is a complex vector describing pairing in this generalized “p-wave” orbital basis. In what follows we consider the class of ESP states in which the direction along which the Cooper pairs have zero spin projection is fixed, either as a spontaneously broken symmetry direction, or by spin-orbit coupling. The general form of the GL free energy functional is constructed from invariants of the maximal symmetry group from products of Ai and A*i through 4th order [17],
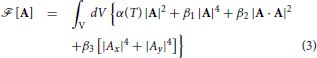
where α(T) determines the onset of pairing in the E1u representation, i.e., α(Tc) ≡ 0, and thus, α(T) ≈ α′(T − Tc). The fourth order coefficients, β1,2,3, determine the magnitude of the condensation energy density and the relative stability of phases belonging to the E1u symmetry class. The first three terms in Equation (3) are invariant under the larger group, i.e., U(1) × SO(2)Lz × ZOrbit2 × P × T, while the last term is an additional invariant that is allowed in the case of Sr2RuO4 by the lower symmetry, U(1) × D4h.
It is convenient to express the bulk order parameter in terms of an amplitude and a normalized complex vector, A = Δ a, with |a|2 ≡ a · a* = 1. The normalized order parameter is then parametrized by two angles, The resulting GL functional is then
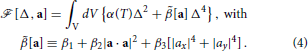
For T < Tc, minimization with respect to Δ leads to Δ2min = − α(T)/2[a], and a condensation energy given by 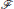 [a] = −α(T)2/4[a], with [a] > 0 for global stability. The ground state is then determined by the normalized order parameter that minimizes [a] = β1 + β2(1 − sin2 φ sin2(2ϑ)) + β3(1 − sin2(2ϑ)). In the case of 2D 3He we have β3 = 0, in which case there are two possible ESP ground states; for β1 > 0 and β2 > 0 the chiral AM state which breaks time-reversal and 2D parity is preferred. There are two degenerate chiral ground states which are time-reversed partners of one another, . However, for −β1 < β2 < 0 the in-plane polar state with a = cos ϑ + sin ϑŷ, for, ϑ ∈ [0, 2π] minimizes the GL functional. This phase has a continuous degeneracy with respect to orientation of polar axis in the x − y plane. Tetragonal anisotropy lifts the continuous degeneracy of the in-plane polar state. For β2 < 0 and β3 > 0 the polar state aligns along a [110] direction, e.g., . However, for the polar state aligns along a [100] direction, e.g., a = . The phase diagram is shown in Figure 1. Note that the weak-coupling prediction for the β parameters favor a chiral ground state independent of the measure of anisotropy, i.e., β3. Furthermore, substantial corrections to weak-coupling theory are required to stabilize an in-plane polar state. In fact the helical state, which belongs to a different irreducible representation (A1u), is a more likely competitor to the chiral state since these two states are degenerate in the weak-coupling limit without spin-orbit coupling. In addition, AFM spin-fluctuations can lead to attractive, sub-dominant, pairing interactions in even parity, “d-wave,” channels. Here we consider fluctuations within the E1u representation, and neglect possible low-lying fluctuations of the “helical” phase (A1u) or even-parity, B1g or B2g, “d-wave” states.
[a] = −α(T)2/4[a], with [a] > 0 for global stability. The ground state is then determined by the normalized order parameter that minimizes [a] = β1 + β2(1 − sin2 φ sin2(2ϑ)) + β3(1 − sin2(2ϑ)). In the case of 2D 3He we have β3 = 0, in which case there are two possible ESP ground states; for β1 > 0 and β2 > 0 the chiral AM state which breaks time-reversal and 2D parity is preferred. There are two degenerate chiral ground states which are time-reversed partners of one another, . However, for −β1 < β2 < 0 the in-plane polar state with a = cos ϑ + sin ϑŷ, for, ϑ ∈ [0, 2π] minimizes the GL functional. This phase has a continuous degeneracy with respect to orientation of polar axis in the x − y plane. Tetragonal anisotropy lifts the continuous degeneracy of the in-plane polar state. For β2 < 0 and β3 > 0 the polar state aligns along a [110] direction, e.g., . However, for the polar state aligns along a [100] direction, e.g., a = . The phase diagram is shown in Figure 1. Note that the weak-coupling prediction for the β parameters favor a chiral ground state independent of the measure of anisotropy, i.e., β3. Furthermore, substantial corrections to weak-coupling theory are required to stabilize an in-plane polar state. In fact the helical state, which belongs to a different irreducible representation (A1u), is a more likely competitor to the chiral state since these two states are degenerate in the weak-coupling limit without spin-orbit coupling. In addition, AFM spin-fluctuations can lead to attractive, sub-dominant, pairing interactions in even parity, “d-wave,” channels. Here we consider fluctuations within the E1u representation, and neglect possible low-lying fluctuations of the “helical” phase (A1u) or even-parity, B1g or B2g, “d-wave” states.
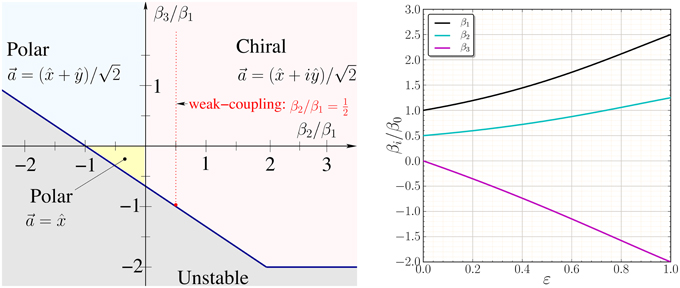
Figure 1. Left: Ginzburg-Landau phase diagram for E1u pairing. The weak-coupling BCS theory predicts the β parameters lie on the dotted red line depending on the degree of anisotropy of the E1u basis functions, implying the chiral AM state is stable. Right: Anisotropy of the GL β parameters in the weak-coupling limit based on the anisotropic pairing model defined in Equation (14) as a function of the anisotropy parameter ϵ calculated from Equations (11–13).
Time Dependent GL Theory—Fluctuations
Consider the Bosonic excitations of the chiral AM ground state with . Space-time fluctuations of the E1u order parameter, 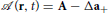 , are represented by two complex amplitudes,
, are represented by two complex amplitudes,
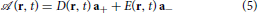
There are two classes of excitations—modes with chirality Lz = +1 represented by the field D(r, t) and modes with the time-reversed chirality, Lz = −1, represented by the field E(r, t)—and altogether four orbital collective modes within the E1u representation. We construct an effective Lagrangian by expanding the GL free energy functional about the ground state. Time-dependent fluctuations introduce an additional invariant, 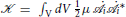 , where μ is the effective inertia of the Cooper pair fluctuations and
, where μ is the effective inertia of the Cooper pair fluctuations and 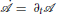 . The effective potential is obtained by expanding the GL functional to 2nd order in the fluctuations
. The effective potential is obtained by expanding the GL functional to 2nd order in the fluctuations 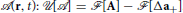 . The Lagrangian,
. The Lagrangian, 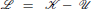 , takes a simplified form when expressed in amplitudes for the normal mode: D± = D±D* and E± = E±E*,
, takes a simplified form when expressed in amplitudes for the normal mode: D± = D±D* and E± = E±E*,
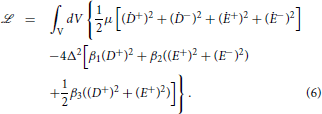
The Euler-Lagrange equations reduce to four uncoupled mode equations,
where MLz C is the excitation gap (“mass”) of the Bosonic mode with quantum numbers Lz, C, and C is the parity under charge conjugation (particle-hole) symmetry [18, 19]. The amplitude D−, which is a cyclic coordinate in the Lagrangian, is a Goldstone mode associated with the broken U(1) gauge symmetry. Indeed for small amplitude and phase fluctuations of the chiral ground state, A(r, t) = Δ(r, t) eiθ(r, t) a+ ≈ Δa+ (1 + δ(r, t) + iθ(r, t)), we identify D− = iΔθ(r, t) with the phase fluctuation and D+ = Δδ(r, t) with the amplitude fluctuation. The amplitude mode of the ground-state order parameter is the Higgs mode for the chiral ground state. In particular, D+ corresponds to an excitation with the same quantum numbers (Lz = +1 and C = +1) as those of the ground state. In the weak-coupling limit the mass of the amplitude mode is determined the pair-breaking energy for dissociation into two Fermions, i.e., M++ = 2mF where mF = Δ is the gap (mass) in the Fermionic spectrum of the broken symmetry phase [20, 21]. Furthermore, since the amplitude mode has the same quantum numbers as the condensate, the mass of the amplitude mode is unshifted, relative to that of two dissociated Fermions, by polarization effects of the underlying Fermionic vacuum. We use this to fix the inertia term in the effective Lagrangian as μ = (2β1 + β3), and thus the mass scale for all the Bosonic modes of the effective Lagrangian.
Collective modes of the Cooper pair condensate with quantum numbers distinct from those of the ground state were discussed soon after the formulation of BCS theory by Anderson [22], Bogoliubov et al. [23], Tsuneto [24], Vaks et al. [25], Bardasis and Schrieffer [26], and Vdovin [27]. Generalizations of the amplitude mode were discovered theoretically in the context of superfluid 3He by Maki [28], Wölfle [29], Sauls and Serene [30]. The observation of these Bosonic modes using acoustic spectroscopy played an important role in identifying the symmetries of the superfluid phases of 3He [31, 32]. In this context the collective modes for E1u pairing symmetry with the time-reversed chirality (Lz = −1), both of which are massive, correspond to the “clapping modes” of superfluid 3He-A in the weak-coupling limit of an isotropic 2D chiral AM state (See Table III in Wölfle [29]). In particular, the masses of the E± modes in the effective Lagrangian are given by
Note that in the weak-coupling limit () for an isotropic (β3 = 0) 2D chiral ground state the time-reversed modes are degenerate, and lie well below the Fermionic continuum edge at 2Δ. However, the degeneracy of the E± modes is lifted by tetragonal anisotropy of the Fermi surface and pairing basis functions, which leads to β3 ≠ 0. The crystal field splitting of the E± modes is shown in Figure 2. In the left panel the splitting of the modes in the weak-coupling limit () is plotted as a function of β3/β1. The soft E+ mode, i.e., M− + → 0 for β3 → −2β2, is the dynamical signature of the boundary of the unstable region of the GL phase diagram shown in Figure 1.
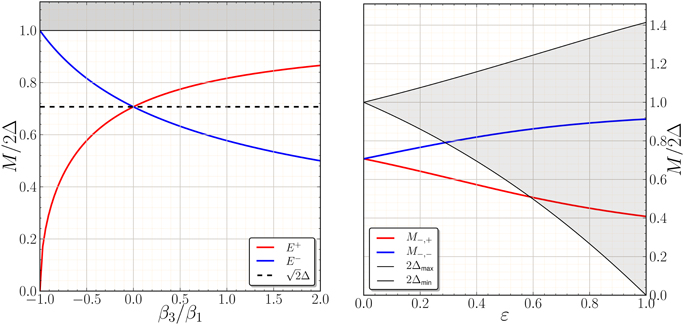
Figure 2. Left: Masses of the E± modes vs. the GL anisotropy parameter, β3/β1, in the weak-coupling limit, . Right: E± masses based on the weak-coupling β parameters defined in Equations (11–13) for the anisotropic E1u basis functions defined in Equation (14). The maximum and minimum of the pair-breaking edge, 2|Δ(p)|, bound the gray shaded region.
Weak-Coupling GL Theory for Anisotropic E1u Pairing
For quantitative predictions of the effects of anisotropy of the Fermi surface and pairing interaction on the collective mode spectrum we require the angle-resolved density of states on the Fermi surface, n(p), and the anisotropy of the pairing basis functions, {Yx(p), Yy(p)}, that define the E1u orbital order parameter in momentum space, Δ(p) = Ax Yx(p) + Ay Yy(p). For a single-band Fermi surface the GL functional for ESP states in the weak-coupling limit can be expressed in terms of Fermi-surface averages of the mean-field order parameter defined on the Fermi surface [33, 34],
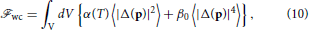
where α(T) = ln(T/Tc), β0 = 7ζ(3)Nf/(4πTc)2, Nf is the single-spin density of states at the Fermi energy, and 〈…〉 ≡ ∫ d2p n(p)(…) is the angle-average over the Fermi surface. The pairing basis functions are normalized with respect to the anisotropic Fermi surface, 〈Y*i(p)Yj(p)〉 = δij for i, j ∈ {x, y}. Evaluating the angular averages in Equation (10) gives the following results for the GL material parameters in the weak-coupling limit,
These results are obtained by using the transformation properties of the basis functions under the group operations of D4h: specifically, . A key result is that the ratio of GL parameters, , is independent of anisotropy [17]. Thus, the chiral AM ground state with broken time-reversal symmetry is favored independent of the anisotropy of the E1u basis functions and Fermi surface anisotropy in the weak-coupling limit.
Cylindrical Symmetry
For cylindrical symmetry, e.g., a Fermi disk for 2D 3He-A, we have and d2p = pf dϕ. The normalized p-wave basis functions are then and , where ϕ is the azimuthal angle defining the unit vector normal to the edge of the Fermi disk. Thus, for the chiral ground state the excitation gap (Fermion mass), , is also isotropic. These basis functions also lead to the following results for the E1u GL β parameters, , and β3 = 0, the latter as expected for an isotropic Fermi surface with pure p-wave basis functions. These values give the weak-coupling, isotropic results for the E± modes reported in Table 1, i.e., the degenerate “clapping” modes of 2D 3He-A with . Note that the Nambu-Sum rule, ∑CM2Lz,C = (2Δ)2, is obeyed for both classes (Lz = ± 1) of Bosonic modes for 2D 3He-A in the weak-coupling limit [35].
Phase Anisotropy
Recent calculations of pairing instabilities for odd-parity pairing in Sr2RuO4 starting from lattice models based d-band electrons and holes with on-site and near neighbor Hubbard interactions and spin-orbit coupling lead to a helical or chiral ground state, but with strong anisotropy. For the chiral state obtained from pairing on hybridized, quasi-1D α and β bands [9], the phase of Δ(p) changes rapidly upon crossing the [110] planes, leading to a low-energy collective mode [36]. To illustrate the effects of strong phase anisotropy on the collective modes consider an extreme limit in which the E1u basis functions are constant within each quadrant of the Fermi surface, but change sign abruptly upon crossing any of the [110] planes, i.e., Yx = sgn(x − y) and Yy = sgn(y + x). These basis functions have constant amplitude, but are discontinuous in phase (±π) across the [110] planes. They give the following results for the E1u GL β parameters, β1 = 2β0, β2 = β0, and β3 = −2β0. For the E± modes this leads M− − → 2Δ and M− + → 0. The soft E+ mode is a dynamical signature of the approach to the unstable region of the GL phase diagram for β3→ −2β2 as shown in Figure 1.
Amplitude Anisotropy
Multi-band models leading to a chiral superconducting state also exhibit strong anisotropy of the amplitude of the order parameter, in particular, an excitation gap |Δ(p)| with nodal, or near nodal, directions on the Fermi surface [10, 11]. Strong anisotropy of the Cooper pair amplitudes in momentum space leads to physical properties that are quite distinct from the predictions based on cylindrical symmetry of the γ band of Sr2RuO4, including the splitting of the E± modes, and in some cases a low-energy collective mode. To illustrate the effects of anisotropy of the pairing interaction on the collective mode spectrum, as well as signatures of a chiral ground state with strong anisotropy, we consider the following model for the anisotropic E1u basis functions defined on the γ band, or hybridized α and β bands,
Tetragonal anisotropy is parametrized by the function I(p), which is invariant under D4h. The E1u basis functions are normalized, , and in the limit ε → 1 exhibit strong anisotropy with a minimum excitation gap, Δmin ∝ (1 − ε) → 0 as ε→ 1 in the [100] directions. The anisotropy of the excitation gap for the chiral ground state is shown in the left panel of Figure 3, while the corresponding β parameters calculated from Equations (11–13) are shown in the right panel of Figure 1. The amplitude anisotropy has no effect on the ratio, β2/β1, that determines the stability of the chiral state, but has a strong effect on the ratio, β3/β1, that determines the effective potential for the E± modes, and thus the splitting of the these modes by anisotropy, as shown in the right panel of Figure 2. Note that in addition to the splitting of the E± modes the masses of the E± modes cross the continuum edge (2Δmin) of unbound Fermion pairs. Thus, we expect the E± modes to become resonances with finite lifetimes for sufficiently strong gap anisotropy. However, the theory for the lifetimes of the E± modes is outside the TDGL Lagrangian for the Bosonic spectrum, and requires a microscopic theory of the correlated Fermionic vacuum, including the mechanism and effects of spontaneous symmetry breaking, and most importantly the interaction and coupling between the Fermionic and Bosonic excitations of the chiral superconducting phase.
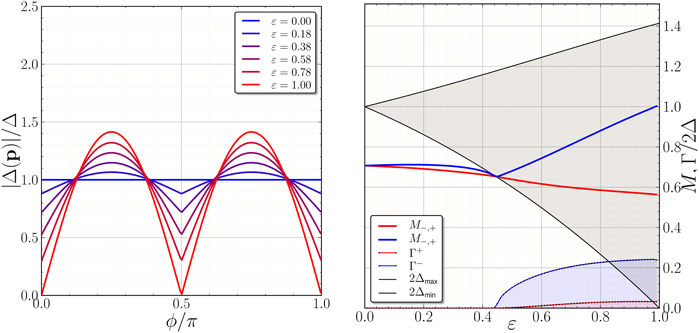
Figure 3. Left: Anisotropy of the excitation gap, |Δ(p)|, based on Equations (14), exhibiting deep gap minima along [110] directions in the limit ϵ → 1. Right: Masses and Linewidths of the E± modes resulting from gap anisotropy calculated from the Equations (20) and (21) at T = 0.
Beyond TDGL
A microscopic formulation of the electrodynamics of the excitations of p-wave superconductors, including the coupling of Bosonic modes to a transverse (EM) electromagnetic field, is developed in Hirschfeld et al. [37] and Yip and Sauls [38] for 3D isotropic Fermi systems with p-wave, spin-triplet pairing. For a 3D chiral p-wave superconductor in the clean limit the coupled set of linearized dynamical equations for the Bosonic mode spectra, including the reaction of the Fermionic vacuum to the excitation of Bosonic modes, as well as the coupling of Bosonic and Fermionic excitations to the EM field are formulated in Yip and Sauls [38]. We have extended this theory to 2D chiral superconductors with anisotropic, quasi-2D Fermi surfaces, multi-band pairing and weak disorder, to make predictions for signatures of anisotropic chiral and helical superconductivity based on the Bosonic mode spectrum and the microwave response for recent theoretical models for the superconducting state of Sr2RuO4 [39]. Here we summarize some of the results from the microscopic theory that reflect the coupling between Bosonic and Fermionic degrees of freedom that are beyond the TDGL Lagrangian dynamics for chiral ground states.
The dynamics of the order parameter is formulated in terms of the space- and time-dependent mean-field pairing self-energy, which for spin-triplet fluctuations is given by
where V(p, p′) = V1(Y*+(p)Y+(p′) + Y*−(p)Y−(p′)) is the pairing interaction in the spin-triplet E1u channel, is the anomalous Keldysh pair-propagator, the energy integration is over the bandwidth of attraction near the Fermi level, −Ωc ≤ ε ≤ + Ωc with Ωc ≪ Ef, and the momentum integration is an average over the Fermi surface defined by the Fermi momentum p. Below we discuss the orbital dynamics for an ESP chiral ground state of the form , with Δ(p) ≡ Δ Y+(p), with , and the spin component of the order parameter, , is fixed along the direction ẑ. The orbital fluctuations of the Cooper pairs are represented by two complex fields,
where the notation is equivalent to that in Equation (5) of the TDGL theory. The solution to the linearized Eilenberger equations for the non-equilibrium pair-propagator, , in terms of the time-dependent order parameter, , and the coupling of charge currents to the EM field, leads to coupled “gap equations” for the orbital fluctuations of the Cooper pairs [39],
where d′(p; r, t) ≡ D*(r, t) Y+(p) + E*(r, t) Y−(p), η′ ≡ vp′ · q generates the dispersion of both Fermionic and Bosonic excitations, and we have expressed the gap equations in terms of Fourier modes. Note in particular that the cross-coupling terms between d(p; q, ω) and d′(p; q, ω) are proportional to the complex amplitudes, Δ(p)2 and Δ*(p)2. The Tsuneto function [40],
determines (i) the coupling of the EM field to the Bosonic modes, (ii) the mass shifts for the Bosonic modes D± and E±, (iii) finite lifetimes of Bosonic modes arising from coupling to the un-bound continuum, i.e., when M ≥ 2 min[|Δ(p)|], and (iv) coupling of the EM field to the Fermionic spectrum, including absorption of EM radiation by creation of unbound Fermionic quasiparticles for ħω ≥ 2|Δ(p)|. Finally, the term γ(p) is the log-divergent integral that determines the BCS instability and equilbrium gap function, Δ(p). Thus, we can regulate the divergence and eliminate the pairing interaction, V1, in the dynamical equations for d(p) and d′(p) in favor of the self-consistently determined equilibrium gap function, Δ(p), using the identity, .
Energies and Lifetimes of the E± Modes
The Bosonic modes are obtained from the eigenvalue spectrum of the homogeneous equations, i.e., for 𝔸 = 0. In the q = 0 limit the eigen-modes are the linear combinations D± = D(ω) ± D*(−ω) and E± = E(ω) ± E*(−ω) as in the TDGL theory, with D− representing the phase mode and D+ the corresponding amplitude mode. For the modes with time-reversed chirality we obtain
where the functions λnm(ω) are moments of the q = 0 Tsuneto function. For the anisotropic E1u model with basis functions given in Equation (14) with x = cosϕ and y = sinϕ, we have for the anisotropic chiral ground state, Δ(p) = Δeiϕ I(ϕ). The corresponding moments λnm are then given by
For the 2D chiral p-wave ground state the gap is isotropic on the Fermi circle, in which case λ10 = λ00 = 2λ11 = λ(ω), with
leading to the degenerate E± modes with M−,+ = M−,− = Δ(T), in agreement with the weak-coupling limit of the TDGL theory; however now valid at any temperature.
The effects of anisotropy of the pairing state on the E± modes are computed by solving the eigenvalue equations, Equations (20), (21), and (22) numerically. The minimum and maximum of the anisotropic gap function are shown as a function of the anisotropy parameter ε in Figure 3; 2Δmin marks the minimum in the continuum edge of un-bound Fermion pairs. The degeneracy of the E± modes is resolved by the anisotropy, however the splitting of the modes for T → 0 and relatively weak anisotropy, , is much smaller than the prediction based on the GL β parameters. The splitting of the two modes is generally smaller at lower temperatures, and becomes strongly suppressed by the asymmetry in level repulsion between the E± modes and the continuum edge at 2Δmin as the higher energy mode approaches the continuum edge.
At sufficiently large anisotropy the continuum edge of un-broken Fermion pairs at 2Δmin intercepts the excitation energy of E± modes. This opens a channel for the E± mode to dissociate into un-bound Fermion pairs, and thus leads to an intrinsic lifetime for the E± mode(s), τ± = ħ/Γ±, where Γ± is the width of the E± resonance. The latter are calculated perturbatively from Equations (20), (21), and (22) and are shown in the right panel of Figure 3, onsetting precisely at an anisotropy such that M−,± = 2Δmin. Note also that close to 2Δmin the asymmetry in the level repulsion drives M−,−→ M−,+. The large asymmetry in Γ± reflects the different phase space for pair dissociation of the E± modes governed by Im λ10(ω) ≫ Im λ11(ω), i.e., the former is an isotropic average over the spectrum of un-bound Fermion pairs, whereas the latter preferentially weights regions of the Fermi surface near the gap maximum. Thus, two key results of a self-consistent theory of coupled Boson-Fermion excitations are: (i) the mass spliting of the E± mode spectrum is strongly suppressed by the asymmetry in the level repulsion from the un-bound Fermion pairs, and (ii) there is a large asymmetry in the lifetimes of the E± modes that results from the different phase space available for dissociation into un-bound Fermion pairs by E± Bosons. Neither of these effects could be anticipated a priori from the TDGL theory for the Bosonic excitations.
Microwave Excitation of the E± Modes
Indeed key signatures of an anisotropic chiral ground state in Sr2RuO4, are the excitation and decay channels for the E± modes. Both depend on the charge conjugation parity of the modes. Consider an EM field incident normal on a surface of Sr2RuO4 defined by the four-fold axis of symmetry, ẑ, and an axis lying in the x − y plane, i.e., q ⊥ ẑ, and with linear polarization also in the x − y plane, i.e., 𝔸 ⊥ẑ and 𝔸 ⊥ q. The EM field couples directly to the Fermionic degrees of freedom (particles and holes), generating a current [37, 39],
Note that the effects of the pairing correlations on the Fermionic contribution to the charge current - the opening of a gap in the Fermionic spectrum and the a.c. response of the negative energy continuum (condensate)—are encoded in the Tsuneto function, λ(p; ω, q). For T → 0 and low frequencies, ω < 2Δmin, only the negative energy continuum (condensate) responds as an a.c. supercurrent—π/2 out of phase with the electric field—with zero dissipation. The supercurrent, and thus the self-consistently determined EM field, are screened by the Meissner effect and penetrate a distance of order the London penetration depth, Λ. This length scale is typically large compared to the coherence length of the superconductor, Λ ≫ ξ ≫ ħ/pf. In this limit the EM response is dominated by the bulk excitation spectrum. For a chiral ground state the EM field also couples directly to the E± Bosonic modes as shown in Equations (20, 21). The Bosonic modes also generate a charge current,
Thus, the total current, 𝕁 = 𝕁F + 𝕁B, can be expressed in terms of a response function, 𝕁i = 𝕂ij(ω, q) 𝔸j(q, ω), that encodes both Fermionic and Bosonic contributions to the a.c. surface impedance. The response function 𝕂ij(q, ω) determines both dissipative and non-dissipative contributions to the current. In particular, the microwave power absorption spectrum can be expressed as a sum over the modes contributing to the Joule losses of the electric field and current that penetrate into the superconductor, Re[𝕁(q, w) · 𝔼*(q, ω)]. To calculate the power spectrum requires a solution of the boundary value problem for the incident, reflected and transmitted EM fields. This boundary value problem determines 𝔸(q, ω) in terms of 𝕂ij and the value of the EM field in vacuum at the surface, B0. For a detailed discussion of the boundary solution see Yip and Sauls [38].
For weak anisotropy, ε = 0.1, the Bosonic modes have well defined excitation energies, ħω±(q) = M−,± + c2±|q|2/2M−,±, with , and carry current for finite q at frequencies below the un-bound Fermion pair continuum, ħω < 2Δmin, supported by the condensate, represented by λ(p; q, ω) > 0. Resonant excitation of the E± modes occurs over the frequency band, M−,± < ħ ω< 2Δmin, spanned by the dispersion of the E± modes. Thus, excitation of the E± leads to an absorption band that is sharply peaked near threshold as shown in the left panel of Figure 4 for ε = 0.1 and E+. Note also, the broad band of dissipation from dissociation Cooper pairs into un-bound Fermion pairs is sharply peaked at 2Δmax. For strong anisotropy, the E± modes broaden into resonances. However, the E+ resonance has a narrow linewidth due to limited phase space for decay into Fermion pairs. Furthermore, the excitation of ground-state Cooper pairs into un-bound Fermion pairs is suppressed well below 2Δmax. Thus, even for strong gap suppression along [100] directions there remains a strong absorption resonance from the weakly damped E+ Bosonic mode. Observation of the E+ mode, and other signatures of the E± Bosonic spectrum, would provide direct evidence of an anisotropic chiral ground state in Sr2RuO4.
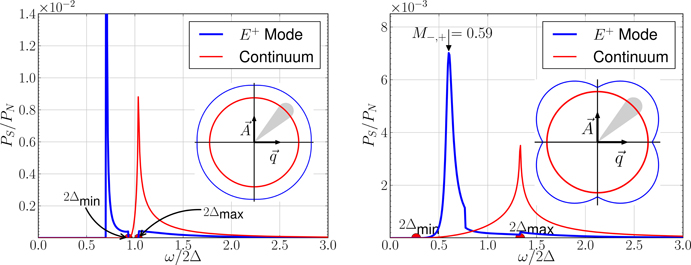
Figure 4. Power absorption spectra normalized to the high-frequency limit of the normal-state, PN(ω), for T = 0, penetration depth, Λ/ξ = 10, and polarization q ⊥ 𝔸 along [100] directions. For this polarization direction only the E+ mode is excited. Left: weak anisotropy with ε = 0.1. A sharp E+ absorption band (blue) and a broad band of dissipation from pair dissociation that is sharply peaked at 2Δmax (red) are shown. Right: strong anisotropy with ε = 0.8. A sharp E+ absorption band (blue) survives weak hybridization with the un-bound continuum. Dissipation from pair dissociation remains sharply peaked at 2Δmax.
Summary
Chiral superconductors which break time-reversal symmetry necessarily belong to a higher dimensional representation of the crystalline point group. In the cases of Sr2RuO4, 2D 3He-A, and UPt3 this is a two-dimensional orbital representation. An important consequence is that a chiral ground state supports Bosonic excitations of the time-reversed Cooper pairs. These excitations are degenerate for 2D 3He-A with an excitation gap, M = Δ, below the continuum edge of un-bound Fermion pairs. Crystalline anisotropy lifts the degeneracy, and for strong anisotropy can generate a low-lying Bosonic mode. Strong amplitude anisotropy also leads to low-lying Fermions, and thus a channel for the Bosonic modes to decay in to un-bound Fermion pairs. Selection rules and phase space considerations are shown to generate to large asymmetries in the lifetimes and hybridization of the Bosonic modes with the continuum of un-bound Fermion pairs. The excitation of the Bosonic modes by microwave radiation could provide clear signatures of an anisotropic chiral ground state. A detailed theory of microwave spectroscopy of anisotropic chiral superconductors which includes the analysis of selection rules, the effects of band structure and Fermi surface anisotropy, spin-orbit coupling and weak disorder will be forthcoming as a separate report [39].
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The research of HW and JS was supported by the National Science Foundation (Grant DMR-1106315), while that of SC is supported by the Institute for Basic Science of Korea (Grant IBS-R009-Y1). JS and SC acknowledge the hospitality of the Aspen Center for Physics, and its support through National Science Foundation Grant No. PHYS-1066293, where part of this work was carried out. JS also acknowledges the hospitality of the KITP and its support through NSF Grant No. PHY11-25915. We acknowledge discussions with Sri Raghu, Catherine Kallin, Steve Simon and Thomas Scaffidi that were important in motivating this work, and Andrea Damascelli for his comments on the role of spin-orbit coupling in Sr2RuO4.
Footnotes
1. ^Invited Talk at SCES14, July 7-11, 2014, Grenoble, France.
References
1. Rice TM, Sigrist M. Sr2RuO4: an electronic analogue of 3He? J Phys Cond Mat. (1995) 7:L643–8. doi: 10.1088/0953-8984/7/47/002
2. Layzer A, Fay D. Spin-fluctuation exchange mechanism for P-wave pairing in liquid 3He. Int J Magn. (1971) 1:135.
3. Leggett AJ. Theoretical description of the new phases of liquid 3He. Rev Mod Phys. (1975) 47:331–414. doi: 10.1103/RevModPhys.47.331
4. Balian R, Werthamer NR. Superconductivity with pairs in a relative p-state. Phys Rev. (1963) 131:1553. doi: 10.1103/PhysRev.131.1553
5. Brinkman WF, Anderson PW. Anisotropic superfluidity in 3He: consequences of the spin-fluctuation model. Phys Rev. (1973) A8:2732. doi: 10.1103/PhysRevA.8.2732
6. Brinkman WF, Serene JW, Anderson PW. Spin-fluctuation stabilization of anisotropic superfluid states. Phys. Rev. A (1974) 10:2386–94. doi: 10.1103/PhysRevA.10.2386
7. Braden M, Sidis Y, Bourges P, Pfeuty P, Kulda J, Mao Z, et al. Inelastic neutron scattering study of magnetic excitations in Sr2RuO4. Phys Rev B (2002) 66:064522. doi: 10.1103/PhysRevB.66.064522
8. Haverkort MW, Elfimov IS, Tjeng LH, Sawatzky GA, Damascelli A. Strong spin-orbit coupling effects on the fermi surface of Sr2RuO4 and Sr2RhO4. Phys Rev Lett. (2008) 101:026406. doi: 10.1103/PhysRevLett.101.026406
9. Raghu S, Kapitulnik A, Kivelson SA. Hidden quasi-one-dimensional superconductivity in Sr2RuO4. Phys Rev Lett. (2010) 105:136401. doi: 10.1103/PhysRevLett.105.136401
10. Wang QH, Platt C, Yang Y, Honerkamp C, Zhang FC, Hanke W, et al. Theory of superconductivity in a three-orbital model of Sr2RuO4. Eur Phys Lett. (2013) 104:17013. doi: 10.1209/0295-5075/104/17013
11. Scaffidi T, Romers JC, Simon SH. Pairing symmetry and dominant band in Sr2RuO4. Phys Rev B (1981) 89:220510. doi: 10.1103/PhysRevB.89.220510
12. Veenstra CN, Zhu ZH, Raichle M, Ludbrook BM, Nicolaou A, Slomski B, et al. Strong spin-orbit coupling effects on the fermi surface of Sr2RuO4 and Sr2RhO4. Phys Rev Lett. (2014) 112:127002. doi: 10.1103/PhysRevLett.112.127002
13. Vorontsov AB, Sauls JA. Crystalline Order in superfluid 3He films. Phys Rev Lett. (2007) 98:045301. doi: 10.1103/PhysRevLett.98.045301
14. Levitin LV, Bennett RG, Casey A, Cowan B, Saunders J, Drung D, et al. Phase diagram of the topological superfluid 3He confined in a nano-scale slab geometry. Science (2013) 340:841–4. doi: 10.1126/science.1233621
15. Kallin C, Berlinsky AJ. Is Sr2RuO4 a chiral p-wave superconductor? J Phys Condens Mat. (2009) 21:164210. doi: 10.1088/0953-8984/21/16/164210
16. Hicks CW, Brodsky DO, Yelland EA, Gibbs AS, Bruin JAN, Barber ME, et al. Strong increase of Tc of Sr2RuO4 under both tensile and Compressive strain. Science (2014) 344:283–5. doi: 10.1126/science.1248292
17. Hess D, Tokuyasu T, Sauls JA. Broken symmetry and Unconventional superconductivity in uniaxial crystals. Physica B (1990) 163:720. doi: 10.1016/0921-4526(90)90318-O
18. Serene JW. Order parameter modes, zero Sound Symmetries in superfluid 3He. In: Adams ED, Ihas G, editors. Quantum Fluids Solids - 1983, Vol. 103. New York, NY: A.I.P. (1983). p. 305.
19. Fishman RS, Sauls JA. Particle-hole symmetry violation in normal liquid 3He. Phys Rev B (1985) 31:251–9. doi: 10.1103/PhysRevB.31.251
20. Higgs PW. Broken symmetries and the masses of gauge bosons. Phys Rev Lett. (1964) 13:508–9. doi: 10.1103/PhysRevLett.13.508
21. Littlewood P, Varma C. Gauge-invariant theory of the dynamical interaction of charge density waves and Superconductivity. Phys Rev Lett. (1981) 47:811. doi: 10.1103/PhysRevLett.47.811
22. Anderson PW. Random-phase approximation in the theory of superconductivity. Phys Rev. (1958) 112:1900–16. doi: 10.1103/PhysRev.112.1900
23. Bogoliubov NN, Tolmachev VV, Shirkov DV. New Methods in the Theory of Superconductivity. Moscow: Academy of Science (1958).
24. Tsuneto T. Transverse collective excitations in superconductorselectromagnetic absorption. Phys Rev. (1960) 118:1029. doi: 10.1103/PhysRev.118.1029
25. Vaks VG, Galitskii VM, Larkin AI. Collective excitations in a superconductor. Zh Eskp Teor Fiz. (1961) 41:1655.
26. Bardasis A, Schrieffer JR. Excitonsplasmons in superconductors. Phys Rev. (1961) 121:1050. doi: 10.1103/PhysRev.121.1050
27. Vdovin YA. Effects of p-state pairing in fermi systems. In: Alekseeva A. I., editors. Methods of Quantum Field Theory to the Many Body Problem, Moscow: Gosatomizdat (1963). p. 94–109.
28. Maki K. Propagation of zero sound in the Balian-Werthamer State. J Low Temp Phys. (1974) 16:465. doi: 10.1007/BF00654896
30. Sauls JA, Serene JW. Coupling of order-parameter modes with ℓ > 1 to zero sound in 3He-B. Phys Rev B (1981) 23:4798. doi: 10.1103/PhysRevB.23.4798
31. Halperin WP, Varoquaux E. Order parameter collective modes in superfluid 3He. In: Halperin WP, Pitaevskii LP, editors. Helium Three. Amsterdam: Elsevier Science Publishers (1990). p. 353.
32. Sauls JA. Broken symmetry non-equilibrium superfluid 3He. In: Godfrin H, Bunkov Y, editors. Topological DefectsNon-Equilibrium Symmetry Breaking Phase Transitions - Lecture Notes for the 1999 Les Houches Winter School. Amsterdam: Elsievier Science Publishers (2000). p. 239–65.
33. Sauls JA. Fermi-liquid theory of unconventional superconductors. In: Bedell KS, Wang Z, Meltzer DE, Balatsky AV, Abrahams E, editors. Strongly Correlated Electronic Materials: The Los Alamos Symposium 1993. Reading, MA: Addison-Wesely (1994). p. 106–32.
34. Ali S, Zhang L, Sauls JA. Thermodynamic potential for superfluid 3He in silica aerogel. J Low Temp Phys. (2011) 162:233–42. doi: 10.1007/s10909-010-0310-4
35. Volovik G, Zubkov M. Higgs bosons in particle physics and in condensed matter. J Low Temp Phys. (2014) 175:486–97. doi: 10.1007/s10909-013-0905-7
36. Chung S, Raghu S, Kapitulnik A, Kivelson S. Charge and spin collective modes in a quasi-one-dimensional model of Sr2RuO4. Phys Rev B (2012) 86:064525. doi: 10.1103/PhysRevB.86.064525
37. Hirschfeld PJ, Wölfle P, Sauls JA, Einzel D, Putikka, WO. Electromagnetic absorption in anisotropic superconductors. Phys Rev B (1989) 40:6695. doi: 10.1103/PhysRevB.40.6695
38. Yip SK, Sauls JA. Circular dichroism and birefringence in unconventional superconductors. J Low Temp Phys. (1992) 86:257–90. doi: 10.1007/BF01151804
39. Wu H, Chung SB, Sauls JA. Collective modes electromagnetic response of anisotropic chiral superconductors. Phys. Rev. B. (2015). Available online at: http://eolus.phys.northwestern.edu/publications/arxiv/wu-23-05-2015.html
40. McKenzie RH, Sauls JA. Collective Modes and Nonlinear acoustics in superfluid 3He-B. arXiv 1309.6018 (2013) p. 1–62. Available online at: http://arxiv.org/abs/1309.6018
Keywords: superconductivity, strontium ruthenate, collective modes, chirality, broken time-reversal, microwave spectroscopy, superfluid 3He, anisotropic pairing
Citation: Sauls JA, Wu H and Chung SB (2015) Anisotropy and strong-coupling effects on the collective mode spectrum of chiral superconductors: application to Sr2RuO4 Front. Phys. 3:36. doi: 10.3389/fphy.2015.00036
Received: 28 February 2015; Accepted: 12 May 2015;
Published: 05 June 2015.
Edited by:
Peter Fischer, Lawrence Berkeley National Laboratory, USAReviewed by:
Mikael Fogelström, Chalmers University of Technology, SwedenCongjun Wu, University of California, San Diego, USA
Copyright © 2015 Sauls, Wu and Chung. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: James A. Sauls, Department of Physics and Astronomy, Northwestern University, 2145 Sheridan Road, Evanston, 60208 IL, USA,c2F1bHNAbm9ydGh3ZXN0ZXJuLmVkdQ==
 James A. Sauls
James A. Sauls Hao Wu
Hao Wu Suk Bum Chung
Suk Bum Chung