Magnetic reconnection in current carrying plasmas, in particular when the plasma is collisionless, is an efficient channel of dissipating the energy temporarily stored in electric currents that are generated in one or the other way in the mechanical plasma flow. When collisions (including anomalous) dominate, reconnection is a slow diffusion process, proceeding on resistive time-scales and properly described by fluid theory [1].
In the absence of resistive friction and Ohmic losses, the agent transforming the stored energy is the current-related magnetic field. Contacting fields of opposite direction may reorganize, locally annihilate the antiparallel components and provide the liberated energy for direct plasma heating and particle/plasma acceleration. In this case reconnection may become very fast proceeding on electron-plasma time scales. Its onset is subject to the scales of the current layer in that it goes on. Distributed currents filling the entire bulk plasma do barely support reconnection. Also field-aligned currents flowing along strong magnetic fields experience negligible reconnection even when restricted to flux tubes, unless the current is so strong that it winds the magnetic field up into spirals. This is believed to occur in stellar magnetic loops like on the sun during solar eruptions.
The relevant set-ups for collisionless reconnection are currents flowing across moderately strong magnetic fields when two plasmas carrying fields of opposite directions encounter each other, the classical model case of reconnection. Such cases are abundant in space and all kinds of astrophysical magnetized objects. Oppositely polarized solar magnetic loops impacting on each other are but one example. The currents produced in the contact region of the two plasmas are fed by the mechanical plasma motion and are restricted to a finite range across the magnetic field only.
The important parameter for collisionless reconnection to occur is the transverse scale of the currents (see Figure 1). In a broad current layer this scale exceeds the ion gyroradius. Here an mhd-fluid description is appropriate since all particles contributing to the current are magnetized. Such layers are subject to “slow reconnection” only if plasma instabilities give rise to anomalous diffusion. Narrower layers of widths in the intermediate region of scales between ion and electron gyroradii require distinguishing between electron and ion dynamics. Ions become non-magnetic while electrons maintain their magnetization. Finally, on scales below the electron gyroradius electrons also become non-magnetic. Current layers that narrow that their transverse widths drop below the electron gyroradius are completely determined by electron inertia and undergo prompt collisionless reconnection for the reason that electrons non-diffusively pass across the layer, crossing the transition region from magnetic fields of one polarity to the opposite. Here electrons escape magnetic slavery, allowing the opposite magnetic fields to get in touch, annihilate and quickly though not instantaneously to reorganize. This process, present in collisionless reconnection, is based on generation of electron viscosity [2, 3] in the thin current layers. The timescale of this fast local reconnection process is determined by the plasma being a dielectric. Thus, it is at the electron plasma time scale.
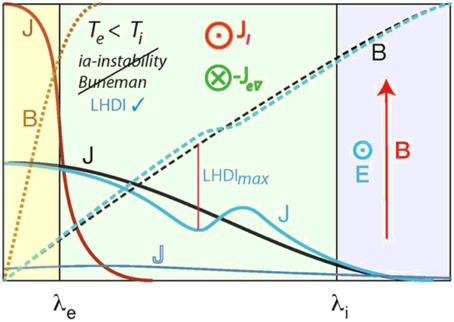
Figure 1. Schematic of the three cases of current sheets J of different widths but same strength. Open J: Broad current sheet, width > ion inertial length λi. The current is distributed, density gradients are very weak. Such current sheets are either stable or undergo mechanical turbulence when evolving large-scale eddies. Black J: Current sheet of intermediate width λe < width < λi between electron and ion inertial scales (green background). In such layers ions are non-magnetic, while electrons are magnetized. The current is carried by nonmagnetic ions (red Ji) which are accelerated in the convection electric field (E). Electron-gradient-drift current (green Je∇ of magnetized electrons in current-density gradient are the second current source. In such sheets not ion-acoustic or Buneman instabilities can be generated. They are unstable with respect to the Lower-hybrid-drift instability (LHDI) which maximizes in the steepest density gradient (red vertical bar) and may cause current bifurcation shown as the blue current profile corresponding to a weak deformation of magnetic field strength (dashed blue line) and a weak antiparallel magnetic component only. Brown J: Narrow current sheets of widths comparable to λe have very steep current density profile and are carried mainly by non-magnetized electrons. Such sheets are subject to several kinds of electron inertia driven instabilities causing electron viscosity. Magnetic fields in such sheets are antiparallel across the sheet and thus unstable to prompt collisionless reconnection.
Electron viscosity has three sources: the first source is the anisotropy of the electron thermal pressure which under collisionless conditions in the local magnetic frame is diagonal, while in the frame of the central current layer it assumes all six independent components for the reason that the magnetic field is locally inclined against the current frame. The second source is electron inertia leading to an inertial contribution to the electron current. The third source is due to so-called Speiser orbits of electrons meandering in the center of the current layer by experiencing mirror reflection from the oppositely directed magnetic fields outside the electron inertial scale width of the current sheet center. The physics of reconnection takes place in this region.
Collisionless currents of widths on the intermediate scale between the ion and electron gyro-radii consist of three parts: the primary unmagnetized ion current which is driven by the convection electric field of the flow of the two approaching oppositely magnetized plasma streams. Pushing the nonmagnetic ions along this field carries the current while, at the same time, accelerates the ions over one ion inertial length thereby heating them up. The second contribution is the magnetized electron-pressure-drift current which pushes the electrons in the direction opposite to the ion flow thus as well contributing to the main current. Finally one has the Hall currents [4] that are carried by magnetized electrons in the crossed convection electric and magnetic fields. The Hall currents stir the electrons around, causing a weak quadrupolar Hall magnetic field. They close most efficiently along the magnetic field to regions away from the current center, while giving rise to (kinetic) Alfvén waves. The Alfvén waves are kinetic for the reason that ions are nonmagnetic and the transverse size of their source region is of the order of the ion inertial scale thus matching the required transverse wavelength of kinetic Alfvén waves. They carry the field-aligned currents, transport hot electrons away from the current sheet toward the footpoints of the magnetic field and replace them by cool electrons from the environment thereby cooling the electron component.
Observations in space show that electrons, in addition to being magnetic, are indeed cooler than ions by several times but less than up to an order of magnitude in temperature [5]. The important conclusion is that for these reasons neither Buneman nor ion acoustic waves can be excited here as their instability conditions are not met. The relevant waves are modified-two stream (lower-hybrid-drift) waves with frequency near the lower hybrid frequency, and possibly also weak oblique whistlers with, however, energy flow along the field.
In this region no reconnection takes place. There are no oppositely directed magnetic field components which could support reconnection nor any reason for liberating electrons from magnetic slavery. Just slow field diffusion becomes possible. Reconnection is strictly restricted to narrow current layers inside the electron inertial scale distance. This has been confirmed many times [6] by numerical PIC simulations with and without guide fields.
The authors of the paper in question [7] make a very interesting and also very important case of the dynamics of a current layer of width in this intermediate region referring to inertial scales rather than gyro-radii, which is well justified for plasma-β ~ 1. Their finding is, using a combination of ion-acoustic/Buneman waves and whistlers, that such moderately broad current sheets are nonlinearly unstable. They should break off, as the authors suggest, into many narrower current filaments and thus cause fast (collisionless) reconnection.
Reference to spatial bifurcation of the current is most interesting as it strongly supports observations of current layer bifurcation [8] respectively splitting of the main current layer, an important and so far barely understood phenomenon to which the present paper of the authors indeed makes an important contribution. The author's suggestion is based on the derivation of a Landau–Ginzburg equation for the electron current speed which allows constructing the thermodynamic free energy. Discussion of this energy, as usual, allows distinguishing between stable and unstable regions. The finding of the authors is that in the domain of scales of interest the current layer is unstable with respect to bifurcation/splitting.
The problem with that paper is, however, that the authors insist on referring to reconnection. As explained above, in the intermediate region there is no reconnection. Moreover reference to ion-acoustic or Buneman modes is unjustified for the conditions are not satisfied for these waves to become unstable. Pressure-gradient drifts are slow. In addition pressure gradient-current driven whistlers are very weak with group velocity parallel only to the magnetic field.
This, however, does not imply the proposed mechanism to be wrong. It is only misplaced. It refers to current layers which may undergo reconnection somewhere while reconnection is not the central point of what the authors really demonstrate. At the contrary, since electrons are magnetic while ions are not, the intermediate scale current is clearly unstable though neither to Buneman nor ion-acoustic waves. It is unstable to the modified-two stream (lower-hybrid drift) instability which has a very low threshold such that one expects the current necessarily to bifurcate once the author's mechanism is applied to lower-hybrid-drift waves. The growth rate of the modified two-stream/lower-hybrid-drift instability is roughly the lower-hybrid frequency [9] which it can even slightly exceed. Using it instead of ion-acoustic waves should lead to similar results.
The value of this investigation thus lies not in a contribution to reconnection, a process that today is quite well understood playing an important role in collisionless dissipation of magnetic turbulence [10, 11]. The theory rather provides a consistent view of bifurcation of moderately thick current layers, an observational fact in near-Earth space [8].
The location of strongest lower-hybrid-drift instability is at the pressure-gradient turning point on the current profile. In the vicinity of this place the current will break off, according to the theory in Guo and Wang [7], splitting into two current maxima separated by, say, one ion inertial scale or a larger fraction of it. This splitting produces weak antiparallel magnetic field components only which locally act to weaken the main magnetic field a bit.
Reconnection among these weak components may occur in the centers of the two bifurcation branches on scales less than the electron inertial scale, if only electron viscosity is generated there and becomes large enough. This is barely the case because the weak antiparallel field components produced in the bifurcation are insufficient for demagnetizing the electrons in this region. Observations in the Earth's magnetic tail [8] do not support such an effect though clearly find current bifurcation. In any case any possible annihilation of antiparallel magnetic fields will be weak only, dissipating little of the main current energy.
Breaking off into many small current filaments in reconnection is observationally found and in 3d-simulations confirmed [11] of being caused by the three-dimensionality of the reconnection process in the main current layer center below the electron inertial scale. Here, under 3d-conditions, collisionless reconnection evolves turbulently for a number of various reasons, in particular for the freedom gained by including the third dimension. In three dimensions it is reconnection in the electron inertial scale current layers that causes the turbulent break-off of the current. Another reason for the appearance of many electron scale current filaments in collisionless plasma is genuine plasma turbulence resulting from decaying and inertial range cascading of large eddies down to the electron scale [10]. This has primarily nothing in common with reconnection though, however, reconnection becomes the ultimate dissipation process of turbulence once the current eddy filaments approach the electron inertial scale.
Asking under which conditions current layer bifurcation by the originally proposed mechanism [7] could indeed take place, causing multiple break-off of the current, one is led to consider current layers that become driven extremely hard by persistent external forces like relativistic convection in relativistic plasma encounters. In this case the pressure gradients on the edges of the layer could possibly become comparable to the size of the layer causing large gradient drifts. However, in such cases other effects like shock waves will come into play as well modifying the evolution of the current layer.
In summary, the proposed mechanism of current bifurcation [7] resulting from phase transition is intriguing in particular as such bifurcations have indeed been observed in near-Earth space suggesting that they are a common feature of moderately broad current layers. It has always been a problem of understanding what happens to broad current layers and how they may reorganize into narrow once which may then undergo reconnection and dissipate their energy. Classical electrodynamics tells that parallel currents attract each other until merging into a single broad current. The usual way of approaching the problem of production of narrow current filaments is via the assumption that the plasma undergoes the transition to turbulence, generating large mechanical eddies in the flow which cascade down to electron scale structures. Examples are found in solar wind turbulence for which it has been shown that the dissipation is via reconnection [10]. This, however, requires a source of turbulence which is thought to be found in the generation of mhd-waves in the bulk plasma.
Any mechanism is of large interest demonstrating the splitting of currents into few or many narrow layers. Guo and Wang [7] show a way out of this dilemma, though under barely realized conditions in the currents sheet which, in contrast to turbulence, do not necessarily lead to reconnection. It will be very interesting to apply this mechanism to the more realistic conditions that are prevalent in broader than electron scale current layers.
It is also interesting to learn that phase transitions can, in principle, take place in high temperature plasmas as well which is something which was suspected but never demonstrated sufficiently convincingly.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
2. Hesse M, Schindler K, Birn J, Kuznetsova M. The diffusion region in collisionless magnetic reconnection. Phys Plasmas (1999) 6:1781. doi: 10.1063/1.873436
3. Treumann RA, Baumjohann W. Superdiffusion revisited in view of collisionless reconnection, Ann Geophys. (2014) 32:643. doi: 10.5194/angeo-32-643-2014
4. Øieroset M, Phan TD, Fujimoto M, Lin RP, Lepping RP. In situ detection of collisionless reconnection in the Earth's magnetotail. Nature (2001) 412:414. doi: 10.1038/35086520
5. Artemyev AV, Baumjohann W, Petrukovich AA, Nakamura R, Dandouras I, Fazakerley A, et al. Proton/electron temperature ratio in the magnetotail. Ann Geophys. (2011) 29:2253 doi: 10.5194/angeo-29-2253-2011
6. Pritchett PL. Onset and saturation of guide-field magnetic reconnection. Phys Plasmas (2005) 12:062301. doi: 10.1063/1.1914309
7. Guo Z, Wang X. Onset of fast magnetic reconnection via subcritical bifurcation. Front Phys. (2015) 03:00018. doi: 10.3389/fphys.2015.00018
8. Runov A, Nakamura R, Baumjohann W, Zhang TL, Volwerk M, Eichelberger H-U, et al. Cluster observations of a bifurcated current sheet. Geophys Res Lett. (2003) 30:1036. doi: 10.1029/2002GL016136
9. Davidson RD. Quasi-linear stabilization of lower-hybrid-drift instability. Phys Fluids (1978) 21:1373. doi: 10.1063/1.862379
10. Treumann RA, Baumjohann W. Ideal MHD turbulence: the inertial range spectrum with collisionless dissipation, Front Phys. (2015) 03:00022. doi: 10.3389/fphys.2015.00022
Keywords: collisionless reconnection, current bifurcation, turbulence, magnetotail reconnection, free energy of current layer
Citation: Treumann RA and Baumjohann W (2015) Broad current sheets, current bifurcation, and collisionless reconnection—An Opinion on “Onset of fast magnetic reconnection via subcritical bifurcation” by Z. Guo and X. Wang. Front. Phys. 3:40. doi: 10.3389/fphy.2015.00040
Received: 20 April 2015; Accepted: 26 May 2015;
Published: 08 June 2015.
Edited by:
Hermann Lühr, Deutsches GeoForschungsZentrum GFZ, GermanyReviewed by:
Stephan Christoph Buchert, Swedish Institute of Space Physics, SwedenCopyright © 2015 Treumann and Baumjohann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rudolf A. Treumann,YXJ0dEBpc3NpYmVybi5jaA==
 Rudolf A. Treumann
Rudolf A. Treumann Wolfgang Baumjohann
Wolfgang Baumjohann