- 1School of Management, University of Leicester, Leicester, UK
- 2e-Humanities Group, Royal Netherlands Academy of Arts and Sciences (KNAW), Amsterdam, Netherlands
- 3Groupe de Recherche pour des Applications de Physique en Economie et Sociologie (GRAPES), Liège Angleur, Belgium
Diffusion of knowledge is expected to be huge when agents are open minded. The report concerns a more difficult diffusion case when communities are made of stubborn agents. Communities having markedly different opinions are for example the Neocreationist and Intelligent Design Proponents (IDP), on one hand, and the Darwinian Evolution Defenders (DED), on the other hand. The case of knowledge diffusion within such communities is studied here on a network based on an adjacency matrix built from time ordered selected quotations of agents, whence for inter- and intra-communities. The network is intrinsically directed and not necessarily reciprocal. Thus, the adjacency matrices have complex eigenvalues; the eigenvectors present complex components. A quantification of the slow-down or speed-up effects of information diffusion in such temporal networks, with non-Markovian contact sequences, can be made by comparing the real time dependent (directed) network to its counterpart, the time aggregated (undirected) network, - which has real eigenvalues. In order to do so, small world networks which both contain an odd number of nodes are studied and compared to similar networks with an even number of nodes. It is found that (i) the diffusion of knowledge is more difficult on the largest networks; (ii) the network size influences the slowing-down or speeding-up diffusion process. Interestingly, it is observed that (iii) the diffusion of knowledge is slower in IDP and faster in DED communities. It is suggested that the finding can be “rationalized,” if some “scientific quality” and “publication habit” is attributed to the agents, as common sense would guess. This finding offers some opening discussion toward tying scientific knowledge to belief.
1. Introduction
Locating, structuring, thereafter simulating stylized facts on the diffusion of knowledge becomes increasingly difficult (see e.g., [1]) due to the huge accumulation of big data. Therefore, it is quite needed to downsize the investigations in order to pin point “microscopic phenomena” contributing to the formation of “macroscopic features.” This process of looking at the nonlinear dynamics of interacting intelligent populations [2], in socio-physics, is equivalent to the observation of vortices or solitons, in fluid mechanics [3, 4], before attempting to observe and to describe turbulence [5].
It is nowadays commonly accepted that analyzing and modeling real-world phenomena can be made on complex networks [6]. In recent times, interesting observations on the diffusion of knowledge in structuring time dependent networks have followed such a path [7, 8]. In that respect, it was shown how time ordering interactions, thus causality, affect the interpretation of dynamical processes: in particular, by comparing contrasting features on moderate size time aggregated networks and on their sub-structured time dependent counterparts. Scholtes et al. [7], Scholtes et al. [8] also showed that some community detection can be made by means of spectral clustering.
Here, a sort of inverse approach is presented. Considering a well defined set of interactions on a network, it will be observed that a difference in the diffusion of knowledge occurs depending on the sub-network size and structure. Numerical results are presented from the comparison of several (small) networks, either when the time ordering of nodes is taken into account or when the network is seen after some time aggregation.
In order to do so, several networks, approximately of the same size, but containing different types of sites and links have been studied. These networks look like small world networks. Moreover, it is imposed that the nodes belong to two communities made of stubborn agents, in order to keep a systematic topological structure, i.e., the diffusion of knowledge is supposed to exist, but without a modification of the state of the recipient, - as when insults are exchanged between agents. Such communities having markedly different opinions have been previously studied in general frameworks [9–11]. Such communities are, for example, the Neocreationist and Intelligent Design Proponents (IDP), on one hand, and the Darwinian Evolution Defenders (DED), on the other hand [12, 13]. Previous reports on these communities studied along the lines of opinion formation, as well as of behavior choice and agent reactions [14, 15], within a socio-physics context pertaining to the diffusion of ideas have been presented and are very briefly recalled in Section 2.
The case of knowledge diffusion within such communities is studied from time ordered selected quotations of agents, whence after building networks, each mimicked by its adjacency matrix, with ranks and rows ordered to define inter- and intra-community links. These networks are intrinsically directed and not necessarily reciprocal. Thus, the adjacency matrices have complex eigenvalues, and the eigenvectors present complex components [16]. The content of the citations is not studied, but perusal of these indicate that they are more “negative arguments” than “positive ones.” However, the diffusion of “knowledge” exists, but without a modification of the state of the recipient, e.g., like when insults are exchanged in many social worlds. There is hardly a search for consensus in such “controversies,” indeed.
In Section 2.3, the large 77 × 77 matrix, i.e., a 77 network, is presented. In Section 2.4, it is explained that several sub-networks can be extracted for further study: they correspond to small world networks which contain either an odd or an even number of nodes, in order to pin point the relevance of complex eigenvalues of the pertinent matrix, due to triads of agents. In so doing, it might be possible to observe some possible symmetry (or “transitivity”) effects, if any. Thereafter, in Section 2.5, the time aggregated (thus, undirected) network counterpart, - which has an adjacency matrix which is symmetric, whence has necessarily only real eigenvalues, is constructed and analyzed.
A quantification of the slow-down or speed-up effects of information diffusion in such temporal networks, with non-Markovian contact sequences, can be made by comparing the real time dependent (directed) network to its counterpart, the time aggregated (undirected) network, - which has real eigenvalues; see Sections 3 and 4.
2. Perspective on Specific Stubborn Agents
With the aim of capturing the dynamical aspects of the interaction between Neocreationist and Intelligent Design Proponents (IDP) and the Darwinian Evolution Defenders (DED), agents of the IDP and DED groups, the degree of activity of each group and the corresponding degree of impact on the community can be monitored [17, 18]. From a mere opinion formation point of view, it could be shown that if DED would have simply outlined scientific data, i.e., not stating Darwin theory is “proved,” but instead noting that it is the best frame to date, they would have lost the debate against the IDP [19, 20].
In order to gain insight on the degree of interrelations due to the activity of such antagonistic social groups [21, 22], a directed network of citations can be constructed, by applying the procedure found in Garcia Cantù Ross and Ausloos [17] and recalled in Section 2.1.
2.1. Network Construction
In order to build the network, the main agents of the Intelligent Design (ID) movement were first selected. From a paper by Pennock [23], criticizing ID, the founders of the ID movement are first identified. Next, the ID web pages and their corresponding links were examined, starting from the URL of the Discovery Institutes Center for Science and Culture (CSC)1. Thereafter, the connections of this predefined ID community with the defenders of the other community, the Darwins evolution theory defenders are selected. This is helped by considering the increasing impact of the ID movement has impelled. the latter has by reaction activated social and scientific organizations around the world. Among the most important ones, the non-profit organization National Center for Science Education (NCSE)2 plays a relevant role in coordinating the activity of people defending the teaching of evolutionary biology in the USA.
A citation network has been constructed as follows, in brief searching for nodes (agents of any community citing their own community or the opponents):
• Starting from a list containing the name of some of the IDP W. Dembski, M. Behe and S. Meyer, and using Google Scholar Internet search tool, their main publications were selected.
• Next another list was created with the different authors citing the agents of the previous list, while as objectively as possible recording their general positions upon either one of the two sides of the debate.
• A node number was arbitrarily given to each agent.
• The node or agent was endowed with an attribute according to the apparent community position.
• For each pair of agents a directed link was drawn if, according to the outcome of the Google Scholar search process, there is a citation.
N.B. the data was downloaded and examined between Oct. 01 and Nov. 15, 2007.
2.2. Network Characteristics
The network is composed of two subgraphs, one with 37 and the other with 40 agents, corresponding to IDP and DED communities, respectively. There are 170 and 128 links in IDP and DED intra-communities, respectively, and 217 inter-community links. Notice that no weight is given to any link. One can distinguish between directed links (DL) and undirected links (UL): such a latter link connects a pair of nodes in both directions (A cites B and B cites A); by extension, a Directed Triangle (DT) is the shortest cycle of a graph formed by ONLY directed links (DL) (A cites B cites C cites A, but B does not cite A, etc.). However, the set-up of such adjacency matrices is such that it is impossible to report whether A cited B, before or after C cited B, for example. Moreover, it is also obvious that a DT is a chronologically absurd feature, - except if there are different citations, but this is not recorded in the present procedure. Nevertheless, the adjacency matrices are usually non-symmetric. Thus, systems of unspecified (i.e., directed or undirected) links are at first only those to be considered. One should remind the reader here that the sum of an adjacency matrix and of its transpose, leads to a symmetric matrix with different weights w for directed (w = 1) and for undirected (w = 2) links.
Nevertheless, individuals leading the transfer of opinion between IDP and DED communities can be identified by analyzing the number of directed triangles and of undirected links of the citation network. It was found [17] that the three main nodes in the ID community make up for 56% of the IDP triangles and 41% of the inhomogeneous ones, while 5 nodes in the DE community make up for 51% of the inhomogeneous triangles. Thus, it can be safely assumed that a few so called opinion leaders can well describe the activity of the whole group to which they belong.
Whence, it should be obvious to the reader that in such small networks, it is hard to get a convincing power law of the degree distributions. However, it seems easily induced that the preferential attachment mode is pertinent for each community, with different “scholarly constraints,” as it will be deduced in Section 3 and argued upon in Section 5.
It is worth calculating the number of triangles associated to each group, i.e., depending on the type of nodes on the triangle edges. The results for the different possible types of triangles are given in Table 1. We emphasize that triangles containing elements of different communities are the most abundant ones. Conversely, among the 348 triangles sustaining the network, 72 (thus 0.21 %) are homogeneous, relating only nodes of the same community. Thus, it is obvious that the interactions induce some non trivial dynamics [16, 24], leading to real and complex eigenvalues.
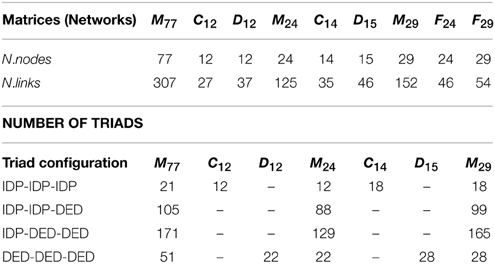
Table 1. Number of nodes, links, and triads, with unspecified (directed or undirected) edges between indicated types of nodes, in the various networks represented by the various adjacency matrices of indicated size.
2.3. A 77 × 77 Real Asymmetric Matrix
The adjacency matrices can be summarized as
in which a matrix element mij takes the value 1 or 0 depending on whether or not a citation of i by j has taken place, as recorded and explained in Garcia Cantù Ross and Ausloos [17], Rotundo and Ausloos [24]. The matrices C0 (37 × 37) and D0 (40 × 40) indicate whether agents of community i have been quoted by others of the same community i. Self-citations are disregarded, mii = 0, i.e., all diagonal terms in M0, C0, and D0 are 0; see [24] for the list of all finite matrix elements. In contrast, F0, i.e.,
emphasizes links between different communities, i.e., agents of community j quoting those of community i(≠ j); i ← j. A and B are obviously rectangular matrices describing inter-community links. A and B are (40 × 37) and (37 × 40) matrices respectively. All C0, A, B and D0 matrices are given in the Supplementary Material; from such matrices, the network, not shown for space saving, can be easily reconstructed through any good classical graph software.
Moreover, since each square matrix M0, C0, D0, F0 has non-negative elements, the Perron-Frobenius theorem states that there exists at least one non-negative eigenvalue greater or equal in absolute value than all other eigenvalues; its corresponding eigenvector has non-negative components [25, 26].
The Perron-Frobenius theorem, applied in its version for non-negative matrices only, indicates that there may exist eigenvalues of the same absolute value as the maximal one.
The EVs of the above 4 matrices, M0, C0, D0, and F0, have been computed. The EVs of interest are given in Table 2. In the framework of this paper only these relevant EVs are indicated.
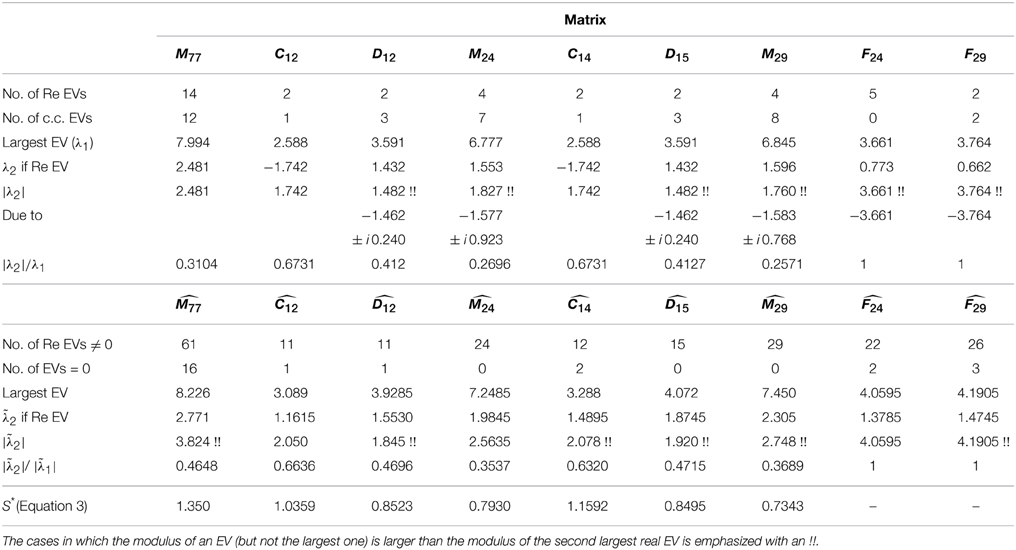
Table 2. Characteristics of the main eigenvalues (EVs) for the various adjacency matrices pertinent to the investigated networks.
2.4. Reduced Size “Core Networks”
To proceed on knowledge diffusion on a network, it should be recognized that some knowledge is lost when the agent is not well connected, i.e., has a node degree = 1, either being at the end of a “dangling bond,” - like a sink or a source in fluid mechanics. The same can be thought for a node degree = 2. The role of these agents is likely marginal in contrast to those sinks and sources which are hubs of the network. In fact for the diffusion of knowledge, a triad graph seems the most basic graph to consider. Thus, for the present study, a few nodes of the whole network can be eliminated from the start.
The following procedure has been applied: in order to emphasize the role of inter-community connecting agents, all agents in the A and B rectangular matrices are kept when ai,j = 1 and bi,j = 1, whence reducing the entire community network to its relevant core according to inter-community links. Next, the most important agents in the C and D matrices are conserved as nodes relevant for intra-community knowledge transfer. Remembering that an odd or an even number of nodes might lead to different sets of (real or complex) eigenvalues, it is interesting to compare two related networks different by only one node unit. It results that the following cases are be considered:
• A network made of 12 ISP
• A network made of 12 DED
• A network made of 24 nodes : 12 DED and 12 IDP
• A network made of 14 IDP
• A network made of 15 DED
• A network made of 29 nodes : 14 IDP and 15 DED
Each network is represented by its adjacency matrix: C12, D12, M24, C14, D15, and M29. Moreover, in order to investigate further any effect in the inter community “knowledge sharing,” the corresponding F matrices, i.e., F24 and F29 have to be specifically used. Recall that none of these 8 matrices are symmetric.
2.5. Aggregation Matrix (or Network) Construction
The above networks, reproducing citations, contain some directed links (and UL as well). For each considered (“time-dependent”) network, an “aggregated network” can be defined though a (new) adjacency matrix, e.g., Mi,j → , etc., - for the 8 cases outlined here above. These new 8 matrices are necessarily symmetric.
3. Results
For each (16) matrix, the eigenvalues (and eigenvectors) have been calculated. The main characteristic results relevant to the present investigation are given in Table 2. To distinguish between the number of real EVs ≠ 0 or 0 is not the presently relevant subject. However, it is at once pointed out that the largest EV is of course real and positive in each case, but the magnitude of the most negative EV might be larger than the “Next to Largest” Re (positive) EV, a fortiori if the latter is negative. Thus, in Table 2, and in view of preparing the following sections and discussion, both the strictly “Next to Largest” Re (positive) EV is given but also the EV having the “Next to Largest Modulus.” It can be seen from this Table that the networks containing DED are those for which the distinction on the notion of “next to largest” EV is relevant.
4. Slow-down or Speed-up Knowledge Diffusion
It has been shown that changes of diffusion dynamics in temporal networks as compared to their static counterparts are due to the change of connectedness or conductance of the corresponding second-order aggregate network. These changes influence the process of knowledge diffusion through a slow-down or speed-up factor which can be computed based on the second-order aggregate networks corresponding to a particular non-Markovian temporal network and its Markovian counterpart. This basically consists in comparing two corresponding adjacency matrix features. In the present case, where the usual temporal aspects is masked but replaced by a sequential one (of quotations), the matter consists in comparing the original adjacency matrix and its symmetrized counterpart.
It was interestingly shown that the convergence time of random walks is related to the second largest eigenvalue of the transition matrix T. For a primitive stochastic matrix with (not necessarily real) eigenvalues 1 = λ1 > |λ2| > |λ3| ≥ … ≥ |λn|, it was shown that the number of steps k after which the total variation distance Δ(πk; π) between the visitation probabilities πk and the stationary distribution π of a random walk falls below ϵ is proportional to 1/ln(|λ2|). For a matrix T(2) capturing the statistics of two-paths in an empirical temporal network and a matrix representing the Markovian model derived from the symmetrized network, an analytical prediction for the change of convergence speed S*, due to non-Markovian properties can be derived as
where λ2 and 2 denote the second largest eigenvalue of T(2) and respectively. Thus, a diffusion slow-down exists if S*(T(2)) ≥ 1. A diffusion speed-up exists if S*(T(2)) ≤ 1. To calculate S*(T(2)), in the present cases, observe that Eq. (3) must be adapted to take into account the (“normalizing”) λ1 value; see ad hoc line in Table 2.
In the present network cases, a temporal network adjacency matrix can have its “second largest eigenvalue,” i.e., to be considered as the “next to largest” eigenvalue, either real (positive or negative, in fact) or be a c.c. eigenvalue with a large modulus.
The relevant results are given in Table 2 last line. For a global view of the data, one can rank the S*(T(2)) values in decreasing order: this corresponds to rank the networks as follows: M77, C14, C12, which have a slow-down feature, while D12, D15, M24, and M29 possess a speed-up feature.
It is deduced that
(i) The diffusion of knowledge is more difficult on the large (complete) network, but this could have been expected;
(ii) The same type of hierarchy constraint on the network size is found either for the slowing-down or speeding up processes;
(iii) However, the IDP and DED sub-networks are markedly different: the diffusion of knowledge is slower for IDP, but faster for DED; this (a priori unexpected finding) might nevertheless be “rationalized,” if one attempts to introduce some “level of scientific quality” in the behavior of the various agents. This perspective offers some opening discussion toward tying psychology, intellect, scientific knowledge to belief. However, one cannot completely neglect the fact that the DED might have more use in publishing thoughts than IDP, who might be less prone to practically publish, whence be quoted;
(iv) Another interesting point pertains to the relative influence of the agents on the (reduced, but pertinent) networks: the diffusion of knowledge is markedly in favor of the DED, since the M24 and M29 corresponding speeds are obviously on the up side.
5. Conclusion
As a conclusion, let a brief summary be given tying the “questions” to the “answers.” In the main text, it has been studied whether the diffusion of knowledge can be measured in and outside distinct communities, necessarily made of stubborn agents on small world-like networks. This speed of knowledge diffusion is obtained from the eigenvalues of the corresponding adjacency matrices for the whole set of agents and for their sub-communities. In particular, it has been found that the Neocreationist and Intelligent Design Proponents (IDP), on one hand, and the Darwinian Evolution Defenders (DED), on the other hand behave quite differently in processing the knowledge. A quantification of the slow-down or speed-up effects of information diffusion in such temporal networks, with non-Markovian contact sequences, has been made. It is observed that the diffusion of knowledge is slower in IDP and faster in DED communities. It is argued that the finding can be “rationalized,” if some “scientific quality” and “publication habit” are attributed to the agents, as common sense would suggest. This finding offers some opening discussion toward tying scientific knowledge to belief, and subsequent diffusion of both in small worlds.
Moreover, a brief observation has been made on the community size effect, and its substructure. It is observed that the diffusion of knowledge is more difficult on large networks. It is also observed that the number of triads with heterogeneous agents seems a relevant “parameter.” In the present cases, a speed-up process effect is markedly greater when two DED agents are involved, whence again likely pointing to some behavior origin in the more usual scientific arguing methods prone to such a community. Since it has been found in [16] that the origin of complex eigenvalues is related to the structure of triads, further work on the relationship between the (density of) different types of triads and the speed of knowledge diffusion should be interesting.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This paper is part of scientific activities in COST Action TD1210 “Analyzing the dynamics of information and knowledge landscapes.”
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fphy.2015.00043
Footnotes
1. ^see http://www.discovery.org/csc/
2. ^see http://www.ncseweb.org/
References
1. Vitanov NK, Ausloos MR. Knowledge epidemics and population dynamics models for describing idea diffusion. In: Scharnhorst A, Boerner K, and van den Besselaar P, editors. Models of Science Dynamics: Encounters Between Complexity Theory and Information Sciences. Berlin; Heidelberg: Springer Verlag (2012). pp. 69–125.
2. Vitanov NK, Jordanov IP, Dimitrova ZI. On nonlinear dynamics of interacting populations: coupled kink waves in a system of two populations. Commun Nonlin Sci Numerical Simul. (2009) 14:2379–88. doi: 10.1016/j.cnsns.2008.07.015
3. Vitanov NK. Breather and soliton wave families for the sine-Gordon equation. Proc R Soc Lond A (1998) 454:2409–23. doi: 10.1098/rspa.1998.0264
4. Vitanov NK. Convective heat transport in a fluid layer of infinite Prandtl number: upper bounds for the case of rigid lower boundary and stress-free upper boundary. Eur Phys J B (2000) 15:349–55. doi: 10.1007/s100510051136
5. Kantz H, Holstein D, Ragwitz M, Vitanov NK. Markov chain model for turbulent wind speed data. Physica A (2004) 342:315–21. doi: 10.1016/j.physa.2004.01.070
6. Costa LF, Oliveira ON, Travieso G, Rodrigues A, Villas Boas PR, Antiqueira L, et al. Analyzing and modeling real-world phenomena with complex networks: a survey of applications. Adv Phys. (2011) 60:329–412. doi: 10.1080/00018732.2011.572452
7. Scholtes I, Wider N, Pfitzner R, Garas A, Tessone CJ, Schweitzer F. Slow-Down vs. speed-up of information diffusion in non-markovian temporal networks. (2013). arXiv preprint arXiv:1307.4030.
8. Scholtes I, Wider N, Pfitzner R, Garas A, Tessone CJ, Schweitzer F. Causality-driven slow-down and speed-up of diffusion in non-Markovian temporal networks. Nat Commun. (2014) 5:5024. doi: 10.1038/ncomms6024
9. Galam S, Moscovici S. Towards a theory of collective phenomena: consensus and attitude changes in groups. Eur J Soc Psychol. (1991) 21:49–74. doi: 10.1002/ejsp.2420210105
10. Galam S, Jacobs F. The role of inflexible minorities in the breaking of democratic opinion dynamics. Physica A (2007) 381:366–76. doi: 10.1016/j.physa.2007.03.034
11. Martins ACR, Galam S. Building up of individual inflexibility in opinion dynamics. Phys Rev E (2013) 87:042807. doi: 10.1103/PhysRevE.87.042807
12. Scott EC. Antievolution and creationism in the United States. Annu Rev Anthropol. (1997) 26:263–89. doi: 10.1146/annurev.anthro.26.1.263
13. Greenwalt K. Establishing religious ideas: evolution, creationism, and intelligent design. Notre Dame JL Ethics Pub Pol'y (2003) 17:321.
14. Sznajd-Weron K, Sznajd J. Opinion evolution in closed community. Int J Mod Phys C (2000) 11:1157–65. doi: 10.1142/S0129183100000936
15. Lambiotte R, Ausloos M. Coexistence of opposite opinions in a network with communities. J Stat Mech Theor Exp. (2007) 2007:P08026. doi: 10.1088/1742-5468/2007/08/P08026
16. Rotundo G, Ausloos M. Complex-valued information entropy measure for networks with directed links (digraphs). Application to citations by community agents with opposite opinion. Eur Phys J B (2013) 86:169. doi: 10.1140/epjb/e2013-30985-6
17. Garcia Cantù Ross A, Ausloos M. Organizational and dynamical aspects of a small network with two distinct communities: neo creationists vs. Evolution defenders. Scientometrics (2009) 80:457–72. doi: 10.1007/s11192-008-2065-0
18. Tierney WG, Holley KA. Intelligent design and the attack on scientific inquiry. Cult Stud Crit Methodol. (2008) 8:39–49. doi: 10.1177/1532708607305125
19. Galam S. Public debates driven by incomplete scientific data: the cases of evolution theory, global warming and H1N1 pandemic influenza. Physica A (2010) 389:3619–31. doi: 10.1016/j.physa.2010.04.039
20. Galam S. Collective beliefs versus individual inflexibility: the unavoidable biases of a public debate. Physica A (2011) 390:3036–54. doi: 10.1016/j.physa.2011.03.021
21. Palevitz BA. Falling Off a tightrope: compromise and accomodation in the war between creationism and evolution. Bioscience (2000) 50:926–9. doi: 10.1641/0006-3568(2000)050[0926:FOATCA]2.0.CO;2
22. Pizzo A. The communication strategies of neocreationism between the United States and Europe. J Sci Commun. (2006) 5:1–4.
23. Pennock RT. Creationism and intelligent design. Ann Rev Genomics Hum Genet. (2003) 4:143–63. doi: 10.1146/annurev.genom.4.070802.110400
24. Rotundo G, Ausloos M. Organization of networks with tagged nodes and biased links: a priori distinct communities. The case of intelligent design proponents and darwinian evolution defenders. Physica A (2010) 389:5479–94. doi: 10.1016/j.physa.2010.07.029
25. Meyer, C. Matrix Analysis and Applied Linear Algebra, ch. 8.3. (2000). Available online at : http://www.matrixanalysis.com/Chapter8.pdf
Keywords: diffusion of controversial knowledge, stubborn communities, small world networks, neocreationists, evolutionists
Citation: Ausloos M (2015) Slow-down or speed-up of inter- and intra-cluster diffusion of controversial knowledge in stubborn communities based on a small world network. Front. Phys. 3:43. doi: 10.3389/fphy.2015.00043
Received: 25 February 2015; Accepted: 31 May 2015;
Published: 19 June 2015.
Edited by:
Serge Galam, Centre National de la Recherche Scientifique, FranceReviewed by:
Anna Carbone, Politecnico di Torino, ItalyWoo-Sung Jung, Pohang University of Science and Technology, South Korea
Copyright © 2015 Ausloos. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marcel Ausloos, School of Management, University of Leicester, University Road, Leicester LE1 7RH, UK,bWE2ODNAbGUuYWMudWs=;bWFyY2VsLmF1c2xvb3NAdWxnLmFjLmJl
 Marcel Ausloos
Marcel Ausloos