Biochemical reactions in crowded environments: revisiting the effects of volume exclusion with simulations

Molecular crowding is ubiquitous within cells and affects many biological processes including protein-protein binding, enzyme activities and gene regulation. Here we revisit some generic effects of crowding using a combination of lattice simulations and reaction-diffusion simulations with the program ReaDDy. Specifically, we implement three reactions, simple binding, a diffusion-limited reaction and a reaction with Michaelis-Menten kinetics. Histograms of binding and unbinding times provide a detailed picture how crowding affects these reactions and how the separate effects of crowding on binding equilibrium and on diffusion act together. In addition, we discuss how crowding affects processes related to gene expression such as RNA polymerase-promoter binding and translation elongation.

1. Introduction

The interior of cells is a crowded environment, quite different from the dilute solutions usually studied in vitro [1–3]. For example, in bacterial cells, macromolecules can occupy up to 40 % of the volume during phases of rapid growth [4], and the water content can drop far below this level upon exposure to increased osmotic pressure [5]. The importance of molecular crowding for understanding processes in cells is increasingly appreciated. Its consequences have been studied extensively in the context of protein-protein binding [2, 6], protein folding [7–10], enzyme activity [11–13], and gene regulation [14–18]. Beyond these fundamental aspects, crowding has direct consequences to understand drought-tolerance of plants [19, 20] and possibly neurodegenerative diseases in humans that are based on protein aggregation [21, 22].

Molecular crowding is ubiquitous, and the complexity of its direct and indirect effects can be bewildering. Some effects of crowding are generic [2, 3]. For example, binding equilibria are typically shifted toward the bound state [2, 6, 23] and diffusion is slowed down [24–26]. In the case of enzymes, both effects apply to the binding of the substrate to the enzyme, with opposite consequences. In addition, the reaction rate may be affected by specific changes in the molecular configuration of the enzyme that are induced by crowding or, in the case of multi-subunit enzymes, by increased binding between the subunits. As a result, different enzymes can exhibit rather different behavior upon increased crowding, as illustrated by the tabulated collection of experimental results in Zhou et al. [13].

In this article, we address the generic effects of crowding. We use a simple lattice model to disentangle the different contributions to the effects of crowding due to binding equilibria and diffusion as well as the dependence on the particle size. We specifically study molecular binding and enzymatic reactions. As a complement, we perform simulations with the reaction-diffusion simulation package ReaDDy [27]. On the one hand, our approach is tutorial in nature and provides a simple rationalization and illustration of well-studied effects. On the other hand, it also provides some new insight. For example, in the case of a receptor-ligand pair, histograms of the binding times allow us to reconcile the reduced diffusion rate with the surprisingly crowding-independent binding rate.

Even though the effects we consider are generic, our main interest here is in gene expression, in particular reaction involving the macromolecular machines that process the genetic information, RNA polymerase and ribosomes. These machines are rather large molecular complexes, and for molecules of such size diffusion is strongly reduced [28]. As a consequence, reactions are expected to be diffusion-limited or close to the diffusion limit. Specifically for ribosomes, it was recently proposed that the slow diffusion of ternary complexes (tRNAs charged with amino acids and GTP-activated elongation factor Tu) imposes a fundamental limitation on the speed of translation, which necessitates the large concentrations of elongation factors in rapidly growing bacteria [29] (elongation factor Tu is the most abundant protein in E. coli [30]). Such a limitation would be aggravated during growth under increased osmotic pressure. Likewise, RNA polymerase is a big molecular machine that diffuses slowly in the cell, such that binding to promoters, which usually determines the rate of transcription, might become diffusion limited.

The paper is organized as follows: We start by introducing the computation methods we use, the lattice model and ReaDDy. Then we study simple implementations of two elementary reactions, binding between two binding partners (which could represent two proteins or molecular complexes or a protein and its binding site on DNA) in Section 3 and a diffusion-limited enzymatic reaction in Section 4. Both cases are based on a ligand or substate that needs to find a target site (the binding partner or enzyme) by diffusion. In Section 5, we study the effects of the size of the crowders and in Section 6 we combine everything to address an enzymatic reaction with Michaelis-Menten kinetics. We close with an extended discussion, where we apply the insight from these simulations to several processes relevant to gene expression, in particular to the speed of translation and to promoter finding by RNA polymerase.

2. Simulation Methods

2.1. Lattice Model

The effects of molecular crowding on biochemical reactions was studied using Monte Carlo simulations of particles on a three-dimensional lattice with periodic boundary conditions. The simulation box has the volume V Ωl³, where l is the lattice spacing and Ω the total number of lattice sites, chosen as the linear extension of the smallest particle type. The system contains three types of particles: Target particles (receptors or enzymes), particles searching for the target (ligands or substrates, respectively) and crowders. Their numbers are denoted as R, L, and C, respectively. For now, all particles are taken to occupy exactly one lattice site. We will consider particles of different sizes below, but throughout this study, all molecules on our lattice simulations are taken to have a square geometry. We will consider a single target particle (receptor or enzyme) and take this particle to be static in the center of the simulation box. A ligand bound to the target particle is taken to occupy the same lattice site as the target particle. The other particles are initially placed randomly on the lattice, occupying the volume fraction ϕ ≈ (R + L)/Ω, see Figure 1A.

FIGURE 1

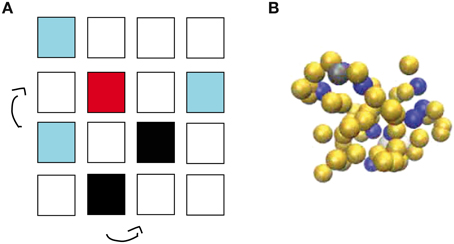
Figure 1. Simulation methods used in this work. (A) Schematic view of the lattice implementation, in which L ligands (light blue) and C crowders (black) diffuse by hopping to one of the six nearest neighbor lattice sites until a ligand finds a target (red). Molecules have square geometry and diffusion is only allowed if the site of destination is unoccupied. Note that the simulations use a three-dimensional lattice rather than the two-dimensional one depicted schematically here. (B) Snapshot from the off-lattice simulation package ReaDDy. L ligands (dark blue), a single target (gray) and C crowders (yellow) diffuse and react in a simulation box with volume V.

At each simulation time step (of duration τ), the crowders and ligands move to each neighbor site with probability 1/6. This move is accepted if the chosen neighboring lattice site is free and rejected if it is occupied. Thus, steric effects or excluded volume are the only interactions considered, and on a free lattice, these particles diffuse with diffusion constant D = l²/(6τ). These moves are performed in a random-sequential fashion: In every simulation step, we randomly choose L times a ligand and C times a crowder and update their position, thus that on average all particles are updated once per simulation step. If a ligand finds the target and the target is free, the complex ligand-target is always formed. Thus, this reaction is taken as diffusion-limited. Only when the target is already occupied by another ligand, the move to form the complex is rejected. Once the complex has been formed, the bound ligand can dissociate from the target with the unbinding rate k_ub. Below, we will consider different scenarios of complex dissociation to describe receptor-ligand complexes and enzyme-substrate reactions.

2.2. Off-lattice Simulations (ReaDDy)

In addition to the lattice implementation, we run simulations with the off-lattice simulation software ReaDDy [27], see Figure 1B. This simulation package describes biochemical reaction-diffusion processes via interacting spherical molecules. Their diffusion is described by a memoryless Langevin equation, which is solved numerically with an Euler discretization with a constant time step Δt,

$\begin{array}{cc}x(t+\Delta t)=x(t)-D\Delta t\frac{\nabla V(x(t))}{k_{B}T}+\sqrt{2D\Delta t}{\eta }_t.& (1)\end{array}$

Here, x(t) is a three-dimensional vector indicating particle positions at time t, D is the reactant diffusion constant, V(x(t)) is the particles' interaction potential, k_B is Boltzmann's constant, T is the temperature and η is a normally distributed random number with zero mean and variance one.

The steric interactions implemented in ReaDDy are given by a harmonic potential, in which the potential force constant k_pot is optimized by finding the largest simulation time step Δt for which there is no overlapping between particles [27]. Throughout this study we use the recommended potential force constant k_pot = 50 kJmol⁻¹ nm⁻¹ [27]. In ReaDDy, reactions are understood as uni- or bimolecular reaction events in which particles either are transformed into other particles, or events that lead to molecule synthesis or degradation. Thus, the concentration of molecules as a function of time can be described by the following set of ordinary differential equations [31]:

$\begin{array}{cc}\frac{d{C}_{P1}(t)}{dt}=\dots =\frac{d{C}_{Pn}(t)}{dt}=k^1{C}_R(t).& (2)\end{array}$

for the first order molecular reactions and

$\begin{array}{cc}\frac{d{C}_{P1}(t)}{dt}=\dots =\frac{d{C}_{Pn}(t)}{dt}=k^2{C}_{R_1}(t)C_{R_2}(t),& (3)\end{array}$

for the second order molecular reactions. In the latter expressions, C_Rn(t) and C_Pn(t) are the concentration of the nth reactant and product species, and k¹ and k² are the first and second order reaction rates, respectively. We note that the macroscopic second order reaction rate k² is the product of the probability for the reactants to be in close contact with the rate at which the reactants in contact transform into the product, k²_micro. Since diffusion is explicitly simulated by ReaDDy, only k²_micro is set as an input in the simulations. For all simulations, we consider k²_micro = 10⁸ s⁻¹. Computationally, a reaction takes place with a reaction probability p_rea, obtained from the Poisson probability of having at least one reaction event with rate k^1,2_micro within time interval Δt, e.g., p_rea = 1 − e^{k1,2_micro Δt}. We note that the molecular diffusion constant D and the reaction rates k¹ and k² are set in ReaDDy assuming dilute conditions, e.g., ϕ = 0. By increasing levels of molecular crowding the kinetics and thermodynamics of the reactions are influenced.

To compare the results from both types of simulations, the length and time units of the lattice simulations must be converted to nanometers and seconds. In ReaDDy, we run simulations with spherical particles of radius r = 3 nm that diffuse within a solid square lattice of volume V = 49× 49 × 49 nm³ = 1.13 × 10⁵ nm³. This volume is chosen in such a way that the total volume is 1000 times the molecules' volume, as in the lattice simulation. This choice defines our lattice in the 10 × 10 × 10 lattice constant to correspond to l = 4.9 nm. The time scale τ of the lattice simulations then corresponds to l²/(6D), which can be used to convert the reaction rates. However, a small difference remains between the capture areas from which binding occurs, so that the binding probabilities P_b are not exactly the same in both methods. To correct for that difference, we adjust the unbinding rate, such that in the absence of crowding the binding probabilities agree between the two methods. This adjustment corresponds to an approximately two-fold increase of the unbinding rate, which thus corrects the corresponding two-fold increase of the binding rate due to different “target volumes.” This adjustment procedure can be viewed as an instance of renormalizing the binding binding/unbinding rate by including unbinding events that are too short for the particle to diffuse away in the bound state [32].

3. Effects of Crowding on Molecular Binding

We start by considering the simple case of binding between a receptor and a ligand in the presence of crowders. We emphasize that we consider a rather generic scenario here, where the receptor and ligand do not necessarily describe the typical case of a protein receptor and a small molecule ligand, but could, for example, also correspond to two proteins, to a regulatory binding site on DNA and a transcription factor, or even to an enzyme and its substrate (provided the actual reaction is very slow, as we will discuss below). Effects of excluded volume on such a reaction have been studied extensively in the past; in particular, it is well-known that crowding shifts the binding equilibrium toward the bound state [2, 3, 6]. The lattice model allows us to provide a rather intuitive explanation of these effects. In addition, we use our simulations to investigate the effects of crowding on the kinetics, which are more subtle.

3.1. Binding Equilibrium

In the simulations of receptor-ligand binding, a ligand reaching the target particle (receptor) forms the receptor-ligand complex unless the receptor is already occupied by another ligand. Thus, the binding reaction is diffusion-limited (a reaction-limitation could be introduced by accepting the binding move with a probability smaller than one but we do not consider this case here). The complex can dissociate again with a rate k_ub. Unbinding is implemented by randomly choosing a neighbor site of the complex and moving the ligand there, provided that site is free. At the same time, the receptor becomes free again and available for another binding event. Thus, the binding reaction, L + R ⇌ LR, is fully reversible and can be characterized by the dissociation constant K_d,0, where the index zero indicates the absence of crowder molecules.

Figure 2A shows results from simulations of a lattice with volume V = 10 × 10 × 10 l³, i.e., with Ω = 1000 lattice sites, where crowders, ligands and the receptor all occupy one lattice site each. In dilute conditions, the unbinding event is set to take place (unless otherwise stated) at a rate k_ub(0) = 1/60 τ⁻¹. To ensure equilibration, the simulations are run until 10,000 binding events have taken place. Figure 2A shows the probability P_b that the receptor is occupied, as a function of the number of ligands for different values of volume occupation ϕ. P_b is determined as the ratio of the time the receptor was occupied and the total simulation time. The symbols represent our simulation results for ϕ = 0, 0.2, 0.3, and 0.5, the lines indicate the corresponding results from the binding equilibrium condition (no free parameters, discussed below), P_b = C/(C + K_d(ϕ)), where the dissociation constant is expressed in units of numbers of molecules in the simulation box. Although qualitatively the behavior is similar for all values of ϕ, increasing volume occupation increases the receptor occupancy by shifting the curves to the left. Thus, as ϕ increases, less ligands are needed to saturate the receptor. For large numbers of ligands, the effect of the crowders is negligible, because the receptor is already saturated. In Figure 2B we plot the dissociation constant K_d(ϕ), which is obtained by interpolation from the simulations as the ligand concentration for which P_b = 0.5, as a function of the volume occupation ϕ. K_d(ϕ) decreases linearly with the volume fraction, indicating the shift of the equilibrium toward the bound state.

FIGURE 2

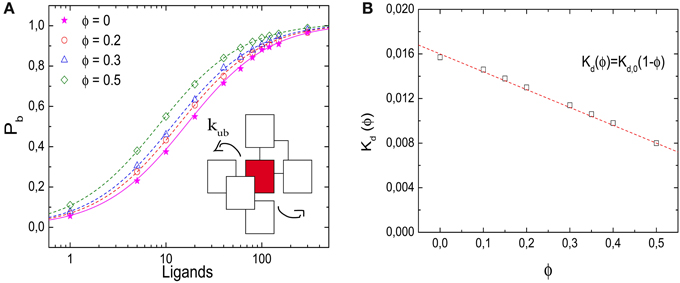
Figure 2. Effects of molecular crowding on binding equilibria. (A) Probability for the receptor to be occupied, P_b, as a function of the number of ligands for four different values of volume occupation, ϕ = 0, 0.2, 0.3, and 0.5. Crowding shifts the curves toward lower ligand concentrations. Simulation data are in agreement with Equation (6) (lines). (Inset) Representation of the unbinding reaction. The ligand steps from the target to one of the six nearest neighbor sites with a rate k_ub. (B) Dissociation constant K_d(ϕ) as a function of ϕ. The data points are obtained from the simulations by interpolation (see text) and the line is K_d(ϕ) = K_d,0(1 − ϕ). Simulation parameters: V = 10 × 10 × 10 l³, D = 1/6 l²τ⁻¹ and K_d,0 = 1/60.

Since the effect of crowders and excluded volume on the dissociation constant is purely thermodynamic rather than kinetic, it can be understood based on the statistics of states of the lattice with the receptor free and occupied, see [33]. We include this argument here for completeness. At equilibrium, the probability for the receptor to be occupied P_b, is obtained as the ratio of the number of possible states S_b, in which a ligand is bound to the receptor and the total number of states, i.e., S_b plus the number of states when the receptor is free, S_ub. We note that the states with an occupied receptor are weighted with the Boltzmann factor due to the binding energy E_b,

$\begin{array}{cc}{P}_b=\frac{S_b{e}^{-E_b/kT}}{S_b{e}^{-E_b/kT}+S_{ub}}=\frac{1}{1+\frac{S_{nb}}{S_b}{e}^{E_b/kT}}.& (4)\end{array}$

The ratio S_nb/S_b is obtained by dividing all the possible ways in which C crowders and L ligands can be organized in a lattice with Ω lattice sites, over all the possible ways in which C crowders and (L − 1) ligands can be distributed in Ω lattice sites. This ratio is thus given by

$\begin{array}{cc}\frac{S_{ub}}{S_b}=\frac{\left(\begin{array}{c}\Omega \\ L+C\end{array}\right)\left(\begin{array}{c}L+C\\ L\end{array}\right)}{\left(\begin{array}{c}\Omega \\ L+C-1\end{array}\right)\left(\begin{array}{c}L+C-1\\ L\end{array}\right)}\approx \frac{\Omega }{L}\left(1-\frac{(L+C)}{\Omega }\right)=\frac{(1-\varphi )}{L/\Omega },& (5)\end{array}$

with L/Ω being the dimensionless ligand concentration. Introducing the latter expression into Equation (4) leads to

$\begin{array}{cc}{P}_b=\frac{1}{1+\frac{K_d(\varphi )}{L/\Omega }},& (6)\end{array}$

with the crowding-dependent dissociation constant K_d(ϕ) = e^E_b/kT (1 − ϕ). The limiting value for ϕ = 0 is the microscopic dissociation constant for the binding reaction without interfering crowders, K_d,0 = e^E_b/kT. We note that this dissociation constant as well as the ligand concentration L/Ω are dimensionless, but can be converted to per-volume units as [L] = L/V = l⁻³ × L/Ω and likewise for the dissociation constants. The microscopic dissociation constant K_d,0 can also be related to the kinetic parameters of the model via the detailed balance condition, k_ub/τ⁻¹ = e^E_b/kT. The latter relation is used to determine the lines in Figures 2A,B.

Equation (6) thus shows that, as ϕ increases, the dissociation constant is diminished and a lower ligand concentration is needed to saturate the receptor as observed in the simulations. An alternative interpretation of the result is that the volume is reduced by the excluded volume, so that the available volume is Ω(1 − ϕ) l³, which effectively increases the ligand concentration. We note however that this interpretation is only valid in the simplest case that we consider here, as it depends on the assumption that all particles have the same size. In that case, the available volume is independent of the spatial arrangement of the particles, which is not the case for particles of different sizes, as discussed below.

3.2. Kinetics of Binding and Unbinding

Next we consider the impact of the crowders on the kinetics of binding and unbinding. To that end, we determine binding and unbinding rates from our simulations as the inverse of the average time the receptor is free before a binding event and occupied before an unbinding event. In Figure 3A we plot the binding rate k_b for three different ligand concentrations as a function of the occupied volume fraction. The binding rate is given by 1 l³ L⁻¹ τ⁻¹ and depends on the ligand concentration, but not the level of crowding, suggesting that diffusion of the ligand to the target is not affected by crowding. The observation of a constant binding rate indicates that the effect of crowding on the dissociation constant discussed above is entirely due to the decrease of the unbinding rate k_ub(ϕ). In Figure 3B we plot k_ub(ϕ) as a function of the excluded volume fraction ϕ. As expected, k_ub(ϕ) decreases linearly as the level of ϕ increases, consistent with the expression k_ub = K_d,0τ⁻¹ (1 − ϕ). Such a linear decrease can be understood as a simple exclusion rule for the complex dissociation step, where the ligand moves from the receptor site to one of its neighbors. The rate for that step is simply reduced by a factor corresponding to the probability that this site is free, (1 − ϕ). We can thus conclude that for the simple case with crowders and ligands of the same size, the shift of the binding equilibrium toward the bound state is caused by crowders blocking unbinding.

FIGURE 3

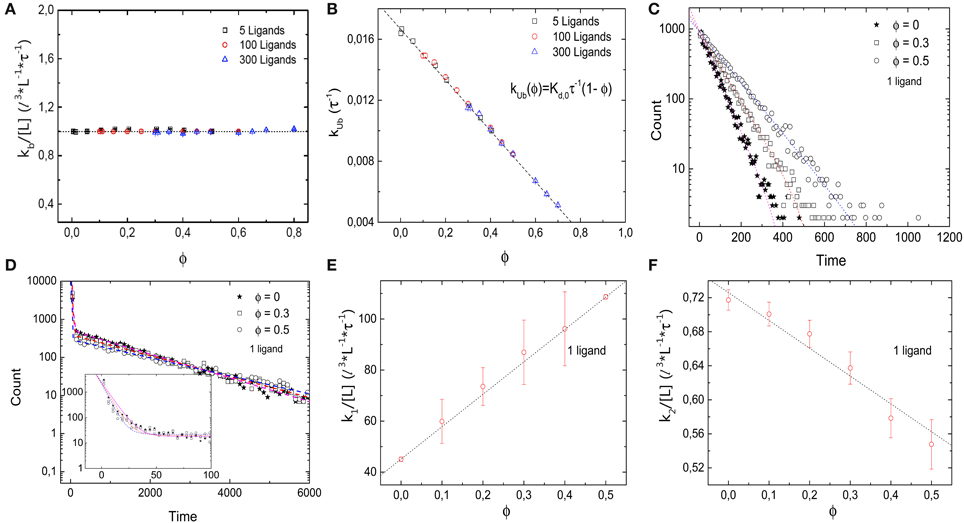
Figure 3. Kinetics of the simple binding reaction model. (A) Binding rate k_b and (B) unbinding rate k_ub, as a function of the volume occupation fraction ϕ. k_b remains constant for all values of ϕ. Thus, diffusion of the ligand toward the target is not affected by crowding. k_ub decays as ϕ increases, in agreement with the expression k_ub = K_d,0τ⁻¹ (1 − ϕ). (C) Histograms of the duration of 10,000 unbinding events for the case of a single ligand for different values of ϕ. The data follow a single exponential. (D) Histograms of the duration of 10,000 binding events for ϕ = 0, 0.3, 0.5 and a single ligand. A double exponential decay is observed with a fast and slow component in the binding kinetics. Inset: closeup of the histogram for short times with smaller bin size. (E) Fast rebinding is enhanced when levels of molecular crowding increase. (F) Slow rebinding is negatively affected when ϕ increases, since the diffusion of the ligand toward the target is hindered. Simulation parameters as in Figure 2.

The rates presented so far are based on the mean values of times between binding and unbinding events. To get a more detailed picture of the effects of crowders, we next consider histograms of these times. Figure 3C shows the histograms of the durations of the bound state before unbinding for the case of a single ligand and three different volume occupation values. The simulation data follow a single exponential (correlation coefficient of fit R² = 0.984, 0.995, and 0.998 for ϕ = 0, 0.2, and 0.5, respectively), with a characteristic time scale that increases as the volume occupation increases, in agreement with an unbinding rate reduced by crowding. For the binding times, the picture is more complex: Figure 3D shows the histograms of the durations of all binding events for the same three cases. In all cases, the simulation data can be described by a double exponential (correlation coefficient of fit R² = 0.999 for the three values of ϕ = 0, 0.2, and 0.5), P(t) = N₁ exp(−k₁t) + N₂ exp(−k₂t), which indicates the existence of a fast and a slow component in the binding kinetics. The corresponding two rates k₁ and k₂ are plotted individually as functions of the volume fraction in Figures 3E,F, respectively. These plots show that they exhibit opposite dependencies on crowding. The rate for rapid rebinding, k₁, increases with increasing volume fraction ϕ, while the rate of the slow component decreases. This result can be interpreted in the following way: crowding enhances rapid rebinding of a ligand still close to the receptor upon unbinding, as the crowders hinder the diffusive motion of the ligand away from the receptor and thus keep it close for a longer time. At the same time, the crowders hinder the diffusive motion to the receptor when the ligand needs to diffuse there from further away. Thus, the constant binding rate, independent of the presence and concentration of crowders conceals the more subtle balance between two opposing effects, namely an increased rate for rapid rebinding and a reduced rate for binding during longer periods of unoccupied receptor. Both effects are related to an effect of crowding on diffusion, but in one case away from the target and in the other toward the target. One could however, consider coarse-grained rates and consider the short-lived unbinding events as part of the bound state [32]. In that case, the binding rate would be reduced by crowding and the unbinding rate would be reduced even more.

3.3. Binding in Off-Lattice Simulations

In addition, we simulated the same receptor-ligand binding reaction using the off-lattice reaction-diffusion dynamics software ReaDDy [27]. These simulations allow us to cross-check the results and to test for possible lattice artifacts. Figure 4A shows the probability P_b that the target is occupied as a function of the number of ligands for different values of ϕ. Comparable quantitative results are found for both implementations of molecular crowding. As in the lattice simulations, increasing volume occupation levels ϕ leads to a decrease in the dissociation constant. In Figures 4B,C we show the rates of binding and unbinding as functions of the volume occupation. The binding rate is independent of the volume fraction, while the unbinding rate decreases as the volume fraction of crowders increases. Just as in the lattice model, the unbinding rate follows k_ub = k_ub(0)(1 − ϕ). We can thus conclude that the effects of crowding on P_b are due to the slower dissociation rate. Next, in Figure 4D we plot the histograms of 1700 binding events for the cases ϕ = 0 and 0.1. As in the lattice implementation, the histograms follow a double exponential distribution (R² = 0.996 and 0.998 for ϕ = 0 and 0.1, respectively). Thus, simulations with ReaDDy also show a slow and a fast component of the binding kinetics. We note that although for both implementations the simulation time increases quadratically with particle number, the simulation times in ReaDDy are about 2 orders of magnitude larger than in our implementation (data not shown). This is primarily due to the computationally expensive evaluation of the steric potential in ReaDDy.

FIGURE 4

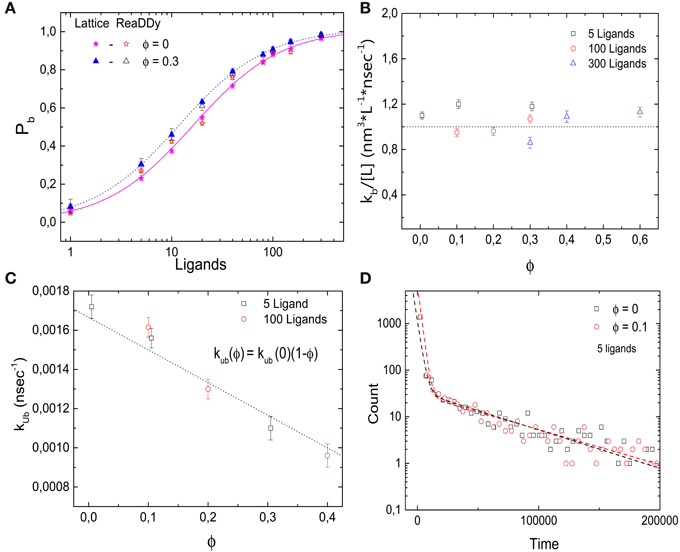
Figure 4. Effects of molecular crowding on binding equilibria simulated with ReaDDy. (A) Probability for the target (receptor) to be occupied P_b as a function of the number of ligands, for two levels of volume occupation ϕ = 0 and 0.3. Crowding shifts the probabilities towards lower number ligands. Similar behavior is observed for the lattice implementation and for ReaDDy. (B) Binding rate k_b stays constant as the levels of volume occupation increase. (C) Unbinding rate decays as ϕ increases, following the relation k_ub = k_ub(0)(1 − ϕ). (D) Histograms of 1700 binding events for two different values of volume occupation ϕ = 0 and 0.3. A double exponential decay is observed, indicating the presence of a slow and a fast component of the dynamics, as in the lattice implementation. Simulation parameters: V = 49 × 49 × 49 nm³, k_ub(0) = 1.6 × 10⁶ s⁻¹, r = 3 nm, D = 166.6 μm² s⁻¹ and T = 20°C. The data from lattice simulations in (A) are the same as in Figure 2A.

4. Effect of Crowding on Diffusion-Limited Reactions

We have seen above that crowders do not affect the rate of formation of the receptor-ligand complex, because they suppress binding events involving large-distance diffusion of the ligand to the receptor, but also enhance (re-)binding for ligands close to the receptor and the two effect compensate each other. We now consider the reaction between an enzyme (replacing the receptor) and its substrate (replacing the ligand). Specifically, we consider a reaction that is diffusion-limited and very efficient, converting every incoming substrate into the corresponding product P, i.e., we consider the irreversible reaction L + R → LR → P + R. In contrast to the receptor-ligand binding considered above, in this case, immediate rebinding of the substrate is not possible, because the released molecule is the product rather than the substrate. Thus, one can expect that the balance between the different effects of the crowder is perturbed and different behavior can be expected in this case. Clearly, the reaction we consider here is a limiting case; a more general and more realistic scenario, namely Michaelis-Menten kinetics, that allows both the unbinding of the substrate and release of the product will be considered below.

4.1. Lattice Simulations

We study the enzyme-substrate reaction under steady-state condition with constant substrate and product concentrations. To implement this case, we use the same simulations as above with only a difference in the unbinding process. Instead of unbinding of the ligand, we now simulate a reaction that transforms the substrate into the product. In addition, we need to implement an additional reaction that keeps the substrate and product concentrations constant. In our lattice simulation, these two events are implemented in one single step: When a substrate is bound to the enzyme (i.e., occupies the target site), the reaction occurs with rate k_r and simultaneously the product is released and removed from the simulation and a new substrate molecule is introduced at a random position. Thus, we keep the product concentration zero and the substrate concentration at its initial value. Effectively, the reaction is described as a unbinding process to a random position in space rather than a neighbor site of the enzyme. Clearly, this dynamics does not satisfy detailed balance; energy input is required to keep the concentrations and thus the chemical potential constant.

In Figure 5A, we plot the probability that the target site, the enzyme, is occupied as a function of the number of substrates in the box. In contrast to the ligand-receptor binding reaction considered above, increased crowder numbers now shift the function to the right, that is, toward larger ligand numbers, so that the occupation of the enzyme (as well as the overall reaction rate) is reduced by the crowders. We note that the effect is rather modest, but nevertheless it is important that the effect is the opposite of what we observed above. Although the process does not correspond to a binding equilibrium, the data are well-described by Equation (6), with an effective dissociation constant K*_d(ϕ) = k_r/k_b, where k_r is the reaction rate and k_b the diffusion-limited binding rate. The effective dissociation constant (determined as the substrate concentration for which P_b = 0.5) is plotted in Figure 5B as a function of the volume fraction of crowders. It increases with increasing volume fraction and can be described by

$\begin{array}{cc}{K}_d^{\ast }(\varphi )=\frac{k_r}{k_b}=\frac{k_r}{k_b^0{(1-\varphi )}^{\kappa }}& (7)\end{array}$

with κ ≃ 0.5 (obtained from the fit to the binding rate below).

FIGURE 5

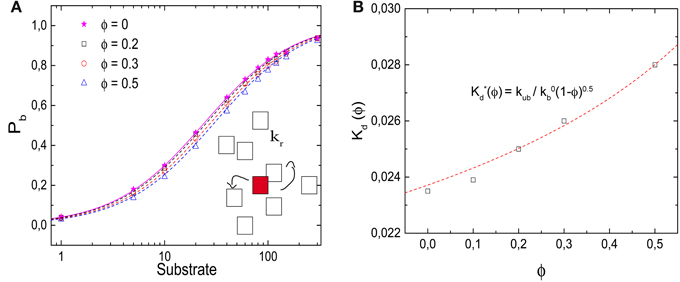
Figure 5. Effects of molecular crowding on a diffusion-limited reaction. (A) Probability P_b for the target (enzyme) to be occupied P_b as a function of the number of substrates, for ϕ = 0, 0.2, 0.3, and 0.5. Molecular crowding shifts P_b toward larger number of ligand. Thus, more ligands are needed to saturate the receptor when ϕ increases. (Inset) Representation of the reaction model, in which a product P is synthesized with a rate k_r. (B) Dissociation constant K*_d(ϕ) (obtained as the substrate concentration for which P_b = 0.5) as a function of ϕ, which increases as a function of ϕ. The line is obtained from Equation (7) with κ = 0.5, as obtained from the fit in Figure 6B. Simulation parameters as in Figure 2, and k_r = 1/60 τ⁻¹.

This functional form is not entirely surprising: Our reaction is diffusion-limited, thus the binding rate is proportional to the diffusion coefficient (k_b = 4πσ D, where σ ≃ l is the reaction radius of the interacting particles). Experiments for different concentrations and species of crowding agents have shown that the change in the diffusion constant of different proteins due to crowding can be described by the phenomenological expression D(ϕ)/D(ϕ = 0) = (1 − ϕ)^κ [15, 24]. In the presence of different crowding agents, diffusion measurements for the protein carbon monoxide hemoglobin have been fitted with a value of κ = 0.36 [15, 24].

That our result for the effective dissociation constant shows the same dependence as experimentally observed for diffusion indicates that, in contrast to the binding reaction studied above, here the entire effect of crowding is via the (diffusion-limited) binding rate. This is indeed the case, as one can see in Figures 6A,B, where we plot the reaction rate (which serves as an effective unbinding rate) and the binding rate individually as functions of the volume fraction, respectively. The bare reaction rate is unaffected by crowding, while the binding rate decreases with increasing volume fraction, with the same functional dependence as the effective dissociation constant,

$\begin{array}{cc}{k}_b(\varphi )=k_b^0{(1-\varphi )}^{\kappa }.& (8)\end{array}$

FIGURE 6

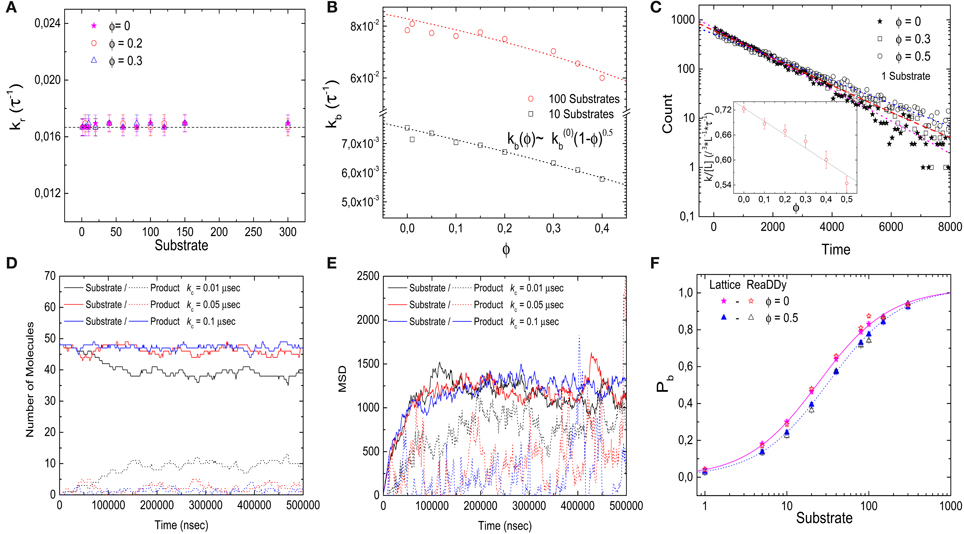
Figure 6. Kinetics of the diffusion-limited reaction. (A) Reaction rate k_r as a function of the number of substrate molecules for different levels of volume occupation ϕ. k_r stays constant and has a value of k_r = 1/60 τ⁻¹ for all substrate numbers and levels of ϕ. (B) Binding rate k_b decays as ϕ increases. The simulation data is fitted with Equation (8), resulting in κ ≃ 0.5 (lines). (C) Binding time histograms fitted with a single-exponential. (Inset) The characteristic time increases as the levels of volume occupation increase. (D,E) Trajectories of the implementation of the diffusion-limited reaction with ReaDDy. Number of particles (D) and mean square displacement (E) from the target as functions of time for different charging rates. The solid lines represent the substrate particles (ligands) that can bind and react, the dashed lines represent the product that needs to be recharged with rate k_c before it can bind again. (F) Comparison of the binding probability P_b as a function of the number of ligands at different crowding levels for ReaDDy simulations and the lattice model (data from Figure 5A). Simulation parameters (ReaDDy): V = 49 × 49 × 49 nm³, k_r = 1.6 × 10⁶ s⁻¹, r = 3 nm and T = 20°C.

This dependence was used for the fit to determine κ ≃ 0.5 (with correlation coefficient R² = 0.98 and 0.96 for 10 and 100 substrates, respectively). As a side remark, we note that the results for the binding rate of this reaction can be used to determine the effect of crowding on the diffusion coefficient, which would be more difficult to obtain from the mean square displacement due to the effect of confinement in the finite simulation volume.

Next, we consider the histograms of the ligand binding times, which are shown in Figure 6C. In contrast to the binding reaction considered above (Figure 3D), the simulation data for this reaction are well-described by a single exponential (correlation coefficient of fit R² = 0.998, 0.995, and 0.998 for ϕ = 0, 0.3, and 0.5, respectively). When ϕ is increased, the characteristic time increases, that is, the ligand-receptor encounter needs more time to take place. This result corresponds to the slow component of the binding scenario discussed above. In fact the two results show good quantitative agreement. We therefore conclude that our description of a diffusion-limited reaction completely uncouples the effect of molecular crowding on diffusion from the effect on binding equilibria.

4.2. Off-Lattice Simulations

Next, we implement this reaction in ReaDDy. We note that the reaction described on the lattice is idealized in the sense that removal of the product and re-introduction of substrate to keep the substrate concentration constant occur simultaneously at different positions on the lattice. For the off-lattice case, this idealization is less straightforward and it is easier to uncouple these processes. Thus, we include an additional reaction in these simulations: A product can be converted back into a substrate with rate k_c. Indeed such processes are realized for example in translation, where tRNAs leave the ribosome uncharged, i.e., not carrying an amino acid and get recharged by tRNA synthetases. The product constitutes an additional molecular species which we take to diffuse with the same diffusion coefficient as the substrate, but not to bind to the enzyme/target.

To compare the ReaDDy simulations with our lattice model, two difficulties must be solved: In the first place, we want to keep the substrate (charged ligand) concentration as unaffected as possible. On the other hand, the product or uncharged ligand must diffuse far from the receptor and be charged at a random position within the simulation box. These two requirements are antagonistic, meaning that on average, fast recharging implies short diffusion, and long diffusion implies slow recharging. Thus, we run simulations for different values of the recharging rate k_c in order to obtain an adequate value to simulate our ideal reaction.

Figure 6D shows simulation time courses for the number of molecules with 50 charged and no uncharged ligands as initial condition. For a small recharging rate, k_c = 0.01 μs⁻¹, the charged ligand number decreases to about 40 molecules. For a fast charging rate k_c = 0.1 μs⁻¹, the charged ligand number stays almost constant at 50 molecules with slight fluctuations. However, the mean square displacement of the substrate and product particles from the origin of the simulation box, which we use as a measure of the distance of the target, shows that for the high recharging rate, the products (uncharged ligand) are on average closer to the target than the substrate/charged ligand. Even for the low recharging rate, a small difference in mean square displacement can still be seen. To balance the two requirements, we therefore used an intermediate charging rate of k_c = 0.05 μs⁻¹. For this value, the number of charged ligands does not change drastically (Figure 6D), and the uncharged ligand diffuses far from the ligand before it gets recharged, see Figure 6E.

Using this intermediate value of the recharging rate (and all other simulation parameters as above), we determine the target occupation P_b as a function of the number of ligands for different levels of crowding (Figure 6F). As the volume occupation increases, P_b is shifted to the right, toward larger ligand concentrations, in quantitative agreement with the lattice simulations.

5. Effects of Crowder Size

So far, we have only considered crowders with the same size as the diffusing ligand or substrate molecules. However, effects of molecular crowding on biochemical reactions are known to be dependent on the reactants' size and geometry [6]. Specifically, large particles experience entropic attraction forces in the presence of smaller crowders. Such forces are known as depletion forces and have been studied extensively, both theoretically and experimentally [34, 35].

Here we are interested in the case of crowders smaller than the ligand/substrate. In the lattice simulations we thus consider ligands occupying more than one lattice site, specifically cubic particles occupying 8 sites. We implemented this situation in two ways, explicitly with crowders occupying a single site and ligands occupying n = 8 sites (small crowders model, SC) and in an approximate way, where the different sizes are taken into account implicitly, by allowing up to n = 8 crowders to occupy the same site, while the presence of a single crowder already excludes a ligand from that site (multiple crowders model, MC). In the latter, n is the maximal number of crowders allowed to occupy the same lattice site (which can have any integer value, while in the first model only sizes n = k³ with integer k are possible). We note that in the first implementation, the lattice constant corresponds to the size of the crowder, while in the second it corresponds to the size of the ligand. Thus, to compare the two implementations, one needs to account for the different unit lengths as well as the corresponding different unit times, which are defined via the diffusion over the lattice spacing.

The effect of the crowders on the binding equilibrium can be calculated in the same way as above, by counting the number of configurations S_ub and S_b by distributing L or L − 1 ligands and C crowders on the lattice [33]. This leads to the probability that the receptor is occupied as given by

$\begin{array}{cc}{P}_b=\frac{1}{1+\frac{K_d(\varphi )}{[L]}}\text{with}{K}_d(\varphi )=K_{d,0}{(1-\varphi )}^n.& (9)\end{array}$

Thus, small crowders have a stronger effect on binding than crowders of the same size as the ligands. This results is confirmed by the simulations. Figure 7A shows P_b as a function of the number of ligands for different levels of molecular crowding. Here, gray-filled symbols show data from simulations where multiple crowders can occupy one lattice site, half-filled colored symbols (pink and green) represent simulations with small crowder particles on the lattice and the red-filled symbols show results from ReaDDy simulations. For the latter, crowders have a radius r = 1.5 nm to obtain a volume 8 times smaller than the ligands. Symbols show averages of our simulations after running over 3000 binding events. Half-saturation of the receptor at ϕ = 0.2, is reached at ≃ 3 ligands, whereas for the case where crowders and ligands have the same size, i.e., n = 1, half-saturation occurs at ≃13 ligands. Lines represent Equation 9 and show good agreement with the simulations. The effective dissociation constant is plotted, for the multiple crowder approximation, as a function of the volume fraction ϕ in Figure 7B. Comparison of the data for crowders with the same size as the ligand and with an 8-fold smaller volume, shows that for the same occupied volume fraction, the small crowders shift the dissociation constant more strongly toward the bound state than the larger crowders. Thus, only for crowders of the same size as the ligand, the effect of crowding can be identified with a reduction of the available volume by the volume occupied by the crowders. For the smaller crowders, the available volume is reduced by a larger amount. This observation can be explained by the fact that the volume from which large particles are excluded is determined by the spatial arrangement of small particles. This additional volume exclusion effect can also be interpreted as due to an additional attractive force between the large particles (here the ligand and the target). The effect of crowder size is also known from scaled particle theory, however in that theory non-linear ϕ-dependencies are already present for crowders of the same size as the ligands [6].

FIGURE 7

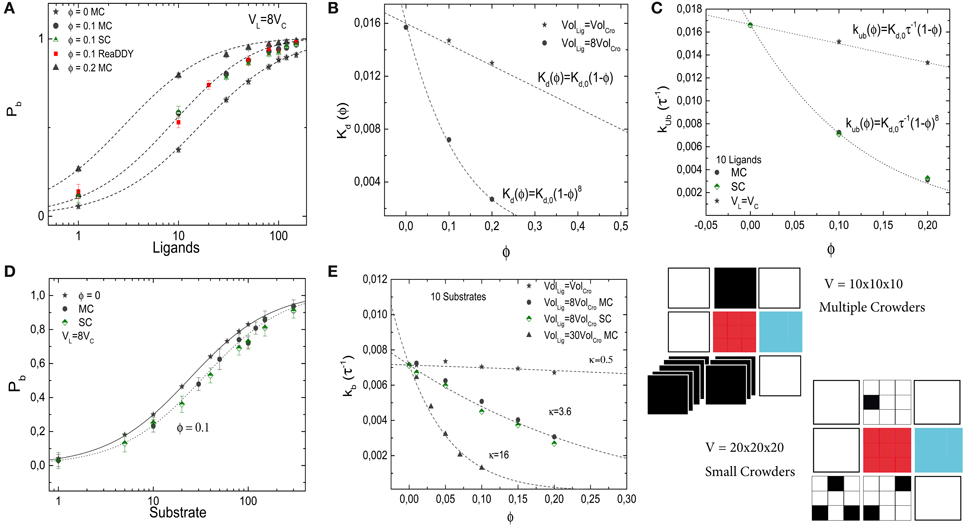
Figure 7. Effects of crowder size on the binding of a ligand to a receptor (A–C) and on the diffusion-limited enzymatic reaction (D,E). In all panels, gray-filled symbols represent the implementation in which multiple crowders can occupy the same lattice site (MC), half-filled symbols (green and pink) represent the implementation of the small crowders (SC) and the red symbols show results from ReaDDy. In general, good agreement between the methods is observed. (A) P_b of the simple binding reaction as a function of the number of ligands for different crowder sizes and volume occupation fractions ϕ. The lines are from Equation (9) with no free parameters. (B) Dissociation constant as a function of ϕ for two different crowder sizes. Smaller crowders have a stronger effect on the dissociation constant than crowders with the same size as the ligands. (C) Unbinding rate as a function of crowder volume fraction. (D) P_b for a diffusion-limited reaction at different crowder volumes. (E) Corresponding binding rate. The lines show fits with Equation (8) (R² = 0.96, 0.995, and 0.994 in descending order). The simulation parameters are as in Figures 2, 5.

Next, we plot the unbinding rate as a function of the volume fraction for smaller crowders, see Figure 7C. Independent of the crowder size, the effect of crowding on the dissociation constant is entirely mediated by the unbinding rate. Results are in good agreement with the expression for the unbinding rate k_ub = K_d,0 τ⁻¹ (1 − ϕ)ⁿ, with n = 1 and 8 for crowders with the same size as the ligands, and crowders 8-fold smaller than the ligands, respectively. No strong difference between the two different implementations is observed.

Next, we study the effect of small crowders on ligand diffusion using again the diffusion-limited reaction in which the target converts a substrate (the ligand) into a product (which is instantaneously replaced by a new substrate inserted into the simulation box at a random position). As for the crowders with the same size as the ligand, binding to the target is weaker in the presence of the crowders and the dissociation constant increases with increasing volume fraction due to a reduction of the binding rate (the effective unbinding rate, given by the reaction rate, remains constant by construction of the reaction model). Figure 7D shows P_b as a function of L for two different volume fractions of crowders, which are again 8-fold smaller than ligands. In Figure 7E, we plot the binding rate k_b as a function of volume fraction for a fixed number of ligands, L = 10, and three different crowder sizes (gray and green symbols). When crowders and ligands have the same size n = 1, the decrease in the binding rate is modest. Reducing the sizes of the crowders increases the effect of crowding. As above, the dependence of the binding rate on the volume fraction can be described by k_b = k⁰_b(1 − ϕ)^κ, with κ ≃ 0.5, 3.6 and 16 for crowders with the same size as the ligands, 8-fold smaller than the ligands and 30-fold smaller than the ligands, respectively. For the case of crowders being 8-fold smaller than the ligands, where we tested both implementations of smaller crowders, no strong difference is observed between the two different implementations.

6. Enzymatic Reaction

Finally, to consider the combined effect of crowding on diffusion, binding and reactions, we simulate an enzymatic reaction with Michaelis-Menten kinetics [36], i.e., L + R ⇔ LR → P + R. This reaction is implemented in our lattice model by combining the two reactions studied above: The substrate binds to the target (the enzyme) as before, but then two events may occur. The substrate may unbind from the target with rate k_ub as in the binding reaction studied in Section III. Alternatively, the reaction can take place and a product is released with rate k_r. In this case, we again remove the product from the simulation box and re-insert a substrate molecule at a random position. In the absence of crowders, the synthesis of product proceeds with a rate

$\begin{array}{cc}\frac{dP}{dt}=\frac{k_r[R][L]}{K_M+[L]},& (10)\end{array}$

with the Michaelis constant K_M = (k_r + k_ub) / k_b. In the two limiting cases where either k_r or k_ub = 0 are negligibly small, the reaction reduces to the two reactions considered above. In the following, we will modulate these two parameters such that k_ub + k_r is kept constant (= 1/60 τ⁻¹). Thus, in the absence of crowding, the reactions have the same Michaelis constant, but differ in their maximal reaction rate, see Figure 8A. By contrast, when crowders interfere in the reaction, the maximal reaction rate may be limited by different physical processes. If unbinding is negligible, the reaction is diffusion-limited, and thus hindered by crowding. The Michaelis constant is increased by crowders, K_M ≈ k_r/k_b × (1 − ϕ)^−κ. As we have seen, this increase can be attributed to a reduced binding rate, and the value of κ is strongly dependent on crowder size. In the other limit, the reaction is limiting and the binding/unbinding process has enough time to reach equilibrium before a reaction takes place. In that case, the Michaelis constant is decreased by the crowders, K_M ≈ k_ub × (1 − ϕ)ⁿ/k_b due to a reduced unbinding rate. For a given concentration of substrate, the rate of product formation is reduced in the first case, but increased in the second. These opposing limiting behaviors are plotted as dashed lines in Figures 8B,C.

FIGURE 8

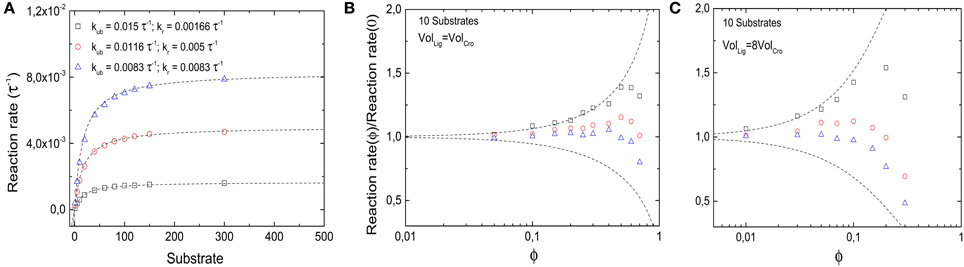
Figure 8. Effects of molecular crowding on a reaction with Michaelis-Menten kinetics. (A) Overall product synthesis rate in absence of crowding (ϕ = 0) as a function of the number of substrates for different set of parameters k_ub and k_r (in units of the inverse simulation time steps τ⁻¹, all other parameters are as in Figure 2). (B) Ratio between the overall synthesis rate in the presence of crowders and the overall synthesis product rate without crowding as a function of crowder volume fraction ϕ. Non-monotonic behavior is obtained for all sets of parameters. For small values of ϕ, binding equilibrium effects are dominant, shifting the ratio to values >1; for large values of ϕ, the slow diffusion dominates, as the reactions become diffusion-limited and the ratio decreases again. The maximal reaction rate is found at an intermediate value of ϕ. (C) The same as in (B), but for crowders 8-fold smaller than substrates. The qualitative behavior is the same as in (B), but the presence of smaller crowders shifts the maximums toward lower values of ϕ. The dashed lines in (B,C) represent the theoretical limits of k_ub ≫ k_r (top) and k_ub ≪ k_r (bottom).

The latter competitive effects lead to a non-monotonic behavior of the reaction rate for parameters that lie between the limit cases, as shown by the symbols in Figures 8B,C. In these cases, the reaction rate is increased by crowding at low volume fractions of crowders, but decreases for large volume fractions. This observation can be explained as a transition between the reaction-limited and the diffusion-limited case, as increasing volume fractions decrease the unbinding rate. Thus, the volume fraction for which the reaction rate is maximal can be estimated by k_r = k_ub(1 − ϕ)ⁿ, which leads to a diffusion-limitation for ϕ ≳ 1−(k_r/k_ub) for n = 1. This estimate also indicates that for smaller crowders (larger n), the maximal reaction rate occurs for smaller volume fractions. This expectation is confirmed by simulations, shown in Figure 8C. Here decreasing reaction rates are seen for volume fractions below the typical intracellular crowding level of 0.3.

Experimentally, both increases and decreases of enzyme activity with increasing levels of crowding have been seen [13]. However, often these observations do not reflect simply the shift in equilibrium binding, in particular, when substrates are small compare to the crowders. Rather, crowding can also affect the activity of an enzyme by modulating its conformation or by inducing oligomerization [11, 37]. However, there is evidence for decreased activity due to diffusion-limitation in several cases [11, 38].

7. Discussion: Crowding Effects on Gene Expression

In the preceding sections we have discussed generic effects of molecular crowding on two elementary types of reactions, simple binding/unbinding and an enzymatic reaction converting a substrate into a product. These two reaction paradigms can be used to describe many different processes in cells, including some that are not enzymatic in a strict sense. An example for the latter is binding of RNA polymerase to a promoter and initiation of transcription, which can be described (within a minimal mathematical representation) by Michaelis-Menten kinetics with the promoter taking the role of the enzyme [39, 40]. In the following, we will thus discuss some applications of these two elementary reactions to processes in gene expression.

7.1. Transcription Factors

Most efforts to study the impact of molecular crowding on gene expression have been devoted to the binding of transcription factors to their binding sites on the chromosome [14, 15, 41]. For most transcription factors, this is a typical case of equilibrium binding and indeed most models for gene regulation are based on the assumption of a binding equilibrium for transcription factors [42, 43]. As discussed above as well as in a large body of previous work, one generically expects such binding to be strengthened by crowding. Interestingly, this holds both for specific binding to the functional binding sites and for (sequence-independent) non-specific binding. Since the molecules involved are the same, the relative strength of specific and non-specific binding should not be affected. Thus, the increase in binding is mainly at the cost of the cytoplasmic fraction of the transcription factors, in agreement with the observation that transcription factors spends most of the time bound to DNA [44, 45].

The strengthening of non-specific binding by crowding should also have an interesting consequence for the dynamics. Transcription factors diffuse in the cell by a combination of three-dimensional cytoplasmic diffusion and one-dimensional diffusion (sliding) along DNA while non-specifically bound [45]. The one-dimensional diffusion coefficient is typically considerably smaller than the diffusion coefficient for three-dimensional diffusion. Thus, unless the transcription factor is bound to DNA in close proximity to a specific binding site, where sliding plays an important role, non-specific binding to DNA can mostly be interpreted as inhibiting cytoplasmic diffusion. Thus the effective diffusion coefficient can be approximated as D_eff = D (1 − P_{b, ns}), where D is the cytoplasmic diffusion coefficient. Assuming that the crowders in the cell are mostly proteins and thus similar in size to the transcription factor of interest, one should expect crowding to have a relatively mild effect on the transcription factor's diffusion in the cytoplasm with D(ϕ) ≃ D(1 − ϕ). However, since non-specific binding is strengthened by crowding, the inhibition of cytoplasmic diffusion is also enhanced and cytoplasmic diffusion is interrupted by pauses on the DNA that get longer and longer with increasing volume fraction of the crowders. Recent Brownian Dynamics simulations [46] indeed showed an increase in the fraction of time spend bound to DNA, however the overall effect on search times, the time required to find a binding site on the DNA, was found to be only weakly affected by crowding, as the opposing effects of crowding seem to keep each other in balance.

7.2. Transcription

As mentioned above, the initiation of transcription can be described by Michaelis-Menten kinetics with RNA polymerase reversibly binding to the promoter and irreversibly starting to elongate an RNA chain. Thus, the promoter formally takes the role of the enzyme and converts free RNA polymerases into transcribing RNA polymerases. Contrary to many transcription factors, RNA polymerase is a relatively big protein with a molecular weight of ≈ 400 kDa [47]. Thus, its size is larger than that of the typical crowder and crowding effects can be expected to be more pronounced. However, to address the effect of crowding on the initiation of transcription, we first need to estimate whether this reaction is diffusion-limited. For a large protein complex such as RNA polymerase, the cytoplasmic diffusion coefficient is approximately 1 μm²/s [28, 48], which is reduced due to non-specific binding to approximately 0.2 μm²/s [48, 49]. Thus, the diffusion-limited binding rate to a promoter can be estimated to be about 0.1 μM⁻¹s⁻¹. This value could be increased due to sliding along the DNA, which effectively increases the size of the target to be reached by cytoplasmic diffusion. However, the importance of sliding is unclear, recent studies have questioned it plays an important role at all and it will clearly be limited by the presence of other DNA-bound proteins including the transcription factors bound near a promoter. Since typical transcription rates are of the order of a few per minute, however, for most cases, with a concentration of RNA polymerases of 5–10 μM, transcription should not be limited by diffusion. An exception might be the transcription of ribosomal RNA, which exhibits much larger transcription rates, up to 80 per minute. Notably, the cellular RNA polymerase pool is quite large, exceeding numbers needed for transcription. One can speculate that a smaller pool would make transcription initiation diffusion-limited at least for highly transcribed genes such as those encoding ribosomal RNA and thus not be sufficient for the high transcription rates required on these genes.

However, for most genes, the initiation of transcription should not be limited by diffusion of RNA polymerase and thus crowding can be expected to enhance polymerase binding to the promoter and thus transcription.

7.3. Translation

Similar to the case of RNA polymerase, one can argue that the initiation of translation could be limited by diffusion of the ribosome, which is an even bigger molecular machine than RNA polymerase; however it does not exhibit non-specific binding to DNA. Contrary to RNA polymerase however, the pool of free ribosomes appears to be rather small [50]. To a first approximation, ribosomes are translating all the time, an observation that can be interpreted as efficient use to maximize the return of an expensive investment [51, 52]. Thus, initiation of translation on any specific mRNA could well be limited by the diffusion of ribosomes. However, different mRNAs compete for ribosomes and such a limitation would not result in inefficient use of ribosomes but rather in the translation of a different mRNA. Thus, the cell's objective here may not be affected by a diffusion limitation.

The elongation process is also quite different for translation compared to transcription. Elongation of the growing polypeptide chain requires that the next amino acid is delivered to the ribosome by a ternary complex containing a tRNA charged with the amino acid and a GTP-activated elongation factor Tu. This complex is again a large molecular complex with a small diffusion coefficient and a molecular size exceeding the size of typical crowders. Assuming a concentration of a few μM for typical ternary complex species [53], binding to the ribosome is expected to occur with rate ~ 10 s⁻¹ [29]. Thus, peptide chain elongation may proceed rather close to the diffusion limit and the large concentration of ternary complexes in cells (EF-Tu is the most abundant protein in E. coli cells [30]) is likely required to avoid such limitation to ensure efficient cellular use of ribosomes. Indeed, from a proteome partitioning point of view, the optimal solution would be to set the Michaelis constant of translation elongation as low as possible. Thus, the actual value must be set by some limitation such as a diffusion limitation, which results in a lower limit for the Michaelis constant [29]. Thus any increase in the level of crowding should slow down translation and, via to the close link between protein synthesis and cell growth, have a negative effect on cell growth. We note, however, that such a limitation could be circumvented by local ternary complex pools. Indeed it has been suggested that tRNAs are recharged while associated with the ribosome [54]. The dynamics is then similar to a high recharging rate in the recharging process in our ReADDy simulations (Figure 6) and crowding would not have the expected negative effect. However, definitive proof for such local recharging is still lacking.

8. Concluding Remarks

In this paper, we used a simple computational approach to discuss the effects of molecular crowding on several simple enzymatic reactions, specifically for relatively big molecular substrates. We used a combination of lattice and off-lattice simulations to revisit the two elementary consequences of molecular crowding, namely enhanced binding and reduced diffusion. The balance between these two effects can be subtle as indicated by the example of the binding rate, which remains unaffected due to an increase in rapid rebinding events and, at the same time, a decrease in binding event involving diffusive arrival of ligands. The lattice model provides a rather intuitive picture of these situations (as well as a very efficient computational implementation).

In addition, we have discussed applications of these effects to steps in gene expression, such as transcription factor-DNA binding, promoter finding by RNA polymerase and translation elongation. Our estimates show that some of these processes may come close to the diffusion limit and that such diffusion limitation may be physiologically important, specifically for translation elongation.

The methods we used here can be applied more generally and there are a number of possible extensions to this work, such as addressing the effects of spatial clustering of targets (binding sites/enzymes) and the built-up of local concentrations.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Fulton AB. How crowded is the cytoplasm? Cell (1982) 30:345–7. doi: 10.1016/0092-8674(82)90231-8

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Zimmerman SB, Minton AP. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu Rev Biophys Biomol Struct. (1993) 22:27–65. doi: 10.1146/annurev.bb.22.060193.000331

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Ellis RJ. Macromolecular crowding: obvious but underappreciated. Trends Biochem Sci. (2001) 26:597–604. doi: 10.1016/S0968-0004(01)01938-7

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Zimmerman SB, Trach SO. Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli. J Mol Biol. (1991) 222:599–620. doi: 10.1016/0022-2836(91)90499-V

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cayley DS, Record MTJr. Large changes in cytoplasmic biopolymer concentration with osmolality indicate that macromolecular crowding may regulate protein DNA interactions and growth rate in osmotically stressed Escherichia coli K-12. J Mol Recongnit. (2004) 17:488–96. doi: 10.1002/jmr.695

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Minton AP. Excluded volume as a determinant of macromolecular structure and reactivity. Biopolymers (1981) 20:2093–120. doi: 10.1002/bip.1981.360201006

CrossRef Full Text | Google Scholar

7. van den Berg B, Ellis RJ, Dobson CM. Effects of macromolecular crowding on protein folding and aggregation. EMBO J. (1999) 18:6927–33. doi: 10.1093/emboj/18.24.6927

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Cheung MS, Klimov D, Thirumalai D. Molecular crowding enhances native state stability and refolding rates of globular proteins. Proc Natl Acad Sci USA. (2005) 102:4753–8. doi: 10.1073/pnas.0409630102

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Mittal J, Best RB. Dependence of protein folding stability and dynamics on the density and composition of macromolecular crowders. Biophys J. (2010) 98:315–20. doi: 10.1016/j.bpj.2009.10.009

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gnutt D, Gao M, Bryski O, Heyden M, Ebbinghaus S. Effekte des volumenausschlusses in lebenden zellen. Angew Chem. (2015) 127:2578–81. doi: 10.1002/ange.201409847

CrossRef Full Text | Google Scholar

11. Derham BK, Harding JJ. The effect of the presence of globular proteins and elongated polymers on enzyme activity. Biochim Biophys Acta (2006) 1764:1000–6. doi: 10.1016/j.bbapap.2006.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Norris MGS, Malys N. What is the true enzyme kinetics in the biological system? An investigation of macromolecular crowding effect upon enzyme kinetics of glucose-6-phosphatase dehydrogenase. Biochem Biophys Res Commun. (2011) 405:388–92. doi: 10.1016/j.bbrc.2011.01.037

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhou H-X, Rivas G, Minton AP. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu Rev Biophys. (2008) 37:375–97. doi: 10.1146/annurev.biophys.37.032807.125817

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Matsuda H, Putzel GG, Backman V, Szleifer I. Macromolecular crowding as a regulator of gene transcription. Biophys J. (2014) 106:1801–10. doi: 10.1016/j.bpj.2014.02.019

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Morelli MJ, Allen RJ, ten Wolde PR. Effects of macromolecular crowding on genetic networks. Biophys J. (2011) 101:2882–91. doi: 10.1016/j.bpj.2011.10.053

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Tan C, Saurabh S, Bruchez MP, Schwartz R, LeDuc P. Molecular crowding shapes gene expression in synthetic cellular nanosystems. Nat. Nanotechnol. (2013) 8:602–8. doi: 10.1038/nnano.2013.132

PubMed Abstract | CrossRef Full Text | Google Scholar

17. McGuffee SR, Elcock AH. Diffusion, crowding and protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput Biol. (2010) 6:e1000694. doi: 10.1371/journal.pcbi.1000694

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Roberts E, Magis A, Ortiz JO, Baumeister W, Luthey-Schulten Z. Noise contributions in an inducible genetic switch: a whole-cell simulation study. PLoS Comput Biol. (2011) 7:e1002010. doi: 10.1371/journal.pcbi.1002010

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Hoekstra FA, Golovina EA, Buitink J. Mechanisms of plant desiccation tolerance. Trends Plant Sci. (2001) 6:431–8. doi: 10.1016/S1360-1385(01)02052-0

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Thalhammer A, Bryant G, Sulpice R, Hincha D. Disordered Cold Regulated15 proteins protect chloroplast membranes during freezing through binding and folding, but do not stabilize chloroplast enzymes in vivo. Plant Physiol. (2014) 166:190–201. doi: 10.1104/pp.114.245399

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ellis RJ, Hartl F-U. Protein folding in the cell: competing models of chaperonin function. FASEB J. (1996) 10:20–26.

PubMed Abstract | Google Scholar

22. Minton AP. Influence of macromolecular crowding upon the stability and state of association of proteins: predictions and observations. J Pharma Sci. (2005) 94:1668–75. doi: 10.1002/jps.20417

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Kim JS, Yethiraj A. Crowding effects on protein association: effects of interactions between crowding agents. J Phys Chem B (2011) 115:347–53. doi: 10.1021/jp107123y

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Muramatsu N, Minton AP. Tracer diffusion of globular proteins in concentrated protein solutions. Proc Nat Acad Sci USA. (1988) 85:2984–8. doi: 10.1073/pnas.85.9.2984

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Han J, Herzfeld J. Macromolecular diffusion in crowded solutions. Biophys J. (1993) 65:1155–61. doi: 10.1016/S0006-3495(93)81145-7

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Kim JS, Yethiraj A. Effects of macromolecular crowding on reaction rates: a computational and theoretical study. Biophys J. (2009) 96:1333–40. doi: 10.1016/j.bpj.2008.11.030

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Schöneberg J, Noe F. Readdy - A software for particle-based reaction-diffusion dynamics in crowded cellular environments. PLoS ONE (2013) 8:e74261. doi: 10.1371/journal.pone.0074261

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Kumar M, Mommer MS, Sourjik V. Mobility of cytoplasmic, membrane, and DNA-binding proteins in Escherichia coli. Biophys J. (2010) 98:552–9. doi: 10.1016/j.bpj.2009.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Klumpp S, Scott M, Pedersen S, Hwa T. Molecular crowding limits translation and cell growth. Proc Natl Acad Sci USA. (2013) 110:16754–9. doi: 10.1073/pnas.1310377110

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Krab IM, Parmeggiani A. EF-Tu, a GTPase odyssey. Biochem Biophys Acta (1998) 1443:1–22. doi: 10.1016/S0167-4781(98)00169-9

PubMed Abstract | CrossRef Full Text

31. Atkins P, de Paula J. Physical Chemistry. Oxford: Oxford University Press (2002).

Google Scholar

32. Zon JS, Morelli MJ, Tanase-Nicola S, ten Wolde PR. Diffusion of transcription factors can drastically enhance the noise in gene expression. Biophys J. (2006) 91:4350–67. doi: 10.1529/biophysj.106.086157

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Phillips R, Kondev J, Theriot J, Garcia H. Physical Biology of the Cell. 2nd Edn., New York, NY: Garland Science, Taylor and Francis Group LLC (2012).

Google Scholar

34. Asakura S, Oosawa F. Interaction between particles suspended in solutions of macromolecules. J Polymer Sci. (1958) 33:183–92. doi: 10.1002/pol.1958.1203312618

CrossRef Full Text

35. Benton LA, Smith AE, Young GB, Pielak GJ. Unexpected effects of macromolecular crowding on protein stability. Biochemistry (2012) 51:9773–5. doi: 10.1021/bi300909q

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Michaelis L, Menten ML. Die Kinetik der Invertinwirkung. Biochem Z. (1913) 49:333–69.

Google Scholar

37. Jiang M, Guo Z. Effects of macromolecular crowding on the intrinsic catalytic efficiency and structure of enterobactin-specific isochorismate synthase. J Am Chem Soc. (2007) 129:730–1. doi: 10.1021/ja065064+

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Totani K, Ihara Y, Matsuo I, Ito Y. Effects of macromolecular crowding on glycoprotein processing enzymes. J Am Chem Soc. (2008) 130:2101–7. doi: 10.1021/ja077570k

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Record MT, Reznikoff WS, Craig MA, McQuade KL, Schlax PJ. Escherichia coli RNA polymerase (Eσ70), promoters, and the kinetics of the steps of transcription initiation. In: Neidhardt FC, editor. Escherichia coli and Salmonella, 2nd Edn. Washington DC: ASM Press (1996). p. 792–820.

40. Dennis PP, Ehrenberg M, Bremer H. Control of rrna synthesis in Escherichia coli: a systems biology approach. Microbiol Mol Biol Rev. (2004) 68:639–68. doi: 10.1128/MMBR.68.4.639-668.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Tabaka M, Kalwarczyk T, Holyst R. Quantitative influence of macromolecular crowding on gene regulation kinetics. Nucl Acids Res. (2013) 42:727–38. doi: 10.1093/nar/gkt907

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Ackers GK, Johnson AD, Shea MA. Quantitative model for gene regulation by λ phage repressor. Proc Natl Acad Sci USA. (1982) 79:1129–33. doi: 10.1073/pnas.79.4.1129

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, et al. Transcriptional regulation by the numbers: models. Curr Opin Gen Dev. (2005) 15:116–24. doi: 10.1016/j.gde.2005.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Kao-Huang Y, Revzin A, Butler AP, O'Conner P, Noble DW, von Hippel PH. Nonspecific dna binding of genome-regulating proteins as a biological control mechanism: measurement of DNA-bound Escherichia coli lac repressor in vivo. Proc Natl Acad Sci USA. (1977) 74:4228–32. doi: 10.1073/pnas.74.10.4228

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Elf J, Li G-W, Xie XS. Probing transcription factor dynamics at the single-molecule level in a living cell. Science (2007) 316:1191–4. doi: 10.1126/science.1141967

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Brackley CA, Cates ME, Marenduzzo D. Intracellular facilitated diffusion: searchers, crowders, and blockers. Phys Rev Lett. (2013) 111:108101. doi: 10.1103/PhysRevLett.111.108101

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Berg D, Chamberlin M. Physical studies on ribonucleic acid polymerase from Escherichia coli B. Biochemistry (1970) 9:5055–64. doi: 10.1021/bi00828a003

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Bakshi S, Dalrymple RM, Li W, Choi H, Weisshaar JC. Partitioning of RNA polymerase activity in Live Escherichia coli from analysis of single-molecule diffusive trajectories. Biophys J. (2013) 105:2676–86. doi: 10.1016/j.bpj.2013.10.024

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Bratton BP, Mooney RA, Weisshaar JC. Spatial distribution and diffusive motion of RNA polymerase in live Escherichia coli. J Bacteriol. (2011) 193:5138–46. doi: 10.1128/JB.00198-11

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Bremer H, Dennis PP. Modulation of chemical composition and other parameters of the cell by growth rate. In: Neidhardt FC, editor. Escherichia coli and Salmonella, 2nd Edn. Washington DC: ASM Press (1996). p. 1553–69.

51. Scott M, Gunderson CW, Mateescu EM, Zhang Z, Hwa T. Interdependence of cell growth and gene expression: origins and consequences. Science (2010) 330:1099–102. doi: 10.1126/science.1192588

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Klumpp S, Hwa T. Bacterial growth: global effects on gene expression, growth feedback and proteome partition. Curr Opin Biotech (2014) 28:96–102. doi: 10.1016/j.copbio.2014.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Dong H, Nilsson L, Kurland CG. Co-variation of tRNA abundance and codon usage in Escherichia coli at different growth rates. J Mol Biol. (1996) 260:649–63. doi: 10.1016/j.cell.2010.02.036

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Cannarozzi G, Schraudolph NN, Faty M, von Rohr P, Friberg MT, Roth AC, et al. A role for codon order in translation dynamics. (2010) Cell 141:355–67.

PubMed Abstract | Google Scholar