A commentary on
Asking photons where they have been
by Danan, A., Farfurnik, D., Bar-Ad, S., and Vaidman, L. (2013). Phys. Rev. Lett. 111:240402. doi: 10.1103/PhysRevLett.111.240402
In a recent letter, Danan et al. [1] devised an elegant experiment investigating the past of photons inside two Mach-Zehnder interferometers, one inside the other—yet drew the wrong conclusions. Namely, that—based on weak measurements on pre- and post-selected states—some photons have been inside the inner interferometer but they never entered and never left. And, consequently, a “common sense” approach describing the past of a photon in terms of a trajectory, or a set of trajectories, for example [2–4], should be abandoned.
But if weak measurements are carried out such that zero photons leave the inner interferometer—that is complete destructive interference is not disturbed, as should be the case—these measurements, which we show how to implement, do not find the photons to have been inside. Further, we argue that the story told by the two-state vector formulation (TSVF) that Danan et al. advocate is in fact contradictory.
By vibrating the mirrors in their key setup of Figure 2B in Danan et al. [1], from which they draw their main conclusions, Danan et al. were able to cause light reaching the quad-cell photo-detector D to acquire vertical shifts, each significantly smaller than the beam width—essentially performing weak measurements on the pre-selected state , and the post-selected state . The presence of detector peaks at the vibrational frequencies of mirrors A and B indicates that some photons have been near these mirrors.
Now imagine that both mirrors A and B are made to vibrate at precisely the same frequency, such that whenever A is rotated by a small angle δθ, B is rotated by −δθ, i.e., in the opposite direction. By simple geometry, and provided that the distances from A and B to the beam-splitter on the way to F are equal, it is easy to see that complete destructive interference at F is not disturbed, as shown in our Figure 1.
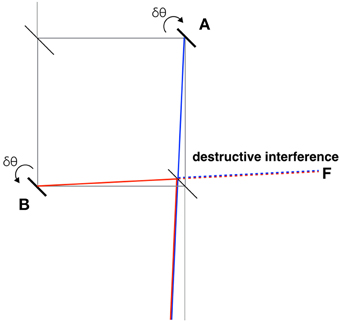
Figure 1. Rotating mirror A by a small angle δθ, and mirror B by −δθ, does not disturb complete destructive interference. This is because the signals from A and B reach the bottom-right beam-splitter at precisely the same position, and the reflected part of the signal from A and the transmitted part of the signal from B (two dotted lines) overlap completely. The distances from A and B to the bottom-right beam-splitter are assumed to be equal; any required phase shift may be implemented as a delay. Note that here δθ is exaggerated for clarity.
What happens to the detector peaks corresponding to mirrors A and B? The weak values of the projection operators at A and B are +1 and −1 respectively. The minus sign for mirror B corresponds, according to weak measurement theory, to an average vertical shift for the photons arriving at the detector that is in the opposite direction of that due to A—the two thus cancelling each other out. Classically, by electromagnetism, eliminating light leakage from the inner interferometer by restoring complete destructive interference means that the all-important detector peaks at the vibrational frequency of mirrors A and B now disappear!
The story told by Danan et al.'s TSVF is the following. Since the forward-evolving state (from the source) and the backward-evolving state (from the detector) are both present at mirror A and at mirror B, the photons have been there, which raises the question: was each photon shifted at the detector in one direction due to it bouncing (as a whole photon) off mirror A and simultaneously shifted in the opposite direction due to it bouncing (as a whole photon) off mirror B?—whose answer has to be no since a joint weak measurement at A and B, to see if the photon was on paths A and B simultaneously, gives the result zero. One can see this from the fact that |A〉 〈A| |B〉 〈B| is identically zero, as |A〉 and |B〉 are orthogonal [5].
But there are three possible, mutually exclusive, stories of where photons have or have not been in the inner interferometer, provided the question can be asked in the first place: (1) some, or all, photons have simultaneously been on paths A and B, which was ruled out, (2) no photons have been near A and no photons have been near B, which is our position, (3) some photons have been near A while other photons have been near B. Quantum mechanics contradicts this last story. The initial peaks corresponding to the different vibrational frequencies of A and B were a result of a non-zero probability amplitude at F. This is now zero since complete destructive interference has been restored. The peaks therefore disappear. From the Schrodinger evolution, there is no shift for some photons at the detector, due to mirror A, offsetting an opposite one for other photons due to mirror B. And ultimately, nothing to suggest that any photons have been near mirror A or B.
More to the point, the weak measurements on paths A and B could have equally been carried out using two separate, external measuring devices placed there. Each would give a non-zero reading, corresponding to the weak values +1 and −1 respectively. Complete destructive interference in this case, as in Danan et al.'s original setup, is not preserved, this time because of entanglement with the measuring devices. (The part of the photon superposition at A is now linked with the external measuring device placed there. And the part of the photon superposition at B is now linked with the external measuring device placed there. For photons, entanglement provides which-path information that prevents complete destructive interference from taking place, much like in the famous Bohr-Einsten [6] double-slit thought experiment.) Crucially, by Danan et al.'s logic that wherever the forward- and backward-evolving states overlap the photon was there [1], as the weak value is non-zero, one would conclude that the photon was physically detected at both A and B, which is absurd! [5].
Strange weak measurements are nothing new. Weak measurements are known to record, for example, faster-than-light speeds, and were as such investigated as a possible candidate for explaining the OPERA detector superluminal neutrino measurements that later turned out to be erroneous [7, 8]. In fact, pre- and post-selection—a key ingredient of weak measurement—can by itself give rise, in the presence of disturbance, to anomalous values, as a statistical feature. This was recently demonstrated by Ferrie and Combes [9] who showed that in a simple model of a coin, the result of a single coin toss can turn out to be 100 heads! They argued that anomalous weak values are not inherently quantum, but can arise purely as a result of classical back action with pre- and post-selection. Others disagree, for instance [10].
We now turn to Danan et al.'s Figure 2C in Danan et al. [1], where they block the lower path. According to their TSVF, both the forward- and backward-evolving states are non-zero at mirror A and at mirror B (which vibrate at different frequencies)—yet no detector peaks are observed! They attribute this to an insufficient number of photons reaching the detector. But even if the detector were sensitive enough, the TSVF fails to simply explain the peaks' diminished size.
In standard quantum mechanics, when the lower path is blocked the intensity of the light reaching the detector is proportional to the squared modulus of the probability amplitude leaking from the inner interferometer (reflected from mirror F) which is very small. But when the lower path is not blocked, interference with the quantum state reflected from C results in an intensity at the detector that has a term linear in the modulus of the probability amplitude leaking from the inner interferometer, not as small—which is how we got the peaks corresponding to mirrors A and B in the first place. Thus, contrary to Danan et al.'s claim that “the photons tell us that they have been in the parts of the interferometer through which they could not pass,” these peaks resulted from photons passing right through the inner interferometer in question.
In conclusion, if weak measurements are performed such that zero photons leave the inner interferometer, meaning as close to zero as practically possible, as should be the case—which we show how to achieve—detector peaks corresponding to photons having been in the inner interferometer no longer appear. Claims such as “some photons have been inside the inner interferometer but they never entered and never left” should not arise.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I thank Onur Hosten and Brian D. Josephson for useful comments. Qubet Research is a start-up in quantum information.
References
1. Danan A, Farfurnik D, Bar-Ad S, Vaidman L. Asking photons where they have been. Phys Rev Lett. (2013) 111:240402. doi: 10.1103/PhysRevLett.111.240402
2. Hosten O, Rakher MT, Barreiro JT, Peters NA, Kwiat PG. Counterfactual quantum computation through quantum interrogation. Nature (2006) 439:949. doi: 10.1038/nature04523
3. Salih H, Li ZH, Al-Amri M, Zubairy MS. Protocol for direct counterfactual quantum communication. Phys Rev Lett. (2013) 110:170502. doi: 10.1103/PhysRevLett.110.170502
4. Salih H. Tripartite counterfactual quantum cryptography. Phys Rev A (2014) 90:012333. doi: 10.1103/PhysRevA.90.012333
5. Resch KJ, Lundeen JS, Steinberg AM. Experimental realization of the quantum box problem. Phys Lett A (2004) 324:125. doi: 10.1016/j.physleta.2004.02.042
7. Berry MV, Brunner N, Popescu S, Shukla P. Can apparent superluminal neutrino speeds be explained as a quantum weak measurement? J Phys A Math Theor. (2011) 44:492001. doi: 10.1088/1751-8113/44/49/492001
8. Adam T, Agafonova N, Aleksandrov A, Anokhina A, Aoki S, Ariga A, et al. Measurement of the neutrino velocity with the OPERA detector in the CNGS beam using the 2012 dedicated data. J High Energy Phys. (2013) 1:153. doi: 10.1007/JHEP01(2013)153
9. Ferrie C, Combes J. How the result of a single coin toss can turn out to be 100 heads. Phys Rev Lett. (2014) 113:120404. doi: 10.1103/PhysRevLett.113.120404
Keywords: quantum information, wave-particle duality, Mach-Zehnder interferometer, weak measurement, post-selection, counterfactuality
Citation: Salih H (2015) Commentary: “Asking photons where they have been” - without telling them what to say. Front. Phys. 3:47. doi: 10.3389/fphy.2015.00047
Received: 21 July 2014; Accepted: 10 June 2015;
Published: 30 June 2015.
Edited by:
Lorenzo Pavesi, University of Trento, ItalyReviewed by:
Yutaka Shikano, Institute for Molecular Science, JapanCopyright © 2015 Salih. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hatim Salih,c2FsaWguaGF0aW1AZ21haWwuY29t
 Hatim Salih
Hatim Salih