- 1Department of Physics and Astronomy, University of Oklahoma, Norman, OK, USA
- 2Instituto de Física, Universidade de São Paulo, São Paulo, Brazil
A variety of supersymmetric models give rise to a split mass spectrum characterized by very heavy scalars but sub-TeV gauginos, usually with a wino-like LSP. Such models predict a thermally-produced underabundance of wino-like WIMP dark matter so that non-thermal DM production mechanisms are necessary. We examine the case where theories with a wino-like LSP are augmented by a Peccei-Quinn sector including an axion-axino-saxion supermultiplet in either the SUSY KSVZ or SUSY DFSZ models and with/without saxion decays to axions/axinos. We show allowed ranges of PQ breaking scale fa for various cases which are generated by solving the necessary coupled Boltzmann equations. We also present results for a model with radiatively-driven naturalness but with a wino-like LSP.
1. Introduction
Supersymmetric models with anomaly-mediated SUSY breaking [1, 2] (AMSB) provided a strong raison d'être for considering the case of a wino-like lightest SUSY particle, or LSP. Originally, such models were built with a “sequestered”—rather than a hidden– SUSY breaking sector. The sequestered sector could be located on a brane which was separated from the visible sector brane in an extra dimensional space-time. In such a case, tree level supergravity contributions to soft SUSY breaking terms were absent and the dominant contribution to soft terms came from the superconformal anomaly. Since the soft terms were all of order , then values of gravitino mass m3∕2 ~ 30–100 TeV were required to generate a weak-scale sparticle mass spectrum. The weak-scale gaugino masses were expected to occur in the ratio M1:M2:M3 ~ 3:1:8, resulting in a wino-like LSP as the dark matter candidate. The thermally-produced relic density of a wino-like LSP is typically [3, 4]
The measured dark matter abundance is then saturated for a wino of mass TeV. For lighter winos, non-thermal production mechanisms such as WIMP production from moduli decay were invoked [5].
While the simplest AMSB models provided solutions to the SUSY flavor, CP and gravitino problems, they retain the problem of predicting tachyonic slepton masses. More recently, they may have fallen into disfavor due to the discovery [6, 7] of the Higgs boson with mass mh = 125.5 ± 0.5 GeV. In the minimal AMSB model, this value of Higgs mass requires m3∕2 ~ 1000 TeV so that the sparticle mass spectrum lies in the multi-TeV region which seems to seriously compromise even the most conservative measures of naturalness [8, 9].
Even well-before the Higgs discovery, related models with a wino-like LSP were emerging. These include
• models with strong moduli stabilization [19],
• pure gravity mediation [20–25] and
These models differ from the original mAMSB model in that they predict a split spectrum with scalars ranging from 25 TeV all the way to ~ 108 TeV– well beyond the reach of collider experiments. In contrast, the gauginos typically lie in the 0.1–3 TeV region so that the lower range of values would be accessible to LHC searches. In most of these models, the gauginos adopt either the AMSB-form [10, 20–24] or a mixed anomaly plus loop contribution form [14–18, 26, 27] which also typically gives rise to a wino-like LSP. The SUSY μ parameter is variable between these several models and may be as small as ~1 TeV [14–18, 25] or as high as hundreds of TeV [20–24]. While the predicted thermal abundance of wino-like WIMPs saturates the measured value for a wino mass of ~2.5 TeV (so the gaugino spectrum would be well beyond reach of LHC), for lower M2 values a thermal underabundance of WIMPs is expected and some non-thermal DM production mechanism is needed. Usually, this has involved some form of moduli production and decay [5, 28–30] (for recent reviews, see Baer et al. [31], Kane et al. [32]).
In the present paper, we instead look at non-thermal wino production from the Peccei-Quinn (PQ) sector1. By invoking a PQ sector in supersymmetric models [34] the axion supermultiplet also contains an R-parity-even spin-0 saxion s and an R-parity-odd spin-1/2 axino ã. This approach has several advantages:
• a PQ sector seems necessary to solve the strong CP problem in the QCD sector [35–41],
• invoking PQ charges for Higgs multiplets offers a means to forbid the appearance of a Planck scale μ term while re-generating a weak-scale μ term (solution to the SUSY μ problem) [42, 43],
• while the presence of the PQ sector can act to augment the wino abundance– for instance by axino and/or saxion decays– the axion abundance can always be adjusted to make up any remaining DM abundance which may be needed.
To explore this situation, we will adopt a benchmark model which encapsulates the dark matter physics expected in the above list of models. This benchmark point– labeled as CSB for “charged SUSY breaking” [10]– contains scalar masses around the 72 TeV region while gauginos lie in the 0.2–2 TeV range. The thermally-produced WIMP abundance is predicted to be – a factor ~ 60 below the measured value. Such a low thermal WIMP abundance requires additional dark matter production mechanisms to match experiment. In the case presented here, the dark matter is actually composed of both WIMPs and axions. While WIMPs can be produced thermally, they can also be produced via axino, saxion and gravitino production and decay in the early universe and via WIMP freeze-in [44]. In addition, saxions produced via coherent oscillations (CO) can inject late-time entropy into the early universe, thus diluting any relics already present. Axions can be produced as usual via CO [45–51], but can also be produced thermally and via saxion decay.
While the models listed above are motivated by a variety of theoretical and phenomenological considerations, we note that collectively the entire set is highly fine-tuned in the electroweak sector, since the weak scale values of and μ2 would have to be adjusted to very high precision to gain a Z mass of just 91.2 GeV. Thus, for contrast, we also examine a SUSY model with radiatively-driven naturalness [52, 53] but with a wino-like LSP [54] with fine-tuning at just the 10% level (labeled as RNSw).
In Section 2, we briefly review a variety of models with split spectra and a wino-like LSP. We also present a SUSY model with radiatively-driven naturalness and a wino-like LSP for comparison. In Section 3, we briefly review our coupled-Boltzmann equation evaluation of mixed axion/wino dark matter (more details can be found in Bae et al. [55]). In Section 4, we present the results of our coupled Boltzmann computation of the mixed axion/wino dark matter abundance in the CSB and RNSw benchmark models. In Section 5, we expand our two benchmark points to model lines to examine how our results depend on the SUSY mass spectrum. Our overall conclusions and a summary plot are given in Section 6.
2. Survey of Some Models with a Wino-like LSP
2.1. PeV SUSY
In Wells [3, 10], it is argued that the PeV scale (with m(scalars) ~ m3/2 ~ 1 PeV = 1000 TeV) is motivated by considerations of wino dark matter and neutrino mass while providing a decoupling solution [56–59] to the SUSY flavor, CP, proton decay and gravitino/moduli problems. This model invoked “charged SUSY breaking” (CSB) where the hidden sector superfield S is charged under some unspecified symmetry. In such a case, the scalars gain masses via
while gaugino masses, usually obtained via gravity-mediation as
are now forbidden. Then the dominant contribution to gaugino masses comes from AMSB:
Saturating the measured dark matter abundance with thermally-produced winos requires TeV which in turn requires the gravitino and scalar masses to occur at the ~1000 TeV (or 1 PeV) level. The author of Wells [3], Wells [10] remains agnostic as to the magnitude of μ, although μ ≫ M2 is expected.
2.2. Split SUSY
In Split SUSY [11–13, 60–62], SUSY is still required for gauge coupling unification and for a dark matter candidate, but naturalness is eschewed in favor of a multi-verse solution to the gauge hierarchy problem. In such a case, matter scalars can exist with masses typically at some intermediate scale TeV while SUSY fermions (gauginos and higgsinos) are protected by chiral symmetry and can be much lighter. Split SUSY can be realized under charged SUSY breaking as in PeV-SUSY or via Scherk-Schwartz SUSY breaking in extra dimensions [11]. Here, one might expect
where the authors remain agnostic concerning whether the wino or bino might be lighter. Typically, binos should overproduce dark matter so that a wino/higgsino admixture might be expected.
2.3. G2MSSM
In string/M-theory models which are compactified on a manifold of G2 holonomy [14–18], one expects a gravitino mass m3/2 ~ 25 − 100 TeV along with a cosmologically relevant moduli field with similar mass [63]. The matter scalar masses are of order ~ m3∕2 but gaugino masses can be much lighter. Typically, a wino LSP is to be preferred [29]. The superpotential μ term is generated with value ~1 TeV so that these models tend to be more electroweak-natural than split SUSY.
2.4. Models with Strong Moduli Stabilization (Kallosh-Linde or KL)
In string theory, an outstanding problem exists in the need for vacuum stabilization of moduli fields. In the KKLT construction [64], one constructs a stable supersymmetric anti-deSitter vacuum, but then uplifts to a deSitter vacuum via SUSY breaking. In KKLT, the volume modulus mass mσ is expected to be comparable to the gravitino mass m3∕2. These models give rise to soft SUSY breaking terms characterized by comparable moduli- and anomaly-mediated contributions [65–67]. However, these models suffer from vacuum destabilization during inflation unless the Hubble constant H < m3/2. Such inflationary models, while possible, are often unwieldy and inelegant [19]2.
An alternative approach known as strong vacuum stabilization invokes instead a racetrack superpotential for the volume modulus, leading to a far heavier modulus mass GeV and allowing for vacuum stability in models of chaotic inflation [19]. In this Kallosh-Linde (KL) case [69], the soft SUSY breaking scalar masses are comparable to m3/2, but the gaugino and trilinear soft terms are suppressed by a factor of m3/2/mσ. The dominant contribution to gaugino masses comes from anomaly-mediation. Requiring a wino LSP without too much relic density then fixes m3/2 ≲ 1000 TeV. Thus, one gains a model of split SUSY with PeV-scale scalar masses but with TeV-scale gauginos with an AMSB mass pattern. The μ parameter is also expected to be ~ m3/2 [70] so a high degree of electroweak fine-tuning is needed.
2.5. Pure Gravity-mediation
In pure gravity mediation (PGM) models [20–24], it is assumed that matter scalar masses are developed at tree level and so have masses TeV while gaugino masses are suppressed since no SUSY breaking fields are assumed to be singlets under any symmetries. The gaugino masses arise via anomaly mediation so the wino is expected to be the LSP. The μ term and SUSY breaking bilinear B are also expected to be at the m3∕2 scale leading to
although a recent incarnation also allows for light higgsinos [25].
2.6. Spread SUSY
In Spread SUSY [26, 27], additional spatial dimensions are assumed so that the 4-d reduced Planck scale MP is enhanced by a volume factor over the fundamental scale M*. Then, if the hidden sector SUSY breaking field X is charged under some symmetry, gaugino masses are generated only via anomaly- mediation while scalar masses are generated via gravity-mediation. One expects a mildly split– or spread– SUSY spectrum characterized by
where the wino is the LSP with sub-TeV masses and the matter scalar masses may lie in the 102 − 103 TeV range while the higgsinos are intermediate between these two.
2.7. Natural SUSY with Wino-like LSP
In SUSY with radiatively-driven naturalness [52, 53], the W, Z, h mass scale arises naturally due to a supersymmetric μ parameter with μ ~ 100 − 300 GeV (the closer to mZ the better) while is driven radiatively to small rather than large values. The TeV-scale top squark masses are highly mixed which uplifts mh to ~ 125 GeV whilst suppressing radiative corrections to the scalar potential which influence the values of mh,Z. While one expects a higgsino-like LSP under conditions of gaugino mass universality, models with non-universal gaugino masses allow for a bino-like or wino-like LSP without sacrificing naturalness [54]. Mixed axion-higgsino dark matter has been previously calculated in Bae et al. [55, 71, 72] while the mainly bino-like LSP case is largely excluded due to overproduction of WIMPs [55, 71]. Here, we consider the wino-like LSP case which typically yields a thermally-produced wino abundance of for winos with GeV (at least an order-of-magnitude lower than expectations for a similarly massive higgsino LSP).
2.8. Two Benchmark Points
In order to compute the mixed axion/wino dark matter relic abundance in the SUSY axion models, we must specify both the PQ and the MSSM parameters. On the MSSM side, we adopt two SUSY benchmark models for illustration. We generate the SUSY model spectra with Isajet 7.83 [73]. We understand a ~ ±2 GeV theoretical uncertainty on the Isasugra RGE-improved one-loop calculation of mh which includes leading two-loop effects.
The first has been listed as benchmark CSB since it occurs in the rather simple and elegant charged SUSY breaking model of Wells [10]. It is rather similar to the Kallosh-Linde [19] benchmark from the study of Baer and List [74]. We take the CSB benchmark to be illustrative of the large class of models with multi-TeV scalars but with sub-TeV gauginos with a wino as LSP. The CSB benchmark model is listed in Table 1.
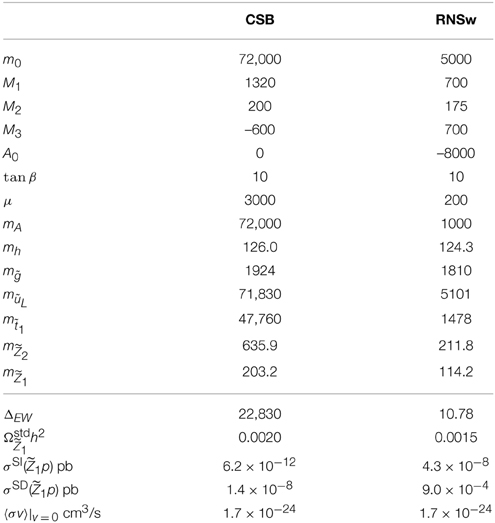
Table 1. Masses and parameters in GeV units for two benchmark points computed with Isajet 7.83 and using mt = 173.2 GeV.
Along with the CSB benchmark, we adopt a natural SUSY benchmark with a wino as LSP. It is taken from Baer et al. [54] and denoted as RNSw (radiatively-driven natural SUSY with a wino LSP).
We also list at the bottom of Table 1 the value of the thermally-produced relic abundance of winos along with spin-independent and spin-dependent direct detection cross sections and the thermally-averaged neutralino annihilation cross section times velocity in the v → 0 limit. This latter quantity enters indirect detection rates for gamma ray and anti-matter signals from neutralino halo annihilations. For the RNSw benchmark, the direct and indirect detection rates are naively at the edge of exclusion. However, the expected event rate for direct WIMP detection is proportional to the WIMP local abundance. In our case, where WIMPs make up only a fraction of the DM abundance, the expected rates should be multiplied by a factor to account for a possibly suppressed local abundance. Likewise, the indirect detection rates should be multiplied by a factor of η2 to account for a possible reduced WIMP local abundance in WIMP-WIMP annihilation reactions. Once we impose the η and η2 factors, then the direct/indirect detection rates are safely below the experimental limits.
3. Brief Review of Coupled Boltzmann Calculation
To accurately estimate the mixed axion/neutralino dark matter production rate in the early universe, it is necessary to evaluate the coupled Boltzmann equations which track dark matter number densities and energy densities in an intertwined manner. The exact equations used are presented in Bae et al. [55] and will not be repeated here. In our calculations, we use a combination of IsaReD [75] and micrOMEGAs [76] for the evaluation of the wino annihilation cross-section (〈σv〉). The wino annihilation rate includes co-annihilation effects but no Sommerfeld enhancement.
The relevant equations track the following number and energy densities:
1. neutralino densities including thermal production and production via decays of heavier partices (e.g., axinos, saxions and gravitinos) followed by possible subsequent re-annihilation,
2. thermally-produced axinos along with axino production via heavy particle decays and diminution of axinos due to their decays,
3. thermally produced saxions along with diminution via their decays,
4. thermally-produced gravitinos [77] along with gravitino decay [78],
5. thermally-produced axions along with axion production via heavy particle decays,
6. axion production via coherent oscillations (CO) and
7. saxion production via CO along with saxion decays.
8. Along with these, we track the radiation density of SM particles.
The above eight components result in 16 coupled Boltzmann equations: one for the number density and one for the energy density of each component. Together with the Friedmann equation (where ρT is the energy density summed over all contributions and MP is the reduced Planck scale) the Boltzmann equations form a closed system which may be solved numerically.
For the SUSY KSVZ model, the various axino (, and ) and saxion branching fractions (s → gg, ) can be found in Choi et al. [79], Baer and Lessa [80], Baer et al. [81]. In addition, the model-dependent decays s → aa, ãã are effectively parameterized [82, 83] by where qi are the charge assignments of PQ multiplets and vi are their vevs after PQ symmetry breaking and . We will take ξ = 0 or 1 which effectively turns off or on saxion decays to axinos/axions [71]. The decay s → ãã augments the LSP abundance whilst the decay s → aa leads to dark radiation parameterized by the effective number of extra neutrinos present in the early universe ΔNeff. The Planck Collaboration reported by the combined data (95%; Planck+WP+highL+H0+BAO) [84]3. We require the upper bound ΔNeff < 1 as a reference value lest too much dark radiation is produced. Excluded points with ΔNeff > 1 are color-coded in our results.
For the SUSY DFSZ model, axino and saxion decay rates are very different from the KSVZ case. While in the KSVZ model axino and saxion decay primarily to gauge bosons and gauginos, in SUSY DFSZ then typically (where ϕ = h, H, A), , and , and s → pairs of Higgs bosons, vector bosons and electroweak-ino pairs. Complete formulae for the DFSZ decay rates are found in Bae et al. [72].
The thermal production rates for SUSY KSVZ (which are proportional to TR) are found in Covi et al. [85], Brandenburg and Steffen [86], Strumia [87], Graf and Steffen [88] while thermal production rates for SUSY DFSZ (which are mostly independent of TR) are obtained from Chun [89], Bae et al. [90, 91]. In Chun [89], Bae et al. [90, 91], explicit estimation is conducted for thermal axino density in SUSY DFSZ model. For thermal saxion and axion production, it is reasonable to expect annihilation/production rates which are similar to axinos, so we adopt an approximate thermal production rates for saxion and axion in SUSY DFSZ model as in Bae et al. [55], We include production of particles via both decays and inverse decays [55]: the latter effects are important in SUSY DFSZ where saxions and axinos are maximally produced at T ~ m(particle) which leads to a freeze-in effect [44] which manifests itself essentially as delayed saxion/axino decays.
An example of the evolution of various energy densities ρi vs. the cosmic scale factor R∕R0 is shown in Figure 1 for the SUSY DFSZ model. R0 is taken to be the scale factor at the end of reheating (T = TR). In the figure, GeV while ms = m3∕2 = 72 TeV for the CSB benchmark point. We also take mã = 40 TeV and ξ = 1 so that saxion decay to axions is turned on. At R∕R0 = 1, the universe is indeed radiation dominated (gray curve) while including a thermal population of WIMPs, saxions, axions, axinos and gravitinos. It also includes a CO-component of saxions. As R∕R0 increases (decreasing temperature as denoted by the green dashed line), the oscillating saxion field begins to decay– mainly via s → aa– so that the population of thermal/decay-produced axions (red curve) increases beyond its otherwise thermal trajectory around and below . The neutralino abundance (dark blue) begins to freeze-out around , but then is augmented by decaying CO saxions and also by axinos (which decay slightly after saxions). Decaying gravitinos add, but only marginally, to the neutralino abundance around . At , the axion mass turns on and the axion field begins to oscillate as non-relativistic matter (brown curve). Also, at , the neutralinos become non-relativistic. Together, the combined neutralino-axion CDM ultimately dominates the universe at around . The ultimate dark matter density is composed of ~ 25% wino-like WIMPs and ~ 75% cold axions with a modest-but-not-yet-excluded contribution of relativistic axions (ΔNeff = 0.68) as dark radiation.
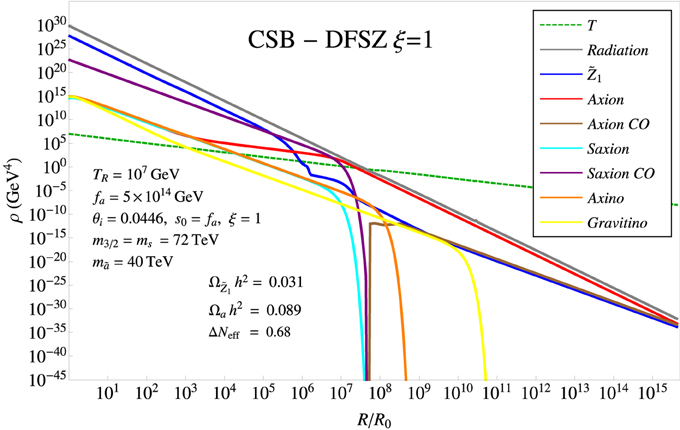
Figure 1. Evolution of various energy densities vs. scale factor R∕R0 for the CSB benchmark case in SUSY DFSZ with ξ = 1 and other parameters as indicated in the figure.
4. Mixed Axion-wino Dark Matter
In the following subsections, we compute the neutralino and axion relic abundances for the two benchmark points through numerical integration of the Boltzmann equations as discussed in Section 3. To gain more general results, we will scan over the PQ scale fa and the axino mass which we take to be bounded by m3∕2:
with ms fixed as ms = m3∕2. In many supergravity models, saxion mass is generated by the same operators as those for the MSSM scalars while axino mass is highly model dependent and can be much smaller than m3∕2 [82, 83, 92, 93]. For this reason, we consider the above parameter range for our general analyses.
For simplicity, we will fix the initial saxion field strength, which sets the amplitude of coherent saxion oscillations, to si = fa (θs ≡ si∕fa = 1). In addition– for points which are DM-allowed () and obey BBN and dark radiation constraints– the initial axion mis-alignment angle θi is set to the required value such that
where where f(θi) is the anharmonicity factor and 0 < θi < π. Turner [48], Lyth [49], Bae et al. [50], Visinelli and Gondolo [51] parametrize the latter as .
In the SUSY DFSZ case, unlike the SUSY KSVZ model, the bulk of our results do not depend strongly on the re-heat temperature (TR) since the axion, axino and saxion TP rates are largely independent of this quantity. Nonetheless, the gravitino thermal abundance is proportional to TR and since gravitinos are long-lived they may affect BBN or WIMP abundance constraints if TR is sufficiently large. In order to avoid the BBN constraints on gravitinos, we choose GeV, which results in a sufficiently small (would-be) gravitino abundance. As a result, gravitinos typically do not contribute significantly to the neutralino abundance, as discussed above.
For each of the CSB and RNSw benchmark points, we consider two different cases: ξ = 0 (saxion decay to axions/axinos turned off) and ξ = 1 (saxion decay to axions/axinos turned on). We adopt a KSVZ model with SU(2)L singlet heavy quark states so that the axion superfield only has interactions with SU(3)c and U(1)Y gauge superfields. We discuss the case of SU(2)L doublet heavy quark states in Section 6 for completeness.
4.1. CSB Benchmark in SUSY KSVZ
4.1.1. ξ = 0 Case
In this section, we will examine the CSB benchmark in the SUSY KSVZ case. We start with the case where saxion decays into axinos and axions are turned off (ξ = 0). Results for this benchmark are shown in Figure 2, where we plot (blue points) and (green points) vs. fa for the scan over parameters defined in Equation (4.1). In the figure, red points violate BBN bounds on late-decaying neutral relics [94] while otherwise the points are BBN safe. We also show the measured abundance of CDM by the solid horizontal line. Points above this line are excluded by overproduction of dark matter while points below the line are allowed. The dashed horizontal gray line denotes the 50% CDM abundance so that blue points above this line have WIMP-dominated CDM while green points above this line have axion-dominated CDM.
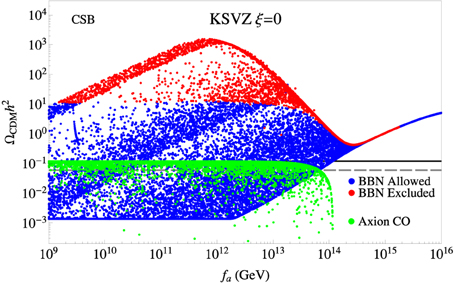
Figure 2. The wino-like WIMP (blue) and axion (green) relic densities from a scan over SUSY KSVZ parameter space for the CSB benchmark case with ξ = 0. The gray dashed line shows the points where DM consists of 50% axions and 50% neutralinos.
In Figure 2, one can see that there are three branches of the neutralino CDM density for GeV. These branches reflect three regions of axino mass. The uppermost branch corresponds to the case of . In this case, axinos decay only into plus SM particles. Since the axion sector does not have a direct coupling to a SU(2)L gauge supermultiplet, axino decays into (mostly wino-like) happen only through the bino-wino mixing, which is very tiny in the MSSM. Therefore, for this branch the axino decay occurs well-after the neutralino freeze-out, enhancing the neutralino abundance well above the measured CDM density for all values of fa. Moreover– for GeV– BBN constrains the model due to the long-lived axino.
The middle branch corresponds to . In this region axinos can decay directly into . Since is mostly bino-like and axinos directly couple to through the U(1)Y anomalous coupling, their life-time is much shorter than in the case. Although the axinos decay after neutralino freeze-out for all fa, the neutralino density can still be smaller than the observed CDM density for GeV. Hence, both axion-dominated or neutralino-dominated dark matter scenarios are possible in this region. For GeV, all points in the branch are excluded by BBN.
The lowermost branch corresponds to . In this region, axinos can decay to gluinos through the SU(3)c anomaly coupling so that the axino life-time becomes much shorter than the previous two cases. For GeV, axinos decay before neutralino freeze-out in the bulk of this parameter region, so the neutralino CDM density takes its standard thermal value ~ 0.002. In the case where the axino mass is close to the gluino mass, however, axinos can decay after neutralino freeze-out and augment the WIMP abundance. As fa increases, axinos more often decay after freeze-out and hence increasingly augment the neutralino relic density. By GeV, axinos always decay after freeze-out and always augment the neutralino abundance. Despite the enhancement of the neutralino abundance, there are points where the DM is axion-dominated up to GeV.
For GeV, the contribution to the WIMP abundance is mostly from CO-produced saxion decays; these augment the abundance for larger fa since the saxion CO production rate increases with fa. On the other hand, the contribution from TP axinos is highly suppressed for large fa, since the axino thermal production decreases with fa. Once the TP axino abundance becomes negligible, the LSP relic abundance becomes independent of the axino mass and all the branches discussed above collapse into a single line, as seen in Figure 2.
4.1.2. ξ = 1 Case
In Figure 3, we show vs. fa for the same CSB benchmark point but now where saxion decays into axinos and axions are allowed: ξ = 1. For the lower ( GeV) range, saxion decays have a smaller impact on the neutralino abundance and the results are similar to the CSB/KSVZ ξ = 0 case. For higher fa values, CO-produced saxions become important and since s → aa and ãã decays are now allowed, there is a large injection of relativistic axions. The lower disjoint narrow band at GeV and occurs for points where mã > ms∕2, so s → ãã is kinematically forbidden. The band tends to swing downward at GeV since the axino contribution to the WIMP relic density decreases due to suppressed axino thermal production. In this band, all constraints are satisfied for fa up to 4 × 1014 GeV. For higher values of fa, overproduction of dark radiation (ΔNeff > 1) occurs and for GeV then enhanced CO-produced saxions followed by decays to WIMPs start to augment the WIMP abundance.
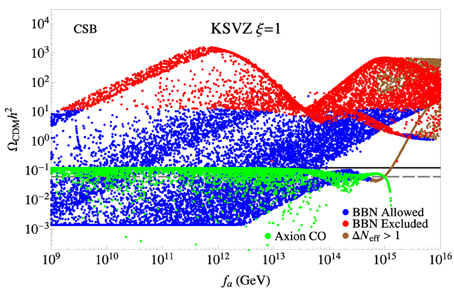
Figure 3. The wino-like WIMP and axion relic densities from a scan over SUSY KSVZ parameter space for the CSB benchmark case with ξ = 1. The gray dashed line shows the points where DM consists of 50% axions and 50% neutralinos.
There is also a broad band of blue (BBN-allowed) and red (BBN-excluded) points at large GeV with very high where the additional neutralino abundance arises from s → ãã decays. Finally we point out that, unlike the ξ = 0 case, the extremely large fa region ( GeV) still shows a dependence on the axino mass: this is responsible for the distinct branches. Although thermal production of axinos is neglegible in this regime, axinos are non-thermally produced from saxion decays and can influence the final neutralino abundance.
4.2. CSB Benchmark in SUSY DFSZ
4.2.1. ξ = 0 Case
In this section, we will examine the CSB benchmark in the SUSY DFSZ case. As before, we start with the ξ = 0 case, shown in Figure 4. The first noteworthy point is that the large μ value enhances the saxion (axino) decay rate to Higgs (higgsinos). As a result the saxion and axino lifetimes are suppressed and the entire fa range is BBN safe. Unlike the KSVZ case, there are two branches for neutralino CDM density, since in the DFSZ case, the axino decay is determined by the μ-term interaction. The upper branch corresponds to with higgsino-like . The axino decay into or can be through wino-higgsino or bino-higgsino mixing, so it is normally suppressed by . For GeV, axinos decay before neutralino freeze-out, and thus the neutralino density takes its standard value. For GeV, axinos tends to decay after neutralino freeze-out so the neutralino density gradually increases as fa increases. In most of parameter space, axions constitute the bulk of dark matter, but wino-like neutralinos can be the dominant dark matter in the region of 1012 GeV GeV. By GeV, the neutralino density is typically larger than the measured CDM result so the parameter/model choices would be excluded.
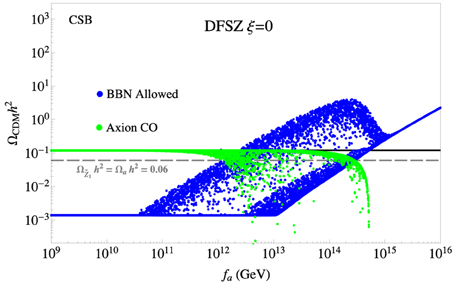
Figure 4. The wino-like WIMP and axion relic densities from a scan over SUSY DFSZ parameter space for the CSB benchmark case with ξ = 0. The gray dashed line shows the points where DM consists of 50% axions and 50% neutralinos.
The lower branch corresponds to . Due to its large interaction, the axino tends to decay before neutralino freeze-out for GeV. Therefore, the neutralino relic abundance is usually fixed at its thermally-produced value for much of the lower range of fa. Once GeV, the neutralino abundance is always enhanced due to decays of axinos and saxions. Still, the CDM abundance tends to be axion-dominated for GeV. For higher fa there is a short interval where wino-like WIMPs can dominate the DM abundance. Finally, for GeV, WIMP CDM is always overproduced. We also point out that for very large fa values, as in the KSVZ ξ = 0 scenario, the thermal production of axinos is neglegible hence the neutralino relic abundance becomes independent of mã.
4.2.2. ξ = 1 Case
For the CSB benchmark with SUSY DFSZ and ξ = 1, the results are shown in Figure 5. The low fa behavior of the plot is similar to the CSB/DFSZ case with ξ = 0: the CDM density is dominated by axions. For higher fa values, where CO-produced saxions become important, the saxion lifetime is shortened by the additional contributions from s → aa, ãã decays. However, most of the points for GeV are forbidden due to overproduction of dark radiation. The lower blue-brown band at GeV occurs when mã > ms∕2 so that additional WIMP production from s → ãã is dis-allowed.
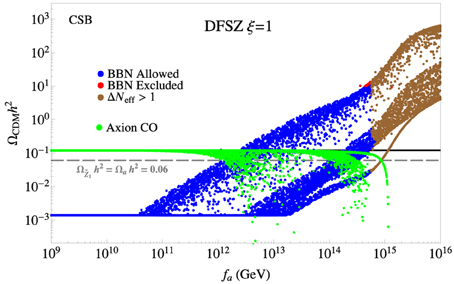
Figure 5. The wino-like WIMP and axion relic densities from a scan over SUSY DFSZ parameter space for the CSB benchmark case with ξ = 1. The gray dashed line shows the points where DM consists of 50% axions and 50% neutralinos.
4.3. RNSw Benchmark in SUSY KSVZ
In this subsection we examine dark matter production in the SUSY RNSw benchmark case. The RNSw benchmark model has values ms = m0 ≡ m3∕2 = 5 TeV which is far smaller than that of the CSB benchmark so that saxions (and also axinos since we take their mass to be bounded by m3∕2) are typically much longer-lived than in the CSB case.
4.3.1. ξ = 0 Case
In Figure 6, we plot vs. fa for the SUSY KSVZ case using the RNSw benchmark point with ξ = 0. In this case, mã is always larger than , so there are only two branches for the neutralino density: and . Long-lived axinos are already augmenting the neutralino relic density even at fa values as low as 109 GeV. As we move to higher fa values, the axinos and saxions are longer-lived, thus contributing even more to the WIMP abundance. For fa values ≳ 4 × 1012 GeV, the model is already excluded due to overproduction of WIMPs. The points reach even higher values as fa increases until GeV. For 4 × 1012 GeV GeV, the axino contribution decreases due to suppression of the thermal production. For GeV, then CO-produced saxions decay into gluino pairs and tend to augment the WIMP abundance. However, this is inconsequential since the model already overproduces WIMP dark matter. A large BBN forbidden region occurs, but it is already in the WIMP-overproduction region so adds no further constraints.
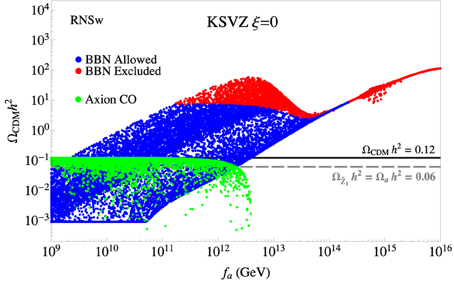
Figure 6. The wino-like WIMP and axion relic densities from a scan over SUSY KSVZ parameter space for the RNSw benchmark case with ξ = 0. The gray dashed line shows the points where DM consists of 50% axions and 50% neutralinos.
4.3.2. ξ = 1 Case
For the RNSw benchmark case in SUSY KSVZ with ξ = 1, as shown in Figure 7, the low fa behavior of is very similar to the ξ = 0 case, since at low fa saxion production is not very relevant and saxions decay well-before neutralino freeze-out. For GeV, as in the ξ = 0 case, the model over-produces WIMPs and is excluded. At even larger values of fa, in the DM-excluded region, the ξ = 1 case begins to differ from ξ = 0. An additional branch of appears: the lowermost branch swings downward due to the suppressed axino and saxion TP as in the ξ = 0 case, but never reaches the DM-allowed line. The upper two branches occur where ms > 2mã so that CO-production of saxions keeps increasing the WIMP abundance. This region is also excluded by the BBN constraint from late-decaying saxions followed by axino cascade decays.
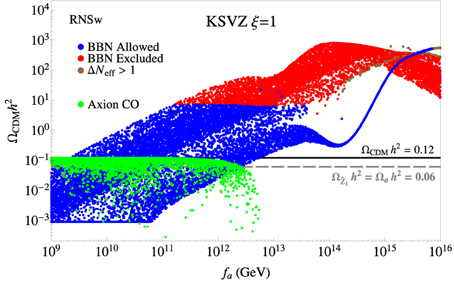
Figure 7. The wino-like WIMP and axion relic densities from a scan over SUSY KSVZ parameter space for the RNSw benchmark case with ξ = 1. The gray dashed line shows the points where DM consists of 50% axions and 50% neutralinos.
4.4. RNSw Benchmark in SUSY DFSZ
In this subsection, we examine the RNSw benchmark model in the SUSY DFSZ model. Since μ(RNSw)≪μ(CSB), saxions in the RNSw/DFSZ case will tend to be longer lived.
4.4.1. ξ = 0 Case
In Figure 8 we show RNSw in the SUSY DFSZ case with ξ = 0. In this case, mã is always larger than μ, so there is no region corresponding to the upper branch in Figure 4. For low fa, in contrast to RNSw in the SUSY KSVZ case, the axino lifetime is smaller and the WIMP abundance remains at its thermally-produced value for GeV. For higher fa values, the WIMP abundance is augmented by axino and saxion decays after freeze-out. Ultimately, the model over-produces WIMPs for GeV. The model tends to be axion-dominated for GeV and WIMP dominated for a narrow range of fa just beyond this value until WIMP overproduction is reached and the model becomes excluded. This is in contrast to the CSB benchmark with DFSZ and ξ = 0, where the allowed region extends to GeV since saxions and axinos are shorter-lived due to much larger masses and stronger interactions (μ(RNSw) ≪ μ(CSB)).
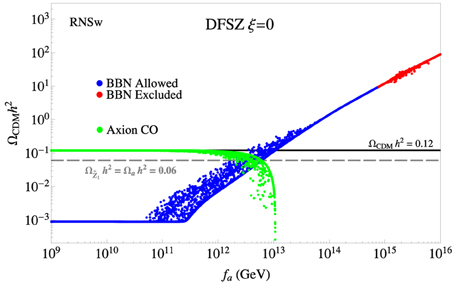
Figure 8. The wino-like WIMP and axion relic densities from a scan over SUSY DFSZ parameter space for the RNSw benchmark case with ξ = 0. The gray dashed line shows the points where DM consists of 50% axions and 50% neutralinos.
4.4.2. ξ = 1 Case
In Figure 9 we show results for the RNSw benchmark in SUSY DFSZ with ξ = 1. While the low fa behavior is similar to the results from the ξ = 0 case, the high fa behavior is different. The decays s → aa and s → ãã allow the saxion to decay more quickly than in the ξ = 0 case for a common value of fa. Thus, the DM-allowed region extends to larger fa values: in this case up to GeV. For these high fa values, the relic density band again splits into two branches: one with heavy axinos (lower-branch), where s → ãã is closed, and one with light axinos (upper branch), where s → ãã is open, thus augmenting the WIMP abundance. The points with GeV tend to be doubly-excluded by overproduction of WIMPs and by overproduction of dark radiation.
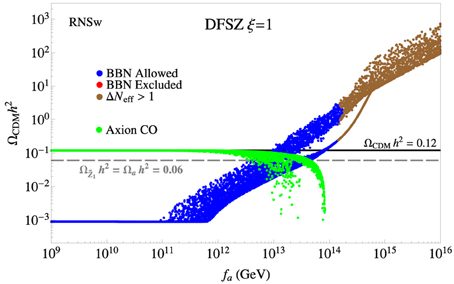
Figure 9. The wino-like WIMP and axion relic densities from a scan over SUSY DFSZ parameter space for the RNSw benchmark case with ξ = 1. The gray dashed line shows the points where DM consists of 50% axions and 50% neutralinos.
5. Dependence of Mixed Axion-wino Abundance on Sparticle Mass Spectra
In the previous sections we have investigated the DM-allowed range of fa for two SUSY benchmark models with wino-like LSPs, fa and mã as free parameters and ms = m0. In this section, we investigate how our results might change as a function of the MSSM spectrum. To explore this issue, we extend our two benchmark points into model lines in the MSSM sector. For brevity, we consider here only the DFSZ model– which provides a solution to the SUSY μ problem– to see the impacts of axino/saxion production/decays on the CDM density. Actually, even in the presence of late-decaying axinos and saxions, the most important factor that determines the WIMP abundance is the WIMP-WIMP annihilation cross section since the augmented density is determined mainly by annihilation cross section evaluated at the heavy particle decay temperature: this is the case of so-called WIMP re-annihilation after non-thermal WIMP production from heavy particle decay [79, 80]. For this reason, the behavior of our plots is similar for both DFSZ and KSVZ models, and so we will show only the DFSZ case and then briefly comment on the KSVZ case.
5.1. CSB Model Line
For the CSB benchmark, we will now allow m3∕2 to vary while keeping tanβ fixed at 10 with μ = 3 TeV and mA = m3∕2. For the CSB model-line, we require m3∕2 ≳ 32 TeV so the mass of the lightest wino-like chargino is always above the limit GeV established from LEP2 searches. The upper limit on m3∕2 occurs at ~ 115 TeV where the predicted value of mh climbs above 128 GeV. Here, we allow for an expected theory error in the Isasugra calculation of mh at about ±2.5 GeV.
We show the thermally-produced neutralino abundance for the CSB model line in Figure 10. Here, we see that ranges from around 0.0007 at the lower limit to about 0.005 at the upper limit as compared to 0.002 for the CSB benchmark. Roughly speaking, the thermally-produced wino abundance will provide either more or less room in general for non-thermally produced winos and axions.
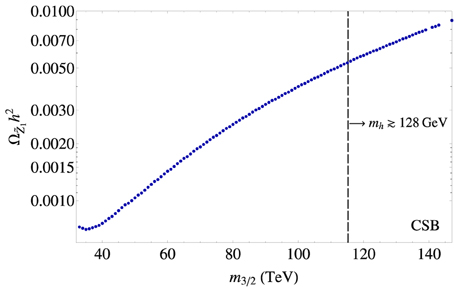
Figure 10. Plot of thermally-produced neutralino abundance vs. m3∕2 along the CSB model line with tanβ = 10 and μ = 3 TeV.
In Figure 11, we show the value of which is produced from the coupled Boltzmann calculation of mixed axion-wino CDM vs. fa for the minimal and maximal values of m3∕2 which are allowed along the CSB model line. The blue curves provide the calculated envelope of values for the lower limit of m3∕2 ~ 32 TeV. At low fa, lies at the TP-value ~ 0.0006 since thermally-produced axinos always decay before neutralino freeze-out. As fa climbs above ~ 1011 GeV, then the lighter axinos start decaying after neutralino freeze-out whilst the heavier axinos still decay before freeze-out. The region between the two blue curves shows the range of which is generated for 0.4 TeV < mã < 32 TeV. We see that values of fa up to ~ 1015 GeV are dark-matter-allowed for very heavy axinos. However, at values of GeV, then too much dark radiation is produced from s → aa decays in addition to WIMP overproduction so that the parameter space is doubly-excluded.
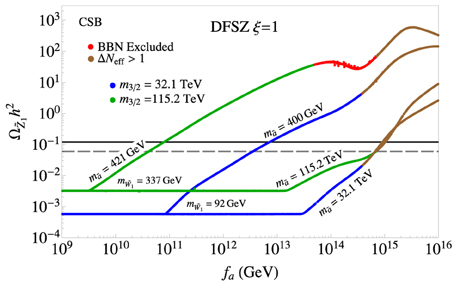
Figure 11. Plot of thermally- and non-thermally-produced neutralino abundance vs. fa along the CSB model line in the DFSZ ξ = 1 case for a light (m3∕2 = 32 TeV, blue envelope) and heavy (m3∕2 = 115 TeV, green envelope) CSB mass spectrum where mã ranges from 400 GeV up to m3∕2.
The heavy end of the CSB model line m3∕2 = 115 TeV is shown by the envelope of green curves. For the light axino with mã = 421 GeV, the thermally-produced value of is obtained only for the short range of GeV. For this heavy CSB spectra, the gauginos are all sufficiently heavy and thus the axino can decay only into so that the axino lifetimes are much longer than that in the case for light spectra. The upper range of the green envelope comes from light axino masses where mã = 421 GeV is the threshold for decay hence augmenting neutralino density at low fa, while the lower envelope is established by the heaviest axino mass values. For the upper part of the envelope, the red points denote the on-set of BBN bounds on late decaying saxions as ruling out GeV. For the lower part of the envelope, with axino masses ranging to 115 TeV, then values of fa up to 7 × 1014 GeV are possible.
In the case of KSVZ model, the spectrum dependence is similar to the DFSZ model. For the light spectum (m3∕2 = 32 TeV), the neutralino abundance tends to be smaller due to its large annihilation cross section. For the heavy spectrum (m3∕2 = 115 TeV), the cross section becomes larger, so the neutralino abundance becomes smaller. Nevertheless, the allowed range of fa for the heavy spectrum is slightly larger than that for light spectrum since the saxion mass is larger (ms = m3∕2) so that its decay can occur earlier.
5.2. RNSw Model Line
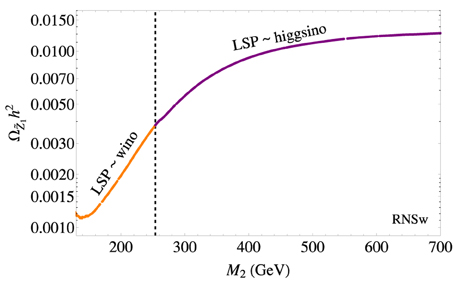
For the RNSw benchmark, we will instead allow the GUT scale SU(2)L gaugino mass M2 to vary while keeping m0 = 5 TeV, m1∕2 = 700 GeV, A0 = −8 TeV and tanβ fixed at 10 with μ = 200 GeV and mA = 1 TeV. For the RNSw model-line, the lower limit on M2 is again set by the limit from LEP2 searches for wino-like charginos. The upper limit on M2 ≲ 250 GeV is set from simply requiring a wino-like LSP: for higher M2 values, the lightest neutralino becomes increasingly higgsino-like, a case which was shown in Bae et al. [55, 72]. The naturalness value ΔEW remains fixed at around 10 since varying M2 hardly affects it [54].
We show the thermally-produced neutralino abundance for the RNSw model line in Figure 12. The lower range of occurs at 0.0012 for M2 ~ 140 GeV. The maximal value reaches up to ~ 0.004 before entering the higgsino-like LSP region. Since the thermally-produced wino abundance increases with M2, the allowed enhancement from non-thermal production decreases as M2 increases. Furthermore, since the non-thermal production (from saxion and axino decays) grows with fa, we expect the maximum allowed value for fa to decrease as M2 increases. This is shown in Figure 13, where we plot the upper limit on fa, denoted as , vs. M2 along the RNSw model line in the DFSZ ξ = 1 case. The axino mass is mã = 0.4 TeV (green dots) or mã = 5 TeV (black dots). The upper limit comes only from the overproduction of WIMPs in this case since violation of BBN bounds and overproduction of dark matter occurs at higher fa in this model.
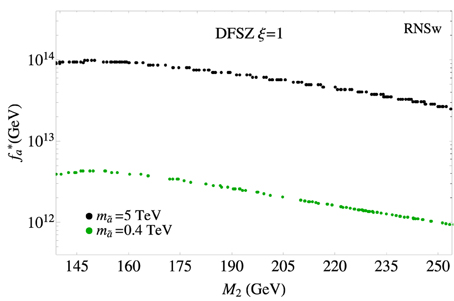
Figure 13. Plot of upper limit of fa allowed from the RNSw model line in the DFSZ case with ξ = 1 vs. M2 for mã = 400 GeV and mã = 5 TeV.
In the KSVZ model, on the other hand, axinos are longer-lived than in the DFSZ model, so the allowed range of fa is smaller than that in the DFSZ case. As we have seen in Figure 7, only a small region, GeV, is allowed for , while GeV is allowed for mã = 5 TeV.
6. Conclusion
In this paper we have examined mixed axion/wino cold dark matter production in two SUSY benchmark models with a wino as LSP. The first– labeled as CSB– is typical of a variety of models (PeV-SUSY, some split SUSY variations, KL, PGM, spread SUSY) with a thermally-underproduced wino-like WIMP abundance. The second, labeled as RNSw, is a model with radiatvely-driven naturalness but with a wino-like rather than a higgsino-like LSP. Our calculation of mixed axion/wino dark matter production stands in contrast to the more commonly examined case of non-thermal WIMP production due to late decaying moduli fields [5, 28, 29]. We find it a more appealing method for augmenting the dark matter abundance since it also provides a solution to the strong CP problem and– in the case of SUSY DFSZ– provides for a solution to the SUSY μ problem.
We have presented results for the wino-like WIMP abundance and axion abundance as a function of the axion decay constant fa and the axino mass mã. In the bulk of the parameter space, WIMPs are thermally under-produced at low and intermediate fa values (~ 109 − 1011 GeV) so that the DM abundance tends to be axion-dominated. The axions are dominantly produced via coherent oscillations of the axion field [45–51]. This has important consequences for direct and indirect WIMP detection experiments since it anticipates a greatly reduced local abundance of WIMPs and hence diminished prospects for wino-like WIMP detection. This can actually allow for wino-like WIMP dark matter to evade the recent Fermi [95], Geringer-Sameth and Koushiappas [96] searches for gamma ray emission from dwarf-spheroidal galaxies since in this case the expected event rate is expected to be reduced by a factor .
A grand overview of our results is presented in Figure 14, where we show the allowed range of fa as a bar for each of the two benchmark points and for each of the eight SUSY PQ models considered. For all the models, no GUT scale values of fa ( GeV) are allowed. This is due to the rather large value of ms ~ m3∕2 in our benchmark models. In these cases, saxions always decay to SUSY particles and no entropy dilution of WIMPS and axions is possible (see Bae et al. [55, 72] for more details).
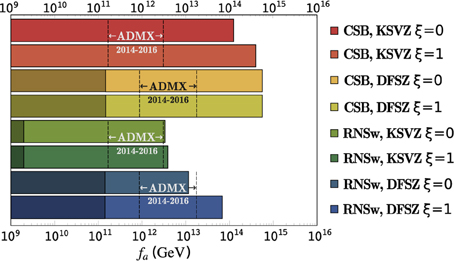
Figure 14. Range of fa which is allowed in each PQMSSM scenario for the CSB and RNSw benchmark models. Darker-shaded regions indicate the range of fa where θi > 3 which might be considered unnatural. We also show the fa range which is expected to be probed by the ADMX experiment in the next few years.
In addition to the SUSY KSVZ case with SU(2)L singlet heavy quark states which has been presented here, we have also investigated SUSY KSVZ models including SU(2)L doublet heavy quark states so that the axion superfield has couplings with SU(2)L gauge superfields. In the case of doublet heavy quarks, axino decays to the wino-like neutralino are not suppressed, even for . Therefore, there is no separate branch like the uppermost one in Figures 2, 3 and thus there are only two branches determined by . The basic features of plots with doublet heavy quarks are similar to the case with singlet heavy quarks since the dominant axino decay mode is into gluinos for both cases. The allowed range of fa values is extended only slightly for doublet KSVZ heavy quarks as compared to the case of singlet heavy quarks shown in this paper.
For sufficiently heavy axinos, all models shown in this paper are DM-allowed for the lower range of GeV, since WIMPs are underproduced. In these cases, the remaining abundance is made up of axions. Even though one might expect a low axion abundance at low fa in the case where the initial mis-alignment angle is θi ~ (1), due to anharmonicity effects the necessary axion abundance can always be obtained by taking θi ~ π [48–51]. In this case, one might wonder about fine-tuning of the axion abundance such that the axion fields sits atop the peak of its potential. Thus, for cases where θi > 3, we shade these regions as darker in Figure 14. The non-shaded regions may be more natural as far as the expected initial axion field value goes.
We should note that for KSVZ models, regions with θi < 3 at low fa occur only if the wino LSP constitutes more than ~ 90% of total CDM density since axion CO-production is very low for . Then, the CSB benchmark in the SUSY KSVZ model most naturally allows for the lowest fa values while the CSB benchmark in the DFSZ model allows for the highest fa values. The range of fa values obtained for the RNSw benchmark is more constrained than the CSB case. The upper bounds on fa for the two benchmark models are well-maintained even when the points are extended to model lines, as was shown for the DFSZ ξ = 1 case in Section 5.
Finally, we denote the range of fa values which are expected to be probed in the next few years by the Axion Dark Matter Search Experiment (ADMX) [97]4. The values shift between KSVZ and DFSZ models since the domain wall number NDW = 1 for KSVZ and 6 for DFSZ and . We also note that a possible ADMX technique of open resonators [98] may allow even lower values of fa to be probed in the future.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the William I. Fine Theoretical Physics Institute (FTPI) at the University of Minnesota for hospitality while the bulk of this work was completed. The computing for this project was performed at the OU Supercomputing Center for Education & Research (OSCER) at the University of Oklahoma (OU). AL thanks Fundacão de Amparo à Pesquisa do Estado de São Paulo (FAPESP) for supporting this work. This work was funded in part by the US Department of Energy Office of High Energy Physics.
Footnotes
1. ^An earlier look at non-thermal production of winos in AMSB models was given in Baer et al. [33].
2. ^Recent introduction of nilpotent superfields can simplify these models [68].
3. ^As this paper was being finalized, this value was updated [84] to Neff = 3.15 ± 0.23.
4. ^The ADMX experiment is a super-cooled microwave cavity axion search experiment located at the University of Washington. For details, see e.g., Kusenko and Rosenberg [97].
References
1. Randall L, Sundrum R. Out of this world supersymmetry breaking. Nucl Phys B (1999) 557:79. doi: 10.1016/S0550-3213(99)00359-4
2. Giudice GF, Luty MA, Murayama H, Rattazzi R. Gaugino mass without singlets. JHEP (1998) 9812:027.
3. Wells JD. Implications of supersymmetry breaking with a little hierarchy between gauginos and scalars. In: 11th International Conference on Supersymmetry and the Unification of Fundamental Interactions (SUSY 2003). Tucson, AZ (2003).
4. Arkani-Hamed N, Delgado A, Giudice GF. The well-tempered neutralino. Nucl Phys B (2006) 741:108. doi: 10.1016/j.nuclphysb.2006.02.010
5. Moroi T, Randall L. Wino cold dark matter from anomaly mediated SUSY breaking. Nucl Phys B (2000) 570:455. doi: 10.1016/S0550-3213(99)00748-8
6. Aad G, et al., (ATLAS Collaboration). Observation of a new particle in the search for the standard model higgs boson with the ATLAS detector at the LHC. Phys Lett B (2012) 716:1. doi: 10.1016/j.physletb.2012.08.020
7. Chatrchyan S, et al., (CMS Collaboration). Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys Lett B (2012) 716:30. doi: 10.1016/j.physletb.2012.08.021
8. Baer H, Barger V, Mustafayev A. Neutralino dark matter in mSUGRA/CMSSM with a 125 GeV light Higgs scalar. JHEP (2012) 1205:091. doi: 10.1007/JHEP05(2012)091
9. Baer H, Barger V, Mickelson D, Padeffke-Kirkland M. SUSY models under siege: LHC constraints and electroweak fine-tuning. Phys Rev D (2014) 89:115019. doi: 10.1103/PhysRevD.89.115019
11. Arkani-Hamed N, Dimopoulos S. Supersymmetric unification without low energy supersymmetry and signatures for fine-tuning at the LHC. JHEP (2005) 0506:073. doi: 10.1088/1126-6708/2005/06/073
12. Giudice GF, Romanino A. Split supersymmetry. Nucl Phys B (2004) 699:65. [Erratum-ibid: B (2005) 706:65]. doi: 10.1016/j.nuclphysb.2004.08.001
13. Arkani-Hamed N, Dimopoulos S, Giudice GF, Romanino A. Aspects of split supersymmetry. Nucl Phys B (2005) 709:3. doi: 10.1016/j.nuclphysb.2004.12.026
14. Acharya BS, Bobkov K, Kane G, Kumar P, Vaman D. An M theory Solution to the hierarchy problem. Phys Rev Lett. (2006) 97:191601. doi: 10.1103/PhysRevLett.97.191601
15. Acharya BS, Bobkov K, Kane GL, Kumar P, Shao J. Explaining the electroweak scale and stabilizing moduli in M theory. Phys Rev D (2007) 76:126010. doi: 10.1103/PhysRevD.76.126010
16. Acharya BS, Bobkov K, Kane GL, Shao J, Kumar P. The G(2)-MSSM: an M theory motivated model of particle physics. Phys Rev D (2008) 78:065038. doi: 10.1103/PhysRevD.78.065038
17. Acharya BS, Kane G, Kuflik E, Lu R. Theory and phenomenology of μ in M theory. JHEP (2011) 1105:033. doi: 10.1007/JHEP05(2011)033
18. Acharya BS, Kane G, Kumar P. Compactified String theories – generic predictions for particle physics. Int J Mod Phys A (2012) 27:1230012. (for a review). doi: 10.1142/S0217751X12300128
19. Kallosh R, Linde AD. Landscape, the scale of SUSY breaking, and inflation. JHEP (2004) 0412:004. doi: 10.1088/1126-6708/2004/12/004
20. Ibe M, Yanagida TT. The lightest higgs boson mass in pure gravity mediation model. Phys Lett B (2012) 709:374. doi: 10.1016/j.physletb.2012.02.034
21. Ibe M, Matsumoto S, Yanagida TT. Pure gravity mediation with m3∕2 = 10-100TeV. Phys Rev D (2012) 85:095011. doi: 10.1103/PhysRevD.85.095011
22. Bhattacherjee B, Feldstein B, Ibe M, Matsumoto S, Yanagida TT. Pure gravity mediation of supersymmetry breaking at the LHC. Phys Rev D (2013) 87:015028. doi: 10.1103/PhysRevD.87.015028
23. Evans JL, Ibe M, Olive KA, Yanagida TT. Universality in pure gravity mediation. Eur Phys J C (2013) 73:2468. doi: 10.1140/epjc/s10052-013-2468-9
24. Evans JL, Ibe M, Olive KA, Yanagida TT. Peccei-quinn symmetric pure gravity mediation. Eur Phys J C (2014) 74:2931. doi: 10.1140/epjc/s10052-014-2931-2
25. Evans JL, Ibe M, Olive KA, Yanagida TT. Light higgsinos in pure gravity mediation. Phys Rev D (2015) 91:055008. doi: 10.1103/PhysRevD.91.055008. [arXiv:1412.3403 [hep-ph]]. Available online at: http://arxiv.org/abs/1412.3403
27. Hall LJ, Nomura Y, Shirai S. Spread supersymmetry with wino LSP: gluino and dark matter signals. JHEP (2013) 1301:036. doi: 10.1007/JHEP01(2013)036
28. Gelmini GB, Gondolo P. Neutralino with the right cold dark matter abundance in (almost) any supersymmetric model. Phys Rev D (2006) 74:023510. doi: 10.1103/PhysRevD.74.023510
29. Acharya BS, Kane G, Watson S, Kumar P. A Non-thermal WIMP Miracle. Phys Rev D (2009) 80:083529. doi: 10.1103/PhysRevD.80.083529
30. Allahverdi R, Dutta B, Sinha K. Successful supersymmetric dark matter with thermal Over/under-abundance from late decay of a visible sector Scalar. Phys Rev D (2013) 87:075024. doi: 10.1103/PhysRevD.87.075024
31. Baer H, Choi KY, Kim JE, Roszkowski L. Dark matter production in the early universe: beyond the thermal WIMP paradigm. Phys Rept. (2015) 555:1. doi: 10.1016/j.physrep.2014.10.002
32. Kane GL, Kumar P, Nelson BD, Zheng B. Dark matter production mechanisms with a non-thermal cosmological history - a classification. Available online at: http://arxiv.org/abs/1502.05406
33. Baer H, Dermisek R, Rajagopalan S, Summy H. Neutralino, axion and axino cold dark matter in minimal, hypercharged and gaugino AMSB. JCAP (2010) 1007:014. doi: 10.1088/1475-7516/2010/07/014
34. Kim JE. A common scale for the invisible xion, local SUSY GUTs and saxino decay. Phys Lett B (1984) 136:378. doi: 10.1016/0370-2693(84)92023-9
35. Peccei RD, Quinn HR. CP conservation in the presence of instantons. Phys Rev Lett. (1977) 38:1440. doi: 10.1103/PhysRevLett.38.1440
37. Wilczek F. Problem of strong P and T invariance in the presence of instantons. Phys Rev Lett. (1978) 40:279. doi: 10.1103/PhysRevLett.40.279
38. Kim JE. Weak interaction singlet and strong CP invariance. Phys Rev Lett. (1979) 43:103. doi: 10.1103/PhysRevLett.43.103
39. Shifman MA. Vainshtein AI, Zakharov VI. Can confinement ensure natural CP invariance of strong interactions? Nucl Phys B (1980) 166:493. doi: 10.1016/0550-3213(80)90209-6
40. Dine M, Fischler W, Srednicki M. A simple solution to the strong CP problem with a harmless axion. Phys Lett B (1981) B104:199. doi: 10.1016/0370-2693(81)90590-6
41. Zhitnitskij AR. On possible suppression of the axion hadron interactions. (In Russian). Sov J Nucl Phys (1980) 31:260. [Yad Fiz 31:497].
42. Kim JE, Nilles HP. The mu problem and the strong CP problem. Phys Lett B (1984) 138:150. doi: 10.1016/0370-2693(84)91890-2
43. Chun EJ, Kim JE, Nilles HP. A natural solution of the mu problem with a composite axion in the hidden sector. Nucl Phys B (1992) 370:105. doi: 10.1016/0550-3213(92)90346-D
44. Hall L, Jedamzik K, March-Russell J, West SM. Freeze-in Production of FIMP dark matter. JHEP (2010) 1003:080. doi: 10.1007/JHEP03(2010)080
45. Preskill J, Wise MB, Wilczek F. Cosmology of the invisible axion. Phys Lett B (1983) 120:127. doi: 10.1016/0370-2693(83)90637-8
46. Abbott LF, Sikivie P. A cosmological bound on the invisible axion. Phys Lett B (1983) 120:133. doi: 10.1016/0370-2693(83)90638-X
47. Dine M, Fischler W. The not so harmless axion. Phys Lett B (1983) 120:137. doi: 10.1016/0370-2693(83)90639-1
49. Lyth DH. Axions and inflation: Sitting in the vacuum. Phys Rev D (1992) 45:3394. doi: 10.1103/PhysRevD.45.3394
50. Bae KJ, Huh JH, Kim JE. Update of axion CDM energy. JCAP (2008) 0809:005. doi: 10.1088/1475-7516/2008/09/005
51. Visinelli L, Gondolo P. Dark matter axions revisited. Phys Rev D (2009) 80:035024. doi: 10.1103/PhysRevD.80.035024
52. Baer H, Barger V, Huang P, Mustafayev A, Tata X. Radiative natural SUSY with a 125 GeV higgs boson. Phys Rev Lett. (2012) 109:161802. doi: 10.1103/PhysRevLett.109.161802
53. Baer H, Barger V, Huang P, Mickelson D, Mustafayev A, Tata X. Radiative natural supersymmetry: reconciling electroweak fine-tuning and the Higgs boson mass. Phys Rev D (2013) 87:115028. doi: 10.1103/PhysRevD.87.115028
54. Baer H, Barger V, Huang P, Mickelson D, Padeffke-Kirkland M, Tata X. Natural SUSY with a bino- or wino-like LSP. Phys Rev D (2015) 91:075005 doi: 10.1103/PhysRevD.91.075005
55. Bae KJ, Baer H, Lessa A, Serce H. Coupled boltzmann computation of mixed axion neutralino dark matter in the SUSY DFSZ axion model. JCAP (2014) 1410:082. doi: 10.1088/1475-7516/2014/10/082
57. Cohen AG, Kaplan DB, Nelson AE. The More minimal supersymmetric standard model. Phys Lett B (1996) 388:588. doi: 10.1016/S0370-2693(96)01183-5
58. Arkani-Hamed N, Murayama H. Can the supersymmetric flavor problem decouple? Phys Rev D (1997) 56:6733. doi: 10.1103/PhysRevD.56.R6733
59. Moroi T, Nagai M. Probing supersymmetric model with heavy sfermions using leptonic flavor and CP violations. Phys Lett B (2013) 723:107. doi: 10.1016/j.physletb.2013.04.049
60. Pierce A. Dark matter in the finely tuned minimal supersymmetric standard model. Phys Rev D (2004) 70:075006. doi: 10.1103/PhysRevD.70.075006
61. Arvanitaki A, Davis C, Graham PW, Wacker JG. One loop predictions of the finely tuned SSM. Phys Rev D (2004) 70:117703. doi: 10.1103/PhysRevD.70.117703
62. Arvanitaki A, Graham PW. Indirect signals from dark matter in split supersymmetry. Phys Rev D (2005) 72:055010. doi: 10.1103/PhysRevD.72.055010
63. Acharya BS, Kane G, Kuflik E. Bounds on scalar masses in theories of moduli stabilization. Int J Mod Phys A (2014) 29:1450073. doi: 10.1142/S0217751X14500730
64. Kachru S, Kallosh R, Linde AD, Trivedi SP. De sitter vacua in string theory. Phys Rev D (2003) 68:046005. doi: 10.1103/PhysRevD.68.046005
65. Choi K, Falkowski A, Nilles HP, Olechowski M, Pokorski S. Stability of flux compactifications and the pattern of supersymmetry breaking. JHEP (2004) 0411:076. doi: 10.1088/1126-6708/2004/11/076
66. Choi K, Falkowski A, Nilles HP, Olechowski M. Soft supersymmetry breaking in KKLT flux compactification. Nucl Phys B (2005) 718:113. doi: 10.1016/j.nuclphysb.2005.04.032
67. Choi K, Jeong KS, Okumura KI. Phenomenology of mixed modulus-anomaly mediation in fluxed string compactifications and brane models. JHEP (2005) 0509:039. doi: 10.1088/1126-6708/2005/09/039
68. Kallosh R, Linde A. Inflation and uplifting with nilpotent superfields. JCAP (2015) 1501:025. doi: 10.1088/1475-7516/2015/01/025
69. Linde A, Mambrini Y, Olive KA. Supersymmetry breaking due to moduli stabilization in string theory. Phys Rev D (2012) 85:066005. doi: 10.1103/PhysRevD.85.066005
70. Dudas E, Linde A, Mambrini Y, Mustafayev A, Olive KA. Strong moduli stabilization and phenomenology. Eur Phys J C (2013) 73:2268. doi: 10.1140/epjc/s10052-012-2268-7
71. Bae KJ, Baer H, Lessa A. Dark radiation constraints on mixed axion/neutralino dark matter. JCAP (2013) 1304:041. doi: 10.1088/1475-7516/2013/04/041
72. Bae KJ, Baer H, Chun EJ. Mixed axion/neutralino dark matter in the SUSY DFSZ axion model. JCAP (2013) 1312:028. doi: 10.1088/1475-7516/2013/12/028
73. Paige F, Protopopescu S, Baer H, Tata X. Available online at: http://www.nhn.ou.edu/~isajet/
74. Baer H, List J. Post LHC8 SUSY benchmark points for ILC physics. Phys Rev D (2013) 88:055004. doi: 10.1103/PhysRevD.88.055004
75. Baer H, Balázs C, Belyaev A. Neutralino relic density in minimal supergravity with coannihilations. JHEP (2002) 0203:042. doi: 10.1088/1126-6708/2002/03/042
76. Belanger G, Boudjema F, Pukhov A, Semenov A. micrOMEGAs3.1 : a program for calculating dark matter oservables. Comput Phys Commun. (2014) 185:960. doi: 10.1016/j.cpc.2013.10.016
77. Pradler J, Steffen FD. Constraints on the reheating temperature in gravitino dark matter scenarios. Phys Lett B (2007) 648:224.
78. Kohri K, Moroi T, Yotsuyanagi A. Big-bang nucleosynthesis with unstable gravitino and upper bound on the reheating temperature. Phys Rev D (2006) 73:123511. doi: 10.1103/PhysRevD.73.123511
79. Choi K-Y, Kim JE, Lee HM, Seto O. Neutralino dark matter from heavy axino decay. Phys Rev D (2008) 77:123501. doi: 10.1103/PhysRevD.77.123501
80. Baer H, Lessa A, Rajagopalan S, Sreethawong W. Mixed axion/neutralino cold dark matter in supersymmetric models. JCAP (2011) 1106:031. doi: 10.1088/1475-7516/2011/06/031
81. Baer H, Kraml S, Lessa A, Sekmen S. Reconciling thermal leptogenesis with the gravitino problem in SUSY models with mixed axion/axino dark matter. JCAP (2010) 1011:040. doi: 10.1088/1475-7516/2010/11/040
83. Kim JE Seo M-S. Mixing of axino and goldstino, and axino mass. Nucl Phys B (2012) 864:296. doi: 10.1016/j.nuclphysb.2012.06.018
84. Ade PAR et al., (Planck Collaboration). Planck 2013 results. XVI. Cosmological parameters. Astron Astrophys. (2014) 571:A16. doi: 10.1051/0004-6361/201321591
85. Covi L, Kim H-B, Kim JE, Roszkowski L. Axinos as dark matter. JHEP (2001) 0105:033. doi: 10.1088/1126-6708/2001/05/033
86. Brandenburg A, Steffen FD. Axino dark matter from thermal production. JCAP (2004) 0408:008. doi: 10.1088/1475-7516/2004/08/008
87. Strumia A. Thermal production of axino dark matter. JHEP (2010) 1006:036. doi: 10.1088/1475-7516/2004/08/008
88. Graf P, Steffen FD. Axions and saxions from the primordial supersymmetric plasma and extra radiation signatures. JCAP (2013) 1302:018. doi: 10.1103/PhysRevD.83.075011
89. Chun EJ. Dark matter in the kim-nilles mechanism. Phys Rev D (2011) 84:043509. doi: 10.1103/PhysRevD.84.043509
90. Bae KJ, Choi K, Im SH. Effective interactions of axion supermultiplet and thermal production of axino dark matter. JHEP (2011) 1108:065. doi: 10.1007/JHEP08(2011)065
91. Bae KJ, Chun EJ, Im SH. Cosmology of the DFSZ axino. JCAP (2012) 1203:013. doi: 10.1088/1475-7516/2012/03/013
92. Goto T, Yamaguchi M. Is axino dark matter possible in supergravity? Phys Lett B (1992) 276:103. doi: 10.1016/0370-2693(92)90547-H
93. Chun EJ, Kim JE, Nilles HP. Axino mass. Phys Lett B (1992) 287:123. doi: 10.1016/0370-2693(92)91886-E
94. Jedamzik K. Big bang nucleosynthesis constraints on hadronically and electromagnetically decaying relic neutral particles. Phys Rev D (2006) 74:103509. doi: 10.1103/PhysRevD.74.103509
95. Ackermann M et al., (Fermi Collaboration). Phys Rev Lett. (2011) 107:241302. doi: 10.1103/PhysRevLett.107.241302
96. Geringer-Sameth A, Koushiappas SM. Exclusion of canonical WIMPs by the joint analysis of Milky Way dwarfs with Fermi. Phys Rev Lett. (2011) 107:241303. doi: 10.1103/PhysRevLett.107.241303
97. Kusenko A, Rosenberg LJ. Working group report: non-wIMP dark matter. Available online at: http://arxiv.org/abs/1310.8642
Keywords: axions, dark matter, winos, DFSZ, KSVZ, supersymmetry, WIMPs
Citation: Bae KJ, Baer HA, Lessa A and Serce H (2015) Mixed axion-wino dark matter. Front. Phys. 3:49. doi: 10.3389/fphy.2015.00049
Received: 12 March 2015; Accepted: 22 June 2015;
Published: 10 July 2015.
Edited by:
Shinji Tsujikawa, Tokyo University of Science, JapanReviewed by:
Bhupal Dev, University of Manchester, UKNishita Desai, Universität Heidelberg, Germany
Copyright © 2015 Bae, Baer, Lessa and Serce. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kyu J. Bae, Howard A. Baer, and Hasan Serce, Physics and Astronomy, University of Oklahoma, Norman, 73019 OK, USA,YmFlQG5obi5vdS5lZHU=;YmFlckBuaG4ub3UuZWR1;c2VyY2VAb3UuZWR1
Andre Lessa, Instituto de Fisica, Universidade de Sao Paulo, Sao Paulo, Brazil,bGVzc2FAaWYudXNwLmJy
 Kyu J. Bae1*
Kyu J. Bae1* Howard A. Baer
Howard A. Baer Hasan Serce
Hasan Serce