Mechanical generation of spin current

We focus the recent results on spin-current generation from mechanical motion such as rigid rotation and elastic deformations. Spin transport theory in accelerating frames is constructed by using the low energy expansion of the generally covariant Dirac equation. Related issues on spin-manipulation by mechanical rotation are also discussed.

1. Introduction

Spin current, a flow of spins, is a key concept in the field of spintronics. It is generated by using angular momentum conversion among magnetic angular momentum due to magnetization dynamics, photon angular momentum, angular momentum due to orbital motion of electron, and spin angular momentum [1–3]. Meanwhile, mechanical angular momentum carried by condensed matter systems due to macroscopic motion has not been utilized for spin-current generation, which might be useful in nano-electromechanical systems (NEMS). In the following, we provide the theory of the coupling between mechanical angular momentum and spin current, and show that spin current can be generated from mechanical motion including rigid rotation and elastic deformations (Figure 1).

FIGURE 1

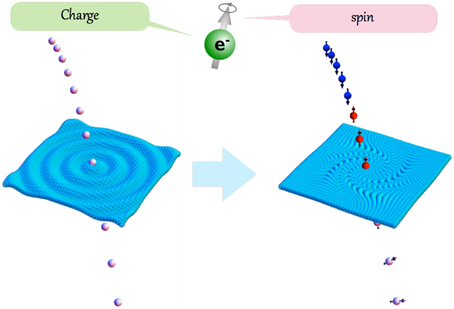
Figure 1. Concept of spin-mechatronics system. Left: coupling between charge current and mechanical motion yields electro-mechanical systems. Right: coupling between spin current and mechanical motion will open up a new field of spintronics.

1.1. Magnetism and Mechanical Rotation

Let us give a brief reivew on the coupling between magnetic moment and mechanical rotation. In 1915 Einstein and de Haas carried out the experiment that reveals a close relationship between magnetism and mechanical angular momentum. They measured the mechanical torque exerted by a reversal of the magnetization of an iron cylinder (Figure 2) [4]. In the same year, Barnett discovered the reciprocal effect, magnetization induced by rotation (Figure 3) [5]. He measured magnetization of iron which is rotated with the angular velocity Ω, and shows that the magnetization M is given by

$\begin{array}{ll}M=\chi \Omega ∕\gamma ,& (1)\end{array}$

where χ is the magnetic susceptibility and γ is the gyromagnetic ratio. The result means that an effective magnetic field,

$\begin{array}{ll}{B}_{\Omega }=\Omega ∕\gamma ,& (2)\end{array}$

is induced in the rotating body. Both Einstein-de Haas and Barnett's experiments established conversion between magnetic and mechanical angular momentum.

FIGURE 2

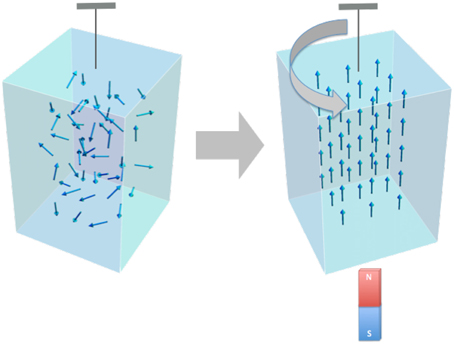
Figure 2. Einstein-de Haas effect. Modulation of magnetization of iron by applying the external magnetic filed, magnetic angular momentum is changed. As a result, the mechanical angular momentum is induced for compensating the modulation of the annular momentum.

FIGURE 3

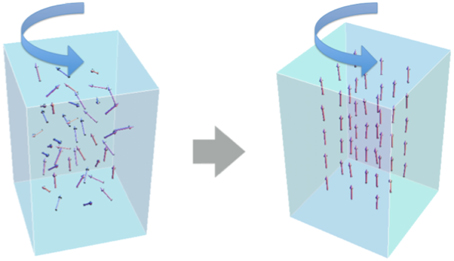
Figure 3. Barnett effect. Magnetization is induced by applying mechanical rotation since an effective magnetic field, emerges in a rotating body.

Recently much attention has been paid to the coupling between mechanical rotation and magnetism in the context of spintronics. Rapid progress in nanotechnology has allowed us to investigate the coupling of nano-magnetism and mechanical rotation [6–8]. There have been theoretical studies on the coupling between magnetic moment and mechanical motion [9–22]. Experiments on mechanical manipulation of nuclear spin have been carried out [23–25], where the Barnett field has been measured by using nuclear magnetic resonance (NMR) spectroscopy. Both a sample and an NMR coil are rotated synchronously at ultra high speed and the NMR frequency is shifted by the field because of the lifting of energy levels split by the external magnetic field. The results provide direct evidence of the coupling between the nuclear magnetic moment and mechanical rotation.

1.2. Toward Mechanical Generation of Spin Current

Our goal is to study mechanical generation of spin current. It is highly challenging because the phenomenon involves non-inertial motion of a body, i.e., rotation and acceleration, and the microscopic coupling has not been clarified. To study effects of mechanical motion on spin current, one has to extend condensed matter theory in an inertial frame to that in non-inertial frames. In the following, we construct quantum theory in accelerating systems and theoretically show that spin current can be generated from mechanical motion, including rigid rotation and elastic deformations.

The outline of this article is as follows. In Section 2, the Dirac equation in both inertial and non-inertial frames are summarized. In Section 3, the Pauli equation in the rotating frame is derived and mechanical generation of spin current by rigid rotation is presented. In Section 4, spin diffusion in the presence of elastic deformation is discussed and spin-current generation by surface acoustic waves is shown. In Section 5, renormalization of spin-rotation coupling is investigated. This article ends with a few concluding remarks in Section 6.

2. Electron in Non-inertial Frames

In this section, we derive the Pauli equation in non-inertial frames which includes inertial effects due to mechanical motion on electron spin. Conventionally, the Pauli equation is derived from low energy expansion of the special relativistic Dirac equation. However, this cannot describe effects induced by acceleration of a body since the special relativity is the theory in inertial systems. To describe spin transport phenomena with inertial effects, we start with the general relativistic Dirac equation that is the fundamental theory of spinor in non-inertial frames.

2.1. Electron in an Inertial Frame

Before going into the non-inertial frame, let us review the derivation of the Pauli equation in an inertial frame. Lagrangian of the special relativistic Dirac equation is given by

$\begin{array}{ll}{ℒ}=\overline{\text{Ψ}}[i{\gamma }^{a}c(p_a-q{A}_a)-m{c}^2]\text{Ψ},& (3)\end{array}$

where Ψ is the 4-spinor wave function, γ^a(a = 0, 1, 2, 3) is the Dirac matrix, which satisfies the anti-commutation relation: {γ^a, γ^b} = 2η^ab, with the Minkowski metric η^ab = diag(−, +, +, +), q is charge, m is mass, c is the speed of light, and A_a is the U(1) gauge potential. The Dirac matrix is related as γ⁰(x) = iβ, ${\gamma }^i(x)=i\beta {\alpha }_i$ with $\beta =\left(\begin{array}{cc}I& O\\ O& -I\end{array}\right)$ and $\alpha =\left(\begin{array}{cc}O& \sigma \\ \sigma & O\end{array}\right)$, where I is the 2 × 2 unit matrix and σ_i is the Pauli matrix.

The Dirac equation contains the electron and positron components. The special relativistic Dirac Hamiltonian is given by

$\begin{array}{ll}{H}_D=\beta m{c}^2+c\alpha ·\pi +q{A}_0,& (4)\end{array}$

where π = p − qA. As the energy gap between the electron and positron states is much larger than the energy scales of condensed matter systems, we reduce the Dirac equation to the Pauli equation using the low energy-expansion developed by Foldy and Wouthuysen [26] and Tani [27]. The Hamiltonian H_D is divided into two parts: ${\in }$ = qA₀ and ${𝓞}$ = cα · π. By successive unitary transformation, $H^{\prime }=U_F{H}_0{U}_F^{†}-i\hslash U_F{\partial }_t{U}_F^{†}$, $H^{″}=U_F{H}^{\prime }{U}_F^{†}-i\hslash U_F{\partial }_t{U}_F^{†}$, …, where $U_F=exp(-i\beta {𝒪}∕2m{c}^2)$, we obtain the block-diagonalized Hamiltonian up to the order of 1/m:

$\begin{array}{ll}{H}^{″}=\beta [m{c}^2+\frac{{\pi }^2}{2m}+\frac{q\hslash }{2m}\sigma ·B]+q{A}_0.& (5)\end{array}$

The second and third terms are the kinetic term and the Zeeman term. The Hamiltonian up to the order of 1/m² leads to the spin-orbit coupling and the Darwin term:

$\begin{array}{l}\frac{-1}{8m^2{c}^4}\left[{𝒪},\left[{𝒪},{\epsilon }\right]+i\hslash {\partial }_t{𝒪}\right]=\frac{q\lambda }{2\hslash }\sigma ·(\pi \times E-E\times \pi )\\ -\frac{q\lambda }{2}\text{div}E,& (6)\end{array}$

where λ = ℏ²/4m²c². While the spin-orbit coupling, λ, is small in vacuum since it originates from the expansion of ${𝓞}$(1/m²), the coupling is enhanced by quantum many body effects in materials (see Section 6 of this article). Actually, large spin-orbit coupling in Pt is widely used for the conversion between charge and spin currents, which are known as spin Hall effect (SHE) [28–34] and inverse spin Hall effect [35]. Hamiltonian with spin-orbit coupling:

$\begin{array}{ll}{H}_e^{(1∕m^2)}=\frac{{\pi }^2}{2m}-e{A}_0-\frac{e\hslash }{2m}\sigma ·B-\frac{e\lambda }{\hslash }\sigma ·(\pi \times E)& (7)\end{array}$

gives rise to the spin-dependent velocity

$\begin{array}{ll}v=\frac{1}{i\hslash }\left[r,H_e\right]=\frac{\pi }{m}-\frac{e\lambda }{m}\sigma \times E.& (8)\end{array}$

The second term is known as the anomalous velocity, which is responsible for the spin Hall effect (Figure 4).

FIGURE 4

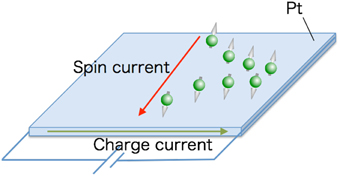
Figure 4. Spin Hall effect. Spin current is generated by strong spin-orbit coupling in Pt and it flows perpendicular to the charge current.

2.2. Electron in Non-inertial Frames

To include inertial effects due to mechanical motion, we start with the generally covariant Dirac Lagrangian [36–38]:

$\begin{array}{ll}{{ℒ}}_G=\overline{\text{Ψ}}[i{e}_a^{\mu }{\gamma }^{a}c(p_{\mu }-q{A}_{\mu }+i\hslash {\Gamma }_{\mu })-m{c}^2]\text{Ψ},& (9)\end{array}$

where the vierbein $e_a^{\mu }$ is a local orthonomal base and can be regarded as a square root of the metric tensor g^μν(x): $e_a^{\mu }{\eta }^{ab}{e}_b^{\nu }=g^{\mu \nu }$. The general relativistic version of the Dirac matrix is given by ${\gamma }^{\mu }(x)=e_a^{\mu }(x){\gamma }^a$ since it satisfies the anti-commutation relation: {γ^μ(x), γ^ν(x)} = 2g^μν(x). The Lagrangian includes the spin connection ${\Gamma }_{\mu }={\omega }_{\mu }^{ab}{\Sigma }_{ab}$, where ${\omega }_{\mu }^{ab}=e_{\lambda }^a({\partial }_{\mu }{\delta }_{\nu }^{\lambda }+{\Gamma }_{\mu \nu }^{\lambda })e^{\nu b}$ with the Christoffel symbol ${\Gamma }_{\mu \nu }^{\lambda }$ and the generator of the Lorentz transformation ${\Sigma }_{ab}=\frac{1}{4}\left[{\gamma }_a,{\gamma }_b\right]$. Especially, the spatial component of the generator is spin operator for the 4-spinor: ${\Sigma }_{ij}=\frac{1}{2}{ϵ}_{ijk}\left(\begin{array}{cc}{\sigma }_k& O\\ O& {\sigma }_k\end{array}\right)$. It should be noted that the general relativistic Lagrangian includes the spin-dependent gauge field Γ_μ(σ), which is responsible for the spin-dependent inertial effects and the mechanical generation of spin current as discussed below.

3. Spin Current Generation by Rigid Rotation

In this section, we show spin-current generation due to rigid rotation by using low energy expansion of the general relativistic Dirac equation.

3.1. Electron in a Rigidly Rotating Frame

Firstly, let us reconsider Einstein-de Haas and Barnett effects from the point of view of the Dirac equation in a rotating frame. The coordinate transformation from a rigidly rotating frame to an inertial frame is given by

$\begin{array}{ll}d{r}^{\prime }=dr+\left(\Omega \times r\right)dt,d{t}^{\prime }=dt,& (10)\end{array}$

where Ω is the angular velocity of the rotation with respect to an inertial frame. From the line element

$\begin{array}{l}d{s}^2=-c^{2}d{t{}^{\prime }}^2+d{r{}^{\prime }}^2=\left[-1+{(\Omega \times r∕c)}^2\right]c^{2}d{t}^2+2(\Omega \times r∕c)\\ cdtdr+d{r}^2=g_{\mu \nu }d{x}^{\mu }d{x}^{\nu },& (11)\end{array}$

the metric leads to $g_{00}=-1+{(\Omega \times \mathbf{\text{r}}∕c)}^2$, g_0i = g_i0 = (Ω × r/c)_i, g_ij = δ_ij (i, j = 1, 2, 3), where we assume |Ω × r/c| ≪ 1. The vierbein and inverse vierbein are given by

$\begin{array}{ll}{e}_0^0=1,e_j^0=0,e_0^i=-{(\Omega \times r∕c)}_i,e_j^i={\delta }_j^i,& (12)\end{array}$

and

$\begin{array}{ll}{e}_0^{\alpha }={\delta }_0^{\alpha }+{\eta }^{\alpha i}{(\Omega \times r∕c)}_i,e_i^{\alpha }={\delta }_i^{\alpha }.& (13)\end{array}$

The space-time dependent Dirac matrix becomes γ⁰(x) = −i β, iγⁱ(x) = iβ[(Ω × r/c)ⁱ + αⁱ], and the Christoffel symbols are given by

$\begin{array}{l}{\Gamma }_{00}^0={\Gamma }_{i0}^0={\Gamma }_{ij}^0={\Gamma }_{jk}^i=0,\\ {\Gamma }_{00}^i=\frac{{ϵ}_{ijk}{\Omega }_j{(\Omega \times r∕c)}_k}{c}+{\partial }_0{(\Omega \times r∕c)}_i,\\ {\Gamma }_{j0}^i=-\frac{{ϵ}_{ijk}{\Omega }_k}{c},& (14)\end{array}$

where ${\partial }_0=c^{-1}{\partial }_t$. Thus, the spin connection reads

$\begin{array}{ll}{\Gamma }_0(x)=\frac{{\gamma }^i{\gamma }^j{ϵ}_{ijk}{\Omega }_l}{4c}=\frac{i\Sigma ·\Omega }{2c},& (15)\end{array}$

$\begin{array}{ll}{\Gamma }_i(x)=0,& (16)\end{array}$

where $\Sigma =\frac{1}{2}\left(\begin{array}{cc}\sigma & O\\ O& \sigma \end{array}\right)$. The time component of the spin connection consists of the inner product of the spin operator and the angular velocity of the rotation, and appears in the following Hamiltonian:

$\begin{array}{ll}{\bar{H}}_D=\beta m{c}^2+(c\alpha -\Omega \times r)·\pi +q{A}_0-\hslash \Omega ·\Sigma .& (17)\end{array}$

The last term −ℏΩ·Σ is spin-rotation coupling. Velocity operator of the Dirac particle in the rotating frame is given by

$\begin{array}{ll}v=\frac{1}{i\hslash }\left[r,H\right]=c\alpha -\Omega \times r.& (18)\end{array}$

This consists of the combination of the velocity in an inertial frame cα and the rotation velocity Ω × r. By using the relation (cα − Ω × r) · π = cα · π −(r × π) · Ω, the Hamiltonian in the rotating frame ${\bar{H}}_D$ is related to that in an inertial frame $H_D=\beta m{c}^2+c\alpha ·\pi +q{A}_0$ as ${\bar{H}}_D=H_D-(\mathbf{\text{r}}\times \pi +\hslash \Sigma )·\Omega$. It agrees with the Hamiltonian obtained by the unitary transformation: $U{H}_D{U}^{†}-i\hslash U{\partial }_t{U}^{†}$ with U = exp[J·Ωt/iℏ] and J = r × π + ℏΣ.

Now let us derive an effective Hamiltonian for an electron in the rotating frame by the Foldy-Wouthuysen-Tani (FWT) transformation. The Hamiltonian H is divided into ${{\epsilon }}^{\prime }=q{A}_0-\Omega ·(\mathbf{\text{r}}\times \pi +\hslash \Sigma )$ and ${𝓞}$ = cα · π. Using the unitary transformation $U_F=exp(-i\beta {𝒪}∕2m{c}^2)$, the Hamiltonian to the order of 1/m is given by

$\begin{array}{l}{\bar{H}}_D^{\prime }=\beta [m{c}^2+\frac{{\pi }^2}{2m}+\frac{q\hslash }{2m}\sigma ·B]+q{A}_0\\ -(r\times \pi +\hslash \Sigma )·\Omega .& (19)\end{array}$

We obtain the kinetic term and Zeeman term as well as the coupling of the total angular momentum J = r × π + Σ and the rotation frequency Ω. The electron sector of the Hamiltonian is written as

$\begin{array}{ll}{\bar{H}}_e^{(1∕m)}=\frac{{\pi }^2}{2m}-e{A}_0-r\times \pi ·\Omega -\frac{e\hslash }{2m}\sigma ·(B+B_{\Omega }),& (20)\end{array}$

where B_Ω = mΩ/e is known as the Barnett field, which is the effective magnetic field due to mechanical rotation and the quantum mechanical origin of the Barnett effect.

The expansion of the order of 1/m² yields the spin-orbit coupling and the Darwin terms augmented by inertial effects [39–41]:

$\begin{array}{l}\frac{-1}{8m^2{c}^4}[{𝒪},[{𝒪},{{\epsilon }}^{\prime }]+i\hslash {\partial }_t{𝒪}]=\frac{q\lambda }{2\hslash }\sigma ·(\pi \times E^{\prime }-E^{\prime }\times \pi )\\ -\frac{q\lambda }{2}\text{div}{E}^{\prime },& (21)\end{array}$

where E′ = E +(Ω × r) × B. It means that the conventional electric field E appeared in the couplings is modified as E → E′ = E +(Ω × r) × B. This result is in accord with the general relativistic transformation of electromagnetic fields in the rotating frame:

$\begin{array}{ll}{E}^{\prime }=E+(\Omega \times r)\times B,& (22)\end{array}$

$\begin{array}{ll}{B}^{\prime }=B,& (23)\end{array}$

where E and B are electromagnetic fields in the rest frame. It should be noted that these relations are not the Lorentz transformations in the special relativity but the general coordinate transformations in the general relativity. The Lorentz transformation of the electromagnetic fields is written as

$\begin{array}{ll}{E}^{″}∕c=\gamma (E∕c+\beta \times B)-\frac{{\gamma }^2}{\gamma +1}(\beta ·E∕c)\beta ,& (24)\end{array}$

$\begin{array}{ll}{B}^{″}=\gamma (B-\beta \times E∕c)-\frac{{\gamma }^2}{\gamma +1}(\beta ·B)\beta ,& (25)\end{array}$

with $\gamma =1∕\sqrt{1-{\beta }^2},$ and β = v₀/c, where E″ and B″ are the electromagnetic field in the inertial frame, whose relative velocity to the rest frame is v₀. In the case of β ⊥ E, β ⊥ B and |v₀/c| ≪ 1, the Lorentz transformations are reduced to

$\begin{array}{llll}{E}^{″}∕c& =& E∕c+\beta \times B,& (26)\end{array}$

$\begin{array}{llll}{B}^{″}& =& B-\beta \times E∕c.& (27)\end{array}$

The special relativistic transformations Equations (26) and (27) have a symmetry for E/c and B, while the general relativistic relations Equations (22) and (23) do not. Such an asymmetry originates from the space-time asymmetry of a general coordinate transformation [41, 42].

3.2. Spin Current from Rigid Rotation

Now we discuss spin current generation from rigid rotation. As derived above, Hamiltonian for electron in the rotating frame is given by

$\begin{array}{l}{\bar{H}}_e=H_e-(r\times \pi +\frac{\hslash }{2}\sigma )·\Omega \\ -\frac{e\lambda }{\hslash }\sigma ·\left[\pi \times \left\{(E+\Omega \times r)\times B\right\}\right].& (28)\end{array}$

Even in the absence of E, when we have both magnetic field B and rotation Ω, the anomalous velocity is induced in the rotating frame as

$\begin{array}{ll}{v}_{\sigma }=-\frac{e\lambda }{m}\sigma \times \left\{E+(\Omega \times r)\times B\right\}.& (29)\end{array}$

In the case of Ω || B || e_z, where e_z is the unit vector along the z-axis, the term (Ω × r) × B becomes ΩrBe_r with the unit vector along the radial direction e_r. Accordingly, the z-polarized spin current flows along the azimuthal direction (Figure 5). The spin current is estimated as

$\begin{array}{ll}{J}_s=en\text{Tr}{\sigma }_z{v}_{\sigma }=2ne\kappa {\omega }_{c}r{e}_{\varphi },& (30)\end{array}$

where r is the distance from the rotation axis, e_ϕ is the unit vector of the azimuthal direction, n is the electron density, and ω_c = eB/m is the cyclotron frequency. The dimensionless parameter κ is given by $\kappa =\tilde{\lambda }{k}_F^2·\frac{\hslash \Omega }{{ϵ}_F}$, where $k_F,{ϵ}_F={\hslash }^2{\mathbf{\text{k}}}_F^2∕2m$ are the Fermi wave number and the Fermi energy, respectively, and $\tilde{\lambda }$ is the spin-orbit coupling in a material. In the case of Pt, $\tilde{\lambda }{k}_F^2\approx 0.6$, and when B = 1T and Ω = 1 kHz, the spin current becomes $J_s\approx 10^8$A/m² [39].

FIGURE 5

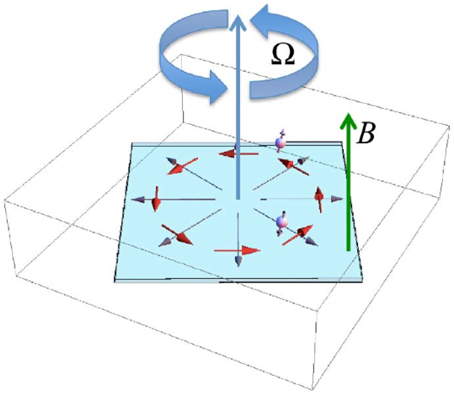
Figure 5. Spin Hall effect in the rotating frame where an external magnetic field is applied along the rotation axes. In this case, the effective electric field is induced in the radial direction and the spin current flows along the azimuthal direction.

4. Spin Current Generation by Elastic Motion

The spin current generation from rigid rotation requires strong spin-orbit coupling as discussed above. On the contrary, in the following we will show an alternative mechanism for mechanical generation of spin current in non-magnets where spin-orbit coupling is not necessary.

4.1. Spin Diffusion Under Time-dependent Field

From now on, we pursue a new route for generating spin current by considering spin-rotation coupling:

$\begin{array}{ll}{H}_{SR}=-\frac{\hslash }{2}\sigma ·B.& (31)\end{array}$

First let us consider applying stationary rotation. In this case, the Barnett field is induced in a material and electron spins align to the rotation axis because of the spin relaxation. However, spin currents cannot be generated since an equilibrium spin state is eventually reached. To generate spin currents, the Barnett field should be time-dependent so that a nonequilibrium spin state is realized. In the following, we investigate spin transport by using the generalized spin diffusion equation in the presence of non-stationary rotation.

When the mechanical rotation, Ω, is applied along the z-axis, the bottom of the energy band of the electron is shifted by ℏΩ/2 due to the Barnett effect. The number density of up (down) spin electron is given by

$\begin{array}{ll}{n}_{\uparrow (\downarrow )}={\displaystyle {\int }_{\pm \hslash \Omega ∕2}^{{\mu }_{\uparrow (\downarrow )}}}d\epsilon N_0(\epsilon ),& (32)\end{array}$

where N₀ is the density of states for electrons, μ_↑ and μ_↓ are the spin-dependent electro-chemical potentials for up and down spin electrons, respectively (Figure 6). Thus, the spin density can be estimated as n_↑ − n_↓ ≈ N₀ δμ, where δμ = μ_↑ − μ_↓ is the spin accumulation. Here the density of state is assumed to be constant for simplicity. Generally, spin relaxation occurs in two processes (Figure 6):

1. on-site spin flip with the spin lifetime, τ_sf,

2. spin diffusion with the diffusion constant, D.

FIGURE 6

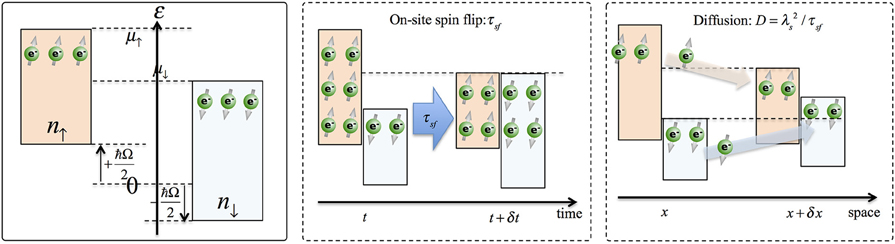
Figure 6. Electron spin states in a rotating frame and spin-diffusion. In a rotating frame, the magnetization by the Barnett field due to mechanical rotation should be included when calculating the spin density (left panel). Spin relaxation occurs in both on-site spin flip (middle panel) and spin diffusion processes (right panel).

The on-site spin flip with the spin lifetime is expressed as ${\tau }_{\text{sf}}^{-1}{N}_0\delta \mu$ and the spin diffusion process as $D{\nabla }^2(N_0\delta \mu )$. Then, the continuity equation for spin density becomes ${\partial }_t(n_{\uparrow }-n_{\downarrow })={\tau }_{\text{sf}}^{-1}{N}_0\delta \mu +D{\nabla }^2(N_0\delta \mu )$. Thus, we obtain the extended spin diffusion equation in the presence of spin-rotation coupling [43]:

$\begin{array}{ll}\left({\partial }_t-D{\nabla }^2+{\tau }_{\text{sf}}^{-1}\right)\delta \mu =\hslash {\partial }_t\Omega ,& (33)\end{array}$

The time-derivative of rotation frequency ∂_tΩ appears in the right-hand side of Equation (33) and this term vanishes when the rotation is stationary as mentioned above.

The z-polarized spin current can be calculated as $J_s=\frac{{\sigma }_0}{e}\nabla \delta \mu$, where σ₀ is the conductivity and δμ is the solution of Equation (33). Therefore, to generate spin current, we need space-time dependent mechanical rotation. To realize such rotation, we focus on an elastic deformation induced by surface acoustic waves, which is suitable for spin-current generation as shown in the next section.

4.2. Electron in Elastic Materials

The coordinate transformation from a local rest frame in an elastic material to the laboratory frame is given by dr′ = dr + vdt, dt′ = dt, where v(t, r) is the velocity field due to elastic deformations, and then, the metric tensor becomes $g_{00}=-1+v^2∕c^2,g_{0i}=g_{i0}=v_i∕c,g_{ij}={\delta }_{ij}$, and the vierbein is given by $e_0^0=1,e_j^0=0,e_0^i=-v_i∕c,e_j^i={\delta }_j^i$. In this case, the spin connection is given by Γ₀ = iΣ · ω/2, Γ_i = 0, where ω = ∇ × v is the vorticity of the lattice motion. This result shows that spin-rotation coupling Σ·Ω in the rigidly rotating frame is extended to“spin-vorticity coupling" Σ·ω/2 in the presence of elastic deformation. The Dirac Hamiltonian is written as

$\begin{array}{l}{H}_D=\beta m{c}^2+c\alpha ·\pi -e{A}_0+\frac{e}{2}A·v-\frac{1}{2}\left\{v,\pi \right\}\\ -\frac{\hslash }{2}\Sigma ·\omega ,& (34)\end{array}$

and the lowest order of the FWT transformation leads to the Hamiltonian for electron:

$\begin{array}{l}{H}_e=\frac{{\pi }^2}{2m}-e{A}_0-\frac{e\hslash }{2m}\sigma ·B+\frac{e}{2}A·v-\frac{1}{2}\left\{v,\pi \right\}\\ -\frac{\hslash }{2}\sigma ·\frac{\omega }{2}.& (35)\end{array}$

The last term is the spin-vorticity coupling, which is responsible for spin-current generation due to surface acoustic waves.

4.3. Spin Current from Surface Acoustic Wave

Let us consider the generation of spin current due to surface acoustic waves (SAWs) in nonmagnetic metals or semiconductors¹. Our setup is illustrated in Figure 7. The SAW traveling along the x-axes induces the local rotational motion along the z-axes whose angular velocity is given by [47, 48]

$\begin{array}{ll}\Omega (x,y,t)=\frac{{\omega }_s^2{u}_0}{2c_t}exp\left\{-k_{t}y+i(kx-\omega t)\right\},& (36)\end{array}$

where ω_s and u₀ are the frequency of the mechanical resonator and the amplitude, respectively, and c_t is the transverse sound velocity, k is the wave number, $k_t=k\sqrt{1-{\xi }^2}$ is the transverse wave number, and ξ is given by ξ = (0.875+1.12ν)/(1+ν) with the Poisson ratio ν. The frequency ω_s is related to k, c_t, and ξ as ω_s = c_tkξ. Inserting Equation (36) into the spin-diffusion Equation (33), the solution leads to the SAW induced spin current [43]:

$\begin{array}{l}{J}_s=\frac{{\sigma }_0}{e}\frac{\partial }{\partial y}{\displaystyle {\int }_0^{\infty }}d{t}^{\prime }{\displaystyle {\int }_0^{\infty }}d{y}^{\prime }\frac{\theta (t-t^{\prime })e^{-(t-t)(1+{\lambda }_s^2{k}^2)∕{\tau }_{\text{sf}}}}{\sqrt{4\pi D(t-t^{\prime })}}\\ \left[e^{-\frac{{(y-y^{\prime })}^2}{4D(t-t^{\prime })}}+e^{-\frac{{(y+y^{\prime })}^2}{4D(t-t^{\prime })}}\right]e^{-k_t{y}^{\prime }-i\omega t^{\prime }},& (37)\end{array}$

where ${\lambda }_s=\sqrt{D{\tau }_{\text{sf}}}$ is the spin diffusion length, and we use the boundary condition J_s = 0 on the surface y = 0. Especially, in the case of ω_sτ_sf ≪1, the solution is reduced to

$\begin{array}{ll}{J}_s\approx \frac{\hslash {\sigma }_0}{2e}{\tau }_{\text{sf}}{\omega }_s^4\frac{u_0}{c_t^2}\frac{\sqrt{1-{\xi }^2}}{\xi }exp\left[-k_{t}y+i(kx-{\omega }_{s}t)\right].& (38)\end{array}$

FIGURE 7

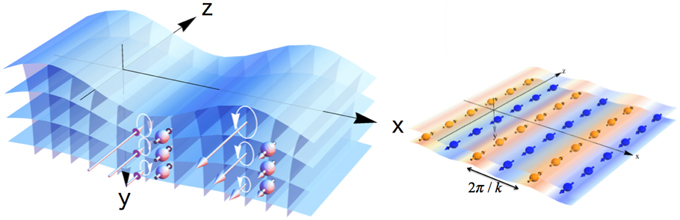
Figure 7. Spin-current generation by spin-vorticity coupling. Spin current flows along the gradient of vorticity due to the SAW (left figure). Magnetic stripe patterns are induced on the surface of non-magnets (right figure).

As shown in Figure 7, the spin current flows along the y-axes, namely parallel to the gradient of the effective magnetic field due to the vorticity of the lattice motion. As a result, the magnetic stripe pattern is induced on the surface of the non-magnetic metal or semi-conductor. Experimentally, spin precession controlled by SAW was observed by using the time-resolved polar magneto-optic Ker effect (MOKE) in which the spatial and time resolution of the order of 10 μm and 10 ns have been acheived [49, 50]. MOKE measurements for metallic multilayer are also performed [51]. Since in-plane spin polarization is induced in our setup, transversal of longitudinal MOKE measurements are relevant to the SAW-induced spin accumulation.

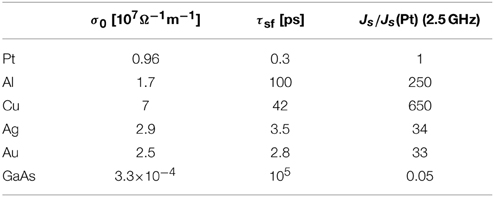
The spin current depends strongly on σ₀ and τ_sf. Table 1 shows the amplitude of the spin current for Pt, Al, Cu, Ag, Au, and n-dopoed GaAs normalized by that for Pt in the case of ω_s = 2.5 GHz. In the case of u₀ = 0.01 nm, J_s(Pt) becomes 10⁴ A/m². Remarkably, the spin current for Al or Cu is much larger than that for Pt since the generated spin current is proportional to σ₀ and τ_sf.

TABLE 1

Table 1. Spin current generated by SAWs.

Conventionally, the generation of spin current in nonmagnetic materials has required strong spin-orbit coupling because the spin Hall effect is used. This means that materials with short spin lifetime has been suitable for spin-current generation. On the contrary, the mechanism proposed in this section requires longer spin lifetimes to generate larger spin currents. In other words, Al and Cu, which have been regarded as good materials for a spin conducting channel, can be favorable for generating spin current.

As expressed in Equation (38), the generated spin current oscillates with the frequency ω_s. The AC nature of the spin current has several advantages: one of the valuable applications would be for the spin-torque ferromagnetic resonance (ST-FMR) [52], where AC spin currents excite magnetization dynamics of nanomagnets in the several GHz range. In Liu et al. [52], an AC charge current is converted into an AC spin current via the SHE which requires materials with the large spin-Hall angle such as Pt and Ta whereas our method does not rely on the SHE and Cu or Al can be used. This indicates that the predicted AC spin current can provide an alternative route for the ST-FMR, namely, a “rare-metal-free” ST-FMR.

5. Renormalization of Spin-rotation Coupling

It is well known that conventional Zeeman coupling and spin-orbit coupling are enhanced by quantum many body effect in materials. In this section, spin-rotation or spin-vorticity coupling and augmented spin-orbit coupling derived in the previous sections are also enhanced by the similar mechanism.

5.1. Bloch Theorem in the Presence of Rotation

Let us consider an electron in a periodic potential in the presence of mechanical rotation.

Firstly, we recall conventional Bloch's theorem. We begin with an electron Hamiltonian in the laboratory frame: $H_0=\frac{{\mathbf{\text{p}}}^2}{2m}+V_0({\mathbf{\text{r}}}_0)$, where V₀ is a microscopic periodic crystal potential. When the crystal lattice has translational symmetry, where primitive lattice vectors a_i(i = 1, 2, 3), eigenfunction for H₀ can be written as ${\psi }_{n,{\mathbf{\text{k}}}^{}}(\mathbf{\text{r}})=e^{i{\mathbf{\text{k}}}^{\prime }·\mathbf{\text{r}}}{u}_{n,{\mathbf{\text{k}}}^{\prime }}(\mathbf{\text{r}})$. Here n is the band index, R is given by $\mathbf{\text{R}}=\sum _i{m}_i{\mathbf{\text{a}}}_i$ with integer m_i, and u_{u, k} satisfies u_{u, k}(r + R) = u_{n, k}(r). This is known as Bloch's theorem. In the presence of an external magnetic field, Hamiltonian has the magnetic translation symmetry [53], and the Bloch's eigenfunction is modified as ${\psi }_{n,{\mathbf{\text{k}}}^{\prime }}(\mathbf{\text{r}})=e^{i{\mathbf{\text{k}}}^{\prime }·\mathbf{\text{r}}}{u}_{n,{\mathbf{\text{k}}}^{\prime }}(\mathbf{\text{r}})$, where the generalized crystal momentum ℏk′ = p + eA is introduced.

As discussed above, mechanical rotation Ω can be regarded as an effective magnetic field, namely, the Barnett field B_Ω = Ω/γ. Accordingly, the wave function for electron in the rotating frame should be treated as a similar eigenfunction in the presence of magnetic fields. The Hamiltonian in the rigidly rotating frame $\bar{H}$ is derived as $\bar{H}=U{H}_0{U}^{†}-i\hslash U\frac{\partial U^{†}}{\partial t}=H_0-\mathbf{\text{J}}·\Omega$, where U = exp[J · Ωt/iℏ] is the unitary transformation with the generator of rotation $\mathbf{\text{J}}=\mathbf{\text{r}}\times \mathbf{\text{p}}+\frac{\hslash }{2}\sigma$. The Hamiltonian can be rewritten as

$\begin{array}{ll}{H}_R=\frac{{(p+e{A}_g)}^2}{2m}+V_0(r)-e{\varphi }_g-\frac{e\hslash }{2m}\sigma ·\frac{B_g}{2},& (39)\end{array}$

where A_g = −(m/e)Ω × r, ${\varphi }_g=(m∕e){(\Omega \times \mathbf{\text{r}})}^2∕2$, and B_g = ∇ × A_g. The field B_g is known as the gravitomagnetic field, which is related to the Barnett field B_Ω as B_Ω = B_g/2. Compared with the Hamiltonian in the presence of electromagnetic fields, $H=\frac{{(\mathbf{\text{p}}+e\mathbf{\text{A}})}^2}{2m}+V_0(\mathbf{\text{r}})-e{\varphi }_g-\frac{g}{2}\frac{e\hslash }{2m}\sigma ·\mathbf{\text{B}}$ with the electron g-factor g, the vector potential, which represents the Coriolis effect, A_g, and the scalar potential ϕ_g, the centrifugal force, appears in $\bar{H}$ and the spin-rotation coupling can be interpreted as the effective Zeeman coupling with g = 1. Since the symmetry of the Hamiltonian is similar to the magnetic translational symmetry, the eigenfunction of $\bar{H}$ is given by ${\psi }_{n,{\mathbf{\text{k}}}_g}(\mathbf{\text{r}})=e^{i{\mathbf{\text{k}}}_g·\mathbf{\text{r}}}{u}_{n,{\mathbf{\text{k}}}_g}(\mathbf{\text{r}})$ with ℏk_g = p + eA [54].

5.2. Renormalization by Interband Mixing

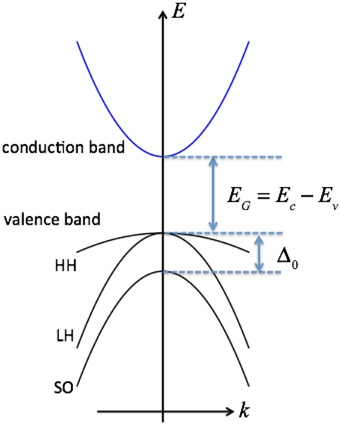
We extend the conventional k·p perturbation [55, 56] to that in the presence of rotation [54]. It is shown that spin-rotation coupling and spin-orbit coupling can be renormalized by the interband mixing in the case of the simple band structure such as GaAs and InSb by using the 8 × 8 Kane model [55] (in which the band structure is shown in Figure 8). We obtain an effective Hamiltonian for the conduction electrons [54]:

$\begin{array}{l}{H{}^{\prime }}^{*}=\frac{{\hslash }^2{k}_g^2}{2m^{*}}+V-(1+\delta g)\frac{\hslash }{2}\sigma ·\Omega \\ +q(\lambda +\delta {\lambda }_{\text{S}})\sigma ·(k_g\times E)+\frac{q}{2}(\lambda +\delta {\lambda }_{\text{D}})\text{div}E,& (40)\end{array}$

where

$\begin{array}{cc}\frac{1}{m^{*}}=\frac{1}{m}+\frac{2P^2}{3{\hslash }^2}(\frac{2}{E_G}+\frac{1}{E_G+{\Delta }_0})& \left(41\right)\end{array}$

$\begin{array}{cc}\delta g=-\frac{4m}{{\hslash }^2}\frac{P^2}{3}(\frac{1}{E_G}-\frac{1}{E_G+{\Delta }_0}),& \left(42\right)\end{array}$

$\begin{array}{cc}\delta {\lambda }_{\text{S}}=-\frac{P^2}{3}(\frac{1}{E_G^2}-\frac{1}{{(E_G+{\Delta }_0)}^2}),& \left(43\right)\end{array}$

$\begin{array}{cc}\delta {\lambda }_D=\frac{P^2}{3}(\frac{2}{E_G^2}+\frac{1}{{(E_G+{\Delta }_0)}^2}).& \left(44\right)\end{array}$

FIGURE 8

Figure 8. Band structure in the 8 × 8 Kane model.

Here, E_G is the energy gap between the conduction and valence bands, Δ₀ is the spin-orbit gap, and P is the Kane momentum matrix element. Thus, both spin-rotation and spin-orbit couplings are renormalized by the interband mixing in materials with non-zero spin-orbit gap Δ₀. In this derivation, we use the simple Hamiltonian ${\bar{H}}^{\prime }$. If we include the augmented spin-orbit coupling, The relations above are modified as E → E′, and therefore, the spin-orbit coupling due to mechanical rotation is also renormalized by the interband mixing.

Conventionally, the renormalized Zeeman coupling obtained from the 8 × 8 Kane model is given by (2 + δg)/2μ_Bσ · B, while spin-rotation coupling is modulated as $-(1+\delta g)\frac{\hslash }{2}\sigma ·\Omega$. The difference stems from that of g factors for the usual magnetic field and the gravitomagnetic field. For lightly doped n-InSb at low temperature, g = −49 has been reported. In this case, δg = −51 [55], and then, spin-rotation coupling becomes about 50 times as large as the bare coupling.

6. Discussion and Conclusions

In this article, we review mechanical generation of spin current by using the low energy expansion of the generally covariant Dirac equation. We have found various inertial effects on electron spins that have been ignored in conventional condensed matter theory. According to general relativity, inertial effects are represented by connections, or gauge fields. Especially, the Dirac equation in non-inertial frames contains spin-dependent connections, and thus, spin-dependent gauge fields appears in the Hamiltonian for electrons in accelerating bodies, and are responsible for generating spin current.

Mechanical generation of spin current as well as mechanical manipulation of spins stem from the intrinsic property of spinor, which is sensitive to curvature of space-time. This year is the 100th anniversary since Einstein's clarification of the coupling between magnetism and mechanical motion as well as his construction of the general relativity. Relying on both fundamental concepts, we are pursuing a new development of spintronics, where spin and mechanical motion are gracefully harmonized.

Funding

This work was financially supported by Grant-in-Aid for Scientific Research C (15K05153), Grant-in-Aid for Young Scientists B (20463797), Grants-in-Aid for Scientific Research A (26247063), and Grant-in-Aid for Scientific Research on Innovative Area, Nano Spin Conversion Science (Grant No. 26103005) from MEXT.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank E. Saitoh, K. Harii, H. Chudo, and M. Ono for valuable discussions.

Footnotes

1. ^Note that spin-generation due to SAWs in magnets has been carried out by Uchida et al. [44–46], where they use magnetization dynamics induced by SAWs.

References

1. Maekawa S, Valenzuela S, Saitoh E, Kimura T (eds.). Spin Current. Oxford, UK: Oxford University Press (2012).

Google Scholar

2. Zutic I, Fabian J, Sarma SD. Spintronics: fundamentals and applications. Rev Mod Phys. (2004) 76:323–410. doi: 10.1103/RevModPhys.76.323

CrossRef Full Text | Google Scholar

3. Maekawa S (ed.). Concepts in Spin Electronics. Oxford, UK: Oxford University Press (2006).

Google Scholar

4. Einstein A, de Haas WJ. Experimental proof of the existence of Ampere's molecular currents. Verh Dtsch Phys Ges. (1915) 17:152.

Google Scholar

5. Barnett SJ. Magnetization by rotation. Phys Rev. (1915) 6:239–70. doi: 10.1103/PhysRev.6.239

CrossRef Full Text | Google Scholar

6. Wallis TM, Moreland J, Kabos P. Einstein–de Haas effect in a NiFe film deposited on a microcantilever. Appl Phys Lett. (2006) 89:122502. doi: 10.1063/1.2355445

CrossRef Full Text | Google Scholar

7. Zolfagharkhani G, Gaidarzhy A, Degiovanni P, Kettemann S, Fulde P, Mohanty P. Nanomechanical detection of itinerant electron spin flip. Nat Nanotechnol. (2008) 3:720–723. doi: 10.1038/nnano.2008.311

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Tejada J, Zysler RD, Molins E, Chudnovsky EM. Evidence for quantization of mechanical rotation of magnetic nanoparticles. Phys Rev Lett. (2010) 104:027202.

PubMed Abstract | Google Scholar

9. Kovalev AA, Bauer GEW, Brataas A. Magnetovibrational coupling in small cantilevers. Appl Phys Lett. (2003) 83:1584. doi: 10.1063/1.1603338

CrossRef Full Text | Google Scholar

10. Chudnovsky EM. Universal decoherence in solids. Phys Rev Lett. (2004) 92:120405. doi: 10.1103/PhysRevLett.92.120405

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chudnovsky EM, Garanin DA, Schilling R. Universal mechanism of spin relaxation in solids. Phys Rev. (2005) B72:094426. doi: 10.1103/PhysRevB.72.094426

CrossRef Full Text | Google Scholar

12. Chudnovsky EM, Garanin DA. Damping of a nanocantilever by paramagnetic spins. Phys. Rev. (2014) B89:174420. doi: 10.1103/PhysRevB.89.174420

CrossRef Full Text | Google Scholar

13. Kovalev AA, Bauer GEW, Brataas A. Nanomechanical magnetization reversal. Phys Rev Lett. (2005) 94:167201. doi: 10.1103/PhysRevLett.94.167201

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kovalev AA, Bauer GEW, Brataas A. Current-driven ferromagnetic resonance, mechanical torques, and rotary motion in magnetic nanostructures. Phys Rev B (2007) 75:014430. doi: 10.1103/PhysRevB.75.014430

CrossRef Full Text | Google Scholar

15. Kovalev AA, Hayden LX, Bauer GEW, Tserkovnyak Y. Macrospin Tunneling and Magnetopolaritons with Nanomechanical Interference. Phys Rev Lett. (2011) 106:147203. doi: 10.1103/PhysRevLett.106.147203

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bretzel S, Bauer GEW, Tserkovnyak Y, Brataas A. Barnett effect in thin magnetic films and nanostructures. Appl Phys Lett. (2009) 95:122504. doi: 10.1063/1.3232221

CrossRef Full Text | Google Scholar

17. Bauer GEW, Bretzel S, Brataas A, Tserkovnyak Y. Nanoscale magnetic heat pumps and engines. Phys Rev B (2010) 81:024427. doi: 10.1103/PhysRevB.81.024427

CrossRef Full Text | Google Scholar

18. Chudnovsky EM, Martinez-Hidalgo X. Tunneling with dissipation and decoherence for a large spin. Phys Rev B (2002) 66:054412. doi: 10.1103/PhysRevB.66.054412

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Calero C, Chudnovsky EM, Garanin DA. Quantum dynamics of a nanomagnet in a rotating field. Phys Rev B (2005) 72:024409. doi: 10.1103/PhysRevB.72.024409

CrossRef Full Text | Google Scholar

20. Calero C, Chudnovsky EM. Rabi spin oscillations generated by ultrasound in solids. Phys Rev Lett. (2007) 99:047201. doi: 10.1103/PhysRevLett.99.047201

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Calero C, Chudnovsky EM, Garanin DA. Magneto-elastic waves in crystals of magnetic molecules. Phys Rev B (2007) 76:094419. doi: 10.1103/PhysRevB.76.094419

CrossRef Full Text | Google Scholar

22. Garanin DA, Chudnovsky EM. Quantum entanglement of a tunneling spin with mechanical modes of a torsional resonator. Phys Rev X (2011) 1:011005. doi: 10.1103/PhysRevX.1.011005

CrossRef Full Text | Google Scholar

23. Chudo H, Ono M, Harii K, Matsuo M, Ieda J, Haruki R, et al. Observation of Barnett fields in solids by nuclear magnetic resonance. Appl Phys Exp. (2014) 7:063004. doi: 10.7567/APEX.7.063004

CrossRef Full Text

24. Chudo H, Harii K, Matsuo M, Ieda J, Ono M, Maekawa S, et al. Rotational doppler effect and barnett field in spinning NMR. J Phys Soc Jpn. (2015) 84:043601. doi: 10.7566/JPSJ.84.043601

CrossRef Full Text

25. Harii K, Chudo H, Ono M, Matsuo M, Ieda J, Okayasu S, et al. Line splitting by mechanical rotation in nuclear magnetic resonance. Jpn J Appl Phys. (2015) 54:050302. doi: 10.7567/JJAP.54.050302

CrossRef Full Text

26. Foldy LL, Wouthuysen SA. On the dirac theory of spin 1/2 particles and its non-relativistic limit. Phys Rev. (1950) 78:29–36. doi: 10.1103/PhysRev.78.29

CrossRef Full Text | Google Scholar

27. Tani S. Connection between particle models and field theories, I. Prog Theor Phys. (1951) 6:267–85. doi: 10.1143/ptp/6.3.267

CrossRef Full Text | Google Scholar

28. Dyakonov MI, Perel VI. Current-induced spin orientation of electrons in semiconductors. Phys Lett. (1971) 35A:459–60. doi: 10.1016/0375-9601(71)90196-4

CrossRef Full Text | Google Scholar

29. Hirsch JE. Spin hall effect. Phys Rev Lett. (1999) 83:1834–47. doi: 10.1103/PhysRevLett.83.1834

CrossRef Full Text | Google Scholar

30. Murakami S, Nagaosa N, Zhang SC. Dissipationless quantum spin current at room temperature. Science (2003) 301:1348–51. doi: 10.1126/science.1087128

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Sinova J, Culcer D, Niu Q, Sinitsyn NA, Jungwirth T, MacDonald AH. Universal intrinsic spin hall effect. Phys Rev Lett. (2004) 92:126603. doi: 10.1103/PhysRevLett.92.126603

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Kato YK, Myers RC, Gossard AC, Awschalom DD. Observation of the spin hall effect in semiconductors. Science (2004) 306:1910–3. doi: 10.1126/science.1105514

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wunderlich J, Kaestner B, Sinova J, Jungwirth T. Experimental Observation of the spin-hall effect in a two-dimensional spin-orbit coupled semiconductor system. Phys Rev Lett. (2005) 94:047204. doi: 10.1103/PhysRevLett.94.047204

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Kimura T, Otani Y, Sato T, Takahashi S, Maekawa S. Room-temperature reversible spin hall effect. Phys Rev Lett. (2007) 98:156601. doi: 10.1103/PhysRevLett.98.156601

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Saitoh E, Ueda M, Miyajima H, Tatara G. Conversion of spin current into charge current at room temperature: inverse spin-hall effect. Appl Phys Lett. (2006) 88:182509. doi: 10.1063/1.2199473

CrossRef Full Text | Google Scholar

36. Brill DR, Wheeler JA. Interaction of neutrinos and gravitational fields. Rev Mod Phys. (1957) 29:465–79. doi: 10.1103/RevModPhys.29.465

CrossRef Full Text | Google Scholar

37. Birrell ND, Davies PCW. Quantum Fields in Curved Space. Cambridge: Cambridge University Press (1982).

Google Scholar

38. Nakahara, M. Geometry, Topology and Physics. Bristol: Institute of Physics Publishing (1998).

Google Scholar

39. Matsuo M, Ieda J, Saitoh E, Maekawa S. Effects of mechanical rotation on spin currents. Phys Rev Lett. (2011) 106:076601. doi: 10.1103/PhysRevLett.106.076601

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Matsuo M, Ieda J, Saitoh E, Maekawa S. Spin current generation due to mechanical rotation in the presence of impurity scattering. Appl Phys Lett. (2011) 98:242501. doi: 10.1063/1.3597220

CrossRef Full Text | Google Scholar

41. Matsuo M, Ieda J, Saitoh E, Maekawa S. Spin-dependent inertial force and spin current in accelerating systems. Phys Rev B (2011) 84:104410. doi: 10.1103/PhysRevB.84.104410

CrossRef Full Text | Google Scholar

42. Schiff LI. A question in general relativity. Proc Natl Acad Sci USA. (1939) 25:391–5. doi: 10.1073/pnas.25.7.391

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Matsuo M, Ieda J, Harii K, Saitoh E, Maekawa S. Mechanical generation of spin current by spin-rotation coupling. Phys Rev B (2013) 87:18402(R). doi: 10.1103/PhysRevB.87.180402

CrossRef Full Text | Google Scholar

44. Uchida K, Adachi H, An T, Ota T, Toda M, Hillebrands B, et al. Long-range spin seebeck effect and acoustic spin pumping. Nat Mater. (2011) 10:737–41. doi: 10.1038/nmat3099

PubMed Abstract | CrossRef Full Text

45. Uchida K, An T, Kajiwara Y, Toda M, Saitoh E. Surface-acoustic-wave-driven spin pumping in Y3Fe5O12/Pt hybrid structure. Appl Phys Lett. (2011) 99:212501. doi: 10.1063/1.3662032

CrossRef Full Text | Google Scholar

46. Uchida K, Adachi H, An T, Nakayama H, Toda M, Hillebrands B, et al. Acoustic spin pumping: direce generation of spin currents from sound waves in Pt/Y3Fe5O12 hybrid structures. J Appl Phys. (2012) 111:053903. doi: 10.1063/1.3688332

CrossRef Full Text

47. Landau LD, Lifshitz EM. Theory of Elasticity. New York, NY: Pergamon (1959).

48. Maekawa S, Tachiki M. Surface acoustic attenuation due to surface spin wave in ferro and antiferromagnets. AIP conf Proc. (1976) 29:542. doi: 10.1063/1.30437

CrossRef Full Text | Google Scholar

49. Sanada H, Sogawa T, Gotoh H, Onomitsu K, Kohda M, Nitta J, et al. Acoustically induced spin-orbit interactions revealed by two-dimensional imaging of spin transport in GaAs. Phys Rev Lett. (2011) 106:216602. doi: 10.1103/PhysRevLett.106.216602

PubMed Abstract | CrossRef Full Text

50. Hernández-Mínguez A, Biermann K, Lazić S, Hey R, Santos PV. Kerr detection of acoustic spin transport in GaAs(110) quantum wells. Appl Phys Lett. (2010) 97:242110. doi: 10.1063/1.3524218

CrossRef Full Text | Google Scholar

51. Suzuki Y, Katayama T, Yoshida S, Tanaka K, Sato K. New magneto-optical transition in ultrathin Fe(100) films. Phys Rev Lett. 68:3355 (1992).

PubMed Abstract | Google Scholar

52. Liu L, Pai CF, Li Y, Tseng HW, Ralph DC, Buhrman RA. Spin-torque switching with the giant spin hall effect of tantalum. Science (2012) 336:555–8. doi: 10.1126/science.1218197

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Zak J. Magnetic translation group. Phys Rev. (1964) 134:A1602–6. doi: 10.1103/PhysRev.134.A1602

CrossRef Full Text | Google Scholar

54. Matsuo M, Ieda J, Maekawa S. Renormalization of spin-rotation coupling. Phys Rev B (2013) 87:115301. doi: 10.1103/PhysRevB.87.115301

CrossRef Full Text | Google Scholar

55. Kane EO. Band structure of indium antimonide. J Phys Chem Solids (1957) 1:249–61. doi: 10.1016/0022-3697(57)90013-6

CrossRef Full Text | Google Scholar

56. Winkler R. Spin–Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems. Berlin; Heidelberg: Springer-Verlag (2006).