Dynamics of hydrofracturing and permeability evolution in layered reservoirs

Introduction

Fluid overpressure in the Earth's crust is a major controlling factor for the mechanics of fracturing and faulting in a variety of geological settings [1]. Overpressure yields a feedback on the background stress regime at depths in the crust and enhances the potential brittle deformation of rocks [2, 3], so that existing fractures and joints open and the frictional resistance along fault planes is reduced.

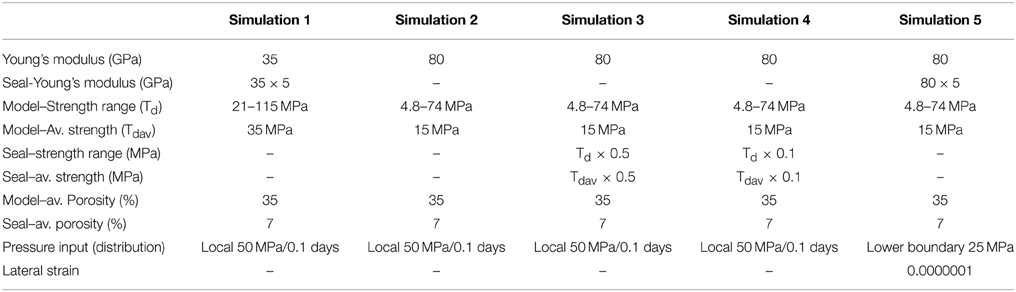
In general stress fields within the Earth's crust can change as a function of fluid pressure, tectonic stresses or material heterogeneities. In confined sedimentary basins (impermeable fault zones and cap rocks) as well as regions of low-grade metamorphism, high fluid pressure develops and often becomes near-lithostatic to eventually trigger fluid assisted fracturing or hydrofracturing (Figure 1). This phenomenon may also result in the permutation of the local stress tensor so that induced fractures become horizontal, a process that is sensitive to tectonic diagenesis and may trigger small scale seismic events or fault reactivation [4–8]. In addition, [9] indicated that heterogeneity and contrasting mechanical properties in rocks can also induce changes in the principal stress magnitude and intrusive bodies e.g., horizontal dykes and sills may render the process of stress permutation at least at the local scale [10, 11].

FIGURE 1

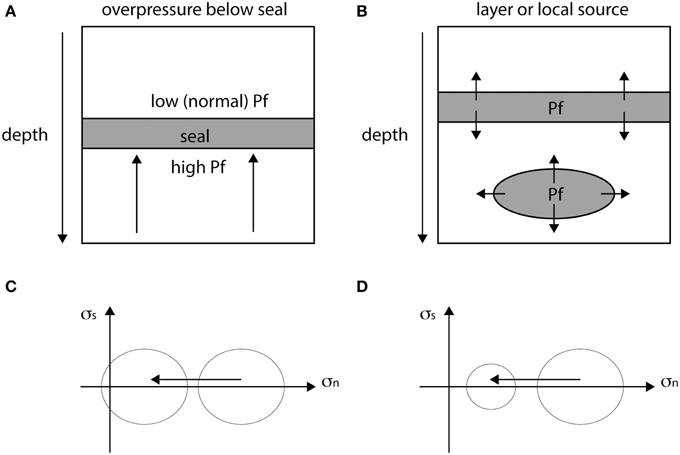
Figure 1. (A) Fluid overpressure below a seal in a sedimentary basin. (B) Fluid overpressure developing in a source region that is either a layer or an elliptical area. (C) Mohr circle diagram showing how an increase in fluid pressure shifts the Mohr circle from its initial compressive stress state at the right side to the left into the tensile regime leading to failure. (D) Mohr diagram of effective stress state where fluid overpressure reduces the differential stress and fluidizes the system. The reduction of differential effective stress is found in sedimentary basins below seals [51].

The mechanism of hydrofracturing is a highly dynamic process and consists of at least a two-way feedback between the hydraulic and mechanical domains of a geological system. In porous rocks the mechanical behavior of the solid material is related to its intrinsic porosity, which due to poroelastic effects is one of the governing factors for the permeability evolution. Effective stress perturbations due to pressure variations and fracturing influence the primary porosity and increase the bulk permeability of the host rock [12]. Hydrofracture propagation facilitates the development of permeable pathways, which significantly enhance flow rates. This behavior impacts on fluid migration in geological systems in a number of ways for instance reservoir quality [13–15], episodic expulsion and entrapment of ore-forming fluids [16] as well as the activation of geothermal circulation/venting with the induction of pressure and temperature anomalies [11, 17]. Miller and Nur [18] describe the “toggle switch” behavior of hydrofractures leading to sudden permeability enhancement or reduction associated with a switch from high to low pressure and backwards. Vass et al. [19] study the impact of chemical fracture sealing over the evolution of joint and faults created by overpressures due to fluid flow. Aochi et al. [20] model the seismicity induced along a fault by hydrofracture or fluid flow. Kobchenko et al. [21] image how fractures get activated and transport fluid during heating of low permeability rocks.

Most of the previous numerical tools used to study fracturing do not take the real time effects of material properties (e.g., stress-effective porosity evolution and vice versa due to poroelasticity) on the developing fracture patterns into account. Neither do they account for the seepage forces due to fluid circulation. This process is complex and depends also on the fracture geometry, fluid pressure diffusion and the strain field conditions. In the presented paper, we show how these factors influence the formation of different fracture patterns that develop under high fluid pressure gradients. The present work is a continuation of [22], in which a 2D coupled model with Darcy based fluid pressure diffusion is introduced and implemented to study hydrofracturing in homogeneous porous rocks. The model permits the quantitative and qualitative study of the evolution of the effective stress field in accordance with porosity-effective pressure elevation, the dynamic interaction with the initiation and growth of fractures in terms of deformation-induced permeability variations and the respective pattern formation. In the current work, we consider layered heterogeneous rock configurations to discuss the corresponding effects of material properties (e.g., stiffness, breaking strength) and initial noise in the system on the developing structures. In addition, we give an example of how layer-confined vertical fractures develop into normal faults, and how this transition changes the permeability (fluid flow) in a multi-layer sedimentary sequence [23]. The assigned numerical scheme [22] conceded a similar approach of poroelasticity and fluid flow in granular media [24–26], during hydrofracture or aerofracture [27–31], shearing of gouge layers in faults [32, 33] or instabilities during sedimentation [34–37].

Fracturing in the brittle crust mainly takes place in extensional and shear modes depending on the balance between the differential stress (σ₁ − σ₃) and rock tensile strength T. Theoretically, the predominant state of triaxial compressive stress due to gravity loading [38] favors only shear failure in rocks at depth, therefore for extensional fractures to open under these conditions, an additional force is needed to produce tensile stresses. This additional force is thought to come from the fluid pressure that builds up in pores and existing cracks [39–41].

For a fluid saturated rock mass in the crust, stresses that act on fluid and solid should be separated from stresses that act on the solid alone. Solid stresses can be defined by Terzaghi's law where normal effective stress ${\sigma }_{ij}^{\prime }$ is given by

$\begin{array}{ll}{\sigma }_{ij}^{\prime }={\sigma }_{ij}-P_f{\delta }_{ij}& \left(1\right)\end{array}$

with σ_ij being the total normal stress, P_f the pore fluid pressure and δ_ij the Kronecker delta with the sign convention of positive compressive stress. A Mohr diagram is often used to illustrate the respective failure mode in Rock Mechanics. In Figure 1 the Mohr circle represents a 2D stress state in the Earth's crust with σ₁ and σ₃ being compressive on the right hand side. Excess in fluid pressure P_f reduces the value of the effective stresses, driving Mohr's circle toward the left along the σ_n-axis from its initial compressive stress state. When the least effective stress transects the composite Mohr-Coulomb failure envelop in the tensile regime the rock fails.

In order to understand the effects of fluid pressure on fracturing and vice versa in heterogeneous systems one has to look at the evolution of fluid pressure gradients and the respective poroelastic response as a result of stress perturbations in the porous matrix [3, 24, 42–45]. For tensile fracturing in overpressured rocks the order of magnitude of the effect of pore pressure pertaining to Biot's poroelastic response on Terzaghi's effective stress state can be approximated by the pore-fluid factor λ_v [5, 40].

$\begin{array}{ll}{\lambda }_v=\frac{P_f}{{\sigma }_v}=\frac{v}{1-v-(1-2v){\alpha }_p}& \left(2\right)\end{array}$

which is the ratio of pore fluid pressure to vertical stress. Depending on the poroelastic factor α_p (0–1 for most rocks) and the Poisson ratio v of the rock, the pore pressure required for hydraulic extensional fracturing is hydrostatic if (λ_v < 0.4) in near surface extensional regimes, superhydrostatic (0.4 < λ_v < 1.0) in low permeable and well cemented rocks and superlithostatic when (λ_v ≥ 1.0) in compressional regimes at depth.

However, using Terzaghi's law in three dimensions assuming that all principal stresses are affected by fluid pressure in the same way is a simplification [46–49]. First of all the term fluid pressure has to be well defined. For example Cobbold and Rodrigues [50] argue that the fluid overpressure should be used in Terzaghi's law. Second of all the behavior of the rock depends on the mechanical and hydraulic boundary conditions, so that the fluid overpressure term in Equation (1) is not a scalar and the differential stress may change as well. These effects are observed by Hillis [51] for several sedimentary basins where overpressure leads to a reduction of the differential stress and the least principal stress is linked to the fluid pressure. In a simplified version the horizontal effective stress below a seal in an over pressurized zone in a sedimentary basin can be expressed by

$\begin{array}{ll}{\sigma }_3^{\prime }={\kappa }_e\left({\sigma }_1-P\right),& \left(3\right)\end{array}$

where P is the local overpressure and κ an elastic proportionality [50]. In this case the fluid overpressure affects the vertical and horizontal stress differently and as a consequence the differential stress is reduced (Figure 1). Rocks are porous so that fluid can percolate through the rock, therefore the actual force that acts on the walls of pores or cracks and leads to rock failure (hydrofracturing) is the fluid pressure gradient (leading to seapage forces, [50]). The fluid pressure in a simplified system can be expressed by the following equation [50]

$\begin{array}{ll}P=\rho gz-\left(\frac{q\mu }{k}\right)z+\left(\frac{Q\mu }{2k}\right)z^2,& \left(4\right)\end{array}$

with the first term representing the hydrostatic fluid pressure (as a function of density ρ, gravity g and depth z), the second term representing fluid overpressure build up below a seal as a function of influx of fluid (with q = darcy velocity, μ = fluid viscosity and k = permeability) and the last term representing a source term, which could be fluid generation in a layer (with Q the fluid production, Figure 1). The last two terms in equation 4 lead to fluid assisted fracturing [50].

Materials and Methods

In order to numerically simulate the development of fluid assisted fractures and hydrofractures, we employ a coupled two-dimensional hydro-mechanical approach to model a 2D pressurized sedimentary section in the Earth's crust (Figure 2). The model is explained in detail in Ghani et al. [22]. The approach combines the continuum description of fluid pressure with a discrete description of deformable elastic solid where the later is represented by a hybrid triangular lattice-particle model and is blanketed over a stationary square grid (larger grid constant) of fluid pressure such that the boundaries of the two lattices coincide with each other. Accommodating local mass to momentum conservation a pressure gradient evolves for a given solid-fluid configuration according to local strain conditions through a poro-elasto-plastic relationship. The model is grounded on the same hypothesis as Flekkøy et al. [24], which emphasizes the growth of hydro-driven fractures in the light of instantaneous and synergistic evolution of rock permeability and interstitial pressure diffusion in the porous elastic medium. In the following subsections we outline the constitutive elements of the coupled scheme [23].

FIGURE 2

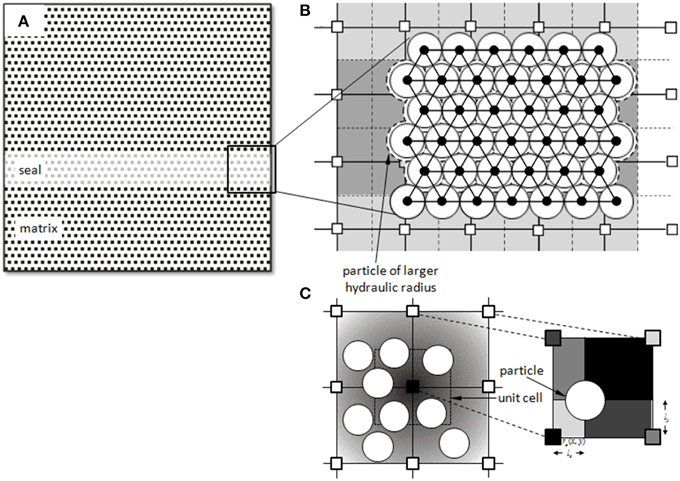
Figure 2. The figure shows the initial model configuration and the fluid-solid interaction criteria [23]. (A) Sketch shows a single layered cap-rock geometry, where a sub-horizontal low permeable layer is sandwiched between a permeable matrix. (B) Sketch illustrating how the coupled particle-lattice model overlays the pressure grid field in physical space. The linear dark gray background depicts transactions of hydrostatic to lithostatic fluid pressures due to a low permeable seal. (C) Sketch showing the fluid-solid interaction according to the smoothing function, with the gray background depicting the pressure gradient toward the central fluid node.

It is assumed that the seepage force at local scale as a function of the evolution of fluid pressure gradients induces localized perturbations in the effective stress field which may lead to rock deformation. Therefore, the continuum fluid phase is determined exclusively in terms of the pressure field P(x, y), where (x, y) are the coordinates of the two-dimensional grid space. The inertia of the fluid is not considered in the model, which is justified for a fluid flow with low Reynolds number as in the concerned case where the fracture aperture or the particle movement is comparable to the diameter of the particles.

Using Darcy law in order to express the seepage velocity through the porous media, a time dependent governing Equation (5) of pressure diffusion is established from the mass conservation of fluid and solid [27, 33, 35].

$\begin{array}{ll}\varphi \beta \left[\frac{\partial P}{\partial t}+u\nabla ·P\right]=\nabla ·\left[\left(1+\beta P\right)\frac{K}{\mu }\nabla \text{P}\right]-\left(1+\beta P\right)\nabla u,& \left(5\right)\end{array}$

where ϕ = 1 − ρ is the porosity, β is the fluid compressibility, P is the fluid pressure and u is the solid velocity field. K and μ stand for permeability and fluid viscosity respectively. The implementation of the diffusion equation is obtained by an Alternate Direction Implicit (ADI) method [52]. In the model, the pressure gradient over a given volume develops according to the permeability K, which is an explicit output of the discrete elastic model as a function of variation in local porosity ∅(x, y). The local permeability K(∅) is determined through a Kozeny-Carman relation given by Carman [53]

$\begin{array}{ll}K\left(\varnothing \right)=\frac{r^2}{45}\frac{{\varnothing }^3}{{\left(1-\varnothing \right)}^2},& \left(6\right)\end{array}$

where r is a fixed grain size (1 μm) and 45 is an empirical constant valid for a packing of spherical grains.

The DEM elasto-plastic module “Latte” of the software package “Elle” [54, 55] is used to simulate brittle deformation in porous rocks. The setup is a 2D hybrid lattice-particle model in which the discrete elements are connected with linear elastic springs. The DEM model determines the discrete description of isotropic elastic continua of a real system with an elastic spring constant k as a function of the macro-scale elastic material property E. This setup can thus be used to simulate plain strain deformation problems according to linear elasticity theory [24] with

$\begin{array}{ll}k=\frac{\sqrt{3}}{2}El,& \left(7\right)\end{array}$

where l stands for the two dimensional model thickness of a given configuration. In order to model heterogeneous material i.e., layered sedimentary rocks, local changes in spring constant k describe the corresponding variation in the mechanical properties (stiffness) of the material. A standard over-relaxation algorithm [56] is used to obtain the equilibrium configuration of the elastic system after each simulation time step (based on the net forces applied on each node). In the plastic part of the model, springs break and imitate local failure of the material if the force acting on them exceeds a prescribed threshold (σ_c) corresponding to the local tensile strength. The average threshold of the tensile strength is related to the stress intensity factor $K_I={\sigma }_I\sqrt{c}$, where σ_I is the critical stress for the relevant displacement of fracture walls and c is the characteristic length of micro-cracks in the material [24]. Broken springs get removed from the network and the associated particles lose cohesion but are still subject to repulsive forces when they meet.

Deformation mechanics of the coupled continuum-elastic model is governed by a mutual momentum exchange between the solid and fluid phase at the scale of a unit volume cell of the continuum system. The net force $F_i^n$ acting on a particle i is composed of three components, interaction force f_e from neighboring particles (either connected with a spring or repulsive forces), seepage force f_p resulting from interstitial fluid pressure and external forces, which are gravity f_g and tectonic forces determined by imposed large scale strains (via forces implemented on the lateral boundaries of the model). The net force is given as

$\begin{array}{ll}{F}_i^n=f_e+f_p+f_g.& \left(8\right)\end{array}$

In the elastic part of the model, each spring inherits a spring constant k and an equilibrium length a, which is identical to the sum of the initial radii of two connected particles. The inter-particle force f_e, which acts along the connected elastic springs is proportional to the given spring constant

$\begin{array}{ll}{f}_e={\displaystyle \sum _j}{k}_{ij}\left(\left|{\vec{a}}_{ij}\right|-\left|{\vec{x}}_{i-}{\vec{x}}_j\right|\right)·{\widehat{n}}_{ij},& \left(9\right)\end{array}$

where the sum is over all connected neighbor nodes j, ${\vec{x}}_i$ and ${\vec{x}}_j$ are the positions of the connected nodes, and ${\widehat{n}}_{ij}$ is the unit vector pointing from the centroid of node i to node j.

The seepage force is generated due to the gradient of the non-hydrostatic part of the pressure field and is a result of the momentum exchange between the elastic material and the viscous fluid flowing in the reservoir. Assuming negligible fluid-solid friction at the interface surface, the only coupling force is the pore pressure gradient ΔP induced by a fluid source in the reservoir. The pressure force f_p on the surface normal of a given particle configuration in the unit grid cell (Figure 2) of surface area dA is calculated by an area-weight smoothing function.

$\begin{array}{ll}{f}_p=-\int PdA,& \left(10\right)\end{array}$

where P = P₀ − ρ_fgz, with P₀ the local fluid pressure in the reservoir at some reference depth z, ρ_f the fluid density, and g the gravity constant.

In the coupled model the term gravitational force incorporates the gravity effects of both the fluid and solid where the later together with the hydrostatic part of pore pressure determines the effective stress field σ_eff = (ρ_s − ρ_f)gz in the system. The gravity force on each particle in the elastic module is inferred using the formulation

$\begin{array}{ll}{f}_i^g={\rho }_s\pi R_i^{2}gC,& \left(11\right)\end{array}$

where ρ_s is the solid mass density, $R_i^2=r_i^{2}S$ with S the dimension of the real system (1000 m), g is the acceleration of gravity and C = 2/3 is a scale factor derived in Ghani et al. [22] to acquire a compatible one dimensional lithostatic stress for an isotropic 2D linear elastic solid.

The two way interaction between the porous solid and the hydrodynamic phase is achieved through the use of a projection operator from the discrete space to the fluid grid space, using a smoothing function s(r_i − r₀), which distributes the weight of a particle over the four neighboring fluid grid nodes as shown in Figure 2C.

$s\left(r_i-r_0\right)=\{\begin{array}{c}\left(1-\frac{l_x}{\Delta x}\right)\left(1-\frac{l_y}{\Delta y}\right)if{l}_x<\Delta x,l_y<\Delta y\\ 0otherwise& \left(12\right)\end{array}$

where r_i(x, y), r₀(x, y) are the positions of the particle and grid node respectively, l_x = |x_i − x₀| and l_y = |y_i − y₀| are the relative distances and Δx, Δy are the lattice constant along the x and y coordinates. This setup is also called “cloud in cell” method which renders the translation of mass m and velocity v of individual particles into continuous local particle density $\rho \left(r_0\right)={\sum }_{i}s\left(r_i-r_0\right)$ and velocity fields $u\left(r_0\right)={\displaystyle {\sum }_i{u}_{i}s\left(r_i-r_0\right)}$, where subscript i runs over the number of particles present in a unit area associated with a particular grid node at position r₀. The same smoothing function is also used to obtain the drag force $f_p=-{\sum }_{k}s\left(r_i{-r}_0\right){\left(\nabla P∕{\rho }_n\right)}_k$ on a single particle due to fluid pressure, index k runs over four nearest grid nodes. The basic approximations to this approach are the multiplication of the calculated 2D solid fraction with 2/3, as well as setting of a lower cutoff of the 2D solid fraction e.g., ρ_min = 0.25, detailed descriptions are given in Ghani et al. [22]. This type of model for the fluid-solid coupling and mapping from 2D to 3D has been validated by successful comparison with experiments on mixed fluid/dense granular flows, in aerofracture [27, 30, 31] or instabilities during sedimentation [25, 26, 34, 35].

Two different approaches have been used in order to account for anisotropies in the model, we insert single layers and multi-layers of dissimilar material and sedimentary properties. A single horizontal layer is defined in the lower half section of the model in order to depict a sealed reservoir which inherits different stiffness values and low permeability relative to the underlying reservoir and overburden rock (Figures 2A,B). In the multi-layered model, four layers of low permeability and high stiffness are considered at regular intervals along the vertical coordinate. According to the boundary conditions considered, loading includes an increase of fluid pressure in the fluid lattice (corresponding to phase transition, fluid source or fluid injection in this zone), a vertical loading due to gravity, or a horizontal loading due to tectonic strains by moving the lateral boundary walls. In all models, the elastic system is constrained by elastic walls at the two lateral and the bottom boundaries, whereas the upper boundary is set free in order to attain an equilibrium under gravity loading. The elastic walls are described as linear elastic springs so that the force on any interacting particle from a wall is proportional to the distance that the particle is pushed into the wall. For instance, the force by a lateral wall on the particle i contacted at location x = x_w is

$f_i=\{\begin{array}{c}-k_w\left(x_i+r_i-x_w\right)n_x,if{x}_i+r_i-x_w>0\\ 0else& \left(13\right)\end{array}$

where k_w is a spring constant for wall interaction r_i is the particle radius, n_x is a unit vector along the x-axis. In the elastic domain, relaxation and plastic deformation (i.e., sliding and rearrangement of the relative grain positions) is assumed to be instantaneous relative to the diffusion of the fluid pressure. This amounts to neglect the inertial terms and the propagation of seismic waves and equilibrate elastic stresses with seepage forces and gravity. After each time dependent diffusion step of fluid pressure, the elastic equilibrium is acquired on account of the elasto-plastic deformation in the material by the subjected seepage forces and other loadings.

At layer interfaces, the elastic constant of springs is taken as an average of the constants of the respective boundary particles. This presents a gradual change of mechanical properties corresponding to models of layered sedimentary rocks. The Young's modulus, the breaking strength of springs and the layer thicknesses are predefined in the models. The respective constituents of the elastic system are assumed to be homogeneous corresponding to their material properties on large scale, however, in order to grasp the effect of the inherited disorder of a real material, we set a pseudo-random distribution of the breaking strength (Figure 3). Natural disorder in geological media corresponds to the ubiquitous presence of Griffith's micro-cracks, variation in their densities and lengths and other defects, which are present at the grain scale. It has been demonstrated that fracture patterns that are observed both in the field and laboratory can be numerically reproduced by implying realistic normal distributions of breaking strength in DEM models[57–60]. The overall breaking strength of the model material, and its failure mode, is sensitive to the lower values of the quenched distribution [61–63].

FIGURE 3

Figure 3. Strength distribution of springs for the different simulations showing dimensionless (left hand side) and scaled values (right hand side). (A) Represents the distribution used in experiments 1–4 whereas (B) represents the layer properties used for experiment 5.

The subsequent model setup is thus analogous to confined reservoirs with seal layers of very low permeability. In each simulation the coupled model starts from a fully relaxed state and is progressively loaded in small steps. The model is subject to a random pressure source that complies a probability distribution function (0 ≤ P ≤ 1) with a maximum pressure in the middle of the lower permeable layer (below the seal)—this represents a possible phase transition in this lower layer associated with a pressure rise, or the arrival of fluid from the bottom. An increase in pore pressure in the source layer creates a linear pressure gradient across the impermeable seal, which ultimately develops high buoyancy forces in the surrounding matrix. This causes high concentration of stresses in the seal layer and depending on material properties of the model constituents it triggers different patterns of successive fracture propagation at relatively weak rock elements (intrinsic flaws). The induction of the fractures accommodates the strain and eventually the stress relief in the elastic system following a rearrangement of particle positions. This concurrently promotes a local change in the background porosity, which by influencing the permeability results in diffusion of pore overpressure in the fractured zone. The evolution of the pore fluid pressure provides a feedback to the stress field in the system and leads to fracture growth along the pressure gradient and results in a regular fracture network. The cycle is echoed successively following the two-way temporal and spatial feedback between hydraulic pressure and strain evolution and associated fracturing in the porous matrix until both the continuity equation and the discrete grains are relaxed, a dynamic stationary equilibrium is found and fracturing ceases.

A varying range of mechanical and hydraulic properties are used in the simulation setup in order to realistically represent the mechanism of quasi-static hydro-driven brittle deformation in heterogeneous rocks in the shallow crust. This involves a switch from sub-vertical to horizontal tensile fracturing as a function of the direction of the principal stress tensor due to high pressure gradients in high pressurized systems [5, 64] as well as in low permeability fault zones [7].

Results

We present 5 different simulations where the first four have a geometry with one horizontally aligned low-permeable layer—similar to a cap-rock, whereas the fifth simulation contains multiple layers. Figure 4A illustrates the initial configuration of the single layered models where a horizontal layer with a thickness of 10% of the model height is emplaced in the lower half of the simulation. Tectonic loading is not included in these models. The fifth example shows fracture formation under an extensional stress regime in addition to abnormal fluid pressure and the developing patterns in a multilayer system.

FIGURE 4

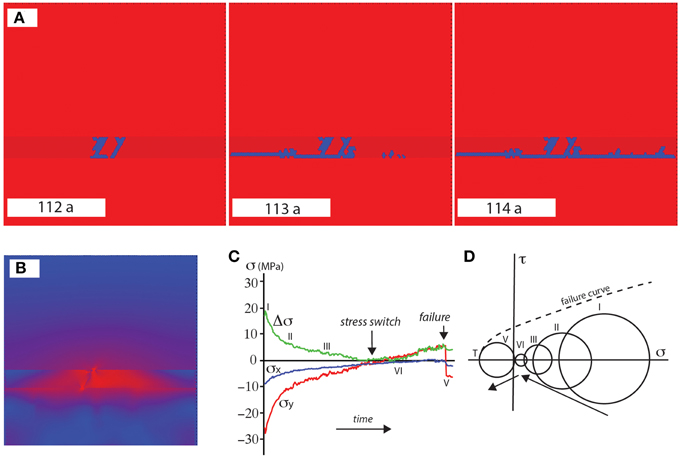
Figure 4. (A) Shows a simulation of the development of initial layer perpendicular fractures in a stiffer impermeable seal (dark red layer) followed by layer parallel fractures. Time proceeds from left to right and fractures are represented by blue color. Fluid is injected randomly in the lowest soft and permeable layer. This creates a high pressure drop across the seal and results in permeability changes through fracturing. (B) The figure shows the differential stress state on the onset of fracturing in the system, where the blue color represents low and the red high differential stress. The less permeable seal shows high stress concentrations whereas the layer below the seal shows low stresses due to high fluid pressures. The high differential stress that is accumulated in the stiffer seal layer is relieved with time following fracturing in the seal. (C) Graph showing the evolution of the magnitude of the stress in the × (horizontal) and y (vertical) direction and the differential stress in the seal. A switch from compressive to a tensile state of vertical stress is seen in the seal and at the interface. The low permeability of the seal results in conditions for layer parallel fracturing. (D) Mohr circle description of the stress states graphed in c illustrating the complexity of stress changes as a function of an increase in fluid pressure.

In all the simulations the solid skeleton (elastic lattice) of the reference model has a resolution of 100 × 150 disc-shaped particles which define an area of 1:1 km, the model thus bears a linear gravitational loading of a 1 km long sedimentary column in the uppermost crust with a Poisson ratio of 1/3. The mechanical parameters and other characteristics for the respective simulation examples are given in Table 1, a low average porosity of 7% is taken for seal layers compared to 35% of the surrounding matrix. As boundary conditions the coupled system is confined mechanically at the lateral and lower boundaries until otherwise described whereas hydraulically it is restrained at the side boundaries. The distribution of breaking strengths for the different simulations are shown in Figures 5A,B. The overall breaking strength of the model material will be at the lower end of the distribution.

TABLE 1

Table 1. Showing parameters for different experiments.

FIGURE 5

Figure 5. Figure illustrating the progressive fracture development (from left to right) in three different simulations where the matrix is shown in red and the fractures shown in blue color [23]. (A) Figures show the development of irregular hydrofractures around an elliptical source in a weak rock unit. Because the seal has a comparatively high strength the growing fractures cannot propagate into the seal layer and change from a vertical to a sub-horizontal direction below the seal. This deflection indicates that the impermeable seal influences fluid pressure diffusion and the stress fields because high fluid pressure gradients build up. (B,C) illustrate the developing fracture patterns correspond to a seal layer that is 0.5 and 0.1 times weaker than the seal shown in simulation (A). The simulations illustrate that the seal with a lower strength has a higher probability of seal failure and as a consequence vertical fractures propagate through the seal. With time the vertically growing fractures from the source zone link up with the fragmented parts of the much weaker seal layer.

In the first simulation we attempt to model bedding parallel and bedding normal fractures in a heterogeneous medium, structures that can be found in limestone sequences of the Oman Mountains. Figure 4A shows the model evolution where red is the matrix, darker red the stiff seal layer and blue fractures. In the simulation the Young's modulus of the seal layer is taken to be 10 times higher than the surrounding matrix. In addition the breaking strength of springs in the horizontal seal layer are set to be 10 times lower than the strength of the matrix. The material has a background Young's modulus of 35 GPa and a breaking strength in the range of 21–115 MPa. The breaking strength of the whole aggregate will be controlled mainly by the lower values and thus be around 21–25 MPa. The fluid has a compressibility of 4.5 × 10⁻¹⁰ Pa⁻¹, a viscosity of 0.001 Pas and one time step in the model is equivalent to 0.1 days. Fluid pressure input is fast enough for fluid pressure gradients to build up.

The development of the fracture pattern in Figure 4A shows that the layer first develops layer perpendicular fractures. These are initiated by the fluid pressure gradient, however their orientation is given by the heterogeneous gravity-induced stress field so that the lowest stress is horizontal. During successive increase in fluid pressure the initial fractures cannot drain the system and a horizontal fracture develops at the lower boundary of the seal. In the closed and confined system, seepage forces generated by the accumulated pore pressure counter the lithostatic stress component σ_v. The vertical compressive stress reduces in a non-linear fashion and gradually turns into the tensile regime (Figure 4C). In the absence of any tectonic loading a subsequent increase in fluid pressure results in the directional switch of the compressive stress components, upon which the system is subjected to overburden uplift at the layer interface as well as the concentration of stresses in the low permeable seal layer (Figure 4B). The simulation exhibits two patterns of hydrofracture growth due to a high Young's modulus of the seal layer. Fluid pressure gradients and a high stress concentration in the seal lead to layer perpendicular fractures. In addition as shown in graph (Figure 4C), the vertical stress component reduces faster than the horizontal component which leads to a second set of successive layer parallel fractures at the seal and source layer interface. This results in tensile/hybrid tensile shear fracturing along the layer interface and eventually leads to seal failure. A graph showing the evolution of the stresses in the vertical (y) and the horizontal (x) directions and the corresponding trend of a Mohr diagram during the simulation are illustrated respectively in (Figures 4C,D). The Mohr diagram can be explained as follows: first both stresses, the vertical and the horizontal decrease due to the high fluid pressure gradients. The horizontal stress meets the simulation walls on the left and right hand side, which is mimicking an endless system. The vertical stress can act against the free upper surface that is only confined by gravity. Therefore, extension in this direction is easier so that the originally highest vertical stress becomes the smallest principal stress and eventually is tensile leading to layer parallel fracturing. This effect is enhanced by the sealing layer that leads to higher fluid pressure gradients in the vertical direction. In this scenario an increase in fluid pressure does not simply lead to a movement of the Mohr circle toward the left hand side of the Mohr diagram, but to an initial decrease of mean and differential stress, a flip of the stress direction and finally a small increase in differential stress leading to the final failure.

The presumed setup is analogous to confined reservoirs with seal rocks of low permeability. Seals in fluid filled layered reservoirs are commonly soft rocks i.e., shales, however, during the evolution of sedimentary basin the mechanical compaction and other diagenetic processes may increase the stiffness of the soft seal up to a significant order of magnitude, which may change the conditions for hydrofracturing, their arrest and propagation over time [65, 66]. If an increase in internal fluid pressure is the main forcing, it seems that a soft layer on top of the seal behaves as stress obstruction for fracture propagation. In this case the heterogeneous system may fail in the form of layer parallel shearing at the macro scale and thus facilitate fluid migration along layer contacts. This is in agreement with field studies [67, 68], which indicate that vertically growing fractures preferentially propagate through stiff rocks rather than through soft layers. On this basis one may predict that bedding parallel veins are a sign of abnormal fluid pressure.

Figure 5 illustrates three simulation runs in which the sandwiched seal layer has different properties than the one shown in Figure 4. The three layers in the model contain the same default value of Young's modulus, however the breaking strength of springs in the enclosed seal layer of the simulation shown in Figures 5B,C is 0.5 and 0.1 times weaker than that of the simulation shown in Figure 5A (Table 1). The material has a Young's modulus of 80 GPa and a breaking strength range of 5–74 MPa with a large-scale overall breaking strength of 15 MPa (Figure 3). The layered heterogeneities have a great influence on the fracture propagation and variable fracture pattern development. In addition, because the breaking strength of the matrix is low compared to the model shown in Figure 4, the fluid pressure gradient at the source is high enough to fracture the weaker matrix around the source where fluid pressure gradients are highest.

In the simulation shown in Figure 5A vertical tension fractures nucleate at the source zone in the lower layer and propagate upward (Figure 5A, timestep: 400, 40 days) under the influence of gravity and pressure gradients. Once the fractures reach the seal they are obstructed and stop to propagate vertically (Figure 5A, timestep: 700, 70 days). Because the mechanical properties of matrix and source layer are the same, the stress concentration in the seal is not high enough to promote fracture propagation across the seal. Since the seal is impermeable, the continuous buildup of fluid pressure does re-orient the principal stresses in the source layer so that the fractures below the seal propagate sideways and the seal does not fracture (Figure 5A, timestep: 750, 75 days).

The second and third simulation in Figures 5B,C show a different scenario. In this case the weak impermeable seal (strength 1/5th and 1/10th of matrix) tends to fail concurrently with the upward propagation of hydrofractures along the pressure gradient. Figure 5B shows an intermediate case of fracture patterns between the extremes shown in Figures 5A,C. Even though the impermeability of the seal layer is a prerequisite for the generation of fluid pressure gradients below the seal, the actual failure of a seal is highly dependent on the presence of vertical discontinuities within the seal layer. Reduction in strength of the seal layer leads to vertical hydrofractures that gradually form from horizontal fractures.

The patterns of simulation 5a are similar to field examples of hydrofractures where large veins develop in the basement of the Oman Mountains in relatively weak schist. The veins are thick and show orientations that are very similar to the hydrofractures in the simulated examples, they look like sheets and steep conjugate shear like fractures.

In the following, we illustrate how tectonic deformation, fluid pressure gradients and gravity can influence the development of fracture networks in multilayer systems (Figure 6). The model setup consists of four hard layers of low permeability that are interbedded in a regular sequence with soft permeable layers. The model contains the same default values of the material parameters that are used in the last three simulations, however the Young's modulus of the impermeable layers is considered to be five times higher than that of the permeable layers (Table 1). For the first 250 days the model was subjected to gravity and fluid pressure input in order to build up a realistic hydraulic gradient in the system. Fluid pressure at the top of the box is set to 0 MPa whereas the bottom boundary is set to 10 MPa (assuming hydrostatic pressures). After 250 days a lateral tensile strain was introduced in the system, with a horizontal constant extension rate in order to model tectonic forcing and fluid pressure rise up to lithostatic levels (27 MPa).

FIGURE 6

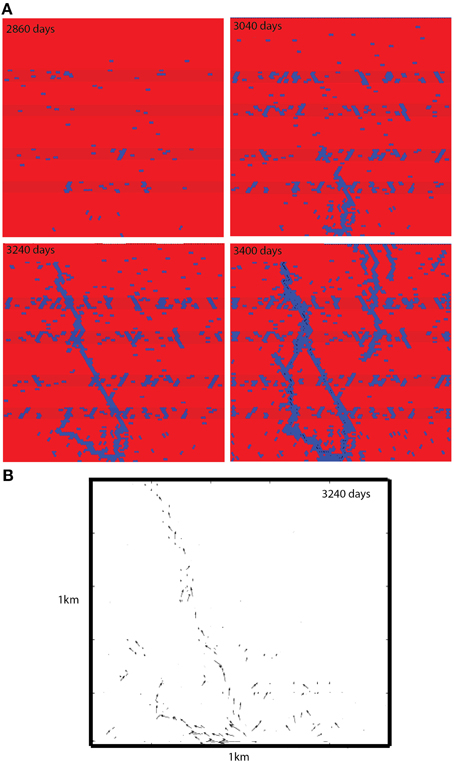
Figure 6. (A) Figure shows a simulation with several stiff layers, a fluid source at the bottom of the model and a horizontal component of extension. Fractures are shown in blue. During the first time step fracturing is mainly taking place in the stiffer layers. From the second figure onwards a fault develops that nucleates at the fluid source and propagates upwards connecting all layers and draining the system. In the stiff layers vertical fractures develop with a defined spacing. One time-step in the model corresponds to 0.1 days. The observed pattern is very similar to the field example (Figure 7B). (B) Shows the resultant directional fluid field, where fluid drains through the system along the connected pathway. The fluid pathway is shown for the third time slice in the simulations shown in (A).

Once tectonic strain builds up, the hard layers fracture and develop a characteristic spacing, whereas the soft permeable matrix does not fracture. After 3040 days and an extension of 0.54 m the fluid pressure gradients are high enough to fracture the soft matrix and a larger scale fracture develops that propagates through the first layers. The hard layers show a clear spacing of fractures and the larger scale fracture is running through the whole system linking the bottom of the simulation with the top and producing a fluid pathway. With progressive deformation the upward growing fractures interact with the local fractures in the hard layers and eventually turn into large-scale normal faults that run through the whole layer pack. This observation is consistent with field example in the Oman Mountains where faults are often associated with vein sets and affirms that the same deformation sequence is responsible for some of the veins and fault sets. The draining of the system by the permeable large-scale fault can also be observed in Figure 6B illustrating the development of fluid pathways through the model. Note that the local layer perpendicular fractures are not part of this large-scale fluid cell. Our model shows a behavior that is often observed in real system and can also be found in the Oman mountains. Layer perpendicular veins develop first but they are mainly associated with local fluid flow and develop because of the mechanical properties of specific layers. If the spacing is uniform this implies that tectonic forces are the main driver for these structures. Once strain becomes larger and fluid pressures are involved, the vein network develops into mature large-scale faults that localize fluid flow and can drain a high pressure system. This scenario may be present in the Oman mountains where layer perpendicular veins develop in hard carbonate beds and large-scale normal faults cut through the whole sequence and seem to drain deeper fluids [64].

In this section we present outcrop analogs of fluid filled fractures or veins observed in the Oman Mountains in Oman [69–71] and discuss the contrasting driving forces, fluid pressure, gravity and tectonic stresses that may be active during the formation of these structures. The Oman Mountains are thought to have experienced significantly high fluid pressures [64, 68, 72] and are composed of a Permian to Cretaceous well-bedded dolomite and limestone sequence that overlies pre-Permian basement rocks. The geological history includes southwards directed overthrusting of the Oman ophiolite sequence, a large-scale extensional event, the development of several strike slip systems and the final uplift of the mountains [64, 69–71, 73]. Especially extension and strike slip deformation were accompanied by several generations of regional fractures and faults, which are cemented with calcite and minor quartz. Bedding perpendicular vein sets often follow stress oriented anastomosing patterns with regular spacing showing single extensional or conjugate extensional shear patterns [59]. These regularly spaced patterns seem to be overprinted by chaotic and very closely spaced veins that indicate the existence of high fluid pressure gradients. Fracture/vein localization seems to be influenced by the layer succession, where deformation is commonly linked to competent carbonate beds or along the layer interfaces (Figure 7A). Figure 7 shows both, layer perpendicular veining across a competent bed and layer parallel veining along the lower and upper boundaries of the competent bed. The bedding parallel veins are thought to be partly associated with the permutation of the effective stress field due to high fluid pressures. Moreover, most of the faults that are associated with vein sets appear to act as fluid flow contributors showing increased veining along the fault plane (Figure 7B) [64].

FIGURE 7

Figure 7. (A) Bedding normal and parallel calcite veins in a limestone layer from the Oman Mountains. The layer is about 10 cm thick. (B) Example of a normal fault in the Oman Mountains (width of view is 2 m). In this case one can observe that a set of extension veins develops first which are later on cut by a normal fault. Veins and faults both seem to form in the same stress field.

In Figure 8 we show three outcrop examples of vein sets that we think show different driving forces, where outcrop photographs are shown in Figures 8A,C,E and fracture patterns are redrawn in Figures 8B,D,F. Figures 8A,B shows linear vein sets of well-defined spacing in a bedding plane on the very top of the sedimentary sequence in the Oman Mountains. The outcrop is situated just below a large-scale thrust where the Oman ophiolite with some exotic sedimentary units was thrust over the Permian to Cretaceous sequence. Though the veins in the layer follow several orientations they overall show a clear direction and spacing. We interpret the regularity of the pattern to reflect a heterogeneous stress field as a function of tectonic stresses indicating that fluid pressure was not the dominant pattern forming force. These structures should be termed tectonic fractures/veins, they may be fluid assisted but clear indicators are missing. The second example in Figures 8C,D shows veins in another locality of the same sequence as those shown in Figure 8A. In this case the veins still show a systematic orientation. However, the intensity of the veins is spatially highly variable, so that some of the veins form patches where the host-rock cannot be seen anymore. We argue that such a feature indicates that fluid pressure gradients start to become more important in the production of the veins. Especially the patches of vein material may be formed by local cells of high fluid pressure. Therefore, in contrast to Figure 8A, the veins shown in Figure 8C may be termed fluid assisted tectonic fractures/veins since fluid pressure is important but some orientation symmetry is still present indicating an influence of tectonic stresses. Finally, the veins exposed in the basement rocks (pre-Permian) of the Oman Mountains are shown in Figures 8E,F. These veins are found to be very thick, jagged, and highly chaotic. Some of the veins are sub-horizontal while others follow a vertical zig-zag pattern. Neither spacing nor any preferred orientation are visible that may indicate the influence of tectonic stresses. In this case it is clear that high fluid pressure gradients and gravity did play the main role in pattern formation, which promotes the hypothesis that the developed veins are real hydrofractures.

FIGURE 8

Figure 8. Different vein patterns in the uppermost Cretaceous carbonate units (A–D) and pre-Permian rocks (E,F) of the Oman Mountains. (A) Photograph of well-oriented and regularly spaced linear vein geometries exhibiting a dominant influence of tectonic stresses, (B) sketch of the vein pattern showing clear spacing and orientation. (C) Photograph of a layer surface showing calcite patches surrounded by regularly spaced veins indicating that fluid pressure and tectonic stresses interacted, with local high fluid pressure gradients producing the patches. (D) Sketch of (C) illustrating a narrow spacing of veins and patches with 100% mineralization. (E) Thick basement veins that have zigzag geometries indicating a dominant role of fluid pressure gradients and gravity. (F) Sketch of e illustrating the chaotic geometry of the veins in the basement.

Discussion

The proposed two-dimensional hybrid hydro-elastic model successfully reproduces realistic patterns of fractures and faults that are associated with fluid pressure gradients as well as gravity and tectonic loading. The coupled model inherits a two-way feedback between the continuum and elastic domains and imitates the evolution of field scale veins and fracture networks in a layered sedimentary system. The presence of large pressure gradients due to permeability contrasts between the seal and the surrounding layers, and the dynamic link between fluid pressure and fracture growth causes oscillations of the stress field in the adjacent rock units immediately after a fracture forms.

In the first example we compare the numerical results with bedding parallel and irregular vein sets in layered limestone as shown in Figures 7A, 8E. It is observed that heterogeneity in the lithology and mechanical properties e.g., Young's modulus and breaking strength distribution influence the evolution of buoyancy, fracture patterns and localization in seal and host rock layers. It is well established that hydrofractures in layered sedimentary rock sequences are more likely to develop in and propagate through stiff rather than soft layers due to concentration of stresses in the stiffer layers.

The layer contact is also considered to be an important parameter that represents a discontinuity in the matrix. Layer contacts in the solid continua tend to break easier and are case sensitive to the elevated effective stress gradient and tend to open up and thus influence the pattern formation of growing fractures [74, 75]. In our simulation, a high contrast in mechanical and material properties between the layers causes a weak bedding contact that fails once it is subject to high fluid pressure gradients. Most cap rocks in fluid filled layered reservoirs are shales that are composed of parallel-aligned clay minerals. Compaction and other diagenetic processes during the evolution of basins may result in further reduction of the clay's permeability, an increase in stiffness or the development of mechanical weak pockets in intrinsic strength [66], which may further alter the conditions of fracturing in layered reservoirs over time.

In this contribution we are simulating uniaxial strain models (gravity loading in undrained or tectonically relaxed basins), in which the minor horizontal stress σ_h increases with increasing P_f as consequence of poroelastic effects and eventually favors the propagation of fractures in the horizontal direction, a scenario that is usually associated with accretionary wedges [39, 76]. In the presence of a free upper surface the derived stress field faces relatively less resistance in the vertical direction so that the system may expand vertically. If stresses are confined in the horizontal direction σ_h may become larger in magnitude than σ_v so that conditions for horizontal fracture propagation are approached [50]. Bedding parallel veins have generally been attributed to represent local principal stress permutations as a function of basinal supra-hydrostatic fluid pressure [64]. One should however note that seal thickness is also pivotal for pattern formation and fracture spacing. The strength distribution of the matrix is another crucial material property that can regulate the dynamics of induced fractures and is commonly simplified in numerical studies. A weaker seal layer will likely fail in a vertical direction during the ascending growth of fractures and will thus contribute to channeling of pressurized fluid flow across the seal to more permeable layers. Conversely a seal with a comparably high strength turns up to be a stress barrier to the vertically propagating fractures. Restriction in fracture propagation results in an increase in fluid pressure, which may cause a switch in the direction of principal effective stresses in the permeable host layer and subsequently divert the growth of the initially vertically induced fractures to near horizontal fracture sets. This situation is reached during the emplacement of sills where fluid pressure is at or above the lithostatic [77]. This observation is consistent with Flekkøy et al. [24], who state that in a geological context a vertical permeability variation is not enough to induce cap rock fracturing if the fluid pressure is the only driving force but that the background heterogeneity in the material properties is also important.

The developing fracture patterns in the simulations depend strongly on the fluid pressure gradient. This is inconsistent with the idea that fluid pressure in rocks only moves the Mohr circle toward the tensile regime to induce extensional fractures [50]. This simplification leads to the wrong prediction of patterns and does not separate a fracture that is produced by fluid pressure gradients from a fracture that is produced by tectonic stresses. Our model shows that fluid pressure gradients can be extremely important in pattern formation (Figure 9). In the presence of fluid pressure gradients, gravity and tectonic stresses, it is observed that a whole set of fracture patterns can develop depending on the dominant driving force in the system. Fractures that are produced by fluid pressure gradients only can look fundamentally different from tectonically induced fractures.

FIGURE 9

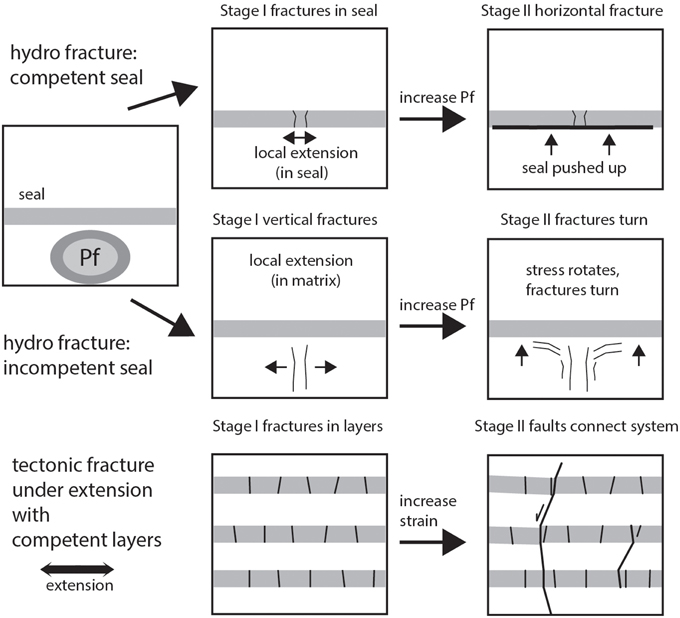
Figure 9. Summary figure illustrating different fracture patterns that develop below and in a competent vs. an incompetent seal and fracture and fault patterns that develop in a layered sequence that is extended. Hydrofractures tend to develop around sources of high fluid pressures where fluid pressure gradients fracture the matrix or bend competent layers leading to fractures. During extension fractures are well spaced along the beds and at higher strain faults connect different layers and drain systems of high fluid pressure.

It is also evident that permeability as such is a dynamic property that changes simultaneously with the deformation of an overpressure system. Fracture networks in Figure 6 show that there is a strong correlation between layer perpendicular fracturing and faulting. Layered systems that are subjected to non-hydrostatic tectonic stresses in the presence of high fluid pressure gradients along anisotropies undergo a transition from layer fracturing to large scale shearing [78]. Fracturing in the model takes place on the local scale whereas faulting seems to drain the whole system and forms a large-scale connectivity [19]. Vertical fractures in stiff layers accommodate the additional strain locally with only a minor increase in stress, however under the prevailing conditions of fluid overpressure the differential stress can increase up to a critical limit leading to the development of large-scale faults. The stress drops significantly when the whole system fails along large-scale normal faults and high fluid pressure gradients along the fault may weaken the fault plane [79]. This has strong correlation with fluid drain where the growing fractures and the fluid pressure in the system influence each other depending on the effective permeability of the interconnected fracture network. This behavior is similar to what is observed in the Oman Mountains, where veins and faults correlate and stable isotopes seems to indicate that faults drain the system [64]. After their formation the faults usually behave as plastic systems and deter any further stress accumulation unless they are fully healed by the mineralization of the fracturing fluid. This phenomenon has strong influences on the strength of the fault planes and the subsequent earthquake events which may sometime turn into catastrophic failure [54].

The process of hydrofracturing has direct applications in many fields e.g., Geothermal reservoirs [80–82], normal oil and gas reservoirs, or CO₂ sequestration [83], where formation fluid pressure gradients play a role in cap-rock failure or permeability creation for the transport of pressurized fluid. We believe that our model can form a basis for better understanding of the influence of fluid pressure gradients and tectonic stresses on the development of natural fractures in reservoirs. In subsequent work we will expand the model to look more closely at seismic patterns that develop under variable boundary conditions.

In conclusion, our coupled numerical model can simulate the dynamic evolution of hydrofracturing. The model can reproduce realistic geometries of the field scale fracture and vein networks and demonstrates how the pattern changes depending on the material properties (i.e., stiffness and breaking strength distribution) and the applied external forces e.g., high fluid pressure gradient, gravity and lateral tectonic forces. Results of the model indicate that layers of low permeability may result in local perturbation of the effective stress field in host rocks and subsequently causes diversion of the direction of growing hydrofractures. Hydrofracturing in the model produces a non-static permeability in an over-pressured system, where the permeability does adjust to the local fluid pressures and accordingly the evolved stresses. We tested the model for a number of different combinations of high fluid pressure gradients, gravity and tectonic stresses to produce complex patterns. We are able to define the first proxies that can be used to determine whether natural fracture, vein and fault networks are mainly due to tectonic stresses or high fluid pressure gradients.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Sections of this manuscript are presented in the Thesis of Dr. IG, which is available here: http://ubm.opus.hbz-nrw.de/volltexte/2013/3543/. This study was carried out within the framework of Deutsche Wissenschaftliche Gesellschaft für Erdöl, Erdgas und Kohle (German Society for Petroleum and Coal Science and Technology) research project 718 “Mineral Vein Dynamics Modelling,” which is funded by the companies ExxonMobil Production Deutschland GmbH, GDF SUEZ E&P Deutschland GmbH, DEA Deutsche Erdoel AG and Wintershall Holding GmbH, within the basic research program of the WEG Wirtschaftsverband Erdoel- und Erdgasgewinnung e.V. We thank the companies for their financial support and their permission to publish these results. This work has received funding from the European Union's Seventh Framework Programme for research, technological development and demonstration under grant agreement no 316889 and support from the Alsace region within the REALISE program.

References

1. Fyfe WS, Price NJ, Thompson AB. Fluids in the Earth's Crust: Their Significance in Metamorphic, Tectonic, and Chemical Transport Processes. New York, NY: Elsevier Scientific Pub. Co. (1978).

Google Scholar

2. Hubbert MK, Rubey WW. Role of fluid pressure in mechanics of overthrust faulting: I. mechanics of fluid-filled porous solids and Its application to overthrust faulting. Geol Soc Am Bull. (1959) 70:115–66. doi: 10.1130/0016-7606(1959)70[115:ROFPIM]2.0.CO;2

CrossRef Full Text | Google Scholar

3. Secor DT. Role of fluid pressure in jointing. Am J Sci. (1965) 263:633–46. doi: 10.2475/ajs.263.8.633

CrossRef Full Text | Google Scholar

4. Segall P, Fitzgerald SD. A note on induced stress changes in hydrocarbon and geothermal reservoirs. Tectonophysics (1998) 289:117–28. doi: 10.1016/S0040-1951(97)00311-9

CrossRef Full Text | Google Scholar

5. Sibson RH, Scott J. Stress/fault controls on the containment and release of overpressured fluids: examples from gold-quartz vein systems in Juneau, Alaska; Victoria, Australia and Otago, New Zealand. Ore Geol Rev. (1998) 13:293–306. doi: 10.1016/S0169-1368(97)00023-1

CrossRef Full Text | Google Scholar

6. Sibson RH. Fluid involvement in normal faulting. J Geodyn. (2000) 29:469–99. doi: 10.1016/S0264-3707(99)00042-3

CrossRef Full Text | Google Scholar

7. Collettini C, De Paola N, Goulty NR. Switches in the minimum compressive stress direction induced by overpressure beneath a low-permeability fault zone. Terra N. (2006) 18:224–31. doi: 10.1111/j.1365-3121.2006.00683.x

CrossRef Full Text | Google Scholar

8. Leclère H, Fabbri O, Daniel G, Cappa F. Reactivation of a strike-slip fault by fluid overpressuring in the southwestern French–Italian Alps. Geophys J Int. (2012) 189:29–37. doi: 10.1111/j.1365-246X.2011.05345.x

CrossRef Full Text | Google Scholar

9. Hu JC, Angelier J. Stress permutations: three-dimensional distinct element analysis accounts for a common phenomenon in brittle tectonics. J Geophys Res. (2004) 109:B09403. doi: 10.1029/2003JB002616

CrossRef Full Text | Google Scholar

10. Bonafede M, Danesi S. Near-field modifications of stress induced by dyke injection at shallow depth. Geophys J Int. (1997) 130:435–48. doi: 10.1111/j.1365-246X.1997.tb05659.x

CrossRef Full Text | Google Scholar

11. Jamtveit B, Svensen H, Podladchikov YY, Planke S. Hydrothermal vent complexes associated with sill intrusions in sedimentary basins. Geol Soc Lond Spec Publ. (2004) 234:233–41. doi: 10.1144/GSL.SP.2004.234.01.15

CrossRef Full Text | Google Scholar

12. Wangen M. Effective permeability of hydrofractured sedimentary rocks. In: Andreas GK, Robert H, editors. Norwegian Petroleum Society Special Publications. Oxford, UK: Elsevier (2002). pp. 61–74. doi: 10.1016/s0928-8937(02)80007-8

CrossRef Full Text

13. Hunt JM. Generation and migration of petroleum from abnormally pressured fluid compartments. AAPG Bull. (1990) 74:1–12.

Google Scholar

14. Roberts SJ, Nunn JA. Episodic fluid expulsion from geopressured sediments. Mar Petrol Geol. (1995) 12:195–204. doi: 10.1016/0264-8172(95)92839-O

CrossRef Full Text | Google Scholar

15. Nunn JA, Meulbroek P. Kilometer-scale upward migration of hydrocarbons in geopressured sediments by buoyancy-driven propagation of methane-filled fractures. AAPG Bull. (2002) 86:907–18. doi: 10.1306/61EEDBD4-173E-11D7-8645000102C1865D

CrossRef Full Text | Google Scholar

16. Cathles LM, Smith AT. Thermal constraints on the formation of mississippi valley-type lead-zinc deposits and their implications for episodic basin dewatering and deposit genesis. Econ Geol. (1983) 78:983–1002. doi: 10.2113/gsecongeo.78.5.983

CrossRef Full Text | Google Scholar

17. Krynauw JR, Hunter DR, Wilson AH. Emplacement of sills into wet sediments at Grunehogna, western Dronning Maud Land, Antarctica. J Geol Soc. (1988) 145:1019–32. doi: 10.1144/gsjgs.145.6.1019

CrossRef Full Text | Google Scholar

18. Miller SA, Nur A. Permeability as a toggle switch in fluid-controlled crustal processes. Earth Planet Sci Lett. (2000) 183:133–46. doi: 10.1016/S0012-821X(00)00263-6

CrossRef Full Text | Google Scholar

19. Vass A, Koehn D, Toussaint R, Ghani I, Piazolo S. The importance of fracture-healing on the deformation of fluid-filled layered systems. J Struct Geol. (2014) 67:94–106. doi: 10.1016/j.jsg.2014.07.007

CrossRef Full Text | Google Scholar

20. Aochi H, Poisson B, Toussaint R, Rachez X, Schmittbuhl J. Self-induced seismicity due to fluid circulation along faults. Geophys J Int. (2013) 196:1544–63. doi: 10.1093/gji/ggt356

CrossRef Full Text | Google Scholar

21. Kobchenko M, Panahi H, Renard F, Dysthe DK, Malthe-Sørenssen A, Mazzini A, et al. 4D imaging of fracturing in organic-rich shales during heating. J Geophys Res. (2011) 116:B12201. doi: 10.1029/2011JB008565

CrossRef Full Text

22. Ghani I, Koehn D, Toussaint R, Passchier CW. Dynamic development of hydrofracture. Pure Appl Geophys. (2013) 170:1685–703. doi: 10.1007/s00024-012-0637-7

CrossRef Full Text | Google Scholar

23. Ghani I. Dynamic Development of Hydrofractures. PhD thesis, University of Mainz, Germany (2013). pp.1–90. Available online at: http://ubm.opus.hbz-nrw.de/volltexte/2013/3543/

24. Flekkøy EG, Malthe-Sorenssen A, Jamtveit B. Modeling hydrofracture. J Geophys Res Solid Earth (2002) 107:1–11. doi: 10.1029/2000JB000132

CrossRef Full Text

25. Vinningland JL, Johnsen O, Flekkøy EG, Toussaint R, Måløy KJ. Experiments and simulations of a gravitational granular flow instability. Phys Rev E. (2007a) 76:051306. doi: 10.1103/PhysRevE.76.051306

CrossRef Full Text | Google Scholar

26. Vinningland JL, Johnsen Ø, Flekkøy EG, Toussaint R, Måløy KJ. Granular Rayleigh-Taylor instability: experiments and simulations. PhysRevLett (2007b) 99:048001. doi: 10.1103/PhysRevLett.99.048001

CrossRef Full Text | Google Scholar

27. Johnsen Ø, Toussaint R, Måløy KJ, Flekkøy EG. Pattern formation during central air injection into granular materials confined in a circular Hele-Shaw cell. Physical Rev E. (2006) 74:011301. doi: 10.1103/PhysRevE.74.011301

CrossRef Full Text | Google Scholar

28. Johnsen Ø, Toussaint R, Måløy KJ, Flekkøy EG, Schmittbuhl, J. Coupled air/granular flow in a linear Hele-Shaw cell. Phys Rev E. (2008a) 77:011301. doi: 10.1103/PhysRevE.77.011301

CrossRef Full Text | Google Scholar

29. Johnsen Ø, Chevalier C, Lindner A, Toussaint R, Clément E, Måløy KJ, et al. Decompaction and fluidization of a saturated and confined granular medium by injection of a viscous liquid or a gas. Phys Rev E. (2008b) 78:051302. doi: 10.1103/PhysRevE.78.051302

CrossRef Full Text

30. Niebling M, Toussaint R, Flekkøy EG, Måløy KJ. Estudios numéricos de Aerofractures en medios poros/Numerical Studies of Aerofractures in Porous Media. Rev Cubana Fis. (2012a) 29:1E, 1E66.

31. Niebling MJ, Toussaint R, Flekkøy EG, Måløy KJ. Dynamic aerofracture of dense granular packings. Phys Rev E. (2012b) 86:061315. doi: 10.1103/PhysRevE.86.061315

CrossRef Full Text | Google Scholar

32. Goren L, Aharonov E, Sparks D, Toussaint R. Pore pressure evolution in deforming granular material: a general formulation and the infinitely stiff approximation. J Geophys Res. (2010) 115:B09216. doi: 10.1029/2009JB007191

CrossRef Full Text | Google Scholar

33. Goren L, Aharonov E, Sparks D, Toussaint R. The mechanical coupling of fluid-filled granular material under shear. Pure Appl Geophys. (2011) 168:2289–323. doi: 10.1007/s00024-011-0320-4

CrossRef Full Text | Google Scholar

34. Niebling MJ, Flekkøy EG, Måløy KJ, Toussaint, R. Mixing of a granular layer falling through a fluid. Phys Rev E. (2010a) 82:011301. doi: 10.1103/PhysRevE.82.011301

CrossRef Full Text | Google Scholar

35. Niebling MJ, Flekkøy EG, Måløy KJ, Toussaint, R. Sedimentation instabilities: impact of the fluid compressibility and viscosity. Phys Rev E. (2010b) 82:051302. doi: 10.1103/PhysRevE.82.051302

CrossRef Full Text | Google Scholar

36. Vinningland JL, Johnsen Ø, Flekkøy EG, Toussaint R, Måløy KJ. Influence of particle size in Rayleigh Taylor granular flow instability. Phys Rev E. (2010) 81:041308. doi: 10.1103/PhysRevE.81.041308

CrossRef Full Text

37. Vinningland JL, Toussaint R, Niebling M, Flekkøy EG, Måløy, KJ. Family-Vicsek scaling of detachment fronts in Granular Rayleigh Taylor Instabilities during sedimenting granular/fluid flows. Eur Phys J Spec Top. (2012) 204:27–40. doi: 10.1140/epjst/e2012-01550-2

CrossRef Full Text | Google Scholar

38. Zoback MD. Reservoir Geomechanics. Cambridge, UK: Cambridge University Press (2007). doi: 10.1017/CBO9780511586477

CrossRef Full Text | Google Scholar

39. Engelder T, Lacazette A. Natural hydraulic fracturing. In: Stephansson NBAO, editor. Rock Joints: Proceedings of the International Symposium on Rock Joints. Rotterdam; Loen: A.A. Balkema (1990). pp. 35–44.

40. Olson JE, Laubach SE, Lander RH. Natural fracture characterization in tight gas sandstones: integrating mechanics and diagenesis. AAPG Bull. (2009) 93:1535–49. doi: 10.1306/08110909100

CrossRef Full Text | Google Scholar

41. Segall P. Formation and growth of extensional fracture sets. Geol Soc Am Bull. (1984) 95:454–62.

Google Scholar

42. Biot MA. General theory of three-dimensional consolidation. J Appl Phys. (1941) 12:155–64. doi: 10.1063/1.1712886

CrossRef Full Text | Google Scholar

43. Secor DT. Mechanics of Natural Extension Fracturing at Depth in the Earth's Crust. Report 68–52, Geological Survey of Canada (1969). pp. 3–48.

44. Rice JR, Cleary MP. Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents. Rev Geophys. (1976) 14:227–41. doi: 10.1029/RG014i002p00227

CrossRef Full Text | Google Scholar

45. Adachi J, Siebrits E, Peirce A, Desroches J. Computer simulation of hydraulic fractures. Int J Rock Mech Min Sci. (2007) 44:739–57. doi: 10.1016/j.ijrmms.2006.11.006

CrossRef Full Text | Google Scholar

46. Cleary MP, Wong SK. Numerical simulation of unsteady fluid flow and propagation of a circular hydraulic fracture. Int J Numer Anal Methods Geomech (1985) 9:1–14. doi: 10.1002/nag.1610090102

CrossRef Full Text | Google Scholar

47. Meyer BR. Design formulae for 2-D and 3-D vertical hydraulic fractures: model comparison and parametric studies. In: SPE Unconventional Gas Technology Symposium. Louisville, KY: Society of Petroleum Engineers, Inc. (1986).

48. Gordeyev YN, Zazovsky AF. Self-similar solution for deep-penetrating hydraulic fracture propagation. Transp Porous Media. (1992) 7:283–304. doi: 10.1007/BF01063964

CrossRef Full Text | Google Scholar

49. Tzschichholz F, Herrmann HJ, Roman HE, Pfuff M. Beam model for hydraulic fracturing. Phys Rev B. (1994) 49:7056–9. doi: 10.1103/PhysRevB.49.7056

CrossRef Full Text | Google Scholar

50. Cobbold PR, Rodrigues N. Seepage forces, important factors in the formation of horizontal hydraulic fractures and bedding-parallel fibrous veins (‘beef’ and ‘cone-in-cone’). Geofluids (2007) 7:313–22. doi: 10.1111/j.1468-8123.2007.00183.x

CrossRef Full Text | Google Scholar

51. Hillis RR. Pore pressure/stress coupling and its implications for rock failure. In: Van Rensbergen P, Hillis RR, Maltman AJ, Morley CK, editors. Subsurface Sediment Mobilization, Vol. 216. London, UK: Geological Society of London Special Publication (2003). pp. 359–368. doi: 10.1144/gsl.sp.2003.216.01.23

CrossRef Full Text

52. Press WH. Numerical Recipes in C: The Art of Scientific Computing. Cambridge, UK: Cambridge University Press (1992).

53. Carman PC. Fluid flow through granular beds. Trans Inst Chem Eng. (1937) 15:150.

Google Scholar

54. Koehn D, Arnold J, Malthe-Sørrenssen A, Jamtveit B. Instabilities in stress corrosion and the transition to brittle failure. Am J Sci. (2003) 303:956–71. doi: 10.2475/ajs.303.10.956

CrossRef Full Text | Google Scholar

55. Bons PD, Koehn D, Jessell MW. Microdynamics simulation. In: Springer Lecture Series in Earth Sciences. Berlin; Heidelberg: Springer (2008). p. 406. doi: 10.1007/978-3-540-44793-1

CrossRef Full Text

56. Allen DNG. Relaxation Methods. New York, NY: McGraw-Hill (1954).

Google Scholar

57. Malthe-Sørenssen A, Walmann T, Jamtveit B, Feder J, Jøssang T. Modeling and characterization of fracture patterns in the Vatnajökull Glacier. Geology (1998a) 26:931–4.

Google Scholar

58. Malthe-Sørenssen A, Walmann T, Feder J, Jøssang T, Meakin P, Hardy HH. Simulation of extensional clay fractures. Phys Rev E (1998b) 58:5548–64. doi: 10.1103/PhysRevE.58.5548

CrossRef Full Text | Google Scholar

59. Koehn D, Arnold J, Passchier CW. Fracture and vein patterns as indicators of deformation history: a numerical study. Geol Soc Lond Spec Publ. (2005) 243:11–24. doi: 10.1144/GSL.SP.2005.243.01.03

CrossRef Full Text | Google Scholar

60. Virgo, S, Abe, S, Urai, JL. The evolution of crack seal vein and fracture networks in an evolving stress field: insights from discrete element models of fracture sealing. J Geophys Res Solid Earth. (2014) 119:8708–27. doi: 10.1002/2014jb011520

CrossRef Full Text

61. Hansen A, Hinrichsen EL, Roux, S. Scale-invariant disorder in fracture and related breakdown phenomena. Phys Rev B. (1991) 43:665. doi: 10.1103/PhysRevB.43.665

CrossRef Full Text | Google Scholar

62. Toussaint R, Pride SR. Interacting damage models mapped onto Ising and percolation models. Phys Rev E. (2005) 71:046127. doi: 10.1103/PhysRevE.71.046127

CrossRef Full Text | Google Scholar

63. Toussaint R, Hansen A. Mean-field theory of localization in a fuse model. Phys Rev E. (2006) 73:046103. doi: 10.1103/PhysRevE.73.046103

CrossRef Full Text | Google Scholar

64. Hilgers C, Kirschner DL, Breton JP, Urai JL. Fracture sealing and fluid overpressures in limestones of the Jabal Akhdar dome, Oman mountains. Geofluids (2006) 6:168–84. doi: 10.1111/j.1468-8123.2006.00141.x

CrossRef Full Text | Google Scholar

65. Valkø P, Econimedes MJ. Hydraulic Fracture Mechanics. New York, NY: John Wiley (1995).

Google Scholar

66. Brenner SL, Gudmundsson A. Arrest and aperture variation of hydrofractures in layered reservoirs. Geol Soc Lond Spec Publ. (2004) 231:117–28. doi: 10.1144/GSL.SP.2004.231.01.08

CrossRef Full Text | Google Scholar

67. Gudmundsson A, Brenner SL. How hydrofractures become arrested. Terra Nova (2001) 13:456–62. doi: 10.1046/j.1365-3121.2001.00380.x

CrossRef Full Text | Google Scholar

68. Holland M, Saxena N, Urai JL. Evolution of fractures in a highly dynamic thermal, hydraulic, and mechanical system - (II) Remote sensing fracture analysis, Jabal Shams, Oman Mountains. Geoarabia (2009a) 14:163–94.

Google Scholar

69. Boudier F, Bouchez JL, Nicolas A, Cannat M, Ceuleneer G, Misseri M, et al. Kinematics of oceanic thrusting in the Oman ophiolite: model of plate convergence. Earth Planet Sci Lett. (1985) 75:215–22. doi: 10.1016/0012-821X(85)90103-7

CrossRef Full Text

70. Breton JP, Bechennec F, Le Metour J, Moen-Maurel L, Razin P. Eoalpine (Cretaceous) evolution of the Oman Tethyan continental margin: insights from a structural field study in Jabal Akhdar (Oman Mountains). Geoarabia (2004) 9:41–58.

71. Searle MP. Structural geometry, style and timing of deformation in the Hawasina window, Al Jabal al Akhdar and Saih Hatat culminations, Oman mountains. Geoarabia (2007) 12:99–130.

Google Scholar

72. Holland M, Urai JL, Muchez P, Willemse EJM. Evolution of fractures in a highly dynamic thermal, hydraulic, and mechanical system - (I) Field observations in Mesozoic Carbonates, Jabal Shams, Oman Mountains. Geoarabia (2009b) 14:57–110.

Google Scholar

73. Gomez-Rivas E, Bons PD, Koehn D, Urai JL, Arndt M, Virgo S, et al. The Jabal Akhdar Dome in the Oman Mountains: evolution of a dynamic fracture system. Am J Sci. (2014) 314:1104–39. doi: 10.2475/07.2014.02

CrossRef Full Text

74. Cooke ML, Underwood CA. Fracture termination and step-over at bedding interfaces due to frictional slip and interface opening. J Struct Geol. (2001) 23:223–38. doi: 10.1016/S0191-8141(00)00092-4

CrossRef Full Text | Google Scholar

75. Gudmundsson A. Emplacement and arrest of sheets and dykes in central volcanoes. J Volcanol Geothermal Res. (2002) 116:279–98. doi: 10.1016/S0377-0273(02)00226-3

CrossRef Full Text | Google Scholar

76. Fischer MP, Engelder T, Brown KM, Bekins B, Clennell B, Dewhurst D, et al. Heterogeneous hydrofracture development and accretionary fault dynamics: comment and reply. Geology (1994) 22:1052–4.

77. Gudmundsson A. Fluid overpressure and stress drop in fault zones. Geophys Res Lett. (1999) 26:115–8. doi: 10.1029/1998GL900228

CrossRef Full Text | Google Scholar

78. Bercovici D, Ricard Y, Schubert G. A two-phase model for compaction and damage: 1. General theory. J Geophys Res Solid Earth. (2001) 106:8887–906. doi: 10.1029/2000JB900430

CrossRef Full Text | Google Scholar

79. Zoback MD, Harjes HP. Injection-induced earthquakes and crustal stress at 9 km depth at the KTB deep drilling site, Germany. J Geophys Res. (1997) 102:18477–91. doi: 10.1029/96JB02814

CrossRef Full Text

80. Gentier S, Rachez X, Peter-Borie M, Blaisonneau A. Hydraulic stimulation of geothermal wells: modeling of the hydro-mechanical behavior of a stimulated fractured rock mass. In: The Proceedings of the XII International Congress of Rock Mechanics. Beijing (2011).

81. Neuville A, Toussaint R, Schmittbuhl J. Fracture roughness and thermal exchange: a case study at Soultz-sous-Forets, C.R.A.S. Geoscience (2009) 342:616. doi: 10.1016/j.crte.2009.03.006

CrossRef Full Text

82. Neuville A, Toussaint R, Schmittbuhl J. Hydro-thermal flows in a self-affine rough fracture. Phys Rev E. (2010) 82:036317. doi: 10.1103/PhysRevE.82.036317

CrossRef Full Text | Google Scholar

83. Cappa F, Rutqvist J, Yamamoto K. Modeling crustal deformation and rupture processes related to upwelling of deep CO2 rich fluids during the 1965-1967 Matsushiro Earthquake Swarm in Japan. J Geophys Res. (2009) 114:B10304. doi: 10.1029/2009JB006398

CrossRef Full Text | Google Scholar