Zebra pattern in rocks as a function of grain growth affected by second-phase particles

1. Introduction

The zebra texture is a periodic pattern which is encountered worldwide in geological formations and is often associated with hydrothermal mineralization. Zebra banding occurs in claystones [1], siderite ores [2, 3], and sphalerite mineralization [4]. The process of the zebra pattern formation varies depending on the rock hosting this structure. Here we focus on the origin of zebra banding occurring in dolostones that is often found in the vicinity of Pb-Zn mineralization. The banding consists of alternating dark and light layers which are built up by a single mineral phase, namely dolomite. Despite the color the only macroscopically recognizable difference is the grain size, which can differ by several orders of magnitude between the coarse grained light and the fine grained dark regions. The pattern appears very symmetric and the layers comprise of monotonic thickness and spacing at the local scale (Figure 1). On a microscale other differences become visible between the dark and the light regions (Figure 1). The fine grained areas are always accompanied by a high density of opaque second-phase material. Furthermore, the crystals in the fine grained layers exhibit lobate grain boundaries whereas the grain boundaries in the light regions display a more polygonal geometry. The overall structure of the coarse grained layers is very similar to the type of veins or crack fillings where the crystals grow toward the central part of the opening and thus form a median line.

FIGURE 1

Figure 1. Examples of zebra textures at different scales. The left picture shows an outcrop in the area of the San Vicente mine. On the right side a hand specimen and two thin sections are shown. The area of the displayed thin sections is 1 cm² which is equivalent to the area of the simulation. The two micrographs show zebra banding with different spacing between the dark and the light layers.

In order to be able to compare the outcome of our numerical simulations with natural specimens, representative samples on which analytical analysis can be performed were collected at the San Vicente mine in Central Peru. This location is a good general example of an ore deposit where numerous of the described zebra textures occur with a high diversity of layer spacing and thickness. The San Vicente mine is a case example of an ore deposit with many typical characteristics of hydrothermal Pb-Zn mineralization which is associated with the zebra textures where ore occurs along and within the bands [5]. The San Vicente mine is hosted in dolomitized platform carbonates in basin flanks in a foreland thrust belt in front of the Andean mountains with larger ore bodies bound to specific lithological units.

Different theories about the origin of the zebra textures in dolostones have been formulated. It is widely accepted that the formation of the structure consists of several phases of which the dark fine grained dolomite is the first one. This first phase represents the replacement of the initial limestone by dolomite [5–15]. What exactly triggers the development of the subsequent phases, which build up the coarse grained regions and are responsible for the final appearance of the pattern, is still a point of debate.

A selection of existing models will be presented in this paragraph. Zebra dolomites occurring in Northern Canada can be related to pre-existing structures in the initial limestone [14]. Prior to the dolomitization the limestone comprised of rhythmic sedimentary structures with a higher porosity/permeability. During the replacement of the limestone by dolomite the fluid flow was focused in these high permeability zones leading to higher dissolution and dolomitization rates and the formation of layers. Studies carried out on zebra dolomites in Belgium, Spain and Canada concluded that the pattern evolved during fracturing due to tectonic stress [8, 9] or hydrofracturing during the pulsed influx of dolomitizing brines [12, 13, 15]. The light coarse grained dolomite bands are interpreted as being at least partly void filling cements which precipitated into extensional fractures [12]. Based on the high symmetry of the banding it has been stated that the process which leads to the formation of the zebra texture has to involve self-organization [7, 10, 11]. The pattern of the zebra dolomite is found to be much too cyclic to be related solely to pre-existing sedimentary features [7]. The concept of self-organization can produce symmetric or rhythmic patterns out of an initially unordered system. An example of such a self-organizing process which produces equidistant concentric banding are the Ostwald-Liesegang rings which evolve during a reaction-diffusion process [16]. The necessary conditions for self-organization processes were found to be present in rocks hosting the zebra patterns [7]. The rhythmic pattern may evolve during dolomitization due to cyclic dissolution/precipitation processes focused in the white layers [7]. Another self-organizing concept which may explain the monotonic thickness and equidistant occurrence of the zebra patterns was introduced by Merino et al. [10] and Merino et al. [11]. In this model the crystals in the light layers displace the host rock during growth (displacive vein growth). The growth of this second dolomite phase not only pushes away the primary dolomite in the dark bands, but also induces a stress field around the light layers. This stress field, which arises from the crystallization stress, is thought to prevent the growth of new material in the direct vicinity [11]. A more general model for the development of banded structures in rocks is the crystal zoning model [3]. In this model a phase transition front collects impurities during its propagation. If a critical value of collected material is reached, the front switches from collecting to releasing particles. This approach can generate a periodic layered distribution of impurities similar to mud bands in snow sediments or the opaque second-phase material in the fine grained layers of the zebra dolomite. Even though this theory does not account for the difference in grain size between the dark and light regions, it may be regarded as a possible process which triggers the formation of the zebra pattern.

It can be summarized that several different models of zebra dolomite formation exist which are either based on focused fracturing or dissolution, self-organizational concepts or simply link the textures to preexisting structural features in the dolomitized limestone. A consensus has therefore not been found yet, and the suggested models sometimes contradict each other. Because the dolomitizing fluids which are likely to be linked to the pattern formation are capable of delivering the metal content to the respective deposit, a general model of the zebra texture formation can widen the understanding of hydrothermal systems that build up economic Pb-Zn mineralization.

Pattern formation in geological systems is often related to self-organization processes. The pattern emerges out of an initially unordered system which is out of equilibrium and in which feedback reactions occur [17, 18]. Especially the genesis of a rhythmic pattern like the one discussed in this paper are likely to involve some kind of self-organization [7]. The concept of self-organization applies to a broad range of scientific problems like Biology [19], Chemistry [20], Geochemistry [17, 18], and Mechanics [21]. Especially when dealing with two phase systems like a fluid saturated rock were mechanical and/or chemical reactions take place, self-organization is likely to occur. As the concept of self-organization is a general approach, findings achieved in one scientific field may also be applicable to another. That self-organization occurs in the type of hydrological system studied in this communication was already proposed by Ortoleva et al. [18], where banded Pb-Zn mineralization was linked to geochemical self-organization.

In this communication we present a simple generic model which can explain the differences in color and grain size in the layers of the zebra pattern. Our model starts with the replacement of the initial impurity rich limestone by dolomite according to the crystal zoning model where the scattered second-phase is redistributed along the propagation direction of the reaction front. The complete dolomitization is followed by a grain growth process that is influenced by second-phase particle densities. This simulation setup involves feedback between the redistribution of second-phase material and grain growth. Moreover, the hydrological system has to be assumed to be out of equilibrium. As already pointed out by Fontbote [7] the host rock and the infiltrating dolomitizing fluid will account for the “out-of-equilibrium condition.” These are general principles which are present during self-organized pattern formation [17, 18].

2. Numerical Model

2.1. Setup

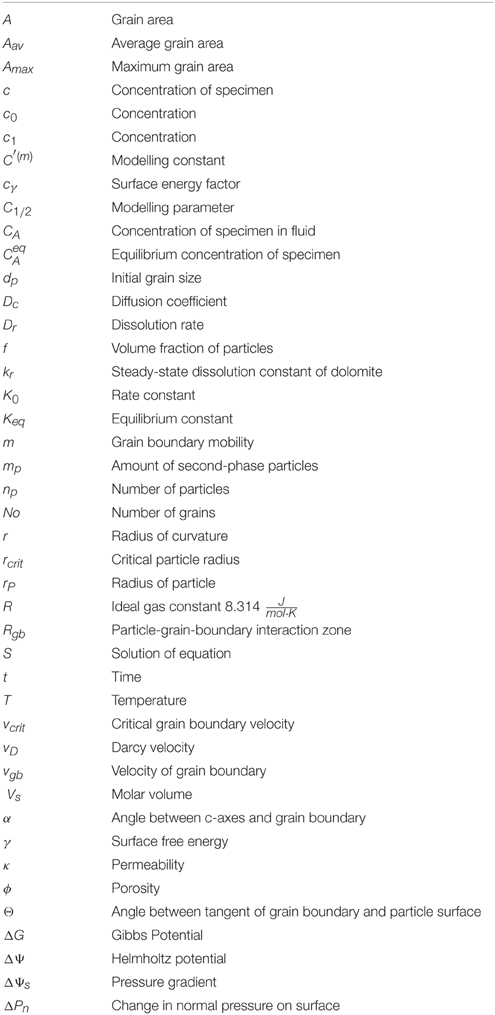
The numerical simulations were carried out in 2D at the scale of a thin section (1 cm²) using the modeling environment “ELLE.” In our simulations two grids are mapped onto each other (Figure 2). The background is represented by nodes distributed on a hexagonal grid that is stationary and records impurity content, concentration and mineralization. The second grid is a mobile boundary-model consisting of line segments that are connected by nodes, where the line segments represent grain boundaries of growing crystals. The two grids are linked to each other so that the impurity content in the hexagonal grid can influence the simulation of grain boundary migration in the boundary model.

FIGURE 2

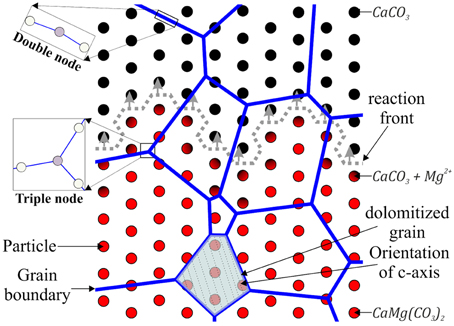
Figure 2. Schematic section of the model showing the basic elements used to simulate the dolomitization and the grain growth. The nodes which are distributed on a hexagonal lattice build up the background of the simulation. The nodes have a value of Mg²⁺-concentration and the parameters of the second-phase (radius and densities) assigned to them. The later influences the migration rate of the grain boundaries. The top layer is built up by the boundary model consisting of connected nodes (either double or triple) which represent the grains. Only grains which are dolomitized can grow whereas the driving force for migration is derived from the surface energy, which is a function of the orientation of the c-axis of the considered crystal and the adjacent grains.

During the simulation of the pattern formation two main processes are active, an initial replacement of calcite by dolomite along a reaction front and a subsequent coarsening of grains as a function of variations in surface energy. Both processes affect impurity distributions whereas the grain growth process itself is also affected by the redistributed scatter of impurities.

2.2. Dolomitization and Second-phase Redistribution

The dolomitization in our model is simulated as a replacement of the initial calcite (CaCO₃) by dolomite (CaMg(CO₃)₂) due to a concentration change of Mg²⁺ in the nodes of the hexagonal grid. Usually the replacement process in large hydrothermal systems involves convective fluid flow but because the area of our simulation is comparatively small we assume that on such a scale convection can be neglected and a general transport equation can be applied:

$\begin{array}{cc}{\left(\frac{\partial c}{\partial t}\right)}_x=v_D{\left(\frac{\partial c}{\partial x}\right)}_t+D_f{\left(\frac{{\partial }^{2}c}{\partial x^2}\right)}_t& \left(1\right)\end{array}$

This expression describes the change in concentration (c) in the x-direction over time (t) due to advection (v_D) and diffusion (D_f) of a specimen. As a simplification we assume the diffusivity to be constant and isotropic. If we consider the transport of a specimen in the saturated zone with non-turbulent flow (Re < 1) we can calculate the advection part of Equation (1) using Darcys law:

$\begin{array}{cc}{v}_D=\frac{\kappa }{\varphi }·\Delta P& \left(2\right)\end{array}$

The velocity in this equation is a function of the pressure gradient (ΔP) in the respective environment, the permeability (κ) and the porosity (ϕ) of the considered medium. Compared to the advection speed the diffusivity usually contributes only a small amount to the overall concentration change and therefore the Darcy velocity will be the critical term in Equation (1). As a consequence the propagation of the reaction front is mainly governed by the Darcy velocity. In order to apply Equations (1) and (2) to our simulation we initially set a constant pressure gradient, a randomly distributed porosity and an initial concentration in the hexagonal grid. These parameters are then used to calculate the concentration change in the nodes due to the propagation of a fluid supersaturated with Mg²⁺. The associated concentration change in the nodes is proportional to the calculated Darcy velocity combined with the constant diffusivity. The Darcy velocity itself is calculated using the initially defined pressure gradient and the local porosity/permeability. A threshold for the concentration of Mg²⁺ was set, above which we consider the node to be completely dolomitized. In addition the porosity increases by about 13% [22] when a node is changed completely to dolomite. Once a grain becomes dolomitized the slower grain growth process can start. However, the grain boundary migration only begins in the considered grain if the adjacent grains are also dolomitized as we assume grain growth to appear along dolomite/dolomite boundaries (Figure 2).

The initial scatter of impurities is alternated by the advancing reaction front similar to the crystal zoning model [3]. The reaction front in our model is capable of collecting second-phase particles whereas the collected amount is inversely proportional to the size of the impurities and proportional to the concentration change between two time steps (Equation 3). For the collection process we applied a size dependent step-function [f(r_p)] assuming that the mobility of second-phase particles during replacement is similar to the mobility associated with grain boundary migration described by Gottstein and Shvindlerman [23]. Furthermore, we chose a function [f(c)] which relates the amount of collected impurities to the concentration change between two time steps which is directly proportional to the replacement rate. The impurities should become mobile during replacement as the calcite/dolomite transition is accompanied by an increase of the crystallographic order. The originating dolomite crystals will prefer a low internal energy state and therefore tend to build in fewer impurities in their lattices. This cleansing process of the crystals can be compared to the generation of impurity free crystals from melt during industrial zone melting [3] even though the transition in our model is between two mineral phases and not a change of the state of matter. The Equation (3) outlines how we calculated the amount of particles collected by the advancing front, if the threshold for collection is not exceeded.

$\begin{array}{cc}m=C_{1/2}·f(r_p)·f(c);S=[0;1]& \left(3\right)\end{array}$

$\begin{array}{l}f(r_P)=1-tanh(r_P)r_P<r_{crit}\\ f(c)=2·(c_1-c_0)c_{0/1}<0.5\end{array}$

Here m_p is the amount of the second-phase which is collected by the reaction front, r_p is the radius of the second-phase particles, r_crit is the threshold of the particle size, c₀ is the concentration of the contaminant in the previous time step and c₁ is the concentration in the current time step, respectively. The factor C_1∕2 is used to control the amount of particles collected or released by the front. As the threshold for dolomitization in our simulation was set to 0.5, the maximum solution of f(c) is 1 but will usually be much lower. Once the loading-threshold of the reaction front is reached the collecting force of the front breaks down and the process switches to releasing particles [acc. [3]]. The release of second-phase particles in our model is a function of particle size and concentration change according to:

$\begin{array}{l}f(r_P)=tanh(r_p)r_p<r_{crit}\\ f(c)=1-\left(2·(c_1-c_0)\right)c_{0/1}<0.5\end{array}$

2.3. Grain Growth

Static grain growth can be divided into normal and abnormal grain growth. During normal grain growth the coarse grains grow and small grains shrink [24]. The driving force for this process is usually derived from the specific surface energy (γ) of the material and the local radius of curvature (r) of the grain boundary. This driving force is proportional to the reduction of the Gibbs free energy (ΔG) [25].

The energy for grain boundary migration derived from the reduction of the Gibbs free energy is largest for surfaces with a small radius of curvature (Equation 8). In general the reduction of the surface free energy of the crystals tends to generate curved boundaries and the direction of the migration depends on the curvature of the considered crystal. Typically the grain boundary will migrate toward its center of curvature [26]. If the reduction of the Gibbs free energy is the main driving force and the surface energy of the crystals is isotropic, the grain boundaries tend to produce a polygonal pattern with straight boundaries. Once all the grains have roughly the same size, the resulting structure is a so-called foam structure with angles of ≈ 120° at triple junctions [27].

In this study we simulated grain growth where grain boundaries interact with a dispersed second-phase. In order to find a kinetic rate-law governing the propagation of boundaries we chose a first order rate law for dissolution/precipitation based on transient state theory [28]. The general form of the applied equation is:

$\begin{array}{cc}{D}_r=k_r{V}_s\left[1-exp\left(\frac{C_A}{C_A^{eq}}\right)\right]& \left(4\right)\end{array}$

In this expression D_r is the dissolution rate [m∕s], k_r is a rate constant [molm⁻²s⁻¹] at a given temperature and pH, V_s is the molar volume [m³mol⁻¹], C_A is the concentration of the specimen in the fluid and $C_A^{eq}$ is the equilibrium concentration of the solute. If we use the expression for the equilibrium constant K_eq:

$\begin{array}{cc}{C}_A^{eq}\approx K_{eq}=K_{0}exp\left(\frac{\Delta P_n{V}_s}{RT}\right)exp\left(\frac{\Delta {\Psi }_s}{RT}\right)& \left(5\right)\end{array}$

and assume an equilibrium saturation and no stress acting on the crystal surface, we can derive an expression for the dissolution or precipitation rate at constant fluid pressure under saturated conditions as Koehn et al. [29, 30]:

$\begin{array}{cc}{D}_r=k_r{V}_s\left[1-exp\left(-\frac{\Delta {\Psi }_s}{RT}\right)\right]& \left(6\right)\end{array}$

where R is the universal gas constant and T is the temperature [K]. We then get a temperature dependent rate law for dissolution/precipitation processes using the Helmholtz free energy change ΔΨ_s. Further details on the derivation can be found in Koehn et al. [29, 30]. If we now substitute ΔΨ_s with ΔG we can describe the process by means of Gibbs free energy reduction. This energy change is closely related to the change of the radius of curvature (Δr) of the considered grain. If this energy reduction is the main driving force for grain boundary migration, the velocity of a point on the grain boundary can be calculated using the surface energy (γ), the grain boundary mobility (m) and the radius of curvature (r) as:

$\begin{array}{cc}\Delta r\approx \left(\frac{-m\gamma }{r}\right)\leftrightarrow v=\frac{\partial r}{\partial t}=\frac{-m\gamma }{r}& \left(7\right)\end{array}$

Based on Equation (7) the velocity of a grain boundary (v) is a function of the reduction of r over time or the grain boundary mobility (m) and the surface free energy (γ, respectively [31]. We can simplify this expression and determine the energy of a point on the grain boundary by:

$\begin{array}{cc}\Delta E_r=\frac{\gamma }{r}& \left(8\right)\end{array}$

This expression can be regarded as the apparent activation energy and we substitute the energy change in Equation (6) by ΔE_r. Hereby it is possible to formulate a general rate law depending on the reduction of the Gibbs free energy with a temperature dependent Arrhenius term which is often used to describe grain growth processes. To compute the migration rate of a grain boundary in our simulation we then applied:

$\begin{array}{cc}{v}_{gb}=k_r{V}_s\left[1-exp\left(-\frac{\Delta E_r}{RT}\right)\right]& \left(9\right)\end{array}$

By implementing a uniform surface energy γ, isotropic grain growth will be simulated and the developing grains will generate a foam structure. In order to resemble grain boundary migration which produces a more dolomite-like crystal shape we adopted a function for anisotropic grain growth developed by Bons et al. [27], in which the surface energy of the grains is a function of the c-axis orientation of the considered- and the adjacent grain. By relating the surface energy to the angle between the grain boundary and the c-axis, the problem is reduced to a function of γ over 90° (Figure A1a). The shape of this function determines to a certain extent the geometry of the developing grains. The energy state of the considered boundary segment is a function of four angles for any node on a boundary but will be a function of six angles for a node at a triple junction. The value of the surface energy of a single node is derived by adding up the energies of the adjacent boundary segments and accounting for the length of every segment. The energy state of a single segment is the product of its length and the sum of the energy values according to the function in Figure A1a. The process developed by Bons et al. [27] also accounts for low energy boundaries related to coincident side lattices. In Figure A1b the distribution of the calculated surface energy of a simulation consisting of 10.000 time step is shown. The distribution of the surface energies shows two distinct peaks at ≈ 0.2 and ≈ 0.5 Jm⁻². This bimodal distribution is caused by the underlying function (Figure A1a).

In contrast to normal grain growth, abnormal grain growth can occur in aggregates where some large grains exist in an otherwise fine grained matrix. The larger grains will then grow at the cost of many small grains which will shrink or disappear [25].

In this work we mainly focus on normal static grain growth, but depending on the distribution of the developing grain sizes, abnormal grain growth may occur at later stages of the simulations. The shift from normal to abnormal grain growth might be caused by the anisotropic distribution of surface energies [32] or by the distribution of impurities.

2.4. Drag Force of Mobile Particles

Fluid films, inclusions, melt, pore size, and the chemical composition of fluids can all change the grain boundary mobility [24, 25, 33]. In our simulation we focus on the interaction of a second-phase volume fraction with a migrating grain boundary. This second-phase can for example be fluid filled pores or a different mineral phase [23–25, 33–35]. The interaction between the grain boundary and an impurity, which results in reduction of the driving force for migration, can be quantified by the so-called Zener drag. Zener formulated equations to calculate the influence of second-phase particles on a moving grain boundary based on laboratory experiments [36]. That the results achieved during laboratory studies can approximate the interaction of crystal growth and a dispersion of second-phase particles in geological systems was shown by Mas and Crowley [34], who achieved a quantitative analysis of the relationship between second-phases and the grain size in marble. It was found that already volume fractions of ≈ 5% will have a significant effect on the grain size in natural systems and even a very fine grained second-phase can have a remarkable effect on the growth rate as long as the volume fraction is sufficiently high enough.

When a moving grain boundary encounters a single, coherent, spherical second-phase particle, this obstacle initially applies an attraction force to the crystal surface. In order to migrate over the obstacle, the grain boundary has to increase its area proportional to the size of the impurity. During progressive boundary migration the particle will then exert a drag force on the surface (Figure 3A). The area increase of the grain boundary and the drag force both result in additional energy needed for further grain boundary migration, whereas the effective drag force is primarily dependent on the size of the considered particle [25]. In order to calculate the drag force of a single second-phase particle the assumption has to be made that the surface tensions of the particle and the grain boundary are in equilibrium. If this is assumed and the grain boundary meets the obstacle at an angle of 90°, the two tensions will cancel out leaving only one surface tension (γ) [36]. This surface tension is the internal energy of the matrix/matrix boundary and not of the matrix/particle interface [25]. The general equation of the Zener drag (F_Z) is then

$\begin{array}{cc}{F}_z=2\pi \gamma r_p·cos\Theta ·sin\Theta & \left(10\right)\end{array}$

where γ is the resulting surface tension, r_p is the radius of the particle and Θ is the angle between the tangent to the pinned matrix boundary at its intersection with the particle and the tangent to the boundary when no particle is present. The maximum pinning force occurs at Θ = 45°. In this case the product of the two trigonometric functions equals 1∕2, leaving:

$\begin{array}{cc}{F}_z=\pi \gamma r_p& \left(11\right)\end{array}$

which is the equation for the maximum Zener-force of a single coherent spherical particle, disregarding the shape of the actual grain boundary [36].

FIGURE 3

Figure 3. (A) Basic concept of the Zener drag applied to a grain boundary by a single coherent, spherical particle. In the first stage when the grain boundary encounters a particle it will be attract by it. In order to move over the particle the grain boundary has to increase its area which is associated with a higher energy needed for further migration. During progressive grain boundary migration the particle will exert a drag force on the particle. This force is highest for angles of 45° between the bend grain boundary and an imaginary undeformed boundary. The area increase and the applied drag force from particle result in a higher energy needed for grain boundary migration and therefore slow down or even inhibit further grain boundary migration [after Nes et al. [36]]. (B) Concept of the Zener pressure applied to a grain boundary by multiple spherical, coherent particles of the same radius. The Zener pressure is the drag force of a distribution of particles which are present in the particle-boundary interaction-zone (R_gb). The assumption for the validity of this concept is that the volume fraction of particles equals the area fraction of particles on the grain boundary [after Nes et al. [36]].

It is very unlikely that there is just one single particle at one grain boundary in a natural system. It is more reasonable to consider a dispersion of particles with different radii (r_p). The effective driving force for grain growth (F_eff) will then be reduced by the cumulative attraction forces of all particles with the same radius (r_p). This can be written as

$\begin{array}{cc}\Delta F_{eff}=F_{eff}-{\displaystyle \sum _{i=1}^{n_p}{n}_i}{F}_{z_i}& \left(12\right)\end{array}$

with n_i being the number of particles with the radius r_p, n_p the maximum number of these particles and F_zi the Zener drag of a particle with the considered radius [23].

In order to simulate the drag force of several particles on a grain boundary we chose Equation (13), which gives a good estimate for the drag force resulting from a volume fraction of particles. This equation is based on the assumption that the particles contributing to the drag force all have the same radius. A zone of interaction between the particles and the grain boundary (R_gb) has to be defined (Figure 3B), which has approximately the diameter of a single particle (2r_p). Furthermore, only second-phase particles which are in the interaction zone (R_gb) behind the moving grain boundary will contribute to the drag force because the impurities in the particle-boundary interaction zone (R_gb) in front of the boundary will produce an attractive force. Finally it is assumed that the volume distribution of particles equals the area distribution (f) on the grain boundary. The equation to calculate the drag force resulting from a volume distribution of second-phase particles is:

$\begin{array}{cc}{P}_z=\frac{3}{2}f\frac{\gamma }{R_{gb}}{R}_{Gb}\approx 2r_p& \left(13\right)\end{array}$

We simplified the process of calculating the impurity-depending drag force by computing the volume fraction of impurities in one node of the hexagonal grid and introducing this value as the area fraction of second-phase particles in Equation (13) (Figure 3B).

To simulate the interaction of a grain boundary with a fraction of impurities we calculated the drag force resulting from the scatter of second-phase particles in the background of the model. The derived drag force reduces the apparent activation energy or driving force for grain boundary migration according to:

$\begin{array}{cc}{D}_r=k_r{V}_s\left[1-exp\left(-\frac{\left[\left(\gamma \frac{1}{r}\right)-\left(\frac{3}{2}f\frac{\gamma }{R_{gb}}\right)\right]}{RT}\right)\right]& \left(14\right)\end{array}$

This is the equation on which our simulation of anisotropic grain growth hindered by a dispersed second-phase is based. The final average and the maximum grain size are both affected by the size and number of impurities present in a volume [23, 33, 35–41].

In addition to applying a drag force on grain boundaries, second-phase particles are not stationary during grain growth. A moving grain boundary can capture particles and shift them in its propagation direction if the grain boundary migration rate is sufficiently low and the diameter of the second-phase particles is small enough. During continuous grain growth the grain boundary will be loaded with progressively more particles that are smaller than a critical size [23]. As the value of the grain boundary velocity derived from the driving force is crucial to the loading process, it is also possible that a loaded grain boundary detaches itself from the particles when the driving force increases. At this point the grain boundary velocity will have the value of a boundary without any particle. Grain boundary migration can therefore take place in two regimes, an impurity controlled regime, with a slow grain boundary migration and an impurity-free regime with a fast grain boundary migration [26]. According to the theory of mobile particles by Gottstein and Shvindlerman [23] we chose a threshold for the radius of the second-phase and for the velocity of the migrating boundary. The amount of the second-phase particles that are redistributed by a moving grain boundary is inversely proportional to the particle size and to the velocity of the grain boundary according to:

$\begin{array}{cc}{m}_p=C_1·f(r)·f(v_{gb})S=[0;1]& \left(15\right)\end{array}$

$\begin{array}{l}f(r)=1-tanh(r_p)r_p<r_{crit}\\ f(v_{gb}=1-tanh(v_{gb})v_{gb}<v_{crit}\end{array}$

It can be inferred that the maximum drag force and therefore the maximum grain size achieved during grain growth are both a function of the size and the dispersion of the second-phase [25, 35]. In order to quantify this relationship Equation (16) can be used to estimate the maximum achievable grain size.

$\begin{array}{cc}{A}_{max}={C^{\prime }}^{(m)}·\frac{d_p}{f}& \left(16\right)\end{array}$

Where A_max is the maximum grain area, d_p is the initial grain size, f is the volume fraction of the second-phase and C^′(m) is a constant that depends on the model assumptions. The dispersion of the second-phase particles has a high impact on final grain size whereby the smallest grain size is reached when the particles are not randomly dispersed and most of them lie on grain corners [25].

3. Results

3.1. Initial Setup

Prior to every simulation a constant pressure gradient, a random distribution of porosity, second-phase particle radii and densities were assigned to the nodes of the hexagonal grid. Particle distributions are aligned horizontally in order to mimic an initial sedimentary layering with graded beds. Such a sedimentary layering can often be found in limestones and may be caused by cyclic sedimentary deposition. Banding in calcareous rocks might as well be of biological origin of which Stromatolites, Stromatoporoids or algae mats are good examples. In addition compaction during diagenesis might form a layered distribution of impurities resulting from pressure solution and subsequent precipitation. An example of a banded dolomite which was found in the Upper Silesian Pb-Zn district in Poland compared with the initial impurity scatter in our model is shown in Figure A2. The Upper Silesian ore deposit is of the same type as the one hosting the San Vicente mine in Peru but a zebra pattern is not frequently observed in this region.

The c-axis orientation of grains varies randomly throughout the model (Figure A1c). We chose the area of the model as being equivalent to 1 cm², the time scale of a single time step was set to 1 h for the dolomitization and once the volume was completely dolomitized the time scale was switched to 10a in order for grain growth to occur. According to the chosen spatial scale one node in the hexagonal grid is thought to equal a spherical volume with a diameter of ≈ 45 μm in which a fraction of impurities can be present.

3.2. Dolomitization and Second-phase Redistribution

Initially a reaction front progresses through the material. This front changes calcite to dolomite, a reaction that includes an increase in porosity (up to 13%). The reaction is induced by an influx of fluid from the lower boundary of the model and is calculated using an advection-diffusion algorithm (see Section 2.2). We use intermediate Péclet and Damköhler numbers to avoid too pronounced fingering in the front. This setup leads to a wavy front in the simulations (Figure 4A) with an intermediate width. During the progression of the reaction the second-phase particles are collected within the front and move with the front until a threshold is reached and the front loses particles again. Behind the front the particle densities are generally lower unless the front is oversaturated and releases particles. The progressing reaction front enhances the initial second-phase distribution (horizontal sedimentary layering). A zonation in concentration change is clearly visible in Figure 4A. The development of channels is minimal but the shape of the front is clearly irregular. The second-phase particle loading process (Equation 3) is displayed in Figure 4B. The highest densities of mobile particles are present close to the actual replacement where the concentration change nearly exceeds the threshold for dolomitization. Once the reaction front has changed the material to dolomite grain boundary migration becomes active (Figure 2).

FIGURE 4

Figure 4. Simulated reaction front after 2500 time steps. (A) Concentration (c) of Mg²⁺. The Bottom part is already dolomitized (black) and the grain growth process could already start. Different layers of concentration change are visible and these different bands of Mg²⁺ could be interpreted as metastable phase in the transition from pure calcite to dolomite. The fluid flow follows the initially set pressure gradient (ΔP). (B) The advancing dolomitization front collects second-phase material along its propagation direction. The amount of captured particles depends on the size of the particles and the concentration change in the front between two time steps. The mobile particles (red) are moving together with the advancing front and represent the amount of second-phase material which is released from the crystal lattices by the dolomitization process.

3.3. Grain Growth with Zener Pressure

Based on the analyzed natural samples, in which saddle dolomite is present in the coarse layers, we assumed a temperature of at least 80°C [22, 42]. This temperature regime is also found in the literature for the area of the San Vicente mine where the involved fluids are characterized as brines with a temperature of ≈ 75–160°C and a pH of ≈ 5 [11, 43, 44]. The pH in the work of Spangenberg et al. [44] was determined through geochemical analyses on sulfates giving the hydrogeochemical parameters of the mineralizing brine. The dolomitizing brine probably percolated through the same underlying detrital rocks generating a similar slightly acidic fluid. The in situ pH of general dolomitizing brines presented in the work of Merino and Canals [11] is also 5. However, a change in pH and/or T will accelerate or slow down the precipitation rate of dolomite as both affect the dissolution constant (k_r) used in Equation (14). We estimated the value of k_r trough an extrapolation to pH 5 from a series of experiments carried out by Gautelier et al. [45]. The measurement of the steady-state dolomite dissolution rate in the work of Gautelier et al. [45] was performed at a maximum temperature of 80°C and is in the temperature range we consider appropriate for our simulations. The value of the surface free energy for limestone is 0.27 Jm⁻² [46] whereas the value for dolomite is poorly known. We therefore based the distribution of the surface energy in our model on the work of Austen et al. [47]. Although the simulated process is thought to be situated in a burial environment with an average depth of 2 km, we neglected the pore pressure and the stresses acting on the crystals assuming that these play only a minor role.

We first tested the implementation of Equation (9) with the chosen constants by comparing the analytical solution with the outcome of the simulation. In Figures A3a,b the derived velocities for different surface energies (0.2–0.8 Jm⁻²) are plotted against an increasing radius of curvature. The theoretical solution (Figure A3b) and the values computed during the simulation (Figure A3a) fit well. The boundary velocity is inversely proportional to the radius of curvature (r) and proportional to the surface energy (γ) in accordance to theory [27, 31]. We further tested the reliability of our applied rate law by simulating the shrinking of a single circular grain (Figure A3c). The radius of curvature will decrease with time and the time steps can therefore be related to a relative radius. As the energy for grain boundary migration is a function of the radius of curvature and the surface energy in our simulation, the different surface energies (0.2–0.8 Jm⁻²) can be related to different grain boundary mobility. A linear decrease of the grain area over time is expected for an isotropic surface energy distribution and the shrinking rate should be proportional to the grain boundary mobility [27], which is the case for the outcome of our simulation.

The maximum grain size and the reduction of grain numbers in our simulation are different for isotropic grain growth, anisotropic grain growth and anisotropic grain boundary migration influenced by second-phase particles (Figure 5). The reduction of the grain number shows an exponential decrease in all three cases, whereas the actual rate is highest for the isotropic case. The difference in the average grain size between anisotropic grain growth and the impurity-controlled growth seems small but is still significant considering that either one or no impurity was assigned to every node in the hexagonal grid, which gives a small volume fraction. Furthermore, the distribution of the surface energy along grain boundaries according to Figure A2a results in grain shapes which are similar to the ones observed in the natural samples. In contrast to the foam structure achieved by isotropic grain growth the angles at triple junctions differ significantly from 120° and the grain shapes are more irregular. In the case of impurity-controlled growth the shapes become even more irregular and the average grain size is slightly smaller.

FIGURE 5

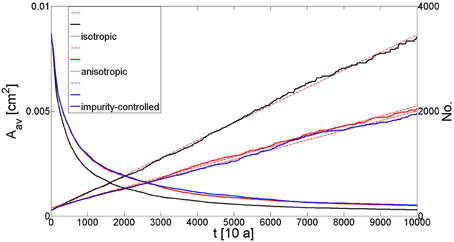
Figure 5. Graph showing the number of grains and the average grain size during simulations with 10.000 time steps (100 ka). The exponential decrease of grain numbers is visible in all three simulation. The maximum grain size is achieved by isotropic grain growth and the smallest maximum grain size is found in the impurity controlled regime. This area increase is inverse proportional to the number of grains at the end of the simulation.

Figure 6 shows simulations with different particle densities with initial distributions shown in Figure A4a. The maximum grain size depends inversely on the particle densities with larger grains in aggregates with lower second-phase densities (Figure 6). There is a large difference in the maximum grain size between a simulation with one or zero mobile impurity and a simulation with a maximum of 15 second-phase particles per node. Grain growth stops and a stable grain size is achieved at time step 2500 in the simulation with 15 mobile impurities per node whereas in the simulation with fewer impurities the maximum grain size is still increasing at time step 7500.

FIGURE 6

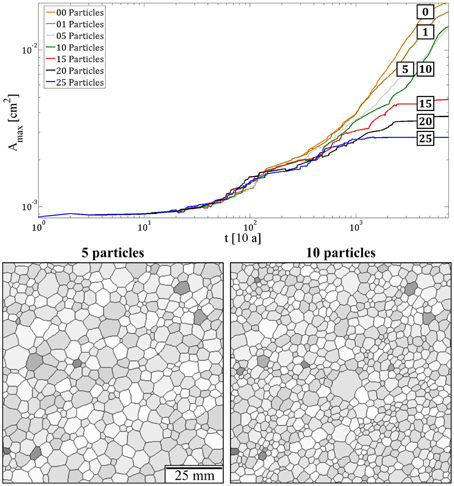
Figure 6. Top: Graph showing the evolution of the maximum grain size during simulations of 7500 time steps. Bottom: The grain size distribution for the case of 5 and the case for 10 impurities per point in the hexagonal grid.

Abnormal grain growth appeared during the simulation with a maximum of 10 impurities assigned to every node in the hexagonal grid (Figure 6). This process is likely to be caused by the redistribution of second-phase particles during grain growth in combination with a energetic advantageous orientation of the c-axis in the large grain compared to its adjacent neighboring crystals. The anhedral shape of the grain boundaries of the large grain leads to an additional driving force, which is probably the reason for the abnormal grain growth of those crystals.

The redistribution of second-phase particles during a simulation with exclusively mobile particles is shown in Figure 7. Every node in the hexagonal grid had either one or zero particles assigned to it and the distribution of the impurity radii is shown in Figure A4a. At the end of the simulation the highest particle densities occur on grain boundaries and especially at triple junctions. This is in good agreement with the simulations carried out by Shelton and Dunard [39] and with our observations on natural samples. In thin sections the grain boundaries in the fine grained layers of the zebra dolomite appear dark, which implies that the grain boundaries captured particles. This can be seen in Figure 7B where an electron-backscattered image of a fine grained band in between two coarse grained bands is shown. The second-phase particle distribution appears to be non-random, with highest particle densities in the fine grained layer and specifically along grain boundaries (Figure 7C). In accordance with the simulations the highest particle densities in the real samples occur at the triple junctions.

FIGURE 7

Figure 7. (A) Particle redistribution during the simulation of anisotropic grain growth shown in Figure 5. The left picture in (A) shows the initial impurity distribution and the right image shows the second-phase particle scatter after 10,000 time steps of the simulation. (B) Backscattered SEM image showing a fine grained layer in the center. The highest particle densities occur in the fine grained part which is indicated by the black line. (C) Combined backscattered and second-electron image showing the area indicated by the blue dotted line in (B). Larger second-phase particles are lined up along the grain boundary (black circles) and the highest density of impurities is visible at the triple junction.

3.4. Pattern Formation

To model the formation of the zebra texture we combined the simulation of the dolomitization and associated impurity redistribution with the simulation of grain growth influence by second-phase particle densities. The initial distribution of the impurities (Figure A4b) represents graded bedding with one sedimentary cycle consisting of 15 single layers with a change in the mean grain size of 0.05 μm from one to the subsequent layer (Figure 8). The reaction front moves from the bottom to the top of the simulation following a predefined pressure gradient and redistributes the impurities along its way.

FIGURE 8

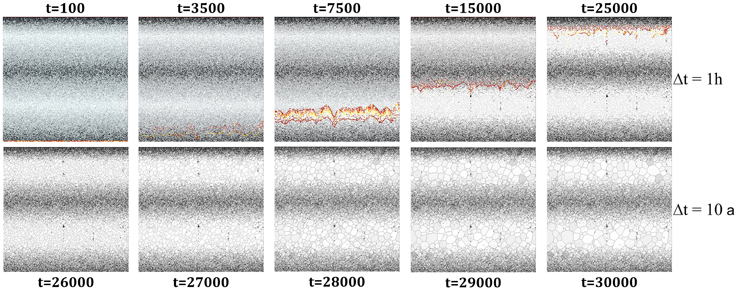
Figure 8. Simulation of the zebra pattern formation by combining the simulation of the dolomitization and the grain growth. Both simulated processes redistribute the initial impurity scatter. The bifurcation is achieved because the initial set graded bedding distribution of particle size is superimposed by the size-dependent shift of the reaction front. A secondary redistribution is then performed during the propagation of the grain boundaries.

The advancing reacting front collects the second-phase particles whereas the amount of particles depends on the radius of the impurities (Equation 3). The width of the front expands successively with time and the amount of particles collected by the front rapidly increases as soon as the front enters regions with smaller second-phase particle radii. Areas with larger particles sizes are not cleared as effective as areas with smaller particles sizes (Equation 3). The dolomitizing front leaves layers with high particle densities behind and releases impurities in small patches when the loading threshold of the front is exceeded (top of Figure 8). Since the amount of collected particles is related to the concentration change between two time steps (Equation 3) the loading process is also related to the development of fingers in the front so that the critical loading value is reached faster in regions between pronounced fingers (Figure 8).

Once the dolomitization front has passed through the sample the time scale is changed so that grain growth becomes active. Due to the layered distribution of second-phase particle densities, which were superimposed by the dolomitization front, high grain boundary migration rates only occur in regions with low impurity densities. This produces larger and potentially more isotropic grains, whereas areas with high particle densities only show minor grain growth. Because of the bifurcation of growth rates due to the impurity concentrations a pattern consisting of layers with a large, and layers with a smaller grain size develops. The grain growth process itself will then also account for the secondary redistribution of particle densities and leads to a secondary cleaning of the growing grains. As an additional result of the bifurcation of the growth rate, the larger grains in the low density second-phase areas are cleaned more effectively by the grain boundary migration as this process is much longer active in these grains than in the grains located in regions with high impurity densities. The stable grain size achieved in the light and dark layers is in good agreement with the natural samples (Figure 9). The grain sizes are found to vary between 80 and 150 μm in the dark and 0.5–5 mm in the light layers [12]. The crystals in the simulations have final grain sizes ranging from ≈ 200 μm in the impurity rich to 2 mm in the impurity free layers.

FIGURE 9

Figure 9. (A) Initial distribution of second-phase particles for the simulations in (B,C). (B) Result of a grain growth simulation without the redistribution performed by the reaction front after 3500 time steps. A stable grain size is reached and no pronounced banding is observable. (C) Result of s simulation of dolomitization followed by grain boundary migration after 30,000 time steps. The redistribution of the second-phase material leads to a bifurcation in grain growth rates and this causes banding. (D) Scan of a thin section. The area of the scan is equivalent to the area of the simulation. The location of the dark and light layers as well as the grain size differences are in good agreement with the result of the simulation shown in (B).

4. Discussion

A combination between second-phase particle redistribution by a replacement front and subsequent grain growth can generate patterns similar to zebra textures observed in natural samples. We therefore put forward a process of pattern formation based on the bifurcation of the overall grain boundary migration rate, where this dichotomy in grain boundary mobility is caused by a layered distribution of second-phase particle densities.

Our simulation of the calcite-dolomite replacement governed by a general transport equation can produce instabilities in the reaction front leading to fingering. This is due to the increasing porosity which accompanies the replacement process and can be compared to the general process of reactive infiltration instabilities [48]. Even though our simulation of the dolomitization is a simplified model of the natural process it is sufficient to simulate the impurity redistribution mechanism which we assume to be crucial for the textural evolution. The basis for the second-phase rearrangement is the crystal zoning model [3] combined with the theory of particle mobility during grain boundary migration [23]. We had to estimate the parameters for the impurity-loading process of the reaction front because the actual values have not yet been determined experimentally. We applied general laws for second-phase particle mobility during the replacement because we assumed that the process is similar to the shifting of particles during grain boundary migration. The mechanism which is of high importance for the pattern formation is the impurity size dependent shift as it superimposes the initial graded bedding distribution in our simulations. The size dependence of the impurity sweep can superimpose a graded bedding structure and build up a layered scatter of impurities. The particle collecting and precipitating reaction front will cleanse areas consisting of second-phase particles with a smaller grain size more efficiently. The resulting structure will consist of equidistant, almost particle free layers alternating with high particle density layers. Thus, the initial layering controls where the respective bands will be formed. We propose that this process produces a basic conditions for formation of banded structures in rocks.

We could further show that our model can reliably calculate grain boundary velocities in a system with mobile second-phase particles (Equation 14). Particle numbers and maximum grain size relationships (Equation 16) are in good agreement with the general theory of grain boundary motion in the presence of impurities [23, 25, 49]. Our simulation can show that during progressive grain boundary migration the impurities will line up along grain boundaries [38, 39, 49] and that surviving grains comprise of a core which is not affected by grain growth [50]. Both simulated processes comprise of some simplification but reflect the natural processes to the extent needed to show how a layered pattern can be generated by combining these two mechanisms.

Based on our simulations we can suggest a general hypothesis for the development of the initial zebra textures or the development of banded structures in crystalline materials. The crucial point in our theory is the development of an equidistant layered distribution of impurity densities. Without the redistribution of the initial impurity scatter by the reaction front no bifurcation in grain growth rates is observed (Figure 9). If the differences in second-phase particle radii and densities are high enough grain growth rate bifurcation might also be observable without the redistribution by the reaction front. However, the dolomitization front will always enhance the banding. Based on that we propose that the layered scatter of the second-phase can either evolve by superimposing a pre-existing structure (like a graded bedding distribution in our model), it could be generated out of an initially random distribution of particles which has been shown be the crystal zoning model developed by [3] or could even be solely of sedimentary origin. The model shown in this communication generates structures which are similar to the ones observed in the natural samples. Even on a microscale the simulations give results which are in good agreement with the samples. The noticeable high densities of opaque material along grain boundaries in the thin sections are also observable in our simulations and are generated by the mobility of the second-phase particles during grain growth. We can therefore conclude that the crucial parameters needed for zebra texture evolution are the initial porosity of the limestone, the saturation of the hydrothermal fluid with respect to dolomite and the porosity change associated with the calcite-dolomite replacement. We would like to point out that the actual redistribution process of second-phase material in our simulation is a strong simplification of the natural process. Pattern formation in natural materials, especially when it happens on a localized scale often involves self-organization [17, 18]. If the process of impurity redistribution as it is simulated in our model is active in every environment where an impurity rich limestone is replaced by dolomite, zebra textures would occur in much more regions than they actually do. Therefore, some critical parameters must be present which produce the layered distribution of second-phase material.

On the large scale these critical parameters could be related to the geometry of the specific tectonic environment and over-pressured fluid systems in which large hydrothermal Pb-Zn mineralization are formed, whereas on the small scale variations in porosity or impurity content could trigger banding or not.

Our model may represent the initial trigger of the pattern formation but can not explain all features, like the elongated shape of the light crystals and the sometimes observed macropores along the median line. It is conceivable, that after the formation of the two maximum grain sizes in our model another process might become active. The final pattern could be formed by one of the existing models (see Section 1). For instance, the grain coarsening could lead to a feedback with the fracturing as the yield stress will drop with increasing grain size leading to a late fracturing of median lines or preferred dissolution along them. The initial sedimentary bedding related anisotropy is in good agreement with the work of Morrow [14]. As suggested by Fontbote [7] a self-organization process is expected to be crucial for the pattern formation. However, whether hydrofracturing, focused dissolution or crystal growth accompanied by the displacement of the fine grained bands is the final stage of pattern formation cannot be said with certainty. Further research is needed to combine the model introduced in this work with either one of the pre-existing theories or with an additional process which has not yet been regarded.

Funding

This work has received funding from the European Union's Seventh Framework Programme for research, technological development and demonstration under grant agreement no 316889.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Peter Chung for the help with the SEM measurements and Piotr Szymczak for organizing the field trip to the Pb-Zn district in Poland. The comments of the two reviewers helped a lot to improve this paper in terms of accuracy and illustrative examples.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/article/10.3389/fphy.2015.00074

References

1. Loughnan FC, Roberts FI. Composition and origin of the ‘zebra rock’ from the East Kimberley region of Western Australia. Aust J Earth Sci. (1990) 37:201–5. doi: 10.1080/08120099008727920

CrossRef Full Text | Google Scholar

2. Strmić Palinkaš S, Spangenberg JE, Palinkaš LA. Organic and inorganic geochemistry of Ljubija siderite deposits, NW Bosnia and Herzegovina. Miner Deposita (2009) 44:893–913. doi: 10.1007/s00126-009-0249-z

CrossRef Full Text | Google Scholar

3. Krug HJ, Brandstädter H Jacob KH. Morphological instabilities in pattern formation by precipitation and crystallization processes. Int J Earth Sci. (1996) 85:19–28.

Google Scholar

4. Wallace MW, Both RA, Morales Ruano S Hach-Ali F, Lees T. Zebra textures from carbonate-hosted sulfide deposits; sheet cavity networks produced by fracture and solution enlargement. Econ Geol. (1994) 89:1183–91. doi: 10.2113/gsecongeo.89.5.1183

CrossRef Full Text | Google Scholar

5. Leach DL, Taylor RD, Fey DL, Diehl SF, Saltus RW. Chap. A of mineral deposit models for resource assesment, Scientific Investigation Report 2010-5070-A. In: A Deposit Model for Mississippi Valley-Type Lead-Zinc Ores. Reston, VA: U.S. Geological Survey (2010). p. 52.

Google Scholar

6. Fontboté L, Gorzawski H. Genesis of the Mississippi Valley-type Zn-Pb deposit of San Vicente, Central Peru: geologic and isotopic (Sr, O, C, S)evidence. Econ Geol. (1990) 85:1402–37. doi: 10.2113/gsecongeo.85.7.1402

CrossRef Full Text | Google Scholar

7. Fontboté L. Self-organization fabrics in carbonate-hosted ore deposits: the example of digenetic crystallization rhythmites (DCRs). In: Fenoll Hach-Ali P, Torres-Ruiz J, Gervilla F, editors. Current Research in Geology Applied to Ore Deposits, Proceedings of the Second Biennial SGA Meeting. Granada (1993). pp. 11–4. Available online at: http://archive-ouverte.unige.ch/unige:29376

8. López-Horgue MA, Iriarte E, Schröder S, Fernandéz-Mendiola PA, Caline B. An example on the tectonic origin of zebra dolomites: the San Martín beach outcrop (Santoña, North Spain). Geol Acta (2009) 47:85–8.

9. López-Horgue MA, Iriarte E, Schröder S, Fernandéz-Mendiola PA, Caline B, Corneyllie H, et al. Structurally controlled hydrothermal dolomites an Albian corbonates of the Asón valley, Basque Cantabrian Basin, Northern Spain. Mar Petrol Geol. (2010) 27:1069–92. doi: 10.1016/j.marpetgeo.2009.10.015

CrossRef Full Text

10. Merino E, Canals A, Fletcher RC. Genesis of self-organized zebra textures in burial dolostones: displacive veins, induced stress, and dolomitization. Geol Acta (2006) 4:383–93.

Google Scholar

11. Merino E, Canals A. Self-accelerating dolomite-for-calcite replacement: self-organized dynamics of burial dolomitization and associated mineralization. Am J Sci. (2011) 311:573–607. doi: 10.2475/07.2011.01

CrossRef Full Text | Google Scholar

12. Nielsen P, Swennen R, Muchez PH, Keppens E. Origin of Dinantian zebra dolomites south of the Brabant-Wales Massif, Belgium. Sedimentology (1998) 45:727–43. doi: 10.1046/j.1365-3091.1998.00171.x

CrossRef Full Text | Google Scholar

13. Swennen R, Vandegisnste V, Ellam E. Genesis of zebra dolomites (Cathedral Formation: Canadian Cordillera Fold and Thrust Belt, British Columbia. J Geochem Explor. (2003) 78–9:571–7. doi: 10.1016/S0375-6742(03)00065-7

CrossRef Full Text | Google Scholar

14. Morrow DW. Zebra and boxwork fabrics in hydrothermal dolomites of northern Canada: indicators for dilational fracturing, dissolution or in situ replacement? Sedimentology (2014) 61:915–51. doi: 10.1111/sed.12094

CrossRef Full Text | Google Scholar

15. Vandeginste V, Swennen R, Gleeson SA, Ellam RM, Osadetz K, Roure F. Zebra dolomitization as a result of focused fluid flow in the Rocky Mountains Fold and Thrust Belt, Canada. Sedimentology (2005) 52:1067–95. doi: 10.1111/j.1365-3091.2005.00724.x

CrossRef Full Text | Google Scholar

16. Cartwright JHE, Garca-Ruiz JM, Villacampa AI. Pattern formation in crystal growth: Liesegang rings. Comput Phys Commun. (1999) 121–2:411–3. doi: 10.1016/S0010-4655(99)00370-7

CrossRef Full Text | Google Scholar

17. Ortoleva P. Macroscopic self organization at geological and other first order phase transitions. In: Vidal C, Pacault A, editors. Non-Equilibrium Dynamics in Chemical Systems - Proceedings of the International Symposium. Bordeaux (1984). doi: 10.1007/978-3-642-70196-2_14

CrossRef Full Text | Google Scholar

18. Ortoleva P, Merino E, Moore C, Chadam J. Geochemical self-organization I: reaction-transport feedbacks and modeling approach. Am J Sci. (1987) 287:979–1007. doi: 10.2475/ajs.287.10.979

CrossRef Full Text | Google Scholar

19. Karsenti E. Self-organization in cell biology: a brief history. Nat Rev Mol Cell Biol. (2008) 9:255–62. doi: 10.1038/nrm2357

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Taylor AF, Tinsley MR. Chemical self-organization: a path to patterns. Nat Chem. (2009) 1:340–1. doi: 10.1038/nchem.310

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Parteli EJR, da Silva LR, Andrade Jr JS. Self-organized percolation in multi-layered structures. J Stat Mech. (2010) 2010:p03026. doi: 10.1088/1742-5468/2010/03/p03026

CrossRef Full Text | Google Scholar

22. Machel HG. Concepts and models of dolomitization: a critical reappraisal. Geol Soc Lond Spec Pub. (2004) 235:7–63. doi: 10.1144/GSL.SP.2004.235.01.02

CrossRef Full Text | Google Scholar

23. Gottstein G, Shvindlerman LS. Theory of grain boundary motion in the presence of mobile particles. Acta Metall Mater. (1993) 41:3267–75. doi: 10.1016/0956-7151(93)90056-X

CrossRef Full Text | Google Scholar

24. Davis NE, Newman J, Wheelock PB, Kronenberg AK. Grain growth kinetics of dolomite, magnesite and calcite: a comparative study. Phys Chem Miner. (2011) 38:123–38. doi: 10.1007/s00269-010-0389-9

CrossRef Full Text | Google Scholar

25. Evans B, Renner J, Hirth G. A few remarks on the kinetics of static grain growth in rocks. Int J Earth Sci. (2001) 90:88–103. doi: 10.1007/s005310000150

CrossRef Full Text | Google Scholar

26. Urai JL, Means WD, Lister GS. Dynamic recrystallization of minerals. In: Hobbs BE, Heard HC, editors. Mineral and Rock Deformation: Laboratory Studies: The Paterson Volume. American Geophysical Union (1986). pp. 161–200. doi: 10.1029/GM036p0161

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Bons PD, Jessell MW, Evans L, Barr T, Stüwe K. Modelling of anisotropic grain growth in minerals. In: Tectonic Modeling: A Volume in Honor of Hans Ramberg. Vol. 193. Geological Society of America Memoirs (2000). pp. 1–11.

28. Lasaga AC. Kinetic Theory in the Earth Sciences. Princeton: Princeton University press (1998). doi: 10.1515/9781400864874

CrossRef Full Text | Google Scholar

29. Koehn D, Arnold J, Jamtveit B, Malthe-Sørenssen A. Instabilities in stress corrosion and the transition to brittle failure. Am J Sci. (2003) 303:956–71. doi: 10.2475/ajs.303.10.956

CrossRef Full Text | Google Scholar

30. Koehn D, Renard F, Toussaint R, Passchier CW. Growth of stylolite teeth patterns depending on normal stress and finite compaction. Earth Planet Sci Lett. (2007) 257:582–95. doi: 10.1016/j.epsl.2007.03.015

CrossRef Full Text | Google Scholar

31. Bons PD, Jessell MW, Becker J. Grain boundary migration. In: Bons PD, Koehn D, Jessell M, editors. Microdynamics Simulation. Berlin; Heidelberg: Springer (2008). pp. 115–26. doi: 10.1007/978-3-540-44793-1

CrossRef Full Text

32. Hwang NM. Simulation of the effect of anisotropic grain boundary mobility and energy on abnormal grain growth. J Mater Sci. (1998) 33:5625–9. doi: 10.1023/A:1004472400615

CrossRef Full Text | Google Scholar

33. Freund D, Rybacki E, Dresen G. Effect of impurities on grain growth in synthetic calcite aggregates. Phys Chem Miner. (2001) 28:737–45. doi: 10.1007/s002690100196

CrossRef Full Text | Google Scholar

34. Mas DL, Crowley PD. The effect of second-phase particles on stable grain size in regionally metamorphosed polyphase calcite marbles. J Metamorph Geol. (1996) 14:155–62. doi: 10.1046/j.1525-1314.1996.05805.x

CrossRef Full Text | Google Scholar

35. Olgaard DL, Evans B. Effect of second-phase particles on grain growth in calcite. J Am Ceram Soc. (1986) 69:C-272–7.

Google Scholar

36. Nes E, Ryum N, Hunderi O. On the Zener drag. Acta Metall. (1985) 33:11–22. doi: 10.1016/0001-6160(85)90214-7

CrossRef Full Text | Google Scholar

37. Brimhall JL, Klein MJ, Huggins RA. Influence of a finely dispersed second phase on recrystallization. Acta Metall. (1966) 14:459–66. doi: 10.1016/0001-6160(66)90313-0

CrossRef Full Text | Google Scholar

38. Harun A, Holm EA, Clode MP, Miodownik MA. On computer simulation methods to model Zener pinning. Acta Mater. (2006) 54:3261–73. doi: 10.1016/j.actamat.2006.03.012

CrossRef Full Text | Google Scholar

39. Shelton RK, Dunard DC. Computer modeling of particle pushing and clustering during matrix crystallization. Acta Mater. (1996) 44:4571–85. doi: 10.1016/1359-6454(96)00082-1

CrossRef Full Text | Google Scholar

40. Urai JL, Jessell M. Recrystallization and grain growth in minerals: recent developments. In: Gottstein G, Molodov D, editors. Recrystallization and Grain Growth, Proceedings of the first Joint International Conference, RWTH Aachen. Aachen: Springer Verlag (2001). pp. 87–96.

41. Weygand D, Bréchet Y, Lépinoux J. Inhibition of grain growth by particle distribution: effect of spatial heterogeneities and of particle strength dispersion. Mater Sci Eng A (2000) 292:34–9. doi: 10.1016/S0921-5093(00)00990-4

CrossRef Full Text | Google Scholar

42. Warren J. Dolomite: occurrence, evolution and economically important associations. Earth Sci Rev. (2000) 52:1–81. doi: 10.1016/S0012-8252(00)00022-2

CrossRef Full Text | Google Scholar

43. Spangenberg JE, Macko SA. Organic geochemistry of the San Vicente zinclead district, eastern Pucará Basin, Peru. Chem Geol. (1998) 146:1–23. doi: 10.1016/S0009-2541(97)00158-7

CrossRef Full Text | Google Scholar

44. Spangenberg JE, Fontboté L, Macko SA. An evaluation of the inorganic and organic geochemistry of the San Vicente mississippi valley-type zinc-lead district, central Peru; implications for ore fluid composition, mixing processes, and sulfate reduction. Econ Geol. (1999) 94:1067–92. doi: 10.2113/gsecongeo.94.7.1067

CrossRef Full Text | Google Scholar

45. Gautelier M, Oelkers EH, Schott J. An experimental study of dolomite dissolution rates as a function of pH from -0.5 to 5 and temperature from 25 to 80°C. Chem Geol. (1999) 157:13–26. doi: 10.1016/S0009-2541(98)00193-4

CrossRef Full Text | Google Scholar

46. Clark SPJ. Handbook of Physical Constants. New York, NY: Geological Society of America (1966).

Google Scholar

47. Austen KF, Wrigth K, Slater B, Gale JD. The interaction of dolomite surfaces with metal impurities: a computer simulation study. Phys Chem Chem Phys. (2005) 7:4150–6. doi: 10.1039/b510454h

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Chadam J, Hoff D, Merino E, Ortoleva P, Sen A. Reactive infiltration instabilities. J Appl Math. (1986) 36:207–21. doi: 10.1093/imamat/36.3.207

CrossRef Full Text | Google Scholar

49. Moelans N, Blanpain B, Wollants P. Phase field simulations of grain growth in two-dimensional systems containing finely dispersed second-phase particles. Acta Mater. (2006) 54:1175–88. doi: 10.1016/j.actamat.2005.10.045

CrossRef Full Text | Google Scholar

50. Jessell MW, Kostenko O, Jamtveit B. The preservation potential of microstructures during static grain growth. J Metamorph Geol. (2003) 21:481–91. doi: 10.1046/j.1525-1314.2003.00455.x

CrossRef Full Text | Google Scholar

List of Symbols