Fermion unification model based on the intrinsic SU(8) symmetry of a generalized Dirac equation

A natural generalization of the original Dirac spinor into a multi-component spinor is achieved, which corresponds to the single lepton and the three quarks of the first family of the standard model of elementary particle physics. Different fermions result from similarity transformations of the Dirac equation, but apparently there can be no more fermions according to the maximal multiplicity revealed in this study. Rotations in the fermion state space are achieved by the unitary generators of the U(1) and the SU(3) groups, corresponding to quantum electrodynamics (QED based on electric charge) and chromodynamics (QCD based on color charge). In addition to hypercharge the dual degree of freedom of hyperspin emerges, which occurs due to the duplicity implied by the two related (Weyl and Dirac) representations of the Dirac equation. This yields the SU(2) symmetry of the weak interaction, which can be married to U(1) to generate the unified electroweak interaction as in the standard model. Therefore, the symmetry group encompassing all the three groups mentioned above is SU(8), which can accommodate and unify the observed eight basic stable fermions.

1. Introduction

In the prevailing standard model (SM) of elementary particle physics (see e.g., the modern textbook by Schwartz [1] or the earlier one by Kaku [2]) the various fermions involved (one lepton doublet and three quark doublets, respectively coming in three generations) are assumed to be massless. This notion is in contradiction to the observations but enforced on the SM by the assumption that chiral symmetry is broken. The fermions then acquire mass subsequently through the Higgs mechanism [3, 4], in which the main effect is to give the vector gauge bosons of the weak interactions mass, but which in addition can also make the fermions massive by help of the Yukawa coupling terms [1]. The Dirac equation [5] in its standard form is fundamental in all of this and thought to be well understood. Thus, the massless fermions of the SM are commonly described in the Weyl representation [6, 7], which involves only the two-component spinors associated with the Pauli spin matrices [8]. Still it remains unclear whether the neutrinos [9, 10] are Dirac or Majorana fermions.

However, the assumption of massless fermions appears not to be acceptable any more, in particular when facing the ample empirical evidence [11] corroborating that even neutrinos have small but non-zero masses. They are revealed by and consistent with the neutrino oscillations [12] which have clearly been observed in the last two decades. As a consequence, massive neutrinos have to be considered [13]. In order to explain their masses the see-saw mechanism [12] was invented, which is not compatible with the SM by involving Majorana mass terms [14–17]. Clearly, any realistic extension of the standard model (SM) will have to consider finite fermion masses at the start, an assumption which causes yet serious conflict with the broken chiral symmetry (and the gauge fixation) that is seen as the essence of weak interactions. To remedy these problems one may require substantial revision of the SM.

Here we make a first step in revisiting thoroughly the Dirac equation assuming that the mass term is given in the Dirac equation to highlight its intrinsic symmetry properties. We show that the Dirac equation for a massive and charged fermion has a rich hidden intrinsic symmetry that has long been overlooked theoretically, but in practice already emerged through experimental evidence and was included in the SM in the guise of the various SU(N) (with N = 1, 2, 3) external symmetry groups by which the different massless fermion are assembled in multiplets. We shall reconsider the Dirac equation for a massive fermion and scrutinize its intrinsic (not space-time related) hidden symmetry, together with the resulting symmetry groups. A corresponding generalization of the original Dirac spinor into an internal multi-component spinor associated with the SU(8) symmetry group is achieved, which includes the single lepton and the three quarks [18] of the first family of the SM of elementary particle physics in a natural way.

The various known stable and fundamental fermions come empirically in the one electron-neutrino doublet and three colored up- and down-quark doublets. It will be shown that these different fermions do all result from similarity transformations of the Dirac equation, but apparently there can be no more fermions according to the maximal multiplicity revealed in this study. The corresponding rotations in the fermion state space are achieved by the unitary generators of the U(1) and the SU(3) groups, corresponding to quantum electrodynamics (QED based on electric charge) and chromodynamics (QCD based on color charge). In addition to hypercharge, the dual degree of freedom of hyperspin emerges from the consideration of the duplicity implied by the two related (Weyl and Dirac) representations of the Dirac equation. This yields naturally the SU(2) symmetry of the weak interaction, which can then be married to U(1) to generate the unified electroweak interaction as in the standard model. The resulting number of basic fermions and the dimension of their state space as considered here originate solely from intrinsic symmetry and appear to be complete. Therefore, the apt symmetry group encompassing the three above mentioned groups would be SU(8), which can accommodate and thus unify all observed massive fermions.

2. Mass Shell Condition and Pauli Matrices

Why do the Pauli matrices occur in the Dirac equation? Their key property is that they permit to linearize the kinetic energy term that goes with the momentum squared in the relativistic (and also non-relativistic) dispersion relation of a particle, which is given by

$\begin{array}{ll}{E}^2-{\mathbf{\text{p}}}^2=m^2=P^{\mu }{P}_{\mu },& (1)\end{array}$

stating the mass shell condition for a free particle. The relativistic covariant four-momentum operator is associated with the temporal or spatial derivative as P_μ = (E, − p) = i∂_μ = i(∂ ∕ ∂t, ∂ ∕ ∂x). Using the generators of three-dimensional rotations we can formally take the square root of the momentum term. In terms of Pauli matrices [8] we obtain

$\begin{array}{ll}{(\mathbf{\sigma }·\mathbf{\text{p}})}^2={\mathbf{\text{p}}}^2{1}_2.& (2)\end{array}$

The symbol 1₂ denotes the 2 × 2 unit matrix, and σ_x, σ_y, and σ_z are the Pauli spin matrices:

$\begin{array}{ll}{\sigma }_x=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),{\sigma }_y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),{\sigma }_z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)& (3)\end{array}$

satisfying the relation:

$\begin{array}{ll}{\sigma }_i{\sigma }_j+{\sigma }_j{\sigma }_i=2{\delta }_{ij}{1}_2.& (4)\end{array}$

This is how spin emerges in normal quantum mechanics, namely via the spinor representation of the rotation group! To most people this appears to be well known, yet in the literature and even in textbooks the fermion spin often is still associated with relativity, a notion that is obviously not correct. Coming then to Lorentz invariance, the task appears to linearize the mass shell condition. Dirac [5] solved this problem by introducing his famous 4 × 4 matrices. Let us now reconsider them and for that purpose introduce generally the kinetic helicity operator as

$\begin{array}{ll}H(\mathbf{\text{p}})=\mathbf{\sigma }·\mathbf{\text{p}}.& (5)\end{array}$

For algebraic simplicity we will in the following calculation omit the argument of H and just use it without annotation if no confusion can arise. The mass shell condition can now be written simply as

$\begin{array}{ll}{E}^2-H^2=m^2={(\beta E+\gamma H)}^2,& (6)\end{array}$

where we introduced two new, genuinely relativistic operators β and γ. Multiplying the above equation out we obtain the algebraic requirements that

$\begin{array}{ll}{\beta }^2=1;{\gamma }^2=-1;\beta \gamma +\gamma \beta =0.& (7)\end{array}$

Like with the Pauli matrices as the SU(2) generators, these requirements cannot be satisfied with pure numbers but in explicit representation require to invoke matrices that should be real by the following argument. The quantum mechanical four-vector operator P^μ = i∂^μ is purely imaginary, and the spin operator is complex (σ_y is purely imaginary). Introducing complex matrices for β or γ would lead to confusion of relativity with quantum mechanics. Note that when decomposing the left-hand side of Equation (6) such that it appears as a squared number on the right-hide side, then for consistency the square of γ must be negative. Thus, γ is playing the role of the imaginary unit. Furthermore, the algebra of β and γ is not closed but requires another member which naturally is obtained as α = βγ and thus anticommutes with the two operators defining it. Also, by its definition we obtain the results α² = 1 and that αβγ = 1. To avoid confusion and to simplify notation we mention explicitly that we use the same symbols for the operators and their respective matrix representations.

Consequently, in terms of 2 × 2 matrices we only have two reasonable options for β and γ, and thus α. The matrices chosen in the Weyl representation are taken as our standard and defined as

$\begin{array}{ll}\alpha =\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right),\beta =\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),\gamma =\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right).& (8)\end{array}$

Note that α and β are connected by the similarity transformation that is enabled by the unitary operator $U(\gamma )=\frac{1}{\sqrt{2}}(1-\gamma )$, which obeys U^† = U^T = U⁻¹. Then α = UβU⁻¹, and of course U commutes with γ. Therefore, we can use either the standard Dirac or the chiral Weyl representation, for which the gamma matrices as defined as 4 × 4 matrices as follows:

$\begin{array}{ll}{\gamma }_W^{\mu }=(\beta 1_2,\gamma \mathbf{\sigma }),& (9)\end{array}$

$\begin{array}{ll}{\gamma }_D^{\mu }=(-\alpha 1_2,\gamma \mathbf{\sigma }).& (10)\end{array}$

Note that in both γ appears at the spin (defining kinetic helicity) term. One also obtains ${\gamma }_W^{\mu }=U{\gamma }_D^{\mu }{U}^{-1}$, a relation that is well known in the literature.

Now, we can also reconsider the so-called chiral (matrix) operator defined as ${\gamma }^5=i{\gamma }_0{\gamma }_x{\gamma }_y{\gamma }_z$ in any representation. Using the fact that σ_xσ_yσ_z = i1₂, it takes in Weyl representation the form:

$\begin{array}{ll}{\gamma }_W^5=-\beta {\gamma }^3{1}_2=\alpha 1_2,& (11)\end{array}$

and obeys ${({\gamma }^5)}^2=1_4$, where 1₄ stands for the 4 × 4 unit matrix. Similarly, we obtain

$\begin{array}{ll}{\gamma }_D^5=-\alpha {\gamma }^3{1}_2=\beta 1_2.& (12)\end{array}$

By use of γ⁵, appropriate projection operators can be defined as $P_{R,L}=\frac{1}{2}(1_4\pm {\gamma }^5)$, which are idempotent and represent a decomposition of the identity operator. We obtain in the Weyl representation:

$\begin{array}{ll}{P}_{R,L}=\frac{1}{2}(1_2\pm \alpha )1_2& (13)\end{array}$

With their help, any spinor field can be decomposed into its right- and left-chiral component, which means we have ψ = P_R ψ + P_L ψ = ψ_R + ψ_L. Left and right chiral projections are at the heart of symmetry breaking and essential for the weak interactions as considered in the SM. By its definition, γ⁵ anticommutes with all gamma matrices, which means {γ⁵, γ^μ} = 0, where the curly brackets denote the anticommutator. Consequently, we obtain ${\gamma }^{\mu }{P}_{R,L}=P_{L,R}{\gamma }^{\mu }$. Moreover, the operation with γ⁵ on the Dirac equation flips the sign of mass. This property of chirality (symmetry operation based on γ⁵) will become important in the subsequent section.

3. The Intrinsic Symmetries

3.1. Space-time Symmetry

The main purpose of this section is to discuss the hidden intrinsic symmetries of Dirac's equation, which was revisited in the previous section in order to provide the necessary material for the subsequent derivations. Before we present them let us for completeness also briefly review the external space-time symmetries, with emphasis on chirality. Time inversion of a scalar field is defined as 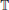ϕ(t) = ϕ(−t) and space inversion alike as ℙϕ(x) = ϕ(−x). Close inspection of the Dirac equation in Weyl representation, when being written out (we omit the unit matrix at the time derivative to ease the notation) explicitly as

$\begin{array}{ll}i\left(\beta \frac{\partial }{\partial t}+\gamma \mathbf{\sigma }·\frac{\partial }{\partial \mathbf{\text{x}}}\right)\psi =m\psi ,& (14)\end{array}$

shows that the temporal and spatial terms in Equation (14) are invariant under the time-reversal and parity operators if they are defined as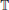 ${T}$ = τ and ${P}$ = βℙ. Furthermore, the kinetic helicity term remains invariant under the operation of ${C}$ = γτ. Here we introduced the spin flip operator τ that is defined as τ = −iσ_y ℂ, and ℂ denotes the complex conjugation operator that transmutes a complex number z into its conjugate z*. This operator turned out to be convenient when treating the complex two-component Majorana equation [17]. It is anti-unitary, obeys τ^† = −τ = τ⁻¹ and τ² = −1 and anticommutes with all Pauli matrices,

$\begin{array}{ll}\left\{\tau ,\mathbf{\sigma }\right\}=\mathbf{0},& (15)\end{array}$

which means τ flips the spin by changing the sign of σ from plus to minus when being commuted with it. So what ${C}$ does is to change the sign of the imaginary unit, but more essentially it reverses the spin and also changes the sign of the charge (coupling constant) in the covariant derivate which means ${C}$D_μ(q) = D_μ(−q)${C}$. Therefore, traditionally [2] this operator was named charge conjugation which transforms ψ into ${\psi }^{{C}}={C}\psi =-i{\gamma }_y{\psi }^{*}$, where the asterisk means complex conjugation and the phase factor in front is apt convention. If we now multiply the three symmetry operators we get ${C}$${P}$${T}$ = γτ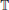βℙτ = αℙ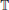, which is the usual CPT operation [1] under which all bilinear forms of the Dirac equation are invariant.

Finally there is another important symmetry operator which reverses the sign of the mass. We name this new symmetry operator as ${M}$ = α1₂ (here in the Weyl representation) the mass conjugation. We emphasize that ${M}$ is based on the operation of chirality as introduced in Equations (11) and (12). Written in terms of Dirac matrices this transformation corresponds to ψ^${M}$ = ${M}$ψ = γ⁵ψ. To our best knowledge mass sign-reversal or conjugation has not been considered before in the discussion of the space-time symmetries of Dirac's equation. However, it turns out to be important to permit formally negative masses. Consequently, we extend the CPT invariance to include ${M}$ such that ${M}$${C}$${P}$${T}$ = α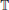γτβℙτ = ℙ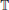 is obtained, which is the pure space time symmetry of the Klein-Gordon [19, 20] equation,

$\begin{array}{ll}\left(\frac{{\partial }^2}{\partial t^2}-\frac{{\partial }^2}{\partial {\text{x}}^2}+m^2\right)\varphi =0.& (16)\end{array}$

It does not depend on the sign of the mass, since it was obtained from the quadratic mass shell condition (Equation 1). Its space-time and related symmetries including an electromagnetic field are composed in Table 1.

TABLE 1

Table 1. Symmetry operations.

With this table we conclude the discussion of the known external or space time symmetry of the Dirac equation, and turn to its intrinsic symmetry which is the key theme of this paper and related to various possible representations.

3.2. Combinatorial Symmetry Yielding Quarks

As we already stressed in connection with the discussion of the chirality or mass reversal ${M}$, there are formally many possible choices of the signs at the three basic components of the Dirac equation. We refer to the mass shell condition (Equation 6) written in terms of the normal quantum mechanical operators of energy E and of kinetic helicity H given by Equation (5), and the genuine relativistic operators β and γ. At the mass term we have the trivial unity operator. When linearizing (taking the “square root” so to speak) we obtain 2³ = 8 possible sign combinations. In the standard Dirac equation only one of them is considered, namely all terms are conventionally assumed to have a positive sign. Out of the eight options in total, four are redundant because they correspond to a simple multiplication of the whole operator equation by a minus sign. The following four decompositions still remain:

$\begin{array}{ll}\begin{array}{c}-\beta E-\gamma H=m\\ +\beta E-\gamma H=m\\ -\beta E+\gamma H=m\\ +\beta E+\gamma H=m\end{array}& (17)\end{array}$

Note that according to Equations (5) and (8) these four equations are of course 4 × 4 matrix equations. Here we have chosen the four options with a positive sign at the mass, the other four with a negative sign at the mass produce merely redundant duplications. Only the bottom equation was chosen by Dirac, the others were not considered. However, they should not be disregarded because they have an equivalent physical meaning and represent three more independent fermionic degrees of freedom! They were simply overlooked but should be treated as equivalent to Dirac's choice. There seems to remain another ambiguity, the sign of γ. We could also have defined it by its transposed matrix to start with. However, as inspection of Equation (17) shows, the system is unaffected by reversing the sign of γ.

In bold conclusion, the full linearization of Equation (6) produces not one but four independent fermions, and only just four and not more, because of the combinatorial possibilities remaining when removing the redundancy in the different “roots” of the mass shell condition.

Letting the above operator equations then act on spinor fields produces four Dirac-type equations, the bottom one in Equation (17) giving the standard Dirac equation (Equation 14) of the literature. For the sake of clarity we write the four versions explicitly

$\begin{array}{ll}\begin{array}{c}(-\beta E-\gamma H){\psi }_{\alpha }=m{\psi }_{\alpha }\\ (+\beta E-\gamma H){\psi }_{\beta }=m{\psi }_{\beta }\\ (-\beta E+\gamma H){\psi }_{\gamma }=m{\psi }_{\gamma }\\ (+\beta E+\gamma H)\psi =m\psi \end{array}& (18)\end{array}$

Mathematically speaking, the bottom equation already yields all the solutions that exist to the well known standard Dirac equation, which describes a Dirac spinor field containing particles and antiparticles, both having two opposite kinetic helicity states. Operating, respectively, from the top with α, β, and γ on the other three equations shows that their spinors are related: ψ = αψ_α = βψ_β = γψ_γ. Note that the chiral symmetry is not broken, since the effects of the operator α is accounted for. So all four solutions describe fermions having the same mass. These particles have already been detected experimentally. The last is the electron, and the other three are the quarks, which as shown here all are the natural outcome of Dirac's equation when the combinatorial symmetry is taken seriously. Also, there are exactly four fermions obtained in this way, a lepton and three quarks (following the established nomenclature, although the name assignments are at this point still arbitrary) as indicated by the indices α, β and γ, which signify their connection with the standard Dirac equation.

Clearly, the lepton state space is one-dimensional and associated with the U(1) symmetry group, whereas the quark state space is three-dimensional and thus genuinely related with the SU(3) group describing mixing among the quark color states themselves. The fundamental gauge-field theory for each fermion is quantum hypercharge dynamics (QYD) coupling to their hypercharges with generators Y_α, Y_β, Y_γ, and Y. They are all represented by the unit operator (matrix) multiplied by their individual hypercharges y_α, y_β, y_γ, and y, respectively for the three quarks and the lepton, and measured in units of the elementary electric charge e. For a detailed discussion of hypercharges in the SM see for example, the Tables 29.1, 30.1 in the modern textbook of Schwartz [1].

When considering each fermion on its own, for example the lepton, we may choose its hypercharge to be either y = 1 or y = −1, but apparently SU(4) group theory prefers −1. The opposite charge is implied respectively for the antiparticle by the charge conjugation symmetry of Dirac's equation. However, since there is equality among the leptons and quarks, according to their individual Dirac equations and as seen from their hypercharge gauge-field theory QYD, these four fermions are allowed to mix among themselves. The corresponding unifying symmetry group is SU(4) [2, 21], which is unitary and four-dimensional in its fundamental representation. Thus, we can define a related hypercharge operator Y₄ as a purely diagonal 4 × 4 matrix, which has the y_α, y_β, y_γ and y on its trace, and can conveniently be written as Y₄ = diag{y_α, y_β, y_γ, y} with the lepton at the end. Since all fifteen generators of the SU(4) are given by traceless matrices, each nontrivial operator that does not involve the unit matrix 1₄ must also be represented by a traceless matrix, while being a linear combination of these generators. In fact Y₄ can be directly chosen as being proportional to the generator λ₁₅ [21]. Thus, we obtain $Y_4=diag\left\{\frac{1}{3},\frac{1}{3},\frac{1}{3},-1\right\}$. Consequently, the trace of Y₄ must vanish, yielding the group-theoretical requirement that

$\begin{array}{ll}{y}_{\alpha }+y_{\beta }+y_{\gamma }+y=0.& (19)\end{array}$

Conventionally, also suggested by the SU(4) group theory, we choose y = −1 for the electron, and therefore the quark hypercharges must sum up to +1. As there is equality [imposed by SU(4)] among the quarks, their hypercharges must be the same, $y_{\alpha }=y_{\beta }=y_{\gamma }=\frac{1}{3}$. The fractional charges simply reflect that there are three quarks and the dimension of their subspace is 3, associated with SU(3) in its fundamental representation. This quantization of charges, which in U(1) could still be continuous, emerges solely from the intrinsic symmetry of the Dirac equation, and appears to be fundamental and does not require to consider the various SM anomalies [1], which are usually exploited to corroborate the assignments of fermion hypercharges. When assembling the four fermion species into a large spinor ${\text{Ψ}}^{†}=({\psi }_{\alpha }^{†},{\psi }_{\beta }^{†},{\psi }_{\gamma }^{†},{\psi }^{†})$, we can write the combined Dirac equation concisely as

$\begin{array}{ll}i\left(\tilde{\beta }\frac{\partial }{\partial t}+\tilde{\gamma }\mathbf{\sigma }·\frac{\partial }{\partial \mathbf{\text{x}}}\right)\text{Ψ}=m\text{Ψ},& (20)\end{array}$

where the beta matrix is diagonal in the large spinor space, $\tilde{\beta }=diag\left\{-\beta ,\beta ,-\beta ,\beta \right\}$ and the gamma matrix alike, $\tilde{\gamma }=diag\left\{-\gamma ,-\gamma ,\gamma ,\gamma \right\}$. Multiplication of Equation (20) by the diagonal matrix Ũ = diag{α, β, γ, 1}, transmutes all negative signs in $\tilde{\beta }$ and $\tilde{\gamma }$ into positive ones, and the spinor components of Ψ into standard Dirac spinors. Writing the large spinor as a quadruplet, with the first three indices referring to the quarks and the last one to the lepton, we obtain the Dirac equation in the standard form,

$\begin{array}{ll}i{\gamma }^{\mu }{\partial }_{\mu }\text{Ψ}=m\text{Ψ},& (21)\end{array}$

yet for the full fermion quadruplet which now has a convenient form to be used in connection with the Yang-Mills theory [1, 2, 22]. Given the number of four fermion degrees of freedom, we conclude that the SU(4) symmetry group unifies leptons and quarks.

3.3. Representation Symmetry Yielding Hyperspin Doublets

In spite of the revelation of the intrinsic SU(3) symmetry of quarks in the Dirac equation and the SU(4) symmetry unifying lepton and quarks, we have not yet exhausted all possibilities. We recall the two versions of the Dirac gamma matrices in Equations (9) and (10), referred to as the Weyl and Dirac representations. Why does this duality exist? Following the reasoning of the previous section, there must be a physical meaning to this fact, which has its origin in the two choices of α and β for the relativistic, real matrix operators appearing at the energy E in Equation (6). In contrast, the antisymmetric real matrix operator γ appearing at the kinetic helicity H is the same in the both representations. Facing this puzzling duplication of the Dirac equation, again the logical consequence should be that this duality indicates two intrinsic degrees of freedom. Thus, there must be yet another set of lepton and three quarks, which come in doublets related to this representation duality. We may call this double degree of freedom appropriately hyperspin, as its symmetry group is SU(2). Let us scrutinize this notion. We can write

$\begin{array}{ll}i\left(\beta \frac{\partial }{\partial t}+\gamma \mathbf{\sigma }·\frac{\partial }{\partial \mathbf{\text{x}}}\right){\text{Ψ}}_W=m{\text{Ψ}}_W,& (22)\end{array}$

$\begin{array}{ll}i\left(-\alpha \frac{\partial }{\partial t}+\gamma \mathbf{\sigma }·\frac{\partial }{\partial \mathbf{\text{x}}}\right){\text{Ψ}}_D=m{\text{Ψ}}_D,& (23)\end{array}$

and combine the two large spinors into a doublet ${\widehat{\text{Ψ}}}^{†}=({\text{Ψ}}_W^{†},{\text{Ψ}}_D^{†})$. We recall that α and β are related by the similarity transformation α = UβU⁻¹, where $U(\gamma )=\frac{1}{\sqrt{2}}(1-\gamma )$, and therefore, like in the previous section, we can write in the Weyl representation after Equation (9) the grand-multiplet Dirac equation finally as

$\begin{array}{ll}i{\gamma }^{\mu }{\partial }_{\mu }\widehat{\text{Ψ}}=m\widehat{\text{Ψ}},& (24)\end{array}$

since U(−α)U⁻¹ = β. Here the doublet spinor is ${\widehat{\text{Ψ}}}^{†}=\left({\text{Ψ}}^{†},{\left(\frac{1}{\sqrt{2}}(1-\gamma )\text{Ψ}\right)}^{†}\right)$, and we can choose without loss of generality Ψ = Ψ_W. The upper component in the hyperspin doublet by construction encompasses a lepton and three quarks, and the lower component alike, with the previously assigned hypercharges −1 and $\frac{1}{3}$. Apparently, the symmetry group for the doublets is SU(2) which has three generators.

The overarching symmetry group is then SU(8) which corresponds to the eight independent fermion degrees of freedom. We identified SU(8) from inspecting the representation multiplicity of the Dirac equation. In conclusion, grand unification, originally proposed by Pati and Salam as a combination of SU(4) with SU(2) [23] or by Georgi and Glashow as SU(5) [24], is suggested to be governed by SU(8) which turns out to be the natural unitary transformation leading to mixing of all eight different fermions.

Returning to the standard Dirac equation for a moment, we could have, by use of P_μ = (E, −p_x, −p_y, −p_z), linearized the mass shell condition generally in the following way:

$\begin{array}{ll}(\pm {\gamma }_0)E+(\pm {\gamma }_x)p_x+(\pm {\gamma }_y)p_y+(\pm {\gamma }_z)p_z=\pm m.& (25)\end{array}$

Following our previous reasoning, we obtain 2⁵ = 32 combinations of the possible plus and minus signs in front of the gammas and the mass term, at which we can select the positive sign, since the minus leads to redundant duplication. Thus, we are left with 16 intrinsic independent degrees of freedom. This number corresponds to the four fermions, one lepton and three quarks, each of them having four degrees of freedom in terms of particle and antiparticle with two spin orientations or kinetic helicity states. Yet there is in principle a multitude of possible similarity transformations, such as the one leading to the Majorana representation [2, 9]. However, this seems not to be physical in the sense that it breaks helicity H into its components and violates charge conjugation by requiring the Majorana field to be charge-self-conjugated [7, 10]. If we want the helicity operator to remain intact, which we consider indispensable, we have to go back to our decomposition (Equation 6), which allows only two similarity transformations and thus implies the hyperspin doublet introduced above.

All fermions considered so far carry hypercharges, yet the neutrino has no electric charge. Why is this so? The solution to this problem has been given by the theory of weak interactions. It was invented by Weinberg [4], Glashow [25], and Salam [26] making the crucial assumption that the basic fermion fields are right- and left-chiral two-component Weyl fields as obtained by the chiral projection discussed in Section 2. They are then assembled into hypercharged left-chiral doublets transforming under SU(2) and right-chiral singlets transforming under U(1), and thus chiral symmetry is maximally broken. How can one generate the electric charges as observed? This is achieved by unifying these two symmetries into the electroweak interaction as now described in many textbooks [1, 2].

However, with the hyperspin doublets introduced in the previous subsection, the weak interaction emerges naturally without breaking the chiral symmetry, and moreover with implementation of the full Dirac spinor for a massive fermion. Let us discuss just the lepton doublet which is given by ${\widehat{\psi }}^{†}=\left({\psi }^{†},{\left(\frac{1}{\sqrt{2}}(1-\gamma )\psi \right)}^{†}\right)$.

As SU(2) is two-dimensional, the hypercharge operator is to be defined as $Y=\frac{y}{2}{1}_2$. The generators of SU(2) are given by the spin three vector $\mathbf{\text{S}}=\frac{1}{2}\mathbf{\sigma }$, and thus the general global phase of $\widehat{\psi }$ can be written as

$\begin{array}{ll}exp\left(i{g}^{\prime }{\vartheta }^{\prime }Y+ig(\mathbf{\vartheta }·\mathbf{\text{S}})\right).& (26)\end{array}$

Here we use conventional notation with g′ for the hypercharge coupling constant and g for the hyperspin coupling constant, and the corresponding constant scalar and vector theta angles which are real. We just need to consider the two diagonal-matrix generators Y and $S_z=\frac{1}{2}{\sigma }_z$, which can be mixed by a rotation of their phase-angle space (here we took ϑ_z = ϑ) such that

$\begin{array}{ll}\left(\begin{array}{c}{\vartheta }^{\prime }\\ \vartheta \end{array}\right)=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}{\omega }^{\prime }\\ \omega \end{array}\right).& (27)\end{array}$

Here θ is the associated rotation angle that is still to be determined. Inserting the new coordinates into the operators appearing in the phase factor (Equation 26) of the spinor ψ, and letting ϑ_x = ϑ_y = 0, we obtain

$\begin{array}{ll}{g}^{\prime }{\vartheta }^{\prime }Y+g(\mathbf{\vartheta }·\mathbf{\text{S}})=Q{\omega }^{\prime }+R\omega .& (28)\end{array}$

with the new matrices

$\begin{array}{ll}Q(y)=\frac{1}{2}\left(\begin{array}{cc}y{g}^{\prime }cos\theta +gsin\theta & 0\\ 0& y{g}^{\prime }cos\theta -gsin\theta \end{array}\right),& (29)\end{array}$

and similarly

$\begin{array}{ll}R(y)=\frac{1}{2}\left(\begin{array}{cc}-y{g}^{\prime }sin\theta +gcos\theta & 0\\ 0& -y{g}^{\prime }sin\theta -gcos\theta \end{array}\right).& (30)\end{array}$

Close inspection of Equations (29) and (30) shows that if g′ cosθ = g sinθ = e for a particular angle θ_W these matrices become more transparent. The condition implies that $tan{\theta }_W=\frac{g^{\prime }}{g}$, which defines the Weinberg-Glashow angle [4, 25]. Once it is fixed by the ratio of the coupling constants, the entity Q(y) turns out to be the electromagnetic charge operator given by

$\begin{array}{ll}Q(y)=\frac{e}{2}\left(\begin{array}{cc}y+1& 0\\ 0& y-1\end{array}\right),& (31)\end{array}$

with the electric charge obtained as $e=g{g}^{\prime }∕\sqrt{g^2+g^{\prime 2}}$. Similarly, we get

$\begin{array}{ll}R(y)=\frac{1}{\sqrt{g^2+g^{\prime 2}}}\left(\begin{array}{cc}-y{g}^{\prime 2}+g^2& 0\\ 0& -y{g}^{\prime 2}-g^2\end{array}\right),& (32)\end{array}$

For the lepton doublet, with y = −1 for the electron, we therefore obtain

$\begin{array}{ll}Q(-1)=e\left(\begin{array}{cc}0& 0\\ 0& -1\end{array}\right),& (33)\end{array}$

corresponding to the uncharged neutrino (top) and the negatively charged electron (bottom). For the three quarks with $y=\frac{1}{3}$, we get

$\begin{array}{ll}Q\left(\frac{1}{3}\right)=e\left(\begin{array}{cc}\frac{2}{3}& 0\\ 0& -\frac{1}{3}\end{array}\right),& (34)\end{array}$

corresponding to the positively charged up-quark (top) and the negatively charged down-quark (bottom). The electric charges of the three color variants of up and down quarks are of course the same.

3.4. Relation to the Observed Mass Pattern

The observed fermion mass pattern can be explained by breaking the rotation symmetry of the SU(8) spinor state at the cost of introducing (at most) 8 different coupling constants and a scalar field, as is implemented in the standard model by introducing the Higgs field coupled with the fermion field. We add a coupling term between the 8-component spinor $\widehat{\text{Ψ}}$ and a scalar field ϕ with 8 coupling constants in a diagonal matrix in the form $\text{diag}(c_1,c_2,\cdots ,c_8)\varphi \widehat{\text{Ψ}}$ to the r.h.s. of the generalized Dirac equation. If the scalar field takes two different vacuum expectation values as a realization, it is possible to obtain different masses for fermions.

The first case is the symmetric (or zero) vacuum expectation value, ϕ = 0. The SU(8) symmetry is retained in the spinor and the original generalized Dirac equation is restored with all the fermion species having the same mass m. The second case is a non-zero vacuum expectation value, ϕ = ϕ₀ ≠ 0, breaking the SU(8) symmetry in the spinor. Combination of the original mass term with the coupling term yields an effective mass term as $\text{diag}\left((m+c_1{\varphi }_0),(m+c_2{\varphi }_0)\cdots ,(m+c_8{\varphi }_0)\right)\widehat{\text{Ψ}}$. Therefore, m + c_iϕ may be regarded as the effective mass for each fermion species.

4. Conclusion and Discussion

We have shown that the different variants of how to decompose the mass shell condition (Equation 6) leads plausibly to eight different but coequal representations of the Dirac equation, which can in a physically meaningful way be interpreted as describing eight massive fermions. The corresponding large Dirac spinor $\widehat{\psi }$ assembles them, while being arranged in four doublets of leptons (neutrino and electron) and quarks (up and down), coming in three forms (which traditionally are refereed to as color-charge variants). Of course, the quark ordering is arbitrary and thus general rotations according to SU(3) in the quark state space are permitted and mixing among them is allowed.

The intrinsic symmetry group for the massive hypercharged fermion is SU(8), which breaks into subgroups. There is SU(2) for the “Dirac-Weyl doublets” of the fermions. The lepton and quarks can mix among themselves according to the symmetry group SU(4). The eight fermion species all have at this stage the same mass, as we started from the mass-shell condition (Equation 6) with a given single mass. Naturally, this mass would be seen as the electron mass, which is the only one that has precisely been measured, and which sets a fundamental spatial scale for the fermions by the electron Compton wavelength. Consequently, one may speculate that the measured or inferred fermion mass splitting is expected to occur as the result of coupling with the scalar field ϕ. The SU(8) symmetry is broken by the scalar field in this scenario.

Whereas the fermions of the SM (except for the electron the theory of which was invented long ago by Dirac [5]) and their complex physical properties were gradually established on experimental grounds, no basic theoretical derivation like for the electron was presented before for the characteristics of quarks. Here we have shown that a new equation is indeed not necessary as the generalized Dirac equation already contains these fermions, including their spin, isospin, and electric as well as color charge. The generalized Dirac equation actually encompasses the eight stable fundamental fermions of the first family of the SM, owing to its rich intrinsic symmetry which was revealed in this paper.

SU(8) in our model comes solely from the intrinsic symmetry of the generalized Dirac equation, and is different from the other unification scenarios based on the SU(8) group, such as the boson-fermion balanced SU(8) unification incorporating graviton and gravitinos [27], the SU(8) unification including flavors or chiral family [28, 29], or the SU(8) unification including supersymmetry [30]. Still, it is worth noting that the generalized spinor in our model has the same construction as that proposed by Yablon [31]. One cannot argue that the 4 different versions of the Dirac equation derived here are the same, simply because they deliver the same observables. The wave function or the spinor is not the same among the 4 versions, and the intrinsic states (or spinors) are in apparent degeneracy, as far as the energy of the free fermion fields is concerned. The association of the lepton field with the quark fields is not arbitrary in our generalized Dirac equation. As described in the hypercharge operator $Y_4=\text{diag}(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1)$, the SU(4) symmetry group, as a subgroup of SU(8), gives the fractional charge in a natural way, which justifies its association with a single lepton and three quarks.

Author Contributions

EM drafting the work. YN substantial contributions to the design of the work.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

EM gratefully acknowledges the institutional support by the Extraterrestrial Physics Division headed by Robert Wimmer-Schweingruber at the Institute for Experimental and Applied Physics of Kiel University in Germany. He also appreciates the support by the Space Research Institute in Graz, Austria, where during a 2-week stay essential ideas of this paper were developed.

References

1. Schwartz MD. Quantum Field Theory and the Standard Model. Cambridge: Cambridge University Press (2014).

Google Scholar

2. Kaku M. Quantum Field Theory: A Modern Introduction. New York, NY: Oxford University Press (1993).

3. Higgs PW. Broken symmetries and the masses of gauge bosons. Phys Rev Lett. (1964) 13:508–9. doi: 10.1103/PhysRevLett.13.508

CrossRef Full Text | Google Scholar

4. Weinberg S. A model of leptons. Phys Rev Lett. (1967) 19:1264–6. doi: 10.1103/PhysRevLett.19.1264

CrossRef Full Text | Google Scholar

5. Dirac PAM. The quantum theory of the electron. Proc R Soc Lond Math Phys Sci A (1928) A117:610–24. doi: 10.1098/rspa.1928.0023

CrossRef Full Text | Google Scholar

6. Weyl H. Elektron und graviton. I. Z Phys. (1929) 56:330–52. doi: 10.1007/BF01339504

CrossRef Full Text | Google Scholar

7. Pal PB. Dirac, Majorana, and Weyl fermions. Am J Phys. (2011) 79:485–98. doi: 10.1119/1.3549729

CrossRef Full Text | Google Scholar

8. Pauli W. Zur quantenmechanik des magnetischen elektrons. Z Phys. (1927) 43:601–23. doi: 10.1007/BF01397326

CrossRef Full Text | Google Scholar

9. Majorana E. Teoria simmetrica dell' elettrone e del positrone. Nuovo Cim. (1937) 14:171–84. doi: 10.1007/BF02961314

CrossRef Full Text | Google Scholar

10. Case KM. Reformulation of the Majorana theory of the neutrino. Phys Rev. (1957) 107:307–16. doi: 10.1103/PhysRev.107.307

CrossRef Full Text | Google Scholar

11. Fukugita M, Yanagida T. Physics of Neutrinos and Applications to Astrophysics. Berlin: Springer (2003).

Google Scholar

12. Mohapatra RN, Pal PB. Massive Neutrinos in Physics and Astrophysics. Singapore: World Scientific (2004).

Google Scholar

13. Mohapatra RN, Smirnov AY. Neutrino mass and new physics. Annu Rev Nucl Part Sci. (2006) 56:569–628. doi: 10.1146/annurev.nucl.56.080805.140534

CrossRef Full Text | Google Scholar

14. Mannheim PD. Introduction to Majorana masses. Int J Theor Phys. (1984) 23:643–74. doi: 10.1007/BF02214135

CrossRef Full Text | Google Scholar

15. Schechter J, Valle JWF. Neutrino masses in SU(2) ⊗ U(1) theories. Phys Rev D (1980) 22:2227–35. doi: 10.1103/PhysRevD.22.2227

CrossRef Full Text | Google Scholar

16. Aste A. A direct road to Majorana fields. Symmetry (2010) 2:1776–809. doi: 10.3390/sym2041776

CrossRef Full Text | Google Scholar

17. Marsch E. A new route to the Majorana equation. Symmetry (2013) 5:271–86. doi: 10.3390/sym5040271

CrossRef Full Text | Google Scholar

18. Gell-Mann M. A schematic model of baryons and mesons. Phys Letts. (1964) 8:214–5. doi: 10.1016/S0031-9163(64)92001-3

CrossRef Full Text

19. Klein O. Elektrodynamik und wellenmechanik vom standpunkt des korrespondenzprinzips. Z Phys. (1927) 41:407–22. doi: 10.1007/BF01400205

CrossRef Full Text | Google Scholar

20. Pauli W, Weisskopf V. Über die quantisierung der skalaren relativistischen wellengleichung. Helv Phys Act. (1934) 7:709–31.

Google Scholar

21. Sbaih MAA, Srour MKH, Hamada MS, Fayad HM. Lie algebra and representation of SU(4). Electron J Theor Phys. (2013) 10:9–26.

Google Scholar

22. Yang CN, Mills F. Conservation of isotopic spin and isotopic gauge invariance. Phys Rev. (1954) 96:191–5. doi: 10.1103/PhysRev.96.191

CrossRef Full Text | Google Scholar

23. Pati JC, Salam A. Lepton number as the fourth “color.” Phys Rev D (1974) 10:275–89. doi: 10.1103/PhysRevD.10.275

CrossRef Full Text | Google Scholar

24. Georgi H, Glashow SL. Unity of all elementary-particle forces. Phys Rev Lett. (1974) 32:438–41. doi: 10.1103/PhysRevLett.32.438

CrossRef Full Text | Google Scholar

25. Glashow SL. Partial-symmetries of weak interactions. Nucl Phys. (1961) 22:579–88. doi: 10.1016/0029-5582(61)90469-2

CrossRef Full Text

26. Salam A. Elementary particle theory. In: Svartholm N, editor. Stockholm: Almquist and Forlag (1968). 367 p.

Google Scholar

27. Adler S. SU(8) family unification with boson fermion balance. Int J Mod Phys. (2014) 29:1450130. doi: 10.1142/S0217751X14501309

CrossRef Full Text

28. Kim CW, Roiesnel C. SU(8) grand unification. Phys Lett. (1980) 93B:343–6. doi: 10.1016/0370-2693(80)90528-6

CrossRef Full Text | Google Scholar

29. Chkareuli JL. The SU(8) GUT for chiral families. Phys Lett B (1993) 300:361–6. doi: 10.1016/0370-2693(93)91346-O

CrossRef Full Text | Google Scholar

30. León J, Quirós M, Ramón Medranom J. Towards a realistic supersymmetric SU8 model. Phys Lett B (1982) 118:365–8. doi: 10.1016/0370-2693(82)90205-2

CrossRef Full Text | Google Scholar

31. Yablon JR. Grand unified SU(8) gauge theory based on baryons which are Yang-Mills magnetic monopoles. J Mod Phys. (2013) 4:94–120. doi: 10.4236/jmp.2013.44A011

CrossRef Full Text | Google Scholar