Protocol for Counterfactually Transporting an Unknown Qubit

Quantum teleportation circumvents the uncertainty principle using dual channels: a quantum one consisting of previously-shared entanglement, and a classical one, together allowing the disembodied transport of an unknown quantum state over distance. It has recently been shown that a classical bit can be counterfactually communicated between two parties in empty space, “Alice” and “Bob.” Here, by using our “dual” version of the chained quantum Zeno effect to achieve a counterfactual CNOT gate, we propose the first protocol for transporting an unknown qubit counterfactually, that is without any physical particles traveling between Alice and Bob—no classical channel and no previously-shared entanglement.

1. Introduction

In contrast to classical information, quantum states cannot be faithfully copied—as proven by the no-cloning theorem [1]. In fact doing so would not only violate the uncertainty principle, but would also violate the rule against faster-than-light signaling [2]. Teleporting an unknown qubit, whereby an identical version appears elsewhere, was presumed to firmly belong to the realm of science fiction—until Bennett et al. [3] showed it possible using previously-shared entanglement and a classical channel, such as a phone line. The original qubit, in accordance with no-cloning, is duly destroyed in the process. Quantum teleportation has since been extended to systems with continuous variables [4], and has been demonstrated in numerous key experiments [5–9].

Here, we wonder: Is the disembodied transport of an unknown qubit over distance possible, even in principle, without recourse to previously-shared entanglement or a classical channel?—and intriguingly, without physical particles traveling between Alice and Bob? The answer, as we show, is surprisingly yes.

It has recently been shown that a classical bit can be counterfactually transferred between two parties in empty space [10, 11]. The key ideas behind direct counterfactual quantum communication—a version of which has recently been realized experimentally [12]—are interaction-free measurement [13, 14] and the quantum Zeno effect [15–19]. Interaction-free measurement is based on the fact that the presence of a blocking object inside an interferometer destroys interference even if no particle hits the object. This has the interesting consequence that sometimes the presence of such an object can be inferred without the object directly interacting with any particles. Noh [20] used this to design a counterfactual quantum key distribution protocol whereby, for shared random bits, no information-carrying photons travel between Alice and Bob. The quantum Zeno effect on the other hand refers to the fact that repeated measurement of an evolving quantum system inhibits its evolution, “freezing” it in its initial state—an effect reminiscent of the proverbial watched kettle that never boils. The quantum Zeno effect can arbitrarily boost the efficiency of interaction-free measurements.

2. Methods

We start by generalizing the action of the Mach-Zehnder chained quantum Zeno effect (CQZE) in Salih et al. [10] to the case of Bob effecting a quantum superposition of blocking and not blocking the channel, showing first how it can function as a fully counterfactual, though not practical, CNOT gate, for only one of Alice's input states. Consider the Mach-Zehnder interferometry Zeno setup of Figure 1A. The first concept we require here is Bob effecting a quantum superposition of blocking and not blocking the transmission channel [13, 14, 16]. Although this is easier to imagine from a practical point of view for the Michelson version we discuss later in this section, this Mach-Zehnder version is easier to explain. Here, BS stands for beamsplitter. The action of BS on Alice's photon is the following, |10〉 → cos θ |10〉 + sin θ |01〉 and |01〉 → cos θ |01〉 − sin θ |10〉, where the state |10〉 corresponds to the photon being on the left of BS, the state |01〉 corresponds to the photon being on the right of BS, and $cos\theta =\sqrt{R}$, with R being the reflectivity of BS. We set θ = π∕2N, where N is the number of beamsplitters. Let the initial combined state of Bob's quantum object together with Alice's photon, impinging on the first beamsplitter BS from the top left, be (α |pass〉 + β |block〉) ⊗ |10〉. The state |pass〉 corresponds to Bob's object not blocking the channel, and has probability amplitude α. The state |block〉 corresponds to Bob's object blocking the channel, and has probability amplitude β.

FIGURE 1

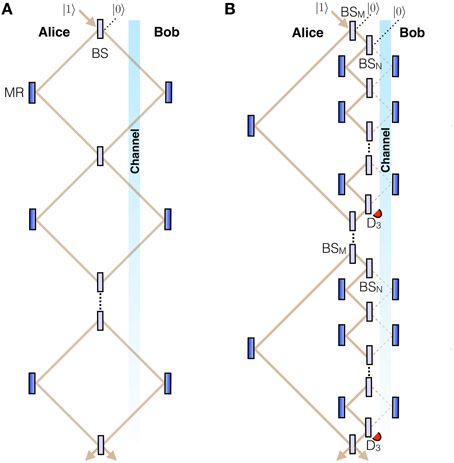
Figure 1. Proposal for counterfactual Mach-Zehnder CNOT. Bob effects a quantum superposition of blocking and not blocking the channel, not practical for this Mach-Zehnder scenario, which acts as the CNOT's control qubit. (A), Partially counterfactual CNOT gate. Beamsplitters BS are highly reflective, with reflectivity R = cos²π∕2N, where N is the total number of BSs. The gate, however, only works for one of Alice's inputs (“0”). Moreover, it is not counterfactual for the part of the superposition where Bob does not block, in which case the photon passes through the channel. (B), Fully counterfactual CNOT gate based on the chained quantum Zeno effect (CQZE). Between successive BS_Ms, of which there are M, there are N beamsplitters BS_N. While the scheme only works for Alice's “0” input, complete counterfactuality is ensured as any photon going into the channel would be lost due to measurement by Bob's object or else end up at one of the detectors D₃: the chained quantum Zeno effect. For large enough M and N, the probability amplitude of the photon being in the channel is virtually zero.

In the following, starting from the second BS, we post-select before each BS the state corresponding to the photon not hitting Bob's object. If the photon hits Bob's object, we assume it is absorbed. But the exact nature of the interaction does not matter, only that the photon is lost; the protocol fails. Immediately after the first BS, the combined state is rotated to (α |pass〉 + β |block〉) ⊗ (cos θ |10〉 + sin θ |01〉), which immediately before the second BS, given the photon is not lost to Bob's object, becomes (1− |β|²sin²θ)^1∕2[α |pass〉 ⊗ (cosθ |10〉 + sin θ |01〉) + β |block〉 ⊗ |10〉]. We have multiplied by the square root of the probability that the photon is not lost to Bob's object, (1− |β| ²sin²θ)^1∕2. And immediately after the second BS this state is rotated to (1− |β| ²sin²θ)^1∕2[α |pass〉 ⊗ (cos 2θ |10〉 + sin 2θ |01〉) + β| block〉 ⊗ (cos θ |10〉 + sin θ |01〉)], which immediately before the third BS, given the photon is not lost to Bob's object, becomes (1− |β| ²sin²θ)[α |pass〉⊗(cos 2θ |10〉 + sin 2θ |01〉) + β| block〉⊗ |10〉]. And immediately after the third BS, this state is rotated to (1− |β| ²sin²θ)[α |pass〉⊗(cos 3θ |10〉 + sin 3θ |01〉) + β| block〉⊗(cos θ |10〉 + sin θ |01〉)].

Thus, after n beamsplitters the combined state has evolved as,

$\begin{array}{cc}\begin{array}{l}(\alpha |\text{pass}\rangle +\beta |\text{block}\rangle )\otimes |10\rangle \to \hfill \\ {(1-{\left|\beta \right|}^2{\sin }^2\theta )}^{(n-1)/2}[\alpha |\text{pass}\rangle \otimes (\cos n\theta |10\rangle +\sin n\theta |01\rangle )+\hfill \\ \beta |\text{block}\rangle \otimes (\cos \theta |10\rangle +\sin \theta |01\rangle )].\hfill \end{array}\hfill & \left(1\right)\hfill \end{array}$

And after N beamsplitters, with N very large, the combined state of Bob's quantum object and Alice's photon becomes (α |pass〉 |01〉 + β |block〉 |10〉). The factor (1− |β|²sin²θ)^(n−1)∕2 squared is the probability that Alice's photon is not lost due to measurement by Bob's object, which brings about the Zeno effect. We thus have a CNOT gate, with Bob's as the control bit, |block〉 ≡ |0〉, and |pass〉 ≡ |1〉, and Alice's as the target bit, |10〉 ≡ |0〉, and |01〉 ≡ |1〉, albeit for only one of Alice's possible input states, namely |0〉. Moreover, the scheme is only counterfactual for the part of the superposition corresponding to Bob blocking and is not counterfactual for the part of the superposition corresponding to Bob not blocking, where Alice's photon gradually “leaks” into the channel.

We now show how to achieve complete CNOT counterfactuality, for Alice's input state |0〉, using the chained quantum Zeno effect (CQZE) setup of Figure 1B. Here, Alice's photon goes through M beamsplitters BS_M, with θ_M = π∕2M. Between successive BS_Ms the photon goes through N beamsplitters BS_N, with θ_N = π∕2N. The state |100〉 corresponds to Alice's photon being on the left of BS_M, the state |010〉 corresponds to the photon being on the right of BS_M and on the left of BS_N, and the state |001〉 corresponds to the photon being on the right of BS_N. For the m-th cycle,

$\begin{array}{cc}\begin{array}{l}(\alpha |\text{pass}\rangle +\beta |\text{block}\rangle )\otimes |010\rangle \to \hfill \\ {(1-{\left|\beta \right|}^2{\sin }^2{\theta }_N)}^{(n-1)/2}[\alpha |\text{pass}\rangle \hfill \\ \otimes (\cos n{\theta }_N|010\rangle +\sin n{\theta }_N|001\rangle )+\hfill \\ \beta |\text{block}\rangle \otimes (\cos {\theta }_N|010\rangle +\sin {\theta }_N|001\rangle )].\hfill \end{array}\hfill & \left(2\right)\hfill \end{array}$

And after N beamsplitters BS_N, with N very large, the combined state of Bob's quantum object and Alice's photon becomes (α |pass〉 |001〉 + β |block〉 |010〉). The factor ${(1-{\left|\beta \right|}^2{sin}^2{\theta }_N)}^{(n-1)∕2}$ squared is the probability that the photon is not lost due to measurement by Bob's object, which brings about the Zeno effect. But Alice's single photon is initially in the state |100〉, as shown in Figure 1B, with all unused ports in the vacuum state. After the m-th BS_M,

$\begin{array}{cc}\begin{array}{l}(\alpha |\text{pass}\rangle +\beta |\text{block}\rangle )\otimes |100\rangle \to \hfill \\ {(1-{\left|\alpha \right|}^2{\sin }^2{\theta }_M)}^{(m-1)/2}[\alpha |\text{pass}\rangle \otimes (\cos {\theta }_M|100\rangle \hfill \\ +\sin {\theta }_M|010\rangle )+\hfill \\ \beta |\text{block}\rangle \otimes (\cos m{\theta }_M|100\rangle +\sin m{\theta }_M|010\rangle )].\hfill \end{array}\hfill & \left(3\right)\hfill \end{array}$

And after the M-th BS_M, with M very large, the combined state of Bob's quantum object and Alice's photon ≃ (α |pass〉 |100〉 + β |block〉 |010〉). The factor ${(1-{\left|\alpha \right|}^2{sin}^2{\theta }_M)}^{(m-1)∕2}$ squared is the probability that Alice's photon is not lost through detection by one of her D₃s, which bring about the Zeno effect for the part of the superposition corresponding to Bob not blocking. We thus have a fully counterfactual CNOT gate, with Bob's as the control bit, |pass〉 ≡ |0〉, and |block〉 ≡ |1〉, and Alice's as the target bit, |100〉 ≡ |0〉, and |010〉 ≡ |1〉, again for only one of Alice's possible input states, |0〉.

Complete counterfactuality is ensured: Any photon going into the channel would either be lost due to measurement by Bob's object or else end up at one of the detectors D₃. This is the most direct, intuitive definition of counterfactuality. Defining counterfactuality in terms of weak measurements, for instance, has proven controversial [21, 22]. Moreover, by Equations (2) and (3), the probability amplitude of the photonic state |001〉 corresponding to the photon being in the channel is virtually zero for large enough M and N. Nevertheless, the scheme is not practical, and more fundamentally, it only works for one of Alice's input states.

Let us now consider a more versatile Michelson version, showing in principle how to achieve a counterfactual quantum CNOT gate for all possible input values. Here, the function of BS in the Mach-Zehnder CQZE setup of Figure 1B is achieved by the combined action of switchable polarization rotator SPR and polarizing beamsplitter [10, 23] PBS, as shown in Figure 2. Bob's quantum object QO_B exists in a superposition of blocking and not blocking the channel. Here, H(V) refers to horizontal (vertical) polarization. The action of $SP{R}_i^{H(V)}$, in Alice's H(V)-input setup, on her photon is the following,

$\begin{array}{cc}|H(V)\rangle \to \cos {\theta }_i|H(V)\rangle +\sin {\theta }_i|V(H)\rangle .& \left(4\right)\end{array}$

$\begin{array}{cc}|V(H)\rangle \to \cos {\theta }_i|V(H)\rangle -\sin {\theta }_i|H(V)\rangle .& \left(5\right)\end{array}$

with i = 1, 2 corresponding to SPRs with different rotation angles. We set rotation angle θ₁₍₂₎ = π∕2M(N), with SPR₁₍₂₎ switched on once per cycle when the photon, or part of it rather, is moving in the direction from SM₁₍₂₎ toward PBS₁₍₂₎. This is in contrast to Salih et al. [10] where switchable polarization rotators are switched on when the photon is moving in the direction from switchable mirror SM₁₍₂₎ toward PBS₁₍₂₎ and on the way back, leading to an undesired rotation in the last outer cycle, tiny for large M. The current scheme avoids this undesired rotation and resulting error altogether. Switchable mirror SM₁₍₂₎ is initially turned off allowing the photon in, but is then turned on for M(N) cycles before it is turned off again, allowing the photon out.

FIGURE 2

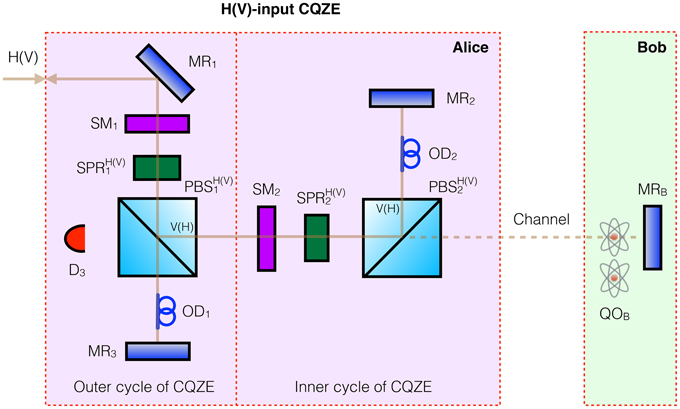
Figure 2. Proposal for fully counterfactual CNOT gate based on Michelson CQZE. By using polarizing beamsplitter PBS^H(V) that passes H(V) photons and reflects V(H), this setup can take H(V) input from Alice, i.e., “0”(“1”), but not yet a superposition. Bob implements his qubit as a superposition of blocking and not blocking the channel using his quantum object QO_B. Switchable mirror SM₁₍₂₎ is initially turned off allowing the photon in, but is then turned on for M(N) outer(inner) cycles before it is turned off again, allowing the photon out. The combined action of switchable polarization rotators SPR and polarizing beamsplitters PBS achieves the function of beamsplitters BS in the Mach-Zehnder version of Figure 1. MR stands for mirror, and OD for optical delay. Again, complete counterfactuality is ensured as any photon going into the channel would either be lost due to measurement by Bob's object QO_B or else end up at detector D₃: the chained quantum Zeno effect. For large enough M and N, the probability amplitude of the photon being in the channel is virtually zero.

The Michelson CQZE setup of Figure 2 takes H(V) polarized photons as input, with PBS^H(V) passing H(V) photons and reflecting V(H) as shown. Alice sends an H(V) photon into the H(V)-input CQZE setup. By a similar evolution to Equations (2) and (3), in the part of the superposition corresponding to Bob not blocking the channel, Alice's exiting photon is H(V) polarized, while in the part of the superposition corresponding to Bob blocking the channel, Alice's exiting photon is V(H) polarized.

This means that Alice can encode her bit using polarization. She encodes a “0”(“1”) by sending an H(V) photon into the corresponding H(V)-input CQZE setup. But can Alice encode a quantum superposition of “0” and “1”?

Crucially, the answer is yes. She first passes her photon through PBS_L in order to separate it into H and V components as shown in Figure 3A. The H(V) component is then fed into the corresponding H(V)-input CQZE setup. Bob can block or not block the transmission channel—or a quantum superposition of blocking and not blocking—for both H and V components which are recombined using PBS_R, Figure 3A. The polarization of Alice's exiting photon is determined by Bob's bit choice. This is our dual chained quantum Zeno effect.

FIGURE 3

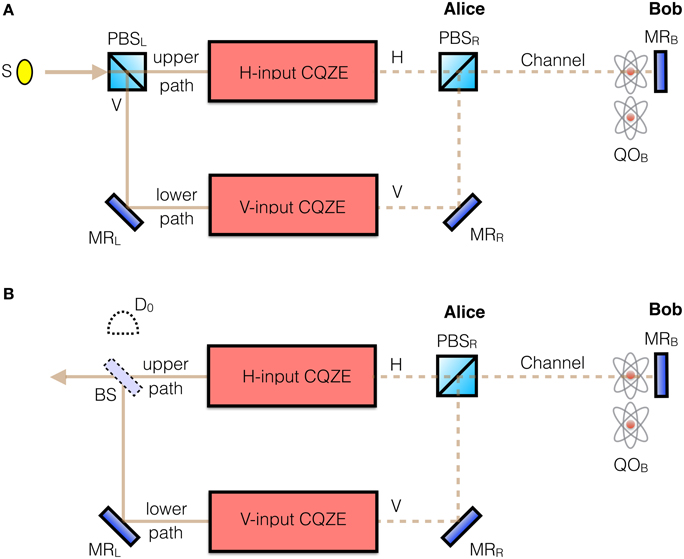
Figure 3. Proposal for fully counterfactual general input CNOT gate based on a dual CQZE. (A), Alice sends a photon in the qubit state α |H〉 + β |V〉, while Bob's quantum object QO_B is in the qubit state λ |pass〉 + μ |block〉. Alice's incoming photon is first separated into H and V components using polarizing beamsplitter PBS_L, which are then, respectively fed into the H-input and V-input CQZE modules from Figure 2. (B), For Alice's exiting photon, PBS_L is replaced by a 50:50 beamsplitter BS. If it is not detected at D₀, then the photon exits toward the left in the correct state. For the case of Alice initially sending an H photon, as in the first step of our protocol, there is no need for BS, the photon exits toward the left in the correct state. S stands for single photon source.

Starting with Equations (2) and (3), and adapting for the Michelson CQZE setup of Figure 2, the probability that the photon avoids detection by detector D₃ in all cycles is ${(1-{\left|\alpha \right|}^2{sin}^2{\theta }_M)}^M$. And the probability that the photon avoids being lost due to measurement by Bob's object in all cycles is ${\prod }_{m=1}^M{(1-{\left|\beta \right|}^2{sin}^2{m\theta }_M{sin}^2{\theta }_N)}^N$ for large N. Thus, the ideal case efficiency of this counterfactual CNOT gate is,

$\begin{array}{cc}{(1-{\left|\alpha \right|}^2{\sin }^2{\theta }_M)}^M{\displaystyle \prod _{m=1}^M{(1-{\left|\beta \right|}^2{\sin }^{2}m{\theta }_M{\sin }^2{\theta }_N)}^N}.& \left(6\right)\end{array}$

In Figure 4 we plot this maximum efficiency for different Ms and Ns, for $\alpha =\beta =1∕\sqrt{2}$. Given perfect implementation, we see that efficiency approaches unity for N >> M >> 1. For instance for M = 50 and N = 1250, ideal efficiency is already 95%.

FIGURE 4

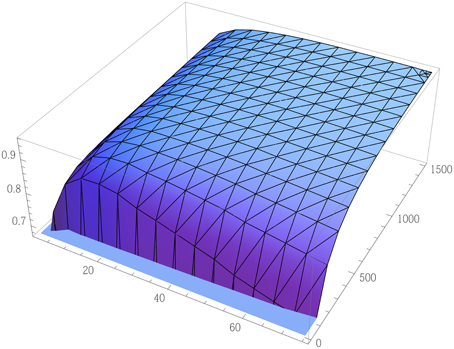
Figure 4. Ideal case efficiency of counterfactual CNOT. The efficiency of an ideally implemented counterfactual CNOT gate, with Alice encoding a quantum superposition of “0” and “1,” plotted against the number of outer and inner cycles M and N, with M up to 75, and N up to 1500. Bob's control qubit is assumed an equal superposition here. Efficiency approaches unity for N >> M >> 1. Errors or loss caused by imperfect optical elements and by noise in the channel, as well as decoherence of Bob's quantum object, all of which have an adverse effect, are ignored here.

Complete counterfactuality is ensured: Any photon going into the channel would either be lost due to measurement by Bob's object or else end up at detector D3. Moreover, the probability amplitude of the photonic state corresponding to the photon being in the channel is virtually zero for large enough M and N.

Unlike the Mach-Zehnder scenario discussed above where, for Bob not blocking, the last BS_M causes an undesired rotation—tiny for large M—in this Michelson implementation, a small number of outer cycles M does not lead to output errors from the counterfactual CNOT gate, but would instead lead to more instances of the gate failing through photon loss. However, a small number of inner cycles N would lead to output errors as well as more photon loss, as would imperfect implementation.

Salih et al. [10], Figure 4, contains an analysis for the case of transferring classical bits counterfactually in the presence of imperfections, for the two cases of Bob blocking the channel and that of Bob not blocking the channel. We see that the CQZE is sensitive to rotation errors by polarization rotators SPR as well as noise randomly blocking the channel. We expect a similar effect for our counterfactual quantum CNOT gate. A detailed analysis in the presence of imperfections, more crucial for a large number of cycles implementation, is left to a future study.

Note that in their experimental implementation of the CQZE of Salih et al. [10], in the single-photon regime, Cao et al. [12] managed to mimic the action of switchable mirrors, whose direct realization would have been challenging, by using slightly tilted semi-reflective mirrors. They post-selected only the photons that emerged in the correct spatial and temporal modes corresponding to the desired number of cycles.

Now, consider the most general case where Alice sends a photon in the superposition λ |H〉 + μ |V〉, with Bob's object in the superposition α |pass〉 + β |block〉. We get the following superposition for Alice's exiting photon, from the upper path H-input CQZE module and the lower path V-input CQZE module, Figure 3B,

$\begin{array}{cc}\begin{array}{l}\lambda (\alpha |\text{pass}\rangle |\text{H}\rangle +\beta |\text{block}\rangle |\text{V}\rangle )\otimes |\text{upper path}\rangle +\\ \mu (\alpha |\text{pass}\rangle |\text{V}\rangle +\beta |\text{block}\rangle |\text{H}\rangle )\otimes |\text{lower path}\rangle .\end{array}& \left(7\right)\end{array}$

All we need now is to combine the two photonic states from the upper and lower paths. This is done by replacing PBS_L in Figure 3A by a 50:50 beamsplitter BS, as shown in Figure 3B. We define the upper path as above or to the right of BS, and the lower path as below or to the left of BS. Let's rename the states (α |pass〉 |H〉 + β |block〉 |V〉) and (α |pass〉 |V〉 + β |block〉 |H〉) as |↖〉 and |↙〉, respectively. We can rewrite the exiting state, Equation (7), as (λ |↖〉 |upper path〉 + μ |↙〉 |lower path〉). Feeding this state into BS, which applies a π∕2-rotation to the path qubit, gives,

$\begin{array}{cc}\begin{array}{l}1/\sqrt{2}(\lambda |\nwarrow \rangle +\mu |\swarrow \rangle )\otimes |\text{lower path}\rangle +\\ 1/\sqrt{2}(\lambda |\nwarrow \rangle -\mu |\swarrow \rangle )\otimes |\text{upper path}\rangle .\end{array}& \left(8\right)\end{array}$

Which means we can obtain the desired state λ|↖〉 + μ|↙〉 with 50% probability upon measuring the path qubit. We will shortly deal with the other 50%. This measurement is carried out at D₀, Figure 3B, without destroying the photon when ideal [24, 25]. If the photon is not detected there we know it is in the other path traveling toward the left, in the correct state. So starting with the most general input states we have got,

$\begin{array}{cc}\begin{array}{l}(\alpha |\text{pass}\rangle +\beta |\text{block}\rangle )\otimes (\lambda |\text{H}\rangle +\mu |\text{V}\rangle )\to \\ \lambda (\alpha |\text{pass}\rangle |\text{H}\rangle +\beta |\text{block}\rangle |\text{V}\rangle )+\\ \mu (\alpha |\text{pass}\rangle |\text{V}\rangle +\beta |\text{block}\rangle |\text{H}\rangle ).\end{array}& \left(9\right)\end{array}$

Rewriting using the equivalent binary states we get,

$\begin{array}{cc}\begin{array}{l}(\alpha |0\rangle +\beta |1\rangle )\otimes (\lambda |0\rangle +\mu |1\rangle )\to \\ \lambda (\alpha |0\rangle |0\rangle +\beta |1\rangle |1\rangle )+\\ \mu (\alpha |0\rangle |1\rangle +\beta |1\rangle |0\rangle ).\end{array}& \left(10\right)\end{array}$

We have thus shown in principle how to achieve a fully counterfactual quantum CNOT gate using our dual CQZE setup.

3. Results and Discussion

We now show in principle how to counterfactually transport an unknown qubit. Using two CNOT gates, the network of Figure 5A swaps the input states (α |0〉 + β |1〉) and |0〉, effectively transferring α |0〉 + β |1〉 from one side (top) to the other (bottom) [26].

FIGURE 5

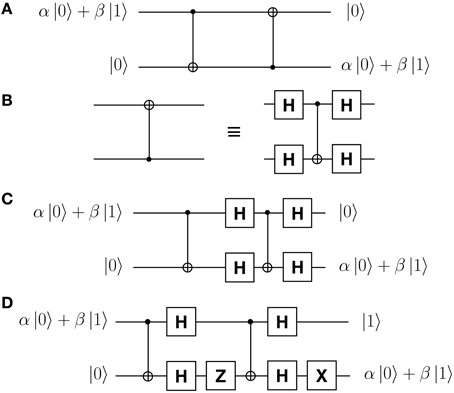
Figure 5. Network for quantum state transfer. (A), By means of two CNOT gates a qubit α |0〉 + β |1〉 can be transferred from one side (top) to the other (bottom). Our counterfactual CNOT gate has Bob's as the control qubit, which is a problem since in this network the control qubits of the two CNOT gates are on opposite sides. (B), By means of four Hadamard gates the control and target qubits of any CNOT gate can be interchanged. (C) Applying (B) to (A), the control qubits of both CNOT gates are now on the same side, Bob's. This network forms the basis of our protocol for counterfactually transporting an unknown qubit. (D), In case of a Z-gate before the right hand side CNOT, we need an X-gate at the end in order for the state α |0〉 + β |1〉 to be correctly transferred. This network is relevant to one of the two possible paths for Alice's exiting photon from the Dual CQZE setup of Figure 3B.

Can we use our counterfactual CNOT gate in this network—with Bob's quantum object as the control qubit—to counterfactually transport an unknown state from Bob to Alice? The problem with the network is that the control qubits of the two CNOT gates are on opposite sides. But there is a way around it. By means of four Hadamard gates, the network of Figure 5B interchanges the control and target qubits of a CNOT gate [27]. Applying this to the network of Figure 5A we get the network of Figure 5C which forms the basis of our protocol,

$\begin{array}{cc}\begin{array}{l}(\alpha |0\rangle +\beta |1\rangle )\otimes |0\rangle \stackrel{\text{CNOT}}{\to }\\ \alpha |00\rangle +\beta |11\rangle \stackrel{H^{\otimes 2}}{\to }\\ \alpha |++\rangle +\beta |--\rangle \stackrel{\text{CNOT}}{\to }\\ \alpha |++\rangle +\beta |+-\rangle \stackrel{H^{\otimes 2}}{\to }\\ |0\rangle \otimes (\alpha |0\rangle +\beta |1\rangle ).\end{array}& \left(11\right)\end{array}$

What about the case of Alice's exiting photon ending up on path D₀, which has 50% probability? From Equation (8), the combined state of Bob's object and Alice's photon in this path is, λ(α |pass〉 |H〉 + β |block〉 |V〉) − μ(α |pass〉 |V〉 + β |block〉 |H〉), which in binary is, λ(α |0〉 |0〉 + β |1〉 |1〉) − μ(α |0〉 |1〉 + β |1〉 |0〉). This is equivalent to the output of a CNOT gate but with Alice applying a Z-gate to her input qubit. Incorporating this in the network of Figure 5C we get the network of Figure 5D. It turns out that an X-gate is needed at the end for the state α |0〉 + β |1〉 to be transferred from one side (top) to the other (bottom),

$\begin{array}{cc}\begin{array}{l}(\alpha |0\rangle +\beta |1\rangle )\otimes |0\rangle \stackrel{\text{CNOT}}{\to }\\ \alpha |00\rangle +\beta |11\rangle \stackrel{H^{\otimes 2}}{\to }\\ \alpha |++\rangle +\beta |--\rangle \stackrel{I\otimes Z}{\to }\\ \alpha |+-\rangle +\beta |-+\rangle \stackrel{\text{CNOT}}{\to }\\ \alpha |--\rangle +\beta |-+\rangle \stackrel{H^{\otimes 2}}{\to }\\ \alpha |11\rangle +\beta |10\rangle \stackrel{I\otimes X}{\to }\\ |1\rangle \otimes (\alpha |0\rangle +\beta |1\rangle ).\end{array}& \left(12\right)\end{array}$

We have finally arrived at our protocol for counterfactually transporting an unknown qubit.

3.1. Protocol for Counterfactual Quantum Transportation

Alice starts by sending an H-photon into the dual CQZE setup of Figure 3, with Bob's quantum object, his qubit to be counterfactually transported, in a superposition of blocking and not blocking the channel: α |pass〉 + β |block〉. Alice then applies a Hadamard transformation to (the polarization of) her exiting photon, as does Bob to his qubit. Alice sends her photon back into the dual CQZE setup. If her exiting photon is not found in path D₀, she knows it is in the other path traveling toward the left. She applies a Hadamard transformation to (the polarization of) her photon, as does Bob to his qubit. The photon is now in the state α |H〉 + β |V〉. If Alice's exiting photon is found instead in path D₀, she first applies a Hadamard transformation to (the polarization of) her photon, as does Bob to his qubit. She then applies an X-transformation to her qubit. The photon is now in the state α |H〉 + β |V〉. Bob's qubit has been counterfactually transported to Alice. His original qubit ends up in the state |0〉 or |1〉 randomly; in other words destroyed.

3.2. Fidelity

Let us now look at the fidelity of our counterfactual transport as a function of the number of outer and inner cycles M and N. We have mentioned that a small number of inner cycles N would lead to output errors for our counterfactual CNOT gate. These output errors only occur for the case of Bob blocking the channel as the number of inner cycles is irrelevant for the case of Bob not blocking the channel. Take the case of Alice sending an H-photon into the counterfactual CNOT gate, with Bob blocking. For asymptotically large N, with N >> M, and given perfect implementation, the counterfactual CNOT outputs a V-photon. However, for finite N we have the recursion relations [10],

$\begin{array}{cc}ϵ[m,N]=\cos (\frac{\pi }{2M})ϵ[m-1]-\sin (\frac{\pi }{2M}){\cos }^N(\frac{\pi }{2N})\eta [m-1].& \left(13\right)\end{array}$

$\begin{array}{cc}\eta [m,N]=\sin (\frac{\pi }{2M})ϵ[m-1]+\cos (\frac{\pi }{2M}){\cos }^N(\frac{\pi }{2N})\eta [m-1].& \left(14\right)\end{array}$

Where η[M, N] is the unnormalized probability amplitude for the photon exiting in the correct state |V〉, and ϵ[M, N] is the unnormalized probability amplitude for the photon exiting in the incorrect state |H〉. We have the initial conditions η[0, N] = 0, and ϵ[0, N] = 1. The case of Alice sending a V-photon into the counterfactual CNOT gate is analogous. Using Equation (11) we get the following expression for the fidelity of our counterfactual qubit transport,

$\begin{array}{cc}\begin{array}{l}Fidelity=[\frac{|\alpha {|}^2}{2}(1+\eta [M,N]+ϵ[M,N])\\ {+\frac{|\beta {|}^2}{2}(1+\eta [M,N]-ϵ[M,N])]}^2.\end{array}& \left(15\right)\end{array}$

For example, for M = 2 and N = 50, with $\alpha =\beta =\frac{1}{\sqrt{2}}$, we already have a fidelity of 99%. Figure 6 plots fidelity, which simplifies to $\frac{{(1+\eta \left[M,N\right])}^2}{4}$ for $\alpha =\beta =\frac{1}{\sqrt{2}}$, against M and N, for M up to 10 and N up to 100.

FIGURE 6

Figure 6. Ideal case fidelity of counterfactual transport. The fidelity of our protocol for counterfactually transporting an unknown qubit plotted against the number of outer and inner cycles, M and N, for M up to 10 and N up to 100, with $\alpha =\beta =\frac{1}{\sqrt{2}}$. Implementation imperfections are ignored.

We have so far not said anything about how Bob may practically implement his qubit. Tremendous recent advances mean that there are several candidate technologies. Perhaps most promising for our purpose here are trapped-ion techniques [28–30], whereby a carefully shielded and controlled ion can be placed in a quantum superposition of two spatially separated states—one of which in our case blocks the channel. Trapped ions offer relatively long decay times, needed for a large-number-of-cycles implementation of the protocol. Moreover, the Hadamard transformation, key to this protocol, can be directly applied by means of suitable laser pulses. Note that in our protocol a smaller number of outer cycles, as explained above, does not lead to output errors, but rather to more instances of photon loss. This opens the door for practical implementation by post-selecting Alice's photon not lost. Such an implementation also helps with decoherence of Bob's quantum object by shortening the time required for qubit transport. It also helps with errors caused by imperfect optical elements and by noise in the channel—as a larger number of cycles would amplify such errors. Shorter qubit transport time could pose a different challenge however. Switchable optical elements such as switchable mirrors and polarization rotators, implemented in the single-photon regime, need to be turned on or off quickly enough to achieve the precise timing described in the protocol. The question of whether our protocol is implementable using current technology is an interesting one whose answer has to wait.

We have proposed a protocol for the counterfactual, disembodied transport of an unknown qubit—much like in quantum teleportation except that Alice and Bob do not require previously-shared entanglement nor a classical channel. No physical particles travel between them either. Here, Bob's qubit is gradually “beamed up” to Alice. In the ideal asymptotic limit, efficiency and fidelity approach unity as the probability amplitude of the photon being in the channel approaches zero. This brings into sharp focus both the promise and mystery of quantum information.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I thank Sam Braunstein, M. Suhail Zubairy, M. Al-Amri, Zheng-Hong Li, Gilles Puetz, and Nicolas Gisin for useful comments received in 2013 on an initial draft. This paper was first posted on the arXiv on April 8, 2014, arXiv:1404.2200.

References

1. Wootters WK, Zurek WH. A single quantum cannot be cloned. Nature (1982) 299:802–3. doi: 10.1038/299802a0

CrossRef Full Text | Google Scholar

2. Gisin N. Quantum cloning without signaling. Phys Lett A (1998) 242:1. doi: 10.1016/S0375-9601(98)00170-4

CrossRef Full Text | Google Scholar

3. Bennett CH, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters WK. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys Rev Lett. (1993) 70:1895. doi: 10.1103/PhysRevLett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Vaidman L. Teleportation of quantum states. Phys Rev A (1994) 49:1473. doi: 10.1103/PhysRevA.49.1473

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bouwmeester D, Pan J-W, Mattle K, Eibl M, Weinfurter H, Zeilinger A. Experimental quantum teleportation. Nature (1997) 390:575–9. doi: 10.1038/37539

CrossRef Full Text | Google Scholar

6. Furusawa A, Sorensen JL, Braunstein SL, Fuchs CA, Kimble HJ, Polzik ES. Unconditional quantum teleportation. Science (1998) 282:706–9. doi: 10.1126/science.282.5389.706

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Riebe M, Häffner H, Roos CF, Hänsel W, Benhelm J, Lancaster GPT, et al. Deterministic quantum teleportation with atoms. Nature (2004) 429:734–7. doi: 10.1038/nature02570

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Barrett MD, Chiaverini J, Schaetz T, Britton J, Itano WM, Jost JD, et al. Deterministic quantum teleportation of atomic qubits. Nature (2004) 429:737–9. doi: 10.1038/nature02608

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sherson JF, Krauter H, Olsson RK, Julsgaard B, Hammerer K, Cirac I, et al. Quantum teleportation between light and matter. Nature (2006) 443:557–60. doi: 10.1038/nature05136

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Salih H, Li Z-H, Al-Amri M, Zubairy MS. Protocol for direct counterfactual quantum communication. Phys Rev Lett. (2013) 110:170502. doi: 10.1103/PhysRevLett.110.170502

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Quantum mechanics: exchange-free communication. Nature (2013) 497:9. doi: 10.1038/497009b

CrossRef Full Text

12. Cao Y, Li Y-H, Cao Z, Yin J, Chen Y-A, Ma X, et al. Direct counterfactual communication with single photons. arXiv:1403.5082 (2014).

Google Scholar

13. Dicke RH. Interactionfree quantum measurements: a paradox? Am J Phys. (1981) 49:925–30. doi: 10.1119/1.12592

CrossRef Full Text | Google Scholar

14. Elitzur AC, Vaidman L. Quantum mechanical interaction-free measurements. Found Phys. (1993) 23:987–97. doi: 10.1007/BF00736012

CrossRef Full Text | Google Scholar

15. Kwiat PG, Weinfurter H, Herzog T, Zeilinger A, Kasevich MA. Interaction-free measurement. Phys Rev Lett. (1995) 74:4763–6. doi: 10.1103/PhysRevLett.74.4763

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kwiat PG, White AG, Mitchell JR, Nairz O, Weihs G, Weinfurter H, et al. High-efficiency quantum interrogation measurements via the quantum zeno effect. Phys Rev Lett. (1999) 83:4725–8. doi: 10.1103/PhysRevLett.83.4725

CrossRef Full Text | Google Scholar

17. Misra B, Sudarshan ECG. The Zenos paradox in quantum theory. J Math Phys. (1977) 18:756–63. doi: 10.1063/1.523304

CrossRef Full Text | Google Scholar

18. Peres A. Zeno paradox in quantum theory. Am J Phys. (1980) 48:931–2. doi: 10.1119/1.12204

CrossRef Full Text | Google Scholar

19. Agarwal GS, Tewari SP. An all-optical realization of the quantum zeno effect. Phys Lett A (1994) 185:139–42. doi: 10.1016/0375-9601(94)90837-0

CrossRef Full Text | Google Scholar

20. Noh T-G. Counterfactual Quantum Cryptography. Phys Rev Lett. (2009) 103:230501–4. doi: 10.1103/PhysRevLett.103.230501

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Vaidman L. Comment on “Protocol for Direct Counterfactual Quantum Communication.” Phys Rev Lett. (2014) 112:208901. doi: 10.1103/PhysRevLett.112.208901

CrossRef Full Text | Google Scholar

22. Salih H, Li Z-H, Al-Amri M, Zubairy MS. Salih et al. reply. Phys Rev Lett. (2014) 112:208902. doi: 10.1103/PhysRevLett.112.208902

CrossRef Full Text

23. Salih H. Tripartite counterfactual quantum cryptography. Phys Rev A (2014) 90:012333. doi: 10.1103/PhysRevA.90.012333

CrossRef Full Text | Google Scholar

24. Nogues G, Rauschenbeutel A, Osnaghi S, Brune M, Raimond JM, Haroche S. Seeing a single photon without destroying it. Nature (1999) 400:239–42. doi: 10.1038/22275

CrossRef Full Text | Google Scholar

25. Haroche S. Nobel lecture: controlling photons in a box and exploring the quantum to classical boundary. Rev Mod Phys. (2013) 85:1083. doi: 10.1103/RevModPhys.85.1083

CrossRef Full Text | Google Scholar

26. Mermin ND. From classical state swapping to quantum teleportation. Phys Rev A (2001) 65:012320. doi: 10.1103/PhysRevA.65.012320

CrossRef Full Text | Google Scholar

27. Mermin ND. Copenhagen computation: how i learned to stop worrying and love Bohr. IBM J Res Dev. (2004) 48:53–62. doi: 10.1147/rd.481.0053

CrossRef Full Text | Google Scholar

28. Hosten O, Rakher MT, Barreiro JT, Peters NA, Kwiat PG. Counterfactual quantum computation through quantum interrogation. Nature (2006) 439:949–52. doi: 10.1038/nature04523

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Monroe C, Meekhof DM, King BE, Wineland DJ. A schrdinger cat superposition state of an atom. Science (1996) 272:1131–6. doi: 10.1126/science.272.5265.1131

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wineland D. Nobel lecture: superposition, entanglement, and raising Schrdingers cat. Rev Mod Phys. (2013) 85:1103–14. doi: 10.1103/RevModPhys.85.1103

CrossRef Full Text | Google Scholar