- D-GESS, Computational Social Science, Eidgenössische Technische Hochschule Zurich, Zurich, Switzerland
The introduction of participatory rating mechanisms on online sales platforms has had substantial impact on firms' sales and profits. In this note, we develop a dynamic model of consumer influences on ratings and of rating influences on consumers, focussing on standard five-star mechanisms as implemented by many platforms. The key components of our social influence model are the consumer trust in the “wisdom of crowds” during the purchase phase and indirect reciprocity during the rating decision. Our model provides an overarching explanation for well-corroborated empirical regularities. We quantify the performance of the voluntary rating mechanism in terms of realized consumer surplus with the no-mechanism and full-information benchmarks, and identify how it could be improved.
1. Introduction
Rating mechanisms have a straightforward positive effect on firms' profits, while the underlying consumers' purchase and rating behaviors are driven by complex dynamic social influence processes. Indeed, such processes may undermine the “wisdom of crowds,” and eventually damage social welfare. In this note, we develop a model with which we can quantify the effects of rating mechanisms on consumer surplus. We compare the resulting effects with the no-mechanism and full-information benchmarks, and suggest ways in which the rating mechanisms could be improved.
Across different types of products and online sales platforms, rating mechanisms have been shown to improve sales [1–10] and consumer satisfaction [11], despite the issue of fake/manipulated reviews [12–14]. From the point of view of the consumer, understanding the representativeness of ratings is key. For that, we need to model why agents contribute and understand which ratings are fake. Perhaps most importantly, we need to identify the role of social influence in ranking dynamics, because social influence can undermine the “wisdom of crowds” [15, 16] and thus lead to bad rating performance.
Review aggregation mechanisms on online sales platforms rely on consumers to engage in costly feedback provision voluntarily. Related to the “tragedy of the commons” [17] and game-theoretic models of voluntary contributions to public goods [18, 19], the question is how can the provisioning of ratings be explained in light of the private interests [20, 21] of individuals to free-ride on others' ratings without providing own feedback themselves. We shall build a model of voting behaviors with four types of agents: egoist, altruist, reciprocator, fake. All types rely on ratings in the purchase decision, but differ in their rating behaviors. Egoist never votes. Altruist votes so as to maximize the rating's informational content for future consumers. Reciprocator votes only if experiencing a positive utility. Fake votes to boost the product's rating, provided some cost constraint is satisfied.
The dynamics resulting from our model are consistent with the following four well-established empirical regularities:
1. High ratings increase sales.
2. Ratings initially decrease.
3. Thereafter, ratings increase.
4. Ratings polarize over time.
Our model departs from standard economic models of “rational” voluntary participation [18, 19] or “rational” voting [22–24], and instead considers opinion dynamics allowing for “social influence” as used by sociophysicists (see reviews by Castellano et al.[25] and Galam [26]). Closest to our study is the recent social-influence-in-rating literature [27–30] which we synthesize in the formulation of our model, relying on a rich model with four behavioral types. The model explains empirical regularities with a single model, particularly contrarian dynamics regarding initial-rating vs. end-of-sequence-rating dynamics.
2. Materials and Methods
2.1. The Model
At each period t = 1, 2, …, a unique new agent i is drawn from a continuum of agents. With probability πA, πE, πR, πF > 0, respectively (such that πA + πE + πR + πF = 1), the agent is altruist, egoist, reciprocator, fake.
Agent i decides whether to buy a product of unknown quality q. q is drawn uniformly at random from [0, 6]. Agent i will derive a private gross benefit from the product equal to qi distributed normally according to N[q, σ2] around the true quality with some finite σ > 0. Moreover, i associates a private cost with purchase of the product, ri, drawn uniformly at random from [0, 6], so that his utility finally is expressed by ui = qi − ri. The reserve utility from deciding not to purchase the product is assumed to be zero. Hence, agent i prefers to purchase the product ex ante if and only if Ei(q) > ri, where Ei(q) is individual i's expectation concerning the quality of the product (in terms of the product's “benefit”) and ri represents its corresponding cost.
In the presence of a rating provided by previous consumers, τt ∈ [1, 5], i's prior about the utility of the product coincides with τt (i.e., agent i believes the “wisdom of crowds”): . If no rating has been given, i's prior on q is assumed to be the ex ante expected quality of q, Ei(q) = 3 (hence write τt = 3 for any period t where no rating is given).
2.1.1. Purchase
An agent i (of any type) decides to purchase the product in period t if .
2.1.2. Rating-Welfare Link
Given true quality q and rating τ, the ex ante welfare of purchase is , which is maximal at τ = q, where social welfare is q2∕2. Given τ = q+δ (rating with some ‘error’), the expression becomes q2+qδ−1∕2(q2−2qδ+δ2) = q2∕2−δ2∕2, which is < q2∕2 and decreasing in the absolute size of the error, |δ|.
Provided τ = q, the ex ante welfare over the whole quality range is . In the absence of rating, this welfare reduces to . Given some erroneous rating τ = q + δ for some δ ≠ 0, , which is > 27 provided δ2 < 3, i.e., the rating is within ca. 1.7 of the true q.
2.1.3. Rating
Agent i, after an ex post experienced quality of qi that is derived from the purchase, can vote on the product in period t so that the period-(t + 1) rating becomes , where is a choice from a standard discrete five-star voting range, . (Agents who do not purchase the good cannot vote). If the agent does not vote, τt+1 = τt.
The ex ante welfare-optimal voting rule is such that i chooses so as to minimize the rating error measured by . We shall refer to voting behavior where i chooses a higher (lower) vote such that () when experiencing a positive (negative) utility as reciprocative. The fake voting behavior always gives provided the marginal impact on τt+1, measured by , is larger than some constant c (cost of providing a fake vote). The following voting behaviors are assumed (see Figure 1 for illustration):
Egoist. The egoist never votes.
Altruist. The altruist always votes welfare-optimally.
Reciprocator. The reciprocator gives a reciprocative vote after a positive utility,
otherwise he does not vote.
Fake. The fake votes five-star if , otherwise he does not vote.
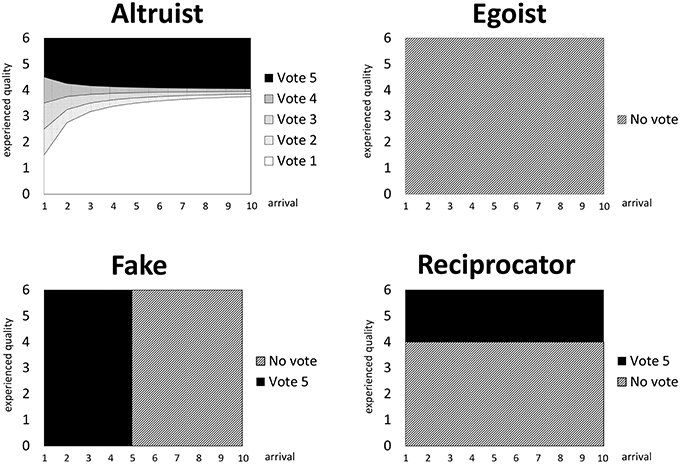
Figure 1. Voting patterns of different behavioral types. The six different voting behaviors (1 star, 2 stars, 3 stars, 4 stars, 5 stars, no vote) are illustrated for each of our four behavioral types (egoist, altruist, reciprocator, fake) as a function of an individual's ex post experienced quality qi (y-axis)—here, supposing ri < 4, c = 1∕7 and τt = 4—while varying the arrival total of votes t (x-axis) that the product has thus far received.
3. Results
3.1. Theoretical Predictions
We shall now derive the theoretical predictions resulting from our behavioral dynamics.
3.1.1. Remark
Egoists have no impact on ratings. Hence, the rating dynamics are predicted by analysis of the dynamic interactions between altruists, reciprocators and fakes, and is describable as a Markov chain. In fact, we will associate all consumers that are not captured by these dynamics with egoism, and not analyze their behavior in further detail. (This behavioral type is “needed” only to argue why many consumers will never vote).
3.1.2. Fake Votes
Over-ratings due to fake voting are expected as long as . Eventually, as t grows and the impact of fake votes is thus reduced, there will be no more fake voting, which will have seized at the very latest by t > 4∕c − 1 provided c > 0 (when for all t even if τt = 1). Before, if over-rating due to fake voting exceeds true quality by more than 1.7, then negative ex ante welfare effects occur as too many consumers will buy the product and experience negative utility.
3.1.3. Altruist Convergence
Altruists' votes polarize over time, meaning that the support (w.r.t. ri) over which agents vote either one- or five-star given any level of τt grows over time. This is a function of the diminishing influence individual star levels have on the rating as t increases. If all agents were altruists, then the process would converge in expectation to the true underlying quality [31].
3.1.4. Over-rating and Reciprocation
Suppose the agent does not purchase the good because he observed a low rating, foregoing an otherwise negative utility. Such an agent has no way of reciprocating as only purchasers can vote. Hence, reciprocity is restricted to situations when the reciprocator derives positive utility from following positive purchase recommendation. As a result, provided t > 4∕c−1 (i.e., only reciprocators and altruists continue to vote), E(τt+1; τt = q) > q because altruists at q will not increase τt+1 beyond τt in expectation. Any reciprocator with ri < qi, however, which in expectation are 50%, will increase the rating beyond the true quality. Reciprocators with ri > qi will end up not voting at all. Note that, as long as τt > 5−1.7 = 3.3, this tendency to over-rate has no negative effect on welfare compared with no-rating.
3.1.5. Empirical Regularities and Simulation Results
Empirical regularities are established on Jindal and Liu [14]'s amazon.com data-mining project (>5 million reviews collected during one calendar month). The short time span of collection is ideally suited for our purposes as (absolute and relative) qualities of products are likely not to change over the sample and thus such phenomena likely play no role. Our focus is on “long” rating sequences from product categories books, music, DVDs, and manufactured products. Four hundred and fifty two products were randomly selected conditional on receiving >50 votes, resulting in a sample of products with 61–1226 votes. Votes for each product are recorded in the order they were posted. The average number of votes is 155 (90% between 61 and 276 votes). The impact of rankings on sales [1–10] is reflected in our data by that fact that products attracting more votes also tend to have higher final ratings (coefficient 0.0006, p-value < 0.001).
Previous empirical analysis of social dynamics focusses on initial ratings [27–29], the main aggregate finding being negative trends, suggestive of initial fake reviews [12–14]. In our data, the initial average vote is 4.35, compared, for example, with 3.89 for the 61st and 4.44 for the 277th votes. Splitting sequences into ordered windows representing 20 subsequent ratings, we obtain negative time trends for the first (–0.0118, p < 0.001), second (–0.0021, p = 0.062), and third (–0.0021, p = 0.058) windows, compared with positive trends overall (0.0002, p < 0.001), indicating a lower “turning point” somewhere between volume 60 and 120. [Trends are positive for the fourth window (0.0089, p = 0.876), fifth window (0.0018, p = 0.175), and thereafter (<0.0001 but >0, p > 0.9)].
Rating variation within a given sequence is typically substantial. From first to final rating, the average maximal difference is 1.33 (a maximum of 3.75 is reached by a particular product). Much of this is due to initial ratings of the sequences which may lie far from (above) the final rating, but even ratings after the 20th reveal substantial changes. The maximal difference between rating 20 and the end of a sequence is 0.46 on average with a maximum of 1.60. Dependent on the total number of votes contributing to a rating, the interpretation concerning a given product's quality may therefore indeed be very different, with implications for the realized welfare-rating link. Note that the variation after ranking 20 is no longer in the range of welfare-detrimental effects compared with no-rating.
The distribution of individual stars evolves as follows. Initially, 283 of the 452 star votes are five-star, 103 four-star, 29 three-star, 13 two-star, and 24 one-star. The respective 11th votes are 249, 112, 31, 20, and 40, displaying a drop in five-star votes. Thereafter, the respective 61st vote frequencies are 237, 88, 32, 29, and 66. Note that the sharpest drop in five-star votes occurs in the first 11 ratings. This suggests that fake reviews are likely to occur within the first 10 votes, but not thereafter.
Figure 2 illustrates the dynamics in ratings and the shares of individual star votes over time.
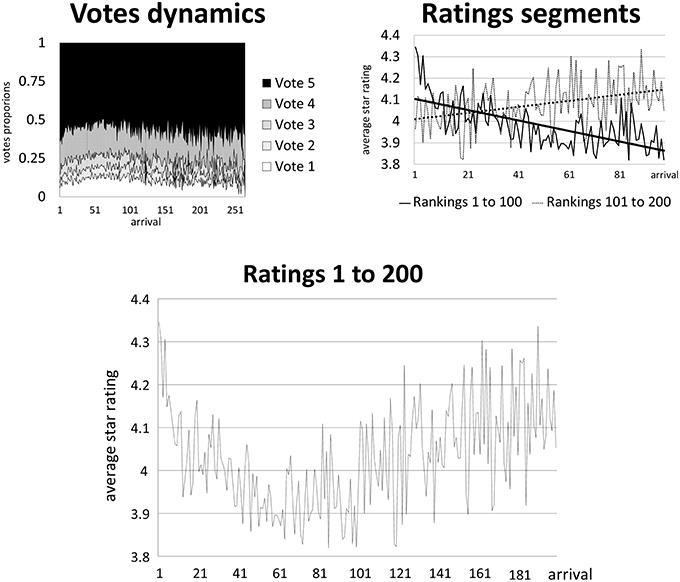
Figure 2. Dynamics in rankings and votes. The x-axes indicate the order in which votes arrive, the y-axes indicate either the votes proportions or the average star rating.
To test the impact of sequence dynamics on the arrival of the individual star votes, we perform ordered probit regressions to test how these change with ratings and volume of sequences over time, allowing for product fixed effects due to differences in qualities across products, for example. For the ordered probit tests, let j denote the index of a product and i the order in a sequence. A latent variable on each product at each order determines the expressed rating: when the variable falls within a k−th interval, the i+1-th expressed rating on j is k (for the five star ratings): where μ1 = −∞, μ6 = ∞. To test whether the observed valence has an influence on the next rating, we specify where is the rating of the first i votes on product j, δj is the fixed effect for product j and the noise (assumed to be i.i.d. normal). α represents the influence of the information released in the observed rating: α < 0 (> 0) implies that larger ratings decrease (increase) chances that the next vote is high. The value of β represents the impact of order, independently of the information in the rating.
For the whole data set, we obtain a positive effect of rating (coefficient 0.2749, p-value < 0.001) and a negative effect for volume (−0.0003, p < 0.001). Qualitatively, the same result is obtained for votes 1-61 (rating 0.2318, p = 0.360; order −0.0041, p < 0.001). A completely different result in terms of ratings' effects, however, is obtained for votes excluding the first twenty 21–61 (rating –0.6117, p < 0.001; order −0.0052, p < 0.001).
To test the implications of our model, we ran five different ensembles of simulations of our model, each consisting of 30 simulations with different random generator seeds. In one of the five simulations ensembles, each type was present with an equal (one quarter) share of the population. In the remaining four simulation ensembles, one type was removed, and only the other three types were present (one third of the population each). For all the simulations, there were 500 products (recall we had 452 in our amazon data sample). The standard deviation of the distribution of experienced qualities was 0.1 and the cost of faking a vote was 0.15. Simulations had an ending condition of 250,000 (500 products, 500 votes on average each) as the total number of votes needed for a simulation to end.
Simulation results summarize as follows. Including all types in our model, yields similar patterns to the ones observed in the amazon data. Excluding altruists or fakes leads to too few votes, and to dynamics that do not match the data at all. Excluding reciprocators (or egoists) leads to similar dynamics, but overall to star levels that are too low (too high) compared with the simulations that included all types. Figure 3 illustrates.
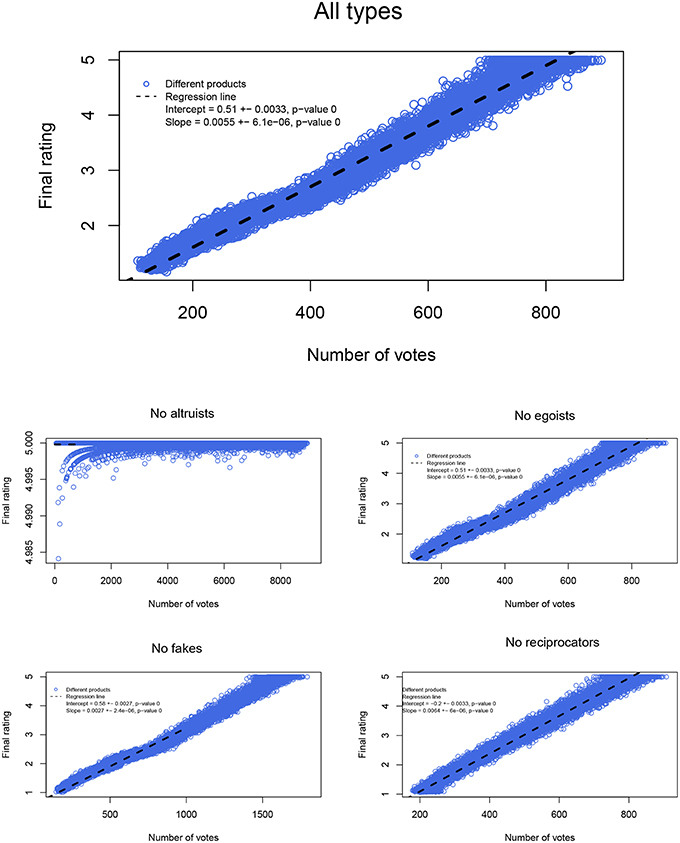
Figure 3. Simulated dynamics. The average final ratings obtained (y-axes) as per different length of series (i.e., number of votes on the x-axes) for the different simulation ensembles are illustrated. The simulations either include all four behavioral types (one simulation with egoist, altruist, reciprocator, fake), or three of the four (four simulations with one type deleted).
4. Discussion
Social dynamics, even in the narrow context of online product ratings, cannot be explainable by a single behavioral model. First and foremost, fake votes have to be separated from informative votes. Moreover, agents without social preferences (egoists) will not vote. The remaining voting behaviors are classifiable into altruistic/welfare-optimal voting (in the sense of aggregate reliability) and reciprocative voting.
Concerning fake votes, our theoretical model predicts that these will seize to arrive after some volume is reached, during which they may actually lead to welfare-decreasing “errors” in rating w.r.t. the true quality of the product. Our empirical analysis indicates that fake voting is a phenomenon typically associated with the first 10 votes only. However, in that period, over-rating explainable by fake votes may be in order of magnitude of over 3 of a maximum of five stars.
The initial over-rating is “corrected” by subsequent votes (votes arriving after 40–80). Indeed, the negative trends in ratings are reversed after the very-early fake votes are corrected for. This correction is associated with “altruistic” voting, characterized by a polarization of votes toward use of “extreme” star-ratings (one and five stars). The resulting bimodality of the distribution of stars bears similarity with box-office performances of movies [32, 33], but the main difference of our model compared to these studies lies in the dynamic and interdependent nature of the emergence of bimodality in our setting. Toward the end of rating sequence, an upward bias is introduced which stems from reciprocative voting. Reciprocative voting is restricted to praise of products and therefore leads to higher votes as corresponds to the true quality perception of consumers.
Our model has several implications which are in line with the rating-influences-sales literature [1–10]. First, very-early ratings should be mistrusted by consumers because of fake votes, providing rationality grounds for the empirical finding that high volume of votes in ratings, by itself, has been shown to have a positive effect on sales. Beyond a critical volume of votes, however, (higher) ratings are informative and therefore also –rationally– justify their empirically observed positive effect on sales. However, the most informative rating typically is not the final rating as reciprocative ratings behaviors create upward biases. An especially informative point to consider is where ratings' sequences reach their lower turning point.
Finally, rating aggregation mechanisms could be improved to explicitly maximize informativeness of the rating. There is some recent literature on how this may be achieved theoretically [34] and using data [35]. In terms of our findings, meaningful corrections to the crude averaging of votes would include discount of very-early high votes (fake), smoothing/discounting over initial windows (fake and reciprocity), and trend correction for very long sequences (reciprocity). We view this paper as a starting point for serious applied and quantitative work related to identifying behavioral types and rating mechanism design.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication. Parts of this research were based on joint work with Gabrielle Demange.
Funding
ANR grant “NET” and ERC Advanced Investigator Grant “Momentum” (Grant No. 324247).
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
First and foremost, the author thanks Gabrielle Demange for collaborating through most of this project, to Bing Liu for sharing his data, and to Madis Ollikainen for research assistance with the simulations. Further thanks go to Dirk Helbing, Bora Erdamar, Rafael Treibich, Michael Mäs, Mehdi Moussaid, members of COSS, three anonymous referees, as well as participants at the Conference on Economic Design 2013 in Lund, Sweden, and at the Workshop on Rating, Ranking, and Recommendation Systems at Paris School of Economics in Paris, France.
References
1. Luca M. Reviews, Reputation, and Revenue: The Case of Yelp. com. Cambridge, MA: Harvard Business School (2011).
2. Chevalier JA, Mayzlin D. The effect of word of mouth on sales: online book reviews. J Market Res. (2006) 43:345–54. doi: 10.1509/jmkr.43.3.345
3. Cabral L, Hortacsu A. The dynamics of seller reputation: evidence from EBAY*. J Ind Econ. (2010) 58:54–78. doi: 10.1111/j.1467-6451.2010.00405.x
4. Jolivet G, Jullien B, Postel-Vinay F. Reputation and Prices on the e-Market:Evidence from a Major French Platform. Toulouse: Institut d'Economie Industrielle (IDEI) (2013). Available online at: http://ideas.repec.org/p/ide/wpaper/27408.html
5. Ghose A, Ipeirotis P, Sundararajan A. Opinion mining using econometrics: a case study on reputation systems. In: Proceedings of the 44th Annual Meeting of the Association for Computational Linguistics. Sydney: ACL (2007).
6. Luca M, Vats S. Digitizing Doctor Demand: The Impact of Online Reviews on Doctor Choice. Cambridge, MA: Harvard Business School (2013).
7. Kumar N, Benbasat I. Research note: the influence of recommendations and consumer reviews on evaluations of website. Inform Systems Res. (2006) 17:425–39.
8. Leskovec J, Adamic L, Adamic B. The dynamics of viral marketing. ACM Trans Web. (2007) 1:1–39. doi: 10.1145/1232722.1232727
9. Danescu-Niculescu-Mizil C, Kossinets G, Kleinberg J, Lee L. How opinions are received by online communities: a case study on Amazon.com helpfulness votes. In: Proceedings of WWW. Madrid (2009) p. 141–50.
10. Moe W, Trusov M. The value of social dynamics in online product ratings forums. J Market Res. (2011) 48:444–56. doi: 10.1509/jmkr.48.3.444
12. Mayzlin D, Dover Y, Chevalier J. Promotional reviews: an empirical investigation of online review manipulation. Am Econ Rev. (2014) 104:2421–55. doi: 10.1257/aer.104.8.2421
13. Luca M, Zervas G. Fake it Till You Make It: Reputation, Competition, and Yelp Review Fraud. Harvard Business School NOM Unit Working Paper (2013) p. 14-006.
14. Jindal N, Liu B. Opinion spam and analysis. In: Proceedings of First ACM International Conference on Web Search and Data Mining. New York, NY (2008).
16. Lorenz J, Rauhut H, Schweitzer F, Helbing D. How social influence can undermine the wisdom of crowd effect. Proc Natl Acad Sci USA. (2011) 108:9020–25. doi: 10.1073/pnas.1008636108
17. Hardin G. The tragedy of the commons. Science (1968) 162:1243–8. doi: 10.1126/science.162.3859.1243
18. Isaac M, McCue K, Plott C. Public goods provision in an experimental environment. J Public Econ. (1985) 26:51–74. doi: 10.1016/0047-2727(85)90038-6
19. Ledyard JO. Public goods: a survey of experimental research. In: Kagel JH, Roth AE, editors. The Handbook of Experimental Economics. Princeton, NJ: Princeton University Press (1997). p. 111–94.
20. Nash J. Equilibrium points in n-person games. Proc Natl Acad Sci USA. (1950) 36:48–9. doi: 10.1073/pnas.36.1.48
21. Olson M. The Logic of Collective Action: Public Goods and the Theory of Groups, Second Printing with New Preface and Appendix (Harvard Economic Studies). Revised ed. Harvard Economic Studies, v. 124. Harvard University Press (1971). Available online at: http://www.amazon.com/exec/obidos/redirect?tag=citeulike07-20&path=ASIN/0674537513
23. Feddersen T. Rational choice theory and the paradox of not voting. J Econ Perspect. (2004) 18:99–112. doi: 10.1257/089533004773563458
24. Feddersen T, Sandroni A. A theory of participation in elections. Am Econ Rev. (2006) 96:1271–82. doi: 10.1257/aer.96.4.1271
25. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys. (2009) 81:591–646. doi: 10.1103/RevModPhys.81.591
26. Galam S. Sociophysics: a review of Galam models. Int J Modern Phys C. (2008) 19:409–40. doi: 10.1142/S0129183108012297
27. Li X, Hitt LM. Self-selection and information role of online product reviews. Inform Systems Res. (2008) 19:456–74. doi: 10.1287/isre.1070.0154
28. Wu F, Huberman BA. How public opinion forms. WINE (2008) 5385:334–41. doi: 10.1007/978-3-540-92185-1_39
29. Godes D, Silva JC. Sequential and temporal dynamics of online opinion. Market Sci. (2012) 31:448–73. doi: 10.1287/mksc.1110.0653
30. Muchnik L, Aral S, Taylor S. Social influence bias: a randomized experiment. Science (2013) 341:647–51. doi: 10.1126/science.1240466
31. List C, Goodin R. Epistemic democracy: generalizing the condorcet Jury theorem. J Polit Philos. (2001) 9:277–306. doi: 10.1111/1467-9760.00128
32. Chakrabarti AS, Sinha S. Self-organized coordination in collective response of non-interacting agents: emergence of bimodality in box-office success. (2013) arXiv:1312.1474.
33. Wasserman M, Mukherjee S, Scott K, Zeng X, Radicchi F, Amaral L. Correlations between user voting data, budget, and box office for films in the internet movie database. J Associat Inf Sci Technol. (2015) 66:858–68. doi: 10.1002/asi.23213
34. Lambert N, Horner J. Motivational feedback. In: Workshop on Rating, Ranking, and Recommendation Systems. Paris (2014).
Keywords: rating dynamics, social influence, amazon data, voluntary contribution dynamics, wisdom of the crowds
Citation: Nax HH (2016) The Logic of Collective Rating. Front. Phys. 4:15. doi: 10.3389/fphy.2016.00015
Received: 19 October 2015; Accepted: 15 April 2016;
Published: 04 May 2016.
Edited by:
Serge Galam, Centre National de la Recherche Scientifique, FranceReviewed by:
Krzysztof Malarz, Akademia Górniczo-Hutnicza University of Science and Technology, PolandBikas K. Chakrabarti, Saha Institute of Nuclear Physics, India
Copyright © 2016 Nax. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Heinrich H. Nax, aG5heEBldGh6LmNo
 Heinrich H. Nax
Heinrich H. Nax