Direct Measurement of Axial Momentum Imparted by an Electrothermal Radiofrequency Plasma Micro-Thruster

1. Introduction

Over the past decade, neutral-gas heating has been experimentally studied both in low-pressure high-power (with and without an applied magnetic field) radiofrequency (rf) discharges [1] and in high-pressure low-power rf discharges [2]. When neutral pressure varies along the axis or across a radius, ionization and transport become coupled and this greatly affects the plasma steady-state [3]. It has been analytically shown [3, 4] that the transport process varies with collisionality (effectively operating pressure and discharge geometry) and power, and also with neutral gas heating [5], thereby yielding very different radial and axial profiles of neutral and charged particle densities and temperatures inside the plasma cavity. The plasma parameters will also vary with the rf power coupling mechanism [6], i.e., the rf electrode configuration and operating conditions. When these rf discharges are considered for use as thrusters, it is necessary to have a detailed understanding of how axial momentum is imparted in the presence of a plasma flow and plasma expansion in vacuum.

Electric thrusters such as ion gridded thrusters, hall effect thrusters, arcjets and resisto-jets are routinely used on satellites [7, 8]. Their usefulness is maximized compared to cold gas and chemical thrusters when their specific impulse exceeds a few hundred seconds but their miniaturization often leads to decreased performances while remaining costly (i.e., gridded engines and Hall effect thrusters require an additional electron neutralizer, usually a Hollow Cathode which needs a certain period of time to achieve optimum operating characteristics). Low-cost low-volume and low-weight thrusters using “green” and safe propellants suitable for use on micro-satellites such as “CubeSats” (based on the 10 cm by 10 cm by 10 cm modular unit) are not readily available. Electrothermal thrusters such as resisto-jets and arcjets aim at heating the propellant and are often in part chemical. For example, arcjets commonly operate with hydrazine or ammonia. Some recent arcjets are essentially cathode spot vacuum arc discharges and erode the cathode producing a stream of metallic blobs and ions. Pulsed Plasma Thrusters also operate by eroding the electrodes and can be scaled down. To date it is extremely difficult to obtain actual thrust balance measurements of microthrusters in general. The recently developed Pocket Rocket concept is essentially an instant “on” radio frequency plasma heated gas thruster [2].

Fruchtman [3] has reported on the effect of the energy deposited in the neutral gas by a collisional plasma and this has been recently confirmed experimentally using volume-average ro-vibrational spectroscopic measurements of neutral gas temperatures in a small-diameter collisional radiofrequency plasma jet known as Pocket Rocket [2, 9]. Neutral gas heating in Pocket Rocket mostly results from ion-neutral collisions in the bulk plasma (charge-exchange and elastic) and from heating at the plasma cavity radial walls [6, 10]. Recent 1D3v Particle In Cell simulations of this plasma jet [11] have provided details on the neutral and charged particles density profiles along the expansion which closely relate to the “open system” analytical analysis by Fruchtman [3], where a net mass flow is considered. Direct measurements of the axial momentum generated by a xenon rf plasma jet expanding in vacuum are reported as a function of two parameters; rf power and gas flow. In essence it is a proof of concept that this type of plasma device generates thrust rather than a test of a space qualified ready system. Future refinements to the rf and gas delivery systems are expected to improve the overall efficiency of the system by a factor of 2–3.

2. Experimental Set Up

Experiments are carried out in the 1 m-diameter 2 m-long Wombat vacuum chamber [12] recently upgraded with a new vacuum pumping system (scroll, turbomolecular, and cryogenic pumps) and a suite of access and viewing ports (Figure 1). The small diameter Pocket Rocket plasma thruster called (MiniPR), is attached to a thrust balance comprising a grounded open cube frame (0.3 × 0.3 × 0.3 m³) suspended from four “chimneys” (Figure 1). A laser-displacement sensor system [13, 14] positioned near the top of the thrust balance mounting is used to measure the displacement of the thrust balance and hence the axial force imparted by the plasma heated gas flow. The base pressure is measured to be about 7 × 10⁻⁷ Torr using an ion gauge and a baratron gauge located 2 m downstream of the thrust balance.

FIGURE 1

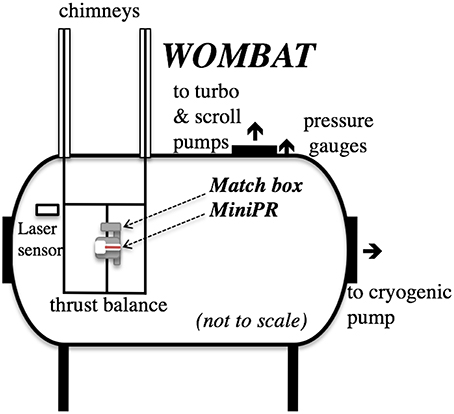
Figure 1. Schematic of the Wombat vacuum chamber showing the MiniPR electrothermal radiofrequency plasma thruster body with Match box mounted on the thrust balance.

Calibration of the thrust balance is carried out in air using precise weights attached to a wire hanging from a pulley (shown in Charles et al. [15]) and yields a typical force-displacement calibration factor of about 0.1 mN/μm. The procedure consisted in recording the balance displacement in μm in air using a motor to drive the pulley and sequentially apply an increasing gravitational force (generated by zero up to 10 weights of 2.1 g each) to yield the calibration factor. The balance would be returned to its resting position of zero displacement (no weight) prior to pump down. Following cold gas and plasma thrust measurements under vacuum, Wombat would be pressurized and the calibration process repeated in air to check the initial calibration factor. The discrepancy was <2.5%.

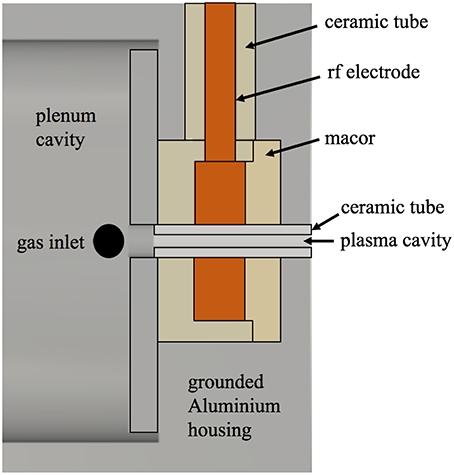
A cartoon of MiniPR is shown in Figure 2 and is fully described in Charles et al. [15, 16]. Briefly, it comprises an 18 mm long 1.5 mm inner diameter ceramic alumina tube plasma cavity having a central annular 5 mm wide rf copper electrode and two grounded 3 mm-wide aluminum electrodes (forming the grounded 8.5 cm diameter aluminum housing), each separated by two macor rings, one 3 mm wide (gas inlet side) and the other 4 mm wide (plasma exhaust side). A 40 mm-diameter 24 mm-long aluminum cavity which acts as gas plenum is terminated by a 26 mm-diameter, 12 mm-deep viewing window (not shown on Figure 2 for clarity).

FIGURE 2

Figure 2. Cartoon showing MiniPR main components.

Xenon propellant gas is introduced via the plenum, flows along the alumina tube, and expands into vacuum. The complete gas line consists of a flow controller placed outside the vacuum system, a gas line feed-through mounted on Wombat and a 4 m long 1 mm inner diameter teflon tube for direct gas injection into the plenum cavity (Figure 2). To minimize vibration noise only the turbomolecular/scroll pumping system is used.

MiniPR's central rf annular electrode is attached to a variable frequency solid state impedance matching network [16] in a grounded aluminum box (“Match box” on Figure 1) via a 20 cm long semi-rigid RG401 coaxial cable. A frequency adjustable MKS generator is used to send power into the match using a 1 m-long coaxial cable inside vacuum and a 4 m-long cable outside vacuum. With the present configuration there is significant power loss (30–50%) in the 12 turns 16 mm-diam 35 mm-long inductance of the solid state matching network [16]. The operating resonant frequency is initially determined for each rf power (typically around 13.8 MHz) by carrying out a number of short plasma shots of a few seconds in duration. This frequency is subsequently used to generate the plasma and obtain direct thrust measurement. Both the rf cable and gas lines inside vacuum are anchored at one position at the top of the thrust balance mounting to minimize mechanical resistance and maintain adequate sensitivity of the thrust balance. This challenging configuration is very distinct from previous thrust measurements using higher-power lower-pressure inductive rf thrusters (in which axial momentum is primarily imparted by accelerated ions rather than neutrals) which did not require mechanical contact between the gas injector and the plasma cavity or between the rf antenna and the plasma cavity [13, 14].

3. Momentum Results and Discussion

3.1. Experimental Thrust Components

The two parameters of interest are the rf power and the xenon gas flow rate. Measurements of the axial momentum imparted by MiniPR are obtained as follow: the manual and automatic gas valves outside vacuum are both opened to inject a constant xenon flow which initially generates substantial oscillations of the balance before a “baseline” position is reached after about one minute. A series of 20 s long plasma shots are subsequently carried out to measure the thrust component imparted by the plasma for varying rf power and a constant flow of 52.5 sccm (5.16 mg.s⁻¹) or for varying xenon flow (the latter is obtained by a fine control of the flow controller which changes the baseline) and a constant rf power of 32 W. The measured thrust is the total thrust F_total and since the ionization degree in the discharge is low (no neutral depletion with the plasma “on”) F_total can be written as

$\begin{array}{ll}{F}_{total}=F_{plasma}+F_{coldgas}& (1)\end{array}$

where F_plasma is the axial force generated by the plasma and F_{cold gas} is the axial force generated by the cold gas flow. After completion of the plasma “shots” the manual shut off gas valve is closed leaving a displacement which corresponds to the F_{cold gas} or “no plasma” thrust component (fortunately, closing the gas valve generates less oscillations than opening the gas valve). For the present study the thrust gain is defined as

$\begin{array}{ll}G=\frac{F_{plasma}}{F_{coldgas}}& (2)\end{array}$

Although the cold gas force would be reduced by the formation of the plasma in highly ionized plasmas (i.e., at high rf power), here the ionization rate is <1% [6] and it is assumed that gas heating does not significantly alters the chocked flow approximation discussed below.

3.2. Effect of Radiofrequency Power

F_total and F_{cold gas} are shown on Figure 3 vs. increasing rf power and constant gas flow of 52.5 sccm (5.16 mg.s⁻¹), giving an operating plenum pressure of 7.7 Torr (1026 Pa). Since the flow is constant, F_{cold gas} is constant and measured to be about 0.8 ± 0.25 mN. Four data sets (Series 1 to 4) were sequentially taken over the course of three consecutive days (without breaking vacuum) yielding an experimental error of ±0.25 mN. Series 1 on day 1 (red filled circles), series 2 on day 2 (open triangles), and series 4 on day 3 (green crosses) were carried out using continuous plasma excitation. Since a rf power larger than about 20 W was required for plasma ignition, series 3 (blue filled squares) was carried out on day 2 using pulsed plasma excitation with a period of 1 ms and a 50 percent duty cycle yielding time-averaged values of 12 and 16.7 W, respectively. Other points in series 3 were obtained using increasing duty cycle values of 20, 40, 60, 80, and 100% to yield increasing time-averaged power values of 10–50 W.

FIGURE 3

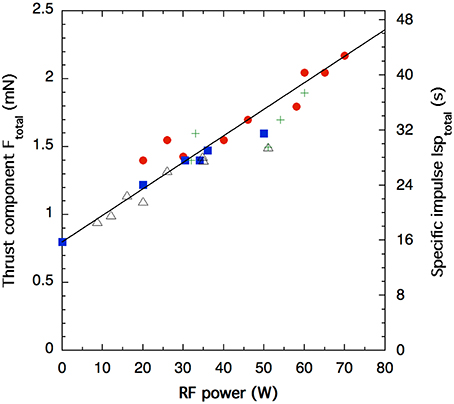
Figure 3. F_total thrust component and I_sptotal specific impulse measured as a function of rf power for four data sets: series 1 (filled red circles), series 2 (open triangles), and series 4 (green crosses) respectively taken on days 1, 2, and 3 for continuous plasma excitation and series 3 (filled blue squares) taken on day 2 for pulsed plasma excitation. The xenon gas flow is constant at 52.5 sccm. The error bar on thrust components is ±0.25 mN. A solid black line is added as a visual guide.

Neglecting the neutral gas pressure term, the axial momentum generated by the cold gas can be approximated for an isentropic choked flow regime [17] by the momentum term

$\begin{array}{ll}{F}_{coldgas}=ṁc_s& (3)\end{array}$

where ṁ is the xenon mass flow rate and $c_s=\sqrt{\frac{{\gamma }_{Xe}RT}{m_{Xe}}}$ is the xenon gas sound speed (T is the gas temperature, R = 287 J.kg⁻¹K⁻¹ is the universal gas constant, γ_Xe is the specific heat capacity for xenon and m_Xe is the xenon molar mass). At T~300 K, c_s is about 170 m.s⁻¹ which yields F_{cold gas} of 0.87 mN very close to the experimental value of 0.8 ± 0.25 mN. As a result of the measurement procedure and the absence of a gas flow valve directly located at the plenum, it is expected that the measured value of F_{cold gas} may be somewhat below the true cold gas thrust due to the residual gas trapped in the small diameter 4 m long teflon tubing gas line which requires hours to be effectively pumped out. This uncertainty may be combined with other effects related to the geometric details of the orifice/nozzle, its sonic surface, and the “free jet” expansion [18, 19].

The results on Figure 3 show that F_total and hence F_plasma increases linearly with rf power and the thrust gain G (defined in Equation 2) is about 1 for a rf power of 40 W. Any gain in thrust is attributed to an increase in the gas exhaust velocity due to neutral gas heating by the plasma. Figure 3 also shows the result of the “effective” or total specific impulse defined as

$\begin{array}{ll}{I}_{s{p}_{total}}=\frac{F_{total}}{ṁg_0}=\frac{(G+1)F_{coldgas}}{ṁg_0}~(G+1)I_{s{p}_{coldgas}}& (4)\end{array}$

where g₀ is the standard gravitational acceleration constant (9.81 m.s⁻²) and

$\begin{array}{ll}{I}_{s{p}_{coldgas}}=\frac{c_s}{g_0}\text{and}{I}_{{\text{sp}}_{\text{plasma}}}=\frac{{\text{Gc}}_{\text{s}}}{{\text{g}}_0}& (5)\end{array}$

are the “cold gas” specific impulse and “plasma” specific impulse, respectively (I_sptotal = I_spplasma + I_{spcold gas}). From Equations 5, I_{spcold gas} is 15.8 s and I_spplasma increases linearly with rf power (Figure 3). This linear variation of F_plasma and I_spplasma with rf power is consistent with a similar variation of plasma density vs. power measured in a previous prototype in the vicinity of the rf electrode for constant argon gas flow [6].

3.3. Effect of Gas Flow

Figure 4 shows thrust and specific impulse measurements obtained for a constant rf power of 32 W and varying xenon gas flow rate from 16.4 to 52.5 sccm (1.61–5.16 mg.s⁻¹), giving a plenum pressure increasing from 3.2 Torr (426 Pa) to 7.7 Torr (1026 Pa). Visual inspection of the discharge through windows on Wombat shows that the most luminous part of the discharge is located in the plasma cavity only (not in the plenum) and that a noticeable “sphere-shaped” plasma plume extending a few mm out is only seen for flows exceeding 30 sccm. From Equation (5), I_{spcold gas} is constant at 15.8 s in this case but F_{cold gas} increases linearly with flow (Equation 3): the open circles on Figure 4 are direct measurements of F_{cold gas} while the open triangles are calculated using Equation (3) (isentropic chocked flow approximation with 1 sccm of Xenon corresponding to 0.0983 mg.s⁻¹ as detailed in Goebel and Katz [7], p. 464). For the lowest gas flow rate of 16.4 sccm (1.61 mg.s⁻¹), F_total is 0.75 mN, i.e., three times greater than the cold gas thrust value F_{cold gas} of 0.25 mN. Hence for this condition the thrust gain for the plasma is G = 2 and from Equation (4), I_sptotal is 48 s, i.e., three times that the I_{spcold gas} value. With the plasma “on” at a fixed forward rf power, the effect of increasing the xenon gas flow leads to a decrease of I_sptotal and an increase of F_total (Figure 4). At a flow rate of 41 sccm (4.03 mg.s⁻¹), F_total is 1.4 mN (G = 1) and remains constant thereafter.

FIGURE 4

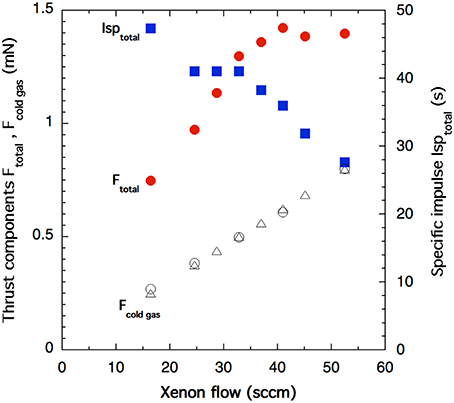
Figure 4. Total F_total (filled red circles) and cold gas F_{cold gas} (open circles) thrust components and total specific impulse I_sptotal (filled blue squares) measured vs. xenon gas flow rate for constant rf power of 32 W and a driving frequency of 13.78 MHz; cold gas specific impulse I_{spcold gas} is constant at ~16 s; F_{cold gas} (open triangles) is calculated using Equation (3). The error bar on thrust components is ± 0.25 mN.

In a typical DC arcjet [20] or cascaded arc [21], the electron density is very high (~10¹⁵cm⁻³) with the discharge near Local Thermal Equilibrium (neutral gas temperature approaching electron temperature) and the energy transfer is dominated by elastic electron-neutral collisions. In such high electron density mode typical of an arc or a filament there are often issues with stability of the arc and electrode erosion but interesting thruster characteristics have been reported for non-reactive gases such as helium [22]. Although MiniPR operating at higher powers and higher pressures may well exhibit a filamentary type of discharge, the currently investigated plasma coupling mode corresponds to an electron density in the 10¹²cm⁻³ range for a pressure of a few Torr for which propellant heating mostly results from ion-neutral collisions (elastic and charge exchange) in the volume and neutral collisions with the plasma cavity wall (resisto-jet effect) which is bombarded by the ion flux especially in the rf electrode region where a self-bias is present. Using a total ion-neutral collisions cross-section of about ${\sigma }_{X{e}^{+}-Xe}~10^{-18}{m}^2$ for xenon [23], the corresponding mean free path ${\lambda }_i=\frac{1}{n_g{\sigma }_{X{e}^{+}-Xe}}$ at a mid cavity pressure of 3.85 Torr (513 Pa), half of the plenum pressure for 52.5 sccm gas flow rate, and a neutral gas density of $n_g~1.36\times 10^{23}$m⁻³ is 7.35 microns yielding 200 collisions across a plasma cavity diameter of 1.5 mm (about two thirds of which would be ion-neutral charge exchange collisions).

The observed decrease of the I_sp with increasing flow (Figure 4) is most likely due to the plasma power being shared among an increasing number of gas atoms and a consequent decrease in the upstream temperature and sound speed. The saturation of the thrust with increasing flow is not presently understood and is being investigated. It is likely that the increasing collisionality affects the radial and axial form of the electric fields that heat the ions which subsequently heat the neutrals (the low ionization degree gives rise to weak electric fields within the plasma plume). Flow rates above 40 sccm leads to higher rates for elastic and charge exchange collisions which could result in a poorer collimation of charged particles inside the choked flow and therefore in lower momentum along the axial direction. Higher mass flow rates of xenon also represents higher pressures in the plenum, where a secondary plasma could be triggered thereby distributing the applied rf power to the plasma plume, decreasing the charge production and leading to lower thrust.

Since Figure 3 corresponds to a flow of 52.5 sccm (maximum investigated flow in Figure 4), and I_sptotal increases by a factor of two when the flow is decreased to 16.4 sccm (Figure 4), a linear extrapolation suggests that a specific impulse of about 100 s could be obtained for a power of 70 W. An increase of power efficiency by a factor of two to four can be expected by optimizing this type of plasma jet for space use, including investigation of the role of the plasma cavity geometry, the type of material use for the rf electrode and plasma cavity, and optimizing the rf match configuration. For a thrust gain G of about 2 (16.4 sccm on Figure 4), the corresponding gas velocity is about three times the sound speed (510 m.s⁻¹) which yields an estimated gas temperature of about 1600 K in good agreement with typical results recently obtained by ro-vibrational spectroscopy in argon in a similar geometry [15].

The results indicate that the choked flow approximation is appropriate. The sonic surface at the exit of the cavity can be determined by computer fluid simulation as shown by Charles et al. [15] and it is this surface averaged velocity which should determine the cold gas flow under choked flow approximation. Downstream of this sonic surface, the gas will expand and accelerate. The latter is still under investigation: there is an axial pressure gradient and the approximation looses its validity downstream of the plasma cavity.

The Hollow Cathode Thruster which has been flown by Surrey Satellite Technology Ltd on TechDemoSat-1 has similar performance: tests with xenon performed on the ground indicated that the Hollow Cathode Thruster would provide 85 s of specific impulse, 1.5 mN of thrust. It required 50–60 W during heating and 40–60 W during discharge at nominal conditions [24].

4. Conclusions

In summary, direct measurements of plasma and cold gas axial thrust components generated by a xenon rf plasma jet have been performed. The cold gas thrust and specific impulse are in agreement with calculations made assuming an isentropic choked flow regime. The momentum gain from the plasma increases linearly with rf power and the I_sp increases with decreasing gas flow. At low flow rates the thrust and I_sp are consistent with an upstream gas temperature of 1600 K reported previously for a similar system operating outside vacuum [15]. The tests with varying rf power showed a possible advantage of MiniPR: when pulsed, the thrust was that expected for a continuous plasma. Consequently, it would be possible to use this thruster with a switch on time in the microsecond range, and combined with gas puffing would allow controlled thrusts down into the micro-Newton range.

Author Contributions

All authors contributed as a team effort. The experiments were carried out at the Australian National University by the authors affiliated to that institution.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was partially funded by the Australian Space Research Program [Wombat upgrade as part of the Australian Plasma Thruster (APT) project] of the Department of Industry, Innovation, Science, Research and Tertiary Education (Australian Government), the Australian Research Council Discovery Project (Pocket Rocket thruster research as part of the DP140100571 project), and Lockheed Martin US (Pocket Rocket thruster Research and Development contract).

References

1. Aanesland A, Liard L, Leray G, Jolly J, Chabert P. Direct measurements of neutral density depletion by two-photon absorption laser- induced fluorescence spectroscopy. Appl Phys Lett. (2007) 91:121502. doi: 10.1063/1.2786601

CrossRef Full Text | Google Scholar

2. Greig A, Charles C, Hawkins R, Boswell R. Direct measurement of neutral gas heating in a radio-frequency electrothermal plasma micro-thruster. Appl Phys Lett. (2013) 103:074101. doi: 10.1063/1.4818657

CrossRef Full Text | Google Scholar

3. Fruchtman A. Energizing and depletion of neutrals by a collisional plasma. Plasma Sources Sci Technol. (2008) 17:024016. doi: 10.1088/0963-0252/17/2/024016

CrossRef Full Text | Google Scholar

4. Fruchtman A, Makrinich G, Chabert P, Rax JM. Enhanced plasma transport due to neutral depletion. Phys Rev Lett. (2005) 95:115002. doi: 10.1103/PhysRevLett.95.115002

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Liard L, Raimbault J-L, Rax J-M, Chabert P. Plasma transport under neutral gas depletion conditions. Phys Plasmas (2007) 40:5192. doi: 10.1088/0022-3727/40/17/026

CrossRef Full Text | Google Scholar

6. Charles C, Boswell R. Measurement and modeling of a radiofrequency micro-thruster. Plasma Sources Sci Technol. (2012) 21:022002. doi: 10.1088/0963-0252/21/2/022002

CrossRef Full Text | Google Scholar

7. Goebel DM, Katz I. Fundamentals of Electric Propulsion. Hoboken, NJ: Wiley (2008).

Google Scholar

8. Charles C. Plasmas for spacecraft propulsion. J Phys D Appl Phys. (2009) 42:163001. doi: 10.1088/0022-3727/42/16/163001

CrossRef Full Text | Google Scholar

9. Boswell RW. Plasma Micro-Thruster. International Patent WO 2012151639 A1. Madison, CT: IFI CLAIMS Patent Services.

10. Greig A, Charles C, Paulin N, Boswell R. Volume and surface propellant heating in an electrothermal radio-frequency plasma micro-thruster. Appl Phys Lett. (2014) 105:054102. doi: 10.1063/1.4892656

CrossRef Full Text | Google Scholar

11. Charles C, Hawkins R, Boswell R. Particle in cell simulation of a radiofrequency plasma jet expanding in vacuum. Appl Phys Lett. (2015) 106:093502. doi: 10.1063/1.4914109

CrossRef Full Text | Google Scholar

12. Charles C, Boswell RW, Bish A. Variable frequency matching to a radiofrequency source immersed in vacuum. J Phys D Appl Phys. (2013) 46:365203. doi: 10.1088/0022-3727/46/36/365203

CrossRef Full Text | Google Scholar

13. Lafleur T, Takahashi K, Charles C, Boswell RW. Direct thrust measurements and modelling of a radio-frequency expanding plasma thruster. Appl Phys Lett. (2011) 18:080701. doi: 10.1063/1.3610570

CrossRef Full Text | Google Scholar

14. Takahashi K, Lafleur T, Charles C, Alexander P, Boswell RW. Electron diamagnetic effect on axial force in an expanding plasma: experiments and theory. Phys Rev Lett. (2011) 107:235001. doi: 10.1103/PhysRevLett.107.235001

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Charles C, Bish A, Boswell RW, Dedrick J, Greig A, Hawkins R, et al. A short review of experimental and computational diagnostics for radiofrequency plasma micro-thrusters. Plasma Chem Plasma Process. (2016) 36:29–44. doi: 10.1007/s11090-015-9654-5

CrossRef Full Text | Google Scholar

16. Charles C, Boswell RW, Bish A. Low-weight fixed ceramic capacitor impedance matching system for an electrothermal plasma microthruster. J Propul Power (2014) 30:1117. doi: 10.2514/1.B35119

CrossRef Full Text | Google Scholar

17. Wilcox DC. Basic Fluid Mechanics, 3rd Edn. San Diego, CA: DCW Industries (2007).

18. Murphy HR, Miller DR. Effects of nozzle geometry on kinetics in free-jet expansion. J Phys Chem. (1984) 88:4474.

Google Scholar

19. Arakoni RA, Ewing JJ, Kushner MJ. Microdischarges for use as microthrusters: modelling and scaling. J Phys D Appl Phys. (2008) 41:105208. doi: 10.1088/0022-3727/41/10/105208

CrossRef Full Text | Google Scholar

20. Zube DM, Myers RM. Thermal nonequilibrium in a low-power arcjet nozzle. J Propul Power (1993) 9:545.

Google Scholar

21. Van de Sanden MCM, de Regt JM, Schram DC. Recombination of argon in an expanding plasma jet. Phys Rev E (1993) 47:2792.

PubMed Abstract | Google Scholar

22. Willmes GF, Burton RL. Low-Power helium pulsed arcjet. J Propul Power (1999) 15:440.

Google Scholar

23. Piscitelli D, Phelps AV, de Urquijo J, Basurto E, Pitchford LC. Ion mobilities in Xe/Ne and other rare-gas mixtures. Phys Rev E (2003) 68:046408. doi: 10.1103/PhysRevE.68.046408

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Lamprou D, Lappas VJ, Shimizu T, Gibbon D, Perren M. Hollow cathode thruster design and development for small satellites. In: IEPC-2011-151 Proceedings, The 32nd International Electrical Propulsion Conference. Wiesbaden (2011).

Google Scholar