- GREMI UMR7344, Centre National de la Recherche Scientifique, Université d'Orléans, Orléans, France
Molecular Dynamics simulations are carried out for investigating atomic processes of platinum sputtering. Sputtered Pt atom energy distribution functions (EDF) are determined at different sputtering argon ionenergies: 100, 500, and 1000 eV. Calculated EDF show a cross-over from Thompson theory to binary collision model when increasing argon ion energy and Pt atom sputtered energy. Implanted argon ion number is depending on its kinetic energy, while it is not the case in binary collision approximation. Finally sputtering yields are greater for Thompson theory than for binary collision model at low energy, but converge to the close values at high energy.
Introduction
Platinum in the form of dispersed nanoclusters is a well-known catalysts used in many applications [1] as fuel cells and chemical sensors, for example. Due to its high cost, it has been necessary to find deposition techniques suitable for lowering its quantity and at the same time retaining or increasing its catalyst activity and its selectivity. Among the various existing possibilities, plasma sputtering deposition has attracted attention due to its simplicity, scalability in the industry [2–4] and in the case of noble metal catalyst, its capability for controlling catalyst shape, size, and concentration profile in catalytic active layers [5–11]. This capability is largely dependent of the sputtering conditions as bias potential of the sputtering target or as the nature of the plasma forming elements. Sputtering yield, impinging ion retention and energy distribution of sputtered particles are often the main information that are searched for. Many works have been carried out both analytically and by simulations for recovering this information. A very popular simulation tool, able to determine sputtering yield, i.e., sputtered atom energy distribution function, is the SRIM software (version 2013 with 2008 stopping power parameters) [12, 13], which considers an amorphous target and ignores the interaction between trapped sputtering ions, and consequently the effect of their accumulation in the target. This is due to the fact that calculation always considers a pristine target. Moreover, interactions between incoming ion and target atoms, and between target atoms are treated in the frame of binary collision approximation [12] which means essentially that these collisions are statistically independent, and so that many-body effects occurring during collision cascades are not treated. On the other hand, a new empirical formula [14, 15], called Yamamura formula, is available for calculating the sputtering yield based on the Sigmund theory [16] using the Ziegler-Biersack-Littmark (ZBL) [17] screened repulsive potential and including the Lindhard electronic stopping power [18]. This model also includes a correction at sputtering ion low energy by including the sputtering threshold energy [14]. In that case, the sputtering rate can be calculated through the Yamamura formula:
where E is the incoming sputtering ion energy, mg and ms are the masses of ion and target atom in a.m.u., respectively, and the numerical factor in units of Å−2. Us is the target surface binding energy. Eth is the sputtering threshold energy. Sn(E) is the stopping power. Γ, Q, and α* are (fitting) parameters as defined in Yamamura and Tawara [14].
Moreover, the Thompson model [19, 20], issued from collision cascade theory, is able to provide an empirical formula of the sputtered atom energy distribution function. Basically, in a binary collision approach, the main ingredient is to calculate the collision differential cross-section of an incident ion with a surface atom, which recoils upon impact, leading for a collision cascade (the extent of the collision cascade being dependent of the transferred energy). The interaction potential in this case is a purely repulsive potential, and thus suitable for high energy (above 1 keV) impinging ions. The overall process is treated statistically in including a recoil density. Assuming that sputtering is issued from such random collisions and also from focused collision cascade, the energy distribution function f(E) of this model reads [19–22]:
where Ecoh is the cohesive energy of the target material, E is the energy of the ejected atoms, is the kinetic energy mass transfer factor, for which mg and ms are gas/plasma phase atom (e.g., argon) and target sputtered atom masses, respectively, and EAr+ is the kinetic energy of the impinging Ar ions.
As the sputtering process is of atomic nature, simulating at the atomic level the mechanism of atom ejection is of primary importance. Besides these well practiced method, Molecular Dynamics (MD) simulations which are calculating all trajectories of a system of particles are very attractive, as they give insights in all coupled dynamical processes, including many-body effects [23]. Thus, studying sputtering phenomena using MD allows overcoming approximations involved in binary collision approximations and empirical modeling [23–30], even if not so much studies have been carried out, especially at ion energy below 1 keV.
The present work is addressing the determination of sputtering yields, retention rates, and sputtered atom energy distribution functions (EDF) in the case of platinum sputtering at various incoming sputtering argon ion energies, thanks to MD theory. The results are compared with SRIM, Yamamura and Thompson model calculations in order to show how MD simulations are able to give a complementary insight of sputtering phenomena.
MD Simulations
In MD simulations, a system evolution is followed at the atomic/molecular scale by solving a set of Newton equations of motions:
where is the position of atom i at time t with mass mi, and V is the interaction potential between all involved species.
The platinum target is modeled by a (100) 50 × 50 × 25 lattice units simulation cell, i.e., a target of size 196 × 196 × 98 Å3, comprising 150,000 platinum atoms. This target is divided in three zones. The bottom layer is composed of six layers of atoms. These atoms are immobilized. In an intermediate zone (layers 7–20) the target temperature is controlled by a Berendsen thermostat for dissipating the ion transferred energy. This second region is thick enough for preventing the cascading atoms to collide with the atoms belonging to the bottom zone, where atoms are immobilized. In the third outermost surface zone (top five remaining layers) the target atoms can move freely, upon impact. This remaining zone is thick enough for allowing any sputtered atom to escape the surface with the right energy, i.e., without any artificial damping coming from the thermostat. In this way, we avoid to externally control the entire target.
The damping constant of the Berendsen thermostat is chosen to be the thermal relaxation time calculated from the electron-phonon coupling theory [31, 32] and is expressed as:
ΘD is the Debye surface temperature, Ts the target temperature, L the Lorentz number, n the electron density, e the electron charge, kB the Boltzmann constant, Z the valence, me the electron mass, κ the thermal conductivity, εF the Fermi energy and Tk is the kinetic temperature. For Pt, τ = 1.2 ps.
Incoming argon ions are randomly placed at a height between 12 and 23 Å above the platinum target and are released toward the surface every 2 ps for allowing correct thermal relaxation of the target. This is ensured by the fact that such a delay between each ion injection is smaller than the thermal relaxation constant τ. The initial velocity of the incoming ions is normal to the target surface (see Figure 1) and corresponds to three chosen kinetic energies: 100, 500, and 1000 eV, respectively corresponding to velocities 219, 490, and 693 Å.ps−1. These three energy values are explored for the following reasons: 100 eV is closed to the sputtering threshold which gives enough statistics for obtaining an energy distribution function of the sputtered atoms. Five-hundred electronvolt is typical of sputtering energy in experiments. The 1000 eV energy is chosen for evaluating the “common” idea that SRIM yields are correct from this energy and above. So if MD yields are close to SRIM results, this will give the indication that MD is correctly operating. Due to the high velocities, the integration time step is fixed to 0.1 fs. The Pt target atoms are located at the crystal position and their velocities are randomly chosen in the Maxwell-Boltzmann distribution at the target temperature, Ts = 300 K here. It should be noticed that Ar+ ions are treated as fast neutral in the present MD simulations. This is justified while they are neutralized by free electrons of the Pt target before they impact the surface.
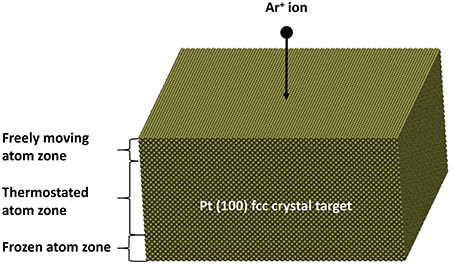
Figure 1. Initial configuration of the simulation. Small spheres are Pt atoms at the crystal position. The incoming Ar ion is at random location above the surface and it is directed to the Pt surface.
In this work, the interactions between target Pt atoms are modeled using embedded Atom Model (EAM) potential [33–36], while Ar-Pt and Ar-Ar interactions are described by pairwise repulsive Moliere potentials.
EAM potential V(r) is of the form:
where Ei is the potential energy of an atom i, ϕ(rij) is the pair energy term as a function of the interatomic distance rij between atoms i and j, and Fi(ρi) is the many-body embedding energy term as a function of the local electron density ρi, at the position of atom i. The local electron density is calculated as a linear sum of the partial electron density contributions from the neighboring atoms:
where fj(rij) is the contribution from atom j to the electron density at the site of the atom i. The pair energy term is defined as:
where re is the equilibrium spacing between nearest neighbors, A, B, α, and β are four adjustable parameters, and κ and λ are two additional parameters for the cutoff distances. The electron density function is taken to have the same form as the attractive term in the pair potential with the same values.
The electron density function is given by:
The Moliere potential takes the simple form of the universal form for the screened Coulomb potential [23]:
For which with aB = 0.529177 Å and Z1 and Z2 are the atomic number of the collision partners. This potential is suitable for the energy range of the argon ions and captures the essential physics of the ion interactions with target atoms.
The simulations have been carried out using the LAMMPS GNU open source code [37]1, on a 40 core Intel Xeon High Performance Computer (ALINEOS SA). One run lasts for 15 days using 9 core for describing 4 ns of the process corresponding to 4 107 iterations. CPU time is high due to the numerous interactions with and within the large Pt target (150,000 atoms).
Results and Discussion
Calculation of sputtering rates and argon retention and energy distribution of sputtered Pt atoms are carried out at three energies of the sputtering argon ions: 100, 500, and 1000 eV. High 1000 eV energy is chosen as it is expected that SRIM is better suited for high energy and is known to be questionable at lower energies.
On Figure 2 are plotted the values of sputtering yields Γ using Yamamura formula, SRIM and MD simulations, and argon retention rate τ only using SRIM and MD, at these three energies.
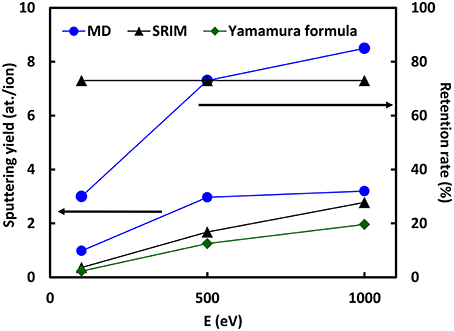
Figure 2. Pt sputtering yields and Ar retention rates as a function of Ar+ ion sputtering energies at normal incidence.
MD simulations are providing a sputtering rate which is over the SRIM values but being closer to SRIM at higher energies values. Yamamura formula sputtering yields are always under both MD and SRIM. Concerning the comparison of SRIM and MD, similar overestimation of MD compared to SRIM has already been observed for Ar sputtering of Cu [26]. This can be due to the fact that Ar retention in the Pt target is reducing Pt atom binding, despite many-body effects insuring Pt cohesion are operating.
Figure 3 displays the EDF of the sputtered Pt atoms at the three considered energies. The number of incident Argon atom is 2000 and released one after each other every 2 ps (i.e., every 20,000 time steps), allowing enough relaxation of the Pt target and thus preventing interaction between collision cascades of two successive argon ions. The SRIM simulations are considering 5000 incident ions. The Yamamura formula does not required any simulations.
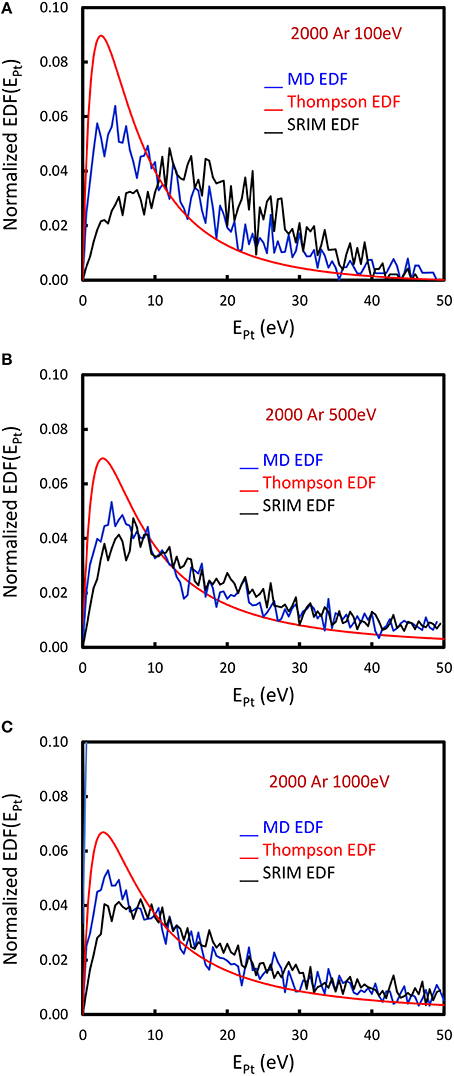
Figure 3. Energy distribution function (EDF) of the sputtered Pt atoms. Ar ion kinetic energy of (A) 100 eV, (B) 500 eV, (C) 1000 eV.
Comparison with SRIM and Thompson formula is very interesting. At all incident Ar+ kinetic energy, MD EDF maximum is located at the same energy of Thompson EDF, which is always located at a fixed position, Ecoh/2, while SRIM maximum is shifted toward higher energies. When increasing Ar+ ion energy the SRIM EDF maximum is shifting toward Thompson and MD EDF maxima. The tail of the EDFs above 10 eV are all different for the three different methods: the MD EDF tail is situated between the rapidly decreasing Thompson EDF tail and the SRIM one. When increasing incident Ar+ kinetic energy, the MD and SRIM EDF tails are almost overlapping.
This shows that the Thompson EDF is consistent with MD simulations at low incident Ar+ kinetic energy, almost on the entire range of the sputtered energies. At this low incident Ar+ kinetic energy, the Thompson formula is almost overlapping with the MD EDF below 10 eV sputtered Pt atom energy, while SRIM is coinciding above 10 eV.
Thus, MD simulations are reproducing features of both SRIM calculations and Yamamura analytical formula, for all incident Ar+ kinetic energies, i.e., between sputtering threshold and 1000 eV. Above 1000 eV, it has already been demonstrated that MD becomes close to SRIM [24].
For further comparison, the mean kinetic energies deduced from these EDFs can also be compared, and reported in Figure 4.
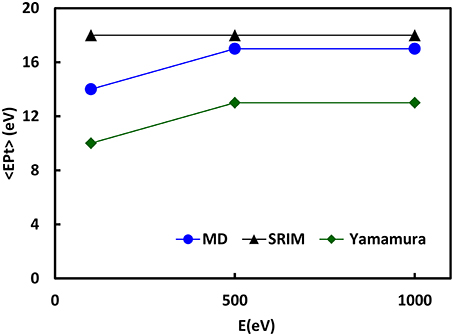
Figure 4. Mean kinetic energies of sputtered Pt as a function of the Ar+ incoming kinetic energy at normal incidence and for the three different calculation methods.
The evolution of mean kinetic energies also illustrates the differences highlighted above between the three methods. MD and SRIM mean kinetic energies are close above 500 eV. In fact, SRIM does not exhibit any change of the Pt mean kinetic energy, while MD deals with a lower Pt mean kinetic energy at lower Ar+ incoming kinetic energy. While Pt mean kinetic energy evolution for Thompson model is similar, the values are systematically 20% lower. This can be considered not so much different, but when looking at the EDFs, the main difference lies in the EDF high energy tail region, for which more numerous high energy sputtered Pt are present for the MD EDF than for Yamamura EDF. This can result in important differences in film properties/structure when studying deposition of Pt on a substrate. So discussing deposited film properties only using the mean kinetic energy parameter is not sufficient for qualifying the energy effects during sputtered atom deposition.
Conclusion
MD simulations of Pt plasma sputtering are carried out for understanding properties of sputtered Pt atoms, especially the EDF, the sputtering rates as well as retention rates. Comparison with popular semi-empirical and binary collision models shows that MD simulations can be applied successfully over a broad range of Ar+ kinetic energies and sputtered Pt energies. Moreover, it exhibits a cross-over from the Yamamura model at low sputtering energy and to the SRIM model at energies higher than 10 eV. The study of other parameters also shows that MD and SRIM are very close at energies above 500 eV. While SRIM model is already known to fail at low sputtered Pt energy, it is anticipated that MD describes correctly interactions at low energies.
Author Contributions
PB run simulations and write the article. SC and JB contributed to discussions of the results and to the writing of the article.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
CNRS is gratefully acknowledged for granting SIMMEPAC project.
Footnotes
References
1. Chen A, Holt-Hindle P. Platinum-based nanostructured materials: synthesis, properties, and applications. Chem Rev. (2010) 110:3767–804. doi: 10.1021/cr9003902
3. Westwood WD. Sputter Deposition AVS Education Committee Book Series, Vol. 2. New York, NY: AVS (2003).
4. Kelly PJ, Arnell RD. Magnetron sputtering: a review of recent developments and applications. Vacuum (2000) 56:159–72. doi: 10.1016/S0042-207X(99)00189-X
5. Andreazza P, Andreazza-Vignolle C, Rozenbaum JP, Thomann A-L, Brault, P. Nucleation and initial growth of platinum islands by plasma sputter deposition. Surf Coat Technol. (2002) 151–2:122–7. doi: 10.1016/S0257-8972(01)01604-8
6. Caillard A, Brault P, Mathias J, Charles C, Boswell R, Sauvage T. Deposition and diffusion of platinum nanoparticles in porous carbon assisted by plasma sputtering. Surf Coat Technol. (2005) 200:391–4. doi: 10.1016/j.surfcoat.2005.01.033
7. Rabat H, Brault P. Plasma sputtering deposition of PEMFC porous carbon platinum electrodes. Fuel Cells (2008) 8:81–6. doi: 10.1002/fuce.200700036
8. Brault P, Josserand C, Bauchire J-M, Caillard A, Charles C, Boswell RW. Anomalous diffusion mediated by atom deposition into a porous substrate. Phys. Rev. Lett. (2009) 102:045901. doi: 10.1103/PhysRevLett.102.045901
9. Cavarroc M, Ennadjaoui A, Mougenot M, Brault P, Escalier R, Tessier Y, et al. Performance of plasma sputtered Fuel Cell electrodes with ultra-low Pt loadings. Electrochem Commun. (2009) 11:859–61. doi: 10.1016/j.elecom.2009.02.012
10. Brault P. Review of low pressure plasma processing of proton exchange membrane fuel cell electrocatalysts. Plasma Processes Polym. (2016) 13:10–8. doi: 10.1002/ppap.201500171
11. Matsumyia M, Shin W, Izu N, Murayama N. Nano-structured thin-film Pt catalyst for thermoelectric hydrogen gas sensor. Sens Actuat B (2003) 93:309–15. doi: 10.1016/S0925-4005(03)00223-5
12. Ziegler JF, Ziegler MD, Biersack JP. SRIM – The stopping and range of ions in matter (2010). Nucl Instrum Methods Phys Res B (2010) 268:1818–23. doi: 10.1016/j.nimb.2010.02.091
13. Stoller RE, Toloczko MB, Was GS, Certain AG, Dwaraknath S, Garner FA. On the use of SRIM for computing radiation damage exposure. Nucl Instrum Methods Phys Res B (2013) 310:75–80. doi: 10.1016/j.nimb.2013.05.008
14. Yamamura Y, Tawara H. Energy dependence of ion-induced sputtering yields from monoatomic solids at normal incidence. At Data Nucl Data Tables (1996) 62:149–253.
15. Ono T, Kenmotsu T, Muramoto T. Simulation of the sputtering process. In: Depla D, Mahieu S, editors. Reactive Sputter Deposition. Berlin: Springer-Verlag (2009). p. 1–42.
16. Sigmund P. Theory of sputtering. I. Sputtering yield of amorphous and polycrystalline targets. Phys Rev. (1969) 184, 383.
17. Ziegler JF, Biersack JP, Littmark U. The Stopping and Range of Ions in Solids. New York, NY: Pergamon Press (1985).
18. Lindhard J, Scharff M. Energy dissipation by ions in the keV region. Phys Rev. (1961) 124:128–30.
19. Thompson W. II. The energy spectrum of ejected atoms during the high energy sputtering of gold. Philos Mag. (1968) 18:377–414.
21. Meyer K, Schuller IK, Falco CM. Thermalization of sputtered atoms. J Appl Phys. (1981) 52:5803–5.
22. Gras-Marti A, Valles-Abarca JA. Slowing down and thermalization of sputtered particle fluxes: energy distributions. J Appl Phys. (1983) 54, 1071–5.
23. Graves DB. Brault P. Molecular dynamics for low temperature plasma-surface interaction studies. J Phys. D (2009) 42:194011. doi: 10.1088/0022-3727/42/19/194011
24. Urbassek HM. Molecular-dynamics simulation of sputtering. Nucl Instrum Methods Phys Res B (1997) 122, 427–41.
25. Brault P, Neyts E. Molecular dynamics simulations of supported metal nanocatalyst formation by plasma sputtering. Catal Today (2015) 256:3–12. doi: 10.1016/j.cattod.2015.02.004
26. Bringa EM, Johnson RE. Molecular dynamics study of non-equilibrium energy transport from a cylindrical track: I. Test of “spike” models. Nucl Instrum Methods Phys Res B (1998) 143:513–35.
27. Bringa EM, Johnson RE, Dutkiewicz L. Molecular dynamics study of non-equilibrium energy transport from a cylindrical track: Part II Spike models for sputtering yield. Nucl Instrum Methods Phys Res B (1999) 152:267–90.
28. Bringa EM, Johnson RE, Jakas M. Molecular-dynamics simulations of electronic sputtering. Phys Rev B (1999) 60:15107–16.
29. Kress JD, Hanson DE, Voter AF, Liu CL, Liu X-Y, Coronell DG. Molecular dynamics simulation of Cu and Ar ion sputtering of Cu (111) surfaces. J Vac Sci Technol A (1999) 17:2819–25.
30. Liu X-Y, Daw MS, Kress JD, Hanson DE, Arunachalamb V, Coronell DG, et al. Ion solid surface interactions in ionized copper physical vapor deposition. Thin Solid Films (2002) 422:141–9. doi: 10.1016/S0040-6090(02)00870-2
31. Flynn CP, Averback RS. Electron-phonon interactions in energetic displacement cascades. Phys Rev B (1988) 38:7118–20.
32. Hou Q, Hou M, Bardotti L, Prevel B, Melinon P, Perez A. Deposition of AuN clusters on Au(111) surfaces. I. Atomic-scale modelling. Phys Rev B (2000) 62:2825–34. doi: 10.1103/PhysRevB.62.2825
33. Daw MS, Baskes MI. Embedded-atom method: derivation and application to impurities, surfaces, and other defects in metals. Phys Rev B (1984) 29:6443.
34. Foiles S, Baskes M, Daw M. Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys Rev B (1986) 33:7983.
35. Daw MS, Foiles SM, Baskes MI. The embedded-atom method: a review of theory and applications. Mater Sci Rep. (1993) 9:251–310.
36. Foiles SM, Baskes MI. Contributions of the embedded-atom method to materials science and engineering. MRS Bull. (2012) 37:485–91. doi: 10.1557/mrs.2012.93
Keywords: plasma sputtering, molecular dynamics simulation, atom energy distribution function, sputtering rate, low temperature plasmas
Citation: Brault P, Chuon S and Bauchire J-M (2016) Molecular Dynamics Simulations of Platinum Plasma Sputtering: A Comparative Case Study. Front. Phys. 4:20. doi: 10.3389/fphy.2016.00020
Received: 26 January 2016; Accepted: 25 April 2016;
Published: 10 May 2016.
Edited by:
Agnes Granier, Centre National de la Recherche Scientifique, FranceReviewed by:
Thomas Mussenbrock, Ruhr University Bochum, GermanyStephanos Konstantinidis, National Fund for Scientific Research, Belgium
Copyright © 2016 Brault, Chuon and Bauchire. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pascal Brault, cGFzY2FsLmJyYXVsdEB1bml2LW9ybGVhbnMuZnI=
 Pascal Brault
Pascal Brault Sotheara Chuon
Sotheara Chuon Jean-Marc Bauchire
Jean-Marc Bauchire