An addendum on
Protocol for Counterfactually Transporting an Unknown Qubit
by Salih, H. (2016). Front. Phys. 3:94. doi: 10.3389/fphy.2015.00094
We give a simpler, more precise formulation for Equations (1–3) in Salih [1], and consequently for transport fidelity, Equation (15). This does not affect the validity of the protocol nor the scientific conclusions of the paper. The fidelity of counterfactual transport for finite inner and outer cycles is re-evaluated and plotted in Figure 1 below.
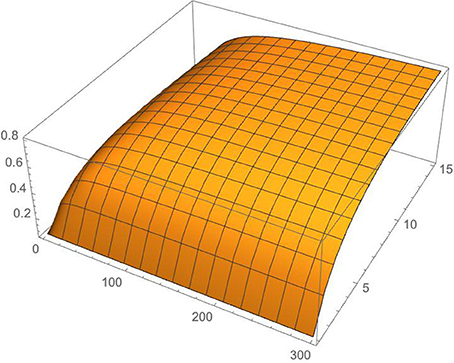
Figure 1. Ideal case fidelity of counterfactual transport. Fidelity is plotted against the number of outer and inner cycles, M and N, for M up to 15 and N up to 300, with . For M = 15 and N = 300 fidelity is already above 80%. The fidelity of our protocol for counterfactual transport approaches unity for N ≫ M ≫ 1. Implementation imperfections are ignored.
First, the revised Equations (1–3) from Salih [1],
Second, the revised Equation (15) from Salih [1] for the approximate fidelity of counterfactual transport, which gets more precise the larger the number of inner cycles, N, gets,
Note that while a smaller number of outer cycles, M, does not lead to output errors in our counterfactual CNOT gate (the key step in our protocol) for either the case of Bob blocking the channel or the case of Bob not blocking the channel, it does lead to reduced fidelity for the case of Bob effecting a superposition of blocking and not blocking the channel. The reason is that for the component of the superposition where Bob does not block, the probability amplitude of Alice's photon is multiplied by a factor of cosθM after each outer cycle. This can be ignored, however, for large M. Given ideal implementation, the fidelity of our protocol for counterfactual transport approaches unity for N≫M≫1, where N and M are the number of inner and outer cycles respectively.
We draw the reader's attention to the fact that the posting of our protocol on the arXiv in 2014 [2] has triggered a number of related papers including, Guo et al. [3], Li et al. [4], Vaidman [5], and Shenoy-Hejamadi and Srikanth [6]. We plan a separate reply to Vaidman's Comment [5].
We finally cite Hosten et al. [7], who first introduced the chained quantum Zeno effect in the context of counterfactual computation, a second time.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Salih, H. Protocol for counterfactually transporting an unknown qubit. Front Phys. (2016) 3:94. doi: 10.3389/FPHY.2015.00094
3. Guo, Q, Cheng, LY, Chen, L, Wang, HF, and Zhang, S. Counterfactual quantum-information transfer without transmitting any physical particles. Sci Rep. (2015) 5:8416. doi: 10.1038/srep08416
4. Li, ZH, Al-Amri, M, and Zubairy, MS. Direct counterfactual transmission of a quantum state. Phys Rev A (2015) 92:052315. doi: 10.1103/PhysRevA.92.052315
5. Vaidman, L. Comment on “Direct counterfactual transmission of a quantum state”. Phys. Rev. A (2015) 93:066301. doi: 10.1103/PhysRevA.93.066301
6. Shenoy-Hejamadi, A, and Srikanth, R. Counterfactual distribution of Schrdinger cat states. Phys. Rev. A (2015) 92:062308. doi: 10.1103/PhysRevA.92.062308
Keywords: interaction-free measurement, Zeno effect, counterfactual communication, entanglement generation, quantum teleportation
Citation: Salih H (2016) Addendum: Protocol for Counterfactually Transporting an Unknown Qubit. Front. Phys. 4:23. doi: 10.3389/fphy.2016.00023
Received: 17 February 2016; Accepted: 16 May 2016;
Published: 05 July 2016.
Edited and reviewed by: Lorenzo Pavesi, University of Trento, Italy
Copyright © 2016 Salih. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hatim Salih, c2FsaWguaGF0aW1AZ21haWwuY29t
 Hatim Salih
Hatim Salih