Quantum Probabilistic Models Revisited: The Case of Disjunction Effects in Cognition

1. Introduction

The process of decision-making is a research field that has always triggered a vast amount of interest among several fields of the scientific community. Throughout time, many frameworks for decision-making have been developed, namely the Expected Utility hypothesis, which is characterized by a specific set of axioms that enable the computation of the person's preferences with regard to choices under uncertainty [1]. Later, Savage [2] proposed an extension to this theory: the Subjective Expected Utility theory. In this extension, uncertainty is described by subjective probabilities, since not all uncertainty can be described using an objective probability distribution. However, human behavior tends to violate the axioms of Expected Utility, leading to the well known Allais paradox [3]. Human behavior also tends to violate the axioms of the Subjective Expected Utility framework, leading to the Ellsberg paradox [4].

1.1. Background

In the 70s, the cognitive psychologists Amos Tversky and Daniel Kahneman decided to put to the test the axioms of the Expected Utility hypothesis. They performed a set of experiments in which they demonstrated that people usually violate the Expected Utility hypothesis and the laws of logic and probability in decision scenarios under uncertainty [5–9]. This means that, when people need to make a decision under scenarios with high levels of uncertainty, ambiguity and risk, they tend to violate the laws of probability theory, leading to decision paradoxes [3, 4].

One of these paradoxes was demonstrated in the article of Tversky and Shafir [10] and corresponds to the violation of Savage's Sure Thing Principle, also known as disjunction effects, under the Prisoner's Dilemma Game. This principle is fundamental in classical probability theory and states that, if one prefers action A over B under the state of the world X, and if one also prefers A over B under the complementary state of the world X, then one should always prefer action A over B even when the state of the world is unspecified [2]. Violations of the Sure Thing Principle imply violations of the classical law of total probability [11].

Quantum cognition has emerged as a research field that aims to build cognitive models using the mathematical principles of quantum mechanics. Given that classical probability theory is very rigid in the sense that it poses many constraints and assumptions (single trajectory principle, obeys set theory, etc.), it becomes too limited (or even impossible) to provide simple models that can capture human judgments and decisions since people are constantly violating the laws of logic and probability theory [12–14].

In this sense, psychological (and cognitive) models benefit from the usage of quantum probability principles because they have many advantages over classical counterparts [15]. They can represent events in vector spaces through a superposition state, which comprises the occurrence of all events at the same time. In quantum mechanics, the superposition principle refers to the property that particles must be in an indefinite state. That is, a particle can be in different states at the same time. Under a psychological point of view, a quantum superposition can be related to the feeling of confusion, uncertainty or ambiguity [16]. This vector space representation does not obey the distributive axiom of Boolean logic and to the law of total probability. This enables the construction of more general models that can mathematically explain cognitive phenomena such as violations of the Sure Thing Principle [17, 18], which is the focus of this study. Quantum probability principles have also been successfully applied in many different fields of the literature, namely in biology [19, 20], economics [21, 22], perception [23, 24], jury duty [25], etc.

One of the pioneering contributions to the Quantum Cognition field comes from the works of Aerts and Aerts [26]. The authors designed a quantum machine, which consists in a particle that can move across the surface of a sphere. An elastic, representing some experiment is introduced in this sphere. The particle then moves orthogonally to the elastic and the elastic breaks uniformly into two parts. With this geometric representation, one can easily compute the probabilities of the particle falling into each side of the elastic. The model was extended with an ϵ parameter that represents the evolution from a quantum structure to a classical one. This parameter varies between [0, 1], where 0 corresponds to maximum lack of knowledge (quantum structure) and 1 to zero lack of knowledge (classical knowledge). Between this interval, there is the possibility of exploring other types of structures that are neither classical nor quantum. The authors also made several experiments to test the variation of probabilities when posing yes∕no questions. According to their experiment, most participants formed their answer at the moment the question was posed. This behavior goes against classical theories, because in classical probability, it would be expected that the participants have a predefined answer to the question and not form it at the moment of the question. A further discussion about this study can be found in the works of Aerts [27–29], Gabora and Aerts [30], and Aerts et al. [31].

In other subsequent works, namely in Aerts [32], the author uses the formalisms of quantum mechanics in order to accommodate disjunction effects. The author, represents concepts as vectors and membership weights as quantum weights, in a complex Hilbert Space. By using quantum interference effects and quantum superpositions, the author was able to model accurately the disjunction of concepts present in experimental data.

1.2. The Article's Main Statement

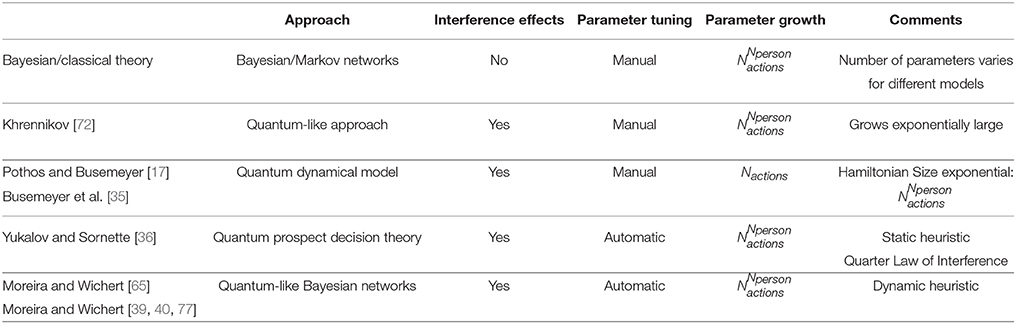
In this article, we provide an overview and discussion of the most important state-of-the-art quantum cognitive models that are able to explain the paradoxical findings of experiments that violate the Sure Thing Principle (ex: the Prisoner's Dilemma game [33]). We conduct a deep comparison of and discussion on several quantum models: the Quantum-Like Approach [34], the Quantum Dynamical Model [35], the Quantum Prospect Decision Theory [36] and Quantum Bayesian Networks [37–40]. We discuss these models in terms of three metrics: (1) incorporation of quantum interference effects, (2) how to find values for quantum parameters, and (3) scalability of the model for more complex decision problems.

The first metric checks if the model uses quantum interference effects to predict actions chosen under uncertainty. Following the work of Yukalov and Sornette [36], toward uncertainty, human beings tend to have aversion preferences. They prefer to choose an action that brings them a certain but lower propensity/utility instead of an action that is uncertain but can yield a higher propensity/utility [41]. This can be simulated through quantum interference effects, in which one outcome is enhanced (or diminished) toward the opposite outcome.

The second metric takes into account the problem of finding values for quantum parameters. In quantum mechanics, a quantum state is modeled by probability amplitudes [42]. These amplitudes are a component of the wave function and this wave function represents a quantum state. Associated with each probability amplitude is a quantum parameter representing the phase of the wave. The interpretation of this parameter under the psychology literature is still not clear, although various works have presented interpretations [17]. Moreover, when applying quantum principles to cognition (or to any other subject), one will need to set these quantum parameters in such a manner that they will lead to accurate predictions. In this metric, we will check how easy it is for the analyzed models to set these parameters.

The third and last metric consists of determining if the model can be extended to more complex scenarios. Although there are many experiments that report violations of the Sure Thing Principle [17, 35, 43, 44], these experiments consist of very small scenarios that are modeled by, at most, two random variables. Therefore, many of the proposed models in the literature are only effective under such small scenarios and become intractable (or even cannot be applied) under more complex situations. These metrics will be analyzed with more detail in Section 8 of the present work.

It is important to note that the goal of this work is the following: we have collected a set of models from the literature that attempt to tackle violations of the Sure Thing Principle in a quantum fashion, and then we compare the collected models. For this comparison, we just show, through a mathematical description of each model, their advantages and disadvantages. That is, we compare these models with the three metrics proposed: number of parameters involved in the model, the scalability of the quantum interference effects and their usage. We will also show that classical models also suffer from the same parameter growth problem as quantum approaches. However, because these models must obey set theory and the laws of classical probability, it is not possible to use them to make predictions in situations where the Sure Thing Principle is being violated.

1.3. Outline

We will start this article with a motivational problem, in which the Sure Thing Principle is found to be violated under the Prisoner's Dilemma Game (Section 2). In Section 3, we will show that a classical approach cannot accommodate violations of the Sure Thing Principle because these approaches obey set theory and consequently the laws of probability theory. We will make a full step-by-step description of the most influential models of the literature. We will show how one could apply them to predict the results concerned with violations of the Sure Thing Principle in the Prisoner's Dilemma Game. In Section 4, we will cover the Quantum-Like Approach [34]. In Section 5, we will analyze the Quantum Dynamical Model [17]. In Section 6, we will describe the Quantum Prospect Decision Theory [36]. In Section 7, we will provide an overview of Quantum-Like Bayesian Networks [37–40]. We then engage in a deeper discussion of these approaches and give thought to the advantages/disadvantages of each model in Section 8. We finish this article by presenting the main conclusions of this work by providing some insights regarding various trends in quantum probabilistic models (Section 9).

2. Violation of the Sure Thing Principle: The Prisoner's Dilemma Game

The Prisoner's Dilemma game corresponds to an example of the violation of the Sure Thing Principle. In this game, there are two prisoners who are in separate solitary confinements with no means of speaking to or exchanging messages with each other. The police offer each prisoner a deal: they can either betray each other (defect) or remain silent (cooperate). For understanding purposes, we provide an example of a payoff matrix for the Prisoner's Dilemma Game (Figure 1). The payoff matrix represents the rewards that each player receives for a given action.

FIGURE 1

Figure 1. Example of a payoff matrix for the Prisoner's Dilemma Game.

The dilemma of this game is the following. Taking into account the payoff matrix, the best choice for both players would be to cooperate. However, the action that yields a bigger individual reward is to defect. If player A has to make a choice, he has two options: if B has chosen to cooperate, the best option for A is to defect because he will be set free; if B has chosen to defect, then the best action for A is also to choose to defect because he will spend less time in jail than if he cooperates.

To test the veracity of the Sure Thing Principle under the Prisoner's Dilemma game, several experiments were performed in the literature in which three conditions were tested:

• Participants were informed that the other participant chose to defect.

• Participants were informed that the other participant chose to cooperate.

• Participants had no information about the other participant's decision.

Table 1 summarizes the results of several works in the literature that have performed this experiment using different payoffs. Note that all entries of Table 1 show a violation of the Sure Thing Principle and, consequently, the law of total probability. In a classical setting, assuming neutral priors, it is expected that:

$\begin{array}{l}Pr( P_2 = Defect | P_1 = Defect )\ge Pr( P_2 = Defect )\\ \ge Pr( P_2 = Defect | P_1 = Cooperate )\end{array}$

TABLE 1

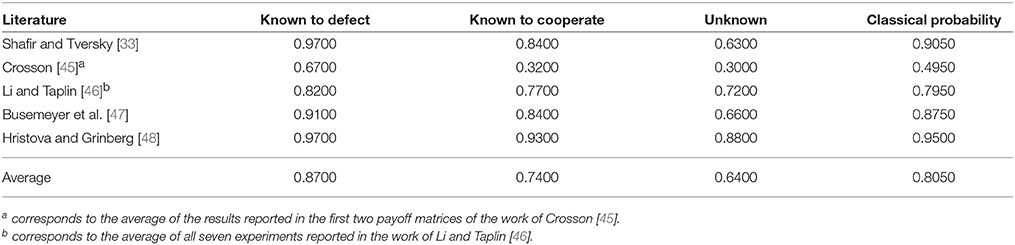
Table 1. Works of the literature reporting the probability of a player choosing to defect under several conditions.

However, this is not consistent with the experimental results reported in Table 1. Note that Pr(P₂ = Defect | P₁ = Defect) corresponds to the probability of the second player choosing the Defect action given that he knows that the first player chose to Defect. In Table 1, this corresponds to the entry Known to Defect. In the same manner, Pr(P₂ = Defect | P₁ = Cooperate) corresponds to the entry Known to Cooperate. The observed probability during the experiments concerned with player 2 choosing to defect, Pr(P2 = Defect), corresponds to the unknown entry of Table 1 because there is no evidence regarding the first player's actions. Finally, the entry Classical Probability corresponds to the classical probability Pr(P₂ = Defect), which is computed through the law of total probability assuming neutral priors (a 50% chance of a player choosing either to cooperate or to defect):

$\begin{array}{l}Pr(P_2=Defect)=Pr(P_1=Defect)\\ ·Pr(P_2=Defect|P_1=Defect)\\ +Pr(P_1=Cooperate)·Pr(P_2=Defect|P_1=Cooperate)\end{array}$

For simplicity, we will use the following notation. The probability of Player 2 choosing to defect will be Pr(P2 = D). In the same way, the probability of Player 2 choosing to cooperate will be Pr(P2 = C).

In the next sections, we will introduce the most representative models in the quantum cognition literature that are able to solve problems concerning violations of the Sure Thing Principle and also show that a classical model cannot accommodate violations of the Sure Thing Principle. We will also demonstrate how quantum models work when trying to predict the probabilities of the average results of the Prisoner's Dilemma Game, reported in Table 1.

3. A Classical Markov Model of the Prisoner's Dilemma Game

A Markov Model can be generally defined as a stochastic probabilistic undirected graphical model that satisfies the Markov property. This means that the probability distribution of the next state depends on the current state and not on previous states. These probabilistic models are very useful for modeling systems that change states according to a transition matrix that specifies some probability distribution or some transition rules that depend solely on the current state.

One can apply a dynamical Markov process to model the Prisoner's Dilemma Game in the following manner. Having as reference the work of Pothos and Busemeyer [17], the Prisoner's Dilemma is a 2-person game and can be modeled in a four-dimensional classical Markov model. Initially, the states can be represented by all possible actions of the players: Cooperate (C) and Defect (D). These are represented in a state vector in which all possible actions are equally likely to be chosen:

$\begin{array}{l}{P}_I=\left[\begin{array}{c}\begin{array}{l}D D\\ D C\\ C D\\ C C\end{array}\end{array}\right]=\left[\begin{array}{c}\begin{array}{l}1\\ 1\\ 1\\ 1\end{array}\end{array}\right]·\frac{1}{4}\end{array}$

The probability of the second player choosing to Defect given that the action of the other player is unknown is given by Equation (35) and consists of the multiplication of this initial probability state P_I by a transition function T(t):

$\begin{array}{ll}{P}_F=T(t)·P_I& (1)\end{array}$

The transition function T(t) is represented by a matrix containing positive real numbers and with the constraint that each row must sum to one (normalization axiom). In other words, this matrix represents the new probability distribution across the player's possible actions over some time period t [17].

$\begin{array}{ll}\frac{d}{dt}T(t)=K·T(t)\Rightarrow T(t)=e^{K.t}& (2)\end{array}$

In Equation (2), the matrix K corresponds to an intensity matrix. It is a matrix representation of all payoffs of the players. A solution to the above equation is given by T(t) = e^K.t, which allows one to construct a transition matrix for any time point from the fixed intensity matrix. These intensities can be defined in terms of the evidence and payoffs for actions in the task. In other words, the intensity matrix performs a transformation on the probabilities of the current state to favor defection or cooperation, which are represented by the parameters μ_d and μ_c, respectively [17].

$\begin{array}{ll}K{A}_d=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\otimes \left[\begin{array}{cc}{\mu }_d& 1\\ 1& -{\mu }_d\end{array}\right]K{A}_c=\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]\otimes \left[\begin{array}{cc}{\mu }_c& 1\\ 1& -{\mu }_c\end{array}\right]& (3)\end{array}$

$\begin{array}{ll}KA=K{A}_d+K{A}_c=\left[\begin{array}{cccc}-1& {\mu }_D& 0& 0\\ 1& -{\mu }_D& 0& 0\\ 0& 0& -1& {\mu }_C\\ 0& 0& 1& -{\mu }_C\end{array}\right]& (4)\end{array}$

In the work of Pothos and Busemeyer [17], the authors proposed the incorporation of dissonance effects to simulate the change of mind to dissolve contradictory beliefs that a player can experience. This is given by the parameter γ and corresponds to the payoffs of the players (Equation 5).

$\begin{array}{ll}KB=\left[\begin{array}{cccc}-1& 0& \gamma & 0\\ 0& -\gamma & 0& 1\\ 1& 0& -\gamma & 0\\ 0& \gamma & 0& -1\end{array}\right]& (5)\end{array}$

Thus, the final intensity matrix K is given by:

$\begin{array}{ll}K=KA+KB=\left[\begin{array}{cccc}-2& {\mu }_D& \gamma & 0\\ 1& -\gamma -{\mu }_D& 0& 1\\ 1& 0& -1-\gamma & {\mu }_C\\ 0& \gamma & 1& -{\mu }_C-1\end{array}\right]& (6)\end{array}$

To compute the final probability of a player defecting, we need to sum the components of the column vector P_F that correspond to the second player choosing the action Defect. Note that the four components of the column vector P_F correspond to [ DD DC CD CC ], where C corresponds to Cooperate and D to Defect. The first letter represents the action chosen by the first player, and the second letter corresponds to the action of the second player. Thus, the probability of player 2 choosing the action Defect corresponds to the summation of the first and the third components of the column vector P_F:

$\begin{array}{ll}Pr( P_2 = Defect ) = P_{F[1st\_dim]} + P_{F[3rd\_dim]}& (7)\end{array}$

In Equation (7), we do not need to perform any normalization in the end because the operation in Equation (1) together with the intensity matrix K ensures that the values computed are already probability values. Moreover, there is no possible combination of parameters resulting from Equation (7) that will satisfy the results observed in Table 1. This occurs because, although we have parameterized the Markov Model, the model will always satisfy the laws of classical probability theory. Thus, there is no possible optimization that can predict the violation of the Sure Thing Principle in such situations. This was already noticed in the previous works of Pothos and Busemeyer [17] and Busemeyer et al. [35].

In the next sections, we explain several quantum approaches proposed in the literature that can accommodate violations ofthe Sure Thing Principle.

4. The Quantum-Like Approach

The Quantum-Like Approach has its roots in contextual probabilities. This model was proposed by A. Khrennikov and corresponds to a general contextual probability space from which the classical and quantum probability models can be derived [34, 49].

4.1. Contextual Probabilities: The Växjö Model

In the Växjö Model, the context relates to the circumstances that form the setting for an event in terms of which it can be fully understood, clarifying the meaning of the event. For instance, in domains outside of physics, such as cognitive science, one can have mental contexts. In social sciences, we can have a social context. The same idea is applied to many other domains, such as economics, politics, game theory, and biology.

Associated with a context, there is a set of observables. In quantum mechanics, an observable corresponds to a self-adjoint operator on a complex Hilbert Space. Under the Växjö Model, these observables correspond to the set of possible events with their respective values.

$\begin{array}{ll}P{r}_{context}=(\mathcal{C},\mathcal{O},\pi )& (8)\end{array}$

For instance, for a context C ∈ ${C}$ and for an observable a ∈ ${O}$ having values α, the probability of the value of one observable is expressed in terms of the conditional (contextual) probability involving the values of an observable. That is, the probability distribution π is given by:

$\begin{array}{ll}\pi (\mathcal{O},\mathcal{C})=Pr( a = \alpha | C )& (9)\end{array}$

If we move into the quantum mechanics realm, Equation (9) can be interpreted as the selection with respect to the result a = α of a measurement performed in a.

For the contextual probability model, the Växjö framework corresponds to a model M described by M = (${C}$, ${O}$, π(${O}$, ${C}$)). Again, ${C}$ is a set of contexts, ${O}$ is the set of observables, and π(${O}$, ${C}$) corresponds to a probability distribution of some observables belonging to a specific context.

In addition, assume for a context C ∈ ${C}$ that there are two dichotomous observables a, b ∈ ${O}$ and that each of these observables can take some values α ∈ a and β ∈ b, respectively.

The Växjö Model can be built from the general structure of the quantum law of total probability. That is, the formula is a combination of the classical probability theory with a supplementary term called the interference term (Equation 10). This term does not exist in classical probability and enables the representation of interferences between quantum states.

$\begin{array}{ll}Pr(b=\beta )=Classical\_Probability(b=\beta )+Interference\_Term& (10)\end{array}$

Under this representation, we can replace Classical_Probability by the classical total probability and also replace the quantum Interference_Term by a supplementary measure, represented by δ(β | a, C). Under the Växjö Model, the term δ(β | a, C) corresponds to:

$\begin{array}{ll}\delta (\beta |a,C)=Pr(b=\beta )-{\displaystyle \sum _{\alpha \in a}P}r(a=\alpha |C)Pr(b=\beta |a=\alpha ,C)& (11)\end{array}$

Equation (11) can be written in a similar way to the classical probability in the following manner:

$\begin{array}{ll}Pr(b=\beta |C)={\displaystyle \sum _{\alpha \in a}P}r(a=\alpha |C)Pr(b=\beta |a=\alpha ,C)+\delta (\beta |a,C)& (12)\end{array}$

If we perform the normalization of the probability measure of supplementary δ(β | a, C) by the square root of the product of all probabilities, we obtain:

$\begin{array}{ll}{\lambda }_{\theta }=\frac{\delta (\beta |a,C)}{2\sqrt{{\displaystyle {\prod }_{\alpha \in a}Pr(a=\alpha |C)Pr(b=\beta |a=\alpha ,C)}}}& (13)\end{array}$

From Equation (13), the general probability formula of the Växjö Model can be derived. For two variables, it is given by:

$\begin{array}{l}Pr(b=\beta |C)={\displaystyle \sum _{\alpha \in a}P}r(a=\alpha |C)Pr(b=\beta |a=\alpha ,C)\\ +2{\lambda }_{\theta }\sqrt{{\displaystyle \prod _{\alpha \in a}P}r(a=\alpha |C)Pr(b=\beta |a=\alpha ,C)}& (14)\end{array}$

If we look closely at Equation (14), we can see that the first summation of the formula corresponds to the classical law of total probability. The second term of the formula (the one that contains the λ_θ parameter) does not exist in the classical model and is called the interference term.

4.2. The Hyperbolic Interference

Although the Quantum-Like Approach provides great possibilities compared with the classical one, it appears that it cannot completely cover data from psychology and that a quantum formalism was not enough to explain some paradoxical findings (see [50]), so hyperbolic spaces were proposed [51–53].

From Equation (14), if $Pr(b=\beta )-\sum _{\alpha \in a}Pr(a=\alpha |C)Pr(b=\beta |a=\alpha ,C)$ is different from zero, then various interference effects occur. To determine which type of interference occurred, one tests the Växjö Model for quantum probabilities. This can be determined by normalizing the supplementary measure in a quantum fashion, just as presented in Equation (13).

If we are under a quantum context, then the quantum interference term will be:

$\begin{array}{ll}\delta (\beta |a,C)=2\sqrt{{\displaystyle \prod _{\alpha \in a}P}r(a=\alpha |C)Pr(b=\beta |a=\alpha ,C)}\cos (\theta )& (15)\end{array}$

In a quantum context because the supplementary term δ(β | a, C) is being normalized in a quantum fashion, then we automatically know that the indicator term λ_θ will always have to be smaller than 1 to obtain quantum probabilities, λ_θ ≤ 1. Thus, under trigonometric contexts, the Växjö Model for quantum probabilities becomes:

$\begin{array}{l}{\lambda }_{\theta }=\cos (\theta ) \to Pr(\beta |C)={\displaystyle \sum _{\alpha \in a}P}r(\alpha |C)Pr(\beta |\alpha ,C)\\ +2\sqrt{{\displaystyle \prod _{\alpha \in a}P}r(\alpha |C)Pr(\beta |\alpha ,C)}\cos (\theta )& (16)\end{array}$

If, however, the probability Pr(b = β) was not computed in a trigonometric space (that is, it is not quantum), then, it is straightforward that the quantum normalization applied in Equation (13) will yield a value larger than 1. Because we are not in the context of quantum probabilities, the quantum normalization factor will fail to normalize the interference term and will produce a number larger than the normalization factor. Under these circumstances, the Växjö Model incorporates the generalization of hyperbolic probabilities, arguing that the context in which these probabilities were computed was Hyperbolic [49, 53, 54].

Under Hyperbolic contexts, the Växjö Model contextual probability formula becomes:

$\begin{array}{l}{\lambda }_{\theta }=\cosh (\theta ) \to Pr(\beta |C)={\displaystyle \sum _{\alpha \in a}P}r(\alpha |C)Pr(\beta |\alpha ,C)\\ \pm 2\sqrt{{\displaystyle \prod _{\alpha \in a}P}r(\alpha |C)Pr(\beta |\alpha ,C)}\cosh (\theta )& (17)\end{array}$

In summary, according to the values computed by the indicator function λ_θ, the Växjö Model enables the computation of probabilities in the following contexts:

• If | λ_θ | = 0, then there is no interference, and the Växjö Model collapses to classical probability theory.

• If | λ_θ | ≤ 1, then we fall into the realm of quantum mechanics, and the context becomes a Hilbert space. The indicator function is then replaced by the trigonometric function cos(θ).

• If | λ_θ | > 1, then we fall into the realm of hyperbolic numbers, and the context becomes a hyperbolic space. The indicator function is then replaced by the hyperbolic function cosh(θ).

4.3. Quantum-Like Probabilities as an Extension of the Växjö Model

The probabilities that emerge from the Växjö model for trigonometric spaces (i.e., quantum probabilities), do not provide a complete description of a quantum system because it can violate the positivity axiom of probability theory [49].

In this sense, an algorithm was proposed in the literature that extends the Växjö model and is able to accommodate the positivity axiom. The algorithm proposed is the Quantum-Like Representation Algorithm (QLRA), and it was proposed by Khrennikov [55–59].

As already mentioned, quantum complex amplitudes can be obtained from classical probability by using Born's rule [60, 61]. In the QLRA, for any trigonometric context C, one can simplify Born's rule for two dichotomous variables using (Equation 19) [49].

$\begin{array}{l}Pr(\beta |C)=Pr({\alpha }_1|C)Pr(\beta |{\alpha }_1,C)+Pr({\alpha }_2|C)Pr(\beta |{\alpha }_2,C)+\\ +2\sqrt{Pr({\alpha }_1|C)Pr(\beta |{\alpha }_1,C)}\\ \sqrt{Pr({\alpha }_2|C)Pr(\beta |{\alpha }_2,C)}\cos \theta & (18)\end{array}$

Equation (18) can be simplified in the following manner:

$\begin{array}{l}Pr(\beta |C)=|\sqrt{Pr({\alpha }_1|C)Pr(\beta |{\alpha }_1,C)}\\ +e^{i{\theta }_{\beta |\alpha ,C}}\sqrt{Pr({\alpha }_2|C)Pr(\beta |{\alpha }_2,C)}{|}^2& (19)\end{array}$

Equation (19) corresponds to the representation of the quantum law of total probability through the Växjö model. In this equation, the angle θ_{β|α, C} corresponds to the phase of a random variable and incorporates the phase of both A = α₁ and A = α₂ in the following manner: θ_{β|α, C} = θ_β|α1 − θ_β|α2.

One should note that the Quantum-Like Approach can be extended to more complex decision scenarios, that is, with more than two random variables. However, this will lead to the very difficult task of tuning an exponential number of quantum θ parameters. Peter Nyman noticed this problem when he generalized the Quantum-Like Approach for 3 dichotomous variables [52, 62–64].

4.4. Modeling the Prisoner's Dilemma using the Quantum-Like Approach

If we want to compute the average probabilities reported in Table 1 for the Prisoner's Dilemma game, then we would need to make the following substitutions to Equation (18):

$\begin{array}{l}Pr({\alpha }_1|C)·Pr(\beta |{\alpha }_1,C)=Pr(P_1=Defect|C)\\ ·Pr(P_2=Defect|P_1=Defect)=0.5\times 0.87=0.435\\ Pr({\alpha }_2|C)·Pr(\beta |{\alpha }_2,C)=Pr(P_1=Cooperate|C)\\ ·Pr(P_2=Defect|P_1=Cooperate)\\ =0.5\times 0.74=0.37\end{array}$

The main problem of the Växjö model and the Quantum-Like Approach is that it can only address very small decision scenarios and the fitting of the θ parameter has to be done fitted to data. To compute the probability of a player choosing to defect, Pr(P₂ = Defect), one would proceed as follows:

$\begin{array}{l}Pr(P_2=Defect)=0.435+0.37+2·\sqrt{0.435}·\sqrt{0.37}·\cos (\theta )\end{array}$

To achieve the observed result, θ must be equal to 1.7779 to achieve the final probability Pr(P₂ = Defect) = 0.64. However, this method does not provide any other means to find this θ parameter except by extrapolating the observed data.

5. The Quantum Dynamical Model

In the works of Busemeyer et al. [11], Pothos and Busemeyer [17], and Busemeyer et al. [35], the authors present a model to perform quantum time evolution. This model requires the creation of a doubly stochastic matrix, which represents the rotation of the participants' beliefs. The double stochasticity is a requirement to preserve unit length operations and to obtain a probability value that does not require normalization. The participants' actions are represented by a superposition vector with all possible actions: [ψ_DD ψ_DC ψ_CD ψ_CC], where C corresponds to Cooperate and D to Defect.

The doubly stochastic matrix that the model requires can only be computed by the use of an auxiliary Hamiltonian matrix, which needs to be self-adjoint. For instance, to explain the average results of the Prisoner's Dilemma game, the Hamiltonian matrix is given by Equation (20), where μ_D and μ_C correspond to parameters representing the payoffs of the defect and cooperate actions, respectively.

$\begin{array}{l}H{A}_d=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\otimes \left[\begin{array}{cc}{\mu }_D& 1\\ 1& -{\mu }_D\end{array}\right]\frac{1}{\sqrt{1+{\mu }_D^2}}\\ H{A}_c=\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]\otimes \left[\begin{array}{cc}{\mu }_C& 1\\ 1& -{\mu }_C\end{array}\right]\frac{1}{\sqrt{1+{\mu }_C^2}}\\ HA=H{A}_d+H{A}_c=\left[\begin{array}{cccc}\frac{{\mu }_D}{\sqrt{1+{\mu }_D^2}}& \frac{1}{\sqrt{1+{\mu }_D^2}}& 0& 0\\ \frac{1}{\sqrt{1+{\mu }_D^2}}& -\frac{{\mu }_D}{\sqrt{1+{\mu }_D^2}}& 0& 0\\ 0& 0& \frac{{\mu }_C}{\sqrt{1+{\mu }_C^2}}& \frac{1}{\sqrt{1+{\mu }_C^2}}\\ 0& 0& \frac{1}{\sqrt{1+{\mu }_C^2}}& -\frac{{\mu }_C}{\sqrt{1+{\mu }_C^2}}\end{array}\right]& (20)\end{array}$

The dynamical model also takes dissonance effects into account. That is, the participants might have been confronted by some information that conflicted with his/her existing beliefs to simulate the dissonance effect when the participants had to decide on an action. Thus, the Quantum Dynamical Model makes use of a second Hamiltonian matrix, HB.

$\begin{array}{l}H{B}_d=\left[\begin{array}{cccc}+1& 0& +1& 0\\ 0& 0& 0& 0\\ +1& 0& -1& 0\\ 0& 0& 0& 0\end{array}\right]·\frac{-\gamma }{\sqrt{2}}H{B}_c=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& -1& 0& +1\\ 0& 0& 0& 0\\ 0& +1& 0& +1\end{array}\right]·\frac{-\gamma }{\sqrt{2}}\\ HB=H{B}_d+H{B}_c=\left[\begin{array}{cccc}\frac{-\gamma }{\sqrt{2}}& 0& \frac{-\gamma }{\sqrt{2}}& 0\\ 0& \frac{\gamma }{\sqrt{2}}& 0& \frac{-\gamma }{\sqrt{2}}\\ \frac{-\gamma }{\sqrt{2}}& 0& \frac{\gamma }{\sqrt{2}}& 0\\ 0& \frac{-\gamma }{\sqrt{2}}& 0& \frac{-\gamma }{\sqrt{2}}\end{array}\right]& (21)\end{array}$

The general Hamiltonian matrix combines the matrices from Equations (20) and (21). In the end, the final matrix needs to be self-adjoint and, consequently, symmetric. To explain the average results of the Prisoner's Dilemma game, the final Hamiltonian matrix is given by:

$\begin{array}{l}H=HA+HB=\\ \left[\begin{array}{cccc}\frac{-\gamma }{\sqrt{2}}+\frac{{\mu }_D}{\sqrt{1+{\mu }_D^2}}& \frac{1}{\sqrt{1+{\mu }_D^2}}& \frac{-\gamma }{\sqrt{2}}& 0\\ \frac{1}{\sqrt{1+{\mu }_D^2}}& \frac{\gamma }{\sqrt{2}}-\frac{{\mu }_D}{\sqrt{1+{\mu }_D^2}}& 0& \frac{-\gamma }{\sqrt{2}}\\ \frac{-\gamma }{\sqrt{2}}& 0& \frac{\gamma }{\sqrt{2}}+\frac{{\mu }_C}{\sqrt{1+{\mu }_C^2}}& \frac{1}{\sqrt{1+{\mu }_C^2}}\\ 0& \frac{-\gamma }{\sqrt{2}}& \frac{1}{\sqrt{1+{\mu }_C^2}}& \frac{-\gamma }{\sqrt{2}}-\frac{{\mu }_C}{\sqrt{1+{\mu }_C^2}}\end{array}\right]& (22)\end{array}$

Next, we need to create a unitary matrix. In quantum mechanics, a unitary matrix restricts the allowed evolution of quantum systems, ensuring that the sum of probabilities of all possible outcomes of any event is always 1. This means that the matrix must be doubly stochastic (all rows and columns sum to 1). In the Quantum Dynamical Model, this matrix encodes all state transitions that a person can experience while choosing a decision. A unitary matrix is computed by a differential equation called Schrödinger's equation:

$\begin{array}{ll}\frac{\delta }{\delta t}U(t)=-i·H·U(t)\Rightarrow U(t)=e^{-i·H·t}& (23)\end{array}$

The parameter t corresponds to the time evolution. Under the Dynamical Quantum Model, this parameter was set to π∕2, corresponding to the average time that a participant takes to make a decision (approximately 2 seconds) [17, 35]. Also, in the book of Busemeyer and Bruza [16], the authors state that the time parameter was set to π∕2, because it produces a probability that reaches its maximum.

The initial belief state corresponds to a quantum state representing a superposition of the participant's beliefs.

$\begin{array}{ll}{Q}_i=\frac{1}{2}\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]& (24)\end{array}$

By multiplying the unitary matrix with the initial superposition belief state, one can compute the transition of the participants' beliefs at each time. The final vector Q_f represents the amplitude distribution across states after deliberation.

$\begin{array}{ll}{Q}_F=U·Q_i=U·\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]·\frac{1}{2}& (25)\end{array}$

Having the final state Q_F, one can compute probabilistic inferences by computing the sum squared magnitude of the rows of interest in the final belief state. Note that the four components of the column vector Q_F respectively correspond to [ DD DC CD CC ], where C corresponds to Cooperate and D to Defect. The first letter represents the action chosen by the first player, and the second letter corresponds to the action of the second player. Thus, the probability of player 2 choosing the action Defect corresponds to the summation of the squared magnitude of the first and the third components of the column vector Q_F:

$\begin{array}{l}Pr(P_2=Defect)=|Q_{F[1st\_dim]}{|}^2+|Q_{F[3rd\_dim]}{|}^2\\ Pr(P_2=Cooperate)=|Q_{F[2nd\_dim]}{|}^2+|Q_{F[4th\_dim]}{|}^2& (26)\end{array}$

To explain the average results observed in the Prisoner's Dilemma Game, in the work of Pothos and Busemeyer [17], the authors chose the following parameters:

• μ_D = 0.51. This parameter corresponds to a participant choosing the defect action.

• μ_C = 0.51. This parameter corresponds to a participant choosing the cooperate action.

• γ = 0.6865. This parameter corresponds to the simulation of the dissonance effect.

Using the above parameters, one can estimate the average results of Table 1 to be Pr(P₂ = Defect) = 0.64. The Quantum Dynamical model shows that quantum probability is a very general framework and can lead to many different probabilities. These probabilities just depend on the way one chooses to fit these free parameters. This has also been shown in the previous study of Moreira and Wichert [65]. To illustrate this concept, we decided to fix one of the parameters μ_D, μ_C or γ and vary the others between the interval [−1, 1]. Figures 2–4 show all possible probabilities that can be obtained with the presented Dynamical Quantum Model for the Prisoner's Dilemma game¹ The value of these figures is to show how sensitive quantum parameters are and how challenging it is to find values for these parameters.

FIGURE 2

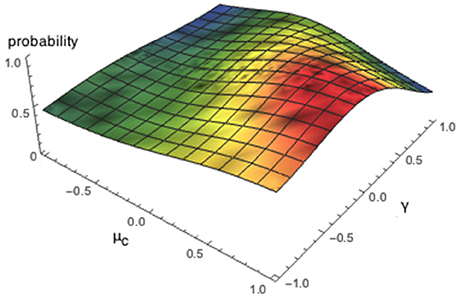
Figure 2. Illustration all possible probabilities, Pr(P₂ = Defect), that can be obtained by varying the parameters γ and μ_C.

FIGURE 3

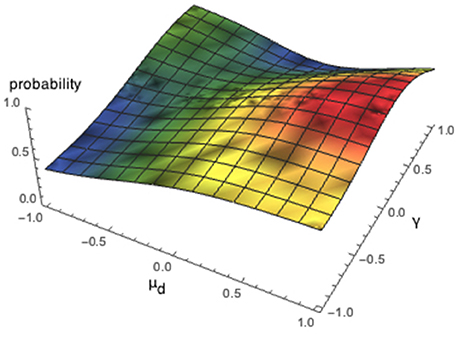
Figure 3. Illustration of all possible probabilities, Pr(P₂ = Defect), that can be obtained by varying the parameters γ and μ_D.

FIGURE 4

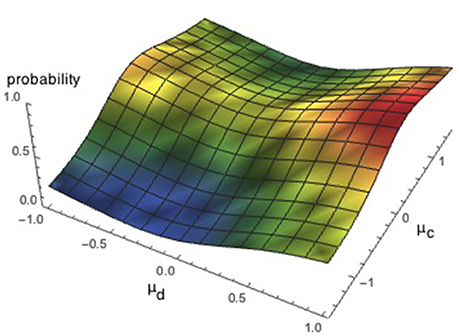
Figure 4. Illustration of all possible probabilities, Pr(P₂ = Defect), that can be obtained by varying the parameters μ_D and μ_C.

In the Quantum Dynamical Model, the parameters used are based on a psychological setting. The incorporation of parameters to model dissonance effects and the payoffs of the players provide an approximation for the psychology of the problem that is not observed in other quantum cognitive models of the literature. However, one great disadvantage of the Quantum Dynamical Model is related to Hamiltonian matrices. Creating a manual Hamiltonian is a very hard problem because it is required that all possible interactions of the decision problem are known, and this specification must be made in such a way that the matrix is doubly stochastic. A recent work from Yearsley and Busemeyer [66] describes how to construct Hamiltonians for quantum models of cognition. The Hamiltonian matrix grows exponentially with the complexity of the decision problem, and the computation of a unitary operator from such matrices is a very complex process. Most of the time, approximations are used because of the complexity of the calculations involved in the matrix exponentiation operation.

6. The Quantum Prospect Decision Theory

The Quantum Prospect Decision Theory was developed by Yukalov and Sornette [36, 67] and developed throughout many other works [68–71]. The foundations of this theory are very similar to the previously presented Quantum-Like Approach.

In the Quantum-Like Approach, we start with two dichotomous observables. In the Quantum Prospect Decision Theory, these observables are referred to as intensions. An intension can be defined by an intended action, and a set of intended actions is defined as a prospect.

Each prospect can contain a set of action modes, which are concrete representations of an intension. Making a comparison with the Quantum-Like Approach, a prospect can be seen as a random variable, and the set of action modes are the assignments that each random variable can have. For instance, the intension to play can have two representations: play action A or play action B.

Following the work of Yukalov and Sornette [36], two intensions A and B have the respective representations: A = x where x ∈ a₁, a₂ and B = y, where y ∈ b₁, b₂. The corresponding state of mind is given by:

$\begin{array}{ll}| {\psi }_s(t)\rangle ={\displaystyle \sum _{i,j}{c}_{i,j}}(t)| A_i B_j\rangle & (27)\end{array}$

Equation (27) represents a linear combination of the prospect basis states. From a psychological perspective, the state of mind is a fixed vector characterizing a particular decision-maker with his/her beliefs, habits, principles, etc. That is, it describes each decision-maker as a unique subject.

The prospect states corresponding to the intensions A and B are given by Equation (28). The ψ symbol corresponds to quantum amplitudes associated with the prospect state. Under the Quantum Prospect Decision Theory, these amplitudes represent the weights of the intended actions while a person is still deliberating about them.

$\begin{array}{l}|{\pi }_{A=a_1}\rangle =c_{11}|A=a_{1}B=b_1\rangle +c_{12}|A=a_{1}B=b_2\rangle \\ |{\pi }_{A=a_2}\rangle =c_{21}|A=a_{2}B=b_1\rangle +c_{22}|A=a_{2}B=b_2\rangle & (28)\end{array}$

The probabilities of the prospects can be obtained by computing the squared magnitude of the prospect states (just as in the Quantum-Like Approach and the Quantum Dynamical Model). Consequently, the final probabilities are given by:

$\begin{array}{l}Pr({\pi }_{A=a_1})=Pr(A=a_1,B=b_1)+Pr(A=a_1,B=b_2)\hfill \\ +q({\pi }_{A=a_1})=|{\psi }_{11}{|}^2+|{\psi }_{12}{|}^2+q({\pi }_{A=a_1})\hfill \\ Pr({\pi }_{A=a_2})=Pr(A=a_2,B=b_1)+Pr(A=a_2,B=b_2)\hfill \\ +q({\pi }_{A=a_2})=|{\psi }_{21}{|}^2+|{\psi }_{22}{|}^2+q({\pi }_{A=a_2})\hfill & (29)\end{array}$

where the interference term q is defined by:

$\begin{array}{l}q({\pi }_{A=a_1})=2·\phi ({\pi }_{A=a_1})\sqrt{Pr(A=a_1,B=b_1)}\hfill \\ ·\sqrt{Pr(A=a_1,B=b_2)}\hfill \\ q({\pi }_{A=a_2})=2·\phi ({\pi }_{A=a_2})\sqrt{Pr(A=a_2,B=b_1)}\hfill \\ ·\sqrt{Pr(A=a_2,B=b_2)}\hfill & (30)\end{array}$

In Equation (30), the symbol φ corresponds to the uncertainty factor and is given by Equation (31).

$\begin{array}{l}\phi ({\pi }_{A=a_1})=\cos (arg({\psi }_{11}·{\psi }_{12}))\\ \phi ({\pi }_{A=a_2})=\cos (arg({\psi }_{21}·{\psi }_{22}))& (31)\end{array}$

The interference term corresponds to the effects that emerge during the process of deliberation, that is, while a person is making a decision. These interference effects result from conflicting interests, ambiguity, emotions, etc. [36].

One can notice that the Quantum Prospect Decision Theory is very similar to the Quantum-Like Approach proposed by Khrennikov [72]. Both theories end up with the same quantum probability formula. However, the Quantum Prospect Decision Theory provides some heuristics for how to choose the uncertainty factors. This information will be addressed in the next section.

6.1. Choosing the Uncertainty Factor

To accommodate the violations of the Sure Thing Principle, the uncertainty factor must be set in such a way that it will enable accurate predictions. Two methods were proposed by Yukalov and Sornette [36] to estimate the uncertainty factor: the Interference Alternation method and the Interference Quarter Law.

• Interference Alternation - Under normalized conditions, the probabilities of the prospects p(π_j) must sum to 1. This normalization only occurs if one characterizes the interference term as an alternation such that the interference effects disappear while summing the probability of the prospects. This results in the property of the interference alternation, given by:

$\begin{array}{ll}{\displaystyle \sum _{j}q}({\pi }_j)=0& (32)\end{array}$

The interference alternation property is in accordance with the findings of Epstein [41]: the destructive interference effects can be associated with uncertainty aversion. This leads to a less probable action under uncertainty conditions. In contrast, the probabilities of other actions that contain less uncertainty are enhanced through constructive quantum interference effects. This uncertainty aversion happens quite frequently in situations where the Sure Thing Principle is violated. This implies that one of the probabilities of the prospects must be enhanced, whereas the other must be decreased.

$\begin{array}{l}sign[\phi ({\pi }_{A=a_1})]=-sign[\phi ({\pi }_{A=a_2})]\\ \text{where} |\phi ({\pi }_{A=a_i})|\in [0,1]& (33)\end{array}$

• Interference Quarter Law - The interference terms generated by quantum probabilistic inferences have a free quantum parameter, which is the uncertainty factor (Equation 31). The Interference Quarter Law corresponds to a quantitative estimation of this parameter. The modulus of the interference term q can be quantitatively estimated by computing the expectation value of the probability distribution of a random variable ξ in the interval [0, 1]:

$\begin{array}{ll}q\equiv {\displaystyle {\int }_0^1\xi ·pr(\xi ) d\xi =\frac{1}{4}}& (34)\end{array}$

The probability distribution p(ξ) is given by Equation (49) and can be computed by taking the average of two probability distributions.

$\begin{array}{ll}pr(\xi )=\frac{1}{2}[p{r}_1(\xi )+p{r}_2(\xi )]=\delta (\xi )+\frac{1}{2}\Theta (1-\xi )& (35)\end{array}$

One of the probability distributions, (p₁(ξ)), is concentrated in the center and is described by a Dirac function δ(ξ).

$\begin{array}{ll}p{r}_1(\xi )=2·\delta (\xi )& (36)\end{array}$

The other probability distribution,(p₂(ξ)), is a uniform distribution in the interval [0, 1].

$\begin{array}{ll}p{r}_2(\xi )=\Theta (1-\xi ) \text{where} \Theta (\xi )=\{\begin{array}{cc}0,& \text{if }\xi <0\\ 1,& \text{if }\xi \ge 0\end{array}& (37)\end{array}$

For a more detailed proof of the Interference Quarter Law, the reader should refer to Yukalov and Sornette [36].

6.2. The Quantum Prospect Decision Theory Applied to the Prisoner's Dilemma Game

In this section, we apply the Quantum Prospect Decision Theory to try to predict the average results for the Prisoner's Dilemma Game reported in Table 1.

The probability of a player defecting (and cooperating), given that one does not know what the action of the other player was, is given by Equation (38). For simplicity, we will assume the following notation: Defect (D) and Cooperate (C).

$\begin{array}{l}Pr(P_2=D)=Pr(P1=D,P2=D)\\ +Pr(P1=C,P2=D)+Interferenc{e}_d\\ Pr(P_2=C)=Pr(P1=D,P2=C)\\ +Pr(P1=C,P2=C)+Interferenc{e}_c& (38)\end{array}$

The interference terms are given by:

$\begin{array}{l}Interferenc{e}_d=2·\phi (P2=D)\\ ·\sqrt{Pr(P1=D,P2=D)·Pr(P1=C,P2=D)}\\ Interferenc{e}_c=2·\phi (P2=C)\\ ·\sqrt{Pr(P1=D,P2=C)·Pr(P1=C,P2=C)}& (39)\end{array}$

The uncertainty factors are given by:

$\begin{array}{l}\phi (P_2=D)=\frac{interferenc{e}_d}{2·\sqrt{pr(P_1=D,P_2=D)·Pr(P_1=C,P_2=D)}}\\ \phi (P_2=D)=\frac{interferenc{e}_c}{2·\sqrt{pr(P_1=D,P2=C)·Pr(P1=C,P2=C)}}& (40)\end{array}$

According to the Interference Quarter Law and to the Alternation Law, the probabilities for acting under uncertainty are given by:

$\begin{array}{l}Pr(P_2=D)=Pr(P_1=D,P_2=D)\hfill \\ +Pr(P_1=C,P_2=D)-0.25\hfill \\ Pr(P_2=C)=Pr(P_1=D,P_2=C)\hfill \\ +Pr(P_1=C,P_2=C)+0.25\hfill & (41)\end{array}$

For the Prisoner's Dilemma Game,

$\begin{array}{l}Pr(P_1=D,P_2=D)=Pr(P1=D)·Pr(P_2=D|P1=D)\hfill \\ =0.5\times 0.87=0.435\hfill \\ Pr(P_1=C,P_2=D)=Pr(P1=C)·Pr(P_2=D|P1=C)\hfill \\ =0.5\times 0.74=0.37\hfill \end{array}$

Then, the final predicted probabilities are given by:

$\begin{array}{ll}\begin{array}{l}\begin{array}{l}Pr(P_2=D)=0.435+0.37-0.25=0.555\\ Pr(P_2=C)=0.065+0.13+0.25=0.445\end{array}\hfill \end{array}& (42)\end{array}$

The average probability to defect for the Prisoner's Dilemma Game in Table 1 when the first player's action is unknown is 0.64. That means that, with the Quarter Interference Law together with the Interference Alternation property, the Prospect Quantum Decision Theory obtained an error of 13%.

7. Probabilistic Graphical Models

In this section, we introduce the concepts of classical and Quantum-Like Bayesian Networks, as well as some approaches in the literature that formalized traditional Bayesian Networks into a Quantum-Like Approach.

7.1. Classical Bayesian Networks

A classical Bayesian Network can be defined by a directed acyclic graph structure in which each node represents a different random variable from a specific domain and each edge represents a direct influence from the source node to the target node. The graph represents independence relationships between variables, and each node is associated with a conditional probability table that specifies a distribution over the values of a node given each possible joint assignment of values of its parents [73].

The full joint distribution [74] of a Bayesian Network, where X is the list of variables, is given by:

$\begin{array}{ll}Pr(X_1,\dots ,X_n)={\displaystyle \prod _{i=1}^{n}P}r(X_i|Parents(X_i))& (43)\end{array}$

The formula for computing classical exact inferences on Bayesian Networks is based on the full joint distribution (Equation 43). Let e be the list of observed variables and let Y be the remaining unobserved variables in the network. For some query X, the inference is given by:

$\begin{array}{ll}Pr(X|e)=\alpha Pr(X,e)=\alpha \left[{\displaystyle \sum _{y\in Y}P}r(X,e,y)\right]& (44)\end{array}$

$\begin{array}{l}\text{Where} \alpha =\frac{1}{{\displaystyle {\sum }_{x\in X}Pr(X=x,e)}}\end{array}$

The summation is over all possible y, i.e., all possible combinations of values of the unobserved variables y. The α parameter corresponds to the normalization factor for the distribution Pr(X|e) [74]. This normalization factor comes from some assumptions that are made in Bayes rule.

7.2. Classical Bayesian Networks for the Prisoner's Dilemma Game

We represent the Prisoner's Dilemma Game under a Bayesian Network structure in which we assume neutral priors: there is a 50% of a player choosing the actions Defect or Cooperate (Figure 5). The decision of the first participant is then followed by the decision of the second participant. The probability distribution of the second player is obtained (or learned) from the experimental data for the averaged results in Table 1 when the actions of the first player are observed. Using this data, the goal is to try to determine the probability of the second player choosing to defect given that it is not known what action the first player chose.

FIGURE 5

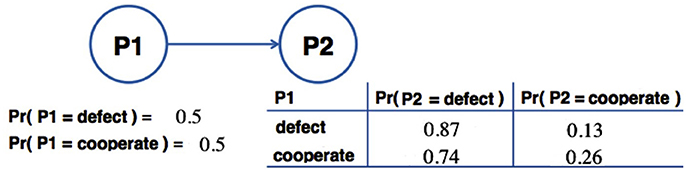
Figure 5. Bayesian Network representation of the Average of the results reported in the literature (last row of Table 1). The random variables that were considered are P₁ and P₂, corresponding to the actions chosen by the first participant and second participant, respectively.

To compute the probability Pr(P₂ = Defect), two operations are required: the computation of the full joint probability distribution (Equation 43) and the computation of the marginal probability.

The full joint probability distribution can be easily computed by multiplying all possible assignments of the network with each other. Table 2 shows the computation of these probabilities.

TABLE 2

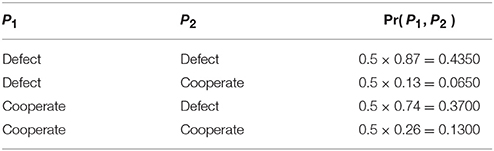
Table 2. Classical full joint probability distribution representation of the Bayesian Network in Figure 5.

The marginalization formula is used when we want to perform queries to the network. For instance, in the Prisoner's Dilemma Game, we want to know what the probability is of the second player choosing to defect given that we do not know what the other player has chosen, Pr(P₂ = Defect). This is obtained by summing the entries of the full joint probability (Table 2) that have P₂ = Defect. That is, we sum up the first and third rows of this table. Equation (45) shows this operation. For simplicity, we have used the following notation: D = Defect and C = Cooperate.

$\begin{array}{l}Pr(P2=D)=Pr(P1=D)·Pr(P2=D|P1=D)+Pr(P1=C)\\ ·Pr(P2=D|P1=C)=0.8050& (45)\end{array}$

In Equation (45), one can see that the classical Bayesian Network was not able to predict the observed results in Table 1 using classical inference. One might think that, if we parameterize the Bayesian Network to take into account the player's actions and dissonance effects, there could be a possibility of obtaining the required results. This line of thought is legitimate, but one must take into account that, in the end, the probabilistic inferences computed through the Bayesian Network must obey set theory and the law of total probability. This means that, even if we parameterize the network, we cannot find any closed form optimization that could lead to the desired results. This happened with the previous example of the Markov Model in Section 3. Although we parameterized the player's actions and dissonance effects, we could not arrive at the desired results because they go against the laws of probability theory, and Markov Models (as well as Bayesian Networks) must obey these laws.

7.3. Quantum-Like Bayesian Networks in the Literature

There are two main works in the literature that have contributed to the development and understanding of Quantum Bayesian Networks. One belongs to Tucci [37] and the other to Leifer and Poulin [38].

In the work of Tucci [37], it is argued that any classical Bayesian Network can be extended to a quantum one by replacing real probabilities with quantum complex amplitudes. This means that the factorization should be performed in the same manner as in a classical Bayesian Network. Thus, the Bayesian Network of Figure 5 could be represented by a Quantum Bayesian Network with the following matrices tables (the ordering of the probability amplitudes in the matrices are the same as the ones in Figure 5):

$\begin{array}{l}{P}_1=\left[\begin{array}{c} a·e^{i{\theta }_1}\sqrt{1-|a·e^{i{\theta }_1}{|}^2}·e^{i{\theta }_2}\end{array}\right]\\ P_2=\left[\begin{array}{l}b·e^{i{\theta }_3}\sqrt{1-|b·e^{i{\theta }_3}{|}^2}·e^{i{\theta }_4}\\ c·e^{i{\theta }_5}\sqrt{1-|c·e^{i{\theta }_5}{|}^2}·e^{i{\theta }_6}\end{array}\right]\end{array}$

One significant problem with Tucci's work is related to the non-existence of any methods to set the phase parameters e^iθ. The author states that one could have infinite Quantum Bayesian Networks representing the same classical Bayesian Network depending on the values that one chooses to set the parameter. This requires that one knows a priori which parameters would lead to the desired solution for each node queried in the network (which we never know). Thus, for these experiments, Tucci's model cannot predict the results observed because one does not have any information about the quantum parameters.

In the work of Leifer and Poulin [38], the authors argue that, to develop a Quantum Bayesian Network, quantum versions of probability distributions, quantum marginal probabilities and quantum conditional probabilities are required (Table 3). The authors performed a preliminary study of these concepts. Generally speaking, a quantum probability distribution corresponds to a density matrix contained in a Hilbert space, with the constraint that the trace of this matrix must sum to 1. In quantum probability theory, a full joint distribution is given by a density matrix, ρ. This matrix provides the probability distribution of all states that a Bayesian Network can have. The marginalization operation corresponds to a quantum partial trace [75, 76].

TABLE 3

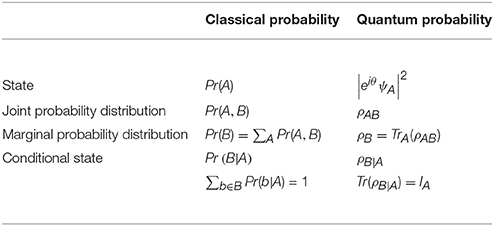
Table 3. Relation between classical and quantum probabilities used in the work of Leifer and Poulin [38].

In the end, the models of Tucci [37] and Leifer and Poulin [38] fail to provide any advantage relative to the classical models because they cannot take into account interference effects between random variables. Thus, they provide no advantages in modeling decision-making problems that try to predict decisions that violate the laws of total probability.

A more recent work from Moreira and Wichert [65] suggested defining the Quantum-Like Bayesian Network in the same manner as in the work of Tucci [37], replacing real probability numbers by quantum probability amplitudes.

In this sense, the quantum counterpart of the full joint probability distribution corresponds to the application of Born's rule to Equation (43):

$\begin{array}{ll}Pr(X_1,\dots ,X_n)={\left|{\displaystyle \prod _{i=1}^N{\psi }_{(X_i|Parents(X_i))}}\right|}^2& (46)\end{array}$

The general idea of a Quantum-Like Bayesian network is that, when performing probabilistic inference, the probability amplitude of each assignment of the network is propagated and influences the probabilities of the remaining nodes. In other words, every assignment of every node of the network is propagated until the node representing the query variable is reached. Note that, by taking multiple assignments and paths at the same time, these trails influence each other in producing interference effects.

The quantum counterpart of the Bayesian exact inference formula corresponds to the application of Born's rule to Equation (44), leading to:

$\begin{array}{ll}Pr(X|e)=\alpha {\left|{\displaystyle \sum _y{\displaystyle \prod _{x=1}^N{\psi }_{(X_x|Parents(X_x),e,y)}}}\right|}^2& (47)\end{array}$

Expanding Equation (47), it will lead to the quantum interference formula:

$\begin{array}{l}Pr(X|e)=\alpha \left({\displaystyle \sum _{i=1}^{\left|Y\right|}{\left|{\displaystyle \prod _x^N{\psi }_{(X_x|Parents(X_x),e,y=i)}}\right|}^2+2·Interference}\right)\end{array}$

$\begin{array}{l}Interference={\displaystyle \sum _{i=1}^{\left|Y\right|-1}{\displaystyle \sum _{j=i+1}^{\left|Y\right|}\left|{\displaystyle \prod _x^N{\psi }_{(X_x|Parents(X_x),e,y=i)}}\right|}}\\ ·\left|{\displaystyle \prod _x^N{\psi }_{(X_x|Parents(X_x),e,y=j)}}\right|·\cos ({\theta }_i-{\theta }_j)& (48)\end{array}$

In the Quantum Dynamical Model, because it uses unitary operators, the double symmetric property of these operators does not require the normalization of the computed values. However, in this approach, because we do not have the constraints of double stochasticity operators, we need to normalize the final scores that are computed to achieve a probability value. In classical Bayesian inference, normalization of the inference scores is also necessary due to assumptions made in Bayes rule. The normalization factor corresponds to α in Equation (48).

Note that, in Equation (48), if one sets (θ_i − θ_j) to π∕2, then cos(θ_i − θ_j) = 0, which means that the quantum Bayesian Network collapses to its classical counterpart. That is, they can behave in a classical way if one sets the interference term to zero. Moreover, in Equation (48), if the Bayesian Network has N binary random variables, we will end up with 2^N free quantum θ parameters. We represent each set of quantum parameters as a single parameter of the full joint probability distribution just like it is presented in Table 4. Approaches to tune those parameters under a Quantum-Like Bayesian Network approach are still an open research question.

TABLE 4

Table 4. Quantum full joint probability amplitude distribution representation of the Bayesian Network in Figure 5.

In the model of Moreira and Wichert [65], if there are many unobserved nodes in the network, then the levels of uncertainty are very high and the interference effects produce changes in the final likelihoods of the outcomes. However, in the opposite scenario, when there are very few unobserved nodes, then the proposed quantum model tends to collapse into its classical counterpart because the uncertainty levels are very low. This work only provides a study on the impact of the quantum parameters in complex decision scenarios. On later works, the same authors have proposed the usage of heuristics to automatically assign values to quantum parameters [39, 77].

7.4. Application of the Quantum-Like Formalism to the Prisoner's Dilemma Game

In this section, we will demonstrate how the proposed Bayesian Network can be applied to the average results presented in Table 1 for the Prisoner's Dilemma game, just as was proposed in the work of Moreira and Wichert [65].

We begin applying the Quantum-Like formalism by creating a Bayesian Network out of the decision problem, in which real classical probabilities are replaced by quantum amplitudes (Figure 6). In the Prisoner's Dilemma Game, if nothing is told to the participants, then there is a 50% chance of the first participant choosing to defect or cooperate. The decision of the first participant is then followed by the decision of the second participant.

FIGURE 6

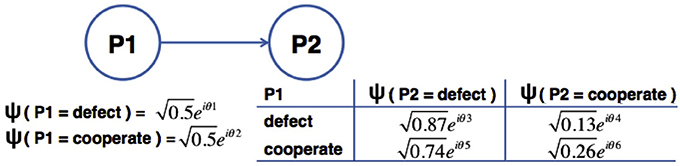
Figure 6. Bayesian Network representation of the Average of the results reported in the literature (last row of Table 1). The random variables that were considered are P1 and P2, corresponding to the actions chosen by the first participant and second participant, respectively.

To compute the probability Pr(P₂ = Defect), two operations are required: the computation of the quantum version of the full joint probability distribution (Equation 46) and the computation of the quantum version of the marginal probability (Equation 48).

The full joint probability distribution can be easily computed by multiplying all possible assignments of the network with each other. For instance, the quantum full joint probability amplitude ψ_{(P1 = Defect, P2 = Defect)} is given by multiplying the prior probability amplitude ψ_{(P1 = Defect)} with the conditional probability amplitude ψ_{(P2 = Defect|P1 = Defect)}. Table 4 shows the computation of these quantum probability amplitudes.

From the quantum version of the full joint probability distribution, one can compute the quantum version of the marginal probability distribution by summing all the entries of Table 4 that contain the assignment P2 = Defect (Equation 49). For simplification purposes, we will consider the following abbreviations: Defect = D and Cooperate = C.

$\begin{array}{l}Pr(P_2=D)=\alpha [|{\psi }_{(P_1=D,P_2=D)}{|}^2+|{\psi }_{(P_1=C,P_2=D)}{|}^2\\ +2·{\psi }_{(P_1=D,P_2=D)}·{\psi }_{(P_1=C,P_2=D)}\cos ({\theta }_A-{\theta }_B)]& (49)\end{array}$

$\begin{array}{l}Pr(P_2=D)=\alpha [|{\psi }_{(P_1=D)}·{\psi }_{(P_2=D|P_1=D)}{|}^2+\\ |{\psi }_{(P_1=C)}·{\psi }_{(P_2=D|P_1=C)}{|}^2+2·{\psi }_{(P_1=D)}\\ ·{\psi }_{(P_2=D|P_1=D)}·{\psi }_{(P_1=C)}·{\psi }_{(P_2=D|P_1=C)}\\ ·\cos ({\theta }_A-{\theta }_B)]& (50)\end{array}$

$\begin{array}{l}Pr(P_2=D)=\alpha [|0.6595{|}^2+|0.6083{|}^2+2\times 0.6595\\ \times 0.6083·\cos ({\theta }_A-{\theta }_B) ]\\ =\alpha [0.8050+0.8023·\cos ({\theta }_A-{\theta }_B)]& (51)\end{array}$

To compute the normalization factor α, we also need to compute Pr(P2 = C):

$\begin{array}{l}Pr(P_2=C)=\alpha [|{\psi }_{(P_1=D)}·{\psi }_{(P_2=C|P_1=D)}{|}^2+|{\psi }_{(P_1=C)}\\ ·{\psi }_{(P_2=C|P_1=C)}{|}^2+2·{\psi }_{(P_1=D)}·{\psi }_{(P_2=C|P_1=D)}\\ ·{\psi }_{(P_1=C)}·{\psi }_{(P_2=C|P_1=C)}·\cos ({\theta }_A-{\theta }_B)]& (52)\end{array}$

$\begin{array}{l}Pr(P_2=C)=\alpha [|0.255{|}^2+|0.3606{|}^2+2\times 0.255\times 0.3606\\ ·\cos ({\theta }_A-{\theta }_B)]=\alpha [0.195+0.1839\\ ·\cos ({\theta }_A-{\theta }_B)]& (53)\end{array}$

The normalization factor α is given by Equation (54).

$\begin{array}{ll}\alpha =\frac{1}{Pr(P_2=D)+Pr(P_2=C)}=\frac{1}{1+0.9862·\cos ({\theta }_A-{\theta }_B)}& (54)\end{array}$

Equation (54) contains two quantum parameters θ. Setting these parameters is still an open research question in the literature, although in some works, various heuristics have been proposed to address this problem [39, 40, 77].

8. Discussion of the Presented Models

The purpose of this section is to present discussion of and a comparison between the existing quantum models in terms of the proposed evaluation metrics: terms of interference, parameter tuning and scalability. The discussion will be mainly focused on the set of parameters that the current quantum cognitive models have that need to be fitted to match the desired predictions. For instance, the Quantum Dynamical Model requires three parameters for such small decision scenarios, whereas the Quantum-Like Approach only needs one, and the Quantum Prospect Decision Theory does not need any parameters because it has a static heuristic to replace the interference term. Note that the Quantum Dynamical Model uses three parameters μ_c, μ_d, γ to predict three probabilities to defect when { known to defect, known to cooperate, unknown }. While the Quantum-Like Approach uses one chosen parameter and two probabilities to defect { known to defect, known to cooperate } to predict one probability to defect when { unknown }. In the end, we will see that the problems that we note for the quantum models are similar to many other classical cognitive models.

8.1. Discussion in Terms of Interference, Parameter Tuning and Scalability

In this section, we analyze the presented works in the literature regarding three different metrics: interference effects, parameter tuning, and scalability.

• Interference Effects. Many works from the literature state that, through quantum interference effects, one could simulate the paradoxical decisions found across many experiments in the literature. Without interference effects, quantum probability converges to its classical counterpart. This metric examines if the analyzed model makes use of any type of quantum interference to explain human decision-making.

• Parameter Tuning. The problem of applying quantum formalisms to cognition is concerned with the number of quantum parameters that one needs to find. These parameters grow exponentially with the complexity of the decision problem, and thus far, very few works in the literature have suggested ways to automatically find these parameters to make accurate predictions.

• Scalability. Most problems of the current models of the literature are concerned with their inability to scale to more complex decision scenarios. Most of these models are built to explain very small paradoxical findings (for example, the Prisoner's Dilemma Game and the Two-Stage Gambling Game). Therefore, this metric consists of analyzing the presented models with respect to their ability to extend and generalize to more complex scenarios.

Table 5 presents a summary of the evaluation of the models presented in this work with respect to the three metrics described above. The parameter growth column is based on the number of parameters that each model generates when we increase the number of unknown random variables in the decision model

TABLE 5

Table 5. Comparison of the different models proposed in the literature.

Starting the discussion with the classical models presented in Sections 3 and 7.1, the probabilistic inferences computed through Bayesian/Markov Networks must obey set theory and the law of total probability. This means that, even if we parameterize the networks, we cannot find any closed form optimization that could lead to the desired results. These networks can be modeled with no parameters (just as was presented in Sections 3 and 7.1), or they can be parameterized. This parameterization can end up with the same size as the full joint probability distribution of the networks. Although these models do not make use of any quantum interference effects and consequently cannot accommodate violations of the Sure Thing Principle, it is worth noting that one can always classically explain behavioral results through appropriate conditionalizations and extensions of classical probabilistic models [16].

The Quantum-Like Approach [72] is based on the direct mapping of classical probabilities to quantum probability amplitudes through Born's rule. This means that one can perform inferences for more complex decision-making scenarios by using the quantum counterpart of the classical marginal probability formula. Thus, the model generates quantum interference effects. The main problem of the Quantum-Like approach concerns the quantum parameters. The current works of the literature do not provide any means to assign values to these quantum parameters. They have to be fitted to explain the observed outcome. Thus, the Quantum-Like approach, although it can be (mathematically) extended to more complex decision scenarios, does not provide any means to assign quantum parameters. Note that, in the Quantum-Like approach, just like in many other models, it is required a mathematical fitting of a set of parameters to make an optimal prediction of the probabilities. So, the Quantum-Like Approach is considered to be a predictive model.

The Quantum Dynamical Model proposed by Pothos and Busemeyer [17] and Busemeyer et al. [35] incorporates quantum interference effects not from the quantum law of probability but by the usage of unitary operators and Hamiltonians. One of the main disadvantages of this model concerns the definition of the Hamiltonian matrices. Creating a Hamiltonian is a very hard problem. It is required that all possible interactions of the decision problem are known, and this specification must be made in such a way that the matrix is doubly stochastic. The unitary matrix also grows exponentially with the complexity of the decision problem, and the computation of a unitary operator from such matrices is a very complex process. Most of the time, approximations are used because of the complexity of the calculations involved in the matrix exponentiation operation. Just as in the Quantum-Like Approach, one needs to fit the quantum parameters so that the final model can give the observed outcome. It is important to note that, in the Quantum Dynamical Model, the parameters used are based on a psychological setting. The incorporation of parameters to model dissonance effects and the payoffs of the players provide an approximation to the psychology of the problem that is not observed in other quantum cognitive models in the literature.

Finally, the Quantum Prospect Theory proposed by Yukalov and Sornette [36] also incorporates quantum interference effects from the quantum law of total probability. This model is very similar, from a mathematical point of view, to the Quantum-Like Approach, with the difference that it proposes laws to compute the quantum interference parameters: the alternation and the quantum quarter laws. Although the model is very precise for very small decision problems (such as the Prisoner's Dilemma), it is not clear how the quantum quarter law and the alternation law would work for more complex problems. For this reason, the Quantum Prospect Theory is a model that enables the usage of quantum interference terms to make predictions under paradoxical scenarios and also provides an automatic mechanism to set the quantum parameters under very small scenarios with a static interference term (q = ±0.25). That is, the interference term is always the same, even for different contextual problems. For this reason, the model is not able to generalize well for more complex decision scenarios.

Regarding Bayesian Networks, it is hard to apply the model proposed in the work of Tucci [37] in paradoxical findings that violate the Sure Thing Principle because the author makes no mention of how to set these parameters. He even argues that a classical Bayesian Network can be represented by an infinite number of quantum Bayesian Networks depending on how one tunes the quantum parameters. Because the model is a Bayesian Network, one is able to perform inferences for any scenario by using the quantum counterpart of the classical marginal probability formula. Thus, in the end, the quantum Bayesian Network proposed by Tucci [37] is scalable and takes into account quantum interference effects; however, it does not give any insights into how to set the quantum parameters that result from the interference.

In the work of Leifer and Poulin [38], the authors create a direct mapping from classical probability to quantum theory. Because they made a quantum Bayesian Network, this model enabled probabilistic inference, and consequently, it can be generalized for any number of random variables through the use of the quantum part of the marginal probability formula. By making the direct mapping from classical to quantum probabilities, the full joint probability distribution is mapped into a density matrix. This means that the interference terms are canceled. The authors also take into account the order in which the operations are performed. Because, the commutativity axiom is not valid in quantum mechanics, we obtain different outcomes if the calculations are performed in a different order. Thus, the quantum Bayesian Network proposed by Leifer and Poulin [38] is scalable and takes into account quantum interference effects; however, by making a direct mapping from classical to quantum, these interference effects will cancel because the network will collapse into its classical counterpart. Thus, in the end, this model does not take advantage of quantum interferences to explain paradoxical decision scenarios.

In the work of Moreira and Wichert [65], the authors also make a direct mapping from classical theory to quantum probability by replacing classical real probability values by complex quantum probability amplitudes using Born's rule. They also applied the same mechanism to derive a quantum-like full joint probability distribution formula and a quantum-like marginal probability distribution for exact inference. In the end, the model is very similar to the Quantum-Like Approach, and it can be modeled for more complex decision-making scenarios very easily due to its graphical structure. Because this model uses quantum probability amplitudes, quantum interference effects arise from the quantum-like exact inference formula. However, the number of parameters grows exponentially large when the levels of uncertainty are high, that is, when there are many unobserved nodes in the network. Although the authors have proposed some dynamic heuristics to address this problem in recent works [39, 40, 77], one needs to take into account that they are heuristics, which means that it can lead to the expected outcome, but it can also lead to completely inaccurate results.

Note that we are aware that the problems that we note in this discussion section about the quantum models are the same in many cognitive science models. However, we are not claiming that it is difficult to find the parameters for a game such as the Prisoner's Dilemma. What we are claiming is that the several models analyzed in this work (Quantum-Like Approach, Quantum Dynamical Model, Quantum-Like Bayesian Networks) contain a set of parameters that need to be fitted to match the desired predictions.

For instance, the Quantum Dynamical Model requires three parameters for such a small decision scenario, whereas the Quantum-Like Approach only needs one, and the Quantum Prospect Decision Theory does not need any parameters, because it has a static heuristic to replace the interference term. The purpose of this discussion section is simply to compare the existing quantum models in terms of the evaluation metrics specified in Table 5.

8.2. Discussion in Terms of Parameter Growth

All models analyzed in this work present different growth rates in what concerns parameters. For instance, the Dynamical Model parameterizes the player's actions plus an additional parameter to model cognitive dissonance effects. Thus, the number of parameters would be static if we consider the N-Person Prisoner's Dilemma Game. That is, instead of having only 2 players, it is extended to N players. In the case of the Quantum-Like Approach, we would have 2^N parameters for the N-Person Prisoner's Dilemma Game. The number 2 comes from the fact that each player has two actions (either defect or cooperate). The same applies to the Classical Networks, the Quantum-Like Bayesian Networks and the Quantum Prospect Theory Model. However, because the authors of this last model presented the Quantum Quarter Law of Interference as a static heuristic, this model does not require any parameters.

At this point, the reader might be thinking that the Quantum Dynamical Model provides great advantages vs. the existing models because the number of parameters required corresponds to the player's actions with an additional cognitive dissonance parameter. Although this line of thought is correct, one should also take into account how the model unfolds. Although the numbers of parameters do not grow exponentially large as in the Quantum-Like Approach, the size of the Hamiltonian does. In fact, it grows exponentially large with the following size: $N_{actions}^{N_{players}}\times N_{actions}^{N_{players}}$, where N_actions represents the number of actions of the players and N_players corresponds to the number of players.

We conclude this section by clarifying that most of the quantum cognitive models proposed in the literature have been directed toward small decision scenarios because of the scarcity of datasets representing complex decision scenarios and violations of the Sure Thing Principle. Consequently, the models proposed are simply overfitting simple decision scenarios. Moreover, we believe that the violations of the Sure Thing Principle tend to diminish with the complexity of the decision scenario. Imagine, for instance, a Three-Stage Gambling game. It will be very hard to find significant data that shows a player wishing to play the last gamble given that he has lost the two previous gambles. More experimental data and more studies are needed for more complex decision scenarios to test the viability of quantum models vs. their classical counterparts.

9. Conclusion

Recent work in cognitive psychology has revealed that quantum probability theory provides another method of computing probabilities without falling into the restrictions that classical probability has in modeling cognitive systems of decision-making. Quantum probability theory can also be seen as a generalization of classical probability theory, because it also includes the classical probabilities as a special case (when the interference term is zero).

Quantum probability has the particularity of enabling the representation of events in a geometric structure. The main advantage of this geometrical representation is the ability to rotate from one basis to another to contextualize and interpret events. This ability does not exist in the classical probability theory and provides great flexibility for decision-making systems. Consequently, quantum probability can be more expressive than its traditional classical counterpart. Under quantum theory, these paradoxical findings can simply be seen as consequences of the geometric flexibility that quantum probability theory offers.

We have collected a set of models from the literature that attempt to tackle violations of the Sure Thing Principle in a Quantum fashion, and then we compared the collected models. To illustrate this comparison, we provided a mathematical description of each model and how they could be applied in a decision scenario. We compared the models in terms of three proposed metrics: the number of parameters involved in the model, the scalability and the usage of the quantum interference effects. We have also performed a more detailed study concerning the growth of the number of quantum parameters when the complexity and the levels of uncertainty of the decision scenario increase. We have also performed this comparison with classical models, namely a Markov Model and a Bayesian Network. The main statement of this work is not to express that quantum models are preferred with respect to the classical models. With this work, we have concluded that purely classical models suffer from the same exponential parameterization growth as quantum models, with the added difficulty that they are not capable of simulating results that violate the Sure Thing Principle. It is worth noting that one can always classically explain behavioral results through appropriate conditionalizations of the classical law of total probability. In the end, classical models are constrained to obey set theory and the laws of probability theory, so there is no closed optimization form that could lead to the paradoxical results found in the experiments violating the Sure thing Principle.

The proposed models of the literature only work for very small decision problems. Most of them do not provide any means to fit the quantum parameters that are required in their models. These models are useful to accommodate the paradoxical violations reported in the literature, but are not able to predict the decisions of the players without a manual fit of the parameters. One should also note that it is very difficult to validate these types of models, especially when the complexity of the decision problem increases. Thus far, in the literature, there are almost no demonstrations of violations of the Sure Thing Principle for more complex decision scenarios. More studies are needed in this direction to validate the viability of quantum models.

This work provides a technical overview of the proposed quantum models of the literature and a discussion of many key aspects of the original studies. With the proposed evaluation metrics, we were able to discuss many key aspects that have been ignored in the literature, namely how the quantum interference terms affect the complexity of the decision problems. Most of the quantum cognitive models proposed in the literature cannot predict the results observed in several experiments of the literature without first knowing the outcome of the experiment. Having this information, they can then fit their models to the desired outcome. Thus, the primary goal of these models is to accommodate the violations of the Sure Thing Principle. The usage of parameters, in some models, with a more clear psychological interpretation are also considered to be explicative. The discussions addressed turn this work into a complement to the study of the original works.

Author Contributions

All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by national funds through Fundação para a Ciência e a Tecnologia (FCT) with reference UID/CEC/50021/2013 and through the PhD grant SFRH/BD/92391/2013. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Footnotes

1. ^These graphs were plotted using the Wolfram Mathematica 10.4.1 software.

References

1. Friedman M, Savage L. The expected-utility hypothesis and the measurability of utility. J Polit Econ (1952) 50:463–74. doi: 10.1086/257308

CrossRef Full Text | Google Scholar

2. Savage LJ. The Foundations of Statistics. New York, NY: John Wiley (1954).

Google Scholar

3. Allais M. Le comportement de l'homme rationel devant le risque: Critique des postulats et axiomes de l'cole americaine. Econometrica (1953) 21:503–46.

4. Ellsberg D. Risk, ambiguity and the savage axioms. Q J Econ. (1961) 75: 643–69. doi: 10.2307/1884324

CrossRef Full Text | Google Scholar

5. Tversky A, Kahnenman D. Judgment under uncertainty: heuristics and biases. Science (1974) 185:1124–31. doi: 10.1126/science.185.4157.1124

PubMed Abstract | CrossRef Full Text

6. Tversky A, Kahneman D. The framing of decisions and the psychology of choice. Science (1981) 211:453–8. doi: 10.1126/science.7455683

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Tversky A, Kahneman D. Rational choice and the framing of decisions. J Business (1986) 59:251–78. doi: 10.1086/296365

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kahneman D, Slovic P, Tversky A. Judgment Under Uncertainty: Heuristics and Biases. Cambridge, UK: Cambridge University Press (1982).

Google Scholar

9. Kahneman D, Tversky A. Prospect theory - an analysis of decision under risk. J Econ. (1979) 47:263–92. doi: 10.2307/1914185

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Tversky A, Shafir E. The disjunction effect in choice under uncertainty. J Psychol Sci. (1992) 3:305–9. doi: 10.1111/j.1467-9280.1992.tb00678.x

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Busemeyer J, Wang Z, Townsend J. Quantum dynamics of human decision making. J Math Psychol. (2006b) 50:220–41. doi: 10.1016/j.jmp.2006.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Busemeyer, J. Cognitive science contributions to decision science. Cognition (2015) 135:43–6. doi: 10.1016/j.cognition.2014.11.010

PubMed Abstract | CrossRef Full Text

13. Busemeyer J, Wang Z. Quantum cognition: key issues and discussion. Top Cogn Sci. (2014) 6:43–6. doi: 10.1111/tops.12074

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Aerts D. Quantum theory and human perception of the macro-world. Front Psychol. (2014) 5:554. doi: 10.3389/fpsyg.2014.00554

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Busemeyer J, Wang Z, Shiffrin R. Bayesian model comparison favors quantum over standard decision theory account of dynamic inconsistencies. Decision (2015) 2:1–12. doi: 10.1037/dec0000017

CrossRef Full Text | Google Scholar

16. Busemeyer J, Bruza P. Quantum Model of Cognition and Decision. Cambridge, UK: Cambridge University Press (2012). doi: 10.1017/CBO9780511997716

CrossRef Full Text | Google Scholar

17. Pothos E, Busemeyer J. A quantum probability explanation for violations of rational decision theory. Proc R Soc B (2009) 276:2171–8. doi: 10.1098/rspb.2009.0121

PubMed Abstract | CrossRef Full Text

18. Khrennikov A, Haven E. Quantum mechanics and violations of the sure-thing principle: the use of probability interference and other concepts. J Math Psychol. (2009) 53:378–88. doi: 10.1016/j.jmp.2009.01.007

CrossRef Full Text | Google Scholar

19. Asano M, Khrennikov A, Ohya M, Tanaka Y, Yamato I. Quantum Adaptivity in Biology: From Genetics to Cognition. Dordrecht: Springer (2015).

Google Scholar

20. Asano M, Basieva I, Khrennikov A, Ohya M, Tanaka Y, Yamato, I. Quantum-like model for the adaptive dynamics of the genetic regulation of e. coli's metabolism of glucose/lactose. J Syst Syn Biol. (2012) 6:1–7.

PubMed Abstract | Google Scholar

21. Khrennikov A. Classical and quantum-like randomness and the financial market. In: Faggini M, Lux T, editors. Coping with the Complexity of Economics. Springer (2009a). p. 67–77. doi: 10.1007/978-88-470-1083-3_5

CrossRef Full Text

22. Haven E, Khrennikov A. Quantum Social Science. New York, NY: Cambridge University Press (2013). doi: 10.1017/CBO9781139003261

CrossRef Full Text | Google Scholar

23. Conte E, Todarello O, Federici A, Vitiello F, Lopane M, Khrennikov A, et al. Some remarks on an experiment suggesting quantum like behavior of cognitive entities and formulation of an abstract quantum mechanical formalism to describe cognitive entity and its dynamics. J Chaos Solit Fract. (2007) 31:1076–88. doi: 10.1016/j.chaos.2005.09.061

CrossRef Full Text | Google Scholar

24. Conte E. Testing quantum consciousness. J NeuroQuantol. (2008) 6:126–39. doi: 10.14704/nq.2008.6.2.167

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Trueblood J, Busemeyer J. A comparison of the belief-adjustment model and the quantum inference model as explanations of order effects in human inference. In: Proceedings of the 32nd Annual Conference of the Cognitive Society, 2010. Portland, OR (2011).

26. Aerts D, Aerts S. Applications of quantum statistics in psychological studies of decision processes. J Found Sci. (1994) 1:85–97. doi: 10.1007/BF00208726

CrossRef Full Text | Google Scholar

27. Aerts D. Quantum structures: an attempt to explain the origin of their appearence in nature. Int J Theor Phys. (1995) 34:1–22. doi: 10.1007/BF00676227

CrossRef Full Text

28. Aerts S. Conditinal probabilities with a quantal and kolmogorovian limit. Int J Theor Phys. (1996) 35:2245. doi: 10.1007/BF02302444

CrossRef Full Text | Google Scholar

29. Aerts S. Interactive probability models: inverse problems on the sphere. Int J Theor Phys. (1998) 37:305–9. doi: 10.1023/A:1026622919418

CrossRef Full Text | Google Scholar

30. Gabora L, Aerts D. Contextualizing concepts using a mathematical generalization of the quantum formalism. J Exp Theor Artif Intell. (2002) 14:327–58. doi: 10.1080/09528130210162253

CrossRef Full Text | Google Scholar

31. Aerts D, Broekaert J, Gabora L. A case for applying an abstracted quantum formalism to cognition. J New Ideas Psychol. (2011) 29:136–46. doi: 10.1016/j.newideapsych.2010.06.002

CrossRef Full Text | Google Scholar

32. Aerts D. Quantum structure in cognition. J Math Psychol. (2009) 53:314–48. doi: 10.1016/j.jmp.2009.04.005

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Shafir E, Tversky A. Thinking through uncertainty: nonconsequential reasoning and choice. Cogn Psychol. (1992) 24:449–74. doi: 10.1016/0010-0285(92)90015-T

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Khrennikov A. Interpretations of Probability. Berlin: Wlater de Gruyter (2009c). doi: 10.1515/9783110213195

CrossRef Full Text

35. Busemeyer J, Wang Z, Lambert-Mogiliansky A. Empirical comparison of markov and quantum models of decision making. J Math Psychol. (2009) 53:423–33. doi: 10.1016/j.jmp.2009.03.002

CrossRef Full Text | Google Scholar

36. Yukalov V, Sornette D. Decision theory with prospect interference and entanglement. Theory Decis. (2011) 70:283–328. doi: 10.1007/s11238-010-9202-y

CrossRef Full Text | Google Scholar

37. Tucci R. Quantum bayesian nets. Int J Mod Phys B (1995) 9:295–337. doi: 10.1142/S0217979295000148

CrossRef Full Text | Google Scholar

38. Leifer M, Poulin D. Quantum graphical models and belief propagation. Ann Phys J. (2008) 323:1899–946. doi: 10.1016/j.aop.2007.10.001

CrossRef Full Text | Google Scholar

39. Moreira C, Wichert A. The synchronicity principle under quantum probabilistic inferences. NeuroQuantology (2015b) 13:111–33. doi: 10.14704/nq.2015.13.1.788

CrossRef Full Text | Google Scholar

40. Moreira C, Wichert A. Quantum-like bayesian networks for modeling decision making. Front Psychol. (2016) 7:11. doi: 10.3389/fpsyg.2016.00011

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Epstein L. A definition of uncertainty aversion. Rev Econ Stud. (1999) 66:579–608. doi: 10.1111/1467-937X.00099

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Peres A. Quantum Theory: Concepts and Methods. New York, NY: Kluwer Academic (1998).

Google Scholar

43. Kuhberger A, Komunska D, Josef P. The disjunction effect: does it exist for two-step gambles? Organ Behav Hum Decis Process. (2001) 85:250–64. doi: 10.1006/obhd.2000.2942

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Lambdin C, Burdsal C. The disjunction effect reexamined: relevant methodological issues and the fallacy of unspecified percentage comparisons. Organ Behav Hum Decis Proces. (2007) 103:268–76. doi: 10.1016/j.obhdp.2006.04.001

CrossRef Full Text | Google Scholar

45. Crosson R. The disjunction effect and reason-based choice in games. J Organ Hum Decis Process. (1999) 80:118–33. doi: 10.1006/obhd.1999.2846

PubMed Abstract | CrossRef Full Text

46. Li S, Taplin J. Examining whether there is a disjunction effect in prisoner's dilemma game. Chinese J Psychol. (2002) 44:25–46. Available online at: http://hdl.handle.net/2440/3240

47. Busemeyer J, Matthew M, Wang Z. A quantum information processing explanation of disjunction effects. In: Proceedings of the 28th Annual Conference of the Cognitive Science Society. Vancouver, BC (2006a).

48. Hristova E, Grinberg M. Disjunction effect in prisonner's dilemma: evidences from an eye-tracking study. In: Proceedings of the 30th Annual Conference of the Cognitive Science Society. Washington, DC (2008).

Google Scholar

49. Khrennikov A. Contextual Approach to Quantum Formalism. Dordrecht: Springer (2010).

Google Scholar

50. Khrennikov A, Basieva I, Dzhafarov E, Busemeyer J. Quantum models for psychological measurements: an unsolved problem. PLoS ONE (2014) 9:e110909. doi: 10.1371/journal.pone.0110909

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Khrennikov A. Representation of the contextual statistical model by hyperbolic amplitudes. J Math Phys. (2005c) 46:1–13. doi: 10.1063/1.1931042

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Nyman P. On the consistency of the quantum-like representation algorithm for hyperbolic interference. J Adv Appl Cliff Algeb. (2011b) 21:799–811. doi: 10.1007/s00006-011-0287-3

CrossRef Full Text | Google Scholar

53. Nyman P. On hyperbolic interferences in the quantum-like representation algorithm for the case of triple-valued observables. J Found Phys. (2011a) arXiv:1108.2194v1.

Google Scholar

54. Khrennikov A. Description of composite quantum systems by means of classical random fields. Found Phys. (2009b) 40:1051–64. doi: 10.1007/s10701-009-9392-8

CrossRef Full Text | Google Scholar

55. Khrennikov A. Classical and quantum mechanics on information spaces with applications to cognitive psychological, social and anomalous phenomena. Found Phys. (1999) 29:1065–98. doi: 10.1023/A:1018885632116

CrossRef Full Text

56. Khrennikov A. Linear representations of probabilistic transformations induced by context transitions. J Phys A (2001) 34:9965–81. doi: 10.1088/0305-4470/34/47/304

CrossRef Full Text | Google Scholar

57. Khrennikov A. Representation of the kolmogorov model having all distinguishing features of quantum probabilistic model. J Phys Lett A (2003) 316:279–96. doi: 10.1016/j.physleta.2003.07.006

CrossRef Full Text | Google Scholar

58. Khrennikov A. From classical statistical model to quantum model through ignorance of information. In: Proceedings of the Third Conference on the Foundations of Information Science. Paris (2005a).

Google Scholar

59. Khrennikov A. Linear and nonlinear analogues of the schrödinger equation in the contextual approach to quantum mechanics. J Doklady Math. (2005b) 72:791–4.

60. Zurek W. Entanglement symmetry, amplitudes, and probabilities: inverting born's rule. J Phys Rev Lett. (2011) 106:1–5. doi: 10.1103/PhysRevLett.106.250402

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Zurek W. Probabilities from entanglement, born's rule from envariance. J Phys Rev A (2005) 71:1–29. doi: 10.1103/PhysRevA.71.052105

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Nyman P. On consistency of the quantum-like representation algorithm. J Theor Phys. (2010) 49:1–9. doi: 10.1007/s10773-009-0171-2

CrossRef Full Text | Google Scholar

63. Nyman P, Basieva I. Representation of probabilistic data by complex probability amplitudes - the case of triple-valued observables. In: Proceedings of the International Conference on Advances in Quantum Theory. Växjö (2011b). doi: 10.1063/1.3567472

CrossRef Full Text

64. Nyman P, Basieva I. Quantum-like representation algorithm for trichotomous observables. J Theor Phys. (2011a) 50:3864–81. doi: 10.1007/s10773-011-0934-4

CrossRef Full Text | Google Scholar

65. Moreira C, Wichert A. Interference effects in quantum belief networks. Appl Soft Comput. (2014) 25:64–85. doi: 10.1016/j.asoc.2014.09.008

CrossRef Full Text | Google Scholar

66. Yearsley J, Busemeyer J. Quantum cognition and decision theories: a tutorial. J Math Psychol. (in press). doi: 10.1016/j.jmp.2015.11.005

CrossRef Full Text | Google Scholar

67. Yukalov V, Sornette D. Quantum decision theory as quantum theory of measurement. Phys Lett A (2008) 372:6867–71. doi: 10.1016/j.physleta.2008.09.053

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Yukalov V, Sornette D. Physics of risk and uncertainty in quantum decision making. Eur Phys J B (2009a) 71:533–48. doi: 10.1140/epjb/e2009-00245-9

CrossRef Full Text | Google Scholar

69. Yukalov V, Sornette D. Processing information in quantum decision theory. Entropy (2009b) 11:1073–1120. doi: 10.3390/e11041073

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Yukalov V, Sornette D. Entanglement production in quantum decision making. Phys Atom Nucl. (2010a) 73:559–62. doi: 10.1134/S106377881003021X

CrossRef Full Text | Google Scholar

71. Yukalov V, Sornette D. Mathematical structure of quantum decision theory. Adv Comp Syst. (2010b) 13:659–98. doi: 10.1142/S0219525910002803

CrossRef Full Text | Google Scholar

72. Khrennikov A. Quantum-like model of cognitive decision making and information processing. J BioSyst. (2009d) 95:179–87. doi: 10.1016/j.biosystems.2008.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Koller D, Friedman N. Probabilistic Graphical Models: Principles and Techniques. Cambridge, MA: The MIT Press (2009).

Google Scholar

74. Russel S, Norvig P. Artificial Intelligence: A Modern Approach. 3rd ed. Edinburgh: Pearson Education (2010).

75. Nielsen MA, Chuang IL. Quantum Computation and Quantum Information. Cambridge, UK: Cambridge University Press (2000).

Google Scholar

76. Rieffel E, Polak W. Quantum Computing: A Gentle Introduction. Cambridge, MA: MIT Press (2011).

Google Scholar

77. Moreira C, Wichert A. The relation between acausality and interference in quantum-like bayesian networks. In: Proceedings of the 9th International Conference on Quantum Interactions. Filzbach (2015a).

Google Scholar