- Departamento de Física, Instituto de Física, Universidade Federal Fluminense, Niterói, Brazil
We present an example where spontaneous symmetry breaking (SSB) may affect not only the behavior of the entanglement at Quantum Phase Transitions (QPT), but also the origin of its non-analyticity. In particular, in the XXZ model, we study the non-analyticities in the concurrence between two spins, which was claimed to be accidental since it had its origin in the optimization involved in the concurrence definition. We show that when one takes into account the effect of the SSB, even though the values of the entanglement measure does not change, the origin of the non-analytical behavior changes. The non-analytical behavior is not due to the optimization process anymore and in this sense it is a “natural” non-analyticity. This is a much more subtle influence of the SSB not observed before. We also show that the value of entanglement between one site and the rest of the chain changes after taking into account the SSB.
1. Introduction
It is now generally accepted that entanglement may help in finding and characterizing Quantum Phase Transitions (QPT), since it may inherit the non-analytic behavior of the ground state energy [1, 2] (see [3] for a review on entanglement and QPT). However, the use of entanglement in the study of QPT is very complex in many particle systems. From one side there are many possible measures. One can, for example, divide the system into two parts and look at the entanglement between them and the way it scales with respect to the size of one of the parts. In this scenario, we would expect the entanglement to scale with the volume, and not the area as has been found in many cases. This scaling with the area is called the area law and was found numerically in many particular models and analytically proved for some class of models. More interestingly, one can relate this entanglement with the ability to approximate the ground state and even obtain critical properties, such as the central charge of the model; see Amico et al. [3] and references. Another possibility is to look at the entanglement between two particles in the system; tracing out the rest. Usually this measure is maximum at the critical point and thus can signal the quantum phase transition, however this is not always true. All these entanglement measures can be written in terms of the reduced density matrices and therefore in terms of correlation functions which contain information about non-analytic behavior of the ground state energy at the critical point [1, 2]. Thus, in principle, they should inherit the non-analytical behavior of the thermodynamical quantities. However, there are non-analytical behaviors in the entanglement measurements which do not correspond to QPT, as first showed by Yang [4], for example. In general, that happens because entanglement measures are defined using optimization procedures which may create accidental non-analytical behavior or even hide genuine ones.
The use of entanglement measures to study QPT are also problematic because most of the measures are difficult to calculate and even more difficult to directly measure. Thus, even though the characterization of entanglement gives more information about the nature of the ground state and its correlation it may be easier to use the usual correlation functions and thermodynamic quantities to study the quantum phase transition. Besides such caveats, the study of the entanglement at QPT is in general more intricate than of thermodynamical quantities, because of the spontaneous symmetry breaking (SSB). At the critical point of a symmetry breaking QPT, the ground state becomes degenerate. In fact, this degenerescency is necessary for the spontaneous breaking of the Hamiltonian symmetry: the emergence of ground states without the Hamiltonian symmetry. However, as the ground state is degenerate, there are many possible ground states; some preserving the symmetry (equal superpositions of symmetry breaking states) others not. Furthermore, while thermodynamical quantities do not depend on which particular degenerate ground state one chooses, entanglement may. Therefore, one has to be careful when choosing the state. In general, states which preserve the symmetry are preferable, since they are simpler: have reduced density matrices with many null entries. But one has to be careful since there are examples where the entanglement depend on the particular ground state used [5, 6] and examples where it does not depend [7].
Here, we show an example of a new and very subtle caveat in the relation between entanglement, SSB and QPT. More specifically, we show that the SSB may change not only the value of the entanglement but also the origin of its non-analytical behavior. Actually, in our example, SSB changes the origin of the non-analytical behavior without even changing the value of the entanglement; a much more subtle influence.
In order to be self-contained, we organize the article as follows: In the next section we make a brief discussion of the model studied. In the following we discuss the subtle SSB effect on the concurrence as a QPT measurement. Then we discuss the same effect on the Von Neumann entropy, which is another kind of entanglement measurement, we then finish with the conclusion.
2. Spin- XXZ Model
We will describe the model closely following [8]. The model is the infinite one dimensional spin- XXZ chain given by the following Hamiltonian
where (u = x, y, z), are the Pauli spin- operators on site j, Δ is the anisotropy parameter, and we consider periodic boundary conditions: . The XXZ model cannot be diagonalized, but its energy spectrum can be obtained by the Bethe ansatz. The Hamiltonian has three symmetries: (i) a discrete parity ℤ2 symmetry over the plane xy: σz → −σz; (ii) a continuous U(1) symmetry that rotates the spins in the xy plane by any angle θ; and (iii) translational invariance. The ℤ2 symmetry implies that and ; while the U(1) symmetry implies that . The translational invariance implies that the reduced density matrix of a single spin does not depend on its position and that of two spins does only depend on the distance between them.
Since we want to analyze the QPT at Δ = −1, the two important phases are:
(i) Δ < −1: the system experiences a SSB, which lead it to a ferromagnetic phase, where all the spins point in the same direction creating a finite magnetization . The critical point at Δ = −1 is of first order.
(ii) −1 < Δ <1: the system is in a gapless phase, where the correlations decay polynomially and all the symmetries are preserved.
The Bethe ansatz solution gives the ground state energy [9, 10] as
where Δ = cosπν. For nearest neighbors we can obtain the correlation from e0(Δ):
For spins further apart, progress has been slow, but there are already some expressions available up to third neighbors [10]. We will not show them here, since they are too lengthy1.
We are interested in the subtleties of SSB in entanglement measurements for two spins in this chain. These entanglement measurements can be determined by the reduced density matrix of the two spins, which can be obtained from the magnetizations and correlations of the two spins. Applying the symmetries of the XXZ model, the state becomes
with r being the distance between the sites and . When the ℤ2 symmetry is broken, the state becomes
with and ; they are the magnetization of each spin along the z direction. Note that the only difference between Equations (5) and (6) are the local magnetization in the z direction. When the ℤ2 symmetry is broken pz and qz become finite and should appear in the reduced density matrix, as they do in Equation (6). Note also that the translational symmetry is still maintained, thus we have .
3. Concurrence and QPT
The first formal and general relation between entanglement and QPT was given in Wu et al. [1]. It is proved that: a discontinuity or a divergence of the ground-state concurrence (the first derivative of the ground state concurrence) can be both necessary and sufficient condition to signal first-order QPT (second-order QPT), except in cases where the non-analyticity is artificial and/or accidental. In sum, the non-analyticity has to come from the matrix elements of the density matrix, not from the mathematical expression for the entanglement measure. At the same time, an explicit example of such an artificial non-analyticity was given for the concurrence of two spins in a XXZ chain [4].
The concurrence is a well known entanglement measure and for two spin 1/2 particles is given by
with the eigenvalues of and the time reversed density matrix. For the symmetric ground state the concurrence has the simple formula:
with
However if one consider the SSB, the expression for the concurrence is a little more complicated and given, as seen in Syljuasen [7], by:
with
The maximization in Equations (7), (8), and (10) appears because the entanglement measure involves an optimization procedure over all possible decompositions of the mixed state in a mixture over pure states. The expressions for the concurrence without taking into account the maximum operation are given by Equations (9) or (11), for symmetric and non-symmetric ground states, respectively. But note that such expression are not valid entanglement measures. Note also that, as expected, Equation (11) reduces to Equations (9) and (10) reduces to Equation (8), when there is no SSB (pz = qz = m = 0).
In Figure 1 we show , which is the concurrence without taking into account the maximum operation neither the SSB. We can see that is discontinuous at Δ = −1, jumping from -1 to 0. This discontinuity has its origins in and , which are both discontinuous at Δ = −1. A discontinuity in the concurrence would indicate a first-order QPT (1QPT), but the true entanglement measure is , not . So does indicate the right transition, but is not an entanglement measure.
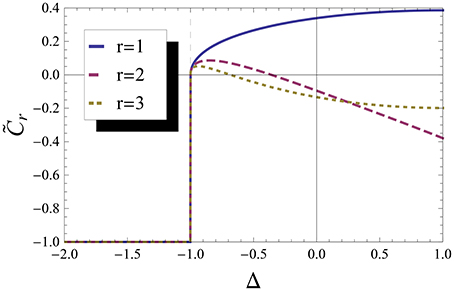
Figure 1. “Concurrence.” “Concurrence” before maximum operation for first, second and third neighbor without taking into account the Spontaneous Symmetry Breaking. We can see that the non analyticity in the concurrence at Δ = −1 is accidental, due to the maximum operation.
In Figure 2 one can see that is continuous and it is possible to check that the first derivative of is discontinuous (we checked it, but one can also guess from the form of the curve of ), which should indicate a second-order QPT (2QPT). In sum, the concurrence indicates a 2QPT, while it is known that at Δ = −1 we have a 1QPT.
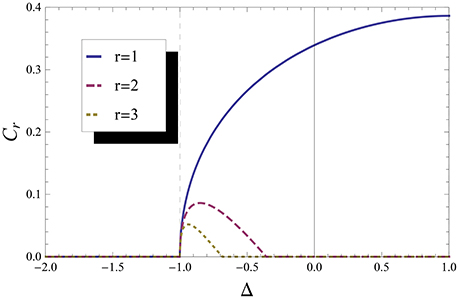
Figure 2. Concurrence. Concurrence for first, second and third neighbor. We can see a non-alalyticity at Δ = −1.
This failure of concurrence to indicate the right order of the QPT was noted in Yang [4] and happens because the discontinuity in the first derivative of comes from the maximum operation and not from the non-analytical behavior of the energy, which is present in the correlation functions and in . Thus, this is an artificial non-analyticity and should not indicate a QPT properly. Note that and also have an “extra” non-analytical behavior (around Δ = −0.5), which originates in the maximization and does not correspond to a QPT. However these results are obtained by not taking into account the effects of the SSB, i.e., using Equation (9) instead of Equation (11).
We now consider the effect of the SSB by taking into account that in the ferromagnetic phase, Δ < −1, all spins are aligned in the same direction: m = ±1 (pz = qz = m). This was first studied in Syljuasen [7], where it was shown that concurrence does not change when considering SSB, even thought the expressions for the concurrence are different: it is Equation (8) for symmetric states and Equation (10) for non-symmetric states. However, Syljuasen [7] does not analyze the origin of the non-analyticity at Δ = −1 when considering the SSB. In order to study this, we ploted Equation (11) in Figure 3. One can see that in the ferromagnetic phase vanishes, so the concurrence goes to zero “naturally” without the need of the maximum operation: for Δ ≤ −1. We can also observe that SSB does not change the “extra” non-analytical behavior of and .
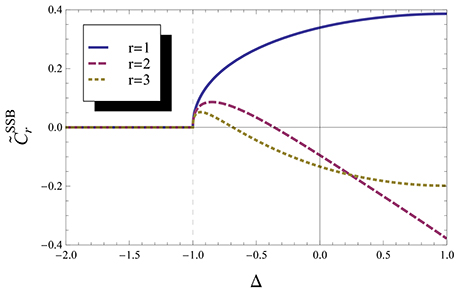
Figure 3. “Concurrence” with SSB. “Concurrence” before maximum operation for first, second and third neighbor taking into account the Spontaneous Symmetry Breaking. We can see that the non-analyticity in the concurrence at Δ = −1, which was accidental due to the maximum operation, happens naturally if we do take into account the symmetry breaking, and that is the only non-analyticity that is changed.
So, we have two facts here:
1) Although the expressions for symmetric and non-symmetric state are different, the entanglement value is the same; something already noted by Syljuasen [7] (and by Osterloh et al. [6] and de Oliveira et al. [5] for the XY model).
2) The origin of non-analyticity in , taking into account SSB, at Δ = −1 is not due to the maximum operation, it comes from the correlation functions and the magnetizations.
Therefore, even tough SSB does not change the behavior of the concurrence, it does change the origin of the non-analyticity: leading an accidental non-analyticity to “natural” one. Note also that SSB only changes the non-analyticity that correspond to a real QPT.
Unfortunately still indicates a 2QPT instead of a 1QPT. That happens because the non-analytic behavior of the energy, which would indicate the correct 1QPT, is contained in the correlation function , but this is canceled by the term pz+qz in Equation (21). Thus, in some sense one could still argue that this is an accidental non-analytical behavior, but of different nature.
4. Von Neumann Entropy and QPT
Another interesting fact is the raise of a discontinuity in the entanglement between one site and the rest of the chain given by the von Neumann entropy for one site when we take into account the SSB.
The von Neumann entropy for one site is given by the equation:
where x is one of the two eigenvalues of the reduced density matrix of one site, that is
with mi = m = 〈σz〉. Thus, the von Neumann entropy is:
Figure 4 depicts this von Neumann entropy taking into account the SSB (red dashed line) and without this SSB (blue line). It shows that without SSB this entropy indicates that the ferromagnetic phase is maximally entangled: it is a macroscopic superposition of two states with finite and opposite magnetizations. Such state is very sensitive to external perturbations. Taking into account the SSB, the entanglement goes to zero as it should for the separable ferromagnetic state at this phase; in this case the system chooses one of the two ferromagnetic configurations. Therefore, in this case the SSB influences directly the entanglement behavior at the QPT, and has to be taken into account for the entanglement to signals the 1QPT. Such influence of the SSB has also been found out in other models [5, 6].
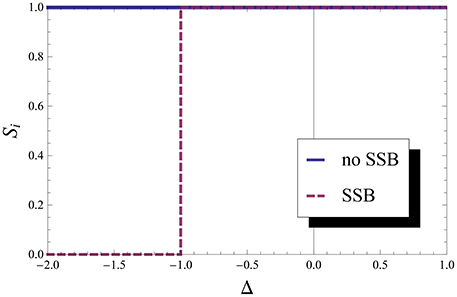
Figure 4. Von Neumann entropy for one particle. Von Neumann entropy of particle i with and without SSB, which shows the entanglement between this particle with all other particles in the chain. We can see that it can indicate 1QFT at Δ = −1 if we take into account SSB.
5. Conclusion
We have studied the influence of SSB in the entanglement between two spins and between one spin and the rest of the chain in the one dimensional spin- XXZ model.
We first showed that, although SSB does not change the behavior of the concurrence at the first-order Quantum Phase Transition, as first noted by Syljuasen [7], it does change the origin of non-analyticity behavior from an accidental one to a “natural” one. This is a much more subtle influence. Unfortunately, the “natural” non-analyticity still indicates a second-order Quantum Phase Transition instead of the correct first-order Quantum Phase Transition.
We also showed that the behavior of the entanglement between one site and the rest is affected by the SSB at the first-order Quantum Phase Transition. It only signals the phase transition when taking into account the SSB.
We thus give further evidence that the use of entanglement to study QPT may be much more intricate than at first glance. One has to be cautious at least about: (i) accidental non-analytic behavior due to optimizations in the entanglement measure adopted; (ii) effects of the SSB in the entanglement value and (iii) effects of spontaneous symmetry break in the origin of the non-analyticities.
Author Contributions
LPJ did all the calculations. TRO participated in all the discussions and supervised the work.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Both authors acknowledge financial support from the Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES). This work was performed as part of the Brazilian National Institute of Science and Technology for Quantum Information.
Footnotes
1. ^Note that there are typos in Equations (19) and (20) from Shiroishi and Takahashi [10]. In (19) we only need to sum a . In (20) we need to go to Kato et al. [11] [note that Equation (5.4) has the same typo] and use Equations (5.10), (B.11), and (B.12) to calculate and find the error in .
References
1. Wu LA, Sarandy MS, Lidar DA. Quantum phase transitions and bipartite entanglement. Phys Rev Lett. (2004) 93:250404. doi: 10.1103/PhysRevLett.93.250404
2. Wu L-A, Sarandy MS, Lidar DA, Sham LJ. Linking entanglement and quantum phase transitions via density functional theory. Phys Rev A (2006) 74:052335. doi: 10.1103/PhysRevA.74.052335
3. Amico L, Fazio R, Osterloh A, Vedral V. Entanglement in many-body systems. Rev Mod Phys. (2008) 80:517. doi: 10.1103/RevModPhys.80.517
4. Yang M-F. Reexamination of entanglement and the quantum phase transition. Phys Rev A (2005) 71:030302(R). doi: 10.1103/PhysRevA.71.030302
5. de Oliveira TR, Rigolin G, de Oliveira MC Miranda E. Symmetry-breaking effects upon bipartite and multipartite entanglement in the XY model. Phys Rev A (2008) 77:032325. doi: 10.1103/PhysRevA.77.032325
6. Osterloh A, Palacios G, Montangero S. Enhancement of pairwise entanglement from ℤ2 symmetry breaking. Phys Rev Lett. (2006) 97:257201. doi: 10.1103/PhysRevLett.97.257201
7. Syljuasen OF. Entanglement and spontaneous symmetry breaking in quantum spin models. Phys Rev A (2003) 68:060301(R). doi: 10.1103/PhysRevA.68.060301
8. Justino L, de Oliveira TR. Bell inequalities and entanglement at quantum phase transitions in the XXZ model. Phys Rev A (2012) 85:052128. doi: 10.1103/PhysRevA.85.052128
9. Yang CN, Yang CP. One-dimensional chain of anisotropic spin-spin interactions. II. Properties of the ground-state energy per lattice site for an infinite system. Phys. Rev. (1966) 150:321–39. doi: 10.1103/PhysRev.150.321
10. Shiroishi M, Takahashi M. Exact Calculation of Correlation Functions for Spin-1/2 Heisenberg Chain. J Phys Soc Jpn. (2005) 74:47–52. doi: 10.1143/JPSJS.74S.47
Keywords: quantum phase transitions, entanglement, spontaneous symmetry breaking, XXZ model, non-analytic behavior of entanglement
Citation: Pereira LJ and de Oliveira TR (2016) Effects of Spontaneous Symmetry Break in the Origin of Non-analytic Behavior of Entanglement at Quantum Phase Transitions. Front. Phys. 4:51. doi: 10.3389/fphy.2016.00051
Received: 16 May 2016; Accepted: 05 December 2016;
Published: 21 December 2016.
Edited by:
James Avery Sauls, Northwestern University, USACopyright © 2016 Pereira and de Oliveira. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thiago R. de Oliveira, dHJvQGlmLnVmZi5icg==
 Leonardo J. Pereira
Leonardo J. Pereira Thiago R. de Oliveira
Thiago R. de Oliveira