Self-organized Criticality via Retro-Synaptic Signals

1. Introduction

Retro-synaptic signals are defined as signals that travel across the synaptic cleft from the post-synaptic unit to the pre-synaptic one [1, 2]. Candidate molecules to be responsible of this type of retrograde communication between two neurons are neurotrophins [3], proteins [4], cell-adhesion molecules [5], lipids [6], and even gases [7]. Previously, it has been reported that retrograde signaling is responsible for network development and apoptosis in the early stages brain formation [8]. Additionally, this type of messaging has been proposed as a mechanism by which neurons compete with their neighbors to supply their targets with appropriate information in exchange for a “reward” that travels in the opposite direction of the action potential resembling the mechanism by which supply networks work in a free-market economy [9]. In this paper we explore the idea that retro-synaptic signals might also be responsible for the emergence of critical behavior in brain networks by studying their effects in a model of neuronal avalanches.

As the name suggests, neuronal avalanches are bursts of activity that resemble a domino effect triggered by spiking in groups of neurons. In the past decade, the observation of cascades of spontaneous neuronal activity, whose sizes and durations are distributed as a power-law, in brain tissue of rat cortex suggested a link between neural dynamics and phase transitions [10]. Consequently, this triggered an avalanche of research in different experimental scenarios [11–17], which confirmed the presence of neuronal avalanches in vivo and ex vivo as a previously unknown modality of brain operation.

It has been reported that neural networks whose dynamics are poised at the border of a phase transition, and whose activity is identified by power-law distribution of events, acquire several benefits for neural computation which include: optimal information transmission and maximum dynamic range [18], maximum information storage [19], and stability of information transmission [20]. However, if brain networks operate at a critical point marking the border between regularity and randomness, how do they reach such dynamical regime?

Self-organized criticality (SOC) has been suggested as a concept to explain the emergence of critical dynamics in natural phenomena [21]. It has been applied to describe the behavior of phenomena as diverse as plate tectonics [22], piles of granular matter [23], forest fires [24], mass extinctions [25], and crashes in the stock market [26], among others. This concept implies the existence of a critical point that becomes an attractor in the collective dynamics of a system. Thus, the control parameter, which is an essential notion in the theory of critical phenomena and phase transitions, does not require to be fine-tuned by an external entity. Rather, the system implements a feedback mechanism based on its internal dynamics that provides it with direct control over its control parameter.

In neural systems, self-organized critical models of neuronal avalanches have been put forward to explain the emergence of critical dynamics in brain tissue. These models can be divided in two categories, those that explain the emergence of critical behavior through plasticity mechanisms such as spike-timing-dependent plasticity [27, 28], short-term plasticity [29], Hebbian-like plasticity processes [30–33], and even non-Hebbian plasticity [34]; and those that explain it through non-plastic mechanisms like axonal re-wiring [35–37] or the balance between neuronal excitation and inhibition [10, 32].

However, few of these models consider the relationship between learning and criticality, which could reveal the effects of this dynamical regime on cognition. Synaptic plasticity has been proposed as the neurobiological basis of learning and memory in brain networks. Some models of critical neuronal avalanches implement synaptic plasticity mechanisms either to explain the emergence of critical behavior in the system [28], or to provide the network with learning capabilities akin to artificial neural networks in machine learning [32]. However, in the latter case it is not clear whether the critical regime survives the synaptic modulation induced by learning, whereas in the former case the implementation of spike-timing-dependent plasticity mechanisms is rather artificial as the system halts for predetermined periods of time in order to apply the synaptic modulation based on the recent activity of the nodes in the system.

Moreover, most models do not take into account the complex configuration of brain networks characterized by the presence of highly-connected units or hubs, as well as the presence of the small-world property which provides the system with an architecture efficient for information transmission across distant regions in the network [38]. Some exceptions are the models presented in Refs. [31–33], which use Apollonian networks to capture both the notion of scale-invariant degree distributions and the small-world property. Lastly, it has been pointed out that non-conservative neural systems such as the one presented in Levina et al. [29] cannot be truly critical, and rather they wander about the critical regime [39, 40].

In this paper we put forward a novel model of self-organized critical neuronal avalanches in neural systems. Our approach differs from others by considering retro-synaptic signals that inform the neuron about the behavior at the level of its local surroundings. We propose a long-term synaptic plasticity mechanism based on this type of signals, which allows the system to reach the critical state autonomously. Such state is robust to the synaptic modulation induced by spike-timing-dependent plasticity mechanisms. Moreover, by considering scale-free structures with high clustering we take into account complex network features such as the small-world property and scale-invariant degree distributions which imply the presence of highly-connected nodes. By considering this type of topologies, our model considers the complex structure of brain networks which are neither regular nor random [38].

2. Model

We present a basic model for neuronal avalanches [41] that resembles the paradigmatic model of SOC: the sand-pile model of Bak et al. [21]. The model consists of N non-leaky integrate-and-fire nodes. Each node j has a membrane potential h_j, which is a continuous variable that is updated in discrete time according to the equation:

$\begin{array}{cc}{h}_j(t+1)=h_j(t)+{\displaystyle \sum _{i=1}^N{A}_{ij}}{w}_{ij}{s}_i(t)+I_{ext}& \left(1\right)\end{array}$

where A denotes the adjacency matrix with entries A_ij = 1 if node i sends an edge to node j, and A_ij = 0 otherwise, w_ij denotes the synaptic weight from node i to node j, s_i(t) ∈ {1, 0} represents the state of node i (active or quiescent, respectively) at time t, and I_ext denotes external input which is supplied to a node depending on the state of the system at time t. The mechanism of external driving works as follows: if there is no activity at time t, then a node is chosen uniformly at random and its membrane potential is increased by a fixed amount through the variable I_ext. If h_i(t) exceeds the threshold θ, then node i emits a spike, which changes the state of this node to active (s_i(t) = 1) and propagates its activity through its synaptic output. Afterwards, the node is reset, i.e., h_i(t + 1) = 0.

The propagation of activity might trigger subsequent activation of neurons. This results in cascading behavior. Here, avalanches take the form of neuronal activity being propagated as a domino effect. While the system is relaxing, external drive stops. This guarantees that the relaxation time occurs at a different time scale than that of the external driving. This corresponds to an infinite separation of time scales between external driving and relaxation dynamics that has been suggested as a necessary condition for critical behavior [42].

In the original model, the synaptic couplings w_ij are set by dividing the control parameter α by the mean connectivity of the network. The parameter α needs to be fine-tuned in order for critical dynamics to emerge. Here, we will set the synaptic weights randomly with values taken from an uniform distribution in the interval (0, 1), and let the system evolve according to a synaptic plasticity mechanism that we describe below.

We introduce a local measure of the performance of a node during simulation time called node success. The node success of node i at time t is the fraction of out-neighbors of this node that become active at time t + 1 when node i spikes at time t, in other words:

$\begin{array}{cc}{\phi }_i(t)=\frac{{\displaystyle {\sum }_{j=1}^N{A}_{ij}{s}_j(t+1)}}{{\displaystyle {\sum }_{j=1}^N{A}_{ij}}}& \left(2\right)\end{array}$

where A is the adjacency matrix of the network, and s_j(t + 1) is the state of node j at time t + 1. The sum in the numerator runs for all out-neighbors j of node i.

Thus, node success measures the performance of an individual spike in terms of the subsequent spikes triggered by such initial activation, which occur within the out-neighborhood of a given node. With this metric we construct a long-term plasticity rule called node-success-driven plasticity (NSDP). The intuition behind the NSDP learning rule is quite straightforward: if a node has very low success, then the node increases the synaptic weight in all of its out-neighborhood, but only if the node is not spiking too often, that is, if the node possesses a low firing rate.

Formally, NSDP is defined by the following equations:

$\begin{array}{cc}{w}_{ij}(t+1)=w_{ij}(t)+\Delta w_{ij}({\phi }_i(t),\Delta t_i)& \left(3\right)\end{array}$

where $\Delta t_i=t-t_{LS}^i$ denotes the time difference between the spike of node i occurring at current time step t and its previous spike which occurred at $t_{LS}^i$ (subscript LS refers to last spike). Whereas,

$\begin{array}{cc}\Delta w_{ij}({\phi }_i(t),\Delta t_i)=A\exp \left\{\frac{-{\phi }_i(t)}{B}\right\}-C\exp \left\{\frac{-\Delta t_i}{D}\right\}& \left(4\right)\end{array}$

with parameters A, B, C, and D taken from ℝ⁺. These parameters are phenomenological, that is, they do not represent a particular physiological property of the living neuron. The action of the first term at the right hand of Equation (4) potentiates the connection (i, j) according to the current node success of i, whereas the second term depresses it depending in the firing rate of i, which is succinctly captured by Δt_i¹.

Network structure plays a significant role on the way that the collective dynamics emerge and behave within a system. Moreover, complex network properties such as the presence of hubs and the small-world property might affect the system's behavior in a way that cannot be anticipated by studying simple heterogeneous structures such as random networks or homogeneous structures such as fully-connected networks. Therefore, we consider five different network types in order to compare the onset of the critical regime in systems under the mechanism of NSDP:

i. random,

ii. out-degree scale-free with low mean clustering coefficient (CC),

iii. out-degree scale-free with high mean CC,

iv. in-degree scale-free with low mean CC, and

v. in-degree scale-free with high mean CC.

Our networks are directed, and for every node in the network the out- and the in-degree is larger than zero. This implies that every node in the system is able to receive and transmit spikes. Out-degree scale-free networks exhibit a power-law in the out-degree distribution, whereas their in-degree distribution follows a Poisson distribution. A power-law out-degree distribution implies the presence of a small fraction of nodes with many outgoing connections that we call broadcasting hubs. On the other hand, an in-degree scale-free network exhibits a power-law in-degree distribution. This implies the existence of a small fraction of nodes with many incoming connections that we call absorbing hubs.

The purpose of tuning the overall clustering coefficient in a network results in different degrees of the small-world property on it Holme and Kim [43]. Therefore, high and low levels of the mean clustering coefficient result in high and low degrees of the small-world property in our scale-free networks. Taken together, the small-world property and the presence of hubs will result in collective dynamics that differ from random structures as we show below.

3. Assessment of Critical Behavior

Our first concern lies on how to determine that the collective dynamics of the system are in the critical state. Critical dynamics feature the presence of power-law distribution of events (e.g., size and duration of avalanches). Thus, a simple and straightforward way to look for criticality is to inspect the distribution of avalanche sizes and durations. If the distribution resembles a power-law distribution, then we have reasons to suspect that the system is undergoing a phase transition.

We assess the quality of such a power-law through the mean-squared deviation Δγ from the best-matching power-law distribution with exponent γ obtained through regression in log-log scales. Our choice of using this method is due to its simplicity, and justified by the asymptotic unbiasedness of the estimation. When this error function is at its minimum, that is, when the data is best approximated by a power-law distribution of avalanche sizes with exponent γ, is when the system is at the critical state.

A power-law fit of the distribution of avalanche sizes is by no means a sufficient condition for a system to be critical, but it is a necessary one. Other tests for criticality that we perform are:

i. Analysis of the relationship between the critical exponents of avalanche sizes and their durations: From the theory of critical phenomena, we know that at criticality the distribution of several observables follow power-law distributions with mathematical expressions linking each other [44]. In particular, there is a power-law positive correlation between avalanche sizes and their durations which only occurs at criticality [16, 45].

ii. Analysis of the largest eigenvalue Λ associated to the matrix of synaptic weights: Larremore et al. studied the spectral decomposition of the weight matrix of a system at criticality, and concluded through analytical inspections along with numerical simulations that the largest eigenvalue of the weight matrix governs the network's dynamic range. When this value is unity, the system is in a critical state and its dynamic range is maximized [46].

iii. Analysis of data collapse: At criticality the dynamics of a system show no particular scale, thus resulting in a fractal geometry of its observables [44, 47]. A standard procedure to analyse the critical regime in a model of neuronal avalanches is to observe if avalanches exhibit a fractal structure. To this purpose, the average “shape” of avalanches is estimated by keeping track of the the lifetime of an avalanche and the number of nodes involved at each avalanche step. If the system is at criticality, then avalanches of different sizes would exhibit the same shape up to a scaling function, in such a way that data could be collapsed in order to observe how avalanche shapes resemble each other [14].

Our fist approach to analyse the critical behavior of our systems will involve estimating the Δγ function due to its ease to be be implemented in running time. When more formal analyses are required we will use the tests described above.

4. Results

During our experiments, we consider three different system sizes: 128, 256, and 512 for each of the different network types considered (i.e., scale-free and random), and 20 different trials per network, which result from generating 20 different networks for each type. We fix the parameters B, C, and D in Equation (4) to 0.1, 0.001, and 10, respectively; and we vary parameter A according to the system's size. This value is set around 10⁻⁴, 10⁻⁵, and 10⁻⁶ for sizes 128, 256, and 512, respectively.

4.1. Distribution of Avalanche Sizes Can Be Approximated by a Power-Law

To start our examination of the critical state of our systems under NSDP we proceed by having a look at the distribution of avalanche sizes at the end of simulation time. We observe a power-law distribution of avalanche sizes that is identified by a straight line in a log-log plot of the distribution until finite size effects take on. In Figure 1A we present only the mean values of these distributions for the sake of clarity. The labeling in Figure 1 and in subsequent figures is as follows: SF[indeg, lowCC] stands for in-degree scale-free networks with low mean CC, SF[indeg, highCC] stands for in-degree scale-free networks with high mean CC, SF[outdeg, lowCC] stands for out-degree scale-free networks with low mean CC, SF[outdeg, lowCC] stands for out-degree scale-free networks with high mean CC, and RN stands for random networks.

FIGURE 1

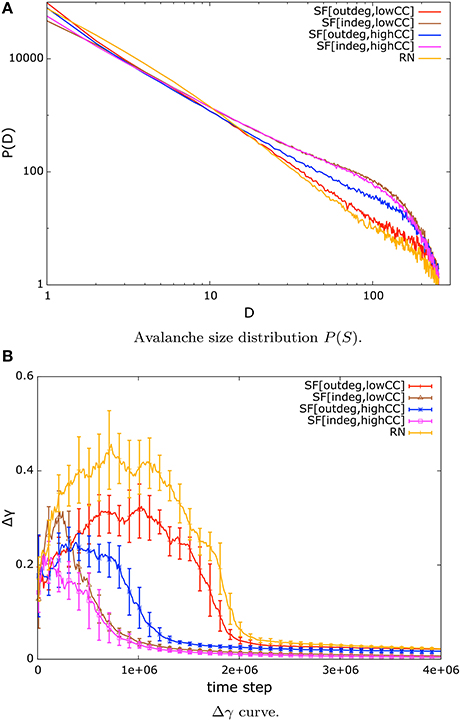
Figure 1. (A) Double logarithmic plots of the distribution of avalanche sizes of scale-free and random nets of size N = 256 under weight modulation by NSDP. The distribution follows a power-law for approximately two decades. Power-law distribution of avalanche sizes is a signature of criticality. (B) Evolution of Δγ for systems under NSDP. Systems converge toward a low error (< 0.05) for the power-law approximation of avalanche size distribution, which implies that this distribution is well-approximated by a power-law. (We present mean and standard deviations from our trials).

Next, we analyse the error of the power-law approximation to our data, that is, the Δγ curve. We present the evolution of the fitting error in Figure 1B. At the beginning of the simulation the systems are not in a critical state. This can be observed in the shape of the Δγ curve in Figure 1B during the first one million time steps of simulation time where the error is large. However, after some time the fitting error settles around a value <0.05. This implies that the distribution of avalanche sizes is well approximated by a power-law distribution for the systems considered in our simulations.

If the synaptic weights of our systems are initialized randomly from the unit interval without applying the NSDP synaptic mechanism, their distribution of avalanche sizes will not resemble a power-law distribution. In Figure 2 we present the distribution of avalanche sizes and Δγ curve (inset) for systems in which the weights have been initialized with random values from the unit interval, but without applying the NSDP synaptic mechanism. In this case, the fitting-error is large (inset) reflecting the fact that the avalanche-size distribution does not resemble a power-law distribution. Thus, NSDP is responsible for the emergence of power-law behavior in our randomly initialized systems.

FIGURE 2

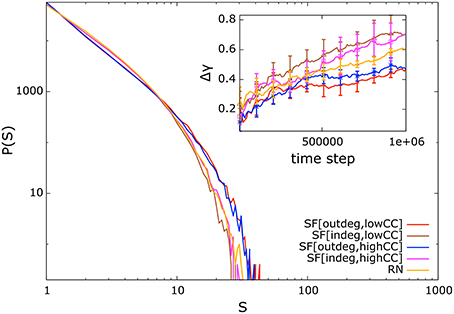
Figure 2. Distribution of avalanche sizes and Δγ curve (inset) for systems comprising 128 nodes without introducing NSDP mechanisms. Here, the avalanche-size distribution does not resemble a power-law distribution as in Figure 1.

Once observing that the distribution of avalanche sizes can be well approximated by a power-law (Figure 1), the remaining question is about the exponent of such power-law distribution. We observe that the value of such exponent lies close to −1.5 as it has been reported in several systems at criticality. We present the evolution of the value of the exponent γ in Figure 3A.

FIGURE 3

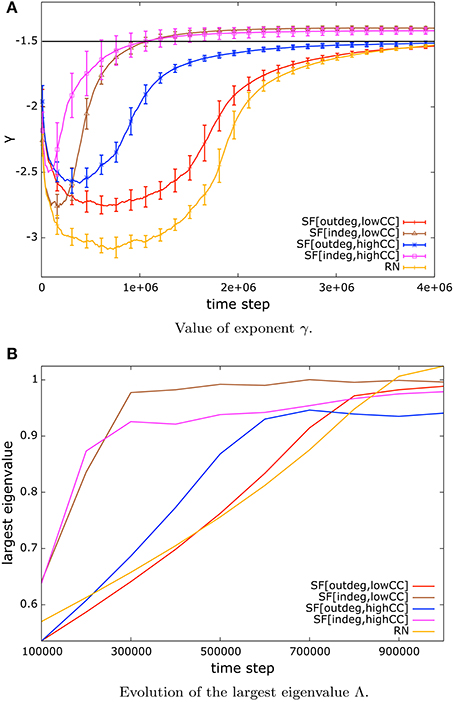
Figure 3. (A) Value of exponent γ of the power-law distribution of avalanche sizes of systems under NSDP. The value of the exponent lies close to −1.5 (black solid line) as it has been reported elsewhere for systems at criticality. The speed of convergence to this value depends on network topology. (B) Evolution of the largest eigenvalue Λ associated to the matrices of synaptic weights for networks of 128 nodes. The value settles around unity once NSDP mechanisms take place. This implies that the system is at the critical state.

As can be seen in Figure 3A, the speed of convergence to a low error regime and an exponent of γ = −1.5 depends on topology, for instance, in-degree scale-free networks converge faster than any other type of networks. This can be explained by the presence of absorbing hubs and to some extent to the high amount of small-world-ness in these networks. On the other hand random networks and out-degree scale-free networks with low mean clustering coefficient exhibit the slowest convergence which can be attributed to low clustering within the network, and the absence of hubs.

4.2. Largest Eigenvalue Λ Close to Unity

As mentioned in Section 3, based on the work by Larremore et al. [46] we analyse the value of the largest eigenvalue Λ associated to the matrix of synaptic weights. It has been shown that a system at criticality is identified by a value of Λ = 1. In the column Λ_NSDP of Table 1 we present the value of the largest eigenvalue for weight matrices under NSDP mechanisms. As it can be seen, the value of Λ is very close to unity for systems under this type of synaptic modulation. This implies that although initialized with random weights the system self-organizes into a configuration of the weight matrix such that it gives rise to a largest eigenvalue Λ close to unity, which implies that the system is at criticality.

TABLE 1

Table 1. Largest eigenvalue Λ of matrix W of synaptic weights for systems under NSDP mechanisms (Λ_NSDP), STDP mechanisms (Λ_STDP), and both NSDP and STDP mechanisms (Λ_STDP+NSDP).

Moreover, we present the evolution of the largest eigenvalue Λ for networks of size N = 128 in Figure 3B. Our systems start with random synaptic couplings which results in a largest eigenvalue Λ ≪ 1, however as NSDP mechanisms start to modulate the synaptic weights, the value of Λ increases and settles around unity, which identifies the critical state in the system.

The convergence to a largest eigenvalue close to unity depends on topology. Here we observe a situation similar to that of the convergence to a low error regime and to the exponent γ = −1.5. In-degree scale-free networks converge faster than any other type of network to Λ = 1. This can be explained by the presence of absorbing hubs in the network.

4.3. Distribution of Avalanche Lifetimes Can Be Approximated by a Power-Law

A system at criticality exhibits power-law distributions of several observables [45]. Our systems under NSDP exhibit distributions of avalanche durations that can be approximated by power-laws whose exponent τ lies in the interval [−2.2, −1.6] depending on network type. This is shown in Figure 4A for scale-free networks of 256 nodes. It has been pointed out in experimental settings as well as analytically that the exponent τ of critical avalanche durations lies close to −2 [10].

FIGURE 4

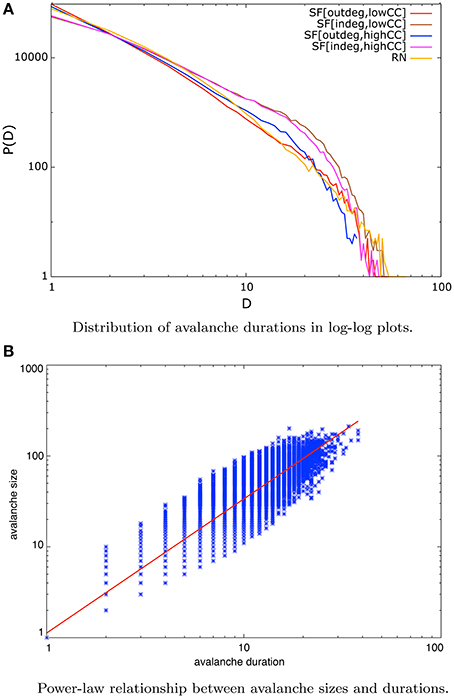
Figure 4. (A) Distribution of avalanche durations in log-log plots for scale-free nets of all sizes considered under the NSDP protocol. This distribution also exhibits a decreasing linear trend for more than a decade which implies that can be approximated by a power-law. (B) Linear relationship on logarithmic axes between avalanche sizes and durations for in-degree scale-free nets of 128 nodes and high mean CC. This behavior implies a power-law correlation of the form S ~ D^β. In blue dots we present our data whereas in red we present the best-fit approximation. A relationship of this type is a signature of criticality.

This fact is also related to the observation of a power-law correlation between avalanche sizes and their durations of the form S ~ D^β. This has been reported as a signature of criticality [14–16].

In Figure 4B we show this behavior for in-degree scale-free networks of size N = 128 and high mean clustering coefficient. Each blue dot in this plot is an avalanche denoted by its size and its duration, whereas the red straight line is the best-fit approximation to the data with an exponent β = 1.4 in this particular example. This apparent linear trend in double logarithmic axes reveal a power-law relationship between avalanche sizes and durations.

It has been pointed out that the exponent β that relates avalanche size to avalanche duration can be predicted by the following expression [14]:

$\begin{array}{cc}\beta =\frac{\tau -1}{\gamma -1}& \left(5\right)\end{array}$

where τ is the exponent related to avalanche durations, and γ is the exponent related to avalanche sizes. The exponent β then is used to verify the data collapse for avalanche shapes (see next section) [14, 48].

4.4. Avalanche Shapes and Data Collapse

In this section we present the average avalanche shape under the regime of NSDP. The shape of an avalanche is defined as the number of nodes involved in an avalanche per time step, or better said, per avalanche time (or step). In our model all avalanches start with only one node becoming active, this corresponds to the first avalanche step. In subsequent time steps we record the number of nodes that become active and average them until the avalanche stops. There are avalanches that involve a single node and therefore occur in a single time step, but also there are avalanches that span to the whole network and that take more than one time step to develop. By the end of each simulation we end up with the number of nodes that on average become active in the second avalanche time, the third avalanche time, and so on.

The plot of avalanche step and the average numbers of nodes involved in each step defines the shape of the avalanche for a given network. The maximum avalanche duration corresponds to the largest number of time steps in which an avalanche takes place for a given network and size.

In Figure 5 we present the average avalanche shapes for in-degree scale-free networks of sizes 128, 256, and 512 and low mean clustering coefficient. The similarity of the avalanche shapes among different system sizes suggests a fractal structure underlying the avalanche dynamics. This is expected to occur in a system at criticality [14, 44, 45]. However, our analysis differs from that of Refs. [14, 48] as these authors consider the average number of nodes involved in a single avalanche conditioned on avalanche duration, whereas we consider all avalanches during a simulation, and average the number of nodes involved for a particular avalanche time-step. The particular shape of the avalanches in our systems, which differs from an inverted parabola [14, 45], might be the result of these three factors: the consideration of all avalanches without conditioning on avalanche duration when averaging avalanche time-step and the number of nodes involved, the model dynamics, and the heterogeneous structure of the networks considered. However, confirming such claim is beyond the scope of this paper.

FIGURE 5

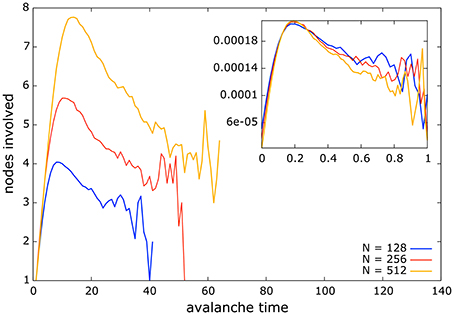
Figure 5. Average avalanche shape for all networks and sizes considered under the regime of NSDP. The similarity of shapes among different sizes suggest the possibility of data collapsing in these systems. This fact implies that avalanches possess a fractal structure which is also a signature of criticality. Inset: data collapse for avalanche shapes shown in main figure. Data collapsing reveals the fractal nature of avalanches in a system at criticality.

In the inset of Figure 5 we show an example of the data collapse resulting from the avalanches shown in the main outset figure. To obtain such data collapse each curve is divided by its duration which gives a normalized avalanche time, and then the heights of the curves are rescaled by their duration raised to the exponent β linking the exponents of avalanche sizes and their durations (Equation 5) [14, 45, 48].

The fact that avalanche shapes from different system sizes can be re-scaled to match each other with certain accuracy not only suggests a fractal nature of the avalanche dynamics but also gives an insight of how avalanches might look in larger system sizes than the ones considered here.

This concludes our examination of the critical state for our systems under the synaptic modulation of NSDP. As synaptic weights were initialized uniformly at random, and the system reached the critical state as a result of node activity based solely in the two rules that define our NSDP mechanism, we conclude that this model exhibits SOC.

5. Spike-Timing-Dependent Plasticity

Once we verified that our long-term plasticity rule allows the system to reach the critical state autonomously, we became interested in studying whether this type of plasticity could coexist with other plasticity mechanisms such as spike-timing-dependent plasticity (STDP). STDP is an asymmetric learning rule in brain networks that captures the temporal correlations between pre- and post-synaptic neurons, which has been proposed as a mechanism for learning and memory in the brain [49]. STDP is a local rule responsible of long-term synaptic modulation that emphasizes the precise timing of each individual spike, it also incorporates and extends the essential mechanism of Hebbian learning by including the notion of long-term potentiation (LTP) and long-term depression (LTD) of synapses based on the differences in activation times for pre- and post-synaptic neurons [50]. Potentiation is achieved when the pre-synaptic node fires shortly before the post-synaptic one. Depression is achieved when the opposite occurs, namely, the post-synaptic neuron fires shortly before the pre-synaptic unit.

We implement STDP mechanisms in our model through the following set of equations:

$\begin{array}{cc}{w}_{ij}(t+1)=w_{ij}(t)+\Delta w_{ij}(\Delta t)& \left(6\right)\end{array}$

where Δt = t_post−t_pre denotes the difference between the spiking times of pre- and post-synaptic neurons, and:

$\Delta w_{ij}(\Delta t)=\{\begin{array}{ll}{a}_p\exp \left\{\frac{-\Delta t}{T_p}\right\}\hfill & \text{if }\Delta t\ge \text{0}\hfill \\ -a_d\exp \left\{\frac{\Delta t}{T_d}\right\}\hfill & \text{if}\Delta t<\text{0}\hfill \end{array}$

where parameters a_p and T_p set the amount and duration of LTP, whereas a_d and T_d set the amount and duration of LTD. In our experiments we set a_p = a_d = 0.1. Observations of STDP in brain tissue suggest that the time window for potentiation is typically shorter than the depression time window [49], for that reason we let T_p = 10 time steps and T_d = 20 time steps. However, it also has been observed that the time-window and the amount of potentiation/depression vary across species and brain structures [50]. A single theoretical model of synaptic plasticity cannot account for all experimental facts [51].

Before applying STDP mechanisms into the system we allow criticality to set in for a period of time in function of system size by fine-tuning the value of the weights w_ij for each network. For networks of 128 nodes, we let the system reach the critical state for 10⁶ time steps before introducing STDP mechanisms. For sizes 256 and 512 we do likewise for 2 × 10⁶ and 3 × 10⁶, respectively. This allows for rare avalanches that span to the whole system to coexist with smaller avalanches which occur frequently. Afterwards, we introduce STDP mechanisms for the same amount of time in which we drove the system to criticality without STDP. By the end of each simulation we end up with systems whose first half of the time were driven to criticality, whereas their second half were under STDP and NSDP regime.

When we introduce STDP mechanisms into a system whose dynamics are already at criticality, we observe that the critical regime vanishes as a consequence of the synaptic modulation induced by the activity of the neurons in the network. This behavior is captured by the shape of the avalanche size distribution, which no longer features a straight line (Figure 6A), as well as in the increasing error in the Δγ curve (Figure 6B), which measures the deviation from the data to the best matching power-law distribution. In Figure 6 we present an example of this behavior for in-degree scale-free networks of size N = 512 and low mean clustering coefficient. Also, the departure from criticality post-STDP is captured by the largest eigenvalue associated to the matrix of synaptic weights. Once STDP mechanisms set in, the value of Λ is less than unity (see column Λ_STDP in Table 1).

FIGURE 6

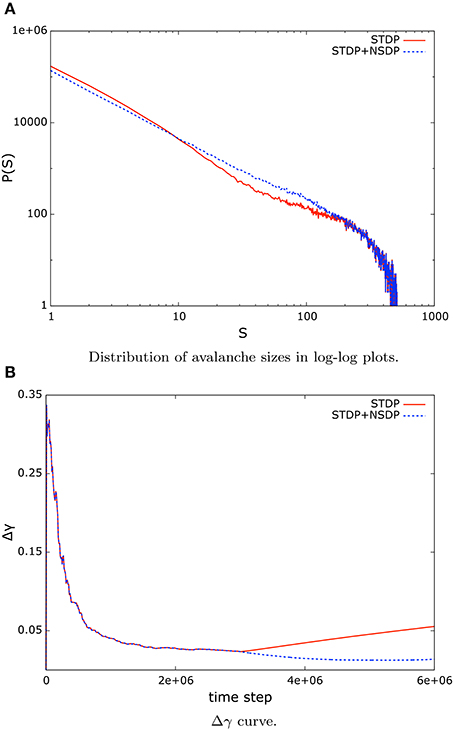
Figure 6. (A) The shape of the distribution of avalanche sizes differs from a straight line when STDP sets in (red, solid line), which indicates a deviation from the critical regime. However, when NSDP is present in the system, the synaptic modulation induced allows the system to stay in the critical regime and exhibit a power-law distribution (blue, dashed line). (B) The error function Δγ shows an increasing trend once STDP mechanisms take place in the system (red, solid line). However, if NSDP mechanisms are also present the system stays in the critical regime. A situation that is observed by the low error in the power-law fit (blue, dashed line).

However, if we combine STDP mechanisms with NSDP mechanisms, the synaptic modulation resulting from the activity of nodes in the system allows the system to stay in the critical regime. We can verify the status of the critical state by looking at the value of the largest eigenvalue Λ when STDP is used in combination with NSDP mechanisms. Column Λ_STDP+NSDP in Table 1 shows the value of the largest eigenvalue for systems under STDP mechanisms combined with NSDP mechanisms. Here, we observe that the value of the largest eigenvalue is close to unity, unlike the case where STDP was applied solely in the system. In Figure 6 we show how the avalanche size distribution is well approximated by a power-law when STDP is applied in combination with NSDP (blue dashed lines).

Thus, NSDP allows the system to stay in the critical regime while STDP mechanisms occur in the system. This implies that learning and memory mechanisms could in principle occur during criticality in neural systems as long as a compensatory process (such as NSDP) is also present in the system. In such a regime, a neural system could acquire the benefits of these two worlds, namely, the capacity of learning through STDP modulation, and optimal information processing through critical dynamics.

6. Discussion

6.1. Retro-Synaptic Signals

NSDP is a mechanism that achieves SOC in the systems examined. The weight modulation induced through NSDP is sufficient to drive the system to the critical state. Interestingly, this modulation is activity-dependent and local. Naturally, the nodes in the system are not aware of the global state of the dynamics such as criticality or power-law behavior; they are programmed to maximize their node success (in response of the activity of their out-neighbors) as long as they are not firing too often, that is, if their firing rate is not very high. If nodes follow these two rules, they will reach the critical state no matter how their synaptic weights were initialized in the first place. Moreover, NSDP serves as a compensatory mechanism that allows the system to stay at criticality when STDP is modulating synapses according to the activity of the neurons. However, how realistic is a long-term plasticity mechanism like NSDP in real brain networks?

The work presented in here suggests the hypothesis that through signals that carry information regarding the success of a spike from a pre-synaptic unit in terms of the subsequent spikes triggered at the post-synaptic neighborhood a neural system is able to reach a critical state without external supervision or tuning.

A signal of this kind will have to travel in the opposite direction of an emitted spike, that is, from post- to pre-synaptic unit, without it being a spike by itself. Rather, this type of retro-synaptic signal will have to be some type of molecule emitted by a post-synaptic unit at the moment it becomes active and emits a spike. The released molecules would travel in the extracellular medium until they are captured by vesicles in the pre-synaptic unit, which in turn will modulate its outbound synaptic strength in function of the seized molecules from the post-synaptic neighborhood.

Another mechanism of retro-synaptic signal might start with the release of molecules (other than neurotransmitters) from the pre-synaptic unit at the moment of a spike. This molecules could travel back to the pre-synaptic neuron carrying information about the success of the most recent spike emitted by this unit. For instance, if the post-synaptic unit seizes such molecules at the moment of spiking, then the absence of those molecules in the extracellular medium and the consequent inability of the pre-synaptic node to catch them back would inform this neuron that its most recent spike was successful in triggering subsequent spikes.

In the Introduction to this paper, we mentioned some candidate mechanisms for retro-synaptic signaling in brain networks. In our particular context, we would require that this messaging also implements long-term synaptic modulation over post-synaptic units. To date, retrograde signals have been proposed as a mechanism by which neurons compete with their neighbors to supply their targets with appropriate information in exchange for a “reward” that travels in the opposite direction of the action potential. This mechanism has an analogy in the way supply networks work in a free-market economy; and it is also analogous to the mechanism of node-success maximisation described in this paper. It has been suggested that this type of competition in neural systems might allow the brain to self-organize into functional networks [9] giving rise to some sort of Darwinian neurodynamics.

Thus, the idea of retro-synaptic signals modulating synaptic efficacies in function of successful spikes triggering subsequent activity is a valid one. Moreover, as we have shown, this mechanism of plastic modulation could be the basic ingredient by which neural systems exhibit complex behavior such as critical dynamics with all the benefits on information processing implied by it.

Retro-synaptic signaling might provide a biological interpretation of the first term of Equation (4) for the NSDP mechanism. What about the second term which penalizes the increment of synaptic weight if a node's firing rate is high? How do single neurons know if they are spiking too often? An answer to this question can be given in terms of the depletion of synaptic resources of a single neuron. If a neuron is spiking often, its synaptic resources deplete, and a certain amount time is required in order to be replenished. The interplay between depletion and replenishment is the underlying mechanism behind the model of Levina et al. [29] that has been shown to exhibit SOC.

We have shown how different topologies reach the critical state at different speeds, with in-degree scale-free networks being the topology that converges faster to such state, and random networks the topology that reaches it last. In the case of in-degree scale-free networks, absorbing hubs might be responsible for an increased activity within the system specially when combined with a high mean clustering coefficient, which implies that the small-world property is present in a higher degree. Absorbing hubs possess a larger firing rate due to the accumulation of activity from their in-neighborhood, which triggers constant firing in this particular type of nodes. Clustering, which ultimately is related to the small-world property, implies that nodes receive and send connections from common neighbors; this increases the chances of sustained activity within a group of nodes which leads to an improvement of the spiking activity in the overall network. Therefore, the presence of absorbing hubs and the small-world property can be deemed responsible for the speed of convergence to the critical state in in-degree scale-free networks.

Out-degree scale-free networks contain absorbing hubs as well although in an amount not comparable to in-degree scale-free networks. Broadcasting hubs are not as effective as absorbing hubs in maximizing the spiking activity within the network not only because the success of spikes emitted by them are in function of the membrane potential of the nodes in their out-neighborhood, but also because the firing rate of the broadcasting hubs might not be comparable to that of the absorbing hubs, as the former might possess a small in-degree in combination with a large out-degree. An analysis of the interplay between in-degree and out-degree in the context of scale-free networks at criticality is beyond the scope of the current study, but we refer the reader to Hernandez-Urbina et al. [52] for a throughout description of the topic. Lastly, random networks do not imply a particular property of their nodes. In fact, given that their in- and out-degree distributions follow a Poisson distribution, nodes with large in- or out-degrees are rare, which means that absorbing/broadcasting hubs occur rarely. Moreover, random networks exhibit a low mean clustering coefficient that implies that nodes are not as assembled in groups as in the other network types considered. This leads to spiking activity that is not comparable to that of the scale-free networks considered in our simulations, and thus to a slower convergence toward the critical regime.

As for the values of parameters A, B, C, and D, we have pointed out that they do not represent a particular property of the living cell. The emergence of critical behavior in the systems considered is robust for the choice of parameters described above across all networks (scale-free and random) in a particular system size. Further direction of work points toward an analysis of the range of tolerance for the values of these parameters in different network structures, as well as, a variation of the model in which these values are also dynamic and in function of system dynamics.

Lastly, we showed how NSDP regularizes the synaptic modulation induced by STDP. This results in long-term plasticity that reflects the modulation induced by learning and memory (STDP), and at the same time provides the synaptic requirements for the network to self-organize toward the critical regime (NSDP). However, we should point out that NSDP is not reversing the weight modulation induced by STDP per se. Both plasticity learning rules have their own action mechanisms: STDP alters the weights at the synaptic output of a pre-synaptic node capturing the temporal correlations existing between the spikes of this node and nodes in its out-neighborhood; whereas NSDP alters the weights at the synaptic output of a pre-synaptic node in function of its node success and its firing rate. Thus, NSDP is allowing for STDP modulation to occur at the right amount required for the system to maintain the critical state of its collective dynamics. Otherwise STDP would destroy the critical state by favoring clustered local activity which in turn would make large avalanches non-existent [53]. This behavior is captured by the deviation in the Δγ curve and the deviation from unity of the largest eigenvalue Λ associated to the weight matrix.

6.2. The Backpropagation Algorithm

The backpropagation algorithm is an extensively used method to train artificial neural networks (ANNs) in supervised learning scenarios in the context of machine learning. As the name suggests, the backpropagation algorithm uses retrograde signals to communicate the fitting error back to the network while training an ANN. The error is then used to estimate the weight updates at each network connection, afterwards the error is re-estimated with the new weights and the process is repeated until convergence. Unlike the neurons that we have considered here, ANNs consist of non-spiking nodes, that is, non-threshold units. Therefore, there is no direct map between ANNs and networks of spiking nodes. Spiking nodes are all-or-none units that fire only when their membrane potential goes beyond a certain threshold. On the contrary, nodes in ANNs are continuous gateways whose activation function needs to be differentiable everywhere for the backpropagation algorithm to work. We believe that NSDP could in principle supply the basic requirements for the design of a backpropagation algorithm in spiking neurons.

There have been some efforts toward developing versions of the backpropagation algorithm for networks of spiking units, such as the SpikeProp algorithm and others [54–56]. Moreover, recently there has been a line of research regarding the plausibility of developing deep learning methods based on spiking networks [57–59]. It has also been shown that deep learning architectures based on spiking neurons outperform those based on non-spiking neurons as the latter are expensive to implement on serial computers [59]. Additionally, it has been shown that neuromorphic electronic architectures based on spiking units offer an efficient solution for developing compact sensory-motor neural processing systems for robotic applications [58]. When deep learning techniques are implemented in a VLSI architecture, the system benefits from the parallel and asynchronous nature of spiking units responding to signals coming from external sensors.

To the best of our knowledge there has not been a study which relates deep learning methods based on spiking neurons and SOC. We believe that NSDP could provide the link between these two concepts, and at the same time provide a learning algorithm based on the ideas behind backpropagation. This is an interesting direction of research due to the benefits on information processing that the critical regime entails.

6.3. To Tune or Not to Tune

Lastly, we conclude this presentation by considering the question of fine-tuning. In this paper, we have shown how systems self-organize into a critical state through NSDP. Thus, we became relieved from the task of fine-tuning the control parameter α, but instead we acquire a new task: that of estimating the appropriate values for parameters A, B, C, and D in Equation(4). Is there no way to be relieved from tuning any parameter in the system?

The issue of tuning or not tuning depends mainly on what we understand by control parameter. This notion, along with the concepts of order parameter and phase transitions are inherited from the theory of statistical mechanics. There, a control parameter can be thought of a knob or dial that when turned the system exhibits some quantifiable change. We say that the system self-organizes if nobody turns that knob but the system itself. In order to achieve this, the elements comprising the system require a feedback mechanism to be able to change their inner dynamics in response to their surroundings².

Let S be a system in which we observe critical dynamics when the control knob is turned and left in a particular configuration. System S requires an external entity to turn the dial in order to make the system exhibit critical behavior in some order parameters (e.g., critical exponents). In order to make S be able to turn the dial by itself we would have to alter its internal configuration, and here is where the new need for tuning emerges. To create a new internal configuration we would have to “plug” new connections in a particular way which would result in system S^⋆, which is now able to turn its own control knob. It could be argued that we have just changed the place of fine-tuning from control dial to internal mechanisms. If that is the case, then the question about fine-tuning control parameters is in the realm of definitions and semantics. System S is the model we introduced in Section 2, whereas S^⋆ is the same model plus NSDP mechanisms. The latter does not require an external entity to turn the dial for the system to exhibit critical dynamics. However, its internal dynamics are configured in a particular way in order to allow feedback mechanisms at the level of individual elements. Did we fine-tune their configuration? Yes. Otherwise, we would have not achieved what was desired, as nothing comes out of nothing. Did we change control parameter from α to A, B, C, and D? No, the control parameter is still intact, and now it is “in the hands” of the system. However, the nodes know nothing about criticality; their only objective is to maximize their success as long as they are not spiking too much. Unlike them, when we -as external entities- turned the dial, we had the purpose of taking the system into (or out of) the critical regime. When we say that the control parameter is now in “their hands” we do not mean that their objective is to give rise to a particular collective behavior. Rather, the control parameter (the dial) is changing as a result of their individual objectives.

Lastly and most importantly, the new configuration stresses the difference between global and local mechanisms. The control parameter α (the dial) is an external quantity that observes and governs the global (i.e., the collective), whereas NSDP provides the system with local mechanism that have an effect over the collective. This is the main feature of a complex system.

Author Contributions

VH wrote the code and performed the simulations. VH and JH wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^Naturally, this quantity differs from the firing rate, as the latter is a time averaged quantity, whereas Δt_i is stochastic in nature.

2. ^For instance, in the model by Levina et al. [29] this is achieved by the combined action of large cascading and the replenishing of synaptic resources; in our model this is achieved by the maximizing of node success as long as the firing rate is not high.

References

1. Harris KD. Stability of the fittest: organizing learning through retroaxonal signals. Trends Neurosci. (2008) 31:130–6. doi: 10.1016/j.tins.2007.12.002

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Regehr WG, Carey MR, Best AR. Activity-dependent regulation of synapses by retrograde messengers. Neuron (2009) 63:154–70. doi: 10.1016/j.neuron.2009.06.021

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zweifel LS, Kuruvilla R, Ginty DD. Functions and mechanisms of retrograde neurotrophin signalling. Nat Rev Neurosci. (2005) 6:615–25. doi: 10.1038/nrn1727

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kalinovsky A, Scheiffele P. Transcriptional control of synaptic differentiation by retrograde signals. Curr Opin Neurobiol. (2004) 14:272–9. doi: 10.1016/j.conb.2004.05.011

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dalva MB, McClelland AC, Kayser MS. Cell adhesion molecules: signalling functions at the synapse. Nat Rev Neurosci. (2007) 8:206–20. doi: 10.1038/nrn2075

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Chevaleyre V, Takahashi KA, Castillo PE. Endocannabinoid-mediated synaptic plasticity in the cns. Annu Rev Neurosci. (2006) 29:37–76. doi: 10.1146/annurev.neuro.29.051605.112834

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kishida KT, Klann E. Sources and targets of reactive oxygen species in synaptic plasticity and memory. Antiox Redox Signal. (2007) 9:233–44. doi: 10.1089/ars.2007.9.ft-8

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Purves D. Body and Brain: A Trophic Theory of Neural Connections. Massachusetts: Harvard University Press (1988).

Google Scholar

9. Lewis SN, Harris KD. The neural marketplace: I. general formalism and linear theory. bioRxiv (2014). 013185. doi: 10.1101/013185

CrossRef Full Text | Google Scholar

10. Beggs J, Plenz D. Neuronal avalanches in neocortical circuits. J Neurosci. (2003) 23:11167. doi: 10.1080/23311940.2016.1150408

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Petermann T, Thiagarajan T, Lebedev M, Nicolelis M, Chialvo D, Plenz D. Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc Natl Acad Sci USA. (2009) 106:15921–6. doi: 10.1073/pnas.0904089106

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Klaus A, Yu S, Plenz D. Statistical analyses support power law distributions found in neuronal avalanches. PLoS ONE (2011) 6:e19779. doi: 10.1371/journal.pone.0019779

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo DR. Criticality in large-scale brain fMRI dynamics unveiled by a novel point process analysis. Front Physiol. (2012) 3:15. doi: 10.3389/fphys.2012.00015

PubMed Abstract | CrossRef Full Text

14. Friedman N, Ito S, Brinkman BA, Shimono M, DeVille RL, Dahmen KA, et al. Universal critical dynamics in high resolution neuronal avalanche data. Phys Rev Lett. (2012) 108:208102. doi: 10.1103/PhysRevLett.108.208102

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Bellay T, Klaus A, Seshadri S, Plenz D. Irregular spiking of pyramidal neurons organizes as scale-invariant neuronal avalanches in the awake state. eLife (2015). 4:e07224. doi: 10.7554/eLife.07224

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Shew WL, Clawson WP, Pobst J, Karimipanah Y, Wright NC, Wessel R. Adaptation to sensory input tunes visual cortex to criticality. Nat Phys. (2015). 11:659–63. doi: 10.1038/nphys3370

CrossRef Full Text | Google Scholar

17. Scott G, Fagerholm ED, Mutoh H, Leech R, Sharp DJ, Shew WL, et al. Voltage imaging of waking mouse cortex reveals emergence of critical neuronal dynamics. J Neurosci. (2014) 34:16611–20. doi: 10.1523/JNEUROSCI.3474-14.2014

PubMed Abstract | CrossRef Full Text

18. Kinouchi O, Copelli M. Optimal dynamical range of excitable networks at criticality. Nat Phys. (2006) 2:348–51. doi: 10.1038/nphys289

CrossRef Full Text | Google Scholar

19. Haldeman C, Beggs J. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys Rev Lett. (2005) 94:58101. doi: 10.1103/PhysRevLett.94.058101

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Bertschinger N, Natschläger T. Real-time computation at the edge of chaos in recurrent neural networks. Neural Comput. (2004) 16:1413–36. doi: 10.1162/089976604323057443

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Bak P, Tang C, Wiesenfeld K. Self-organized criticality. Phys Rev A (1988) 38:364.

Google Scholar

22. Gutenberg B, Richter CF. Magnitude and energy of earthquakes. Ann Geophys (1956) 9:1–15.

PubMed Abstract

23. Frette V, Christensen K, Malthe-Sørenssen A, Feder J, Jøssang T, Meakin P. Avalanche dynamics in a pile of rice. Nature (1996) 379:49–52.

Google Scholar

24. Bak P, Chen K, Tang C. A forest-fire model and some thoughts on turbulence. Phys Lett A (1990) 147:297–300.

Google Scholar

25. Bak P. How Nature Works. Oxford: Oxford University Press (1997).

Google Scholar

26. Johansen A, Sornette D. Stock market crashes are outliers. Eur Phys J B (1998) 1:141–3.

Google Scholar

27. Shin C, Kim S. Self-organized criticality and scale-free properties in emergent functional neural networks. Phys Rev E (2006). 74:045101. doi: 10.1103/PhysRevE.74.045101

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Meisel C, Gross T. Adaptive self-organization in a realistic neural network model. Phys Rev E (2009) 80:061917. doi: 10.1103/PhysRevE.80.061917

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Levina A, Herrmann J, Geisel T. Dynamical synapses causing self-organized criticality in neural networks. Nat Phys. (2007) 3:857–60. doi: 10.1038/nphys758

CrossRef Full Text | Google Scholar

30. de Arcangelis L, Perrone-Capano C, Herrmann HJ. Self-organized criticality model for brain plasticity. Phys Rev Lett. (2006) 96:028107. doi: 10.1103/PhysRevLett.96.028107

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Pellegrini GL, de Arcangelis L, Herrmann HJ, Perrone-Capano C. Activity-dependent neural network model on scale-free networks. Phys Rev E (2007) 76:016107. doi: 10.1103/PhysRevE.76.016107

PubMed Abstract | CrossRef Full Text | Google Scholar

32. de Arcangelis L, Herrmann HJ. Learning as a phenomenon occurring in a critical state. Proc Natl Acad Sci USA. (2010) 107:3977–81. doi: 10.1073/pnas.0912289107

PubMed Abstract | CrossRef Full Text | Google Scholar

33. de Arcangelis L, Herrmann HJ. Activity-dependent neuronal model on complex networks. Front Physiol. (2012) 3:62. doi: 10.3389/fphys.2012.00062

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Magnasco MO, Piro O, Cecchi GA. Self-tuned critical anti-hebbian networks. Phys Rev Lett. (2009) 102:258102. doi: 10.1103/PhysRevLett.102.258102

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Bornholdt S, Rohlf T. Topological evolution of dynamical networks: global criticality from local dynamics. Phys Rev Lett. (2000) 84:6114. doi: 10.1103/PhysRevLett.84.6114

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Bornholdt S, Röhl T. Self-organized critical neural networks. Phys Rev E (2003) 67:066118. doi: 10.1103/PhysRevE.67.066118

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Rybarsch M, Bornholdt S. Avalanches in self-organized critical neural networks: a minimal model for the neural soc universality class. PLoS ONE (2014) 9:e93090. doi: 10.1371/journal.pone.0093090

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Sporns O. Networks of the Brain. Cambridge, MA: The MIT Press (2010).

Google Scholar

39. Bonachela JA, Muñoz MA. Self-organization without conservation: true or just apparent scale-invariance? J Stat Mech. (2009). 2009:P09009. doi: 10.1088/1742-5468/2009/09/P09009

CrossRef Full Text | Google Scholar

40. Bonachela JA, De Franciscis S, Torres JJ, Muñoz MA. Self-organization without conservation: are neuronal avalanches generically critical? J Stat Mech. (2010). 2010:P02015. doi: 10.1088/1742-5468/2010/02/P02015

CrossRef Full Text | Google Scholar

41. Eurich C, Herrmann J, Ernst U. Finite-size effects of avalanche dynamics. Phys Rev E (2002) 66:066137. doi: 10.1103/PhysRevE.66.066137

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Jensen HJ. Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems, Vol. 10. Cambridge: Cambridge University Press (1998).

Google Scholar

43. Holme P, Kim BJ. Growing scale-free networks with tunable clustering. Phys Rev E (2002) 65:026107. doi: 10.1103/PhysRevE.65.026107

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Sornette D. Critical Phenomena in Natural Sciences: Chaos, Fractals, Self-Organization and Disorder: Concepts and Tools. Berlin: Springer Science and Business Media. (2004).

45. Beggs J, Timme N. Being critical of criticality in the brain. Front Physiol. (2012) 3:163. doi: 10.3389/fphys.2012.00163

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Larremore DB, Shew WL, Restrepo JG. Predicting criticality and dynamic range in complex networks: effects of topology. Phys Rev Lett. (2011) 106:058101. doi: 10.1103/PhysRevLett.106.058101

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Kadanoff LP. Theories of matter: infinities and renormalization. arXiv preprint arXiv:1002.2985 (2010).

Google Scholar

48. Sethna JP, Dahmen KA, Myers CR. Crackling noise. Nature (2001) 410:242–50. doi: 10.1038/35065675

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Bi GQ, Poo MM. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci. (1998) 18:10464–72.

PubMed Abstract | Google Scholar

50. Bi GQ, Poo MM. Synaptic modification by correlated activity: hebb's postulate revisited. Annu Rev Neurosci. (2001) 24:139–66. doi: 10.1146/annurev.neuro.24.1.139

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Morrison A, Diesmann M, Gerstner W. Phenomenological models of synaptic plasticity based on spike timing. Biol Cybern. (2008) 98:459–78. doi: 10.1007/s00422-008-0233-1

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Hernandez-Urbina V, Underwood TL, Herrmann JM. The success of complex networks at criticality. arXiv preprint arXiv:1507.07884 (2015).

Google Scholar

53. Hernandez-Urbina V, Herrmann JM. Small-world structure induced by spike-timing-dependent plasticity in networks with critical dynamics. arXiv preprint arXiv:1507.07879 (2015).

Google Scholar

54. Bohte SM, Kok JN, La Poutre H. Error-backpropagation in temporally encoded networks of spiking neurons. Neurocomputing (2002) 48:17–37. doi: 10.1016/S0925-2312(01)00658-0

CrossRef Full Text | Google Scholar

55. Ponulak F, Kasinski A. Supervised learning in spiking neural networks with resume: sequence learning, classification, and spike shifting. Neural Comput. (2010) 22:467–510. doi: 10.1162/neco.2009.11-08-901

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Sporea I, Grüning A. Supervised learning in multilayer spiking neural networks. Neural Comput. (2013) 25:473–509. doi: 10.1162/NECO_a_00396

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Nessler B, Pfeiffer M, Buesing L, Maass W. Bayesian computation emerges in generic cortical microcircuits through spike-timing-dependent plasticity. PLoS Comput Biol. (2013) 9:e1003037. doi: 10.1371/journal.pcbi.1003037

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Sheik S, Pfeiffer M, Stefanini F, Indiveri G. Spatio-temporal spike pattern classification in neuromorphic systems. In: Lepora NF, Mura A, Krapp HG, Verschure PFMJ, Prescott TJ, editors. Biomimetic and Biohybrid Systems. London: Springer (2013). p. 262–73.

59. O'Connor P, Neil D, Liu SC, Delbruck T, Pfeiffer M. Real-time classification and sensor fusion with a spiking deep belief network. Front Neurosci. (2013) 7:178. doi: 10.3389/fnins.2013.00178

PubMed Abstract | CrossRef Full Text | Google Scholar