- Department of Cognitive Sciences, University of California, Irvine, Irvine, CA, USA
Two non-boolean methods are discussed for modeling context in behavioral data and theory. The first is based on intuitionistic logic, which is similar to classical logic except that not every event has a complement. Its probability theory is also similar to classical probability theory except that the definition of probability function needs to be generalized to unions of events instead of applying only to unions of disjoint events. The generalization is needed, because intuitionistic event spaces may not contain enough disjoint events for the classical definition to be effective. The second method develops a version of quantum logic for its underlying probability theory. It differs from Hilbert space logic used in quantum mechanics as a foundation for quantum probability theory in variety of ways. John von Neumann and others have commented about the lack of a relative frequency approach and a rational foundation for this probability theory. This article argues that its version of quantum probability theory does not have such issues. The method based on intuitionistic logic is useful for modeling cognitive interpretations that vary with context, for example, the mood of the decision maker, the context produced by the influence of other items in a choice experiment, etc. The method based on this article's quantum logic is useful for modeling probabilities across contexts, for example, how probabilities of events from different experiments are related.
1. Introduction
Probability functions are special kind of functions on event algebras. Following Birkhoff and von Neumann [1], a lattice event algebra is a structure of the form,
where X is a nonempty set, is a set of subsets of X, ⊆ is the set-theoretic subset relation, X and the empty set ∅ set are in , and for all A and B in , A ⋓ B is the ⊆-least upper bound in of A and B, and A ⋒ B is the ⊆-greatest lower bound in of A and B. 𝖃 is said to be complemented if and only if for all A in there exists a B in , called the complement of A, such that A ⋓ B = X and A ⋒ B = ∅. (Throughout this article, ⋓ and ⋒ will always denote, respectively, the ⊆-least upper bound and ⊆-greatest lower bound operators on some collection of sets. The complement of A will often be denoted by A⊥.) A special kind of lattice event algebra has been used throughout science and mathematics to describe the domain of finitely additive probability functions. It is where
i.e., where ⋓ = set-theoretic union, ∪, ⋒ = set-theoretic intersection, ∩, and set-theoretic complementation, −, is a complementation operation for 𝖃. This special event algebra is called a set-theoretic boolean algebra.
Probability theory began in the seventeenth century with the study of gambling games. Part of the assumptions underlying such games was that the occurrence of each event that was the basis of a wager could be determined to have happened or could be determined not to have happened. The non-happening of an event A was viewed as the occurrence of another event, the complement of A, −A. Ambiguous or indefinite outcomes were not allowed. In the nineteenth century Boole formulated the logical structure underlying such gambling situations as a set-theoretic boolean algebra. One principle of this algebra is the Law of the Excluded Middle: For each event A, either A happens or −A happens, or in algebraic notation, A ∪ −A = X, where X is the sure event. Another is the Distributive Law, for all A, B, C, A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
During the late 1920s to early 1930s, the validity of the Law of the Excluded Middle and the Distributive Law were called into question as general logical principles: The mathematician Brouwer concluded that the Law of the Excluded Middle was improper for some kinds of mathematical inference, and the mathematician von Neumann found the Distributive Law to be too restrictive for the structure of events in quantum physics. Both Brouwer and von Neumann constructed new logics that generalized boolean algebras.
Brouwer's logic became known as intuitionistic logic. This article uses the special form of it that is a topology open sets. Brouwer developed his intuitionistic logic for philosophical considerations in the foundations of mathematics. Here intuitionistic logic is used for entirely different purposes: It has a more flexible algebraic structure than boolean algebras, and this flexibility is exploited to described how context can affect probability in organized manners.
2. Topological Algebra of Events
is said to be a topological algebra if and only if is a topology of open subsets with universal set X, and for each A in ,
A is the ⊆-largest element of that is in X – A,
that is,
A is called the pseudo complement of A. For the special case where 𝔗 is a boolean algebra (and thus each element of is both an open and closed set), is set-theoretic complementation, −. A “topological probability function” is defined on as follows:
Definition 1. A topological probability function ℙ is a function from into the closed interval [0,1] of the reals such that for all A and B in ,
• ℙ(X) = 1, ℙ(∅) = 0,
• if A ⊆ B then ℙ(A) ≤ ℙ(B), and
• topological finite additivity: ℙ(A ∪ B) = ℙ (A) + ℙ (B) − ℙ (A ∩ B).
If 𝔗 is a boolean algebra, then topological finite additivity is logically equivalent to the usual concept of finite additivity for probability functions. In this article, a finitely additive probability function on a set-theoretic boolean algebra is called a boolean probability function.
A topology with a topological probability function is a generalization of a set-theoretic boolean algebra with a finitely additive probability function. Topologies are much richer algebraically than boolean algebras, and this richness is useful for describing probabilistic concepts that are difficult or impossible to formulate in a boolean algebra, for example, various concepts of ambiguity, vagueness, and incompleteness. This article uses topologies to formulate a specific concept of “context” that applies to some decision situations. This is done through the use of properties of the pseudo complementation operation ∸.
Definition 2. Let be a topological algebra. Then A in is said to be a refutation if and only if there exists a B in such that A = B.
One interpretation of is based on the operations of “verification” and “refutation” used in the philosophy of science. For this interpretation, an underlying empirical domain is assumed along with a scientific theory about its events. An event is said to be “verified” if its occurrence is empirically verified or it is a direct consequence of the underlying theory. An event A is said to be “refuted” if and only if the assumption of its occurrence is inconsistent with known facts and theory about its occurrence. Event A can be refuted by verifying an event B such that A ∩ B = ∅. A can also be refuted by showing its occurrence is inconsistent with known verifiable events and fundamental tenets of the theory underlying the empirical domain. Under this interpretation, the refutation of A is the largest open set S in the topology that refutes A. It follows that A ∩ S = ∅ and thus S = A. The refutation of A, A, is the largest open set T that refutes A. Because A ∩ A = ∅, A refutes A. However, is often the case that A is not verifiable—i.e., it is only the case that A is refutable. In such a situation A ⊂ A. Because of this, it is often the case that for verifiable A, A ∪ A is not the sure event. This reflects that in most cases that verifiability should not be identified with truth and refutation with falsehood.
Refutations play a different role in defining context for topological algebras. Their key properties for this are given in the following theorem.
Theorem 1. Let be a topological algebra. Then the following six statements hold for all A and B in .
1. if A ⊆ B then B ⊆ A.
2. A ⊆ A.
3. A = A.
4. (A ∪ B) = A ∩ B and A ∪ B ⊆ (A ∩ B).
5. A ∩ B = ∅ iff ( A ∩ B = ∅).
6. There does not exists C in such that A ⊂ C ⊂ A.
Proof. Statements 1–4 follow from Theorem 3.13 of Narens [2]. Statements 5 and 6 follow from Theorem 8 of Narens [3].
The key difference between set-theoretic boolean algebras and topological algebras is that in set-theoretic boolean algebras
for all B in the algebra, whereas for topological algebras that are not boolean it can be shown that there exist events A and D such that
By Statement 5 of Theorem 1, such a D in Equation 1 cannot be a refutation.
Let be a topological algebra. Define ≡ on as follows: For all A and B in , A ≡ B if and only if A = B. Then ≡ is an equivalence relation on , and each ≡-class is called a contextual class. The ≡-class to which A belongs, A≡, is called the contextual class for A. Note if A∩B = ∅, then A and B belong to different contextual classes by Statement 5 of Theorem 1.
In psychology, context viewed as an operation that changes an event's interpretation. This is often done in formalizations by making a distinction between a description of an event E (gamble, etc.) given in an instruction and the interpretation of that description in a context , , that can vary with instructions, emotional states, or other forms of context.
The contextual classes of a topological algebra are highly structured. In particular, each contextual class A≡ has a ⊆-maximal element, the refutation A, and that these maximal elements form the following boolean algebra.
Theorem 2. Define ⊎ on the set of refutations as follows: For all A and B in , A ⊎ B = (A ∪ B). Then
is a boolean lattice, that is, for all A, B, C in , A ∩ (B ⊎ C) = (A ∩ B) ⊎ (A ∩ C).
Proof. Theorem 3.16 of Narens [2].
In general 𝕽 is not a set-theoretic boolean algebra, because there may exists an element A in such that A ∪ A is a proper subset of X. When A ∪ A = X for all A in , 𝕽 is called a stone algebra, and it can be shown that = − on , that is, 𝕽 is a set-theoretic boolean algebra. Stone algebras are useful in applications, because a topological probability function ℙ on a stone algebra 𝔗 is also a finitely additive probability function on 𝕽, and for each A in , ℙ( A) can be viewed as the upper boolean probability of the topological probabilities of the events in the contextual class A≡.
There are many ways contextual classes can be used in psychology. One way is to provide generalizations of the standard theory for rational decision making, SEU (Subjective Expected Utility.) For gambling situations, SEU assumes a gamble g = (a1, A1 ⋯ an, An) is composed of a series of terms of the form ai, Ai, where ai, Ai stands for receiving outcome ai if the event Ai occurs, and where is a partition of the sure event X. In determining the utility of gambles in SEU, the subjective probability P(Ai) of Ai is independent of the outcome ai across gambles. That is, SEU requires that if bi, Ai is a term in another gamble h that partitions X, then P(Ai) is also the probability assigned to Ai in the computation of h. Some in the literature have question whether this is a valid rationality principle. In any case, one might want to investigate psychological models where such independence is violated. This is done in a model of Narens [3] called “DSEU” (“Descriptive Subjective Expected Utility”). In DSEU, the nature of the outcome a in a term a, A can influence the implied subjective judgment of the probability of the event A, e.g., where a is a catastrophe such as losing one's life vs. a is winning $5. Narens models the various interpretations of an event occurring in different gambles as events in a contextual class of a topological algebra. Strong disjointness (i.e., C ∩ D) guarantees that contextual interpretations of gambles remain gambles. Narens [3] shows that subjective judgments of the utilities of the contextual interpretations of gambles and their associated subjective probability of events are rational in the sense that there is a SEU model that has a submodel that is isomorphic to the judgments made on the subjective interpretations of gambles. The existence of such a submodel shows that any irrationality observed in the DSEU model by standard tests (e.g., making a Dutch Book) will transfer to SEU, making SEU irrational by such tests, which is impossible by known results.
3. A Behavioral Quantum Probability Theory
3.1. Orthomodular Event Lattices
In making decisions involving probabilistic phenomena, people's behavior often violate economic and philosophic principles of rationality. Various theories in economics and psychology have been developed to account for these violations, Prospect Theory of Kahneman and Tversky [4] being currently the most influential. Almost always the accounts assumed an underlying boolean algebra of events. The deviations from SEU are modeled by changing or generalizing characteristics of a finitely additive probability function. Relatively recently, a different approach has been taken: Change the event space to accommodate the violations of economic and philosophic rationality. Topological event spaces of the previous section are one example of such an approach. More commonly in the literature are modeling techniques inspired by von Neumann's approach to quantum mechanics, for example, Busemeyer and Bruza [5].
In his classic Mathematische Grundlagen der Quantenmechanik, von Neumann [6] modeled probabilistic quantum phenomena using closed subspaces of a Hilbert space as events. The seminal article by Birkhoff and von Neumann [1], “The Logic of Quantum Mechanics,” isolated the algebraic properties of the event spaces that von Neumann thought underly the probability theory inherent in quantum phenomena. The logic consisted of the following:
• A lattice event algebra with a complementation operation ⊥.
• ⊥ satisfies the properties of DeMorgan's Laws, that is, for all A and B in ,
A complementation operation that satisfies DeMorgan's Laws is called an othrocomplementation operation.
• 𝖃 satisfies the modular law, that is for all A, B, and C in ,
For lattice algebras, the modular law is a generalization of the distributive law, B ⋓ (A ⋒ C) = (B ⋓ A) ⋒ (B ⋓ C). Thus, the von Birkhoff-von Neumann logic is a generalization of a boolean lattice algebra, that is, of an orthocomplemented lattice algebra satisfying the above distributive law. It applies to the lattice algebra of all subspaces of a finite dimensional Hilbert space. However, as Husimi [7] pointed out, the lattice algebra of closed subspaces of an infinite dimensional Hilbert space does not satisfy the modular law. He suggested replacing the modular law with the following consequence of it that he called the orthomodular law: For all A, B, C,
Today, Husimi's suggestion won out and the term quantum logic applies to lattice event algebras with orthocomplementation satisfying the orthomodular law. In this article, lattice terminology is used instead, and such lattices are called orthomodular lattices.
In psychology, ideas derived from quantum mechanics have been implemented in various ways, from borrowing methods that assume some physics, to using only Hilbert space probability theory, to using only orthomodular lattices. All of these have foundational issues: Why should methods based on physical laws, e.g., methods based on the conservation of energy, apply to psychology? How does one derive the geometrical properties of Hilbert space used in quantum probability from psychological considerations? What does orthomodularity have to do with how experiments are designed and conducted? To my knowledge, the first two questions has not been adequately addressed in the literature. This article makes some progress on the third.
3.2. Counterfactuals in Behavioral Experiments
The behavioral modeling described in this section concerns a simplified experimental situation. It differs from a similar model presented in Narens [8] in that minor errors and ambiguities in the construction of that model are eliminated and the material is presented in a more clear manner. The version presented here is also more general.
The assumed simplified situation makes for easier mathematical modeling and philosophical analysis, which are the principal goals of this article. The cost for this is a loss of realism and a design that may require much larger numbers of subjects than is practical for usual psychological experimentation.
The experimental situation under consideration has a large population of subjects, where each is put into exactly one of a finite number of experiments. In psychology, this is called a between-subject paradigm.
Each experiment has a finite, nonempty set of choices—called outcomes—and each of an experiment's subjects must choose exactly one of the experiment's outcomes. Different experiments are assumed to have different outcomes. Thus, each outcome occurs only in one experiment.
To simplify the presentation, only a specific case involving two experiments is considered throughout most of this article. The definitions, concepts, and methods of proof developed for this specific case are formulated in manners so that they generalize to the case of finitely many experiments. Such a generalization is briefly discussed in Section 3.5.
The (experimental) paradigm (P) has two experiments, (A) and (B). Experiment (A) has a set of 3 outcomes, , and experiment (B) has a set of 3 outcomes, . (P), which spans (A) and (B), has the set six outcomes, . The set of (P)'s subjects, , is randomly divided in half, with one of the halves participating in (A) and the other in (B). In each experiment, the identity of each subject is recorded along with the outcome she chose. Thus, the number of subjects, N, and the number Nx of subjects who chose outcome x, x = a, b, c, d, e, f, are known. This is the collected data of (P).
Paradigm (P) also has a theory that connects its experiments (A) and (B). This connection is described counterfactually, for example,
If subject s in experiment (A) chose an outcome in event E in the power-set of were instead originally put in experiment (B), then she would have chosen an outcome in event F in the power-set of .
Such counterfactuals exist only in theory, not in data: For a subject s who chose some outcome of E in and in experiment (A), it is not possible to determine from (P)'s data alone whether or not s's choice would have been in , where in experiment (B), and F ≠ ∅. Such a determination must be a consequence of the theory posited by paradigm (P).
Definition 3. Let s be a subject in paradigm (P) and o be an outcome in . Then s is said to have actually chosen o if and only if o is an outcome in an experiment of (P), s is a subject in that experiment, and s chose o. s is said to have counterfactually chosen o if and only if
(i) s is a subject in (A), o is an outcome in (B) and s would have chosen o if she were placed in (B) instead of (A), or
(ii) s is a subject in (B), o is an outcome in (A) and s would have chosen o if she were placed in (A) instead of (B).
Let E be an event in . Then s is said to have paradigmatically chosen E if and only if s actually chose some element of E or s counterfactually chose some element of E.
Theoretical assumptions of (P). The following three theoretical assumptions are made about (P):
(T1) Each subject in paradigmatically choses exactly one outcome from each of (P)'s experiments; and each of (P)'s outcomes is paradigmatically chosen by some subject in .
(T2) Each subject who actually chose the outcome c in would have counterfactually chosen the outcome d in , and each subject who actually chose the outcome d in would have counterfactually chosen the outcome c in .
(T3) For x = a, b, c, d, e, f, let ≪ x ≫ be the set of (P)'s subjects that paradigmatically chose x. Then for y = a, b and z = e, f, ≪ y ≫ ⊈ ≪ z ≫ and ≪ z ≫ ⊈ ≪ y ≫. (Note by (T2) that ≪ c ≫ = ≪ d ≫.)
(T1) is a general theoretical assumption that extends to paradigms having finitely many experiments. (T2) and (T3) are theoretical assumptions that are specific to properties of (P). Section 3.5 describes modified versions of them that apply more widely to paradigms having finitely many experiments.
By assumption, . However, there are situations where outcomes in and are needed to be identified. This accomplished through the use of counterfactual statements. Assumption (T2) above is an example of this: For the purposes of analysis and drawing conclusions about (P), it counterfactually identifies c and d as being the same outcome.
The following notation and concepts are useful.
Definition 4. The following notation is used throughout this article.
• < E > is the set of all subjects s of (P) who actually chose some element e in E.
• ≪ E ≫ is the set of all subjects s of (P) who paradigmatically chose some element e in E.
• | < E > | is the number of subjects in < E >.
• |≪ E ≫ | is the number of subjects in ≪ E ≫.
The following definition provides a method for identifying events across experiments.
Definition 5. Throughout this article for each , σ(G) denotes the event in such that G ⊆ σ(G) and for each of (P)'s subjects p, if p has a paradigmatic choice in G then all of her paradigmatic choices are in σ(G). (From the latter, it follows that she has no paradigmatic choices in .) H is said to be a proposition if and only if for some K and H = σ(K). Such a H is also called the proposition associated with K. Note that for each K in , the proposition associated with K, σ(K), exists.
Notation For each , let and .
The following lemma is a simple consequence of Definition 5.
Lemma 1. Let H be the proposition. Then < −H > = − < H >.
Proof. Each subject p makes one unique actual choice. If this choice is in −H then p is in < −H > and therefore p must be in − < H >, i.e., < −H > ⊆ − < H >. If p is in − < H >, then her actual choice is in −H, i.e., − < H > ⊆ < −H >.
Definition 6. The following notation is used throughout this article:
• For each event F in is the proposition associated with F.
• o for an outcome in is the proposition associated with {o}.
• It follows from (P)'s assumptions that c = d = the proposition associated with {c, d}. Throughout this article, let k stand for the proposition associated with {c, d}. Thus, c = d = k.
• stands for the set of propositions in .
Elements of are described later in Figure 1.
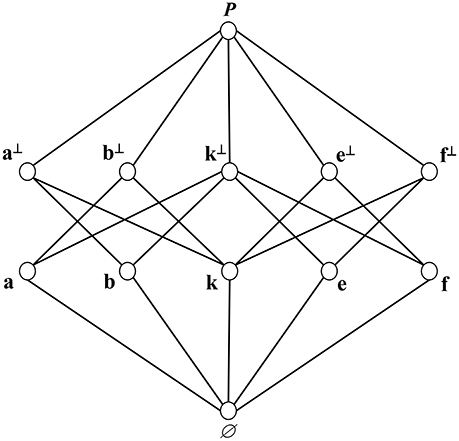
Figure 1. Hasse diagram for . ⊆ corresponds to elements of (nodes) being directly connected by edges to higher elements (higher nodes).
It follows from 's theory and data that ∅ is a proposition and is a proposition.
It will be shown that the proposition a is {a, e, f}.
{a} ⊆ {a, e, f}. Because each subject paradigmatically selects exactly one outcome in , it follows that b ∉ a and c ∉ a, and thus by assumption (T2), d ∉ a. By assumption (T1) each subject who paradigmatically chooses some element of a must also paradigmatically choose some element in . This element cannot be d. Therefore, it is either e or f. If it is e, then another subject who paradigmatically chose a must have chosen f, for otherwise a ⊆ e, contradicting assumption (T3). Similarly if a subject who chose an element of a paradigmatically chose f, then another subject who paradigmatically chose and element of a must have paradigmatically chosen e. Thus, it has been shown that a = {a, e, f}. Similarly b = {b, e, f}. Note that
However {e, f} is not a proposition. Note that the proposition that is the ⊆-greatest-lower bound of a and b is the empty set, ∅.
Definition 7. Let E and F be, respectively, the propositions associated with E and F. Then the following definitions hold:
• E⊥ = σ(< −E >).
• E ⋓ F = σ(< E > ∪ < F >).
• E ⋒ F = σ(< E > ∩ < F >).
Note by Lemma 1 and the meanings of “< >” and “∪” that for all E and F in ,
Lemma 2. Let C, D, and E, respectively be, respectively, propositions associated with C, D, and E. Then C⊥ is a proposition, C =C⊥⊥, and D ⊆ E iff E⊥ ⊆ D⊥.
Proof. C⊥ = σ(C) is a proposition by Definition 7.
By Equation (3),
Because
and
it follows that D ⊆ E iff E⊥ ⊆ D⊥.
Lemma 3. ⋓ is the ⊆-least upper bound operation on .
Proof. Let F and G, respectively, be propositions associated with F and G. Then, because
it follows that
and therefore F ⋓ G is a proposition. Then
and
making F ⋓ G an upper bound of F and G. Suppose H is the proposition associated with H and is such that F ⊆ H and G ⊆ H. Then
Thus
and therefore,
showing that F ⋓ G is the least upper bound of F and G.
Lemma 4. ⋒ is the ⊆-greatest lower bound operation on .
Proof. Let F and G, respectively, be propositions associated with F and G. Then, because < F > ∩ < G > = < F ∩ G >, it follows that
and therefore F ⋒ G is a proposition. Thus,
and
making F ⋒ G a lower bound of F and G. Suppose the proposition H associated with H is such that
Then < F > ⊇ < H > and < G > ⊇ < H >, and thus
and therefore,
showing that F ⋒ G is the greatest lower bound of F and G.
Lemma 5. is a complemented lattice event algebra.
Proof. is clearly the ⊆-largest element of and ∅ is clearly the ⊆-smallest element of .
Because, by Lemmas 3 and Lemma 4, ⋓ and ⋒ are, respectively, the ⊆-least upper bound and ⊆-greatest lower bound operators on , 𝕻 is a lattice event algebra. The following shows that ⊥ is a complementation operation on 𝕻.
Let E and F, respectively, be the propositions associated with E and F. Then, by E⊥ = σ(−E) and Equation (3),
and
Lemma 6. The complemented lattice event algebra satisfies DeMorgan's Laws.
Proof. It is a well-known result of lattice theory (e.g., Theorem 2.14 of [2]) that DeMorgan's Laws for 𝕻 are equivalent to the following: For all E and F in ,
Equation (4) follows from Lemma 2.
The above lemmas show that the description of the experimental situation gives rise to an orthocomplemented lattice. Aerts and Gabora [9] have a similar result for a different psychological paradigm: They show that their empirical data is representable as an orthocomplemented lattice that they imbed in a Hilbert space.
Theorem 3 given later shows that also satisfies the Orthomodular Law. The proof, which generalizes to a wide class of paradigms with finitely many experiments, uses a probability function that is defined on the set of 𝕻's propositions. The probability theory for this function is developed in the following two sections.
3.3. Probability Theory for 𝕻
Definition 8. Throughout the rest of this article, let ℙ be the following function on : For each E in ,
ℙ is called (P)'s propositional probability function.
The following is the intended interpretation of ℙ: For each proposition E in , ℙ(E) is the probability that a randomly chosen paradigm subject actually chose some outcome e in E. If the subjects in < E > are known through data and theory, then the value of ℙ(E) completely computable from data.
Propositions E that span experiments are necessarily partially based on counterfactuals. Because of this, they are theoretical in nature. Nevertheless, as discussed at the end of Section 3, for paradigm (P), ℙ's value for a proposition F is estimable from data to a good approximation. As discussed at the end of Section 3 this is not generally true of other paradigms. However, for the special case where a proposition comes from one of a paradigm's experiments it is generally true by an analog of the following argument given for (P).
Because of the large numbers of subjects participating in (P)'s experiments and the way they were randomly assigned in equal numbers to each of (P)'s experiments, it follows that for each E in ,
where ≈ stands for “approximately” and | < E⋆ > | for “the number of subjects in (B) that counterfactually chose some outcome in E.” Thus, for E in ,
which is computable since | < E > | and are known from data.
Thus for each proposition E in and similarly for each proposition F in , ℙ(E) and ℙ(F) are estimable to a good approximation from data. For where G spans experiments can be more complicated. For such spanning propositions, theoretical assumptions as well as data are needed to calculate ℙ's probabilities. As discussed at the end of Section 3, this is possible for paradigm (P) but may not be possible for other paradigms where the the theory may not complete enough to estimate all spanning propositions.
3.4. Logical and Probabilistic Structure of Orthomodular Event Lattices
Figure 1 is a Hasse diagram of the lattice . The set-theoretic boolean algebra generated by has 26 = 64 elements. The elements at the bottom of Figure 1 but above ∅ are called atoms. They are lattice elements E such that there there does not exist a lattice element F such that ∅ ⊂ F ⊂ E. Figure 1 has 5 atoms, a, b, k, e, f. The set-theoretic boolean algebra generated by these atoms has 25 = 32 elements. has 12 elements—a substantial reduction from 64 or 32.
In Figure 1, the lattice-theoretic intersection ⋒ of atoms, e.g., a ⋒ f, is the proposition ∅. This is a consequence of assumption (T3).
The following concepts are useful for the understanding of the structure of orthomodular lattices.
Definition 9. is said to be an ortholattice if and only if 𝖃 is a complemented lattice event algebra satisfying DeMorgan's Laws.
Definition 10. Let be an ortholattice. Then the following definitions hold.
1. Events C and D in are said to be orthogonal, in symbols, C⊥D if and only if C ⊆ D⊥.
2. ℚ is said to be an orthoprobability function on 𝖃 if and only if
• ℚ is a function from into the real interval [0,1];
• ℚ(X) = 1 and ℚ(∅) = 0; and
• for all C and D in , if C ⊥ D then ℚ(C ⋓ D) = ℚ(C) + ℂ(D).
ℚ is said to be ⊂-monotonic if and only if for all C and D in , if C ⊂ D then ℚ(C) < ℚ(D).
3. An event lattice of the form where is said to be a subalgebra of 𝖃. Note that 𝖄 has the same ⊆-maximal and minimal elements, X and ∅, as 𝖃, and that the operations of 𝖄 are the restrictions of the operations of 𝖃 to .
4. A complemented lattice event algebra is said to be an O6 subalgebra of 𝖃 if and only there exist F and G in such that the following two statements hold:
• and
• ∅ ⊂ F ⊂ G ⊂ X and ∅ ⊂ G⊥ ⊂ F⊥ ⊂ X.
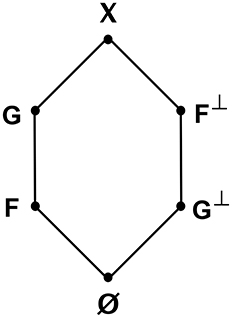
Figure 2 shows a Hasse diagram of an O6 subalgebra of 𝖃 when is a set of propositions.
Lemma 7. Suppose is an ortholattice that has no O6 subalgebra. Then 𝖃 is orthomodular.
Proof. Theorem 2 (pp. 22–23) of Kalmbach [10]. (Also Theorem 2.25 of [2].)
Lemma 8. ℙ is a ⊂ -monotonic orthoprobability function on .
Proof. Suppose F and G are arbitrary elements of such that G ⊆ F⊥. We first show
It is immediate that < F > ⊆ < F ⋓ G > and < G > ⊆ < F ⋓ G >. Thus,
Suppose s is in
Then is is in σ(F) or s is in σ(G). Without loss of generality, suppose s is in σ(F) = F. Then
and Equation (5) follows from Equations (6) and (7).
By the definitions of “proposition” and “⊥” and Equation (3), < F⊥ > = < − F > = − < F >. Thus, < F > ∩ < F⊥ > = ∅, and therefore, because G ⊆ F⊥, < F > ∩ < G > = ∅. Thus,
Therefore,
showing ortho-additivity.
To show monotonicity suppose F and H are arbitrary elements of such that F ⊂ H. Then < F > ⊂ < H >. Then, by the definition of ℙ, ℙ(F) < ℙ(H).
Theorem 3. is an orthomodular lattice and ℙ is an orthoprobability function on 𝕻.
Proof. By Lemma 8, ℙ is a monotonic orthoprobability function on 𝕻. Suppose 𝕻 is not an orthomodular lattice. A contradiction will be shown. Then by Lemma 7 there exists a sublattice of 𝕻 that has a Hasse diagram of the form displayed in Figure 2. By the monotonicity of ℙ,
and by the ortho-additivity of ℙ,
Equations (8) and (9) contradict one another, because, by the monotonicity of ℙ, ℙ(G⊥) < ℙ(F⊥).
The literature has studied orthomodular lattices as generalizations of the logic underlying quantum mechanics. Unfortunately, not all orthomodular lattices admit orthoprobability functions [11]. This in itself is a clue that for science something more than general orthomodular lattices are needed. For 𝕻, the probability function ℙ was derived directly from (P)'s theory and empirical considerations.
3.5. Generalizations and Properties of Paradigm Probability Functions
Thus far, our analysis has focussed on the paradigm (P) and the probabilistic structure 𝕻. Although the analysis sometimes used special features of them, care was taken to present, when possible, concepts and methods of proof that generalized to a wider class experimental situations and a wider class of probabilistic structures. There are, however, some conditions special to 𝕻 and ℙ that do not apply to all between-subject paradigms involving finitely many experiments. These are concerned with the use of 𝕻's atoms.
The boolean algebra spans (P)'s experiments. Its set of atoms is , which is the set of outcomes of (P)'s experiments. (P)'s data consist of records of the choices in made by its subjects. In shifting the analysis from 𝕭 to 𝕻, it is desirable to keep the data intact. (P)'s theoretical axioms and concepts does this by making the propositions a, b, k, e, and f the atoms of 𝕻. (k results from theoretical assumption (T2) that requires the identification of c and d.) This allows the collected data about to be transferred to a, b, k, e, f. Concepts and theorems can exploit this transfer. For example, this transfer is needed to implement the important concept of “actually determined” in obtaining consequences of (P)'s theory and data.
Many of the previous results about 𝕻 generalize to a paradigm (Q) involving finitely many experiments, (A1), …, (An), where (Q) has disjoint experimental outcomes, disjoint subject populations, and where for 1 ≤ i, j ≤ n, Ai's subject population is randomly sampled from (Q)'s subject pool and is the same size as Aj's subject population. In particular, with appropriate generalizations of (P)'s theory, Lemmas 2 to 8 and Theorem 3 generalize to (Q)'s lattice of propositions using the methods of proof similar to the those presented for 𝕻 and ℙ.
(Q)'s theory consists of a set of statements describing relationships among subjects' responses across experiments. Among these are statements that generalize (T1), (T2), and (T3) of (P)'s theory in the following manner:
(T*1) Each of (Q)'s subjects paradigmatically choses an outcome from each of (Q)'s experiments; and each of (Q)'s outcomes is paradigmatically chosen by at least one of (Q)'s subjects.
(T*2) Identifications of outcomes across experiments are made.
(T*3) The atomic propositions of (Q)'s propositional lattice consist of propositions that correspond to the outcomes that were not identified in (T⋆2) along with propositions corresponding to each set of mutually identified outcomes in (T⋆2).
“< >” and ℙ have analogous definitions and results for (Q) to those for (P).
3.6. Comparison with Quantum Probability
Many researchers of the formal foundations of quantum mechanics have speculated that the underlying probability theory for quantum mechanics is not interpretable in a physically acceptable manner into a boolean probability theory (e.g., [1, 12–14]). Others have disagreed (e.g., [15]), producing a long-running controversy that continues to the present (e.g., 16).
Von Neumann was well aware of foundational difficulties presented in his seminal 1932 book, Mathematische Grundlagen der Quantenmechanik. It appears to me that such difficulties are sharply increased and compounded by the importation of formalisms involving probability from quantum mechanics to cope with the difficult contextual issues presented in the behavioral sciences.
Rédei [17] writes the following about the evolution of von Neumann's position about the nature of probability in quantum mechanics.
What von Neumann aimed at in his quest for quantum logic in the years 1935–1936 was establishing the quantum analog of the classical situation, where a Boolean algebra can be interpreted as being both the Tarski-Lindenbaum algebra of a classical propositional logic and the algebraic structure representing the random events of a classical probability theory, with probability being an additive normalized measure on the Boolean algebra satisfying [monotonicity], and where the probabilities can also be interpreted as relative frequencies. The problem is that there exist no “properly non-commutative” versions of this situation: The only (irreducible) examples of non-commutative probability spaces probabilities of which can be interpreted via relative frequencies are the modular lattices of the finite (factor) von Neumann algebras with the canonical trace; however, the non-commutativity of these examples is somewhat misleading because the non-commutativity is suppressed by the fact that the trace is exactly the functional that insensitive for the non-commutativity of the underlying algebra. So it seems that while one can have both a non-classical (quantum) logic and a mathematically impeccable non-commutative measure theory, the conceptual relation of these two structures cannot be the same as in the classical commutative case—as long as one views the measure as probability in the sense of relative frequency. This must have been the main reason why after 1936 von Neumann abandoned the relative frequency view of probability in favor of what can be called a “logical interpretation.” In this interpretation, advocated by von Neumann explicitly in his address to the 1954 Amsterdam Conference, (quantum) logic determines the (quantum) probability, and vice versa, i.e., von Neumann sees logic and probability emerging simultaneously.
Von Neumann did not think, however, that this rather abstract idea had been worked out by him as fully as it should. Rather, he saw in the unified theory of logic, probability, and quantum mechanics a problem area that he thought should be further developed. He finishes his address to the Amsterdam Conference with these words [18]:
I think that it is quite important and will probably shade a great deal of new light on logics and probably alter the whole formal structure of logics considerably, if one succeeds in deriving this system from first principles, in other words for a suitable set of axioms. All the existing axiomatizations of this system are unsatisfactory in this sense, that they bing in quite arbitrarily algebraical laws which are not clearly related to anything that one believes to be true or that one has observed in quantum theory to be true. So, while one has very satisfactorily formalistic foundations of projective geometry of some infinite generalizations of it, including orthogonality, including angles, none of them are derived from intuitively plausible first principles in the manner in which axiomatizations in other areas are.
Now I think that at this point lies a very important complex of open problems, about which one does not know well of how to formulate them now, but which are likely to give logics and the whole dependent system of probability a new slam.
Von Neumann's concerns about probability theory in quantum mechanics do not hold for the multi-experiment behavioral paradigms presented in this article. The paradigms' orthomodular lattice event structures follows directly from their experimental designs and theories linking experiments. This produces an orthoprobability probability function ℚ for a paradigm's lattice of propositions, 𝕼. Because for propositions, actual probabilities coincide paradigmatic probabilities, ℚ can be estimated through a relative-frequency process for events for which the underlying theory and collected data specify to a good approximation which subjects paradigmatically chose outcomes for those events. Paradigm (P) is an example where such a relative frequency approach applies to all of its events: Its event lattice has twelve elements. Of these, the probabilities of two, and ∅, are determined by definition. Five others, a, b, k, e, f, are atoms and their actual probabilities are estimable by collected data and thus, as described earlier, their paradigmatic probabilities are estimable. The remaining five are complements of the five atoms and these have as probabilities 1 minus the probability of its atom, and thus they too are estimable. Now consider the general case 𝕼 where F and G are lattice disjoint propositions where it is known which subjects chose an element of F and which chose an element of G. If it is the case that F ∪ G ⊂ F ⋓ G then more information is required to estimate the number of subjects who are in F ⋓ G. The additional information has to come from the paradigm's theory. For (P), its theory tells us that a ⋓ f = {a, b, e, f}, which is the complement of k and thus has number of subjects . This number is known because and |k| are known.
4. Conclusions
Both the topological probability and the quantum-like paradigm theories presented here are applicable to a variety of psychological experimental situations where Kolmogorov probability theory appears inadequate for modeling cognitive processes. Although very different in how they handle probabilities, they both can often offer explanations for puzzling behavioral phenomena. From a modeling point of view, this is not entirely surprising: After all, both are generalizations of Kolmogorov probability, and, as such, both have greater freedom to model behavioral data than the Kolmogorov theory. However, because of their algebraic structural differences, they are likely to suggest different cognitive mechanisms producing the data. Topological probability functions are arguably “rational” in the sense that they do not violate the key ideas of rationality inherent in the Dutch Book Argument and the SEU model.
The probability theory of quantum mechanics and the psychological paradigm probability theory developed here share many formal characteristics, but at a fundamental level they are about different kinds of uncertainty. The uncertainty in paradigm probability theory is manufactured by the random assignment of subjects to experiments by the scientist. It is not an inherent part of the subjects, outcomes, or of the paradigm's theory. The subjects in an experiment have actual and counterfactual choices. These choices, as well as the theory connecting the paradigm's experiments, are modeled in deterministic manners. All of this is very different than the probability theory of quantum mechanics, where the uncertainty results from the randomness inherent an ensemble of particles.
Systems satisfying the Kolmogorov axioms for probability produce a probability theory founded on a σ-additive boolean probability function. Such probability functions have come to dominate the probability theories of mathematics, statistics, and science. They are usually conceptualized as a single boolean probability function defined over all relevant situations. They are often interpreted as measuring the propensity of an event to occur or a subjective degree of belief that an event will occur. Such a propensity or degree are considered to be completely associated with the event, and, as a consequence, does not depend on the situation to which an event belongs. In this sense, propensity (or degree of belief) is noncontextual.
Kolmogorov probability theory can be generalized to become contextual by allowing events that belong to different situations to have different propensities (or different degrees of belief). These situations are characterized as having different probability functions. This causes various challenging issues in behavioral science, e.g., the identification of random variables across situations, or descriptions of the relationships of random variables across different probabilistic situations. Dzharafov and Kujala [19] and Dzharafov et al. [20] have laid out a foundation for such a generalization. It produces an alternative to the single probability function interpretation of the Kolmogorov theory that have many features in common with the probability theory underlying quantum mechanics. There are several other quantum-like probability theories in the literature that are not discussed in this article (e.g., the probability theory of [21]). It is beyond the scope of this article to go into their foundations or relationships to the alternative probability theories described in this article.
Context is an ill-understood concept in the behavioral sciences. While there are many psychological experiments illustrating its ubiquity and importance in psychological phenomena, e.g., framing effects in cognitive psychology, there is very little theory and experimentation describing the relationship of contexts across different experiments. I believe part of the reason for this has been the lack of mathematical theories designed to model contextual relationships. For particle physics, this kind of modeling was accomplished by von Neumann. His method has been imported by Busemeyer and colleagues and others into the behavioral science (e.g., [5]). This has produced some interesting new phenomena (e.g., [22]) and has been used as a unifying foundation for explaining many puzzling psychological phenomena. Not surprisingly, this importation has raised new, serious foundational and methodological issues.
Narens [2] interprets many results from lattice theory—most known in the 1930s—as suggesting there are not many alternatives to boolean algebras that are useful event spaces for modeling probabilistic experimental phenomena, except for those that are distributive (e.g., topological algebras) or orthomodular (e.g., closed subspaces of a Hilbert space). This means that rich mathematical theories of probabilistic context are likely very limited without giving up much more structure from Kolmogorov probability theory, particularly, without greatly reducing the parts of the event space displaying forms of “probabilistic additivity.”
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Funding
The research for this article was supported by grant SMA-1416907 from NSF.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fphy.2017.00004/full#supplementary-material
References
1. Birkhoff G, von Neumann J. The logic of quantum mechanics. Ann Math. (1936) 37:823–43. doi: 10.2307/1968621
2. Narens L. Probabilistic Lattices with Applications to Psychology. Singapore: World Scientific (2015). doi: 10.1142/9345
3. Narens L. Multimode utility theory. J Math Psychol. (2016b) 75:42–58. doi: 10.1016/j.jmp.2016.02.003
4. Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk. Econometrica (1979) 47:263–91. doi: 10.2307/1914185
5. Busemeyer JR, Bruza PD. Quantum Models of Cognition and Decision. Cambridge: Cambridge University Press (2012).
8. Narens L. Probabilistic frames for non-Boolean phenomena. Philos Trans A Math Phys Eng Sci. (2016a) 374:20150105. doi: 10.1098/rsta.2015.0102
9. Aerts D, Gabora L. A theory of concepts and their combinations I: the structure of the sets of contexts and properties. Kybernetes (2005) 34:167–91. doi: 10.1108/03684920510575799
11. Greechie RJ. Orthomodular lattices admitting no states. J Comb Theory (1971) 10:119–32. doi: 10.1016/0097-3165(71)90015-X
13. Suppes PC. Probability concepts in quantum mechanics. Philos Sci. (1961) 28:378–89. doi: 10.1086/287824
14. Suppes PC. The probabilistic argument for a non-classical logic of quantum mechanics. Philos Sci. (1966) 33:14–21. doi: 10.1086/288067
15. Sneed JD. Quantum mechanics and classical probability theory. Synthese (1970) 21:34–64. doi: 10.1007/BF00414187
17. Rédei M. Von Neumann's concept of quantum logic and quantum probability. In: Rédei M, Stöltzner M, editors, John von Neumann and the Foundations of Quantum Mechanics. Dordrecht: Kluwer (2001).
18. von Neumann J. Unsolved problems in mathematics. In: Rédei M, Stöltzner M, editors, John von Neumann and the Foundations of Quantum Physics. Dordecht: Kluwer Academic (2001). p. 231–46.
19. Dzhafarov EN, Kujala JV. Conversations on contextuality. In: Dzhafarov EN, Jordan JS, Zhang R, Cervantes VH, editors. Contextuality from Quantum Physics to Psychology. World Scientific Press (2015). p. 1–22.
20. Dzhafarov EN, Kujala JV, Cervantes VH. Contextuality-by-default: a brief overview of ideas, concepts, and terminology. In: Lecture Notes in Computer Science, Vol. 9535 (2016). p. 12–23.
21. Foulis DJ, Randall CH. Operational statistics. I. Basic concepts. J Math Phys. (1972) 13:1667–75. doi: 10.1063/1.1665890
Keywords: non-boolean methods, Hilbert space, intuitionistic logic, quantum logic, event lattices
Citation: Narens L (2017) Topological and Orthomodular Modeling of Context in Behavioral Science. Front. Phys. 5:4. doi: 10.3389/fphy.2017.00004
Received: 26 May 2016; Accepted: 18 January 2016;
Published: 14 February 2017.
Edited by:
Emmanuel E. Haven, University of Leicester, UKReviewed by:
Irina Basieva, Graduate School for the Creation of New Photonics Industries, RussiaTomas Veloz, University of British Columbia, Canada
Copyright © 2017 Narens. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Louis Narens, bG5hcmVuc0B1Y2kuZWR1
 Louis Narens
Louis Narens