- 1Space Research Institute, Austrian Academy of Sciences, Graz, Austria
- 2Institut für Geophysik und Extraterrestrische Physik, Technische Universität Braunschweig, Braunschweig, Germany
- 3Institut für Theoretische Physik, Technische Universität Braunschweig, Braunschweig, Germany
- 4Deutsches Zentrum für Luft- und Raumfahrt, Institut für Planetenforschung, Berlin, Germany
A mini-review is given about two recent discoveries in the solar wind turbulence research on ion-kinetic scales: the existence of sideband waves (or breakdown of the linear mode wave picture) and the wavevector anisotropy leading to a persistent filament formation in a wide range of plasma beta.
1. Introduction
The solar wind is a radial outflow of the plasma originating in the solar corona, and is unique in that the plasma develops into turbulence in interplanetary space while retaining the collisionless state of the medium. Understanding or explaining the fact that the solar wind is in a turbulent state is not trivial, and should be regarded as a challenge even in fundamental physics because turbulence is an energy transport process from one scale to another, and the energy transport cannot proceed without some dissipation mechanism to thermalize the constituent particles. How the Alfvénic fluctuations in the solar wind influence the physics of energy cascade and dissipation in heliospheric plasma turbulence is an interesting and important question.
Physical processes become increasingly more complex from magnetohydrodynamic (MHD) scales onto the ion-kinetic scales (at about 400 km down to 100 km or even shorter in the solar wind). Individual particle motion, gyration, and electrostatic oscillation interact with the incident waves on kinetic scales and the energy transfer is possible between the electromagnetic fields and the plasma particles via various channels of dynamics. Moreover, waves become dispersive and dissipative on the kinetic scales. Here, the notion of dispersion means a transport of the fluctuation energy of the magnetic field into that of the electric field, while the notion of dissipation means an energy transport from the electric or magnetic field into the particle thermal motion. Current understanding of solar wind turbulence is summarized in extensive review articles [1–3].
Two questions remain particularly interesting and challenging as to ion-kinetic scale turbulence in the solar wind, “What kinds of wave modes are there in solar wind turbulence?” and “What kinds of spatial structures do the turbulent fields exhibit?” In this mini-review, we offer an up-to-date summary of the studies on the wave modes and the spatial structures in solar wind turbulence on the ion-kinetic scales. The results are obtained by the four-spacecraft measurements using the Cluster magnetometer data in the solar wind [4] and by direct numerical simulations using the hybrid plasma code AIKEF [5].
2. Linear Mode Picture
The picture of linear modes is widely applied to interpreting fluctuations in space plasma. Ion-kinetic waves have on one hand a character of small-wavelength extension of the magnetohydrodynamic waves (Alfvén mode, and fast and slow magnetosonic modes); On the other hand, wave-particle interactions influence the wave dynamics such as resonance with particle motions or wave damping. Theoretically, each ion-kinetic mode is obtained by a linearly perturbing the Vlasov equation (typically assuming a Maxwellian plasma) and solving the equation under a given set of parameters like the wavenumber, the propagation angle to the mean magnetic field, the plasma parameter beta, the ion-to-electron temperature ratio, and the Alfvén speed with respect to the speed of light. The solution is obtained in the form of dispersion relation and damping rate, that is, frequencies in complex numbers as a function of the wavenumbers. Analytic solutions are obtained only in few cases. The numerical algorithm to find the dispersion relations involves a use of the modified Bessel functions, and is described, for example, in the books by Stix [6] and Gary [7].
For a quasi-parallel propagation to the mean magnetic field, possible ion-kinetic modes (assuming a temperature isotropy) are the whistler mode, the ion-cyclotron mode, and the ion-acoustic mode. For a quasi-perpendicular propagation, there are four possible ion-kinetic modes as a transition of the quasi-parallel modes: the kinetic Alfvén mode, the kinetic slow mode, the oblique whistler mode, and the ion Bernstein mode. Figure 1 upper panels show sketches of the dispersion branches for the whistler and the ion-cyclotron modes for a propagation angle of 5 degree to the mean magnetic field at different values of plasma beta, 0.1, 1, and 5. The lower panels show sketches of the kinetic Alfvén mode, the whistler mode, and the ion Bernstein mode for a propagation angle of 85 degree and at different values of plasma beta.
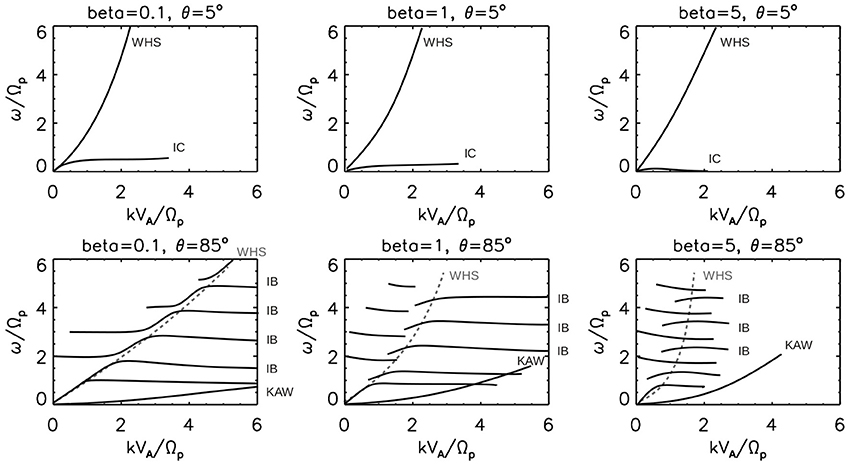
Figure 1. Sketches of dispersion relations for ion-kinetic wave modes under the condition of small damping. An electron-proton plasma is assumed here. Dispersion relations are shown under different conditions: quasi-parallel propagation angle from the mean magnetic field (5°) and quasi-perpendicular propagation (85°), and three different values of ion beta (0.1, 1, and 5). Wave modes represent the whistler mode (WHS), the ion cyclotron mode (IC), the ion Bernstein mode (IB), and the kinetic Alfvén wave (KAW). Temperature is isotropic and the electron-to-ion temperature is 10. The Alfvén speed to the light speed is . Dispersion relations are numerically obtained by implementing the solutions of the linear Vlasov equation as in Gary [7].
Ion-Cyclotron Mode
Ion-cyclotron mode is smoothly connected from the MHD Alfvén mode with a left-hand temporal field rotation sense around the mean magnetic field. The frequencies of the ion-cyclotron mode approach the resonance at the ion gyro-frequency for the parallel propagation. The resonance frequency becomes lower for oblique propagations or for a larger value of beta. The electromagnetic ion-cyclotron mode can propagate along the magnetic field line and deposit the energy over a large distance. For example, 1-Hz ion-cyclotron waves transfer the energy from the radiation belt down to the Earth ionosphere and cause pulsating proton aurora [8]. There is evidence for the ion-cyclotron mode in the solar wind (inner heliosphere) [9]. The velocity distribution functions of ions show a peak at the apparent phase speed for the ion-cyclotron mode in the parallel direction to the mean magnetic field and an arc shape centered at the apparent phase speed for the ion-cyclotron mode, a sign of the pitch angle scattering by the ion-cyclotron mode.
Numerical simulations indicate that the ion-cyclotron mode can heat and accelerate the helium alpha particles, as well [10–13].
Kinetic Alfvén Mode
Kinetic Alfvén mode is obtained as a quasi-perpendicular limit of the ion-cyclotron mode and hence a small-wavelength extension of the MHD Alfvén mode. At a propagation angle of about 70 degrees, the sense of the dispersion relation or the curvature of the dispersion branch becomes flipped from a converging sense of the frequency increase toward the ion-cyclotron resonance frequency into a diverging sense of the frequency increase such as that of the whistler mode. The kinetic Alfvén mode has very low frequencies (below the ion gyro-frequency) and are only moderately damped, and is considered as one of the most relevant or dominant mode in the solar wind. In fact, a number of spacecraft observations are favorably interpreted as realization of the kinetic Alfvén mode in a frequency range between 0.1 and 100 Hz in the spacecraft frame: from the multi-spacecraft k-filtering technique [14, 15] and by other techniques [16–20]. Recent numerical simulations for forced hybrid kinetic turbulence suggest that the kinetic Alfvén mode dominates ion-scale turbulence in a high-beta plasma, and the whistler mode in a low-beta plasma [21].
2.1. Kinetic Slow Mode
Kinetic slow mode is a small-wavelength extension of the MHD slow mode and has as low frequencies as that of the kinetic Alfvén mode (depending on the value of beta). While the slow mode is generally considered as a strongly Landau-damped mode, the slow mode acquires only a moderate damping rate for nearly perpendicular propagations. Compressive fluctuations in the solar wind may be slow mode waves [22, 23] or pressure-balanced structures between the magnetic field and the plasma in the solar wind [24, 25].
2.2. Whistler Mode
The whistler mode is smoothly connected from the MHD fast mode with a right-hand field rotation sense around the mean magnetic field [26]. The existence of the whistler mode is indicated in various regions in space plasmas, e.g., as magnetospheric chorus [27], magnetotail right-hand waves [28, 29], magnetosheath or magnetospheric lion roar waves [30, 31], magnetopause-waves [32], and waves departing from magnetic reconnection [33]. In the ion-kinetic domain, the frequencies of the whistler mode are increasingly higher at larger wavenumbers. The dispersion branch begins to split into resonance branches at the ion gyro-frequency and its harmonics as the ion Bernstein mode. The frequencies between different Bernstein modes still retain the dispersion branch for the whistler mode In a low-beta plasma, the quasi-perpendicular whistler mode is more smoothly connected from lower frequencies to higher frequencies. In a high-beta plasma, in contrast, the whistler mode branch almost vanishes because of the resonant splitting into the ion Bernstein mode. Several cases of the solar wind observations are interpreted as the whistler mode on the ion-kinetic scales [34] and the electron-kinetic scales [35, 36].
2.3. Ion Bernstein Mode
The ion Bernstein mode is a set of ion resonance branches that appear as a break-up of the whistler branch at the ion gyro-frequency (fundamental mode) as well as the harmonics (second order and higher order). The Bernstein mode can be both electrostatic and electromagnetic, and is particularly suited for transferring the fluctuation energy toward higher frequencies by three-wave couplings [37]. The ion Bernstein mode is extensively studied in Tokamak, fusion, and laboratory plasmas [38–42]. Several observational studies indicate the ion Bernstein mode in the solar wind [43, 44].
3. Sideband Waves
3.1. Sideband Activity
Small-amplitude fluctuations in the plasma can develop into turbulence by exciting daughter waves in a successive way. The fluctuations can appear as sideband waves associated with the linear modes. The fundamental or the most likely process to generate the sideband waves is the three-wave coupling. The coupling itself is a coherent process such that the frequencies, the wavevectors, and the initial phases of the interacting and the generated waves must fulfill the wave resonance conditions, ω1 + ω2 = ω3 for the frequencies, for the wavevectors, ϕ1 + ϕ2 = ϕ3 for the initial phases. Therefore, some mechanism is needed to make the wave phase random or incoherent such as dissipation of the fluctuation energy or thermal motion of the plasma. A coupling of four waves (such as wave transmission and wave reflection out of two interacting waves) or even more participating waves is possible but the probability becomes lower when more participating waves are involved in the interactions.
The three-wave coupling is irrelevant from the physics of the linear modes. If the daughter wave happens to have a frequency of some linear modes (onto the same branch or a different branch), the daughter wave can be supported by the plasma as a background medium, and can propagate over a large distance and can exist for a longer time. Sideband waves are formed if there is a frequency mismatch between the daughter wave and the linear modes, and if there is a continuous pumping of the daughter wave. Sideband or nonlinear modes can be any propagating wave components other than the linear mode fluctuations. The lifetime of the sideband waves plays an important role in turbulence evolution. Sideband waves may break into other frequencies and wavevectors through successive wave-wave interactions.
Wave couplings can happen even for smaller fluctuation amplitudes because the nonlinear effect caused by a spatial gradient (or a wavenumber) can compete against the small amplitudes. In the fluid picture, the nonlinear terms such as the advection or the Lorentz force represent a combination of (1) self-coupling between different scales of the flow velocity or the magnetic field and (2) mediation by a wavenumber (which comes from the spatial derivative, the nabla operator).
3.2. Frequency Mismatch
Using four-point tetrahedral measurements of Cluster, both the frequencies and the wavevectors in the three-dimensional space can be determined in the solar wind. Furthermore, the frequencies can be corrected for the Doppler shift (a product of the wavevector with the flow velocity vector) and the frequencies can be studied in the plasma rest frame co-moving with the plasma flow. Figure 2 left exhibits a histogram of the frequency-wavevector occurrence in the co-moving frame using 9 time intervals of Cluster's solar wind measurements and 512 discrete wave components therein [44]. Frequencies are normalized to the proton cyclotron frequency, and the wavenumbers (the magnitude of the wavevector) are normalized by multiplying the proton inertial length (Alfvén speed divided by the proton cyclotron frequency). Comparison with the theoretically estimated or expected dispersion relations shows no clear or strong agreement in the wave data with the linear mode waves such as the kinetic Alfvén mode or the ion Bernstein modes. The majority of the detected waves in the solar wind do not agree with the frequencies of the linear mode, but appear either as sideband waves associated with the linear mode or as a concentration below the ion gyro-frequency that does not belong to any linear modes. The sideband formation around the linear mode is also indicated on other time intervals of the Cluster data, e.g., around the frequencies of the kinetic Alfvén mode [45–47].
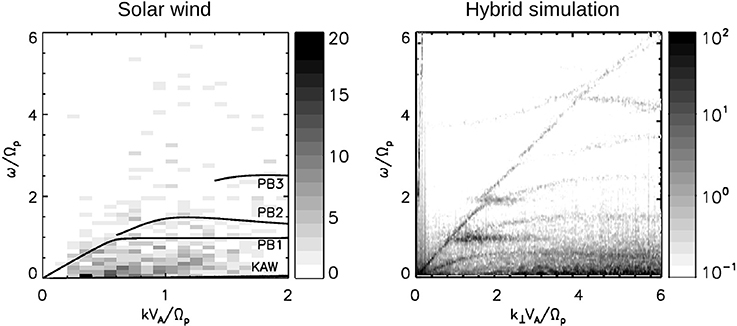
Figure 2. (Left) Histogram of wave components (rest-frame frequencies and wavenumbers) observed by the Cluster spacecraft, adapted from Perschke et al. [44] with the dispersion relations over-plotted for kinetic Alfvén waves (KAW) and proton Bernstein modes (fundamental mode denoted by PB1; second and third harmonics by PB2 and PB3, respectively). (Right) Magnetic energy distribution in the wavenumber-frequency domain obtained from hybrid plasma turbulence simulation, adapted from Comişel et al. [49]. Color bar scales are in units of events on the left and the square of the magnetic fluctuation amplitude normalized to the mean magnetic field magnitude on the right.
The existence of sideband waves is also confirmed in the hybrid plasma simulations (Figure 2 right). Moreover, the frequency spread around the linear mode grows together with the turbulence evolution. That is, the sideband spread serves as an index of turbulence evolution for distinct linear modes [48–50]. The sideband spread can be measured by computing the variance of the fluctuation energy around the linear mode frequency as:
where ω0 denotes the linear mode frequency at a given value of the wavenumber and E(k, ω) the fluctuation energy as a function of the frequency ω and the wavenumber k. If multiple wave modes co-exist in the turbulence data, the frequency range for the integration needs to be specified such as ω− and ω+ for the lower and upper limits. Hybrid plasma simulations show that the sideband activity evolves when the fluctuations evolve into turbulence by exciting waves at smaller wavelengths and that the evolution profile depends on the wave modes [48, 50].
Using 31 solar wind events and 2,328 discrete waves therein, the wavenumber-frequency spectra are fitted into a scaling of the frequency deviation (as measured by the standard deviation) as σ ∝ k1.6 such that the frequency deviation is inflated more rapidly at higher wavenumbers [47]. A hydrodynamic scaling of the frequency deviation is σ ∝ k2/3 (in the Lagrangian-frame), and is asymptotic at higher wavenumbers.
So far, not many unambiguous observational studies are available which indicate the frequency deviation from the linear mode waves in the solar wind. The E-over-B method (the ratio of the electric to the magnetic field fluctuations) can determine the dispersion relation experimentally, but one has to assume that there is only one wave mode at each frequency and that the fluctuations are of electromagnetic type and not of electrostatic type. The frequency deviation is contributed not only by wave-wave interactions but also by a random sweeping by large-scale flow variations and large-scale wave motions. In future studies of kinetic plasma turbulence, the origin of the frequency deviation should be more systematically studied.
4. Filament Formation
4.1. Origin of Turbulent Filaments
Magnetohydrodynamic (or Alfvénic) turbulence develops primarily into filaments of magnetic flux along the mean magnetic field. The reason for the filament formation lies in the fundamental wave-wave coupling of the Alfvén waves. In the MHD picture, the combination of the dispersion relation for the Alfvén mode with the three-wave coupling constrains that the parallel component of the wavevector is either zero (for one incident wave) or a constant (for the other incident wave) [51]. That is, the energy cascade is strictly perpendicular in this treatment. The wavevector of the daughter wave has a larger value of the perpendicular component of the wavevector. Also, it is worth noting that the three-wave coupling (in the wavevector sense) is successfully demonstrated in a laboratory plasma experiment [52].
In the ion-kinetic picture, propagation directions are typically given as an input to solving for the dispersion relations in the linear Vlasov theory. However, incorporation of the dispersion relation into the three-wave coupling predicts that the wavevectors evolve increasingly in the perpendicular direction. For both the whistler and the kinetic Alfvén modes, three-wave coupling favors energy cascade perpendicular to the mean magnetic field [53]. Numerical simulations of plasma turbulence indicate that the perpendicular wavevector geometry is more valid: magnetohydrodynamic simulations [54], ion kinetic or hybrid simulations [48, 55, 56], gyro-kinetic simulations [57], and particle-in-cell simulations [58–60].
4.2. Visualization of the Wavevector Geometry
Two scenarios are possible as to describing how the wavevectors are organized: parallel and perpendicular wavevector geometries. The parallel wavevector geometry (also referred to as the slab geometry) reflects the picture of packets of Alfvén waves propagating parallel and anti-parallel to the mean magnetic magnetic field with different wavelengths. The perpendicular wavevector geometry (also referred to as the quasi-two-dimensional geometry) reflects the picture of turbulence evolving in the plane perpendicular to the mean magnetic field. In terms of the Alfvén mode, the dispersion relation becomes a zero-frequency mode such that coherent structures develop in the perpendicular wavevector geometry.
Spacecraft measurements in the solar wind indicate that both of the wavevector geometries are possible: the parallel wavevector geometry on large (magnetohydrodynamic) scales (or referred to as the outer scales) [61] or high-speed streams [62], and the perpendicular wavevector geometry on small scales from magnetohydrodynamic down to ion-kinetic scales [63, 64] or low-speed streams [62].
Using the Cluster spacecraft data, the magnetic energy can be determined directly in the three-dimensional ion-kinetic wavevector domain by integrating the spectra over the frequencies. Figure 3 left displays a characteristic or typical example of the wavevector anisotropy [64]. The energy distribution extends preferentially in the perpendicular direction to the mean magnetic field. In contrast, the spectral energy falls down more quickly in the parallel direction and most of the fluctuation energy is confined to small parallel wavenumbers, that is, there are large-scale structure along the mean magnetic field and many different fluctuation scales perpendicular to the mean field.
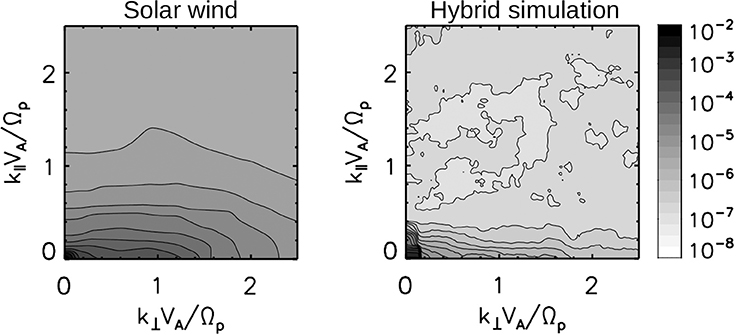
Figure 3. Magnetic energy distribution as a function of the parallel and perpendicular wavenumbers derived from the solar wind observation (left) [64] and the hybrid plasma simulation (right) [64]. Ion beta value is close to unity in the both cases. Color bar scales are in units of nT2 on the left and the squared amplitude to the mean magnetic field on the right.
The picture of the perpendicular wavevector geometry is also confirmed by the hybrid plasma simulations [63, 64] for different values of plasma beta observed by the Cluster spacecraft (both low-beta and high-beta plasmas). The energy spectrum (for magnetic field fluctuations) extends in the perpendicular direction to the mean magnetic field and does not develop in the parallel direction. The type of the wavevector geometry can be measured by measuring the variance of the spectral extension in the parallel and perpendicular directions, and computing the ratio as follows:
The degree of wavevector anisotropy A changes with the value of plasma parameter beta, that is, the wavevector anisotropy becomes weaker at higher values of ion beta. A possible interpretation is that parallel and oblique propagating waves are generated more in the high-beta plasma. Yet, it is not known if the fluctuations are more compressive in the high-beta plasma. An empirical scaling law is found to characterize the wavevector anisotropy as a function of plasma beta, A ∝ β−0.3 [63].
5. Outlook
Understanding the fundamental processes of plasma turbulence is of particularly importance not only because of its dispersive-dissipative nature in the collisionless state but also because of its versatile applications and implications to astrophysical turbulence problems such as solar corona, star formation, interstellar medium, and galactic cosmic ray.
As a conclusion, we address several challenging questions or tasks that should be resolved using the running or upcoming space plasma observation programs such as MMS [65], Solar Orbiter [66], Solar Probe Plus [67], and THOR concept [68].
1. Control parameters: Wave modes and wave-particle interactions depend on the values of plasma parameter beta. In a high-beta plasma, the thermal spread of the distribution function is larger and there are increasingly more particles that can resonate with waves and absorb the energy from the wave electric field even at higher frequencies. On the other hand, nonlinearities (of waves and plasma motions) depend on the fluctuation amplitudes. It is an important task to systematically understand how the plasma develops into turbulence at different values of beta and amplitude.
2. Sideband waves: While both spacecraft measurements and numerical simulations indicate the existence of sideband waves in turbulent plasmas, the properties of the sideband waves remain unknown such as the lifetime, the fluctuation sense, and the amplitude. Understanding the lifetime of the sideband waves is important on constructing a phenomenological model. In fluid turbulence, in contrast, eddy damping or eddy turnover time is considered as the typical time scale, and is an essential ingredient in Kolmogorov's phenomenology.
3. Electron-scale kinetics: Waves in the plasma become even more diverse on electron-kinetic scales: whistler mode; electron cyclotron mode; lower hybrid mode; electron Bernstein modes, and upper hybrid mode. For example, the lower hybrid mode serves as an effective channel of dissipation, since this mode can heat electrons through cyclotron resonance and ions through perpendicular Landau resonance. In addition, small-scale magnetic reconnection may occur spontaneously when a thin current sheet is formed and the electron motion becomes non-gyrotropic.
4. Coherent structures: Kinetic turbulent fluctuations in the plasma do not all have to be propagating waves. Coherent structures such as vortices, current sheets, density enhancements or cavities, discontinuities, and flux tubes may also appear in turbulence originating either in the fluid-like behavior of electrons or in wave-wave resonance. Coherent structures do not propagate intrinsically, and can be regarded as a zero-frequency mode. A new method should be developed to distinguish between propagating waves and coherent structures in the spacecraft data, and if such a task is done, our picture of plasma turbulence will significantly be improved if turbulence is more wave-like or structure-like, or under what conditions waves or structures appear.
5. Field decompositions: Magnetic field fluctuations can be decomposed into different bases. Decomposition into right-hand and left-hand field rotation senses is one possibility, and comes from the notion that the magnetic helicity is an invariant in ideal MHD. In practice, the method of Stokes parameter analysis using the Hilbert transform can be implemented to the fluctuation data [69]. Decomposition into compressible and incompressible fluctuations is another possibility. If the dispersion relation analysis is applied to these fluctuation components (field rotation sense, compressible or incompressible sense), the knowledge on the wave modes will be improved.
6. Wave-particle interactions: The kinetic picture of plasma differs from the fluid treatment of plasma in that the velocity distribution function serves as as an internal degree of freedom. For example, an unstable velocity distribution can drive waves by a micro-instability, while waves can decay and the distribution function becomes deformed when the wave damping, e.g., Landau or cyclotron resonance, is effective. Understanding non-Maxwellian features in association with the turbulent fluctuations is an important task using hybrid simulations [56] or Vlasov simulations [70, 71].
Author Contributions
YN on drafting and coordination of the work. UM on improving the quality of the manuscript.
Funding
The work conducted in Braunschweig is financially supported by Collaborative Research Center 963, Astrophysical Flow, Instabilities, and Turbulence - AstroFIT, and MO 539/20-1, DECODE: Detection of wave coupling cascade in space plasmas of the German Science Foundation. The work conducted in Graz is financially supported by Austrian Space Applications Programme at Austrian Research Promotion Agency, FFG ASAP-12 SOPHIE, Solar Orbiter wave observation program in the heliosphere under contract 853994.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors acknowledge and thank the following colleagues for discussion: H. Comişel for the hybrid simulation results, C. Perschke and K.-H. Glassmeier for the Cluster data analysis results, Y. Nariyuki about the turbulence control parameters, and E. Marsch, B. T. Tsurutani, and S. P. Gary about the kinetic processes.
References
1. Marsch E. Kinetic physics of the solar corona and solar wind. Living Rev Solar Phys. (2006) 3:1. doi: 10.12942/lrsp-2006-1
2. Petrosyan A, Balogh A, Goldstein ML, Léorat, J, Marsch E, Petrovay K, et al. Turbulence in the solar atmosphere and solar wind. Space Sci Rev. (2010) 156:135–238. doi: 10.1007/s11214-010-9694-3
3. Bruno R, and Carbone V. The solar wind as a turbulence laboratory. Living Rev Solar Phys. (2013) 10:2. doi: 10.12942/lrsp-2013-2
4. Escoubet CP, Fehringer M, Goldstein M. The cluster mission. Ann Geophys. (2001) 19:1197–200. doi: 10.12942/lrsp-2013-2
5. Müller J, Simon S, Motschmann U, Schüle J, Glassmeier KH, Pringle GJ. Adaptive hybrid model for space plasma simulations. Comp Phys Comm. (2011) 182:946–66. doi: 10.1016/j.cpc.2010.12.033
7. Gary SP. Theory of Space Plasma Microinstabilities. Cambrige Atmospheric and Space Science Series. Cambridge: Cambridge University Press (1993).
8. Nomura R, Shiokawa K, Sakaguchi K, Otsuka Y, Connors M. Polarization of Pc1/EMIC waves and related proton auroras observed at subauroral latitudes. J Geophys Res Space Phys. (2012) 117:A02318. doi: 10.1029/2011JA017241
9. Marsch E, Tu CY. Evidence for pitch angle diffusion of solar wind protons in resonance with cyclotron waves. J Geophys Res. (2001) 106:8357–61. doi: 10.1029/2000JA000414
10. Maneva YG, Viñas AF, Ofman L. Turbulent heating and acceleration of He++ ions by spectra of Alfvén-cyclotron waves in the expanding solar wind: 1.5-D hybrid simulations. J Geophys Res Space Phys. (2013) 118:2842–53. doi: 10.1002/jgra.50363
11. Maneva YG, Viñas AF, Moya PS, Wicks RT, Poedts S. Dissipation of parallel and oblique Alfvén-cyclotron waves – Implications for heating of alpha particles in the solar wind. Astrophys J. (2015) 814:33. doi: 10.1088/0004-637X/814/1/33
12. Ofman L, Viñas AF, Maneva Y. Two-dimensional hybrid models of H+ – He++ expanding solar wind plasma heating. J Geophys Res Space Phys. (2014) 119:4223–38. doi: 10.1002/2013JA019590
13. Ozak N, Ofman L, Viñas AF. Ion heating in inhomogeneous expanding solar wind plasma: the role of parallel and oblique ion-cyclotron waves. Astrophys J. (2015) 799:77. doi: 10.1088/0004-637X/799/1/77
14. Sahraoui F, Goldstein ML, Belmont G, Canu P, Rezeau L. Three dimensional anisotropic k spectra of turbulence at subproton scales in the solar wind. Phys Rev Lett. (2010) 105:131101. doi: 10.1103/PhysRevLett.105.131101
15. Roberts OW, Li X, Li B. Kinetic plasma turbulence in the fast solar wind measured by Cluster. Astrophys J. (2013) 769:58. doi: 10.1088/0004-637X/769/1/58
16. Bale SD, Kellogg PJ, Mozer FS, Horbury TS, Rème H. Measurement of the electric fluctuation spectrum of magnetohydrodynamic turbulence. Phys Rev Lett. (2005) 94:215002. doi: 10.1103/PhysRevLett.94.215002
17. Salem CS, Howes GG, Sundkvist D, Bale SD, Chaston CC, Chen CHK, et al. Identification of kinetic Alfvén wave turbulence in the solar wind. Astrophys J Lett. (2012) 745:L9. doi: 10.1088/2041-8205/745/1/L9
18. TenBarge JM, Podesta JJ, Klein KG, Howes GG. Interpreting magnetic variance anisotropy measurements in the solar wind. Astrophys J. (2012) 753:107. doi: 10.1088/0004-637X/753/2/107
19. Kiyani KH, Chapman SC, Sahraoui F, Hnat B, Fauvarque O, Khotyaintsev YV. Enhanced magnetic compressibility and isotropic scale invariance at sub-ion Larmor scales in solar wind turbulence. Astrophys J. (2013) 763:10. doi: 10.1088/0004-637X/763/1/10
20. Chen CHK, Boldyrev S, Xia Q, Perez JC. Nature of subproton scale turbulence in the solar wind. Phys Rev Lett. (2013) 110:225002. doi: 10.1103/PhysRevLett.110.225002
21. Cerri SS, Califano F, Jenko F, Told D, Rincon F. Subproton-scale cascades in solar wind turbulence: driven hybrid-kinetic simulations. Astrophys J Lett. (2016) 822:L12. doi: 10.3847/2041-8205/822/1/L12
22. Howes GG, Bale SD, Klein KG, Chen CHK, Salem CS, TenBarge JM. The slow-mode nature of compressible wave power in solar wind turbulence. Astrophys J Lett. (2012) 753:L19. doi: 10.1088/2041-8205/753/1/L19
23. Klein KG, Howes GG, TenBarge JM, Bale SD, Chen CHK, Salem CS. Using synthetic spacecraft data to interpret compressible fluctuations in solar wind turbulence. Astrophys J. (2012) 755:159. doi: 10.1088/0004-637X/755/2/159
24. Yao S, He JS, Tu CY, Wang LH, Marsch E. Small-scale sressure-balanced structures driven by oblique slow mode waves measured in the solar wind. (2013) Astrophys J. 774:59. doi: 10.1088/0004-637X/774/1/59
25. Zhao JS, Voitenko Y, Yu MY, Lu JY, Wu DJ. Properties of short-wavelength oblique Alfvén and slow waves. Astrophys J. (2014) 793:107. doi: 10.1088/0004-637X/793/2/107
26. Gary SP. Low-frequency waves in a high-beta collisionless plasma: polarization, compressibility and helicity. J Plasma Phys. (1986) 35:431–47. doi: 10.1017/S0022377800011442
27. Katoh Y. A simulation study of the propagation of whistler-mode chorus in the Earth's inner magnetosphere. Earth Planets Space (2014) 66:6. doi: 10.1186/1880-5981-66-6
28. Tsurutani BT, Smith EJ. Magnetosonic waves adjacent to the plasma sheet in the distant magnetotail: ISEE-3. Geophys Res Lett. (1984) 11:331–4. doi: 10.1029/GL011i004p00331
29. Tsurutani BT, Richardson IG, Thorne RM, Butler W, Smith EJ, Cowley SWH, et al. Observations of the right-hand resonant ion beam instability in the distant plasma sheet boundary layer. J Geophys Res. (1985) 90:12159–72. doi: 10.1029/JA090iA12p12159
30. Baumjohann W, Treumann RA, Georgescu E, Haerendel G, Fornaçon KH, Auster HU. Waveform and packet structure of lion roars. Ann Geophys. (1999) 17:1528–34. doi: 10.1007/s00585-999-1528-9
31. Baumjohann W, Georgescu E, Fornaçon KH, Auster HU, Treumann RA, Haerendel G. Magnetospheric lion roars. Ann Geophys. (2000) 18:406–10. doi: 10.1007/s00585-000-0406-2
32. Vaivads A, Santolik O, Stenberg G, André M, Owen CJ, Canu P, et al. Source of whistler emissions at the daysidemagnetopause. Geophys Res Lett. (2007) 34:L09106. doi: 10.1029/2006GL029195
33. Eastwood JP, Phan TD, Bale SD, Tjulin A. Observations of turbulence generated by magnetic reconnection. Phys Rev Lett. (2009) 102:035001. doi: 10.1103/PhysRevLett.102.035001
34. Narita Y, Gary SP, Saito S, Glassmeier KH, Motschmann U. Dispersion relation analysis of solar wind turbulence. Geophys Res Lett. (2011) 38:L05101. doi: 10.1029/2010GL046588
35. Narita Y, Nakamura R, Baumjohann W, Glassmeier KH, Motschmann U, Giles B, et al. On electron-scale whistler turbulence in the solar wind. Astrophys J Lett. (2016) 827:L8. doi: 10.3847/2041-8205/827/1/L8
36. Stansby D, Horbury TS, Chen CHK, Matteini L. Experimental determination of whistler wave dispersion relation in the solar wind. Astrophys J Lett. (2016) 829:L16. doi: 10.3847/2041-8205/829/1/L16
37. Jenkins TG, Austin TV, Smithe DN, Loverich J, Hakim AH. Time-domain simulation of nonlinear radiofrequency phenomena. Phys Plasmas (2013) 20:012116. doi: 10.1063/1.4776704
38. Cardinali A, Castaldo C, Cesario R, De, Marco F, Paoletti F. Analysis of the heating scenarios of the ion Bernstein wave (IBW) experiment in Frascati Tokamak Upgrade. Nucl Fusion (2002) 42:427–40. doi: 10.1088/0029-5515/42/4/307
39. Intrator T, Myra JR, D'Ippolit DA. Three-dimensional finite-element model of the ion Bernstein wave antenna and excitation of coa xial electrostatic edge modes in the tokamak fusion test reactor. Nucl Fusion (2003) 43:531–8. doi: 10.1088/0029-5515/43/7/304
40. Toida M, Suzuki T, Ohsawa Y. Collective behavior of ion Bernstein waves in a multi-ion-species plasma. Phys Plasmas (2004) 11:3028–34. doi: 10.1063/1.1712977
41. Korsholm SB, Stejner M, Bindslev H, Furtula V, Leipold F, Meo F, et al. Measurements of intrinsic ion Bernstein waves in a Tokamak by collective Thomson scattering. Phys Rev Lett. (2011) 106:165004. doi: 10.1103/PhysRevLett.106.165004
42. Zhang XJ, Zhao YP, Wan BN, Gong XZ, Lin Y, Zhang WY. Experimental observation of ion heating by mode-converted ion Bernstein waves in tokamak plasmas. Nucl Fusion (2012) 52:082003. doi: 10.1088/0029-5515/52/8/082003
43. Perschke C, Narita Y, Gary SP, Motschmann U, Glassmeier KH. Dispersion relation analysis of turulent magnetic field fluctuations in fast solar wind. Ann Geophys. (2013) 31:1949–55. doi: 10.5194/angeo-31-1949-2013
44. Perschke C, Narita MU, Glassmeier KH. Multi-spacecraft observations linear modes and sideband waves in ion-scale solar wind turbulence. Astrophys J. (2014) 793:L25. doi: 10.1088/2041-8205/793/2/L25
45. Roberts OW, Li X, Jeska L. Evidence of the ion cyclotron resonance at proton kinetic scales in the solar wind. Astrophys J. (2015a) 802:1. doi: 10.1088/0004-637X/802/1/1
46. Roberts OW, Li X, Jeska L. A statistical study of the solar wind turbulence at ion kinetic scales using the k-filtering technique and Cluster data. Astrophys J. (2015b) 802:2. doi: 10.1088/0004-637X/802/1/2
47. Perschke C, Narita Y, Motschmann U, Glassmeier KH. Observational test for a random sweeping model in solar wind turbulence. Phys Rev Lett. (2016) 116:125101. doi: 10.1103/PhysRevLett.116.125101
48. Comişel H, Verscharen D, Narita Y, Motschmann U. Spectral evolution of two-dimensional kinetic plasma turbulence in the wavenumber-frequency domain. Phys Plasmas (2013) 20:090701. doi: 10.1063/1.4820936
49. Comişel H, Constantinescu V, Narita Y. Origin of the filament structure in space plasmas. Geosci Lett. (2014) 1:12. doi: 10.1186/s40562-014-0012-x
50. Comişel H, Narita Y, Motschmann U. Dispersion relation as a channel of plasma turbulence evolution. Earth Planet Space (2015) 67:32. doi: 10.1186/s40623-015-0191-5
52. Howes GG, Drake DJ, Nielson KD, Carter TA, Kletzing CA, Skiff F. Toward astrophysical turbulence in the laboratory. Phys Rev Lett. (2012) 109:255001. doi: 10.1103/PhysRevLett.109.255001
53. Gary SP. Test for wavevector anisotropy in plasma turbulence cascades. Astrophys J. (2013) 769:36. doi: 10.1088/0004-637X/769/1/36
54. Matthaeus WH, Gosh S, Ougton S, Roberts DA. Anisotropic three-dimensional MHD turbulence. J Geophys Res. (1996) 101:7619–30. doi: 10.1029/95JA03830
55. Valentini F, Califano F, Veltri P. Two-dimensional kinetic turbulence in the solar wind. Phys Rev Lett. (2010) 104:205002. doi: 10.1103/PhysRevLett.104.205002
56. Verscharen D, Marsch E, Motschmann U, Müller J. Kinetic cascade beyond magnetohydrodynamics of solar wind turbulence in two-dimensional hybrid simulations. Phys Plasmas (2012) 19:022305. doi: 10.1063/1.3682960
57. Howes GG, Tenbarge JM, Dorland W, Quataert E, Schekochihin AA, Numata R, et al. Gyrokinetic simulations of solar wind turbulence from ion to electron scales. Phys Rev Lett. (2011) 107:035004. doi: 10.1103/PhysRevLett.107.035004
58. Saito S, Gary SP, Li H, Narita Y. Whistler turbulence: particle-in-cell simulations. Phys Plasmas (2008) 15:102305. doi: 10.1063/1.2997339
59. Gary SP, Chang O, Wang J. Forward cascade of whistler turbulence: three-dimensional particle-in-cell simulations. Astrophys J. (2012) 755:142. doi: 10.1088/0004-637X/755/2/142
60. Chang O, Gary SP, Wang J. Whistler turbulence at variable electron beta: three-dimensional particle-in-cell simulations. J Geophys Res Space Phys. (2013) 118:2824–33. doi: 10.1002/jgra.50365
61. Chen CHK, Mallet A, Schekochihin AA, Horbury TS, Wicks RT, Bale SD. Three-dimensional structure of solar wind turbulence. Astrophys J. (2012) 758:120. doi: 10.1088/0004-637X/758/2/120
62. Dasso S, Milano LJ, Matthaeus WH, Smith CW. Anisotropy in fast and slow solar wind fluctuations. Astrophys J. (2005) 635:L181–4. doi: 10.1086/499559
63. Comişel H, Narita Y, Motschmann U. Wavevector anisotropy of plasma turbulence at ion kinetic scales: solar wind observations and hybrid simulations. Nonlin Processes Geophys. (2014) 21:1075–83. doi: 10.5194/npg-21-1075-2014
64. Narita Y, Comişel H, Motschmann U. Spatial structure of ion-scale plasma turbulence. (2014) Front Phys. 2:13. doi: 10.3389/fphy.2014.00013
65. Burch JL, Moore TE, Torbert RB, Giles BL. Magnetospheric Multiscale overview and science objectives. Space Sci Rev. (2016) 199:5–21. doi: 10.1007/s11214-015-0164-9
66. Müller D, Marsden RG, St. Cyr OC, Gilbert HR. Solar Orbiter: exploring the Sun-heliosphere connection. Solar Phys. (2013) 285:25–70. doi: 10.1007/s11207-012-0085-7
67. Fox NJ, Velli MC, Bale SD, Decker R, Driesman A, Howard RA, et al. The Solar Probe Plus mission: humanity's first visit to our star. (2016) Space Sci Rev. 204:7–48. doi: 10.1007/s11214-015-0211-6
68. Vaivads A, Retinò A, Soucek J, Khotyaintsev YV, Valentini F, Escoubet CP, et al. Turbulence Heating ObserveR - satellite mission proposal. J Plasma Phys. (2016) 82:905820501. doi: 10.1017/S0022377816000775
69. Comişel H, Nariyuki Y, Narita Y, Motschmann U. On the role of ion-scale whistler waves in space and astrophysical plasma turbulence. Ann Geophys. (2016) 34:975–84. doi: 10.5194/angeo-34-975-2016
70. Perrone D, Valentini F, Servidio S, Dalena S, Veltri P. Vlasov simulations of multi-ion plasma turbulence in the solar wind. Astrophys J. (2013) 762:99. doi: 10.1088/0004-637X/762/2/99
Keywords: solar wind turbulence, ion-kinetic scale, sideband waves, filaments
Citation: Narita Y and Motschmann U (2017) Ion-Scale Sideband Waves and Filament Formation: Alfvénic Impact on Heliospheric Plasma Turbulence. Front. Phys. 5:8. doi: 10.3389/fphy.2017.00008
Received: 11 December 2016; Accepted: 08 February 2017;
Published: 23 February 2017.
Edited by:
Hermann Lühr, Deutsches Geoforschungszentrum GFZ, GermanyReviewed by:
Xochitl Blanco-Cano, National Autonomous University of Mexico, MexicoLeon Ofman, The Catholic University of America, USA
Copyright © 2017 Narita and Motschmann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yasuhito Narita, eWFzdWhpdG8ubmFyaXRhQG9lYXcuYWMuYXQ=
 Yasuhito Narita
Yasuhito Narita Uwe Motschmann3,4
Uwe Motschmann3,4