Edge-Corrected Mean-Field Hubbard Model: Principle and Applications in 2D Materials

This work reviews the current progress of tight-binding methods and the recent edge-modified mean-field Hubbard model. Undercoordinated atoms (atoms not fully coordinated) exist at a high rate in nanomaterials with their impact overlooked. A quantum theory was proposed to calculate electronic structure of nanomaterials by incorporating bond order-length-strength (BOLS) correlation to mean-field Hubbard model, i.e., BOLS-HM. Consistency between the BOLS-HM calculation and density functional theory (DFT) calculation on 2D materials verified that (i) bond contractions and potential well depression occur at the edge of graphene, phosphorene, and antimonene nanoribbons; (ii) the physical origin of the band gap opening of graphene, phosphorene, and antimonene nanoribbons lays in the enhancement of edge potentials and hopping integrals due to the shorter and stronger bonds between undercoordinated atoms; (iii) the band gap of 2D material nanoribbons expand as the width decreases due to the increasing under-coordination effects of edges which modulates the conductive behaviors; and (iv) non-bond electrons at the edges and atomic vacancies of 2D material accompanied with the broken bond contribute to the Dirac-Fermi polaron (DFP) with a local magnetic moment.

Introduction

2D Materials demonstrate extraordinary properties compared with bulk material and attract overwhelming attentions. For example, band gap (E_G) occurs of graphene nanoribbons(GNRs) while bulk graphite is a good conductor; E_G expands monotonically with the inverse of ribbon width of GNR [1] and, bare or Hydrogen ended [2]; unexpected magnetism [3–6] and quantum hall effect [7, 8] were detected at the edge and defect sites of GNRs while bulk graphite is diamagnetism; few-layered phosphorene [9, 10] shows high carrier motilities of 1,000 cm²V⁻¹s⁻¹, and a high current on/off ratio of up to 10⁵ at room temperature; Antimony(Sb), non-hygroscopic, gray metal with a layered structure similar to that of BP [11]. Antimonene is stable at high temperature as high as 1,000 K [12] and becomes semiconducting when it is a one atomic layer [13].

Once the size of nanomaterials decreases, the ratio of under-coordinated atoms located at surface, edges, and defects increase compared to the total atomic number. Under-coordination effects induce tunability to the properties of nanomaterials, in contrast with the constant properties in bulky species. For example, the quantities such as the Young's modulus, melting point, dielectric constant, and the extensibility of a solid can change with the solid size [14–16]. The binding energy of core electronic levels also generally shift to energies that are lower (larger in absolute value) than those of the bulk as size decreases or when the atom locates around under-coordinated sites such as surface, edge, and nano-islands [17].

The involvement of the broken bonds and the non-bonding states make the materials at the nanoscale much complicated and hardly to be understood. Some experimental and theoretical studies have been conducted on size dependent properties of noble metal nanostructures, electronic structure of metal nanoparticles and GNRs, and the water anomalies in literature. However, fundamental progress in theory is still lagging far behind the experimental and theoretical exploitations. Recently, bond order-length-strength (BOLS) correlation derived non-bonding electron polarization theory [16, 18, 19] were proposed to address those problems and obtained great success [20, 21]. Under the light shed by BOLS theory, we will explore the mysteries brought by broken bond and non-bond of nanomaterial.

Multi-scale computational modeling of materials is becoming a reliable tool to underpin scientific investigations and to complement traditional theoretical and experimental approaches [22–24]. At the atomic scale, the ab initio approaches were developed to model the material purely based on Quantum mechanics law without fitting from experimental data, such as Hartree-Forck theory and density functional theory (DFT) [25, 26]. At the large scale above ~1,000 atoms, the classical force field of MD is fit for simulations. Tight-binding (TB) approach, although developed earlier than DFT [27], is developing fast in recent decades and widely used in the investigation of system of 100–1,000 atoms as reviewed in articles [28–30]. However, under-coordinated modifications at edge, defect and surface sites to conventional TB method are usually neglected in low-dimensional systems or investigated case by case [31, 32].

Edge modification can be presented in the edge Hamiltonian matrix element as a function of distance between edge atoms by fitting distance-dependent TB parameters [33]. Edge effects were also modeled for a specific system, like graphene, from the geometrical perturbation [34], curvature-strain [35, 36], and enhancement of hopping integral at edge [37] and so on.

By extending the BOLS mechanics, a quantum theory of BOLS-corrected Hubbard model (BOLS-HM) was proposed with applications for 2D materials graphene, phosphorene, and antimonene nanoribbons of electronic, lattice vibronic, catalytic, and magnetic properties of the material under consideration.

In this themed report, we firstly reviewed the current progresses of TB calculations (conventional TB, density functional TB, spin-polarized Hubbard model, and edge states), and proposed our BOLS-HM model. Then, the applications of BOLS-HM model on the electronic structure and magnetism of GNRs, E_G expansion of phosphorene, and electronic properties of antimonene were reviewed and discussed. Finally, we summarized the themed report.

Principle

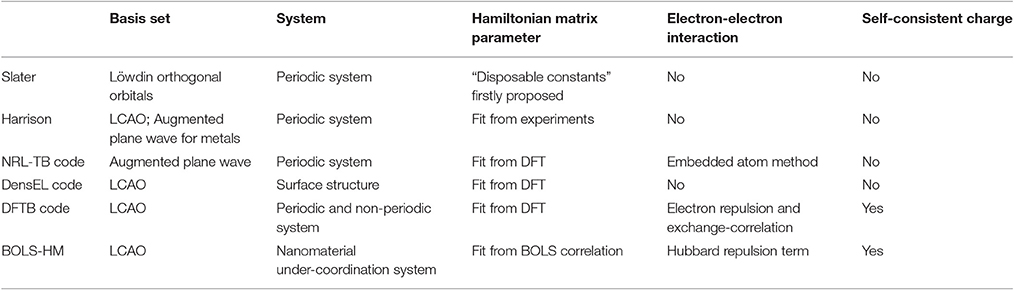
The starting point for any discussion of the tight-binding method for electronic and atomic structure calculations must be Slater and Koster [27]. TB method is developing fast in recent decades and widely used in the investigation of large system as reviewed in articles [28–30] and books [38, 39]. TB method is a parameterized and semi-empirical calculation method which can deal with much larger system with typically two to three orders of magnitude faster than ab initio methods do [29]. TB parameters and codes have been developed by various groups, such as Harrison [40], Papaconstantopoulos with NRL-TB code [28], Bowler with DensEL code [41], and Seifert with DFTB code [30, 42].

Table 1 summarized the TB methods of Slater and Koster [27], Harrison [40], Papaconstantopoulos with NRL-TB code [28], Bowler with DensEL code [41], and Seifert with DFTB code [30, 42]. The comparison is considered from basis set, applicable system, parameterization of Hamiltonian matrix, electron-electron interaction, and self-consistent charges. It can be seen from the table that in early years (before 1990's) TB parameters were mainly fit from experiments but now are mainly from DFT results. There still lacks a TB method designed to nanomaterial and under-coordination system.

TABLE 1

Table 1. Comparison of current TB methods with BOLS-HM.

The main advantage of BOLS-HM is that it is designed for nanomaterial and under-coordination systems, since BOLS correlation theory focuses on the bond length, energy, elastic, electronic, optic, dielectric, and other properties of under-coordination system. Besides, BOLS-HM not only improves the Hamiltonian matrix element, it can also predict the physical and chemical properties of nanostructures such as the splitting between the bonding and anti-bonding band of GNR and of valence d band of noble metals, induced by the enhancement of Hamiltonian integrals and by the localized electron-electron repulsions.

Conventional TB

TB is firstly based on two assumptions: Born-Oppenheimer approximation [38, 39] and Single electron approximation [27]. Without considering electron-electron interaction, the simplest TB Hamiltonian of one electron in a unit cell is written as:

$H_0^{\text{TB}}(r)=-\frac{{\hslash }^2}{2m}{\nabla }^2+V(r)=H_{atom}(r-R_i)+V_{\text{cry}}(r) (1)$

where the first term is the kinetic energy T of electron and V(r) is the periodic potential from ion-cores, which can be divided into atomic potential V_atom(r) and crystal potential V_cry(r).

As Slater and Koster stated in the paper [27]:

“In fact, if we were going to use n atomic orbitals per unit cell, we could make any n linear combinations of the original orbitals, form Bloch sums of these modified orbitals, and solve a secular problem using the modified Bloch sums, and in every case come out with the same answer in the end. The advantage in one choice of atomic orbitals over another is convenience in calculating the matrix components or solving the secular equation…”

Thus, choosing a proper basis set, although cannot change the final answer, can indeed make the calculation much simpler and of more efficiency. Bloch [43] provided the formal mechanism for dealing with periodic systems, such as crystals, by means of the Bloch sum in form of LCAO.

Solution of energy states of Equation (1) is transferred to an eigenvalue problem of: ${\text{H}}_0^{\text{TB}}{\text{c}}_{\text{k}}={\epsilon }_{\text{k}}\text{S}{\text{c}}_{\text{k}}$, with overlap integral matrix $S_{ivjv\prime }=\int {\varphi }_{iv}^{*}·{\varphi }_{jv\prime }\mathbf{\text{d}}r$ and Hamiltonian matrix element:

$H_{ijvv\prime }^{\text{TB}}=\{\begin{array}{ll}{\Delta }_{iv}\hfill & \text{if}i=j,v=v\prime \hfill \\ t_{ijvv\prime }\hfill & \text{if}i\text{and}j\text{are neighbors}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array} (2)$

where, t_ijvv′ is the off-diagonal element between v^th orbital at i^th atom and v^′th orbital at the equivalent nearest j^th atoms. However, the atomic orbitals, ϕ_v,i(r − R_i), are not ideal for the purposes of analysis, as the orbitals on different atomic sites are not orthogonal to one another.

Löwdin [44] provided a scheme for creating an orthogonal basis set, Löwdin functions, which are defined as

$u_{v,i}={\displaystyle \sum _{j,v\prime }{S}_{ivjv\prime }^{-1/2}{\varphi }_{jv\prime }} (3)$

where S is the overlap matrix.

While Bloch functions are periodic and non-localized, Wannier functions [45] construct orthogonal “atomic” wave functions which can take non-periodic terms into account. Wannier function can be expressed as Wannier [45]:

$a_{v,i}(r-R_i)=N^{-1/2}{\displaystyle \sum _k\exp (-\text{i}k{R}_i){\psi }_{v,k}(r)} (4)$

where ψ_v,k(r) is the Bloch sum.

Unlike other basis set which are expanded in k-space, Wannier function is a real-space basis set and can be a powerful tool in the study of the electronic and dielectric properties of materials [45].

Besides the above, many other excellent basis sets have also been proposed and widely applied in the electronic structure modeling of materials, such as linear muffin-tin orbital (LMTO) proposed by Slater [46] and used in LMTO-TB calculation [47, 48] and Gaussian-type orbital (GTO) proposed by Boys [49]. To choose a proper basis set for a system is an important part in saving time and improving the efficiency and accuracy in the electronic structure calculations.

Density-Functional TB Method

As discussed, the single-electron Hamiltonian $H_0^{\text{TB}}$ only considers the potential energy from ion cores in crystal and neglects the interaction among electrons.

The total energy of a system of M electrons in the field of N nuclei at positions R_i may be written within DFT as a functional of a charge density n(r) [50]:

$\begin{array}{l}E={\displaystyle \sum _v<{\Psi }_v(r)}|-\frac{{\hslash }^2}{2m}{\nabla }^2+V(r)+\frac{1}{2}{\displaystyle \int \frac{n(r\prime )}{\left|r-r\prime \right|}}dr\prime |{\Psi }_v(r)>\\ +E_{\text{XC}}[n(r)]+\frac{1}{2}{\displaystyle \sum _{i,j}^N\frac{Z_i{Z}_j}{|R_i-R_j|}} (5)\end{array}$

where the first sum includes kinetic energy T and potential energy V(r) from crystal ion-cores and potential energy from other electrons V_e, the second term is the exchange-correlation (XC) contribution, and the last term covers the ion-ion core repulsion, E_rep.

For 0^th order density-functional tight-binding (DFTB), charge-density n(r) which should be solved by self-consistent field (SCF) method in DFT is now approximated by the input charge-density n₀(r). And the total energy $E_0^{\text{DFTB}}$ becomes,

$\begin{array}{l}{E}_0^{\text{DFTB}}={\displaystyle \sum _v<{\Psi }_v(r)}|-\frac{{\hslash }^2}{2m}{\nabla }^2+V(r)+\frac{1}{2}{\displaystyle \int \frac{n_0(r\prime )}{\left|r-r\prime \right|}}dr\prime \\ +V_{\text{XC}}[n_0]|{\Psi }_v(r)>+\frac{1}{2}{\displaystyle \sum _{i,j}^N\frac{Z_i{Z}_j}{|R_i-R_j|}}\\ ={\displaystyle \sum _v<{\Psi }_v(r)}\left|H_0^{\text{KS}}\right|{\Psi }_v(r)>+E_{\text{rep}} (6)\end{array}$

This non-self-consistent-charge (non-SCC) DFTB approach has been successfully applied to various problems in different systems and materials [33]. Moreover, second-order SCC-DFTB [50] has also been included n(r) = n₀(r) + δn(r) in the corresponding Hamiltonian terms in Equation (6), and also been widely used and accepted [51]. However, DFTB [50] is purely parameterized by DFT results without considering experimental results and complicated to be realized.

Spin-Polarized Hubbard Model

In incompletely filled electron shells with narrow energy bands, the correlations between electrons are too strong to be neglected as done in conventional TB. The Coulomb repulsion between electrons at the same atomic site will change the band structure significantly. The Hubbard model, named after Hubbard [52], includes the onsite repulsion which stems from the Coulomb repulsion between electrons at each atomic site in Hamiltonian. Using the real-space Wannier functions a_v,i(r − R_i) as basis set, Hamiltonian is expressed in second quantization form as [52]:

$\begin{array}{l}H={\displaystyle \sum _{i,\sigma }{\Delta }_i}{c}_{i,\sigma }^{+}{c}_{i,\sigma }+{\displaystyle \sum _{<i,j>,\sigma }{t}_{ij}(c_{i,\sigma }^{+}{c}_{j,\sigma }+c_{j,\sigma }^{+}{c}_{i,\sigma })}\\ +{\displaystyle \sum _{ijkl,\sigma }<ij|1/r|kl>}{c}_{i,\sigma }^{+}{c}_{j,-\sigma }{c}_{k,\sigma }^{+}{c}_{l,-\sigma }\\ \text{With}<ij|1/r|kl>\\ =e^2{\displaystyle \int \frac{a_{\sigma }{(r-R_i)}^{*}{a}_{-\sigma }(r-R_j)a_{\sigma }{(r\prime -R_k)}^{*}{a}_{-\sigma }(r\prime -R_l)}{r-r\prime }}\\ drdr\prime & (7)\end{array}$

where spin sign σ = ±1/2 and $c_{i,\sigma }^{+}\text{and}{c}_{i,\sigma }$ are the creation and annihilation operator in Wannier representation, indicating to create and to annihilate an electron at the lattice vector R_i. The first and second terms are the same as the $H_0^{\text{TB}}$. The last term is the inter-electron potential energy, which is usually a multi-center integral. Hubbard [52] indicated that the single center integral U =< ii, σ|1/r|ii,−σ > is about 10 eV, much greater than other two-center, three-center integrals. Thus, the simplified Hamiltonian becomes:

$H={\displaystyle \sum _{i,\sigma }{\Delta }_i}{c}_{i,\sigma }^{+}{c}_{i,\sigma }+{\displaystyle \sum _{<i,j>,\sigma }{t}_{ij}(c_{i,\sigma }^{+}{c}_{j,\sigma }+c_{j,\sigma }^{+}{c}_{i,\sigma })}+{\displaystyle \sum _{i,\sigma }U}{n}_{i,\sigma }{n}_{i,-\sigma } (8)$

where $n_{i,\sigma }=c_{i,\sigma }^{+}{c}_{i,\sigma }$ represents the particle-number operator at site R_i and spin σ. Equation (8) is called Hubbard model with last term Un_i↑n_i↓.

Hubbard model plays a significant role in the conductor-insulator transition of metal and magnetism of narrow band [53]. For example, Hubbard-Mott insulators [54] are a class of materials that should conduct electricity under conventional band theories, but are insulators when measured (particularly at low temperatures). This effect is due to electron-electron interactions in narrow bands which are not considered in conventional band theory. The Coulomb repulsions of semi-localized electrons in narrow bands are strong enough to split the band into two subbands and generate the Mott band gap [55]. This situation is very similar to nanomaterials with limited quantity of electrons and semi-localized electrons at edge and surfaces.

Shockley and Tamm Edge States

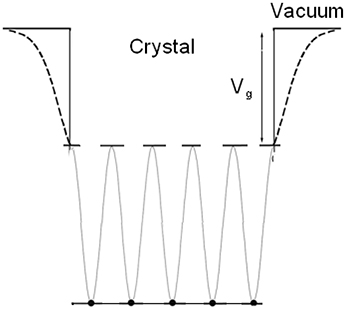
At the surface, the termination of a crystal obviously causes deviation from perfect periodicity. Surface states that are calculated in the framework of near-free electron approximation are called Shockley states [56] and those from a tight-binding model are called Tamm states [57]. However, there is no real physical distinction between the two terms, only the mathematical approach in describing surface states is different.

A simplified model of the crystal potential in one dimension is used: the periodic crystal potential jumps abruptly to the vacuum level V_g at surface, as shown in Figure 1.

FIGURE 1

Figure 1. Simplified one-dimensional potential model.

The one-dimensional surface wave function at E state can be expressed as:

$\Psi (x)=A\exp \left[-\sqrt{2m(V_g-E)}\frac{x}{\hslash }\right] (9)$

The Shockley states and the Tamm states are suitable to describe periodical systems. However, the simplification of the stepped potential prevents the method applied in nanomaterials or imperfect surface where the change of multi-well potential at surface should be considered.

BOLS-Corrected Hubbard Model

The BOLS is an extension of the “atomic coordination number (CN)—atomic size” correlation mechanism of Goldschmidt, Pauling, and Feibelman to energy domain. The shorter and stronger bonds between undercoordinated atoms provide significant modification to atomic cohesive energy (E_c) and associated properties when the fraction of the undercoordinated atoms is increased. The consequence of the broken bond follows the BOLS correlation [14, 16]:

$\{\begin{array}{ll}{c}_z\hfill & =d_i/d_B=2/\left\{1+\exp \left[\left(12-z\right)/\left(8z\right)\right]\right\}\hfill \\ \hfill & \left(\text{Bond}\text{Strain}\right)\hfill \\ c_z^{-m}\hfill & =E_i/E_B\left(\text{Bond}\text{Strength}\right)\hfill \\ z_{zB}{c}_z^{-m}\hfill & =E_{ic}/E_{Bc}\left(\text{Atomic}\text{Cohesive}\text{Energy}\right)\hfill \end{array} (10)$

where m is the bond nature indicator; subscript i and B denote the i^th under-coordinated atom and bulk value, respectively. z_zB = z/z_B is the reduce coordination with z_B = 12 being the bulk standard. First equation indicates that: as the CN z decreases, bond length (d_i) becomes shorter compared with bulk value (d_B); the curve of z-d dependence is illustrated in Figure 2A, compared with measurements of Au particles, carbon nanotubes, Pt, Ir, Ti, Zr, and Zn chains [14]. The second equation indicates the single bond energy increases by $c_z^{-m}$ as length decreases. The atomic cohesive energy E_c will change as the sum over all the bonds of the atom.

FIGURE 2

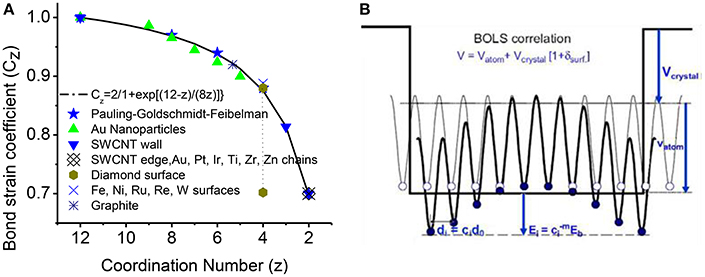
Figure 2. (A) The BOLS correlation mechanism (solid line) formulated from the atomic “CN-radius.” The formulation has been further verified by the measurement (scattered symbols) from Au particles, carbon nanotubes, Pt, Ir, Ti, Zr, and Zn chains [14]. (B) Schematic illustration of the broken-bond induced potential trapping at the terminating edges up to two inter-atomic layers [58, 59]. Reprinted with permission of Sun [14].

Figure 2B illustrates the BOLS correlation and the quantum trapping of potential and energy [14, 16]. Instead of single potential well of Quantum confinement, multi-well quantum trapping happens to nanostructures. At the edge and surface of nanostructures (particle, rod, chain, etc.), the remaining bonds of the under-coordinated atoms to contract spontaneously with an association of bond strength gain up to two inter-atomic layers. The localized strain in turn causes potential well depression with a consequence of localized densification of charge, energy and mass, which is called as Quantum trapping of the charge and energy.

Any detectable quantity localized nearby the broken bonds can be formulated by the above parameters of bond strain (d), bond energy (E), and atomic cohesive energy (E_C) change as shown in Equation (10). The BOLS theory has enabled unification of the unusual performance of detectable quantities Q(z), such as mechanical, thermal, acoustic, chemical, electronic, dielectric, ferroelectric, optic, and magnetic properties and the transport dynamics of electrons, phonons, and photons at the skins of nanostructures of various shapes, as summarized in Sun [14] and listed in Table 2.

TABLE 2

Table 2. Formulation of the measurable quantities on the bonding parameters [14].

Q of a nanostructure can be expressed as a function q(m, z, d, E_B), as sampled in Table 2. Properties of a nanosolid with size (K) depends on shape (τ), and bond nature (m) [16, 60]. BOLS correlation has already been verified of bond identities in the metal nanoparticles, metal surfaces, carbon nanotubes, graphene nanoribbons, etc. [61, 62].

Applying variational principle to the TB Hamiltonian, Hamiltonian matrix element of secular equations becomes:

$H_{ijvv\prime }^{TB}=\{\begin{array}{l}{\displaystyle \sum _j{e}^{\text{i}k·(R_j-R_i)}}{\displaystyle \int {\varphi }_{iv}^{\ast }(r-R_i)}·\hfill \\ (H_{\text{atom}}+V_{\text{cry}})·{\varphi }_{jv\prime }(r-R_j)dr\left(\text{1}-,\text{2}-\text{D}\right)\hfill \\ {\displaystyle \int {\varphi }_{iv}^{\ast }(r-R_i)}·(H_{\text{atom}}+V_{\text{cry}})·\hfill \\ {\varphi }_{jv\prime }(r-R_j)dr\left(\text{0}-\text{D}\right)\hfill \end{array} (11)$

where V_cry is the ion-cores' potential subtracting the i^th atomic potential.

Writing ϕ_iv(r − R_i) as |iv >, as far as the v and v′ orbitals are concerned, the Hamiltonian matrix element $H_{ijv{v}^{\prime }}^{TB}$ becomes:

$\{\begin{array}{ll}{\Delta }_{iv}\hfill & =<iv|H_{\text{atom}}+V_{\text{cry}}|iv>=\hfill \\ \hfill & {\epsilon }_v+\alpha \left(\text{Diagonal Elements}\right)\hfill \\ t_{ijvv\prime }\hfill & =\{\begin{array}{l}{\displaystyle \sum _j{e}^{\text{i}k·(R_j-R_i)}}<iv|V_{\text{cry}}|jv\prime >\hfill \\ =f(r)·{\beta }_{ijvv\prime }\left(\text{Off - diagonal}\right)\hfill \\ <iv|H_{\text{atom}}+V_{\text{cry}}|jv\prime \hfill \\ >={\beta }_{ijvv\prime }\left(\text{0 - D Off - diagonal}\right)\hfill \end{array}\hfill \end{array}$

with,

$\{\begin{array}{l}\alpha =<iv|V_{\text{cry}}|iv>\left(\text{Onsite integral}\right)\hfill \\ {\beta }_{ijvv\prime }=<iv|V_{\text{cry}}|jv\prime >\left(\text{Hopping integral}\right)\hfill \end{array} (12)$

where the diagonal element Δ_i consists of the eigen-energy ε_v = < iv|H_atom|iv > of the v^th level plus the onsite integral α. ${\beta }_{ijv{v}^{\prime }}$ is the hopping exchange integral of the nearest neighbor j^th atom. f (r) is the periodic factor, ${\displaystyle \sum _j}{e}^{\text{i}\text{k}·({\text{R}}_j-{\text{R}}_i)}$. Since the atomic orbitals of a same atom are orthogonal to each other, $<iv\left|H_{\text{atom}}\right|i{v}^{\prime }>=0$; also, due to the localization of atomic Hamiltonian, $<iv\left|H_{\text{atom}}\right|j{v}^{\prime }>=0$.

CN Imperfection Induced Quantum Trapping

According to the BOLS correlation theory, CN imperfection at edges of low-dimensional nanostructures or at surface skin of 0-D nanoparticles causes the remaining bonds of the under-coordinated atoms to contract spontaneously with an association of bond strength gain, which in turn causes potential well depression with a consequence of localized densification of charge, energy, and mass. BOLS considered that the shorter and stronger bonds between undercoordinated atoms provide significant modification to the Hamiltonian matrix elements.

Since BOLS considered the effective CN of three layers from surface or edges, the modification to potential multi-well at three-layer edges is adopted. As illustrated in Figure 2A, the broken-bond induces potential trapping at the terminating edges up to three atomic layers. Compared with the Tamm model approximating original periodic potential jumping to vacuum level, as shown in Figure 2B, BOLS consideration of the quantum entrapment of potential multi-well at “surface skin” better describes the real nanomaterial observed experimentally [58].

Enhancement of Onsite and Hopping Integrals

In the present BOLS-HM, we took the following relations of effective coordination number (z), bond length (d), single bond energy (E), potential (V), and Hamiltonian integrals α an ${\beta }_{ijv{v}^{\prime }}$ into consideration, the modification of under-coordinated site i to the bulk B can be expressed as,

$\{\begin{array}{ll}{C}_z(z_i)=\frac{d_i(z_i)}{d_{iB}}=\frac{2}{1+\text{exp}\left(\frac{12-z_i}{8z_i}\right)}\hfill & \left(\text{Bond Contract}\right)\hfill \\ C_z^{-m}=\frac{E_i(z_i)}{E_{iB}}=\frac{V(z_i)}{V_B}\hfill & \left(\text{Bond Energy; Potential}\right)\hfill \\ \begin{array}{l}\frac{\alpha (z_i)}{{\alpha }_B}=\frac{<{\phi }_i\left(r\right)|V(z_i)|{\phi }_i(r)>}{<{\phi }_i\left(r\right)|V_B|{\phi }_i(r)>}\hfill \end{array}\hfill & \hfill \\ \cong \frac{V(z_i)}{V_B}\cong C_z^{-m}\hfill & \left(\text{Onsite Integral}\right)\hfill \\ \frac{{\beta }_{ij}(z_i)}{{\beta }_{ijB}}=\frac{<{\phi }_i\left(r\right)|V(z_i)|{\phi }_j(r)>}{<{\phi }_i\left(r\right)|V_B|{\phi }_j(r)>}\hfill & \hfill \\ =\frac{E_i(z_i)}{E_{iB}}=C_z^{-m}\hfill & \left(\text{Hopping Integral}\right)\hfill \end{array} (13)$

C_z is the bond contraction coefficient and m is a constant of bond nature indicator. As the effective CN becomes imperfect at the edge, the edge bond will be shortened by C_z and strengthened by $C_z^{-m}$; and the potential well of the neighbor atom will become closer and deepened in energy space proportional to bond energy. BOLS-HM considers the relative ratio of a quantity at under-coordinated atom and in bulk. Since the main contribution of V_cry to the ratio of integral at i^th atomic site is the atomic potential from the neighbor j^th atom V_ij, the α(z_i) and β_ij(z_i) are both considered as $C_z^{-m}$ proportional to the bond energy and potential well depression compared to those of bulk.

Determining the bond nature indicator m is accomplished by the consistency between predictions of BOLS correlation theory and experimental results on the various quantities as shown in Table 2. For example, based on the Young's modulus [63, 64], the melting temperature [65, 66] of carbon nanotube and the energy shift of C1s level of grapheme [67], we obtained the bond nature parameter m = 2.56 of carbon. Figure 3 compares the relation between hopping integrals and the C-C bond length derived by BOLS-HM and obtained by TB fitting from DFT results [33]. It should be noted that DFT treats low dimensional systems with vacuum slabs; while BOLS-HM develops the relations from the consistency between BOLS correlation theory and the experimental results.

FIGURE 3

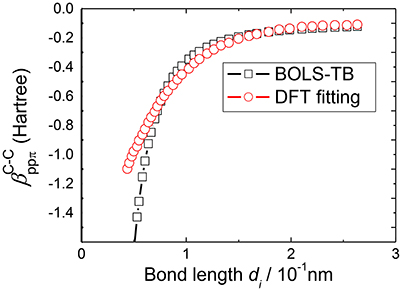
Figure 3. Correlation between the β_ij and the bond length d derived by BOLS–TB compared with previous TB fitting from the DFT results [33].

Onsite Repulsion Effects

Since limited amount of electrons exist in nanomaterial compared with tremendous amount of electrons in bulk, the electron-electron repulsion at each atom, especially at edge sites, will induce considerable changes to electronic structure. As discussed, the Hubbard model [52] includes the onsite repulsion which stems from the Coulomb repulsion between electrons at each atomic site in Hamiltonian by introducing the Hubbard term Un_i↑n_i↓.

BOLS-HM considers the relation of d_i and U_i as:

$\{\begin{array}{ll}{C}_z(z)=d_i(z_i)/d_{iB}\hfill & \left(\text{Bond Contraction}\right)\hfill \\ U_i\propto d_i{(z_i)}^{-3}\hfill & \left(\text{Volume}\right)\hfill \\ U_i(z_i)/U_j(z_j)={[C_z(z_i)/C_z(z_j)]}^{-3}\hfill & \left(\text{Repulsion Energy}\right)\hfill \end{array} (14)$

where i^th atom locates at edge sites and j^th atom at the interior with coordination number of z_j. Hubbard U is the onsite repulsion energy which should contain the information of the relative ratio of the electron density, ${\left[C_z(z_i)/C_z(z_j)\right]}^{-3}$.

Application of BOLS-HM in 2D Materials

Electronic Structure of Graphene Nanoribbons

Challenges

The principle for the EG expansion with width is not clear, apart from the EG disparity between experiments and calculations. Either the carrier confinement [68–70] or the edge energy pinning couldn't be changed by E_G expansion and it also couldn't be observed [37] when calculations for the edge and for the interior were identical which were computed by hopping integrals employed in band structure. At the edge, the hopping integral is extremely greater comparing with the integral in the GNR interior [69]. It's obvious that the E_G is determined intrinsically by the crystal potential and hence the Hamiltonian matrix, but the density and energy of carriers in GNR is of a great importance to the transport dynamics though from our proposition.

Hamiltonian of GNRs

As far as the π and π* orbitals of the C 2p_z electrons are concerned, the Hamiltonian matrix elements are

$\{\begin{array}{l}{\Delta }_i={\epsilon }_{2p_z}+<2p_z|V_{cry}|2p_z>={\epsilon }_{2p_z}+\alpha \hfill \\ \left(\text{Diagonal Elements}\right)\hfill \\ t_{ij}=f_{ij}(x)·<2p_{zi}|V_{cry}|2p_{zj}>=f_{ij}(x)·{\beta }_{ij}\hfill \\ \left(\text{Off}-\text{diagonal}\text{Elements}\right)\hfill \end{array} (15)$

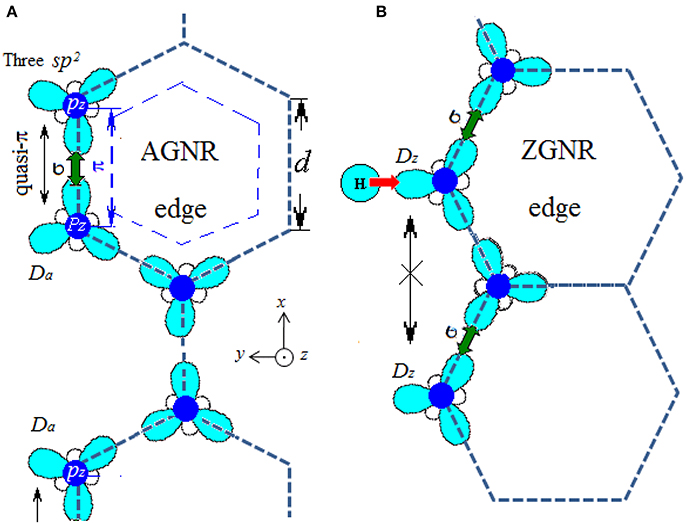
where the onsite energy Δ_i is the sum of the exchange integral and the eigen-energy of the p_z electron, ε_2pz. V is the crystal potential and V_i is the i^th intra-atomic potential; α is the onsite exchange integral of negative value; β_ij is the hopping integral and $f_{ij}(\text{x})={\displaystyle \sum _j}exp\left[\text{i}\text{k}·({\text{X}}_i-{\text{X}}_j)\right]$. Considered structures of armchair-edge GNR (AGNR) and reconstructed zigzag-edge GNR (RecGNR) are shown in Figure 4. Since periodic direction is along x axis, wave vector k is parallel to x.

FIGURE 4

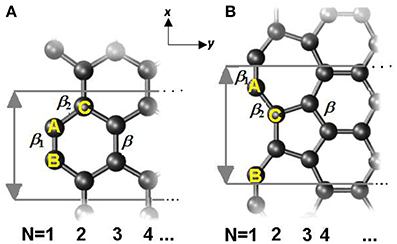
Figure 4. Illustration of structure of (A) AGNR and (B) RecGNR edges. The reconstructed edge consists of 7- and 5-atom rings. Periodic direction is along x axis and ribbon width in y axis. The hopping integrals are indicated as β, β ₁, and β ₂. N indicates the counting of ribbon width; the numbers also mark the atomic position. Reprinted with permission from Zhang et al. [71].

BOLS-HM Parameter for Graphene

The following relations of effective coordination number (z), bond coefficient (C_z), single bond energy (E), potential (V), and hopping integral were be taken into consideration in the present BOLS-HM.

$\{\begin{array}{lll}{\beta }_{ij}(z_i)\hfill & =<{\phi }_i\left(r\right)|V-V_i|{\phi }_j(r)\hfill & \hfill \\ \hfill & >\propto E_i(z_i)\hfill & \left(\text{Overlap}\text{integral}\right)\hfill \\ \frac{{\beta }_1}{\beta }\hfill & =\frac{C_z{(2)}^{-2.56}}{C_z{(3)}^{-2.56}}=1.49\hfill & \left(\text{Bare edge integral}\right)\hfill \\ \frac{{\beta }_2}{\beta }\hfill & =\frac{C_z{(2.5)}^{-2.56}}{C_z{(3)}^{-2.56}}=1.17\hfill & \left(\text{Bare edge-interior integral}\right)\hfill \\ \frac{{\beta }_3}{\beta }\hfill & ={C_{zH}}^{-2.56}=1.11\hfill & \left(\text{H-edge integral}\right)\hfill \end{array} (16)$

Abbreviation of the bond contraction coefficient is C_z. C_zH corresponds to the C-C bond length coefficient terminated with H. Subscripts B corresponds to bulk. From the measured melting point [65, 66] of carbon nanotubes, elastic modulus [63, 64], and the C1s electron binding energy shift [67], we have obtained m = 2.56.

In conducting the edge-modified TB calculations, the β_ij are enlarged by C(z)^−2.56 for under-coordinated atoms, as shown in Figure 4. The β₁ and β₂ (reduced from β_ij, β for the bulk) at the edge are proportional to the bond energy. Therefore, β₁ > β₂ > β = 2.4 eV. The H-end edge bond contraction coefficient, C_H, is defined as the bond length ratio between GNR edge and interior, and taken as 96% according to DFT relaxation results [68]. Hence, the Hamiltonian as an example, of AGNR is

$\begin{array}{c}\hfill H=\begin{array}{c}\hfill \left|\begin{array}{ccccccc}\hfill A\hfill & \hfill B\hfill & \hfill C\hfill & \hfill D\hfill & \hfill E\hfill & \hfill F\hfill & \hfill \hfill \\ \hfill \Delta \prime \hfill & \hfill {\beta }_1{f}_1^{\ast }\hfill & \hfill {\beta }_2{f}_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill \\ \hfill {\beta }_1{f}_1\hfill & \hfill \Delta \prime \hfill & \hfill 0\hfill & \hfill {\beta }_2{f}_2^{*}\hfill & \hfill 0\hfill & \hfill \beta f_1\hfill & \hfill \hfill \\ \hfill {\beta }_2{f}_2^{*}\hfill & \hfill 0\hfill & \hfill \Delta \hfill & \hfill \beta f_1\hfill & \hfill \beta f_2^{*}\hfill & \hfill 0\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill {\beta }_2{f}_2\hfill & \hfill \beta f_1^{*}\hfill & \hfill \Delta \hfill & \hfill 0\hfill & \hfill \beta f_2\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \beta f_2\hfill & \hfill 0\hfill & \hfill \Delta \hfill & \hfill \beta f_1^{*}\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \beta f_2^{*}\hfill & \hfill \beta f_1\hfill & \hfill \Delta \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill \end{array}\right|\hfill \end{array}\hfill \end{array}$

With

$\begin{array}{l}{f}_1={\displaystyle \sum _B\exp (\text{i}k·d_{BA})}=\cos (k/\sqrt{3})+i\sin (k/\sqrt{3})\\ f_2={\displaystyle \sum _C\exp (\text{i}k·d_{AC})}=\cos (k/2\sqrt{3})+i\sin (k/2\sqrt{3})\end{array}$

The first Brillion zone is $k\in (\pi /\sqrt{3})\left[-1,1\right]$. The direction of k is along the x axis. $\sqrt{3}a$ is the lattice constant of the unit cell of AGNR.

Considering Hamiltonian matrix, state vector matrix ${\text{C}}_{\text{k}}=|{\text{c}}_v(\text{k}),{\text{c}}_{v^{\prime }}(\text{k}),\dots >$ at a specific k point applies the equation:

$C_k^{T}H{C}_k=\Sigma (17)$

where Σ is a diagonal matrix with diagonal elements of ${\epsilon }_v\text{,}{\epsilon }_{v^{\prime }},$ etc. C_k is an orthogonal matrix with $<{\text{c}}_v(\text{k})|{\text{c}}_{v^{\prime }}(\text{k})>=0$. Through diagonalizing the Hamiltonian Matrix, by using QR (orthogonal and upper triangular matrix decomposition) iteration [72], Arnoldi Iteration [73], or Jacobi method [74], the eigen-energies and eigen-vectors can be obtained at each k point. High symmetry k-points are usually calculated first such as Γ point at the center of Brillouin zone and M point at center of an edge of simple cubic.

E_G Opening GNRs

In Figure 5, band structures of bare and H-end RecGNR-8 are compared clearly. Both BOLS-HM and DFT calculation results are plot. By the method of BOLS-HM and DFT, a very small E_G (~0.1 eV) is generated near Γ point. E_G indeed is dominated by the quantum entrapment of electrons at edges. The bond which is dangling results in an additional state at the Fermi level. The electron entrapment could pin and polarize the non-bonding electron locally [19]. Dangling bonds generates localized energy state near E_F (blue line), but does not determine E_G [2, 75].

FIGURE 5

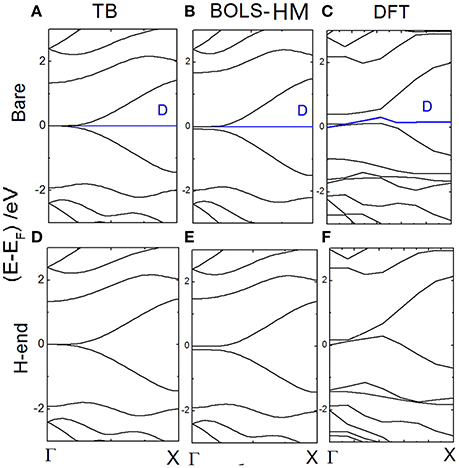
Figure 5. The energy dispersion of bare RecGNR-8 calculated by (A) TB; (B) BOLS-HM; (C) DFT; The energy dispersion of H-end RecGNR-8 calculated by (D) TB; (E) BOLS-HM; and (F) DFT. Reprinted with permission from Zhang et al. [71].

Figure 6 compares size-dependent E_G (N) calculated by conventional TB and by BOLS-HM scheme. AGNR with or without hydrogenation were both considered by BOLS-HM. E_G is always zero when N = 3p+2 (p is a natural number) calculated by TB. E_G opens with or without hydrogenation calculated by BOLS-HM, accord with the E_G observations of DFT calculation [68, 76] and STM results [77]. Hydrogenation does not determine the E_G opening, but the hopping integral enhancement does.

FIGURE 6

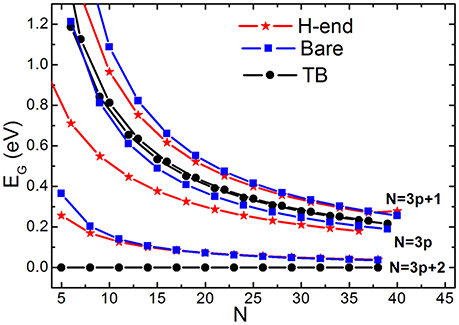
Figure 6. E_G vs. ribbon width (N) of the in bare and H-end AGNRs calculated by TB and BOLS-HM. Reprinted with permission from Zhang et al. [71].

Spin and Magnetism of GNR

Challenges

There was a puzzle about the mechanism of the edge-discriminative generation of the (Dirac-Fermi Polarons) DFPs [78]. The DFPs have been observed as a sharp density of states at Fermi energy (E_F) by scanning tunneling microscopy/spectroscopy [79, 80]. However, it is not likely to form DFPs at a clean graphite surface, the interior of GNR, or the armchair edge. Below the surface of graphene, the charge density fluctuations attribute to charge donations of impurities [81]. It has been suggested that the interlayer interaction should generate the DFPs [82]. However, the mechanism only applies to graphene of two or more layers [83–85]. Clarifying the principle of the DFPs generating [86] is a burning desire.

Spin-Polarized BOLS-HM Parameters of Graphene

In the TB Hubbard model, the spin-polarized Hamiltonian can be expressed as:

$\begin{array}{l}{H}_{\sigma }={\displaystyle \sum _{i,\sigma }{\Delta }_i}{c}_{i,\sigma }^{+}{c}_{i,\sigma }+{\displaystyle \sum _{<i,j>,\sigma }{\beta }_{ij}(f_{ij}{c}_{i,\sigma }^{+}{c}_{j,\sigma }+f_{ij}^{\ast }{c}_{j,\sigma }^{+}{c}_{i,\sigma })}\\ +{\displaystyle \sum _i{U}_i{\widehat{n}}_{i,\sigma }{\widehat{n}}_{i,-\sigma }}& (18)\end{array}$

Where σ is the spin with sign. f_ij is the periodic factor. Subscript D denotes dangling σ-bond. The last term is the Hubbard electron repulsion.

We establish the Hamiltonian matrix for atomic vacancy, zigzag, armchair, reconstructed zigzag in the BOLS-HM calculations. Owing to the truth that orbitals have different symmetries in the z-direction [87], the hopping integral t_D between the dangling σ–electron orbital and the p_z orbital of the nearest neighbors is about −0.5 eV [88]. Spin-polarized electronic structures are solved by self-consistent field scheme.

Local Spin Density of States

Considering spin-polarized Hamiltonian, spin-polarized electronic structures can be obtained by diagonalizing the Hamiltonian matrix using the mean-field method as described. Local spin density of states (LSDOS) of spin σ at i^th atom, g_iσ(E), can be calculated from the spin-polarized electronic structure.

LDOS at i^th atom [g_i(E)] is calculated according to the atomic contribution (c_ivk) to the LCAO eigen-vector c_vk and expressed as:

$g_i(E)=\frac{1}{A}{\displaystyle \sum _{v,k}{c}_{ivk}^2\exp \left[-\frac{1}{2}{\left(\frac{E-{\epsilon }_{vk}}{{\sigma }_s}\right)}^2\right]} (19)$

Figure 7 illustrates the calculation results of LDOS of AGNR-20. Density distribution at each atomic position and at difference energy can be obtained. Arrows in left panel indicates the quantum trapping of bonding electrons and polarization of anti-bonding states at edge sites obtained by BOLS-HM.

FIGURE 7

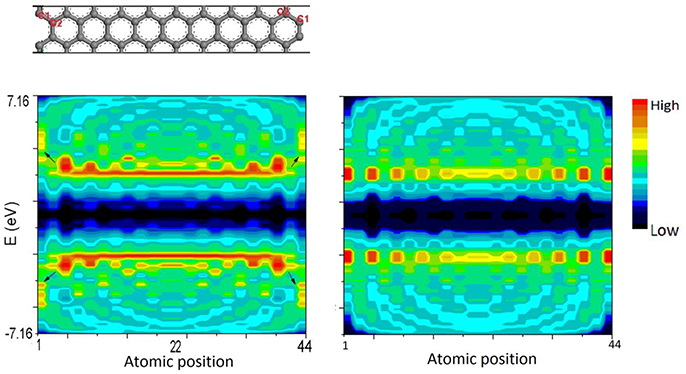
Figure 7. LDOS contour of AGNR-20 calculated by BOLS-HM (left) compared with conventional TB (right). C1 and C2 are the edge sites.

The BOLS-HM derived LDOS of a hydrogenated vacAGNR (H-vacAGNR) with ribbon width N = 20 is shown in Figure 8. A sharp resonant peak at vacancy site near E_F can be observed, which is consistent with that identified experimentally from graphite surface vacancy [89].

FIGURE 8

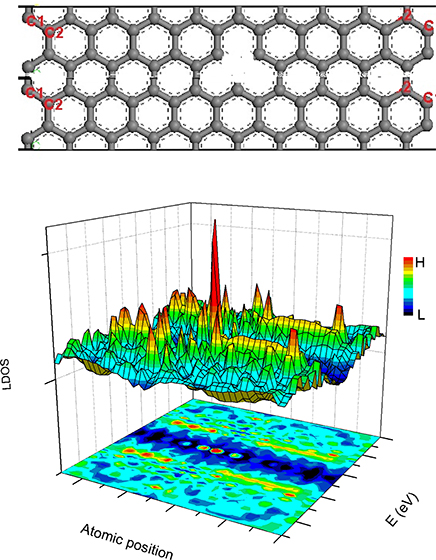
Figure 8. The structure of vacAGNR-20 (up) and the BOLS-HM derived LDOS of the defective AGNR (down). Reprinted with permission from Zhang et al. [90].

Magnetism of Dirac-Fermi Polarons

As Figure 9 shows, the local spin density of states (LSDOS) with and without hydrogenation are compared intuitively, as well as the spin electron density in real space. Zigzag edges and atomic defects demonstrates a spin-density as high as 0.7~1.0 electron/ų of dangling σ-bond. Surprisingly, after hydrogenation, zigzag edge still has a low magnetism, due to the contribution of p_z electrons trapped at edges. Meanwhile, we found armchair edge exhibiting an extremely low spin-density.

FIGURE 9

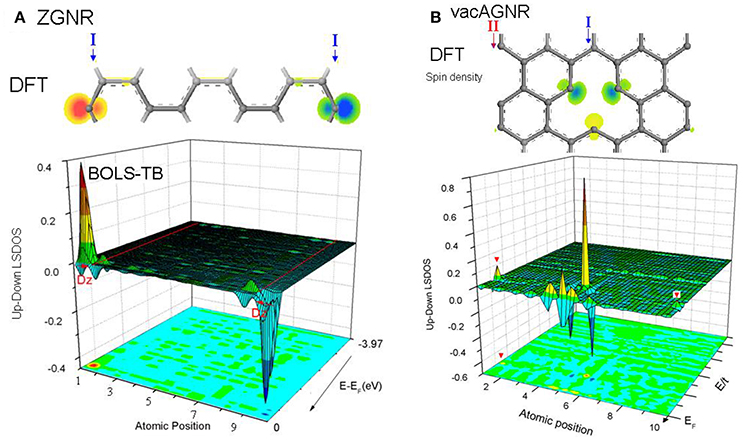
Figure 9. DFT-derived spin electron density and BOLS-HM derived difference LSDOS for (A) ZGNR and (B) H-ZGNR. Zigzag edge manifest a strong local magnetism caused by both D_z and trapped edge p_z electron. Hydrogenation annihilates D_z but leaves a weak magnetism. Reprinted with permission from Zhang et al. [90].

The sp² hybridization of GNR edges are shown in Figure 10 to help to understanding the results of magnetism of DFPs. At armchair edge in Figure 10A, each edge atom loses one of its neighbors and leaves a dangling electron. Due to the short distance (d) between two atoms along the edge, triple bonds are formed between two atoms and the sp2 hybrid may also change. At zigzag edge in Figure 10B, atoms along the edge have a longer distance ($\sqrt{3}d$) and leave the dangling σ bond which may provide edge Dirac states.

FIGURE 10

Figure 10. Hybrid sp² orbitals of carbon atom are plotted at edges of (A) AGNR and (B) ZGNR.

E_G Expansion of Black Phosphorene

Challenges

Few-layer phosphorene [9, 10] shows high carrier motilities, up to 1,000 cm²V⁻¹s⁻¹, and a high current on/off ratio of up to 10⁵ at room temperature. These values make this material a promising candidate for field-effect transistors [91–93]. Modulating the band gap of phosphorene nanoribbon (PNR) [94, 95] is crucial for the semiconducting applications. Because of its anisotropy, the electronic properties are affected considerably by the orientation of the PNRs [96, 97], leading to promising applications. However, the physical origin behind the E_G modulation is still unclear.

BOLS-HM Scheme

According to BOLS-HM, the perturbation to the crystal potential can be expressed as follows V_cry (N) = V_cry (∞) (1+Δ_N). V_cry (N) and V_cry (∞) denote the crystal potential of nanomaterial size (N) and the bulk, respectively. Δ_N is a size-dependent perturbation to the crystal potential. The relationship can also be described as Froyen and Harrison [31]:

$\begin{array}{l}\Delta =\frac{V_{cry}(N)-V_{cry}(\infty )}{V_{cry}(\infty )}=\frac{E_g(N)-E_g(\infty )}{E_g(\infty )}\\ ={\displaystyle \sum _{i\le 3}{\gamma }_i}\left(\frac{E_i}{E_b}-1\right)={\displaystyle \sum _{i\le 3}{\gamma }_i}\left(C_i^{-m}-1\right)\\ {\gamma }_i=\frac{V_i}{V}=\tau C_i{N}^{-1}& (20)\end{array}$

γ_i is the surface-to-volume ratio, and τ is the dimensionality with τ = 1, 2, 3 for a nanoparticle, nanoribbon, or nanofilm, respectively. The bond index m is intrinsic to a specific material. The expressions indicate the size-dependent V_cry and E_G are a function of shape and surface-to-volume ratio of a nanomaterial.

Figure 11 compares the DFT-derived E_G vs. the ribbon width(N) of zigzag and armchair PNRs with theoretical prediction of BOLS-HM [98]. The m of the PNRs in Equation (20) was optimized to be 4.60 based on the measured data. Using the optimized m-values, we calculated, plotted, and compared the theoretical curves. The necessary values of the reference bandgap energy E_bZ = 0.82 eV and E_bA = 0.43 eV were obtained. They are very close to the bulk value of two typical edge materials. A further refinement of the derived m, E_bZ, and E_bA values was achieved by carefully matching the DFT calculations to the whole nanoribbon length ranges.

FIGURE 11

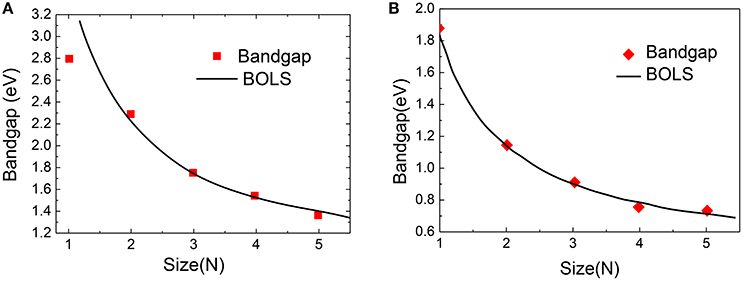
Figure 11. BOLS reproduction of the DFT calculated size-dependency of (A) zigzag PNRs and (B) armchair PNRs. Reprint with permission from Liu et al. [98].

Electronic Properties of Antimonene

Encouragingly, the 2D material has been found in group V elements. Antimony(Sb), non-hygroscopic, gray metal with a layered structure similar to that of BP [11]. Antimonene is stable at high temperature as high as 1,000 K [12] and becomes semiconducting when it is a one atomic layer [99]. Because there are a large number of dangling bonds and broken bonds in the edge of antimonene nanoribbon (SbNR) [100], the bond parameters of the surface atoms are different from the internal atoms. Like other 2D material, the E_G modulation is crucial for its potential applications while the physical origin is not conclusive yet.

Though antimony belongs to rhombohedral system, hexagonal coordinate system is convenient to describe its structure. We identify the SbNR structures by the number of N along the ribbon orientations. Vacuum slabs of 10 Å were inserted in the width direction and the z axis. DFT calculation was performed by CASTEP using PBE functional. Figure 12 compares the DFT-derived E_G vs. the ribbon width(N) of zigzag and armchair PNRs with theoretical prediction of BOLS-HM. The reproduction of these quantities confirms the importance of the size of nanoribbons, which supports the proposals that the origin of these novel properties is mainly due to the change of the bond length and strength in different sizes of SbNRs.

FIGURE 12

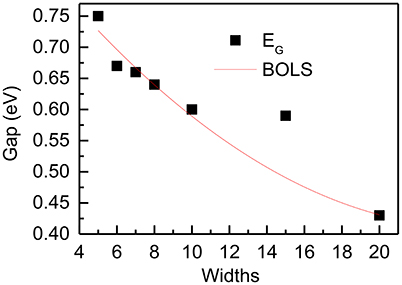
Figure 12. DFT-derived band gap dependence of width of the zigzag SbNRs. The red lines correspond to the BOLS theoretical prediction.

Summary

In this work, a quantum theory was proposed to calculate the under-coordinated effects on the electronic structure of materials by incorporating BOLS correlation theory to mean-field Hubbard model. The whole process of BOLS-HM dealing with the chemical bonds can be summarized as:

1. Input the effective coordination number z, the bond length at the under-coordinated sites to calculate the increase of bond energy, and the mortification of the inter-atomic matrix elements according to BOLS correlation.

2. Construct the Bloch sums ψ_v,k(r) of wave functions for low-dimentional nanomaterial.

3. Construct the Hamiltonian matrix with strong correlation Hubbard model of the nanosystem.

4. Solve the spin-polarized electronic structure self-consistently to get eigenenergy and eigenvectors ${\text{C}}_{\text{k}}=|{\text{c}}_v(\text{k}),{\text{c}}_{v^{\prime }}(\text{k}),\dots >$ for each k point.

5. Based on the eigenenergy and eigenvector results, properties such as Mulliken charge, Mayer bond order, local density of states can thus be obtained.

By virtue of BOLS-HM, we clarified that (i) bond contractions and potential well depression occur at the edge of graphene, phosphorene, and antimonene nanoribbons; (ii) the physical origin of the band gap opening of graphene, phosphorene, and antimonene nanoribbons lays in the enhancement of edge potentials and hopping integrals due to the shorter and stronger bonds between undercoordinated atoms; (iii) the band gap of 2D material nanoribbons expand as the width decreases which modulates the conductive behaviors; and (iv) non-bond electrons at the edges and atomic vacancies of 2D material accompanied with the broken bond contribute to the DFP with a local magnetic moment. Although, this work shows the BOLS-HM applications on three kinds of 2D materials, the potential applications are not limited to those materials but applied on other species such as Mo/WS₂.

Author Contributions

XZ coordinates the project. XZ and TW proposed the theoretical model. TW, WC, and DP wrote the manuscript. SW did the DFT calculations.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Financial supports from National Natural Science Foundation (No. 51605306) of China, Guangdong Innovation Youth Fund (No. 2015KQNCX144), and Natural Science Foundation of Guangdong (No. 2016A030310060), and of SZU (No. 827000131), Shenzhen foundation fund (No. JCYJ20160427105015701) are gratefully acknowledged.

References

1. Hod O, Barone V, Peralta JE, Scuseria GE. Enhanced half-metallicity in edge-oxidized zigzag graphene nanoribbons. Nano Lett. (2007) 7:2295–9. doi: 10.1021/nl0708922

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Barone V, Hod O, Scuseria GE. Electronic structure and stability of semiconducting graphene nanoribbons. Nano Lett. (2006) 6:2748–54. doi: 10.1021/nl0617033

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lehtinen PO, Foster AS, Ma Y, Krasheninnikov AV, Nieminen RM. Irradiation-induced magnetism in graphite: a density functional study. Phys Rev Lett. (2004) 93:187202. doi: 10.1103/PhysRevLett.93.187202

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Pereira VM, Guinea F, Lopes dos Santos JMB, Peres N, Castroneto AH. Disorder induced localized states in graphene. Phys Rev Lett. (2006) 96:036801. doi: 10.1103/PhysRevLett.96.036801

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Palacios JJ, Fernández-Rossier J, Brey L. Vacancy-induced magnetism in graphene and graphene ribbons. Phys Rev B (2008) 77:195428. doi: 10.1103/PhysRevB.77.195428

CrossRef Full Text | Google Scholar

6. Cervenka J, Katsnelson MI, Flipse CFJ. Room-temperature ferromagnetism in graphite driven by two-dimensional networks of point defects. Nat Phys. (2009) 5:840–4. doi: 10.1038/nphys1399

CrossRef Full Text | Google Scholar

7. Enoki T, Kobayashi Y, Fukui KI. Electronic structures of graphene edges and nanographene. Int Rev Phys Chem. (2007) 26:609–45. doi: 10.1080/01442350701611991

CrossRef Full Text | Google Scholar

8. Soldano C, Mahmood A, Dujardin E. Production properties and potential of graphene. Carbon (2010) 48:2127–50. doi: 10.1016/j.carbon.2010.01.058

CrossRef Full Text | Google Scholar

9. Lu SB, Miao LL, Guo ZN, Qi X, Zhao CJ, Zhang H, et al. Broadband nonlinear optical response in multi-layer black phosphorus: an emerging infrared and mid-infrared optical material. Opt Express (2015) 23:11183–94. doi: 10.1364/OE.23.011183

CrossRef Full Text | Google Scholar

10. Guo Z, Zhang H, Lu S, Wang Z, Tang S, Shao J, et al. From black phosphorus to phosphorene: basic solvent exfoliation, evolution of raman scattering, and applications to ultrafast photonics. Adv Funct Mater. (2016) 25:6996–7002. doi: 10.1002/adfm.201502902

CrossRef Full Text | Google Scholar

11. Cheung CH, Fuh HR, Hsu MC, Lin YC, Chang CR. Spin orbit coupling gap and indirect gap in strain-tuned topological insulator-antimonene. Nanoscale Res. Lett. (2016) 11:459. doi: 10.1186/s11671-016-1666-4

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Lei T, Liu C, Zhao JL, Li JM, Li YP, Wang JO, et al. Electronic structure of antimonene grown on Sb2Te3 (111) and Bi2Te3 substrates. J Appl Phys. (2016) 119:015302. doi: 10.1063/1.4939281

CrossRef Full Text | Google Scholar

13. Zhang S, Yan Z, Li Y, Chen Z, Zeng H. Atomically thin arsenene and antimonene: semimetal-semiconductor and indirect-direct band-gap transitions. Angew Chem. (2015) 54:3112–5. doi: 10.1002/anie.201411246

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Sun CQ. Size dependence of nanostructures: impact of bond order deficiency. Prog Solid State Chem. (2007) 35:1–159. doi: 10.1016/j.progsolidstchem.2006.03.001

CrossRef Full Text | Google Scholar

15. Sun CQ. Oxidation electronics: bond-band-barrier correlation and its applications. Prog Mater Sci. (2003) 48:521–685. doi: 10.1016/S0079-6425(03)00010-0

CrossRef Full Text | Google Scholar

16. Sun CQ. Thermo-mechanical behavior of low-dimensional systems: the local bond average approach. Prog Mater Sci. (2009) 54:179–307. doi: 10.1016/j.pmatsci.2008.08.001

CrossRef Full Text | Google Scholar

17. Yang DQ, Sacher E. Strongly enhanced interaction between evaporated Pt nanoparticles and functionalized multiwalled carbon nanotubes via plasma surface modifications: effects of physical and chemical defects. J Phys Chem C (2008) 112:4075–82. doi: 10.1021/jp076531s

CrossRef Full Text | Google Scholar

18. Sun CQ, Fu SY, Nie YG. Dominance of broken bonds and unpaired nonbonding pi-electrons in the band gap expansion and edge states generation in graphene nanoribbons. J Phys Chem C (2008) 112:18927–34. doi: 10.1021/jp807580t

CrossRef Full Text | Google Scholar

19. Sun CQ, Sun Y, Ni Y, Zhang X, Pan J, Wang XH, et al. Coulomb repulsion at the nanometer-sized contact: a force driving superhydrophobicity, superfluidity, superlubricity, and supersolidity. J Phys Chem C (2009) 113:20009–19. doi: 10.1021/jp907726b

CrossRef Full Text | Google Scholar

20. Sun CQ, Nie Y, Pan J, Zhang X, Ma SZ, Wang Y, et al. Zone-selective photoelectronic measurements of the local bonding and electronic dynamics associated with the monolayer skin and point defects of graphite. RSC Adv. (2012) 2:2377–83. doi: 10.1039/c2ra00512c

CrossRef Full Text | Google Scholar

21. Sun CQ. Dominance of broken bonds and nonbonding electrons at the nanoscale. Nanoscale (2010) 2:1930–61. doi: 10.1039/c0nr00245c

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Ghoniem NM, Busso EP, Kioussis N, Huang H. Multiscale modelling of nanomechanics and micromechanics: an overview. Philos Mag. (2003) 83:3475–528. doi: 10.1080/14786430310001607388

CrossRef Full Text | Google Scholar

23. Dimitri DV. Multiscale modelling of nanostructures. J Phys Condens Matter (2004). 16:R1537. doi: 10.1088/0953-8984/16/50/R01

CrossRef Full Text | Google Scholar

24. Fu CC, Torre JD, Willaime F, Bocquet JL, Barbu A. Multiscale modelling of defect kinetics in irradiated iron. Nat Mater. (2005) 4:68–74. doi: 10.1038/nmat1286

CrossRef Full Text | Google Scholar

25. Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev. (1964) 136:B864. doi: 10.1103/PhysRev.136.B864

CrossRef Full Text | Google Scholar

26. Kohn W. Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev. (1965) 140:A1133. doi: 10.1103/PhysRev.140.A1133

CrossRef Full Text

27. Slater JC, Koster GF. Simplified LCAO method for the periodic potential problem. Phys Rev. (1954) 94:1498. doi: 10.1103/PhysRev.94.1498

CrossRef Full Text | Google Scholar

28. Papaconstantopoulos DA, Mehl MJ. The Slater–Koster tight-binding method: a computationally efficient and accurate approach. J Phys Condens Matter (2003) 15:R413. doi: 10.1088/0953-8984/15/10/201

CrossRef Full Text | Google Scholar

29. Goringe CM, Bowler DR, Hernández E. Tight-binding modelling of materials. Rep Prog Phys. (1997) 60:1447. doi: 10.1088/0034-4885/60/12/001

CrossRef Full Text | Google Scholar

30. Seifert G, Joswig JO. Density-functional tight binding—an approximate density-functional theory method. Wiley Interdiscip Rev Comput Mol Sci. (2012) 2:456–65. doi: 10.1002/wcms.1094

CrossRef Full Text | Google Scholar

31. Froyen S, Harrison WA. Elementary prediction of linear combination of atomic orbitals matrix elements. Phys Rev B (1979) 20:2420–22. doi: 10.1103/PhysRevB.20.2420

CrossRef Full Text | Google Scholar

32. Harrison WA. Overlap interactions and bonding in ionic solids. Phys Rev B (1986) 34:2787–93. doi: 10.1103/PhysRevB.34.2787

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Porezag D, Frauenheim T, Köhler T, Seifert G, Kaschner R. Construction of tight-binding-like potentials on the basis of density-functional theory: application to carbon. Phys Rev B (1995) 51:12947–57. doi: 10.1103/PhysRevB.51.12947

CrossRef Full Text | Google Scholar

34. Lammert PE, Crespi VH. Geometrical perturbation of graphene electronic structure. Phys Rev B (2000) 61:7308–11. doi: 10.1103/PhysRevB.61.7308

CrossRef Full Text | Google Scholar

35. Karasev MV. Graphene as a quantum surface with curvature-strain preserving dynamics. Russ J Math Phys. (2011) 18:64–72. doi: 10.1134/S1061920811010079

CrossRef Full Text | Google Scholar

36. Wakabayashi K, Okada S, Tomita R, Fujimoto S, Natsume Y. Edge states and flat bands of graphene nanoribbons with edge modification. J Phys Soc Jpn. (2010) 79:034706. doi: 10.1143/JPSJ.79.034706

CrossRef Full Text | Google Scholar

37. Wang ZF, Li Q, Zheng H, Ren H, Su H, Shi QW, et al. Tuning the electronic structure of graphene nanoribbons through chemical edge modification: a theoretical study. Phys Rev B Condens Matter (2007) 75:113406. doi: 10.1103/PhysRevB.75.113406

CrossRef Full Text | Google Scholar

38. Yu PY, Cardona M. editors. Tight-binding or LCAO approach to the band structure of semiconductors. Fundamentals of Semiconductors, 3rd Edn. Berlin, Heidelberg: Springer (2005), p. 68–71.

PubMed Abstract

39. Szabó A, Ostlund NS. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. Mineola, TX; New York, NY: Courier Dover Publications (1989).

Google Scholar

40. Harrison WA. Electronic Structure and the Properties of Solids - The Physics of Chemical Bond. San Francisco: CA: Freeman (1980).

Google Scholar

41. Bowler D. DensEl: A. Tight Binding Code. Available online at: http://www.ucl.ac.uk/~ucapdrb/DensEl.html

42. Seifert G. The DFTB Website. Available online at: http://www.dftb.org

43. Bloch F. Über die quantenmechanik der elektronen in kristallgittern. Z Phys A Hadrons Nuclei (1929) 52:555–600.

Google Scholar

44. Lowdin PO. On the non-orthogonality problem connected with the use of atomic wave functions in the theory of molecules and crystals. J Chem Phys. (1950) 18:365–75. doi: 10.1063/1.1747632

CrossRef Full Text | Google Scholar

45. Wannier GH. The structure of electronic excitation levels in insulating crystals. Phys Rev. (1937) 52:191–7. doi: 10.1103/PhysRev.52.191

CrossRef Full Text | Google Scholar

46. Slater JC. An augmented plane wave method for the periodic potential problem. Phys Rev. (1953) 92:603–8. doi: 10.1103/PhysRev.92.603

CrossRef Full Text | Google Scholar

47. Andersen OK, Pawlowska Z, Jepsen O. Illustration of the linear-muffin-tin-orbital tight-binding representation: compact orbitals and charge density in Si. Phys Rev B (1986) 34:5253. doi: 10.1103/PhysRevB.34.5253

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Xie ZL, Dy KS, Wu SY. First-principles real-space tight-binding LMTO calculation of electronic structuresfor atomic clusters. Phys Rev B (1997) 55:1748. doi: 10.1103/PhysRevB.55.1748

CrossRef Full Text | Google Scholar

49. Boys SF. Electronic wave functions. I. A general method of calculation for the stationary states of any molecular system. Proc R Soc Lond A Math Phys Sci. (1950) 200:542–54. doi: 10.1098/rspa.1950.0036

CrossRef Full Text | Google Scholar

50. Elstner M, Porezag D, Jungnickel G, Elsner J, Haugk M, Frauenheim T, et al. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys Rev B (1998) 58:7260–8. doi: 10.1103/PhysRevB.58.7260

CrossRef Full Text | Google Scholar

51. Koskinen P, Häkkinen H, Seifert G, Sanna S, Th F, Moseler M. Density-functional based tight-binding study of small gold clusters. New J Phys. (2006) 8:9. doi: 10.1088/1367-2630/8/1/009

CrossRef Full Text | Google Scholar

52. Hubbard J. Electron correlations in narrow energy band. Proc R Soc Lond A Math Phys Sci. (1963) 276:238–57. doi: 10.1098/rspa.1963.0204

CrossRef Full Text | Google Scholar

53. Hubbard J. The magnetism of iron. Phys Rev B (1979) 19:2626–36. doi: 10.1103/PhysRevB.19.2626

CrossRef Full Text | Google Scholar

54. Mott NF, Peierls R. Discussion of the paper by de Boer and Verwey. Proc Phys Soc. (1937) 49:72. doi: 10.1088/0959-5309/49/4S/308

CrossRef Full Text | Google Scholar

55. Kuiper P, Kruizinga G, Ghijsen J, Sawatzky GA, Verweij H. Character of holes in Li_{x}Ni_{1-x}O and their magnetic behavior. Phys Rev Lett. (1989) 62:221–4. doi: 10.1103/PhysRevLett.62.221

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Shockley W. On the surface states associated with a periodic potential. Phys Rev. (1939) 56:317–23. doi: 10.1103/PhysRev.56.317

CrossRef Full Text | Google Scholar

57. Tamm I. On the possible bound states of electrons on a crystal surface. Phys Z Soviet Union (1932) 1:733.

58. Huang WJ, Sun R, Tao J, Menard LD, Nuzzo RG, Zuo JM. Coordination-dependent surface atomic contraction in nanocrystals revealed by coherent diffraction. Nat Mater. (2008) 7:308–13. doi: 10.1038/nmat2132

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Wang Y, Nie YG, Wang LL, Sun CQ. Atomic-layer- and crystal-orientation-resolved 3d(5/2) binding energy shift of Ru(0001) and Ru(1010) surfaces. J Phys Chem C (2010) 114:1226–30. doi: 10.1021/jp909549f

CrossRef Full Text | Google Scholar

60. Sun CQ. Surface and nanosolid core-level shift: Impact of atomic coordination-number imperfection. Phys Rev B (2004) 69:045105. doi: 10.1103/PhysRevB.69.045105

CrossRef Full Text | Google Scholar

61. Matsui F, Matsushita T, Kato Y, Hashimoto M, Inaji K, Guo FZ, et al. Atomic-layer resolved magnetic and electronic structure analysis of Ni thin film on a Cu(001) surface by diffraction spectroscopy. Phys Rev Lett. (2008) 100:207201. doi: 10.1103/PhysRevLett.100.207201

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Feibelman PJ. Relaxation of hcp(0001) surfaces: a chemical view. Phys Rev B (1996) 53:13740. doi: 10.1103/PhysRevB.53.13740

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Falvo MR, Clary GJ, Taylor RM, Chi V, Brooks FP, Washburn S, et al. Bending and buckling of carbon nanotubes under large strain. Nature (1997) 389:582–4. doi: 10.1038/39282

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Wong EW, Sheehan PE, Lieber CM. Nanobeam mechanics: elasticity, strength, and toughness of nanorods and nanotubes. Science (1997) 277:1971–5. doi: 10.1126/science.277.5334.1971

CrossRef Full Text | Google Scholar

65. An B, Fukuyama S, Yokogawa K, Yoshimura M. Surface superstructure of carbon nanotubes on highly oriented pyrolytic graphite annealed at elevated temperatures. Jpn J Appl Phys. (1998) 37(Pt 1):3809–11.

Google Scholar

66. Sun CQ, Bai HL, Tay BK, Li S, Jiang EY. Dimension, strength, and chemical and thermal stability of a single C-C bond in carbon nanotubes. J Phys Chem B (2003) 107:7544–6. doi: 10.1021/jp035070h

CrossRef Full Text | Google Scholar

67. Son YW, Cohen ML, Louie SG. Half-metallic graphene nanoribbons. Nature (2006) 444:347–9. doi: 10.1038/nature05180

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Son YW, Cohen ML, Louie SG. Energy gaps in graphene nanoribbons. Phys Rev Lett. (2006) 97:216803. doi: 10.1103/PhysRevLett.97.216803

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Liu L, Shen Z. Bandgap engineering of graphene: a density functional theory study. Appl Phys Lett (2009) 95:252104. doi: 10.1063/1.3276068

CrossRef Full Text | Google Scholar

70. Zhang YH, Zhou KG, Xie KF, Zeng J, Zhang HL, Peng Y. Tuning the electronic structure and transport properties of graphene by noncovalent functionalization: effects of organic donor, acceptor and metal atoms. Nanotechnology (2010) 21:065201. doi: 10.1088/0957-4484/21/6/065201

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Zhang X, Kuo JL, Gu M, Bai P, Sun CQ. Graphene nanoribbon band-gap expansion: broken-bond-induced edge strain and quantum entrapment. Nanoscale (2010) 2:2160–3. doi: 10.1039/c0nr00273a

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Francis JGF. The QR transformation, a unitary analogue to the LR transformation I. Comput J. (1961) 4:265–71. doi: 10.1093/comjnl/4.3.265

CrossRef Full Text | Google Scholar

73. Arnoldi WE. The principle of minimized iterations in the solution of the matrix eigenvalue problem. Q Appl Math. (1951) 9:17–29. doi: 10.1090/qam/42792

CrossRef Full Text | Google Scholar

74. Rutishauser H. Handbook series linear algebra: the Jacobi method for real symmetric matrices. Numer Math. (1966) 9:1–10. doi: 10.1007/BF02165223

CrossRef Full Text | Google Scholar

75. Street RA. Hydrogenated Amorphous Silicon. New York, NY: Cambridge University Press (1991).

Google Scholar

76. Yu SS, Wen QB, Zheng WT, Jiang Q. Electronic properties of graphene nanoribbons with armchair-shaped edges. Mol Simul. (2008) 34:1085–90. doi: 10.1080/08927020801958795

CrossRef Full Text | Google Scholar

77. Han MY, Ozyilmaz B, Zhang Y, Kim P. Energy band-gap engineering of graphene nanoribbons. Phys Rev Lett. (2007) 98:206805. doi: 10.1103/PhysRevLett.98.206805

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Fujita M, Wakabayashi K, Nakada K, Kusakabe K. Peculiar localized state at zigzag graphite edge. J Phys Soc Jpn. (1996) 65:1920. doi: 10.1143/JPSJ.65.1920

CrossRef Full Text | Google Scholar

79. Okada S, Oshiyama A. Magnetic ordering in hexagonally bonded sheets with first-row elements. Phys Rev Lett. (2001) 87:146803. doi: 10.1103/PhysRevLett.87.146803

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Nakada K, Fujita M, Dresselhaus G, Dresselhaus MS. Edge state in graphene ribbons: nanometer size effect and edge shape dependence. Phys Rev B (1996) 54:17954–61. doi: 10.1103/PhysRevB.54.17954

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Zhang YB, Brar VW, Girit C, Zettl A, Crommie MF. Origin of spatial charge inhomogeneity in graphene. Nat Phys. (2009) 5:722–6. doi: 10.1038/nphys1365

CrossRef Full Text | Google Scholar

82. Ferro Y, Allouche A. Interpretation of STM images of graphite with an atomic vacancy via density-functional calculations of electronic structure. Phys Rev B (2007) 75:155438. doi: 10.1103/PhysRevB.75.155438

CrossRef Full Text | Google Scholar

83. Ma S, Xia JH, Srikanth V, Sun X, Staedler T, Jiang X et al. Magnetism of amorphous carbon nanofibers. Appl Phys Lett. (2009) 95:263105. doi: 10.1063/1.3272940

CrossRef Full Text | Google Scholar

84. Xu B, Yin J, Xia YD, Wan XG, Jiang K, Liu ZG. Electronic and magnetic properties of zigzag graphene nanoribbon with one edge saturated. Appl Phys Lett. (2010) 96:163102. doi: 10.1063/1.3402762

CrossRef Full Text | Google Scholar

85. Zanolli Z, Charlier JC. Spin transport in carbon nanotubes with magnetic vacancy-defects. Phys Rev B (2010) 81:165406. doi: 10.1103/PhysRevB.81.165406

CrossRef Full Text | Google Scholar

86. Koskinen P, Malola S, Häkkinen H. Evidence for graphene edges beyond zigzag and armchair. Phys Rev B (2009) 80:073401. doi: 10.1103/PhysRevB.80.073401

CrossRef Full Text | Google Scholar

87. Zheng F, Sasaki KI, Saito R, Duan W, Gu BL. Edge states of zigzag boron nitride nanoribbons. J Phys Soc Jpn. (2009) 78:074713. doi: 10.1143/JPSJ.78.074713

CrossRef Full Text | Google Scholar

88. Yazyev OV, Helm L. Defect-induced magnetism in graphene. Phys Rev B (2007) 75:125408. doi: 10.1103/PhysRevB.75.125408

CrossRef Full Text | Google Scholar

89. Ugeda MM, Brihuega I, Guinea F, Gómez-Rodríguez JM. Missing atom as a source of carbon magnetism. Phys Rev Lett. (2010) 104:096804. doi: 10.1103/PhysRevLett.104.096804

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Zhang X, Nie Y, Zheng W, Kuo JL, Sun CQ. Discriminative generation and hydrogen modulation of the Dirac-Fermi polarons at graphene edges and atomic vacancies. Carbon (2011) 49:3615–21. doi: 10.1016/j.carbon.2011.04.064

CrossRef Full Text | Google Scholar

91. Wang X, Jones AM, Seyler KL, Tran V, Jia Y, Zhao H, et al. Highly anisotropic and robust excitons in monolayer black phosphorus. Nat Nanotechnol. (2015) 10:517–21. doi: 10.1038/nnano.2015.71

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Li L, Yu Y, Ye GJ, Ge Q, Ou X, Wu H, et al. Black phosphorus field-effect transistors. Nat Nanotechnol. (2014) 9:372–7. doi: 10.1038/nnano.2014.35

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Qiao J, Kong X, Hu ZX, Yang F, Ji W. Few-layer black phosphorus: emerging 2D semiconductor with high anisotropic carrier mobility and linear dichroism. Nat Commun. (2014) 5.

94. Han X, Stewart HM, Shevlin SA, Catlow CRA, Guo ZX. Strain and orientation modulated bandgaps and effective masses of phosphorene nanoribbons. Nano Lett. (2014) 14:4607–14. doi: 10.1021/nl501658d

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Ramasubramaniam A, Muniz AR. Ab initio. Phys Rev B (2014) 90:085424. doi: 10.1103/PhysRevB.90.085424

CrossRef Full Text | Google Scholar

96. Baringhaus J, Ruan M, Edler F, Tejeda A, Sicot M, Talebibrahimi A, et al. Exceptional ballistic transport in epitaxial graphene nanoribbons. Nature (2013) 506:349–54. doi: 10.1038/nature12952

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Yoon Y, Guo J. Effect of edge roughness in graphene nanoribbon transistors. Appl Phys Lett. (2007) 91:666. doi: 10.1063/1.2769764

CrossRef Full Text | Google Scholar

98. Liu Y, Bo M, Yang X, Zhang P, Sun CQ, Huang Y. Size modulation electronic and optical properties of phosphorene nanoribbons: DFT-BOLS approximation. Phys Chem Chem Phys. (2017) 19:5304–9. doi: 10.1039/C6CP08011A

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Huang YL, Zhang X, Ma ZS, Zhou YC, Zheng WT, Zhou J, et al. Hydrogen-bond relaxation dynamics: resolving mysteries of water ice. Coord Chem Rev. (2015) 285:109–65. doi: 10.1016/j.ccr.2014.10.003

CrossRef Full Text | Google Scholar

100. Wang Y, Ding Y. Electronic structure and carrier mobilities of arsenene and antimonene nanoribbons: a first-principle study. Nanoscale Res Lett. (2015) 10:955. doi: 10.1186/s11671-015-0955-7

PubMed Abstract | CrossRef Full Text | Google Scholar