Environmental Fluctuations and Their Consequences for the Evolution of Phenotypic Diversity

An essential aspect of the current theory of adaptive speciation is the maintenance of phenotypic variation and the evolution of stationary stable phenotypic diversity, a phenomenon known as evolutionary branching. Theoretical and empirical evidence suggest that phenotypic variation can be maintained by favoring rare phenotypes, for example, through frequency-dependent selection. However, even when phenotypic variation is provided, the conditions leading to evolutionary branching are not universal. In order to lead to stable diversification, current models of adaptive speciation, such as the Lotka-Volterra competition model, must resort to strong assumptions that range from using unrealistic shape parameters for the competition and carrying capacity functions, modeling separately the generation of discontinuities in niche space, to increasing the dimensionality of phenotypic traits. Here, we introduce a stochastic version of the Lotka-Volterra competition model. We demonstrate that environmental fluctuations suffice to lead consistently to phenotypic diversification and evolutionary branching. Our observations build upon previous findings identifying a role for stochastic fluctuations on the evolution of phenotypic diversity, emphasize the difference between strong vs. weak assumptions in the stability of the LVC model, and suggest that the conditions for evolutionary branching are more relaxed than anticipated.

1. Introduction

The origins and maintenance of species diversity is one of the foundational questions in evolutionary biology. Theory and empirical evidence suggest that a large number of factors impact species persistence, adaptation, and phenotypic diversification; often believed to antecede the process of speciation [1, 2]. Current theory distinguishes two essential aspects associated to the process of adaptive speciation. The first is the origin and maintenance of phenotypic variation, and the second, the assimilation of such variation in the form of stable discontinuities in the population distribution of phenotypes through a process called evolutionary branching [3–5].

The classic Lotka-Volterra competition (LVC) model describes the evolutionary dynamics of a population and has been extensively used to explore the conditions for evolutionary branching [6, 7]. According to the LVC model, a population of organisms lives on a one-dimensional niche space, where there is a one-to-one mapping between phenotypic traits and niche position. As a consequence, phenotypes are fully specified by their relative position along the niche axis, where distance between phenotypes reflects similarity, and therefore, accessibility to similar resources. In order to subsist, individuals consume the resources available in their niches, such that over time, the frequency of a given phenotypic trait in the population is function of two main forces: the carrying capacity of the environment, and the competition between individuals.

The carrying capacity describes the interaction between organisms and their environment. It is often defined as a limit on the number of individuals that can simultaneously occupy a given position along the niche axis (i.e., have the same phenotypic trait). Such limit encapsulates environmental constraints on the availability of resources and/or the efficiency conferred by phenotypic traits to resource consumption [8]. The carrying capacity constitutes the stabilizing component of selection [9].

The second major force that impacts the frequency of phenotypes in a population is competition. Competition is a function of both the density of individuals with a given phenotypic trait and the similarity between phenotypes. The more common and more similar the phenotypes in a population, the stronger the degree of competition. Due to its dependence on the fraction of individuals with a given trait, competition contributes to the frequency-dependent component of selection.

The LVC model predicts that the maintenance and evolution of phenotypic diversity in a population of competing individuals is function of the relation between the stabilizing and the frequency-dependent components of selection, that is, between carrying capacity and competition [10]. According to the LVC model a population can evolve toward two possible outcomes. On the one hand, the predominance of stabilizing over frequency-dependent selection leads to the evolution of highly similar individuals. On the other hand, the predominance of frequency-dependent over stabilizing selection, results in phenotypic diversification and evolutionary branching [9, 11]; a condition deemed essential to the process of adaptive speciation.

Because the maintenance of phenotypic diversity is a crucial onset of evolutionary branching, understanding the conditions that promote diversity has attracted considerable attention [5, 7, 8, 12, 13]. These and other studies showed that, although in its basic form the LVC model leads to the spontaneous generation of phenotypic diversity (i.e., it is unstable), evolutionary branching is not a granted outcome of the model. Indeed, the frequency-dependent component of selection must be strong in order for diversity to persist [9]. Therefore, in order to observe branching researchers resort to several strong assumptions, such as: the use of unrealistic, non-Gaussian shape parameters in the competition and carrying capacity functions [13], modeling separately the generation of discontinuities on niche space [14], or increasing the dimensionality of phenotypic traits [9].

An aspect that has received less attention in the study of the conditions for evolutionary branching is the role of stochastic fluctuations. In contrast to the assumptions described above, fluctuations are a pervasive phenomenon in ecology [15–17]. For instance, noise can arise as a result of small population sizes (i.e., demographic noise), from the interaction among individuals, or between individuals and their environment (i.e., environmental noise). Studies incorporating some form of stochasticity in their analyses have reached contradictory conclusions. While some have shown that fluctuations can promote diversification [12, 18], alternative mathematical formulations have also shown that fluctuations can also reduce the likelihood of evolutionary branching [19, 20].

Here, we explore the role of environmental fluctuations on the evolution of phenotypic diversity. We study the impact of fluctuations on the availability of resources in niche space. We do this by building an stochastic version of the LVC model that introduces noise in the interaction between individuals and their environment. We show that in the simplest form of the LVC model, that of an asexual population, environmental fluctuations can lead consistently to the evolution of phenotypic diversity and to evolutionary branching. In Section 2, we present the deterministic and stochastic variant of the LVC model. Section 3 describes our results. Finally, in Section 4, we discuss our observations in the context of modeling phenotypic diversification and adaptive speciation.

2. Model

2.1. The (Deterministic) Lotka-Volterra Competition Model

We start our analyses with the classic LVC model. This model describes the evolution of the phenotypic density of a population [ϕ(x, t)], by taking into account two main components. First, the positive contribution of population growth, which is given by a constant growth-rate (r), common to all phenotypes: r ϕ(x, t). A second, negative contribution, describes the combined effect of competition between individuals, α(x, y); and the environment's carrying capacity, K(x). The full dynamics of the population density is given by the following partial integro–differential equation, which summarizes the positive contribution of growth, and the negative, combined contribution of competition and carrying capacity:

$\begin{array}{ll}\frac{\partial \varphi (x,t)}{\partial t}=r \varphi (x,t)-\frac{\varphi (x,t)}{K(x)}{\displaystyle {\int }_{\Omega }\varphi }(y,t) \alpha (x,y)dy.& (1)\end{array}$

The competition and carrying capacity functions, are defined as Doebeli et al. [13]:

$\begin{array}{ll}\alpha (x,y)=\exp \left[-a|x-y{|}^{n_{\alpha }}\right],& (2)\end{array}$

and:

$\begin{array}{ll}K(x)=\exp \left[-k|x{|}^{n_k}\right];& (3)\end{array}$

where a and k are the inverse of the widths of the distributions; n_α and n_k are shape parameters. In the case of Gaussian distributions: n_α = n_k = 2.0.

2.2. The Lotka-Volterra Competition Model with Environmental Fluctuations

Most environmental fluctuations in the wild are caused by a complex mixture of factors that are difficult to tease apart. Here, in order to take into account fluctuations encompassing such variety of factors, we construct an stochastic variant of the LVC model. We define a stochastic carrying capacity function [κ(x, t)], as:

$\begin{array}{ll}\kappa (x,t)=\exp \left[-\xi (t) x^2\right].& (4)\end{array}$

where the parameter k, that previously described the inverse of the width (Equation 3), has been replaced by Gaussian white noise with mean, μ, and variance, σ_ξ. Formally, the stochastic function ξ(t), is defined as:

$\begin{array}{ll}<\xi (t)>=\mu ,& (5)\end{array}$

$\begin{array}{ll}<\xi (t)\xi (t\prime )>={\sigma }_{\xi }\delta (t-t\prime ),& (6)\end{array}$

subject to the constraint ξ(t) > 0 for all t. By setting the variance σ_ξ = 0, and the mean μ = k, we recover the deterministic LVC model. The final stochastic dynamics of the LVC model is defined according to Equation (1), with a deterministic, Gaussian competition function: α(x, y), and a stochastic carrying capacity function defined according to Equations (4–6).

Building upon previous work [21], we were able to obtain a solution for the evolution of the full stochastic LVC model. Assuming no spatio-temporal correlations, the stochastic parameter, ξ, is completely characterized by its probability distribution P(ξ). For simplicity, we assume that P(ξ) follows a Gaussian distribution with mean μ and variance σ_ξ, defined for ξ ≥ 0.

$\begin{array}{ll}P(\xi )=\frac{e^{-{(\xi -\mu )}^2/(2{\sigma }_{\xi }^2)}}{{\sigma }_{\xi }\sqrt{\pi /2} (1+\text{erf}[\mu /({\sigma }_{\xi }\sqrt{2})])}.& (7)\end{array}$

If we marginalize Equation (3) using the probability distribution P(ξ) on both sides, we obtain the following evolution equation:

$\begin{array}{ll}\frac{\partial \varphi (x,t)}{\partial t}=r\varphi (x,t)-\frac{\varphi (x,t)}{\Gamma (x)}{\displaystyle {\int }_{\Omega }\varphi }(y,t) \alpha (x,y)dy.& (8)\end{array}$

Where Γ(x) is defined as:

$\begin{array}{ll}\Gamma (x)=\text{exp}\left(-\mu x^2-\frac{{\sigma }_{\xi }^2{x}^4}{2}\right)\frac{1+\text{erf}\left(\frac{\mu }{{\sigma }_{\xi }\sqrt{2}}\right)}{1+\text{erf}\left(\frac{\mu +{\sigma }_{\xi }^2{x}^2}{{\sigma }_{\xi }\sqrt{2}}\right)} .& (9)\end{array}$

The stationary distribution is the solution of:

$\begin{array}{ll}r\Gamma (x)={\displaystyle {\int }_{\Omega }\varphi }(y)\alpha (x,y)dy.& (10)\end{array}$

All simulations were carried out using the software Mathematica [22].

3. Results

3.1. Phenotypic Diversity is Not a Universal Outcome of the Deterministic LVC Model

As discussed above, the deterministic, Gaussian LVC model does not always lead to evolutionary branching. In fact, when the effect of competition predominates over the effect of the carrying capacity (k > a), the population evolves toward a regime of stabilizing selection, with a consequent reduction in phenotypic diversity. In contrast, when the stabilizing component is stronger than the frequency-dependent component of selection (a > k), the resulting stationary distribution is unstable, and depends on the shape parameters of the carrying capacity and competition functions (n_k and n_α).

In the most frequently studied case, that of a Gaussian distribution (n_α = n_k = 2.0), a carrying capacity of large width (small k), ensures the maintenance of phenotypic diversity. However, under this conditions the model does not lead to branching (Figure 1B). In contrast, by assuming non-Gaussian shape parameters (e.g., n_α = n_k = 4.0), the model leads to evolutionary branching (Figure 1C) [13]; and diversity can persists even for values of a smaller than k, leading to branching approximately at 4a = k [9].

FIGURE 1

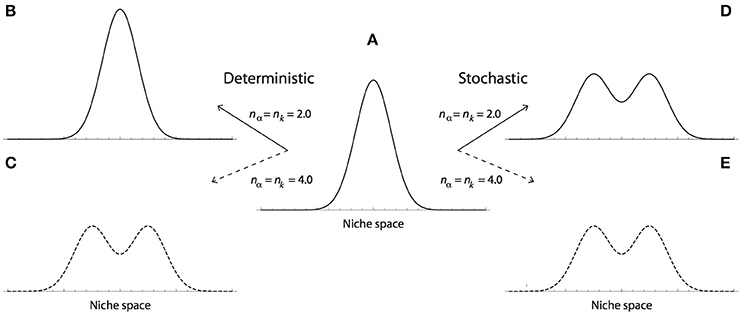
Figure 1. Deterministic vs. stochastic evolutionary dynamics of the Lotka-Volterra competition model. The evolutionary dynamics of the LVC model under a regime of frequency-dependent selection (i.e., a > k); with either deterministic (B,C), or stochastic (D,E) environmental conditions. Under these conditions, the model leads to two possible evolutionary outcomes, which depend on the relation between the shape parameters of the competition and carrying capacity functions (n_α and n_k). The maintenance of phenotypic diversity and evolutionary branching, are illustrated by a unimodal and bimodal phenotypic distributions, respectively. (A) Initial, bell-shaped distribution of phenotypic diversity, ϕ(x, t = 0). (B,C) Under deterministic conditions, evolutionary branching is not a granted outcome of the LVC model. (B) In the case of Gaussian functions (n_α = n_k = 2.0), the model predicts the maintenance of phenotypic diversity. (C) When the carrying capacity and competition functions are quartic (n_α = n_k= 4.0), stabilizing selection remains if: k > a. However, if k < a, frequency-dependent selection leads to branching. (D,E) Stochastic fluctuations lead to branching even in the Gaussian case. (D) Under stochastic conditions, even Gaussian competition and carrying capacity functions (n_α = n_k = 2.0), lead to evolutionary branching. (E) As in the deterministic case, when the carrying capacity and competition functions are quartic (n_α = n_k= 4.0), the model leads to branching. Both axes are in arbitrary units.

Thus, the deterministic LVC model shows that in order for diversification to lead to evolutionary branching, the frequency-dependent component of selection must predominate over the stabilizing component (i.e., a > k). Under these circumstances, the model can lead to branching only if the shape parameters of the carrying capacity and competition functions are larger than 2 (e.g., quartic). We emphasize, however, that under the more plausible biological scenario of a Gaussian function (n_α = n_k = 2.0), phenotypic diversity persist only if a > k; whereas evolutionary branching never happens (Figure 1B).

3.2. Environmental Fluctuations Induce Evolutionary Branching

We wanted to explore the role of stochasticity in the maintenance of phenotypic diversity and the conditions that lead to evolutionary branching. Because of their pervasiveness in nature, we decided to explore fluctuations arising from the interaction between individuals and their environment. Fluctuations arising from the interaction between individuals and their environment can impact the ability of a species to exploit resources, either because phenotypes may fluctuate in their efficiency of resource acquisition/consumption, or because the availability of resources may on itself be subject to fluctuations.

As described above, we constructed an stochastic version of the LVC model by introducing environmental fluctuations as Gaussian random noise in the width of the carrying capacity function (Equations 4–6). The strength of fluctuations in this model can be tuned by the deviation parameter σ_ξ. Larger values of σ_ξ translate into stronger fluctuations, while by setting σ_ξ = 0, we recover the deterministic version of the model. The model assumes no spatio-temporal correlations.

In order to explore the effect of fluctuations on the dynamics of the model, we use as initial conditions a bell-shaped phenotypic distribution: $\varphi (x,0)=c_0{e}^{-x^2/{\sigma }_0^2}$; with c₀ = 0.5, σ₀ = 0.4, and Gaussian shape parameters (i.e., n_α = n_k = 2.0). In agreement with a regime of frequency-dependent selection (Figure 1A), we set competition and carrying capacity functions parameters as: a = 2 and μ = 1. Recall that under these conditions, the model does not lead to evolutionary branching (see for instance [13]).

As illustrated in Figure 1D, we observe that the introduction of environmental fluctuations translates into phenotypic diversity and evolutionary branching. Under the model parameters tested here, the effect of environmental fluctuations on branching seem independent of increments in the shape parameters (Figure 1E). Indeed, the evolution of the marginalized model, defined by Equations (8, 9) and obtained from numerical simulations, shows that phenotypic diversification emerges early during the evolutionary dynamics of a population experiencing environmental fluctuations (Figure 2A). Numeric simulations of Equation (1), using the stochastic carrying capacity described in Equations (4–6), lead to the same result (Figure 2B).

FIGURE 2

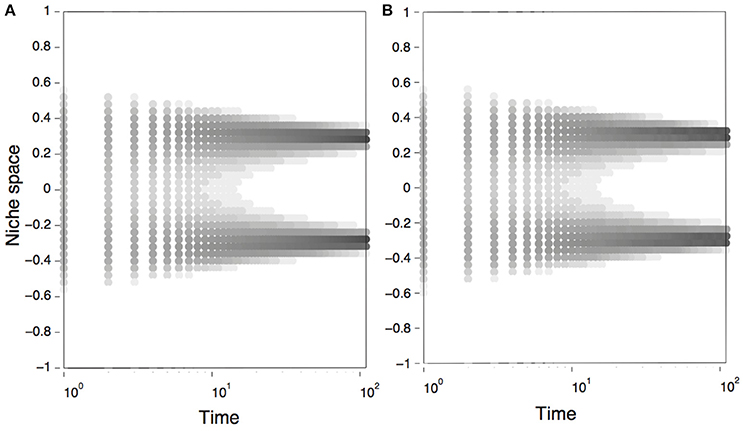
Figure 2. Dynamics of the Lotka-Volterra Competition models studied in this work. Panels show the temporal dynamics, obtained by numerical simulations, of a population using the marginalized model (A), defined by Equations (8–9); and the stochastic model (B), defined by Equations (1, 4–6). As initial conditions we used a bell–shaped distribution of phenotypes ($\varphi (x,0)=c_{0}exp(-x^2/{\sigma }_0^2)$, with c₀ = 0.5, σ₀ = 0.4), Gaussian shape parameters for the competition and carrying capacity function (n_α = n_k = 2.0); and a regime of frequency-dependent selection. Parameters were: r = 1, a = 2, μ = 1, and σ_ξ = 1. Both axes are in arbitrary units.

In order to study the sensitivity of our previous result to the degree of noise in the model, we performed numerical simulations using the previous parameters and different values of σ_ξ, ranging from 0.15 to 0.85. The final solutions for the evolution of the full stochastic equation show complex behaviors (Figure 3). We observe the emergence of branching at values of σ_ξ as small as 0.35.

FIGURE 3

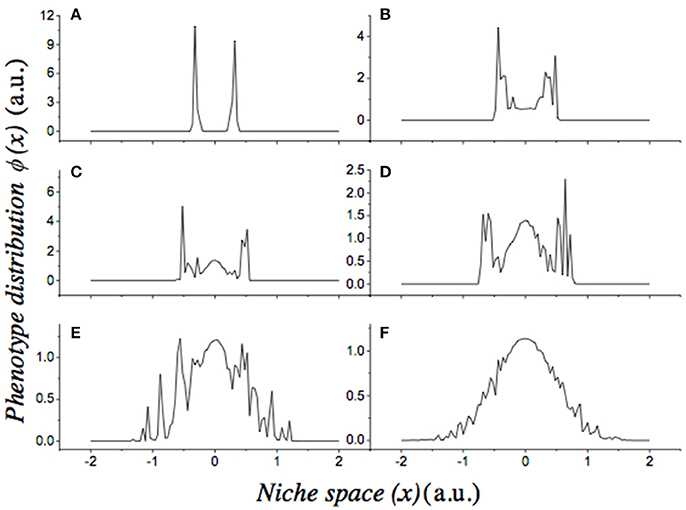
Figure 3. Effect of noise on the stochastic dynamics of the Lotka-Volterra Competition model. Panels show the final phenotypic distributions (ϕ(x)) of independent stochastic simulations carried out under increasing levels of noise [σ_ξ]. From panels (A–F), the values of σ_ξ are: 0.85, 0.65, 0.55, 0.45, 0.35, 0.15, respectively. In all cases, the initial condition is a bell–shaped distribution of phenotypes: $\varphi (x,0)=c_{0}exp(-x^2/{\sigma }_0^2)$, with c₀ = 0.5, σ₀ = 0.4. We used Gaussian shape parameters: n_α = n_k = 2.0; and a regime of frequency-dependent selection. Parameters were: r = 1, a = 2, and μ = 1. Each simulation was performed for 10⁴ time steps. Both axes are in arbitrary units.

As exemplified in Figure 2, our main result shows how the introduction of environmental fluctuations in the deterministic LVC model leads to strong levels of phenotypic diversity, and to evolutionary branching. This result confirms that even in the absence of strong assumptions used by previous models, environmental fluctuations relax the conditions for evolutionary branching.

4. Discussion

The Lotka-Volterra competition model has been extensively used to study the interplay between species interactions, phenotypic diversity and the onset of evolutionary branching [9, 10, 12, 13, 19, 23, 24]. A well-known result of this model is the existence of a link between the interactions of individuals and their environment (i.e., carrying capacity), vs. the interaction between individuals with other individuals (e.g., competition). Such a link can lead to either a regime of stabilizing selection, where a population evolves highly similar individuals; or to a regime of frequency-dependent selection, which leads to phenotypic diversification and evolutionary branching. According to this result, however, phenotypic diversity only evolves under strong levels of frequency-dependent selection and requires strong assumptions, such as modifying the shape parameters of the carrying capacity and competition functions to larger, unrealistic values [9, 13].

Here, we introduced an stochastic version of the LVC model. The model shows that environmental fluctuations can alleviate the strong assumptions required for evolutionary branching in the deterministic LVC model. Notably, and in contrast to previous studies using the deterministic LVC model, preliminary explorations of the stochastic model presented here, seem to render the conditions for branching independent of assumptions in the shape parameters of the carrying capacity and competition functions.

Instead of focusing on a particular source of noise, we sought to model fluctuations as the result of a complex mixture of environmental factors. We introduced fluctuations as white noise in the carrying capacity function, which encodes constraints on the interaction between individuals and their environment. More specifically, one can think of the carrying capacity as a constraint on two properties of an individual's niche [8]. First, niche position, which describes the resource for which the phenotype optimizes efficient consumption. And second, niche width, which captures the change in the efficiency of resource consumption as a function of phenotype divergence. Our model focused on this second property of the interaction between individuals and their environment.

Previous studies exploring the role of fluctuations in the evolution of phenotypic diversity distinguished between demographic and environmental sources of noise. It is well-known that strong competition can result on demographic (i.e., population size) fluctuations [25], which can lead to the extinction of newly evolved phenotypes. Consistent with this intuition, demographic noise can delay evolutionary branching, by driving a population to cycles of diversification and extinction [19, 26].

In contrast to the effect of demographic fluctuations, environmental fluctuations have shown contradictory results [12, 26, 27]. In agreement with our result, a lottery model of a fluctuating fitness optimum showed that fluctuations can facilitate branching [27]. Sasaki and Ellner [27] constructed a model based on a deterministic dynamics and showed that small departures from an homogeneous resource level can lead to strong changes in population diversity. In the work presented here, we reached the same conclusion by exploring the role of temporal fluctuations through a stochastic integro–differential equation.

Under conditions of strong fluctuations, and when individuals respond to the environment in a correlated manner, environmental noise have also been observed to delay evolutionary branching [12]. Because in our model we did not study correlations in the response to fluctuations, we can not compare it directly to the model in Johansson and Ripa [12]. We note, however, that the types of fluctuations introduced in Johansson and Ripa [12], affect the entire population fitness, whereas fluctuations in our model affect explicitly the environmental component of the LVC model (see Equation A6 in Supplementary Material of [12]). Mechanistically, our model introduces fluctuations in the width of the carrying capacity function. Overall, the simulation results we observed, seem to arise naturally from the marginalization of the effective carrying capacity (Equation 9). The probability distribution involved in such marginalization encapsulates distributions with small (i.e, Dirac-delta), to large deviations (e.g., quartic). Consequently, variation in the width parameter of the carrying capacity can affect the kurtosis of the phenotypic distribution for a short interval, thereby mimicking the effect of increasing the shape parameter, which is known to lead to evolutionary branching [13, 28]. Here, we note that in addition to the carrying capacity, alternative formulations of the competition function may have an independent effect on the evolution of phenotypic diversity. The effects of alternative kernel functions have been studied in the absence of noise [29]. In the results presented here, however, and because of arguments on the spatial distribution of individuals [30], we used a constant, Gaussian kernel.

As observed in this and other studies, the resulting effect of environmental noise depends on its mathematical formulation, as well as on correlations in the response to fluctuations. A comparative analysis of existing models incorporating fluctuations and temporal correlations, alternative mathematical formulations of noise, as well as a deeper exploration of the parameters of the stochastic LVC model, will be needed to fully understand the effect of fluctuations on phenotypic diversity. Overall, our work highlights the role of fluctuations as an alternative to the strong assumptions used in previous studies; and adds to the mounting evidence suggesting that the conditions for evolutionary branching are more relaxed than anticipated.

Author Contributions

Both authors contributed equally to the conception of the work, drafting the work, or revising it critically for important intellectual content. Final approval of the version to be published. Agreement to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

MF thanks the hospitality received at the SFI and FONDECYT 1140278.

References

1. Coyne JA, Orr HA. Speciation, Vol. 37. Sunderland, MA: Sinauer Associates (2004).

Google Scholar

2. Thompson JN. Relentless Evolution. Chicago: University of Chicago Press (2013).

Google Scholar

3. Brown JS, Pavlovic NB. Evolution in heterogeneous environments: effects of migration on habitat specialization. Evol Ecol. (1992) 6:360–82.

Google Scholar

4. Abrams PA, Matsuda H, Harada Y. Evolutionarily unstable fitness maxima and stable fitness minima of continuous traits. Evol Ecol. (1993) 7:465–87.

Google Scholar

5. Metz JA, Geritz SA, Meszéna G, Jacobs FJ, van Heerwaarden JS. Adaptive Dynamics: A Geometrical Study of the Consequences of Nearly Faithful Reproduction. IIASA Working Paper. IIASA, Laxenburg. (1995).

Google Scholar

6. Christiansen FB, Loeschcke V. Evolution and intraspecific exploitative competition I. One-locus theory for small additive gene effects. Theor Popul Biol. (1980) 18:297–313.

Google Scholar

7. Doebeli M, Dieckmann U. Evolutionary branching and sympatric speciation caused by different types of ecological interactions. Am Nat. (2000) 156:S77–101. doi: 10.1086/303417

CrossRef Full Text | Google Scholar

8. Ackermann M, Doebeli M, Gomulkiewicz R. Evolution of niche width and adaptive diversification. Evolution (2004) 58:2599–612. doi: 10.1111/j.0014-3820.2004.tb01614.x

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Doebeli M, Ispolatov I. Complexity and diversity. Science (2010) 328:494–7. doi: 10.1126/science.1187468

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Dieckmann U, Doebeli M. On the origin of species by sympatric speciation. Nature (1999) 400:354–7.

PubMed Abstract | Google Scholar

11. Dieckmann U. Adaptive Speciation. Cambridge, UK: Cambridge University Press (2004).

Google Scholar

12. Johansson J, Ripa J. Will sympatric speciation fail due to stochastic competitive exclusion? Am Nat. (2006) 168:572–8. doi: 10.1086/507996

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Doebeli M, Blok HJ, Leimar O, Dieckmann U. Multimodal pattern formation in phenotype distributions of sexual populations. Proc R Soc Lond B Biol Sci. (2007) 274:347–57. doi: 10.1098/rspb.2006.3725

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Scheffer M, van Nes EH. Self-organized similarity, the evolutionary emergence of groups of similar species. Proc Natl Acad Sci USA (2006) 103:6230–5. doi: 10.1073/pnas.0508024103

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Sturmbauer C. Explosive speciation in cichlid fishes of the African Great Lakes: a dynamic model of adaptive radiation. J Fish Biol. (1998) 53:18–36.

Google Scholar

16. Danley PD, Kocher TD. Speciation in rapidly diverging systems: lessons from Lake Malawi. Mol Ecol. (2001) 10:1075–86. doi: 10.1046/j.1365-294X.2001.01283.x

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Bijlsma K, Loeschcke V. Environmental Stress, Adaptation and Evolution, Vol. 83. Berlin: Birkhäuser (2013).

Google Scholar

18. Ives A, Gross K, Klug J. Stability and variability in competitive communities. Science (1999) 286:542–4.

PubMed Abstract | Google Scholar

19. Claessen D, Andersson J, Persson L, de Roos AM. Delayed evolutionary branching in small populations. Evol Ecol Res. (2007) 9:51–69.

Google Scholar

20. Wakano JY, Iwasa Y. Evolutionary branching in a finite population: deterministic branching vs. stochastic branching. Genetics (2013) 193:229–41. doi: 10.1534/genetics.112.144980

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Fuentes MA, Cáceres MO. Computing the non-linear anomalous diffusion equation from first principles. Phys Lett A (2008) 372:1236–9. doi: 10.1016/j.physleta.2007.09.020

CrossRef Full Text | Google Scholar

22. Wolfram Research I. Mathematica. Champaign, IL: Wolfram Research, Inc. (2016).

Google Scholar

23. MacArthur R, Levins R. The limiting similarity, convergence, and divergence of coexisting species. Am Nat. (1967) 101:377–85.

Google Scholar

24. Roughgarden J. Evolution of niche width. Am Nat. (1972) 106:683–718.

Google Scholar

25. May RM. Stability in randomly fluctuating versus deterministic environments. Am Nat. (1973) 107:621–50.

Google Scholar

26. Johansson J, Ripa J, Kuckländer N. The risk of competitive exclusion during evolutionary branching: effects of resource variability, correlation and autocorrelation. Theor Popul Biol. (2010) 77:95–104. doi: 10.1016/j.tpb.2009.10.007

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Sasaki A, Ellner S. The evolutionarily stable phenotype distribution in a random environment. Evolution (1995) 49:337–50.

Google Scholar

28. Sasaki A. Clumped distribution by neighbourhood competition. J Theor Biol. (1997) 186:415–30.

Google Scholar

29. Leimar O, Sasaki A, Doebeli M, Dieckmann U. Limiting similarity, species packing, and the shape of competition kernels. J Theor Biol. (2013) 339:3–13. doi: 10.1016/j.jtbi.2013.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Pigolotti S, López C, Hernández-García E. Species clustering in competitive Lotka-Volterra models. Phys Rev Lett. (2007) 98:258101. doi: 10.1103/PhysRevLett.98.258101

PubMed Abstract | CrossRef Full Text | Google Scholar