- 1Faculty of Pure and Applied Mathematics, Wroclaw University of Science and Technology, Wrocław, Poland
- 2Department of Theoretical Physics, Faculty of Fundamental Problems of Technology, Wroclaw University of Science and Technology, Wrocław, Poland
We investigate a kinetic Ising model with the Metropolis algorithm on the temporal directed random q-regular graph. We introduce a rewiring time τ as a parameter of the model and show that there is a critical τ = τ* above which the model exhibits continuous order-disorder phase transition and below which the transition is discontinuous. We discuss our findings in a light of the very recent results obtained for a generalized kinetic Ising model on quenched and annealed networks.
1. Introduction
Extensive studies have shown that order-disorder phase transitions in the equilibrium Ising model with the nearest-neighbors interactions are very robust to the type of a network. This means that observed transitions are not only continuous but also characterized with the same set of bulk critical exponents on quenched and annealed networks [1]. Moreover, it has been shown recently that even for the non-equilibrium Ising model with the heat-bath dynamics on the directed random q-regular graph (q-RRG) continuous phase transitions are observed [2]. Therefore results obtained in Jȩdrzejewski et al. [3], showing that kinetic Ising model with Metropolis dynamics can also display discontinuous phase transitions, were puzzling and confusing. To solve this puzzle a new generalized model with two heat baths—one for the Ising spins at temperature Ts and second for links of the graph at temperature TL, has been recently proposed [4]. It has been shown that on contrary to the models investigated previously by Lee et al. [1], the kinetic model studied in Jȩdrzejewski et al. [3] is an non-equilibrium one and corresponds to the infinite temperature TL of links. Furthermore, it has occurred that there is a critical temperature at which switch from discontinuous to continuous phase transition is observed (so called tricritical point) [4]. However, the question arose if such a tricriticality could be exclusively explained on the basis of non-equilibrium driving. In other words, would it be possible to observe such a behavior also for other single-spin-flip dynamics (e.g., heat-bath)?
The above question has been asked and answered in Jȩdrzejewski et al. [5]. It has been shown that on the annealed non-equilibrium network, which within the generalized model by Park and Noh [4] corresponds to the infinite temperature of links (TL = ∞), different dynamics leads to completely different results. For example, the model with heat-bath algorithm at TL = ∞ displays a continuous phase transition, and the critical temperature only slightly deviates from the equilibrium one. On the other hand, the generalized Metropolis algorithm gives qualitatively different behavior, which depends on the model's parameter. It has been also observed that generally higher flipping probabilities lead to discontinuous phase transitions. Furthermore, based on results obtained within generalized model with two heat-baths [4] and modified Metropolis algorithm studied in Jȩdrzejewski et al. [5], it has been suggested that tricriticality, i.e., switch from continuous to discontinuous phase transitions is driven by noise.
There are many possibilities to incorporate noise into the system. In Park and Noh [4] it has been introduced by the additional heat-bath for links, whereas in Jȩdrzejewski et al. [5] it has been introduced by the probability of flip in the absence of the energy changes W0: in the original Metropolis algorithm W0 = 1, whereas for the heat-bath dynamics W0 = 1/2. Within the generalized zero-temperature Glauber dynamics, W0 can change continuously [6], which leads to very interesting results [7–9]. The idea of W0 as a parameter has been used in Jȩdrzejewski et al. [5] and it has been shown that there is a tricritical point : for the transition is continuous and for it is discontinuous.
Here we propose another possibility to introduce noise into the system. We investigate the model on a temporal network and introduce rewiring time τ, as a parameter. Because τ = ∞ corresponds to quenched network and τ = 1 to TL = ∞ (i.e., annealed network), one could expect that there is a critical time scale τ* that separates these two regimes. Following very recent studies [4, 5], we analyze a kinetic Ising model with Metropolis dynamics on the temporal directed random regular graph to check whether this type of noise will also lead to tricriticality.
Temporal networks are particularly useful to model social systems [10]. However, if the dynamics on the network is very rapid compared to the dynamics of the contacts then there is no need to model the system as a temporal network [10]. The model we investigate here is not a social model, but it could be treated as such Nyczka and Sznajd-Weron [11]. In fact, the q-neighbor Ising model Jȩdrzejewski et al. [3], reformulated later in terms of the kinetic Ising model on random regular graph, has been inspired by the q-voter model of opinion dynamics [12–15]. This is not entirely clear what it the scale of opinion changes and definitely exploring how opinion dynamics will be influenced by the dynamics of a network is an interesting task. However, this is not a paper about networks. Time-varying graph is for us merely an excuse to incorporate noise into the system and check how it will influence observed phase transitions. Nevertheless, we hope that our results may be also inspiring for people dealing with opinion dynamics on networks and also for this reason we use a graphical representation of so called spinson (spin+person) introduced by Nyczka and Sznajd-Weron [11] to illustrate the model in Figure 1.
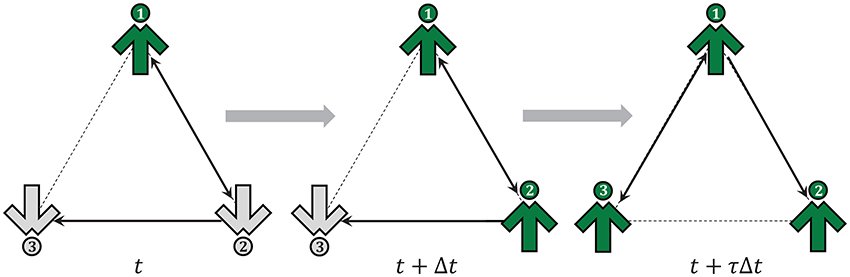
Figure 1. Sample evolution of the system on the temporal directed random regular graph: states at time t, t + Δt and t + τΔt are shown.
2. Model
We investigate a kinetic Ising model with the Metropolis algorithm on the temporal directed random q-regular graph (q-RRG) of size N. We describe such a graph at time t by a non-symmetric adjacency matrix A(t) with elements Aij(t) ≠ Aji(t), i, j = 1, …, N. If node i can be influenced by node j at time t then Aij(t) = 1, otherwise Aij(t) = 0 and therefore in our case:
Above relation means that each node i can be influenced by q nodes but not necessary influences q other nodes. As usually, we set Aii = 0 to avoid self-loops.
Each node of a graph is occupied by exactly one spin described by dynamic variable Si(t) = ±1, i = 1, 2, …, N. The state of spins at time s(t) = (S1(t), S2(t), …, SN(t)) can be changed at each elementary time step due to the interactions between spins and thermal fluctuations. Additionally, in Jȩdrzejewski et al. [3, 5] the adjacency matrix A(t) could change at each elementary time step, i.e., in general A(t + Δt) ≠ A(t). In this paper we introduce a new parameter τ, which denotes a number of elementary steps during which a graph (and simultaneously adjacency matrix) does not change. It means that for a period of time τΔt a graph is fixed. In Figure 1 we present an example of a system of N = 3 nodes with degree q = 1 at three time steps: t, t + Δt, t + τΔt.
At time t a state of a system is given by:
In the next step t + Δt the state of spins changes s(t + Δt) = (+1, +1, −1) ≠ s(t) but adjacency matrix does not change, i.e., A(t + Δt) = A(t). After τ steps spins and links are changed.
The network itself evolves completely randomly, i.e., after each τ steps we choose a new adjacency matrix at random with the constrain given by Equation (1), whereas spin variables change according to Metropolis algorithm, which means that each elementary time step consists of three consecutive steps:
1. We choose randomly one spin i from the uniform distribution U[0, N]
2. We calculate the change of the energy, that would occur after a spin flip:
3. We flip a spin (Si(t + Δt) = −Si(t)) with probability:
As usual one Monte Carlo step (MCS) consists of N elementary steps, which means that Δt = 1/N. As we have mentioned, network changes after each τ steps completely randomly. Another approach has been used very recently in Park and Noh [4]. They have proposed to consider a system in contact with two heat baths: the Ising spins are in thermal contact with the heat bath at temperature TS, whereas the links are in thermal contact with the heat bath at temperature TL. The Hamiltonian for the whole system including the spins and the links was given by:
and not only spin flips but also rewiring was carried out with a certain probability depending on the energy difference:
where for brevity A′ = A(t + Δt), A = A(t), s′ = s(t + Δt), s = s(t). This means that the probability of flipping the spin was given by:
and the probability to accept a new configuration of links by:
The original q-neighbor Ising model, introduced in Jȩdrzejewski et al. [3], is a limiting case of the above model (i.e., corresponds to TL = ∞). In this paper we propose completely different approach—we do not claim that the network itself is in contact with a heat-bath. It changes randomly at regular time intervals. Yet, we could propose a generalized model based on the model with two heat-baths but additionally with two time scales: tS for spins and tL = τtS for links. In such a case the model we consider here would correspond again to TL = ∞. This might be an interesting idea for the future.
We are aware that the complete rewiring at every τ steps is perhaps not the most appropriate in the context of e.g., changing friends in social systems. Probably a continuous rewiring (at every step but only with a certain probability) would be more reliable. Indeed we could generalize our model by introducing a probability of rewiring prew in a single time step. Within such a generalization the model described above would correspond to prew = 1. However, as we have checked, such a generalization would only rescale results, since they depend only on τ/prew, not separately on τ and prew. For example that behavior of the model with τ = 100 and prew = 0.01 is exactly the same as for τ = 104 and prew = 1.
3. Results
Our generalized model reduces to the q-neighbor Ising model for τ = 1 and therefore should display a discontinuous phase transition for q ≥ 4. On the other hand for τ = ∞ it reduces to the equilibrium Ising model on q-RRG, which means that should always display a continuous phase transition. This means that somewhere in between, for a critical τ* we should observe a switch from discontinuous to continuous phase transition. The maximum jump of the order parameter:
and simultaneously the maximum hysteresis has been observed for q = 4. Moreover, also recent papers focused on q = 4 [4, 5] and therefore we will focus here on this value.
We investigate the model by Monte Carlo simulations and estimate the magnetization of the system as an ensemble average over M samples:
where mj is the stationary magnetization in j-th sample, defined as:
here denotes a value of an i-th spin in the j-th sample in the stationary state. All results presented in this paper has been averaged over M = 102 samples.
To check the type of the phase transition between ordered (ferromagnetic) and disordered (paramagnetic) phase we start with two types of initial conditions:
1. ordered, i.e., Si(0) = 1 for all i = 1, …, N,
2. random, i.e., with probability 1/2 initial value of spin Si(0) = 1 and with complementary probability Si(0) = −1.
As long as the phase transition is discontinuous we should obtain two temperatures below which the system is ordered and above which m = 0: T1 for the ordered initial conditions and T2 for the random initial conditions. For τ > τ* spinodal lines T1, T2 should collapse to a single line of a continuous phase transition .
In Figure 2 we present dependence between the stationary value of magnetization m and temperature T for two types of initial conditions for the system size N = 104. It is seen that indeed for small τ results depend on initial conditions. With increasing τ hysteresis decreases and eventually the phase transition between ordered ferromagnetic and disordered paramagnetic phases becomes continuous. It is worth to recall here, that the real phase transitions and simultaneously real size of hysteresis are defined only in the thermodynamic limit N → ∞. If simulated system is too small one can mistakenly draw a conclusion of the continuous phase transition because the hysteresis increases with the system size (see Figure 3). This phenomenon is probably well known to all researchers that are specialized in numerical analysis of the phase transitions but we hope that results presented in Figure 3 and the above comment will be instructive for the newcomers in the field. From Figure 2 one can determine spinodal lines T1(τ) and T2(τ) and this allows to estimate the critical value of τ = τ* above which the transition switches to continuous.
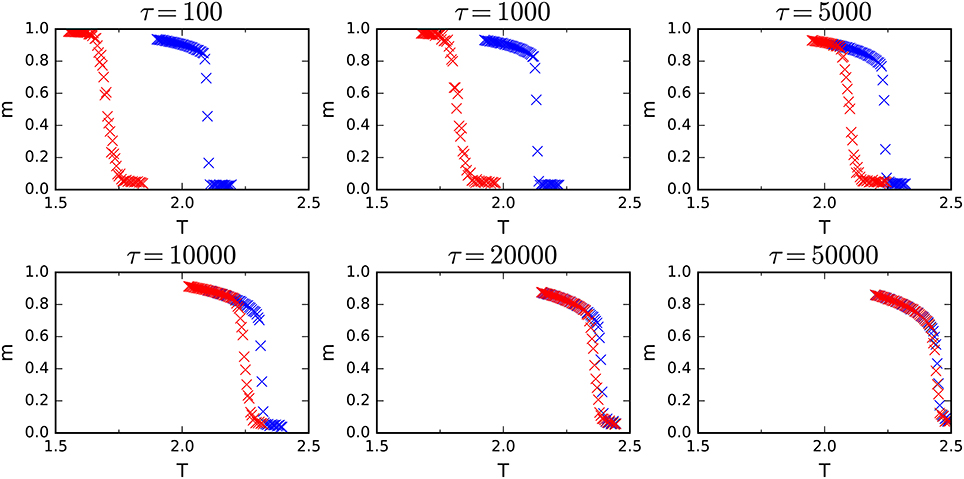
Figure 2. Dependence between the stationary value of magnetization m and temperature T for two types of initial conditions: random (red) and ordered (blue). Panels from top left to bottom right show results for growing rewiring times τ. It is seen that hysteresis decreases with increasing τ and for large τ phase transition is continuous.
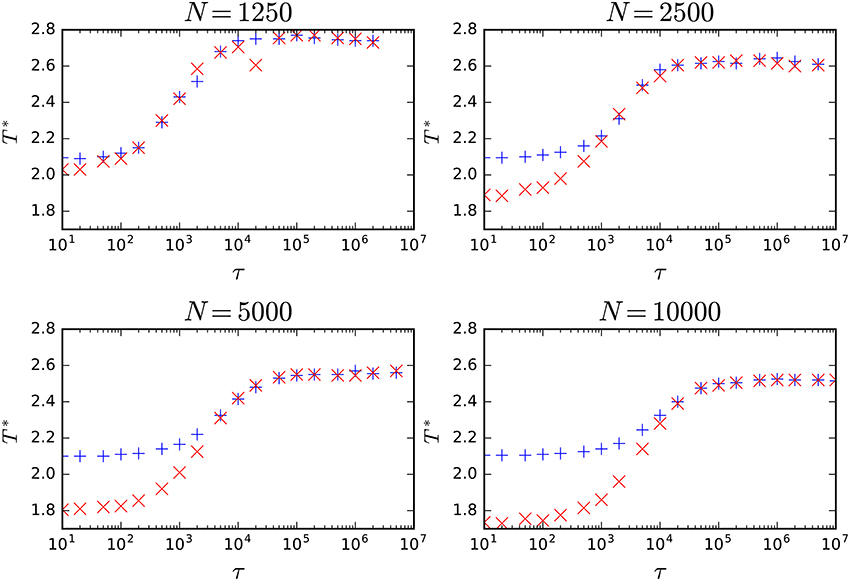
Figure 3. Spinodal lines T*(τ), i.e., dependencies between transition temperatures T1 and T2 and the rewiring time τ above which an order parameter m = 0 for two types of initial conditions, random (x) and ordered (+) respectively. Between these lines both phases—paramagnetic and ferromagnetic—coexist.
It is seen in Figure 3 that with increasing τ spinodal lines are approaching each other and eventually tricritical point is reached at τ*. Tricritical behavior for q = 4 has been also observed by Park and Noh [4] withing the Ising model on fluctuating network with two heat-baths and for the generalized Metropolis algorithm [5].
We would like to stress here that determining the exact value of the critical temperature T*(τ) for intermediates value of 1 < τ < ∞ and hence the critical rewiring time τ* is far from being trivial. In equilibrium statistical mechanics, the standard procedure to identify the universality class and to estimate the critical temperature within the Monte Carlo simulations would be to calculate the reduced fourth order cumulant of the order parameter, widely known as the Binder cumulant, which for the Ising model reduces to Landau and Binder [16]:
Drawing curves for U4 as a function of a temperature for different sizes N one can determine the transition point from the common intersection point.
However, it is far from being obvious if the powerful cumulant intersection method can be applied in non-equilibrium systems. For example it cannot be used to absorbing phase transitions [6]. Nevertheless, we have decided to calculate U4 for several values of τ to check if this method works for our non-equilibrium model. Until now we have measured the rewiring time τ in elementary steps. However, if we want to compare results for different sizes the rewiring time τ should be measured in Monte Carlo steps instead of elementary steps and therefore τ is given in MCS in Figure 4. It is seen in Figure 4 that the method works pretty well for τ ≥ 5MCS. It works even for τ ≈ 1MCS. Although the intersection is not perfect it allows to estimate the critical temperatures, e.g., T*(τ = 1MCS) ≈ 2.3 and T*(τ = ∞) ≈ 2.49, which agrees pretty well with results presented in Figures 2–4 suggest that τ* is of the order of 1MCS but to determine the precise value of the tricritical point τ* is not so easy.
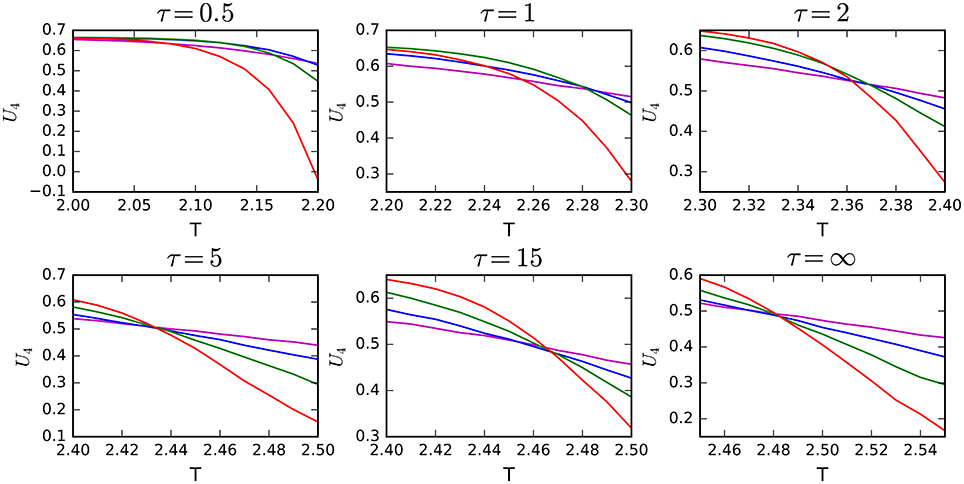
Figure 4. Binder cumulant, i.e., the reduced fourth order cumulant of the order parameter defined by Equation (12), as a function of temperature T for several values of the rewiring times τ measured in the Monte Carlo steps for N = 1,250 (red), N = 625 (green), N = 312 (blue) and L = 161 (magenta).
It should be noticed here that the critical temperature for large values of τ (i.e., almost quenched network) approaches T* ≈ 2.49, which is a significantly lower value that one given by the analytical formula derived by Dorogovtsev et al. for the equilibrium Ising model on networks with an arbitrary distribution of connections [17]:
where J is a coupling constant. For q-RRG degrees k of all nodes are equal to q, i.e., < k2 > = q2 and < k > = q. Moreover, we have assumed that J = 1 and thus the critical temperature should be equal:
which for q = 4 gives T*(4) = 2.88. However, as noticed by Lipowski et al., an Ising model on the directed network is a non-equilibrium model [18] and therefore this is not surprising that our results differ from those obtained by Dorogovtsev et al. [17]. Moreover, our result is consistent with the results for the Ising model on undirected q-RRG, because it has been shown that for the Ising model with the Metropolis dynamics the critical temperature for the annealed network is significantly lower than for the quenched network [5]. Yet another result should be commented here, namely the critical temperature for the Ising model on directed q-RRG with the heat-bath dynamics [2]. In particular for q = 4 the critical temperature has been reported to be close to 3.089, which again is significantly larger value than T* obtained here. Again, this is not very surprising in the light of recent findings by Jedrzejewski et al. because it has been shown numerically and analytically that the critical temperature for the Ising model on the annealed q-RRG with the heat bath dynamics is significantly larger than for the same model with the Metropolis algorithm.
4. Conclusion
The aim of this paper was to check how the random rewiring of a network influences phase transitions in the kinetic Ising model with Metropolis algorithm on q-RRG. It has been shown in Jȩdrzejewski et al. [3] that if a network is rewired in every elementary time step then an order-disorder phase transition becomes discontinuous for q ≥ 4, which has been a puzzling result. Therefore we decided to rewire the network not in every elementary step, but every τ steps and see how this would influence results. We have expected that for large τ the model will reproduce results of the equilibrium Ising model on the quenched q-RRG. However, we did not have an intuition if the quenched limit will be observed only for τ = ∞ or maybe for any τ > 1, or above some critical value τ*. It has occurred that indeed τ* exists but its value is comparable with a length of a single Monte Carlo step. This means that results of the kinetic Ising model on the temporal q-RRG, which changes randomly after each Monte Carlo step, are almost identical with results for the model on the static q-RRG. We have presented here results only for q = 4, but our conclusions are valid also for other values of q > 3. For q = 3 the phase transition is always continuous and there are no phase transitions for q = 1 and q = 2 [2, 3].
Author Contributions
GM conducted all simulations and analyzed results. KS designed and supervised research and wrote the article.
Funding
This work is supported partially by funds from the National Science Centre (NCN, Poland) through grant no. 2016/21/B/HS6/01256 and by PLGrid Infrastructure. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Lee SH, Ha M, Jeong H, Noh JD, Park H. Critical behavior of the Ising model in annealed scale-free networks. Phys Rev E (2009) 80:051127. doi: 10.1103/PhysRevE.80.051127
2. Lipowski A, Gontarek K, Lipowska D. Robust criticality of an ising model on rewired directed networks. Phys Rev E (2015) 91:062801. doi: 10.1103/PhysRevE.91.062801
3. Jȩdrzejewski A, Chmiel A, Sznajd-Weron K. Oscillating hysteresis in the q-neighbor Ising model. Phys Rev E (2015) 92:052105. doi: 10.1103/PhysRevE.92.052105
4. Park JM, Noh JD. Tricritical behavior of nonequilibrium Ising spins in fluctuating environments. Phys Rev E (2017) 95:042106. doi: 10.1103/PhysRevE.95.042106
5. Jȩdrzejewski A, Chmiel A, Sznajd-Weron K. Kinetic Ising models with various single-spin flip dynamics on quenched and annealed random regular graphs. (2017) arXiv:submit/1828985.
6. Godrèche C, Luck JM. Metastability in zero-temperature dynamics: statistics of attractors. J Phys Cond Matt. (2005) 17:S2573–90.
7. Spirin V, Krapivsky PL, Redner S. Freezing in ising ferromagnets. Phys Rev E (2001) 65:016119. doi: 10.1103/PhysRevE.65.016119
8. Radicchi F, Vilone D, Meyer-Ortmanns H. Phase transition between synchronous and asynchronous updating algorithms. J Stat Phys. (2007) 129:593. doi: 10.1007/s10955-007-9416-8
9. Skorupa B, Sznajd-Weron K, Topolnicki R. Phase transition between synchronous and asynchronous updating algorithms. Phys Rev E (2012) 86:051113. doi: 10.1103/PhysRevE.86.051113
10. Holme P, Saramäki J. Temporal networks. Phys Rep. (2012) 519:97–125. doi: 10.1016/j.physrep.2012.03.001
11. Nyczka P, Sznajd-Weron K. Anticonformity or independence?-insights from statistical physics. J Stat Phys. (2013) 151:174–202. doi: 10.1007/s10955-013-0701-4
12. Castellano C, Munoz MA, Pastor-Satorras R. Nonlinear q -voter model. Phys Rev E (2009) 80:034031. doi: 10.1103/PhysRevE.80.041129
13. Nyczka P, Sznajd-Weron K, Cislo J. Phase transitions in the q-voter model with two types of stochastic driving. Phys Rev E Stat Nonlin Soft Matter Phys. (2012) 86(1 Pt 1):011105. doi: 10.1103/PhysRevE.86.011105
14. Mobilia M. Nonlinear q -voter model with inflexible zealots. Phys Rev E Stat Nonlin Soft Matter Phys. (2015) 92:012803.
15. Jedrzejewski A. Pair approximation for the q-voter model with independence on complex networks. Phys Rev E Stat Nonlin Soft Matter Phys. (2017) 95:012307. doi: 10.1103/PhysRevE.95.012307
16. Landau DP, Binder K. A Guide to Monte Carlo Simulations in Statistical Physics. 3rd Edn. New York, NY: Cambridge University Press (2009).
Keywords: kinetic Ising model, Metropolis algorithm, phase transitions, complex networks, temporal networks, opinion dynamics
Citation: Marcjasz G and Sznajd-Weron K (2017) Phase Transitions in the Kinetic Ising Model on the Temporal Directed Random Regular Graph. Front. Phys. 5:24. doi: 10.3389/fphy.2017.00024
Received: 13 March 2017; Accepted: 31 May 2017;
Published: 19 June 2017.
Edited by:
Michel Droz, Université de Genève, SwitzerlandReviewed by:
Kirsten Martens, Centre national de la recherche scientifique (CNRS), FranceAdam Lipowski, Adam Mickiewicz University in Poznań, Poland
Copyright © 2017 Marcjasz and Sznajd-Weron. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Katarzyna Sznajd-Weron, a2F0YXJ6eW5hLndlcm9uQHB3ci5lZHUucGw=
 Grzegorz Marcjasz
Grzegorz Marcjasz Katarzyna Sznajd-Weron
Katarzyna Sznajd-Weron