Nilpotent Quantum Mechanics: Analogs and Applications

The most significant characteristic of nilpotent quantum mechanics is that the quantum system (fermion state) and its environment (vacuum) are, in mathematical terms, mirror images of each other. So a change in one automatically leads to corresponding changes in the other. We have used this characteristic as a model for self-organization, which has applications well beyond quantum physics. The nilpotent structure has also been identified as being constructed from two commutative vector spaces. This zero square-root construction has a number of identifiable characteristics which we can expect to find in systems where self-organization is dominant, and a case presented after the publication of a paper by us on “The ‘Logic’ of Self-Organizing Systems” [1], in the organization of the neurons in the visual cortex. We expect to find many more complex systems where our general principles, based, by analogy, on nilpotent quantum mechanics, will apply.

Introduction

Three main developments form the background to this work. The first is a universal rewrite system, which is a scale-independent and fractal computational process of generating zero-totality alphabets, with seemingly very general application [1], The most immediate applications of the rewrite structure have been found in physics and biology, which brings us to the second development. Nilpotent quantum mechanics is a form of relativistic quantum mechanics/quantum field theory which can be derived from the rewrite system and which minimalizes the whole quantum apparatus to a single operator acting on a universal environment, which is its mirror image. The third development is that both the rewrite structure and nilpotent quantum mechanics require a combination of two vector spaces, each dual to the other, which provides a powerful model for self-organization [1].

Nilpotent quantum mechanics is the most immediately successful application of the universal rewrite system and serves as an almost perfect model for other applications. It is not so much that these applications derive directly from nilpotent quantum mechanics, rather that they derive from the structure which makes this form of quantum mechanics possible. Many characteristics can be described as identifiers of both the rewrite and the nilpotent structures, whether at the quantum mechanical level, or applicable in mathematics, chemistry, biology, or other areas of physics. We have proposed a number of such features as being detectable in systems of very different kinds and as thus being signatures of quantum-like organization or behavior, especially where self-organization is dominant [1], and we have identified a new one in the organization of the neurons in the visual cortex.

The Universal Rewrite System

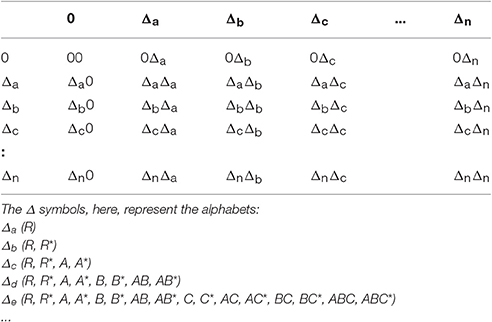
The universal rewrite system provides a computational approach to both mathematics and physics based on the idea of a zero totality alphabet [1]. We successively create alphabets in which “conjugation” represented by * ensures totality zero, and in which new creation is ensured by the regular appearance of anticommutative pairs A, B; C, D; etc., each of which is commutative to all the others:

$\begin{array}{ll}(\mathit{\text{R}},{\mathit{\text{R}}}^{*})(\mathit{\text{R}},{\mathit{\text{R}}}^{*})\Rightarrow (\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*})& (1)\end{array}$

$\begin{array}{ll}(\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*})(\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*})\Rightarrow (\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*},\mathit{\text{B}},{\mathit{\text{B}}}^{*},\mathit{\text{AB}},{\mathit{\text{AB}}}^{*})& (2)\end{array}$

Successive alphabets absorb the previous ones in the sequence, so creating a new cardinality. We may start at any arbitrary zero-totality alphabet but there is no natural beginning or end to the process, which can be summarized in Table 1.

TABLE 1

Table 1. The universal rewrite process.

An Algebra for the Rewrite Process

The rewrite process is more general than any particular mathematical interpretation, but such interpretations include both binary integers and digital logic, in addition to the algebraic series:

(1, −1)

(1, −1) × (1, i₁)

(1, −1) × (1, i₁) × (1, j₁)

(1, −1) × (1, i₁) × (1, j₁) × (1, i₂)

(1, −1) × (1, i₁) × (1, j₁) × (1, i₂) × (1, j₂)

(1, −1) × (1, i₁) × (1, j₁) × (1, i₂) × (1, j₂) × (1, i₃) …

In this interpretation, the anticommutative pairs A, B; C, D; E … are expressed as quaternion units, i₁, j₁; i₂, j₂; i₃…, each of which is commutative to all the others. By the fourth stage, we have repetition, which then continues indefinitely. An incomplete set of quaternion units (for example, i₃ in the sixth alphabet) becomes equivalent to the algebra of complex numbers. Mathematically, we can see the process of the creation of the zero totality alphabets as one of conjugation, followed by repeated cycles of complexification and dimensionalization (where each i is paired with a j).

At the point where the cycle repeats, we have what can be recognized as a Clifford algebra—the algebra of 3-D space, where the vectors i, j, k are constructed from i₁ i₂, j₁ i₂, i₁ j₁ i₂, and i₁, j₁, i₁ j₁ = k₁ and i₂, j₂, i₂ j₂ = k₂ are (mutually commutative) quaternion algebras of the form i, j, k.

(1, −1)

(1, −1) × (1, i)

(1, −1) × (1, i) × (1, j)

(1, −1) × (1, i) × (1, j) × (1, i)

(1, −1) × (1, i) × (1, j) × (1, i) × (1, j)

(1, −1) × (1, i) × (1, j) × (1, i) × (1, j) × (1, i) …

In this algebraic structure, the unit vectors i, j, k have the multiplication rules

$\begin{array}{ll}{\text{i}}^2={\text{j}}^2={\text{k}}^2=1& (3)\end{array}$

$\begin{array}{ll}\text{ij}=-\text{ji}=\mathit{\text{i}}\text{k};\text{jk}=-\text{kj}=\mathit{\text{i}}\text{i};\text{ki}=-\text{ik}=\mathit{\text{i}}\text{j}& (4)\end{array}$

which are essentially those of complexified quaternions, with multiplication rules

$\begin{array}{ll}{(\mathit{\text{i}}\text{i})}^2={(\mathit{\text{i}}\text{j})}^2={(\mathit{\text{i}}\text{k})}^2=1& (5)\end{array}$

compared to those for pure quaternions

$\begin{array}{ll}{\text{i}}^2={\text{j}}^2={\text{k}}^2=\text{ijk}=-1.& (6)\end{array}$

In the Clifford vector algebra, there is a full product between vectors a and b which combines vector and scalar products

$\begin{array}{ll}\text{ab}=\text{a.b}+\mathit{\text{i}}\text{a}\times \text{b}& (7)\end{array}$

It has been shown by Hestenes [2] and others, that using a Clifford vector algebra is a natural way of incorporating spin into quantum mechanics as an automatic consequence of the vector structure of space and momentum. The units are, significantly, isomorphic to those of Pauli matrices.

Clifford vector algebra produces three subalgabras from the products of its basic units (see Table 2). Bivectors (for example, area and angular momentum, in physics) are products of two orthogonal vector units (such as i and j); they are also called pseudovectors and are isomorphic to quaternion units. Trivectors (for example, volume) are products of three orthogonal vector units (i, j, k), and are also called pseudoscalars; their full algebra is that of complex numbers.

TABLE 2

Table 2. The units of Clifford algebra.

Standard Clifford vector algebra notably produces these subalgebras in the reverse order to the universal rewrite system, which generates, in its first four alphabets, scalars, pseudoscalars, quaternions and vectors, along with the scalar subalgebras of pseudoscalars and quaternions.

Significantly, if we take all these algebras as independently true, and hence commutative, as the rewrite structure seems to suggest we should, since each is a complete description of zero totality, then we require an algebra that is a commutative combination of vectors, bivectors, trivectors and scalars, or vectors, quaternions, pseudoscalars and scalars. This turns out to be equivalent to the algebra of the sixth alphabet, a group structure of order 64 with elements, as in Table 3.

TABLE 3

Table 3. The units of the Dirac algebra.

The algebra represented by these group elements is isomorphic to the gamma matrix algebra of the Dirac equation, which defines conventional relativistic quantum mechanics.

Characteristics of the Rewrite Process

The universal rewrite process is characterized by duality, self-similarity, scale-independence and holism; it proceeds by bifurcation at every stage. It can be distinguished from non-universal rewrite processes by the fact that it has no fixed starting or ending point, and by the endless reconstruction of both alphabet and production rules at every bifurcation. The self-similarity follows immediately from the absence of a fixed starting point. It implies that physical applications at some particular level will be matched by applications at other levels, and that the scaling up from small to larger and more complex systems is governed by a principle analogous to the renormalization group in physics, where the structures which the rewrite process generates are maintained by new emergent physical principles.

The observer, who is always placed within the zero totality system (variously described as “the universe,” “nature,” or “reality”), must necessarily start from the minimum representation of a zero totality alphabet, say (R, R*). The stages in the process are all zeros. During the process we go from one zero cardinality or totality to the next. The cardinalities are like Cantor's cardinalities of infinity, but are cardinalities of zero instead. We ensure that they are cardinalities by always including the previous cardinality or alphabet. So (R, R*, A, A*) includes (R, R*). Because they are cardinalities or zero totality alphabets (descriptions of the universe in physical terms), the process is always holistic. We have to include everything.

Now, we have to assume that (R, R*) is not necessarily the beginning, though it is the point where we as observers start from. So, this already “bifurcated” state will have started from a previous alphabet, which we assume we can't access directly. If we describe this as R, then the * or R* character creates the doubling process. Before we create (R, R*), we have to assume that (R) is a zero totality alphabet, but it is a zero we can't access because we have no structure for it. In effect, we are trying to posit an ontology that exists before the epistemology or observation, begins with (R, R*). So, we assume that it must happen without being able to observe it.

Duality is intrinsic to the process. The operation () () ⇒ (,) describes how we proceed from one description of the entire or universe zero totality alphabet to the next alphabet in the hierarchy. The (,) becomes a “bifurcation” or “doubling.” So

$\begin{array}{ll}(\mathit{\text{R}},{\mathit{\text{R}}}^{*})(\mathit{\text{R}},{\mathit{\text{R}}}^{*})\Rightarrow (\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*})& (8)\end{array}$

can be expressed as (R, R*,   A, A*), where (R, R*) (R, R*) is the bifurcation that creates the new zero cardinality (R, R*, A, A*), in effect transforming the second (R, R*) into the new (A, A*). All the “doublings” or “bifurcations” in the process are, in this sense, similar to the initial creation of (R, R*), even when they involve complexification or dimensionalization rather than conjugation. So

$\begin{array}{ll}(\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*})(\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*})\Rightarrow (\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*},\mathit{\text{B}},{\mathit{\text{B}}}^{*},\mathit{\text{AB}},{\mathit{\text{AB}}}^{*})& (9)\end{array}$

can also be written as

$\begin{array}{ll}(\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*})(\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*})\Rightarrow (\mathit{\text{R}},{\mathit{\text{R}}}^{*},\mathit{\text{A}},{\mathit{\text{A}}}^{*}, \mathit{\text{B}},{\mathit{\text{B}}}^{*},\mathit{\text{AB}},{\mathit{\text{AB}}}^{*})& (10)\end{array}$

where the original alphabet (R, R*, A, A*) and its dual (B, B*, AB, AB*) are created by a process similar to the one which created R and R*. For practical purposes, a new character (B) is introduced.

Application to Physics

In applying to physics, we note that the universal rewrite process creates successive models for a zero-totality universe. This is what we mean by physical parameters. We can recognize the algebras of the fundamental parameters mass, time, charge and space as being, respectively, scalar, pseudoscalar, quaternion, and vector, exactly as are generated by the first four alphabets of the universal rewrite system. Here, mass is the source of gravity and includes energy, while charge is a term used to represent the sources of the three non-gravitational interactions [3]. The four alphabets seem to be independent descriptions of the universe which must be simultaneously true, as should all subsequent alphabets following these.

i                      i,j,k     1         i,j,k

time                space   mass   charge

pseudoscalar  vector   scalar quaternion

Now, if we combine the algebras of these quantities, we obtain the 64-part algebra isomorphic to the Dirac gamma algebra that we tabulated in Section An Algebra for the Rewrite Process. But the 8 units of time, space, mass, and charge are not the minimum number of starting units to generate the 64-part algebra. This is, in fact, 5 and its construction always involves the breaking of the symmetry of one of the two 3-D components, space or charge. Typically, we “combine” one of the units of charge with each of those of time, space and mass, to obtain:

ik                   ii, ij,ik                j

energy            momentum         rest mass

ikE                iip_x, ijp_y, ikp_z    jm

pseudoscalar vector                 scalar

The units ik, ii, ij, ik, j correspond to the five base units of the gamma algebra, and the new terms, energy, momentum and rest mass, can be seen to take on aspects of the original charge units, together with the pseudoscalar, vector and scalar properties of their other parent quantities. Now, when we combine the momentum terms into a single vector p and take the complete package (ikE + ip + jm) to represent the properties of a fundamental physical unit (particle or fermion), we find that we can, in this case, immediately solve the problem of indefinite extension of the alphabets since (ikE + ip + jm) is a nilpotent or square root of zero. The equation

$\begin{array}{ll}(ikE+ip+jm)(ikE+ip+jm)=E^2-p^2-m^2=0& (11)\end{array}$

is then simply the relativistic and quantum mechanical conservation of energy and momentum. So, if we take (ikE + ip + jm) as incorporating all the alphabets needed to create a repetitive sequence, when we seek to generate the next alphabet by squaring, we will find that it is zeroed automatically, so zeroing all higher alphabets which incorporate it, and we can describe the world through an indefinite succession of such units.

Simultaneously when we create energy, momentum and rest mass as concepts, the combination of time, space, mass, and charge breaks the symmetry between the weak, strong and electric charges, which then take up the algebraic characteristics of their associated parameters:

ik                        ii, ij, ik            j

weak charge       strong charge   electric charge

‘pseudoscalar     vector               scalar

The reduction of the original 8 units to the composite set of 5 is, in fact, a characteristic symmetry-breaking operation in nature, which is found also in mathematics, chemistry and biology as well as several other aspects of physics. In all these areas, 5 seems to be the number at which symmetry is necessarily broken.

Nilpotent Quantum Mechanics

Nilpotent quantum mechanics is founded on a nilpotent operator which can be expressed in the form (± ikE ± ip + jm), which is an abbreviated expression for a row or column vector, whose 4 terms encompass the four sign variations in E and p. We can use a canonical quantization procedure to replace E and p as operators by E → i∂ /∂t, p → – i▽, for a free fermion, or by covariant derivatives such as E → i∂ /∂t + eΦ …, p → – i▽ + eA +…, for a fermion constrained by any number of potentials of any type or even by curvature terms. The structure of the operator then determines both the complete quantum behavior of the fermion and also that of its environment or “vacuum” by defining a unique phase term which, when operated on, produces an amplitude which squares to zero:

$\begin{array}{ll}{(\text{operator acting on unique phase term})}^2={\text{amplitude}}^2=0& (12)\end{array}$

The process incorporates both Dirac and Klein-Gordon equations in the form

$\begin{array}{ll}(\pm \text{ik}\mathit{\text{E}}\pm \text{i}\text{p}+\text{j}\mathit{\text{m}})(\pm \text{ik}\mathit{\text{E}}\pm \text{i}\text{p}+\text{j}\mathit{\text{m}})\to 0& (13)\end{array}$

where (± ikE ± ip + jm) can stand for either operator or amplitude. This would make the Dirac equation for a free fermion

$\begin{array}{ll}(\mp k\partial /\partial t\mp i\text{i}\nabla +\text{j}m)(\pm \text{ik}E\pm \text{i}\text{p}+\text{j}m)e^{-i(Et-\text{p.r})}=0& (14)\end{array}$

For a fermion under the constraint of a potential or any number of potentials, the phase factor would take a different form but the result would still be a term with the same structure as (± ikE ± ip + jm) being squared to zero.

Characteristics of Nilpotent Quantum Mechanics

Nilpotent quantum mechanics is relativistic and is concerned with fermions. It shares all the standard characteristics of relativistic quantum mechanics using the more conventional formalisms of the Dirac equation, and can be easily transformed into these formalisms using the one-to-one correspondence between the algebraic operators and gamma matrices. However, it also has some characteristics which only become apparent in this mathematical form, but which are necessary for understanding how the process can be scaled up in higher order systems.

Spin ½ and zitterbewegung are among the shared characteristics and can be easily derived using variants of the standard formalisms. Chirality (or the intrinsic left-handedness of fermions and right-handedness of antifermions) emerges in the same way. Fermion uniqueness or Pauli exclusion is obvious in the nilpotent formalism, as any combination state of identical fermions will automatically vanish. However, the nilpotent also creates a completely new meaning for the concept. Because the totality of experience is defined always to be zero, if we take a fermion in any state, say (ikE + ip + jm), subject to any number of constraints that can be built into its operator, and imagine that we can create it from absolutely nothing, then the “vacuum” which defines the rest of the universe for that fermion, must be a kind of mirror image, −(ikE + ip + jm), so that both the superposition and the combination of vacuum and fermion remain at zero:

$\begin{array}{ll}-(\text{ik}\mathit{\text{E}}+\text{i}\text{p}+\text{j}\mathit{\text{m}})+(\text{ik}\mathit{\text{E}}+\text{i}\text{p}+\text{j}\mathit{\text{m}})=0& (15)\end{array}$

$\begin{array}{ll}-(\text{ik}\mathit{\text{E}}+\text{i}\text{p}+\text{j}\mathit{\text{m}})(\text{ik}\mathit{\text{E}}+\text{i}\text{p}+\text{j}\mathit{\text{m}})=0& (16)\end{array}$

To maintain this zero totality in all circumstances, any change in either the fermion or its environment must be reflected in a corresponding change in the other. In effect, this creates a principle of self-organization which can be imagined in systems on a much larger scale, and which will be identifiable by strongly characteristic features which originate in the nilpotent structure and the universal rewrite process.

Another significant aspect of quantum mechanics is that it involves both locality and non-locality. The distinction between the two processes is clear in the nilpotent form. Everything inside the bracket is local; everything outside the bracket is non-local. So the conservation laws of energy and angular momentum are local; superpositions and combination states and interactions with vacuum are non-local. Both processes, however, are holistic in requiring the cooperation of the entire universe, and each produces consequences which affect the other. In nilpotent quantum mechanics, the individual fermion conserves its energy only with respect to the rest of the universe. The fermion is an open system and intrinsically dissipative. The first law of thermodynamics must be accompanied by the second.

Fermions are, in a very fundamental way, incomplete. They have half-integral spin, are only observable when interacting in a pairing with other fermions, and are square roots of algebraic operators which only have meaning when multiplied with other objects of the same kind. In the nilpotent formalism, bosons of spin 1 and spin 0 are formed from fermion-antifermion combinations of the form (± ikE ± ip + jm) (∓ ikE ± ip + jm) and (± ikE ± ip + jm) (∓ ikE ∓ ip + jm), while a fermion-fermion combination can exist in the form (± ikE ± ip + jm) (± ikE ∓ ip + jm) in Cooper pairs, Bose-Einstein condensates and other applications of Berry phase. All these expressions become scalars when multiplied out. All the tendency for aggregation in nature can be seen as stemming from the need for fermions to acquire partners to remove this incompleteness, and it can be linked to the action of a harmonic oscillator, of which the zitterbewegung is a special instance. The same pattern emerges at higher levels, suggesting that the nilpotent model applies well beyond the direct application of quantum principles. It is very likely that a major role in providing the “staircase” that we hope to show leading from the smallest systems to the largest will be provided by the renormalization group procedure.

Dual Space

The most significant aspect of the structure is that it incorporates two full vector spaces with the full Clifford algebra of each. The 64-part algebra requires a Clifford vector algebra for space commutatively combined with its three subalgebras, representing time, mass, and charge. If we take these three subalgebras together, we find that they have the mathematical characteristics of another vector space, entirely commutative to the first. This “space,” however, as a composite of three other parameters, is not an observable quantity. So, the nilpotent structure emerges from combination of two vector spaces, only one of which is observable.

We can call the unobserved space “vacuum space,” and its effects are immediately apparent in spin ½ and the 4-component structure of the fermion wavefunction. Here, the fermion also includes two terms associated with antifermion states. These are a manifestation of the fermion's vacuum, and are responsible for the fermion spending half its time as a real particle and half as a vacuum particle (zitterbewegung), which is also one of many ways of accounting for the fermion's ½ spin.

Another way of looking at this is to relate it to Berry phase, and to attribute this to the fact that the fermion is a singularity with respect to ordinary space. As is well-known, Berry or geometric phase can be described in purely topological terms. If we parallel transport a vector around any complete circuital path in ordinary or simply-connected space, we can expect it to leave the vector pointing in the same direction at both beginning and end of the circuit. However, if the space of the circuit contains a singularity or is multiply-connected, then the vector will gain a phase change of π and end up pointing in the opposite direction from its starting position.

Spin ½ could be seen as indicating that the fermion singularity rotates in its own multiply-connected space. So, we can attribute the same effect to the fact that the fermion is defined as a singularity and that it is defined by a nilpotent connection between two spaces, leading to the conclusion that the dual space structure is actually responsible for the existence of discrete matter in the form of physical singularities. In our understanding, the Berry phase/spin ½/zitterbewegung results from defining a localized point particle simultaneously with defining the non-localized vacuum that determines its relation to the rest of the universe, and that carries the information about its future evolution. We can consider Berry phase to be a particularly significant indicator of the presence of some kind of dual space, nilpotent-related behavior, especially in systems subject to self-organization.

The Holographic Principle

The nilpotent dual spaces are genuinely dual, in that they contain precisely the same information, though in different forms. This duality has many manifestations. For example, the uniqueness of the nilpotent (ikE + ip + jm) and Pauli exclusion could be determined by the “direction” of a line drawn from the origin if iE, p, and m re represented as coordinates on the quaternion axes k, i, and j. Alternatively, we could express Pauli exclusion by the more conventional method of defining fermion wavefunctions as antisymmetric. This leads to a truly remarkable result if we take (ψ₁ψ₂ – ψ₂ψ₁) for two fermions in the nilpotent formalism:

$\begin{array}{ll}(\pm {\text{ik}\mathit{\text{E}}}_1\pm {\text{i}\text{p}}_1+\text{j}{\mathit{\text{m}}}_1)(\pm {\text{ik}\mathit{\text{E}}}_2\pm {\text{i}\text{p}}_2+\text{j}{\mathit{\text{m}}}_2)& (17)\\ -(\pm {\text{ik}\mathit{\text{E}}}_2\pm {\text{i}\text{p}}_2+\text{j}{\mathit{\text{m}}}_2)(\pm {\text{ik}\mathit{\text{E}}}_1\pm {\text{i}\text{p}}_1+\text{j}{\mathit{\text{m}}}_1)\\ =4{\text{p}}_1{\text{p}}_2-4{\text{p}}_2{\text{p}}_1=8\mathit{\text{i}}{\text{p}}_1\times {\text{p}}_2,\end{array}$

for this only has a non-zero value if the fermion spins are oriented in different directions. In effect, the complete information about a fermion state is contained in its instantaneous spin direction, or in the plane to which this is perpendicular. In principle, the orientation of the fermion in real space and in the “vacuum space” created by the quaternion axes k, i, and j carries the same information. Exactly the same duality occurs in the derivation of spin ½ either from the anticommutativity of the momentum operator, which uses real space, or from the Thomas precession, which uses vacuum space, and the duality again informs the holographic principle.

The holographic principle, in which the entire information about a system is found on the bounding area, is thought to be a significant organizing principle for many systems. We have already considered it as “a characteristic signature of a nilpotent, self-organizing system with its planar fractality” [1]. Essentially, it uses the information coded in the E and p terms of the operator (ikE + ip + jm), that is, in two components of the vacuum space, as nilpotency makes the third term redundant. This then becomes equivalent to using the information coded in two components of the dual real space. Significantly, this can also be coded in one dimension of space and one of time, which would be equivalent to using the vacuum space. As space and momentum are conjugate variables, area is also a conjugate of angular momentum, and (ikE + ip + jm) is recognizably an angular momentum operator, with the E term determining the handedness, p the direction and m the magnitude. Since any system which conserves angular momentum or which operates according to the holographic principle (for example, galaxies acting collectively under gravity) can be expressed in this form, then any such system can be seen as a direct analog of the nilpotent fermion, even though it is not intrinsically quantum or relativistic.

The application of the nilpotent operator to the holographic principle also suggests that it can itself be regarded as a quantum hologram, with phase ikE, amplitude ip and reference phase jm. Again, we can recover the entire structure from just two terms, for example, phase and reference phase. Quantum holography has now been officially recognized as occurring in the case of “quantum holographic encoding in a two-dimensional electron gas” [4], but the work of Walter Schempp has already shown that it has extensive practical application in Magnetic Resonance Imaging based on harmonic analysis on the 3D Heisenberg Lie group [5]. The universal rewrite system shows that the repeating unit that we need for the description of a quantum or quantum-like system is a double vector space. The two three dimensional spaces make quantum holography possible via Fourier transform action, and relate to the 3D Heisenberg Lie Group and its nilpotent Lie algebra and their dual/inverses [1].

The holographic paradigm is particularly significant in that the wavefunction is defined only up to an arbitrary fixed phase, which provides a direct meaning for the quantum vacuum in quantum field theory, as ensuring that only relative phases, which encode the 3 + 1 space-time geometries, can be measured. This phase becomes the fixed, though arbitrary, measurement standard for all subsequent measurements, and acts as the holographic basis for a universal and self-organized quantum process in which new fermionic states of matter are produced. After each new emergence, a new arbitrary standard is created, providing a complete history, i.e., hologram or holographic record of past events, which our senses perceive as an unending irreversible evolution. Nature allows us to use our arbitrary standard as the new beginning of a rewrite process (as in Section Characteristics of the Rewrite Process) and to conceive of how self-organization can take place at each new level of complexity. The universal rewrite system implies that the only valid mathematical representations of nilpotent quantum-like systems are all automorphisms of the universe itself, and that this is the mathematical meaning of quantum entanglement [6].

Self-Organization: A New Application

The universal rewrite system provides a blueprint for self-organization mediated through the nilpotent relation between the defined system and the rest of the universe, which emerges in this form of quantum mechanics. The particular characteristics of nilpotent quantum mechanics provide us with a number of identifiers which we have already linked to self-organization, citing specific examples, and which include double 3-dimensionality; a five-fold broken symmetry; geometric phase; spin ½ or equivalent double helical structure; uniqueness of the objects and unique birthordering; irreversibility; dissipation; chirality, harmonic oscillator mechanism, zitterbewegung; fractality of dimension 2; the holographic principle and quantum holography [1]. Self-organization appears to be very general in nature and an almost obvious consequence of a universal rewrite system which reappears at each new level of complexity, so we can expect to find increasing evidence of such identifiers in systems that have been shown to be self-organizing.

A completely new application emerged immediately after our last QI presentation [1]. Our previous work has indicated that geometrical or Berry phase is a particularly significant identifier of nilpotent-like behavior in a system that need not necessarily be quantum. In an earlier paper, we wrote, concerning nilpotent structure (where X² = 0): “each X² signifies a return (in terms of a corresponding unique dual Dirac annihilation operator) to the quantum mechanical vacuum state which takes the form of a universal attractor of fractal dimension 2 …, where the uniqueness of each of the nilpotent quantum mechanical Dirac operators is carried by means of quantum phase, in the form a unique gauge invariant Berry/geometric phase able to encode the requisite relativistic 3 + 1 space time geometric information about the unique fermion state vector, and is ‘scale free’” [7].

Now, new research, by Kaschube et al. published just after “The Logic of Self-Organizing Systems,” shows that the neurons in the visual cortex in the brain of three distantly-related mammals have a quasiperiodic structure. Orientations of the neurons in the flat sheets of the cortex change continuously, repeating over a length known as the “map period” (λ), while appearing to converge on centers known as “pinwheels,” while the pinwheel density per λ² appears to equal π to within a few percent [8]. According to Miller, writing in the same issue: “The result offers insight into the development and evolution of the visual cortex, and strongly suggests that key architectural features are self-organized rather than genetically hard-wired” (our emphasis). Miller also says that “The universality of self-organizing behavior provides a simple and compelling explanation for the arrival of widely divergent evolutionary lines at this common design [9].”

In our interpretation, π might well appear in the density of the squared “map period” of the neurons because the spatial structure of the system requires a geometrical phase. If the “pinwheel” is taken as a “singularity” in the physical space, then we need a double circuit through the “map period” or cycle of orientations to re-establish the original phase state. The singularity would then generate a double map period (2λ) in any direction of the two-dimensional cortical sheet, and each pinwheel singularity would be situated in a circle with radius length λ in this two-dimensional space, creating a pinwheel density/λ² of π. This would coincide directly with our proposal that a characteristic structure for the space of self-organizing systems at all levels of complexity results from a dual vector system, or equivalent, for which a geometrical phase of π becomes an identifying feature.

This is referred to in many publications and very explicitly in the biological context, with the relevant identifying structures, in “A Computational Unification of Scientific Law” and references therein [10]. The underlying Clifford algebra suggests that analogous mathematical models are also possible, one of which is the Klein bottle structure proposed by one of us in earlier work [3]. This has been developed further by Rapoport, along with the appearance of pinwheel structures and the appearance of the identifying π which we associate with the Berry phase, and Rapoport has proposed extensions of the analogy to many seemingly unrelated areas [11, 12]. The fundamental dualities involved can be expressed in many different ways and have been discussed by the authors as the universal basis for physical, chemical, biological, and other systems and their organization in many previous publications. Essentially, where energy is a conserved or near-conserved quantity in any structure, or where there is a definable energy flow, a nilpotent relation can be found between that structure and the rest of the universe, and the analogies presented in Zero to Infinity and earlier works will automatically apply, together with certain identifying characteristics [3]. The structure of the visual cortex is just one example where our prior predictions appear to have been vindicated in a seemingly unexpected and visually striking way. It is our belief that examination of other self-organizing systems will reveal the presence of other characteristic identifiers of a structure analogous to nilpotent quantum mechanics.

Conclusion

Self-organization in Nature has been posited as resulting from a universal rewrite system, which manifests itself at each new structural level. In this system, the totality of the entire universe or anything that can be applied universally is taken to be zero. New zero totality structures or alphabets emerging from a previous one always include it, leading to what has been described here as a succession of alphabets, with zero cardinality by analogy with the well-known succession of infinite cardinalities in mathematics. The process is universal, so is not confined to specific interpretations, but one such interpretation is an algebraic series which becomes a form of Clifford algebra, or an infinite series of sets of quaternion units, with the full set of terms produced by squaring out or multiplying to a higher order. The series of zero totalities has a fractal quality in that combinations of all the alphabets in the series up to any order, as independent units, leads to an alphabet higher up in the series. This appears to be applicable to physics where the first few terms in the series correspond to the successive algebraic properties of the fundamental physical parameters mass, time, charge and space.

A combination of these leads to a higher algebra which appears to correspond to that used in the Dirac equation of relativistic quantum mechanics, which describes the fermionic state, the only known fundamental entity in physics. Interpreting this algebra as a group of order 64, allows us to select sets of 5 generators for the entire combination, which we can show correspond precisely to the algebraic terms that define the Dirac state and that we conventionally identify as the gamma matrices. In addition, the combination of the terms as used in physics has only nilpotent solutions, squaring to zero, suggesting that all higher alphabets incorporating these will automatically produce zero squared and higher order products as well.

The higher order alphabet which incorporates all the alphabets corresponding to the parameters appears to be equivalent to that which would be produced by a double vector or dual space. The nilpotent structure of the fermion (which can also be derived from the conventional form of the Dirac equation using gamma matrices) immediately explains Pauli exclusion and interprets vacuum as corresponding to the “rest of the universe” (zero totality—fermion) which allows a fermion to exist in any particular state, with the fermion and vacuum occupying the two “spaces” required by our algebra. Quantum mechanics can then be structured as the interaction between a nilpotent fermion and the rest of the universe acting like a mirror image creating a totality of zero. The many powerful applications of this kind of quantum mechanics have already been extensively described [3]. If we now interpret the nilpotent fermion plus vacuum combination as an example of a more universal condition, produced by the universal rewrite system, we can extend the application to self-organizing systems in general, and we suggest, among other things, that it is the explanation of the holographic principle being applicable to such systems. We also suggest how it should apply to biological systems, giving an example from the structure of the visual cortex, which we propose is an example of the Berry phase which results from the system and its entire environment occupying two different mathematical “spaces.”

Author Note

This paper is a revised and expanded version of an AAAI technical report on “The ‘Logic’ of Self-Organizing Systems” (2010-08-020). The authors hold the copyright and no permission is required from AAAI for the use and reproduction of material from this report.

Author Contributions

PR: The original ideas of universal rewrite system, the associated algebra and nilpotent quantum mechanics. Joint contribution with PM on recognizing the wide application of these ideas in particular to many areas outside of physics.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Marcer P, Rowlands P. The ‘Logic’ of Self-organizing Systems. AAAI Technical Reports 2010-08-020 (2010).

2. Hestenes D. Space-Time Algebras. New York, NY: Gordon and Breach (1966).

3. Rowlands P. Zero to Infinity: The Foundations of Physics. Singapore; Hackensack, NJ: World Scientific (2007).

Google Scholar

4. Moon CR, Mattos LS, Foster BK, Zeltzer G, Manoharan HC. Quantum holographic encoding in a two-dimensional electron gas. Nat Nanotechnol. (2009) 4:167–72. doi: 10.1038/nnano.2008.415

CrossRef Full Text | Google Scholar

5. Schempp W. Quantum holography and neurocomputer architectures. J Math Imaging Vis. (1992) 2:279–326.

Google Scholar

6. Marcer P, Rowlands P. The Grammatical universe and the laws of thermodynamics and quantum entanglement. AIP Conf Proc. (2010) 1303:161–7. doi: 10.1063/1.3527151

CrossRef Full Text | Google Scholar

7. Marcer P, Rowlands P. Further evidence in support of the universal nilpotent grammatical computational paradigm of quantum physics. AIP Conf Proc. (2010) 1316:90–101. doi: 10.1063/1.3536456

CrossRef Full Text | Google Scholar

8. Kaschube M, Schnabel M, Löwel S, Coppola DM, White LE, Wolf F. Universality in the Evolution of orientation columns in the visual cortex. Science (2010) 330:1113–6. doi: 10.1126/science.1194869

CrossRef Full Text | Google Scholar

9. Miller KD. π = visual cortex. Science (2010) 330:1059–60. doi: 10.1126/science.1198857

CrossRef Full Text | Google Scholar

10. Marcer P, Rowlands P. A Computational Unification of Scientific Law: spelling out a universal semantics for physical reality. In: Amoroso RL, Kauffman LH, Rowlands P, editors. The Physics of Reality Space, Time, Matter, Cosmos. Singapore; Hackensack, NJ: World Scientific (2013), p. 50–9.

Google Scholar

11. Rapoport DL. Klein bottle logophysics, self-reference, heterarchies, genomic topologies, harmonics and evolution. Quantum Biosyst. (2016) 7:1–73, 106–72.

Google Scholar

12. Rapoport DL. Klein bottle logophysics: a unified principle for non-linear systems, cosmology, geophysics, biology, biomechanics and perception. J Phys. (2013) 437. doi: 10.1088/1742-6596/437/1/012024

CrossRef Full Text | Google Scholar