The Physics of Teams: Interdependence, Measurable Entropy, and Computational Emotion

Most of the social sciences, including psychology, economics, and subjective social network theory, are modeled on the individual, leaving the field not only a-theoretical, but also inapplicable to a physics of hybrid teams, where hybrid refers to arbitrarily combining humans, machines, and robots into a team to perform a dedicated mission (e.g., military, business, entertainment) or to solve a targeted problem (e.g., with scientists, engineers, entrepreneurs). As a common social science practice, the ingredient at the heart of the social interaction, interdependence, is statistically removed prior to the replication of social experiments; but, as an analogy, statistically removing social interdependence to better study the individual is like statistically removing quantum effects as a complication to the study of the atom. Further, in applications of Shannon's information theory to teams, the effects of interdependence are minimized, but even there, interdependence is how classical information is transmitted. Consequently, numerous mistakes are made when applying non-interdependent models to policies, the law and regulations, impeding social welfare by failing to exploit the power of social interdependence. For example, adding redundancy to human teams is thought by subjective social network theorists to improve the efficiency of a network, easily contradicted by our finding that redundancy is strongly associated with corruption in non-free markets. Thus, built atop the individual, most of the social sciences, economics, and social network theory have little if anything to contribute to the engineering of hybrid teams. In defense of the social sciences, the mathematical physics of interdependence is elusive, non-intuitive and non-rational. However, by replacing determinism with bistable states, interdependence at the social level mirrors entanglement at the quantum level, suggesting the applicability of quantum tools for social science. We report how our quantum-like models capture some of the essential aspects of interdependence, a tool for the metrics of hybrid teams; as an example, we find additional support for our model of the solution to the open problem of team size. We also report on progress with the theory of computational emotion for hybrid teams, linking it qualitatively to the second law of thermodynamics. We conclude that the science of interdependence advances the science of hybrid teams.

Introduction

One of the major conclusions from modern game theorists, based on findings in the laboratory, is that the societies that cooperate have better social welfare [[1], p. 7–8]. The evidence from the field, however, does not support this claim: Cooperation between competitors is often considered by the judiciary to be collusion [2]; consensus-seeking permits a minority faction to control a majority (e.g., in European Union politics, see [3], p. 29); and central decision-making promotes corruption [4]. Unexplained by traditional theory, misallocations of resources by corrupt activities abound across the globe [5]. In our research, we have concluded that corruption is more likely unchecked in countries, businesses and teams that impede the interdependence spontaneously arising among citizens in a nation with functional checks and balances; China is an example of the corruption that occurs from blocking interdependence (e.g., censorship), replaced by central decision-making [6]:

Much about the Hong'ao dump was not as it appeared on paper, a reconstruction of the disaster shows. The duplicity, involving doctored documents and false identities, illustrates systemic gaps in China's efforts to prevent industrial and transportation accidents, which claim tens of thousands of lives annually and have galvanized public anger over official corruption … like the deadly explosions last year at a toxic chemical storage site in Tianjin … the disaster in Shenzhen suggests that dark pools of mismanagement and corruption persist even in the most developed parts of the country.

Conceptually, interdependence has been known for some time. According to Smith's [7] “invisible hand,” a service provided by one worker exploiting an opportunity is interdependent with another worker providing food, housing, transport, and on in an endless iteration of services across a market free to respond to market demands and signals by the movement of capital and labor sufficient to satisfy demand. But free movement is impeded by barriers established by centralized commands, decisions or procedures (e.g., Dodd-Frank rules in the USA), authoritarian governments (e.g., China), or violent gangs (e.g., Palestine's Hamas; Lebabon's Hezbollah; the US's Mara Salvatrucha).

What we know so far from this our work-in-progress is that reducing interdependence increases errors and the misallocation of resources [8]. We also know from the National Academy of Sciences ([9], p. 33) that while interdependence is important to effective teamwork, the size of a team for a given problem remains an open question. The Academy then contradicted itself by stating “many hands make light work,” indicating its belief that redundancy has a positive effect on teams. Traditional models of subjective social network theory also predict that an increase in redundancy in social networks increases efficiency [10]. We approach team size with our quantum-like model of interdependence. By treating oil firms as teams [11], we theorized that the best size for teams is the least size possible that maintains interdependence across a team to solve a problem identified by a society when its labor and capital are free to move. We discovered that by overstaffing, redundancy reduces interdependence. In this paper, we extend our finding to the size of a nation's military.

Even in American bureaucracies, consensus-seeking, corruption, and mismanagement appear to go hand in hand (e.g., for a cover-up by the Veterans Affairs, see [12]; for unjustified rule-making by the US Treasury, see [13]; for Department of Energy guidance that citizen advisors should “strive for consensus,” see [14]). As an example of the mismanagement associated with consensus-seeking (i.e., minority control; in Lawless [15]), DOE planned to vitrify high-level radioactive wastes into glass for its eventual geologic disposal starting in the 1980s at both its Hanford facility in Washington State and at its Savannah River Site in South Carolina. However, the consensus-seeking Hanford Citizens Advisory Board has not formally motivated DOE to accelerate its Hanford vitrification facility, a project plagued by gross mismanagement now delayed until 2033 [16]. Compare that with the majority-ruled Savannah River Site's Citizen Advisory Board that formally motivated SRS to start its vitrification facility in 1996 and has overseen its safe operations for the more than 20 years hence.

In the literature, Khrennikov [17] suggests now is the time to apply quantum-like models to address open questions in many fields; e.g., business, psychology, and social systems. Busemeyer and Wang ([18], p. 43) add that “Quantum cognition is an emerging field that uses mathematical principles of quantum theory to help formalize and understand cognitive systems and processes.” Wang and Busemeyer [19] reintroduce the concept of complementarity to account for order effects; we use complementarity to account for the stable gap between physical (objective) measures of behavior and self-reported (subjective) observations of behavior (e.g., [20]), as well as for the different interpretations of reality common to individuals (e.g., present-day supporters of Einstein's views on quantum theory vs. Bohr's Copenhagen interpretation; in Lawless [2]), and the different skills held by members of a team, where each may have subjective interpretations and beliefs (e.g., in the search for justice, construing the courtroom as a team, prosecutors, and defense attorneys work together by pursuing different theories of a crime; [11, 21]).

The phenomenon that links these examples is the interdependence between behavior and its interpretations; interdependence between multiple interpretations of social reality; and the interdependence among members of a team multitasking to solve a problem. In its review of teams, the National Academy of Sciences repeatedly cited the presence of interdependence but without addressing the phenomenon theoretically [9]. In this study, we apply quantum-like models to the study of interdependence (e.g., [22], p. 147). From Wendt [23], “humans live in highly interdependent societies” (p. 150); interdependence, however, creates a measurement problem [2], which Wendt ([23], p. 67) describes as “the apparent impossibility of an objective measurement,” and which we have linked to the behavior-cognition gap, for example, between the objective measures of behavior and the self-reported subjective accounts of behavior (e.g., [20]). Wendt ([23], p. 34) adds that a quantum-like model “offers the potential for revealing new social phenomena,” which we demonstrate by determining the size of teams, heretofore an open problem ([9], p. 33).

In the 1940s, Von Neumann and Morgenstern's ([24], Section 4.8.2) theory of games introduced to generations of social scientists a mathematical model of static interdependence in a configuration of arbitrary rewards and punishments promoted as tradeoffs among the choices offered to players with values determined by scientists, not by social reality, producing decades of biased social and political policies from these toy models. Unlike Smith's [7] “invisible hand” or the physical sciences where “reality is not as it appears” to human observers [25], game theory and wide swaths of social science are based on, at best, simple observations of individuals and, at worst, self-reported observations ([26]; e.g., questionnaires, surveys, interviews). The value of actual behaviors vs. self-reports of constructs poorly correlate, if at all, with most of the variance between actual behavior and self-reported behavior unaccounted [20].

Bohr, the quantum physicist, criticized game theory on foundational grounds, leading [24] to decry that if Bohr was correct, how to proceed was “inconceivable” (p. 148). Generalizing from quantum theory, Bohr [27] conceived of humans as dual agents constituted of two independent but interdependent parts in the brain (e.g., motor control and vision; from Rees et al. [28]), viz., a human can serve to enact (objectively) a behavior or to observe (subjectively) a behavior; or a human can hold belief #1 (e.g., conservative) or opposing belief #2 (e.g., liberal), the degree of complementarity between these two parts affecting the tradeoffs common to making decisions in social reality [11], consequently creating a measurement problem long ignored by social scientists [23]; viz., game theory does not recognize the existence of a measurement problem in social reality. Specifically, when measuring a social object interdependent with another, both are affected (e.g., [8]). When playing games, as scientists feed choices to subjects to test preferences and responses, they avoid seeing this problem, one of the reasons that game theorists lament that the “evidence of mechanisms for the evolution of cooperation in laboratory experiments … [has not yet been found in] real-world field settings” ([29], p. 422). Later, Von Neumann ([30], p. 420, footnote 217) grappled with the social science implications of Bohr's ideas for the quantum interaction: “Bohr … was first to point out that the dual description which is necessitated by the formalism of the quantum mechanical description of nature is fully justified by the physical nature of things … [that] may be connected with the principle of psycho-physical parallelism.”

Kelley [31], an eminent social psychologist who spent most of his career studying interdependence with games, finally abandoned the study of interdependence because he could never bridge the gap between the game matrices presented to a pair of players versus the “invisible” matrices subjects responded to during games; i.e., no matter how strongly held, the preferences self-reported by subjects before they participated in games were repeatedly contradicted by their choices made during games.

The inability of scientists to determine the value of the social interaction at the heart of games is mirrored across the social sciences by practitioners who base their theories on observations of the processes of how the best teams should operate, often with self-reported (subjective) surveys that tell us nothing new (e.g., the surveys and interviews of teams at Google; in Duhigg [32]). By infusing social science with the normative values that happen to agree with religious beliefs, presently, social science is, unfortunately, of no value in the engineering of hybrid teams. An exception of sorts is the report by the National Academy of Sciences on the value of interdependence to scientific teams [9]; but, by being non-mathematical, the Academy report offers no guidance to engineer hybrid teams.

In comparison to game theory and other traditional approaches to the study of interdependence in teams, we define interdependence as responsive or reactive to signals in nature between non-independent organisms (e.g., elk grazing in a forest with predators leads to healthier forest grasses; from Carroll [33]). Our physics of interdependence as mutual responsiveness is similar to that of entanglement, where the factors that produce interdependence cannot be factored, remaining opaque or invisible to even well-trained observers [2]. But although the effects of interdependence are often “invisible” to rational human observers [7], we recognize that humans manage or exploit it with the competition between at least two teams vying for the support of each team's ideological beliefs or skills before an audience of neutral individuals freely able to choose, thereby entangling them in one belief and then countered by its contrary belief as they process the information generated by the opposing sides of an argument (viz., a Nash equilibrium), exactly what dictators first seek to suppress [2].

When measuring states of interdependence, the measurement problem's “apparent impossibility of an objective measurement” ([23], p. 67) makes social reality non-deterministic. As an example, Cohen [34] reported that women with HIV partners voluntarily participated in the trial of a new drug designed to prevent HIV infection. Ninety-five percent of the women self-reported to medical staff that they had faithfully taken the medication, but, if true, because the infection spread to many of these women, the results indicated that the trial had failed. Inadvertently, the medical research team recalled that they had also collected blood samples from the women during the trial. Once investigated, researchers discovered that only about 26% of the women had actually taken the drug, saving the trial.

From the HIV example, if “quantum-like effects exist in the social world, expressed as interdependence” ([22], p. 147), the interdependence should produce a complementarity in social-psychological systems that causes interference between the two factors of a human's physical behavior and its very different observation of behavior, a difference ignored by traditional social scientists' belief in the independence of these effects. The interpretations of observations by individuals and scientists are impacted by their beliefs, biases, and experience, producing, for example, interference illusions [35]. Unlike quantum systems where angles of separation between two beams of light produce replicable effects, and whereas we can reliably reproduce Adelson's interferences to create his checkerboard illusion, at this early stage of social application, much remains unknown and surprising as in the example above reported by Cohen [34]. It is likely the reason that wide swaths of social science have recently come under suspicion for being unable to be replicated [36]. The goal of our research project is thus to find a way to objectively study the interference between “behavior” and “observed behavior.”

As another example of how interdependence makes social reality non-deterministic, consider self-esteem, one of the major foci for the clinical practice of psychology over the decades. In the book published by the American Psychological Association (APA), [37] began:

Although, relatively little is known about self-esteem, it is generally considered to be a highly favorable personal attribute, the consequences of which are assumed to be as robust as they are desirable. Books and chapters on mental hygiene and personality development consistently portray self-esteem as one of the premier elements in the highest levels of human functioning … Its general importance to a full spectrum of effective human behaviors remains virtually uncontested. We are not aware of a single article in the psychological literature that has identified or discussed any undesirable consequences that are assumed to be a result of realistic and healthy levels of personal self-regard.

Despite this bold claim by Bednar and Peterson under the imprimatur of the APA, a 30-year meta-analysis of all of the known experimental studies where self-esteem could be measured against actual physical performance for both academics and the workplace by Baumeister [38] found a negligible correlation, confirming that self-reports of self-esteem are unrelated to actual behavior.

As a result, we adopt the spirit imbued in game theory to model interdependence, but we reject game theory as fundamentally observational and a-theoretical. Instead, by using Von Neumann's model of quantum interference and Bohr, we review herein our advances: by taking limits, we derived a quantitative measure in the limit of what constitutes a perfect team, another for the worst team, and another we found as a relative metric of team performance modeled after Kullback–Leibler divergence where redundancy in teams is characterized by the divergence in team size from comparable free market teams [11]. Finally, we review our past research to lay the groundwork for a computational model of emotion in teams characterized as a phase shift between overstaffed and rightly-sized teams.

In his theory of self-replicating automata, Von Neumann [39] addressed energy costs and thermodynamics; Shannon information theory; an individual, traditional, and rational perspective of reality; stability (p. 70); errors (p. 71); parts of self-replicating automata (p. 74); the difficulty of choosing the parts of a self-replicating automata in the right order (p. 76); and common sense in assembling the parts (p. 77). In contrast [11], we use a phase shift in the production of maximum entropy to demarcate teams with good allocations of resources from those that misallocate; interdependence between ideologically opposed power centers reflected as a point of social stability that drives information processing (what we have named as Nash equilibria; e.g., Republican and Democrat political parties; defense and district attorneys; Einstein's and Bohr's view of quantum reality); and a metric for the assembly of teams measured by a decrease in structural entropy production. Regarding Nash equilibria, we exemplify them as checks and balances, the source for the best possible government. Contradicting the results of toy games by game theorists ([1], p. 7) and social scientists, Madison [40] established that good governance occurs where “Ambition must be made to counteract ambition.”

In summary, briefly, our goal is to apply our findings to determine mathematically the performance of hybrid teams. Traditional, but normative, models centered around cooperation, while of value in the creation of stories or religious homilies, are of little value for the engineering of hybrid teams. By extending our research to team emotion, we hope to generalize our research where our most recent goal was to use hybrid team performance as a guide to minimize human error (e.g., [41]).

Review of Prior Research. Mathematical Physics

Martyushev [42] theorized that maximum entropy production (MEP) drove the evolution of systems. Wissner-Gross and Freer [43] added that intelligence maximizes the entropic force with Equation (1),

$\begin{array}{cc}F(X_0)=T{\nabla }_{x}S(X)|X_0& \left(1\right)\end{array}$

where F is the entropic force associated with macrostate X, T the temperature and S the Shannon entropy for state X. To apply Equation (1) to a social system, say with a team of scientists seeking to operate at MEP, we would expect a scientific team to use its intelligence to be able to devote its available energy to the fullest exploration of its chosen problem space in the search for a solution, but barriers encumber exploration, reducing MEP, motivating the need for intelligence to overcome barriers (e.g., bureaucracy; corruption; arbitrary rules; censorship; etc.). We conclude that teams use their collective intelligence to seek MEP to overcome barriers; e.g., to seek the path where multitasking applies the maximum effort to solve a difficult problem. Building on Wissner–Gross and Freer that barriers impede MEP, intelligence in a team is needed to navigate around or to overcome these barriers, helping top teams to better compete to succeed. If, as we hypothesize, redundancy acts as a barrier that increases destructive interference in a team, reducing the “force” in Equation (1), then overstaffing in a team is a barrier that frustrates the application of intelligence to decisions. As one of our steps, we will adopt a method that helps us to look for a sign of the collective effects of intelligence.

Our theory is that excluded spaces are governed by the politics in play operating in a social reality, with bistable interpretations of social reality determined by neutral supporters [44]. In contrast to our approach with bistability, others have suggested that stable beliefs could be implemented with epistemic logics, comprising a Hilbert space semantics of belief states that could lead to a formal derivation of social entanglement. Instead, we let the beliefs held by one subgroup attempting to force its interpretation of social reality on the whole group to be |0>, and its complementary, orthogonal view held by a second subgroup to be |1>, giving as the state (Equation 2) for the combined group:

$\begin{array}{cc}|\Psi >=1/\surd 2(|0>+|1>);& \left(2\right)\end{array}$

the factors in Equation (2) of non-separable states [22] become separable by measurement [2], but the measurement problem ([23], p. 67) means that as we determine the state of one factor, we no longer have reliable information on the state of the other factor. If a state's subsystems are not separable, it is entangled; however, if a state is, or has been made, separable, it cannot be entangled [45, 46].

A social system that controls, stops or blocks the bistable interdependence in Equation (2) should be modeled by Shannon entropy. Pure states are product states, where S(ρ) = 0. Product states are uncorrelated; e.g.,, where AB is the Hilbert space of a composite system [46]. The measurement of one subsystem in a composite, product state system has no affect on its second subsystem ([45], [[47], p. 61–3]). If the interdependence among skill sets does not exist in two or more subsystems, Shannon information governs, the data is iid¹, no correlations exist, and joint entropy is likely greater than the contributions of subsystems, i.e.,

$\begin{array}{cc}H(X,Y)\ge H(X),H(Y)& \left(3\right)\end{array}$

To reflect correlations caused by interference among the sources of information, unlike Shannon entropy, interdependence can be destructive or constructive, captured by Von Neumann's density matrix, ρ, with entropy depicted by Equation (4):

$\begin{array}{cc}\text{S}=-\text{Tr}(\rho \text{log}\rho )& \left(4\right)\end{array}$

If a team is successful in producing a team with members who multitask together to form what appears to be a team with “single mind,” its degrees of freedom (dof) go to 1 (from the equation for cognitive interdependence by Kenny et al. [48], p. 235), accounting for “invisibility,” giving:

$\begin{array}{cc}\text{S}={\text{lim}}_{\text{dof}->\text{1}}\text{log}(\text{dof})=0& \left(5\right)\end{array}$

Interestingly, Einstein was the first to discover the reduction in dof at the quantum level, a critical insight that he shared with Schrodinger ([49], p. 238–9). Like the “single mind” of a team, an example of constructive interference occurs with the melding of the brain into a single mind was given in an interview of Donald Hoffman [50], a cognitive scientist with an evolutionary perspective,

We have two hemispheres in our brain … [that form a] unified single mind. … But when you do a split-brain operation, a complete transection of the corpus callosum, you get clear evidence of two separate consciousnesses.

Interference may be constructive, as when the members of a team work well together. In contrast to Equation (3), to represent Hoffman's “unified single mind” and to further account for the invisibility of interdependence effects, we use subaddivity to get:

$\begin{array}{cc}\text{S}({\rho }_{\text{AB}})\le \text{S}({\rho }_{\text{A}})+\text{S}({\rho }_{\text{B}})& \left(6\right)\end{array}$

Working from Von Neumann's perspective, correlations in joint entropy can become greater or equal to their differences, reflected by Equation (7):

$\begin{array}{cc}\text{S}({\rho }_{\text{AB}})\ge |\text{S}({\rho }_{\text{A}})-\text{S}({\rho }_{\text{B}})|& \left(7\right)\end{array}$

Equation (7) implies that social groups engage in tradeoffs to choose the more fit members of a team, where the best fit is signified by a reduction in joint entropy. Shannon states for subadditivity in a composite system can also be expressed as: H(x, y) ≤ H(x) + H(y) ([51], p. 515–6). From our perspective, subadditivity holds when subsystems are correlated, indicating that the components are interdependent with offsetting entropies, justifying our comments that teams need coaches to compensate for a team's invisible information as it multitasks. At the atomic level, the trace of a density matrix, ρ, isTr(ρ) = 1; for a pure state, ρ² = ρ(idempotent). IfTr(ρ²) = 1, ρis pure and |ψ>_AB is separable; however, ifTr(ρ²) < 1, ρis mixed and |ψ>_AB is entangled ([52], p. 207–8). The degree of mixing determines the departure from a pure state. Based on these considerations, we theorize that interdependence among teammates produces subadditivity, where interdependence specifically means a lack of separability.

Returning to Equation (2), if the two factions in a group, represented by the operators A and B, have reached a single consensus without compromise, the eigenvalues for the operators representing both factions in the group are the same ([[53], p. 256), giving:

$\begin{array}{cc}[A,B]=AB\mathrm{ - }BA=0& \left(8\right)\end{array}$

But interference from social interaction may be destructive; e.g., the rupture of a sports team; a married couple undergoing a divorce; the splitting apart of a business striving to survive a market turndown, like the Maersk Conglomerate [54]. When a group with two factions holds opposed viewpoints, a gap occurs in the group's interpretations of (social, physical) reality. In social-psychological systems, if a binary operator fails to commute ([[53], p. 343], [55] and [56],), it may produce order effects (e.g., [19], p. 2), uncertainty or incompleteness [11], giving:

$\begin{array}{cc}[A,B]=AB\mathrm{ - }BA=iC& \left(9\right)\end{array}$

where C represents a gap, a quantum gap at the atomic level [27] and the incommensurable political gap at the social level, the latter relabeled by us as a Nash equilibrium [4]. This gap at the social level offers a rich, new view of social reality. When the gap is fully driven by both factions with no neutrals on either side, conflict becomes likely [44]. But when neutrals must be wooed by both sides to win a debate, the solicitation of neutrals compels a compromise for the two sides to reach a decision, magnifying the power of neutrals freely able to influence both sides of a debate by helping to avoid a rupture [57]. As a merger of ideas, a compromise satisfies the decision at hand in the heat of the moment, releasing the emotional energy pent up by both factions (emotions are discussed later), energy that had been reserved to continue an intellectual battle associated with a decision under uncertainty. The self-interests of the two sides of a Nash equilibrium act as a quasi-team with neutrals to process information that serves to check (control) the ambitions of both sides [40].

As they form an audience, neutrals, we argue, are the only social element to enter into a superposition (Equation 2), driven into the superposition by the Nash equilibrium that acts like the two cylinders of an engine. As they are wooed to and fro, once neutrals are measured, the trail they leave behind forms limit cycles [4]. Other than the trail left behind, neither side fully grasps the social reality sufficiently well enough to control the neutrals, why dictators, gangs and command economies suppress Nash equilibria and free speech [4]. But in a free society, the result is multiple tradeoffs that a free society exploits to evolve [2], such as finding the optimum size of a team.

Wang and Busemeyer [19] use the concept of complementarity to account qualitatively for order effects; we use complementarity to account for the gap between behavior and self-reported observations of behavior (e.g., [20]), as well as the different interpretations of reality by members of opposing teams (e.g., present-day supporters of Einstein's views on quantum theory vs. Bohr's acausal Copenhagen interpretation; in Lawless [2] and Bohr [27]).

Cohen [58] revised Equation (10) in signal detection theory to arrive at transformations between Fourier pairs, concluding that a “narrow waveform yields a wide spectrum, and a wide waveform yields a narrow spectrum and that both the time waveform and frequency spectrum cannot be made arbitrarily small simultaneously” (p. 45), giving:

$\begin{array}{cc}{\sigma }_{\text{A}}{\sigma }_{\text{B}}\ge 1/2,& \left(10\right)\end{array}$

where σ_A is the standard deviation of variable A (often events), σ_B for variable B (often the time for when events occur) both modeled in Figure 1.

FIGURE 1

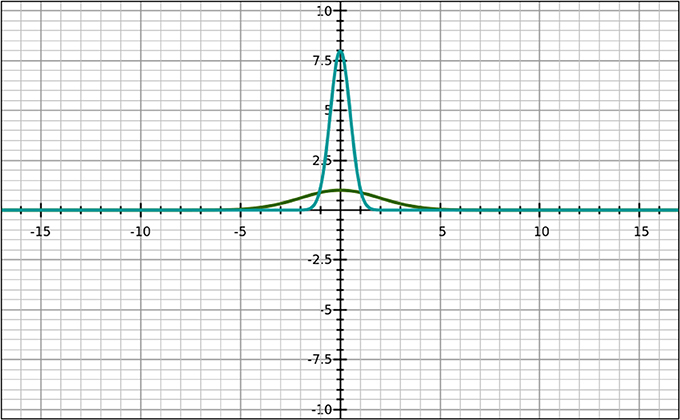
Figure 1. As a notional example, the wide Gaussian is Fourier transformed to the narrow one; the Standard deviation for the latter one is 0.33, that for the wide one about 5.0; the two multiplied together is >1/2.

In quantum theory, the uncertainty relation Equation (10) follows directly from the non-commutativity of Hilbert space operators (Equation 9). Similar relations appear for Fourier pairs in classical field theory as well. By itself, the application of Equation (10) to what follows for the action of teams (Equations 10, 11) can be criticized as a mere analogy and not formally motivated. However, a new discovery of redundancy or overstaffing among oil producers as teams coupled with another discovery (e.g., flawed DOE nuclear waste management teams of scientists and their managers with Equation 14 below; in Lawless [15]) add credibility to our formulation (e.g., [59]).

Based on our prior findings, when the goal of tradeoffs is to find the team members with the right skills for the best team fit, we begin to extend our findings with a revision of Equation (10) to:

$\begin{array}{cc}{\sigma }_{\text{A}}{\sigma }_{\text{B}}->{\sigma }_{\text{skills}}{\sigma }_{\text{interpretations}}\ge 1/2& \left(11\right)\end{array}$

Along with the claims of Smith [7] and Bohr [27], the struggles of Kelley [31] and the findings of Zell and Krizan [20], Equations (5, 11) help us to see that, based strictly on physics, reducing the standard deviation for skills (action) to improve teamwork increases the standard deviation for the interpretations (observations) of the performance of a team's members, accounting for the “invisible” loss of awareness. Accordingly, if the skills of a team approach perfection, the width of different interpretations widens, making it difficult to see what makes a team effective, motivating the need for a coach to improve the performance of a poorly performing team in the search for more successful outcomes for a team's actions (e.g., efforts have recently begun at NSF to train teams of scientists to become better teams of scientists; e.g., [9, 60]).

To study the implications of Equation (10), we decompose a team into a (static) structure that directs its efforts, and its efforts at performing its mission (i.e., dynamic skill roles; actions based on those roles). Assume that the structure of a team is functioning perfectly, allowing the team to use an optimum amount of its available energy to solve the problems that the team was designed to address. Building on our prior success, but speculating, we convert Equation (11) into two components representing the least entropy production (LEP) for the structure of a team and maximum entropy (MEP) to perform a team's mission:

$\begin{array}{cc}{\sigma }_{\text{LEP}}{\sigma }_{\text{MEP}}\ge 1/2& \left(12\right)\end{array}$

Taking limits with the variables in Equation (12) gives us an equation that captures a team's excellence; i.e., as a team's consumption of energy by its structure goes to zero, it's ability to maximize its ability to problem-solve itself becomes a maximum:

$\begin{array}{cc}S=li{m}_{\sigma \text{LEP}->\text{0}}{\sigma }_{\text{MEP}}=\infty & \left(13\right)\end{array}$

With Equation (13) in hand, by inverting it, an account is discovered for what happens when a team fails, splits apart, or implodes [2], giving

$\begin{array}{cc}S=li{m}_{\sigma \text{MEP}->\text{0}}{\sigma }_{\text{LEP}}=\infty & \left(14\right)\end{array}$

The teams represented by Equation (14) might be a couple undergoing divorce; a business team failing (e.g., Maersk Shipping; in Chopping [54]); or a team of scientists forced by managers to not follow rigid scientific practices, exactly what [61] was concerned about. Such an example of scientific malfeasance, driven by management, happened in 1983 with the Department of Energy (DOE) at its Savannah River Site (SRS) in Aiken, SC. Despite its many scientific claims to Congress that DOE waste management practices were safe and equivalent to commercial ones, the file photograph in Figure 2 from SRS points out that from the 1950s until 1983, DOE's waste management practices permitted 90% of its military solid radioactive wastes to be disposed of in ordinary cardboard boxes, allowing these boxes to sit in open trenches exposed to the weather for months at a time, becoming one of the primary sources of radioactively contaminated groundwater across DOE's complex. Public awareness stopped DOE's use of cardboard boxes in 1985. After DOE had openly admitted its past errors and had begun to rectify them, during the cleanup in 2000, renewed public support for DOE accelerated the closure of the same radioactive waste burial ground at SRS [15].

FIGURE 2

Figure 2. At DOE's Savannah River Site from the 1950s until 1985, DOE's waste management permitted 90% of its military solid radioactive wastes to be buried in ordinary cardboard boxes, allowing these boxes to sit in open trenches exposed to the weather for months at a time.

Materials and Methods

The National Academy of Sciences [9] concluded that the problem of team size was an open question, yet implicitly supported redundancy with their consensus speculation that “more hands make light work” (Ch. 1, p. 13). In contrast, to our examples of excluded volumes we add redundancy as a cause of poorly performing oil firm teams [11]. We had found that GDP/capita, our surrogate for the competitiveness of a nation's oil firm teams, was significantly related to its freedom index, less teamwork redundancy, and less redundancy in the number of employees per oil firm. Then with divergence for a distribution of oil firms compared to another for a comparable freedom index, we found a significant regression to indicate that worker redundancy decreased per unit of oil produced as the oil firms were freer to optimize their teams to deploy their capital and labor as they saw fit when drilling for oil. For example, Exxon's production with 15.5 employees/M BBL of oil compares to Sinopec's 124.6 employees/M BBL of oil produced, illustrating that redundancy creates inefficiency.

We first define our four factors: redundancy, economic freedom, military power, and corruption. These factors are mixed objective and subjective, meaning the results will include varying levels of subjectivity.

Redundancy

Redundancy is a quantity measured for interacting human autonomous systems and interfering with other autonomous systems [11]. Redundant are any number of mates that exceed the minimum number of members of a team designed to solve the problem assigned to a team; e.g., a baseball team with more than 9 members on a baseball field has redundant members by that many. In quantum theory, redundant copies of quantum states violate the no-cloning rule ([62], p. 77), and, we argue, interdependent states [11]; e.g., compare Sinopec's 124.6 employees/M BBL of oil produced with Exxon's 15.5, illustrating that authoritarian regimes creates inefficiency with redundancy.

Military Power Ranking

We used the ranking devised by Global Firepower (http://www.globalfirepower.com). Its ranking is based on a nation's weapon diversity and conventional forces without relying on nuclear stockpiles. It includes geographic factors, logistics, natural resources, and industry.

Economic Freedom

An index established by the Heritage foundation based on four broad factors to measure liberty and free markets for 186 nations: rule of law; government size; regulatory efficiency; and open markets. Each factor has three sub-factors (http://www.heritage.org/index/ranking).

Corruption

An index of nations established by Transparency International (https://www.transparency.org). Its factors determine the abuse of power for private gain, and whether the abuse is covert or concealed. The assessment is first to the branches of government, then the public sector, law enforcement, media, businesses, and then other factors.

We measure redundancy with divergence from a Kullback–Leibler-type equation for relative entropy, where D_KL(Q||P) is the Kullback–Leibler's divergence of probability distribution Q from P:

$\begin{array}{cc}{D}_{\text{KL}}(Q||P)={\sum }_{\text{i}}Q(i)log(Q(i)/P(i))& \left(15\right)\end{array}$

The sum of Equation (15) reflects the divergence of distribution Q_i, from distribution P_i, with both distributions normalized. For example, log (P(i)/P(i)) = log 1 = 0. Thus, the more divergence, the larger the separation between two distributions. Based on Equation (15), assuming that a relatively perfect team is possible to solve the problem at hand, we also assume that some structures for desired teams may be closed-ended for a solved problem like those that exist for sports teams; e.g., for a baseball team, designated members take the role of pitcher, catcher, first baseman, etc. Unlike the relatively simple problem of designing a sports team, most business and scientific teams are open-ended whenever competition or innovation are factors. To solve this kind of a structural problem, in business, we look to an industry leader for the best team structure possible for the problem at hand.

To extend these findings to militaries, we hypothesize that redundancy is associated with less freedom in the marketplace and with more corruption. We test this hypothesis with correlations and Kullback–Leibler divergence. We expect that distributions in the real world range from minimum to maximum redundancy; from minimum to maximum freedom; and from minimum to maximum corruption. The nations used in this problem are footnoted below², as is the data for each of them³.

Example:

As an example of the calculations with Equation (15), for China's Military Power Distribution (MPD, or P_MPD), we divided its military power rank (3) by its population in billions (1.374) = 2.183 and the result we divided by 8.1, China's GDP/capita in thousands = 0.370; we summed this result for our top 22 nations = 82.28, which we divided into 0.370 to get the fraction for China, P_China = .0045. We repeated to calculate the Free Market Distribution (FMD) for China (59.4) by dividing by the sum (1296.9) for our Q₁. Next we entered the calculations stepwise into Equation (15) to get for China the following calculation:

$FM{D}^{\ast }Ln(FMD/MPD)={0.044}^{\ast }ln(0.044/0.0045)=\mathrm{0.101.}$

In addition, as one of our methods, we will look for a sign of the collective effects of intelligence.

Results

For a pilot run, we used a convenience sample of 12 nations consisting of some of the largest militaries in the world⁴. We assumed that a country's military could be represented as a team. We compared military size with a country's economic freedom index and its corruption index. For this sample, we first calculated correlations to obtain the following results: As a country's economic freedom index increased positively, its military size per GDP decreased significantly (r = −0.78, p < 0.005) and its corruption level decreased significantly (r = −0.59, p < 0.05). We also found that economic freedom and corruption were inversely correlated significantly (r = −0.77, p < 0.025), indicating that an increase in freedom was associated with a decrease in corruption.

Heartened by these pilot results, we were ready to test our hypothesis with Equation (15). For Q₁, we summed the result of FMD versus MPD to get 1.78. We repeated the process for Q₂ to get another distribution for corruption levels versus MPD for a sum of 1.95. Then we regressed the FMD results individually nation by nation versus MPD (Q₁) with the divergence of corruption from MPD (Q₂) and plotted the result in Figure 3. The result is significant (R², 0.926, p < 0.0001).

FIGURE 3

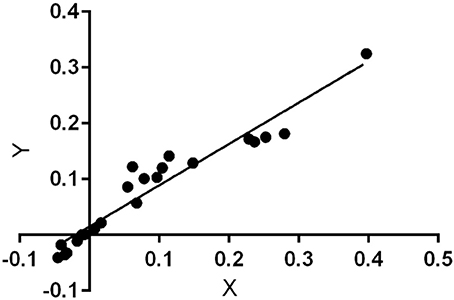
Figure 3. In this figure, we regressed the divergence of freedom from a military distribution with the divergence of corruption from a military distribution. The result indicates a significant regression (R² = 0.926, p < 0.0001). The nations used in this regression are listed in section Materials and Methods.

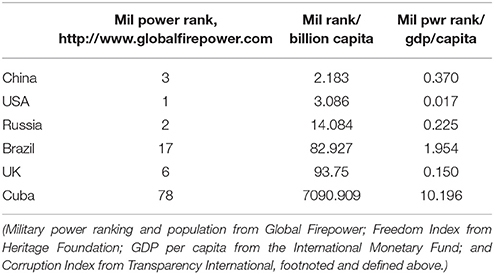
As a side issue, we also looked for signs of intelligence. We found it in our calculations. Consider an abstract from our data in column 4 of the Table 1 below where we see a demarcation between authoritarian and democratically governed militaries. Although fuzzy, we argue that the results in the table's column 4 are signs of intelligence based on information processing; i.e., the military power rank per capita per gdp per capita for China is 0.370 vs. that for the USA of 0.017 and for the UK of 0.15, indicating greater protection per capita by the USA and UK compared to China, Russia, Brazil, and Cuba.

TABLE 1

Table 1. Data rounded off to three significant decimals.

Discussion

We had hypothesized and found in two separate distributions, one for the divergence of GDP for a country's Index of Economic Freedom with its military power ranking per capita, and the other for the divergence of a country's corruption index versus its military power ranking per capita, a significant regression. This indicates that, even with real-world data containing subjective estimations, redundancy increases the more authoritarian is a country's decision-making. As a corollary, the collective effects of intelligence in a society operate best under the freedom to allocate capital and labor for its best uses.

Our results for this study, also backed with correlations, support theory and justify our use of quantum-like models. We found less divergence with our hypothesis for military team size and economic freedom, but more divergence with military team size and corruption, indicating that National Defense improves under the collective effects of intelligent decisions at the level of the team in free markets. It means that a military is leaner and more effective under democracies that under autocracies.

We suspect that redundancy in the market of teams isolates excess teammates from interdependent effects, reducing responsiveness, and converting co-workers into featherbedders. Barriers, like authoritarian leadership and corruption, impede reaching MEP by intelligent teams. And, as we have found, redundancy increases under authoritarian governments, for the possible but corrupt political payoffs that may become necessary to keep civil peace. For example, corruption has stymied the reform of scientific practices in Russia [63] and the transformation of Russian businesses attempting to reduce redundancy [64].

Our model is different from the traditional model, specifically, the cognitive model. As a representative example of the influence of the cognitive model transported from social science to history in the hands of a popular historian⁵, Harari [65] concludes that human groups of no more than 150 can be held together, primarily with gossip, but that larger groups, like Peugeot SA, are “a figment of our collective imagination” (p. 29) based on shared stories, a social construct that forms the “imagined realities” of the cognitive model. But if Harari's account is true, the differences in team distributions between those domiciled in authoritarian regimes versus democracies should be random. Nor would there be any path forward to build teams of machines or robots that could reasonably be expected to advance social welfare in any meaningful way. If Harari's perspective is true, the success of any one's story may be no more than a matter of taste, preference or culture, not a matter for physics or engineering.

That is not what we have found. Our results establish the meaningful differences that interdependent information plays in the interactions and affairs of humans under any and every form of government. Information constraints (barriers) under authoritarian regimes are less able to direct the movement of labor and capital to best solve targeted problems, an added constraint for innovation, one reason the Chinese rely on the theft of intellectual property (see the interview of General M. Hayden, the former CIA and NSA chief, by the editor-in-chief of the Wall Street Journal, [66]). Certainly, obstacles exist in democracies, especially when they become less free to allocate resources to solve the problems targeted (e.g., the Department of Energy's practices included cardboard boxes, seepage basins and other shortcuts to dispose of its radioactive wastes to save money that may eventually cost DOE well over two hundred billions of dollars to remediate its Hanford Site and its Savannah River Site; in Lawless [15]).

Unlike Google's survey of teams [32], guided as it was by traditional social science, we have conjectured and found evidence that an improved theory of human behavior includes both cognitive (subjective surveys like Google's) and behavioral (physical) data which our quantum-like model handles well. By reporting that interdependence is a factor in the best scientific teams, the National Academy has made a nice corrective (9; also see [67]). While we agree with the Academy about the value of interdependence, it would have been better for it to have addressed the theoretical value of interdependence as we did with our quantum-like models to shift the focus from individuals to teams, to how teams disarm “imagined realities” to improve their, and their society's, situational awareness of reality, and to better justify the social tools that humans use to produce superior decisions (e.g., political debate). From our perspective, independent individuals or neutrals are valued as critical to the determination of the winners and losers in a contest where the uncertainty associated with an outcome is high and depends on the persuasion of an audience of neutrals (e.g., in the competition between two equally competent teams competing against each other in politics, in courtrooms, or for the philosophical meaning of quantum reality). The added benefit is that we can generalize these results to mathematical metrics for hybrid teams.

New Work: Emotion

In the HRI community, a lot of research with reinforcement learning (RL) is designed to assist in social interaction where “emotions obviously are important for social interaction” ([68], p. 29). For their research, RL agents require few assumptions, are easy to apply in all kinds of domains, and allow for learning. In contrast, our theory is designed to determine when teams are working well and when not.

In his magisterial review of the literature on emotion, supported by our theory, Zajonc [69] saw that emotion may be interpersonal rather than individual (p. 593), especially during communication (p. 604); emotion exists independently of cognition or is even disconnected from awareness (p. 607) and correlates poorly with self-reports (p. 612), supporting the concept of a mind-body duality (p. 596); habituation indicates a low level of emotion (p. 614); positive emotions lower temperature, T, negative ones increase T (p. 616); and deaf subjects respond more emotionally to spoken texts than normals (p. 619), an effect that, ceteris paribus, suggests expressing a skill is less evident to observers than its absence (p. 619).

In addition, a rise in T occurs with cognitive or social dissonance [2]; energy doubles when expressing a statement in a normal versus an angry voice [70]. Emotions reflect an individual's self-interest (71, p. 439; i.e., less dissonance) and serve to guide social behavior (p. 442) by minimizing marginal expenditures of energy (see also [69], p. 592 and 622).

What if judgments about reality are not rational but guided primarily by experience (where a culture has been ushered into being and molded by experiential learning; [35])? Letting LEP represent the ground state for the structure of a team, a team with its structure at its ground state can devote its availability energy to solving problems, giving experience time to develop into a successful culture. For example, a perfect business team is able to devote its available energy to addressing the problems life offers to it. By way of contrast, when a team's structure exists at an excited state, a business team splitting apart is expending most of its free energy on ripping apart the culture and structure of its team (e.g., Maersk; in Chopping [54]), leaving little available energy to solving the problems it encounters.

Applied to teams by integrating Zajonc and others, we can see that the structure of a team is in a relatively stable state (dof −> 1), and that independent, asocial individuals are in a freer state (maximum dof) than team members. Based on the second law of thermodynamics, comparing a solid substance (ice) and its liquid form (water), energy must be emitted by a group of individuals as a team is formed (e.g., those mergers that reduce redundant employees; in Bunge [72]) and absorbed by a team if it breaks apart.

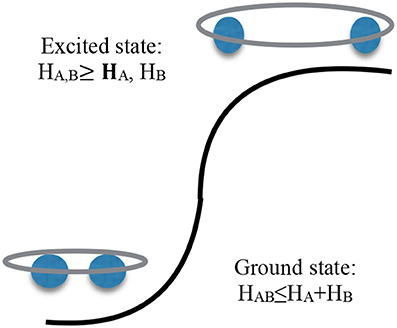
Initially, we use a sigmoid function to model the effort required to hold a team together (see Figure 4). In Equation (16), the effort, f(effort), applied to a team's structure to channel its interactions into a single whole becomes

$\begin{array}{cc}f(effort)=1/(1+exp(-effort))& \left(16\right)\end{array}$

FIGURE 4

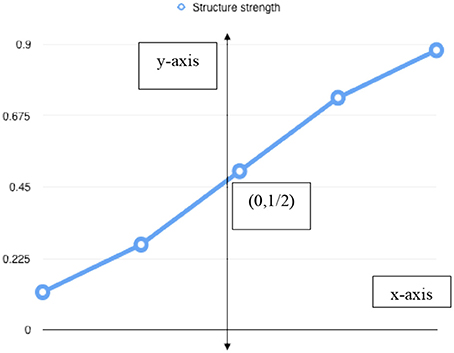
Figure 4. A Monte Carlo simulation of Equation (16) with the y-axis intercept at (0, ½) in the center, with y ranging from 0 to +1 (listed vertically on the far left side). From the y intercept to the right along the x-axis (with x = 0, +1, +2 units) represents increasing effort and emotion; from the left of the intercept along the x-axis represents stability and a team's ground state (where x = -2, -1, 0 units). As the effort to maintain a team's structure approaches zero in the middle of the graph, a critical point is reached. As more effort is required to hold the team's structure together (i.e., moving to the right), it begins to break apart as team members begin to act more and more like redundant, independent individuals.

Results from a Monte Carlo simulation of Equation (16) shown in Figure 4 below indicates that as effort to hold together a team's structure increases beyond a critical point, the team's structure begins to fail. In this simple model, we consider the effort as the potential energy of the team; a well-fitted team then has negative potential energy. Conversely, the less successful the team at solving its designated problems, the more its teammates begin to act as individuals, the more the strength of the team's structure becomes random, causing the cohesion of the team to dissipate. Once the team reaches a critical point (near the y-intercept) in its dissipation, a phase shift has occurred, requiring more and more energy to maintain the team, offsetting a team's successes, destroying the team's structure. Once that happens, joint entropy begins to resume a Shannon-like nature (i.e., Equation 3; e.g., the coming collapse of Sears; in Halzack [73]).

We have also found evidence that a well-fitted team having success at solving the problems it was designed to solve exhibits more intelligence than an under-fitted or over-fitted team with redundant members. The well-fitted team generates less entropy than its individual contributors, an indication that a state of maximum interdependence exists inside of the team, where each member is responsive to every other team member and to the team's mission as well. The state of maximum interdependence, however, can be reversed or blocked. Like quantum computations, the state of interdependence is a resource for a team but also for the society within which the well-fitted team is embedded and to which the well-fitted team contributes. Once a well-fitted team establishes a point of stability, an emotionless baseline, it is operating in a ground state (Figure 5, bottom left). If the joint entropy generated by the team begins to exceed the entropy of any single contributor, the team's interdependence and structure have begun to dissipate (Figure 5, upper right).

FIGURE 5

Figure 5. A notional aspect of the transactions modeled by the sigmoidal function in Equation (16).

We have not addressed the characteristics of the problem targeted, but we suspect that a team must be designed to match its designated problem (e.g., a well-fitted 5-member baseball team is of value in playing against an equally competent 5-member baseball team, but of little value when playing against an equally competent but nine-person baseball team).

Conclusions

Significant impediments exist in the formulation of a science of teams using traditional theories. Specifically, Shannon's information theory and the social sciences, including economics, assume that the human observation of human behavior records the actual behavior that has occurred, even for self-reports of self-observed behavior. In computational social science, this phenomenon has been labeled informally as the “god's eye view,” indicating that the “computer” within which computational action occurs knows immediately whatever action a computational agent takes. In the social sciences, this phenomenon manifests as an observational bias; it allows social scientists to assume that self-reported behavior is actual behavior (e.g., if this assumption was true, deception or denial, such as alcoholic denial or spying, would not exist). We claim that this assumption is unsupported by the evidence, as is the “knowledge” gathered in support, such as the conclusion consonant with widespread religious beliefs that cooperation provides for the best social good. At the heart of these rational, but false models, interdependence is seen as a constraint (information or communication theory) or experimental confound (cognitive science) that must be overcome by traditional social scientists to confirm a theoretical models based on methodological individualism (MI; [26]).

By replacing MI with quantum-like models, we have found computational metrics for good and poor teamwork performance, and a third finding that redundancy is associated with corruption by using relative entropy to model divergence from an oil market leading team, now supported in this study by the size of a nation's military. We have also proposed a new model for a team's emotion as it shifts from a ground state to an excited state. We conclude that, like entanglement at the atomic level, interdependence at the social level is the primary social resource that ordinary humans exploit to innovate and promote social welfare.

Wendt [23] said that quantum-like models should be given a chance to make new discoveries. Who would have even thought that redundancy is a problem, or that it could give insight into the structure of what constitutes the best team. The National Academy of Sciences report on teams points out that team size is an open problem, but while it did not mention redundancy [9], it did speculate that “many hands make light work,” a speculation faulted by our results.

We reject the traditional model of redundancy (e.g., [10]). Cummings [67] found that the more interdisciplinary a science team, the least productive it was as a science team; however, he also found that the best science teams were highly interdependent; i.e., highly responsive to each other. We agree with Cummings, and our results support him.

Excessive team emotion is observable to external observers; e.g., a divorce; a business breakup; a team's collapse. More difficult to observe is the critical point, the transition from a team arguing appropriately [74] over an “invisible” structural issue that, if not resolved, may represent a transition from being a well-fitted team past the critical point until “visible” to those observing a team's transition along the path to becoming ill-fitted as a team's structure breaks down.

For a mathematical physics of teams, a significant impediment has too long existed from accepting the traditional belief that social truth can be established by observing individuals. As exemplars, both built around the statistics of independent, identically distributed data (i.i.d.), information theory and social science, including economics, assume that self-reports record actual behavior, especially self-observed behavior. But the traditional social science model simply does not generalize to hybrid teams; to evolve, to design hybrid teams, this idea that “self-observations record actual behavior” must be rejected.

In contrast, based on our model where interdependence reduces a team's degrees of freedom (dof), thereby obscuring this effect by making it “invisible” to viewers, we propose that ordinary teamwork is characterized by the search for an optimum in the tradeoff between maximum entropy production (MEP) and least entropy production (LEP), where MEP reflects team performance (dynamics; e.g., productivity), LEP determines team structure (statics), and, unexpectedly, the tradeoff generalizes to represent a new and computational model of team emotion. With our theory, we are able to draw several conclusions. First, as a resource, social humans exploit interdependence to innovate and promote social welfare, suggesting that, by increasing and aligning the MEP density across teams, a culture of competition among teams predictably improves social intelligence, innovation and social welfare. Second, however, interdependence precludes replication, causality and truth, exactly what is commonly found in social reality, including social science. And, finally, our local theory of teams appears to scale without limit, limiting the value of independent individuals; but, we theorize, value returns when independent individuals enter into states of superposition driven by the opposed worldviews of competing teams, interdependently entangled until these now individuals superposed to both views are measured to determine the winner of the competition that they are most responsive to.

The best teams have the least redundancy so that they are maximally interdependent among teammates to be responsive to each other as they multitask to solve the problems that they face intelligently. In conclusion, we have found support for our quantum-like model with the solution to the open problem of team size.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Funding

Some of the work was performed while the corresponding author was a senior faculty researcher at the Naval Research Laboratory over the past 2 years, including the Summer 2016 and 2017.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author thanks the reviewers of his manuscript for their very helpful comments, suggestions and corrections.

Footnotes

1. ^iid: independent and identically distributed random variables

2. ^Nations: the top 20 militaries in the world plus Cuba and North Korea were used: China, USA, Russia, Brazil, UK, India, France, Japan, Turkey, Germany, Italy, South Korea, Egypt, Pakistan, Indonesia, Israel, Vietnam, Poland, Taiwan, and Iran.

3. ^For the actual study, we used the top 20 militaries in the world per capita (from http://www.globalfirepower.com) and GDP per capita from the IMF (https://en.wikipedia.org/wiki/List_of_countries_by_GDP_(nominal)_per_capita) versus national Free Market Economy ranking (http://www.heritage.org/index/ranking) and Transparency International's corruption index (https://www.transparency.org/news/feature/corruption_perceptions_index_2016).

4. ^For the pilot study, we used the following sample: USA, China, Cuba, North Korea, India, Israel, Iran, Japan, Mexico, Pakistan, Russia & Turkey; economic freedom index from 2016 http://www.heritage.org/index/ranking; b: the number of military personnel was derived from the 2014 edition of “The Military Balance” published annually by the International Institute for Strategic Studies, except for Cuba, North Korea and Pakistan, with data from http://www.tradingeconomics.com/; and the corruption index was from Transparency International at https://en.wikipedia.org/wiki/Transparency_International.

5. ^His book is a New York Times Bestseller

References

1. Axelrod R. The Evolution of Cooperation. New York, NY: Basic (1984).

Google Scholar

2. Lawless WF. Preventing (another) Lubitz: the thermodynamics of teams and emotion. In: Atmanspacher H, Filk, T, Pothos, E, Editors. Quantum Interactions. LNCS 9535. New York, NY: Springer International (2016). p. 207–15.

Google Scholar

3. WP. White Paper. European Governance (COM (2001) 428 Final; Brussels, 25.7.2001). Brussels: Commission of the European Community (2001).

4. Lawless WF, Sofge DA, Chaudron L, Bartheye O. Bistability, Nash equilibria, (relatively) dark collectives and social physics. Modeling the social behavior of teams. J Enterprise Transform. (2016) 5:241–74. doi: 10.1080/19488289.2015.1123203

CrossRef Full Text | Google Scholar

5. Acemoglu D, Robinson JA. Corruption is just a symptom, not the disease. To end global poverty, stop tolerating national institutions that serve greedy elites and suck poor countries Dry. (2015, December 3). Wall Street Journal. Available online at: http://www.wsj.com/articles/corruption-is-just-a-symptom-not-the-disease-1449174010

6. Buckley C. Collapse in China, safety fears were discussed. New York Times (2016, January 16). Available online at: http://www.nytimes.com/2016/01/17/world/asia/shenzhen-landslide-china.html

7. Smith A. An Inquiry into the Nature and Causes of the Wealth of Nations. Chicago, IL: University of Chicago Press (1776/1977).

8. Lawless WF, Sofge DA. The intersection of robust intelligence and trust: Hybrid teams, firms and systems. In: Mittu R, Sofge D, Wagner A, Lawless WF, Editors. The Intersection of Robust Intelligence and Trust in Autonomous Systems. Berlin: Springer (2016). p. 250–70. doi: 10.1007/978-1-4899-7668-0_12

CrossRef Full Text | Google Scholar

9. Cooke NJ, Hilton ML. (eds.). Enhancing the Effectiveness of Team Science. Committee on the Science of Team Science; Board on Behavioral, Cognitive, and Sensory Sciences; Division of Behavioral and Social Sciences and Education; National Research Council. Washington, DC: National Academies Press (2015).

10. Centola D, Macy M. Complex contagions and the weakness of long ties. Am J Sociol. (2007) 113:702–34. doi: 10.1086/521848

CrossRef Full Text | Google Scholar

11. Lawless WF. The entangled nature of interdependence. Bistability, irreproducibility and uncertainty. J Math Psychol. (2017) 78:51–64. doi: 10.1016/j.jmp.2016.11.001

CrossRef Full Text | Google Scholar

12. Slack D. VA bosses in 7 states falsified Vets' wait times for care. USA Today (2016, April 7). Available online at: http://www.usatoday.com/story/news/politics/2016/04/07/va-wait-time-manipulation-veterans/82726634/

13. DC. MetLife, Inc. versus Financial Stability Oversight Board (FSOB). US District Court for DC, Civilian Action 15-0045, Case 1:15-cv-00045 (2016, 3/39).

14. DOE. U.S. Department of Energy Environmental Management Site-Specific Advisory Board, Policies and Procedures Desk Reference, Office of Intergovernmental and Community Activities (2013). p. 19. Available online at: http://energy.gov/sites/prod/files/2013/07/f2/EM%20SSAB%20Policies%20and%20Procedures%20%28June%202013%29.pdf

15. Lawless WF, Akiyoshi M, Angjellari-Dajcic F, Whitton J. Public consent for the geologic disposal of highly radioactive wastes and spent nuclear fuel. Int J Environ Stud. (2014) 71:41–62. doi: 10.1080/00207233.2014.881165

CrossRef Full Text | Google Scholar

16. GAO. HANFORD WASTE TREATMENT. DOE Needs to Evaluate Alternatives to Recently Proposed Projects and Address Technical and Management Challenges. Report to the Committee on Armed Services, U.S. Senate (2015, May). Available onine at: http://www.gao.gov/assets/680/670080.pdf

17. Khrennikov A. Quantum-like modeling of cognition. Front Phys. (2015) 3:77. doi: 10.3389/fphy.2015.00077

CrossRef Full Text | Google Scholar

18. Busemeyer JR, Wang Z. Quantum cognition: key issues and discussion. Top Cogn Sci. (2014) 6:43–6. doi: 10.1111/tops.12074

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Wang Z, Busemeyer JR. Reintroducing the concept of complementarity into psychology. Front Psychol. (2015) 6:1822. doi: 10.3389/fpsyg.2015.01822

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Zell E, Krizan Z. Do people have insight into their abilities? A metasynthesis? Perspect Psychol Sci. (2014) 9:111–25. doi: 10.1177/1745691613518075

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Freer RD, Perdue WC. Civil Procedure. Cincinatti, OH: Anderson. (1996).

Google Scholar

22. Wang Z, Busemeyer JR. Interference effects of categorization on decision-making. Cognition (2016) 150:133–49. doi: 10.1016/j.cognition.2016.01.019

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wendt A. Quantum Mind and Social Science. Unifying Physical and Social Ontology. Cambridge, UK: Cambridge University Press (2015).

Google Scholar

24. Von Neumann J, Morgenstern O. Theory of Games and Economic Behavior. Princeton, NJ: Princeton University Press (1953). (originally published in 1944).

Google Scholar

25. Rovelli C. Seven Brief Lessons on Physics. Transl. by S. Carnell and E. Segre. New York, NY: Riverhead Books; Penguin Publishing Group (2015). [Original publisher Allen Lane, September 24, 2015].

26. Ahdieh RG. Beyond Individualism and Economics (2009). Available online at: ssrn.com/abstract = 1518836 (Accessed December 5, 2009).

27. Bohr N. Science and the unity of knowledge. In: Leary L, Editor. The Unity of Knowledge. New York, NY: Doubleday (1955). p. 44–62.

28. Rees G, Frackowiak R, Frith C. Two modulatory effects of attention that mediate object categorization in human cortex. Science (1997) 275:835–8. doi: 10.1126/science.275.5301.835

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Rand DG, Nowak MA. Human cooperation. Cogn Sci. (2013) 17:413–25. doi: 10.1016/j.tics.2013.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Von Neumann J. Mathematical Foundations of Quantum Mechanics. Transl. by Beyer RT. Princeton, NJ: Princeton University Press (1955).

Google Scholar

31. Kelley HH. Lewin, situations, and interdependence. J Soc Issues (1992) 47:211–33. doi: 10.1111/j.1540-4560.1991.tb00297.x

CrossRef Full Text | Google Scholar

32. Duhigg C. What google learned from its quest to build the perfect team. New research reveals surprising truths about why some work groups thrive and others falter. New York Times Magazine (2016, February 25). Available online at: http://www.nytimes.com/2016/02/28/magazine/what-google-learned-from-its-quest-to-build-the-perfect-team.html

33. Carroll SB. The Serengeti Rules. The Quest to Discover How Life Works and Why It Matters. Princeton, NJ: Princeton University Press (2016).

Google Scholar

34. Cohen J. Human nature sinks HIV prevention trial. Science (2013) 351:1160. Available online at: http://www.sciencemag.org/news/2013/03/human-nature-sinks-hiv-prevention-trial

35. Adelson EH. Lightness perceptions and lightness illusions. In: Gazzaniga M, Editor. The New Cognitive Sciences, 2nd Edn. Cambridge, MA: MIT Press (2000). p. 339–51.

36. Nosek B, corresponding author from OCS. Open collaboration of science: estimating the reproducibility of psychological science. Science (2015). 349:943 (Suppl. 4716–1 to 4716–9). doi: 10.1126/science.aac4716

CrossRef Full Text | Google Scholar

37. Bednar RL, Peterson SR. Self-Esteem Paradoxes and Innovations in Clinical Practice, 2nd Edition. Washington, DC: American Psychological Association (1995).

38. Baumeister RF, Campbell JD, Krueger JI, Vohs KD. Exploding the self-esteem myth. Sci Am. (2005). 292:70–7. Available online at: https://www.uvm.edu/~wgibson/PDF/Self-Esteem%20Myth.pdf

PubMed Abstract | Google Scholar

39. Von Neumann J. Theory of Self-Reproducing Automata. Champaign, IL: University of Illinois Press (1966).

Google Scholar

40. Madison J. The federalist No. 51. The structure of the government must furnish the proper checks and balances between the different departments. In: Hamilton A, Madison J, Jay J, Editors. Toronto, ON: Bantam Books (1788/1982). Available online at: https://founders.archives.gov/documents/Hamilton/01-04-02-0199

41. Lawless WF, Mittu R, Sofge D, Russell S. Autonomy and Artificial Intelligence. New York, NY: Springer (published in August under the full title: Autonomy and Artificial Intelligence: A threat or savior?) (2017, forthcoming).

42. Martyushev LM. Entropy and entropy production: old misconceptions and new breakthroughs. Entropy (2013) 15:1152–70. doi: 10.3390/e15041152

CrossRef Full Text | Google Scholar

43. Wissner-Gross AD, Freer CE. Causal entropic forces. Phys Rev Lett. (2013) 110:168702. doi: 10.1103/PhysRevLett.110.168702

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Kirk R. More Terrible Than Death. Massacres, Drugs, and America's War in Columbia. New York, NY: Public Affairs (2003).

45. Bruss D. Characterizing entanglement. J Math Phys. (2002) 43:4237. doi: 10.1063/1.1494474

CrossRef Full Text | Google Scholar

46. Suter D, Stolze J. Quantum Computing, Revised and Enlarged, 2nd Edition. Hoboken, NJ: Wiley (2008).

47. Mintert F, Viviescas C, Buchleitner A. Basic concepts of entangled states. In: Springer Lecture Notes Physics, Vol. 768x. New York, NY: Springer. (2009). p. 61–86.

Google Scholar

48. Kenny DA, Kashy DA, Bolger N. Data analyses in social psychology. In: Gilbert DT, Fiske ST, Lindzey G, Editors. Handbook of Social Psychology, 4th Edn. Boston, MA: McGraw-Hill (1998). p. 233–65.

49. Stone AD. Einstein and the Quantum. Princeton, NJ: Princeton University Press (2015).

Google Scholar

50. Gefter A. The evolutionary argument against reality. The cognitive scientist donald hoffman uses evolutionary game theory to show that our perceptions of an independent reality must be illusions. Interview of D.D. Hoffman, Quanta Magazine (2016, April 21). Available onlie at: https://www.quantamagazine.org/20160421-the-evolutionary-argument-against-reality/

51. Nielsen MA, Chuang IL. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge, UK: Cambridge University Press (2011).

Google Scholar

52. uskind L, Friedman A. Quantum Mechanics. New York, NY: Bantam Books (2014).

53. Gershenfeld N. The Physics of Information Technology. Cambridge, MA: MIT Press (2000).

Google Scholar

54. Chopping D. Maersk to split into two separate units. Move comes months after departure of CEO Nils Andersen. Wall Street Journal (2016, September 22). Available online at: http://www.wsj.com/articles/maersk-to-split-into-two-units-1474529401

55. Luce RD. Several unresolved conceptual problems of mathematical psychology. J Math Psychol. (1997) 41:79–87. doi: 10.1006/jmps.1997.1150

CrossRef Full Text | Google Scholar

56. Luce RD. Rationality in choice under certainty and uncertainty. In: Schneider S, Shanteau, J, Editors. Emerging Perspectives in Judgment and Decision Making. Cambridge: Cambridge University Press (2003). p. 64–83. doi: 10.1017/CBO9780511609978.004

CrossRef Full Text | Google Scholar

57. Schlesinger A. The Vital Center. The Politics of Freedom. Rolling Meadows, IL: Riverside Press (1949).

Google Scholar

58. Cohen L. Time-Frequency Analysis: Theory and Applications. Prentice Hall Signal Processing Series. London, UK: Pearson. (1995).

Google Scholar

59. Goodman SN. Aligning statistical and scientific reasoning. Science (2016) 352:1180–1. doi: 10.1126/science.aaf5406

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Cohen J. Promoting Team Science. Santa Barbara, CA (2015, October 14). Available online at: http://www.news.ucsb.edu/2015/016031/promoting-team-science#sthash.bTJSXdKn.dpuf

61. Lilienthal D. Change, Hope and the Bomb. Princeton, NJ: Princeton University Press (1963).

Google Scholar

62. Wooters WK, Zurek WH. The no-cloning theorem. Physics Today (2009, February). p. 76–7. Available online at: http://www.physics.umd.edu/studinfo/courses/Phys402/AnlageSpring09/TheNoCloningTheoremWoottersPhysicsTodayFeb2009p76.pdf

63. Englund W. A fix for Russian science isn't taking hold. Washington Post (2014, December 21). Available online at: https://www.washingtonpost.com/world/europe/a-fix-for-russian-science-isnt-taking-hold/2011/11/28/gIQAMJD99O_story.html?hpid=z3

64. Chow J, Marson J. Renault tries to fix Russian misadventure. French company and nissan try to turn around Russian auto maker AvtoVAZ, but CEO they installed sets off a backlash. Wall Street Journal (2016, April 11). Available onine at: http://www.wsj.com/articles/renault-tries-to-fix-russian-misadventure-1460333219

65. Harari YN. Sapiens. A Brief History of Humankind. New York, NY: HarperCollins (2015).

Google Scholar

66. Baker G. Michael hayden says U.S. Is easy prey for hackers. Former CIA and NSA chief says ‘shame on us’ for not protecting critical information better. Interview by the Wall Street Journal's Editor in Chief (2015, June 21). Available onine at: http://www.wsj.com/articles/michael-hayden-says-u-s-is-easy-prey-for-hackers-1434924058

67. Cummings J. Team Science Successes and Challenges. National Science Foundation Sponsored Workshop on Fundamentals of Team Science and the Science of Team Science. Bethesda, MD (2015, June 2).

68. Moerland TM, Broekens J, Jonker C. Emotion in Reinforcement Learning Agents and Robots: A Survey (2017, May 15). Available online at: https://arxiv.org/pdf/1705.05172.pdf

69. Zajonc RB. Emotion. In: Gilbert DT, Fiske ST, Lindzey G, Editors. The Handbook of Social Psychology 4th Edn. Boston, MA: McGraw-Hill (1998). p. 591–632.

70. Lawless WF. The Quantum of Social Action and the Function of Emotion in Decision-Making. AAAI Technical Report FS-01-02 (2001). Available online at: www.aaai.org

71. Dawkins R. The Selfish Gene. Oxford: Oxford University press (1989).

Google Scholar

72. Bunge J. Bayer-monsanto deal faces heavy regulatory scrutiny. combining two of the world's largest farm suppliers will test politicians wary of consolidation in the $100 billion global market. Wall Street Journal (2016, September 14). Available online at: http://www.wsj.com/articles/bayer-monsanto-deal-faces-heavy-regulatory-scrutiny-1473855922

73. Halzack S. The big missteps that brought an american retail icon to the edge of collapse. Washington Post (2017, June 1). Available online at: https://www.washingtonpost.com/business/capitalbusiness/the-big-missteps-that-brought-an-american-retail-icon-to-the-edge-of-collapse/2017/06/01/19f4bee4-35a3-11e7-b4ee-434b6d506b37_story.html?utm_term=.2323f86cfca4

74. Hackman JR. Six Common Misperceptions About Teamwork. Harvard Business Review (2011). Available online at: blogs.hbr.org/cs/