- Key Laboratory for Thin Film and Microfabrication of Ministry of Education, Department of Micro/Nano-electronics, Shanghai Jiao Tong University, Shanghai, China
As theoretical approaches and technical methods improve over time, the field of computer simulations for water has greatly progressed. Water potential models become much more complex when additional interactions and advanced theories are considered. Macroscopic properties of water predicted by computer simulations using water potential models are expected to be consistent with experimental outcomes. As such, discrepancies between computer simulations and experiments could be a criterion to comment on the performances of various water potential models. Notably, water can occur not only as liquid phases but also as solid and vapor phases. Therefore, the melting temperature related to the solid and liquid phase equilibrium is an effective parameter to judge the performances of different water potential models. As a mini review, our purpose is to introduce some water models developed in recent years and the melting temperatures obtained through simulations with such models. Moreover, some explanations referred to in the literature are described for the additional evaluation of the water potential models.
Introduction
Water is an undeniably important chemical in nature. Scientists from different disciplines are attracted to water because of its significance and ubiquity. Furthermore, life cannot exist without water which is considered as “matrix of life” [1]. As a pivotal solvent, water provides an appropriate environment for chemical reactions and biological processes. In addition, water is distributed across the Earth and even is found in outer space. Except experiments for water exploration, computer simulations become an alternative way to estimate properties under various circumstances. The first water potential model proposed by Bernal and Fowler as early as 1933 [2] was a pioneering work. However, its correctness was proven nearly 40 years later [3, 4] when the computational power became satisfactory enough. Subsequently, an enormous number of water potential models appeared continuously. Improvements during this process stemmed from both modifications based on previous models and original proposals with new ideas.
Most water potential models can be classified into two categories: classical and quantum potential models. The fundamental difference is that the effect of electronic structures of water molecules is treated by solving Schrödinger equations in the latter case. The earliest models are called rigid models, describing water molecule as the combination of point charges and repulsion-dispersion sites. In addition, OH bond lengths and angles are geometrically fixed [5–8]. Parameters of such empirical potential models are commonly fitted to reproduce macroscopic properties at ambient conditions. While rigid models neglect the polarizability of molecules and flexibility of OH bonds, polarizable models can respond to local electrostatic changes that play an important role in solvation and surface phenomena. Several methods are introduced [9] to implement polarizability, including fluctuating charges, charge-on spring, point dipole, and mobile charge densities methods. To mimic water more realistically, intramolecular vibrations should be allowed through the inclusion of flexibility. Hence, flexible models can yield vibrational spectra due to variable bond lengths and angles. Vibrational spectroscopy technologies including infrared spectra and Raman are proficient at detecting structures and dynamics of water, especially in the OH stretch regions [10]. Furthermore, model parameters can be modified using results from either ab initio calculations or experimental data of water clusters [11]. As water clusters have finite particles, experiments are easier to carry out than bulk liquid or ice for deep understanding, such as local structures and hydrogen bond networks [12, 13]. More ambitious works account for electronic structures in computer simulations [14]. For example, quantum potential models consider electronic degrees of freedom in terms of wave functions or electronic density. Especially, density functional theory (DFT) can handle the influence of electronic structures when the exchange-correlation energy is treated by generalized gradient approximations.
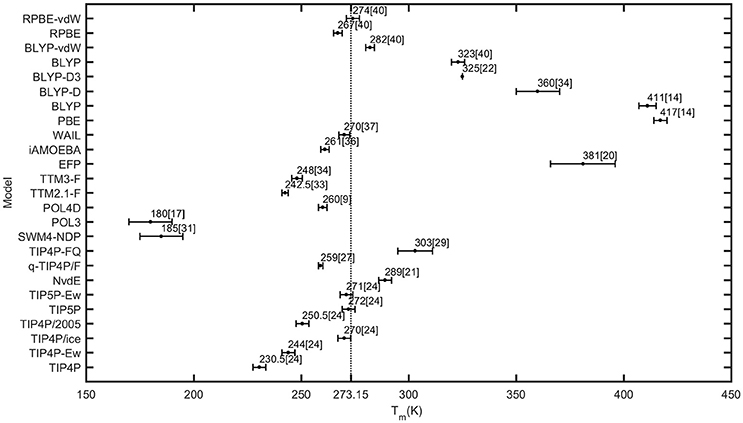
The main goal of water computer simulations is to reproduce macroscopic properties perfectly under various thermodynamic conditions and predict phenomena observed in experiments [15, 16]. In general, characteristics which can quantify the accuracy of water potential models are numerous. Properties appearing in literature include the density of liquid, self-diffusion coefficient, critical point, dielectric constant, phase diagram, radial distribution functions, melting temperature and others. On account of various phases of water, the melting point should be an effective criterion to judge different models (see Figure 1). Namely, models that describe liquid phases well should be examined closely when they describe solid phases or phase transitions [17]. Relevant studies for both bulk water and water clusters have been reported. When compared with bulk water, the melting transition of water clusters is strongly influenced by cluster sizes [18]. Two most popular methods for the melting point estimation are Gibbs free energy calculations and the direct solid-liquid coexistence curve [19, 20]. Regardless of which method is used, the obtained melting temperature is convincing within acceptable and reasonable deviations, and this viewpoint has been confirmed in previous literature [21]. Besides, both isothermal-isobaric (NPT) and isoenthalpic-isobaric (NPH) ensembles are applied in molecular dynamics simulations. In the NPH ensemble, the constant enthalpy ensures that the total system is isolated so that no heat is transmitted between the system and the surroundings [20]. Consequently, the border of liquid and solid will shift until the whole system reaches an equilibrium (Gliq (P; Tm) = Gsolid (P; Tm)). When a NPT simulation is performed, the melting or freezing is monitored by examining the evolution of the total energy of the ice-liquid system or density profile. A temperature higher than the melting point makes ice melt completely, while a lower temperature results in freezing [9]. Computational limits lead to imprecision; in fact, many simulation systems do not contain enough molecules since the size of the simulation cuboid geometry is limited. Consequently, the finite size affects the calculated melting point [22]. Simultaneously, a periodic boundary condition is usually introduced to mimic bulk water, and cutoff strategies (for van der Waals interactions, electrostatic interactions, Lennard-Jones interactions, etc.) are necessary to simplify the calculation of interactive forces. Moreover, the simulation time is unrealistically restricted due to the expensive computational cost, especially in DFT-based simulations.
Melting Temperatures of Various Water Potential Models
Melting Temperatures of Classical Water Potential Models
Classical water potential models take up the majority and have played a dominant role in molecular dynamics simulations of water. Rigid models, e.g., TIP4P, TIP4P-Ew [5], TIP4P/ice [15], TIP4P/2005 [6], TIP5P [23], TIP5P-Ew [8], and NvdE [7], have been studied in detail from various perspectives. Melting temperatures of these models obtained by different researchers are not exactly same but within the uncertainty. Hence, melting points of the mentioned models are adapted qualitatively from the published literature and the form “model-melting point (uncertainty)” is used for a simple expression. Melting temperatures are listed as TIP4P-230.5 (3) K, TIP4P-Ew-244 (3) K, TIP4P/ice-270 (3) K, TIP4P/2005-250.5 (3) K, TIP5P-272 (3) K, TIP5P-Ew-271 (3) K [24], and NvdE-289 (3) K [21] (see Figure 1). For complete comparisons with bulk water, the melting points of 20-molecule water cluster using TIP4P, TIP4P/ice and TIP4P/2005 were estimated within 150 ± 20 K. TIP4P/ice had the highest value followed by TIP4P/2005 and TIP4P [18], which is consistent with bulk water. Deviations from experiments are justified by distinguishing the position of negative charges and the resulting quadrupole moment of these models. One negative charge is located at the bisector of the two OH bonds in TIP4P-like models, while two negative charges in TIP5P and TIP5P-Ew are located at the lone-pair electron sites of the oxygen atom. As for NvdE model, three negative charges are located at the lone-pair sites and the bisector simultaneously. In three-charge models, once the quadrupole moment is closer to the real value, the melting point is more consistent with the experimental value [25]. However, the melting temperature of four-charge models is correlated with a stable tetrahedral distribution of charges. This type of charge distribution enhances the hydrogen bond network providing a higher melting point for the NvdE model compared to TIP4P model. Accounting for the geometry of NvdE which combines two methodologies, the negative charge distribution is inferred to dramatically influence the melting temperature. Conversely, parameters of rigid models are set to match experimental data of target properties at different conditions. For instance, TIP4P/ice was specifically designed to calculate solid phase properties [15], and TIP4P/2005 was designed to reproduce the temperature of maximum density and other common properties [6], although the two models have the similar geometry and charge distribution. Consequently, estimations of anticipated properties like the melting temperature can be guaranteed for specific models, but predictions of other properties mostly fail for exceeding the fit range. Finally, measurements of melting points are associated with phase transitions that are sensitive to pressure and temperature. As the pressure increases, low-density water transforms continuously to high-density water due to interstitial molecules, which was simulated by TIP4P [26]. The relation that a higher pressure corresponds to a lower melting point was proved and the validity of TIP4P was checked concomitantly.
The validity of rigid models is unsurprisingly questionable since they ignore flexible and polarizable features. The flexibility affects intramolecular interactions in terms of variable OH bond lengths and angles. The flexible q-TIP4P/F [27] model with OH stretches described by Morse-type functions determined the melting temperature to be 259 (1) K. The inclusion of such intramolecular interaction indicated no obvious improvements to the melting temperature. In addition to flexibility, the polarizability can reveal the potential to respond instantaneously to heterogenous environments and charge transformations. The TIP4P-FQ model [28] which modifies TIP4P through fluctuating charges contains a self-polarization term, causing stronger interactions between molecules. Then, the corresponding melting temperature was found to be 303 (8) K [29]. Another polarizable model named SWM4-NDP [30] applies the Drude oscillator technique to represent polarizability and has the quadrupole moment assigned at approximately the experimental value. Surprisingly, the melting temperature of SWM4-NDP was 185 (10) K, which was much lower than 273.15 K [31]. The polarizable POL3 [32] model yielded a melting point of 180 (10) K [17] and thus its suitability for ice simulation is limited. In this model, induced dipoles are determined by point dipoles located at the three atom sites and the surrounding electric field. Although induced point dipoles increase the total dipole moment, the total quadrupole moment is rather small. The POL4D model [9] with Rowlinson five-site geometry is polarized in the simplest isotropic linear way. The melting temperature of this model was estimated as 260 (2) K. Importantly, methods treating polarizability and structures of polarizable models can affect the simulated melting temperature, which is clearly demonstrated by deviations from the experimental value [31] (see Figure 1). In most cases, the addition of polarizability tends to lower the melting temperature with an exception of TIP4P-FQ. When the polarizability is introduced based on common rigid models, this modification may destabilize the solid structure and increase the disorder of molecules, which accounts for the lower melting temperature.
In contrast to roughness of empirical potential models, ab initio potential models express the sophisticated representation of Born-Oppenheimer potential energy surface. TTM2.1-F [11] which employed gas phase monomer potential energy and dipole moment surfaces previously yielded a melting value of 242.5 (1.5) K [33]. Later, the flexible and polarizable TTM3-F model [16] having similar structural and dynamical characteristics with the previous version converged at 248 (2.5) K [34]. The highlight of the latter model is the ability to reproduce vibrational spectra both in water clusters and liquid water, which are congruent with experiments [16]. To some extent, this agreement ensures the validity of the designed model. The EFP model [35] is derived from ab initio quantum chemistry with no empirical parameters and water molecules are represented as combinations of five interaction energy terms, including the Coulombic, polarization, exchange repulsion, dispersion and charge transfer interactions. The estimated melting point was 381 (15) K [20] which was substantially higher than the experimental value. The iAMOEBA model [36] is parameterized using the ForceBalance method which utilizes experimental data and high-level ab initio calculation results. Electronic polarizability is treated in a direct approximation, which reduces the computational cost and maintains an accurate description. The melting point was calculated to be 261 (2) K, not far from the experimental value. The WAIL model was created as a problem-specific force field for water using the adaptive force matching method with only electronic structure information as input. Thus, this model determined a melting point of 270 (2.5) K [37]. Although ab initio potential models are desired to predict macroscopic properties and interactions well, the availability of such models that can predict melting temperature is still problematic (see Figure 1). However, information derived from the electronic structure and potential energy surface is encouraging for a deeper understanding of water molecules. Despite this, how to use such information of intermolecular interactions to account for the melting properties remains challenging, which is clearly shown by the rather high melting temperature of the EFP model. TTM2.1-F and TTM3-F that rely on water clusters interactions may underestimate bulk interactions and lead to lower melting temperatures, while iAMOEBA which employs hybrid data and WAIL which uses a quantum mechanics/molecular mechanics procedure, perform well about the melting prediction.
Melting Temperatures of Quantum Water Potential Models
Great caution should be exercised when DFT-based molecular dynamics simulations are performed. Most exchange-correlation functionals fail to predict physical and thermodynamic properties of water, resulting from the lack of delicate interactions. In view of the complexity and accuracy of functionals, Perdew-Burke-Ernzerhof (PBE) and Becke-Lee-Yang-Parr (BLYP) were chosen to determine the melting temperature via Born-Oppenheimer molecular dynamics simulations [14]. When the prerequisite density (ρ = 1 g/cm3) was satisfied, the average pressure of P = 2,500 bar (PBE) and P = 10,000 bar (BLYP) were much higher than the ambient pressure. Melting temperatures corresponding to these unusual pressures were 417(3) K (PBE) and 411 (4) K (BLYP). Supercooled water and overstructured liquid were predicted at ambient conditions, which strongly suggests that pure functionals cannot effectively describe accurate interactions. To this end, an empirical van der Waals (vdW) potential correction for long-range dispersion effects has been verified to dramatically improve descriptions of molecular complexes [38]. The dispersion correction plays a significant role in improving simulation results, yielding superior water densities, radial distribution functions and self-diffusion coefficients. BLYP-D functional [34] estimated the melting temperature as 360 (10) K, showing noticeable progress compared to the original functional. The development of approximate DFT approaches is an active area of research for the chemical accuracy in large systems, such as dispersion-corrected atom-centered potential, nonlocal van der Waals functional and pure density functional [39]. However, BLYP functional with D3 corrections provided a melting value of 325 K [22] which is still higher than the experimental value. Besides, effects of vdW interactions on properties of water are explored by using neural network potentials which produce the accurate potential energy surface. Calculated melting temperatures of revised Perdew–Burke–Ernzerhof (RPBE) and BLYP with and without D3 corrections are displayed as BLYP-323 (3) K, BLYP-vdW-283 (2) K, RPBE-267 (2) K and RPBE-vdW-274 (3) K [40]. The inclusion of vdW forces not only resulted in more realistic structures but also produced a shift of melting temperature toward 273.15 K. Notably, a discrepancy occurs when values of BLYP are compared with earlier reports in term of different settings, but the diminution of the melting point due to vdW corrections is consistent, which further proves the role of vdW corrections. Clearly, DFT-based simulations roughly estimate the melting point because of the inherent complexity and shortcomings of functionals. Higher functionals like hybrid functionals or functionals with advanced dispersion corrections are suggested for excellent performance.
Monte Carlo simulations with second-order Møller-Plesset (MP2) perturbation theory have been performed for understanding structures and properties of liquid water [41]. Similar to DFT-based simulations, MP2-based simulations are also a quantum mechanical method. Moreover, MP2 theory accounts for dispersion interactions and recovers many dynamic correlations. Simulations for the melting temperature of water with MP2 are still missing, but the density of liquid water at ambient conditions (T = 295 K and P = 1 bar) has been obtained, i.e., 1.02 g/mL [41]. To obtain the correct density, DFT with a generalized gradient approximation needs a higher temperature and pressure than MP2. Polarizability and dispersion interactions were found to explain these differences. The TTM3-F model with dispersion and polarizability scale factors was chosen to perform simulations individually to test effects of the dispersion and polarizability [42]. A smaller dispersion interaction leads to less dense liquid water, which indicates that molecules would move faster. Then, a larger pressure is needed on the system to maintain the density at 1 g/cm3. In fact, the correction of vdW interactions in BLYP potential eliminates the demand for higher pressures [34]. Furthermore, a larger polarizability was found to result in overstructured water, which would melt at a higher temperature. Enhanced tetrahedral hydrogen bonds prevent the motion and rotation of molecules at ambient conditions and more energy is needed to break these restrictions [42]. Through the comparison of dispersion and polarizability, the melting point is further explained by the effect of the intermolecular forces which are determined by the essential description of the molecular model.
Summary and Future Outlook
According to modeling principles, water potential models are divided into classical and quantum potential models. Parameters of the former models are fitted to either experimental data or ab initio calculation results. Empirical models describe potential energy in an effective way, whereas ab initio based models are capable of generating Born-Oppenheimer potential energy surfaces. Quantum models describe water at an atomistic level and are transferable across different environments. Empirical models can predict the melting temperature close to the experimental value through specific modifications. These models have excellent advantages in applications due to their simplicity, while theoretical understandings and physical insights are ambiguous. Ab initio water potential models are combined with superior theories based on water clusters, but they fail to reproduce the melting temperature of bulk water in some cases. As for quantum models, high-level principles are included to represent in-depth descriptions. However, interactions between molecules are complex and described in an approximate way. Indeed, DFT-based simulations are likely to evaluate a higher melting point than the experimental value. This review shows that the prediction of the melting temperature is a stringent judgment for water potential models and that it may guide the development of improved potential models.
Ultimately, various intermolecular and intramolecular interactions should be described exactly to reproduce the melting temperature like electrostatic moments, polarizability, dispersion forces and bond vibrations. With regard to theoretical approximations under computational limits, most simulations of melting points are performed in classical molecular dynamics considering the motion of atoms in trajectories governed by Newton equations. Quantum effects influence the motion of water nuclei, especially because hydrogen is the lightest atom. For advanced works, quantum mechanical simulations (such as path-integral, centroid and ring polymer molecular dynamics) in conjunction with superior water potential models (designed for quantum simulations) [27, 37] are expected to generate extraordinary physical insights.
Author Contributions
SD wrote the main manuscript text and prepared figures, SY designed the idea, and JL gave some suggestion and revised the manuscript. All authors reviewed the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (No. 51672176).
References
2. Bernal J, Fowler R. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J Chem Phys. (1933) 1:515–48. doi: 10.1063/1.1749327
3. Barker J, Watts R. Structure of water; a Monte Carlo calculation. Chem Phys Lett. (1969) 3:144–5. doi: 10.1016/0009-2614(69)80119-3
4. Rahman A, Stillinger FH. Molecular dynamics study of liquid water. J. Chem. Phys. (1971) 55:3336–59. doi: 10.1063/1.1676585
5. Horn HW, Swope WC, Pitera JW, Madura JD, Dick TJ, Hura GL, et al. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J Chem Phys. (2004) 120:9665–78. doi: 10.1063/1.1683075
6. Abascal JL, Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J Chem Phys. (2005) 123:234505. doi: 10.1063/1.2121687
7. Nada H, van der Eerden JP. An intermolecular potential model for the simulation of ice and water near the melting point: a six-site model of H2O. J Chem Phys. (2003) 118:7401–13. doi: 10.1063/1.1562610
8. Rick SW. A reoptimization of the five-site water potential (TIP5P) for use with Ewald sums. J Chem Phys. (2004) 120:6085–93. doi: 10.1063/1.1652434
9. Viererblová L, Kolafa J. A classical polarizable model for simulations of water and ice. Phys. Chem. Chem. Phys. (2011) 13:19925–35. doi: 10.1039/c1cp22198a
10. Bakker H J, Skinner J L. Vibrational spectroscopy as a probe of structure and dynamics in liquid water. Chem Rev. (2009) 110:1498–517. doi: 10.1021/cr9001879
11. Fanourgakis GS, Xantheas SS. The flexible, polarizable, Thole-type interaction potential for water (TTM2-F) revisited. J Phys Chem A (2006) 110:4100–6. doi: 10.1021/jp056477k
12. Buck U, Huisken F. Infrared spectroscopy of size-selected water and methanol clusters. Chem Rev. (2000) 100:3863–90. doi: 10.1021/cr990054v
13. Devlin JP, Sadlej J, Buch V. Infrared spectra of large H2O clusters: New understanding of the elusive bending mode of ice. J Phys Chem A (2001) 105:974–83. doi: 10.1021/jp003455j
14. Yoo S, Zeng XC, Xanthes SS. On the phase diagram of water with density functional theory potentials: the melting temperature of ice Ih with the Perdew-Burke-Ernzerhof and Becke-Lee-Yang-Parr functionals. J Chem Phys. (2009) 130:221102. doi: 10.1063/1.3153871
15. Abascal J, Sanz E, Garcia Fernandez R, Vega C. A potential model for the study of ices and amorphous water: TIP4P/ice. J Chem Phys. (2005) 122:234511. doi: 10.1063/1.1931662
16. Fanourgakis GS, Xantheas SS. Development of transferable interaction potentials for water. V. Extension of the flexible, polarizable, Thole-type model potential (TTM3-F, v 3.0) to describe the vibrational spectra of water clusters and liquid water. J Chem Phys. (2008) 128:074506. doi: 10.1063/1.2837299
17. Muchova E, Gladich I, Picaud S, Hoang PN, Roeselova M. The ice- vapor interface and the melting point of ice Ih for the polarizable POL3 water model. J Phys Chem A (2011) 115:5973–82. doi: 10.1021/jp110391q
18. Douady J, Calvo F, Spiegelman F. Effect of an ionic impurity on the caloric curves of water clusters. Eur Phys J D-Atom Mol Opt Plas Phys. (2009) 52:47–50. doi: 10.1140/epjd/e2008-00247-3
19. Habershon S, Manolopoulos DE. Free energy calculations for a flexible water model. Phys Chem Chem Phys. (2011) 13:19714–27. doi: 10.1039/c1cp21520e
20. Brorsen KR, Willow SY, Xantheas SS, Gordon MS. The melting temperature of liquid water with the effective fragment potential. J Phys Chem Lett. (2015) 6:3555–9. doi: 10.1021/acs.jpclett.5b01702
21. Abascal JL, Fernandez RG, Vega C, Carignano MA. The melting temperature of the six site potential model of water. J Chem Phys. (2006) 125:166101. doi: 10.1063/1.2360276
22. Seitsonen AP, Bryk T. Melting temperature of water: DFT-based molecular dynamics simulations with D3 dispersion correction. Phys Rev B (2016) 94:184111. doi: 10.1103/PhysRevB.94.184111
23. Mahoney MW, Jorgensen WL. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J Chem Phys. (2000) 112:8910–22. doi: 10.1063/1.481505
24. García Fernández R, Abascal JL, Vega C. The melting point of ice Ih for common water models calculated from direct coexistence of the solid-liquid interface. J Chem Phys. (2006) 124:144506. doi: 10.1063/1.2183308
25. Abascal JL, Vega C. The water forcefield: Importance of dipolar and quadrupolar interactions. J Phys Chem C (2007) 111:15811–22. doi: 10.1021/jp074418w
26. Saitta A M, Datchi F. Structure and phase diagram of high-density water: the role of interstitial molecules. Phys Rev E (2003) 67:020201. doi: 10.1103/PhysRevE.67.020201
27. Habershon S, Markland TE, Manolopoulos DE. Competing quantum effects in the dynamics of a flexible water model. J Chem Phys. (2009) 131:024501. doi: 10.1063/1.3167790
28. Rick SW, Stuart SJ, Berne BJ. Dynamical fluctuating charge force fields: application to liquid water. J Chem Phys. (1994) 101:6141–56. doi: 10.1063/1.468398
29. Nicholson BF, Clancy P, Rick SW. The interface response function and melting point of the prism interface of ice Ih using a fluctuating charge model (TIP4P-FQ). J Crys Growth (2006) 293:78–85. doi: 10.1016/j.jcrysgro.2006.04.077
30. Lamoureux G, Harder E, Vorobyov IV, Roux B, MacKerell AD. A polarizable model of water for molecular dynamics simulations of biomolecules. Chem Phys Lett. (2006) 418:245–9. doi: 10.1016/j.cplett.2005.10.135
31. Gladich I, Roeselova M. Comparison of selected polarizable and nonpolarizable water models in molecular dynamics simulations of ice Ih. Phys Chem Chem Phys. (2012) 14:11371–85. doi: 10.1039/c2cp41497j
32. Dang LX. The nonadditive intermolecular potential for water revised. J Chem Phys. (1992) 97:2659–60. doi: 10.1063/1.463054
33. Paesani F, Voth GA. Quantum effects strongly influence the surface premelting of ice. J Phys Chem C (2008) 112:324–7. doi: 10.1021/jp710640e
34. Yoo S, Xantheas SS. Communication: The effect of dispersion corrections on the melting temperature of liquid water. J Chem Phys. (2011) 134:121105. doi: 10.1063/1.3573375
35. Gordon MS, Slipchenko L, Li H, Jensen JH. The effective fragment potential: a general method for predicting intermolecular interactions. Annu Rep Comput Chem. (2007) 3:177–93. doi: 10.1016/S1574-1400(07)03010-1
36. Wang LP, Head-Gordon T, Ponder JW, Ren P, Chodera JD, Eastman PK, et al. Systematic improvement of a classical molecular model of water. J Phys Chem B (2013) 117:9956. doi: 10.1021/jp403802c
37. Pinnick ER, Erramilli S, Wang F. Predicting the melting temperature of ice-Ih with only electronic structure information as input. J Chem Phys. (2012) 137:014510. doi: 10.1063/1.4731693
38. Grimme S. Accurate description of Van der Waals complexes by density functional theory including empirical corrections. J Comput Chem. (2004) 25:1463–73. doi: 10.1002/jcc.20078
39. Grimme S, Antony J, Ehrlich S, Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys. (2010) 132:154104. doi: 10.1063/1.3382344
40. Morawietz T, Singraber A, Dellago C, Behler, J. How van der Waals interactions determine the unique properties of water. Proc Natl Acad Sci USA. (2016) 113:201602375. doi: 10.1073/pnas.1602375113
41. Del Ben M, Schönherr M, Hutter J, VandeVondele J. Bulk liquid water at ambient temperature and pressure from MP2 theory. J Phys Chem Lett. (2013) 4:3753–9. doi: 10.1021/jz401931f
Keywords: water melting temperature, classical water model, quantum water model, DFT, MP2
Citation: Du S, Yoo S and Li J (2017) Comparison of the Melting Temperatures of Classical and Quantum Water Potential Models. Front. Phys. 5:34. doi: 10.3389/fphy.2017.00034
Received: 28 May 2017; Accepted: 02 August 2017;
Published: 17 August 2017.
Edited by:
Miguel Rubi, University of Barcelona, SpainReviewed by:
Annarita Laricchiuta, Consiglio Nazionale Delle Ricerche (CNR), ItalyFlorent Calvayrac, University of Maine, France
Copyright © 2017 Du, Yoo and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jinjin Li, bGlqaW5qaW4ucGh5c2ljc0BnbWFpbC5jb20=
 Sen Du
Sen Du Soohaeng Yoo
Soohaeng Yoo Jinjin Li
Jinjin Li