GUT and Flavor Models for Neutrino Masses and Mixing

1. Introduction

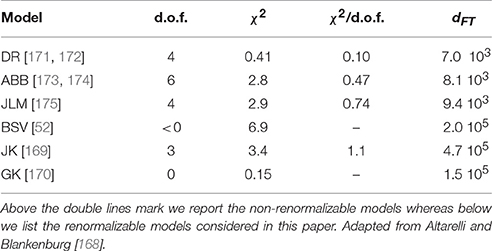
In the course of the last two decades, valuable experimental evidences for three families of massive neutrinos and flavor neutrino oscillations were obtained in various experimental channels, and the parameters which characterize the mixing are now known with a relatively high precision. As a consequence, the existence of non-vanishing neutrino masses and mixing have been firmly established. In spite of the huge amount of available data, many properties of the neutrino physics are yet poorly known or even completely unknown as, just to mention some of them, whether the massive neutrinos are Dirac or Majorana particles [1], what kind of spectrum the neutrino masses obeys, what is the absolute scale of neutrino masses, what is the octant for the atmospheric mixing angle θ₂₃ and what are the values of the CP violating phases in the leptonic sector. In a unified description of fermion masses and mixing, the above-mentioned features must be somehow linked to quark properties which, however, appear so dissimilar to make such a connection very hard to find; this is the well-known flavor problem. Let us take the mixing angles as an example. Quark and neutral leptonic mixings are described by the Cabibbo-Kobayashi-Maskawa matrix V_CKM [2, 3] and the Pontecorvo-Maki-Nakagawa-Sakata matrix U_PMNS [4–7], respectively. Although one can assume an identical parametrization, Figure 1 shows that the absolute values of the matrix elements are quite different: the V_CKM is an almost diagonal matrix, with the largest deviation from 1 coming from the Cabibbo angle in the (12) position while the U_PMNS exhibits a pattern where all but the (13) entry are of the same order of magnitude of ${O}$(1). Since at the end of the day the V_CKM and U_PMNS matrices all come from the Yukawa matrices of the theory, one would naively expect no sort of relations among their entries, which is obviously the case. Unless one decides to take seriously the numerical quark-lepton complementarity relation [8–11] that connects the solar θ₁₂ and atmospheric θ₂₃ leptonic angles to the Cabibbo angle θ_C, θ₁₂ + θ_C ~ π/4. In this case (and also for other similar relations), Grand Unified Theories (GUT) supplemented with the help of family symmetries could provide a simple explanation so that their role in deciphering the flavor problem cannot be neglected. In fact, while GUT groups relate the properties of particles belonging to different species, thus establishing a connections among mass matrices of leptons and quarks, flavor symmetries act on the members of particles of the same species but different families, enabling a strong connection between the matrix elements of a given mass matrix. Thus, one can arrange the theory in such a way that flavor symmetries are mainly responsible for a definite mixing pattern in the neutrino sector and that GUT symmetries introduce the Cabibbo angle in the leptonic sector as a correction to the U_PMNS given by the diagonalization of the charged lepton mass matrix (somehow related to the down quark masses).

FIGURE 1

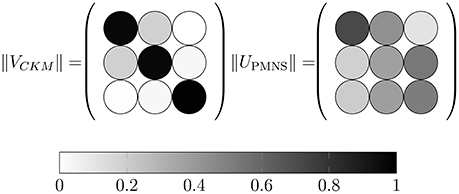
Figure 1. Pictorial representation of the absolute values of the matrix elements of the V_CKM and U_PMNS matrices.

Notice that the additional degree of symmetry involved in these theories allows a substantial decrease of the number of independent parameters compared to the Standard Model case (which amounts to 19) and, quite often, the model produces observable predictions that can be verified by experiments. The typical example in GUT theories is related to the mean life of the proton τ_p; since the new colored gauge bosons and scalars implied by the larger symmetry can mediate proton decay at a rate faster than the age of the Universe, many variations have been ruled out based on the predicted upper limit on τ_p. On the other hand, the less freedom in the elements of the mass matrices subsequent to the imposition of flavor symmetries allowed in the past to derive patterns of leptonic mixing in very good agreement with the old neutrino data which unfortunately do not resist to the comparison with the more precise measurements as we currently have. The typical example is provided by the so-called Tribimaximal mixing (TBM [12–16], more on this and other patterns later in section 4) which predicts θ₁₃ = 0 and requires ad-hoc large corrections to fall over acceptable ranges. Given the vastness of the scientific production in terms of models employing flavor symmetries, we restrict ourselves here to non-abelian discrete symmetries and abelian U(1)'s. While the latter have been inspired by the Froggatt and Nielsen mechanism [17], the former answers to the necessity of explaining the existence of three generations of fermions or at least to unify two of them (that is why non-abelian group), avoiding at the same time the presence of Goldstone and gauge bosons coming from their spontaneous symmetry breaking (that is why discrete). Discrete symmetries can be inspired by different extensions of the Standard Model (SM); for example, one can start with an SU(3) invariant theory and then break it into its discrete groups using large Higgs representations [18]; or one can consider extra dimensional theories [19] (also string inspired), where the new dimensions are properly compactified and the discrete group appears as a remnant of the n-dimensional space-time symmetry [19].

Although the combination GUT ⊕ flavor seems to be even more restrictive in terms of free parameters, the aim of this short review is to show that several attempts in this direction have been done that produced good results. But, before arriving at this conclusion, we will devote section 3 to the understanding of the main prediction for neutrino masses in GUT theories and section 4 on the role played by flavor. Only in section 5 we will investigate the physics opportunity given by the union of these two different types of symmetries.

2. Remarks on Neutrino Masses

2.1. Dirac Mass Term

Dirac neutrino masses can be generated by the same Higgs mechanism that gives masses to quarks and charged leptons in the SM. To this aim, we need to introduce SM singlet fermions ν_Ri and the related Yukawa couplings with the Higgs field; after spontaneous symmetry breaking, the Lagrangian containing the lepton mass terms is given by:

$\begin{array}{ll}\begin{array}{l}{{L}}_{mass}=-\frac{v}{\sqrt{2}}{\displaystyle \sum _{\alpha ,\beta =e,\mu ,\tau }({\overline{\nu }}_{\alpha L}{Y}_{\alpha \beta }^{\nu }{\nu }_{\beta R}+\text{h}.\text{c}.)}\\ -\frac{v}{\sqrt{2}}{\displaystyle \sum _{\alpha ,\beta =e,\mu ,\tau }({\overline{\ell }}_{\alpha L}{Y}_{\alpha \beta }^{\ell }{\ell }_{\beta R}+\text{h}.\text{c}.)},\end{array}\hfill & (1)\hfill \end{array}$

where ℓ_α represents the charged lepton fields, v is the vacuum expectation value (vev) of the Higgs field and Y^ν and Y^ℓ are the Yukawa couplings of neutrinos and charged leptons, respectively, accommodated in 3 × 3 matrices. The diagonalization of Y^ν,ℓ can be performed with a biunitary transformation:

$\begin{array}{ll}{U}_L^{\nu }{}^{†}{Y}^{\nu }{U}_R^{\nu }=Y^{\prime \nu }\text{with}{Y}_{ij}^{\prime \nu }=y_i^{\prime \nu }{\delta }_{ij},\hfill & (2)\hfill \end{array}$

$\begin{array}{ll}{U}_L^{\ell }{}^{†}{Y}^{\ell }{U}_R^{\ell }=Y^{\prime \ell }\text{with}{Y}_{\alpha \beta }^{\prime \ell }=y_{\alpha }^{\prime \ell }{\delta }_{\alpha \beta },\hfill & (3)\hfill \end{array}$

and, consequently, the left and right-handed components of the fields with definite mass are as follows:

$\begin{array}{ll}{\nu }_{kL}={\displaystyle \sum _{\beta =e,\mu ,\tau }{(U_L^{\nu }{}^{†})}_{k\beta }}{\nu }_{\beta L},{\nu }_{kR}={\displaystyle \sum _{\beta =e,\mu ,\tau }{(U_R^{\nu }{}^{†})}_{k\beta }}{\nu }_{\beta R},\hfill & (4)\hfill \end{array}$

$\begin{array}{ll}{\ell }_{\alpha L}^{\prime }={\displaystyle \sum _{\beta =e,\mu ,\tau }{(U_L^{\ell }{}^{†})}_{\alpha \beta }}{\ell }_{\beta L},{\ell }_{\alpha R}^{\prime }={\displaystyle \sum _{\beta =e,\mu ,\tau }{(U_R^{\ell }{}^{†})}_{\alpha \beta }}{\ell }_{\beta R}.\hfill & (5)\hfill \end{array}$

In terms of the mass states defined in Equations (4) and (5), the Lagrangian in (1) can be rewritten as:

$\begin{array}{ll}\begin{array}{l}{{L}}_{mass}=-{\displaystyle \sum _{k=1,2,3}\frac{v{y}_k^{\prime \nu }}{\sqrt{2}}}({\overline{\nu }}_{kL}{\nu }_{kR}+\text{h}.\text{c}.)\\ -{\displaystyle \sum _{\alpha =e,\mu ,\tau }\frac{v{y}_{\alpha }^{\prime \ell }}{\sqrt{2}}}({\overline{\ell }}_{\alpha L}^{\prime }{\ell }_{\alpha R}^{\prime }+\text{h}.\text{c}.)=\end{array}\hfill & (6)\hfill \end{array}$

$\begin{array}{ll}=-{\displaystyle \sum _{k=1,2,3}\frac{v{y}_k^{\prime \nu }}{\sqrt{2}}}{\overline{\nu }}_k{\nu }_k-{\displaystyle \sum _{\alpha =e,\mu ,\tau }\frac{v{y}_{\alpha }^{\prime \ell }}{\sqrt{2}}}{\overline{\ell }}_{\alpha }^{\prime }{\ell }_{\alpha }^{\prime },\hfill & (7)\hfill \end{array}$

with

${\nu }_k={\nu }_{kL}+{\nu }_{kR},{\ell }_{\alpha }^{\prime }={\ell }_{\alpha L}^{\prime }+{\ell }_{\alpha R}^{\prime }.$

More importantly, the mixings driven by $U_L^{\nu ,\ell }$ enter in the leptonic charged current expressed in terms of mass eigenstates as

$\begin{array}{ll}{J}_{CC}^{\mu }={\displaystyle \sum _{k=1,2,3}{\displaystyle \sum _{\alpha =e,\mu ,\tau }{\overline{\nu }}_{kL}}}{\gamma }^{\mu }{(U_L^{\nu }{}^{†}{U}_L^{\ell })}_{k\alpha }{\ell }_{\alpha L}^{\prime },\hfill & (8)\hfill \end{array}$

and give rise to the well known PMNS matrix:

$\begin{array}{ll}{U}_{\text{PMNS}}=U_L^{\ell }{}^{†}{U}_L^{\nu }.\hfill & (9)\hfill \end{array}$

This unitary matrix is generally parametrized in terms of three mixing angles and one CP-violating phase, in a way similar to that used for V_CKM:

$\begin{array}{ll}{U}_{\text{PMNS}}=\left(\begin{array}{ccc}{c}_{12}{c}_{13}& s_{12}{c}_{13}& s_{13}{e}^{-i\delta }\\ -s_{12}{c}_{23}-c_{12}{s}_{23}{s}_{13}{e}^{i\delta }& c_{12}{c}_{23}-s_{12}{s}_{23}{s}_{13}{e}^{i\delta }& s_{23}{c}_{13}\\ s_{12}{s}_{23}-c_{12}{c}_{23}{s}_{13}{e}^{i\delta }& -c_{12}{s}_{23}-s_{12}{c}_{23}{s}_{13}{e}^{i\delta }& c_{23}{c}_{13}\end{array}\right),\hfill & (10)\hfill \end{array}$

where c_ij = cos(θ_ij), s_ij = sin(θ_ij) and θ_ij are the mixing angles (0 ≤ θ_ij ≤ π/2). δ is the Dirac CP-violating phase ranging in the interval 0 ≤ δ < 2π.

The current best-fit values and the allowed 1σ and 3σ ranges for the oscillation parameters as well as for the two independent mass differences $\Delta m_{kj}^2=m_k^2-m_j^2$, as obtained from the flavor transition experiments, are summarized in Table 1. Normal Ordering refers to the situation in which m₁ < m₂ < m₃, whereas for the Inverted Ordering we mean m₃ < m₁ < m₂.

TABLE 1

Table 1. Value of the oscillation parameters obtained from a global analysis from Esteban et al. [20].

The reported values are obtained from the global analysis of Esteban et al. [20].

2.2. Majorana Mass Terms

With the minimal particle content of the SM, namely leptons L_i and the Higgs doublet H:

$\begin{array}{ll}{L}_i={\left(\begin{array}{c}\begin{array}{l}\nu \\ e\end{array}\end{array}\right)}_{iL},H=\left(\begin{array}{c}\begin{array}{l}{\varphi }^{+}\\ {\varphi }^0\end{array}\end{array}\right),\hfill & (11)\hfill \end{array}$

one can generate dimension five operators of the form:

$\begin{array}{ll}{{L}}_5~\frac{y_{ij}}{\Lambda }{\overline{L}}_i{L}_j^c\tilde{H}{\tilde{H}}^T,\hfill & (12)\hfill \end{array}$

where Λ can be understood as the scale where new physics probably sets in and $\tilde{H}=-i{\tau }_2{H}^{*}$. In fact, two SM singlets are built from the product of four SU(2)_L doublets as [21]:

$\begin{array}{ll}2\otimes 2\otimes 2\otimes 2=(3\oplus 1)\otimes (3\oplus 1),\hfill & (13)\hfill \end{array}$

either via the product of two triplets or by the product of two singlets. Since L and H are different fields, we have four possible combinations that can give an overall SU(2)_L singlet:

$\begin{array}{l}{O}_1={\left(L_{i}H\right)}_1{\left(L_{j}H\right)}_1{O}_2={\left(L_i{L}_j\right)}_1{\left(HH\right)}_1\\ O_3={\left(L_i{L}_j\right)}_3{\left(HH\right)}_3{O}_4={\left(L_{i}H\right)}_3{\left(L_{j}H\right)}_3,\end{array}$

where the subscript 1, 3 refer to the SU(2)_L representation. Since (HH)₁ = 0 due to the antisymmetry under the exchange of the two doublets, only O_{1, 3, 4} contribute to neutrino masses. In particular, the explicit form of the bilinear are as follows:

$\begin{array}{ll}{\left(L_i{L}_j\right)}_1~{\nu }_i{e}_j-e_i{\nu }_j{\left(L_i{L}_j\right)}_3~\left(\begin{array}{c}{\nu }_i{\nu }_j\\ {\nu }_i{e}_j+e_i{\nu }_j\\ e_i{e}_j\end{array}\right)\hfill & (14)\hfill \end{array}$

$\begin{array}{ll}{\left(L_{i}H\right)}_1~{\nu }_i{\varphi }^0-e_i{\varphi }^{+}{\left(L_{i}H\right)}_3~\left(\begin{array}{c}\begin{array}{c}{\nu }_i{\varphi }^{+}\\ {\nu }_i{\varphi }^0+e_i{\varphi }^{+}\\ e_i{\varphi }^0\end{array}\end{array}\right)\hfill & (15)\hfill \end{array}$

$\begin{array}{ll}{\left(HH\right)}_3~\left(\begin{array}{c}{\varphi }^{+}{\varphi }^{+}\\ {\varphi }^{+}{\varphi }^0+{\varphi }^0{\varphi }^{+}\\ {\varphi }^0{\varphi }^0\end{array}\right),\hfill & (16)\hfill \end{array}$

from which we realize that O₁, O₃ and O₄ all contain the combination of fields ${\nu }_i{\nu }_j{({\varphi }^0)}^2$ that generate neutrino masses after electroweak spontaneous symmetry breaking. However, giving their different contractions of the SU(2)_L indices, O₁ has a tree-level realization in terms of the interchange of a heavy SM singlet ν_R, the type-I see-saw mechanism [22–26], whereas heavy triplets are needed to realize O₃ and O₄, either with the interchange of a scalar particle (the type-II see-saw mechanism [27]) or of a fermion field (the type-III mechanism [28]), see Figure 2.

FIGURE 2

Figure 2. Tree level realization of the Weinberg operators O₁, O₃ and O₄. From left to right, the intermediate states are: singlet fermion N, scalar triplet Δ_L and fermion triplet Σ fields.

In the first case, the introduction of three right-handed neutrinos N_i ≡ ν_Ri allows for an invariant mass Lagrangian of the form [29]:

$\begin{array}{ll}{{L}}_m=-Y_{ij}{\overline{L}}_i(\tilde{H}{N}_j)+\frac{1}{2}{\overline{N}}^c{}_i{M}_{ij}{N}_j+ h.c.\hfill & (17)\hfill \end{array}$

The first term in this equation is known as the Dirac mass term and it is essentially a copy of the mass term “employed” by the charged fermions and quarks to get their masses. The second term, instead, is a pure Majorana contribution to the neutrino mass. After spontaneous symmetry breaking, ${L}$_m gives rise to the Dirac mass matrix (_mD)ij ≡ Y_ij〈H〉, which is non-hermitian and non-symmetric, and to the Majorana mass matrix M which is symmetric. Assuming all N_i to be very heavy, one can integrate them away so that the resulting light neutrino mass matrix reads:

$\begin{array}{ll}{m}_{\nu }=-m_D{M}^{-1}{m}_D^T.\hfill & (18)\hfill \end{array}$

The type-I see-saw mechanism shows that the light neutrino masses depend quadratically on the Dirac masses but are inversely proportional to the large Majorana mass, so that the scale of new physics is clearly Λ = M.

In the case of type-II mechanism, at least one scalar SU(2)_L triplet must be added to the field content of the SM; for values of the weak hypercharge equal to +1, the triplet has the following components:

$\begin{array}{ll}{\Delta }_L=\left(\begin{array}{c}\begin{array}{c}{\Delta }^{++}\\ {\Delta }^{+}\\ {\Delta }^0\end{array}\end{array}\right),\hfill & (19)\hfill \end{array}$

and the Lagrangian terms that accommodate the new states and are relevant for neutrino masses are:

$\begin{array}{ll}\begin{array}{l}{L}_{\Delta }~\left(k_{ij}{\overline{L}}_i\left(\sigma ·{\Delta }_L^{†}\right)L_j^c-{\mu }_{\Delta }{\tilde{H}}^T\left(\sigma ·{\Delta }_L\right)\tilde{H}+h.c.\right)\\ +m_{\Delta }^2|{\Delta }_L{|}^2,\end{array}\hfill & (20)\hfill \end{array}$

where σ_i are the Pauli matrices and k_ij the new Yukawa couplings induced by the presence of Δ_L. Assuming that the scalar potential has a minimum in the direction 〈Δ_L〉 = (0, 0, v_Δ) (as well as in the standard vacuum 〈H〉 = (0, v)) and that the hierarchy $m_{\Delta }^2\gg {\mu }_{\Delta }v$ is valid, then the light neutrino mass matrix is:

$\begin{array}{ll}{(m_{\nu })}_{ij}~\frac{{\mu }_{\Delta }{v}^2}{m_{\Delta }^2}{k}_{ij};\hfill & (21)\hfill \end{array}$

in this case, the scale of new physics is approximately given by $\Lambda ~m_{\Delta }^2/{\mu }_{\Delta }$.

In the last case of type-III see-saw mechanism, the triplet hyperchargeless fermions Σ can be arranged in the following form:

$\begin{array}{ll}\Sigma =\left(\begin{array}{c}\begin{array}{cc}{\Sigma }^0/\sqrt{2}& {\Sigma }^{+}\\ {\Sigma }^{-}& -{\Sigma }^0/\sqrt{2}\end{array}\end{array}\right),\hfill & (22)\hfill \end{array}$

and the related Lagrangian reads:

$\begin{array}{ll}{{L}}_{\Sigma }-~k_{ij}^{\Sigma }{\overline{L}}_i\tilde{H}{\Sigma }_j+{(m_{\Sigma })}_{ij}Tr\left({\overline{\Sigma }}_i^c{\Sigma }_j\right),\hfill & (23)\hfill \end{array}$

where again $k_{ij}^{\Sigma }$ is a Yukawa coupling matrix. Under the hypothesis that $m_{\Sigma }\gg k^{\Sigma }v$, the light mass matrix assumes the form

$\begin{array}{ll}{m}_{\nu }~-k^{\Sigma }\frac{1}{m_{\Sigma }}{\left(k^{\Sigma }\right)}^T{v}^2,\hfill & (24)\hfill \end{array}$

which is very similar to Equation (18) since, for the purposes of neutrino masses, the state Σ⁰ acts like a right-handed neutrino.

It has to be noted that the Majorana nature of neutrinos modifies the PMNS matrix of Equation (10) to take into account two more independent CP violating phases α and β that cannot be eliminated by a rotation of the neutrino fields; a possible convention for the new U_PMNS is as follows:

$\begin{array}{ll}{U}_{\text{PMNS}}^{\prime }=U_{\text{PMNS}}\times \text{diag}\{1,e^{i\alpha /2},e^{i\beta /2}\}.\hfill & (25)\hfill \end{array}$

Neutrino oscillation data cannot determine whether the massive neutrinos are Dirac or Majorana particles because the new phases cancel out of the oscillation amplitudes.

3. Neutrino Masses and Mixing in GUT Theories

The possibility to generate non-zero neutrino masses through the see-saw mechanism, which requires quite a large B − L scale, fit rather naturally in grand unified models based on the gauge group SO(10) [30]. Putting aside Supersymmetry (SUSY) for the moment, the experimental constraints from the lifetime of the proton and from the weak mixing angle ${sin}^2{\theta }_W$ impose that SO(10) breaks to the SM at least in two or more steps [31, 32]. In a minimal setup which allows for a two-step breaking, the intermediate gauge groups (typically a Pati-Salam group SU(4) × SU(2)_L×SU(2)_R ≡ 4_C2_L2_R [33]) is broken down to the SM at a scale around 10¹² GeV, which is usually also the scale of the Majorana masses. To accomplish this program, the Higgs sector must be carefully chosen in such a way to avoid bad mass relations of the SU(5) type [34]. Let us discuss an example. Consider the following chain:

$\begin{array}{ll}\begin{array}{l}SO(10)\stackrel{M_U-210_H}{\to }{4}_C{2}_L{2}_R\stackrel{M_I-126_H}{\to }SM\stackrel{M_Z-10_H}{\to }\\ SU{\left(3\right)}_{C}U{\left(1\right)}_{EM}\end{array}\hfill & (26)\hfill \end{array}$

where the three mass scales refer to the scale where SO(10) is broken down to the PS (M_U), where PS is broken to the SM (M_I) and finally where the SM group is broken down to the electromagnetism (M_Z). The SO(10) representations used to perform the various stages of symmetry breaking are also indicated. With fermions in the 16 representation, the Yukawa Lagrangian contains two terms:

$\begin{array}{ll}{L}=16\left(h10_H+f{\overline{126}}_H\right)16,\hfill & (27)\hfill \end{array}$

where the couplings h and f are 3 × 3 symmetric matrices in flavor space. In terms of their PS quantum numbers, the Higgses in Equation (26) decompose as:

$\begin{array}{l}10_H=(1,2,2)\oplus (6,1,1),\\ 126_H=(6,1,1)\oplus (\overline{10},3,1)\oplus (10,1,3)\oplus (15,2,2).\end{array}$

Of all the previous sub-multiplets, the ones useful for generating neutrino (and fermion) masses are the (1, 2, 2) ≡ Φ ∈ 10_H entering the last breaking in Equation (26) and that contains an SU(2)_L doublet, the (10, 1, 3) ≡ Δ_R ∈ 126_H to allow for right-handed Majorana masses and the (15, 2, 2) ≡ Σ ∈ 126_H which also contains an SU(2)_L doublet. Using the extended survival hypothesis [31], we assume that both Δ_R and Σ have masses around M_I, and all other multiplets are close to the GUT scale¹.

A comment here is in order. The (1, 2, 2) of the 10_H representation can be decomposed into

$\begin{array}{ll}(1,2,2)=(1,2,+\frac{1}{2})\oplus (1,2,-\frac{1}{2})\equiv H_u\oplus H_d\hfill & (28)\hfill \end{array}$

under the SM group; if $10_H=10_H^{*}$ then $H_u^{*}=H_d$ as in the SM but, as it has been shown in Bajc et al. [37], in the limit V_cb = 0 the ratio m_t/m_b should be close to 1, in contrast with the experimental fact that at the GUT scale m_t/m_b ≫ 1. On the other hand, even though the 10_H is a real representation from the SO(10) point of view, one can choose its components to be either real or complex. In the latter case, $10_H\ne 10_H^{*}$ and then $H_u^{*}\ne H_d$. In order to keep the parameter space at an acceptable level, it is a common practice to introduce an extra symmetry (for instance, the Peccei-Quinn U(1)_PQ [38]) to avoid the Yukawa couplings related to $10_H^{*}$.

For the vev values of the 10_H components we will use the following short-hand notation:

$\begin{array}{ll}{k}_u\equiv \langle {(1,2,2)}_{10}^u\rangle \ne k_d\equiv \langle {(1,2,2)}_{10}^d\rangle .\hfill & (29)\hfill \end{array}$

For the vev of the 126_H, instead, one can take full advantage of the fact that a vev for the doublet Σ (that we call v_{u, d}) can be induced by a term in the scalar potential of the form [39]:

$V=\lambda 126_H\overline{126_H}126_{H}10_H\to \lambda {\Delta }_R\overline{{\Delta }_R}\Sigma \Phi ,$

which gives:

$\begin{array}{ll}{v}_{u,d}~\lambda \frac{v_R^2}{M_{(15,2,2)}^2}{k}_{u,d},\hfill & (30)\hfill \end{array}$

where v_R = 〈(10, 1, 3)〉. According to this, the fermion mass matrices of the model assume the form:

$\begin{array}{ll}\begin{array}{l}{M}_u=h{k}_u+f{v}_u,M_d=h{k}_d+f{v}_d\\ M_{\nu }^D=h{k}_u-3f{v}_u,M_l=h{k}_d-3f{v}_d,M_{\nu }^M=f{v}_R.\end{array}\hfill & (31)\hfill \end{array}$

These relations clearly show why the Yukawa sector requires more than the 10_H; in fact, in the absence of the 126_H (or 120_H) one would get M_d ≡ M_l, which is phenomenologically wrong. The role of the 126_H in SO(10) theories is exactly to break the wrong mass relations and the factor of 3 appearing in Equation (31), derived from the vev of Σ of the 126_H, is the equivalent of the Georgi-Jarlskog factor of the non-minimal SU(5) [40].

Under the hypothesis that the type-I see-saw mechanism is responsible for the light neutrino masses, a fit can be performed which fixes the entries of the h and f couplings to reproduce the low energy observables in the flavor sector (also in the supersymmetric case) in the full three-flavor approach [35, 41, 42]. This partially contradicts the conclusions derived in the two-flavor limit, where the type-I see-saw mechanism has been shown to be incompatible with a large atmospheric mixing. To show this, let us approximate $M_{\nu }^D\approx M_u$ and work in the basis where the charged leptons are diagonal; assuming a small up and down quark mixings λ_C (of the order of the Cabibbo angle), Equation (18) tells us that

$\begin{array}{ll}{m}_{\nu }~4r_R\left(\begin{array}{c}\begin{array}{cc}{m}_c^2/(m_s-m_{\mu })& {\lambda }_C\\ {\lambda }_C& m_t^2/(m_b-m_{\tau })\end{array}\end{array}\right),\hfill & (32)\hfill \end{array}$

so that two non-degenerate eigenvalues can be generated whose squared difference can be made of the correct order of magnitude ~10⁻³ eV², but the atmospheric mixing angle is suppressed by λ_C, thus making this construction incompatible with the data.

Relations of the form (31) are also obtained in the minimal SU(5) scenario with a 5_H and fermions in the reducible 5 ⊕ 10 representation. With this minimal Higgs content, the prediction at the GUT scale is again M_d ≡ M_l. To solve this problem, the scheme proposed in Georgi and Jarlskog [40] involved a slightly more complicated Higgs structure due to the presence of the 45_H representation. It replaces the above wrong relations with the more appropriate m_d = 3m_e and 3m_s = m_μ, which can be derived from the following textures [43]:

$\begin{array}{ll}{Y}_u=\left(\begin{array}{c}\begin{array}{ccc}0& p& 0\\ p& 0& q\\ 0& q& v\end{array}\end{array}\right),Y_d=\left(\begin{array}{ccc}0& r& 0\\ r& s& 0\\ 0& 0& t\end{array}\right),Y_e=\left(\begin{array}{ccc}0& r& 0\\ r& -3s& 0\\ 0& 0& t\end{array}\right),\hfill & (33)\hfill \end{array}$

and whose flavor structure can be obtained, for example, by means of additional symmetries (discussed later). In the context of SO(10), the textures in Equation (33) have been obtained in Harvey et al. [44, 45], in a model with three families of left-handed fermions, 16_{1, 2, 3}, two real 10_H's, three 126_H and one 45_H. Equally successful phenomenological attempts where instead all quark and lepton mass matrices have the same zero texture with vanishing (1,1), (1,3) and (3,3) entries have been proposed in Matsuda et al. [46].

Going beyond the type-I see-saw mechanism for neutrino masses, it has been shown that there exists a very elegant connection between the large atmospheric angle θ₂₃ and the relation m_b = m_τ, if the type-II see-saw is the dominant one [47, 48]. To show this, let us allow the $(\overline{10},3,1)$ component of the 126_H to take a large vev v_L. This generates a “left” mass matrix for the Majorana neutrinos $M_{\nu }^L=f{v}_L$ so that the total light neutrino mass matrix is given by $m_{\nu }=M_{\nu }^L-m_D^T{(M_{\nu }^M)}^{-1}{m}_D$. Under the hypothesis of the dominance of type-II, in the basis where the charged leptons are diagonal we easily get:

$\begin{array}{ll}{m}_{\nu }=M_{\nu }^L\approx M_d-M_l\approx \left(\begin{array}{c}\begin{array}{cc}{m}_s-m_{\mu }& {\theta }_D\\ {\theta }_D& m_b-m_{\tau }\end{array}\end{array}\right),\hfill & (34)\hfill \end{array}$

(θ_D being a small down quark mixing) and a maximal atmospheric mixing necessarily requires a cancellation between m_b and m_τ. However, SM extrapolation of the fermion masses from the electroweak scale up to the GUT scale (but see [49, 50] for the effects of the intermediate mass scales in the running) shows that m_b ~ 1.7m_τ [51], so this mechanism does not seem to fit well with a non-SUSY SO(10) GUT with the 10_H ⊕ 126_H Higgs sector [52]. This conclusion is not altered when the fit takes into account the three families of fermions. On the other hand, in the SUSY case the relation m_b = m_τ is roughly fulfiled for low tan β ~ ${O}$(1) with no threshold corrections but also for larger tan β ~ ${O}$(40) with significant threshold corrections. The quality of the full three-family fits in these cases is comparable.

If we insist on minimality in the Higgs sector, the next combinations are the 120_H ⊕ 126_H and 10_H ⊕ 120_H. Both of them make use of the 120_H representation which, according to the following decomposition under the PS gauge group, contains several bi-doublets useful for fermion masses:

$120_H=(10+\overline{10},1,1)\oplus (6,3,1)\oplus (6,1,3)\oplus (15,2,2)\oplus (1,2,2).$

Models of the first kind (120_H ⊕ 126_H) have been considered predictive when restricted to the second and third generations [37]. However, the predicted ratio m_b/m_τ ~ 3 strongly disfavors a SM (for which m_b/m_τ ~ 2) and SUSY (for which m_b/m_τ ~ 1) fits with neither type-I nor type-II see-saw dominance. The second combination, 10_H ⊕ 120_H [53], in spite of being compatible with the b − τ unification [54], produces either down-quark mass or top-quark mass unrealistically small.

In the case of a non-minimal Higgs content with 10_H ⊕ 120_H ⊕ 126_H, the Yukawa sector contains a large number of independent parameters but, except the supersymmetric case, the use of the 120_H does not improve the fits in the type-II see-saw dominated case. On the other hand, the fits obtained for the type-I scenario, including neutrino observables, are considerably better than the corresponding SUSY as well as better of the 10_H ⊕ 126_H non-SUSY case.

4. Neutrino Masses and Mixing from Flavor Symmetries

4.1. Lepton Mixing from Discrete Symmetry

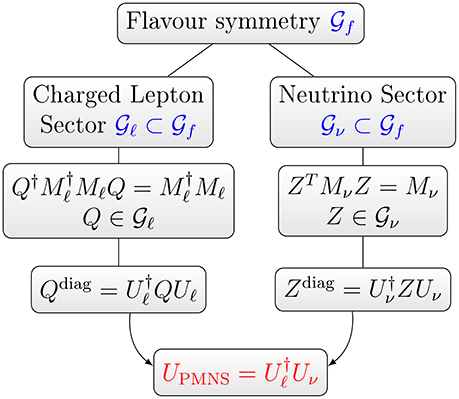
The general strategy to get the leptonic mixing matrix U_PMNS from symmetry consideration is to assume that at some large energy scale the theory is invariant under the action of a flavor symmetry group ${G}$_f; the scalar sector is then built in a suitable way as to be broken to different subgroups in the neutrino sector ${G}$_ν, and in the charged lepton sector, ${G}$_ℓ. The lepton mixing originates then from the mismatch of the embedding of ${G}$_ℓ and ${G}$_ν into ${G}$_f. Let us assume that

$\begin{array}{ll}{{G}}_{\ell }\subset {{G}}_f{{G}}_{\nu }\subset {{G}}_f{{G}}_{\ell }\cap {{G}}_{\nu }=\varnothing .\hfill & (35)\hfill \end{array}$

For Majorana particles, we can write the action of the elements of the subgroups of ${G}$_f on the mass matrix as²

$\begin{array}{ll}{Q}^{†}{M}_{\ell }^{†}{M}_{\ell }Q=M_{\ell }^{†}{M}_{\ell }Q\in {{G}}_{\ell }\hfill & (36\text{a})\hfill \end{array}$

$\begin{array}{ll}{Z}^T{M}_{\nu }Z=M_{\nu }Z\in {{G}}_{\nu }.\hfill & (36\text{b})\hfill \end{array}$

For Dirac neutrinos the last relation must be modified as:

$\begin{array}{ll}{Z}^{†}{M}_{\nu }^{†}{M}_{\nu }Z=M_{\nu }^{†}{M}_{\nu }Z\in {{G}}_{\nu }.\hfill & (37)\hfill \end{array}$

If we restrict ourselves to matrices Z with det Z = 1 and to Majorana neutrinos, then the maximal invariance group of the neutrino mass matrix which leave the neutrino masses unconstrained is the Klein group V = Z₂ ⊗ Z₂ [55–58]. The charged leptonic subgroup ${G}$_ℓ could be either a cyclic group Z_n, with the index n ≥ 3, or a product of cyclic symmetries like, for example, Z₂ ⊗ Z₂. We discard in the discussion possible residual non-abelian symmetries because their character would result in a partial or complete degeneracy of the mass spectrum, and thus incompatible with the current data on charged lepton masses. For the same reason we assume that Z ∈ ${G}$_ν decomposes into three inequivalent representations under ${G}$_ℓ.

The diagonalization of the mass matrices is equivalent, using (36), to a rotation of the group elements Q and Z through unitary matrices as:

$\begin{array}{ll}{Q}^{\text{diag}}=U_{\ell }^{†}Q{U}_{\ell }\hfill & (38\text{a})\hfill \end{array}$

$\begin{array}{ll}{Z}^{\text{diag}}=U_{\nu }^{†}Z{U}_{\nu },\hfill & (38\text{b})\hfill \end{array}$

because both ${G}$_ℓ and ${G}$_ν are abelian. The matrices U_ℓ and U_ν are determined up to unitary diagonal K_{ℓ, ν} and permutation P_{ℓ, ν} matrices:

$\begin{array}{ll}{U}_{\ell }\to U_{\ell }{P}_{\ell }{K}_{\ell }\hfill & (39\text{a})\hfill \end{array}$

$\begin{array}{ll}{U}_{\nu }\to U_{\nu }{P}_{\nu }{K}_{\nu }.\hfill & (39\text{b})\hfill \end{array}$

Thus, up to Majorana phases and permutations of rows and columns, the lepton mixing matrix U_PMNS is given by:

$\begin{array}{ll}{U}_{\text{PMNS}}=U_{\ell }^{†}{U}_{\nu }.\hfill & (40)\hfill \end{array}$

Notice that, as a consequence of the fact that U_PMNS is not completely determined, the mixing angles are fixed up to a small number of degeneracies. For the same reason, the Dirac CP phase δ is determined up to a factor π and the Majorana phases cannot be predicted because the matrix M_ν remains unconstrained in this setup. In Figure 3 we have pictorially summarized the above procedure.

FIGURE 3

Figure 3. Representative scheme of the approach used to construct the U_PMNS.

It is remarkable that, under particular assumptions on the residual symmetry groups in the neutrino and charged lepton sectors³, the construction we have just discussed allow for model (and mass)-independent predictions on the mixing angles (or columns of U_PMNS). As it has been shown in Grimus [59], Hernandez and Smirnov [60, 61], if only a cyclic group from each sector is a subgroup of the full flavor group ${G}$_f, then it is possible to derive non-trivial relations between the mixing matrix in terms of the symmetry transformations which, in turn, provoke the appearance of well-defined connections among different mixing angles, also called sum rules. In particular, non-zero θ₁₃, deviations from maximal mixing for θ₂₃ and predictions for the CP Dirac phase [62, 63] are relevant predictions in (quasi perfect) agreement with the current data. An intersting and useful classification of all possible mixing matrices completely determined by residual symmetries (originated from a finite flavor symmetry group) can be found in Fonseca and Grimus [58].

Since the family symmetry ${G}$_f has to be broken to generate the observed pattern of masses and mixing, the models generally consider an enlarged Higgs sector where Higgs-type fields, called flavons ϕ, are neutral under the SM gauge group and break spontaneously the family symmetry by acquiring a vev

$\begin{array}{ll}ϵ=\frac{\langle \varphi \rangle }{\Lambda },\hfill & (41)\hfill \end{array}$

where Λ denotes a high energy mass scale. If the scale of the vev is smaller (or at least of the same order of magnitude) than Λ, one can consider ϵ as a small expansion parameter which can be used to derive Yukawa matrices with built-in hierarchies and/or precise relations among their entries. In order to do that, it is often necessary that all three lepton families are grouped into triplet irreducible representations, so that the possible choices for ${G}$_f are U(3) and subgroups. To give an example, in the case of SU(3) and for the Weinberg operator of Equation (12), one can consider lepton doublets into a triplet of SU(3) and the Higgs doublet H in a singlet of ${G}$_f [64, 65]; the lowest dimensional SU(3) invariant operator is built using a pair of flavon fields transforming in the 3 of SU(3). For a generic flavon alignment 〈ϕ〉 ∝ (a, b, c)^T, the neutrino mass matrix is then proportional to

$\begin{array}{ll}\left(\begin{array}{c}\begin{array}{ccc}{a}^2& ab& ac\\ ba& b^2& bc\\ ca& cb& c^2\end{array}\end{array}\right).\hfill & (42)\hfill \end{array}$

Special mixing patterns, as the ones discussed below, are obtained assuming particular flavon alignments in the flavor space which, quite frequently, imply well defined relations among the mixing angles and the Dirac CP-violating phase [66–72].

For a model to be consistent, the alignment must descend from the minimization of the scalar potential, without ad-hoc assumptions on the potential parameters. Widely used ingredients for this type of constructions are:

• the presence of additional scalar degrees of freedom, which are called driving fields, and are singlets under the gauge group;

• additional (perhaps cyclic) symmetries, apart from ${G}$_f, which are necessary to forbid those Lagrangian operators which would prevent the desired vacuum alignment.

In SUSY frameworks, both flavons and driving fields are neede to derive the superpotential w of the model. In the limit of unbroken SUSY, the minimum of the related scalar potential V is given by the derivatives of w with respect to the components of the driving fields, which determine a set of equations for the components of the flavon fields. A detailed account of such a procedure has been given in Altarelli and Feruglio [73], to which we refer the interested reader. Here we limit ourselves to a simple representative example, extracted from de Medeiros Varzielas et al. [74]. Suppose that the SM singlet pair (φ₀, φ) is made up of a driving (φ₀) and a flavon (φ) triplet fields in such a way that terms like φ₀φ and ${\phi }_0{\phi }^2$ are flavor invariant; thus, the most general renormalizable superpotential is given by:

$\begin{array}{ll}w=M({\phi }_0\phi )+g({\phi }_0\phi \phi ).\hfill & (43)\hfill \end{array}$

The vacuum minimization conditions for the φ field are then:

$\begin{array}{ll}\begin{array}{l}\frac{\partial w}{\partial {\phi }_{01}}=M{\phi }_1+g{\phi }_2{\phi }_3=0,\\ \frac{\partial w}{\partial {\phi }_{02}}=M{\phi }_2+g{\phi }_3{\phi }_1=0,\\ \frac{\partial w}{\partial {\phi }_{03}}=M{\phi }_3+g{\phi }_1{\phi }_2=0,\end{array}\hfill & (44)\hfill \end{array}$

which are solved by:

$\begin{array}{ll}\phi =v(1,1,1), v=-\frac{M}{g}.\hfill & (45)\hfill \end{array}$

This simple case does not obviously exhaust all possible situations arising after the minimization procedure; in more complicated cases, it could happen that some of the vevs depends on unknown parameters which are not related to the parameters appearing in w. This indicates that there are flat directions in the flavon potential, as one could check by analyzing the flavons and driving fields mass spectrum in the SUSY limit. SUSY breaking effects and radiative corrections are eventually important to give mass to the modes associated to these flat directions.

The presence of driving fields is not a necessary condition for obtaining the correct vacuum alignment. While this implies to deal with longer and more complicated potentials [75–77], one can avoid intricated calculations formulating flavor models in extra dimensions where the scalar fields live in the bulk of the higher-dimensional space [78]. The vacuum alignment is then achieved by the boundary conditions of the scalar fields and the physics at low energy is described by massless zero modes which break the flavor symmetries [79].

4.2. Typical Discrete Patterns

The use of discrete symmetries was first suggested to explain a simplified form of the neutrino mass matrix called Tri-Bi-Maximal mixing (TBM) [12–16]:

$\begin{array}{ll}{U}_{\text{TB}}=\left(\begin{array}{c}\begin{array}{ccc}\sqrt{\frac{2}{3}}& \frac{1}{\sqrt{3}}& 0\\ -\frac{1}{\sqrt{6}}& \frac{1}{\sqrt{3}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{3}}& \frac{1}{\sqrt{2}}\end{array}\end{array}\right),\hfill & (46)\hfill \end{array}$

which implies $s_{12}^2=1/3$, $s_{23}^2=1/2$ and s₁₃ = 0. In this case the matrix m_ν takes the form:

$\begin{array}{ll}{m}_{\nu }=\left(\begin{array}{c}\begin{array}{ccc}x& y& y\\ y& x+v& y-v\\ y& y-v& x+v\end{array}\end{array}\right),\hfill & (47)\hfill \end{array}$

(x, y and v are complex numbers) which can also parametrized as:

$\begin{array}{ll}{m}_{\nu }=m_1{\Phi }_1{\Phi }_1^T+m_2{\Phi }_2{\Phi }_2^T+m_3{\Phi }_3{\Phi }_3^T,\hfill & (48)\hfill \end{array}$

where

$\begin{array}{ll}{\Phi }_1^T=\frac{1}{\sqrt{6}}(2,-1,-1), {\Phi }_2^T=\frac{1}{\sqrt{3}}(1,1,1), {\Phi }_3^T=\frac{1}{\sqrt{2}}(0,-1,1)\hfill & (49)\hfill \end{array}$

are the respective columns of U_TB and m_i are the neutrino mass eigenvalues given by the simple expressions m₁ = x − y, m₂ = x + 2y and m₃ = x − y + 2v [80].

Notice that, in the basis where charged leptons are diagonal, the mass matrix for TBM mixing is the most general matrix which is invariant under the so-called 2-3 (or μ − τ) symmetry [81, 82] under which

$\begin{array}{ll}{m}_{\nu }=A_{23}{m}_{\nu }{A}_{23},\hfill & (50)\hfill \end{array}$

where A₂₃ is given by:

$\begin{array}{ll}{A}_{23}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right),\hfill & (51)\hfill \end{array}$

and, in addition, under the action of a unitary symmetric matrix S_TB which commutes with A₂₃:

$\begin{array}{ll}{m}_{\nu }=S_{TB}{m}_{\nu }{S}_{TB},\hfill & (52)\hfill \end{array}$

where S_TB is given by:

$\begin{array}{ll}{S}_{TB}=\frac{1}{3}\left(\begin{array}{ccc}-1& 2& 2\\ 2& -1& 2\\ 2& 2& -1\end{array}\right).\hfill & (53)\hfill \end{array}$

In practice, the matrices A₂₃ and S_TB realize the action of Z ∈ ${G}$_ν.

For bimaximal (BM) mixing [83], instead, we have $s_{12}^2=s_{23}^2=1/2$ and accordingly:

$\begin{array}{ll}{U}_{\text{BM}}=\left(\begin{array}{ccc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0\\ -\frac{1}{2}& \frac{1}{2}& \frac{1}{\sqrt{2}}\\ \frac{1}{2}& -\frac{1}{2}& \frac{1}{\sqrt{2}}\end{array}\right).\hfill & (54)\hfill \end{array}$

The respective mass matrix is of the form:

$\begin{array}{ll}{m}_{\nu }=\left(\begin{array}{ccc}x& y& y\\ y& z& x-z\\ y& x-z& z\end{array}\right),\hfill & (55)\hfill \end{array}$

that is

$\begin{array}{ll}{m}_{\nu }=m_1{\Phi }_1{\Phi }_1^T+m_2{\Phi }_2{\Phi }_2^T+m_3{\Phi }_3{\Phi }_3^T,\hfill & (56)\hfill \end{array}$

where

$\begin{array}{ll}{\Phi }_1^T=\frac{1}{2}(\sqrt{2},1,1), {\Phi }_2^T=\frac{1}{2}(-\sqrt{2},1,1), {\Phi }_3^T=\frac{1}{\sqrt{2}}(0,-1,1).\hfill & (57)\hfill \end{array}$

The resulting matrix is characterized by the invariance under the action of A₂₃ and also under the application of the real, unitary and symmetric matrix S_BM of the form

$\begin{array}{ll}{m}_{\nu }=S_{BM}{m}_{\nu }{S}_{BM},\hfill & (58)\hfill \end{array}$

with S_BM given by:

$\begin{array}{ll}{S}_{BM}=\left(\begin{array}{c}\begin{array}{ccc}0& -\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}& \frac{1}{2}& -\frac{1}{2}\\ -\frac{1}{\sqrt{2}}& -\frac{1}{2}& \frac{1}{2}\end{array}\end{array}\right).\hfill & (59)\hfill \end{array}$

In this case, are the matrices A₂₃ and S_BM that realize the action of Z ∈ ${G}$_ν on the neutrino mass matrix.

Other examples of special patterns can be found in the literature; among them, a vast production has been devoted to the Golden Ratio mixing (GR), of which two slightly different versions have attracted much attention: in one of them [84–87] the solar angle is given by tanθ₁₂ = 1/ϕ, where $\varphi =(1+\sqrt{5})/2$ is the golden ratio, which implies ${\theta }_{12}=31.7°$; in the other one, suggested in Rodejohann [88], cosθ₁₂ = ϕ/2 and ${\theta }_{12}=36°$.

Since these special patterns mainly differ for the value of the solar angle, we report in Figure 4 the predictions for ${sin}^2{\theta }_{12}$ of GR and TBM and compare them with three different fit results coming from Capozzi et al. [89] (labeled as CLMMP), Forero et al. [90] (labeled as FTV) and Gonzalez-Garcia et al. [91] (labeled as GMS). See the caption for more details.

FIGURE 4

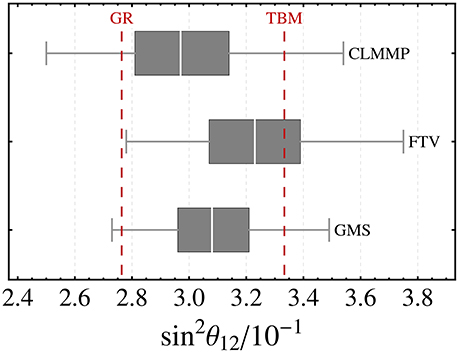
Figure 4. Predictions for sin${}^2{\theta }_{12}$ for GR and TBM mixing patterns (red dashed lines); the box charts represent the value of the global fits (for NO only since the allowed region is the same for both orderings) performed in Capozzi et al. [89] (labeled as CLMMP), Forero et al. [90] (labeled as FTV) and Gonzalez-Garcia et al. [91] (labeled as GMS). The white vertical lines inside the boxes are the best fit values, the gray boxes the 1σ confidence regions and the gray lines the 3σ allowed regions.

The neutrino mass matrices analyzed so far have been derived in the basis where charged leptons are diagonal; then one can ask which features the matrix Q of Equation (36) must have in order to maintain the hermitian product $M_{\ell }^{†}{M}_{\ell }$ diagonal; observing that the most general diagonal $M_{\ell }^{†}{M}_{\ell }$ is left invariant under the action of a diagonal phase matrix with 3 different phase factors, one can easily see that if Qⁿ = 1 then the matrix Q generates a cyclic group Z_n. Examples for n = 3 and n = 4 are the following:

$\begin{array}{l}{Q}_{TB}=\left(\begin{array}{ccc}1& 0& 0\\ 0& \omega & 0\\ 0& 0& {\omega }^2\end{array}\right),{\omega }^3=1\hfill \\ Q_{BM}=\left(\begin{array}{ccc}-1& 0& 0\\ 0& -i& 0\\ 0& 0& i\end{array}\right).& (60)\hfill \end{array}$

We stress again that a realistic flavor model that reproduces all experimental features of neutrino masses and mixing can be realized from a theory invariant under the spontaneously broken symmetry described by ${G}$_f which, in turn, must contain at least the S and Q transformations. These generate the subgroups ${G}$_ν and ${G}$_ℓ, respectively. The breaking of ${G}$_f must be arranged in such a way that it is broken down to ${G}$_ν in the neutrino mass sector and to ${G}$_ℓ in the charged lepton mass sector. In some cases also the symmetry under A₂₃ is part of ${G}$_ℓ and then must be preserved in the neutrino sector or it can arise as a consequence of the breaking of ${G}$_ℓ.

Notice that it is not strictly necessary to deal with diagonal charged leptons because the special patterns analyzed so far can be considered as a good first approximation of the data and suitable corrections, for example coming explicitly from the charged leptons, must be taken into account [92–94].

Many discrete groups with the previous properties have been studied and their potentialities to describe neutrino masses and mixings scrutinized in detail. Just to give some examples, the groups A₄, S₄ and T′ are commonly utilized to generate TBM mixing (see, for example, [73, 95–103]); the group S₄ can also be used to generate BM mixing [83, 104, 105]; A₅ can be utilized to generate GR mixing [84–87] and the groups D₁₀ and D₁₂ can lead to another type of GR [88, 106] and to hexagonal mixing [107, 108]. Excellent reviews in this sector can be found, for instance, in King [65], Altarelli and Feruglio [80], Ishimori et al. [109] and Grimus and Ludl [110].

4.3. TBM and BM from Discrete Symmetries

To make a direct connection with the procedure outlined in section 4.1, we study here two examples on how to get the TBM and BM patterns from ${G}$_f = S₄. This is the permutation group of order four, it has 4! = 24 elements and it is isomorphic to the symmetry group of the cube. The algebra contains two generators, S and T, that satisfy the condition S² = T⁴ = (ST)³ = 1. The group contains five irreducible representations: two singlets 1 and 1′, one doublet 2 and two triplets 3 and 3′. The (non trivial) tensor products are

$\begin{array}{l}{1}^{\prime }\otimes 1^{\prime }=1\\ 1^{\prime }\otimes 2=2\\ 1^{\prime }\otimes 3=3^{\prime }\\ 1^{\prime }\otimes 3^{\prime }=3\\ 2\otimes 2=1_s\oplus 2_s\oplus {1^{\prime }}_a\\ 2\otimes 3=2\otimes 3^{\prime }=3\oplus 3^{\prime }\\ 3\otimes 3=3^{\prime }\otimes 3^{\prime }=1_s\oplus 2_s\oplus {3^{\prime }}_s\oplus 3_a\\ 3\otimes 3^{\prime }=1^{\prime }\oplus 2\oplus 3\oplus 3^{\prime },\end{array}$

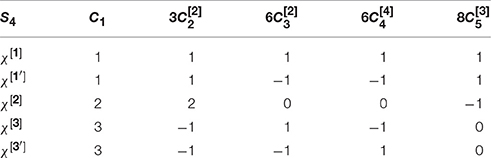
where the subscript s (a) denotes symmetric (antisymmetric) combinations. The S₄ elements can be classified by the order h of each element, where ω^h = e (see Table 2 where the five conjugacy classes and their characters are summarized. As expected, we have 1+3+6+6+8 = 24 elements in each class and the superscript indicates the order of each element in the conjugacy classes). A possible choice for the three dimensional generators is

$\begin{array}{ll}S=\frac{1}{2}\left(\begin{array}{c}\begin{array}{ccc}0& \sqrt{2}& \sqrt{2}\\ \sqrt{2}& -1& 1\\ \sqrt{2}& 1& -1\end{array}\end{array}\right)T=\left(\begin{array}{ccc}1& 0& 0\\ 0& e^{i\pi /2}& 0\\ 0& 0& e^{i3\pi /2}\end{array}\right).\hfill & (62)\hfill \end{array}$

The group S₄ contains another three dimensional representation, whose generators are related to those in Equation (62) through {S, T} → {−S, −T}. The abelian subgroups of S₄ are four Klein groups V, four Z₃ groups and three different Z₄. These are summarized in Table 3.

TABLE 2

Table 2. Characters of the S₄ group.

TABLE 3

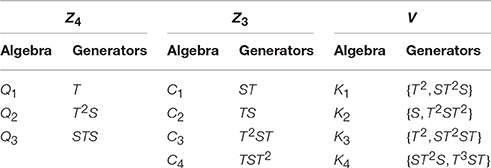
Table 3. Possible independent algebras of S₄ subgroups (same classification as the one adopted in de Adelhart Toorop et al. [111]).

The patterns of interest can be obtained using the following choices of subgroups:

• ${G}$_ℓ = Z₃ and ${G}$_ν = V

These subgroups are useful to reproduce the TBM only. We assume C₃ ∈ Z₃ and K₁ ∈ V as representative algebra. The absolute value of the PMNS matrix is therefore given by:

$\begin{array}{ll}\Vert U_{\text{PMNS}}\Vert =U_{\text{TBM}}=\frac{1}{\sqrt{6}}\left(\begin{array}{ccc}2& \sqrt{2}& 0\\ 1& \sqrt{2}& \sqrt{3}\\ 1& \sqrt{2}& \sqrt{3}\end{array}\right).\hfill & (63)\hfill \end{array}$

Notice that the Jarlskog invariant J_CP [112], defined as:

$\begin{array}{ll}\begin{array}{l}{J}_{\text{CP}}\equiv \Im \left[{(U_{\text{PMNS}})}_{11}{(U_{\text{PMNS}})}_{13}^{\ast }{(U_{\text{PMNS}})}_{31}^{\ast }{(U_{\text{PMNS}})}_{33}\right]=\\ \frac{1}{8}\sin 2{\theta }_{12}\sin 2{\theta }_{23}\sin 2{\theta }_{13}\cos {\theta }_{13}\sin \delta ,\end{array}\hfill & (64)\hfill \end{array}$

is zero. To obtain a realistic mixing pattern with ${\theta }_{13}~9°$ we need to include large corrections.

• ${G}$_ℓ = Z₄ and ${G}$_ν = V

In this case only the BM pattern is possible; therefore both θ₁₂ and θ₂₃ are maximal. Next to leading order corrections of roughly the same order of magnitude of the Cabibbo angle are needed to reproduce the data as discussed, for instance, in Altarelli et al. [105].

• ${G}$_ℓ = V and ${G}$_ν = V

This case, discussed in Lam [113], produces a BM mixing pattern. A representative choice for the subalgebras for ${G}$_ℓ is K₁ and for ${G}$_ν is K₂.

4.4. Other LO Patterns

The fact that the value of the reactor angle is non-zero with high accuracy opens the possibility to use discrete symmetries to enforce the LO leptonic mixing patterns to structures where θ₁₃ is different from zero from the beginning. The various realizations all differ by the amount of the NLO needed to reconcile the theoretical predictions with the experimental data. Some of the new patterns, that have been obtained and studied in specific model realizations, are the following:

• the Trimaximal mixing [114], which referes to schemes where the first or the second column is the same as the corresponding one of TB matrix [107, 115, 116]. In both cases, the good TB prediction of ${\theta }_{12}~35°$ is maintained and θ₁₃ is always different from zero.

• the Tri-Permuting (TP) mixing matrix, introduced in Bazzocchi [117]. The mixing is defined by two maximal angles and a large θ₁₃ according to

$\begin{array}{ll}\sin {\theta }_{12}=\sin {\theta }_{23}=-\frac{1}{\sqrt{2}},\sin {\theta }_{13}=\frac{1}{3},\hfill & (65)\hfill \end{array}$

which corresponds to the following mixing matrix:

$\begin{array}{ll}{U}_{\text{TP}}~\frac{1}{3}\left(\begin{array}{ccc}2& -2& 1\\ 2& 1& -2\\ 1& 2& 2\end{array}\right).\hfill & (66)\hfill \end{array}$

• the Bi-trimaximal (BT) mixing, introduced in King et al. [118] and corresponding to the mixing matrix:

$\begin{array}{ll}{U}_{\text{BT}}=\left(\begin{array}{ccc}{a}_{+}& \frac{1}{\sqrt{3}}& a_{-}\\ -\frac{1}{\sqrt{3}}& \frac{1}{\sqrt{3}}& \frac{1}{\sqrt{3}}\\ a_{-}& -\frac{1}{\sqrt{3}}& a_{+}\end{array}\right),\hfill & (67)\hfill \end{array}$

• where $a_{\pm }=(1\pm \frac{1}{\sqrt{3}})/2$, and leads to the following predictions:

$\begin{array}{ll}\begin{array}{l}\sin {\theta }_{12}=\sin {\theta }_{23}=\sqrt{\frac{8-2\sqrt{3}}{13}}\approx 0.591({\theta }_{12}={\theta }_{23}\approx 36.2°),\\ \sin {\theta }_{13}=a_{-}\approx 0.211({\theta }_{13}\approx 12.2°).\end{array}\hfill & (68)\hfill \end{array}$

4.5. Discrete Symmetries and Invariance Under CP

Let us now enlarge the symmetry content of the theory assuming, in addition to the invariance under the discrete group, also invariance under CP [119–121].

As in section 4.1, we consider that the residual symmetry in the charged sector ${G}$_ℓ is a cyclic group Z_n, n ≥ 3, or the product Z₂ ⊗ Z₂. Under the action of CP, a generic field Φ transforms as [122–124]:

$\begin{array}{ll}\Phi (x)\to {\Phi }^{\prime }(x)=X{\Phi }^{\star }(x_{CP}),\hfill & (69)\hfill \end{array}$

where X is the representations of the CP operator in field space and x_CP is the space-time coordinate transformed under the usual CP transformation $x\to x_{CP}=(x^0,-\mathbf{\text{x}})$. The invariance of the field under ${G}$_f is expressed as:

$\begin{array}{ll}\Phi (x)\to {\Phi }^{\prime }(x)=A\Phi (x),\hfill & (70)\hfill \end{array}$

where A is an element of a non-abelian discrete symmetry group. X can be chosen as a constant unitary symmetric matrix⁴:

$\begin{array}{ll}X{X}^{†}=X{X}^{\star }=1,\hfill & (71)\hfill \end{array}$

in such a way that the square of the CP transformation is the identity, X² = 1. The action of X on the mass matrices, before the symmetry breaking, is given by

$\begin{array}{ll}{X}^{\star }{M}_{\ell }^{†}{M}_{\ell }X={(M_{\ell }^{†}{M}_{\ell })}^{\star }\hfill & (72\text{a})\hfill \end{array}$

$\begin{array}{ll}X{M}_{\nu }X=M_{\nu }^{\star },\hfill & (72\text{b})\hfill \end{array}$

if neutrinos are Majorana particles. If instead neutrinos are Dirac particles, (72b) has to be modified to

$\begin{array}{ll}{X}^{\star }{M}_{\nu }^{†}{M}_{\nu }X={(M_{\nu }^{†}{M}_{\nu })}^{\star }.\hfill & (73)\hfill \end{array}$

The fact that the theory is invariant under the flavor symmetry group ${G}$_f requires that for the generators of the group A the representations X in the field space must satisfy the following relation:

$\begin{array}{ll}{(X^{-1}AX)}^{\star }=A^{\prime }A,A^{\prime }\in \left\{{{G}}_f\right\},\hfill & (74)\hfill \end{array}$

where in general A ≠ A′. Notice that if X is a solution of (71) and (74) also e^iρX, with ρ being an arbitrary phase, is a solution.

Let us now specify this framework to the case where the residual symmetry ${G}$_ν is Z₂ ⊗ CP, with Z₂ contained in the flavor group; the matrix Z representing the generator of the former symmetry and the CP transformation X have to fulfil the constraint

$\begin{array}{ll}X{Z}^{\star }-ZX=0,\hfill & (75)\hfill \end{array}$

which is invariant under (74). In the neutrino sector, the light neutrino mass matrix satisfies both relations:

$\begin{array}{ll}{Z}^T{M}_{\nu }Z=M_{\nu }\hfill & (76\text{a})\hfill \end{array}$

$\begin{array}{ll}X{M}_{\nu }X=M_{\nu }^{\star }.\hfill & (76\text{b})\hfill \end{array}$

Notice that it is always possible to choose a basis where

$\begin{array}{ll}X=\Omega {\Omega }^T{Z}_c={\Omega }^{†}Z\Omega Z_c=\text{diag}\{{(-1)}^{z_1},{(-1)}^{z_2},{(-1)}^{z_3}\},\hfill & (77)\hfill \end{array}$

with z_i = 0, 1. Since Z generates a Z₂ symmetry, two of the three parameters z_i have to coincide and the combination ${\Omega }^T{M}_{\nu }\Omega$ is constrained to be block-diagonal and real. Thus, this matrix can be diagonalized using a rotation R(θ) in the ij-plane of degenerate eigenvalues of Z, where θ is an unconstrained parameter that can be fixed to describe the neutrino mixing parameters. The positiveness of the light neutrino masses is ensured by the diagonal matrix K_ν with elements equal to ±1 or ±i. In this way the matrix M_ν can be diagonalized with unitary matrix defined as

$\begin{array}{ll}{U}_{\nu }\equiv \Omega R_{ij}(\theta )K_{\nu }.\hfill & (78)\hfill \end{array}$

The mass spectrum is not fixed and thus permutations of columns are admitted. The inclusion of the charged leptons into the game proceeds as discussed in section 4.1. So, called U_ℓ the matrix diagonalizing $M_{\ell }^{†}{M}_{\ell }$, the full U_PMNS is given by:

$\begin{array}{ll}{U}_{\text{PMNS}}\equiv U_{\ell }^{†}{U}_{\nu }=U_{\ell }\Omega R_{ij}(\theta )K_{\nu },\hfill & (79)\hfill \end{array}$

up to permutations of rows and columns. To give an explicit example [125], let us assume that U_ℓ = 1 and take Ω to be

$\begin{array}{ll}\Omega =\frac{1}{\sqrt{2}}\left(\begin{array}{ccc}\sqrt{2}\cos \phi & -\sqrt{2}i\sin \phi & 0\\ \sin \phi & i\cos \phi & -1\\ \sin \phi & i\cos \phi & 1\end{array}\right);\hfill & (80)\hfill \end{array}$

this matrix fulfils (77) for Z and X chosen as (Z, X) = $(T^{2}S{T}^{3}S{T}^2,S{X}_0)$, with X₀ ≡ A₂₃. Since z₁ and z₃ of the diagonal combination Ω†ZΩ are equal, the indices ij of the rotation matrix R_ij(θ) in (79) are {i, j} = {1, 3}. Thus, the PMNS mixing matrix simply reads

$\begin{array}{ll}{U}_{PMNS}=\Omega R_{13}(\theta )K_{\nu }.\hfill & (81)\hfill \end{array}$

Extracting the mixing angles from (81) we find:

$\begin{array}{ll}\begin{array}{l}{\sin }^2{\theta }_{12}=\frac{2}{2+(3+\sqrt{5}){\cos }^2\theta },\\ {\sin }^2{\theta }_{13}=\frac{1}{10}\left(5+\sqrt{5}\right){\sin }^2\theta ,\\ {\sin }^2{\theta }_{23}=\frac{1}{2}-\frac{\sqrt{2(5+\sqrt{5})}\sin 2\theta }{7+\sqrt{5}+(3+\sqrt{5})\cos 2\theta },\end{array}\hfill & (82)\hfill \end{array}$

which also call for an exact sum rule among the solar and the reactor mixing angles:

$\begin{array}{ll}{\sin }^2{\theta }_{12}=\frac{{\sin }^2\phi }{1-{\sin }^2{\theta }_{13}}\approx \frac{0.276}{1-{\sin }^2{\theta }_{13}}.\hfill & (83)\hfill \end{array}$

Using for ${sin}^2{\theta }_{13}$ its best fit value ${({sin}^2{\theta }_{13})}^{\text{bf}}=0.0217$, we find for the solar mixing angle ${sin}^2{\theta }_{12}\approx 0.282$ which is within its 3σ range, see Table 1.

Models that explore the predictability of the CP symmetry in conjunction with non-abelian discrete symmetries have been massively explored in the very recent years; for example, the interplay between S₄ and CP has been studied, among others, in Mohapatra and Nishi [126], Feruglio et al. [127], Luhn [128], and Penedo et al. [129], while the role of A₅ has been elucidated in Li and Ding [130], Ballett et al. [131] and Turner [132] and that of several Δ groups in de Medeiros Varzielas and Emmanuel-Costa [133], Bhattacharyya et al. [134], Ma [135], Hagedorn et al. [136] and Ding and King [137].

4.6. The Use of Abelian Symmetries

Let us now investigate the possibility to construct SUSY models where the only flavor symmetry is a continuous U(1) [17]; thus the following procedure can be used:

- given that the flavor symmetry acts horizontally on leptons, the related charges can be written as $e^c~(n_1^{\text{R}},n_2^{\text{R}},0)$ for the SU(2)_L lepton singlets and as $L~(n_1^{\text{L}},n_2^{\text{L}},0)$ for the lepton doublets. Since only charge differences impact the mass hierarchies and the mixing angles, the third lepton charges can be set to zero and one can safely assume a charge ordering as $n_1^{\text{R}}>n_2^{\text{R}}>0$. To prevent flavor-violating Higgs couplings, the Higgs fields H_{u, d} are not charged.

- Once we have assigned U(1) charges to leptons, the Yukawa terms are no longer invariant under the action of the flavor symmetry and new scalar fields θ must be introduced that transforms non-trivially under U(1), with charge n_θ. Thus, the Yukawa part of the Lagrangian is as follows:

$\begin{array}{ll}{{L}}_Y={(Y_e)}_{ij}{L}_i{H}_d{e}_j^c{\left(\frac{\theta }{\Lambda }\right)}^{p_e}+{(Y_{\nu })}_{ij}\frac{L_i{L}_j{H}_u{H}_u}{{\Lambda }_{\text{L}}}{\left(\frac{\theta }{\Lambda }\right)}^{p_{\nu }}+\text{H}\text{.c}\text{.}\hfill & (84)\hfill \end{array}$

where Λ is the cut-off of the effective flavor theory and Λ_L the scale of the lepton number violation, in principle distinct from Λ. Here (_Ye)ij and (_Yν)ij are free complex parameters with modulus of ${O}$(1) while p_e and p_ν are appropriate powers of the ratio θ/Λ needed to compensate the U(1) charges for each Yukawa term. Without loss of generality, we can fix n_θ = −1; consequently, $n_1^{L,R},n_2^{L,R}>0$ for the Lagrangian expansion to make sense. For the neutrino masses we consider that they are described by the effective Weinberg operator, while the extension to see-saw mechanisms is straightforward.

- Once the flavor and electroweak symmetries are broken by the vevs of the flavon and the Higgs fields, the mass matrices arise, with entries proportional to the expanding parameter $ϵ\equiv \frac{\langle \theta \rangle }{\Lambda }<1$.

The lepton charges assignments reported in Table 4, some of them already studied in Altarelli et al. [138], give rise to the following mass matrices [139]:

TABLE 4

Table 4. Examples of charge assignment under U(1).

$\begin{array}{ll}\begin{array}{l}A:Y_e=\left(\begin{array}{ccc}{ϵ}^3& {ϵ}^2& 1\\ {ϵ}^3& {ϵ}^2& 1\\ {ϵ}^3& {ϵ}^2& 1\end{array}\right),Y_{\nu }=\left(\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right),\\ A_{\mu \tau }:Y_e=\left(\begin{array}{ccc}{ϵ}^4& {ϵ}^3& ϵ\\ {ϵ}^3& {ϵ}^2& 1\\ {ϵ}^3& {ϵ}^2& 1\end{array}\right),Y_{\nu }=\left(\begin{array}{ccc}{ϵ}^2& ϵ& ϵ\\ ϵ& 1& 1\\ ϵ& 1& 1\end{array}\right),\\ H:Y_e=\left(\begin{array}{ccc}{ϵ}^7& {ϵ}^5& {ϵ}^2\\ {ϵ}^6& {ϵ}^4& ϵ\\ {ϵ}^5& {ϵ}^3& 1\end{array}\right),Y_{\nu }=\left(\begin{array}{ccc}{ϵ}^4& {ϵ}^3& {ϵ}^2\\ {ϵ}^3& {ϵ}^2& ϵ\\ {ϵ}^2& ϵ& 1\end{array}\right),\end{array}\hfill & (85)\hfill \end{array}$

$\begin{array}{ll}\begin{array}{l}{A}^{\prime }:Y_e=\left(\begin{array}{ccc}{ϵ}^3& ϵ& 1\\ {ϵ}^3& ϵ& 1\\ {ϵ}^3& ϵ& 1\end{array}\right),Y_{\nu }=\left(\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right),\\ H^{\prime }:Y_e=\left(\begin{array}{ccc}{ϵ}^{10}& {ϵ}^6& {ϵ}^2\\ {ϵ}^9& {ϵ}^5& ϵ\\ {ϵ}^8& {ϵ}^4& 1\end{array}\right),Y_{\nu }=\left(\begin{array}{ccc}{ϵ}^4& {ϵ}^3& {ϵ}^2\\ {ϵ}^3& {ϵ}^2& ϵ\\ {ϵ}^2& ϵ& 1\end{array}\right).\end{array}\hfill & (86)\hfill \end{array}$

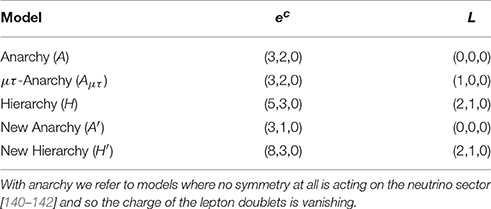
As already remarked, the coefficients in front of ϵⁿ are complex numbers with absolute values of ${O}$(1) and arbitrary phases. Considering that Y_ν is a symmetric matrix, the total number of undetermined parameters that arise in this type of constructions is 30 plus the unknown value of ϵ. In order to establish which models adapt better to the data of Table 1, one cannot use a χ²-based analysis because the minimum is always very close to zero for every (Y_e, Y_ν) pairs; thus, a meaningful comparison of two models is better achieved with the help of a Bayesian analysis. This has been done in Bergstrom [139] and the results of the Bayes factor between all models and A′ are reported in Figure 5.

FIGURE 5

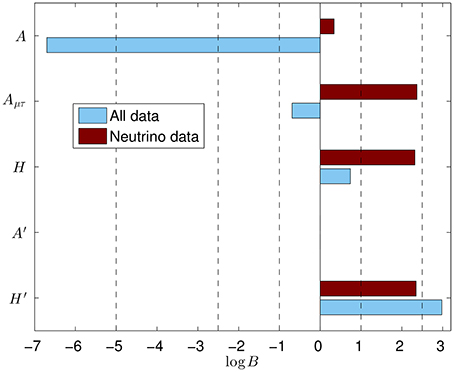
Figure 5. Logarithms of Bayes factors with respect to the model A′ for the models in Table 4 using only neutrino data (dark-red bars) and all data (light-blue bars). Positive values of logB indicate a weak evidence (logB = 1), a moderate evidence (logB = 2.5) and a strong evidence (logB = 5) of the supposed model against the reference one A′. Numerical estimates on ϵ are not reported but values in the range (0.1–0.2) emerged from the analysis as the most appropriate ones.

The relevant features of such an analysis can be summarized as follows: when using only the neutrino data, the hierarchical models are all weakly preferred over the anarchical ones. When also the charged lepton data are taken into account in the analysis, the A model turns out to be strongly disfavored. Adding in the comparison also the H′ and A′ models, the former is the best one: it is moderately better than A_μτ and A′, and weakly preferred over H.

Other possibilities in the direction of using U(1) rely on the fact that the U(1) charges are not completely arbitrary but are determined by an underlying symmetry of the type L_e − L_μ − L_τ for lepton doublets and arbitrary right-handed charges [143–145]. In the limit of exact symmetry, the neutrino mass matrix has the following structure:

$\begin{array}{ll}{m}_{\nu }=m_0\left(\begin{array}{ccc}0& 1& x\\ 1& 0& 0\\ x& 0& 0\end{array}\right),\hfill & (87)\hfill \end{array}$

which leads to a spectrum of inverted type and mixing angles as θ₁₂ = π/4, tanθ₂₃ = x (i.e., large atmospheric mixing for x ~ ${O}$(1)) and θ₁₃ = 0. An important limitation of such a texture is that two eigenvalues have the same absolute values and the solar mass difference cannot be reproduced. Successful tentatives to describe also $\Delta m_{21}^2$ have been presented, for instance, in Lavoura and Grimus [146] and Grimus and Lavoura [147] where, however, either the reactor angle was almost vanishing or the solar angle was too large with respect to its current value. Corrections of ${O}$(λ_${G}$) from the charged lepton sector [92–94] could be invoked to properly shift θ₁₂ from maximal mixing and θ₁₃ from zero, thus allowing a sizable reactor angle, but at the prize of a too large solar-to-atmospheric mass ratio r. A possible solution to the previous issues was discussed in Meloni [145], where the U(1) flavor symmetry was broken by the vevs of two complex fields ϕ and θ (instead of one) of charges Q_ϕ = 1 and Q_θ = −1/2. An appropriate breaking of L_e − L_μ − L_τ in the neutrino sector assures the correct value of $r~{\lambda }_C^2$ and preserves the leading order (LO) prediction of large θ₂₃, whereas the necessary deviations for the solar and reactor angles are instead obtained from the charged lepton mass matrix with complex entries.

5. Where GUT Meets Flavor

The importance of the discovery of neutrino masses and mixing angles is that they provide interesting information on the problem of understanding the origin of three families of quarks and leptons and their mixing parameters. In this respect, as we have already outlined before, the relevance of GUT groups resides on the fact that some of the mass matrices of different fermions are related in a non-trivial way, see for example Equation (31), whereas family symmetries impose stringent constraints on the matrix elements of the same mass matrix. Figure 6 summarizes in concise way how GUT and family symmetries act on the observable fermions (see caption for more details).

FIGURE 6

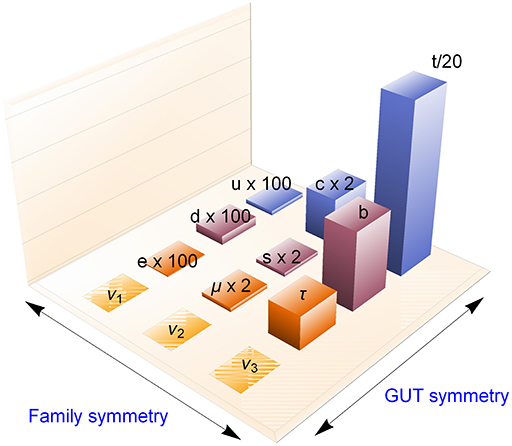
Figure 6. Action of the GUT and family symmetry groups. Given the large hierarchies, the height of the columns are not in scale and the actual values of the fermion masses have been multiplied or divided by the factors on top of each columns.

The next obvious step is to merge these two different type of symmetries in order to construct a flavor sector with very few free parameters. As it was the case for the special patterns of lepton mixing, also in the case with GUT one needs to identify which features of the data are really relevant for the formulation of a model. In this sense, the fact that the reactor angle θ₁₃ is approximately related to the Cabibbo angle θ_C by the relation ${\theta }_{13}~{\theta }_C/\sqrt{2}$ may be a hint of a connection between leptonic and quark mixing [9]. And this is not restricted to the reactor angle only. In fact, as shown in Figure 7, the experimental value of ${sin}^2{\theta }_{12}$ is related to the predictions of exact TBM or GR by a jump of order ${\lambda }_C^2$, or of order λ_C in the case of BM.

FIGURE 7

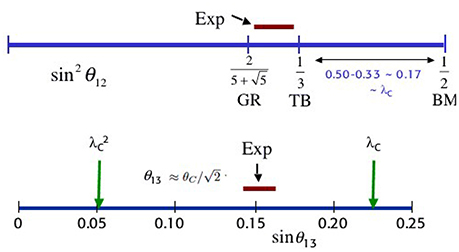
Figure 7. Comparison of the experimental value of the leptonic mixing angles against their exact predictions by TBM, GR and BM mixings. Figure from Altarelli et al. [148].

This idea seems to agree with the empirical observation that θ₁₂ + θ_C ~ π/4, a relation known as quark-lepton complementarity [8]–[11], sometimes replaced by ${\theta }_{12}+{O}({\theta }_C)~\pi /4$ (weak complementarity). If we want to realize in a complete model the previous relations, one possibility is to start from BM and generate universal corrections to the mixing angles of order λ_C, arriving at the following relations:

$\begin{array}{ll}{\sin }^2{\theta }_{12}~\frac{1}{2}+{O}({\lambda }_C){\sin }^2{\theta }_{23}~\frac{1}{2}+{O}({\lambda }_C)\sin {\theta }_{13}~{O}({\lambda }_C),\hfill & (88)\hfill \end{array}$

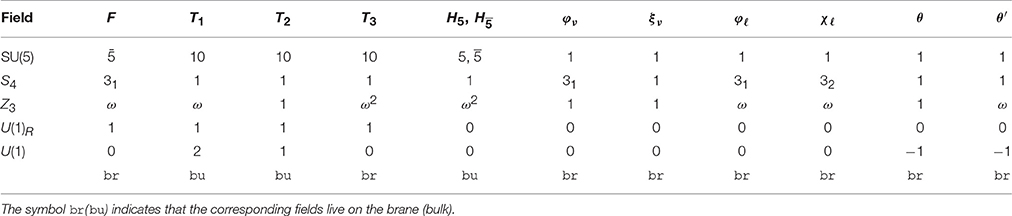
which are all in agreement with the experimental data. These corrections can be appropriately fabricated by charged lepton rotations which differ from the identity by off-diagonal elements whose magnitude is obviously of order of the Cabibbo angle. The game becomes highly non-trivial in GUT theories which demand that also masses for the quarks and the CKM matrix are reproduced at the same time. An example based on SU(5) that permits to realize the program of having the BM structure in the neutrino sector and then to correct it by terms arising from the diagonalization of the charged lepton mass matrix is built as follows [149] (but see [150] for a variant using the A₄ family group). The construction is a SUSY SU(5) model in 4+1 dimensions [151, 152] with a flavor symmetry S₄ ⊗ Z₃ ⊗ U(1)_R ⊗ U(1) [105, 149], where U(1) is the Froggatt-Nielsen (FN) symmetry that leads to the hierarchies of fermion masses and U(1)_R is the usual R-symmetry. The particle assignments are displayed in Table 5 where, for the sake of simplicity, we have not reported the driving fields needed to realize the wanted symmetry breaking pattern. From the table we see that the three $\overline{5}$ are grouped into the S₄ triplet F, while the tenplets T_{1, 2, 3} are assigned to the singlet of S₄. The breaking of the S₄ symmetry is ensured by a set of SU(5)-invariant flavon supermultiplets, which are three triplets φ_ℓ, φ_ν (3₁), χ_ℓ (3₂) and one singlet ξ_ν. The alignment in flavor space of their vevs along appropriate directions will be the source of the BM lepton mixing. The GUT Higgs fields H₅ and $H_{\overline{5}}$ are singlets under S₄ but equally charged under Z₃, so that they are distinguished only by their SU(5) transformation properties. The tenplets T₁ and T₂ are charged under the U(1) flavor group which is spontaneously broken by the vevs of the θ and θ′ fields, both carrying U(1) charges −1 and transforming as a singlet of S₄.

TABLE 5

Table 5. Matter and Higgs assignment of the model.

As a result of symmetries and field assignments to the irreducible representations of SU(5) × S₄, the charged lepton masses are diagonal at LO and exact BM is achieved for neutrinos. Higher dimension vertices in the Lagrangian, suppressed by powers of a large scale Λ, generate corrections to the diagonal charged leptons and to exact BM. We adopt the definitions:

$\begin{array}{ll}\frac{v_{{\phi }_{\ell }}}{\Lambda }~\frac{v_{\chi }}{\Lambda }~\frac{v_{{\phi }_{\nu }}}{\Lambda }~\frac{v_{\xi }}{\Lambda }~\frac{\langle \theta \rangle }{\Lambda }~\frac{\langle {\theta }^{\prime }\rangle }{\Lambda }~s~{\lambda }_C,\hfill & (89)\hfill \end{array}$

where $s=\frac{1}{\sqrt{\pi R\Lambda }}$ is the volume suppression factor and v_ϕ are the vevs of the flavon fields listed in Table 5. This simple (and democratic) choice leads to a good description of masses and mixing. In fact, the charged lepton mass matrix turns out to be:

$\begin{array}{ll}{m}_e~\left(\begin{array}{c}\begin{array}{ccc}{a}_{11}{\lambda }_C^5& a_{21}{\lambda }_C^4& a_{31}{\lambda }_C^2\\ a_{12}{\lambda }_C^4& -c{\lambda }_C^3& \dots \dots \\ a_{13}{\lambda }_C^4& c{\lambda }_C^3& a_{33}{\lambda }_C\end{array}\end{array}\right){\lambda }_C,\hfill & (90)\hfill \end{array}$

where the a_ij are generic complex coefficients of modulus of ${O}(1)$ not predicted by the theory. The corresponding lepton rotation is thus:

$\begin{array}{ll}{U}_{\ell }~\left(\begin{array}{ccc}1& u_{12}{\lambda }_C& u_{13}{\lambda }_C\\ -u_{12}^{*}{\lambda }_C& 1& 0\\ -u_{13}^{*}{\lambda }_C& -u_{12}^{*}{u}_{13}^{*}{\lambda }_C^2& 1\end{array}\right),\hfill & (91)\hfill \end{array}$

(u_ij again of ${O}(1)$) so that ${\theta }_{23}^{\ell }=0$.

The neutrino masses are obtained by Weinberg operators of the form:

$\begin{array}{ll}{(FF)}_1(H_5{H}_5),{(FF)}_{3_1}{H}_5{H}_5{\phi }_{\nu },{(FF)}_{3_1}{H}_5{H}_5{\xi }_{\nu },\hfill & (92)\hfill \end{array}$

which are diagonalized by exact BM, so the mixing angles are easily derived:

$\begin{array}{l}{\sin }^2{\theta }_{12}=\frac{1}{2}-\frac{1}{\sqrt{2}} Re(u_{12}+u_{13}){\lambda }_C{\sin }^2{\theta }_{23}=\frac{1}{2}+{O}({\lambda }_C^2)\\ \sin {\theta }_{13}=\frac{1}{\sqrt{2}}|u_{12}-u_{13}|{\lambda }_C.\end{array}$

We observe that the model produces at the same time the “weak” complementarity relation and the empirical fact that sinθ₁₃ is of the same order than the shift of ${sin}^2{\theta }_{12}$ from the BM value of 1/2, both of order λ_C.

It is important to stress that the predictions of GUT models are valid at the GUT scale and, in order to compare with the experimental results, the evolution of the Yukawa matrices down to the electroweak scale must be performed [153, 154]. Although the final values depend somehow on the details of the model, it is known that in the case of a quasi-degenerate neutrino mass spectrum, the renormalization group corrections to the neutrino parameters can be dramatically large [155, 156]. However, as it has been elucidated in Antusch et al. [157, 158], in SUSY models small tanβ and small neutrino Yukawa couplings are sufficient conditions for having the corrections to the mixing angles (and CP phases) are under control.

The requirement of having a BM mixing as a starting point is not a necessary ingredient to get a good description of fermion observables; as pointed out in Hagedorn et al. [159], even from the TBM at LO one can conceive a model where the corrections to the reactor angle are large enough to meet the experimental value, maintaining at the same time the solar and atmospheric mixing at acceptable values. Also the choice of the discrete group is not restricted to S₄; examples where a large θ₁₃ is obtained after substantial corrections from higher order operators can be found, for example, in King et al. [118], Antusch et al. [154], Cooper et al. [160], Marzocca et al. [161], Antusch et al. [162, 163], Björkeroth et al. [164], Antusch and Hohl [165], Gehrlein et al. [166], and Meroni et al. [167], which employ the A₄, A₅, T′ and Δ(96) groups, respectively, within an SU(5) framework.

If the gauge group is enlarged to SO(10), we loose the advantages of using the SU(5)-singlet right-handed neutrinos since one generation of fermion belongs to the 16-dimensional representation. One possible strategy to separate neutrinos from the charged fermions is to assume the dominance of type-II see-saw with respect to the more usual type-I see-saw.

As we have already seen, in models of this type neutrino masses are described by ${M}$_ν ~ fv_L, where v_L is the vev of the B − L = 2 triplet in the ${\overline{\mathbf{126}}}_H$ Higgs field and f is its Yukawa coupling matrix with the 16. Since one can decide to work in a basis where the matrix f is diagonalized by the BM or by TBM matrices, the results of a fit of the model parameters on the fermion observables performed in one basis lead to the same χ² than the fit in the other basis, thus a χ² analysis cannot decide whether TBM or BM is a better starting point [148]. This is confirmed by the plot in Figure 8, where it is shown that, within uncertainties, the χ² as a function of the reactor angle is equal in the two cases, and this is true also for values of sinθ₁₃ different than the measured value. In particular, the minimum χ² value, χ² = 0.003, is obtained for ${sin}^2{\theta }_{13}~0.015$, just a bit below the experimental value ${sin}^2{\theta }_{13}~0.022$. Nevertheless, as the minimum χ² is quite shallow for ${sin}^2{\theta }_{13}<0.1$, the fit does not exhibit any strongly preferred value of θ₁₃.

FIGURE 8

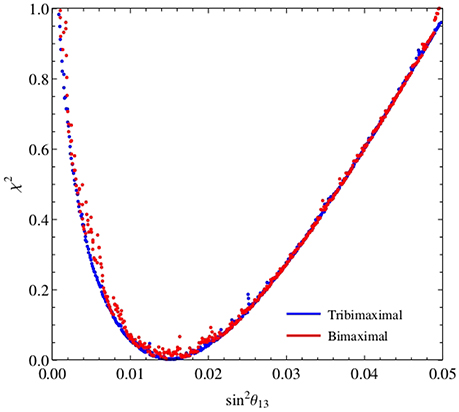
Figure 8. χ² as a function of ${\text{sin}}^2{\theta }_{13}$ in the type-II see-saw SO(10) models obtained when starting in the TBM or BM basis.

Having established that the χ² is not the best variable to decide whether TBM or BM is better, one can consider to measure the amount of fine-tuning needed to fit a set of data by means of the parameter d_FT introduced in Altarelli and Blankenburg [168]:

$\begin{array}{ll}{d}_{FT}={\displaystyle \sum \left|\frac{p_i}{e_i}\right|},\hfill & (93)\hfill \end{array}$

where e_i is the “error” of a given parameter p_i defined as the shift from the best fit value that changes the χ² by one unit, with all other parameters fixed at their best fit values. In Figure 9 we report a study of the fine tuning parameter when the fit is repeated with the same data except for ${sin}^2{\theta }_{13}$. It clearly shows that:

FIGURE 9

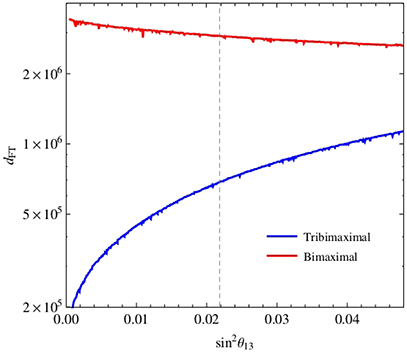
Figure 9. The behavior of the d_FT increases (decreases) with ${\text{sin}}^2{\theta }_{13}$ in the TBM (BM) cases. For the physical value ${\text{sin}}^2{\theta }_{13}~0.022$ it is about 4 times larger in the BM case.

• for the physical value of ${sin}^2{\theta }_{13}$, d_FT is smaller in the TBM case;

• the fine tuning increases (decreases) with sinθ₁₃ for TBM (BM).

A closer inspection of the d_FT parameter reveals a series of interesting features: first of all, that the large values are predominantly driven by the smallness of the electron mass; then, due to the presence of mixing, the d_FT coming from the 33 component of h (mainly responsible for the top mass) is actually one of the largest contributions to the global d_FT because of its relevance to the electron mass in both TBM and BM scenarios. Although this might be surprising, one has to take into account that the dependence of the observables on the parameters is quite complicated due to the off-diagonal elements of the mass matrices.

Other classes of renormalizable and non-renormalizable SO(10) models supplemented by discrete and continuous symmetries have been discussed in the literature. In Altarelli and Blankenburg [168] a model comparison based on a χ² analysis and on the values of d_FT has been carried out with sufficient details to allow for a discrimination in terms of performance in the description of the data. Table 6 has been extracted from Altarelli and Blankenburg [168] and reports the results of such a comparison. The model called BSV [47] (no flavor symmetries involved here) has a minimal Yukawa sector with 10_H and ${\overline{\mathbf{126}}}_H$ and has been compared with the data in Bertolini et al. [52], where the type-I and mixed type-I and type-II cases were considered. As it is well known, the restricted Higgs content calls for complex h and f matrices. Even increasing the number of free parameters, with type-II dominance no good fit of the data can be obtained. The situation changes if one introduces the 120_H of Higgs, as in the model with type-II see-saw dominance introduced by Joshipura and Kodrani (JK) [169]. The relevant feature of this model is the existence of a broken μ − τ symmetry in addition to the parity symmetry which causes hermitian mass matrices. Similarly, Grimus and Kuhbock [170] (GK) also have an extended Higgs sector with 10_H, $\overline{\mathbf{126}}$ and 120_H but their model is based on type-I see-saw dominance.

TABLE 6

Table 6. Comparison of different SO(10) models fitted to the data.

In the class of non-renormalizable SO(10) theories, we can cite the model of Dermisek and Raby (DR) [171, 172]; it contains Higgses in the 10_H, 45_H and ${\overline{\mathbf{16}}}_H$, and it is based on the flavor symmetry S₃ × U(1) × Z₂ × Z₂. In the symmetric S₃ limit only the masses of the third generation are non-vanishing while the second and first generation masses are generated by a symmetry breaking stage. The neutrino masses are obtained through a type-I see-saw mechanism with a hierarchical Majorana mass matrix. Enough freedom to reproduce the observed neutrino properties is guarantee by new SO(10)-singlet neutrino and new scalar fields.

A similar Higgs sector with 10_H, (16 + 16)_H and 45_H representations and a few SO(10) singlets constitute the scalar sector of the model by Albright, Babu and Barr (ABB) [173, 174]. However, this model is based on a flavor symmetry U(1)×Z₂×Z₂ which is mainly used to select the desired terms which in the Lagrangian and reject those that would not help in reproducing the data. A modification of this model has been proposed by Ji, Li, Mohapatra (JLM) [175]; the charged lepton and the down quark mass matrices are the same as in the ABB model but the up and Dirac neutrino mass matrices are modified thanks to new dimension five and six vertices introduced in the theory. The model is based on type-I see-saw and the new operators provide a sufficient number of free parameters to fit the leptonic mixing angles.

The relevant feature of the results presented in Table 6 is that the realistic SO(10) models which are non-renormalizable with type-I see-saw (DR, ABB, JLM), have a χ²/d.o.f. smaller than 1 and a moderate level of fine tuning d_FT, if compared with the relatively more constrained BSV, JK and GK. They all have a large amount of fine tuning and, with the exception of the GK model, a worst χ². The larger fine tuning arises from the more pronounced difficulty of fitting the light first generation of charged fermion masses, together with the neutrino mass differences and mixing angles.

More recently, successful attempts to completely describe neutrino data within S₄ and Δ(27) have been presented in Björkeroth et al. [176–178], where also the ability to provide a framework for the leptogenesis mechanism has been addressed [178].

Beside the models with complete unification at the GUT scale, one can also consider the possibility of supplementing with flavor symmetries models with partial unification, that is theories where the gauge group at the GUT scale is not an unique group. Good examples in this direction are those based on the Pati-Salam group SU(4)_c ⊗ SU(2)_L ⊗ SU(2)_R (PS), as discussed in de Adelhart Toorop et al. [179], where S₄ was employed to recover the quark-lepton complementarity at LO and in King [180, 181], which explores the capabilities of A₄ to describe quark and lepton masses, mixing and CP violation⁵. As usual, these models also need the presence of additional discrete (or continuous U(1)) symmetries to forbid or suppress unwanted operators. In Figure 10, modified from King [181], we sketch a possible particle assignment for models with [PS ⊗ permutation ⊗ discrete] groups, where it is understood that the permutation group contains triplet representations. In both panels, the red, blue and green colors represent the SU(3) triplets, which are accompanied with the light gray particles to complete the fundamental 4 representation of SU(4)_c. The left-handed families are assigned to triplet presentations of the permutation groups and are doublets under SU(2)_L, left panel. On the right panel we consider that the right-handed families are distinguished by different charges of the discrete group and are doublets of SU(2)_R.

FIGURE 10

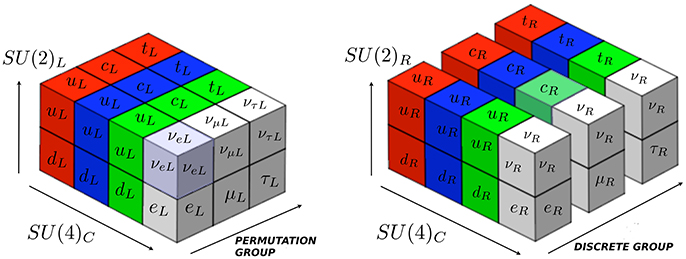
Figure 10. Pictorial representation of a possible particle assignment in models with [PS ⊗ permutation ⊗ discrete] groups. Figure taken and modified from King [181].

6. Conclusions

The question of the theoretical understanding of the experimental numbers of fermion masses and mixing is a very old story. Although neutrinos were considered as a promising tool to access the fundamental properties of particle interactions, the new data helped to discard some theoretical model on lepton mixing (mainly those based on θ₁₃ = 0 at the LO) but many other still offer a viable solution, spanning a wide range of possibilities going from a situation with no structure and no symmetry in the neutrino sector (anarchy) to a maximum of symmetry for the models based on discrete non-abelian flavor groups.

In this respect, neutrinos have not offered so far any crucial insight on the problem of flavor. The extension to include GUT (or Partial Unification) symmetry exacerbates the difficulties in the model building, as also the quark properties must be taken into account and the larger symmetry reduces the useful number of free parameters.

If one is driven by the fact that the quark-lepton complementarity is a real feature of Nature, then models based on SU(5) with a broken S₄ symmetry emerge as one among the most viable and predictive theory, in which fermion masses and mixing are all well reproduced inside their experimental ranges at the prize of small fine-tunings in very few model parameters.

As we have seen in Table 1, the octant of the atmospheric angle, the value of the CP violating phase δ and the neutrino mass orderings are features of the neutrinos that have not been clearly addressed so far. Thus, from the model building point of view, the results coming from the running (for instance, NOνA [183] and T2K [184]) and planned experiments (like DUNE [185]) can certainly help in selecting the class of models that, more than others, will be able to incorporate the new information. In this respect, the emerging indication of δ ~ 3/2π seems to exclude the whole class of models predicting CP-conserving Dirac phase, as many do of those listed in section 4.5.

On the other hand, the uncertainties affecting the already measured mixing angle and mass differences are expected to be reduced to a sub-percent level in the next 5–10 years (as it is the case for the solar parameters measured by the JUNO detector [186]) and, in a framework where the mixing parameters are obtained from a LO neutrino mass texture corrected by charge lepton rotations, this can influence in a critical manner which LO mass matrix is the most useful starting point; with more precise measurements, the jumps described in Figure 7, needed to reconcile the LO predictions with the data, must be chosen more carefully.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author is strongly indebted with Erica Vagnoni and Andrea Di Iura for useful discussions.

Footnotes

1. ^One can safely estimate that the colored states Δ_R and Σ do not give a catastrophic contribution to proton decay [35, 36].

2. ^The charged lepton mass matrix M_ℓ is written in the right-left basis.

3. ^For instance, one can impose relations between the generators of these residual groups and/or force the determinants to assume specific values.

4. ^The requirement that X is a symmetric matrix has been shown in Bajc et al. [119] to be a necessary condition, otherwise the neutrino mass spectrum would be partially degenerate.

5. ^See King [182] for an example of a PS model where, instead of a discrete group, the continuos SO(3) gauged family symmetry has been employed.

References

1. Majorana E. Teoria simmetrica dell'elettrone e del positrone. Nuovo Cim. (1937) 14:171–84.

Google Scholar

2. Cabibbo N. Unitary symmetry and leptonic decays. Phys Rev Lett. (1963) 10:531–3. doi: 10.1103/PhysRevLett.10.531

CrossRef Full Text | Google Scholar

3. Kobayashi M, Maskawa T. CP violation in the renormalizable theory of weak interaction. Prog Theor Phys. (1973) 49:652–7. doi: 10.1143/PTP.49.652

CrossRef Full Text | Google Scholar

4. Pontecorvo B. Mesonium and anti-mesonium. Sov Phys JETP. (1957) 6:429.

5. Pontecorvo B. Inverse beta processes and nonconservation of lepton charge. Sov Phys JETP. (1958) 7:172–3.

Google Scholar

6. Maki Z, Nakagawa M, Sakata S. Remarks on the unified model of elementary particles. Prog Theor Phys. (1962) 28:870. doi: 10.1143/PTP.28.870

CrossRef Full Text | Google Scholar

7. Pontecorvo B. Neutrino experiments and the problem of conservation of leptonic charge. Sov Phys JETP. (1968) 26:984–8.

Google Scholar

8. Raidal M. Relation between the neutrino and quark mixing angles and grand unification. Phys Rev Lett. (2004) 93:161801. doi: 10.1103/PhysRevLett.93.161801

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Antusch S, King SF, Mohapatra RN. Quark-lepton complementarity in unified theories. Phys Lett. (2005) B618:150–61. doi: 10.1016/j.physletb.2005.05.026

CrossRef Full Text | Google Scholar

10. Minakata H, Smirnov AY. Neutrino mixing and quark-lepton complementarity. Phys Rev. (2004) D70:073009. doi: 10.1103/PhysRevD.70.073009

CrossRef Full Text | Google Scholar

11. Frampton PH, Mohapatra RN. Possible gauge theoretic origin for quark-lepton complementarity. J High Energy Phys. (2005) 1:025. doi: 10.1088/1126-6708/2005/01/025

CrossRef Full Text | Google Scholar

12. Harrison PF, Perkins DH, Scott WG. Tri-bimaximal mixing and the neutrino oscillation data. Phys Lett. (2002) B530:167–73. doi: 10.1016/S0370-2693(02)01336-9

CrossRef Full Text | Google Scholar

13. Harrison PF, Scott WG. Symmetries and generalizations of tri - bimaximal neutrino mixing. Phys Lett. (2002) B535:163–9. doi: 10.1016/S0370-2693(02)01753-7

CrossRef Full Text | Google Scholar

14. Xing ZZ. Nearly tri bimaximal neutrino mixing and CP violation Phys Lett. (2002) B533:85–93. doi: 10.1016/S0370-2693(02)01649-0

CrossRef Full Text

15. Harrison PF, Scott WG. mu - tau reflection symmetry in lepton mixing and neutrino oscillations. Phys Lett. (2002) B547:219–28. doi: 10.1016/S0370-2693(02)02772-7

CrossRef Full Text | Google Scholar

16. Harrison PF, Scott WG. Permutation symmetry, tri - bimaximal neutrino mixing and the S3 group characters. Phys Lett. (2003) B557:76. doi: 10.1016/S0370-2693(03)00183-7

CrossRef Full Text | Google Scholar

17. Froggatt CD, Nielsen HB. Hierarchy of quark masses, cabibbo angles and CP violation. Nucl Phys. (1979) B147:277–98. doi: 10.1016/0550-3213(79)90316-X

CrossRef Full Text | Google Scholar

18. Luhn C. Spontaneous breaking of SU(3) to finite family symmetries: a pedestrian's approach. J High Energy Phys. (2011) 3:108. doi: 10.1007/JHEP03(2011)108

CrossRef Full Text | Google Scholar

19. Altarelli G, Feruglio F, Lin Y. Tri-bimaximal neutrino mixing from orbifolding. Nucl Phys. (2007) B775:31–44. doi: 10.1016/j.nuclphysb.2007.03.042

CrossRef Full Text | Google Scholar

20. Esteban I, Gonzalez-Garcia MC, Maltoni M, Martinez-Soler I, and Schwetz T. Updated fit to three neutrino mixing: exploring the accelerator-reactor complementarity. J High Energy Phys. (2017) 1:087. doi: 10.1007/JHEP01(2017)087

CrossRef Full Text | Google Scholar

21. Ibarra A. Neutrino mass models. Acta Phys Polon Supp. (2016) 9:741–68. doi: 10.5506/APhysPolBSupp.9.741

CrossRef Full Text | Google Scholar

22. Minkowski P. μ → eγ at a rate of one out of 10⁹ muon decays? Phys Lett. (1977) 67B:421–8. doi: 10.1016/0370-2693(77)90435-X

CrossRef Full Text | Google Scholar

23. Yanagida T. Horizontal symmetry and masses of neutrinos. In: Proceedings of the Workshop on the Baryon Number of the Universe and Unified Theories, Tsukuba (1979).

Google Scholar

24. Gell-Mann M, Ramond P, Slansky R. Complex spinors and unified theories. In: Supergravity Workshop Stony Brook, (1979). New York, NY. p. 315–21.

25. Glashow SL. The future of elementary particle physics. In: Lévy M, Basdevant JL, Speiser D, Weyers J, Gastmans R, Jacob M, editors. Quarks and Leptons. NATO Advanced Study Institutes Series (Series B. Physics), Boston, MA: Springer (1980), p. 707.

26. Mohapatra RN, Senjanovic G. Neutrino mass and spontaneous parity violation. Phys Rev Lett. (1980) 44:912. doi: 10.1103/PhysRevLett.44.912

CrossRef Full Text | Google Scholar

27. Konetschny W, Kummer W. Nonconservation of total lepton number with scalar bosons. Phys Lett. (1977) 70B, 433–5. doi: 10.1016/0370-2693(77)90407-5

CrossRef Full Text | Google Scholar

28. Foot R, Lew H, He XG, Joshi GC. Seesaw neutrino masses induced by a triplet of leptons. Z Phys. (1989) C44:441.

Google Scholar

29. Altarelli G, Feruglio F. Models of neutrino masses and mixings. New J Phys. (2004) 6:106. doi: 10.1088/1367-2630/6/1/106

CrossRef Full Text | Google Scholar

30. Fritzsch H, Minkowski P. Unified interactions of leptons and hadrons. Ann Phys. (1975) 93:193–266. doi: 10.1016/0003-4916(75)90211-0

CrossRef Full Text | Google Scholar

31. del Aguila F, Ibanez LE. Higgs bosons in SO(10) and partial unification. Nucl Phys. (1981) B177:60–86. doi: 10.1016/0550-3213(81)90266-2

CrossRef Full Text | Google Scholar

32. Deshpande NG, Keith E, Pal PB. Implications of LEP results for SO(10) grand unification. Phys Rev. (1993) D46:2261–4.

Google Scholar

33. Pati JC, Salam A. Lepton number as the fourth color. Phys Rev. (1974) D10:275–89. doi: 10.1103/PhysRevD.10.275

CrossRef Full Text | Google Scholar

34. Georgi H, Glashow SL. Unity of all elementary particle forces. Phys Rev Lett. (1974) 32:438–41. doi: 10.1103/PhysRevLett.32.438

CrossRef Full Text | Google Scholar

35. Altarelli G, Meloni D. A non supersymmetric SO(10) grand unified model for all the physics below M_GUT. J High Energy Phys. (2013) 8:21. doi: 10.1007/JHEP08(2013)021

CrossRef Full Text | Google Scholar

36. Deppisch FF, Gonzalo TE, Graf L. Surveying the SO(10) model landscape: the left-right symmetric case. Phys Rev. (2017) D96:055003. doi: 10.1103/PhysRevD.96.055003

CrossRef Full Text | Google Scholar

37. Bajc B, Melfo A, Senjanovic G, Vissani F. Yukawa sector in non-supersymmetric renormalizable SO(10). Phys Rev. (2006) D73:055001. doi: 10.1103/PhysRevD.73.055001

CrossRef Full Text | Google Scholar

38. Peccei RD, Quinn HR. CP conservation in the presence of instantons. Phys Rev Lett. (1977) 38:1440–3. doi: 10.1103/PhysRevLett.38.1440

CrossRef Full Text

39. Babu KS, Mohapatra RN. Predictive neutrino spectrum in minimal SO(10) grand unification. Phys Rev Lett. (1993) 70:2845–8. doi: 10.1103/PhysRevLett.70.2845

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Georgi H, Jarlskog C. A new lepton - quark mass relation in a unified theory. Phys Lett. (1979) 86B:297–300. doi: 10.1016/0370-2693(79)90842-6

CrossRef Full Text | Google Scholar

41. Joshipura AS, Patel KM. Fermion masses in SO(10) models. Phys Rev. (2011) D83:095002. doi: 10.1103/PhysRevD.83.095002

CrossRef Full Text | Google Scholar

42. Dueck A, Rodejohann W. Fits to SO(10) grand unified models. J High Energy Phys. (2013) 9:24. doi: 10.1007/JHEP09(2013)024

CrossRef Full Text | Google Scholar

43. Arason H, Castano DJ, Piard EJ, Ramond P. Mass and mixing angle patterns in the standard model and its minimal supersymmetric extension. Phys Rev. (1993) D47:232–40. doi: 10.1103/PhysRevD.47.232

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Harvey JA, Ramond P, Reiss DB. CP violation and mass relations in SO(10). Phys Lett. (1980) 92B:309–11. doi: 10.1016/0370-2693(80)90270-1

CrossRef Full Text | Google Scholar

45. Harvey JA, Reiss DB, Ramond P. Mass relations and neutrino oscillations in an SO(10) model. Nucl Phys. (1982) B199:223–68. doi: 10.1016/0550-3213(82)90346-7

CrossRef Full Text | Google Scholar

46. Matsuda K, Fukuyama T, Nishiura H. SO(10) GUT and quark lepton mass matrices. Phys Rev. (2000) D61:053001. doi: 10.1103/PhysRevD.61.053001

CrossRef Full Text | Google Scholar

47. Bajc B, Senjanovic G, Vissani F. How neutrino and charged fermion masses are connected within minimal supersymmetric SO(10). PoS (2001) HEP2001:198.

Google Scholar

48. Bajc B, Senjanovic G, Vissani F. β - τ unification and large atmospheric mixing: a Case for noncanonical seesaw. Phys Rev Lett. (2003) 90:051802. doi: 10.1103/PhysRevLett.90.051802

CrossRef Full Text | Google Scholar

49. Meloni D, Ohlsson T, Riad S. Effects of intermediate scales on renormalization group running of fermion observables in an SO(10) model. J High Energy Phys. (2014) 12:052. doi: 10.1007/JHEP12(2014)052

CrossRef Full Text | Google Scholar

50. Meloni D, Ohlsson T, Riad S. Renormalization group running of fermion observables in an extended non-supersymmetric SO(10) model. J High Energy Phys. (2017) 3:045. doi: 10.1007/JHEP03(2017)045

CrossRef Full Text | Google Scholar

51. Xing Zz, Zhang H, Zhou S. Updated values of running quark and lepton masses. Phys Rev. (2008) D77:113016. doi: 10.1103/PhysRevD.77.113016

CrossRef Full Text | Google Scholar

52. Bertolini S, Schwetz T, Malinsky M. Fermion masses and mixings in SO(10) models and the neutrino challenge to SUSY GUTs. Phys Rev. (2006) D73:115012. doi: 10.1103/PhysRevD.73.115012

CrossRef Full Text | Google Scholar

53. Lavoura L, Kuhbock H, Grimus W. Charged-fermion masses in SO(10): analysis with scalars in 10+120. Nucl Phys. (2006) B754:1–16. doi: 10.1016/j.nuclphysb.2006.07.024

CrossRef Full Text | Google Scholar

54. Bajc B, Senjanovic G. Radiative seesaw and degenerate neutrinos. Phys Rev Lett. (2005) 95:261804. doi: 10.1103/PhysRevLett.95.261804

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Lam CS. Symmetry of lepton mixing. Phys Lett. (2007) B656:193–8. doi: 10.1016/j.physletb.2007.09.032

CrossRef Full Text | Google Scholar

56. Lam CS. Determining horizontal symmetry from neutrino mixing. Phys Rev Lett. (2008) 101:121602. doi: 10.1103/PhysRevLett.101.121602

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Lam CS. The unique horizontal symmetry of leptons. Phys Rev. (2008) D78:073015. doi: 10.1103/PhysRevD.78.073015

CrossRef Full Text | Google Scholar

58. Fonseca RM, Grimus W. Classification of lepton mixing matrices from finite residual symmetries. J High Energy Phys. (2014) 2014:033. doi: 10.1007/JHEP09(2014)033

CrossRef Full Text | Google Scholar

59. Grimus W. Discrete symmetries, roots of unity, and lepton mixing. J Phys G (2013) 40:075008. doi: 10.1088/0954-3899/40/7/075008

CrossRef Full Text | Google Scholar

60. Hernandez D, Smirnov AYu. Lepton mixing and discrete symmetries. Phys Rev. (2012) D86:053014. doi: 10.1103/PhysRevD.86.053014

CrossRef Full Text | Google Scholar

61. Hernandez D, Smirnov AYu. Discrete symmetries and model-independent patterns of lepton mixing. Phys Rev. (2013) D87:053005. doi: 10.1103/PhysRevD.87.053005

CrossRef Full Text | Google Scholar

62. Ge SF, Dicus DA, Repko WW. Z₂ symmetry prediction for the leptonic dirac CP phase. Phys Lett. (2011) B702:220–3. doi: 10.1016/j.physletb.2011.06.096

CrossRef Full Text | Google Scholar

63. Ge SF, Dicus DA, Repko WW. Residual symmetries for neutrino mixing with a large θ₁₃ and nearly maximal δ_D. Phys Rev Lett. (2012) 108:041801. doi: 10.1103/PhysRevLett.108.041801

PubMed Abstract | CrossRef Full Text | Google Scholar

64. King SF, Ross GG. Fermion masses and mixing angles from SU(3) family symmetry. Phys Lett. (2001) B520:243–53. doi: 10.1016/S0370-2693(01)01139-X

CrossRef Full Text | Google Scholar

65. King SF, Luhn C. Neutrino mass and mixing with discrete symmetry. Rept Prog Phys. (2013) 76:056201. doi: 10.1088/0034-4885/76/5/056201

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Barry J, Rodejohann W. Neutrino mass sum-rules in flavor symmetry models. Nucl Phys. (2011) B842:33–50. doi: 10.1016/j.nuclphysb.2010.08.015

CrossRef Full Text | Google Scholar

67. Ballett P, King SF, Luhn C, Pascoli S, Schmidt MA. Testing atmospheric mixing sum rules at precision neutrino facilities. Phys Rev. (2014) D89:016016. doi: 10.1103/PhysRevD.89.016016

CrossRef Full Text | Google Scholar

68. Meloni D. Checking flavour models at neutrino facilities. Phys Lett. (2014) B728:118. doi: 10.1016/j.physletb.2013.11.033

CrossRef Full Text | Google Scholar

69. Petcov ST. Predicting the values of the leptonic CP violation phases in theories with discrete flavour symmetries. Nucl Phys. (2015) B892:400. doi: 10.1016/j.nuclphysb.2015.01.011

CrossRef Full Text | Google Scholar

70. Girardi I, Petcov ST, Titov AV. Determining the dirac CP violation phase in the neutrino mixing matrix from sum rules. Nucl Phys. (2015) B894:733. doi: 10.1016/j.nuclphysb.2015.03.026

CrossRef Full Text | Google Scholar

71. Girardi I, Petcov ST, Titov AV. Predictions for the Leptonic Dirac CP Violation Phase: a Systematic Phenomenological Analysis. Eur Phys J. (2015) C75:345. doi: 10.1140/epjc/s10052-015-3559-6

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Girardi I, Petcov ST, Stuart AJ, Titov AV. Leptonic dirac CP violation predictions from residual discrete symmetries. Nucl Phys. (2016) B902:1–57. doi: 10.1016/j.nuclphysb.2015.10.020

CrossRef Full Text | Google Scholar

73. Altarelli G, Feruglio F. Tri-bimaximal neutrino mixing, A(4) and the modular symmetry. Nucl Phys. (2006) B741:215–35. doi: 10.1016/j.nuclphysb.2006.02.015

CrossRef Full Text | Google Scholar

74. de Medeiros Varzielas I, King SF, Ross GG. Tri-bimaximal neutrino mixing from discrete subgroups of SU(3) and SO(3) family symmetry. Phys Lett. (2007) B644:153–7. doi: 10.1016/j.physletb.2006.11.015

CrossRef Full Text | Google Scholar

75. Grimus W, Lavoura L. S₃ × Z₂ model for neutrino mass matrices. J High Energy Phys. (2005) 2005:013. doi: 10.1088/1126-6708/2005/08/013

CrossRef Full Text | Google Scholar

76. Meloni D, Morisi S, Peinado E. Fritzsch neutrino mass matrix from S₃ symmetry. J Phys G (2011) 38:015003. doi: 10.1088/0954-3899/38/1/015003

CrossRef Full Text | Google Scholar

77. Ferreira PM, Grimus W, Lavoura L, Ludl PO Maximal CP violation in lepton mixing from a model with Delta(27) flavour symmetry. J High Energy Phys. (2012) 2012:128. doi: 10.1007/JHEP09(2012)128

CrossRef Full Text | Google Scholar

78. Kobayashi T, Omura Y, Yoshioka K. Flavor symmetry breaking and vacuum alignment on orbifolds. Phys Rev. (2008) D78:115006. doi: 10.1103/PhysRevD.78.115006

CrossRef Full Text | Google Scholar

79. Burrows TJ, King SF. A₄ x SU(5) SUSY GUT of flavour in 8d. Nucl Phys. (2011) B842:107–21. doi: 10.1016/j.nuclphysb.2010.08.018

CrossRef Full Text | Google Scholar

80. Altarelli G, Feruglio F. Discrete flavor symmetries and models of neutrino mixing. Rev Mod Phys. (2010) 82:2701–29. doi: 10.1103/RevModPhys.82.2701

CrossRef Full Text | Google Scholar

81. Fukuyama T, Nishiura H. Mass matrix of Majorana neutrinos (1997). arXiv:hep-ph/9702253.

Google Scholar

82. Fukuyama T. Twenty years after the discovery of μ−τ symmetry. High Energy Phys. (2017) 2017:033B11. doi: 10.1093/ptep/ptx032

CrossRef Full Text | Google Scholar

83. Barger VD, Pakvasa S, Weiler TJ, Whisnant K. Bimaximal mixing of three neutrinos. Phys Lett. (1998) B437:107–16. doi: 10.1016/S0370-2693(98)00880-6

CrossRef Full Text | Google Scholar

84. Datta A, Ling FS, Ramond P. Correlated hierarchy, Dirac masses and large mixing angles. Nucl Phys. (2003) B671:383–400. doi: 10.1016/j.nuclphysb.2003.08.026

CrossRef Full Text | Google Scholar

85. Kajiyama Y, Raidal M, Strumia A. The Golden ratio prediction for the solar neutrino mixing. Phys Rev. (2007) D76:117301. doi: 10.1103/PhysRevD.76.117301

CrossRef Full Text | Google Scholar

86. Everett LL, Stuart AJ. Icosahedral (A(5)) family symmetry and the golden ratio prediction for solar neutrino mixing. Phys Rev. (2009) D79:085005. doi: 10.1103/PhysRevD.79.085005

CrossRef Full Text | Google Scholar

87. Feruglio F, Paris A. The golden ratio prediction for the solar angle from a natural model with A₅ flavour symmetry. J High Energy Phys. (2011) 2011:101. doi: 10.1007/JHEP03(2011)101

CrossRef Full Text | Google Scholar

88. Rodejohann W. Unified parametrization for quark and lepton mixing angles. Phys Lett. (2009) B671:267–71. doi: 10.1016/j.physletb.2008.12.010

CrossRef Full Text | Google Scholar

89. Capozzi F, Lisi E, Marrone A, Montanino D, Palazzo A. Neutrino masses and mixings: Status of known and unknown 3ν parameters. Nucl Phys. (2016) B908:218–34. doi: 10.1016/j.nuclphysb.2016.02.016

CrossRef Full Text | Google Scholar

90. Forero DV, Tortola M, Valle JWF. Neutrino oscillations refitted. Phys Rev. (2014) D90:093006. doi: 10.1103/PhysRevD.90.093006

CrossRef Full Text | Google Scholar

91. Gonzalez-Garcia MC, Maltoni M, Schwetz T. Updated fit to three neutrino mixing: status of leptonic CP violation. J High Energy Phys. (2014) 11:052. doi: 10.1007/JHEP11(2014)052

CrossRef Full Text | Google Scholar

92. Petcov ST, Rodejohann W. Flavor symmetry L_e−L_μ−Lτ, atmospheric neutrino mixing and CP violation in the lepton sector. Phys Rev. (2005) D71:073002. doi: 10.1103/PhysRevD.71.073002

CrossRef Full Text | Google Scholar

93. Altarelli G, Feruglio F, Masina I. Can neutrino mixings arise from the charged lepton sector? Nucl Phys. (2004) B689:157–71. doi: 10.1016/j.nuclphysb.2004.04.012

CrossRef Full Text | Google Scholar

94. Meloni D, Plentinger F, Winter W. Perturbing exactly tri-bimaximal neutrino mixings with charged lepton mass matrices. Phys Lett. (2011) B699:354–59. doi: 10.1016/j.physletb.2011.04.033

CrossRef Full Text | Google Scholar

95. Ma E. Tribimaximal neutrino mixing from a supersymmetric model with A4 family symmetry. Phys Rev. (2006) D73:057304.

Google Scholar

96. He XG, Keum YY, Volkas RR. A(4) flavor symmetry breaking scheme for understanding quark and neutrino mixing angles. J High Energy Phys. (2006) 04:039. doi: 10.1088/1126-6708/2006/04/039

CrossRef Full Text | Google Scholar

97. Chen MC, King SF. A4 see-saw models and form dominance. J High Energy Phys. (2009) 06:072. doi: 10.1088/1126-6708/2009/06/072

CrossRef Full Text | Google Scholar

98. Altarelli G, Meloni D. A simplest A4 model for tri-bimaximal neutrino mixing. J Phys. (2009) G36:085005. doi: 10.1088/0954-3899/36/8/085005

CrossRef Full Text | Google Scholar

99. Bazzocchi F, Merlo L, Morisi S. Fermion masses and mixings in a S(4)-based model. Nucl Phys. (2009) B816:204–26. doi: 10.1016/j.nuclphysb.2009.03.005

CrossRef Full Text | Google Scholar

100. Grimus W, Lavoura L, Ludl PO. Is S(4) the horizontal symmetry of tri-bimaximal lepton mixing? J Phys. (2009) G36:115007. doi: 10.1088/0954-3899/36/11/115007

CrossRef Full Text | Google Scholar

101. Aranda A. Neutrino mixing from the double tetrahedral group T-prime. Phys Rev. (2007) D76:111301.

Google Scholar

102. Ding GJ. Fermion mass hierarchies and flavor mixing from T-prime symmetry. Phys Rev. (2008) D78:036011. doi: 10.1103/PhysRevD.78.036011

CrossRef Full Text | Google Scholar

103. Frampton PH, Kephart TW, Matsuzaki S. Simplified renormalizable T-prime model for tribimaximal mixing and cabibbo angle. Phys Rev. (2008) D78:073004. doi: 10.1103/PhysRevD.78.073004

CrossRef Full Text | Google Scholar

104. Mohapatra RN, Nussinov S. Bimaximal neutrino mixing and neutrino mass matrix. Phys Rev. (1999) D60:013002. doi: 10.1103/PhysRevD.60.013002

CrossRef Full Text | Google Scholar

105. Altarelli G, Feruglio F, Merlo L. Revisiting bimaximal neutrino mixing in a model with S₄ discrete symmetry. J High Energy Phys. (2009) 2009:020. doi: 10.1088/1126-6708/2009/05/020

CrossRef Full Text | Google Scholar

106. Adulpravitchai A, Blum A, Rodejohann W. Golden ratio prediction for solar neutrino mixing. New J Phys. (2009) 11:063026. doi: 10.1088/1367-2630/11/6/063026

CrossRef Full Text | Google Scholar

107. Albright CH, Dueck A, Rodejohann W. Possible alternatives to tri-bimaximal mixing. Eur Phys J. (2010) C70:1099–110. doi: 10.1140/epjc/s10052-010-1492-2

CrossRef Full Text | Google Scholar

108. Kim JE, Seo M-S Quark and lepton. mixing angles with a dodeca-symmetry. J High Energy Phys. (2011) 2011:97. doi: 10.1007/JHEP02(2011)097

CrossRef Full Text | Google Scholar

109. Ishimori H, Kobayashi T, Ohki H, Shimizu Y, Okada H, Tanimoto M Non-abelian discrete symmetries in particle physics. Prog Theor Phys Suppl. (2010) 183:1–163. doi: 10.1143/PTPS.183.1

CrossRef Full Text | Google Scholar

110. Grimus W, Ludl PO. Finite flavour groups of fermions. J Phys. (2012) A45:233001. doi: 10.1088/1751-8113/45/23/233001

CrossRef Full Text | Google Scholar

111. de Adelhart Toorop R, Feruglio F, Hagedorn C. Finite modular groups and lepton mixing. Nucl Phys. (2012) B858:437–67. doi: 10.1016/j.nuclphysb.2012.01.017

CrossRef Full Text | Google Scholar

112. Jarlskog C. Commutator of the quark mass matrices in the standard electroweak model and a measure of maximal CP violation. Phys Rev Lett. (1985) 55:1039. doi: 10.1103/PhysRevLett.55.1039

CrossRef Full Text | Google Scholar

113. Lam CS. Group theory and dynamics of neutrino mixing. Phys Rev. (2011) D83:113002. doi: 10.1103/PhysRevD.83.113002

CrossRef Full Text | Google Scholar

114. Grimus W, Lavoura L. A model for trimaximal lepton mixing. J High Energy Phys. (2008) 09:106. doi: 10.1088/1126-6708/2008/09/106

CrossRef Full Text | Google Scholar

115. He XG, Zee A. Minimal modification to the tri-bimaximal neutrino mixing. Phys Lett. (2007) B645:427–31. doi: 10.1016/j.physletb.2006.11.055

CrossRef Full Text | Google Scholar

116. Antusch S, King SF, Luhn C, Spinrath M. Trimaximal mixing with predicted θ₁₃ from a new type of constrained sequential dominance. Nucl Phys. (2012) B856:328–41. doi: 10.1016/j.nuclphysb.2011.11.009

CrossRef Full Text | Google Scholar

117. Bazzocchi F. Tri-Permuting Mixing Matrix and predictions for θ₁₃. (2011). arXiv: 1108.2497

Google Scholar

118. King SF, Luhn C, Stuart AJ. A grand delta(96) x SU(5) flavour model. Nucl Phys. (2013) B867:203–35. doi: 10.1016/j.nuclphysb.2012.09.021

CrossRef Full Text | Google Scholar

119. Feruglio F, Hagedorn C, Ziegler R. Lepton mixing parameters from discrete and CP symmetries. J High Energy Phys. (2013) 2013:027. doi: 10.1007/JHEP07(2013)027

CrossRef Full Text | Google Scholar

120. Holthausen M, Lindner M, Schmidt MA. CP and discrete flavour symmetries. J High Energy Phys. (2013) 2013:122. doi: 10.1007/JHEP04(2013)122

CrossRef Full Text | Google Scholar

121. Chen MC, Fallbacher M, Mahanthappa KT, Ratz M, Trautner A. CP violation from finite groups. Nucl Phys. (2014) B883:267–305. doi: 10.1016/j.nuclphysb.2014.03.023

CrossRef Full Text | Google Scholar

122. Ecker G, Grimus W, Neufeld H. Spontaneous CP violation in left-right symmetric gauge theories. Nucl Phys. (1984) B247:70–82. doi: 10.1016/0550-3213(84)90373-0

CrossRef Full Text | Google Scholar

123. Ecker G, Grimus W, Neufeld H. A standard form for generalized CP transformations. J Phys. (1987) A20:L807. doi: 10.1088/0305-4470/20/12/010

CrossRef Full Text | Google Scholar

124. Neufeld H, Grimus W, Ecker G. Generalized CP invariance, neutral flavor conservation and the structure of the mixing matrix. Int J Mod Phys. (1988) A3:603–16. doi: 10.1142/S0217751X88000254

CrossRef Full Text | Google Scholar

125. Di Iura A, Hagedorn C, Meloni D. Lepton mixing from the interplay of the alternating group A₅ and CP. J High Energy Phys. (2015) 2015:037. doi: 10.1007/JHEP08(2015)037

CrossRef Full Text | Google Scholar

126. Mohapatra RN, Nishi CC. S₄ flavored CP symmetry for neutrinos. Phys Rev. (2012) D86:073007. doi: 10.1103/PhysRevD.86.073007

CrossRef Full Text | Google Scholar

127. Feruglio F, Hagedorn C, Ziegler R. A realistic pattern of lepton mixing and masses from S₄ and CP. Eur Phys J. (2014) C74:2753. doi: 10.1140/epjc/s10052-014-2753-2

CrossRef Full Text | Google Scholar

128. Luhn C. Trimaximal TM₁ neutrino mixing in S₄ with spontaneous CP violation. Nucl Phys. (2013) B875:80–100. doi: 10.1016/j.nuclphysb.2013.07.003

CrossRef Full Text | Google Scholar

129. Penedo JT, Petcov ST, Titov AV. Neutrino mixing and leptonic CP violation from S₄ flavour and generalised CP symmetries. (2017). arXiv: 1705.00309

130. Li CC, Ding GJ. Lepton mixing in A₅ family symmetry and generalized CP. J High Energy Phys. (2015) 2015:100. doi: 10.1007/JHEP05(2015)100

CrossRef Full Text | Google Scholar

131. Ballett P, Pascoli S, Turner J. Mixing angle and phase correlations from A5 with generalized CP and their prospects for discovery. Phys Rev. (2015) D92:093008. doi: 10.1103/PhysRevD.92.093008

CrossRef Full Text | Google Scholar

132. Turner J. Predictions for leptonic mixing angle correlations and nontrivial Dirac CP violation from A₅ with generalized CP symmetry. Phys Rev. (2015) D92:116007. doi: 10.1103/PhysRevD.92.116007

CrossRef Full Text | Google Scholar

133. de Medeiros Varzielas I, Emmanuel-Costa D. Geometrical CP violation. Phys Rev. (2011) D84:117901. doi: 10.1103/PhysRevD.84.117901

CrossRef Full Text | Google Scholar

134. Bhattacharyya G, de Medeiros Varzielas I, Leser P. A common origin of fermion mixing and geometrical CP violation, and its test through Higgs physics at the LHC. Phys Rev Lett. (2012) 109:241603. doi: 10.1103/PhysRevLett.109.241603

PubMed Abstract | CrossRef Full Text | Google Scholar

135. Ma E Neutrino mixing geometric CP. violation with delta(27) symmetry. Phys Lett. (2013) B723:161–3. doi: 10.1016/j.physletb.2013.05.011

CrossRef Full Text | Google Scholar

136. Hagedorn C, Meroni A, Molinaro E. Lepton mixing from Δ(3n²) and Δ(6n²) and CP. Nucl Phys. (2015) B891:499–557. doi: 10.1016/j.nuclphysb.2014.12.013

CrossRef Full Text | Google Scholar

137. Ding GJ, King SF. Generalized CP and Δ(3n²) family symmetry for semi-direct predictions of the PMNS matrix. Phys Rev. (2016) D93:025013. doi: 10.1103/PhysRevD.93.025013

CrossRef Full Text | Google Scholar

138. Altarelli G, Feruglio F, Masina I, Merlo L. Repressing anarchy in neutrino mass textures. J High Energy Phys. (2012) 11:139. doi: 10.1007/JHEP11(2012)139

CrossRef Full Text | Google Scholar

139. Bergstrom J, Meloni D, Merlo L. Bayesian comparison of U(1) lepton flavor models. Phys Rev. (2014) D89:093021. doi: 10.1103/PhysRevD.89.093021

CrossRef Full Text | Google Scholar

140. Hall LJ, Murayama H, Weiner N. Neutrino mass anarchy. Phys Rev Lett. (2000) 84:2572–5. doi: 10.1103/PhysRevLett.84.2572

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Haba N, Murayama H. Anarchy and hierarchy. Phys Rev. (2001) D63:053010. doi: 10.1103/PhysRevD.63.053010

CrossRef Full Text | Google Scholar

142. de Gouvea A, Murayama H. Statistical test of anarchy. Phys Lett. (2003) B573:94–100. doi: 10.1016/j.physletb.2003.08.045

CrossRef Full Text | Google Scholar

143. Petcov ST. On pseudodirac neutrinos, neutrino oscillations and neutrinoless double beta decay. Phys Lett. (1982) 110B:245–9. doi: 10.1016/0370-2693(82)91246-1

CrossRef Full Text | Google Scholar

144. Altarelli G, Franceschini R. Neutrino masses with inverse hierarchy from broken L(e) - L(mu) - L(tau): a reappraisal. J High Energy Phys. (2006) 03:047. doi: 10.1088/1126-6708/2006/03/047

CrossRef Full Text | Google Scholar

145. Meloni D. Large θ₁₃ from a model with broken L_e−L_μ−L_τ symmetry. J High Energy Phys. (2012) 02:090. doi: 10.1007/JHEP02(2012)090

CrossRef Full Text | Google Scholar

146. Lavoura L, Grimus W Seesaw model with softly broken L(e) - L(muon) - L(tau). J High Energy Phys. (2000) 09:007. doi: 10.1088/1126-6708/2000/09/007

CrossRef Full Text | Google Scholar

147. Grimus W, Lavoura L. Softly broken lepton number L(e) - L(mu) - L(tau) with non-maximal solar neutrino mixing. J Phys. (2005) G31:683–92. doi: 10.1088/0954-3899/31/7/013

CrossRef Full Text | Google Scholar

148. Altarelli G, Machado PAN, Meloni D. On bimaximal neutrino mixing and GUT's. PoS (2015) CORFU2014:012. arXiv:1504.05514

Google Scholar

149. Meloni D. Bimaximal mixing and large theta13 in a SUSY SU(5) model based on S4. J High Energy Phys. (2011) 10:010. doi: 10.1007/JHEP10(2011)010

CrossRef Full Text

150. Altarelli G, Feruglio F, Hagedorn C. A SUSY SU(5) grand unified model of tri-bimaximal mixing from A₄. J High Energy Phys. (2008) 03:052. doi: 10.1088/1126-6708/2008/03/052

CrossRef Full Text | Google Scholar

151. Kawamura Y. Triplet doublet splitting, proton stability and extra dimension. Prog Theor Phys. (2001) 105:999–1006. doi: 10.1143/PTP.105.999

CrossRef Full Text | Google Scholar

152. Hall LJ, Nomura Y. A Complete theory of grand unification in five-dimensions. Phys Rev. (2002) D66:075004. doi: 10.1103/PhysRevD.66.075004

CrossRef Full Text | Google Scholar

153. Antusch S, King SF, Spinrath M. Measurable neutrino mass scale in A₄× SU(5). Phys Rev. (2011) D83:013005. doi: 10.1103/PhysRevD.83.013005

CrossRef Full Text | Google Scholar

154. Antusch S, King SF, Spinrath M. Spontaneous CP violation in A₄×SU(5) with constrained sequential dominance 2. Phys Rev. (2013) D87:096018. doi: 10.1103/PhysRevD.87.096018

CrossRef Full Text | Google Scholar

155. Chankowski PH, Pokorski S. Quantum corrections to neutrino masses and mixing angles. Int J Mod Phys. (2002) A17:575–614. doi: 10.1142/S0217751X02006109

CrossRef Full Text | Google Scholar

156. Kuo TK, Pantaleone JT, Wu GH. Renormalization of the neutrino mass matrix. Phys Lett. (2001) B518:101–8. doi: 10.1016/S0370-2693(01)01032-2

CrossRef Full Text | Google Scholar

157. Antusch S, Kersten J, Lindner M, Ratz M. Running neutrino masses, mixings and CP phases: analytical results and phenomenological consequences. Nucl Phys. (2003) B674:401–33. doi: 10.1016/j.nuclphysb.2003.09.050

CrossRef Full Text | Google Scholar

158. Antusch S, Kersten J, Lindner M, Ratz M, Schmidt MA. Running neutrino mass parameters in see-saw scenarios. J High Energy Phys. (2005) 2005:024. doi: 10.1088/1126-6708/2005/03/024

CrossRef Full Text | Google Scholar

159. Hagedorn C, King SF, Luhn C. SUSY S₄× SU(5) revisited. Phys Lett. (2012) B717:207–13. doi: 10.1016/j.physletb.2012.09.026

CrossRef Full Text | Google Scholar

160. Cooper IK, King SF, Luhn C. A4xSU(5) SUSY GUT of flavour with trimaximal neutrino mixing. J High Energy Phys. (2012) 2012:130. doi: 10.1007/JHEP06(2012)130

CrossRef Full Text | Google Scholar

161. Marzocca D, Petcov ST, Romanino A, Spinrath M. Sizeable θ₁₃ from the charged lepton sector in SU(5), (Tri-)bimaximal neutrino mixing and dirac CP violation. J High Energy Phys. (2011) 2011:009. doi: 10.1007/JHEP11(2011)009

CrossRef Full Text | Google Scholar

162. Antusch S, Gross C, Maurer V, Sluka C. A flavour GUT model with ${\theta }_{13}^{PMNS}\simeq {\theta }_C/\sqrt{2}$. Nucl Phys. (2013) B877:772–91. doi: 10.1016/j.nuclphysb.2013.11.003

CrossRef Full Text | Google Scholar

163. Antusch S, Gross C, Maurer V, Sluka C. Inverse neutrino mass hierarchy in a flavour GUT model. Nucl Phys. (2014) B879:19–36. doi: 10.1016/j.nuclphysb.2013.11.017

CrossRef Full Text | Google Scholar

164. Björkeroth F, de Anda FJ, de Medeiros Varzielas I, King SF. Towards a complete A₄× SU(5) SUSY GUT. J High Energy Phys. (2015) 2015:141. doi: 10.1007/JHEP06(2015)141

CrossRef Full Text

165. Antusch S, Hohl C. Predictions from a flavour GUT model combined with a SUSY breaking sector. (2017). arXiv: 1706.04274 [hep-ph].

Google Scholar

166. Gehrlein J, Oppermann JP, Schäfer D, Spinrath M. An SU(5) × A₅ golden ratio flavour model. Nucl Phys. (2014) B890:539–68. doi: 10.1016/j.nuclphysb.2014.11.023

CrossRef Full Text | Google Scholar

167. Meroni A, Petcov ST, Spinrath M. A SUSY SU(5)xT' unified model of flavour with large θ₁₃. Phys Rev. (2012) D86:113003. doi: 10.1103/PhysRevD.86.113003

CrossRef Full Text | Google Scholar

168. Altarelli G, Blankenburg G. Different SO(10) paths to fermion masses and mixings. J High Energy Phys. (2011) 2015:133. doi: 10.1007/JHEP03(2011)133

CrossRef Full Text | Google Scholar

169. Joshipura AS, Kodrani BP, Patel KM. Fermion masses and mixings in a mu-tau symmetric SO(10). Phys Rev. (2009) D79:115017. doi: 10.1103/PhysRevD.79.115017

CrossRef Full Text | Google Scholar

170. Grimus W, Kuhbock H. A renormalizable SO(10) GUT scenario with spontaneous CP violation. Eur Phys J. (2007) C51:721–9. doi: 10.1140/epjc/s10052-007-0324-5

CrossRef Full Text | Google Scholar

171. Dermisek R, Raby S. Bi-large neutrino mixing and CP violation in an SO(10) SUSY GUT for fermion masses. Phys Lett. (2005) B622:327–38. doi: 10.1016/j.physletb.2005.07.018

CrossRef Full Text | Google Scholar

172. Dermisek R, Harada M, Raby S. SO(10) SUSY GUT for fermion masses: lepton flavor and CP violation. Phys Rev. (2006) D74:035011. doi: 10.1103/PhysRevD.74.035011

CrossRef Full Text | Google Scholar

173. Albright CH, Barr SM. Construction of a minimal Higgs SO(10) SUSY GUT model. Phys Rev. (2000) D62:093008. doi: 10.1103/PhysRevD.62.093008

CrossRef Full Text

174. Albright CH, Barr SM. Realization of the large mixing angle solar neutrino solution in an SO(10) supersymmetric grand unified model. Phys Rev. (2001) D64:073010. doi: 10.1103/PhysRevD.64.073010

CrossRef Full Text | Google Scholar

175. Ji Xd, Li Yc, Mohapatra RN. An SO(10) GUT model with lopsided mass matrix and neutrino mixing angle θ₁₃. Phys Lett. (2006) B633:755–60. doi: 10.1016/j.physletb.2006.01.005

CrossRef Full Text | Google Scholar

176. Björkeroth F, de Anda FJ, King SF, Perdomo E. A natural S₄×SO(10) model of flavour. (2017). arXiv: 1705.01555 [hep-ph].

177. Björkeroth F, de Anda FJ, de Medeiros Varzielas I, King SF. Towards a complete Δ(27) × SO(10) SUSY GUT. Phys Rev. (2016) D94:016006. doi: 10.1103/PhysRevD.94.016006

CrossRef Full Text | Google Scholar

178. Björkeroth F, de Anda FJ, de Medeiros Varzielas I, King SF. Leptogenesis in a Δ(27) × SO(10) SUSY GUT. J High Energy Phys. (2017) 2017:077. doi: 10.1007/JHEP01(2017)077

CrossRef Full Text | Google Scholar

179. de Adelhart Toorop R, Bazzocchi F, Merlo L. The interplay between GUT and flavour symmetries in a pati-salam x S4 model. J High Energy Phys. (2010) 2010:001. doi: 10.1007/JHEP08(2010)001

CrossRef Full Text

180. King SF. A model of quark and lepton mixing. J High Energy Phys. (2014) 2014:119. doi: 10.1007/JHEP01(2014)119

CrossRef Full Text | Google Scholar

181. King SF. A to Z of flavour with pati-salam. J High Energy Phys. (2014) 2014:130. doi: 10.1007/JHEP08(2014)130

CrossRef Full Text | Google Scholar

182. King SF, Malinsky M. Towards a complete theory of fermion masses and mixings with SO(3) family symmetry and 5-D SO(10) unification. J High Energy Phys. (2006) 2006:071. doi: 10.1088/1126-6708/2006/11/071

CrossRef Full Text | Google Scholar

183. Adamson P, Aliaga L, Ambrose D, Anfimov N, Antoshkin A, Arrieta-Diaz E, et al. Constraints on oscillation parameters from ν_e appearance and ν_μ disappearance in NOvA. Phys Rev Lett. (2017) 118:231801. doi: 10.1103/PhysRevLett.118.231801

CrossRef Full Text | Google Scholar

184. Abe K, Amey J, Andreopoulos C, Antonova M, Aoki S, Ariga A, et al. Combined analysis of neutrino and antineutrino oscillations at T2K. Phys Rev Lett. (2017) 118:151801. doi: 10.1103/PhysRevLett.118.151801

PubMed Abstract | CrossRef Full Text | Google Scholar

185. Acciarri R, Acero MA, Adamowski M, Adams C, Adamson P, Adhikari S, et al. Long-baseline neutrino facility (LBNF) and deep underground neutrino experiment (DUNE). (2016). arXiv:1601.05471

Google Scholar

186. Djurcic Z, Guarino V, Cabrera A, Cabrera H, Kerret C, Guo X, et al. JUNO conceptual design report. (2015). arXiv: 1508.07166 [physics.ins-det].

Google Scholar