- 1Dipartimento di Fisica dell'Università di Pisa, Pisa, Italy
- 2INFN, Pisa, Italy
- 3CP3-Origins and Danish IAS, University of Southern Denmark, Odense, Denmark
- 4CERN, Theory Division, Geneva, Switzerland
We extend the list of theories featuring a rigorous interacting ultraviolet fixed point by constructing the first theory featuring a Higgs-like scalar with gauge, Yukawa and quartic interactions. We show that the theory enters a perturbative asymptotically safe regime at energies above a physical scale Λ. We determine the salient properties of the theory and use it as a concrete example to test whether scalars masses unavoidably receive quantum correction of order Λ. Having at our dispose a calculable model allowing us to precisely relate the IR and UV of the theory we demonstrate that the scalars can be lighter than Λ. Although we do not have an answer to whether the Standard Model hypercharge coupling growth toward a Landau pole at around Λ ~ 1040GeV can be tamed by non-perturbative asymptotic safety, our results indicate that such a possibility is worth exploring. In fact, if successful, it might also offer an explanation for the unbearable lightness of the Higgs.
1. Introduction
The Large Hadron Collider (LHC) data at confirm the Standard Model (SM) and give strong bounds on supersymmetry, on composite Higgs and on other SM extensions that were put forward to tame the quadratically divergent corrections to the Higgs mass in a natural way. The existence of natural solutions apparently ignored by nature challenges even anthropic approaches. This unsettling situation calls for reconsidering the issue of naturalness.
The bulk of the physical corrections to the SM observables are only logarithmically sensitive to a potential UV physical scale because they stem from marginal operators. Physical corrections to the Higgs mass are small in the SM, and can remain small once it is extended to account for dark matter, neutrino masses [1], gravity, and inflation [2]. This is true up to possible power-divergent corrections that may offset the lightness of the Higgs. As well-known, the Higgs propagator Π(q2) at zero momentum q = 0 receives a quadratically divergent correction, which is often interpreted as a large correction to the Higgs mass. Writing only the top Yukawa one-loop contribution, one has
The photon too receives at zero momentum a quadratically divergent correction. In QED one has
This is not interpreted as a large photon mass because it is presumed that some unknown physical cut-off regulates divergences while respecting gauge invariance, that forces the photon to be massless. Similarly, the graviton propagator receives a quadratically divergent correction Πμν, ρσ(0): in part it can be interpreted as a cosmological constant, in part it breaks reparametrization invariance.
The fate of the Higgs mass is not clear. Some regulators (such as dimensional regularization) respect all these symmetries and get rid of all power divergences, including the one that affects the Higgs mass. Other regulators (such as Pauli-Villars and presumably string theory) do not generate a photon mass nor a graviton mass and generate a large Higgs mass, given that it is only protected by scale invariance, which is not a symmetry of the full theory.
One possibility is that the SM is (part of) a theory valid up to infinite energy, such that no physical cut-off exists. Then, once that Equation (2) is interpreted to mean zero, the same divergence in Equation (1) must be interpreted in the same way. Furthermore, in a theory with dimension-less parameters only, one can argue that ∫d4k/k2 = 0 by dimensional analysis. Gravity itself could be described by small dimension-less parameters [2–4], such that it makes sense to extrapolate the SM RGE above the Planck scale.
In this context, one possibility is devising realistic weak-scale extensions of the SM such that all gauge, Yukawa, and quartic couplings flow to zero at infinite energy [3, 4]. However hypercharge must be embedded into a large non-abelian group, in order to be asymptotically free: naturalness then demands new vectors at the weak scale, which have not been observed so far.
The other possibility is that the SM itself might be asymptotically safe. The hypercharge gauge coupling gY becomes non-perturbative at Λ ~ 1040GeV, hitting a “Landau pole.” It is not known what it means. It might mean that the SM is not a complete theory and new physics is needed at lower energy. Otherwise gY and other couplings might run up to constant non-perturbative values as illustrated in Figure 1, such that the SM enters into an asymptotically safe phase. In fact, this possibility was envisioned very early on in the literature [5, 6] triggering lattice studies [7–9] as well as non-perturbative analytic studies such as the one of Gies and Jaeckel [10]. It is fair to say, however, that the fate of the SM depends on non-perturbative effects which are presently unknown; see [11–17] for attempts to compute the non-perturbative region and for related ideas.
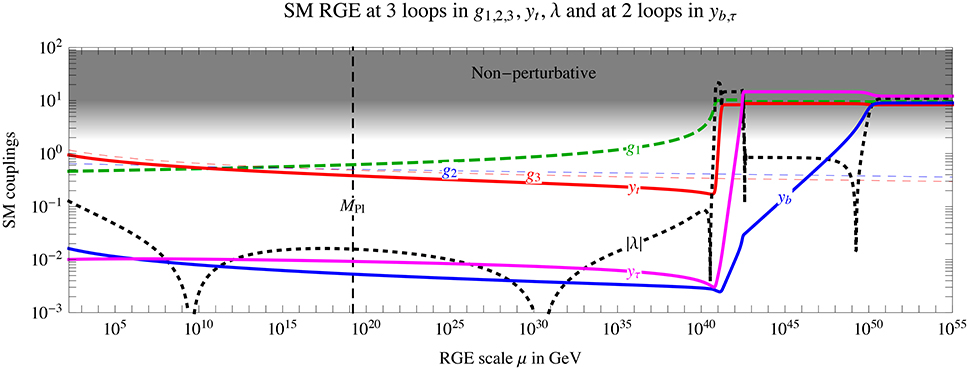
Figure 1. Illustration of a possible RGE running in the SM. We assumed central values for all parameters, and solved the 3 loop RGE equations. In order to obtain an asymptotically safe behavior we artificially removed the bottom and tau Yukawa contributions to the 3-loop term in the RGE. This only affects the running in the non-perturbative region above 1040GeV, where the result cannot of course be trusted. Furthermore, we ignored the Yukawa couplings of the lighter generations, and gravity.
Tavares, Schmaltz and Skiba [18] proposed an alleged no-go argument, according to which Landau makes Higgs obese: i.e., scalars generally receive a mass correction of the order of the would-be-Landau pole scale Λ. In the SM case, this would mean that, whatever happens at 1040GeV, the Higgs mass receives a contribution of order 1040GeV, so that an asymptotically safe Higgs (where asymptotic safety kicks above Λ) cannot be natural.
Later, Litim and Sannino (LS) [19] presented the first four-dimensional example of a perturbative quantum field theory where all couplings that are small at low energy flow to a constant value at higher energy persisting up to infinite energy. This model involves a gauge group SU(Nc) with large Nc, a neutral scalar S and vector-like charged fermions, with asymptotically safe Yukawa couplings and scalar quartics. The model realizes Total Asymptotic Safety (TAS). Another equally relevant property of the model is that without the scalar it cannot be perturbatively safe [19, 20]. Scalars are required to dynamically render the theory fundamental at all scales without invoking supersymmetry, which would keep scalars massless independently of their dynamics.1 In fact supersymmetry makes it harder to realize an asymptotically safe scenario [28, 29] both perturbatively and non-perturbatively. Furthermore, the LS model, on the line of physics, connects two fixed points, a non-interacting infrared free one (the theory at low energy is non-abelian QED-like) to an interacting ultraviolet fixed point. Remarkably the model shares the SM backbone since it features gauge, fermion and needed scalar degrees of freedom, albeit it still misses a gauged Higgs-like state. We therefore extend the LS model in section 2 to further feature a Higgs-like charged scalar H. We rigorously demonstrate that the theory enters a perturbative asymptotically safe regime at energies above a physical scale Λ. We also show that we can determine the RGE flow linking ultraviolet and infrared physics precisely.
In the Appendix (Supplementary Material) we explore theories featuring chiral fermions and show that it is possible to achieve asymptotic safety for the gauge and Yukawa couplings while safety for scalar couplings is challenging.
Having at our disposal a calculable model similar to the SM, we carefully re-consider the naturalness issue in this class of theories in order to offer an answer to the question: Does the Higgs-like scalar H acquire a mass of the order of the scale Λ? In section 3 we do not find any such contribution, de facto, re-opening the issue. We discuss possible caveats and offer our conclusions in section 4.
2. Asymptotically Safe Models with an Higgs-Like Scalar
Litim and Sannino considered a model with gauge group SU(Nc) and gauge coupling g; NF vector-like fermions in the fundamental plus anti-fundamental, and neutral scalars Sij with Yukawa couplings . The number of flavors NF can be fixed to make the one-loop gauge beta function small. Large Nc, NF allows to make arbitrarily small, guaranteeing perturbative control. The new key feature with respect to the analogous construction by Banks and Zaks [30] is that the Yukawa couplings can (non-trivially) make the two-loop gauge beta function negative2, such that, together with , g enters into a perturbative fixed point at large energy. Finally, one verifies that Yukawa couplings and scalar quartics too have a perturbative fixed point. The model satisfies Total Asymptotic Safety (TAS).
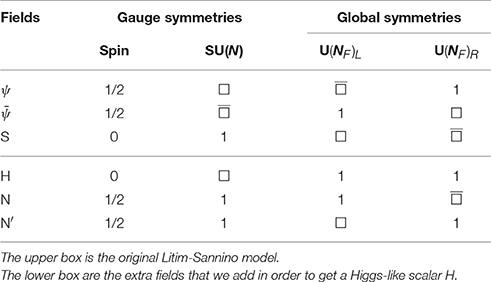
In general the equations βg = βy = βλ = 0 have multiple solutions, that correspond to different global symmetries of the theory. The analysis can be simplified focusing on the maximal global symmetry, U(NF)L ⊗ U(NF)R, which can be realized with complex scalars S. The field content is then summarized by the upper box of Table 1.
The lower box of Table 1 shows the fields that we add: one Higgs-like scalar charged under the gauge group. Its introduction does not affect, in the limit of large Nc, NF, the fixed point for y and g found in Litim and Sannino [19]. We also add singlet fermions Ni, (see Table 1 for the details) in order to allow H to have Yukawa couplings, like the SM Higgs. The allowed Yukawa couplings then are
The scalar potential is
and it is positive if
where η = Tr(S†SS†S)/Tr2(S†S) ranges between η = 1 and η = 1/NF. The bounds in Equation (5) need only to be imposed at the extremal values.
2.1. RGE and Their Fixed Points
Defining the β-functions coefficients as
the relevant RGE are
Notice that yy′ỹ*ỹ′* is left invariant by redefinitions of the phases of all fields, so the model admits one CP-violating phase. Nevertheless, CP is conserved at all fixed points, so that the RGE can be written in terms of real couplings. For simplicity we therefore assume all couplings to be real.
The one-loop gauge beta function can be rewritten as
can be made arbitrarily small in the limit of large Nc, NF. In this limit reduces to
and it vanishes for y2/g2 ≃ 6/13, which corresponds to a negative
Thereby, the gauge coupling has an IR-attractive fixed point g = 0 and a non-trivial UV-attractive fixed point at
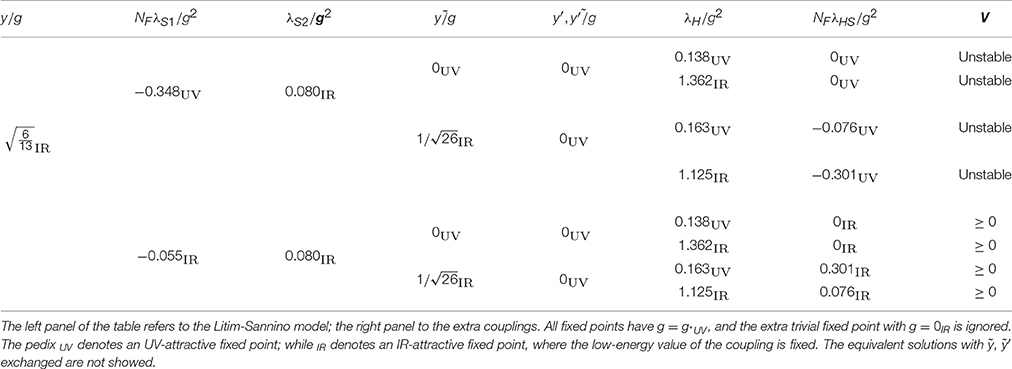
The scalar quartics λS1, λS2 admit two fixed points. At leading order in ϵ:
The solution with the + (−) sign corresponds to a stable (unstable) potential V(S) as determined in Litim et al. [32]. At the stable solution, the fixed point for both quartics, as well as the fixed point for y, are IR-attractive: this means that their low-energy values are univocally fixed, with respect to g, along the RGE trajectory that reaches infinite energy.
So far the new fields that we added just acted as spectators. We must check that they have their own fixed points. By studying the full equations we find that the extra Yukawa couplings y′, ỹ and ỹ′ have 3 inequivalent fixed points. The fixed points with y′ = ỹ′ = 0 lead to fixed points for the quartics, as listed in Table 2. The full potential V(S, H) is stable when V(S) is stable.
All these couplings are perturbative for ϵ ≪ 1, in the sense that higher order corrections are suppressed by powers of ϵ. An explicit solution to the RGE equations is obtained by assuming that all ratios y/g, λ/g2 run remaining constant up to corrections of relative order ϵ. Then one obtains an RGE equation for g
Its solution is
which can be used to define in an RGE-invariant way the transmutation scale Λ in terms of μ and of g(μ). In the limit where the second two-loop term is neglected, Λ becomes the Landau pole scale of one-loop RGE. Imposing the boundary condition g(μ0) = g0 the solution becomes [19]
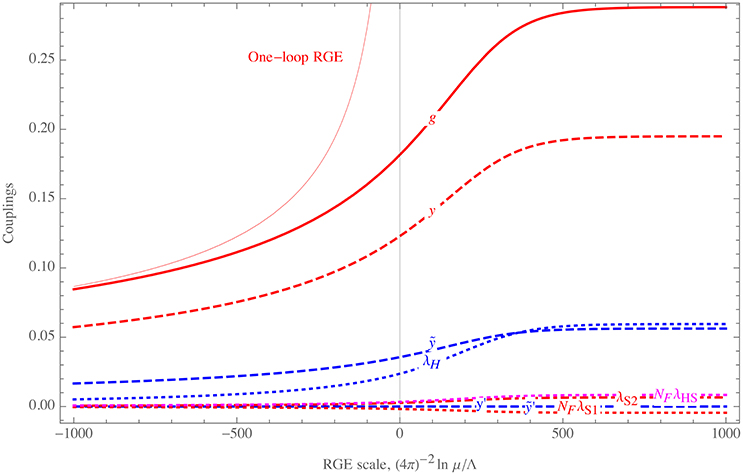
where W(z) is the Lambert function defined by z = WeW. The fixed point g = g* is UV-attractive: this means that g can become smaller at low energy. Figure 2 illustrates a typical RGE running.
3. On the Lightness of Safe Scalars
We now investigate whether scalars can be lighter than the characteristic energy scale Λ where the RG flow displays a cross-over from the Gaussian IR scaling to the UV interacting scaling. This scale is dynamical in nature and arises via dimensional transmutation. Above this scale the theory remains finite at arbitrary short distances avoiding the Landau pole. The precise definition and way to determine this scale is presented in Litim et al. [32].
The authors of Marques Tavares et al. [18] argued that scalars acquire masses of order Λ by elevating a one-loop computation of the top corrections for the SM Higgs to an operatorial one in an alleged theory featuring an asymptotically safe behavior. Their rough analysis used: dimensional analysis, modeling the underlying behavior of the couplings and ad-hoc subtractions to render the result finite. Henceforth according to their result the asymptotically safe Higgs scenario would remain unnatural.
Differently from Marques Tavares et al. [18] we have the precisely calculable model of section 2, containing a scalar H analogous to the Higgs doublet in the SM, with gauge, Yukawa and quartic interactions, that run into a perturbative ultraviolet fixed point as illustrated in Figure 2. Furthermore, the theory connects to a Gaussian IR fixed point. We set all masses to zero, making the classical theory scale invariant, and we determine whether quantum corrections make scalars massive. We perform our computations in such a way that both IR and UV quantum conformality are preserved.
3.1. Perturbative Effects
We start by considering the quantum corrections affecting scalar masses that stem from the standard perturbative approach of summing Feynman diagrams. We therefore fix the renormalization scale at an arbitrary value μ0, and compute the scalar two-point function Π(0). At any loop order, each diagram is proportional to powers of dimension-less coupling constants renormalized at μ0 times a loop integral which is scale-invariant and quadratically divergent at large loop momenta. To ensure short and large distance quantum conformality these divergences are set to zero. As well-known, scale-invariant loop integrals vanish automatically in dimensional regularization.
3.2. Resumming Large Logarithms, Λ Dependence and Meaning
One might be worried that a mere perturbative analysis is insufficient to settle the issue. So, we now comment on potentially different non-perturbative corrections.
A relevant class of dominant non-perturbative corrections are those where couplings get enhanced by large logarithms. At one loop one encounters corrections of relative order Cℓ where and ℓ = ln (E/μ0). The correction Cℓ becomes of order one at energy E much different from μ0. At two loops one encounters corrections of order C2 ℓ2 and C2ℓ.
As well-known, all corrections of order (Cℓ)n can be resummed by solving the one-loop RGE equations; all corrections of order Cn ℓ n−1 are resummed by solving the two-loop RGE equations, and so on. The RGE equations know that Λ is a special scale. In order to compute whether scalar masses receive corrections of order Λ, we must compute and solve the RGE equations for massive parameters. The RGE for squared scalar masses have the following generic form, dictated by dimensional analysis:
The right-handed side in general contains scalar masses, fermion masses and cubic scalar couplings. Without explicit computations it is clear that, if we set all masses to zero at any scale μ0 (for example a scale much above Λ), all masses will remain zero at any other scale μ (for example a scale much below Λ). No scalar mass of order Λ is generated trough RGE evolution when the Λ threshold is crossed.
In fact the RG-invariant scale Λ appears when solving for the RG equations. In models with a single scalar squared mass one has:
with
Here is the quantum dimension of the mass operator. The non-trivial Λ dependence is automatically encoded in the running of the various couplings entering in the above expression. While Λ-dependent, the renormalization of m2 is multiplicative: the additive renormalization of order Λ2 claimed in [18] is absent. This shows that these type of corrections do not introduce an explicit mass-term for the scalars despite the presence of an RG-invariant Λ. In addition, according to our interpretation of the scale Λ no special scheme is privileged.
The ratio m/Λ allows to measure deviations from IR quantum conformality when making the arbitrary choice of the bare mass of the scalar, or any other physical scale. Near IR quantum conformality can, in fact, be naturally ensured in the present framework requiring m ≪ Λ for any μ < Λ. In other words we use Λ as the RG-invariant meter to compare scales.
In order to make the discussion more explicit, we consider the model of section 2 and determine the RGE for the mass term operators that would explicitly break scale symmetry (fermion masses still vanish because of the chiral symmetry). Their one-loop RGE are:
The couplings evolve satisfying g2 ∝ y2 ∝ λ to leading order in ϵ along the UV-attractive asymptotically-safe trajectory connecting the theory to the IR Gaussian fixed point. So the RGE for the masses reduce to independent equations for appropriate linear combinations of the squared masses. Neglecting sub-leading terms in the limit of large Nc, NF the RGE for depends only on itself:
Equation (21) can be integrated analytically, giving
Considering the fixed point with ỹ, λHS ≠ 0, and defining the numerical constants and listed in Table 2, Equation (19) can also be integrated and gives
The factor w can be explicitly written as ratios of Lambert functions using Equation (15), and at ultra-high energies μ, μ0 ≫ Λ it reduces to w ≃ μ/μ0. The solutions to the RGE in this limit can be easily obtained substituting constant couplings in Equations (19) and (20). These expressions say that the various massive parameters mi acquire dimension 1 + (ϵ) at energies above Λ. Our results recover the fact that a massive scalar contributes to the mass of other scalars coupled to it. The physical ratios between different masses in general run by an infinite amount up to infinite energy: this can be seen as a motivation for considering theories where all masses vanish, being generated only at low energy trough dynamical generation of vacuum expectation values or condensates. However, it does not mean that masses receive power-divergent corrections: no mass is generated trough RGE running, if masses vanish at some scale.
3.3. Non-Perturbative Contributions
Finally, we discuss now truly non-perturbative effects, which could give corrections of order Λ2e−1/C. In the model of section 2 the couplings C can be chosen to be arbitrarily small, such that non-perturbative effects, even if present, are exponentially suppressed. In this model there are no new bound states with masses of order Λ, no condensates of order Λ, no new non-perturbative phenomena: The RG invariant scale Λ merely determines the boundary between the IR and the UV regime.
In order to make the discussion more concrete, we discuss two special cases of non-perturbative phenomena.
First, if the fixed point is not fully IR-attractive the quartics could run to low-energy values that violated the positivity condition of the potential, cross the boundary in Equation (5) at a scale μ ~ M exponentially smaller than Λ. If this happens, scalars acquire vacuum expectation values and masses order M trough the Coleman-Weinberg mechanism. Indeed various works proposed extensions of the Standard Model where the weak scale is generated in this way.
Next, we notice that the running of the SM Higgs quartic λH in Figure 1 exhibits a similar, but more complex pattern: there is a 2−3σ hint that λH runs negative between and , see Figure 1. As well-known, this implies a vacuum decay rate suppressed by the non-perturbative factor e−S, where is the action of the Fubini bounce . Here r2 = x2 + y2 + z2 − t2 and E is a free parameter with dimension of mass, that arises because of classical scale invariance. The non-perturbative Fubini bounce also leads to a non-perturbative correction to the Higgs mass of order
Such non-perturbative correction to the Higgs mass is negligibly small, given that vacuum decay is negligibly slow comparte to cosmological time-scale, namely where H0 is the Hubble rate.
We conclude this section by asserting that in an asymptotically safe theory featuring Higgs-like states no masses are generated along the trajectory connecting the IR Gaussian fixed point dynamics to the interacting UV safe one. The intrinsic and calculable RG invariant scale Λ merely determines the boundary between the IR and UV conformal regimes. Furthermore, at this scale no new fundamental degrees of freedom are generated. This is so since the underlying theory is described by the same fundamental degrees of freedom along the entire RG flow3. When introducing explicit conformal symmetry breaking operators such as the Higgs mass term the scale Λ allows us to ensure that deviations from the IR quantum conformal behavior are minimal so that the physical mass m≪Λ for any μ < Λ. This can be naturally achieved in any UV and IR conformal preserving renormalization scheme.
Our results show that the claim that asymptotically safe scalars are never naturally light [18] maximally violates quantum IR (near) conformality by, de facto, elevating the RG invariant scale Λ to the mass scale of the Higgs.
4. Conclusions
In section 2 we extended the Litim-Sannino [19] theory to further contain a Higgs-like scalar H charged under the gauge group and with further Yukawa and quartic interactions. We showed that all couplings are governed by an IR Gaussian fixed point at low energies, and grow at short distance until a scale Λ. Above this scale the couplings enter into a rigorous asymptotically safe regime up to infinite energy, thereby avoiding Landau poles as illustrated in Figure 2.
In Appendix (Supplementary Material) we attempted to make the model more SM-like by adding chiral fermions. Although we succeeded in making the gauge and the Yukawa couplings asymptotically safe we were unable to render the quartic couplings safe as well. Our analysis, however, does not exclude the possibility of building a SM-like chiral theory that is fully asymptotically safe.
In section 3 we investigated the perturbative and non-perturbative quantum corrections to the scalar mass operator. To better elucidate our main points, we determined these corrections for the calculable model of section 2, serving as SM template. We showed that no scalar masses of order of the Renormalization Group (RG) invariant scale Λ are generated along the entire RG trajectory connecting the IR Gaussian fixed point to the UV interacting fixed point. In other words, section 3 shows that, if scalar masses are absent, no scalar masses are generated. If the scalar mass operator is added to the theory, the scalar masses receive the multiplicative RGE corrections of Equation (17) that have been computed in section 3.2 for the explicit model constructed here. These yield a non-trivial and non-quadratic Λ dependence arising solely from the dynamics. The mass of Higgs-like scalars can be naturally small relative to the scale Λ that acts, in this respect, merely as a comparison scale. Our results do not validate the claims made in Marques et al. [18] that, in practice by the use of ad-hoc regularization schemes, elevated the scale Λ to the mass of the Higgs, maximally violating, at least the low energy (near) conformality of the theory. It is worth stressing that, differently from the naive estimates of Marques Tavares et al. [18], never in our computations we had to resort to ad-hoc assumptions or expansions around one of the two fixed points since we can rigorously solve for the flow connecting the IR and UV, including the determination of the non-trivial anomalous dimensions. Our results naturally capture the correct power-law behavior when approaching the UV interacting fixed point as already explained in sections F, G of Litim and Sannino [19].
Our interest further resides in using these computable models to motivate new avenues for the SM near the scale Λ~ 1040GeV, where the hypercharge coupling gY nears its Landau pole. To this end a case-by-case investigation is needed. In particular a phenomenologically viable application to the SM case would deserve a proper dedicated study to firmly establish what happens near the hypercharge Landau pole. Do couplings enter into an asymptotically safe regime, as illustrated in Figure 2? If yes, would the Higgs mass remain naturally small, or non-perturbative dynamics generate condensates of order Λ that affect the Higgs mass? Our explicit example demonstrates that such a possibility is worth exploring.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the grant 669668 – NEO-NAT – ERC-AdG-2014 and the Danish National Research Foundation under the grant DNRF:90. We thank Ara Ioannisian for useful discussions. Martin Schmaltz is thanked for discussions and clarifications of his work during the 2016 CERN workshop Charting the Unknown.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fphy.2017.00049/full#supplementary-material
Footnotes
1. ^It is important to note that scalars without the simultaneous presence of gauge and fermion interactions, are not ultraviolet safe as a large body of analytic and first principle lattice results has demonstrated [21–27].
2. ^It was indeed shown for the first time in Antipin et al. [31], Litim and Sannino [19] and Litim et al. [32] that Yukawa interactions are instrumental, in perturbation theory, to tame the UV behavior of non-asymptotically free gauge theories. In fact without scalars gauge-fermion theories, in perturbation theory, are doomed to remain at best effective field theories [19, 20]. These conditions were further elaborated in Bond and Litim [33] and in Antipin and Sannino [34] for chiral matter. Of course having a fixed point in the Yukawa and gauge coupling is not enough for the theory to be safe, and much more work is required to show that it is safe in all couplings. Beyond perturbation theory one can argue that at large number of matter flavors and finite number of colors one can achieve asymptotic safety as recently summarized and further elucidated in Antipin and Sannino [35]. Exact non-perturbative results have been established for supersymmetric field theories [28].
3. ^Our theory respects the a-theorem inequality Δa > 0 calculated between the UV and IR fixed point in the large Nc and Nf limit [36] and therefore the UV and IR CFTs are distinct, even though the underlying degrees of freedom remain the same along the RG flow.
References
1. Farina M, Pappadopulo D, Strumia A. A modified naturalness principle and its experimental tests. J High Energy Phys. (2013) 1308:022. doi: 10.1007/JHEP08(2013)022
3. Giudice GF, Isidori G, Salvio A, Strumia A. Softened gravity and the extension of the standard model up to infinite energy. J High Energy Phys. (2015) 1502:137. doi: 10.1007/JHEP02(2015)137
4. Pelaggi GM, Strumia A, Vignali S. Totally asymptotically free trinification. J High Energy Phys. (2015) 1508:130. arXiv:1507.06848
7. Gockeler M, Horsley R, Linke V, Rakow PEL, Schierholz G, Stuben H. Is there a Landau pole problem in QED? Phys Rev Lett. (1997) 80:4119. doi: 10.1103/PhysRevLett.80.4119
8. Kim S, Kogut JB, Lombardo MP. On the triviality of textbook quantum electrodynamics. Phys Lett. B502:345–9. doi: 10.1016/S0370-2693(01)00201-5
9. Kim S, Kogut JB, Lombardo MP. Gauged Nambu-Jona-Lasinio studies of the triviality of quantum electrodynamics. Phys Rev. (2001) D65:054015. doi: 10.1103/PhysRevD.65.054015
10. Gies H, Jaeckel J. Renormalization flow of QED. Phys Rev Lett. (2004) 93:110405. doi: 10.1103/PhysRevLett.93.110405
11. Bogoliubov NN, Logunov AA, Shirkov DV. The method of dispersion relations and perturbation theory. Sov Phys JETP (1960) 37:574.
12. Redmond PJ, Uretsky JL. Conjecture concerning the properties of nonrenormalizable field theories. Phys Rev Lett. (1958) 1:147. doi: 10.1103/PhysRevLett.1.147
13. Shirkov DV, Solovtsov IL. Analytic model for the QCD running coupling with universal αs(0) value. Phys Rev Lett. (1997) 79:1209–12. doi: 10.1103/PhysRevLett.79.1209
14. Suslov IM. Exact asymptotics for beta-function in QED. J Exp Theor Phys. (2008) 108:980–4. doi: 10.1134/S1063776109060089
15. Suslov IM. Renormalization group functions of the ϕ4 theory in the strong coupling limit: analytical results. J Exp Theor Phys. (2010) 107:413–29. doi: 10.1134/S1063776108090094.
17. 't, Hooft G. A class of elementary particle models without any adjustable real parameters. Found Phys. (2011) 41:1829. arXiv:1104.4543.
18. Marques Tavares G, Schmaltz M, Skiba W. Higgs mass naturalness and scale invariance in the UV. Phys Rev. (2014) D89:015009. doi: 10.1103/PhysRevD.89.015009
19. Litim DF, Sannino F. Asymptotic safety guaranteed. J High Energy Phys. (2014) 1412:178. doi: 10.1007/JHEP12(2014)178
20. Caswell WE. Asymptotic behavior of nonabelian gauge theories to two loop order. Phys Rev Lett. (1974) 33:244. doi: 10.1103/PhysRevLett.33.244
21. Aizenman M. Proof of the triviality of ϕ4 in D-dimensions field theory and some mean field features of ising models for D > 4. Phys Rev Lett. (1981) 47:1–4. doi: 10.1103/PhysRevLett.47.1
22. Frohlich J. On the triviality of lambda ϕ4 in D-dimensions theories and the approach to the critical point in D > 4 dimensions. Nucl Phys B (1982) 200:281–96. doi: 10.1016/0550-3213(82)90088-8
23. Luscher M, Weisz P. Scaling laws and triviality bounds in the lattice ϕ4 theory. 1. One component model in the symmetric phase. Nucl Phys B (1987) 290:25–60. doi: 10.1016/0550-3213(87)90177-5
24. Luscher M, Weisz P. Scaling Laws and Triviality Bounds in the Lattice ϕ4 Theory. 2. One component model in the phase with spontaneous symmetry breaking. Nucl Phys B (1988). 295:65.
25. Heller UM, Klomfass M, Neuberger H, Vranas PM. Regularization dependence of the Higgs mass triviality bound. Nucl Phys Proc Suppl. (1992) 30:685–9. doi: 10.1016/0920-5632(93)90302-M
26. Wolff U. Precision check on triviality of ϕ4 theory by a new simulation method. Phys Rev. (2009) D79:105002. doi: 10.1103/PhysRevD.79.105002
27. Korzec T, Wolff U. Triviality of in the broken phase revisited. PoS (2015) 2014:305. arXiv:1502.03714
28. Intriligator K, Sannino F. Supersymmetric asymptotic safety is not guaranteed. J High Energy Phys. (2015) 2015:23. doi: 10.1007/JHEP11(2015)023
29. Bajc B, Sannino F. Asymptotically safe grand unification. J High Energy Phys. (2016) 1612:141. doi: 10.1007/JHEP12(2016)141
30. Banks T, Zaks A. On the phase structure of vector-like gauge theories with massless fermions. Nucl Phys. (1982) B196:189–204. doi: 10.1016/0550-3213(82)90035-9
31. Antipin O, Gillioz M, Mlgaard E, Sannino F. The a theorem for gauge-Yukawa theories beyond Banks-Zaks fixed point. Phys Rev. (2013) D87:125017. doi: 10.1103/PhysRevD.87.125017
32. Litim DF, Mojaza M, Sannino F. Vacuum stability of asymptotically safe gauge-Yukawa theories. J High Energy Phys. (2016) 1601:081. doi: 10.1007/JHEP01(2016)081
33. Bond AD, Litim DF. Theorems for asymptotic safety of gauge theories. (2017). Eur Phys J. C77:429. doi: 10.1140/epjc/s10052-017-4976-5
34. Molgaard E, Sannino F. Asymptotically safe and free chiral theories with and without scalars. Phys Rev. (2017) D96:056004.
36. Sannino F. Plenary Talk Held for the ERG 2016 Meeting in Trieste. Available online at: http://indico.ictp.it/event/7608/session/3/contribution/10/material/slides/0.pdf
Keywords: asymptotic safety, beyond standard model physics, naturalness, QFT, fundamental interactions
Citation: Pelaggi GM, Sannino F, Strumia A and Vigiani E (2017) Naturalness of Asymptotically Safe Higgs. Front. Phys. 5:49. doi: 10.3389/fphy.2017.00049
Received: 05 May 2017; Accepted: 27 September 2017;
Published: 24 October 2017.
Edited by:
Stefano Moretti, University of Southampton, United KingdomReviewed by:
Frank Krauss, Durham University, United KingdomTetsuo Shindo, Kogakuin University, Japan
Copyright © 2017 Pelaggi, Sannino, Strumia and Vigiani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesco Sannino, c2Fubmlub0BjcDMtb3JpZ2lucy5uZXQ=
 Giulio M. Pelaggi1,2
Giulio M. Pelaggi1,2 Francesco Sannino
Francesco Sannino