- Institute for Theoretical Physics, Kanazawa University, Kanazawa, Japan
We discuss radiative seesaw models, in which an exact symmetry is imposed. Due to the exact symmetry, neutrino masses are generated at a two-loop level and at least two extra stable electrically neutral particles are predicted. We consider two models: one has a multi-component dark matter system and the other one has a dark radiation in addition to a dark matter. In the multi-component dark matter system, non-standard dark matter annihilation processes exist. We find that they play important roles in determining the relic abundance and also responsible for the monochromatic neutrino lines resulting from the dark matter annihilation process. In the model with the dark radiation, the structure of the Yukawa coupling is considerably constrained and gives an interesting relationship among cosmology, lepton flavor violating decay of the charged leptons and the decay of the inert Higgs bosons.
1. Introduction
Neutrino oscillation experiments show that the neutrinos have tiny masses and mix with each other. It is a clear evidence for physics beyond the standard model (SM), since the SM has no mechanism for giving masses to the neutrinos. The global fit [1] shows that the mass-squared differences of the neutrinos are eV2 and for normal (inverted) mass hierarchy. The cosmological data, on the other hand, gives the upper bound of the sum of the neutrino masses as Σjmνj < 0.23 eV [2], a scale twelve orders of magnitudes smaller than the electroweak scale. It is one of the most important problems of particle physics to reveal the origin of the tiny masses for the neutrinos.
Type-I seesaw mechanism [3–6] is one of the attractive way to realize the tiny masses of the neutrinos, where the right-handed neutrinos are introduced to the SM. If the neutrino Yukawa coupling for the Dirac neutrino mass is (1), the mass of the right-handed neutrino has to be around (1015) GeV to obtain eV-scale neutrinos. The mass scale of (1015) GeV is obviously beyond the reach of collider experiments. Even for the mass of the right-handed neutrinos around (1) TeV, the direct search of the right-handed neutrinos would be difficult because of the tiny neutrino Yukawa couplings of (10−6).
Another attractive way to give the neutrino masses is a radiative generation (the so-called radiative seesaw model). The original idea of radiatively generating neutrino masses due to TeV-scale physics has been proposed by Zee [7], in which the neutrino masses are induced at the one-loop level because of the addition of an isospin doublet scalar field and a charged singlet field to the SM. Another possibility for generating neutrino masses via the new scalar particles is e.g., the Zee-Babu model [8, 9], in which the neutrino masses arise at the two-loop level.
A further extension with a TeV-scale right-handed neutrino has been proposed in Krauss et al. [10]. In this model the neutrino masses are induced at the three-loop level, where the Dirac neutrino mass at the tree level is forbidden due to an exact Z2 symmetry. The right-handed neutrino is odd under the Z2 and becomes a candidate of dark matter (DM). The idea of simultaneous explanation for the neutrino masses via the radiative seesaw mechanism and the stability of DM by introducing an exact discrete symmetry has been discussed in many models (see e.g., [11–46] and the recent review [47] and references therein).
The model proposed by Ma [11] is one of the simplest radiative seesaw model with DM candidates. The model has the Z2-odd right-handed neutrinos Nk and the inert doublet scalar field . The neutrino masses are generated at the one-loop level, in which the Yukawa interactions and the scalar interaction (λ5/2)(H†η)2 contribute to the neutrino mass generation. The mass matrix is expressed as
where Mk is the Majorana mass of the k-th generation of right-handed neutrino, and are the mass of the and , respectively. In this model, we have two scenarios with respect to the DM candidate; the lightest right-handed neutrino N1 or the lighter Z2-odd neutral scalar field ( or ). The phenomenology of the model is studied in Kubo et al. [48], Bouchand and Merle [49], Merle and Platscher [50], Ma and Raidal [51], Suematsu et al. [52], Aoki and Kanemura [53], Suematsu et al. [54], Schmidt et al. [55], Hehn and Ibarra [56], Toma and Vicente [57], Ibarra et al. [58], Merle et al. [59], Lindner et al. [60], Hessler et al. [61], Aristizabal Sierra et al. [62], Gelmini et al. [63], and Ma [64].
A DM candidate can be made stable by an unbroken symmetry. The simplest possibility of such a symmetry is Z2 symmetry as in the above models. However, if the DM stabilizing symmetry is larger than Z2: ZN (N ≥ 4) or a product of two or more Z2s, the DM is consisting of stable multi-DM particles (multicomponent DM system). A supersymmetric extension of the radiative seesaw model of Ma [11] is an example [41–46]. Other possibilities with multicomponent DM are widely discussed in Ma and Sarkar [34], Kajiyama et al. [35, 37], Wang and Han [36], Baek et al. [38], Aoki et al. [39, 40], Bhattacharya et al. [65], Berezhiani and Khlopov [66, 67], Hur et al. [68], Zurek [69], Batell [70], Dienes and Thomas [71, 72], Ivanov and Keus [73], Dienes et al. [74], D'Eramo et al. [75], Gu [76], Bhattacharya et al. [77, 78], Geng et al. [79], Boddy et al. [80], Geng et al. [81], Esch et al. [82], Geng et al. [83], Arcadi et al. [84], DiFranzo and Mohlabeng [85], Aoki and Toma [86], and Aoki et al. [87].
In this paper we study two models of the two-loop extension of the model by Ma [11], we call them as “model A” and “model B,” in which due to the symmetry a set of stable particles can exist. Introducing two new scalar fields, the λ5 term is generated radiatively in the model A [39, 40]. In this model we discuss the three component DM system in which the two new scalar fields and a right-handed neutrino are the DM candidate. Such case has been discussed in Aoki et al. [40], however, we reanalyze the model since the benchmark points studied in Aoki et al. [40], where the masses of both new scalars are several hundred GeV, has been excluded by the recent results of the direct detection DM experiments. In this paper we focus on the case where the mass of one of the scalar DMs is close to the half of the Higgs boson mass to satisfy the constraints from the direct detection. In the model B the right-handed neutrinos have the mass radiatively generated through the one loop of internal new fermion and scalar fields. We identify the lightest right-handed neutrino as dark radiation.
We start in section 2 by writing down a set of the Boltzmann equations of the multicomponent DM system. The model A is discussed in section 3 by following Aoki et al. [40]. In section 4 we discuss the model B and relate dark radiation with the lepton flavor violating decay of the charged leptons and the decay of the inert Higgs bosons. Summery and discussion are given in section 5.
2. Multicomponent Dark Matter Systems
In the case of one-component DM the relic density of DM χ is determined by the Boltzmann equation
where nχ is the DM number density, is the equilibrium number density and is the thermally averaged cross section for χχ → XX′. Here X and X′ stand for the SM particles. The Hubble parameter H is given by , where g* is the total number of effective degrees of freedom, T and MPL are the temperature and the Planck mass, respectively. It is convenient to rewrite the equation in terms of dimensionless quantities; the number per comoving volume Yχ = nχ/s and the inverse temperature x = m/T. Here s is the entropy density and m is the mass of the DM particle. Using the replacement of dx/dt = H|T = m/x, we obtain
The thermally averaged cross section of (10−9) GeV with a DM mass of 100 GeV gives , which is consistent with the observed value of the relic abundance Ωh2 ≃ 0.12 [88].
In the multicomponent DM system three types of processes enter in the Boltzmann equations1:
See Figure 1 for a depiction of three types of processes. Here we assume that none of the DM particles have the same quantum number with respect to the DM stabilizing symmetry. The Boltzmann equations for the DM particle χi with mass mi are
Here x = μ/T and is the reduced mass of the system. The contributions of non-standard annihilations have been discussed in e.g., Aoki et al. [87] for two and three component DM system with a symmetry.
3. Model A
In the following, by extending the one-loop model in Ma [11] we study two of the two-loop radiative seesaw models with symmetry. We refer to them as “model A” and “model B.” Owing to the symmetry, there exist at least two extra stable electrically neutral particles. The multicomponent DM system is realized in the model A, while one of the stable particles plays as the dark radiation in the model B.
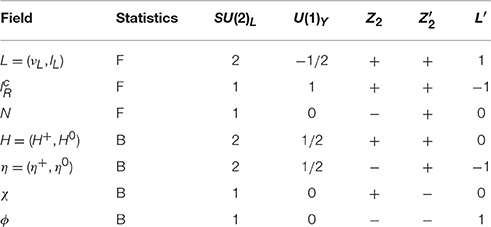
The matter content of the model A is shown in Table 1. In addition to the matter content of the SM model, we introduce the right-handed neutrino Nk, an SU(2)L doublet scalar η, and two SM singlet scalars χ and ϕ. Note that the lepton number L′ of N is zero. The -invariant Yukawa sector and Majorana mass term for N can be described by
where i, j, k (= 1, 2, 3) stand for the flavor indices. The scalar potential V is written as V = Vλ+Vm, where
The is the unbroken discrete symmetry while the lepton number L′ is softly broken by the last term in the potential Vm, the ϕ mass tem. In the absence of this term, there will be no neutrino mass. Note that the “λ5 term,” (λ5/2)(H†η)2, is also forbidden by L′. A small λ5 of the original model of Ma [11] is “natural” according to 't Hooft [100], because the absence of λ5 implies an enhancement of symmetry. In fact, if λ5 is small at some scale, it remains small for other scales as one can explicitly verify [49, 50]. Here we attempt to derive the smallness of λ5 dynamically, such that the λ5 term becomes calculable.
The Higgs doublet field H, the inert doublet field η and the singlet scalar ϕ are respectively parameterized as
where vh is the vacuum expectation value. The tree-level masses of the scalars are given by
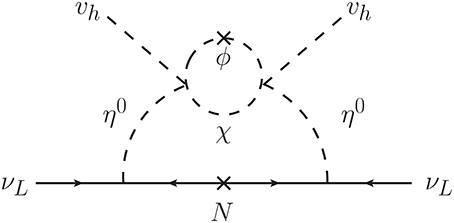
Although the tree-level mass of is the same as that of as shown in Equation (13), the degeneracy is lifted at the one-loop level via the effective λ5 term:
This correction is embedded into the two-loop diagram to generate the neutrino mass (see Figure 2). The 3 × 3 neutrino mass matrix ν can be given by
where we have assumed that .
Using given in Equation (17), the neutrino mass matrix can be approximated as
We see from Equations (17) and (19) that the neutrino mass matrix ν is proportional to . When mχ, mϕR, , , for instance, implies that to obtain the neutrino mass scale of . With the same set of the parameter values we find that , where the smallness is a consequence of the radiative generation of this coupling. As we will see, the product |Yνκ| enters into the semi-annihilation of DM particles which produces monochromatic neutrinos, while the upper bound of |Yν| follows from the μ → eγ constraint.
3.1. Multicomponent Dark Matter System
In the model A there are three type of dark matter candidates ; N1 (the lightest among Nk's) or (or ) with , χ with and ϕR (or ϕI) with . For there are two candidates. In the following discussions we assume that N1 is a DM candidate [40]. The other possibility, -DM, is discussed in Aoki et al. [39].
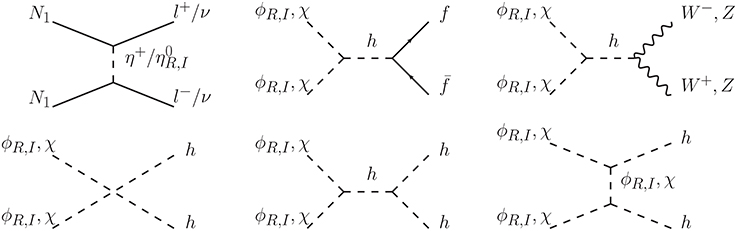
We discuss the three DM system of N1, ϕR, χ. There are three types of DM annihilation process:
Here we have assumed mϕR > mχ and mϕR + mχ < M2, 3. Moreover, since the mass difference between ϕR and ϕI is controlled by the lepton-number breaking mass m5, which is assumed to be much smaller than mϕR. Then mϕR and mϕI are practically degenerate and the contribution of ϕI to the annihilation processes during the decoupling of DMs is nonnegligible. The diagrams for annihilation processes which enter the Boltzmann equation are shown in Figures 3–5. Since the reaction rate of the conversion between ϕR and ϕI can reach chemical equilibrium during the decoupling of DMs, we can sum up the number densities of ϕR and ϕI and compute the relic abundance of [40].
In the multicomponent DM scenario, the effective cross section off the nucleon is given by
In our model, only χ and ϕR scatter with the nucleus, and the right-handed neutrino N1 does not interact with nucleus at tree level. So we can neglect the N1 contribution at the lowest order in perturbation theory. The effective cross sections of ϕR and χ are expressed as
where σχ and σϕR are the spin independent cross sections and given by
Here is the usual nucleonic matrix element [101] and mN is nucleon mass.
The upper bounds on the cross section off the nucleon is obtained by LUX [102] and XENON1T [103]. In the cases of one-component DM system of a real or complex scalar boson, those experimental results give the strong constraint on the masses of those DM particles; the allowed DM mass region is ≃mh/2 and ≳1 TeV [104–106]. In the model A with the multicomponent DM system, the constrains on the cross sections off the nucleon for χ and ϕR are also relatively severe. As a benchmark we take the mass of χ as mχ = mh/2 while vary the mass of ϕR in the following analysis2.
In the original one-loop neutrino mass model in Ma [11], the relic density of N1 tends to be larger than the observational value [48]. The additional contributions coming from the semi-annihilation can enhance the annihilation rate for N1 so that the N1 DM contribution to the total relic abundance can be suppressed. This situation is realized for M1 > mϕR, mχ as can be seen later.
As the benchmark set we take the following values for the parameters.
The masses of heavier right-handed neutrinos are M2 = M3 = 1 TeV. The mass differences between and the sum of mχ and mϕR are so chosen that no resonance appears in the s-channel of the semi-annihilation in Figure 5 (right). The benchmark set satisfies the constraints from the perturbativeness, the stability conditions of the scalar potential [39, 40], the lepton flavor violation (LFV) such as μ → eγ [107] and the electroweak precision measurements [108, 109]. It is noted that κ is bounded as |κ| ≲ 0.4 by the perturbativeness and the stability conditions [39, 40].
Figure 6 shows the relic abundances of , , and and the total relic abundance as a function of mϕR for the benchmark set. The horizontal dashed line stands for the observed value . It is shown that the relic abundance of the χ is Ωχ ≃ Ωobs/2. When ϕR is lighter than N1, the semi-annihilation tends to decrease the relic abundance of N1. For the benchmark set, the total relic abundance is consistent with the observed value around mϕR ≃ 280 GeV.
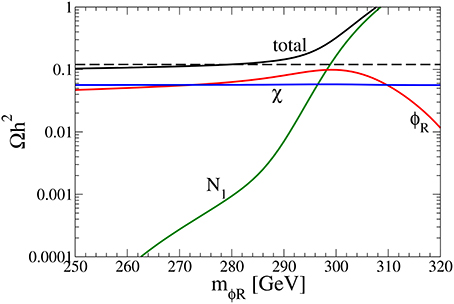
Figure 6. Relic abundances , , and and the total relic abundance as a function of mϕR. The relevant masses and couplings are taken as in Equations (27–31). The horizontal dashed line stands for the observed value .
The left panel in Figure 7 shows the contour plot for the mϕR − γ5 plane where the total relic density of DM can be made consistent with the observed value . We take two values, 10 GeV (black line) and 1 GeV (red line), for the mass difference between and mχ+mϕR in Equation (28). The other parameters are taken as the same in Equations (27–31). We can see the scalar coupling γ5 increases drastically as mϕR increases for mϕR ≳ 290 GeV. It is because the relic density of the N1 DM, , becomes significant for mϕR ≳ 290 GeV, so that should be drastically suppressed. The scalar couplings of DM particles with the SM Higgs boson, γ2 and γ5, and the DM masses are constrained by the DM direct detection experiments. For the χ DM, the effective cross section off nucleon in Equation (24) is cm2 for the benchmark set. It is an order of magnitude smaller than the current experimental bound. For the ϕR DM, the right panel in Figure 7 shows the relation between mϕR and the effective cross section for =10 GeV (black line) and 1 GeV (red line), where the DM relic abundance is consistent with the observation. The plot corresponds to the parameter space in the left panel in Figure 7. The dot and dashed lines indicate the upper bounds of LUX and XENON1T, respectively. The hatched region is excluded by perturbativity. Although the scalar coupling γ5 becomes large for mϕR ≳ 290 GeV and then the cross sections off the nucleon σϕR becomes large, the effective cross section decreases for mϕR ≳ M1(= 300 GeV), since the abundance of ϕR decreases. For the case of 10 GeV, it can be seen that the mass region 288 GeV ≲ mϕR is excluded by LUX and XENON1T data. On the other hand, there are no constraints from the direct DM search experiments on the mass of ϕR for the case of 1 GeV. This is because the relic abundance of ϕR becomes much smaller by the large contribution from the s-channel process of the semi-annihilation. Figure 8 shows the same as in Figure 7 but for M1 = 500 GeV and γ7 = 0.28. >From the right panel in Figure 8, we see that 485 (490) GeV ≲ mϕR ≲ 510 (502) GeV is excluded by the direct detection experiments for 10 (1) GeV.
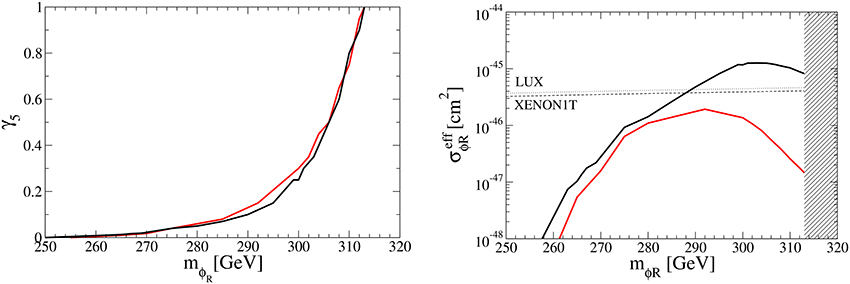
Figure 7. (Left) Contour plot for the total relic density . (Right) The relation between the mϕ and the effective cross sections given in Equation (24). The black dot and dashed lines show the upper limit of the spin independent cross section off the nucleon given by LUX [102] and XENON1T [103], respectively. The hatched region is excluded by perturbativity. In both panels, we take two values, 10 GeV (black line) and 1 GeV (red line), for the mass difference between and mχ+mϕR.
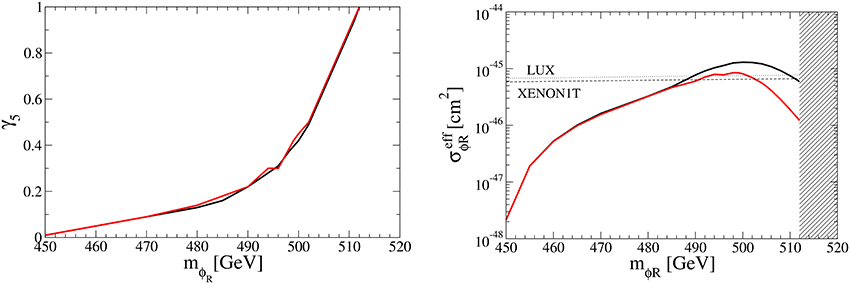
Figure 8. The same as Figure 7 but for M1 = 500 GeV and γ7 = 0.28.
Before we go to discuss indirect detection, we summarize the parameter space, in which a correct value of the total relic DM abundance can be obtained without contradicting the constraint from the direct detection experiments. As in the case of the single SM singlet DM, the constraint is in fact very severe: The mass of χ has to be very close to mh/2, and γ2 (the Higgs portal coupling) also has to be close to 0.004 for an adequate amount of Ωχ. However, as for mϕR and γ5, there exist a certain allowed region. The allowed region in the mϕR − γ5 plane is controlled by the semi-annihilation [especially, the last diagram in Figure 5, which is sensitive to the mass relation (28)] and the DM conversion (especially the right diagram in Figure 4, which is sensitive to γ7). If we increase the mass of the right-handed neutrino DM, the mass of ϕR increases, but how the allowed range in the mϕR-γ5 plane emerges remains the same. If we take the larger γ7, e.g., γ7 = 0.28, in Figure 7, the allowed region for mϕR becomes narrower as 295 GeV ≲ mϕR ≲ 300 GeV. The smaller mϕR (≲ 295 GeV) is excluded by Ωtotal < Ωobs due to the larger DM conversion i.e., the larger annihilation process of ϕRϕR → χχ → XX.
3.2. Indirect Detection
For indirect detections of DM the SM particles produced by the annihilation of DM are searched. Because the semi-annihilation produces a SM particle, this process can serve for an indirect detection. In our model, especially, the SM particle from the semi-annihilation process as shown in Figure 5 is neutrino which has a monochromatic energy spectrum. Therefore, we consider below the neutrino flux from the Sun [110–120] as a possibility to detect the semi-annihilation process of DMs.
The DM particles are captured in the Sun losing their kinematic energy through scattering with the nucleus. Then captured DM particles annihilate each other. The time dependence of the number of DM ni in the Sun is given by Griest and Seckel [114], Ritz and Seckel [115], Bertone et al. [116], Silk et al. [117], Kamionkowski [118], Kamionkowski et al. [119], and Jungman et al. [120]
where i, j, k = χ, ϕR, N1 and Ci is the capture rates in the Sun:
and CA's are the annihilation rate:
Here f(mi) depends on the form factor of the nucleus, elemental abundance, kinematic suppression of the capture rate, etc., varying depending on the DM mass [118–120]. Vij is an effective volume of the Sun with μij = 2mimj/(mi+mj) in the non-relativistic limit. In the Equation (32) we have neglected the DM production processes such as jj → ii and jk → iX because the kinetic energy of the produced particle i is much larger than that corresponding to the escape velocity from the Sun, i.e., ~ 103 km/s [114, 121, 122]. Consequently, the number of the right-hand neutrino DM cannot increase in the Sun, and hence the semi-annihilation process, ϕRχ → N1ν, is the only neutrino production process3, where its reaction rate as a function of t is given by Γ(ϕRχ → Nν; t) = CA(ϕRχ → N1ν)nϕR(t)nχ(t).
Figure 9 shows the mϕR dependence of the neutrino production rate today Γ(ϕRχ → Nν; t0), where s is the age of the Sun, for the same parameter space as in Figure 7 (Figure 9, left) and in Figure 8 (Figure 9, right). The hatched region is excluded by perturbativity. Arrows indicate the excluded regions by the direct detection experiments. For mϕR ≳ M1 where the relic abundance of N1 dominates that of ϕR, the neutrino production rate decreases since the capture rate of the ϕR becomes small. As we can see from Figure 5 a resonance effect for the s-channel annihilation process can be achieved if . Then the smaller neutrino mass difference gives the larger neutrino production rate. For the case of = 1 GeV, the rate Γ(ϕRχ → Nν; t0) reaches about 1018 s−1 at mϕR ≃ 290 GeV for M1 = 300 GeV and 4 × 1017 s−1 at mϕR ≃ 490 GeV for M1 = 500 GeV, respectively.
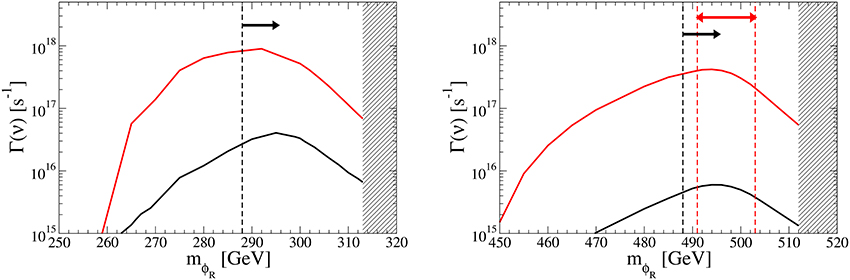
Figure 9. The neutrino production rate Γ(ν) = Γ(ϕRχ → Nν; t0) in the Sun against the ϕR DM mass for M1 = 300 GeV (Left) and 500 GeV (Right). The parameter space, as well as the meaning of colors of the lines in the left and right panel, are the same as in Figures 7, 8, respectively. The hatched region is excluded by perturbativity. Arrows indicate the excluded regions by the direct detection experiments.
The upper limits on the DM DM → XX′ from the Sun are given by IceCube experiment [123]. For instance, the upper limit on the annihilation rate of the DM of 250 (500) GeV into W+W− is 1.13 × 1021 (2.04 × 1020) s−1 and that into τ+τ− is 5.99 × 1020 (7.96 × 1019) s−1, which is at least 102 times larger than the rate Γ(ν) shown in Figure 9. Note however that the energy spectrum of the neutrino flux produced by the W or τ decay is different from the monochromatic neutrino. With an increasing resolution of energy and angle the chance for the observation of the semi-annihilation and hence of a multicomponent nature of DM can increase.
4. Model B
Neutrinos have always played consequential roles in cosmology (see [124], and also [125] and references therein). While they play a role as hot dark matter, the mechanism of their mass generation is directly connected to cosmological problems such as baryon asymmetry of the Universe [126] and dark matter [10–36, 39–48]. Resent cosmological observations with increasing accuracy [88, 127–129] provide useful hints on how to extend the neutrino sector. Here we propose an extension of the neutrino sector such that the tensions among resent different cosmological observations can be alleviated. The tensions have emerged since the first Planck result [88] in the Hubble constant H0 and in the density variance σ8 in spheres of radius 8h − 1 Mpc: The Planck values of 1/H0 and σ8 are slightly larger than those obtained from the observations of the local Universe such as Cepheid variables [128] and the Canada-France- Hawaii Telescope Lensing Survey [130], respectively. The Planck galaxy cluster counts [131] and also the Sloan Digital Sky Survey data [127] yield a smaller σ8.
It has been recently suggested [131–139] that these tensions can be alleviated if the number Neff of the relativistic species in the young Universe is slightly larger than the standard value 3.046 and the mass of the extra relativistic specie is of (0.1) eV [139]. Here we suggest a radiative generation mechanism of the neutrino mass, which is directly connected to the existence of a stable DM particle and also a non-zero ΔNeff = Neff − 3.046.
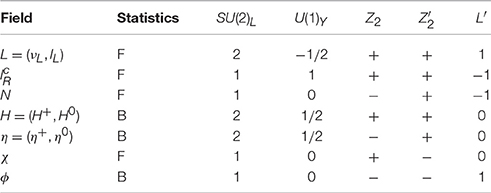
The matter content of the model is shown in Table 2. It is a slight modification of the model A: χ in this model is a Majorana fermion. The -invariant Yukawa sector (the quark sector is suppressed) is described by the Lagrangian
where i, j, k = 1, 2, 3, and we have assumed without loss of generality that the χ mass term is diagonal. We also assume that have only diagonal elements. The most general renormalizable form of the -invariant scalar potential is given by
and the mass terms are
where the m4 term in Equation (39) breaks L′ softly. The scalar fields H, η and ϕ are defined in Equation (10). Since we assume that the discrete symmetry is unbroken, the scalar fields above do not mix with other, so that their tree-level masses can be simply expressed:
The two-loop diagram for the neutrino mass is shown in Figure 10. Because of the soft breaking of the dimension two operator ϕ2, the propagator between ϕ and ϕ can exist, generating the mass of N:
The 3 × 3 two-loop neutrino mass matrix ν is given by
We can also use (45) to obtain an approximate formula for the neutrino mass
where UN is the unitary matrix diagonalizing the mass matrix (MN)ij with the eigenvalues Mk and the mass eigenstates , and we have used the fact that . In the following discussions we choose the theory parameters so as to be consistent with the global fit [1]:
where the values in the parenthesis are those for the inverted mass hierarchy.
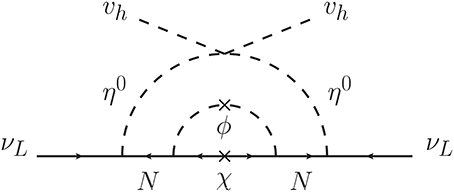
Figure 10. Two-loop radiative neutrino mass of the model B. The upper cross means the soft breaking mass term , which should indicate that there are ϕR and ϕI loops in the inner one-loop diagram. The lower cross indicates the chirality flip of χ. The result (Equation 46) is obtained by using the exact propagators of ϕs and χs.
4.1. Dark Radiation
According to the discussion at the beginning of this section, we identify the lightest right-handed neutrino with dark radiation contributing to ΔNeff 4. Without los of generality we may assume it is with mass ≲ 0.24 eV. The upper bound on the mass is obtained together with 3.10 < Neff < 3.42 in Feng et al. [139]. To simplify the situation, we require that the heavier right-handed neutrinos and decay above the decoupling temperature of . Their decay widths are given by
where we have used and neglected the mass of and νLs. Therefore, and can decay above if
is satisfied, where H(T) is the Hubble constant at temperature T, and g*s(T) is the relativistic degrees of freedom at T. To obtain the effective number of the light relativistic species Neff [125, 140], we have to compute the energy density of at the time of the photon decoupling, where we denote the decoupling temperature of γ, νL and by and , respectively. Further, Tν0 (TN0) stands for the temperature of at the decoupling of γ. The most important fact is that the entropy per comoving volume is conserved, so that sa3 is constant, where s is the entropy density, and a is the scale factor. The effective number Neff follows from and is given by Kolb and Turner [125], Steigman [140], Anchordoqui and Goldberg [141], Steigman et al. [142], Anderhalden et al. [143, 145], Anchordoqui et al. [144], and Weinberg [146]
for Nν = 3, where ρr is the energy density of relativistic species. Since , we need to compute the decoupling temperature to obtain and hence Neff. For 0.05 ≲ ΔNeff ≲ 0.38 [139] we find and also MeV to obtain (which gives ΔNeff = 0.25). To estimate , we compute the annihilation rate ΓN(T) of at T, which is given by
where ζ(3) ≃ 1.202… and nN(T) is the number density of . Then we calculate from , which can be rewritten as5
with .
It turns out that M2, 3 ~ (10) GeV to obtain ΔNeff ~ 0.25 while satisfying M1 ≲ 0.24 eV. To see this, we first find that
which follows from Equation (53) for ΔNeff ~ 0.25. Further we can estimate a part of Equation (49) from the neutrino mass Equation (47) with Mν ~ 0.05 eV:
where we have used . Then using Equation (50) with T ≃ 165 MeV (which corresponds to ΔNeff ≃ 0.25), we obtain
Note that this is an order of magnitude estimate, and indeed M2(3) can not be smaller than 10 GeV to satisfy ΔNeff ≲ 0.38.
Since we require that M1 ≲ 0.24 eV, there exists a huge hierarchy in the right-handed neutrino mass. This has a consequence on the Yukawa coupling matrix Y′ν: To obtain realistic neutrino masses with the mixing parameters given in Equation (48),
has to be satisfied. Note that only enters into the thermally averaged annihilation cross section of , as we can see from Equation (52). Because of ΔNeff ≲ 0.38, on the other hand, can not be made arbitrarily large. The hierarchy (Equation 57) has effects on the LFV radiative decays of the type li→ljγ, so that the LFV decays and ΔNeff are related, as we will see below. In the limit mj≪mi, where mi and mj stand for the mass of li and lj, respectively, the ratio of the partial decay width can be written as Ma and Raidal [51]
Here and are defined in Equations (40) and (47), respectively, and the current upper bounds on the branching fraction of these processes [107, 148] require
From Equation (59) we find that is not constrained by the stringent constraint from μ → eγ, which will be crucial in obtaining a realistic Neff without having any contradiction with Equations (59–61). Furthermore, if is large compared with others and the hierarchy (Equation 57) is satisfied, the ratio is ~ , and from the same reason ΔNeff depends mostly on . A benchmark set of the input parameters is given by
which yields
where we have assumed that are all real so that there is no CP phase. These values are consistent with Equations (48), (59–61). With the same input parameters we find: The lhs of (50) = 5.46 × 10−21 (1.78 × 10−20) GeV for N2 (N3), where the rhs is H = 2.10 × 10−20 GeV with and , and ΔNeff = 0.245.
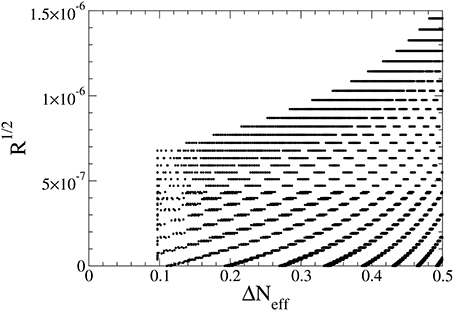
In Figure 11 we plot R1/2 against ΔNeff with GeV and GeV, where we have varied between 221 and 227 GeV. In the black region of Figure 11 the differences of the neutrino mass squared and the neutrino mixing angles are consistent with Equation (48) for the normal hierarchy, and the constraints M1 < 0.24 eV, (Equations 50 and 59–61) are satisfied. If ΔNeff and R1/2 would depend on only, we would obtain a line in the plane. The and dependence in R1/2 cancels, but this is not the case for ΔNeff. This is the reason why we have an area instead of a line in Figure 11. We see from Figure 11 that the predicted region for ΔNeff ≲ 0.1 is absent. The main reason is that we have assumed that M2, M3 ≲ 16 GeV. This has also a consequence on the difference between and , because the mass difference changes the overall scale of the neutrino mass (47). To obtain a larger M2, 3, we can decrease the mass difference, thereby implying an increase of the degree of fine-tuning. Further, the difference between and can not be made arbitrarily large, because it requires a smaller M2, 3, which due to H(T)∝T2 in turn implies that the decoupling temperature has to decrease to satisfy the constraint [Equation (50)]. A smaller , on the other hand, means a larger ΔNeff which is constrained to be below 0.38. This is why is varied only in a small interval in Figure 11.
Since the current upper bound on is 4.2 × 10−13 [107], the model B predicts
which is about two orders of magnitude smaller than the current experimental bounds [148].
Another consequence of the hierarchy (Equation 57) is that the total decay width of ηR depends on , which is approximately (we assume that ηR is the lightest among ηs). Therefore, ΔNeff is basically a function of the decay width. In Figure 12 we show ΔNeff against , the decay width of over , where we have used the same parameters as for Figure 11. decays almost 100 percent into neutrinos and dark radiation , which is invisible. In contrast to this, η+ can decay into a charged lepton and , and the decay width over is the same as . ΓηR should be compared with the decay width for , which is ~ for the same parameter space as for Figure 12, where f and f′ stand for the SM fermions (except the top quark). Therefore, η+ decays almost 100 percent into a charged lepton and missing energy. In Aristizabal Sierra [62], a similar hierarchical spectrum of the right-handed neutrinos in the model of Ma [11] has been assumed (the lightest one has been regarded as a warm dark matter) and collider physics has been discussed. How the inert Higgs bosons can be produced via s-channel exchange of a virtual photon and Z boson [149, 150] is the same, but the decay of the inert Higgs bosons is different because of the hierarchy Equation (57) of the Yukawa coupling constants. As it is mentioned above, the η± decays in the present model almost only into the lightest one and a charged lepton. Therefore, the cascade decay of the heavier right-handed neutrinos into charged leptons will not be seen at collider experiments, because they can be produced only as a decay product of η±. The decay width of η± into an individual charged lepton depends of course on the value of . In the parameter space we have scanned we cannot make any definite conclusion on the difference.
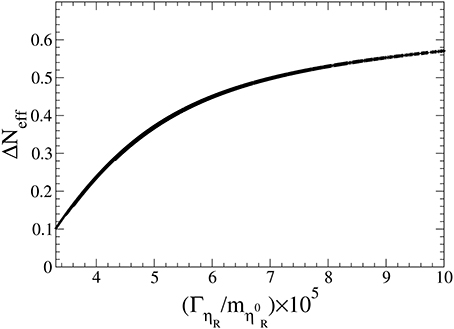
Figure 12. ΔNeff against , where we have used the same parameters as for Figure 11.
4.2. Cold Dark Matter and Its Direct and Indirect Detection
Since the lightest N is dark radiation and the masses of the heavier ones are (10) GeV (as we have seen in the previous subsection), can not be DM candidates, because they decay into N and ν. So, DM candidates are χ and the lightest component of ϕ6. In the case that ηs are lighter than ϕR and the lightest component of ϕ (which is assumed to be ϕR) is DM, a correct relic abundance [88] can be easily obtained, because γ3 for the scalar coupling (η†η)|ϕ|2 is an unconstrained parameter so far. So, in the following discussion we assume that ϕR is DM.
Because of the Higgs portal coupling γ2, the direct detection of ϕR is possible. The current experimental bound of XENON1T [103] of the spin-independent cross section σSI off the nucleon requires |γ2| ≲ 0.05 ~ 0.14 formϕR = 250 ~ 500 GeV. Since γ2 is allowed only below an upper bound (which depends on the DM mass mϕR), γ3 can vary in a certain interval for a given DM mass.
With this remark, we note that the capture rate of DM in the Sun is proportional to σSI, while its annihilation rate in the Sun is proportional to the thermally averaged annihilation cross section, [110–120]. If a pair of ϕRs annihilates into and also , a pair of νL and will be produced, which may be observed on the Earth [121, 122]. The signals will look very similar to those coming from W±, which result from DM annihilation. The annihilation rate as a function of time t is given by Jungman et al. [120]
where CϕR is the capture rate in the Sun,
and CA is given by
We have used f(250 GeV) ≃ 0.5 and f(500 GeV) ≃ 0.2 [120], and we have assumed that all the ηs have the same mass and therefore . In Figure 13 we plot the annihilation rate today ( s) against σSI for mϕR = 250 and 500 GeV with mη fixed at 230 GeV and . The vertical dashed lines are the XENON1T upper bound on σSI [103]. The peak of for mϕR = 250 (500) GeV appears at cm2 and is ≃ 1.7 (0.7) × 1018 s−1, which is two to three orders of magnitude smaller than the upper bound on the DM annihilation rate into W± in the Sun [123].
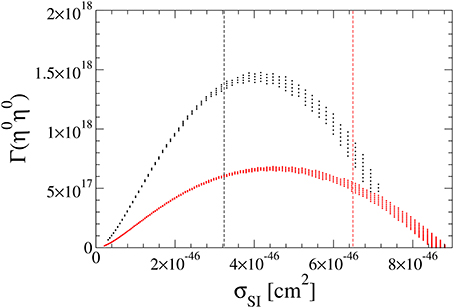
Figure 13. The pair-annihilation rate of ϕR into and in the Sun, , against σSI for mϕR = 250 (black) and 500 (red) GeV, where mη is fixed at 230 GeV (all ηs have the same mass) and . The black (red) vertical dashed line is the XENON1T [103] upper bound on σSI for mϕR = 250 (black) and 500 (red) GeV.
5. Conclusion
We have discussed the extensions of the Ma model by imposing a larger unbroken symmetry . Thanks to the symmetry, at least two stable particles exit. We have studied two models, model A and model B, where the stable particles form a multicomponent DM system in the model A, while they are a DM and dark radiation in the model B.
The model A is an extension of the model of Ma such that the lepton-number violating “λ5 coupling,” which is to obtain small neutrino masses for Yν ~ 0.01, is radiatively generated. Consequently, the neutrino masses are generated at the two-loop level, where the unbroken symmetry acts to forbid the generation of the one-loop mass. Such larger unbroken symmetry implies that the model involves a multi-component DM system. We have considered the case of the three-component DM system: two of them are SM singlet real scalars and the other one is a right-handed neutrino. The DM conversion and semi-annihilation in addition to the standard annihilation are relevant to the DM annihilation processes. We have found that the non-standard processes have a considerable influence on the DM relic abundance. We also have discussed the monochromatic neutrinos from the Sun as the indirect signal of the semi-annihilation of the DM particles. In the cases of one-component DM system of a real scalar boson or of a Majorana fermion the monochromatic neutrino production by the DM annihilation is strongly suppressed due to the chirality of the left-handed neutrino. However, such suppression is absent when DM is a complex scalar boson or a Dirac fermion. Also in a multicomponent DM system, the neutrino production is unsuppressed if it is an allowed process. We have found that the rate for the monochromatic neutrino production in the model A is very small compared with the current IceCUBE [123] sensitivity. However, the resonant effect in the s-channel process of the semi-annihilation can be expected to enhance the rate.
In the model B, the mass of the right-handed neutrinos are produced at the one-loop level. Then the radiative seesaw mechanism works at the two-loop level. Thanks to there exist at least two stable DM particles; a dark radiation with a mass of (1) eV and the other one, DM, is the real part of ϕ. The dark radiation contributes to ΔNeff <1 such that the tensions in cosmology that exist among the observations in the local Universe (CMB temperature fluctuations and primordial gravitational fluctuations) can be alleviated. Because of the hierarchy eV, we are able to relate to the ratio of the lepton flavor violating decays to ΔNeff. The indirect signal of the neutrino from the Sun has also been discussed. It is found that the predicted annihilation rate of the neutrinos is two to three orders of magnitude smaller than the current bound [123]. We have also expressed ΔNeff as a function of the decay width of (which is assumed to be lightest among ηs). It decays 100 percent into left- and right-handed neutrinos, where the heavier right-handed neutrinos decay further into dark radiation (the lightest among them). Dark radiation appears as a missing energy in collider experiments. We also have found that η+ decays 100 percent into a charged lepton and the missing energy. This is a good example in which, through the generation mechanism of the neutrino masses, cosmology and collider physics are closely related.
Author Contributions
All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The work of MA is supported in part by the Japan Society for the Promotion of Sciences Grant-in-Aid for Scientific Research (Grants No. 16H00864 and No. 17K05412). JK is partially supported by the Grant-in-Aid for Scientific Research (C) from the Japan Society for Promotion of Science (Grant No.16K05315).
Footnotes
1. ^Semi-annihilation processes also exist in one-component DM systems when DM is a Z3 charged particle [89, 90, 91, 92, 93, 94, 95] or a vector boson [96, 97, 98, 99].
2. ^Two singlet scalar DM scenario in model has been explored in detail in Bhattacharya et al. [65].
3. ^There are also neutrinos having continuous energy spectrum from the decay of SM particles produced by the standard annihilation. The upper bounds for the production rates of the SM particles are given in Agrawal et al. [121], Andreas et al. [122], and Aartsen et al. [123].
4. ^Within a similar framework of radiative seesaw mechanism, the lightest right-handed neutrino has been regarded as stable warm dark matter in Aristizabal Sierra et al. [62]. In the models proposed in Kajiyama et al. [37] and Baek et al. [38], the topology of the two loop to generate the neutrino mass is basically the same as that of Figure 10. But the matter content of our model is much simpler; we have only two additional extra fields compared with the one-loop model of Ma [11], while in these papers five and four additional ones have to be introduced. Apart from this difference, they have not considered the lightest right-handed neutrino as dark radiation. In Baek et al. [38], however, the Nambu-Goldstone boson associated with the spontaneous breaking of U(1)B−L is regarded as dark radiation.
5. ^We use the relation between T and g*s given in Husdal [147] to solve Equation (53) for .
6. ^Both together can not be DM, because the heavier one decays into .
References
1. Esteban I, Gonzalez-Garcia MC, Maltoni M, Martinez-Soler I, Schwetz T. Updated fit to three neutrino mixing: exploring the accelerator-reactor complementarity. J High Energy Phys. (2017) 1:087. doi: 10.1007/JHEP01(2017)087
2. Ade PAR, Aghanim N, Arnaud M, Ashdown M, Aumont J, Baccigalupi C, Banday AJ, et al. Planck 2015 results. XIII. Cosmological parameters. Astron Astrophys. (2016) 594:A13. doi: 10.1051/0004-6361/201525830
3. Minkowski P. μ → eγ at a rate of one out of 109 muon decays? Phys Lett. (1977) 67B:421–8. doi: 10.1016/0370-2693(77)90435-X
4. Gell-Mann M, Ramond P, Slansky R. Complex spinors and unified theories. Conf Proc. (1979) C790927:315–21.
5. Sawada O, Sugamoto A (Eds.). Proceedings: Workshop on the Unified Theories and the Baryon Number in the Universe Tsukuba (1979).
6. Mohapatra RN, Senjanovic G. Neutrino mass and spontaneous parity violation. Phys Rev Lett. (1980) 44:912. doi: 10.1103/PhysRevLett.44.912
7. Zee A. A theory of lepton number violation, neutrino majorana mass, and oscillation. Phys Lett. (1980) 93B:389. doi: 10.1016/0370-2693(80)90349-4
8. Zee A. Quantum numbers of majorana neutrino masses. Nucl Phys. B (1986) 264:99–110. doi: 10.1016/0550-3213(86)90475-X
10. Krauss LM, Nasri S, Trodden M. A model for neutrino masses and dark matter. Phys Rev. D (2003) 67:085002. doi: 10.1103/PhysRevD.67.085002
11. Ma E. Verifiable radiative seesaw mechanism of neutrino mass and dark matter. Phys Rev. D (2006) 73:077301. doi: 10.1103/PhysRevD.73.077301
12. Nasri S, Moussa S. Model for small neutrino masses at the TeV scale. Mod Phys Lett. A (2002) 17:771–8. doi: 10.1142/S0217732302007119
13. Ma E. Z(3) dark matter and two-loop neutrino mass. Phys Lett. B (2008) 662:49–52. doi: 10.1016/j.physletb.2008.02.053
14. Aoki M, Kanemura S, Seto O. Neutrino mass, dark matter and baryon asymmetry via TeV-scale physics without fine-tuning. Phys Rev Lett. (2009) 102:051805. doi: 10.1103/PhysRevLett.102.051805
15. March-Russell J, McCabe C, McCullough M. Neutrino-flavoured sneutrino dark matter. J High Energy Phys. (2010) 03:108. doi: 10.1007/JHEP03(2010)108
16. Aoki M, Kanemura S, Shindou T, Yagyu K. An R-parity conserving radiative neutrino mass model without right-handed neutrinos. J High Energy Phys. (2010) 07:084. doi: 10.1007/JHEP07(2010)08410.1007/JHEP11(2010)049
17. Kanemura S, Seto O, Shimomura T. Masses of dark matter and neutrino from TeV scale spontaneous U(1)B−L breaking. Phys Rev. D (2011) 84:016004. doi: 10.1103/PhysRevD.84.016004
18. Kanemura S, Nabeshima T, Sugiyama H. Neutrino masses from loop-induced dirac yukawa couplings. Phys Lett. B (2011) 703:66–70. doi: 10.1016/j.physletb.2011.07.047
19. Dev PSB, Pilaftsis A. Minimal radiative neutrino mass mechanism for inverse seesaw models. Phys Rev. D (2012) 86:113001. doi: 10.1103/PhysRevD.86.113001
20. Bhupal Dev PS, Pilaftsis A. Light and superlight sterile neutrinos in the minimal radiative inverse seesaw model. Phys Rev. D (2013) 87:053007. doi: 10.1103/PhysRevD.87.053007
21. Gustafsson M, No JM, Rivera MA. Predictive model for radiatively induced neutrino masses and mixings with dark matter. Phys Rev Lett. (2013) 110:211802. doi: 10.1103/PhysRevLett.110.211802
22. Kajiyama Y, Okada H, Yagyu K. Two loop radiative seesaw model with inert triplet scalar field. Nucl Phys. B (2013) 874:198–216. doi: 10.1016/j.nuclphysb.2013.05.020
23. Law SSC, McDonald KL. A class of inert N-tuplet models with radiative neutrino mass and dark matter. J High Energy Phys. (2013) 09:092. doi: 10.1007/JHEP09(2013)092
24. Hirsch M, Lineros RA, Morisi S, Palacio J, Rojas N, Valle JWF. WIMP dark matter as radiative neutrino mass messenger. J High Energy Phys. (2013) 10:149. doi: 10.1007/JHEP10(2013)149
25. Restrepo D, Zapata O, Yaguna CE. Models with radiative neutrino masses and viable dark matter candidates. J High Energy Phys. (2013) 11:011. doi: 10.1007/JHEP11(2013)011
26. Lindner M, Schmidt D, Watanabe A. Dark matter and U(1)′ symmetry for the right-handed neutrinos. Phys Rev. D (2014) 89:013007. doi: 10.1103/PhysRevD.89.013007
27. Okada H, Yagyu K. Radiative generation of lepton masses. Phys Rev. D (2014) 89:053008. doi: 10.1103/PhysRevD.89.053008
28. Baek S, Okada H, Toma T. Radiative lepton model and dark matter with global U(1)′ symmetry. Phys Lett. B (2014) 732:85–90. doi: 10.1016/j.physletb.2014.03.021
29. Ahriche A, Chen CS, McDonald KL, Nasri S. Three-loop model of neutrino mass with dark matter. Phys Rev. D (2014) 90:015024. doi: 10.1103/PhysRevD.90.015024
30. Ahriche A, McDonald KL, Nasri S. A model of radiative neutrino mass: with or without dark matter. J High Energy Phys. (2014) 10:167. doi: 10.1007/JHEP10(2014)167
31. Kanemura S, Matsui T, Sugiyama H. Neutrino mass and dark matter from gauged U(1)B−L breaking. Phys Rev. D (2014) 90:013001. doi: 10.1103/PhysRevD.90.013001
32. Kanemura S, Sakurai K, Sugiyama H. Probing models of dirac neutrino masses via the flavor structure of the mass matrix. Phys Lett. B (2016) 758:465–72. doi: 10.1016/j.physletb.2016.05.046
33. Simoes C, Wegman D. Radiative two-loop neutrino masses with dark matter. J High Energy Phys. (2017) 04:148. doi: 10.1007/JHEP04(2017)148
34. Ma E, Sarkar U. Revelations of the E(6)/U(1)(N) model: two-loop neutrino mass and dark matter. Phys Lett. B (2007) 653:288–91. doi: 10.1016/j.physletb.2007.08.019
35. Kajiyama Y, Okada H, Toma T. New interpretation of the recent result of AMS-02 and multi-component decaying dark matters with non-Abelian discrete flavor symmetry. Eur Phys J. C (2014) 74:2722. doi: 10.1140/epjc/s10052-014-2722-9
36. Wang W, Han ZL. Radiative linear seesaw model, dark matter, and U(1)B−L. Phys Rev. D (2015) 92:095001. doi: 10.1103/PhysRevD.92.095001
37. Kajiyama Y, Okada H, Toma T. Multicomponent dark matter particles in a two-loop neutrino model. Phys Rev. D (2013) 88:015029. doi: 10.1103/PhysRevD.88.015029
38. Baek S, Okada H, Toma T. Two loop neutrino model and dark matter particles with global B-L symmetry. J Cosmol Astrop Phys. (2014) 1406:027. doi: 10.1088/1475-7516/2014/06/027
39. Aoki M, Kubo J, Takano H. Two-loop radiative seesaw mechanism with multicomponent dark matter explaining the possible excess in the Higgs boson decay and at the Fermi LAT. Phys Rev. D (2013) 87:116001. doi: 10.1103/PhysRevD.87.116001
40. Aoki M, Kubo J, Takano H. Multicomponent dark matter in radiative seesaw model and monochromatic neutrino flux. Phys Rev. D (2014) 90:076011. doi: 10.1103/PhysRevD.90.076011
41. Ma E. Supersymmetric model of radiative seesaw majorana neutrino masses. Ann Fond Broglie (2006) 31:285.
42. Ma E. Supersymmetric U(1) Gauge realization of the dark scalar doublet model of radiative neutrino mass. Mod Phys Lett. A (2008) 23:721–5. doi: 10.1142/S0217732308026753
43. Fukuoka H, Kubo J, Suematsu D. Anomaly induced dark matter decay and PAMELA/ATIC experiments. Phys Lett. B (2009) 678:401–6. doi: 10.1016/j.physletb.2009.06.048
44. Fukuoka H, Suematsu D, Toma T. Signals of dark matter in a supersymmetric two dark matter model. J Cosmol Astrop Phys. (2011) 1107:001. doi: 10.1088/1475-7516/2011/07/001
45. Suematsu D, Toma T. Dark matter in the supersymmetric radiative seesaw model with an anomalous U(1) symmetry. Nucl Phys. B (2011) 847:567–89. doi: 10.1016/j.nuclphysb.2011.02.007
46. Aoki M, Kubo J, Okawa T, Takano H. Impact of inert higgsino dark matter. Phys Lett. B (2012) 707:107–15. doi: 10.1016/j.physletb.2011.12.012
47. Cai Y, Herrero-Garca J, Schmidt MA, Vicente A, Volkas RR. From the trees to the forest: a review of radiative neutrino mass models. (2017). e-Print: arXiv:1706.08524 [hep-ph].
48. Kubo J, Ma E, Suematsu D. Cold dark matter, radiative neutrino mass, μ → eγ, and neutrinoless double beta decay. Phys Lett. B (2006) 642:18–23. doi: 10.1016/j.physletb.2006.08.085
49. Bouchand R, Merle A. Running of radiative neutrino masses: the scotogenic model. J High Energy Phys. (2012) 07:084. doi: 10.1007/JHEP07(2012)084
50. Merle A, Platscher M. Running of radiative neutrino masses: the scotogenic model − revisited. J High Energy Phys. (2015) 11:148. doi: 10.1007/JHEP11(2015)148
51. Ma E, Raidal M. Neutrino mass, muon anomalous magnetic moment, and lepton flavor nonconservation. Phys Rev Lett. (2001) 87:011802. doi: 10.1103/PhysRevLett.87.011802
52. Suematsu D, Toma T, Yoshida T. Reconciliation of CDM abundance and μ → eγ in a radiative seesaw model. Phys Rev. D (2009) 79:093004. doi: 10.1103/PhysRevD.79.093004
53. Aoki M, Kanemura S. Probing the Majorana nature of TeV-scale radiative seesaw models at collider experiments. Phys Lett. B (2010) 689:28–35. doi: 10.1016/j.physletb.2010.04.024
54. Suematsu D, Toma T, Yoshida T. Enhancement of the annihilation of dark matter in a radiative seesaw model. Phys Rev. D (2010) 82:013012. doi: 10.1103/PhysRevD.82.013012
55. Schmidt D, Schwetz T, Toma T. Direct detection of leptophilic dark matter in a model with radiative neutrino masses. Phys Rev. D (2012) 85:073009. doi: 10.1103/PhysRevD.85.073009
56. Hehn D, Ibarra A. A radiative model with a naturally mild neutrino mass hierarchy. Phys Lett. B (2013) 718:988–91. doi: 10.1016/j.physletb.2012.11.034
57. Toma T, Vicente A. Lepton flavor violation in the scotogenic model. J High Energy Phys. (2014) 01:160. doi: 10.1007/JHEP01(2014)160
58. Ibarra A, Yaguna CE, Zapata O. Direct detection of fermion dark matter in the radiative seesaw model. Phys Rev. D (2016) 93:035012. doi: 10.1103/PhysRevD.93.035012
59. Merle A, Platscher M, Rojas N, Valle JWF, Vicente A. Consistency of WIMP Dark Matter as radiative neutrino mass messenger. J High Energy Phys. (2016) 07:013. doi: 10.1007/JHEP07(2016)013
60. Lindner M, Platscher M, Yaguna CE, Merle A. Fermionic WIMPs and vacuum stability in the scotogenic model. Phys Rev. D (2016) 94:115027. doi: 10.1103/PhysRevD.94.115027
61. Hessler AG, Ibarra A, Molinaro E, Vogl S. Probing the scotogenic FIMP at the LHC. J High Energy Phys. (2017) 01:100. doi: 10.1007/JHEP01(2017)100
62. Aristizabal Sierra D, Kubo J, Restrepo D, Suematsu D, Zapata O. Radiative seesaw: warm dark matter, collider and lepton flavour violating signals. Phys Rev. D (2009) 79:013011. doi: 10.1103/PhysRevD.79.013011
63. Gelmini GB, Osoba E, Palomares-Ruiz S. Inert-sterile neutrino: cold or warm dark matter candidate. Phys Rev. D (2010) 81:063529. doi: 10.1103/PhysRevD.81.063529
64. Ma E. Radiative scaling neutrino mass and warm dark matter. Phys Lett. B (2012) 717:235–7. doi: 10.1016/j.physletb.2012.09.046
65. Bhattacharya S, Poulose P, Ghosh P. Multipartite interacting scalar dark matter in the light of updated LUX data. J Cosmol Astrop Phys. (2017) 1704:043. doi: 10.1088/1475-7516/2017/04/043
66. Berezhiani ZG, Khlopov MYu. Physics of cosmological dark matter in the theory of broken family symmetry. (In Russian). Sov J Nucl Phys. (1990) 52:60–4.
67. Berezhiani ZG, Khlopov MYu. Cosmology of spontaneously broken gauge family symmetry. Z Phys. C (1991) 49:73–8.
68. Hur T, Lee HS, Nasri S. A supersymmetric U(1)-prime model with multiple dark matters. Phys Rev. D (2008) 77:015008. doi: 10.1103/PhysRevD.77.015008
69. Zurek KM. Multi-component dark matter. Phys Rev. D (2009) 79:115002. doi: 10.1103/PhysRevD.79.115002
70. Batell B. Dark discrete gauge symmetries. Phys Rev. D (2011) 83:035006. doi: 10.1103/PhysRevD.83.035006
71. Dienes KR, Thomas B. Dynamical dark matter: I. Theoretical overview. Phys Rev. D (2012) 85:083523. doi: 10.1103/PhysRevD.85.083523
72. Dienes KR, Thomas B. Dynamical dark matter: II. An explicit model. Phys Rev. D (2012) 85:083524. doi: 10.1103/PhysRevD.85.083524
73. Ivanov IP, Keus V. Zp scalar dark matter from multi-Higgs-doublet models. Phys Rev. D (2012) 86:016004. doi: 10.1103/PhysRevD.86.016004
74. Dienes KR, Su S, Thomas B. Distinguishing dynamical dark matter at the LHC. Phys Rev. D (2012) 86:054008. doi: 10.1103/PhysRevD.86.054008
75. D'Eramo F, McCullough M, Thaler J. Multiple gamma lines from semi-annihilation. J Cosmol Astrop Phys. (2013) 1304:030. doi: 10.1088/1475-7516/2013/04/030
76. Gu PH. Multi-component dark matter with magnetic moments for Fermi-LAT gamma-ray line. Phys Dark Univ. (2013) 2:35–40. doi: 10.1016/j.dark.2013.03.001
77. Bhattacharya S, Drozd A, Grzadkowski B, Wudka J. Two-component dark matter. J High Energy Phys. (2013) 10:158. doi: 10.1007/JHEP10(2013)158
78. Bhattacharya S, Drozd A, Grzadkowski B, Wudka J. Constraints on two-component dark matter. Acta Phys Polon. B (2013) 44:2373–9. doi: 10.5506/APhysPolB.44.2373
79. Geng CQ, Huang D, Tsai LH. Imprint of multicomponent dark matter on AMS-02. Phys Rev. D (2014) 89:055021. doi: 10.1103/PhysRevD.89.055021
80. Boddy KK, Feng JL, Kaplinghat M, Tait TMP. Self-interacting dark matter from a non-abelian hidden sector. Phys Rev. D (2014) 89:115017. doi: 10.1103/PhysRevD.89.115017
81. Geng CQ, Huang D, Tsai LH. Cosmic ray excesses from multi-component dark matter decays. Mod Phys Lett. A (2014) 29:1440003. doi: 10.1142/S0217732314400033
82. Esch S, Klasen M, Yaguna CE. A minimal model for two-component dark matter. J High Energy Phys. (2014) 09:108. doi: 10.1007/JHEP09(2014)108
83. Geng CQ, Huang D, Lai C. Multi-component dark matter. Int J Mod Phys. A (2015) 30:1545009. doi: 10.1142/S0217751X15450098
84. Arcadi G, Gross C, Lebedev O, Mambrini Y, Pokorski S, Toma T. Multicomponent dark matter from gauge symmetry. J High Energy Phys. (2016) 12:081. doi: 10.1007/JHEP12(2016)081
85. DiFranzo A, Mohlabeng G. Multi-component dark matter through a radiative higgs portal. J High Energy Phys. (2017) 01:080. doi: 10.1007/JHEP01(2017)080
86. Aoki M, Toma T. Implications of two-component dark matter induced by forbidden channels and thermal freeze-out. J Cosmol Astrop Phys. (2017) 1701:042. doi: 10.1088/1475-7516/2017/01/042
87. Aoki M, Duerr M, Kubo J, Takano H. Multi-component dark matter systems and their observation prospects. Phys Rev. D (2012) 86:076015. doi: 10.1103/PhysRevD.86.076015
88. Ade PAR, Aghanim N, Armitage-Caplan C, Arnaud M, Ashdown M, Atrio-Barandela F, et al. Planck 2013 results. XVI. Cosmological parameters. Astron Astrophys. (2014) 571:A16. doi: 10.1051/0004-6361/201321591
89. D'Eramo F, Thaler J. Semi-annihilation of dark matter. J High Energy Phys. (2010) 06:109. doi: 10.1007/JHEP06(2010)109
90. Belanger G, Kannike K, Pukhov A, Raidal M. Impact of semi-annihilations on dark matter phenomenology - an example of ZN symmetric scalar dark matter. J Cosmol Astrop Phys. (2012) 1204:010. doi: 10.1088/1475-7516/2012/04/010
91. Belanger G, Kannike K, Pukhov A, Raidal M. Z3 scalar singlet dark matter. J Cosmol Astrop Phys. (2013) 1301:022. doi: 10.1088/1475-7516/2013/01/022
92. Ko P, Tang Y. Self-interacting scalar dark matter with local Z3 symmetry. J Cosmol Astrop Phys. (2014) 1405:047. doi: 10.1088/1475-7516/2014/05/047
93. Blanger G, Kannike K, Pukhov A, Raidal M. Minimal semi-annihilating ℤN scalar dark matter. J Cosmol Astrop Phys. (2014) 1406:021. doi: 10.1088/1475-7516/2014/06/021
94. Aoki M, Toma T. Impact of semi-annihilation of ℤ3 symmetric dark matter with radiative neutrino masses. J Cosmol Astrop Phys. (2014) 1409:016. doi: 10.1088/1475-7516/2014/09/016
95. Ding R, Han ZL, Liao Y, Xie WP. Radiative neutrino mass with3 dark matter: from relic density to LHC signatures. J High Energy Phys. (2016) 05:030. doi: 10.1007/JHEP05(2016)030
96. Hambye T. Hidden vector dark matter. J High Energy Phys. (2009) 01:028. doi: 10.1088/1126-6708/2009/01/028
97. Arina C, Hambye T, Ibarra A, Weniger C. Intense gamma-ray lines from hidden vector dark matter decay. J Cosmol Astrop Phys. (2010) 1003:024. doi: 10.1088/1475-7516/2010/03/024
98. Khoze VV, McCabe C, Ro G. Higgs vacuum stability from the dark matter portal. J High Energy Phys. (2014) 08:026. doi: 10.1007/JHEP08(2014)026
99. Boehm C, Dolan MJ, McCabe C. A weighty interpretation of the Galactic Centre excess. Phys Rev. D (2014) 90:023531. doi: 10.1103/PhysRevD.90.023531
100. 't Hooft G. Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking. NATO Sci Ser B. (1980) 59:135–57.
101. Ellis JR, Ferstl A, Olive KA. Reevaluation of the elastic scattering of supersymmetric dark matter. Phys Lett. B (2000) 481:304–14. doi: 10.1016/S0370-2693(00)00459-7
102. Akerib DS, Alsum S, Araśjo HM, Bai X, Bailey AJ, Balajthy J, et al. Results from a search for dark matter in the complete LUX exposure. Phys Rev Lett. (2017) 118:021303. doi: 10.1103/PhysRevLett.118.021303
103. Aprile E, Aalbers J, Agostini F, Alfonsi M, Amaro FD, Anthony M, et al. First dark matter search results from the XENON1T experiment. (2017). e-Print: arXiv:1705.06655 [astro-ph.CO].
104. Wu H, Zheng S. Scalar dark matter: real vs complex. J High Energy Phys. (2017) 03:142. doi: 10.1007/JHEP03(2017)142
105. Arcadi G, Dutra M, Ghosh P, Lindner M, Mambrini Y, Pierre M, et al. The waning of the WIMP? A review of models, searches, and constraints. (2017). e-Print: arXiv:1703.07364 [hep-ph].
106. Athron P, Balzs C, Bringmann T, Buckley A, Chrzaszcz M, Conrad J, et al. Status of the scalar singlet dark matter model. Eur Phys J. C (2017) 77:568. doi: 10.1140/epjc/s10052-017-5113-1
107. Baldini AM, Bao Y, Baracchini E, Bemporad C, Berg F, Biasotti M, et al. Search for the lepton flavour violating decay μ+→e+γ with the full dataset of the MEG experiment. Eur Phys J. C (2016) 76:434. doi: 10.1140/epjc/s10052-016-4271-x
108. Barbieri R, Hall LJ, Rychkov VS. Improved naturalness with a heavy Higgs: an Alternative road to LHC physics. Phys Rev. D (2006) 74:015007. doi: 10.1103/PhysRevD.74.015007
109. Baak M, Cth J, Haller J, Hoecker A, Kogler R, Mnig K, et al. The global electroweak fit at NNLO and prospects for the LHC and ILC. Eur Phys J. C (2014) 74:3046. doi: 10.1140/epjc/s10052-014-3046-5
110. Silk J, Olive KA, Srednicki M. The photino, the sun and high-energy neutrinos. Phys Rev Lett. (1985) 55:257–9. doi: 10.1103/PhysRevLett.55.257
111. Krauss LM, Srednicki M, Wilczek F. Solar system constraints and signatures for dark matter candidates. Phys Rev. D (1986) 33:2079–83. doi: 10.1103/PhysRevD.33.2079
112. Freese K. Can scalar neutrinos or massive dirac neutrinos be the missing mass? Phys Lett. (1986) 167B:295–300. doi: 10.1016/0370-2693(86)90349-7
113. Gaisser TK, Steigman G, Tilav S. Limits on cold dark matter candidates from deep underground detectors. Phys Rev. D (1986) 34:2206. doi: 10.1103/PhysRevD.34.2206
114. Griest K, Seckel D. Cosmic asymmetry, neutrinos and the sun. Nucl Phys. B (1987) 283:681–705. doi: 10.1016/0550-3213(87)90293-8
115. Ritz S, Seckel D. Detailed neutrino spectra from cold dark matter annihilations in the sun. Nucl Phys. B (1988) 304:877–908. doi: 10.1016/0550-3213(88)90660-8
116. Bertone G, Hooper D, Silk J. Particle dark matter: evidence, candidates and constraints. Phys Rept. (2005) 405:279–390. doi: 10.1016/j.physrep.2004.08.031
117. Silk J, Moore B, Diemand J, Bullock J, Kaplinghat M, Strigari L, et al. Particle Dark Matter: Observations, Models and Searches. Bertone G, editor. Cambridge: Cambridge University Press (2010). Available online at: http://www.cambridge.org/uk/catalogue/catalogue.asp?isbn=9780521763684
118. Kamionkowski M. Energetic neutrinos from heavy neutralino annihilation in the sun. Phys Rev. D (1991) 44:3021–42. doi: 10.1103/PhysRevD.44.3021
119. Kamionkowski M, Griest K, Jungman G, Sadoulet B. Model independent comparison of direct versus indirect detection of supersymmetric dark matter. Phys Rev Lett. (1995) 74:5174–7. doi: 10.1103/PhysRevLett.74.5174
120. Jungman G, Kamionkowski M, Griest K. Supersymmetric dark matter. Phys Rept. (1996) 267:195–373. doi: 10.1016/0370-1573(95)00058-5
121. Agrawal P, Dolle EM, Krenke CA. Signals of inert doublet dark matter in neutrino telescopes. Phys Rev. D (2009) 79:015015. doi: 10.1103/PhysRevD.79.015015
122. Andreas S, Tytgat MHG, Swillens Q. Neutrinos from inert doublet dark matter. J Cosmol Astrop Phys. (2009) 0904:004. doi: 10.1088/1475-7516/2009/04/004
123. Aartsen MG, Ackermann M, Adams J, Aguilar JA, Ahlers M, Ahrens M, et al. Search for annihilating dark matter in the Sun with 3 years of IceCube data. Eur Phys J. C (2017) 77:146. doi: 10.1140/epjc/s10052-017-4689-9
124. Lee BW, Weinberg S. Cosmological lower bound on heavy neutrino masses. Phys Rev Lett. (1977) 39:165–8. doi: 10.1103/PhysRevLett.39.165
126. Fukugita M, Yanagida T. Baryogenesis without grand unification. Phys Lett. B (1986) 174:45–7. doi: 10.1016/0370-2693(86)91126-3
127. Rozo E, Wechsler RH, Rykoff ES, Annis JT, Becker MR, Evrard AE, et al. Cosmological constraints from the SDSS maxBCG cluster catalog. Astrophys J. (2010) 708:645–60. doi: 10.1088/0004-637X/708/1/645
128. Riess AG, Macri L, Casertano S, Lampeitl H, Ferguson HC, Filippenko AV, et al. A 3% solution: determination of the hubble constant with the hubble space telescope and wide field camera 3. Astrophys J. (2011) 730:119. doi: 10.1088/0004-637X/730/2/119
129. Heymans C, Grocutt E, Heavens A, Kilbinger M, Kitching TD, Simpson F, et al. CFHTLenS tomographic weak lensing cosmological parameter constraints: mitigating the impact of intrinsic galaxy alignments. Mon Not R Astron Soc. (2013) 432:2433. doi: 10.1093/mnras/stt601
130. Benjamin J, Van Waerbeke L, Heymans C, Kilbinger M, Erben T, Hildebrandt H, et al. CFHTLenS tomographic weak lensing: quantifying accurate redshift distributions. Mon Not R Astron Soc. (2013) 431:1547. doi: 10.1093/mnras/stt276
131. Ade PAR, Aghanim N, Armitage-Caplan C, Arnaud M, Ashdown M, Atrio-Barandela F, et al. Planck 2013 results. XX. Cosmology from Sunyaev−Zeldovich cluster counts. Astron Astrophys. (2014) 571:A20. doi: 10.1051/0004-6361/201321521
132. Hamann J, Hasenkamp J. A new life for sterile neutrinos: resolving inconsistencies using hot dark matter. J Cosmol Astrop Phys. (2013) 1310:044. doi: 10.1088/1475-7516/2013/10/044
133. Wyman M, Rudd DH, Vanderveld RA, Hu W. Neutrinos help reconcile planck measurements with the local universe. Phys Rev Lett. (2014) 112:051302. doi: 10.1103/PhysRevLett.112.051302
134. Battye RA, Moss A. Evidence for massive neutrinos from cosmic microwave background and lensing observations. Phys Rev Lett. (2014) 112:051303. doi: 10.1103/PhysRevLett.112.051303
135. Dvorkin C, Wyman M, Rudd DH, Hu W. Neutrinos help reconcile Planck measurements with both the early and local Universe. Phys Rev. D (2014) 90:083503. doi: 10.1103/PhysRevD.90.083503
136. Archidiacono M, Fornengo N, Gariazzo S, Giunti C, Hannestad S, Laveder M. Light sterile neutrinos after BICEP-2. J Cosmol Astrop Phys. (2014) 1406:031. doi: 10.1088/1475-7516/2014/06/031
137. Zhang JF, Li YH, Zhang X. Sterile neutrinos help reconcile the observational results of primordial gravitational waves from Planck and BICEP2. Phys Lett. B (2015) 740:359–63. doi: 10.1016/j.physletb.2014.12.012
138. Battye RA, Charnock T, Moss A. Tension between the power spectrum of density perturbations measured on large and small scales. Phys Rev. D (2015) 91:103508. doi: 10.1103/PhysRevD.91.103508
139. Feng L, Zhang JF, Zhang X. A search for sterile neutrinos with the latest cosmological observations. Eur Phys J. C (2017) 77:418. doi: 10.1140/epjc/s10052-017-4986-3
140. Steigman G. Neutrinos and big bang nucleosynthesis. Adv High Energy Phys. (2012) 2012:268321. doi: 10.1155/2012/268321
141. Anchordoqui LA, Goldberg H. Neutrino cosmology after WMAP 7-Year data and LHC first Z' bounds. Phys Rev Lett. (2012) 108:081805. doi: 10.1103/PhysRevLett.108.081805
142. Steigman G, Dasgupta B, Beacom JF. Precise relic WIMP abundance and its impact on searches for dark matter annihilation. Phys Rev. D (2012) 86:023506. doi: 10.1103/PhysRevD.86.023506
143. Anderhalden D, Diemand J, Bertone G, Maccio AV, Schneider A. The galactic halo in mixed dark matter cosmologies. J Cosmol Astrop Phys. (2012) 1210:047. doi: 10.1088/1475-7516/2012/10/047
144. Anchordoqui LA, Goldberg H, Steigman G. Right-handed neutrinos as the dark radiation: status and forecasts for the LHC. Phys Lett. B (2013) 718:1162–5. doi: 10.1016/j.physletb.2012.12.019
145. Anderhalden D, Schneider A, Maccio AV, Diemand J, Bertone G. Hints on the nature of dark matter from the properties of milky way satellites. J Cosmol Astrop Phys. (2013) 1303:014. doi: 10.1088/1475-7516/2013/03/014
146. Weinberg S. Goldstone bosons as fractional cosmic neutrinos. Phys Rev Lett. (2013) 110:241301. doi: 10.1103/PhysRevLett.110.241301
147. Husdal L. On effective degrees of freedom in the early universe. Galaxies (2016) 4:78. doi: 10.3390/galaxies4040078
148. Patrignani C, Agashe K, Aielli G, Amsler C, Antonelli M, Asner DM, et al. Review of particle physics. Chin Phys. C (2016) 40:100001. doi: 10.1088/1674-1137/40/10/100001
149. Djouadi A. The anatomy of electro-weak symmetry breaking. II. The Higgs bosons in the minimal supersymmetric model. Phys Rept. (2008) 459:1–241. doi: 10.1016/j.physrep.2007.10.005
Keywords: neutrino mass, dark matter, radiative seesaw mechanism, flavor physics, dark radiation
Citation: Aoki M, Kaneko D and Kubo J (2017) Multicomponent Dark Matter in Radiative Seesaw Models. Front. Phys. 5:53. doi: 10.3389/fphy.2017.00053
Received: 04 August 2017; Accepted: 10 October 2017;
Published: 01 November 2017.
Edited by:
Frank Franz Deppisch, University College London, United KingdomReviewed by:
Arindam Das, Korea Institute for Advanced Study, South KoreaMichael Duerr, Deutsches Elektronen-Synchrotron (HZ), Germany
Copyright © 2017 Aoki, Kaneko and Kubo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mayumi Aoki, bWF5dW1pQGhlcC5zLmthbmF6YXdhLXUuYWMuanA=
 Mayumi Aoki
Mayumi Aoki Daiki Kaneko
Daiki Kaneko Jisuke Kubo
Jisuke Kubo