Value of the Axial-Vector Coupling Strength in β and ββ Decays: A Review

In this review the quenching of the weak axial-vector coupling strength, g_A, is discussed in nuclear β and double-β decays. On one hand, the nuclear-medium and nuclear many-body effects are separated, and on the other hand the quenching is discussed from the points of view of different many-body methods and different β-decay and double-β-decay processes. Both the historical background and the present status are reviewed and contrasted against each other. The theoretical considerations are tied to performed and planned measurements, and possible new measurements are urged, whenever relevant and doable. Relation of the quenching problem to the measurements of charge-exchange reactions and muon-capture rates is pointed out.

1. Introduction

The neutrinoless double beta (0νββ) decays of atomic nuclei are of great experimental and theoretical interest due to their implications of physics beyond the standard model of electroweak interactions. Since these processes occur in nuclei, nuclear-structure effects play an important role and they may affect considerably the decay rates. The nuclear effects are summarized as the nuclear matrix elements (NMEs) containing information about the initial and final states of the nucleus and the action of the 0νββ transition operator on them. The NMEs, in turn, are computed numerically using some nuclear-theory framework suitable for the nuclei under consideration. The possible future detection of the 0νββ decay in the next generation of ββ experiments constantly drives nuclear-structure calculations toward better performance. Accurate knowledge of the NMEs is required in order that the data will be optimally used to obtain information about the fundamental nature and mass of the neutrino [1–7]. In addition, the 0νββ decay relates also to the breaking of lepton-number symmetry and the baryon asymmetry of the Universe [8, 9]. A number of nuclear models, including configuration-interaction based models like the interacting shell model (ISM), and various mean field models, have been adopted for the calculations. The resulting computed NMEs have been analyzed in the review articles [4, 10–12]. Most of the calculations have been done by the use of the proton-neutron quasiparticle random-phase approximation (pnQRPA) [13].

The performed 0νββ-decay calculations, as also those of the two-neutrino double beta (2νββ) decay, indicate that the following nuclear-structure ingredients affect the values of NMEs:

(a) The chosen valence space of single-particle orbitals and their nucleon occupancies [14–16].

(b) The effects stemming from the shell closures [10, 17]. These closures are formed by the bunching of single-particle orbitals in the nuclear mean-field potential to form the so-called major shells that are separated by large energy gaps. The gaps occur at “magic numbers” of nucleons and have sometimes drastic effects on nuclear properties.

(c) The nuclear deformation and seniority truncation [18–22]. In ground states of even-even (even number of protons and neutrons) nuclei all nucleons are paired to angular momentum zero and form a superfluid-like state with total angular momentum zero. This is called seniority-zero state. If one pair is broken, extra angular momentum is generated and this contributes to excited states of nuclei. These are called seniority-two states. Breaking more pairs generates higher-seniority states that can mix with the lower-seniority states by the nuclear residual interaction. Cutting the higher-seniority contributions, i.e., performing a seniority truncation, simplifies calculations considerably.

(d) Also, it has to be noted that the adopted closure approximation, i.e., omitting the energy dependence of the involved energy denominator and replacing the contributions coming from the intermediate virtual states by a unit operator (for all other nuclear models, except for the quasiparticle random-phase approximation, QRPA), for the 0νββ-decay calculations does not hold for the calculations of the 2νββ-decay rates [1, 23, 24].

(e) A further important aspect can be added to the list, namely the uncertain value of the weak axial-vector coupling strength g_A, leading to an effective value of g_A in nuclear-model calculations. This deviation (usually quenching) from the free-nucleon value can arise from the nuclear medium effects and the nuclear many-body effects described in more detail in the following sections of this review.

At the nuclear level, β decay can be considered as a mutual interaction of the hadronic and leptonic currents mediated by massive vector bosons W^± [25]. The leptonic and hadronic currents can be expressed as mixtures of vector and axial-vector contributions [26–28]. The weak vector and axial-vector coupling strengths g_V and g_A enter the theory when the hadronic current is renormalized at the nucleon level [29]. The conserved vector-current hypothesis (CVC) [26] and partially conserved axial-vector-current hypothesis (PCAC) [30, 31] yield the free-nucleon values g_V = 1.00 and g_A = 1.27 [25] but inside nuclear matter the value of g_A is affected by many-nucleon correlations and a quenched or enhanced value might be needed to reproduce experimental observations [32–35]. Precise information on the effective value of g_A is crucial when predicting half-lives of neutrinoless double beta decays since the half-lives are proportional to the fourth power of g_A [1, 36].

Since the vector bosons W^± have large mass and thus propagate only a short distance, the hadronic current and the leptonic current can be considered to interact at a point-like weak-interaction vertex with an effective coupling strength G_F, the Fermi constant. The parity non-conserving nature of the weak interaction forces the hadronic current to be written at the quark level (up quark u and down quark d) as a mixture of vector and axial-vector parts:

$\begin{array}{ll}{J}_H^{\mu }=ū(x){\gamma }^{\mu }(1-{\gamma }_5)d(x),& (1)\end{array}$

where γ^μ are the usual Dirac matrices and ${\gamma }_5=i{\gamma }^0{\gamma }^1{\gamma }^2{\gamma }^3$. Renormalization effects of strong interactions and energy scale of the processes must be taken into account when moving from the quark level to the hadron level. Then the hadronic current between nucleons (neutron n and proton p) takes the rather complex form

$\begin{array}{ll}{J}_H^{\mu }=\bar{p}(x)\left[V^{\mu }-A^{\mu }\right]n(x),& (2)\end{array}$

where the vector-current part can be written as

$\begin{array}{ll}{V}^{\mu }=g_{\text{V}}(q^2){\gamma }^{\mu }+\mathrm{\text{i}}{g}_{\text{M}}(q^2)\frac{{\sigma }^{\mu \nu }}{2m_{\text{N}}}{q}_{\nu }& (3)\end{array}$

and the axial-vector-current part as

$\begin{array}{ll}{A}^{\mu }=g_{\text{A}}(q^2){\gamma }^{\mu }{\gamma }_5+g_{\text{P}}(q^2)q^{\mu }{\gamma }_5.& (4)\end{array}$

Here q^μ is the momentum transfer, q² its magnitude, m_N the nucleon mass (roughly 1 GeV) and the weak couplings depend on the magnitude of the exchanged momentum. For the vector and axial-vector couplings one usually adopts the dipole approximation

$\begin{array}{ll}\begin{array}{c}{g}_{\text{V}}(q^2)=\frac{g_{\text{V}}}{{\left(1+q^2/M_{\text{V}}^2\right)}^2};g_{\text{A}}(q^2)=\frac{g_{\text{A}}}{{\left(1+q^2/M_{\text{A}}^2\right)}^2},\end{array}& (5)\end{array}$

where g_V and g_A are the weak vector and axial-vector coupling strengths at zero momentum transfer (q² = 0), respectively. For the vector and axial masses one usually takes M_V = 84 MeV [37] and M_A ~ 1 GeV [37–39] coming from the accelerator-neutrino phenomenology. For the weak magnetism term one can take $g_{\text{M}}(q^2)=({\mu }_p-{\mu }_n)g_{\text{V}}(q^2)$ and for the induced pseudoscalar term it is customary to adopt the Goldberger-Treiman relation [40] $g_{\text{P}}(q^2)=2m_{\text{N}}{g}_{\text{A}}(q^2)/(q^2+m_{\pi }^2)$, where m_π is the pion mass and μ_p − μ_n = 3.70 is the anomalous magnetic moment of the nucleon. It should be noted that the β decays and 2νββ decays are low-energy processes (few MeV) involving only the vector [first term in Equation (3)] and axial-vector [first term in Equation (4)] parts at the limit q² = 0 so that the q dependence of Equation (5) does not play any role in the treatment of these processes in this review. Contrary to this, the 0νββ decays and nuclear muon-capture transitions involve momentum transfers of the order of 100 MeV and the full expression (2) is active with slow decreasing trend of the coupling strengths according to Equation (5).

2. Effective Values of g_A: Preamble

The effective value of g_A can simply be characterized by a renormalization factor q (in case of quenching of the value of g_A it is customarily called quenching factor):

$\begin{array}{ll}q=\frac{g_{\text{A}}}{g_{\text{A}}^{\text{free}}},& (6)\end{array}$

where

$\begin{array}{ll}{g}_{\text{A}}^{\text{free}}=1.2723(23)& (7)\end{array}$

is the free-nucleon value of the axial-vector coupling measured in neutron beta decay [41] and g_A is the value of the axial-vector coupling derived from a given theoretical or experimental analysis. This derived g_A can be called the effective g_A so that from (6) one obtains for its value

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=q{g}_{\text{A}}^{\text{free}}.& (8)\end{array}$

Equations (6)−(8) constitute the basic definitions used in this review.

The effective value of g_A can be derived from several different experimental and theoretical analyses. In these analyses it is mostly impossible to separate the different sources of renormalization affecting the value of g_A: (i) the meson-exchange currents (many-body currents) that are beyond the one-nucleon impulse approximation (only one nucleon experiences the weak decay without interference from the surrounding nuclear medium), usually assumed in the theoretical calculations, (ii) other nuclear medium effects like interference from non-nucleonic degrees of freedom, e.g., the Δ isobars and (iii) the deficiencies in the nuclear many-body approach that deteriorate the quality of the wave functions involved in the decay processes.

The effects (i) and (ii) can be studied by performing calculations using meson-exchange models and allowing non-nucleonic degrees of freedom in the calculations. These calculations that go beyond the nucleonic impulse approximation are described in section 3 in the context of Gamow-Teller β decays for which the related effects are measurable. The calculations yield a fundamental quenching factor q_F and the related fundamentally renormalized effective g_A for the space components (μ = 1, 2, 3) of the axial current (4) via the effects of the virtual pion cloud around a nucleon. The time component of μ = 0, the axial charge ρ₅, is, however, fundamentally enhanced by, e.g., heavy meson exchange and the corresponding effective coupling $g_{\text{A}}^{\text{eff}}({\gamma }_5)$ is discussed in section 8.2, in the context of first-forbidden 0⁺ ↔ 0⁻ transitions for which the effect is measurable.

The ISM has the longest history behind it in studies of the axial quenching in Gamow-Teller β decays. The reason for this is the success of the ISM to describe nuclear spectroscopy of light nuclei and the rather large amount of data on these type of allowed β decays. The results of these studies are presented in section 5. In the same section the ISM results are compared with those obtained by the use of the pnQRPA. In section 6.2 the effective value of g_A is analyzed for the first-forbidden unique β decays for which there are some experimental data available. In section 7 this study is extended to higher-forbidden unique β decays where no experimental data are available and one has to resort to mere theoretical speculations. In section 8 the forbidden non-unique β decays are discussed. Experimentally, there are available data for the above-mentioned first-forbidden non-unique 0⁺ ↔ 0⁻ and other β transitions. For the higher-forbidden non-unique transitions, discussed in section 9, there are scattered half-life and β-spectrum data but more measurements are urgently needed, in particular for the shapes of the β spectra. Unfortunately, in all these studies it is not possible to completely disentangle the nuclear-medium effects (i) and (ii) from the nuclear-model effects (iii).

In the last two sections, 11, 12 more exotic methods to extract the in-medium value of g_A are presented: The spin-multipole strength functions and nuclear muon capture. Measurements of the spin-multipole strength functions, in particular the location of the corresponding giant resonances, help theoretical calculations fine-tune the parameters of the model Hamiltonians such that the low-lying strength of, say 2⁻ states, is closer to reality. Hence, more such measurements are called for. The nuclear muon capture probes the axial current (4) at 100 MeV of momentum transfer and thus suits perfectly for studies of the renormalization of the NMEs related to 0νββ decays. This means that muon-capture experiments for medium-heavy nuclei are urgently needed.

The renormalization of g_A which stems from the nuclear-model effects (iii) depends on the nuclear-theory framework chosen to describe the nuclear many-body wave functions involved in the weak processes, like β and ββ decays. This is why the effective values of g_A can vary from one nuclear model to the other. On the other hand, the different model frameworks can give surprisingly similar results as witnessed in section 9 in the context of the comparison of the measured β spectra with the computed ones. The renormalization of g_A can also depend on the process in question. For the zero-momentum-exchange (q² = 0) processes, like β and 2νββ decays, the renormalization can be different from the high-momentum-exchange (q² ~ 100 MeV) processes, like 0νββ decays (in section 9 the related g_A is denoted as $g_{\text{A},0\nu }^{\text{eff}}$) or nuclear muon captures.

This introduction to the many-faceted renormalization of the axial-vector coupling is supposed to enable a “soft landing” into the review that follows. As can be noticed, the renormalization issue is far from being solved and lacks a unified picture thus far. There is not yet a coherent effort to solve the issue, but rather some sporadic attempts here and there. The most critical issue may be the nuclear many-body deficiencies (iii) that hinder a quantitative assessment of the nuclear-medium effects (i) and (ii) in light, medium-heavy and heavy nuclei. Only gradually this state of affairs will improve with the progress in the ab-initio nuclear methods extendable to nuclei beyond the very lightest ones. Hence, the lack of perfect nuclear many-body theory is reflected in this review as a wide collection of different effective g_A variants, different for different theory frameworks and processes and not necessarily connected to each other (yet). The hope is that in the future the different studies would point to one common low-energy renormalization of g_A for the β and two-neutrino ββ decays and that we would have some idea about the renormalization mechanisms at work in the case of the neutrinoless ββ decays.

On the other hand, there are some attempts to disentangle the nuclear medium effects from the nuclear many-body effects. Examples are the fundamental quenching elaborated in section 3 and the nuclear-medium-independent quenching factor k introduced in section 5.2 for the Gamow-Teller β decays, and in sections 6.2, 7 for the unique-forbidden β transitions. This factor is designed to give hints about the impact of the changes in the complexity of the nuclear model on the value of the effective axial coupling. Also the previously mentioned method based on the examination of β spectra in section 9 is largely nuclear-model independent and seems to be a reasonable measure of the nuclear-medium effects (i) and (ii). More measurements of the β spectra are thus urgently called for.

3. Nuclear-Medium Effects

Based on the early shell-model studies of Gamow-Teller β decays, effects of Δ resonances and meson-exchange currents on the weak axial-vector coupling strength of the space part, A, of the axial current A^μ (4) is expected to be quenched in nuclear medium and finite nuclei. Contrary to this, the coupling strength of the time part, A⁰, of (4) is expected to be enhanced by, e.g., the contributions coming from exchanges of heavy mesons. Many of these modifications in the strengths of the axial couplings stem from processes beyond the impulse approximation where only one nucleon at a time is experiencing a weak process, e.g., β decay, without interference from the surrounding nuclear medium. In fact, based on general arguments concerning soft-pion amplitudes [42] the space part of A^μ is quenched and the time part of A^μ is enhanced relative to the single-particle processes of the impulse approximation.

The origin of the quenching of the space part of A^μ is not completely known and various mechanisms have been proposed for its origin: studied have been the Δ-isobar admixture in the nuclear wave function [43], shifting of Gamow-Teller strength to the Δ-resonance region, and renormalization effects of meson-exchange currents. The β⁻ and β⁺ Gamow-Teller strengths were related to the Δ-isobar region e.g., in Delorme et al. [44] and sizable Δ-resonance effects on β decays of low-lying nuclear states by tensor forces were reported in Oset and Rho [45] and Bohr and Mottelson [46]. In Towner and Khanna[47, 48] very simple nuclear systems were used to study the tensor force and related effects in order to minimize the impact of nuclear many-body complexities. Studied were the tensor effects and their interference with the Δ-isobar current and meson-exchange currents in building up corrections to the Gamow-Teller matrix elements. Also relativistic corrections to the Gamow-Teller operator were included. Large cancellations among the various contributions were recorded and corrections below some 20% were obtained for the light (simple) nuclei. However, recent experimental studies of (p,n) and (n,p) reactions [49] report that the Δ-nucleon-hole admixtures into low-lying nuclear states play only a minor role in the quenching of g_A, in line with the results of Suhonen [43]. Also extended sum rules have been derived for relating g_A to pion-proton total cross sections [50–52], or the method of QCD sum rules has been utilized [53].

In Wilkinson [54] the renormalization of the β-decay operator by the two- or many-nucleon correlations, in terms of inter-nucleonic and intra-nucleonic mesonic currents, leads to the notion effective “fundamentally” renormalized axial coupling g_AeF. The quenching of g_A is then described by the fundamental quenching factor q_F such that q_F > q since q contains, in addition, the quenching stemming from the inadequate treatment of the nuclear many-body problem. From here on the above notation is adopted for the renormalization of g_A stemming from the (fundamental) mesonic-current effects.

In the early study of Ericson [55] of the sum rule for Gamow-Teller matrix elements a (fundamental) quenching of roughly

$\begin{array}{ll}{q}_{\text{F}}=0.9& (9)\end{array}$

was obtained for very light nuclei (A ≤ 17) by the examination of the effects of meson-exchange currents on the pion-nucleon interaction vertex and extending the result to a sum rule for Gamow-Teller matrix elements. This (practically) model-independent study produces the following (fundamentally) renormalized value of the axial coupling strength

$\begin{array}{ll}{g}_{\text{AeF}}=0.9\times 1.27=1.1.& (10)\end{array}$

The above result does not necessarily apply to individual Gamow-Teller transitions between low-energy nuclear states.

The work of Ericson [55] was followed by the works [56, 57] where it was found that the renormalization should be universal for all transitions, in particular applicable to the mentioned Gamow-Teller transitions at low nuclear excitations. The procedure bases on the fact that the partially conserved axial current (PCAC) hypothesis [30, 31] enables one to calculate the full axial-current matrix element in terms of a pion-nucleus vertex [58]. At the low-momentum-exchange limit, relevant for the nuclear β decays, the PCAC leads to the Goldberger-Treiman relation [40, 59] which relates the effective value of g_A to the effective value of the pionic coupling constant g_π by Ericson [55]

$\begin{array}{ll}\frac{g_{\text{A}}^{\text{eff}}}{g_{\pi }^{\text{eff}}}=\frac{g_{\text{A}}^{\text{free}}}{g_{\pi }^{\text{free}}}=\frac{f_{\pi }}{\sqrt{2}{m}_{\text{N}}},& (11)\end{array}$

where m_N is the nucleon mass and f_π = 0.932m_π is the pion decay constant, m_π being the pion mass. The pionic coupling constant is, in turn, renormalized by the effects on the virtual pion field by the presence of other nucleons. For large nuclei (surface effects can be omitted) the renormalization arises from nucleonic short-range correlations leading to voids between nucleons and the renormalization can be understood via an electromagnetic analog: an electric dipole in a correlated dielectric medium is renormalized in a similar way as the pionic coupling constant. There is also a connection to the low-energy scattering of pions on nuclei: the short-range correlations quench the p-wave pion-nucleon amplitude by the same amount as the dielectric effect. For finite nuclei a model-dependent surface factor has to be taken into account [55]. The size renormalization emerges from the nuclear surface layer of a thickness of the order of the pion Compton wavelength and thus the quenching of g_A increases with increasing nuclear radius and, as a consequence, with increasing nuclear mass.

In Rho [57] the pion-nucleus vertex was calculated and the related quenched g_A agreed with the one of Ericson [55] to leading order. In infinite nuclear matter This quenching turns out to be [57]

$\begin{array}{ll}{q}_{\text{F}}^{\infty }=0.76(\mathrm{\text{infinite nuclear matter}})& (12)\end{array}$

leading to the quenched effective axial coupling strength

$\begin{array}{ll}{g}_{\text{AeF}}^{\infty }=0.76\times 1.27=0.96.(\mathrm{\text{infinite nuclear matter}})& (13)\end{array}$

in infinite nuclear matter.

The works of Ericson [55, 56] and Rho [57] were used by Wilkinson [54] to bridge the gap between the infinite nuclear matter and finite nuclei. In Wilkinson [54] it was argued that the fundamental quenching can be described by the formula

$\begin{array}{ll}{q}_{\text{F}}=\sqrt{{(q_{\text{F}}^{\infty })}^2+\left[1-{(q_{\text{F}}^{\infty })}^2\right]/A^{0.17}}& (14)\end{array}$

for finite nuclei of mass number A. This formula includes the short-range correlation effect and the finite-size factor [56, 57] and gives for the fundamental quenching, using (12), between A = 50 − 150 the value q_F = 0.88. This means that the fundamental quenching is practically constant over the range of nuclei of interest to the double beta decay. The corresponding fundamentally quenched value of the axial-vector strength is plotted in Figure 2, and its value is practically 1.1 through the whole range of interest.

In Siiskonen et al. [60] the renormalization of the axial current (and vector and induced pseudoscalar terms of the nucleonic current) was studied for several nuclear systems as a function of transition energy by including effective transition operators up to second order in perturbation theory. Thus, the renormalization of g_A contains both the fundamental and nuclear many-body aspects. It was found that the renormalization was practically constant up to 60 MeV in transition energy, in agreement with the q dependence of g_A in relation (5). The obtained quenchings are as follows

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=1.0 (1s0d\text{ shell});0.98 (1p0f\text{ shell});0.71 {(}^{56}\text{Ni});0.52{(}^{100}\text{Sn}).& (15)\end{array}$

The results (15), obtained by using the nuclear-medium-corrected transition operators have been repeated in Table 1 of section 5.1 and Figure 3 of section 5.2 in order to compare them with the more phenomenological shell-model results. Effective operators have also been used in the connection with the calculations for the double beta decays in a solvable model [69] and for the nucleus ⁹²Mo [70] and the nuclei ⁷⁶Ge and ⁸²Se [71, 72] in the framework of the interacting shell model.

TABLE 1

Table 1. Mass ranges and effective values of g_A extracted from the works of the last column.

As speculated in Wilkinson [54], the mesonic effects (meson-exchange currents) show up as effective two-body contributions to the β-decay operators. These two-body currents quench g_A and this quenching was first estimated in Menéndez [73], in the framework of the chiral effective field theory (cEFT) where both the weak currents and nuclear forces can be described on the same footing and to a given order of approximation (leading order, next-to-leading order, etc.) In Menéndez [73] the two-body currents were replaced by an effective one-body current derived from the cEFT, leading to a momentum-dependent effective coupling $g_{\text{A}}^{\text{eff}}(q^2)$, renormalized with respect to the bare axial coupling of (5). It turned out that the additional quenching is caused by the short-range nucleon-nucleon coupling present in the original two-body current. The additional quenching decreases with increasing q, being the strongest at the zero-momentum-transfer limit, affecting mostly the nuclear β and 2νββ decays. In fact, the strength of the short-range nucleon-nucleon coupling in the two-body current can be adjusted such as to reproduce the empirical quenching of the Gamow-Teller β decays discussed in section 5. As the 0νββ decay is a high-momentum-transfer process (q ~ 100 MeV) it is expected that the two-body currents have not such a drastic effect on the one-body current (4) for the 0νββ decay. Here it should be noted that the one-body current (2) has been fully taken into account in all 0νββ-decay calculations and the two-body currents introduce a renormalization, $g_{\text{A}}^{\text{eff}}(q^2)$, that deviates from the one-body dipole $g_{\text{A}}(q^2)$ of (5) the less the higher the momentum exchange q is. The quenching caused by the two-body currents could probably be measured by using charge-exchange reactions [49] in advanced nuclear-physics infrastructures.

In Menéndez [73] it was estimated, by using the ISM many-body framework in the mass range A = 48 − 136, that the effect of the two-body currents on the value of the 0νββ NME is between −35 and 10% depending on the (uncertain) values of the cEFT parameters, the smallest corrections occurring for A = 48. In Engel [74] the effect of the two-body currents was studied in the framework of the pnQRPA in the mass range A = 48 − 136, and a quenching effect of 10–22% was obtained for the 0νββ NMEs, the 10% effect pertaining to the case of ⁴⁸Ca. A more complete calculation, including three-nucleon forces and consistent treatment of the two-body currents and the nuclear Hamiltonian, was performed in Ekström [75]. Application to the Gamow-Teller β decays in ¹⁴C and ^{22, 24}O nuclei yielded the quenching q = 0.92 − 0.96 by comparison of the computed strengths to that of the Ikeda 3(N−Z) sum rule [35, 76]. This <10% quenching is in line with the trend observed in the studies [73, 74] where the quenching approaced the 10% limit for light nuclei. It should be noted that the two-body meson-exchange currents appear also in neutrino-nucleus scattering [77] but at energies where two nucleons are ejected as a result of the scattering (the so-called two-particle-two-hole exchange currents). The higher energy evokes considerable difficulties in handling the two-body meson-echange currents, as demonstrated in Simo et al. [78].

The meson-exchange currents can cause also enhancement phenomena, like in the case of the renormalization of the one-body weak axial charge density ρ₅ [time part of A^μ in (4)] in the case of the 0⁻ ↔ 0⁺ nuclear β transitions [42, 79]. In this case the γ⁵ operator mediates the first-forbidden non-unique β transition and the corresponding axial-vector coupling strength is enhanced quite strongly. In the work of Kirchbach and Reinhardt [79] the effects of a pionic two-body part of ρ₅ was studied for 4 nuclear masses and the corresponding leading single-particle transitions. This work was extended by Kirchbach et al. [80] and Towner [81] by taking into account also the heavy-meson exchanges. In Towner [81] 6 nuclear masses and a number of single-particle transitions were computed by using nuclear wave functions from the ISM. An interesting investigation of the role of the two-particle-two-hole excitations in the A = 16 nuclei was performed in Towner and Khanna [82]. The renormalization of the weak axial charge by the meson-exchange currents had to be taken into account in order to explain the measured rates of both the 0⁻ → 0⁺ β decay and the 0⁺ → 0⁻ muon capture. The axial-charge enhancement is elaborated further, quantitatively, in section 8.2.

Very recently break-through results in the calculations of the axial charge and axial-vector form factors have been achieved in the lattice QCD (quantum chromodynamics) calculations [83–85]. In the work [84] the result

$\begin{array}{ll}{g}_{\text{A}}^{\text{free}}=1.278(21)(26)(\mathrm{\text{lattice calculation}})& (16)\end{array}$

was obtained, where the first uncertainty is statistical and the second comes from the extrapolation systematics. This computed value is quite compatible with the measured free value of g_A in (7). Also the lattice QCD calculations of the double beta decay are advancing in the two-nucleon (toy) systems (see [86]).

4. Nuclear-Model Effects

The studies on the effective value of the axial-vector coupling strength, g_A, have mainly been performed for β decays in established nuclear many-body frameworks. Also the magnetic moments of nuclei have been studied [87, 88] for simple one-particle and one-hole nuclei in order to pin down the effects of the tensor force in shifting low-energy strength of Gamow-Teller type to higher energies, and thus effectively quenching the spin-isospin operator for Gamow-Teller decays. The used many-body frameworks encompass the interacting shell model (ISM) [89] and the pnQRPA [13, 90]. Also the frameworks of the microscopic interacting boson model (IBM-2) [91] and the interacting boson-fermion-fermion model, IBFFM-2 [92], have been used. Let us discuss next the various many-body aspects of these models that may affect the (apparent) renormalization of the magnitude of g_A. It is appropriate to note here that in all these studies the nuclear many-body framework can be considered more or less deficient and thus the many-body effects cannot be disentangled from the nuclear-medium effects, discussed in section 3.

4.1. Many-Body Aspects of the ISM

The ISM is a many-body framework that uses a limited set of single-particle states, typically one harmonic-oscillator major shell or one nuclear major shell, to describe nuclear wave functions involved in various nuclear processes. The point of the ISM is to form all the possible many-nucleon configurations in the given single-particle space, each configuration described by one Slater determinant, and diagonalize the nuclear (residual) Hamiltonian in the basis formed by these Slater determinants. In this way the many-body features are taken into account exactly but only in a limited set of single-particle states. The problem is to extend the single-particle space beyond the one-shell description due to the factorially increasing size of the sparse Hamiltonian matrix to be diagonalized. In this way only the low-energy features of a nucleus can be described, leaving typically the giant-resonance region out of reach. The other problem with the ISM is to find a suitable (renormalized) nucleon-nucleon interaction to match the limited single-particle space. Since this space is small, the renormalization effects of the two-body interaction become substantial. Typically, mostly in the early works, all the matrix elements of the two-body interaction were fitted such that the computed observables, energies, electromagnetic decays, etc., are as close as possible to the corresponding measured ones (see section 5.1). In some works also perturbative approaches through particle-hole excitations from the valence to the excluded space have been considered (see, e.g., [93–95] and the references therein).

From early on there have been difficulties for the ISM to reproduce the measured β-decay rates [96]. This has lead to a host of investigations of the effective (quenched) value of g_A in the ISM framework (see section 5.1 below). The main limitation of the ISM is its confinement to small single-particle spaces, typically comprising one oscillator major shell or a magic shell, leaving one or two spin-orbit partners out of the model space. From, e.g., pnQRPA calculations [15, 16] and perturbative ISM calculations [72, 97] one knows that inclusion of all spin-orbit partners in the single-particle model space is quite essential. This has been noticed also in the extended ISM calculations where the missing spin-orbit partners have been included at least in an effective way [20, 98]. Even extension of the ISM to include two harmonic-oscillator shells (1s0d and 1p0f shells) has been done for the calculation of the 0νββ decay of ⁴⁸Ca [99].

Several advanced shell-model methods have been devised in order to include larger single-particle spaces into the calculations. One can try to find clever ways to select the most important configurations affecting the observables one is interested in. Such an established algorithm is the Monte Carlo shell model (MCSM) where statistical sampling of the Slater determinants is used [100, 101]. One can also use importance-truncation schemes [102] or very advanced ab initio methods, like the coupled-cluster theory, where the two- and three-body interactions can be derived from the chiral effective field theory (cEFT) [103]. One can also use the in-medium similarity renormalization group (IM-SRG) method, like in Bogner [104], where an ab initio construction of a non-perturbative 1s0d-shell Hamiltonian, based on cEFT two- and three-body forces, has been done. Another new method is the density matrix renormalization group (DMRG) algorithm [105], which exploits optimal ordering of the proton and neutron single-particle orbitals and concepts of quantum-information theory.

All the new methods extend the traditionally used ISM model spaces and the future β-decay calculations using these methods will either confirm or reduce the amount of quenching of g_A observed in the older ISM calculations, described in section 5.1 below. The ab initio methods are already available for the light nuclei, occupying the 0p and 1s0d shells, and later for the medium-heavy and heavy nuclei dwelling in the higher oscillator shells. The quenching problem can only be solved by using many-body methods with error estimates, including a systematic way to improve their accuracy. At the same time the two- and three-body forces used in the calculations should be produced on the same footing as the many-body framework itself, preferably from ab initio principles. One should not forget that also the operators used in the computations should be made effective operators that match the adopted single-particle valence spaces. Using these prescriptions one can eliminate the deficiencies of the nuclear many-body framework and obtain information about the quenching of g_A in the nuclear medium (see section 3), beyond the effects caused by the deficiencies of a nuclear model.

4.2. Many-Body Aspects of the pnQRPA

The random-phase approximation (RPA) is an extension of the Tamm-Dancoff model (TDM) in the description of magic nuclei (at closed major shells) by particle-hole excitations across the magic gaps between closed nuclear major shells [35, 106]. In the RPA the simple particle-hole vacuum, with the single-particle orbitals fully occupied up to the Fermi surface at the magic gap, is replace by the correlated vacuum, containing two-particle–two-hole, four-particle–four-hole, etc. excitations across the magic gap. The use of the correlated vacuum in the RPA enhances the strength of collective transitions [35, 106]. Its quasiparticle version, quasiparticle RPA (QRPA) describes open-shell nuclei, outside the closures of magic shells, by replacing the particle-hole excitations by two-quasiparticle excitations. Usually these quasiparticles are generated by the use of the Bardeen-Cooper-Schrieffer (BCS) theory [107] from the short-range interaction part of the nuclear Hamiltonian in an even-even reference nucleus. The quasiparticles can be viewed as partly particles and partly holes, inducing fractional occupancies of the nuclear single-particle orbitals and leading to a smeared Fermi surface for protons and/or neutrons for open-shell nuclei. The proton-neutron version of the QRPA (pnQRPA) uses two-quasiparticle excitations that are built from a proton and a neutron quasiparticle. This enables description of odd-odd nuclei starting from the even-even BCS reference nucleus.

The strong point of the pnQRPA theory is that it can include large single-particle valence spaces in the calculations. There are no problems associated with leaving spin-orbit-partner orbitals out of the computations. On the other hand, the pnQRPA has a limited configuration space, essentially including two-quasiparticle excitations on top of a correlated ground state [35]. Deficiencies of the pnQRPA formalism have been analyzed against the ISM formalism, e.g., in Menéndez [21] by using a seniority-based scheme (seniority was defined earlier, at point (c) in section (1). In that work the pnQRPA was considered to be a low-seniority approximation of the ISM. But on the other hand, the ground-state correlations of the pnQRPA introduce higher-seniority components to the pnQRPA wave functions and the deficiencies stemming from the incomplete seniority content of the pnQRPA should not be so bad [108]. Also the renormalization problems of the two-body interaction are not so severe as in the ISM due to the possibility to use large single-particle model spaces. On the other hand, it is harder to find a perturbative scheme for the effective Hamiltonian due to the incompleteness of the available many-body configuration space. Due to this, schematic or G-matrix-based boson-exchange Hamiltonians have widely been used (see section 5.2).

In any case, the configuration content of the pnQRPA is limited and extensions and improvements of the theory framework are wanted in order to see how the quenching problem of g_A evolves with these extensions and improvements. Such extensions have been devised, including, e.g., the renormalized QRPA (RQRPA) [109, 110] and similar “fully” renormalized schemes [111–113]. Another possible improvement of the pnQRPA is the relativistic quasiparticle time-blocking approximation (RQTBA), in particular its proton-neutron version, the pn-RQTBA, advocated in Robin and Litvinova [114]. It shows good promise for improvements over the β-decay calculations of the ordinary pnQRPA the use of which clearly points out to need for a quenched value of g_A in β-decay calculations, as discussed in section 5.2.

The (charge-conserving) QRPA framework, with linear combinations of proton-proton and neutron-neutron quasiparticle pairs, phonons [35], can be used to describe (collective) excitations of even-even nuclei (collectivity is where the name phonon stems from). These, in turn, can be used as reference nuclei in building the excitations of the neighboring odd-mass (odd-proton or odd-neutron) nuclei by coupling the QRPA phonons with proton or neutron quasiparticles. This phonon-quasiparticle coupling can be carried out in a microscopic way, based on a realistic effective residual Hamiltonian. This has been achieved, e.g., in the microscopic quasiparticle-phonon model (MQPM) [115, 116] where a microscopic effective Hamiltonian based on the Bonn G matrix has been used to produce the one- and three-quasiparticle states in odd-mass nuclei. This extension of the QRPA has been used to describe β decays, and in particular in connection with the renormalization problem of g_A, as discussed in section 9.

It should be noted that odd-mass nuclei can also be described by starting from an odd-odd reference nucleus, described by the pnQRPA phonons [35]. By coupling either proton or neutron quasiparticles with pnQRPA phonons one can, again, create the states of either a neutron-odd or a proton-odd nucleus. This approach was coined the proton-neutron MQPM (pnMQPM) and was used to describe forbidden beta decays in Mustonen and Suhonen [117]. Although the pnQRPA-based phonons better take into account the Ikeda sum rule [35, 76] and the Gamow-Teller giant-resonance region of the β⁻-type strength function, the pnMQPM lacks the important three-proton-quasiparticle and three-neutron-quasiparticle contributions, essential for good reproduction of the low-energy spectra of odd-mass nuclei. This is why its use in β-decay calculations has been very limited.

4.3. Many-Body Aspects of the IBM

In its simplest version, the interacting boson model (IBM), the theory framework consists of s and d bosons which have as their microscopic paradigms the 0⁺ and 2⁺ coupled collective Fermion pairs present in nuclei. Even a mapping of the collective Fermion pairs to these bosons can be devised [91]. An extension of the IBM is the microscopic IBM (IBM-2) where the proton and neutron degrees of freedom are explicitly separated. The IBM and IBM-2 are sort of phenomenological versions of the ISM, containing the seniority aspect and the restriction to one magic shell in terms of the single-particle valence space. The Hamiltonian and the transition operators are constructed from the s and d bosons as lowest-order boson expansions with coupling coefficients to be determined by fits to experimental data or by relating them to the underlying fermion valence space through a mapping procedure [118, 119]. Thus, the IBM and its extensions use more or less phenomenological operators mimicking the renormalized operators used in the ISM (see section 4.1).

The two versions of the IBM can be extended to include higher-multipole bosons, like g bosons, as well. Further extension concerns the description of odd-mass nuclei by the use of the interacting boson-fermion model (IBFM) and its extension, the microscopic IBFM (IBFM-2) [92]. The IBM concept can also be used to describe odd-odd nuclei by using the interacting boson-fermion-fermion model (IBFFM) and its proton-neutron variant, the proton-neutron IBFFM (IBFFM-2) [120]. Here the problems arise from the interactions between the bosons and the one or two extra fermions in the Hamiltonian, and from the transition operators containing a host of phenomenological parameters to be determined in some way. The IBM-2 and the IBFFM-2 have been used to access the renormalization of g_A, as described in section 10.2.

5. Effective Value of g_A in Allowed Gamow-Teller β Decays

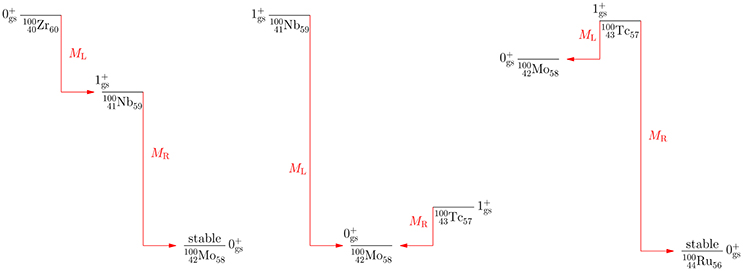
Gamow-Teller decays are mediated by the Pauli spin operator σ and they are thus able to change the initial nuclear spin J_i by one unit. In the renormalization studies the simplest Gamow-Teller transitions are selected, namely the ground-state-to-ground-state ones. In Figure 1 are depicted Gamow-Teller ground-state-to-ground-state β⁻ and β⁺/EC transitions between even-even 0⁺ and odd-odd 1⁺ ground states in the A = 100 Zr-Nb-Mo-Tc-Ru region. Shown are three different situations with a cascade pattern (left panel), lateral feeding to a middle nucleus (middle panel), and lateral feeding from a middle nucleus (right panel). All these transitions are mediated by a Gamow-Teller NME, M_GT, of the Pauli spin operator, defined, e.g., in Suhonen [35]. The corresponding β-decay data can be obtained from ENSDF ¹. In the figure this NME is denoted by M_L (M_R) in the case it is to the left (right) of the central nucleus. The corresponding reduced transition probability B_GT can be written as

$\begin{array}{ll}{B}_{\text{GT}}=\frac{g_{\text{A}}^2}{2J_i+1}{{|M}_{\text{GT}}|}^2,& (17)\end{array}$

where J_i is the spin of the ground state of the initial nucleus, g_A is the weak axial-vector coupling strength, substituted by the effective coupling strength $g_{\text{A}}^{\text{eff}}$ of Equation (8) in practical calculations of the β-decay rates involving nuclear levels of low excitation energy [Hence, the coupling strength g_A is probed at the q² → 0 limit in (5)]. It is worth noting that the Gamow-Teller decays probe only g_A, not g_V which is carried by the vector part (Fermi spin-zero operator) of the β transitions, not active for the here discussed 1⁺ ↔ 0⁺ transitions due to the conservation of angular momentum.

FIGURE 1

Figure 1. Gamow-Teller beta decays in the A = 100 Zr-Nb-Mo-Tc-Ru region.

The comparative half-lives (logft values) of the 1⁺ ↔ 0⁺ Gamow–Teller transitions are given in terms of the reduced transition probabilities as given in Suhonen [35]

$\begin{array}{ll}logft={log}_{10}(f_0{t}_{1/2}\left[s\right])={log}_{10}\left(\frac{6147}{B_{\text{GT}}}\right)& (18)\end{array}$

for the β⁺/EC or β⁻ type of transitions. The half-life of the initial nucleus, t_1/2, has been given in seconds.

Next we inspect the evolution of the quenching concept, based on (17) and (18), in nuclear-structure calculations performed during the last four decades.

5.1. Interacting Shell Model

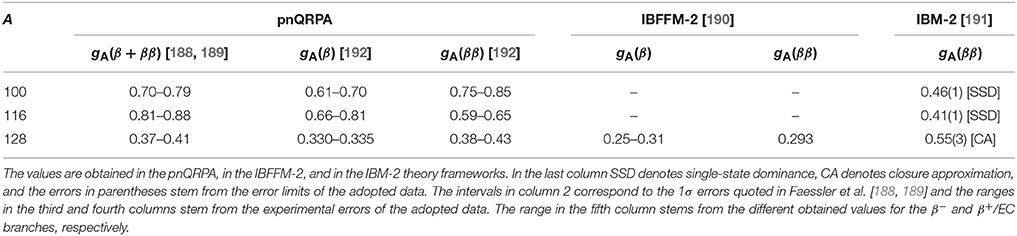
Traditionally the renormalization of the axial-vector coupling strength has been addressed in the context of the ISM in a wealth of calculations pertaining to Gamow-Teller β decays of very light (p-shell), light (sd-shell), and medium-heavy (pf-shell and sdg-shell) nuclei. In these calculations it appears that the value of g_A is quenched. As indicated by the ISM results below, the quenching factor (6) is roughly a decreasing function of the nuclear mass number A, implying stronger quenching with increasing nuclear mass. The studies can be grouped according to the mass regions as follows.

5.1.1. Results for the 0p-Shell Nuclei

A thorough study of the Gamow-Teller β decays of the 0p-shell nuclei was performed in Chou et al. [61]. A 0p − 1s0d cross-shell Hamiltonian derived by Warburton and Brown [121] was used in the calculations. The thus derived phenomenological (the fundamental, section 3, and nuclear-model induced renormalization cannot be disentangled) quenching factor [see Equation (6)] (from a least-squares fit, with one standard deviation error) assumed the value

$\begin{array}{ll}q=0.82\pm 0.02,& (19)\end{array}$

when using the then adopted value $g_{\text{A}}^{\text{free}}=1.26$ in contrast to the presently adopted value of Equation (7). Since the presently adopted free value of g_A is a bit larger, the quenching increases slightly and for the effective value (8) of g_A we have to use

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=(0.82\pm 0.02)\times \frac{1.26}{1.27}\times 1.27=1.03_{-0.02}^{+0.03},& (20)\end{array}$

leading to an effective quenched value of g_A close to unity.

5.1.2. Results for the 1s0d-Shell Nuclei

A pioneering early work of Wilkinson [122] investigated Gamow-Teller β decays in the 0p shell and lower 1s0d shell for the quenching of g_A. In this work Wilkinson obtained a quenching factor which was slightly corrected in Wilkinson [54] based on new experimental data. The corrected value reads (from a least-squares fit, with one standard deviation error)

$\begin{array}{ll}q=0.899\pm 0.035,& (21)\end{array}$

when using the then adopted value $g_{\text{A}}^{\text{free}}=1.25$. Using again the correction for $g_{\text{A}}^{\text{free}}$ we have

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=(0.899\pm 0.035)\times 1.25=1.12_{-0.04}^{+0.05}.& (22)\end{array}$

The same quenching was obtained in Brown et al. [123] by using a different ISM effective Hamiltonian indicating that the quenching is not very sensitive to the detailed aspects of the shell-model analysis. In Wilkinson [54] the empirical result (21) was combined with relativistic corrections to yield

$\begin{array}{ll}q=0.927\pm 0.038.(\mathrm{\text{with relativistic corrections}})& (23)\end{array}$

This yields

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=(0.927\pm 0.038)\times 1.25=1.18\pm 0.05.& (24)\end{array}$

when including the relativistic corrections.

In Wilkinson [122] and Wilkinson [54] it was speculated that the renormalization effects of the Gamow-Teller transitions at low nuclear excitation are of the order expected from fundamental mesonic effects [55–57] (nuclear medium effect, see section 3) or from the lifting of Gamow-Teller strength to higher energies by the nuclear tensor force [87, 88] (nuclear model effect, see section 4). Indeed, by using sum-rule arguments of Ericson [55] the expected quenching by the meson-exchange effects would be around q = 0.93 for nuclei in the vicinity of A = 16. This is in very good agreement with the relativistically corrected empirical result (23).

A full sd-shell analysis of the quenching was performed in Wildenthal [62] with a new set of wave functions derived from a Hamiltonian reproducing the global spectroscopic features of the 1s0d-shell nuclei. The least-squares study (with one standar deviation error) yielded the (empirical) quenching factor q = 0.77±0.02 and thus leads to the global $g_{\text{A}}^{\text{free}}$-corrected 1s0d-shell effective axial-vector coupling of

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=(0.77\pm 0.02)\times 1.25=0.96_{-0.02}^{+0.03},& (25)\end{array}$

which is notably smaller than (22) obtained for the lower 1s0d shell. In the least-squares-fit studues, like this and the one of Chou et al. [61] (see section 5.1.1), the separation of the fundamental quenching (see section 3) from the total quenching is impossible.

5.1.3. Results for the 1p0f(0g_9/2)-Shell Nuclei

In the work [63] 64 Gamow-Teller β decays for the nuclear mass range A = 41−50 were studied. This mass range covers the lower part of the 1p0f shell. The shell-model work was based on Caurier et al. [124] and KB3 two-body interaction was adopted. In Martínez-Pinedo et al. [63] the experimental values of Gamow-Teller matrix elements (extracted by using the free value of g_A) were compared with their computed values by plotting them against each other in an xy plane. The plot was well described by a line with the slope giving a phenomenological quenching factor. From the slope and its error the quenching factor

$\begin{array}{ll}q=0.744\pm 0.015& (26)\end{array}$

was derived, when using the their adopted value $g_{\text{A}}^{\text{free}}=1.26$. Then the $g_{\text{A}}^{\text{free}}$-corrected lower pf-shell quenching amounts to

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=(0.744\pm 0.015)\times 1.26=0.937_{-0.018}^{+0.019}.& (27)\end{array}$

It is interesting to note that with this value of $g_{\text{A}}^{\text{eff}}$ the half-life of the 2νββ decay of ⁴⁸Ca could be predicted [125] in perfect agreement with the later measured value [126]. In the work [127] it was confirmed that the value q = 0.77 reasonably describes the quenching in the A = 48 region. The quenching in the 1s0d and 1p0f shells was also studied in Auerbach et al. [128] for the nucleus ²⁶Mg (1s0d model space) and for the nuclei ⁵⁴Fe and ⁵⁶Ni (1p0f model space) by using both the random-phase approximation and the ISM. The computed β⁺ Gamow-Teller strengths were compared with those derived from the (n,p) charge-exchange reactions. This comparison implied a phenomenological quenched value of $g_{\text{A}}^{\text{eff}}~0.98$, not far from the value (25), extracted in the 1s0d shell by Wildenthal [62] and the value (27), extracted in the 1p0f shell.

The upper 1p0f(0g_9/2)-shell Gamow-Teller transitions were analyzed in Honma [65] in the 0f_5/21p0g_9/2 valence space using a renormalized G-matrix-based two-body interaction, fitted in the mass region A = 63 − 96. A rough phenomenological quenching factor

$\begin{array}{ll}q=0.6& (28)\end{array}$

was adopted in the subsequent calculations of the 2νββ-decay rates of ⁷⁶Ge and ⁸²Se. This, in turn, leads to an upper 1p0f(0g_9/2)-shell effective coupling strength of

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=0.6\times 1.26=0.8,& (29)\end{array}$

which is considerably smaller than (27) obtained for the lower 1p0f shell.

5.1.4. Results for the 0g_7/21d2s0h_11/2-Shell Nuclei

In Caurier et al. [66] an analysis of the Gamow-Teller β decays in the (incomplete) sdg shell (for A = 128 − 130) was performed using the 0g_7/21d2s0h_11/2 single-particle space. A model Hamiltonian based on a renormalized Bonn-C G-matrix with a subsequent fitting of about 300 energy levels of some 90 nuclei in the 0g_7/21d2s0h_11/2 shell was used in the calculations. The resulting phenomenological quenching factor was

$\begin{array}{ll}q=0.57,& (30)\end{array}$

implying a 0g_7/21d2s0h_11/2-shell effective coupling strength of

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=0.57\times 1.26=0.72,& (31)\end{array}$

which is a bit smaller than those obtained in the 1p0f(0g_9/2) shell.

In Caurier et al. [66] also the case of A = 136 was discussed for the 2νββ decay of ¹³⁶Xe using the above-mentioned single-particle space. Comparing the experimentally available [129] (p,n) type of strength function on ¹³⁶Xe (up to excitation energies of 3.5 MeV in ¹³⁶Cs) with the computed one, the authors concluded a phenomenological quenching factor

$\begin{array}{ll}q=0.45& (32)\end{array}$

for A = 136. This leads to a heavily quenched effective axial-vector coupling strength of

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(A=136)=0.45\times 1.26=0.57,& (33)\end{array}$

for the A = 136 region of the 0g_7/21d2s0h_11/2 shell. On the other hand, more recent calculations by Horoi et al. [68, 130] for the 2νββ NMEs of ¹³⁰Te and ¹³⁶Xe suggest a milder quenching and a larger value $g_{\text{A}}^{\text{eff}}(A=130-136)=0.94$ [68] for the effective coupling strength. This is in a rather sharp tension with the results (31) and (33) of Caurier et al. [66].

In Juodagalvis et al. [67] a cross-shell study for the mass region A = 90 − 97 was performed in the single-particle space 1p_1/20g_9/2 for protons and 0g_7/21d0s0h_11/2 for neutrons by using a Bonn-CD-based potential with perturbative renormalization. Again, lack of the full space of spin-orbit partners lead to a strong phenomenological Gamow-Teller quenching

$\begin{array}{ll}q=0.48,& (34)\end{array}$

leading to a cross pf − sdg-shell effective coupling strength of

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=0.48\times 1.26=0.60.& (35)\end{array}$

The above-derived quenching is not far from the quenching q = 0.5 derived in Brown [131] for nuclei in the ¹⁰⁰Sn region using a 0f_5/21p0g_9/2 proton-hole space and 0g_7/21d0s0h_11/2 neutron-particle space.

A quite recent ISM analysis of the nuclei within the mass range 52 ≤ A ≤ 80 was performed by Kumar et al. [64]. There the 1p0f-shell nuclei, 52 ≤ A ≤ 67, were treated by using the KB3G interaction, and the comparison with the experimental β⁻-decay half-lives produced a phenomenological quenching factor leading to the effective coupling strength

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=0.838_{-0.020}^{+0.021}(52\le A\le 67).& (36)\end{array}$

The 0f_5/21pg_9/2-shell nuclei, 67 ≤ A ≤ 80, were computed by using the JUN45 interaction, producing the effective coupling strength

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=0.869\pm 0.019(67\le A\le 80).& (37)\end{array}$

In this work the error estimation is given by the slopes-of-the-lines method [63], discussed in the context of Equation (26) above.

All the results of the ISM analyses have been collected in Table 1. There the mass range (magic shell), value of $g_{\text{A}}^{\text{eff}}$, and the author information are given. Also the results of Siiskonen et al. [60], from section 3, obtained by the use of effective operators in the nuclear medium, have been given for comparison. In addition, the ISM results (adding the ¹⁰⁰Sn results of Siiskonen et al. [60]) for masses 60 ≤ A ≤ 136 have been visualized in Figure 3 of section 5.2. In the figure the results of Honma et al. [65], Caurier et al. [66], Horoi and Neacsu [68], Juodagalvis et al. [67], Kumar et al. [64], and Siiskonen et al. [60] (see the discussions above) have been plotted against the background (the hatched region of Figure 3) of the results of the pnQRPA analyses performed in section 5.2. Looking at the figure makes it obvious that the ISM results of the aforementioned references are commensurate with the results of the (global) analyses of Gamow-Teller transitions performed in the framework of the pnQRPA.

Finally, it is of interest to point out to the recent work [132] where no-core-configuration-interaction formalism, rooted in multireference density functional theory, was used to compute the Gamow-Teller NMEs for T = 1/2 mirror nuclei (pairs of nuclei where either a neutron or a proton is added to an even-even N = Z core nucleus) in the 1s0d and 1p0f shells. The computations were performed in a basis of 10 or 12 spherical harmonic-oscillator shells by using two different Skyrme forces. The computed quenching factors coincide surprisingly closely with those of the ISM quoted in (25) (Wildenthal et al. [62]) for the 1s0d shell and in (26) (Martinez-Pinedo et al. [63]) for the 1p0f shell, despite the big differences in the two nuclear models. This would point to the possibility that the quenching in the 1s0d and 1p0f shells is not so much related to the deficiencies of the nuclear models but rather to omission of effects coming from the nuclear medium, like from the two-body currents and other mesonic effects discussed in section 3.

5.2. Quasiparticle Random-Phase Approximation

Only recently the important aspect of the effective value of g_A has been addressed within the framework of the pnQRPA. The situation with pnQRPA is more involved than in the case of the ISM since the adopted schematic or realistic interactions are usually renormalized separately in the particle-hole (g_ph parameter) and particle-particle (g_pp parameter) [133–136] channels. Typically the particle-hole parameter, g_ph, is fitted to reproduce the centroid of the Gamow-Teller giant resonance (GTGR) obtained from the semi-empirical formula [135, 136]

$\begin{array}{l}\Delta E_{\text{GT}}=E(1_{\text{GTGR}}^{+})-E\left(0_{\text{gs}}^{+}\right)=[1.444\left(Z+\frac{1}{2}\right)A^{-1/3}\\ -30.0(N-Z-2)A^{-1}+5.57]\mathrm{\text{MeV}}.& (38)\end{array}$

The above formula indicates that the difference ΔE_GT between the GTGR and the ground state of the neighboring even-even reference nucleus depends on the proton and neutron numbers (Z,N) of the reference nucleus, as well as on its mass number. For the particle-particle parameter, g_pp, there is no unique way to fix its value, as criticized in Suhonen [137]. Furthermore, the exact value of g_pp depends on the size of the active single-particle model space. In this review several ways how this can be done are discussed. As a result of the g_pp problems and problems with systematic renormalization of the two-body interactions, the fundamental quenching (see section 3) cannot be disentangled from the nuclear-model effects, discussed in section 4.

The first pnQRPA attempts were inspired by a simultaneous description of β and 2νββ decays, as elaborated more in section 10. In Delion and Suhonen [138] 9 isobaric systems, with A = 70, 78, 100, 104, 106, 110, 116, 128, 130, of the type displayed in the right panel of Figure 1 were analyzed by using a spherical pnQRPA with schematic particle-hole and particle-particle forces. The pnQRPA calculations were performed in the even-even reference nuclei. For each GTGR-fixed g_ph the value of g_pp was varied in order to reproduce the experimentally known ratio M_R/M_L which is independent of the value of g_A. The value of g_A was then determined by requiring M_R(th)/M_R(exp) = 1. This produced the mean value

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=0.27& (39)\end{array}$

and the approximate mass dependence $g_{\text{pp}}\approx 0.5/\sqrt{A}$. By using this dependence of g_pp and the above value (39) for g_A the experimental β⁺/EC and β⁻ NMEs of 218 Gamow-Teller transitions were quite well reproduced in Delion and Suhonen [138]. The quite low value obtained for $g_{\text{A}}^{\text{eff}}$ implies that a larger quenching is required than in the ISM due to the simple schematic form of the adopted Hamiltonian in the pnQRPA calculations. in other words, the quenching coming from the many-body effects is stronger for the pnQRPA calculation than for the ISM calculation which is more realistic in terms of two-body interactions and configuration space. In this analysis the effects coming from the nuclear medium (section 3) cannot be disentangled from the many-body effects, unfortunately.

In Pirinen and Suhonen [139] an analysis of 26 β⁻ and 22 β⁺/EC Gamow-Teller transitions of the type depicted in Figure 1 in the mass range A = 100 − 136 was performed. In this study the geometric mean

$\begin{array}{ll}{\bar{M}}_{\text{GT}}=\sqrt{M_{\text{L}}{M}_{\text{R}}}& (40)\end{array}$

of the extracted experimental NMEs was compared with that computed by the use of the pnQRPA with realistic effective forces based on the g_ph- and g_pp-renormalized Bonn-A G matrix. The use of the geometric mean of the left and right NMEs stabilizes the values of the mean NMEs and smoother trends can be obtained. This is based on the fact that the NME for the β⁻ branch is a decreasing function of g_pp and the NME for the β⁺/EC branch is an increasing function of g_pp. Thus, the product of the NMEs of these branches remains essentially constant over a wide range of g_pp values (see the figures in Ejiri and Suhonen [140]).

Like in Delion and Suhonen [138], the pnQRPA calculations of Pirinen and Suhonen [139] were performed in the even-even reference nuclei. The value of g_ph was fixed by the phenomenological centroid (38) of the GTGR separately for each nucleus. In the calculations it turned out that the value g_pp = 0.7 represents a reasonable global value for the particle-particle interaction strength in the model spaces used in the calculations: at least one oscillator major shell above and below those oscillator shells where the proton and neutron Fermi surfaces lie. Furthermore, an average piece-wise linear behavior

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=\{\begin{array}{cc}0.02A-1.6& \text{for }A\le 120\\ \frac{1}{60}A-\frac{43}{30}& \text{for }A\ge 122\end{array}& (41)\end{array}$

of g_A was found in the calculations. These derived values of $g_{\text{A}}^{\text{eff}}$, plotted in Figure 2, were used, in turn, to describe the Gamow-Teller and 2νββ decay rates to the ground state and lowest excited states in the even-even reference nucleus in the A = 100−136 mass region. These results were compared with those obtained by the use of the average value

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(\text{ave})=0.6& (42)\end{array}$

for $g_{\text{A}}^{\text{eff}}$. The average value reproduced surprisingly well the experimentally known 2νββ half-lives in this mass region.

FIGURE 2

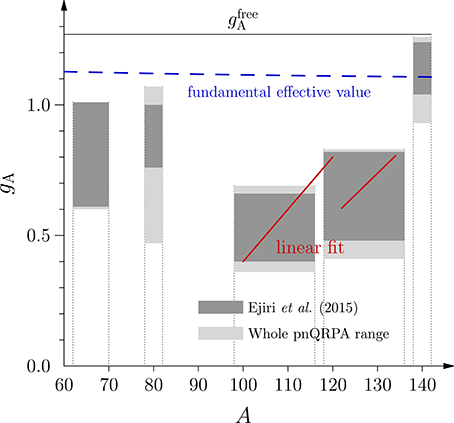
Figure 2. Averaged effective values of g_A [$g_{\text{A}}^{\text{eff}}$ of (45)] in the 5 different mass ranges, plotted from the numbers of Table 2. The legends inside the figure correspond to the following references: Ejiri et al. [140] (dark-hatched boxes); Whole pnQRPA range: combined results of Pirinen and Suhonen [139], Deppisch and Suhonen [141], and Ejiri and Suhonen [140] (light-hatched boxes) illustrate the total range of $g_{\text{A}}^{\text{eff}}$ for each mass region. Also the linear fit (41) and the “fundamentally” quenched g_A, Equation (14), are plotted for comparison.

The work of Pirinen and Suhonen [139] was extended in Deppisch and Suhonen [141] to a wider range of nuclei (A = 62−142) and to a more refined statistical analysis of the results. The same renormalized Bonn-A G matrix as in Pirinen and Suhonen [139] was adopted for the pnQRPA calculations, along with the scaling with the g_ph and g_pp parameters. A Markov chain Monte Carlo statistical analysis of 80 Gamow-Teller transitions in 47 isobaric decay triplets of the kind depicted in Figure 1 was performed. The analysis was also extended to 28 longer isobaric chains and the results were compared with those obtained for the isobaric triplets. Also the measured half-lives of 2νββ decays occurring in the isobaric chains were analyzed. A roughly linearly increasing trend of $g_{\text{A}}^{\text{eff}}$ as a function of the mass number A could be extracted from the analysis of the isobaric triplets for A ≥ 100, in accordance with the result of Pirinen and Suhonen [139]. Similar features were seen also in the fits to longer multiplets. For the range 100 ≤ A ≤ 136 the average (42) was roughly obtained in both analyses.

In contrast to Pirinen and Suhonen [139] also the value of g_pp was kept as a free parameter, the same for the left and right NMEs of transitions in the triplets like in Figure 1, and different for each even-even reference nucleus in the longer chains. Both types of analysis yield a rough average of g_pp ≈ 0.7 for the particle-particle strength parameter in the mass range 100 ≤ A ≤ 136 (see the last column of Table 2), in accordance with the value used in the analysis of Pirinen and Suhonen [139]. At this point it should be noted that the adopted single-particle model spaces used in the calculations correspond to those of Pirinen and Suhonen [139] for 100 ≤ A ≤ 136: at least one oscillator major shell above and below those oscillator shells where the proton and neutron Fermi surfaces lie.

TABLE 2

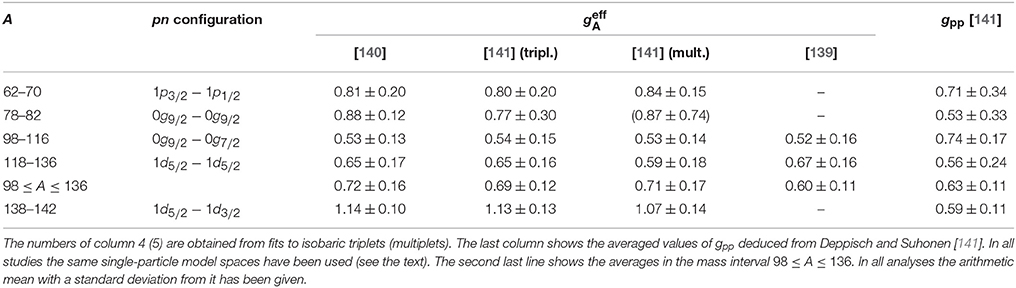
Table 2. Mass ranges, the corresponding leading pn configurations and average effective values (45) of g_A extracted from three different works.

A slightly different analysis of the Gamow-Teller transitions in the mass range 62 ≤ A ≤ 142 was carried out in Ejiri and Suhonen [140]. This is the same mass range as analyzed in Deppisch and Suhonen [141]. Again the g_ph- and g_pp-renormalized Bonn-A G matrix was used in a pnQRPA framework, and the geometric mean (40) was used in the analysis to smooth the systematics. The mass range was divided in 5 sub-ranges according to the leading proton-neutron (pn) configuration influencing the Gamow-Teller decay rate. The reduction of the NME in the chain ${\bar{M}}_{\text{qp}}\to {\bar{M}}_{\text{pnQRPA}}\to {\bar{M}}_{\text{exp}}$ was followed, where ${\bar{M}}_{\text{qp}}$ is the mean two-quasiparticle NME (40) for the leading pn configuration, ${\bar{M}}_{\text{pnQRPA}}$ is the pnQRPA-computed mean NME, and ${\bar{M}}_{\text{exp}}$ is the mean experimental NME, extracted from the experimental decay-half-life data by using $g_{\text{A}}^{\text{free}}=1.27$. The ratio

$\begin{array}{ll}k=\frac{{\bar{M}}_{\text{pnQRPA}}}{{\bar{M}}_{\text{qp}}}& (43)\end{array}$

is a measure of the quenching of the NME when going from a rudimentary many-body approach toward a more sophisticated one. This ratio is independent of the nuclear-matter effects and is usually nuclear-mass dependent (the results of the analysis [140] are quoted in the second column of Table 4 in section 7). The quenching of g_A by the nuclear-medium and many-body (inseparable!) effects was incorporated in the ratio

$\begin{array}{ll}{k}_{\text{NM}}=\langle {\bar{M}}_{\text{exp}}/{\bar{M}}_{\text{pnQRPA}}\rangle ,& (44)\end{array}$

representing an average of the ratio ${\bar{M}}_{\text{exp}}/{\bar{M}}_{\text{pnQRPA}}$ of the experimental NME and the pnQRPA-computed NME over each sub-range of masses. The resulting effective g_A can be extracted from k_NM by using the simple relation

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}=g_{\text{A}}^{\text{free}}{k}_{\text{NM}}=1.27k_{\text{NM}}.& (45)\end{array}$

The resulting values of $g_{\text{A}}^{\text{eff}}$, along with the mass ranges and leading pn configurations are listed in Table 2. The pnQRPA results were obtained by fitting the g_ph parameter to the phenomenological centroid (38) of the GTGR separately for each nucleus, and by adopting g_pp = 0.67, in line with the analyses of Pirinen and Suhonen [139] and Deppisch and Suhonen [141]. Again, the adopted single-particle model spaces correspond to those of Deppisch and Suhonen [141]: at least one oscillator major shell above and below those oscillator shells containing the proton and neutron Fermi surfaces.

In Table 2 also the averaged results of Deppisch and Suhonen [141] and Pirinen and Suhonen [139] are shown for comparison. For Deppisch and Suhonen [141] are shown the results of both the isobaric triplet (tripl.) and multiplet (mult.) fits, as also the averaged g_pp values, extracted from the analysis of the triplet fits of Deppisch and Suhonen [141]. In all the analyses the same single-particle model spaces were used: at least one oscillator major shell above and below those oscillator shells containing the proton and neutron Fermi surfaces. The triplet and multiplet fits of Deppisch and Suhonen [141] are quite consistent, excluding the multiplet fit of mass range 78–82 (the result in parenthesis) which has two fitted multiplets, the other rendering an ambiguous result. The results of Deppisch and Suhonen [141] are very close to those of Pirinen and Suhonen [139] and Ejiri and Suhonen [140]. Most of the (quite small) differences between the various calculations stem from the different ways of treating the value of the particle-particle strength g_pp, which for the studies of Ejiri and Suhonen [140] and Pirinen and Suhonen [139] was kept constant (g_pp = 0.67 and g_pp = 0.7, respectively) but was allowed to vary in the work of Deppisch and Suhonen [141] (see the last column of Table 2).

The numbers of Table 2 have been visualized in Figure 2. Also the linear fit (41) and the “fundamentally” quenched g_A, Equation (14), are plotted for comparison. The plot reveals quite a simple structure of the ranges of $g_{\text{A}}^{\text{eff}}$ within different mass regions. The numbers of Ejiri et al. [140] are given as dark-hatched regions while the light-hatched regions contain the results of Ejiri et al. plus the results of Pirinen et al. [139] and Deppisch et al. [141]. A general decreasing trend of the ranges of $g_{\text{A}}^{\text{eff}}$ (the hatched boxes) can be seen, except for the heaviest masses A ≥ 138. It is noteworthy that there is a small shift in the values of $g_{\text{A}}^{\text{eff}}$ at A = 120 indicated by all the pnQRPA analyses (both light and hatched boxes). Also the linear fit (41) indicates a discontinuity close to this mass number. The most probable cause for this displacement is the change in the nuclear wave functions from the 0g-orbital dominated to the 1d-orbital dominated proton-neutron configuration, as seen in Table 2. A similar, even more drastic, displacement is seen between A = 70–78 where the dominating proton-neutron configuration of the nuclear wave functions shifts from the 1p orbitals to the 0g orbitals.

The obtained pnQRPA ranges can be compared with results obtained by performing combined $g_{\text{A}}^{\text{eff}}$ analyses of β and 2νββ decay rates in the pnQRPA and other models: The light-hatched regions of Figure 2 have been plotted in Figure 18 for comparison with the results of section 10. The result of the linear fit (41) is not included in that plot since the hatched regions are a better way to describe the (large) spread of the pnQRPA results for different masses A. This large spread is not perceivable in the linear fit.

In Figure 3 the light-hatched regions of Figure 2 (combined results of the pnQRPA analyses) have been plotted as a background against the results of the ISM of section 5.1. As can be seen in the figure, the ISM results and the pnQRPA results are in excellent agreement with each other. This is a non-trivial result considering the quite different premises of these two different calculation frameworks. For the masses A ≥ 138 there is no comparison between the two approaches since mid-shell heavy nuclei, with increasing deformation, are hard to access by the ISM due to an overwhelming computational burden.

FIGURE 3

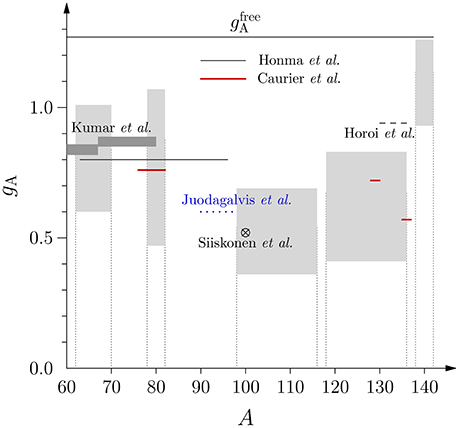
Figure 3. Whole ranges of averaged effective values of g_A from Figure 2 (light-hatched regions) plotted against the ISM results of section 5.1. The ISM results come from Honma et al. [65], Caurier et al. [66], Juodagalvis et al. [67], Kumar et al. [64] (dark-hatched regions), and Siiskonen et al. [60].

6. Quenching of g_A in Forbidden Unique β Decays

The forbidden unique β transitions are the simplest ones that mediate β decays between nuclear states of large angular-momentum difference ΔJ. In particular, if one of the states is a 0⁺ state, then for a Kth forbidden (K = 1, 2, 3, …) unique beta decay the angular momentum of the other involved state is J = K + 1. At the same time the parity changes in the odd-forbidden and remains the same in the even-forbidden decays [35]. The change in angular momentum and parity for different degrees of forbiddenness is presented in Table 3, and they obey the simple rule

$\begin{array}{ll}{(-1)}^{\Delta J}\Delta \pi =-1.\left(\text{Forbidden unique decays}\right)& (46)\end{array}$

TABLE 3

Table 3. Change in angular momentum and parity in Kth forbidden unique β decays with a 0⁺ state as an initial or final nuclear state.

Here it is interesting to note that also the Gamow-Teller decays obey the rule (46) if one of the involved nuclear states has the multipolarity 0⁺.

6.1. Theoretical Considerations

The theoretical half-lives t_1/2 of Kth forbidden unique β decays can be expressed in terms of reduced transition probabilities B_Ku and phase-space factors f_Ku. The B_Ku is given by the NME, which in turn is given by the single-particle NMEs and one-body transition densities. Then (for further details see [35])

$\begin{array}{ll}{t}_{1/2}=\frac{\kappa }{f_{K\text{u}}{B}_{K\text{u}}};B_{K\text{u}}=\frac{g_{\text{A}}^2}{2J_i+1}|M_{K\text{u}}{|}^2,& (47)\end{array}$

where J_i is the angular momentum of the mother nucleus and κ is a constant with value [142]

$\begin{array}{ll}\kappa =\frac{2{\pi }^3{\hslash }^7\text{ln }2}{m_e^5{c}^4{\left(G_{\text{F}}cos{\theta }_{\text{C}}\right)}^2}=6147\text{ s},& (48)\end{array}$

with G_F being the Fermi constant and θ_C being the Cabibbo angle. The phase-space factor f_Ku for the Kth forbidden unique β^± decay can be written as

$\begin{array}{ll}{f}_{K\text{u}}={\left(\frac{3}{4}\right)}^K\frac{(2K)!!}{(2K+1)!!}{\displaystyle {\int }_1^{w_0}}{C}_{K\text{u}}(w_e)p_e{w}_e{(w_0-w_e)}^2{F}_0(Z_f,w_e)\text{d}{w}_e,& (49)\end{array}$

where C_Ku is the shape function for Kth forbidden unique β decays which can be written as (see, e.g., [35, 143])

$\begin{array}{ll}{C}_{K\text{u}}(w_e)={\displaystyle \sum _{k_e+k_{\nu }=K+2}}\frac{{\lambda }_{k_e}{p}_e^{2(k_e-1)}{(w_0-w_e)}^{2(k_{\nu }-1)}}{(2k_e-1)!(2k_{\nu }-1)!},& (50)\end{array}$

where the indices k_e and k_ν (both k = 1, 2, 3…) come from the partial-wave expansion of the electron (e) and neutrino (ν) wave functions. Here w_e is the total energy of the emitted electron/positron, p_e is the electron/positron momentum, Z_f is the charge number of the daughter nucleus and F₀(Z_f, w_e) is the Fermi function taking into account the coulombic attraction/repulsion of the electron/positron and the daughter nucleus². The factor λ_ke contains the generalized Fermi function F_{ke − 1} [144] as the ratio

$\begin{array}{ll}{\lambda }_{k_e}=\frac{F_{k_e-1}(Z_f,w_e)}{F_0(Z_f,w_e)}.& (51)\end{array}$

The integration is performed over the total (by electron rest-mass) scaled energy of the emitted electron/positron, w₀ being the endpoint energy, corresponding to the maximum electron/positron energy in a given transition.

The NME in (47) can be expressed as

$\begin{array}{ll}{M}_{K\text{u}}={\displaystyle \sum _{ab}}{M}^{(K\text{u})}(ab)({\psi }_f\Vert {[c_a^{†}{\tilde{c}}_b]}_{K+1}\Vert {\psi }_i),& (52)\end{array}$

where the factors M^(Ku)(ab) are the single-particle matrix elements and the quantities $({\psi }_f||{[c_a^{†}{\tilde{c}}_b]}_{K+1}||{\psi }_i)$ are the one-body transition densities with ψ_i being the initial-state wave function and ψ_f the final-state wave function. The operator $c_a^{†}$ is a creation operator for a nucleon in the orbital a and the operator ${\tilde{c}}_a$ is the corresponding annihilation operator. The single-particle matrix elements are given (in the Biedenharn-Rose phase convention) by

$\begin{array}{ll}{M}_{K\text{u}}(ab)=\sqrt{4\pi }(a\Vert r^K{\left[Y_K\sigma \right]}_{K+1}{i}^K\Vert b),& (53)\end{array}$

where Y_K is a spherical harmonic of rank K, r the radial coordinate, and a and b stand for the single-particle orbital quantum numbers. The NME (53) is given explicitly in Suhonen [35].

6.2. First-Forbidden Unique β Decays

The first-forbidden unique β transitions are mediated by a rank-2 (i.e., having angular-momentum content 2) parity-changing spherical tensor operator [a special case of the operator (53)], schematically written as ${O}(2^{-})$. For these decays it is customary to modify the general structure of Equations (47)–(49) by replacing the phase-space factor f_{K = 1, u} of (49) by a 12 times larger phase-space factor f_1u, i.e.,

$\begin{array}{ll}{f}_{1\text{u}}=12f_{K=1,\text{u}},& (54)\end{array}$

yielding a factor log12 = 1.079 times larger comparative half-lives (18) than in the standard definition (47).

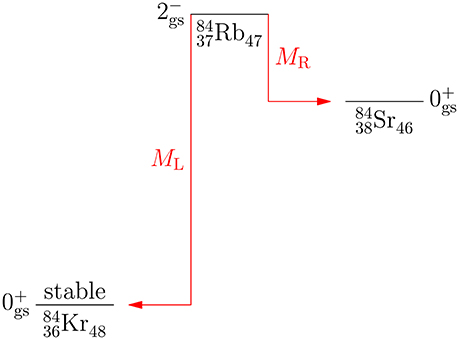
In the quenching studies it is advantageous to use the simplest first-forbidden transitions, namely the ground-state-to-ground-state ones. In Figure 4 are depicted the first-forbidden unique ground-state-to-ground-state β⁻ and β⁺/EC transitions between even-even 0⁺ and odd-odd 2⁻ ground states in the A = 84 Kr-Rb-Sr isobaric chain. Shown is the lateral feeding from a middle odd-odd nucleus to adjacent even-even ground states. In the figure, as also in Figure 1 for the Gamow-Teller transitions, the NME is denoted by M_L (M_R) in case it is to the left (right) of the central nucleus.

FIGURE 4

Figure 4. First-forbidden unique beta decays in the A = 84 Kr-Rb-Sr isobaric chain.

In the early work [145] a systematic schematic analysis of the first-forbidden unique β decays was performed from the point of view of suppression factors stemming from the effect of E1 (electric dipole) giant resonance in the final odd-odd nucleus. In Towner et al. [146] the suppression mechanism of the first-forbidden and third-forbidden β decays of light nuclei (A ≤ 50) was studied by using simple shell-model estimates and first-order perturbation theory. The hindrance was traced to the repulsive T = 1 (isospin 1) particle-hole force.

In the work [147] 19 first-forbidden unique ground-state-to-ground-state β-decay transitions were studied. The interesting transitions are the ones where both M_L and M_R NMEs are known experimentally, like in the case of Figure 4. The experimental values of the NMEs can be deduced by using Equations (47) and (48) and by adopting the free value of the axial-vector coupling strength³. In this case one can use the geometric mean (40) of the left and right NMEs in the analysis, making the analysis more stable. In Ejiri et al. [147] a g_ph- and g_pp-renormalized Bonn-A G matrix was used as the two-nucleon interaction in a pnQRPA framework. The two-quasiparticle and pnQRPA NMEs were compared with the ones extracted from the measured comparative half-lives. Again the relations (44) and (45) can be used to obtain the value

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}\approx 0.45\times 1.27=0.57& (55)\end{array}$

for the effective axial-vector coupling strength using the pnQRPA wave functions. The average of the values of the leading two-quasiparticle NMEs gives in turn

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(2\text{qp})\approx 0.18\times 1.27=0.23,& (56)\end{array}$

implying the ratio

$\begin{array}{ll}k=\frac{{\bar{M}}_{\text{pnQRPA}}}{{\bar{M}}_{\text{qp}}}=0.4& (57)\end{array}$

and thus a drastic nuclear many-body effect when going from the two-quasiparticle level of approximation to the pnQRPA level. The 2qp-NME to pnQRPA-NME comparison is the only one where a clean separation between the nuclear-medium effects and the nuclear-model effects can be achieved, the nuclear-model effect being responsible for the (in this case large) shift in the values of the NMEs.

7. Higher-Forbidden Unique β Decays

Early studies of the quenching in the second- and third-forbidden unique β decays were performed in Towner et al. [146] and Warburton et al. [149]. The work of Towner et al. [146] was discussed in section 6.2. In Warburton et al. [149] these β decays were studied using a simple ISM and the unified model (deformed shell model) for six β transitions in the A = 10, 22, 26, 40 nuclei. The interest for these studies derived from nuclear-structure considerations: how to explain in a nuclear model the hindrance phenomena occurring in certain measured β transitions. Beyond this, the incentive to study the Gamow-Teller (section 5), first-forbidden unique (section 6.2), and higher-forbidden unique (this section) β decays stems from their relation to the Gamow-Teller type of NME involved in 0νββ decays. The 0νββ decays proceed via virtual intermediate states of all multipolarities J^π due to the multipole expansion of the Majorana-neutrino propagator (see, e.g., [1–3, 150–155]). Studies of the quenching of these two-leg (“left-leg” and “right-leg” transitions illustrated in the schematic Figure 5 for the 0νββ decay of ¹¹⁶Cd to ¹¹⁶Sn via the virtual intermediate states in ¹¹⁶In) virtual transitions is of paramount importance to, e.g., estimate the sensitivities of the present and future neutrino experiments to the Majorana-neutrino mass. The possible quenching of these intermediate multipole transitions in the GT type of 0νββ NME can be, in a simplistic approach, condensed into an effective axial coupling, $g_{\text{A},0\nu }^{\text{eff}}$, multiplying the NME:

$\begin{array}{ll}{M}_{\text{GTGT}}^{(0\nu )}={(g_{\text{A},0\nu }^{\text{eff}})}^2{\displaystyle \sum _{J^{\pi }}}(0_f^{+}\Vert {{O}}_{\text{GTGT}}^{(0\nu )}(J^{\pi })\Vert 0_i^{+}),& (58)\end{array}$

where ${{O}}_{\text{GTGT}}^{(0\nu )}$ denotes the transition operator mediating the 0νββ transition through the various multipole states J^π, $0_i^{+}$ denotes the initial ground state, and the final ground state is denoted by $0_f^{+}$ (here, for simplicity, we assume a ground-state-to-ground-state transition). The effective axial coupling relevant for 0νββ decay is denoted as $g_{\text{A},0\nu }^{\text{eff}}$ to emphasize that its value may deviate from the one determined in single beta and 2νββ decays. The remarkable feature of Equation (58) is that the effective axial coupling strength is raised to 2nd power making the value of $g_{\text{A},0\nu }^{\text{eff}}$ play an extremely important role in determining the 0νββ-decay rate which is (neglecting the smaller double Fermi and tensor contributions) proportional to the squared NME and thus to the 4th power of the coupling:

$\begin{array}{ll}0\nu \beta \beta -\text{rate}~{\left|M_{\text{GTGT}}^{(0\nu )}\right|}^2=g_{\text{A},0\nu }^4{\left|{\displaystyle \sum _{J^{\pi }}}(0_f^{+}\Vert {{O}}_{\text{GTGT}}^{(0\nu )}(J^{\pi })\Vert 0_i^{+})\right|}^2.& (59)\end{array}$

FIGURE 5

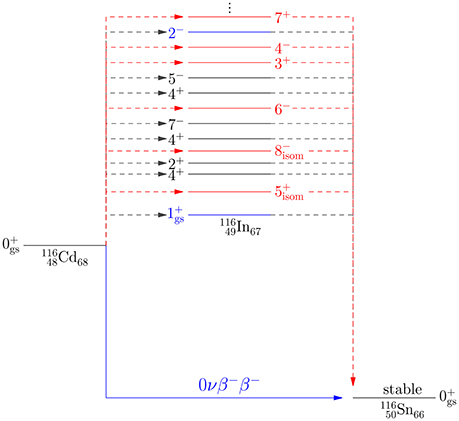
Figure 5. The 0νββ decay of ¹¹⁶Cd to ¹¹⁶Sn via the virtual intermediate states in ¹¹⁶In. The transitions between ¹¹⁶Cd (¹¹⁶Sn) and ¹¹⁶In constitute the left-leg (right-leg) transitions.

The quenching related to the left-leg and right-leg β transitions of Figure 5 can be studied by using the theoretical machinery of section 6.1. In Kostensalo and Suhonen [156] this machinery was applied to 148 potentially measurable second-, third-, fourth-, fifth-, sixth- and seventh-forbidden unique beta transitions. The calculations were done using realistic single-particle model spaces and G-matrix-based microscopic two-body interactions. The results of Kostensalo and Suhonen [156] could shed light on the magnitudes of the NMEs corresponding to the high-forbidden unique 0⁺ ↔ J^π = 3⁺, 4⁻, 5⁺, 6⁻, 7⁺, 8⁻ virtual transitions taking part in neutrinoless double beta decay, as shown in Figure 5.

In Kostensalo and Suhonen [156] the ratio k, Equation (62) below, of the NMEs, calculated by the pnQRPA, M_pnQRPA, and a two-quasiparticle model, M_qp, was studied and compared with earlier calculations for the allowed Gamow-Teller 1⁺ [140] and first-forbidden spin-dipole (SD) 2⁻ [147] transitions. Based on this comparison the expected half-lives of the studied β-decay transitions were predicted. An example case of the expected half-lives of second-, fourth-, and seventh-forbidden β decays is shown in Figure 6. The computed NMEs are corrected by the use of the ratio of the geometric means (40) of the experimental and pnQRPA NMEs,

$\begin{array}{ll}{k}_{\text{NM}}=\frac{{\bar{M}}_{\text{exp}}}{{\bar{M}}_{\text{pnQRPA}}},& (60)\end{array}$

extracted from the GT work of Ejiri and Suhonen [140], to predict the transition half-lives of the figure. In the figure one sees that the expected half-lives range from 4 years to the astronomical 9 × 10²⁹ years. It is expected that the decays to and from isomeric states are not measurable and the decays between the nuclear ground states are masked by transitions to excited states with lesser degree of forbiddenness. Only in some cases the high-forbidden β decay exhausts 100% of the decay rate between two nuclear ground states; one example being the second-forbidden β⁻ transition ${}^{54}\text{Mn}(3_{\text{gs}}^{+}){\to }^{54}\text{Fe}(0_{\text{gs}}^{+})$, with a half-life 4.2(9) × 10⁵ years, shown in Figure 7. Even in this case the measurement will be challenging due to the Gamow-Teller type of electron-capture feeding of the first excited 2⁺ state of ⁵⁴Cr, taking practically 100% of the feeding intensity.

FIGURE 6

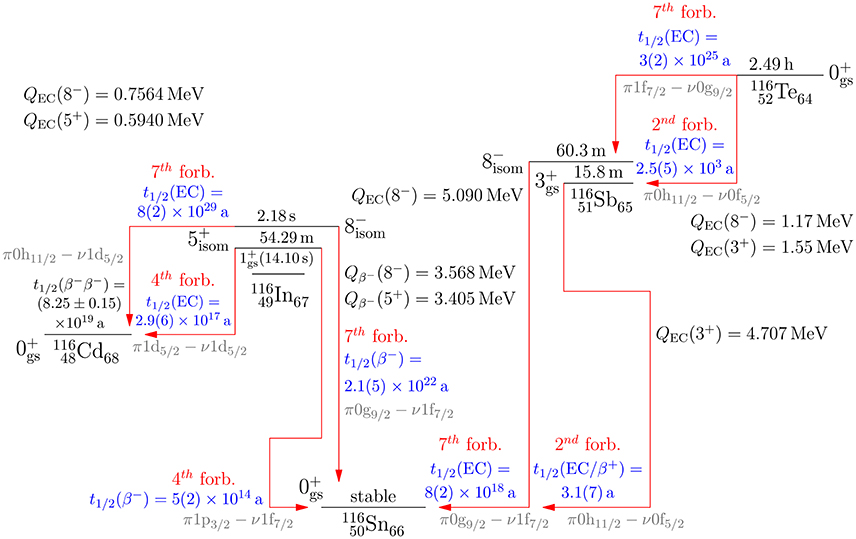
Figure 6. Predicted half-lives and their error estimates (in parenthesis) for β⁻ and EC (electron-capture) transitions in the isobaric chain A = 116. The spin-parity assignments, decay energies (Q values) and life-times of the nuclear ground (gs) and isomeric (isom) states are experimental data and taken from ENSDF (http://www.nndc.bnl.gov/). The 2νββ half-life is taken from Barabash [157]. In addition to the half-lives the degree of forbiddenness and the leading single-particle transition are shown.

FIGURE 7

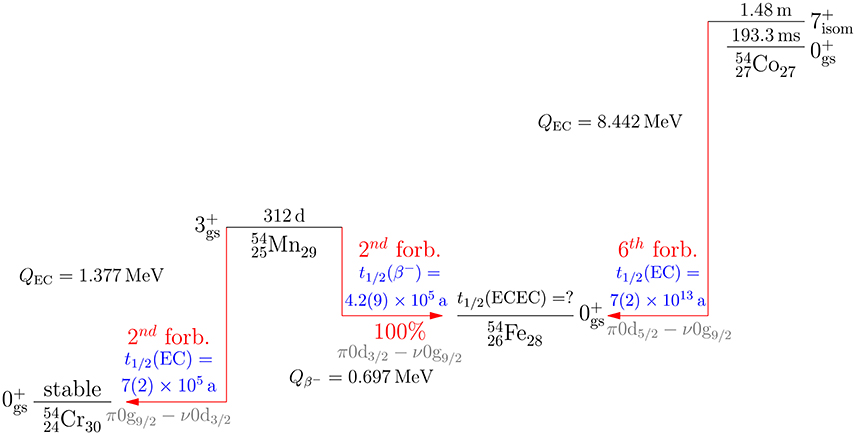
Figure 7. The same as Figure 6 for the second- and sixth-forbidden β decays in the isobaric chain A = 54.

The geometric mean of the EC/β⁺ and β⁻ NMEs, defined in (40), can be generalized to a geometric mean of n NMEs, M_i, i = 1, 2, …n, of successive β transitions with a common mother or daughter nucleus:

$\begin{array}{ll}\bar{M}={\left({\displaystyle \prod _{i=1}^n}{M}_i\right)}^{1/n}.& (61)\end{array}$

Here the aim, as in the case of (40), is to reduce the fluctuations in the computed NMEs by exploiting the compensating trends of the β⁻ and β⁺/EC branches of decay when changing the value of the particle-particle interaction parameter g_pp of the pnQRPA. One can now define the ratio

$\begin{array}{ll}k=\frac{{\bar{M}}_{\text{pnQRPA}}}{{\bar{M}}_{\text{qp}}}& (62)\end{array}$

of the pnQRPA-calculated mean NME, ${\bar{M}}_{\text{pnQRPA}}$, and the mean two-quasiparticle NME, ${\bar{M}}_{\text{qp}}$, computed by using (61). The ratio k is a measure of the evolution of the nuclear-model dependent many-body effects on the computed NME. The ratio (62) is independent of the nuclear-medium effects (the fundamental quenching of section 3) and gives an idea of how the quenching of g_A depends on the degree of complexity of the adopted nuclear model.

In Kostensalo and Suhonen [156] the β transitions were divided in two groups: GROUP 1 contained only non-magic even-even reference nuclei (i.e., nuclei where the pnQRPA and the associated BCS (Bardeen-Cooper-Schrieffer) calculation were performed), whereas GROUP 2 contained (semi)magic reference nuclei. The transitions in GROUP 2 were left out from the analysis of the ratio k of (62) since the BCS results tend to be unstable at magic shell closures. In Figure 8 the ratio k is shown for transitions belonging to GROUP 1. The same k distribution is shown in terms of division to β⁻ and EC/β⁺ decays in Figure 9.

FIGURE 8

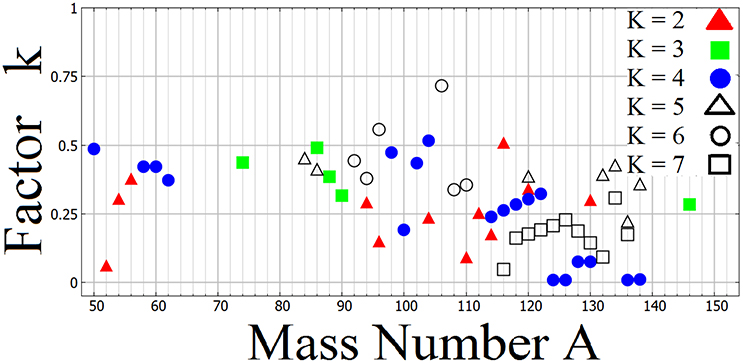
Figure 8. Ratio (62) as a function of the mass number A for β transitions involving solely non-magic reference nuclei. The degree of forbiddenness K is indicated by color and shape of the symbol.

FIGURE 9

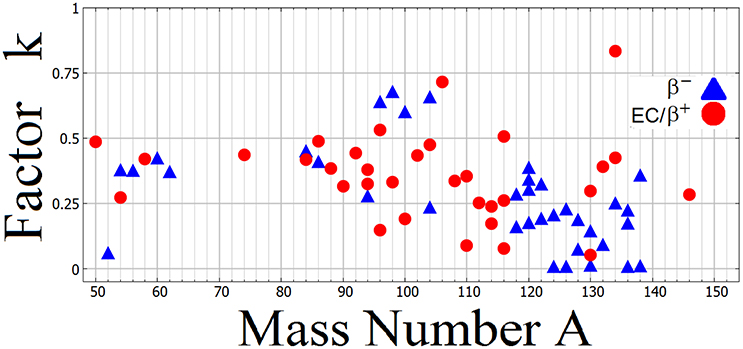
Figure 9. Ratio (62) as a function of the mass number A separated to β⁻ and EC/β⁺ K-forbidden transitions of Figure 8.

From Figure 8 it is visible that the second- and fourth-forbidden β transitions are distributed to masses below A = 62 and above masses A = 92, whereas the third-forbidden decays occupy the mass range 74 ≤ A ≤ 90. The sixth-forbidden decays occur within the range 92 ≤ A ≤ 110 and the seventh-forbidden decays occur above A = 116. The fifth-forbidden decays occur in a scattered way above A = 84. From Figure 9 one observes that most of the β⁻ decays are concentrated above mass A = 118 where also quite low values of k can be obtained. The EC/β⁺ decays, on the other hand, are more concentrated in the middle-mass region 82 ≤ A ≤ 116.

Figure 8 suggests that the values of the ratio (62) can be classified in terms of three mass regions, namely A = 50 − 88 (k ~ 0.4), A = 90 − 120 (values of k have a scattered, decreasing trend), and A = 122 − 146 (a low-k region with k~0.2). The ratios k for the three mass regions and for various degrees of forbiddenness K are shown in Table 4 for β transitions belonging to GROUP 1. A comparison is made to the GT results of Ejiri and Suhonen [140] and SD results of Ejiri et al. [147]. The ratios are also plotted in Figure 10 for illustrative purposes. In the figure one can see that the trend, in terms of the mass number A, is a bit different for the Gamow-Teller and the forbidden (K ≥ 2) transitions. For most of the forbidden transitions, namely K = 3, 4, 5, k has a decreasing tendency as a function of A, in particular for the k = 4 transitions. For K = 2 and K = 7 a slightly increasing tendency is observed. It seems, on average, that the quenching of the forbidden transitions is somewhat stronger than that of Gamow-Teller transitions in the mass region A = 90 − 146.

TABLE 4

Table 4. Ratio (62) for three mass regions and for various degrees of forbiddenness K for β transitions belonging to GROUP 1.

FIGURE 10

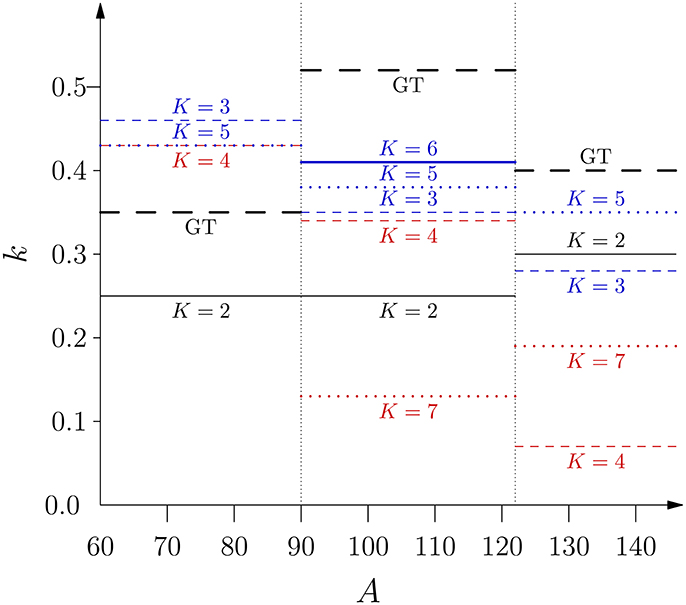
Figure 10. Illustration of the values of the ratio k (62), taken from Table 4, for the three mass regions A = 50−88, A = 90−122, and A = 122−146 for different degrees of forbiddenness K. GT denotes the ratio k for Gamow-Teller transitions.

The numbers in Table 4 suggest that, in the gross, k is independent of the degree of forbiddenness and thus the (low-energy) forbidden unique contributions [obeying the simple rule (46)] to the 0νββ NME (59) should be roughly uniformly quenched. If these conclusions can be generalized to include also the non-unique β transitions, obeying the rule (−1)^ΔJΔπ = +1, one can then speak about an effective axial coupling, $g_{\text{A},0\nu }^{\text{eff}}$, in front of the 0νββ NME in (58), at least for low intermediate excitation energies. The quenching for these low intermediate excitation energies could then be deduced from the hatched regions of Figure 2, implying the effective axial couplings listed in Table 5 for the three mass regions of interest for 0νβ⁻β⁻-decay calculations in the pnQRPA framework. At this point it has to be noted that a “low” excitation energy is still an undefined notion that has to be investigated in future works.

TABLE 5

Table 5. Values of the low-energy effective axial coupling, $g_{\text{A},0\nu }^{\text{eff}}$ of (58), for the three mass regions of interest for 0νβ⁻β⁻-decay calculations in the pnQRPA framework.

Finally, it should be stressed that the use of the low-energy effective axial coupling, $g_{\text{A},0\nu }^{\text{eff}}$, is particular to the pnQRPA many-body framework and reflects the deficiencies of pnQRPA in calculating the magnitudes of the NMEs of the allowed and forbidden unique β-decay transitions. It is not directly related to the more fundamental quenching of the axial-vector coupling strength g_A, related to the meson-exchange currents, delta isobars, two-body weak currents, etc., discussed in section 3, but it is rather a nuclear-model effect, discussed in section 4.

8. Quenching of g_A in Forbidden Non-unique β Decays

The general theory of forbidden beta decays is outlined in Behrens and Buhring [144] and Schopper [158]. Streamlined version of those is given in Mustonen et al. [159].

8.1. Theoretical Considerations

In the forbidden non-unique β decay the half-life can be given, analogously to (47), in the form

$\begin{array}{ll}{t}_{1/2}=\kappa /\tilde{C},& (63)\end{array}$

where $\tilde{C}$ is the dimensionless integrated shape function, given by

$\begin{array}{ll}\tilde{C}={\displaystyle {\int }_1^{w_0}}C(w_e)p{w}_{\text{e}}{(w_0-w_e)}^2{F}_0(Z_f,w_e)\text{d}{w}_e,& (64)\end{array}$

with the notation explained in section 6.1. The general form of the shape factor of Equation (64) is a sum

$\begin{array}{l}C\left(w_e\right)={\displaystyle \sum _{k_e,k_{\nu },K}{\lambda }_{k_e}[M_K{(k_e,k_{\nu })}^2}\\ + m_K{\left(k_e,k_{\nu }\right)}^2-\frac{2{\gamma }_{k_e}}{k_e{w}_e}{M}_K\left(k_e,k_{\nu }\right)m_K\left(k_e,k_{\nu }\right)],& (65)\end{array}$

where the factor λ_ke was given in (51) and Z_f is the charge number of the final nucleus. The indices k_e and k_ν (k = 1, 2, 3…) are related to the partial-wave expansion of the electron (e) and neutrino (ν) wave functions, K is the order of forbiddenness of the transition, and ${\gamma }_{k_e}=\sqrt{k_e^2-{(\alpha Z_f)}^2}$, α ≈ 1/137 being the fine-structure constant. The nuclear-physics information is hidden in the factors M_K(k_e, k_ν) and m_K(k_e, k_ν), which are complicated combinations of the different NMEs and leptonic phase-space factors. For more information on the integrated shape function, see [144, 159].

The quite complicated shape factor (65) can be simplified in the so-called ξ approximation when the coulomb energy of the emitted β particle at the nuclear surface is much larger than the endpoint energy, i.e., ξ = αZ_f/2R≫w₀, where R is the nuclear radius. Then the forbidden non-unique transition can be treated as a unique one of the same ΔJ. Applicability of this approximation has recently been criticized in Mougeot [160].

8.2. First-Forbidden Non-unique β Decays

For the first-forbidden non-unique β decays the shape factor (65) has to be supplemented with a ΔJ = |J_i − J_f| = 0 term $C^{(1)}(w_e)$ [144, 158, 161, 162], where J_i (J_f) is the initial-state (final-state) spin of the mother (daughter) nucleus. Then the shape factor can be cast in the simple form [144, 158, 163]

$\begin{array}{ll}C(w_e)=K_0+K_1{w}_e+K_{-1}/w_e+K_2{w}_e^2,& (66)\end{array}$

where the factors K_n contain the NMEs (6 different, altogether) of transition operators ${O}$ of angular-momentum content (rank of a spherical tensor) ${O}(0^{-})$, ${O}(1^{-})$, and ${O}(2^{-})$, where the parity indicates that the initial and final nuclear states should have opposite parities according to Table 3. In the leading order these operators contain the pieces [148]

$\begin{array}{ll}{O}(0^{-}):g_{\text{A}}({\gamma }^5)\frac{\sigma ·{\text{p}}_e}{M_{\text{N}}};\text{ i}{g}_{\text{A}}\frac{\alpha Z_f}{2R}(\sigma ·\text{r}),& (67)\end{array}$

$\begin{array}{ll}{O}(1^{-}):g_{\text{V}}\frac{{\text{p}}_e}{M_{\text{N}}};g_{\text{A}}\frac{\alpha Z_f}{2R}(\sigma \times \text{r});\mathrm{\text{i}}{g}_{\text{V}}\frac{\alpha Z_f}{2R}\text{r},& (68)\end{array}$

$\begin{array}{ll}{O}(2^{-}):\frac{\mathrm{\text{i}}}{\sqrt{3}}{g}_{\text{A}}{\left[\sigma \text{r}\right]}_2\sqrt{{\text{p}}_e^2+{\text{q}}_{\nu }^2},& (69)\end{array}$

where p_e (q_ν) is the electron (neutrino) momentum, r the radial coordinate, and the square brackets in (69) denote angular-momentum coupling. The matrix elements of the operators (67) and (68) are suppressed relative to the Gamow-Teller matrix elements by the small momentum p_e of the electron and the large nucleon mass M_N or the small value of the fine-structure constant α. The matrix element of (69) is suppressed by the small electron and neutrino momenta. The axial operator σ · p_e and vector operator r trace back to the time component of the axial current A^μ in (4) and vector current V^μ in (3), and the rest of the operators stem from the space components of V^μ and A^μ. The renormalization of these pieces is discussed next.

The ξ approximation to the first-forbidden non-unique transitions has been discussed, e.g., [144, 148, 158]. One of the first analyses of first-forbidden non-unique transitions in this approximation was done in Bohr and Mottelson [148] for nuclei around ²⁰⁸Pb, based on the work of Damgaard and Winther [164]. Assuming certain dominant single-particle configurations around the double-closed shell at A = 208, Bohr and Mottelson obtained two sets of values for the effective vector and axial-vector coupling when analyzing the decay rates mediated by the rank-1 operators ${O}(1^{-})$ in (68). Combining the two obtained values we obtain

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(\text{sp})=(0.5-0.6)\times 1.18=0.46-0.56,& (70)\end{array}$

where the symbol sp refers to single-particle estimate for the states involved in the β decays in odd-A nuclei. It is interesting that also an effective value for the vector coupling was derived:

$\begin{array}{ll}{g}_{\text{V}}^{\text{eff}}(\mathrm{\text{sp}})=0.3-0.7.& (71)\end{array}$

This deviates quite much from the canonical value g_V = 1 dictated by the CVC hypothesis [26]. Hence, strong nuclear-model dependent effects are recorded in this case. In the case of the axial-vector strength the numbers of (70) can be compared with the ones extracted from the first-forbidden unique decays in the two-quasiparticle approximation for odd-odd nuclei. There, in Equation (56), a value $g_{\text{A}}^{\text{eff}}$(2qp) ~ 0.2 was obtained, implying that for the odd-odd systems the quenching is more drastic than for the odd-mass systems. All in all, a proper many-body treatment should reduce the quenching markedly, as shown by the factor k in (57), describing the transition from the two-quasiparticle approximation to the pnQRPA level in the case of the unique-forbidden β transitions.

In Ejiri et al. [145] a schematic study of the six NMEs corresponding to the operators (67)–(69) was performed. The hindrance factors associated with the NMEs were related to the E1 (electric dipole) giant resonance in a semi-quantitative way. The nuclear medium effect, in the form of the meson-exchange currents, on the σ · p_e part of ${O}(0^{-})$ in (67) was discussed in Kubodera et al. [42], Kirchbach and Reinhardt [79] and Towner [81]. This is the well-known (fundamental) enhancement of the γ⁵ NME (axial charge ρ₅, the time component of the axial current, see section 3), stemming from the renormalization of the pion-decay constant and the nucleon mass M_N in nuclear medium [165] and exchange of heavy mesons [80, 81]. In this review the corresponding coupling strength is coined $g_{\text{A}}^{\text{eff}}({\gamma }^5)$ for short. In Kirchbach and Reinhardt [79] a simple nuclear approach to the meson-exchange renormalization $g_{\text{A}}^{\text{eff}}({\gamma }^5)=(1+\delta )g_{\text{A}}^{\text{free}}$ gave the following values of $g_{\text{A}}^{\text{eff}}({\gamma }^5)$ (below are given the studied nuclear masses and the corresponding active single-particle transitions):

$\begin{array}{lll}{g}_{\text{A}}^{\text{eff}}({\gamma }^5)=1.90& A=16& (1{\mathrm{\text{s}}}_{1/2}\to 0{\mathrm{\text{p}}}_{1/2})\\ g_{\text{A}}^{\text{eff}}({\gamma }^5)=1.96& A=18& (1{\mathrm{\text{s}}}_{1/2}\to 0{\mathrm{\text{p}}}_{1/2})\\ g_{\text{A}}^{\text{eff}}({\gamma }^5)=1.84& A=96& (2{\mathrm{\text{s}}}_{1/2}\to 1{\mathrm{\text{p}}}_{1/2})\\ g_{\text{A}}^{\text{eff}}({\gamma }^5)=1.78& A=206& (2{\mathrm{\text{p}}}_{1/2}\to 2{\mathrm{\text{p}}}_{1/2})& (72)\end{array}$

The work of Kirchbach and Reinhardt [79] was extended by Towner [81] to include 6 nuclear masses and several single-particle transitions for each mass. The resulting renormalization by the meson-exchange currents amounted to

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}({\gamma }^5)=2.0-2.3(A=16-208)& (73)\end{array}$

for the masses A = 16 − 208.

The above fundamental renormalization of the axial charge was contrasted with the nuclear-model dependent many-body effects by using the framework of the interacting shell model in several studies in the past. For very low masses, A = 11 [166] and A = 16 [167], some 40−50% enhancement of the axial charge was obtained leading to $g_{\text{A}}^{\text{eff}}({\gamma }^5)=1.8-1.9$. A further study [168] of the A = 11 − 16 nuclei indicated an enhanced axial charge of

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}({\gamma }^5)=2.04\pm 0.04,(A=11-16)& (74)\end{array}$

where the uncertainties come solely from the experimental errors, not from the uncertainties associated with the theoretical analyses. A general study of the first-forbidden non-unique decays was carried on in Warburton et al. [169] for 34 ≤ A ≤ 44, and a further comparison [170] with the measured rate of the β⁻ decay of ⁵⁰K indicated an enhanced value of

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}({\gamma }^5)=1.93\pm 0.09,(A=50)& (75)\end{array}$

where the uncertainty is purely experimental.

A thorough shell-model treatment of the mass A = 205 − 212 nuclei in the lead region was carried out in Warburton [171–173]. There a rather strongly enhanced value of

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}({\gamma }^5)=2.55\pm 0.07(A=205-212)& (76)\end{array}$

was obtained for the axial charge. The uncertainty comes from the least-squares fit to 18 measured β-decay transitions in the indicated mass region. For the σ · r operator (space component of A^μ) essentially no renormalization (quenching, since space components tend to be quenched opposite to the enhancement of the time component, see beginning of section 3) was obtained: $g_{\text{A}}/g_{\text{A}}^{\text{free}}(0^{-})=0.97\pm 0.06$. The value (76) is notably larger than those obtained for the lower masses and also larger than the lead-region results of Towner (73). However, in Kubodera and Rho [165] the theoretical result

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}({\gamma }^5)=2.5\pm 0.3(A=205-212)& (77)\end{array}$

was obtained by adopting an effective Lagrangian incorporating approximate chiral and scale invariance of QCD. This seems to confirm the phenomenological result of Warburton [172, 173]. For further information see the review [174].

For the ${O}(1^{-})$ operator σ × r in (68) the analyses of Warburton [171, 173] yielded the effective values

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(1^{-})~0.6;g_{\text{V}}(1^{-})~0.6(\mathrm{\text{Warburton}})& (78)\end{array}$

due to core-polarization effects caused by the limited model space used. In the work Rydstrom [175] a shell-model study of the first-forbidden transition ${}^{205}\text{Tl}(1/2_{\text{gs}}^{+}){\to }^{205}\text{Pb}(1/2^{-})$ yielded the effective values

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(1^{-})~0.43-0.65;g_{\text{V}}(1^{-})~0.38-0.85.(\mathrm{\text{Rydström }}etal.)& (79)\end{array}$

The shell-model analysis of Suzuki et al. [163] of the N = 126 isotones suggests a large quenching for $g_{\text{A}}^{\text{eff}}(1^{-})$ but a large quenching of $g_{\text{V}}^{\text{eff}}(1^{-})$ is not necessarily needed for most of the studied cases, contrary to (78) and (79), in accordance with the CVC hypothesis [26].

In the work [176] half-lives of a number of nuclei at the magic neutron numbers N = 50, 82, 126 were analyzed by comparing results of large-scale shell-model calculations with experimental data. Both Gamow-Teller and first-forbidden β decays were included in the analysis. By performing a least-squares fit to the experimental data the following quenched weak couplings were extracted: For the enhanced γ⁵ matrix element the value $g_{\text{A}}^{\text{eff}}({\gamma }^5)=1.61$ was obtained and for the σ · r part the quenching $g_{\text{A}}/g_{\text{A}}^{\text{free}}(0^{-})=0.66$ was obtained. For the 1⁻ part the quenched values read

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(1^{-})~0.48;g_{\text{V}}(1^{-})~0.65.(\text{Zhi }etal.)& (80)\end{array}$

Interestingly, also for the first-forbidden unique operator ${O}(2^{-})$ of (69) a quenching

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(2^{-})~0.53(\text{Zhi }etal.)& (81)\end{array}$

was obtained. This is not far from the result $g_{\text{A}}^{\text{eff}}~0.57$ [see Equation (55)] obtained in the analysis of the first-forbidden unique β decays in Ejiri et al. [147].

The above considerations for the vector coupling coefficient g_V are in conflict with the CVC hypothesis [26] and the findings of [177] where the shape of the computed β-electron spectrum was compared with that of the measured one for the fourth-forbidden β⁻ decay of ¹¹³Cd. This comparison confirmed an unquenched value g_V = 1.0 for the vector coupling coefficient, in accordance with the CVC hypothesis. For more discussion of the related method for highly-forbidden β decays, see section 9.

9. Higher-Forbidden Non-Unique β Decays

The shape functions of forbidden non-unique beta decays are rather complex combinations of different NMEs and phase-space factors. Furthermore, their dependence on the weak coupling strengths g_V (vector part) and g_A (axial-vector part) is very non-trivial. In fact, the shape factor C(w_e) (65) can be decomposed into vector, axial-vector and mixed vector-axial-vector parts in the form [177]

$\begin{array}{ll}C(w_e)=g_{\text{V}}^2{C}_{\text{V}}(w_e)+g_{\text{A}}^2{C}_{\text{A}}(w_e)+g_{\text{V}}{g}_{\text{A}}{C}_{\text{VA}}(w_e).& (82)\end{array}$

Integrating equation (82) over the electron kinetic energy, we obtain an analogous expression for the integrated shape factor (64)

$\begin{array}{ll}\tilde{C}=g_{\text{V}}^2{\tilde{C}}_{\text{V}}+g_{\text{A}}^2{\tilde{C}}_{\text{A}}+g_{\text{V}}{g}_{\text{A}}{\tilde{C}}_{\text{VA}},& (83)\end{array}$

where the factors ${\tilde{C}}_i$ in Equation (83) are just constants, independent of the electron energy.

In Haaranen et al. [177] it was proposed that the shapes of β-electron spectra could be used to determine the values of the weak coupling strengths by comparing the computed spectrum with the measured one for forbidden non-unique β decays. This method was coined the spectrum-shape method (SSM). In this study also the next-to-leading-order corrections to the β-decay shape factor were included. In Haaranen et al. [177] the β-electron spectra were studied for the 4th-forbidden non-unique ground-state-to-ground-state β⁻ decay branches ¹¹³Cd(1/2⁺) → ¹¹³In(9/2⁺) and ¹¹⁵In(9/2⁺) → ¹¹⁵Sn(1/2⁺) using the microscopic quasiparticle-phonon model (MQPM) [115, 116] and the ISM. It was verified by both nuclear models that the β spectrum shapes of both transitions are highly sensitive to the values of g_V and g_A and hence comparison of the calculated spectrum shape with the measured one opens a way to determine the values of these coupling strengths. As a by-product it was found that for all values of g_A the best fits to data were obtained by using the canonical value g_V = 1.0 for the vector coupling strength. This result is in conflict with those obtained by analyzing first-forbidden non-unique β decays in section 8.2, where strongly quenched values of g_V were obtained.

The work of Haaranen et al. [177] on the ¹¹³Cd and ¹¹⁵In decays was extended in Haaranen et al. [178] to include an analysis made by using a third nuclear model, the microscopic interacting boson-fermion model (IBFM-2) [92]. At the same time the next-to-leading-order corrections to the β-decay shape factor were explicitly given and their role was thoroughly investigated. A striking feature of the SSM analysis was that the three models yield a consistent result, g_A ≈ 0.92, when the SSM is applied to the available experimental β spectrum [179] of ¹¹³Cd. The result is illustrated in Figure 11 where the three curves overlap best at the values $g_{\text{A}}^{\text{eff}}=0.92$ (MQPM), $g_{\text{A}}^{\text{eff}}=0.90$ (ISM), and $g_{\text{A}}^{\text{eff}}=0.93$ (IBFM-2). The agreement of the β-spectrum shapes computed in the three different nuclear-theory frameworks speaks for the robustness of the SSM in determining the effective value of g_A. For completeness, in Figure 12 are shown the three components (82) as functions of the electron energy for the three different nuclear models used to compute the spectrum shapes of ¹¹³Cd in Figure 11. It is seen that for the whole range of electron energies the two components, C_V(w_e) and C_A(w_e) are roughly of the same size whereas the magnitude of the component C_VA(w_e) is practically the sum of the previous two, but with opposite sign. Hence, for the whole range of electron energies there is a delicate balance between the three terms, and their sum is much smaller than the magnitudes of its constituent components.

FIGURE 11

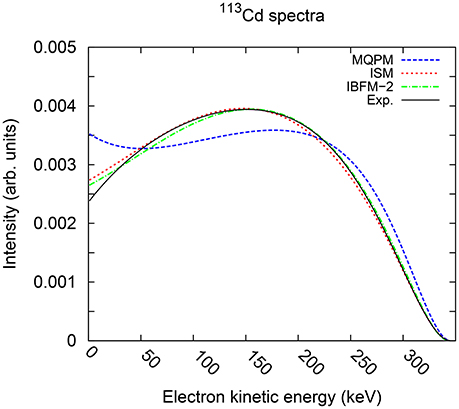
Figure 11. Comparison of the computed β spectra of ¹¹³Cd with the experiment. The next-to-leading-order corrections to the shape factor have been included, and only the best matches are shown in the figure. The canonical value g_V = 1.0 is used for the vector coupling strength. The areas under the curves are normalized to unity.

FIGURE 12

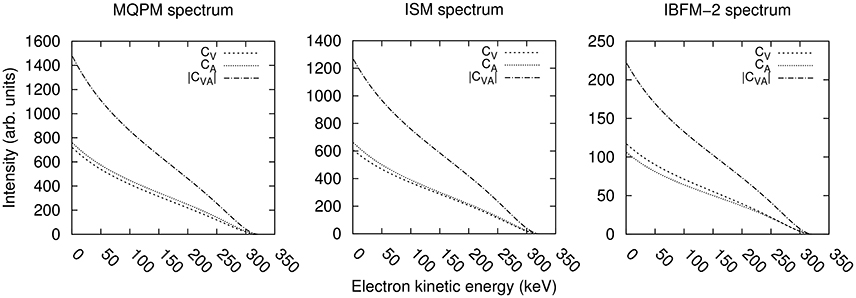
Figure 12. Components C_V, C_A, and C_VA of (82) for the electron spectra of the β⁻ decay of ¹¹³Cd as computed by the three nuclear models discussed in the context of Figure 11. Note that the contribution of C_VA is negative.

The works [177, 178] were continued by the work [180] where the evolution of the β spectra with changing value of g_A was followed for 26 first-, second-, third-, fourth- and fifth-forbidden β⁻ decays of odd-A nuclei by calculating the associated NMEs by the MQPM. The next-to-leading-order contributions were taken into account in the β-decay shape factor. It was found that the spectrum shapes of the third- and fourth-forbidden non-unique decays depend strongly on the value of g_A, whereas the first- and second-forbidden decays were practically insensitive to the variations in g_A. Furthermore, the g_A-driven evolution of the normalized β spectra seems to be quite universal, largely insensitive to small changes of the nuclear mean field and the adopted residual many-body Hamiltonian. These features were also verified in the follow-up work [181], where the ISM was used as the nuclear-model framework. This makes SSM a robust tool for extracting information on the effective values of the weak coupling strengths. This also means that if SSM really is largely nuclear-model independent there is a chance to access the fundamental renormalization factor q_F of section 3 for (highly) forbidden β transitions. It is also worth noting that in the works [180, 181] several new experimentally interesting decays for the SSM treatment were discovered.

Results of the investigations of Kostensalo et al. [180] and Kostensalo and Suhonen [181] are summarized in Tables 6, 7, and in Figures 13–15. Figure 13 displays the β spectra of the second-forbidden non-unique transitions ⁹⁴Nb(6+) → ⁹⁴Mo(4⁺) (left panel) and ⁹⁸Tc(6⁺) → ⁹⁸Ru(4⁺) (right panel) calculated by using the ISM [181]. It is obvious that the shape of the spectra depends sensitively on the value of g_A but not as strongly as the transitions associated with the mother nuclei ¹¹³Cd and ¹¹⁵In, as shown in the figures of Haaranen et al. [177]. It is to be noted that both of the transitions have been observed experimentally since the branching is 100%, but the electron spectra are not yet available.

TABLE 6

Table 6. Dimensionless integrated shape functions $\tilde{C}$ (83) and their vector ${\tilde{C}}_{\text{V}}$, axial-vector ${\tilde{C}}_{\text{A}}$, and mixed components ${\tilde{C}}_{\text{VA}}$ for the forbidden non-unique β decays of ¹³⁵Cs and ¹³⁷Cs.

TABLE 7

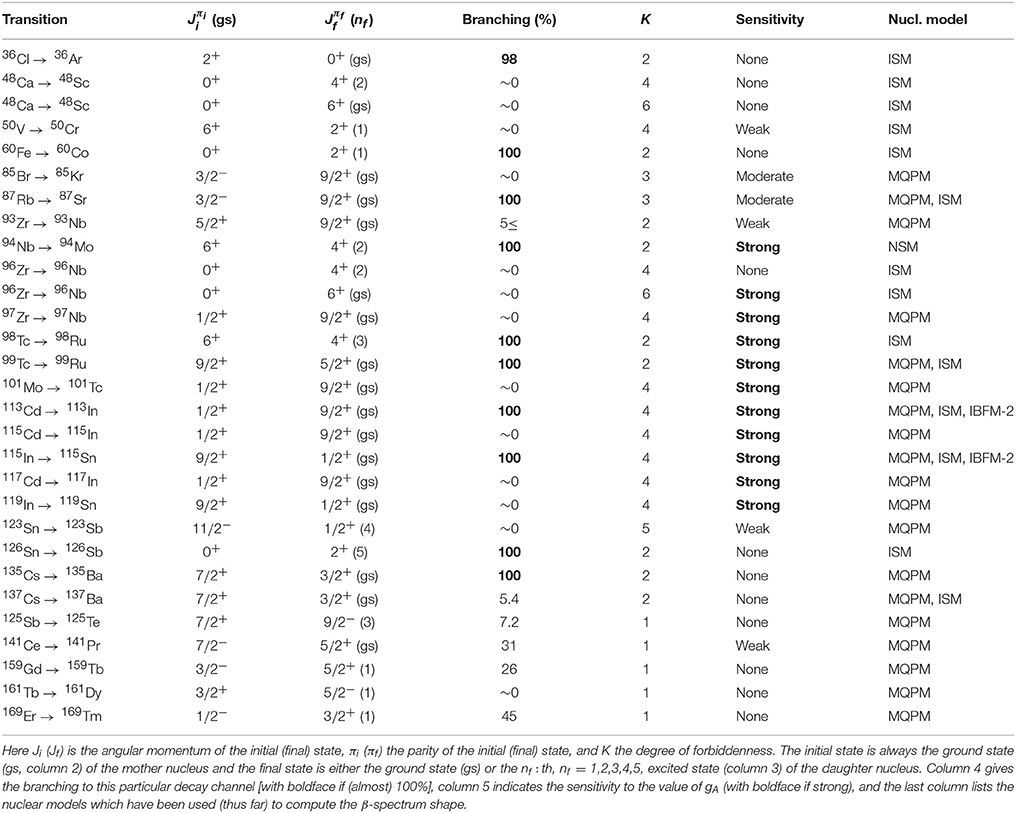
Table 7. List of the studied high-forbidden non-unique β⁻-decay transitions and their sensitivity to the value of g_A.

FIGURE 13

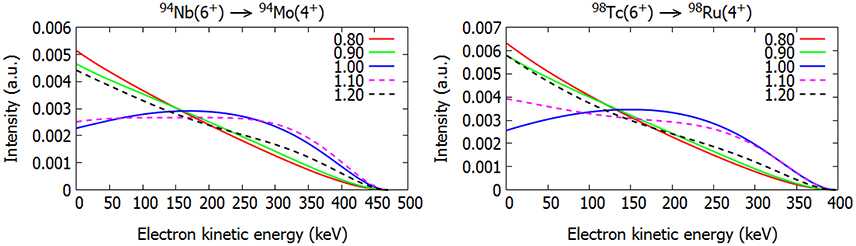
Figure 13. Normalized ISM-computed electron spectra for the second-forbidden non-unique decays of ⁹⁴Nb and ⁹⁸Tc. The value g_V = 1.0 was assumed and the color coding represents the value of g_A.

In Figure 14 a comparison of the MQPM (left panel) and ISM (right panel) calculations [181] for the β spectrum of the second-forbidden non-unique decay transition ⁹⁹Tc(9/2⁺) → ⁹⁹Ru(5/2⁺) is shown. Again there is clear sensitivity to the value of g_A, at the level of the ⁹⁴Nb and ⁹⁸Tc transitions, but the remarkable thing is that the spectrum shapes computed by the two nuclear models agree almost perfectly, giving further evidence in favor of the robustness of the SSM. Again, experimentally, the branching to this decay channel is practically 100% so that the β spectrum is potentially well measurable.

FIGURE 14

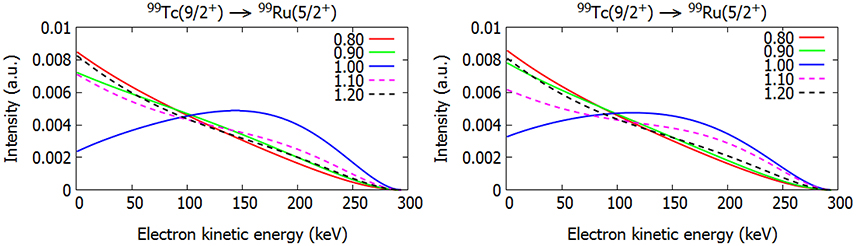
Figure 14. Normalized electron spectra for the second-forbidden non-unique ground-state-to-ground-state β⁻ decay of ⁹⁹Tc as computed by using the MQPM (Left panel) and the ISM (Right panel). The value g_V = 1.0 was assumed and the color coding represents the value of g_A.

Finally, In Figure 15 the β spectrum of the second-forbidden non-unique decay-transition ¹³⁷Cs(7/2⁺) → ¹³⁷Ba(3/2⁺) is shown. Here the spectrum shape is quite independent of the value of g_A and has exactly the same computed shape for the two applied nuclear-model frameworks: the MQPM and the ISM [181]. The robustness of the β-spectrum shape against variations in g_A and the calculational scheme makes the measurement of this spectrum interesting in terms of testing the basic framework of high-forbidden non-unique β decays. The cause of the inertia against variations of g_A is seen in Table 6 in the decomposition (83) of the dimensionless integrated shape function $\tilde{C}$ for the decays of both ¹³⁵Cs and ¹³⁷Cs. It is seen that for these two decays all the components of $\tilde{C}$ are of the same sign, thus adding coherently. Hence, changes in the value of g_A do not affect the spectrum shape, contrary to those decays where there is a destructive interference between the axial-vector and mixed components of (83), like in the cases of Figures 11–14, further analyzed in Table 8.

FIGURE 15

Figure 15. Normalized electron spectra for the second-forbidden non-unique ground-state-to-ground-state β⁻ decay of ¹³⁷Cs as computed by using the MQPM and the ISM. The value g_V = 1.0 was assumed and the color coding represents the nuclear model.

TABLE 8

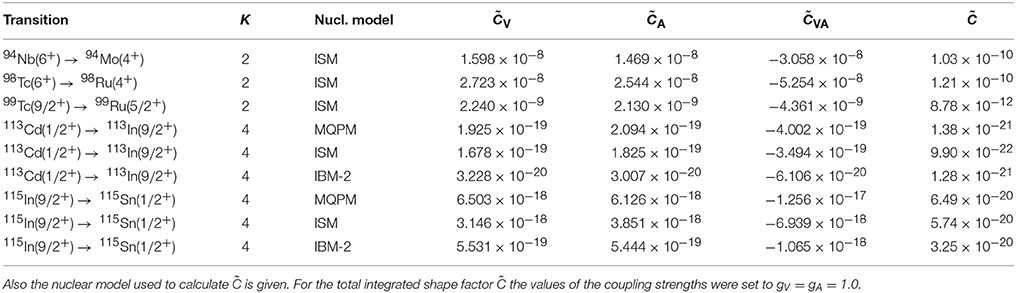
Table 8. Dimensionless integrated shape functions $\tilde{C}$ (83) and their vector ${\tilde{C}}_{\text{V}}$, axial-vector ${\tilde{C}}_{\text{A}}$ and mixed components ${\tilde{C}}_{\text{VA}}$ for the experimentally most promising forbidden non-unique β decays of forbiddenness K.

Table 7 summarizes the exploratory works of Haaranen et al. [177, 178], Kostensalo et al. [180] and Kostensalo and Suhonen [181] in terms of listing the studied decay-transition candidates and their potential for future measurements. Here only the studied non-unique β-decay transitions are listed since the unique forbidden transitions are practically g_A-independent even when the next-to-leading-order terms are included in the β-decay shape factor [177]. The most favorable cases for measurements are the ones that have a strong dependence on g_A and the branching to the final state of interest is close to 100%. By these criteria the best candidates for measurements are the non-unique transitions ⁹⁴Nb(6⁺) → ⁹⁴Mo(4⁺) (second-forbidden), ⁹⁸Tc(6⁺) → ⁹⁸Ru(4⁺) (second-forbidden), ⁹⁹Tc(9/2⁺) → ⁹⁹Ru(5/2⁺) (second-forbidden), ¹¹³Cd(1/2⁺) → ¹¹³In(9/2⁺) (fourth-forbidden), and ¹¹⁵In(9/2⁺) → ¹¹⁵Sn(1/2⁺) (fourth-forbidden). Plans for accurate measurements of (some) of these transitions are on-going in the DAMA (V. Tretyak, private communication) and COBRA collaborations (K. Zuber, private communication). It should be noted that also the transition ⁸⁷Rb(3/2⁻) → ⁸⁷Sr(9/2⁺) could be of interest for measurements since it has a 100% branching and the corresponding β spectrum is moderately sensitive to g_A.

In Table 8 the dimensionless integrated shape functions $\tilde{C}$ (83) have been decomposed into their vector ${\tilde{C}}_{\text{V}}$, axial-vector ${\tilde{C}}_{\text{A}}$ and mixed vector-axial-vector components ${\tilde{C}}_{\text{VA}}$ for the experimentally most promising forbidden non-unique β decays of forbiddenness K of Table 7. In the table also the nuclear model used to calculate $\tilde{C}$ is given. A characteristic of the numbers of Table 8 is that the magnitudes of the vector, axial-vector, and mixed components are of the same order of magnitude, and the vector and axial-vector components have the same sign whereas the mixed component has the opposite sign. This makes the three components largely cancel each other and the resulting magnitude of the total dimensionless integrated shape function is always a couple of orders of magnitude smaller than its components. Thus, the integrated shape function becomes extremely sensitive to the value of g_A, as seen in Figure 13 for the decays of ⁹⁴Nb and ⁹⁸Tc, and in Figure 14 for the decay of ⁹⁹Tc.

For the beta spectrum of the decays of ¹¹³Cd and ¹¹⁵In there are calculations available in three different nuclear-theory frameworks as shown in Figure 11 and Tables 7, 8. As visible in Table 8, an interesting feature of the components of the integrated shape functions $\tilde{C}$ is that the MQPM and ISM results are close to each other whereas the numbers produced by IBM-2 are clearly smaller. Surprisingly enough, the total value of $\tilde{C}$ is roughly the same in all three theory frameworks. This is another indication of the robustness of the SSM.

There are indirect ways to access the quenching of high-forbidden β-decay transitions. One of them is to study electromagnetic decays of analogous structure. In Jokiniemi et al. [182] magnetic hexadecapole (M4) γ transitions in odd-A medium-heavy nuclei were studied by comparing the single-quasiparticle NMEs against the MQPM-computed NMEs to learn about the quenching in the analogous third-forbidden unique β decays (parity change with angular-momentum content 4). The MQPM calculations suggest a strong quenching $g_{\text{A}}~0.33g_{\text{A}}^{\text{free}}~0.4$ for these transitions. This strong quenching could be an artifact of the MQPM framework since there the excitations of an odd-A nucleus are formed by coupling BCS quasiparticles to excitations of the neighboring even-even reference nucleus. Thus, the predicted M4 giant resonance in the odd-A nucleus might not be strong enough to draw low-lying M4 strength to higher excitation energies, around the giant-resonance region.

10. Quenching of g_A in 2νββ Decays

The 2νββ decay rate can be compactly written as

$\begin{array}{ll}{\left[t_{1/2}^{(2\nu )}(0_i^{+}\to 0_f^{+})\right]}^{-1}=g_{\text{A}}^4{G}_{2\nu }{\left|M^{(2\nu )}\right|}^2,& (84)\end{array}$

where G_2ν represents the leptonic phase-space factor (without including g_A) as defined in Kotila and Iachello [183]. The initial ground state is denoted by $0_i^{+}$ and the final ground state by $0_f^{+}$. The 2νββ NME M^(2ν) can be written as

$\begin{array}{ll}{M}^{(2\nu )}={\displaystyle \sum _{m,n}}\frac{M_{\text{L}}(1_m^{+})M_{\text{R}}(1_n^{+})}{D_m},& (85)\end{array}$

where the quantity D_m is the energy denominator and the NMEs M_L and M_R correspond to left-leg and right-leg virtual Gamow-Teller transitions depicted in Figure 16. The summation is in general over all intermediate 1⁺ states, not just the first one as implied by the very schematic Figure 5. On the other hand, the summation in (85) can be dominated by one transition, usually through the lowest 1⁺ state if it happens to be the ground state of the intermediate nucleus. In this case one speaks about single-state dominance. This dominance has been addressed in several works (e.g., [184–186]).

FIGURE 16

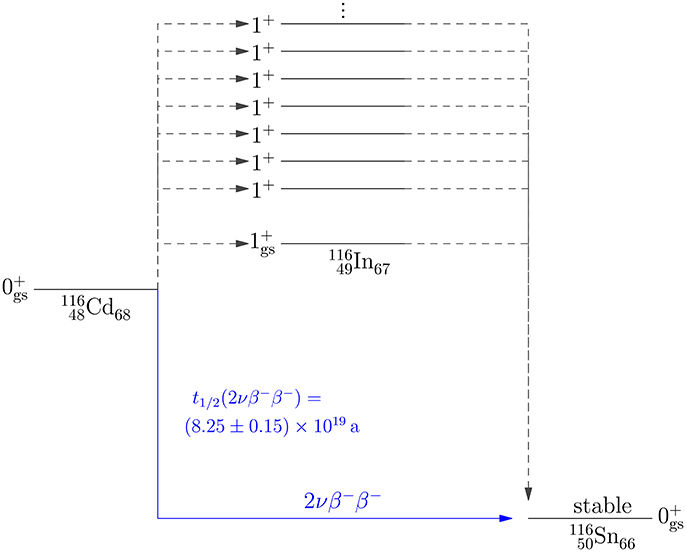
Figure 16. The 2νββ decay of ¹¹⁶Cd to ¹¹⁶Sn via the 1⁺ virtual intermediate states in ¹¹⁶In. The transitions between ¹¹⁶Cd (¹¹⁶Sn) and ¹¹⁶In constitute the left-leg (right-leg) transitions.

The 2νββ decay rate (84) and 0νββ decay rate (59) share the same strong dependence on g_A. It is thus essential to study the renormalization of g_A in beta and 2νββ decays before entering studies of the 0νββ decay. These studies touch only the 1⁺ contribution to the 0νββ decay. However, it is known that contributions from higher multipoles are also very important for the 0νββ decay (see section 7). It is challenging to relate the results emanating from the β and 2νββ decay studies to the value of the 0νββ NME: the former two involve momentum transfers of a few MeV whereas the latter involves momentum exchanges of the order of 100 MeV through the virtual Majorana neutrino. The high exchanged momenta in the 0νββ decay allow for the possibility that the effective value of g_A acquires momentum dependence, as discussed in section 3. In addition, the high exchanged momenta induce substantial contributions from the higher J^π states to the 0νββ decay rate [155]. The renormalization of g_A for these higher-lying states could be different from the renormalization for the low-lying states, the subject matter of this review.

After this preamble we now proceed to discuss the possible renormalization of the axial-vector coupling strength [at zero-momentum limit q → 0 in (5)] as obtained from the combined β-decay and 2νββ-decay analyses performed in different theoretical approaches. It is important to be aware that in all the studies of the present section it is impossible to disentangle between the fundamental, nuclear-matter affected, and the many-body, nuclear-model affected, contributions to the renormalization of g_A.

10.1. Quasiparticle Random-phase Approximation

The simultaneous analysis of both β and 2νββ decays opens up new vistas in attempts to pin down the effective value of the weak axial-vector coupling strength. Indeed, analysis of these two decay modes is possible for few nuclear systems where both the β-decay data (http://www.nndc.bnl.gov/) and 2νββ-decay data [157, 187] are available. The involved transitions, with the available data, are depicted schematically in Figure 17. The aim in using the three pieces of data available for the three isobaric systems is to gain information on the effective value of g_A and the value of the particle-particle interaction parameter g_pp of pnQRPA in the mass regions A = 100,116,128.

FIGURE 17

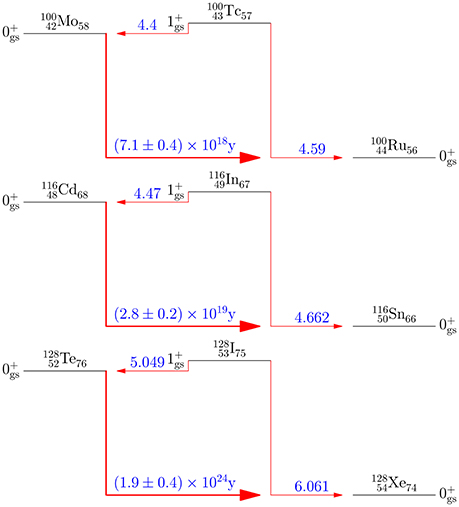
Figure 17. Schematic plot of β and ββ decays in the three isobaric chains (A = 100, 116, 128) with data on both decay modes. Given are the 2νββ half-life and logft values of the left- and right-branch β decays.

The first work to address the quenching in both β and 2νββ decays was [188] where both the beta-decay and 2νββ decay data were analyzed for the A = 100, 116 systems in the framework of the pnQRPA using the method of least squares to fit the pair (g_pp,g_A) to the available three pieces of data, namely the logft values of the left- and right-branch β decays, and the 2νββ half-life (see Figure 17). Realistic model spaces (large and small basis) and a phenomenologically renormalized microscopic G-matrix-based Hamiltonian was used in the investigations. In Faessler et al. [188] the best fit values $g_{\text{A}}^{\text{eff}}=0.74$ (A = 100) and $g_{\text{A}}^{\text{eff}}=0.84$ (A = 116) were obtained in the large single-particle model space. Furthermore, it is interesting to note that in the first version [189] of the paper [188] also results for the A = 128 system were included. There the result $g_{\text{A}}^{\text{eff}}=0.39$ (A = 128) was quoted. These values of $g_{\text{A}}^{\text{eff}}$ have been quoted in Table 9 and plotted in Figure 18 in section 10.2.

TABLE 9

Table 9. Extracted values of g_A for three isobaric chains hosting a 2νββ transition.

FIGURE 18

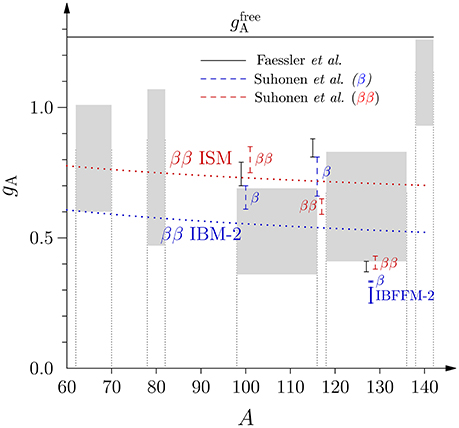
Figure 18. Sketch of the effective values of g_A taken from Table 9 against the light-hatched ranges of $g_{\text{A}}^{\text{eff}}$ in the 5 mass regions of Figure 2 (the combined pnQRPA results). The curves are from the 2νββ analysis of Barea et al. [191] [curves (86)] and the vertical segments display the results of the combined β and 2νββ analyses of Faessler et al. [188, 189] (solid line) and Suhonen and Civitarese [192] (dashed lines). Also the (combined) IBFFM-2 result of Yoshida and Iachello [190] is depicted.

In Suhonen and Civitarese [192, 193] realistic single-particle bases and a G-matrix-based microscopic interaction was used to analyze the A = 100, 116, 128 systems of β and ββ decays. A slightly different approach to the one of Faessler et al. [188, 189] was adopted: by taking the left and right branches of β-decay data of Figure 17 one can fix the pair (g_pp,g_A(β)) by reproducing the available logft values. By using the just determined value of g_pp one can compute the 2νββ NME and half-life and compare with the experimental half-life. This comparison produces a new value of $g_{\text{A}}^{\text{eff}}$, which can be denoted as g_A(ββ). In an ideal case the two effective values of g_A, namely g_A(β) and g_A(ββ), are the same but the over-constrained nature of the problem tends to yield different values to these parameters. The thus obtained values of g_A(β) and g_A(ββ) are quoted in Table 9 and plotted in Figure 18 in section 10.2.

10.2. Interacting Shell Model and Interacting Boson Model

A monotonic behavior of g_A(ββ) was parametrized in Barea et al. [191] by analyzing the magnitudes of 2νββ NMEs produced by the microscopic interacting boson model (IBM-2) [91] and the ISM. In this study the obtained g_A-vs.-A slopes were very flat, having the analytic expressions

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(\mathrm{\text{IBM-2}})=1.269A^{-0.18};g_{\text{A}}^{\text{eff}}(\mathrm{\text{ISM}})=1.269A^{-0.12}.& (86)\end{array}$

These curves have been plotted in Figure 18 together with the results obtained in the pnQRPA analyses of ββ decays in section 10.1. The results of these analyses, together with the the original numbers for g_A(ββ) produced in the IBM-2 calculations of Barea et al. [191] are quoted in Table 9. The IBM-2 numbers are given in the last column of the table and the first two lines refer to the use of the single-state dominance (SSD) hypothesis in the IBM-2 calculations. Based on the analysis in Suhonen and Civitarese [192] this assumption is approximately valid since the magnitudes of the first 1⁺ contribution and the final 2νββ NME are practically the same for the decays of ¹⁰⁰Mo and ¹¹⁶Cd. The last number of the IBM-2 column in Table 9 refers to the assumption of closure approximation (CA) in the IBM-2 calculation. It is well established [1, 23] that such an approximation does not work for the 2νββ decays and thus this number could be dubious. Indeed, in a later publication [190] a more consistent theoretical framework was used (the interacting boson-fermion-fermion model, IBFFM-2 [120]) and in the case of A = 128 values of g_A were obtained that differ notably from the ones obtained in Barea et al. [191]. The IBFFM-2 numbers, based on analysis of both the β and 2νββ decay, are presented in columns 5 and 6 of Table 9. One can see that the IBFFM-2 values of g_A(β) and g_A(ββ) are quite close to those of the pnQRPA-based calculations. The combined β and ββ results of Yoshida and Iachello [190] have also been depicted in Figure 18.

Recent ISM calculations [68, 130] for the 2νββ NMEs of ¹³⁰Te and ¹³⁶Xe, and a subsequent comparison with the experimental NMEs (updated comparison performed in Horoi and Neacsu [68]) suggest a mild quenching and a rather large value of for the effective coupling strength:

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(A=130-136)=0.94.& (87)\end{array}$

This result was already discussed in section 5.1 and it was included in Table 1 of that section. The result (87) was also illustrated in Figure 3 of section 5.2.

From Figure 18 one sees that the results of the pnQRPA analyses of Faessler et al. [188, 189] and Suhonen et al. [192] are consistent with each other, and are in agreement with the 2νββ results of the ISM (the upper dotted curve in Figure 18) for the masses A = 100, 116. For the mass A = 128 both the pnQRPA and IBFFM-2 results deviate strongly from the ISM result, coming closer to the IBM-2 results. Both the ISM and IBM-2 curves follow, in average, the trend of the pnQRPA results of the β-decay analyses of section 5.2 (the light-hatched regions of Figure 18), except for the very heavy masses, A ≥ 138. The differences in the results of the β-decay and 2νββ-decay analyses are not drastic but they still exist. The differences may stem from the fact that not only one 1⁺ state takes part in most of the 2νββ decays. Contributions from the 1⁺ states above the lowest 1⁺ state, sometimes the ground state, interfere with each other and the contribution coming from the lowest one. These interferences have been discussed (e.g., [184, 186]).

11. Spin-multipole Strength Functions, Giant Resonances and the Renormalization of g_A

As discussed in sections 5 and 6 the low-lying Gamow-Teller and higher isovector spin-multipole strengths, in particular the 2⁻ strength, are quenched against nuclear-model calculations. The low-lying spin-multipole strength represents the low-energy tail of the corresponding spin-multipole giant resonance (SMGR). Usually only the low-energy part, with excitation energies E ≤ 5 MeV, of the spin-multipole strength function is experimentally known, and only for low multipoles, like for Gamow-Teller strength [194] or spin-dipole 2⁻ strength [195]. These strength functions have been measured using charge-exchange reactions at low momentum transfers, like the (p,n), (³He,t), (n,p), and (d,²He) reactions [196–198]. As an example, in Figure 19 is shown the strength for isovector spin-dipole excitations from the 0⁺ ground state of ⁷⁶Ge to the 0⁻, 1⁻, and 2⁻ states in ⁷⁶As. The centroid energies of the corresponding giant resonances are roughly 24 MeV (0⁻), 20 MeV (1⁻), and 18 MeV (2⁻) [199].

FIGURE 19

Figure 19. Isovector β⁻ spin-dipole strengths for 0⁻, 1⁻, and 2⁻ states in ⁷⁶As as excited from the 0⁺ ground state of ⁷⁶Ge. The solid envelope curve represents the sum of the three multipole distributions. The excitation energy is relative to the 2⁻ ground state of ⁷⁶As.

The measured strength functions for Gamow-Teller transitions can be pestered by the isovector spin monopole (IVSM) contributions at high energies [200, 201]. The location (38) of the Gamow-Teller giant resonance, GTGR, dictates partly the amount of strength remaining at low energies [at zero-momentum limit q → 0 in (5)], and thus the quenching of the axial-vector coupling strength g_A in model calculations [202]. These calculations have mostly been performed in the framework of the pnQRPA which represents well the centroids of the strong Gamow-Teller peaks, and extensions of the pnQRPA to two- plus four-quasiparticle models, like the proton-neutron microscopic anharmonic vibrator approach (pnMAVA) [203, 204], does not alter the picture very much.

Like in the case of the Gamow-Teller strength, also the location of the SMGRs affect the low-lying strength of, e.g., isovector spin-dipole (J^π = 0⁻, 1⁻, 2⁻, see Figure 19) and spin-quadrupole (J^π = 1⁺, 2⁺, 3⁺) excitations [199, 205]. This is why measurements of such giant resonances could help in solving the quenching problems associated to g_A at low energies.

12. Effective g_A from Nuclear Muon Capture

The (ordinary, non-radiative) nuclear muon capture is a transition between nuclear isobars such that

$\begin{array}{ll}{\mu }^{-}+(A,Z,N)\to {\nu }_{\mu }+(A,Z-1,N+1),& (88)\end{array}$

where a negative muon is captured from an atomic s orbital and as a result the nuclear charge decreases by one unit and a muon neutrino is emitted. The process is schematically depicted in Figure 20 for the capture on ⁷⁶Se, with the final states in ⁷⁶As. Here also the nucleus ⁷⁶Ge is depicted since it ββ decays to ⁷⁶Se. Properties of the μ-mesonic atoms have been treated theoretically in Ford and Wells [206] and experimentally in e.g., [207–210]. Due to the heavy mass of the muon (m_μ = 105 MeV) the process has a momentum exchange of the order of q ~ 100 MeV and is thus similar to the neutrinoless ββ decay where a Majorana neutrino of a similar momentum is exchanged. This means that contrary to β decays all the terms of the hadronic current (2) are activated and that the contributions from the forbidden transitions J > 1 are not suppressed relative to the allowed ones, just like in the case of 0νββ decays. Since the induced currents in (2) are activated the theoretical expressions for the individual capture transitions are rather complex [211–215] whereas the total capture rates are much easier to calculate [216, 217].

FIGURE 20

Figure 20. Double β triplet ⁷⁶Ge, ⁷⁶As, and ⁷⁶Se with the nuclear states shown in the intermediate nucleus ⁷⁶As. These states are populated by the ordinary muon capture (OMC) transitions from ⁷⁶Se.

Most of the theoretical attempts to describe the muon capture to individual nuclear states have concentrated on very light nuclei, A ≤ 20 [207, 213, 218–222] or to the mass region A = 23–40 [209, 210, 214, 215, 223–229]. Also studies in the 1s−0d and 1p−0f shells have been performed [230, 231]. Heavier nuclei, involved in ββ-decays, have been treated in Kortelainen and Suhonen [232, 233]. Interestingly enough, the muon-capture transitions can be used to probe the right-leg virtual transitions of 0νββ decays [231–233], but they can also give information on the in-medium renormalization of the axial current (4) in the form of an effective g_A [210, 223, 225] and an effective induced pseudoscalar coupling g_P (in fact the ratio g_P/g_A) [209, 213–215, 219, 220, 223–225, 227, 228] at high (100 MeV) momentum transfers, relevant for studies of the virtual transitions of the 0νββ decays. A recent review on the renormalization of g_P is given in Gorringe and Fearing [234].

More experimental data on partial muon-capture rates to nuclear states are needed for heavier nuclei in order to access the renormalization of g_A and g_P for momentum transfers of interest for the 0νββ decay. The present (see e.g., [235]) and future experimental muon-beam installations should help solve this problem.

13. Conclusions

The quenching of the weak axial-vector coupling strength, g_A, is an important issue considering its impact on the detectability of the neutrinoless double beta decay. The quenching appeared in old shell-model calculations as a way to reconcile the measured and calculated β-decay rates and strength functions. Later such quenching was studied in other nuclear-model frameworks, like the quasiparticle random-phase approximation and the IBM. The quenching of g_A can be observed in allowed Gamow-Teller decays as also in forbidden β decays. The origins of the quenching seem to be both the nuclear-medium effects and deficiencies in the nuclear many-body approaches, but a clean separation of these two aspects is formidably difficult. Different quenchings have been obtained in different calculations, based on different many-body frameworks. There is not yet a coherent approach to the quenching problem and many different separate studies have been performed. However, when analyzed closer, the obtained quenching of g_A is surprisingly similar in different many-body schemes for different physical processes (e.g., for Gamow-Teller β transitions, for electron spectra of forbidden non-unique β decays) in the mass range from light to medium-heavy nuclei.

Different ways to access the quenching have been proposed, like comparisons with Gamow-Teller β-decay and two-neutrino double-β-decay data. In a promising new method, the SSM, the comparison of the computed and measured electron spectra of high-forbidden non-unique β decays is proposed. The robustness of the method is based on the observations that the computed spectra seem to be relatively insensitive to the adopted mean-field and nuclear models. Measurements of such electron spectra for certain key transitions are encouraged. Also the relation of the quenching problem to the low-lying strength for Gamow-Teller and higher isovector spin-multipole excitations is worth stressing, as also the relation to the corresponding giant resonances, accessible in present and future charge-exchange-reaction experiments. The development of high-intensity muon beams makes measurements of nuclear muon-capture rates easier and enables access to the renormalization of the axial current at momentum exchanges relevant for the neutrinoless ββ decay.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Funding

University of Jyväskylä and Suomen Akatemia.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by the Academy of Finland under the Finnish Center of Excellence Program 2012–2017 (Nuclear and Accelerator Based Program at JYFL).

Footnotes

1. ^ENSDF at NNDC site, http://www.nndc.bnl.gov/

2. ^For positron emission the change Z_f → −Z_f has to be performed in F₀(Z_f, w_e) and F_ke−1(Z_f, w_e), Equation (51) below.

3. ^In Ejiri et al. [147] the Bohr-Mottelson (BM) formulation [148] of first-forbidden decays is used. The difference between the present and the BM formulation can be crystallized into the following relations: $M(\text{BM})=M_{1\text{u}}/\sqrt{4\pi }$, $B(\text{BM})=B_{1\text{u}}/(4\pi g_{\text{A}}^2)$, f₁(BM) = 3f_1u/4. In addition, since g_V(BM) = G_Fg_V and g_A(BM) = G_Fg_A, one has to make replacements g_A(BM) → g_A and g_V(BM) → 1 in order to go from the BM formulation to the present one.

References

1. Suhonen J, Civitarese O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys Rep. (1998) 300:123–214.

Google Scholar

2. Vergados JD, Ejiri H, Šimkovic F. Theory of neutrinoless double beta decay. Rep Prog Phys. (2012) 75:106301. doi: 10.1088/0034-4885/75/10/106301

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Vergados JD, Ejiri H, Šimkovic F. Neutrinoless double beta decay and neutrino mass. Int J Mod Phys E (2016) 25:1630007. doi: 10.1142/S0218301316300071

CrossRef Full Text | Google Scholar

4. Engel J, Menéndez J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Rep Prog Phys. (2017) 80:046301. doi: 10.1088/1361-6633/aa5bc5

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Deppisch FF, Hirsch M, Päs H. Neutrinoless double beta decay and physics beyond the standard model. J Phys G Nucl Part Phys. (2012) 39:124007. doi: 10.1088/0954-3899/39/12/124007

CrossRef Full Text | Google Scholar

6. Rodejohann W. Neutrino-less double beta decay and particle physics. Int J Mod Phys E (2011) 20:1833–930. doi: 10.1142/S0218301311020186

CrossRef Full Text | Google Scholar

7. Rodejohann W. Neutrino-less double beta decay and neutrino physics. J Phys G Nucl Part Phys. (2012) 39:124008. doi: 10.1088/0954-3899/39/12/124008

CrossRef Full Text | Google Scholar

8. Deppisch FF, Harz J, Hirsch M, Huang WC, Päs H. Falsifying high-scale baryogenesis with neutrinoless double beta decay and lepton flavor violation. Phys Rev D (2015) 92:036005. doi: 10.1103/PhysRevD.92.036005

CrossRef Full Text | Google Scholar

9. Deppisch F, Pas H, Suhonen J. Double beta decay versus cosmology: majorana CP phases and nuclear matrix elements. Phys Rev D (2005) 72:033012. doi: 10.1103/PhysRevD.72.033012

CrossRef Full Text | Google Scholar

10. Suhonen J, Civitarese O. Review of the properties of the 0νβ⁻β⁻ nuclear matrix elements. J Phys G Nucl Part Phys. (2012) 39:124005. doi: 10.1088/0954-3899/39/12/124005

CrossRef Full Text | Google Scholar

11. Vogel P. Nuclear structure and double beta decay. J Phys G Nucl Part Phys. (2012) 39:124002. doi: 10.1088/0954-3899/39/12/124002

CrossRef Full Text | Google Scholar

12. Engel J. Uncertainties in nuclear matrix elements for neutrinoless double-beta decay. J Phys G Nucl Part Phys. (2015) 42:034017. doi: 10.1088/0954-3899/42/3/034017

CrossRef Full Text | Google Scholar

13. Suhonen J, Civitarese O. Double-beta-decay nuclear matrix elements in the QRPA framework. J Phys G Nucl Part Phys. (2012) 39:085105. doi: 10.1088/0954-3899/39/8/085105

CrossRef Full Text | Google Scholar

14. Suhonen J, Civitarese O. Effects of orbital occupancies on the neutrinoless ββ matrix element of ⁷⁶Ge. Phys Lett B (2008) 668:277–81. doi: 10.1016/j.physletb.2008.08.056

CrossRef Full Text | Google Scholar

15. Suhonen J, Civitarese O. Effects of orbital occupancies and spin-orbit partners on 0νββ-decay rates. Nucl Phys A (2010) 847:207–32. doi: 10.1016/j.nuclphysa.2010.08.003

CrossRef Full Text | Google Scholar

16. Suhonen J. Effects of orbital occupancies and spin-orbit partners II: 0νββ decays of ⁷⁶Ge, ⁸²Se and ¹³⁶Xe to first excited 0⁺ states. Nucl Phys A (2011) 853:36–60. doi: 10.1016/j.nuclphysa.2011.01.021

CrossRef Full Text | Google Scholar

17. Barea J, Iachello F. Neutrinoless double-β decay in the microscopic interacting boson model. Phys Rev C (2009) 79:044301. doi: 10.1103/PhysRevC.79.044301

CrossRef Full Text | Google Scholar

18. Sarriguren P, Moya de Guerra E, Escuderos A. Spin-isospin excitations and β⁺/EC half-lives of medium-mass deformed nuclei. Nucl Phys A (2001) 691:631–48. doi: 10.1016/S0375-9474(01)00565-6

CrossRef Full Text | Google Scholar

19. Álvarez-Rodríguez R, Sarriguren P, Moya de Guerra E, Pacearescu L, Faessler A, Šimkovic F. Deformed quasiparticle random phase approximation formalism for single- and two-neutrino double β decay. Phys Rev C (2004) 70:064309. doi: 10.1103/PhysRevC.70.064309

CrossRef Full Text | Google Scholar

20. Caurier E, Nowacki F, Poves A. Nuclear-structure aspects of the neutrinoless ββ-decays. Eur Phys J A (2008) 36:195–200. doi: 10.1103/PhysRevLett.113.262501

CrossRef Full Text | Google Scholar

21. Menéndez J, Poves A, Caurier E, Nowacki F. Disassembling the nuclear matrix elements of neutrinoless ββ decay. Nucl Phys A (2009) 818:139–51. doi: 10.1016/j.nuclphysa.2008.12.005

CrossRef Full Text | Google Scholar

22. Rodríguez TR, Martínez-Pinedo G. Energy density functional study of nuclear matrix elements for neutrinoless ββ decay. Phys Rev Lett. (2010) 105:252503. doi: 10.1103/PhysRevLett.105.252503

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Tomoda T. Double beta decay. Rep Prog Phys. (1991) 54:53–126.

PubMed Abstract | Google Scholar

24. Faessler A. Šimkovic F. Double beta decay. J Phys G Nucl Part Phys. (1998) 24:2139–78.

Google Scholar

25. Commins ED, Bucksbaum PH. Weak Interactions of Leptons and Quarks. Cambridge: Cambridge University Press (1983).

Google Scholar

26. Feynmann RP, Gell-Mann M. Theory of the Fermi interaction. Phys Rev. (1958) 109:193–8.

27. Gell-Mann M. Test of the nature of the vector interaction in β decay. Phys Rev. (1958) 111:362–5.

Google Scholar

28. Theis WR. Eine Rangordnung der einzelnen Terme in den schwachen Wechselwirkungen. Z Phys. (1958) 150:590–2.

Google Scholar

29. Zuber K. Neutrino Physics. London: Institute of Physics Publishing Ltd. (2004).

Google Scholar

30. Nambu Y. Axial vector current conservation in weak interactions. Phys Rev Lett. (1960) 4:380–2.

Google Scholar

31. Gell-Mann M, Lévy M. The axial vector current in beta decay. Nuovo Cim. (1960) 16:705–26. doi: 10.1007/BF02859738

CrossRef Full Text | Google Scholar

32. Blin-Stoyle RJ. Renormalization of the axial-vector coupling constant in β-decays. Nucl Phys A (1975) 254:353–69.

Google Scholar

33. Khanna FC, Towner IS, Lee HC. Quenching of axial-vector coupling constant in the β-decay of finite nuclei. Nucl Phys A (1978) 305:349–56.

Google Scholar

34. Haxton WC, Henley EM. Symmetries and Fundamental Interactions in Nuclei. Singapore: World Scientific (1995).

Google Scholar

35. Suhonen J. From Nucleons to Nucleus: Concepts of Microscopic Nuclear Theory. Berlin: Springer (2007).

36. Maalampi J, Suhonen J. Neutrinoless double β⁺/EC decays. Adv High Energy Phys. (2013) 2013:505874. doi: 10.1155/2013/505874

CrossRef Full Text | Google Scholar

37. Bodek A, Avvakumov S, Bradford R, Budd H. Vector and axial nucleon form factors: a duality constrained parametrization. Eur Phys J C (2008) 53:349–54. doi: 10.1140/epjc/s10052-007-0491-4

CrossRef Full Text | Google Scholar

38. Bhattacharya B, Hill RJ, Paz G. Model-independent determination of the axial mass parameter in quasielastic neutrino-nucleus scattering. Phys Rev D (2011) 84:073006. doi: 10.1103/PhysRevD.84.073006

CrossRef Full Text | Google Scholar

39. Amaro JE, Ruiz Arriola E. Axial-vector dominance predictions in quasielastic neutrino-nucleus scattering. arXiv:1510.07532v2 [nucl-th].

40. Goldberger ML, Treiman SB. Form factors in β decay and μ capture. Phys Rev. (1958) 111:354–61.

Google Scholar

41. Patrignani C. et al. (Particle Data Group). Review of particle physics. Chin Phys C (2016) 40:100001. doi: 10.1088/1674-1137/40/10/100001

CrossRef Full Text

42. Kubodera K, Delorme J, Rho M. Axial currents in nuclei. Phys Rev Lett. (1978) 40:755–8.

Google Scholar

43. Suhonen J. QRPA estimate for the Δ(1232) contribution to the Gamow-Teller decay of heavy nuclei. Phys Lett B (1991) 255:159–62.

Google Scholar

44. Delorme J, Ericson M, Guichon P. Quark spin-isospin sum rules and their Adler-Weisberger relation in nuclei. Phys. Lett (1982) 115B:86–90.

Google Scholar

45. Oset E, Rho M. Axial currents in nuclei: the Gamow-Teller matrix element. Phys Rev Lett. (1979) 42:47–50.

Google Scholar

46. Bohr A, Mottelson BR. On the role of the δ resonance in the effective spin-dependent moments of nuclei. Phys Lett. (1981) 100B:10–2.

Google Scholar

47. Towner IS, Khanna FC. Quenching of allowed Gamow-Teller β transitions in mirror nuclei. Phys Rev Lett. (1979) 42:51–4.

Google Scholar

48. Towner IS, Khanna FC. Corrections to the single-particle M1 and Gamow-Teller matrix elements. Nucl Phys A (1983) 399:334–64.

Google Scholar

49. Ichimura M, Sakai H, Wakasa T. Spin-isospin responses via (p,n) and (n,p) reactions. Prog Part Nucl Phys. (2006) 56:446–531. doi: 10.1016/j.ppnp.2005.09.001

CrossRef Full Text | Google Scholar

50. Adler SL. Sum rules for the axial-vector coupling-constant renormalization in β decay. Phys Rev. (1965) 140:B736–47.

Google Scholar

51. Weisberger WI. Unsubtracted dispersion relations and the renormalization of the weak axial-vector coupling constants. Phys Rev. (1966) 143:1302–9.

Google Scholar

52. Kim CW, Primakoff H. Sum rules in nuclear beta decay. Phys Rev. (1966) 147:1034–7.

53. Henley EM. Axial-vector coupling constants and chiral-symmetry restoration. Phys Rev D (1992) 46:431–7.

PubMed Abstract | Google Scholar

54. Wilkinson DH. Renormalization of the axial-vector coupling constant in nuclear β-decay (III). Nucl Phys A (1974) 225:365–81.

Google Scholar

55. Ericson M. Axial vector nuclear sum rules and exchange effects. Ann Phys. (1971) 63:562–76.

Google Scholar

56. Ericson M, Figureau A, Thévenet C. Pionic field and renormalization of the axial coupling constant in nuclei. Phys Lett. (1973) 45B:19–22.

Google Scholar

57. Rho M. Quenching of axial-vector coupling constant in β-decay and pion-nucleus optical potential. Nucl Phys A (1974) 231:493–503.

Google Scholar

58. Blin-Stoyle RJ, Tint M. Theory of partially conserved axial-vector current and mesonic exchange effects in nuclear beta decay. Phys Rev. (1967) 160:803–8.

Google Scholar

59. Goldberger ML, Treiman SB. Decay of the pi meson. Phys Rev. (1958) 110:1178–84.

Google Scholar

60. Siiskonen T, Hjorth-Jensen M, Suhonen J. Renormalization of the weak hadronic current in the nuclear medium. Phys Rev C (2001) 63:055501. doi: 10.1103/PhysRevC.63.055501

CrossRef Full Text | Google Scholar

61. Chou WT, Warburton EK, Brown BA. Gamow-Teller beta-decay rates for A ≤ 18 nuclei. Phys Rev C (1993) 47:163–77.

PubMed Abstract | Google Scholar

62. Wildenthal BH, Curtin MS, Brown BA. Predicted features of the beta decay of neutron-rich sd-shell nuclei. Phys Rev C (1983) 28:1343–66.

Google Scholar

63. Martínez-Pinedo G, Poves A, Caurier E, Zuker AP. Effective g_A in the pf shell. Phys Rev C (1996) 53:R2602–05.

PubMed Abstract

64. Kumar V, Srivastava PC, Li H. Nuclear β⁻-decay half-lives for fp and fpg shell nuclei. J Phys G Nucl Part Phys. (2016) 43:105104. doi: 10.1088/0954-3899/43/10/105104

CrossRef Full Text | Google Scholar

65. Honma M, Otsuka T, Misuzaki T, Hjorth-Jensen M. Effective interaction for f5pg9-shell nuclei and two-neutrino double beta-decay matrix elements. J Phys Conf Ser. (2006) 49:45–50. doi: 10.1088/1742-6596/49/1/011

CrossRef Full Text | Google Scholar

66. Caurier E, Nowacki F, Poves A. Shell model description of the ββ decay of ¹³⁶Xe. Phys Lett B (2012) 711:62–4.

Google Scholar

67. Juodagalvis A, Dean DJ. Gamow-Teller GT₊ distributions in nuclei with mass A = 90–97. Phys Rev C (2005) 72:024306. doi: 10.1103/PhysRevC.72.024306

CrossRef Full Text | Google Scholar

68. Horoi M, Neacsu A. Shell model predictions for ¹²⁴Sn double-β decay. Phys Rev C (2016) 93:024308. doi: 10.1103/PhysRevC.93.024308

CrossRef Full Text | Google Scholar

69. Engel J, Vogel P. Effective operators for double-β decay. Phys Rev C (2004) 69:034304. doi: 10.1103/PhysRevC.69.034304

CrossRef Full Text | Google Scholar

70. Suhonen J, Divari P, Skouras L, Johnstone I. Double beta decay of ⁹²Mo: comparison of the shell model and the quasiparticle random-phase approximation. Phys Rev C (1997) 55:714–9.

Google Scholar

71. Engel J, Hagen G. Corrections to the neutrinoless double-β-decay operator in the shell model. Phys Rev C (2009) 79:064317. doi: 10.1103/PhysRevC.79.064317

CrossRef Full Text | Google Scholar

72. Holt JD, Engel J. Effective double-β-decay operator for ⁷⁶Ge and ⁸²Se. Phys Rev C (2013) 87:064315. doi: 10.1103/PhysRevC.87.064315

CrossRef Full Text | Google Scholar

73. Menéndez J, Gazit D, Schwenk A. Chiral two-body currents in nuclei: Gamow-Teller transitions and neutrinoless double-beta decay. Phys Rev Lett. (2011) 107:062501. doi: 10.1103/PhysRevLett.107.062501

PubMed Abstract | CrossRef Full Text

74. Engel J, Šimkovic F, Vogel P. Chiral two-body currents and neutrinoless double-β decay in the quasiparticle random-phase approximation. Phys Rev C (2014) 89:064308. doi: 10.1103/PhysRevC.89.064308

CrossRef Full Text | Google Scholar

75. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Bacca S, et al. Effects of three-nucleon forces and two-body currents on Gamow-Teller strengths. Phys Rev Lett. (2014) 113:262504. doi: 10.1103/PhysRevLett.113.262504

PubMed Abstract | CrossRef Full Text

76. Ikeda K, Fujii S, Fujita JI. The (p,n) reactions and beta decays. Phys Lett. (1963) 3:271–2.

77. Katori T, Martini M. Neutrino-nucleus cross sections for oscillation experiments. arXiv:1611.07770 [hep-ph].

78. Simo IR, Amaro JE, Barbaro MB, De, Pace A, Caballero JA, Donnelly TW. Relativistic model of 2p-2h meson exchange currents in (anti)neutrino scattering. arXiv:1604.08423 [nucl-th].

79. Kirchbach M, Reinhardt H. On the meson-exchange correction to the axial-charge density for ns_1/2↔n'p_1/2 β-transitions. Phys Lett B (1988) 208:79–83.

Google Scholar

80. Kirchbach M, Riska DO, Tsushima K. The axial exchange charge operator and the nucleon-nucleon interaction. Nucl Phys A (1992) 542:616–30.

Google Scholar

81. Towner IS. Enhancement in axial-charge matrix elements from meson-exchange currents. Nucl Phys A (1992) 542:631–58. doi: 10.1016/0375-9474(92)90261-H

CrossRef Full Text | Google Scholar

82. Towner IS, Khanna FC. Role of 2p-2h states in weak 0⁺−0⁻ transitions in A = 16 nuclei. Nucl Phys A (1981) 372:331–48.

Google Scholar

83. Bhattacharya T, Cirigliano V, Cohen S, Gupta R, Lin HW, Yoon B. Axial, scalar and tensor charges of the nucleon from 2+1+1-flavor lattice QCD. Phys Rev D (2016) 95:054508. doi: 10.1103/PhysRevD.94.054508

CrossRef Full Text | Google Scholar

84. Berkowitz E, Brantley D, Bouchard C, Chang CC, Clark MA, Garron N. et al. An accurate calculation of the nucleon axial charge with lattice QCD. arXiv:1704.01114 [hep-lat].

85. Gupta R, Jang YC, Lin HW, Yoon B, Bhattacharya T. Axial vector form factors of the nucleon from lattice QCD. arXiv:1705.06834 [hep-lat].

86. Tiburzi BC, Wagman ML, Winter F, Chang E, Davoudi Z, Detmold W. et al. Double-β decay matrix elements from lattice quantum chromodynamics. arXiv:1702.02929 [hep-lat].

87. Shimizu K, Ichimura M, Arima A. Magnetic moments and GT-type β-decay matrix elements in nuclei with a LS doubly closed shell plus or minus one nucleon. Nucl Phys A (1974) 226:282–318.

Google Scholar

88. Hyuga H, Arima A, Shimizu K. Exchange magnetic moments. Nucl Phys A (1980) 336:363–406.

Google Scholar

89. Caurier E, Martínez-Pinedo G, Nowacki F, Poves A, Zuker AP. The shell model as a unified view of nuclear structure. Rev Mod Phys. (2005) 77:427–88. doi: 10.1103/RevModPhys.77.427

CrossRef Full Text | Google Scholar

90. Ring P, Schuck P. The Nuclear Many-Body Problem. New York, NY: Springer (1980).

Google Scholar

91. Iachello F, Arima A. The Interacting Boson Model. Cambridge: Cambridge University Press (1987).

PubMed Abstract | Google Scholar

92. Brant S, Paar V. IBFFM yrast states in odd-odd nuclei associated with O(6) and SU(3) limits. Z Phys. (1988) 329:151–9.

93. Kuo TTS, Osnes E. Folded-Diagram Theory of the Effective Interaction in Atomic Nuclei. Springer Lecture Notes in Physics, Vol. 364. Berlin: Springer (1990).

94. Hjorth-Jensen M, Osnes E, Kuo TTS. Phys Rep. (1995) 261:125–270.

95. Engeland T, Hjorth-Jensen M, Kartamyshev M, Osnes E. The Kuo-Brown effective interaction: from ¹⁸O to the Sn isotopes. Nucl Phys A (2014) 928:51–63. doi: 10.1016/j.nuclphysa.2014.03.012

CrossRef Full Text | Google Scholar

96. Towner LS. Quenching of spin matrix elements in nuclei. Phys Rep (1997) 155:263–377.

Google Scholar

97. Kwiatkowski AA, Brunner T, Holt JD, Chaudhuri A, Chowdhury U, Eibach M, et al. New determination of double-β-decay properties in ⁴⁸Ca: high-precision Q_ββ-value measurement and improved nuclear matrix element calculations. Phys Rev C (2014) 89:045502. doi: 10.1103/PhysRevC.89.045502

CrossRef Full Text | Google Scholar

98. Horoi M, Brown BA. Shell-model analysis of the ¹³⁶Xe double beta decay nuclear matrix elements. Phys Rev Lett. (2013) 110:222502. doi: 10.1103/PhysRevLett.110.222502

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Iwata Y, Shimizu N, Otsuka T, Utsuno Y, Menendéz J, Honma M. et al. Large-scale shell-model analysis of the neutrinoless ββ decay of ⁴⁸Ca. Phys Rev Lett. (2016) 116:112502. doi: 10.1103/PhysRevLett.116.112502

CrossRef Full Text | Google Scholar

100. Abe T, Maris P, Otsuka T, Shimizu N, Utsuno Y, Vary JP. Benchmarks of the full configuration interaction, Monte Carlo shell model, no-core full configuration methods. Phys Rev C (2012) 86:054301. doi: 10.1103/PhysRevC.86.054301

CrossRef Full Text | Google Scholar

101. Togashi T, Tsunoda Y, Otsuka T, Shimizu N. Quantum phase transition in the shape of Zr isotopes. Phys Rev Lett. (2016) 117:172502. doi: 10.1103/PhysRevLett.117.172502

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Stumpf C, Braun J, Roth R. Importance-truncated large-scale shell model. Phys Rev C (2016) 93:021301(R). doi: 10.1103/PhysRevC.93.021301

CrossRef Full Text | Google Scholar

103. Jansen GR, Engel J, Hagen G, Navratil P, Signoracci A. Ab initio coupled-cluster effective interactions for the shell model: application to neutron-rich oxygen and carbon isotopes. Phys Rev Lett. (2014) 113:142502. doi: 10.1103/PhysRevLett.113.142502

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Bogner SK, Hergert H, Holt JD, Schwenk A, Binder S, Calci A, et al. Nonperturbative shell-model interactions from the in-medium similarity renormalization group. Phys Rev Lett. (2014) 113:142501. doi: 10.1103/PhysRevLett.113.142501

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Legeza O, Veis L, Poves A, Dukelsky J. Advanced density matrix renormalization group method for nuclear structure calculations. Phys Rev C (2015) 92:051303(R). doi: 10.1103/PhysRevC.92.051303

CrossRef Full Text | Google Scholar

106. Rowe DJ. Nuclear Collective Motion. London: Methuen (1970).

Google Scholar

107. Lane AM. Nuclear Theory. New York, NY: Benjamin (1964).

Google Scholar

108. Escuderos A, Faessler A, Rodin V, Šimkovic F. Contributions of different neutron pairs in different approaches for neutrinoless double-beta decay. J Phys G Nucl Part Phys. (2010) 37:125108. doi: 10.1088/0954-3899/37/12/125108

CrossRef Full Text | Google Scholar

109. Toivanen J, Suhonen J. Renormalized proton-neutron QRPA and its application to double beta decay. Phys Rev Lett. (1995) 75:410–3.

PubMed Abstract | Google Scholar

110. Toivanen J, Suhonen J. Study of several double-beta-decaying nuclei using the renormalized proton-neutron quasiparticle random-phase approximation. Phys Rev C (1997) 55:2314–23.

Google Scholar

111. Raduta AA, Raduta CM, Faessler A, Kaminski WA. Description of the 2νββ decay within a fully renormalized RPA approach. Nucl Phys A (1998) 634:497–524.

Google Scholar

112. Raduta CM, Raduta AA. Deascription of the 2νββ decay within a fully renormalized proton-neutron quasiparticle random-phase approximation approach with a restored gauge symmetry. Phys Rev C (2010) 82:068501.

Google Scholar

113. Raduta CM, Raduta AA, Ursu II. New theoretical results for 2νββ decay within a fully renormalized proton-neutron random-phase approximation approach with the gauge symmetry restored. Phys Rev C (2011) 84:064322. doi: 10.1103/PhysRevC.84.064322

CrossRef Full Text | Google Scholar

114. Robin C, Litvinova E. Nuclear response theory for spin-isospin excitations in a relativistic quasiparticle-phonon coupling framework. Eur Phys J A (2016) 52:205. doi: 10.1140/epja/i2016-16205-0

CrossRef Full Text | Google Scholar

115. Toivanen J, Suhonen J. Microscopic quasiparticle-phonon description of odd-A Xe isotopes. J Phys G Nucl Part Phys. (1995) 21:1491–7.

Google Scholar

116. Toivanen J, Suhonen J. Microscopic quasiparticle-phonon description of odd-mass ^127−133Xe isotopes and their beta decay. Phys Rev C (1998) 57:1237–45.

Google Scholar

117. Mustonen MT, Suhonen J. Microscopic quasiparticle-phonon description of beta decays of ¹¹³Cd and ¹¹⁵In using proton-neutron phonons. Phys Lett B (2007) 657:38–42. doi: 10.1016/j.physletb.2007.09.037

CrossRef Full Text | Google Scholar

118. Otsuka T, Arima A, Iachello F. Nuclear shell model and interacting bosons. Nucl Phys A (1978) 309:1–33.

Google Scholar

119. Otsuka T. Microscopic basis of the interacting boson model. Prog Theor Phys Suppl. (1996) 125:5–48.

Google Scholar

120. Iachello F, Van Isacker P. The Interacting Boson-Fermion Model. Cambridge: Cambridge University Press (1991).

Google Scholar

121. Warburton EK, Brown BA. Effective interactions for the 0p1s0d nuclear shell-model space. Phys Rev C (1992) 476:923–44.

PubMed Abstract | Google Scholar

122. Wilkinson DH. Renormalization of the axial-vector coupling constant in nuclear β-decay (II). Nucl Phys A (1973) 209:470–84.

Google Scholar

123. Brown BA, Chung W, Wildenthal BH. Empirical renormalization of the one-body Gamow-Teller β-decay matrix elements in the 1s−0d shell. Phys Rev Lett. (1978) 40:1631–5.

Google Scholar

124. Caurier E, Zuker AP, Poves A, Martínez-Pinedo G. Full pf shell model study of A = 48 nuclei. Phys Rev C (1994) 50:225–36.

PubMed Abstract | Google Scholar

125. Caurier E, Poves A, Zuker A. A full 0ℏω description of the 2νββ decay of ⁴⁸Ca. Phys Lett B (1990) 252:13–7.

Google Scholar

126. Balysh A, De Silva A, Lebedev VI, Lou K, Moe MK, Nelson MA, et al. Double beta decay of ⁴⁸Ca. Phys Rev Lett. (1996) 77:5186–9.

PubMed Abstract

127. Horoi M, Stoica S, Brown B. Shell-model calculations of two-neutrino double-β decay rates of ⁴⁸Ca with the GXPF1A interaction. Phys Rev C (2007) 75:034303. doi: 10.1103/PhysRevC.75.034303

CrossRef Full Text | Google Scholar

128. Auerbach N, Bertsch GF, Brown BA, Zhao L. β⁺ Gamow-Teller strength in nuclei. Nucl Phys A (1993) 556:190–200.

Google Scholar

129. Puppe P, Frekers D, Adachi T, Akimune H, Aoi N, Bilgier B. et al. High resolution (³He,t) reaction on the double-β decaying nucleus ¹³⁶Xe. Phys Rev C (2011) 84:051305(R). doi: 10.1103/PhysRevC.84.051305

CrossRef Full Text | Google Scholar

130. Neacsu A, Horoi M. Shell model studies of the ¹³⁰Te neutrinoless double-β decay. Phys Rev C (2015) 91:024309. doi: 10.1103/PhysRevC.91.024309

CrossRef Full Text | Google Scholar

131. Brown BA, Rykaczewski K. Gamow-Teller strength in the region of ¹⁰⁰Sn. Phys Rev C (1994) 50:R2270–3.

PubMed Abstract | Google Scholar

132. Konieczka M, Baczyk P, Satula W. β-decay study within multireference density functional theory and beyond. Phys Rev C (2016) 93:042501(R). doi: 10.1103/PhysRevC.93.042501

CrossRef Full Text | Google Scholar

133. Vogel P, Zirnbauer MR. Suppression of the two-neutrino double-beta decay by nuclear-structure effects. Phys Rev Lett. (1986) 57:3148–51.

PubMed Abstract | Google Scholar

134. Civitarese O, Faessler A, Tomoda T. Suppression of the two-neutrino double β decay. Phys Lett B (1987) 194:11–4.

Google Scholar

135. Suhonen J, Faessler A, Taigel T, Tomoda T. Suppression of the β⁺ decays of ¹⁴⁸Dy, ¹⁵⁰Er and ¹⁵²Yb. Phys Lett B (1988) 202:174–8.

Google Scholar

136. Suhonen J, Taigel T, Faessler A. pnQRPA calculation of the β⁺/EC quenching for several neutron-deficient nuclei in mass regions A = 94−110 and A = 146−156. Nucl Phys A (1988) 486:91–117.

Google Scholar

137. Suhonen J. Nuclear matrix elements of ββ decay from β-decay data. Phys Lett B (2005) 607:87–95. doi: 10.1016/j.physletb.2004.12.048

CrossRef Full Text | Google Scholar

138. Delion DS, Suhonen J. Effective axial-vector strength and β-decay systematics. Europhys Lett (2014) 107:52001. doi: 10.1209/0295-5075/107/52001

CrossRef Full Text | Google Scholar

139. Pirinen P, Suhonen J. Systematic approach to β and 2νββ decays of mass A = 100−136 nuclei. Phys Rev C (2015) 91:054309.

Google Scholar

140. Ejiri H, Suhonen J. GT neutrino-nuclear responses for double beta decays and astro neutrinos. J Phys G Nucl Part Phys. (2015) 42:055201. doi: 10.1088/0954-3899/42/5/055201

CrossRef Full Text | Google Scholar

141. Deppisch FF, Suhonen J. Statistical analysis of β decays and the effective value of g_A in the proton-neutron random-phase approximation framework. Phys Rev C (2016) 94:055501. doi: 10.1103/PhysRevC.94.055501

CrossRef Full Text | Google Scholar

142. Hardy JC, Towner IS, Koslowsky V, Hagberg E, Schmeig H. Superallowed 0⁺ → 0⁺ nuclear β-decays: a critical survey with tests of CVC and the standard model. Nucl Phys A (1990) 509:429–460.

Google Scholar

143. Gove NB, Martin MJ. Log-f tables for beta decay. Nucl Data Tables (1971) 10:205–317.

Google Scholar

144. Behrens H, Bühring W. Electron Radial Wave Functions and Nuclear Beta-decay. Oxford: Clarendon Press (1982).

145. Ejiri H, Ikeda K, Fujita J. Hindrance factors for beta decays of hevy nuclei. Phys Rev. (1968) 176:1277–88.

Google Scholar

146. Towner IS, Warburton EK, Garvey GT. Hindrance phenomena in unique first- and third-forbidden β-decay. Ann Phys. (1971) 66:674–96.

Google Scholar

147. Ejiri H, Soukouti N, Suhonen J. Spin-dipole nuclear matrix elements for double beta decays and astro-neutrinos. Phys Lett B (2014) 729:27–32. doi: 10.1016/j.physletb.2013.12.051

CrossRef Full Text | Google Scholar

148. Bohr A, Mottelson BR. Nuclear Structure, Vol. I. New York, NY: Benjamin (1969).

149. Warburton EK, Garvey GT, Towner IS. Unique second- and third-forbidden β decay. Ann Phys. (1970) 57:174–200.

Google Scholar

150. Kortelainen M, Civitarese O, Suhonen J, Toivanen J. Short-range correlations and neutrinoless double beta decay. Phys Lett B (2007) 647:128–32. doi: 10.1016/j.physletb.2007.01.054

CrossRef Full Text | Google Scholar

151. Kortelainen M, Suhonen J. Improved short-range correlations and 0νββ nuclear matrix elements of ⁷⁶Ge and ⁸²Se. Phys Rev C (2007) 75:051303(R).

Google Scholar

152. Kortelainen M, Suhonen J. Nuclear matrix elements of 0νββ decay with improved short-range correlations. Phys Rev C (2007) 76:024315. doi: 10.1103/PhysRevC.76.024315

CrossRef Full Text | Google Scholar

153. Suhonen J, Kortelainen M. Nuclear matrix elements for double-β decay. Int J Mod Phys E (2008) 17:1–11. doi: 10.1142/S0218301308009495

CrossRef Full Text | Google Scholar

154. Hyvärinen J, Suhonen J. Nuclear matrix elements for 0νββ decays with light or heavy Majorana-neutrino exchange. Phys Rev C (2015) 91:024613. doi: 10.1103/PhysRevC.91.024613

CrossRef Full Text | Google Scholar

155. Hyvärinen J, Suhonen J. Analysis of the intermediate-state contributions to neutrinoless double β⁻ decays. Adv High Energy Phys. (2016) 2016:4714829. doi: 10.1155/2016/4714829

CrossRef Full Text | Google Scholar

156. Kostensalo J, Suhonen J. Spin-multipole nuclear matrix elements in the pn quasiparticle random-phase approximation: implications for β and ββ half-lives. Phys Rev C (2017) 95:014322. doi: 10.1103/PhysRevC.95.014322

CrossRef Full Text | Google Scholar

157. Barabash AS. Average and recommended half-life values for two neutrino double beta decay: upgrade-2013. AIP Conf Proc. (2013) 1572:11–5 doi: 10.1063/1.4856538

CrossRef Full Text | Google Scholar

158. Schopper HF. Weak Interactions and Nuclear Beta Decay. Amsterdam: North-Holland (1966).

Google Scholar

159. Mustonen, MT. Aunola M, Suhonen J. Theoretical description of the fourth-forbidden non-unique β decays of ¹¹³Cd and ¹¹⁵In. Phys Rev C (2006) 73:054301. doi: 10.1103/PhysRevC.73.054301

CrossRef Full Text | Google Scholar

160. Mougeot X. Reliability of usual assumptions in the calculation of β and ν spectra. Phys Rev C (2015) 91:055504. doi: 10.1103/PhysRevC.91.055504

CrossRef Full Text | Google Scholar

161. Suhonen J. Calculation of allowed and first-forbidden beta-decay transitions of odd-odd nuclei. Nucl Phys A (1993) 563:205–24.

Google Scholar

162. Ydrefors E, Mustonen MT, Suhonen J. MQPM description of the structure and beta decays of the odd A = 95, 97 Mo and Tc isotopes. Nucl Phys A (2010) 842:33–47. doi: 10.1016/j.nuclphysa.2010.04.005

CrossRef Full Text | Google Scholar

163. Suzuki T, Yoshida T, Kajino T, Otsuka T. β decays of isotones with neutron magic number of N = 126 and r-process nucleosynthesis. Phys Rev C (2012) 85:015802. doi: 10.1103/PhysRevC.85.015802

CrossRef Full Text | Google Scholar

164. Damgaard J, Winther A. First-forbidden β-decays of Tl²⁰⁷ and Pb²⁰⁹. Nucl Phys. (1964) 54:615–24.

Google Scholar

165. Kubodera K, Rho M. Axial-charge transitions in heavy nuclei and in-medium effective chiral Lagrangians. Phys Rev Lett. (1991) 67:3479–82.

PubMed Abstract | Google Scholar

166. Millener DJ, Alburger DE, Warburton EK, Wilkinson DH. Decay scheme of ¹¹Be. Phys Rev C (1982) 26:1167–85.

Google Scholar

167. Warburton EK, Alburger DE, Millener DJ. Shapes of the ¹⁶N and ¹⁵C beta spectra and extraction of matrix elements for ¹⁵C(β⁻)¹⁵N(g.s.). Phys Rev C (1984) 29:2281–9.

Google Scholar

168. Warburton EK, Towner I, Brown BA. First-forbidden β decay: meson-exchange enhancement of the axial charge at A ~ 16. Phys Rev C (1994) 49:824–39.

PubMed Abstract | Google Scholar

169. Warburton EK, Becker JA, Brown BA, Millener DJ. First-forbidden beta decay near A = 40. Ann Phys. (1988) 187:471–501.

Google Scholar

170. Warburton EK. In-medium and core-polarization effects in ${}^{50}\text{K}(0^{-}){\stackrel{{\beta }^{-}}{\to }}^{50}\text{Ca}(0^{+})$. Phys Rev C (1991) 44:1024–9.

PubMed Abstract | Google Scholar

171. Warburton EK. Core polarization effects on spin-dipole and first-forbidden β-decay operators in the lead region. Phys Rev C (1990) 42:2479–86.

PubMed Abstract | Google Scholar

172. Warburton EK. Mesonic enhancement of the weak axial-vector current evaluated from β decay in the lead region. Phys Rev Lett. (1991) 66:1823–6.

PubMed Abstract | Google Scholar

173. Warburton EK. First-forbidden β decay in the lead region and mesonic enhancement of the weak axial current. Phys Rev C (1991) 44:233–60.

PubMed Abstract | Google Scholar

174. Warburton EK, Towner IS. Nuclear medium effects in first forbidden beta decay. Phys Rep. (1994) 242:103–18.

Google Scholar

175. Rydström L, Blomqvist J, Liotta RJ, Pomar C. Structure of proton-deficient nuclei near ²⁰⁸Pb. Nucl Phys A (1990) 512:217–40.

176. Zhi Q, Caurier E, Cuenca-García JJ, Langanke K, Martínez-Pinedo G, Sieja K. Shell-model half-lives including first-forbidden contributions for r-process waiting-point nuclei. Phys Rev C (2013) 87:025803. arXiv:1301.5225 [nucl-th].

Google Scholar

177. Haaranen M, Srivastava PC, Suhonen J. Forbidden nonunique β decays and effective values of weak coupling constants. Phys Rev C (2016) 93:034308. doi: 10.1103/PhysRevC.93.034308

CrossRef Full Text | Google Scholar

178. Haaranen M, Kotila J, Suhonen J. Spectrum-shape method and the next-to-leading-order terms of the β-decay shape factor. Phys Rev C (2017) 95:024327. doi: 10.1103/PhysRevC.95.024327

CrossRef Full Text | Google Scholar

179. Belli P, Bernabei R, Bukilic N, Cappella F, Cerulli R, Dai CJ. et al. Investigation of β decay of ¹¹³Cd. Phys Rev C (2007) 76:064603.

Google Scholar

180. Kostensalo J, Haaranen M, Suhonen J. Electron spectra in forbidden β decays and the quenching of the weak axial-vector coupling constant g_A. Phys Rev C (2017) 95:044313. doi: 10.1103/PhysRevC.95.044313

CrossRef Full Text | Google Scholar

181. Kostensalo J, Suhonen J. g_A-driven shapes of electron spectra of forbidden β decays in the nuclear shell model. Phys Rev C (2017) 96:024317. doi: 10.1103/PhysRevC.96.024317

CrossRef Full Text | Google Scholar

182. Jokiniemi L, Suhonen J, Ejiri H. Magnetic hexadecapole γ transitions and neutrino-nuclear responses in medium-heavy nuclei. Adv High Energy Phys. (2016) 2016:8417598. doi: 10.1155/2016/8417598

CrossRef Full Text

183. Kotila J, Iachello F. Phase-space factors for double-β decay. Phys Rev C (2012) 85:034316. doi: 10.1103/PhysRevC.85.034316

CrossRef Full Text | Google Scholar

184. Civitarese O, Suhonen J. Is the single-state dominance realized in double-β-decay transitions? Phys Rev C (1998) 58:1535–8.

Google Scholar

185. Bhattacharya M, García A, Hindi MM, Norman EB, Ortiz CE, Kaloskamis NI et al. Electron capture decay of ¹¹⁶In and double β decay of ¹¹⁶Cd. Phys Rev C (1998) 58:1247–56.

186. Civitarese O, Suhonen J. Systematic study of the single-state dominance in 2νββ decay transitions. Nucl Phys A (1999) 653:321–37.

Google Scholar

187. Barabash AS. Precise half-life values for two-neutrino double-β decay. Phys Rev C (2010) 81:035501. doi: 10.1103/PhysRevC.81.035501

CrossRef Full Text | Google Scholar

188. Faessler A, Fogli GL, Lisi E, Rodin V, Rotunno AM, Šimkovic F. Overconstrained estimates of neutrinoless double beta decay within the QRPA. J Phys G (2008) 35:075104. doi: 10.1088/0954-3899/35/7/075104

CrossRef Full Text | Google Scholar

189. Faessler A, Fogli GL, Lisi E, Rodin V, Rotunno AM, Šimkovic F. Overconstrained estimates of neutrinoless double beta decay within the QRPA. (2007) arXiv 0711.3996v1 [nucl–th].

Google Scholar

190. Yoshida N, Iachello F. Two-neutrino double-β decay in the interacting boson-fermion model. Prog Theor Exp Phys. (2013) 2013:043D01. doi: 10.1093/ptep/ptt007

CrossRef Full Text | Google Scholar

191. Barea J, Kotila J, Iachello F. Nuclear matrix elements for double-β decay. Phys Rev C (2013) 87:014315. doi: 10.1103/PhysRevC.87.014315

CrossRef Full Text | Google Scholar

192. Suhonen J, Civitarese O. Single and double beta decays in the A = 100, A = 116 and A = 128 triplets of isobars. Nucl Phys A (2014) 924:1–23. doi: 10.1016/j.nuclphysa.2014.01.004

CrossRef Full Text | Google Scholar

193. Suhonen J, Civitarese O. Probing the quenching of g_A by single and double beta decays. Phys Lett B (2013) 725:153–7. doi: 10.1016/j.physletb.2013.06.042

CrossRef Full Text | Google Scholar

194. Frekers D, Puppe P, Thies JH, Ejiri H. Gamow-Teller strength extraction from (³He,t) reactions. Nucl Phys A (2013) 916:219–40. doi: 10.1016/j.nuclphysa.2013.08.006

CrossRef Full Text | Google Scholar

195. Frekers D, Alanssari M, Ejiri H, Holl M, Poves A, Suhonen J. Charge-exchange reactions on double-β decaying nuclei populating J^π = 2⁻ states. Phys Rev C (2017) 95:034619. doi: 10.1103/PhysRevC.95.034619

CrossRef Full Text | Google Scholar

196. Goodman CD, Goulding CA, Greenfield MB, Rapaport J, Bainum DE, Foster CC, et al. Gamow-Teller matrix elements from 0°(p, n) cross sections. Phys Rev Lett. (1980) 44:1755–9.

Google Scholar

197. Taddeucci TN, Goulding CA, Carey TA, Byrd RC, Goodman CD, Gaarde C, et al. The (p,n) reaction as a probe of beta decay strength. Nucl Phys A (1987) 469:125–72.

Google Scholar

198. Akimune H, Ejiri H, Fujiwara M, Daito I, Inomata T, Hazama R, et al. GT strengths studied by (³He,t) reactions and nuclear matrix elements for double beta decays. Phys Lett B (1997) 394:23–8.

Google Scholar

199. Jokiniemi L, Suhonen J. Isovector spin-multipole strength distributions in Double-β-decay triplets. Phys Rev C (2017) 96:034308. doi: 10.1103/PhysRevC.96.034308

CrossRef Full Text | Google Scholar

200. Bes DR, Civitarese O, Suhonen J. Schematic and realistic model calculations of the isovector spin monopole (IVSM) excitations in ¹¹⁶In. Phys Rev C (2012) 86:024314.

Google Scholar

201. Civitarese O, Suhonen J. Strength of J^π = 1⁺ Gamow-Teller and isovector spin monopole transitions in double-β-decay triplets. Phys Rev C (2014) 89:044319. doi: 10.1103/PhysRevC.89.044319

CrossRef Full Text | Google Scholar

202. Delion DS, Suhonen J. Two-neutrino ββ decays and low-lying Gamow-Teller β⁻ strength functions in the mass range A = 70−176. Phys Rev C (2017) 95:034330. doi: 10.1103/PhysRevC.95.034330

CrossRef Full Text | Google Scholar

203. Kotila J, Suhonen J, Delion DS. Two-neutrino double beta decay of ⁷⁶Ge in an anharmonic vibrator approach. J Phys G (2009) 36:045106. doi: 10.1088/0954-3899/36/4/045106

CrossRef Full Text | Google Scholar

204. Kotila J, Suhonen J, Delion DS. Description of the two-neutrino ββ decay of ¹⁰⁰Mo by pnMAVA. J Phys G (2010) 37:015101. doi: 10.1088/0954-3899/37/1/015101

CrossRef Full Text | Google Scholar

205. Auerbach N, Klein A. Structure of isovector spin excitations in nuclei. Phys Rev C (1984) 30:1032–43.

Google Scholar

206. Ford KW, Wells JG. Calculated properties of μ-mesonic atoms. Nucl Phys. (1962) 35:295–302.

Google Scholar

207. Miller GH, Eckhause M, Kane FR, Martin P, Welsh RE. Negative muon capture in carbon leading to specific final states. Phys Lett. (1972) 41B:50–2.

Google Scholar

208. Suzuki T, Measday DF, Roalsvig JP. Total nuclear capture rates for negative muons. Phys Rev C (1987) 35:2212–4.

PubMed Abstract | Google Scholar

209. Gorringe TP, Johnson BL, Armstrong DS, Bauer J, Kovash MA, Hasinoff MD, et al. Hyperfine effect in μ⁻ capture on ²³Na and g_p/g_a. Phys Rev Lett. (1994) 72:3472–5.

Google Scholar

210. Gorringe TP, Armstrong DS, Arole S, Boleman M, Gete E, Kuzmin V et al. Measurement of partial nuon capture rates in 1s−0d shell nuclei. Phys Rev C (1999) 60:055501.

Google Scholar

211. Primakoff H. Theory of muon capture. Rev Mod Phys. (1959) 31:802–22.

Google Scholar

212. Morita M, Fujii A. Theory of allowed and forbidden transitions in muon capture reactions. Phys Rev. (1960) 118:606–18.

Google Scholar

213. Gillet V, Jenkins DA. Muon capture in oxygen-16. Phys Rev. (1965) 140:B32–41.

Google Scholar

214. Parthasarathy R, Sridhar VN. Gamma-neutrino angular correlation in muon capture of ²⁸Si. Phys Rev C (1978) 18:1796–802.

Google Scholar

215. Parthasarathy R, Sridhar VN. Gamma-neutrino angular correlations in muon capture by ²⁸Si. II, Phys Rev C (1981) 23:861–8.

Google Scholar

216. Luyten JR, Rood HPC, Tolhoek HA. On the theory of muon capture by complex nuclei (I). Nucl Phys. (1963) 41:236–74.

Google Scholar

217. Luyten JR, Tolhoek HA. On the theory of muon capture by complex nuclei (II). Nucl Phys. (1965) 70:641–57.

Google Scholar

218. Duck I. Muon capture in the shell model. Nucl Phys. (1962) 35:27–48.

Google Scholar

219. Gmitro M, Kamalov SS, Šimkovic F, Ovchinnikova AA. Ordinary and radiative muon capture on ¹²C. Nucl Phys A (1990) 507:707–14.

Google Scholar

220. Jonkmans G, Ahmad S, Armstrong DS, Azuelos G, Bertl W, Blecher M et al. Radiative muon capture in hydrogen and the induced pseudoscalar coupling. Phys Rev Lett. (1996) 77:4512–5.

PubMed Abstract | Google Scholar

221. Siiskonen T, Suhonen J, Hjorth-Jensen M. Shell-model effective operators for muon capture in ²⁰Ne. J Phys G Nucl Part Phys. (1999) 25:L55–61.

Google Scholar

222. Govaerts J, Lucio-Martinez JL. Nuclear muon capture on the proton and ³He within the standard model and beyond. Nucl Phys A (2000) 678:110–46. doi: 10.1016/S0375-9474(00)00316-X

CrossRef Full Text | Google Scholar

223. Kolbe E, Langanke K, Vogel P. Muon capture, continuum random phase approximation, and in-medium renormalization of the axial-vector coupling constant. Phys Rev C (1994) 50:2576–81.

PubMed Abstract | Google Scholar

224. Brudanin V, Egorov V, Filipova T, Kachalkin A, Kovalenko V, Salamatin A, et al. Measurement of the induced pseudoscalar form factor in the capture of polarized muons by Si nuclei. Nucl Phys A (1995) 587:577–95.

Google Scholar

225. Johnson BL, Gorringe TP, Armstrong DS, Bauer J, Hasinoff MD, Kovash MA, et al. Observables in muon capture on ²³Na and the effective weak couplings ${\tilde{g}}_a$ and ${\tilde{g}}_p$. Phys Rev C (1996) 54:2714–31.

PubMed Abstract | Google Scholar

226. Siiskonen T, Suhonen J, Kuz'min VA, Tetereva TV. Shell-model study of partial muon-capture rates in light nuclei. Nucl Phys A (1998) 635:446–69.

Google Scholar

227. Siiskonen T, Suhonen J, Kuz'min VA, Tetereva TV. Erratum to: Shell-model study of partial muon-capture rates in light nuclei. Nucl Phys A (1999) 651:437–8.

Google Scholar

228. Siiskonen T, Suhonen J, Hjorth-Jensen M. Towards the solution of the C_P/C_A anomaly in shell-model calculations of muon capture. Phys Rev C (1999) 59:R1839–43.

Google Scholar

229. Kortelainen M, Aunola M, Siiskonen T, Suhonen J. Mean-field effects on muon-capture observables. J Phys G Nucl Part Phys. (2000) 26:L33–7.

Google Scholar

230. Eramzhyan RA, Kuz'min VA, Tetereva TV. Calculations of ordinary and radiative muon capture on ^58,60,62Ni. Nucl Phys A (1998) 642:428–48.

Google Scholar

231. Kortelainen M, Suhonen J. Nuclear muon capture as a powerful probe of double-beta decays in light nuclei. J Phys G Nucl Part Phys. (2004) 30:2003–18. doi: 10.1088/0954-3899/30/12/017

CrossRef Full Text | Google Scholar

232. Kortelainen M, Suhonen J. Ordinary muon capture as a probe of virtual transitions of ββ decay. Europhys Lett. (2002) 58:666–72. doi: 10.1209/epl/i2002-00401-5

CrossRef Full Text | Google Scholar

233. Kortelainen M, Suhonen J. Microscopic study of muon-capture transitions in nuclei involved in double-beta-decay processes. Nucl Phys A (2003) 713:501–21. doi: 10.1016/S0375-9474(02)01303-9

CrossRef Full Text | Google Scholar

234. Gorringe T, Fearing HW. Induced pseudoscalar coupling of the proton weak interaction. Rev Mod Phys. (2004) 76:31–92. doi: 10.1103/RevModPhys.76.31

CrossRef Full Text | Google Scholar

235. Cook S, D'arcy R, Edmonds A, Fukuda M, Hatanaka K, Hino Y, et al. MuSIC: delivering the world's most intense muon beam. arXiv:1610.07850 [physics.acc-ph].