- 1School of Business, University of Leicester, Leicester, United Kingdom
- 2GRAPES – Group of Researchers for Applications of Physics in Economy and Sociology, Angleur, Belgium
This short note is intended as a “Letter to the Editor” Perspective in order that it serves as a contribution, in view of reaching the physics community caring about rare events and scaling laws and unexpected findings, on a domain of wide interest: sport and money. It is apparent from the data reported and discussed below that the scarcity of such data does not allow to recommend a complex elaboration of an agent based model,—at this time. In some sense, this also means that much data on sport activities is not necessarily given in terms of physics prone materials, but it could be, and would then attract much attention. Nevertheless the findings tie the data to well-known scaling laws and physics processes. It is found that a simple scaling law describes the gains of teams in recent bicycle races, like the Tour de France. An analogous case, ranking teams in Formula 1 races, is shown in an Appendix.
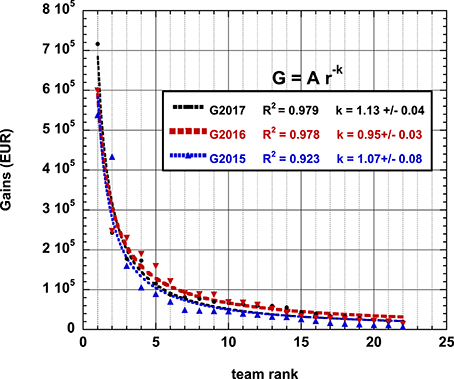
This short note stems from a recent set of aggregated data1 about the financial gains of the teams in the recent Tour de France. The gains of the 22 teams comprised of originally 9 riders, for a 23 day race with 21 stages are accumulated every day according to some pre-established rules2. Usually teams and riders aim at specific “jerseys” (going with money rewards) beside winning a stage.
It is of course trivial to rank the 22 teams according to their final gains at the end of the competition. It is on the other hand unexpected to find that such a size-ranking is best fitted by nothing else that a fine hyperbola with exponent ≃ −1, obtained through a Levenberg-Marquardt algorithm; see Figure 1. Motivated by such an unexpected finding I looked at whether similar data could be obtained for previous Tour de France races. From two different sources3,4, I obtained the equivalent data for 2016 and 2015. Quite unexpectedly, the same hyperbolic law occurs again with a decay exponent ~ −1 ± 0.05; see Figure 1.
Unfortunately, in view of “proving a universal behavior,” one cannot find such data for the other similar top long5 races, like Giro and Vuelta. It is known that these races have not so much money to distribute, — whence there is less “advertisement” of the matter. This likely means that such a kind of (financial) data is not easily available.
From a physics point of view, a few comments are in order. First, the exponent (−1) is reminiscent of Zipf's finding about the “least effort law” [1], when understood as an equilibrium steady state process. However, it can also be understood, as in a recent set of papers on UEFA and FIFA soccer team or country ranking, respectively, in terms of a dissipative structure process, arising from the number of points (“input energy flow”) given each year according to scores in different competitions, thereby leading to a self-organizing system [2–4]. Mutatis mutandis, several riders contribute to the team gains along the race. This is different from a Matthew like effect, in which the winner takes all. A very parsimonious toy model containing ingredients leading to team ranking, under such complex rules, was proposed in Ausloos et al. [3]. The model suggests that peer classes are an extrinsic property of the ranking, as obtained in many non-linear (non-equilibrium) systems under boundary condition constraints.
This is different from individual gains (and ranking) due to individual competitions. For such a case, a model was proposed by Deng et al. [5] in which players ranks and/or prize money are accrued based on their own competition wins/scores. The model is mimicking a tournament, like an inverse tree; as in tennis tournaments with direct elimination; notice that team tournaments can be often also based on direct elimination. However, sometimes, before the direct elimination stage, teams played against each other (home-and-away) in a “round robin” format [2–4].
Let it be observed that cycling competition is a different matter: even though (it seems that) a cyclist race is won by only one individual, it is well-known that this is a team activity [6–8] as usually recognized by the winner in interviews. The to-be-agent-based-model should use ideas based on cooperation beside competition [9–13]—a quite open and intense field of research in “new statistical physics.”
In so doing, it seems that from a rare type of data, one can tie some “pre-universality feature” to a complex world. Beside the aim of this report and findings, one may suggest to look at such similar data in other sports (see Appendix) in view of some accumulation toward more scientific impetus and subsequent work.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer M-XL and handling Editor declared their shared affiliation.
Footnotes
1. ^From http://www.sports.fr/cyclisme/tour-de-france/articles/tour-de-france-le-classement-des-gains-1899047/
2. ^http://www.portailduvelo.fr/tour-de-france-2012-primes-et-gains-de-epreuve-maillot-jaune-vert-a-pois/
3. ^http://videosdecyclisme.fr/tour-de-france-2016-gains-empoches-par-toutes-les-equipes/
4. ^http://www.eurosport.fr/economie/gains-tour-de-france-2015-sky-et-chris-froome-terminent-en-tete-avec-556-630-euros_sto4887058/story.html
5. ^The case of 1 day or a few days races is technically and financially different
References
1. Zipf G. Human Behavior and the Principle of Least Effort. Cambridge, MA: Addison-Wesley Press (1949).
2. Ausloos M, Cloots R, Gadomski A, Vitanov NK. Ranking structures and Rank-Rank Correlations of Countries. The FIFA and UEFA cases. Int J Mod Phys C (2014) 25:1450060. doi: 10.1142/S0129183114500600
3. Ausloos M, Gadomski A, Vitanov NK. Primacy and Ranking. Application to UEFA Team Competition. Phys Scr. (2014) 89:108002. doi: 10.1088/0031-8949/89/10/108002
4. Ausloos M. Intrinsic classes in the Union of European football associations soccer team ranking. Centr Eur J Phys. (2014) 12:773–9. doi: 10.2478/s11534-014-0505-4
5. Deng W, Li W, Cai X, Bulou A, Wang QA. Universal scaling in sports ranking. New J Phys. (2012) 14:093038. doi: 10.1088/1367-2630/14/9/093038
6. Albert E. Riding a line: competition and cooperation in the sport of bicycle racing. Sociol Sport J. (1991) 8:341–61. doi: 10.1123/ssj.8.4.341
7. Hoenigman R, Bradley E, Lim A. Cooperation in bike racing — when to work together and when to go it alone. Complexity (2004) 17:39–44. doi: 10.1002/cplx.20372
8. Baumeister RF, Ainsworth SE, Vohs KD. Are groups more or less than the sum of their members? The moderating role of individual identification. Behav Brain Sci. (2016) 39:e137. doi: 10.1017/S0140525X15000618
9. Challet D, Zhang YC. Emergence of cooperation and organization in an evolutionary game. Physica A (1997) 246:407–18. doi: 10.1016/S0378-4371(97)00419-6
10. Axelrod RM. The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration. Princeton, NJ: Princeton University Press (1997).
11. Sonubi A, Arcagni A, Stefani S, Ausloos M. Effects of competition and cooperation interaction between agents on networks in the presence of a market capacity. Phys Rev E (2016) 94:022303. doi: 10.1103/PhysRevE.94.022303
12. Lawless WF, Sofge DA, Chaudron L, Bartheye O. Bistability, nash equilibria, relatively dark collectives, and social physics: modeling the social behavior of teams. J. Enterprise Transform. (2015) 5:241–74. doi: 10.1080/19488289.2015.1123203
13. Lawless WF. The physics of teams: interdependence, measurable entropy, and computational emotion. Front Phys. (2017) 5:30. doi: 10.3389/fphy.2017.00030
Appendix
F1 Team Ranking
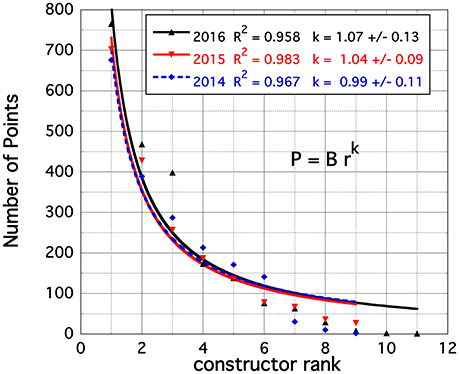
Another case in which team ranking depends on individual member performance occurs in Formula 1 races. According to their place at the end of a race, the pilot gets a certain number of points. There are usually 2 drivers for a team. In fact, such pilots are often competing against each other even though being in a team, There are about 20 races per year. At the end of the year, the teams are compared and ranked according to the number of cumulated points (P) of their drivers. The best team is known as the “best constructor for the year.” The 2014, 2015, and 2016 cases are shown in Figure 2. The rank-size law is also characterized by a decay exponent ~ −1. The analogy is obvious, even though the number of teams is smaller and the matter is not directly the amount of financial gains.
Keywords: financial gain, Universal scaling law, tour de France, competitive teams, self-organization
Citation: Ausloos M (2017) Hint of a Universal Law for the Financial Gains of Competitive Sport Teams. The Case of Tour de France Cycle Race. Front. Phys. 5:59. doi: 10.3389/fphy.2017.00059
Received: 19 September 2017; Accepted: 06 November 2017;
Published: 05 December 2017.
Edited by:
Wei-Xing Zhou, East China University of Science and Technology, ChinaReviewed by:
Ming-Xia Li, East China University of Science and Technology, ChinaAnna Carbone, Politecnico di Torino, Italy
Salvatore Micciche', Università degli Studi di Palermo, Italy
Copyright © 2017 Ausloos. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marcel Ausloos, bWE2ODNAbGUuYWMudWs=; bWFyY2VsLmF1c2xvb3NAdWxnLmFjLmJl
 Marcel Ausloos
Marcel Ausloos