- 1School of Physics, Sun Yat-sen University, Guangzhou, China
- 2ARC Centre of Excellence for Particle Physics at the Terascale, School of Physics, The University of Melbourne, Melbourne, VIC, Australia
- 3ARC Centre of Excellence for Particle Physics at the Terascale, Department of Physics, The University of Adelaide, Adelaide, SA, Australia
- 4ARC Centre of Excellence for Particle Physics at the Terascale, School of Physics, The University of Sydney, Sydney, NSW, Australia
- 5Instituto de Física Corpuscular (CSIC-Universitat de València), Valencia, Spain
A plausible explanation for the lightness of neutrino masses is that neutrinos are massless at tree level, with their mass (typically Majorana) being generated radiatively at one or more loops. The new couplings, together with the suppression coming from the loop factors, imply that the new degrees of freedom cannot be too heavy (they are typically at the TeV scale). Therefore, in these models there are no large mass hierarchies and they can be tested using different searches, making their detailed phenomenological study very appealing. In particular, the new particles can be searched for at colliders and generically induce signals in lepton-flavor and lepton-number violating processes (in the case of Majorana neutrinos), which are not independent from reproducing correctly the neutrino masses and mixings. The main focus of the review is on Majorana neutrinos. We order the allowed theory space from three different perspectives: (i) using an effective operator approach to lepton number violation, (ii) by the number of loops at which the Weinberg operator is generated, (iii) within a given loop order, by the possible irreducible topologies. We also discuss in more detail some popular radiative models which involve qualitatively different features, revisiting their most important phenomenological implications. Finally, we list some promising avenues to pursue.
1. Introduction
The discovery of neutrino oscillations driven by mass mixing is one of the crowning achievements of experimental high-energy physics in recent decades. From its beginnings as the “solar neutrino problem”—a deficit of electron neutrinos from the Sun compared to the prediction of the standard solar model, an anomaly first discovered by the Homestake experiment—through the emergence of the “atmospheric neutrino problem” and its eventual confirmation by SuperKamiokande, to terrestrial verifications by long baseline and reactor neutrino experiments, the existence of non-zero and non-degenerate neutrino masses is now well established [1–17]. In addition, the existence of oscillations proves that the weak eigenstate neutrinos νe, νμ, and ντ are not states of definite mass themselves, but rather non-trivial, coherent superpositions of mass eigenstate fields called simply ν1, ν2, and ν3, with masses m1, m2, and m3, respectively1. The dynamical origin of neutrino mass is at present unknown, including whether neutrinos are Dirac or Majorana fermions. In the former case, neutrinos and antineutrinos are distinct and have a total of four degrees of freedom, exactly as do the charged leptons and quarks. Majorana fermions, on the other hand, are their own antiparticles, and they have just two degrees of freedom corresponding to left- and right-handed helicity. Dirac neutrinos preserve total lepton number conservation, while Majorana neutrino masses violate lepton number conservation by two units. The purpose of this review is to survey one class of possible models, where neutrino masses arise at loop order and are thus called “radiative.” Almost all of the models we examine are for the Majorana mass case. Before turning to a discussion of possible models, we should summarize the experimental data the models are trying to understand or at least accommodate.
The Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix (Uαi) [18, 19] defines the relationship between the weak and mass eigenstates, through
where α = e, μ, τ and i = 1, 2, 3. The PMNS matrix U is unitary, and may be parameterized by three (Euler) mixing angles θ12, θ23, and θ13, a CP-violating Dirac phase δ that is analogous to the phase in the Cabibbo-Kobayashi-Maskawa (CKM) quark mixing matrix, and two Majorana phases α2,3 if neutrinos are Majorana fermions. The standard parametrization is
where cij ≡ cosθij and sij ≡ sinθij. The neutrino oscillation lengths are set by the ratio of squared-mass differences and energy, while the amplitudes are governed by the PMNS mixing angles and the Dirac phase. The Majorana phases do not contribute to oscillation probabilities. The angles θ12, θ23, and θ13 are sometimes referred to as the solar, atmospheric and reactor angles, respectively, because of how they were originally or primarily measured. The “solar” and “atmospheric” oscillation length parameters are, respectively,
where the distinction between the two atmospheric quantities will be discussed below.
A recent global fit [20] obtains the following 3σ ranges for the mixing angle and Δm2 parameters:
where i = 1, 2 depending on the sign of the atmospheric squared-mass difference (see Forero et al. [21] and Capozzi et al. [22] for earlier fits). The sign of has been measured because the Mikheyev-Smirnov-Wolfenstein or MSW effect [23, 24] in the Sun depends on it. The sign of the atmospheric equivalent is, however, not currently known, and is a major target for future neutrino oscillation experiments. Because of this ambiguity, there are two possible neutrino mass orderings: m1 < m2 < m3 which is called either “normal ordering” or “normal hierarchy”, and m3 < m1 < m2 which is termed “inverted.” The global fit results for the other parameters depend somewhat on which ordering is assumed. In Equations (4) and (5) we quote results that leave the ordering as undetermined. See Esteban et al. [20] for a discussion of these subtleties, but they will not be important for the rest of this review. Note that the convention is i = 1 in Equation (5) for normal ordering and i = 2 for inverted ordering.
At the 3σ level, the CP-violating phase δ can be anything. However, there is a local minimum in χ2 at δ ~ −π/2, which is tantalizing and very interesting. It hints at large CP-violation in the lepton sector, and the specific value of −π/2 is suggestive of a group theoretic origin (but beware that the definition of this phase is convention dependent). As with the mass ordering, the discovery of CP violation in neutrino oscillations is a prime goal for future experiments. One strong motivation for this is the cosmological scenario of baryogenesis via leptogenesis [25], and even if other sources of leptonic CP-violation are involved, it is important to experimentally establish the general phenomenon in the lepton sector. At present, we do not know if neutrinos are Dirac or Majorana fermions, so there is no information about the possible Majorana phases α2,3. Neutrinoless double-beta decay is sensitive to these parameters, as is standard leptogenesis.
The final parameter to discuss is the absolute neutrino mass scale. The square root of the magnitude of the atmospheric Δm2 provides a lower bound of 0.05 eV on at least one of the mass eigenvalues. Laboratory experiments performing precision measurements of the tritium beta-decay end-point spectrum currently place a direct kinematic upper bound of about 2 eV on the absolute mass scale [26–28] as quantified by an “effective electron-neutrino mass” , independent of whether the mass is Dirac or Majorana, and the sensitivity of the currently running KATRIN experiment is expected to be about 0.2 eV [29]. With appropriate caution because of model dependence, cosmology now places a strong upper bound on the sum of neutrino masses of about 0.2 eV [30], with the precise number depending on exactly what data are combined. If the neutrino mass sum was much above this figure, then its effect on large-scale structure formation—washing out structure on small scales—would be strong enough to cause disagreement with observations. For Majorana masses, neutrinoless double beta-decay experiments have determined an upper bound on an effective mass defined by
of 0.15−0.33 at 90% C.L., depending on nuclear matrix element uncertainties [31]2. We can thus see that experimentally and observationally, we are closing in on a determination of the absolute mass scale.
The fact that the laboratory and cosmological bounds require the absolute neutrino mass scale to be so low strongly motivates the hypothesis that neutrinos obtain their masses in a different manner from the charged leptons and quarks. A number of approaches have been explored in the literature, with one of them being the main topic of this review: radiative neutrino mass generation. Other approaches will also be briefly commented on, to place radiative models into the overall context of possible explanations for why neutrino masses are so small.
This completes a summary of the neutrino mass and mixing data that any model, including radiative models, must explain or accommodate. As noted above, future experiments and observational programs have excellent prospects to determine the mass ordering, discover leptonic CP violation, observe neutrinoless double beta-decay (0νββ) and hence the violation of lepton number by two units, and measure the absolute neutrino mass scale. In addition, the determination of the θ23 octant—whether or not θ23 is less than or greater than π/4—is an important goal of future experiments. Before turning to a discussion of neutrino mass models, we should review some interesting experimental anomalies that may imply the existence of light sterile neutrinos3 in addition to the active flavors νe,μ,τ (see Gariazzo et al. [32], Kopp et al. [33] for phenomenological fits).
There are three anomalies. The first is > 3σ evidence from the LSND [34, 35] and MiniBooNE [36, 37] experiments of appearance in a beam, with MiniBooNE also reporting a νe signal in a νμ beam. Interpreted through a neutrino oscillation hypothesis, these results indicate an oscillation mode with a Δm2 or order 1 eV2. This cannot be accommodated with just the three known active neutrinos simultaneously with the extremely well-established solar and atmospheric modes that require much smaller Δm2 parameters. This hypothesis thus only works if there are four or more light neutrino flavors, and the additional state or states must be sterile to accord with the measured Z-boson invisible width4. The Icecube neutrino telescope has recently tested the sterile neutrino oscillation explanation of these anomalies through the zenith angle dependence of muon track signals and excludes this hypothesis at about the 99% C.L. [38].
The next two anomalies concern νe and disappearance. Nuclear reactors produce a flux that has been measured by several experiments. When compared to the most recent computation of the expected flux [39, 40], a consistent deficit of a few percent is observed, a set of results known as the “reactor anomaly” [41]. The Gallium anomaly arose from neutrino calibration source measurements by the Gallex and SAGE radiochemical solar neutrino experiments, also indicating a deficit [42–45]. Both deficits are consistent with very short baseline transitions driven by eV-scale sterile neutrinos, and a significant number of experiments are underway to test the oscillation explanation. It should be noted that a recent analysis by the Daya Bay collaboration points to the problem being with the computation of the reactor flux rather than being an indication of very short baseline oscillations [46]. The key point is that if a sterile neutrino was responsible, one should observe the same deficit for all neutrinos from the reactor fuel, independent of nuclear species origin, but this was observed to not be the case. There is also a tension between the appearance and disappearance anomalies when trying to fit both with a self-consistent oscillation scheme [32, 33], and there is a cosmological challenge of devising a mechanism to prevent the active-sterile transitions from thermalizing the sterile neutrino in the early universe, as thermalization would violate the ~ 0.2 eV bound on the sum of neutrino masses.
Because the situation with the above anomalies is unclear, and there are challenges to explaining them with oscillations, this review will focus on neutrino mass models that feature just the three known light active neutrinos. If any of the above anomalies is eventually shown to be due to oscillations, then all neutrino mass models will need to be extended to incorporate light sterile neutrinos, including the radiative models that are our subject in this review.
The rest of this review is structured as follows: section 2 provides a general discussion of schemes for neutrino mass generation and attempts a classification. The structure of radiative neutrino mass models is then described in section 3. Section 4 covers phenomenological constraints and search strategies, including for cosmological observables. Detailed descriptions of specific models are then given in section 5, with the examples chosen so as to exemplify some of the different possibilities that the radiative mechanisms permit. We conclude in section 6, where we discuss some research directions for the future. Appendix gives further details on the relative contributions of the different operators to neutrino masses.
2. Schemes for Neutrino Masses and Mixings
In this section, we survey the many different general ways that neutrinos can gain mass, and attempt a classification of at least most of the proposed schemes. As part of this, we place both the tree-level and radiative models in an overarching context—a systematic approach, if you will, or at least as systematic as we can make it. The number of different kinds of models can seem bewildering, so there is some value in understanding the broad structure of the neutrino mass “theory space.”
Under the standard model (SM) gauge group GSM ≡ SU(3)c × SU(2)L × U(1)Y, the left-handed neutrinos feature as the upper isospin component of
where on the right-hand (RH) side the first entry denotes the representation with respect to the color group SU(3)c, the second SU(2)L (weak-isospin), and the third hypercharge Y, normalized so that electric charge is given by Q = I3 + Y. In the minimal standard model, there is no way to generate non-zero neutrino masses and mixings at the renormalizable level. Dirac masses are impossible because of the absence of RH neutrinos,
as are Majorana masses because there is no scalar isospin triplet
to which the lepton bilinear could have a Yukawa coupling. Thus, the family-lepton numbers Le, Lμ and Lτ are (perturbatively) conserved because of three accidental global U(1) symmetries. The discovery of neutrino oscillations means that the family-lepton number symmetries must be broken. If they are broken down to the diagonal subgroup generated by total lepton number L ≡ Le + Lμ + Lτ, then the neutrinos must be Dirac fermions. If total lepton number is also broken, then the neutrinos are either fully Majorana fermions or pseudo-Dirac5.
The question of whether neutrinos are Dirac or Majorana (or possibly pseudo-Dirac) is one of the great unknowns. The answer is vital for model building, as well as for some aspects of phenomenology. If neutrinos are Majorana, then it is not necessary to add RH neutrinos to the SM particle content. In fact, many of the radiative models we shall review below do not feature them. If RH neutrinos do not exist, then a possible deep justification could be SU(5) grand unification, which is content with a structure per family6. But another logical possibility, motivated by quark-lepton symmetry and SO(10) grand unification, is that RH neutrinos exist but have large (SM gauge invariant) Majorana masses, leading to the extremely well-known type-I seesaw model [47–51]. On the other hand, if neutrinos are Dirac, then RH neutrinos that are singlets under the SM gauge group, as per Equation (8), are mandatory and they must not have Majorana masses even though such terms are SM gauge invariant and renormalizable. Thus, at the SM level, something like total lepton-number conservation must be imposed by hand. Most of the radiative models we shall discuss lead to Majorana neutrinos, though we shall also briefly review the few radiative Dirac models that have been proposed.
The choice of Dirac or Majorana is thus a really important step in model building. It is perhaps fair to say that theoretical prejudice, as judged by number of papers, favors the Majorana possibility. There are a couple of reasons for this. One is simply that Majorana fermions are permitted by the Poincaré group, so it might be puzzling if they were never realized in nature, and the fact is that they constitute the simplest spinorial representation. (Recall that a Dirac fermion is equivalent to two CP-conjugate, degenerate Majorana fermions). Another was already discussed above: even if RH neutrinos exist, at the SM level they can have gauge-invariant Majorana masses, leading to Majorana mass eigenstates overall. Yet another reason is a connection between Majorana masses and an approach to understanding electric charge quantization using classical constraints and gauge anomaly cancellation [52, 53]. Nevertheless, theoretical prejudice or popularity in the literature is not necessarily a reliable guide to how nature actually is, so the Dirac possibility should be given due consideration.
2.1. Dirac Neutrino Schemes
The simplest way to obtain Dirac neutrinos is by copying the way the charged-fermions gain mass. Right-handed neutrinos are added to the SM particle content, producing the gauge-invariant, renormalizable Yukawa term
where the Higgs doublet H transforms as (1, 2, 1/2) with . The Dirac neutrino mass matrix is then
To accommodate the O(0.1) eV neutrino mass scale, one simply takes . The price to pay for this simple and obvious model is a set of tiny dimensionless parameters, some six or seven orders of magnitude smaller than the next smallest Yukawa coupling constant (that for the electron), and smaller even than the value a fine-tuned θQCD needs to be from the upper bound on the neutron electric-dipole moment. This is of course logically possible, and it is also technically natural in the 't Hooft sense [54] because taking yν to zero increases the symmetry of the theory. Nevertheless, it seems unsatisfactory to most people. The really tiny neutrino masses strongly suggest that the generation of neutrino mass proceeds in some different, less obvious manner, one that provides a rationale for why the masses are so small. As well as the Dirac vs. Majorana question, the explanation of the tiny masses has dominated model-building efforts in the literature.
So, how may one produce very light Dirac neutrinos? We highlight three possibilities, but there may be others: (i) a Dirac seesaw mechanism, (ii) radiative models, and (iii) extra-dimensional theories.
2.1.1. Dirac Seesaw Mechanism
In addition to the νL that resides inside the doublet L, and the standard RH neutrino of Equation (8), we introduce a vector-like heavy neutral fermion NL,R ~ (1, 1, 0) and impose total lepton-number conservation with νL,R and NL,R assigned lepton numbers of 1. In addition, we impose a Z2 discrete symmetry under which νR and a new gauge-singlet real scalar S are odd, with all other fields even. With these imposed symmetries, the most general Yukawa and fermion bare mass terms are
leading to the neutral-fermion mass matrix
where
We now postulate the hierarchy mL ≪ mR ≪ MN on the justification that the bare mass term has no natural scale so could be very high, and that the symmetry breaking scale of the new, imposed Z2 should be higher than the electroweak scale. The light neutrino mass eigenvalue is thus
and the eigenvector is dominated by the νL admixture so does not violate weak universality bounds. The inverse relationship of the light neutrino mass with the large mass MN is the seesaw effect, with the postulated small parameter mR/MN causing mν to be much smaller than the electroweak-scale mass mL. The above structure is the minimal one necessary to illustrate the Dirac seesaw mechanism (and has a cosmological domain wall problem because of the spontaneously broken Z2), but the most elegant implementation is in the left–right symmetric model [55]. Under the extended electroweak gauge group SU(2)L×SU(2)R×U(1)B−L, the RH neutrino sits in an SU(2)R doublet with B−L = −1, while NL,R remains as gauge singlets. The scalars are a left–right symmetric pair of doublets HL,R with B−L = 1. The usual scalar bidoublet is not introduced. The Z2 symmetry is then a subgroup of SU(2)R, and S is embedded in the RH scalar doublet. The mass and symmetry breaking hierarchy is then . The absence of the bidoublet ensures the zero in the top-left entry of the mass matrix7. Several tree-level Dirac neutrino mass models have been discussed in Ma and Popov [56]: The SM singlet Dirac fermion NL + NR can be obviously replaced by an electroweak triplet. Alternatively a neutrinophilic two Higgs doublet model [57, 58] is an attractive possibility to obtain small Dirac neutrino masses.
2.1.2. Radiative Dirac Schemes
A generalization of the symmetry structure of the Z2 Dirac seesaw model discussed above provides us with one perspective on the construction of radiative Dirac neutrino mass models. A basic structural issue with such models is the prevention of the tree-level term generated by the renormalizable Yukawa interaction of Equation (10). Some new symmetry must be imposed that forbids that term, but that symmetry must also be spontaneously or softly broken in such a way that an effective operator is produced. In the case of radiative models, this must be made to happen at loop order. One obvious possibility is to demand that “RH neutrino number” is conserved, meaning that invariance under
with all other SM fields as singlets, is imposed. One may then introduce a complex scalar ρ that transforms, for example, as
whose non-zero expectation value spontaneously breaks the symmetry. The effective operator
produced by integrating out new physics at mass scale Λ, is both SM gauge invariant and invariant under the imposed symmetry 8. It generates a neutrino Dirac mass of order
which will be small compared to the weak scale when . If this operator is “opened up”—derived from an underlying renormalizable or ultraviolet (UV) complete theory—at loop-level, then a radiative neutrino Dirac-mass model is produced. Note that in a loop-level completion, the parameter 1/Λn depends on powers of renormalizable coupling constants and a 1/16π2 per loop as well as the actual masses of new, exotic massive particles. See Ma and Popov [56] for a recent systematic study of 1-loop models based on this kind of idea. Note that the Dirac seesaw model discussed earlier is obtained as a truncated special case: the U(1) symmetry with n = 1 is replaced with its Z2 subgroup, the complex scalar field ρ is replaced with the real scalar field S, and the effective operator is opened up at tree-level.
Obviously, the phase part of ρ will be a massless Nambu-Goldstone boson (NGB), but its phenomenology might be acceptable because it only couples to neutrinos. If one wishes to avoid this long range force, one could find a way to make the new U(1) anomaly-free and then gauge it so that the NGB gets eaten, or one may use a discrete subgroup of the U(1) to forbid Equation (10). See Wang and Han [60] for a discussion of the Z2 case for 1-loop models that also include a dark matter candidate.
The above is simply an example of the kind of thinking that has to go into the development of a radiative Dirac neutrino model—we are not claiming it is the preferred option. To our knowledge, a thorough analysis of symmetries that can prevent a tree-level Dirac mass and thus guide the construction of complete theories has not yet been undertaken in the literature. That is one of the reasons this review will discuss Majorana models at greater length than Dirac models.
2.1.3. Extra-Dimensional Theories
One way or another, the effective coefficient in front of must be made small. Seesaw models achieve this by exploiting powers of a small parameter given by the ratio of symmetry breaking and/or mass scales. Radiative models augment the seesaw feature with 1/16π2 loop factors and products of perturbative coupling constants. In warped or Randall-Sundrum extra-dimensional theories [61, 62], the geometry of fermion localization in the bulk [63, 64] can lead to the suppression of Dirac neutrino masses through having a tiny overlap integral between the profile functions for the neutrino chiral components and the Higgs boson [63, 65–68]. The phenomenological implications of Dirac neutrinos in extra-dimensional set-ups have been studied in De Gouvea et al. [69], where it is shown that these effects can be encoded in specific dimension-six effective operators.
One can also have a “clockwork” mechanism [70, 71] to generate exponentially suppressed Dirac masses. In the same way, it is also useful to have low-scale seesaw [72]. This mechanism can be implemented with a discrete number of new fields or via an extra spatial dimension [73].
2.2. Majorana Neutrino Schemes
We now come to our main subject: radiative Majorana neutrino mass generation. We also briefly review tree-level seesaw schemes, both for completeness and for the purposes of comparison and contrast to the loop-level scenarios. In the course of the discussion below, an attempt will be made to classify the different kinds of radiative models. This is a multidimensional problem: no single criterion can be singled out as definitely the most useful discriminator between models. Instead, we shall see that several overlapping considerations emerge, including ΔL = 2 effective operators, number of loops, number of Higgs doublets, nature of the massive exotic particles, whether or not there are extended symmetries and gauge bosons, distinctive phenomenology, and whether or not the models address problems or issues beyond just neutrino mass (e.g., dark matter, grand unification, …).
The main distinctive feature of Majorana neutrino mass is, of course, that it violates lepton-number conservation by two units. It is thus extremely useful to view the possibilities for the new physics responsible from a bottom-up perspective, meaning SM gauge-invariant, ΔL = 2 low-energy effective operators that are to be derived from integrating out new physics that is assumed to operate at scales higher than the electroweak. This approach permits the tree-level seesaw [47–51, 74–80] and radiative models to be seen from a unified perspective.
Taking the particle content of the minimal SM, it is interesting that the simplest and lowest mass-dimension effective operator one can produce is directly related to Majorana neutrino mass generation. This is the famous Weinberg operator [81]
where the SU(2) indices and Lorentz structures are suppressed (one can check that there is only one independent invariant even though there are three different ways to contract the SU(2) indices of the four doublets.). We say the singular “operator” for convenience, but it is to be understood that there are also family indices so we really have a set of operators. This is a mass dimension five operator, so enters the Lagrangian with a 1/Λ coefficient, where Λ is the scale of the new physics that violates lepton number by two units. Replacing the Higgs doublets with their vacuum expectation values (VEVs), one immediately obtains the familiar Majorana seesaw formula,
displaying the required suppression of mν with respect to the weak scale v when ϵ ≡ v/Λ ≪ 1, so that the ΔL = 2 new physics operates at a really high scale.
The Weinberg operator can be immediately generalized to the set
where the number of primes is equal to n. One obtains ever more powerful seesaw suppression,
as n increases.
The task now is to derive, from an underlying renormalizable or UV complete theory, one of the Weinberg-type operators as the leading contribution to neutrino mass. This process has come to be termed “opening up the operator.” The choices one makes about which operator (what value of n) is to dominate and how it is to be opened up determine the type of theory one obtains. Here are some possible choices:
1. Open up O1 at tree-level using only exotic massive fermions and scalars as the new physics.
2. Open up O1 at j-loop level using heavy exotics only.
3. Open up O1 at j-loop level using both light SM particles and heavy exotics.
4. Open up at tree-level using heavy exotics only.
5. Open up at j-loop level using heavy exotics only.
6. Open up at j-loop level using both light SM particles and heavy exotics.
Option 1 leads, in its simplest form, precisely to the familiar type-I [47–51], type-II [74–79] and type-III [80] seesaw mechanisms, as we review in the next subsection. Option 2 leads to a certain kind of radiative model, to be contrasted with that arising from option 3. The difference between the two can be expressed in terms of the matching conditions used to connect an effective theory below the scale Λ of the ΔL = 2 new physics to the full theory above that scale, as outlined in Figure 1. For scenario 2, the effective Weinberg operator has a non-zero Wilson coefficient at Λ, and for all scales below that. In scenario 3, on the other hand, the Weinberg operator has a coefficient at scale Λ that is loop-suppressed compared to the Wilson coefficients of other, non-Weinberg-type ΔL = 2 operators9 at that scale, where these other operators are obtained by integrating out the heavy fields only. If the matching is performed at tree-level approximation, then the coefficient of the Weinberg operator at Λ in fact vanishes. Under renormalization group mixing, the non-zero ΔL = 2 operators will, however, generate an effective Weinberg operator as the parameters are run to scales below Λ. If the matching is performed at loop-level, then the Weinberg operator will have a non-zero coefficient at scale Λ, but it will be loop-suppressed compared to the coefficients of the relevant non-Weinberg operators. Below Λ, the Weinberg operator coefficient will, once again, receive corrections from the renormalization group running and operator mixing. Option 3 will be a major topic in this review, and it motivates the enumeration of all SM gauge-invariant ΔL = 2 operators, not just those in the Weinberg class, since the non-Weinberg operators describe the dominant ΔL = 2 processes at scale Λ. Opening up the non-Weinberg operators at tree-level then provides a systematic method of constructing a large class of theories that generate neutrino masses at loop order.
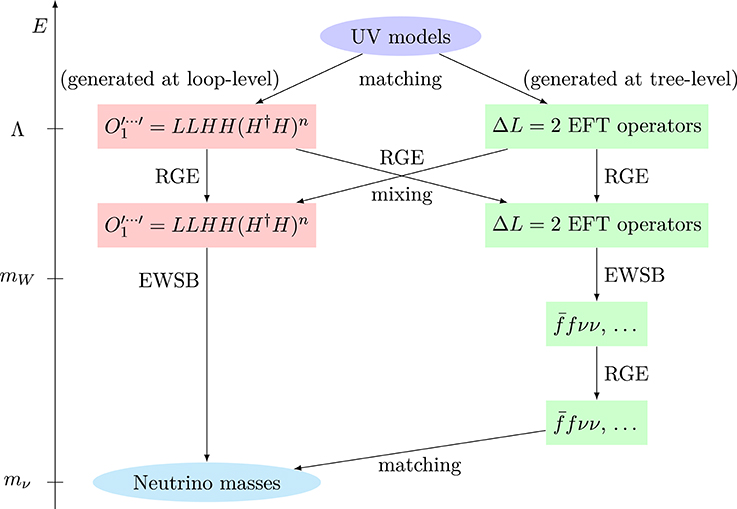
Figure 1. Running and matching for (radiative) Majorana neutrino masses. See Appendix for a discussion of the relative contribution of the different operators.
Options 4-6 obviously repeat the exercise, but with two more powers of ϵ which help suppress the neutrino mass. With these options, one needs to ensure that generated from the new physics dominates over O1 and all lower-dimensional operators . Option 6 is similar to 3 in that the effective theory between the weak and new physics scales contains some non-Weinberg type of ΔL = 2 operator(s) that dominate at scale Λ.
2.2.1. Tree-Level Seesaw Mechanisms
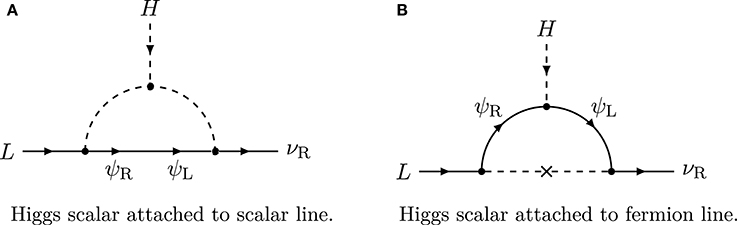
The three familiar seesaw models may be derived in a unified way by opening up the Weinberg operator O1 at tree level in the simplest possible way, using as the heavy exotics only scalars or fermions. The available renormalizable interactions are then just of Yukawa and scalar-scalar type. The opening-up process is depicted in Figure 2. The type-I and type-III seesaw models are obtained by Yukawa coupling LH with the two possible choices of (1, 1, 0) and (1, 3, 0) fermions, both of which can have gauge-invariant bare Majorana masses. The type-II model is the unique theory obtained from Yukawa coupling the fermion bilinear to a (1, 3, 1) scalar multiplet, which in turn couples to H†H†, a cubic interaction term in the scalar potential10. The seesaw effect is obtained in this case by requiring a positive quadratic term for the triplet in the scalar potential, that on its own would cause the triplet's VEV to vanish, but which in combination with the cubic term induces a small VEV for it.
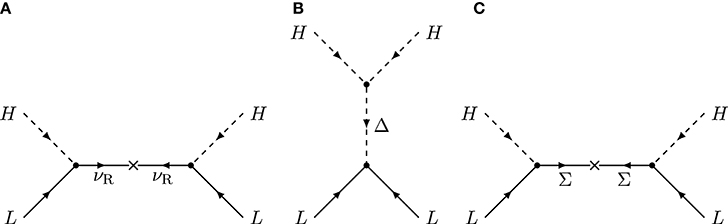
Figure 2. Minimally opening up the Weinberg operator at tree-level using either exotic massive fermions or scalars. (A) Type-I seesaw model. The massive exotic particle integrated out to produce an effective Weinberg operator at low energy is a SM gauge-singlet Majorana fermion, the right-handed neutrino νR. (B) Type-II seesaw model. The massive exotic is a (1, 3, 1) scalar Δ coupling to LL and H†H†. It gains a small induced VEV from the latter coupling. (C) Type-III seesaw model. The massive exotic is a (1, 3, 0) fermion Σ whose middle component mixes with the left-handed neutrino.
As is clear from Figure 2, there are two interaction vertices for all three cases, and there is only one type of exotic per case. An interesting non-minimal tree-level seesaw model realizing option 4 is obtained by allowing four vertices instead of two, and two exotic multiplets: a (1, 4, −1/2) scalar that couples to HHH† and a (1, 5, 0) massive fermion that Yukawa couples to the exotic scalar quadruplet and the SM lepton doublet [82–84]. The resulting model produces the generalized Weinberg operator which has mass-dimension nine. This model is a kind of hybrid of the type-II and type-III seesaw mechanisms, because it features both a small induced VEV for the quadruplet and a seesaw suppression from mixing with the fermion quintuplet.
2.2.2. Radiative Schemes and Their Classification
As noted above, there are many different kinds of radiative neutrino mass models and there is probably no single classification scheme that is optimal for all purposes. We thus discuss a few different perspectives, some much more briefly than others. Two will be treated at length: (i) the ΔL = 2 effective operator approach, and (ii) classification by loop-order openings of the Weinberg operator.
A. Standard model ΔL = 2 effective operators. This approach can be considered as stemming from the observations made about options 3 and 6 in section 2.2: when both light SM particles and heavy exotics appear in the neutrino mass loop graph, it is useful to first consider integrating out the heavy exotics at tree-level. This produces effective ΔL = 2 operators that are of non-Weinberg type. They must be of different type, because if they were not, then the heavy exotics would produce the Weinberg operator without participation by light SM particles, leading either to a class 1 model (if O1 is produced at tree-level) or a class 2 model (if O1 is produced at loop level). An exhaustive list of gauge-invariant, non-Weinberg ΔL = 2 operators is thus needed.
Such a list was provided by Babu and Leung (BL) [85], based on the following assumptions: (i) the gauge group is that of the SM only, (ii) no internal global symmetries are imposed apart from baryon number, (iii) the external lines are SM quarks, SM leptons and a single Higgs doublet, and (iv) no operators of mass dimension higher than 11 were considered. We first comment on these assumptions. Clearly, if the gauge symmetry was extended beyond that of the SM, then some combination of effective operators might be restricted to having a single coefficient, and others might be forced to vanish, compared to the SM-gauge-group-only list. Similar observations follow for imposed global symmetries. It is sensible to impose baryon number conservation, because otherwise phenomenological constraints will force the new physics to such high scales that obtaining neutrino masses of the required magnitude (at least one at 0.05 eV) will be impossible. The case of a single Higgs doublet can readily be generalized to multiple Higgs doublets, given that the gauge quantum numbers are the same. This would obviously enrich the phenomenology of the resulting models, and if additional symmetries were also admitted, then it would change the model-building options. The point is simply that H†H is invariant under all possible internal symmetries, while is not. (Admitting additional Higgs doublets is also interesting for generalized-Weinberg-operator models, because then a symmetry reason can exist for, say, being generated without also generating what would otherwise be dominant LLH1,2H1,2 operators.) The addition of non-doublet scalar multiplets into the external lines is a more serious complication. Some discussion of the possible roles of additional scalars that gain non-zero VEVs that contribute to neutrino mass generation will be given in later sections. Another restriction worth noting in the BL list is the absence of the gauge-singlet RH neutrinos. In assumption (iv), the point to highlight is the absence of SM gauge fields. Babu and Leung did actually write down the mass-dimension-7 operators containing gauge fields, and Bhattacharya and Wudka [86] further examined them. As far as we know, however, no complete analysis has been undertaken for the dimension-9 and -11 cases. Finally, it is sensible to stop at dimension 11 because at any higher order the contribution to neutrino mass will be insufficiently large. The BL list, as enumerated from O1 to O60, took operators that could be thought of as products of lower-dimension operators with the SM invariants HH† and the three dimension-4 charged-fermion Yukawa terms as implicit. de Gouvea and Jenkins [87] extended their list by explicitly including the latter cases, thereby augmenting the operator count to O75.
Operators meeting all of these requirements exist at all odd mass dimensions [85, 88, 89], starting with the Weinberg operator O1 as the unique dimension-5 case (up to family indices). The dimension-7 list is as follows:
We follow the BL numbering scheme, which was based on tracking the number of fermion fields in the operator rather than the mass dimension. The operators are separated in three groups with 2, 4, and 6 fermions. Some comments now need to be made about the schematic notation and what features are suppressed. The field-string defining each operator above completely defines the flavor content of that operator. Thus L ~ (1, 2, −1/2) is the lepton doublet, Q ~ (3, 2, 1/6) is the quark doublet, ec ~ (1, 1, 1) is the isosinglet charged anti-lepton, dc ~ is the isosinglet anti-down, is the isosinglet anti-up, and H ~ (1, 2, 1/2) is the Higgs doublet. The color indices and the different possible Lorentz structures are suppressed. In general, there are a number of independent operators corresponding to each flavor-string. For the dimension-7 list, operators O3 and O4 each have two independent possibilities for the contraction of the isospin indices, as explicitly defined above, but obviously a unique color contraction. Babu and Leung specify the independent internal-index contractions, but only make general remarks on the Lorentz structures, and we shall follow suit. To assist the reader to understand the notation, we write out the above operators more completely in standard 4-component spinor notation, but for scalar and pseudoscalar Lorentz structures only and with isospin indices suppressed:
Of course, these operators feature quark and charged-lepton fields in addition to neutrinos and Higgs bosons, so they do not by themselves produce neutrino masses. The charged fermion fields have to be closed off in a loop or loops to produce a neutrino self-energy graph which then generates a Weinberg-type operator, as per options 3 and 6. In fact, using this procedure and naive dimensional analysis one can estimate their matching contribution to the Weinberg operator, as done in de Gouvea and Jenkins [87]. In addition, every dimension-7 operator in Equation (24) may be multiplied by H†H to produce a dimension-9 generalization of that operator, just as is a generalization of O1. At dimension 9, there are many more operators. Six of the flavor strings feature four fermion fields and three Higgs doublets:
Note that the operators O61,66,71 are the products of O1 and the three SM Yukawa operators. Another 12 are six-fermion operators:
Although absent from the BL list another such operator is , which generates the correct neutrino mass scale only for a very low lepton-number violation scale. In case it consists entirely of the first generation SM fermions it is strongly constrained by 0νββ (generated at tree level by this operator). The large number of dimension-11 operators can be found listed in Babu and Leung [85] and de Gouvea and Jenkins [87].
de Gouvea and Jenkins [87] and Angel et al. [90] performed general analyses of diagram topologies for opening up these operators at tree-level using massive exotic scalars and either vector-like or Majorana fermion exotics, and consequently producing neutrino mass at various loop levels. The operators
can give rise to 1-loop neutrino mass models, while
can produce 2-loop models. The set
can form the basis for neutrino mass to be generated at three or more loops.
In each of these cases, one may derive an indicative upper bound on the scale of new physics from the requirement that at least one neutrino mass be at least 0.05 eV in magnitude. For example, for operators involving first generation11 quarks this bound can be estimated as follows: Operator O19, which can be opened up to give a 3-loop neutrino mass contribution, has the lowest upper bound on the new physics scale of about 1 TeV (apart from ). The highest is about 4 × 109 TeV for the 1-loop case of O4a. These estimates come from an examination of the loop contribution to neutrino mass only, and do not take into account other phenomenological constraints that will exist for each complete model. As part of that, any unknown coupling constants, such as Yukawas that involve the exotic fermions and/or scalars were set to unity. In a realistic theory, many of these constants would be expected to be less than one, which would bring the scale of new physics to lower values. In any case, one can see that the required new physics, even for 1-loop models, is typically more testable than the type-I, II, and III seesaw models. Some high loop models, as the O19 case demonstrates, have very low scales of new physics and some may even be ruled out already. At the dimension-11 operator level, so not explicitly discussed here, there are even examples which can at best produce a 5-loop neutrino mass contribution. Those models are definitely already excluded. Examples of full models that are associated with specific operators will be presented in later sections.
B. Number of loops. A complementary perspective on the spectrum of possible radiative neutrino mass models is provided by adopting the number of loops as the primary consideration rather than the type of ΔL = 2 effective operator that dominates the new physics. Equations (28–30) already form the basis for such a classification for type 3 and type 6 scenarios, but a more general analysis will also capture the type 2 and type 5 possibilities.
At j-loop order, neutrino masses are typically given by
for the O1 associated options 2 and 3, and
for the cases of options 5 and 6, where GeV, and Λ is the new-physics scale where lepton number is violated by two units. All coupling constants, and for some models also certain mass-scale ratios, are absorbed in the dimensionless coefficient C. In order to explain the atmospheric mass splitting lower bound of 0.05 eV, we obtain an upper limit on the new physics scale Λ of 105C TeV for 3-loop models and 10 C TeV for 5-loop models corresponding to the O1 cases, and 10 C1/3 TeV for the case at 3-loop order. Constraints from flavor physics severely constrain the scale of new physics and the couplings entering in C. In addition, in models which feature explicit ΔL = 2 lepton-number violation through trilinear scalar interactions, the latter cannot be arbitrarily large because otherwise they have issues with naturalness (see Herrero-García et al. [91] for the case of the Zee model) and charge/color breaking minima (see Frere et al. [92], Alvarez-Gaume et al. [93] and Casas and Dimopoulos [94] for studies in the context of supersymmetry and Herrero-Garcia et al. [95] for the case of the Zee-Babu model). Thus, apart from a few 4-loop models [96–98] which compensate the loop suppression by a high multiplicity of particles in the loop, the vast majority of radiative neutrino mass models generate neutrino mass at 1-, 2-, or 3-loop level. We therefore focus on these cases.
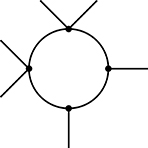
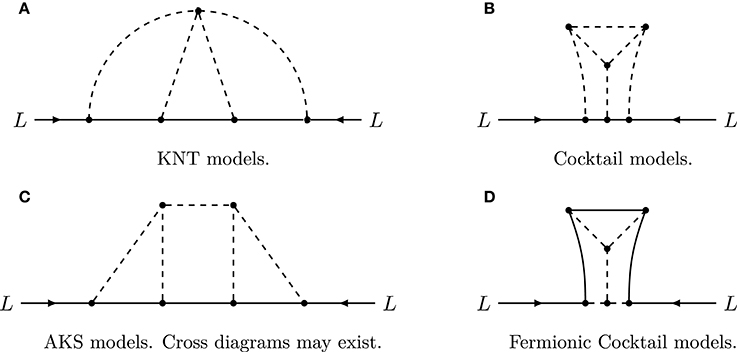
1-loop topologies for O1 = LLHH. The opening up of the Weinberg operator at 1-loop level has been systematically studied in Ma [99] and Bonnet et al. [100]. The authors of Bonnet et al. [100] identified 12 topologies which contribute to neutrino mass. Among all the topologies and possible Lorentz structures, topology T2 cannot be realized in a renormalizable theory. For the other topologies, the expression for neutrino mass and the possible particle content for electroweak singlet, doublet, and triplet representations is listed in the appendix of Bonnet et al. [100]. The divergent ones, T4-1-i, T4-2-ii, T4-3-ii, T5 and T6, need counter-terms to absorb the divergences, which are indeed tree-level realizations of the Weinberg operators. Furthermore, for T4-1-ii, there is no mechanism to forbid or suppress the tree-level contribution from Weinberg operator, such as extra discrete symmetry or U(1). Therefore, there are in total six topologies which generate neutrino mass via a genuine12 1-loop diagram: T1-i, T1-ii, T1-iii, T3, T4-2-i, T4-3-i, which are depicted in Figure 3. Depending on the particle content, the topologies do not rely on any additional symmetry. However, the topologies T4-x-i require a discrete Z2 symmetry in addition to demanding Majorana fermions in the loop with lepton-number conserving couplings. This is difficult to achieve in a field theory, as lepton-number is necessarily broken by neutrino mass. For example, in topology T4-2-i the scalar connected to the two Higgs doublets H is necessarily an electroweak triplet and thus its direct coupling to two lepton doublets L is unavoidable. This coupling induces a type-II seesaw tree-level contribution to neutrino mass. Similar arguments hold for the other topologies T4-x-i.
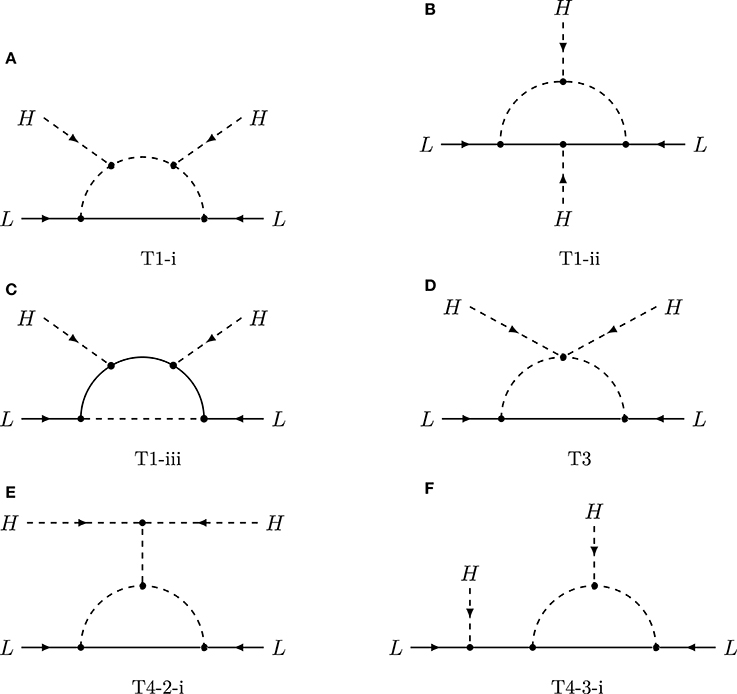
Figure 3. Feynman diagram topologies for 1-loop radiative neutrino mass generation with the Weinberg operator O1 = LLHH. Dashed lines could be scalars or gauge bosons if allowed.
1-loop topologies for . A similar analysis has been performed for 1-loop topologies that give rise to the dimension-7 generalized Weinberg operator [101]. Of the 48 possible topologies, only the eight displayed in Figure 4 are relevant for genuine 1-loop models. For specific cases, not all of these eight diagrams will be realized. The three-point vertices can be Yukawa, gauge or cubic scalar interactions, while the four-point vertices only contain scalar and gauge bosons.
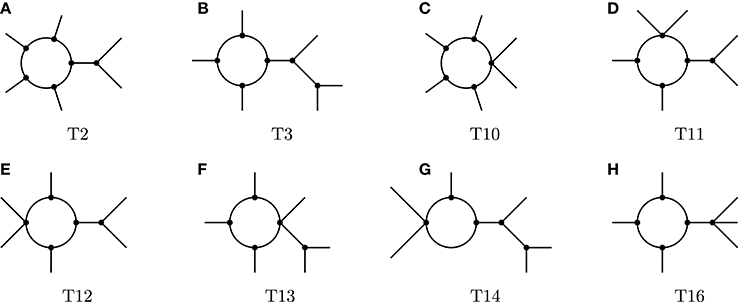
Figure 4. Topologies that can give rise to genuine 1-loop openings of the dimension-7 Weinberg operator .
2-loop topologies for O1 = LLHH. A systematic analysis of 2-loop openings of O1 was performed in Aristizabal Sierra et al. [102]. Figure 5 displays the topologies identified in this study as able to contribute to genuine 2-loop models. There are additional 2-loop diagrams – that were termed “class II” – that have the form of one of the 1-loop topologies of Figure 3 with one the vertices expanded into a 1-loop subgraph. They remark the class II topologies may be useful for justifying why a certain vertex has an unusually small magnitude.
Figure 5. Topologies for genuine 2-loop completions of the Weinberg operator O1 = LLHH. Solid dots denote interaction vertices. Crossed lines without a dot at the intersection denote a non-planar configuration.
C. Other considerations. We now briefly survey other perspectives on classifying or discriminating between neutrino mass models.
One suggested criterion is complexity [103]. While recognizing that sometimes nature appears to favor minimal possibilities (in an Occam's razor approach), and at other times not (e.g., the old problem of why there are three families), it does make sense to rank neutrino mass models on some sensible measure of how complex they are. Law and McDonald [103] proposes a hierarchy based on (i) whether or not the model relies on the imposition of ad hoc symmetries, (ii) the number of exotic multiplets required, and (iii) the number of new parameters. Interestingly, they construct radiative models that are even simpler, on the basis of these criteria, than the 1-loop Zee-Wolfenstein model [104, 105]. However, like the Zee-Wolfenstein model, while these models generate non-zero neutrino masses, they fail phenomenologically. Thus, we must conclude that if nature utilizes the radiative mechanism, it will be non-minimal.
Another consideration for Majorana mass models is the important phenomenological connection to 0νββ decay [106–108]. Just as Majorana neutrino mass models may be systematically constructed through opening up ΔL = 2 effective operators, models for 0νββ decay can be analysed by opening up the ūūddēē family of operators. The neutrino mass and 0νββ decay considerations are of course connected, but the nature of the relationship is model-dependent. An interesting situation would emerge in a hypothetical future where 0νββ decay is observed, but the standard Majorana neutrino exchange contribution through mββ is contradicted by, for example, cosmological upper bounds on the absolute neutrino mass scale. That would point to a non-minimal framework, which may be connected with radiative neutrino mass generation.
A further interesting aspect is the existence or otherwise of a deep theoretical reason for a given radiative model. At first sight, each such model looks random. However, some of them can be connected with, for example, grand unified theories (GUTs). One simple point to make is that exotics, such as scalar leptoquarks, that often feature in radiative models can be components of higher-dimension multiplets of SU(5) and SO(10). Also, by contributing to renormalization group running, some of them can assist with gauge coupling constant unification [109]. If they are to be light enough to play these roles, while other exotics within the multiplets have, for example, GUT-scale masses, then we face a similar issue to the famous doublet-triplet splitting problem. Nevertheless, this is a starting point for investigating the possible deeper origin of some of the required exotics. Another interesting GUT-related matter was analysed in depth in de Gouvêa et al. [88]. A necessary condition for a ΔL = 2 operator of a certain mass dimension to be consistent with a GUT origin is that it occurs as a term in an effective operator of the same mass dimension derived with grand unified gauge invariance imposed. For example, the dimension-7 operator O3a from Equation (24) does not appear as a component in any SU(5) operator of the same dimension. On the other hand, other SM operators are embedded in the same GUT operator, with only one of them being able of giving the dominant contribution to neutrino masses. In addition to the question of the mere existence of SM-level operators in GUT decompositions, grand unification also imposes relations between SM-level operators, including some that violate baryon number and generate B−L violating nucleon decays and/or neutron-antineutron oscillations, leading to additional constraints. In the end, the authors of de Gouvêa et al. [88] conclude that only a small subset of SM ΔL = 2 operators are consistent with grand unification.
Another strategy for uncovering a deeper origin for a radiative model is by asking if a given model has some close connection with the solution of important particle physics problems beyond just the origin of neutrino mass. One that has been explored at length in the literature is a possible connection to dark matter. Examples of such models will be given in more detail in later sections. Here, we simply mention some systematic analyses of what new symmetries can be imposed in radiative models to stabilize dark matter [110, 111]. Farzan et al. [110] classified the symmetries Gν that can be imposed in order to ensure that the first non-zero contribution to O1 occurs at a given loop order, by forbidding all potential lower-order contributions. All standard model particles are singlets under Gν, implying that the lightest of the exotics that do transform under this symmetry must be stable if the symmetry remains exact, establishing a connection with dark matter. Restrepo et al. [111] performed a systematic analysis of radiative models in a certain class in order to find those that have viable dark matter candidates. The considered models are those that generate mass at 1-loop level using exotics that are at most triplets under weak isospin, and where the stabilizing symmetry is Z2. They found 35 viable models. A similar analysis, but requiring 2-loop neutrino mass generation, can be found in Simoes and Wegman [112].
Besides dark matter, radiative neutrino mass models may also be connected to other physics beyond the SM such as the anomalous magnetic moment of the muon, the strong CP problem, the baryon asymmetry of the Universe or B-physics anomalies, among others. Phenomenology related to radiative neutrino mass models is briefly discussed in section 4 in general and an example of a possible connection to the recent B-physics anomalies is presented in section 5.4.
3. Radiative Generation of Neutrino Masses
We adopt the classification of radiative neutrino mass models according to their Feynman diagram topology13, but refer to the other classification schemes where appropriate. In particular, we indicate the lowest-dimensional non-trivial ΔL = 2 operator which is generated beyond the Weinberg operator LLHH. These ΔL = 2 operators capture light particles which are in the loop to generate neutrino mass and are very useful to identify relevant low-energy phenomenology.
In the subsections 3.1–3.3 we classify Majorana neutrino mass models proposed in the literature according to their topology and specifically discuss models with SM gauge bosons in the loop in section 3.4. In section 3.5 we review Dirac neutrino mass models and briefly comment on models based on the gauge group SU(3)c × SU(3)L × U(1)X in section 3.6.
3.1. 1-Loop Majorana Neutrino Mass Models
This section is divided into several parts: (i) 1-loop UV completions of the Weinberg operator, (ii) 1-loop seesaws, (iii) UV completions with additional VEV insertions, (iv) 1-loop UV completions of the higher dimensional operators and (v) other 1-loop models. Notice that the first part includes models with multi-Higgs doublets, while the second part discusses external fields which transform under an extended symmetry. Besides the genuine topologies discussed in section 2, there are models based on the non-genuine 1-loop topologies in Figure 6.
3.1.1. Weinberg Operator LLHH
We follow the general classification of UV completions of the Weinberg operator at 1-loop [100] discussed in section 2.2.2. The six genuine topologies are shown in Figure 3. Analytic expressions for all 1-loop topologies are listed in the appendix of Bonnet et al. [100].
Here we list the theories falling into respective categories. As the topologies stay the same while incorporating multiple Higgs doublets, theories with more than one Higgs doublet will also be listed here. Models in which the generation of neutrino mass relies on additional VEVs connected to the neutrino mass loop diagram are discussed in section 3.1.3. We first discuss the models based on topology T3, the only one with a quartic scalar interaction, before moving on to the other topologies.
T3
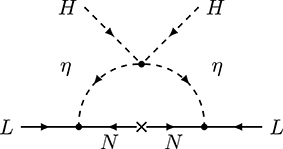
Topology T3 is one of the most well-studied. It was first proposed in Ma [99] and its first realization, the scotogenic model with a second electroweak scalar doublet and sterile fermion singlets (at least two) both odd under a Z2 symmetry, was later proposed in Ma [113]. See section 5.3 for a detailed discussion of the model. Its appeal lies in the simultaneous explanation of dark matter, which is stabilized by a Z2 symmetry. A crucial ingredient is the quartic scalar interaction (H†η)2 (see Equation 95) of the SM Higgs boson H with the electroweak scalar doublet η in the loop. This scalar interaction splits the masses of the neutral scalar and pseudoscalar components of η. Neutrino masses vanish in the limit of degenerate neutral η scalar masses. Several variants of the scotogenic model have been proposed in the literature: with triplet instead of singlet fermions [114–116], an extension with an additional singlet scalar [117], one fermionic singlet and two additional electroweak scalar doublets [118], scalar triplets [119], colored scalars and fermions [120, 121], a vector-like fermionic lepton doublet, a triplet scalar, and a neutral [122, 123] or charged [124] singlet scalar, vector-like doublet and singlet fermions and doublet scalar, which contains a doubly charged scalar [125], higher SU(2) representations [126–129], an extended discrete symmetry with Z2 × Z2 [130, 131] or Z2 × CP [132], a discrete flavor symmetry based on S3 [133], A4 [134–137], Δ(27) [138, 139], which is either softly-broken or via electroweak doublets, and its embedding in (grand) unified theories [137, 140–143]. Finally, the authors of Megrelidze and Tavartkiladze [144] proposed the generation of neutrino mass via lepton-number-violating soft supersymmetry-breaking terms. In particular the generation of the dimension-4 term with left-handed sleptons leads to models based on the topology T-3 with supersymmetric particles in the loop. Another variant involves a global continuous dark symmetry [145], Hagedorn, (in prep), termed the generalized scotogenic model.
T1-i
Ma [146] discusses a supersymmetrized version of the scotogenic model, which is based on topology T3 and we discuss in detail in section 5.3. The topology necessarily differs from T3 because the term (H†η)2 is not introduced by D-terms. An embedding of this model in SU(5) is given in Ma [147]. In a non-supersymmetric context, the same topology is discussed in Farzan [117], which introduces one real singlet scalar, in the context of a (dark) left–right symmetric model [148, 149], and in Budhi et al. [150], Kashiwase and Suematsu [151], and Budhi et al. [152], which introduce multiple singlet scalars to connect the two external Higgs fields. The term (H†η)2, which is essential to generate topology T3, is neglected in Budhi et al. [150], Kashiwase and Suematsu [151], and Budhi et al. [152] and thus neutrino mass is generated via topology T1-i. One of the singlet scalars in the neutrino mass model can be the inflaton via a non-minimal coupling with the Ricci-scalar. The term (H†η)2 can be explicitly forbidden by imposing a U(1) symmetry, which is softly broken by the CP-violating mass term χ2 of a complex scalar field χ [153]. Finally the authors of Lu and Gu [154] proposed a model with electroweak singlet and triplet scalars as well as fermions and study the dark matter phenomenology and leptogenesis.
T1-ii
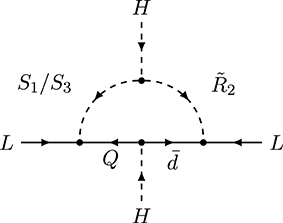
Among the models based on the topology T1-ii, there are four possible operators which models are based on. Besides models with only heavy new particles, there are models with SM charged leptons, down-type quarks, or up-type quarks in the loop, which are based on the operators O2 and O3, respectively. We first discuss the models based on operator O2. The first radiative Majorana neutrino mass model, the Zee model [104], is based on this operator. See section 5.1.1 for a detailed discussion of its phenomenology. Several variants of the Zee model exist in the literature. The minimal Zee-Wolfenstein model [105] with a Z2 symmetry to forbid tree-level FCNCs has been excluded by neutrino oscillation data [155, 156], while the general version with both Higgs doublets coupling to the leptons is allowed [ 91, 157]. Imposing a Z4 symmetry [158] allows to explain neutrino data and forbid tree-level FCNCs in the quark sector. Previously in Aranda et al. [159] a flavor-dependent Z4 symmetry was used to obtain specific flavor structures in the quark and lepton sector. A supersymmetric version of the Zee model has been proposed in Leontaris and Tamvakis [160], Haba et al. [161], Cheung and Kong [162], and Kanemura et al. [163]. Its embedding into a grand unified theory has been discussed in Zee [104], Tamvakis and Vergados [164] and Fileviez Perez and Murgui [165], and in models with extra dimensions in Chang and Ng [166] and Chang et al. [167].
Other flavor symmetries beyond Z4 have been studied in Babu and Mohapatra [168, 169], Koide and Ghosal [170], Kitabayashi and Yasue, [171], Adhikary et al. [172], Fukuyama et al. [173], Aranda et al. [174, 175], and Okamoto and Yasue [176] studied the Zee model when the third generation transforms under a separate SU(2) × U(1) group. Babu and Mohapatra [168, 169] studied large transition magnetic moments of the electron neutrino, which was an early, now excluded, explanation for the solar neutrino anomaly. General group theoretic considerations about the possible particle content in the loop are discussed in Ma [99].
Models with multiple leptoquarks, which mix among each other, also generate neutrino mass via topology T1-ii. We discuss this possibility in more detail in section 5.4.1. They induce the operator O3 if the leptoquark couples down-type quarks to neutrinos. Well-studied examples of leptoquarks are down-type squarks in R-parity violating SUSY models, which generate neutrino masses, as was first demonstrated in Hall and Suzuki [177]. Specific examples with multiple leptoquarks which mix with each other were discussed in Nieves [178], Chua et al. [179], Mahanta [180], Aristizabal Sierra et al. [181], Helo et al. [182], Päs and Schumacher [183], Cheung et al. [184], Doršner et al. [185]. There are several supersymmetric models [179, 186–190] which generate neutrino mass via different down-type quarks or charged leptons in the loop and consequently induce the operators O3 and O2, respectively. Finally, there are models with only heavy particles in the loop such as the inert Zee model [191] or supersymmetric models with R-parity conservation [192, 193].
T1-iii
This topology was first proposed in Ma [99] and it naturally appears in the supersymmetrized version of the scotogenic model [146, 147, 194–203] together with topology T1-i. The topology can be used to implement the radiative inverse seesaw [204–206], which resembles the structure of the inverse seesaw [207, 208]. This model has been extended by a softly-broken non-Abelian flavor symmetry group [209–211] in order to explain the flavor structure in the lepton sector. The SUSY model in Ma and Sarkar [212] generates neutrino mass via sneutrinos and neutralinos in the loop. This mechanism was first pointed out in Hirsch et al. [213]. In the realization of Ma and Sarkar [212], the masses of the real and imaginary parts of the sneutrinos are split by the VEV of a scalar triplet, which only couples to the sneutrinos via a soft-breaking term and thus does not induce the ordinary type-II seesaw. Similarly it has been used in a model with vector-like down-type quarks [214, 215], which requires mixing of the SM quarks with the new vector-like quarks. This model leads to the operator O3.
3.1.2. 1-Loop Seesaws and Soft-Breaking Terms
For completeness we also include the two possible 1-loop seesaw topologies T4-2-i and T4-3-i which have been identified in Bonnet et al. [100]. Topology T4-2-i always involves a electroweak scalar triplet like in the type-II seesaw mechanism and topology T4-3-i contains an electroweak singlet or triplet fermion like in the type-I or type-III seesaw mechanism, respectively. Based on our knowledge, there are currently no models based on topologies T4-2-i and T4-3-i in the literature.
Finally, although the topology T4-2-ii shown in Figure 6C has been discarded in Bonnet et al. [100], because it is generally accompanied by the tree-level type-II seesaw mechanism, there are three models based on this topology [216–218]. They break lepton number softly by a dimension-2 term and thus there is no tree-level contribution by forbidding the “hard-breaking” dimension-4 terms which are required for the type-II seesaw mechanism. Similar constructions may be possible for other topologies and lead to new interesting models.
3.1.3. Additional VEV Insertions
The above discussed classification technically does not cover models with additional scalar fields, which contribute to neutrino mass via their vacuum expectation value in contrast to being a propagating degree of freedom in the loop. Inspired by the above classification, we similarly classify these new models according to the topologies in Figure 3 by disregarding the additional VEV insertions.
T1-i
There are several radiative neutrino mass models which are based on a U(1) symmetry, which is commonly broken to a remnant Z2 symmetry: there are models based on a global Peccei-Quinn U(1)PQ symmetry [219, 220], which connects neutrino mass to the strong CP problem, a local U(1)B−L symmetry [221–223] and local dark U(1) symmetry [224–226]. The authors of Ho et al. [221] systematically study radiative neutrino mass generation at 1-loop (but also 2-, and 3-loop) level based on a gauged U(1)B−L symmetry, which is broken to a ZN symmetry. The models in Chang and Wong [224], Dasgupta et al. [219], Lindner et al. [225], Adhikari et al. [227], Kownacki and Ma [226] also have a contribution to neutrino mass at 2-loop order based on a Cheng-Li-Babu-Zee (CLBZ) topology.
T1-ii
All of the models with additional VEV insertions rely on the breaking of a symmetry: left–right symmetry [228–230], a more general SU(2)1×SU(2)2 symmetry [231], a flavor symmetry [232–234], U(1)B−L [235], and dilation symmetry [236]. All these models lead to the operator O2. Foot et al. [236] discusses in particular the following two 1-loop models: the scale-invariant Zee model and a scale-invariant model with leptoquarks which induces O3. Finally, there is the inert Zee model with a flavor symmetry [237, 238].
T1-iii
The model in Nomura et al. [239] relies on the VEVs of a scalar triplet and a septuplet which are subject to strong constraints from electroweak precision tests in particular from the T (or ρ) parameter. The minimization of the potential is not discussed, but the VEVs can in principle be introduced via the linear term in the scalar potential, which leads to the operator at 2-loop level, because the linear term for the septuplet is only induced at the 1-loop level. The topology can also be generated by new heavy lepton-like doublets and sterile fermions, which are charged under a new gauged dark U(1) in addition to a Z2 symmetry [240].
T3
There are several variants of the scotogenic model with additional VEV insertions. Most of them are based on an extended symmetry sector, such as a discrete Z3 instead of a Z2 symmetry [241, 242], dilation symmetry [236, 243–245], a gauged U(1)B−L [246–250], global U(1)B−L [251], a general gauged U(1) [252–254], continuous U(1) flavor symmetry [255, 256], a discrete flavor symmetry based on D6 [257], A4 [258–262] or S4 [263], and different LR symmetric models without a bidoublet [264]. Apart from additional symmetries, the mixing of the fermionic singlet with a fermionic triplet in the loop requires the VEV of an electroweak triplet with vanishing hypercharge [265–267]. Finally, the two models discussed in Okada and Yagyu [268, 269] rely on a similar topology as the scotogenic model, but with triplet VEVs instead of electroweak doublet VEVs.
T4-2-i
Based on our knowledge, there are currently no models based on topology T4-2-i in the literature.
T4-3-i
Wang and Han [270] proposed a model which reduces to topology T4-3-i after breaking of the U(1)B−L symmetry. As the Majorana mass term for the fermionic pure singlet is not introduced, there is no inverse seesaw contribution to neutrino mass after the breaking of the U(1)B−L symmetry and neutrino masses are generated at 1-loop level.
T4-1-i/ii
These types of models contain a triplet scalar which couples to the lepton doublet as per the tree-level type-II seesaw. However, the neutral component of the triplet scalar gets an induced VEV at 1-loop and thus generates neutrino masses effectively at 1-loop. The model in Nomura and Okada [271] is based on topology T4-1-i shown in Figure 6A, which is finite due to additional VEV insertions on the fermion line. The model in Kanemura and Sugiyama [272] is based on topology T4-1-ii shown in Figure 6B. The tree-level contribution is forbidden by a discrete symmetry and renormalizability of the theory. However, at loop-level neutrino mass is generated by a dimension-7 operator with two additional SM singlet fields s1. Note in both cases an extra symmetry such as U(1)B−L or a discrete symmetry and lepton number is needed to forbid the contribution from the tree-level type-II seesaw. Topology T4-1-ii is also induced in the SUSY model in Figueiredo [273] and Franceschini and Mohapatra [201] after the breaking of SUSY and the discrete Z4 symmetry.
3.1.4. Higher-Dimensional Weinberg-Like Operators
Apart from UV completions of the Weinberg operator, there are a few models which induce one of the higher dimensional operators with additional Higgs doublets at 1-loop level.
Dimension-7 ()
The first model which induced the dimension-7 operator at 1-loop level in a two Higgs doublet model was proposed in Kanemura and Ota [274]. It was realized using at most adjoint representations and an additional softly-broken Z5 symmetry and an exact Z2 symmetry and thus allows to use the topologies T12 (Figure 4E) and T31 (Figure 7), which would otherwise be accompanied by the dimension-5 operator O1. If the Zee model is extended by a triplet Majoron [275, 276] the operator is induced at tree-level. After closing the loop of charged leptons via topology T3 (Figure 4B), the dimension-7 operator is obtained. Cepedello et al. [101] systematically studies the possible 1-loop topologies of and explicitly shows several models: the only genuine model without representations beyond the adjoint of SU(2) is based on topology T11, while the other models use quadruplets or even larger representations to realize the other genuine topologies.
Dimension-9 ()
In Law and McDonald [277] and Baldes et al. [278] neutrino masses are generated via a radiative inverse seesaw. The mass of the additional SM singlets is induced at tree-level and then first transmitted to the neutral components of new electroweak doublets via a 1-loop diagram, before it induces neutrino mass via the seesaw. It leads to the dimension-9 operator via the four VEV insertions on the scalar line of the 1-loop diagram. There is also a 2-loop contribution, which may dominate neutrino mass depending on the masses of the new particles.
Dimension-11 ()
The model proposed in Aranda and Peinado [279] relies on the VEV of a 7-plet χ, which is induced via a non-renormalizable coupling, linear in χ, to six electroweak Higgs doublets.
As can be seen from the discussion above, in order to generate Weinberg-like effective operators at dimension larger than five, typically extra symmetries (in some cases large discrete symmetries), new large representations, a large number of fields or a combination of all the previous need to be invoked. This makes the model-building of such scenarios much more involved than for the case of the Weinberg operator.
3.1.5. Other 1-Loop Models
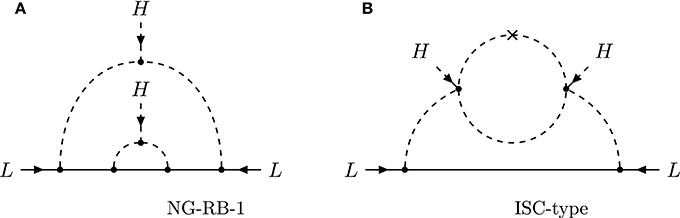
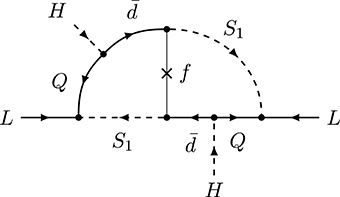
Apart from the models in the general classification [100], it is possible to generate neutrino mass via a radiative inverse seesaw mechanism shown in Figure 8 at 1-loop order, which has been proposed in Ahriche [280]. Tree-level contributions are forbidden by a softly-broken Z4 symmetry. The soft-breaking is indicated by the cross on the scalar line. Note the cross on the fermion line in the loop denotes a Majorana mass term, while the other two denote Dirac mass terms.
Finally we would like to comment on one further possibility to generate neutrino mass at 1-loop order. If the neutrino masses vanish at tree-level in type-I seesaw model, then 1-loop electroweak corrections give the leading contribution [281]:14 non-zero neutrino masses are induced by finite 1-loop diagrams with either a Z-boson or a Higgs boson. The UV divergent part of the 1-loop corrections to the Weinberg operator cancel due to the absence of a tree-level contribution. This has been explicitly shown in Pilaftsis [281] with a calculation in the mass basis. In terms of the classification of 1-loop topologies, these diagrams correspond to the topologies T3 and T1-iii for the Higgs and Z-boson in the loop, respectively. The vanishing of the tree-level contribution can be achieved using a specific texture in the seesaw model with SM singlet fermions S [285] in addition to the right-handed neutrinos N
in the basis (ν, N, S). In the limit μS → 0 the tree-level contribution to the active neutrinos exactly vanishes and neutrino masses are generated at 1-loop order. This construction has been denoted minimal radiative inverse seesaw [285].
This texture can be obtained by imposing a U(1) symmetry under which S is charged. After it is spontaneously broken by the VEV of a SM singlet scalar η, the Yukawa interaction SNη generates the term MN without generating a Majorana mass term μS for the fermionic singlets S or a coupling of S to the SM lepton doublets L at the renormalizable level.
3.2. 2-Loop Majorana Neutrino Mass Models
The possible 2-loop topologies of the Weinberg operator have been discussed in Aristizabal Sierra [102]. We will closely follow this classification. All possible genuine 2-loop topologies are shown in Figure 5. Analytic expressions for the 2-loop diagrams are summarized in the appendix of Aristizabal Sierra [102] and are based on the results in McDonald and McKellar [286] and Angel et al. [287]. Most topologies can be considered as variations of a few 2-loop models discussed in the literature: (i) variations of the Cheng-Li-Babu-Zee (CLBZ) topology [76, 288, 289], (ii) the Petcov-Toshev-Babu-Ma (PTBM) topology [290–292], and the so-called rainbow (RB) topology [102]. In the following we will further distinguish between fermion and scalar lines and show in Figures 9, 10B the relevant diagrams of genuine topologies and the internal-scalar-correction (ISC)-type topology which are used in the following discussion. The first two subsections discuss models based on genuine topologies, the third one models based on non-genuine topologies, and the last one models based on multiple topologies.
3.2.1. Genuine 2-Loop Topologies
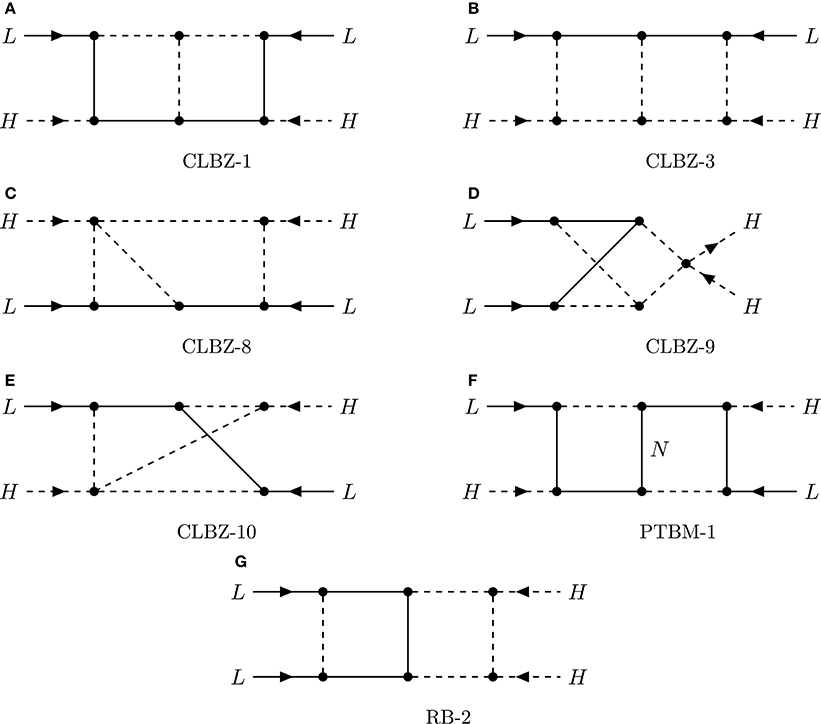
The relevant diagrams for the genuine topologies are shown in Figure 9.
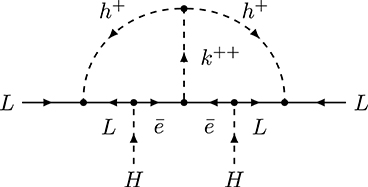
CLBZ-1
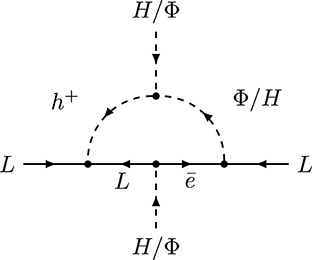
The topology CLBZ-1 is displayed in Figure 9A. The first model was independently proposed and studied by Zee [288] and Babu [289], and is commonly called Zee-Babu model (See a more detailed discussion in section 5.1.2). It also leads to the operator O9. A scale-invariant version of the model has been proposed in Foot et al. [236]. It has been extended to include a softly-broken continuous Le − Lμ − Lτ flavor symmetry [293, 294] or discrete flavor symmetry [295], and has been embedded in a SUSY model [296, 297]. The same topology has also been used for models with quarks instead of charged leptons inside the loop. They rely on the introduction of a leptoquark and a diquark [298–300] and lead to operator O11. Similarly, there is a version without light fields in the loop [221, 301–303]. The models in Ho et al. [221] are part of a systematic study of models based on a gauged U(1)B−L which is broken to a ZN symmetry.
CLBZ-3
Topology CLBZ-3 is depicted in Figure 9B and only differs from topology CLBZ-1 in the way how the Higgs VEVs are attached to the loop diagram: Topology CLBZ-3 has the Higgs VEVs attached to two of the scalar lines, while they are attached to the internal fermion lines for CLBZ-1. Cheng and Li [76] listed several possible neutrino mass models, including the first 2-loop model which was based on topology CLBZ-3 with an effective scalar coupling. A possible UV completion was presented with an electroweak quintuplet scalar. This UV completion leads to the operator (with an additional VEV insertion from an electroweak quintuplet scalar). All models [221, 304–307] based on topology CLBZ-3 only contain heavy fields.
CLBZ-8
The topology is shown in Figure 9C. Variants of the Zee-Babu model have also been embedded in grand unified theories [308]. In case of SU(5), there is a 5-plet of matter particles in the loop which leads to the effective operators O9 and O11.
CLBZ-9
Topology CLBZ-9 which is displayed in Figure 9D has been utilized in a model with two diquarks [215].
CLBZ-10
The same paper also introduces another model with two diquarks which is based on topology CLBZ-10, shown in Figure 9E.
PTBM-1
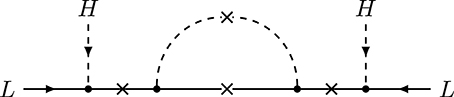
The first model to utilize the topology Figure 9F, although in presence of a tree-level contribution, was presented in Petcov and Toshev [290], Babu and Ma [291], Branco et al. [292] and Babu and Ma [309]. Neutrino mass receives a 2-loop correction via the exchange of two W-bosons as shown in Figure 9F. This idea has been recently revived and experimentally excluded in the context of extra chiral generations [310], but the mechanism can still work in the case of vector-like leptons. Lepton number is violated by the SM singlet Majorana fermion N in the center of the diagram and thus there is a tree-level contribution in addition to the 2-loop contribution to neutrino mass. Lepton number can equally well be broken by the type-III seesaw, when the fermionic singlet is replaced by a fermionic triplet [311]. The model in Babu and Julio [312] has one of the W-bosons replaced by scalar leptoquarks and it is consequently not accompanied by a tree-level contribution. The 1-loop contribution induced by the mixing of the leptoquarks vanishes, because the left-chiral coupling of one of the leptoquarks is switched off [313]. All models with W bosons will lead to operators with derivatives in the classification according to ΔL = 2 operators. Finally, Angel et al. [287] proposed a model with a scalar leptoquark and colored octet fermion.
3.2.2. Genuine Topologies with Additional VEV Insertions
Similar to the 1-loop models, we also categorize the models with additional VEV insertions following the classification of Aristizabal Sierra et al. [102].
CLBZ-1
There are several models based on topology CLBZ-1 (shown in Figure 9A), which all induce the operator O9. Bamba et al. [314] discusses a possible connection of neutrino mass with dark energy. Porto and Zee [315] proposed a model with one electroweak Higgs doublet field per lepton generation, an extension of the so-called private Higgs scenario. Finally, Lindner et al. [316] discusses an extension of the Zee-Babu model by a global U(1)B−L symmetry, which is spontaneously broken to a Z2 subgroup. This implies the existence of a Majoron and a DM candidate.
CLBZ-3
Chang and Keung [317] proposed a variant of the Zee-Babu model with an additional triplet Majoron, which is based on topology CLBZ-3 which is displayed in Figure 9B.
CLBZ-9
The topology CLBZ-9 is depicted in Figure 9D. The model in Guo [318] is based on a dark U(1) symmetry with only heavy fields in the loop.
RB-2
The model proposed in Kajiyama et al. [319] is based on U(1)B−L, which is broken to Z2. Apart from the VEV breaking U(1)B−L, neutrino mass is generated by a diagram with topology RB-2 which is shown in Figure 9G.
3.2.3. Non-Genuine Topologies
The relevant non-genuine 2-loop topologies are shown in Figure 10.
NG-RB-1
The non-genuine topology NG-RB-1 (Figure 10A) is generated in Nomura and Okada [320]. There are no lower-order contributions due to the U(1) symmetry, which is broken to Z2 as in the above-mentioned models.
Other non-genuine topologies
There are several models which generate vertices or masses of particles at loop level. The models in Aoki et al. [321, 322] realize an ISC-type topology which is shown in Figure 10B by softly breaking lepton number with a dimension-2 scalar mass insertion in the internal scalar loop. Similarly, Ma and Sarkar [323] discusses a supersymmetric model where the scalar-quartic coupling is induced after supersymmetry is softly broken and thus an ISC-type topology is induced for neutrino mass. The models in Kajiyama et al. [324] and Baek et al. [325] have only heavy particles in the loop and can be considered as a 1-loop scotogenic model, where the Majorana mass term for the SM singlet fermions is generated at 1-loop order. Thus, neutrino mass is effectively generated at 2-loop order. It can be considered as an RB-type topology. In contrast to the topology RB-2, the SM Higgs fields are attached to the outer scalar line (the one on the left in Figure 9G). Both models break U(1)B−L to a discrete ZN subgroup. Ghosh et al. [326] proposes another model based on an RB-type topology, where the Higgs fields couple to the fermions in the outer loop. The model features a stable dark matter candidate due to an imposed Z2 symmetry. Moreover, neutrino mass relies on the spontaneous breaking of an extended lepton number symmetry to a discrete Z2 subgroup. The models in Ma [327], Nasri and Moussa [328], Chao [329], Ma and Wudka [330] and Nomura and Okada [331] realize the type-I seesaw by generating the Dirac mass terms at 1-loop order, and the model in Okada and Orikasa [332] generates a radiative type-II seesaw contribution by generating the triplet VEV at 1-loop level, and thus the Weinberg operator at 2-loop level. Finally, Witten [333] and Arbelàez Rodríguez et al. [334] firstly generate the right-handed neutrino mass at 2-loop level in the context of a GUT, which induces the active neutrino mass via the usual seesaw mechanism. Similarly Law and McDonald [335] and Baldes et al. [278] realize a radiative inverse seesaw. The mass of additional singlets is generated at 2-loop order. The model is based on an additional gauged U(1) symmetry (which is spontaneously broken to its Z2 subgroup) to forbid the generation of neutrino mass at tree-level via the seesaw mechanism. The model can explain the matter-antimatter asymmetry of the universe, but not account for the dark matter abundance [278].
3.2.4. Models Based on Several Topologies
Several models in the literature [144, 221, 336–351] are based on multiple 2-loop topologies. We highlight three examples. Megrelidze and Tavartkiladze [144] proposed to generate neutrino mass via lepton-number-violating soft supersymmetry-breaking terms using the so-called type-II-B soft seesaw with electroweak triplet superfields. Integrating out the scalar components of the electroweak triplets leads to the dimension-5 lepton-number-violating term . Neutrino mass is generated at 2-loop via a diagram based on topology CLBZ-1 and diagrams which generate the couplings of the scalar component of the electroweak triplet superfield to two lepton doublets L on the one hand and the two electroweak Higgs doublets Hu on the other hand at the 1-loop level. Another interesting class of models are based on internal electroweak gauge bosons, which are based on CLBZ-type topologies and discussed in Chen et al. [345, 346], del Aguila et al. [347], Chen et al. [348], del Aguila et al. [349], King et al. [350] and Geng and Tsai [351]. All of them introduce a doubly-charged scalar and a coupling of the doubly-charged scalar to two W-bosons, which can be achieved via a mixing of the doubly-charged scalar with the doubly-charged scalar in an electroweak triplet scalar. Neutrino mass is typically generated via topologies CLBZ-1 and CLBZ-3 and induces the operator
This possibility is further discussed in section 3.4. Gauge bosons similarly can play an important role in the generation of neutrino mass in extended technicolor (ETC) models as discussed in Appelquist and Shrock [352, 353] and Appelquist et al. [354]. These models contain many SM singlet fermions and only a few elements of the neutral fermion mass matrix are directly generated by condensates, while many elements are generated at 1-loop (or higher loop) level via loop diagrams with ETC gauge bosons. In particular the relevant Dirac mass terms relevant for the active neutrino masses are generated at 1-loop level and thus neutrino mass is effectively generated at 2-loop (or even higher loop) level.
3.3. 3-Loop Majorana Neutrino Mass Models
Unlike 1-loop and 2-loop topologies, there is no systematic classification of all 3-loop topologies. Thus, we restrict ourselves to the existing 3-loop models in the literature and do not consider other topologies or different fermion flow for the given topologies. Most of the existing 3-loop models can be categorized in four basic types of diagrams shown in Figure 11 where we do not specify the Higgs insertions. The remaining models are either based on a combination of the listed topologies or the combination of a loop-induced vertex at 1- or 2-loop inside a loop diagram.
3.3.1. The KNT Models
The first 3-loop radiative neutrino mass model was proposed in Krauss et al. [355] with the topology shown in Figure 11A by Krauss, Nasri and Trodden (KNT) and it leads to the operator O9. We refer to radiative neutrino mass models sharing the same topology as KNT models and discuss them in more detail in section 5.2. A systematic study with several different variants can be found in Chen et al. [356]. The models of Chen et al. [357], Ahriche and Nasri [358], Ahriche et al. [359], Chen et al. [356], Ahriche et al. [360–364] also generate the operator O9, the models of Chen et al. [356], Nomura et al. [365] and Cheung et al. [366] the operator O11 with down-type quarks, while the models in Okada and Okada [367], Chen et al. [356], Okada and Yagyu [368] and Cheung et al. [369] only have new heavy states in the loop.
3.3.2. AKS-Type Models
Neutrino mass can also arise at 3-loop order from the diagram shown in Figure 11C. The first model of such topology was proposed by Aoki, Kanemura, and Seto (AKS) in Aoki et al. [370] and is based on the operator with two Higgs doublets Hi. We will refer to it as the AKS model and more generally to models based on this topology as AKS-type models. It contains a second Higgs doublet and several SU(2)L singlets. The exotic particles can also be all electroweak singlets [221, 371]. The model in Gu [371] leads to the operator O9. Other variants include colored exotic particles such as leptoquarks [356, 372, 373], which generate the operators O11, 12, or electroweak multiplets [356, 374, 375] generating the operators O1,9. Note cross diagrams may be allowed in specific models.
3.3.3. Cocktail Models
The third class of models are based on the two cocktail diagrams shown in Figures 11B,D. The name for the diagram has been coined by Gustafsson et al. [376], which proposed a 3-loop model with two W-bosons based on topology Figure 11B and consequently generated the operator , which are discussed in more detail in section 3.4. The same model has also been studied in Geng et al. [377]. The models in Hatanaka et al. [378] and Alcaide et al.[379] are based on the same topology, but with W bosons replaced by scalars. While Alcaide et al. [379] induces operator , the model of Hatanaka et al. [378] leads to operator O9. Finally, the fermionic cocktail topology Figure 11D is used in the models of Nishiwaki et al. [380], and Kanemura et al. [381], both of which generate operator O9.
Apart from the three classes of models, there are a few models which do not uniquely fit in any of the three classes. The model in Jin et al. [382] is based on topologies Figures 11A,C with two W-bosons and thus generates the operator . Nomura et al. [383] generates the mass of new exotic fermions at 2-loop level via a CLBZ-type diagram, which in turn generate neutrino mass at 1-loop. Geng and Huang [384] studies a 2-loop model based on the operator O8, which itself is generated at 1-loop order.
Most of the 3-loop models need to impose extra discrete symmetries such as Z2 or a continuous U(1) symmetry to forbid lower-loop or tree-level contributions, unless accidental symmetries exist and thus partly require other VEV insertions. One example is to employ higher dimensional representation of SU(2)L [362], e.g., septuplet, in the spirit of minimal dark matter [385, 386] such that undesirable couplings are forbidden by the SM gauge group alone. Due to the existence of the extra imposed or accidental symmetries, 3-loop models serve as a natural playground for DM physics.
3.4. Models with Gauge Bosons
The first model [290–292] with gauge bosons in the loop uses the topology PTBM-1 and leads to operators built from two lepton doublets including covariant derivatives. However, it also has a tree-level contribution, while models based on operators with right-handed charged leptons are genuine radiative neutrino mass models.
In del Aguila [107] two LNV effective operators with gauge bosons, i.e., present in covariant derivatives, were considered, which allowed to have neutrinoless double beta decay rates generated at tree level thanks to new couplings to the SM leptons15. Interestingly, depending on the chirality of the outgoing leptons in 0νββ, there are two new operators (beyond the standard contribution from the Weinberg operator which involves left-handed electrons). For left–right (LR) chiralities of the outgoing electrons, there is a dimension-7 operator:16
For right-right (RR) chiralities, there is a dimension-9 operator as define in Equation (34). After electroweak symmetry breaking, these operators generate the relevant vertices for 0νββ at tree level: and , respectively. The contributions of and to 0νββ are depicted in Figures 12B,C respectively, where the red point denotes the effective operator insertion.
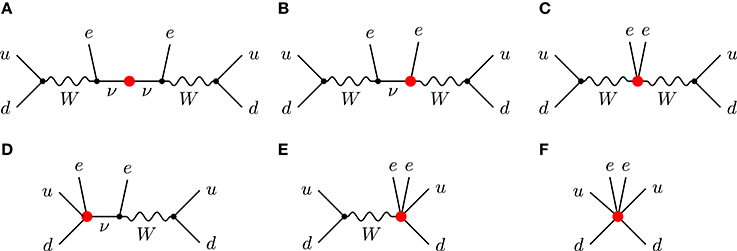
Figure 12. Possible contributions to 0νββ. The red dot indicates the ΔL = 2 effective vertex. Figure reproduced from del Aguila [349].
The lowest order contributions from these operators to neutrino masses occur at 1- and 2-loop orders, respectively, via the diagrams of Figure 13. The dominant contributions come from matching (see also Babu and Leung [85], de Gouvêa et al. [87], Angel et al. [90] and de Gouvêa et al.[88] for estimates of the matching contributions to neutrino masses of LNV operators), which using dimensional analysis can be estimated to be given by del Aguila et al. [107]:
for and by
for . Notice that the appearance of the chirality-flipping charged lepton masses is expected in order to violate lepton number in the LH neutrinos, which naturally generates textures in the neutrino mass matrix.

Figure 13. Lowest order contributions of (left, at 1-loop order) and (right, at 2-loop order) to neutrino masses. The red dot indicates the ΔL = 2 effective vertex. Figure reproduced following del Aguila [107].
Possible tree-level UV completions which have new contributions to 0νββ at tree level were outlined in del Aguila et al. [107]. See also del Aguila [349], which provides a summary of two examples of models generating and , respectively. The UV model of [347] generates 0νββ at tree level, while neutrino masses are generated as expected at 2-loop order. It includes a doubly-charged singlet, a Y = 1 triplet scalar and a real singlet. In order to prevent tree-level neutrino masses as in type-II seesaw via the latter field, a discrete Z2 symmetry, which was spontaneously broken by the VEV of the singlet, was added. Recently a variation has been studied, in which the Z2 symmetry is exact, such that there is a good dark matter candidate, which is a mixture of singlet and triplet [379]. In this case, the contributions to 0νββ and to neutrino masses are further shifted by one extra loop, i.e., they are generated at 1- and 3-loop orders, respectively. Gustafsson et al. [376, 387] studied also a specific model with a dark matter candidate, named the cocktail model, which generated at 1-loop order, i.e., 0νββ at 1-loop order and therefore neutrino masses at 3-loop order. It includes a singly-charged singlet, a doubly-charged singlet and a Y = 1 scalar doublet, together with a discrete symmetry Z2 under which all the new fields except the doubly-charged are odd. Other models generating were presented in Chen et al. [345, 346, 348], King et al. [350], Geng and Tsai [351], and Liu and Gu [388].
3.5. Radiative Dirac Neutrino Mass Models
Although Majorana neutrinos are the main focus of research, Dirac neutrinos are a viable possibility to explain neutrino mass. It is noteworthy that the first radiative neutrino mass model [389] was based on Dirac neutrinos. In recent years, there has been an increased interest in Dirac neutrinos and, in particular, there are a few systematic studies on the generation of Dirac neutrino mass beyond the simple Yukawa interaction, which include both tree-level and loop-level realizations, besides several newly-proposed radiative Dirac neutrino mass models, which we will outline below.
Ma and Popov [56] and Wang and Han [60] performed a study of Dirac neutrino mass according to topology at tree-level and 1-loop level. There are only two possible one-particle-irreducible topologies for the Dirac Yukawa coupling at 1-loop, which are shown in Figure 14. The simplest radiative Dirac neutrino mass models are based on a softly-broken Z2 symmetry, which is required to forbid the tree-level contribution, and generate the topologies in Figure 14. Wang et al. [390] studied scotogenic-type models with a U(1)B−L symmetry at 1- and 2-loop order. Finally, Kanemura et al. [391] takes a model-independent approach and discusses the possible flavor structures of the induced Dirac mass term under a number of constraints: The fermion line only contains leptons and each lepton type can appear at most once.
1-Loop Models
Many of the proposed 1-loop models are realized in a left–right symmetric context without SU(2) triplet scalars [56, 389, 392–397]. Rajpoot [398] attempted the generation of Dirac neutrino masses in the context of a model where hypercharge emerges as diagonal subgroup of U(1)L×U(1)R. To our knowledge the generation of Dirac neutrino mass at 1-loop level with a softly broken Z2 was first suggested in Kanemura et al. [399] based on topology Figure 14B. Farzan and Ma [400] implements the first scotogenic model of Dirac neutrino mass by using a dark Z2 and softly-broken Z2. Both of these possibilities have been studied in more detail in the systematic studies outlined above. Another way to explain the smallness of Dirac neutrino mass is via a small loop-induced VEV [401]. Finally, Borah and Dasgupta [402] discusses a left–right symmetric model with pseudo-Dirac neutrinos. The tree-level Majorana mass terms are not allowed, because the bidoublet is absent and the coupling of the left-handed triplet to leptons is forbidden by a discrete symmetry.
2-Loop Models
Two explicit models of Dirac neutrino mass have been discussed in Bonilla et al. [403] and Kanemura et al. [404] apart from the general classification [390]. They are both based on a U(1) symmetry, a dark U(1) and lepton number, respectively. The U(1) symmetry is broken to a discrete subgroup and thus both models feature a stable dark matter candidate.
3-Loop Model
Finally, a Dirac neutrino mass term can also be induced via a global chiral anomaly term [405]. The five-dimensional anomaly term with the pseudo-scalar a and the (dual) field strength tensor Fμν () is induced at 1-loop level and leads to a Dirac mass term at 2-loop order, being effectively a 3-loop contribution.
3.6. 331 Models
Another interesting class of models is based on the extended gauge group SU(3)c × SU(3)L × U(1)X. The SM gauge group can be embedded in several different ways and is determined by how the hypercharge generator is related to the generator T8 of SU(3)L and the generator X of U(1)X,
where β is a continuous parameter. In addition to one radiative Dirac neutrino mass model [406], several radiative Majorana neutrino mass models have been proposed at 1-loop level [407–423], 2-loop order [424–429], 3-loop order [430], and even at 4-loop order [98]. As lepton number violation (LNV) in 331 models and in particular neutrino mass generation has been discussed in a recent review [431], we refer the interested reader to it for a detailed discussion. However, we highlight one model based on gauged lepton number violation [419–421], which generates neutrino mass via lepton number violation in the 1-loop diagram shown in Figure 15 with the SU(3)L×U(1)X gauge bosons, where Hi denotes the SM Higgs doublets, 〈1〉χ the VEV in the third component of SU(3)L and Nc the third partner of νL in the triplet of SU(3)L. Note that lepton number is broken by the mixing of the gauge bosons in the vertex at the top of the diagram.
4. Phenomenology
In this section we revisit the most relevant phenomenological implications of radiative neutrino mass models. The possible signals are very model dependent, as each radiative model has its own particularities that should be studied on a case-by-case basis. However, in the following we will try to discuss generic predictions of these models, making use of simplified scenarios and/or of effective operators, and referring to particular examples when necessary.
4.1. Universality Violations and Non-standard Interactions
In the SM, leptonic decays mediated by gauge interactions are universal. Several scenarios of physics beyond the SM have universality violations, that is, decays into different families (up to phase space-factors) are no longer identical17. These may or may not be related to neutrino masses, as lepton number is not violated in these interactions. Indeed, for instance a two Higgs doublet model with general Yukawa interactions breaks universality, irrespective of neutrino masses. In tree-level neutrino mass models, there are also violations of universality, mediated by the (singly) charged scalar boson in the type-II seesaw model, or due to the non-unitarity of the leptonic mixing matrix in type-I and type-III seesaw models when the extra neutral fermions are heavy [432, 433].
In some of the radiative models there can be violations of universality. One illustrative example of this case is due to the presence of a singly-charged singlet h with mass (as in the Zee and Zee-Babu models, see section 5.1). The relevant interaction is , where f is an antisymmetric matrix in flavor space and . Integrating out the singlet, one obtains the following dimension 6 effective operator [434]
One can see that this operator involves left-handed leptons, like charged currents in the SM18. This implies that it interferes constructively with the W boson, modifying among others the muon decay rate [435]. Therefore, the Fermi constant which is extracted from muon decay in the SM, , and that in a model with a singly-charged singlet, , are different, i.e., . Their ratio obeys to leading order in f:
The new Fermi constant is subject to different constraints. For example, from measurements of the unitarity of the CKM matrix, as the Fermi constant extracted from hadronic decays should be equivalent to that from leptonic decays, we can bound feμ:
Also leptonic decays which in the SM are mediated by charged-current interactions are not universal anymore. The ratio of leptonic decays among the different generations can be tested via the effective couplings given by
All these lead to strong limits on the f couplings depending on the mass on the singlet [95].
Furthermore, the new singly-charged scalar via the effective operator in Equation (39) induces neutrino interactions that cannot be described by W-boson exchange and are termed non-standard neutrino interactions (NSIs). Equation (39) is usually rewritten after a Fierz identity as
where are the NSI parameters given by
These could be in principle probed at neutrino oscillation experiments. However, typically whenever NSIs are induced, lepton flavor violating (LFV) processes are also generated, which are subject to stronger constraints. This is particularly the case for the four-lepton dimension 6 operators, due to gauge invariance. Models with large NSI are difficult to construct, and typically involve light mediators [436, 437]. We refer the reader to Davidson et al. [438], Ibarra et al. [439], Gavela et al. [440], Biggio et al. [441, 442], Antusch et al. [443] and Ohlsson [444] for studies of NSIs and their theoretical constraints.
4.2. Lepton Flavor Violation
One of the common predictions shared by most neutrino mass models (radiative or not) is the existence of LFV processes involving charged leptons with observable rates in some cases. Indeed, neutrino oscillations imply that lepton flavors are violated in neutrino interactions, and as in the SM neutrinos come in SU(2) doublets together with the charged leptons, also violations of lepton flavors involving the latter are expected. Which is the most constraining LFV observable is, however, a model-dependent question. It is thus convenient to use a parametrization that allows for a model-independent description of these processes. For each of the models one can then compute the relevant coefficients and apply the following formalism. We follow the notation and conventions of Porod et al. [445]19.
The general LFV Lagrangian can be written as
The first term contains the ℓ−ℓ−γ interaction Lagrangian, given by
where e is the electric charge, q is the photon momentum, are the standard chirality projectors and the indices {α, β} denote the lepton flavors. The first term in Equation (48) corresponds to the monopole interaction between a photon and a pair of leptons whereas the second is a dipole interaction term. In this parametrization the form factors vanish when the photon is on-shell, i.e., in the limit of q2 → 0. Similarly, the interaction Lagrangians with the Z and Higgs bosons are given by20
where p is the ℓβ 4-momentum, and
with the SM Higgs h. The general 4-lepton interaction Lagrangian can be written as
where in this case the indices {α, β, γ, δ} denote the lepton flavors and we have defined ΓS = 1, ΓV = γμ and ΓT = σμν. It is clear that the Lagrangian in Equation (51) contains all possible terms allowed by Lorentz invariance. Finally, the general 2ℓ2q 4-fermion interaction Lagrangian (at the quark level) can be split in two pieces
where
Here γ denotes the d-quark flavor and we are neglecting the possibility of quark flavor violation, which is beyond the scope of this review 21.
The parametrization used implies that the operators appearing in Equations (51), (53), and (54) have canonical dimension six. Therefore, the Wilson coefficients , and scale as 1/Λ2, where Λ is the new physics energy scale at which they are generated. Note this scale is unrelated to the scale at which lepton number is violated. The same comment applies to the dipole coefficients in Equation (48). In contrast, the rest of the coefficients discussed in this section, , and SL,R, are dimensionless (although their leading new physics contribution appears at order v2/Λ2). If we restrict the discussion to flavor violating coefficients, they all vanish in the SM. Therefore, they encode the effects induced by the new degrees of freedom present in specific models.
It should be noted that all operators in the general LFV Lagrangian in Equations (48–54) break gauge invariance. For instance, they contain new charged lepton interactions, but not the analogous new interactions for the neutrinos, their SU(2)L doublet partners which are partly discussed in the previous subsection. This type of parametrization of LFV effects is correct at energies below the electroweak symmetry breaking scale, but it may miss relevant correlations between operators that are connected by gauge invariance in the underlying new physics theory. See for instance Pruna and Signer [450] for a discussion of LFV in terms of gauge-invariant operators.
We now proceed to discuss the LFV processes with the most promising experimental perspectives in the near future. We will provide simple analytical expressions in terms of the coefficients of the general LFV Lagrangian and highlight some radiative neutrino mass models with specific features leading to non-standard expectations for these processes. By no means this will cover all the models constrained by these processes, but will serve as a review of the novel LFV scenarios in radiative neutrino mass models.
Note, however, that there are other processes, which may yield stringent constraints in particular models: for instance in models with leptoquarks, the latter can mediate semi-leptonic τ-decays and leptonic meson decays at tree level. The LFV decays have also been investigated in several radiative models, although they typically have very low rates, see for instance Ghosal et al. [451] and Li et al. [452].
4.2.1. ℓα → ℓβγ
The most popular LFV process is ℓα → ℓβγ. There are basically two reasons for this: (1) for many years, the experiments looking for the radiative process μ → eγ have been leading the experimental developments, with the publication of increasingly tighter bounds, and (2) in many models of interest these are the processes where one expects the highest rates. In fact, many phenomenological studies have completely focused on these decays, neglecting other LFV processes that may also be relevant.
The experimental situation in radiative LFV decays is summarized in Table 1. As one can easily see in this table, muon observables have the best experimental limits. This is due to the existing high-intensity muon beams. The current limit for the μ → eγ branching ratio has been obtained by the MEG experiment, BR(μ → eγ) < 4.2·10−13 [453], slightly improving the previous bound also obtained by the same collaboration. This bound is expected to be improved by about one order of magnitude in the MEG-II upgrade [454]. The bounds in τ decays are weaker, with the branching ratios bounded to be below ~ 10−8, and some improvements are expected as well in future B-factories [456].
The decay width for ℓα → ℓβγ is given by Hisano et al. [457]
where α is the fine structure constant. Only the dipole coefficients , defined in Equation (48), contribute to this process. General expressions for these coefficients can be found in Lavoura [458].
The μ → eγ limit is typically the most constraining one in most radiative neutrino mass models. One can usually evade it by adopting specific Yukawa textures that reduce the μ − e flavor-violating entries (see for example Schmidt et al. [459]) or simply by globally reducing the Yukawa couplings by increasing the new physics scale. However, in some cases this is not possible. A simple example of such situation is the scotogenic model [113] with a fermionic dark matter candidate. The singlet fermions in the scotogenic model only couple to the SM particles via the Yukawa couplings. Therefore, these Yukawa couplings must be sizable in order to thermally produce singlet fermions in the early universe in sufficient amounts so as to reproduce the observed DM relic density. This leads to some tension between the DM relic density requirement and the current bounds on LFV processes, although viable regions of the parameter space still exist [459, 460]. In contrast, in other radiative models the tight connection between neutrino masses and LFV implies suppressed ℓα → ℓβγ rates. This is the case of bilinear R-parity violating models [461–463], see section 5.5 for a detailed discussion of this type of supersymmetric neutrino mass models.
4.2.2. ℓα → ℓβℓδℓδ
We now consider the ℓα → ℓβℓδℓδ 3-body decays. One can distinguish three categories: , (with β ≠ δ) and (also with β ≠ δ). These processes have received less attention even though the experimental limits on their branching ratios are of the same order as for the analogous ℓα → ℓβγ decays. We summarize the current experimental bounds and future sensitivities for the ℓα → ℓβℓδℓδ 3-body decays in Table 2. We note that an impressive improvement of four orders of magnitude is expected in the μ → eee branching ratio sensitivity thanks to the Mu3e experiment at PSI [464].
The ℓα → ℓβℓδℓδ decay width receives contributions from several operators of the general LFV Lagrangian. In the case of the first category, , the decay width is given by Porod et al.[445]
in case of the second category, (with β ≠ δ), the expression is given by Abada et al. [467]
whereas for the third category, (with β ≠ δ), the decay width is given by Abada et al. [467]
Here we have defined
The masses of the leptons in the final state have been neglected in Equations (56–58), with the exception of the contributions given by the dipole coefficients , where infrared divergences would otherwise occur.
The dipole coefficients , which contribute to ℓα → ℓβγ, also contribute ℓα → ℓβℓδℓδ. It is easy to see how: the Feynman diagram contributing to ℓα → ℓβγ can always be supplemented with a flavor-conserving ℓδ−ℓδ−γ additional vertex resulting in a diagram contributing to ℓα → ℓβℓδℓδ22. In fact, such diagrams have been shown to be dominant in many models, the most popular example being the Minimal Supersymmetric Standard Model (MSSM). In this case, known as dipole dominance scenario, a simple proportionality between the decays widths of both LFV decays can be established. For example, in the β = δ case this proportionality leads to
which implies , making the radiative decay the most constraining process.
The dipole dominance assumption is present in many works discussing LFV phenomenology. However, it can be easily broken in many radiative neutrino mass models. This can happen in two ways:23
• Due to tree-level LFV: In many radiative neutrino mass models the 4-lepton operators receive contributions at tree-level. The most prominent example of such models is the Zee-Babu model, in which the doubly-charged scalar k++ mediates unsuppressed decays. In such case one can easily find regions of parameter space where , see Herrero-Garcia et al. [95] for a recent study.
• Due to loop-level LFV: Kubo et al. [468], Aristizabal Sierra et al. [469], Suematsu et al. [470], and Adulpravitchai et al. [471] explored the LFV phenomenology of the scotogenic model but only considered μ → eγ. However, this assumption has been shown to be valid only in some regions of the parameter space. In fact, box diagrams contributing to 4-lepton coefficients can actually dominate, dramatically affecting the phenomenology of the scotogenic model [460, 472]. Qualitatively similar results have been found in other variants of the scotogenic model [129, 266]24. In fact, this feature is not specific of the scotogenic model and its variants: one can find other radiative neutrino mass models with loop contributions dominating over the dipole. For instance, Z-penguin contributions have been found to be dominant in the angelic model [90] and RνMDM models [473].
This clearly shows that radiative neutrino mass models typically have a very rich LFV phenomenology with new (sometimes unexpected) patterns and correlations.
4.2.3. μ−e Conversion
The most spectacular improvements in the search for LFV are expected in μ − e conversion experiments. Several projects will begin their operation in the near future, with sensitivities that improve the current bounds by several orders of magnitude. The experimental situation is shown in Table 3.
The conversion rate, normalized to the the muon capture rate Γcapt, is given by Kuno and Okada [479] and Arganda et al. [480]
Z and N are the number of protons and neutrons in the nucleus and Zeff is the effective atomic charge [481]. GF is the Fermi constant, α is the electromagnetic fine structure constant, pe and Ee are the momentum and energy of the electron, mμ is the muon mass and Fp is the nuclear matrix element. and (with X = L, R and K = S, V) are effective couplings at the nucleon level. They can be written in terms of effective couplings at the quark level as
The numerical values of the relevant GK factors can be found in Kuno and Okada [479], Kosmas et al. [482] and Porod et al. [445]. For coherent μ − e conversion in nuclei, only scalar (S) and vector (V) couplings contribute and sizable contributions are expected only from the u, d, s quark flavors. The gXK(q) effective couplings can be written in terms of the Wilson coefficients in Equations (48), (53), and (54) as
where Qq is the quark electric charge (Qd = −1/3, Qu = 2/3) and for d-quarks (u-quarks), with X = L, R and K = S, V.
Radiative neutrino mass models can also be probed by looking for μ − e conversion in nuclei. As already pointed out, the search for this LFV process is going to be intensified in the next few years and, in case no observation is made, it will soon become one of the most constraining observables for this type of models. Similarly to the leptonic LFV 3-body decays discussed above, the dipole coefficients also enter the μ − e conversion rate, potentially dominating it. In this case, one can derive a simple relation [483]
where f(Z, N) is a function of the nucleus ranging from 1.1 to 2.2 for the nuclei of interest. The reader is referred to de Gouvea and Vogel [484] and Crivellin et al. [485] for a discussion on the complementarity of μ → eγ and μ − e conversion in nuclei. One can easily depart from this dipole dominance scenario in radiative neutrino mass models due to the existence of sizable contributions to other LFV operators. For instance, non-dipole contributions have been shown to be potentially large in the scotogenic model in Toma and Vicente [472] and Vicente and Yaguna [460]. The dipole coefficients may also be reduced due to partial cancellations in non-minimal models, see for example Ahriche et al. [360, 361] and Rocha-Moran and Vicente [266]. Finally, as already pointed out in the case of ℓα → ℓβℓδℓδ decays, some radiative neutrino mass models contain new states that mediate LFV processes at tree level. For instance, in R-parity violating models with trilinear terms (discussed in section 5.5), the superpotential terms induce μ − e conversion at tree level [486]. This easily breaks the expectation in Equation (67).
Finally, we point out that the experiments looking for μ → eee and μ − e conversion in nuclei will soon take the lead in the search for LFV. Therefore, even if dipole contributions turn out to be dominant in a given model, μ → eee and μ − e conversion in nuclei might become the most constraining LFV processes in the near future. Prospects illustrating this point for specific radiative neutrino mass models have been presented in Angel et al. [90], Vicente and Yaguna [460], and Klasen et al. [487].
4.2.4.
In many radiative neutrino mass models, there can also be contributions to lepton-flavor violating Higgs (HLFV) decays, like h → τ−μ+, τ−e+ and their CP-conjugates. These same interactions, however, also generate LFV processes such as τ → μ(e)γ, as no symmetry can prevent the latter [488], which are subject to much stronger constraints. In the effective field theory with just the 125 GeV Higgs boson, HLFV decays involving the tau lepton can be sizable, and ATLAS and CMS constraints on its flavor violating couplings (shown in Table 4) are comparable or even stronger than those coming from low-energy observables [489–491]. However, in UV models, specially in radiative neutrino mass models, the situation is generally the opposite.
Table 4. Experimental 95 % C.L. upper bounds on HLFV decays from ATLAS and CMS in the tau sector using the 13 TeV data sets.
The relevant gauge-invariant effective operators that generate HLFV are the Yukawa operator:
and derivative operators like
or
plus their Hermitian conjugates. In Herrero-García et al. [491] all the possible tree-level realizations of these operators were outlined, some of which include particles that are present in radiative neutrino mass models, as we will see below. In Figure 16, we show some possible UV completions of operators , and . The authors concluded that only can have sizable rates, and in particular only for UV completions that involve scalars, like in a type-III two-Higgs doublet model.
Figure 16. Different 1-loop UV completions of the Yukawa operator given in Equation (68), and the derivative operators given in Equation (69) and in Equation (70). F and F1,2 are fermion fields and S1,2 scalar fields. The Zee-Babu and the scotogenic models are examples of radiative models with HLFV generated at 1-loop order. Figure reproduced from Herrero-García et al. [491].
After electroweak symmetry breaking the Yukawa operator gives rise to the interaction Lagrangian in Equation (50). For instance, the SL,R couplings are given by
where Df is the SM flavor-diagonal contribution, not relevant for the present discussion, and CY is the Wilson coefficient of the operator defined in Equation (68). Focusing on the contributions from the Yukawa operator, the branching ratio of the Higgs into a tau and a muon reads:
Most radiative neutrino mass models generate HLFV at 1-loop order [491]25. For instance, the doubly-charged scalar singlet and the singly-charged scalar singlet of the Zee-Babu model (see section 5.1) generate respectively the derivative operators and at 1-loop order. The scotogenic model (see section 5.3) also generates HLFV at 1-loop order ().
We can estimate the loop-induced HLFV in radiative neutrino mass models. Denoting a generic Yukawa coupling of the fermions and scalars with the SM leptons as Y, and a scalar quartic coupling with the Higgs as λih, and taking into account that the amplitude of h → μτ involves a tau mass, one can estimate the dominant contribution to be [491]:
where M is the largest mass in the loop. In all these models, in addition to the loop factor, there are in general limits from charged LFV processes, as usually all radiative neutrino mass models have charged particles that can generate ℓα → ℓβγ. As τ → μγ typically gives the constraint , we get:
well below future experimental sensitivities. Thus, unless cancellations are invoked (which are difficult to achieve in all possible radiative decays), HLFV rates are very suppressed, well below future experimental sensitivities.
One class of models which can have large HLFV are those with another Higgs doublet such that both the SM and the new scalar doublet couple to the lepton doublets [488, 499–502]. In such scenarios, both Yukawa couplings cannot be diagonalized simultaneously, which leads to LFV Higgs interactions. One example is the Zee model discussed in section 5.1, which can have BR(h → μτ) up to the percent level [91].
4.3. Anomalous Magnetic Moments and Electric Dipole Moments
The anomalous magnetic moments (AMMs) and electric dipole moments (EDMs) of the SM leptons receive new contributions in radiative neutrino mass models (see Raidal et al. [503] for a review on the topic). These are contained in the dipole coefficients that also contribute to the radiative ℓα → ℓβγ decays, typically leading to tight correlations between these observables. Using the effective Lagrangian in Equation (48), the anomalous magnetic moment aα and the electric dipole moment dα of the charged lepton ℓα are given by Raidal et al. [503]
The experimental values for the AMMs and EDMs of charged leptons are collected in Table 5. In particular the muon AMM received a lot of intention in recent years due to the discrepancy between the experimentally measured value given in Table 5 and the SM prediction [504]
with the errors due to electroweak, lowest-order, and higher-order hadronic contributions.

Table 5. Experimental values for AMMs and EDMs [504].
There are many examples of radiative neutrino mass models leading to sizable effects in these two observables. For some examples in the case of AMMs see for instance Dicus et al. [234], Babu and Julio [312], Nomura et al. [239], Nomura and Okada [299], Chiang et al. [206], and Lee et al. [505]. In some cases, the new contributions effects can help close the gap between the theory prediction and the experimental measurement of the muon AMM, although in other cases they increase the disagreement, depending on their sign. We refer to the recent review [506] for a guide regarding new physics contributions to the muon AMM.
Regarding lepton EDMs, some examples in radiative neutrino models are given in Borah and Dasgupta [402, 397], and Chiang et al. [206]. In this case one requires CP-violating new physics in the lepton sector, something that is easily accommodated in new Yukawa couplings.
4.4. Neutrinoless Double Beta Decay
One of the main experimental probes to test the Majorana/Dirac nature of neutrinos is neutrinoless double beta decay (0νββ), in which a nucleus (A, Z) decays into another nucleus (A, Z + 2) and two electrons [507]. In order to have sizable 0νββ rates, the nuclei should not have single beta decays. This is achieved with even-even nuclei which, thanks to the nuclear pairing force, are lighter than the odd-odd nucleus, making single beta decays kinematically forbidden. The current strongest experimental limits are obtained using 136Xe by EXO-200 [508] and KamLAND-Zen [509, 510] which yield lower bounds of the lifetime of 1.1·1025 y and 1.9·1025 y at 90 % C.L, respectively. Uncertainties in the nuclear matrix elements translate into uncertainties in the extracted values of |mee| (see Equation 6), whose current strongest upper limits are in the ballpark of ~0.15 eV. For further details regarding the present and future experimental situations see Dell'Oro et al. [511].
The observation of 0νββ decay would imply that lepton number is violated by two units (ΔL = 2), and therefore that neutrinos are Majorana particles [512]. However, quantitatively, this contribution to neutrino masses occurs at 4-loop order and is therefore extremely suppressed, much lighter than the observed neutrino masses (see Duerr et al. [513] for a quantitative study of this statement). So, even if it is true that neutrinos will necessarily be Majorana if 0νββ is observed, the main contribution to their masses may no be necessarily related to 0νββ.
We will mainly focus in this section on radiative models which have new direct contributions to neutrinoless double beta decay beyond the standard ones mediated by the light Majorana neutrinos, which are indirect, as they are generated by the new particles at higher-loop order (via light neutrino masses). For general reviews on the subject the interested reader is referred to Rodejohann [514], Bilenky and Giunti [515] and Dell'Oro et al. [511].
In Päs et al. [516, 517] a general phenomenological formula for the process including both long and short-range interactions was given. The authors considered all possible Lorentz structures for the quarks involved in the process and the outgoing electrons. In del Aguila et al. [107] effective operators that involve gauge bosons were considered, such that there are new effective vertices of the W-boson and the electrons.
In Figure 12 (reproduced from del Aguila et al. [349]) all possible contributions to 0νββ are shown, with the red dot representing the ΔL = 2 vertex. Figure 12A shows the light neutrino contribution, while Figure 12F involves a dimension-9 effective operator. In Bonnet et al. [106] a systematic classification of possible UV models stemming from the dimension 9 operator was performed (Figure 12F). See also Helo et al. [182] for scalar-mediated UV completions and its connection to neutrino masses. Figures 12D,E involve new vertices between quarks, leptons and gauge bosons. Figures 12B,C involve new vertices with just leptons and gauge bosons and no quarks. In del Aguila et al. [107] operators that involve gauge bosons were considered, such that there are new effective vertices of the W-boson and the electrons, as in Figures 12B,C. See section 3.4 for a discussion of the effective operators that generate the latter diagrams and their connection to neutrino masses. A systematic classification of UV models for all the dimension-7 operators was given in Helo et al. [108]. Many (if not all) of these particles can be present in radiative neutrino mass models.
We outline in the following two typical new contributions to 0νββ from radiative neutrino mass models:
1. New particles that couple to quarks. For instance, leptoquarks as in Hirsch et al. [518, 519] and Kohda et al. [298]. In R-parity violating SUSY (see section 5.5) there can be new contributions to 0νββ from new states, see Mohapatra [520], Babu and Mohapatra [521], and Hirsch et al. [522, 523]. Another simple example due to exchange of color octet scalars and fermions that couple to quarks and leptons simultaneously is given in Choubey et al. [524]. A model with two scalar diquarks, a dilepton and a second Higgs doublet is given in Brahmachari and Ma [525]. See other examples in Gu [526] and Helo et al. [182].
2. New particles that open operators that involve gauge bosons del Aguila et al. [107], see discussion in section 3.4.
Let us also mention that, in addition to 0νββ, there are also limits on other lepton number violating elements mαβ of the neutrino mass matrix in flavor basis (where the charged lepton mass matrix is diagonal), different from the mee (which equals mββ) one, stemming from meson decays, tau decays, e+p collider data among other processes [527]. Also indirect bounds using neutrino oscillations and the unitarity of the PMNS matrix can be set [528]. However, both the direct and indirect (even if much stronger than the direct) bounds obtained are typically very weak [527, 528]. μ−e+ conversion also offers a possibility to test the meμ element, however typically the rates are not competitive with those of 0νββ, although of course they test a different element and flavor effects could be relevant. A study of the contributions from effective operators was performed in Berryman et al. [529], while a doubly-charged scalar was studied in detail in Geib and Merle [530].
Lepton number violation can also be searched for at colliders. This is specially interesting for channels that do not involve electrons, as it is necessarily the case for 0νββ. Those will be discussed in section 4.5. Also the connection of lepton number violation to the matter-antimatter asymmetry of the universe will be discussed in section 4.6.
4.5. Collider Searches
Radiative neutrino mass models generally have a much lower UV scale than the GUT scale, which makes them testable at either current or future colliders. The diversity of exotic particles and their interaction with the SM particles in radiative neutrino mass models leads to an extremely rich phenomenology at colliders. Processes pertaining to the Majorana nature of neutrino masses or LFV couplings between the exotic particles and the SM, i.e., processes violating lepton number and/or lepton flavor, are often chosen as signal regions in collider searches due to the low SM background26. Of course, there are searches for exotic particles in general if they are not too heavy and the couplings are sizable 27. In the following, we sketch different search strategies at colliders, which often utilize the low SM background for LNV and LFV processes. We thus discuss LNV and LFV processes separately before discussing general searches for new particles, which rely on processes without any LNV/LFV.
4.5.1. Lepton Number Violation
At the LHC, the most sought-after channel of LNV28 are same-sign leptons
where ℓ denotes e or μ, and X can be any number of jets, or other SM objects. The details of the production and the actual content of X are very model-dependent: typically heavy states are produced and decay to final states with same-sign dilepton due to their Majorana nature. We will take a doubly-charged scalar as a simple example to illustrate the basics of this search strategy. A doubly-charged scalar ϕ++ is an SU(2)L singlet with hypercharge Y = 2. They can be pair-produced via Drell-Yan process and subsequently decay to two same-sign dileptons. For large masses the photon-initiated process becomes important and leads to an enhancement [532]. Assuming the branching fraction of ϕ++ → e+e+ is 100%, the signature for pair-produced doubly-charged scalars is four electrons and thus ZZ production is the main SM background. To reduce the SM background, discriminating variables such as the same-sign dilepton mass, the difference between the opposite sign dilepton mass and the Z boson mass, and the scalar sum of the lepton pT can be utilized. ATLAS [533] has excluded doubly-charged SU(2)L singlet scalar with mass lower than 420 GeV at 95% CL with LHC Run 2 data. The improved limit can be extracted from the CMS search for doubly-charged component of an SU(2)L triplet [534]. In Sugiyama et al. [535], del Aguila and Chala [536, 537] and Kanemura et al. [538] studies of doubly-charged scalars and how to discriminate the multiplet to which they belong were performed.
The sensitivities of 0νββ searches detailed in section 4.4 and the same-sign dilepton searches at the LHC can be compared in any specific model (see for example [539–541]). Specifically in Helo et al. [539] and Peng et al. [540] a simplified model with a scalar doublet S ~ (1, 2, 1) and a Majorana fermion F, which has the same matter content as the scotogenic model, is adopted. In this model, the reach of tonne-scale 0νββ generally beats that of the LHC. In the parameter space region where the heavy particle masses are near the TeV scale, however, the two probes are complementary.
4.5.2. Lepton Flavor Violation
As described in section 4.2, lepton flavor violating processes are commonly predicted in radiative neutrino mass models, which can also be probed at colliders. The actual production topology of the LFV processes varies from model to model. For example, in models with the leptoquark , there are two possible decay channels, or [542]. The dilepton final states are produced from
where X can represent , multiple jets and leptons, and the former contributes dominantly for normal ordering in the minimal model with two leptoquarks. SUSY stop searches in the dilepton final states have the same signatures and their collider bounds can be translated into that of the leptoquark. This has been done for the LHC 8 TeV run [543] and the limit was mS1 ≳ 600 GeV [214]. Note that this limit in LFV channel is stronger than lepton flavor conserving ones (mS1 ≳ 500 GeV) as the SM background is lower. The stop search has been updated for LHC Run 2 [544, 545], though a recast for leptoquarks in LFV dilepton final states still awaits further analysis.
Alternatively, LFV processes can also be studied in an independent manner. In the framework of effective operators with two flavor-diagonal quarks and two flavor-off-diagonal leptons, constraints from LHC searches for LFV final states are interpreted as lower limits on the UV cut-off scale [546]. Compared with the limits derived from low energy precision measurements [449, 546], LHC delivers less stringent limits for light quarks. For heavier quarks, however, competitive limits of ΛUV ≳ 600−800 GeV can already be set for operators with right-handed τ leptons using only LHC Run 1 data.
4.5.3. Searches for New Particles
Radiative neutrino mass models may contain exotic particles such as vector-like quarks (VLQs), vector-like leptons (VLLs), scalar leptoquarks, singly- or doubly-charged scalars, colored octet fermions or scalars, and electroweak multiplets. Note that the examples here are far from complete and searches for each individual particle require their own dedicated discussion. In Cai et al. [214], LHC searches for exotic particles in UV complete models based on ΔL = 2 dimension 7 operators are discussed systematically. Here we will only present a simple summary about a handful of new particles.
Vector-Like quarks
We refer by VLQs to new SU(3)c triplets which mix with the SM quarks and Higgs via Yukawa couplings [547]. The VLQs include different SU(2) representations: two singlets T and B with hypercharge 2/3 and −1/3; three doublets (T, B), (X, T), and (B, Y) with hypercharge 1/6, 7/6, and −5/6; and two triplets (X, T, B), and (T, B, Y) with hypercharge 2/3 and −1/3. They can be pair produced at the LHC via gluon fusion and quark-antiquark annihilations. Single production is model-dependent and can be dominant for large vector-like quark masses and large mixings [547]. The mass splitting among the components of the fields is suppressed by the mixing angles between the SM quarks and the vector-like quarks, which in turn suppresses the decays between the component fields. Therefore, VLQs will dominantly decay to either a gauge boson or a Higgs plus a SM quark. Both ATLAS and CMS have performed searches for VLQs and have set lower limits on the VLQs masses up to 990 GeV at the 95% confidence level (CL) depending on the representations and the decay branching ratio [548–559].
Vector-like leptons
VLLs are the colorless version of VLQs. Similar to VLQs, VLLs mix with the SM leptons via Yukawa couplings with Higgs. Due to the absence of right-handed neutrinos, there are less VLLs: two singlets N and E with hypercharge 0 and 1; two doublets (N, E) and (E, D) with hypercharge 3/2 and 1/2; and triplets (P, N, E) and (N, E, D) with hypercharge 0 and 1, respectively. Detailed studies have been performed in Altmannshofer et al. [560], Falkowski et al. [561], Dermisek et al. [562], and Kumar and Martin [563]. Contrary to the colored VLQs, VLLs are dominantly pair produced at the LHC via Drell-Yan process as the phase space suppression is less significant in the parameter space of interest at the moment. They can also be singly produced in association with W, Z or H, which can be dominant if the pair production channel is phase space suppressed and sizable mixing parameters are assumed. Likewise VLLs decay either to a SM lepton and a boson, W or Z, or Higgs. So far there is no dedicated search for VLLs at colliders, though SUSY searches for sleptons or charginos can be used to derive bounds on VLLs (see Altmannshofer et al. [560] and Hamada et al.[564] for example).
Leptoquarks
Leptoquarks appear frequently in theories beyond the SM such as grand unified theories [565, 566]. As its name suggests, a leptoquark, which can be either a scalar or a vector [542], possesses both non-zero lepton and baryon numbers. Here we will focus on scalar leptoquarks. At hadron colliders, leptoquarks are primarily produced in pairs via gluon fusion and quark-antiquark annihilation. Each leptoquark subsequently decays to one quark and one charged or neutral lepton. Both ATLAS [567, 568] and CMS [569–571] have performed searches for leptoquarks in final states with two charged leptons plus multiple jets. Assuming 100% branching fraction of the leptoquark decay into a charged lepton and a quark, current searches at the LHC Run 2 with 13 TeV center of mass energy have excluded leptoquarks with masses less than 1,130 GeV [569], 1,165 GeV [570] and 900 GeV [571] at 95% CL for leptoquark couplings to the first, second and third generations respectively.
Charged scalars singlets
Singly- and doubly-charged scalars are introduced in various radiative neutrino mass models (see Babu and Julio [158], Zee [288], and Babu [289], for instance). As singlets under SU(3)c × SU(2)L, the singly (doubly) charged scalar can only couple to the lepton doublet (right-handed charged lepton) bilinear. So the doubly-charged scalar can only decay to a pair of charged leptons, which leads to LNV signature at colliders (see discussion in section 4.5.1 for details). As for the singly-charged scalar, it decays to a charged lepton and a neutrino whose LNV effects can not be detected at the LHC. Singly-charged scalars are mainly produced in pairs via the Drell-Yan pair process. They are searched for in final states with two leptons plus 29. SUSY searches for sleptons and charginos at the LHC share the same signature as the singly-charged scalars. Thus, we can in principle recast the slepton search in The ATLAS Collaboration [574] and extract the limit for our singly-charged scalars. Note a slepton can also be produced via a W-boson, while singly-charged scalar only via a virtual photon.
Higher-dimensional electroweak multiplet
SU(2)L higher-dimensional representations can also be incorporated in radiative neutrino mass theories [126–129, 362, 473, 575, 576]. While the mass splittings among the component fields for scalar multiplets can be generally large due to couplings to the SM Higgs, those for fermion multiplets are only generated radiatively and are typically MeV, with the neutral component being the lightest. This small mass splitting results in lifetimes ns. At the LHC, charged component field can be produced in pair via electroweak interaction and decay to the neutral component plus a very soft pion, which leads to a disappearing track signature. For a triplet with a lifetime of about 0.2 ns, the current LHC searches set the lower mass limit to be 430 GeV at 95% CL [577–579].
4.6. Generation of the Matter-Antimatter Asymmetry of the Universe
The matter-antimatter asymmetry of the universe has been inferred independently (and consistently) by big bang nucleosynthesis (BBN) predictions of light elements, and by the temperature anisotropies of the cosmic microwave background. In order to generate it, the Sakharov conditions need to be fulfilled [580]. There should be:
• Processes that involve baryon number violation (BNV).
• Processes in which both charge conjugation (C) and charge and parity conjugation (CP) are violated.
• Departure from thermal equilibrium, so that (i) the number densities of particles and antiparticles can be different, and (ii) the generated baryon number is not erased.
In the standard model, it is well-known that due to the chiral nature of weak interactions B+L is violated by sphaleron processes, while B−L is preserved [581]. Also C and CP are violated in the quark sector (in the CKM matrix), although the amount is too small to generate the required CP asymmetry. In the lepton sector (with massive neutrinos) CP can be violated, and there are in fact hints of δ ~ −π/2 [20]. However, the measurement of the Higgs mass at 125 GeV implies that the phase transition is not strongly first-order, with no departure from thermal equilibrium. Therefore, the SM has to be extended to explain the matter-antimatter asymmetry which raises the question whether this new physics is related to neutrino masses or not.
When sphalerons are active and in thermal equilibrium, roughly at temperatures above the electroweak phase transition, B+L can be efficiently violated. Therefore, one natural option in models of Majorana neutrinos is that an asymmetry in lepton number is generated, which is converted by sphalerons into a baryon asymmetry. This is known as leptogenesis [25] (see Davidson et al. [582] for a review on the topic), the most popular example being the case of type-I seesaw, where the out-of-equilibrium decays of the lightest of the heavy right-handed neutrinos into lepton and Higgs doublets and their conjugates, at a temperature equal or smaller than its mass, generate the lepton asymmetry due to CP-violating interactions.
The scotogenic model and its variants, see section 5.3, have been studied in detail regarding the generation of the baryon asymmetry from particle decays with TeV-scale masses. Ma [583] briefly discusses leptogenesis within the scotogenic model. This discussion is extended in Kashiwase and Suematsu [584, 585] and Racker [586] to include resonant leptogenesis. Resonant leptogenesis has also been studied in a gauge extension of the scotogenic model [224–226] in Kashiwase and Suematsu [252] and resonant baryogenesis in an extension with new colored states in Dev and Mohapatra [587]. Hambye et al. [588] and Babu and Ma [589] consider extensions of the scotogenic model by an additional charged or neutral scalar to achieve viable non-resonant leptogenesis. The baryon asymmetry can similarly be enhanced by producing the SM singlet fermions in the scotogenic model non-thermally beyond the usual thermal abundance [590]. Leptogenesis via decays of an inert Higgs doublet or a heavy Dirac fermion were studied in Lu and Gu [119, 154] in scotogenic-like models, respectively. In Chen and Law [127] leptogenesis was studied in a scotogenic-like model with fermionic 5-plets and a scalar 6-plet, via the decays of the second-lightest fermionic 5-plet. Baldes et al. [278] demonstrated the feasibility to generate the correct matter-antimatter asymmetry via leptogenesis in the model proposed in Ma [335]. It also showed that any pre-existing baryon asymmetry in the two models proposed in Ma [335] and Law and McDonald [277] is washed out at temperatures above the mass of their heaviest fields.
In radiative models with extra scalars coupled to the Higgs field, the phase transition can generally be stronger, as they contribute positively to the beta function of the Higgs and therefore, they help to stabilize the Higgs potential. Moreover, in these models there are typically extra sources of CP violation. These two ingredients allow the possibility of having electroweak baryogenesis. In particular, the strong first-order phase transition has been discussed using an effective potential in Bertolini et al. [591], and in Aoki et al. [592] for the model of Aoki et al. [370]. Also in the case of a supersymmetric radiative model in Kanemura et al. [202].
However, in general the new states can also destroy a pre-existing asymmetry, irrespective of their production mechanism, as they violate necessarily lepton number by two units [593–596]. The new particles typically have gauge interactions, so that they are in thermal equilibrium at lower temperatures than those at which the asymmetry is generated (by high-scale baryogenesis or by leptogenesis, for instance30) potentially washing it out.
Some works have focused on the fact that if LNV is observed at the LHC, one could falsify leptogenesis, as the wash-out processes would be too large [597–599]. Similarly, observations of 0νββ rates beyond the one generated by the light neutrinos could impose constraints for the first family [600]. LFV processes could be used to extend it to all families. See Deppisch et al. [531] for further discussions about LNV processes in leptogenesis.
The limits on radiative models due to the requirement of not washing-out any pre-existing asymmetry are model-dependent. A more systematic way to go is to consider the LNV effective operators related to radiative models [81, 85, 87]. These operators lead to wash-out processes if they are in thermal equilibrium above the electroweak phase transition, and therefore their strength can be bounded by this requirement.
4.7. A Possible Connection to Dark Matter Models
In many radiative neutrino mass models the generation of neutrino masses at tree-level is forbidden by a symmetry, . This symmetry can be global or gauge, continuous or discrete (a typical example is a Z2 parity), imposed or accidental (a by-product of other symmetries in the model). If is preserved after electroweak symmetry breaking, the lightest state transforming non-trivially under it, the so-called lightest charged particle (LCP), is completely stable and, in principle, could constitute the dark matter (DM) of the universe. This opens up an interesting connection between radiative neutrino masses and dark matter. DM may be produced via its coupling to neutrinos and thus the annihilation cross section is closely related to neutrino mass. This has been studied using an effective Lagrangian for light, MeV-scale, scalar DM [601] in a scotogenic-like model and for fermionic DM [460, 468–472] in the scotogenic model. A key signature of this close connection is a neutrino line from DM annihilation. The constraints from neutrino mass generation on the detectability of a neutrino line has been recently discussed in El Aisati et al. [602].
Based on the general classification of 1-loop models [100], the authors of Restrepo et al. [111] performed a systematic study for models compatible with DM stabilized by a discrete Z2 symmetry. They focused on the topologies T1-x and T3. The topologies T4-2-i and T4-3-i require an additional symmetry to forbid the tree-level contribution and thus were not studied in Restrepo et al. [111]. A similar classification for 2-loop models has been presented in Simoes and Wegman [112] based on the possible 2-loop topologies discussed in Aristizabal Sierra et al. [102]. Symmetries forbidding tree and lower-order loop diagrams have been discussed in Farzan et al. [110]. In section 5.3 we discuss the prototype example of such models: the scotogenic model.
Besides dark matter being stabilized by a fundamental symmetry, it may be stable due to an accidental symmetry. For example, higher representations of SU(2)L cannot couple to the SM in a renormalizable theory, which leads to an accidental Z2 symmetry at the renormalizable level. This has been dubbed minimal dark matter [385, 386]. After the initial proposal to connect the minimal dark matter paradigm and radiative neutrino mass generation [126], it has been conclusively demonstrated that the minimal dark matter paradigm cannot be realized in 1-loop neutrino mass models [473, 575, 576]. However, there is a viable variant of the KNT model at 3-loop order [362], which realizes the minimal dark matter paradigm without imposing any additional symmetry beyond the SM gauge symmetry.
Finally, the DM abundance in the universe may be explained by a light pseudo-Goldstone boson (pGB) associated with the spontaneous breaking of a global symmetry. It is commonly called Majoron in case the lepton number plays the role of the global symmetry. The possibility of pGB dark matter has been discussed in one of the models in Dasgupta et al. [219] which provides a pGB dark matter candidate after the breaking of a continuous U(1) symmetry to its Z2 subgroup in addition to the LCP. Recently the authors of Ma et al. [603] proposed an extension of the Fileviez-Wise model [120] to incorporate a Majoron DM candidate which simultaneously solves the strong CP problem.
5. Selected Examples of Models
In the following subsections, we list and discuss different benchmark models for neutrino mass that are qualitatively different. We start with the most well-studied models, which are the Zee model, discussed in section 5.1.1, that is the first 1-loop model for Majorana neutrino masses, and the Zee-Babu model, revisited in section 5.1.2, which is the first 2-loop model. In section 5.2 we discuss the first 3-loop model [355], which was proposed by Krauss, Nasri, and Trodden and is commonly called KNT-model, and its variants. It is also the first model with a stable dark matter candidate. The scotogenic model is discussed in section 5.3. It generates neutrino mass at 1-loop order and similarly to the KNT-model it features a stable dark matter candidate due to the imposed Z2 symmetry. These are the most well-studied models in the literature. However, this preference is mostly due to the historic development (and also simplicity) and we are proposing a few other interesting benchmark models in the following subsections.
5.1. Models with Leptophillic Particles
There are only three different structures which violate lepton number (LN) by two units that can be constructed with SM fields [76]:
The three different structures can couple respectively to a SU(2) triplet scalar with Y = 1 (we denote it by Δ), a singly-charged SU(2) singlet scalar (we call it h+) and a doubly-charged SU(2) singlet scalar (we call it k++).
In all cases, we could assign LN equal to −2 to the new fields so that such interactions preserve it. However, dimension-3 terms in the scalar potential will softly break LN, as there is no symmetry to prevent them. In the first case, the triplet can have in the potential the lepton-number violating term (with ΔL = 2) with the SM Higgs doublet H
Then, after electroweak symmetry breaking, the triplet gets an induced VEV (strongly bounded by the T parameter to be ≲O(1) GeV), and neutrino masses are generated at tree-level via the type-II seesaw.
If only the singly-charged scalar h+ is present, a ΔL = 2 term can be constructed with two Higgs doublets, the SM Higgs H and an extra Higgs doublet Φ
In this case, however, neutrino masses are not induced by the Higgs VEV at tree-level, but they are generated at 1-loop order. This is known as the Zee model [104, 105].
For the case of the doubly-charged scalar, one can construct the ΔL = 2 term precisely with two singly-charged scalars h+
Notice that no other combination with SM fields exist, given the large electric charge of k++. In this case, neutrino masses are generated at 2-loop order. This is known as the Zee-Babu model [76, 604].
These are the simplest radiative models. By using particles that couple to a lepton and a quark (leptoquarks), one can also have ΔL = 2 interactions and generate neutrino masses at a different number of loops. In the following, we will discuss the Zee and Zee-Babu models.
5.1.1. The Zee Model
In addition to the SM content with a Higgs scalar doublet H, the Zee model [104, 105] contains an extra Higgs scalar doublet Φ and a singly-charged scalar singlet h+, which is shown in Table 6. It is an example of the operator . Several aspects of the phenomenology of the model have been studied in Petcov [605], Zee [288], Bertolini and Santamaria [606, 607], Yu et al. [608, 609], Frampton and Glashow [610], Jarlskog et al. [611], Ghosal et al. [451], Kanemura et al. [612], Balaji et al. [613], Koide [614], Brahmachari and Choubey [615], Frampton et al. [616], Assamagan et al. [617], He [156], Kanemura et al. [618], and Aristizabal Sierra and Restrepo [619]. While the Zee-Wolfenstein version where just the SM Higgs doublet couples to the leptons has been excluded by neutrino oscillation data [155, 156], the most general version of the Zee model in which both couple remains allowed [157] and has been recently studied in Herrero-García et al. [91] (see also Babu and Julio [158] and Aranda et al. [159] for a variant with a flavor-dependent Z4 symmetry).
The Yukawa Lagrangian is
where and eR are the SU(2) lepton doublets and singlets, respectively, and with τ2 being the second Pauli matrix. Due to Fermi statistics, f is an antisymmetric Yukawa matrix in flavor space, while Y1 and Y2 are completely general complex Yukawa matrices. Furthermore, the charged-lepton mass matrix is given by
where tan β = sβ/cβ = v2/v1 with and and . Without loss of generality, one can work in the basis where mE is diagonal.
Assuming CP-invariance there are two CP-even neutral scalars (one of which is the 125 GeV Higgs boson, with mass mh, and the other is a heavy one with mass mH), one neutral CP-odd scalar with mass mA, and two charged-scalars of masses , whose mixing due to the trilinear term in Equation (81) is given by
Interestingly, μZee cannot be arbitrarily large, as it contributes at 1-loop level to the mass of the light Higgs. Demanding no fine-tuning, we can estimate |μZee| ≲ 4π mh ≃ 1.5 TeV.
The Yukawa couplings of Equation (83), together with the term in the potential given in Equation (81), imply that lepton number is violated by the product mE(Y1v2 − Y2v1)fμZee. Therefore, neutrino masses will be necessarily generated, in particular the lowest order contribution appears at 1-loop order, as shown diagram of Figure 17, where the charged scalars run in the loop. The neutrino mass matrix is given by:
with φ being the mixing angle for the charged scalars given in Equation (85). Therefore, in the Zee model, due to the loop and the chiral suppressions, the new physics scale can be light. From the form of the mass matrix it is clear that if one takes Y2 → 0 (Zee-Wolfenstein model), the diagonal elements vanish, yielding neutrino mixing angles that are not compatible with observations.
Neglecting me ≪ mμ, mτ and taking feμ = 0, the following Majorana mass matrix is obtained
Notice that if the term proportional to the muon mass is neglected, one neutrino remains massless. In order to obtain correct mixing angles, we need both and different from zero [91, 491], as they enter in the 1-2 submatrix of Equation (87). This implies that LFV mediated by the scalars will be induced. In fact, in the model large LFV signals are generated, like τ → μγ and μ − e conversion in nuclei. Moreover, also a full numerical scan of the model performed in in Herrero-García et al. [91] showed that large LFV Higgs decays are possible, in particular BR(h → τμ) can reach the percent level. BR(h → τe) is roughly two-orders of magnitude smaller than BR(h → τμ). The singly-charged h also generates violations of universality, as it interferes constructively with the W boson, as well as non-standard interactions, see section 4.1, which however are too small to be observed [91].
In Herrero-García et al. [91] it was also shown that the model is testable in next-generation experiments. While normal mass ordering (NO) provided a good fit, inverted mass ordering (IO) is disfavored, and if θ23 happens to be in the second octant, then IO will be ruled-out. Notice also that the lightest neutrino is required to be massless for IO, as it has also been obtained in He and Majee [157]. Furthermore, future τ → μγ (μ − e conversion) will test most regions of the parameter space in NO (IO). Regarding direct searches at the LHC, the new scalars have to be below ~2 TeV, which implies that they can be searched for similarly as in a two-Higgs doublet model (with an extra charged scalar that could be much heavier). Particularly, the charged scalars are searched for at colliders. See the discussion in section 4.5.
Let us mention that an interesting modification of the Zee model was proposed in Babu and Julio [158] (see also Aranda et al. [159]), where a Z4 symmetry was imposed, being able to reduce significantly the number of parameters. In that case, among the predictions of the model, is that the spectrum should be inverted. Other flavor symmetries beyond Z4 in this framework have been studied in Babu and Mohapatra [168, 169], Koide and Ghosal [170], Kitabayashi and Yasue, [171], Adhikary et al. [172], Fukuyama et al. [173], Aranda et al. [174, 175].
5.1.2. The Zee-Babu Model
The Zee-Babu model contains, in addition to the SM, two SU(2) singlet scalar fields with electric charges one and two, denoted by h+ and k++ [76, 604] as shown in Table 7. It is a UV completion of the operator . Several studies of its phenomenology exist in the literature [95, 435, 620–622].
The leptonic Yukawa Lagrangian reads:
where like in the Zee model, due to Fermi statistics, f is an antisymmetric matrix in flavor space. On the other hand, g is symmetric. Charged lepton masses are given by , which be take to be diagonal without loss of generality.
Lepton number is violated by the simultaneous presence of the trilinear term μZB in Equation (82), together with mE, f, g. Note that the trilinear term cannot be arbitrarily large, as it contributes to the charged scalar masses at loop level, and can also lead to charge-breaking minima, if |μZB| is large compared to the charged scalar masses. For naturalness considerations we demand |μZB| ≪ 4π min(mh, mk). See Nebot et al. [435] and Herrero-Garcia et al. [95] for detailed discussions.
As lepton number is not protected, neutrino masses are generated radiatively, in particular at 2-loop order, via the diagram of Figure 18. The mass matrix is approximately given by (see for instance McDonald and McKellar [286], Nebot et al. [435] and Herrero-Garcia et al. [95] for more details)
where M is the heaviest mass of the loop, either that of the singly-charged singlet h+ or of the doubly-charged singlet k++. A prediction of the model is that, since f is a 3 × 3 antisymmetric matrix, det f = 0, and therefore . Thus, at least one of the neutrinos is exactly massless at this order.
In the model, both NO and IO can be accommodated. The phenomenology of the singly-charged scalar is similar to that discussed in the Zee model, apart from the fact that in the Zee model the charged singlet mixes with the charged component of the doublet. Some of the most important predictions of the model are due to the presence of the doubly-charged scalar k++. Firstly, k++ mediates trilepton decays () at tree-level which unlike, in the Zee model, are not suppressed by the small charged lepton masses, as well as radiative decays (ℓi → ℓjγ). Secondly, k++ can be pair-produced at the LHC via Drell-Yan, decaying among other final states into same-sign leptons which yields a clean experimental signature. See the discussion in section 4.5.
5.2. KNT-Models
The first radiative neutrino mass model at 3-loop order is the KNT model [355] which has one fermionic singlet N and two singly-charged scalars S1,2 in addition to the SM particles. A discrete Z2 symmetry is imposed, under which only S2 and N are odd. We list the quantum numbers of the exotic particles in Table 8.
The Z2 symmetry forbids the usual type-I seesaw contribution at tree-level. The relevant Lagrangian is expressed as
where the flavor indices of f and g are all suppressed. With this setup, neutrino masses are generated first at 3-loop order as shown in Figure 19. The neutrino mass matrix is then
where the function F is defined in Ahriche and Nasri [358]. This matrix is, however, only rank one and thus can give exactly one non-zero neutrino mass. Adding more copies of N can increase the rank of the matrix. The phenomenology of this model including flavor physics, dark matter, Higgs decay, electroweak phase transition and collider searches is discussed in detail in Ahriche and Nasri [358].
This model is subject to constraints from LFV experiments such as μ → eγ which requires three copies of N for the neutrino mixing to be in agreement with the observations31. Meanwhile in order to be consistent with the measurements of muon anomalous magnetic moment and the 0νββ decay, strong constraints are imposed. For MS1,S2 ⩾ 100 GeV, and , it can satisfy all flavor constraints while reproducing the neutrino mixing data.
Assuming a mass hierarchy MN < MS2, the lightest fermion singlet is stable and serves as a good DM candidate. This is also the first radiative neutrino mass theory with a stable DM candidate running in the loop. If the DM relic density is saturated and all previously discussed constraints are satisfied, the DM mass cannot exceed 225 GeV while the lighter charged scalar S2 cannot be heavier than 245 GeV. If the fermion singlets have very small mass splitting, DM coannihilation effects should be taken into account. With about 5% mass splitting, the DM relic density increases by 50%.
As discussed in section 4.5.3, the singly-charged scalars can be pair-produced at the LHC and subsequently decay to a pair of charged leptons and the fermion singlets which appear as missing transverse energy. This signature is exactly the same as the direct slepton pair production in SUSY theories. ATLAS has performed the search for sleptons in this channel with 36.1 fb−1 data of TeV [574] and has ruled out slepton masses below ~500 GeV in the non-compressed region. The actual constraint on MS2 depends on the decay branching ratio of S2 to different leptons and in principle will be substantially relaxed compared to the ATLAS search.
With the same topology, a lot of variations of the KNT model can be constructed. Chen et al. [356] discusses several possibilities to replace the electron with other SM fermions32 or vector-like fermions. A similar model in which the electron is replaced by a fermion doublet with hypercharge 5/2 and S1,2 with doubly-charged scalar is discussed in Okada and Yagyu [368]. The Z2-odd particles in this model form instead the outer loop.
5.3. The Scotogenic Model
The most popular model linking dark matter to the radiative generation of neutrino masses is the one proposed by E. Ma in 2006. We will refer to it as scotogenic model [113]33. In the scotogenic model, the SM particle content is extended with three singlet fermions, Ni (i = 1, 2, 3), and one SU(2)L doublet, η, with hypercharge ,
This setup is supplemented with a Z2 parity, under which the new states are odd and all the SM particles are even34. The newly-introduced particles with their respective charges of the scotogenic model are shown in Table 9. The gauge and discrete symmetries of the model allow us to write the Lagrangian terms involving the fermion singlets
We do not write the kinetic term for the fermion singlet as it takes the standard canonical form. YN is an arbitrary 3 × 3 complex matrix, whereas the 3 × 3 Majorana mass matrix MN can be taken to be diagonal without loss of generality. We highlight that the usual neutrino Yukawa couplings with the SM Higgs doublet are not allowed due to the Z2 symmetry. This is what prevents the light neutrinos from getting a non-zero mass at tree-level. The scalar potential of the model is given by
Neutrino masses are induced at the 1-loop level via the diagram in Figure 20
where the masses of the scalar ηR and pseudo-scalar part ηI of the neutral scalar are given by
with the electroweak VEV . Neutrino mass vanishes in the limit of λ5 = 0 and thus degenerate masses for the neutral scalars ηR,I, because it is possible to define a generalized lepton number which forbids a Majorana mass term.
In the scotogenic model, the Z2 parity is assumed to be preserved after electroweak symmetry breaking. This will be so if 〈η〉 = 0. In this case, the lightest Z2-odd state (to be identified with the LCP defined in section 4.7) will be stable and, if neutral, will constitute a potentially good DM candidate. The LCP in the scotogenic model can be either a fermion or a scalar: the lightest singlet fermion N1 or the lightest neutral η scalar (ηR or ηI). As the neutrino Yukawa couplings are generally required to be small to satisfy LFV constraints, the DM phenomenology for a scalar LCP is generally the same as in the inert doublet model [624, 625]. Recently it has been pointed out [626] that late decay of the lightest SM singlet fermion N1 may repopulate the dark matter abundance and thus resurrect the intermediate dark matter mass window between mW, the mass of the W boson, and 550 GeV. In the case of a fermionic LCP, for which the annihilation cross section is governed by the neutrino Yukawa couplings, the connection of the dark matter abundance with neutrino masses leads to a very constrained scenario due to the bounds from lepton flavor violation [460, 468–472].
Many scotogenic variations have been proposed since the publication of the minimal model described above. All these models are characterized by neutrino masses being induced by new dark sector particles running in a loop [114–135, 138, 139, 141–143, 204, 261, 265]. One of them involves a global continuous dark symmetry, instead of a discrete dark symmetry [145], Hagedorn, (in prep). A gauge dark symmetry was considered in Yu [253] and a scale-invariant version presented in Ahriche et al. [245]. The collider [627–630] and dark matter [631–634] phenomenologies of different scotogenic variants have also been discussed in detail. Finally, we point out that the authors of Merle and Platscher [635] identified a potential problem in this family of models, since some parameter regions lead to the breaking of the Z2 parity at high energies. This problem, how it can be escaped and its phenomenological implications have been explored in Merle et al. [636], Merle and Platscher [267], and Lindner et al. [637].
5.4. Models with Leptoquarks
Leptoquarks are common ingredients of radiative neutrino mass models. For example neutrino mass can be generated at loop level by two leptoquarks which mix via a trilinear coupling to the SM Higgs boson [178–185]. Neutrino mass generation at 1-loop order with all possible leptoquarks has been systematically studied in in Aristizabal Sierra et al. [181]. At 1-loop order and especially at a higher-loop order, leptoquarks usually appear together with other exotic particles such as vector-like quarks and leptons, charged scalar singlets and electroweak multiplets [214]. We will review two models here, one at 1-loop and one at 2-loop order.
5.4.1. A 1-Loop Model
Without introducing exotic fermions, the only possible topology that can contribute at 1-loop order to the Weinberg operator is T1-ii shown in Figure 3 as we need the fermion arrow to flip only once. With this topology and leptoquarks as the only exotic particles, the only UV completion we can realize is depicted in Figure 21. The relevant scalar leptoquarks35 are S1, S3 and with quantum numbers detailed in Table 10. The relevant Lagrangian reads
following the convention in in Doršner et al. [185] with all generation indices suppressed. Apparently only the leptoquark component fields with electric charge can contribute. These leptoquarks, in the interaction basis , will mix with each other through the λ1,3 terms in Equation (98)36. We will consider simplified scenarios where either S1 or S3 appears together with . For the model with S1,3, the squared-mass matrix will be diagonalized with angle θ1,3 and the mass eigenvalues are m1 and m2. So the neutrino mass matrix is expressed as [181, 185]
where Md = diag(md, ms, mb) with md,s,b being the down, strange and bottom quark masses. Due to the hierarchy of down-type quark masses, the neutrino mass matrix will be approximately rank-2 with one nearly massless neutrino. Current neutrino oscillation data put lower bounds on the product of Yukawa couplings ranging from 10−12 to 10−7 for leptoquarks with TeV scale masses [181]. On the other hand, low energy precision experiments constrain the Yukawa couplings from above. For example, μ − e conversion in titanium bounds the first generation Yukawa couplings with
for 1 TeV leptoquark masses. Their decay branching fractions are dictated by the same couplings that determine the neutrino masses and mixings, which leads to a specific connection between the decay channels of the leptoquark and the neutrino mixings. Generally LFV decays with similar branching ratios to final states with muon and tau are expected in some leptoquark decays. This neutrino mass model can also be tested at colliders. The leptoquarks running in the loop can be created in pairs and decay to final states containing leptons plus jets with predicted branching ratios. We refer to section 4.5 for further details on searches of leptoquarks at colliders.
Päs and E. Schumacher [183] explored the possibility to explain the anomalous b → sll transitions with S3 and . Different texture of the Yukawa coupling matrices y3 and ỹ2 were considered and leptoquark masses in the the range of 1 to 50 TeV can reproduce the neutrino masses and mixings in addition to RK [639].
5.4.2. A 2-Loop Model
Based on the gauge-invariant effective operator , which violates lepton number by two units, a UV complete radiative neutrino mass model at 2-loop order containing leptoquark S1 and fermion color octet f can be constructed [287]. We list their quantum numbers in Table 11 for the convenience of the readers.
The general gauge invariant Lagrangian for the exotic particles is then expressed as
where generation indices for all parameters and fields are suppressed. We demand baryon number conservation to forbid the terms and which induce proton decay. With this setup, Majorana neutrino mass will be generated at 2-loop order as shown in Figure 22. Generally the contribution to the neutrino mass matrix is proportional to the down-type Yukawa coupling squared which is dominated by the third generation unless strong hierarchy in λLQλdf exists. As a result, we can simplify the formula for the neutrino mass matrix to
with the CKM-matrix element Vtb and Iαβ as a function of mf and mS1 whose exact form can be read from Angel et al. [287]. The indices α and β label the leptoquark copies. This neutrino mass matrix is only rank one if there is only one leptoquark flavor assuming the dominance of the bottom-quark loop37. At least two leptoquarks are needed to fit to the current neutrino oscillation data in this model, where one neutrino mass eigenvalue is nearly vanishing. Among all flavor processes, μ − e conversion in nuclei, μ → eγ and μ → eee give the most stringent constraints.
The leptoquark S1 can explain the recent anomalies observed in semileptonic B decays, i.e., the violation of lepton flavor universality (LFU) of [639] and [640–645]. In the parameter space with relatively large , the combination of left- and right-handed couplings induces scalar and tensor operators, which lift the chirality suppression of the semi-leptonic B-decay B → D(*)ℓν and produce sizable effects in the LFU observables [313].
5.5. Supersymmetric Models with R-Parity Violation
Supersymmetric models with R-parity violation naturally lead to non-zero neutrino masses and mixings. These models have been regarded as very economical, since no new superfields besides those already present in the MSSM are required. Moreover, their phenomenology clearly departs from the standard phenomenology in the usual SUSY models, typically providing new experimental probes.
With the MSSM particle content, one can write the following superpotential, invariant under supersymmetry, as well as the gauge and Lorentz symmetries,
Here is the MSSM superpotential, whereas
The ϵ coupling has dimensions of mass, {i, j, k} denote flavor indices and gauge indices have been omitted for the sake of clarity. The first three terms in break lepton number (L) whereas the last one breaks baryon number (B). The non-observation of processes violating these symmetries impose strong constraints on these parameters, which are required to be rather small [646]. Also importantly, their simultaneous presence would lead to proton decay, a process that has never been observed and whose rate has been constrained to increasingly small numbers along the years. For this reason, it is common to forbid the couplings in Equation (104) by introducing a discrete symmetry called R-parity. The R-parity of a particle is defined as
where s is the spin of the particle. With this definition, all SM particles have Rp = +1 while their superpartners have Rp = −1, and the four terms in are forbidden. Furthermore, as a side effect, the lightest supersymmetric particle (LSP) becomes stable and can be a dark matter candidate.
However, there is no fundamental reason to forbid all four couplings in . When R-parity is conserved both lepton and baryon numbers are conserved, but in order to prevent proton decay just one these two symmetries suffices. Furthermore, the breaking of R-parity by L-violating couplings generates non-zero neutrino masses, and thus constitutes a well-motivated scenario beyond the standard SUSY models. This scenario (with only L-violating couplings) can be theoretically justified by replacing R-parity by a less restrictive symmetry, such as baryon triality [647].
We can distinguish two types of R-parity violating (RPV) neutrino mass models:
• Bilinear R-parity violation (b-p): In this case the only RPV term in the superpotential is the bilinear , which breaks lepton number by one unit. This leads to the generation of one mass scale for the light neutrinos at tree-level via a low-scale seesaw mechanism with the neutralinos playing the role of the right-handed neutrinos. The second (necessary) mass scale is induced at the 1-loop level. Therefore, this can be regarded as a hybrid radiative neutrino mass model.
• Trilinear R-parity violation (t-p): When one allows for the violation of R-parity with the trilinear superpotential terms , lepton number is also broken by one unit and Majorana neutrino masses are generated at the 1-loop level. Therefore, this setup constitutes a pure radiative neutrino mass scenario.
We now proceed to discuss some of the central features of these two types of leptonic RPV models, highlighting the most remarkable experimental predictions. Although in general one can have both types of leptonic RPV simultaneously, we will discuss them separately for the sake of clarity.
Neutrino Masses with b-p
Bilinear R-parity violation [177] is arguably the most economical supersymmetric scenario for neutrino masses. The bilinear ϵi = (ϵe, ϵμ, ϵτ) terms in the superpotential come along with new terms in the soft SUSY breaking potential. Therefore, the number of new parameters in b-p with respect to the MSSM is 6, without modifying its particle content, and they suffice to accommodate all neutrino oscillation data. For a comprehensive review on b-p see Hirsch and Valle [648].
The ϵi couplings induce mixing between the neutrinos and the MSSM neutralinos. In the basis , the neutral fermion mass matrix is given by
Here is the standard MSSM neutralino mass matrix and m ∝ ϵ is the matrix containing the neutrino-neutralino mixing. Assuming the hierarchy (naturally fulfilled if ϵ ≪ mW), one can diagonalize the mass matrix in Equation (106) in the seesaw approximation, , obtaining
where Λi = μvi + vdϵi are the so-called alignment parameters. Here M1,2 are the usual gaugino soft mass terms, μ is the Higgsino superpotential mass term, is the VEV and are the sneutrino VEVs (induced by ϵi ≠ 0). The special (projective) form of mν implies that it is a rank 1 matrix, with only one non-zero eigenvalue, identified with the atmospheric mass scale. Furthermore, one can obtain two leptonic mixing angles in terms of the alignment parameters,
The generation of the solar mass scale, which is much smaller (), requires one to go beyond the tree-level approximation. This makes b-p a hybrid radiative neutrino mass model, since loop corrections are necessary in order to reconcile the model with the observations in neutrino oscillation experiments. An example of such loops is shown in Figure 23, where the bottom–sbottom diagrams are displayed. These are found to be the dominant contributions to the solar mass scale generation in most parts of the parameter space of the model. Other relevant contributions are given by the tau-stau and neutrino-sneutrino loops [649–651]. In all cases two p projections are required, hence leading to the generation of ΔL = 2 Majorana masses for the light neutrinos.
Figure 23. Bottom–Sbottom diagrams for solar neutrino mass in the b-p model. Open circles correspond to small R-parity violating projections, full circles correspond to R-parity conserving projections and crosses indicate genuine mass insertions which flip chirality. hb ≡ Yb is the bottom quark Yukawa coupling. Figure reproduced from Diaz et al. [650].
The most important consequence of the breaking of R-parity at the LHC is that the LSP is no longer stable and decays. In fact, this is the only relevant change with respect to the standard MSSM phenomenology. Since the p couplings are constrained to be small, they do not affect the production cross-sections or the intermediate steps of the decay chains, and hence only the LSP decay is altered in an observable way. For instance, the smallness of the p couplings typically imply observable displaced vertices at the LHC, see for instance de Campos et al. [652]. Furthermore, in b-p there is a sharp correlation between the LSP decay and the mixing angles measured in neutrino oscillation experiments [653–656]. This connection allows to test the model at colliders. For instance, for a neutralino LSP one finds
A departure from this value would rule out the model completely. Interestingly, these correlations are also found in extended models which effectively lead to bilinear p [657–659].
Neutrino Masses with t-p
Supersymmetry with trilinear p has many similarities with leptoquark models. Once the trilinear RPV interactions are allowed in the superpotential, the sfermions become scalar fields with lepton and/or baryon number violating interactions, defining properties of a leptoquark. For instance, the right sbottom has the same quantum numbers as the leptoquark S1 discussed in section 5.4.2 and the λ′ coupling in Equation (104) originates a Yukawa interaction exactly like λLQ in Equation (101)38. For this reason, neutrino mass generation takes place in analogous ways, t-p being a pure radiative model.
As already discussed, the breaking of R-parity leads to the decay of the LSP. This is the most distinctive signature of this family of models. However, in contrast to b-p, the large number of free parameters in t-p exclude the possibility of making definite predictions for the LSP decay. Nevertheless, one expects novel signatures at the LHC, typically with many leptons in the final states [661]. Other signatures, already mentioned in section 4.2, include LFV observables, see for instance de Gouvea et al. [486].
6. Conclusions and Outlook
The discovery of neutrino oscillations and its explanation in terms of massive neutrinos has been one of the most exciting discoveries in particle physics in recent years and a clear sign of lepton flavor violation and physics beyond the SM. Neutrino masses being the first discovery of physics beyond the SM may be related to the fact that the lowest-order effective operator, the Weinberg operator, generates Majorana neutrino masses. This may point to Majorana neutrinos and consequently lepton number violation introducing a new scale beyond the SM. The magnitude of this scale, and that of lepton flavor violation, are unknown.
The sensitivity to many lepton flavor violating processes will be increased by 2-4 orders of magnitude in the next decade and thus test lepton flavor violation at scales of TeV. In particular the expected improvement of up to 4 orders of magnitude for μ − e conversion and the decay μ → eee, but also other processes, will yield strong constraints on the parameter space of currently allowed models or even more excitingly lead to a discovery. Moreover, the LHC is directly probing the TeV-scale and several possible options for colliders are discussed to probe even higher scales. These exciting experimental prospects, together with the simplicity of the explanation for the smallness of neutrino mass, are the main motivations to study radiative neutrino mass models.
Radiative neutrino mass models explain the lightness of neutrinos without introducing heavy scales. The main idea is that neutrino masses are absent at tree-level, being generated radiatively at 1- or higher-loop orders. This, together with the suppressions due to the possible presence of SM masses and/or extra Yukawa and quartic couplings, implies that the scale of these models may be in the range of TeV. This is also theoretically desirable, because all new particles are light and no hierarchy problem is introduced.
The plethora of neutrino mass models studied in the last decades is overwhelming, reaching the hundreds. We believe that at this point an ordering principle for the theory space is necessary to (i) help scientists outside the field to acquire an overview of the topic, (ii) cover the theory space and spot possible holes, (iii) try to draw generic phenomenological conclusions that can be looked for experimentally, and last but not least (iv) serve as reference for model-builders and phenomenologists.
One can choose to systematically classify the different possibilities and models in different complementary ways: in terms of (i) the effective operators they generate after integrating out the heavy particles at tree-level, (ii) the number of loops at which the Weinberg operator is generated, and (iii) the possible topologies within a particular loop order39. In the first case, the contribution of the matching to the Weinberg operator can be easily estimated, and possible UV completions can be outlined. The second option also sheds light on the scale of the new particles. Finally, the study of possible topologies, which have been analyzed up to 2-loop order, helps to systematically pin down neutrino mass models.
We presented selected examples of radiative neutrino mass models in section 5 which serve as benchmark models and discussed their main phenomenological implications such as lepton flavor-violating processes and direct production of the heavy particles at colliders. The phenomenology is generally very rich and quite model-dependent including extra contributions to neutrinoless double beta decay, electric dipole moments, anomalous magnetic moments, and meson decays. Furthermore, radiative neutrino mass models may solve the dark matter problem with a weakly-interacting massive particle running in the loop generating neutrino mass. Also, the new states can play a crucial role for the matter-antimatter asymmetry, although not necessarily in a positive way, and therefore extra bounds can be set on the lepton number violating interactions.
From our work, we have found that there are several interesting avenues that can be pursued in the future:
• If anomalies in B-physics [639–645], or in the muon anomalous magnetic moment [662], persist, their connection to radiative models should be further pursued.
• There are only a few studies of the matter anti-matter asymmetry in radiative neutrino mass models and more detailed studies are required.
• A systematic classification of models generated from effective operators with covariant derivatives40 would help to pin down the possible models involving gauge bosons.
• Further studies of the symmetries that allow the generation of Dirac masses at loop level.
• Beyond the LHC, radiative neutrino mass models can be further tested specially if a future collider has initial leptonic states. If those are same sign, one could directly test the neutrino mass matrix by producing for instance the doubly-charged scalar of the Zee-Babu model [622].
To conclude, it is interesting that there are many combinations of what one may call “aesthetically reasonable” particles—those that have SM multiplet assignments and hypercharges that are not too high—that couple to SM particles in such a way as to realize neutrino mass generation at loop level. Radiative mass generation, as well as being a reasonable hypothesis for explaining the smallness of neutrino masses, also provides many phenomenological signatures at relatively low new-physics scales. So, even if nature realizes the seesaw mechanism with heavy right-handed neutrinos, given the difficulty of testing such a paradigm, falsifying radiative models by means of studying in detail their phenomenology and actively searching for their signals seems the only way to strengthen the case of the former by reducing as much as possible the theory space. Not to mention all the useful insights learned on such a journey.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge the use of the TikZ-Feynman package [663]. JHG acknowledges discussions with Arcadi Santamaria and Nuria Rius. This work was supported in part by the Australian Research Council through the ARC Centre of Excellence for Particle Physics at the Terascale (CoEPP) (CE110001104). A.V. acknowledges financial support from the “Juan de la Cierva” program (27-13-463B-731) funded by the Spanish MINECO as well as from the Spanish grants FPA2014-58183-P, Multidark CSD2009-00064, SEV-2014-0398 and PROMETEOII/ 2014/084 (Generalitat Valenciana).
Footnotes
1. ^The possibility of additional neutrino-like states will be discussed below.
2. ^The effective mass mββ depends on the Majorana phases and thus provides a unique probe for them.
3. ^Sterile neutrinos are not charged under the SM gauge group.
4. ^MiniBooNE also has a mysterious excess in their low-energy bins that cannot be explained by any oscillation hypothesis.
5. ^Pseudo-Dirac neutrinos are a special case of Majorana neutrinos where the masses of two Majorana neutrinos are almost degenerate and the breaking of lepton number is small. However, they should not be confused with Dirac neutrinos.
6. ^RH neutrinos could obviously be added as a singlet of SU(5).
7. ^If one does not impose left–right discrete symmetry on the Lagrangian, then there will be no cosmological domain wall problem. The Dirac seesaw mechanism does not require this discrete symmetry.
8. ^This construction resembles the well-known Froggatt-Nielsen mechanism [59].
9. ^The other ΔL = 2 operators also play an important role in the classification of radiative neutrino mass models and will be discussed in detail in section 2.2.2.
10. ^Note that the LL ~ (1, 1, −1) option is irrelevant for tree level mechanisms because it does not produce the required bilinear.
11. ^The bound on the scale of new physics is generally higher for operators involving heavier quarks.
12. ^In a genuine n-loop neutrino mass model, only diagrams starting from n-loop order contribute to neutrino mass. There are no tree level or lower order loop contributions.
13. ^Note that diagrams with scalar or vector bosons are equivalent from a topological point of view.
14. ^The finite 1-loop corrections to the active neutrino mass matrix in the seesaw model were first discussed in Grimus and Neufeld [282] with an arbitrary number of right-handed neutrinos, left-handed lepton doublets, and Higgs doublets. The finite 1-loop corrections are particularly important in case of delicate cancellations in the tree-level neutrino mass terms, which have been studied in Aristizabal Sierra and Yaguna, [283] using the result of Grimus and Lavoura [284].
15. ^In general, 0νββ is generated in these models at a lower order than neutrino masses.
16. ^There are other operators which, however, are simultaneously generated with the Weinberg operator, which dominates as it is dimension 5 [107].
17. ^Higher order effects break universality in a tiny amount due to Higgs interactions, i.e, by the charged lepton Yukawa couplings.
18. ^In models with an extra Higgs doublet coupled to the leptons, other operators can be formed by integrating out the second Higgs doublet. In those cases, the electrons involved are right-handed and therefore there is no interference with the W boson. An example is the Zee model, see Herrero-García et al. [91].
19. ^See Lee et al. [446], Lee and Shrock [447] and Marciano and Sanda [448] for pioneering work on LFV processes.
20. ^Note the different choice of Lorentz structures in Equations (48), (49). The two forms can be related via the Gordon-identity.
21. ^Carpentier and Davidson [449] provides a comprehensive collection of constraints on quark flavor violating operators.
22. ^We clarify that this is only true for the processes and (with β ≠ δ). The process (with β ≠ δ) does not receive contributions from penguin diagrams, but only from boxes.
23. ^In some models, cancellations due to certain Yukawa textures can affect some decays (like μ → eγ), but it is virtually impossible to cancel all radiative decays simultaneously.
24. ^Interestingly, the authors of Chowdhury and Nasri [129] have shown that in variants of the scotogenic model with higher SU(2) representations the LFV rates become larger due to additive effects from the components of the large multiplets.
25. ^Also in type-I seesaw (and inverse seesaw), and in the MSSM, HLFV is generated at 1-loop order [494–498].
26. ^Theoretically there is no SM background. Realistically, however, object misidentification, undetected particles and fake objects can result in similar final states at the detector level.
27. ^Some of the exotic particles may also show up in tree-level neutrino mass models. The interested reader is referred to the recent review [531] for the collider tests of specific tree-level models.
28. ^Strictly speaking the process is not necessarily LNV, because X may carry lepton number as well, for example in form of neutrinos. Currently the searches are limited to electrons and muons. However, τ-leptons may also be used to search for LNV.
29. ^Long-lived charged particles have been searched at the LHC using anomalously high ionization signal [572], also in the context of dark matter [573]. However, charged scalars in radiative neutrino mass models usually have sizable couplings to SM leptons and decay promptly.
30. ^In this last case, of course, the presence of low scale LNV can be regarded as being less motivated, as in principle there would already be an explanation for neutrino masses (at least for one neutrino).
31. ^Less copies of N means less contribution to the neutrino mass matrix, which in turn generally leads to larger Yukawa couplings to generate the same neutrino mass scale and thus more likely to violate constraints from LFV processes.
32. ^The authors of Chen et al. [356] also point out that up-quarks are not feasible due to gauge invariance.
33. ^The scotogenic model has been extensively studied, sometimes referring to it with different names. For instance, some authors prefer the denomination radiative seesaw. In this review we will stick to the more popular name scotogenic model, which comes from the Greek word skotos (σ oτoσ), darkness. scotogenic would then mean created from darkness.
oτoσ), darkness. scotogenic would then mean created from darkness.
34. ^The Z2 symmetry can obtained from the spontaneous breaking of an Abelian U(1) factor, see for instance Aristizabal Sierra et al. [623].
35. ^We follow the nomenclature in Doršner et al. [638] and Buchmuller et al. [542] for the names of the leptoquarks, where subscripts indicate dimension of the SU(2)L representations.
36. ^Aristizabal Sierra et al. [181] considered the most general interactions with all possible leptoquarks and found in total four mass matrices for leptoquarks with electric charges , , and .
37. ^The contributions of the strange and down quarks are suppressed by and thus have been neglected in the discussion of Angel et al. [287].
38. ^There are, however, additional couplings that supersymmetry forbids but would be allowed for general leptoquarks. Therefore, t-p can then be regarded as a constrained leptoquark scenario. See Deshpande and He [660] for a paper on t-p as a possible explanation for the B-meson anomalies that highlights the similarities between this setup and leptoquark models.
39. ^A fourth complementary classification in terms of particles can be done, which will appear in a future publication Cai, (in prep).
40. ^All possible dimension-7 operators with SM fields and right-handed neutrinos have been listed in Bhattacharya and Wudka [86].
References
1. Hirata KS, Inoue K, Kajita T, Kifune T, Kihara K, Nakahata M, et al. Results from one thousand days of real time directional solar neutrino data. Phys Rev Lett. (1990) 65:1297–300. doi: 10.1103/PhysRevLett.65.1297
2. Hirata KS, Inoue K, Ishida T, Kajita T, Kihara K, Nakahata M, et al. Observation of a small atmospheric νμ/νe ratio in Kamiokande. Phys Lett. (1992) B280:146–52. doi: 10.1016/0370-2693(92)90788-6
3. Fukuda Y, Hayakawa T, Ichihara E, Inoue K, Ishihara K, Ishino H, et al. Evidence for oscillation of atmospheric neutrinos. Phys Rev Lett. (1998) 81:1562–7. doi: 10.1103/PhysRevLett.81.1562
4. Cleveland BT, Daily T, Davis R Jr, Distel JR, Lande K, Lee CK, et al. Measurement of the solar electron neutrino flux with the Homestake chlorine detector. Astrophys J. (1998) 496:505–26. doi: 10.1086/305343
5. Hampela W, Handta J, Heussera G, Kikoa J, Kirstena T, Laubensteina M, et al. GALLEX solar neutrino observations: Results for GALLEX IV. Phys Lett. (1999) B447:127–33.
6. Abdurashitov JN, Gavrin VN, Gorbachev VV, Gurkina PP, Ibragimova TV, Kalikhov AV, et al. Measurement of the solar neutrino capture rate with gallium metal. Phys Rev. (1999) C60:055801.
7. Fukuda S, Fukuda Y, Ishitsuka M, Itow Y, Kajita T, Kameda J, et al. Solar B-8 and hep neutrino measurements from 1258 days of Super-Kamiokande data. Phys Rev Lett. (2001) 86:5651–5. doi: 10.1103/PhysRevLett.86.5651
8. Ahmad QR, Allen RC, Andersen TC, D Anglin J, Barton JC, Beier EW, et al. Direct evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory. Phys Rev Lett. (2002) 89:011301. doi: 10.1103/PhysRevLett.89.011301
9. Altmann M, Balata M, Belli P, Bellotti E, Bernabei R, Burkert E, et al. Complete results for five years of GNO solar neutrino observations. Phys Lett. (2005) B616:174–90. doi: 10.1016/j.physletb.2005.04.068
10. Ahn MH, Aliu E, Andringa S, Aoki S, Aoyama Y, Argyriades J, et al. Measurement of neutrino oscillation by the K2K experiment. Phys Rev. (2006) D74:072003. doi: 10.1103/PhysRevD.74.072003
11. Michael DG, Adamson P, Alexopoulos T, Allison WW, Alner GJ, Anderson K, et al. Observation of muon neutrino disappearance with the MINOS detectors and the NuMI neutrino beam. Phys Rev Lett. (2006) 97:191801. doi: 10.1103/PhysRevLett.97.191801
12. Abe S, Ebihara T, Enomoto S, Furuno K, Gando Y, Ichimura K, et al. Precision measurement of neutrino oscillation parameters with KamLAND. Phys Rev Lett. (2008) 100:221803. doi: 10.1103/PhysRevLett.100.221803
13. Abe K, Abgrall N, Ajima Y, Aihara H, Albert JB, Andreopoulos C, et al. Indication of electron neutrino appearance from an accelerator-produced off-axis muon neutrino beam. Phys Rev Lett. (2011) 107:041801. doi: 10.1103/PhysRevLett.107.041801
14. Abe Y, Aberle C, Akiri T, dos Anjos JC, Ardellier F, Barbosa AF, et al. Indication of reactor disappearance in the double chooz experiment. Phys Rev Lett. (2012) 108:131801. doi: 10.1103/PhysRevLett.108.131801
15. An FP, Bai JZ, Balantekin AB, Band HR, Beavis D, Beriguete W, et al. Observation of electron-antineutrino disappearance at Daya Bay. Phys Rev Lett. (2012) 108:171803. doi: 10.1103/PhysRevLett.108.171803
16. Ahn JK, Chebotaryov S, Choi JH, Choi S, Choi W, Choi Y, et al. Observation of reactor electron antineutrino disappearance in the RENO experiment. Phys Rev Lett. (2012) 108:191802. doi: 10.1103/PhysRevLett.108.191802
17. Abe K, Adam J, Aihara H, Akiri T, Andreopoulos C, Aoki S. Precise measurement of the neutrino mixing parameter θ23 from Muon neutrino disappearance in an off-axis beam. Phys Rev Lett. (2014) 112:181801. doi: 10.1103/PhysRevLett.112.181801
18. Pontecorvo B. Inverse beta processes and nonconservation of lepton charge. Sov Phys JETP. (1958) 7:172–3.
19. Maki Z, Nakagawa M, Sakata S. Remarks on the unified model of elementary particles. Prog Theor Phys. (1962) 28:870–80. doi: 10.1143/PTP.28.870
20. Esteban I, Gonzalez-Garcia MC, Maltoni M, Martinez-Soler I, Schwetz T. Updated fit to three neutrino mixing: exploring the accelerator-reactor complementarity. J High Energy Phys. (2017) 1:087. doi: 10.1007/JHEP01(2017)087
21. Forero DV, Tortola M, Valle JWF. Neutrino oscillations refitted. Phys Rev. (2014) D90:093006. doi: 10.1103/PhysRevD.90.093006
22. Capozzi F, Fogli GL, Lisi E, Marrone A, Montanino D, Palazzo A. Status of three-neutrino oscillation parameters, circa 2013. Phys Rev. (2014) D89:093018. doi: 10.1103/PhysRevD.89.093018
23. Mikheev SP, Smirnov AYu. Resonant amplification of neutrino oscillations in matter and solar neutrino spectroscopy. Nuovo Cim. (1986) C9:17–26. doi: 10.1007/BF02508049
26. Lobashev VM. The search for the neutrino mass by direct method in the tritium beta-decay and perspectives of study it in the project KATRIN. Nucl Phys. (2003) A719:153–60. doi: 10.1016/S0375-9474(03)00985-0
27. Kraus C, Bornschein B, Bornschein L, Bonn J, Flatt B, Kovalik A, et al. Final results from phase II of the Mainz neutrino mass search in tritium beta decay. Eur Phys J. (2005) C40:447–68. doi: 10.1140/epjc/s2005-02139-7
28. Aseev VN, Belesev AI, Berlev AI, Geraskin EV, Golubev AA, Likhovid NA, et al. An upper limit on electron antineutrino mass from Troitsk experiment. Phys Rev. (2011) D84:112003. doi: 10.1103/PhysRevD.84.112003
29. Osipowicz A, Blümer H, Drexlin G, Eitel K, Meisel G, Plischke P, et al. KATRIN: a next generation tritium beta decay experiment with sub-eV sensitivity for the electron neutrino mass. Lett. Intent (2001). Available online at: https://arxiv.org/pdf/hep-ex/0109033.pdf
30. Ade PAR, Aghanim N, Arnaud M, Ashdown M, Aumont J, Baccigalupi C, et al. Planck 2015 results. XIII. Cosmological parameters. Astron Astrophys. (2016) 594:A13. doi: 10.1051/0004-6361/201525830
31. Agostini M, Allardt M, Bakalyarov AM, Balata M, Barabanov I, Baudis L, et al. Background free search for neutrinoless double beta decay with GERDA Phase II. (2017) Nature 544:47. doi: 10.1038/nature21717
32. Gariazzo S, Giunti C, Laveder M, Li YF. Updated global 3+1 analysis of short-baseline neutrino oscillations. J High Energy Phys. (2017) 6:135. doi: 10.1007/JHEP06(2017)135
33. Kopp J, Machado PAN, Maltoni M, Schwetz T. Sterile neutrino oscillations: the global picture. J High Energy Phys. (2013) 5:050. doi: 10.1007/JHEP05(2013)050
34. Athanassopoulos C, Auerbach LB, Burman RL, Caldwell DO, Church ED, Cohen I, et al. Evidence for νμ → νe neutrino oscillations from LSND. Phys Rev Lett. (1998) 81:1774–7. doi: 10.1103/PhysRevLett.81.1774
35. Aguilar-Arevalo A, Auerbach LB, Burman RL, Caldwell DO, Church ED, Cochran AK, et al. Evidence for neutrino oscillations from the observation of anti-neutrino(electron) appearance in a anti-neutrino(muon) beam. Phys Rev. (2001) D64:112007. doi: 10.1103/PhysRevD.64.112007
36. Aguilar-Arevalo AA, Bazarko AO, Brice SJ, Brown BC, Bugel L, Cao J, et al. A Search for electron neutrino appearance at the Δm2 ~ 1eV2 scale. Phys Rev Lett. (2007) 98:231801. doi: 10.1103/PhysRevLett.98.231801
37. Aguilar-Arevalo AA, Brown BC, Bugel L, Cheng G, Church ED, Conrad JM, et al. Improved search for oscillations in the miniBooNE experiment. Phys Rev Lett. (2013) 110:161801. doi: 10.1103/PhysRevLett.110.161801
38. Aartsen MG, Ackermann M, Adams J, Aguilar JA, Ahlers M, Ahrens I, et al. Search for sterile neutrino mixing using three years of IceCube DeepCore data. Phys Rev. (2017) D95:112002. doi: 10.1103/PhysRevD.95.112002
39. Mueller TA, Lhuillier D, Fallot M, Letourneau A, Cormon S, Fechner M, et al. Improved predictions of reactor antineutrino spectra. Phys Rev. (2011) C83:054615. doi: 10.1103/PhysRevC.83.054615
40. Huber P. On the determination of anti-neutrino spectra from nuclear reactors. Phys Rev. (2011) C84:024617. doi: 10.1103/PhysRevC.84.024617
41. Mention G, Fechner M, Lasserre T, Mueller TA, Lhuillier D, Cribier M, et al. The reactor antineutrino anomaly. Phys Rev. (2011) D83:073006. doi: 10.1103/PhysRevD.83.073006
42. Hampel W, Heusser G, Kiko J, Kirsten TA, Laubenstein M, Pernicka E, et al. Final results of the Cr-51 neutrino source experiments in GALLEX. Phys Lett. (1998) B420:114–26.
43. Abdurashitov JN, Gavrin VN, Girin SV, Gorbachev VV, Ibragimova TV, Kalikhov AV, et al. Measurement of the response of the Russian-American gallium experiment to neutrinos from a Cr-51 source. Phys Rev. (1999) C59:2246–63.
44. Abdurashitov JN, Gavrin VN, Gorbachev VV, Gurkina PP, Ibragimova TV, Kalikhov AV, et al. Measurement of the solar neutrino capture rate with gallium metal. III: results for the 2002–2007 data-taking period. Phys Rev. (2009) C80:015807. doi: 10.1103/PhysRevC.80.015807
45. Kaether F, Hampel W, Heusser G, Kiko J, Kirsten T. Reanalysis of the GALLEX solar neutrino flux and source experiments. Phys Lett. (2010) B685:47–54. doi: 10.1016/j.physletb.2010.01.030
46. An FP, Balantekin AB, Band HR, Bishai M, Blyth S, Cao D, et al. Evolution of the reactor antineutrino flux and spectrum at Daya bay. Phys Rev Lett. (2017) 118:251801. doi: 10.1103/PhysRevLett.118.251801
47. Minkowski P. μ → eγ at a Rate of One Out of 109 Muon Decays? Phys Lett. (1977) B67:421–8. doi: 10.1016/0370-2693(77)90435-X
49. Gell-Mann M, Ramond P, Slansky R. Complex spinors and unified theories. Conf Proc. (1979) C790927:315–21.
50. Mohapatra RN, Senjanovic G. Neutrino mass and spontaneous parity violation. Phys Rev Lett. (1980) 44:912. doi: 10.1103/PhysRevLett.44.912
51. Glashow SL. The future of elementary particle physics. NATO Sci Ser B (1980) 61:687. doi: 10.1007/978-1-4684-7197-7_15
52. Foot R, Joshi GC, Lew H, Volkas RR. Charge quantization in the standard model and some of its extensions. Mod Phys Lett. (1990) A5:2721–32. doi: 10.1142/S0217732390003176
53. Babu KS, Mohapatra RN. Is there a connection between quantization of electric charge and a majorana neutrino? Phys Rev Lett. (1989) 63:938. doi: 10.1103/PhysRevLett.63.938
54. 't Hooft G. Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking. NATO Sci Ser B (1980) 59:135–57.
55. Roy P, Shanker OU. Observable neutrino dirac mass and supergrand unification. Phys Rev Lett. (1984) 52:713–6. doi: 10.1103/PhysRevLett.52.713
56. Ma E, Popov O. Pathways to naturally small dirac neutrino masses. Phys Lett. (2017) B764:142–4. doi: 10.1016/j.physletb.2016.11.027
57. Wang F, Wang W, Yang JM. Split two-higgs-doublet model and neutrino condensation. EuroPhys Lett. (2006) 76:388–94. doi: 10.1209/epl/i2006-10293-3
58. Gabriel S, Nandi S. A new two Higgs doublet model. Phys Lett. (2007) B655:141–7. doi: 10.1016/j.physletb.2007.04.062
59. Froggatt CD, Nielsen HB. Hierarchy of quark masses, cabibbo angles and CP violation. Nucl Phys. (1979) B147:277–98.
60. Wang W, Han ZL. Naturally small dirac neutrino mass with intermediate SU(2)L multiplet fields. J High Energy Phys. (2016) 4:166. doi: 10.1007/JHEP04(2017)166
61. Randall L, Sundrum R. A Large mass hierarchy from a small extra dimension. Phys Rev Lett. (1999) 83:3370–3. doi: 10.1103/PhysRevLett.83.3370
62. Randall L, Sundrum R. An alternative to compactification. Phys Rev Lett. (1999) 83:4690–3. doi: 10.1103/PhysRevLett.83.4690
63. Grossman Y, Neubert M. Neutrino masses and mixings in nonfactorizable geometry. Phys Lett. (2000) B474:361–71. doi: 10.1016/S0370-2693(00)00054-X
64. Gherghetta T, Pomarol A. Bulk fields and supersymmetry in a slice of AdS. Nucl Phys. (2000) B586:141–62. doi: 10.1016/S0550-3213(00)00392-8
65. Huber SJ, Shafi Q. Neutrino oscillations and rare processes in models with a small extra dimension. Phys Lett. (2001) B512:365–72. doi: 10.1016/S0370-2693(01)00736-5
66. Moreau G, Silva-Marcos JI. Neutrinos in warped extra dimensions. J High Energy Phys. (2006) 1:048. doi: 10.1088/1126-6708/2006/01/048
67. Agashe K, Okui T, Sundrum R. A common origin for neutrino anarchy and charged hierarchies. Phys Rev Lett. (2009) 102:101801. doi: 10.1103/PhysRevLett.102.101801
68. Chang WF, Ng JN, Wu JMS. Discrete dirac neutrino in warped extra dimensions. Phys Rev. (2009) D80:113013. doi: 10.1103/PhysRevD.80.113013
69. De Gouvea A, Giudice GF, Strumia A, Tobe K. Phenomenological implications of neutrinos in extra dimensions. Nucl Phys. (2002) B623:395–420. doi: 10.1016/S0550-3213(01)00621-6
70. Choi K, Im SH. Realizing the relaxion from multiple axions and its UV completion with high scale supersymmetry. J High Energy Phys. (2016) 1:149. doi: 10.1007/JHEP01(2016)149
71. Kaplan DE, Rattazzi R. Large field excursions and approximate discrete symmetries from a clockwork axion. Phys Rev. (2016) D93:085007. doi: 10.1103/PhysRevD.93.085007
72. Hambye T, Teresi D, Tytgat MHG. A clockwork WIMP. J High Energy Phys. (2017) 7:47. doi: 10.1007/JHEP07(2017)047
73. Giudice GF, McCullough M. A clockwork theory. J High Energy Phys. (2017) 2:036. doi: 10.1007/JHEP02(2017)036
74. Magg M, Wetterich C. Neutrino mass problem and gauge hierarchy. Phys Lett. (1980) B94:61–4. doi: 10.1016/0370-2693(80)90825-4
76. Cheng TP, Li LF. Neutrino masses, mixings and oscillations in SU(2) × U(1) models of electroweak interactions. Phys Rev. (1980) D22:2860.
77. Lazarides G, Shafi Q, Wetterich C. Proton lifetime and Fermion masses in an SO(10) model. Nucl Phys. (1981) B181:287–300.
79. Mohapatra RN, Senjanovic G. Neutrino masses and mixings in Gauge models with spontaneous parity violation. Phys Rev. (1981) D23:165.
80. Foot R, Lew H, He XG, Joshi GC. Seesaw neutrino masses induced by a triplet of leptons. Z Phys. (1989) C44:441.
81. Weinberg S. Baryon and Lepton nonconserving processes. Phys Rev Lett. (1979) 43:1566–70. doi: 10.1103/PhysRevLett.43.1566
82. Kumericki K, Picek I, Radovcic B. TeV-scale seesaw with quintuplet fermions. Phys Rev. (2012) D86:013006. doi: 10.1103/PhysRevD.86.013006
83. Picek I, Radovcic B. Enhancement of h → γγ by seesaw-motivated exotic scalars. Phys Lett. (2013) B719:404–8. doi: 10.1016/j.physletb.2013.01.056
84. Liao Y. Cascade seesaw for tiny neutrino mass. J High Energy Phys. (2011) 6:98. doi: 10.1007/JHEP06(2011)098
85. Babu KS, Leung CN. Classification of effective neutrino mass operators. Nucl Phys. (2001) B619:667–89. doi: 10.1016/S0550-3213(01)00504-1
86. Bhattacharya S, Wudka J. Dimension-seven operators in the standard model with right handed neutrinos. Phys Rev. (2016) D94:055022. doi: 10.1103/PhysRevD.94.055022
87. de Gouvea A, Jenkins J. A survey of lepton number violation via effective operators. Phys Rev. (2008) D77:013008. doi: 10.1103/PhysRevD.77.013008
88. de Gouvêa A, Herrero-García J, Kobach A. Neutrino masses, grand unification, and baryon number violation. Phys Rev. (2014) D90:016011. doi: 10.1103/PhysRevD.90.016011
89. Kobach A. Baryon number, lepton number, and operator dimension in the standard model. Phys Lett. (2016) B758:455–7. doi: 10.1016/j.physletb.2016.05.050
90. Angel PW, Rodd NL, Volkas RR. Origin of neutrino masses at the LHC: ΔL = 2 effective operators and their ultraviolet completions. Phys Rev. (2013) D87:073007. doi: 10.1103/PhysRevD.87.073007
91. Herrero-García J, Ohlsson T, Riad S, Wirén J. Full parameter scan of the Zee model: exploring Higgs lepton flavor violation. J High Energy Phys. (2017) 4:130. doi: 10.1007/JHEP04(2017)130
92. Frere JM, Jones DRT, Raby S. Fermion masses and induction of the weak scale by supergravity. Nucl Phys. (1983) B222:11–9.
93. Alvarez-Gaume L, Polchinski J, Wise MB. Minimal low-energy supergravity. Nucl Phys. (1983) B221:495.
94. Casas JA, Dimopoulos S. Stability bounds on flavor violating trilinear soft terms in the MSSM. Phys Lett. (1996) B387:107–12.
95. Herrero-Garcia J, Nebot M, Rius N, Santamaria A. The zee–babu model revisited in the light of new data. Nucl Phys. (2014) B885:542–70. doi: 10.1016/j.nuclphysb.2014.06.001
96. Nomura T, Okada H. A four-loop Radiative Seesaw Model. Phys Lett. (2017) B770:307–13. doi: 10.1016/j.physletb.2017.05.002
97. Nomura T, Okada H. Four-loop neutrino model inspired by diphoton excess at 750 GeV. Phys Lett. (2016) B755:306–11. doi: 10.1016/j.physletb.2016.02.022
98. Cárcamo Hernández AE, Kovalenko S, Schmidt I. Radiatively generated hierarchy of lepton and quark masses. J High Energy Phys. (2017) 2:125. doi: 10.1007/JHEP02(2017)125
99. Ma E. Pathways to naturally small neutrino masses. Phys Rev Lett. (1998) 81:1171–4. doi: 10.1103/PhysRevLett.81.1171
100. Bonnet F, Hirsch M, Ota T, Winter W. Systematic study of the d=5 Weinberg operator at one-loop order. J High Energy Phys. (2012) 7:153. doi: 10.1007/JHEP07(2012)153
101. Cepedello R, Hirsch M, Helo JC. Loop neutrino masses from d = 7 operator. J High Energy Phys. (2017) 7:079. doi: 10.1007/JHEP07(2017)079
102. Aristizabal Sierra D, Degee A, Dorame L, Hirsch M. Systematic classification of two-loop realizations of the Weinberg operator. J High Energy Phys. (2015) 3:40. doi: 10.1007/JHEP03(2015)040
103. Law SSC, McDonald KL. The simplest models of radiative neutrino mass. Int J Mod Phys. (2014) A29:1450064. doi: 10.1142/S0217751X1450064X
104. Zee A. A theory of lepton number violation, neutrino majorana mass, and oscillation. Phys Lett. (1980) B93:389. doi: 10.1016/0370-2693(80)90349-4
105. Wolfenstein L. A theoretical pattern for neutrino oscillations. Nucl Phys. (1980) B175:93–6. doi: 10.1016/0550-3213(80)90004-8
106. Bonnet F, Hirsch M, Ota T, Winter W. Systematic decomposition of the neutrinoless double beta decay operator. J High Energy Phys. (2013) 3:55. doi: 10.1007/JHEP03(2013)055
107. del Aguila F, Aparici A, Bhattacharya S, Santamaria A, Wudka J. Effective Lagrangian approach to neutrinoless double beta decay and neutrino masses. J High Energy Phys. (2012) 6:146. doi: 10.1007/JHEP06(2012)146
108. Helo JC, Hirsch M, Ota T. Long-range contributions to double beta decay revisited. J High Energy Phys. (2016) 6:6. doi: 10.1007/JHEP06(2016)006
109. Hagedorn C, Ohlsson T, Riad S, Schmidt MA. Unification of gauge couplings in radiative neutrino mass models. J High Energy Phys. (2016) 9:111. doi: 10.1007/JHEP09(2016)111
110. Farzan Y, Pascoli S, Schmidt MA. Recipes and ingredients for neutrino mass at loop level. J High Energy Phys. (2013) 3:107. doi: 10.1007/JHEP03(2013)107
111. Restrepo D, Zapata O, Yaguna CE. Models with radiative neutrino masses and viable dark matter candidates. J High Energy Phys. (2013) 11:11. doi: 10.1007/JHEP11(2013)011
112. Simoes C, Wegman D. Radiative two-loop neutrino masses with dark matter. J High Energy Phys. (2017) 4:148. doi: 10.1007/JHEP04(2017)148
113. Ma E. Verifiable radiative seesaw mechanism of neutrino mass and dark matter. Phys Rev. (2006) D73:077301. doi: 10.1103/PhysRevD.73.077301
114. Ma E, Suematsu D. Fermion triplet dark matter and radiative neutrino mass. Mod Phys Lett. (2009) A24:583–9. doi: 10.1142/S021773230903059X
115. Chao W. Dark matter, LFV and neutrino magnetic moment in the radiative seesaw model with fermion triplet. Int J Mod Phys. (2015) A30:1550007. doi: 10.1142/S0217751X15500074
116. von der Pahlen F, Palacio G, Restrepo D, Zapata O. Radiative type III seesaw model and its collider phenomenology. Phys Rev. (2016) D94:033005. doi: 10.1103/PhysRevD.94.033005
117. Farzan Y. A minimal model linking two great mysteries: neutrino mass and dark matter. Phys Rev. (2009) D80:073009. doi: 10.1103/PhysRevD.80.073009
118. Hehn D, Ibarra A. A radiative model with a naturally mild neutrino mass hierarchy. Phys Lett. (2013) B718:988–91. doi: 10.1016/j.physletb.2012.11.034
119. Lu, W-B, Gu, P-H. Mixed inert scalar triplet dark matter, radiative neutrino masses and leptogenesis. Nucl Phys. (2017) B924:279–311. doi: 10.1016/j.nuclphysb.2017.09.005
120. Fileviez Perez P, Wise MB. On the origin of neutrino masses. Phys Rev. (2009) D80:053006. doi: 10.1103/PhysRevD.80.053006
121. Liao Y, Liu JY. Radiative and flavor-violating transitions of leptons from interactions with color-octet particles. Phys Rev. (2010) D81:013004. doi: 10.1103/PhysRevD.81.013004
122. Farzan Y, Pascoli S, Schmidt MA. AMEND: a model explaining neutrino masses and dark matter testable at the LHC and MEG. J High Energy Phys. (2010) 10:111. doi: 10.1007/JHEP10(2010)111
123. Okada H, Orikasa Y. Radiative neutrino model with an inert triplet scalar. Phys Rev. (2016) D94:055002. doi: 10.1103/PhysRevD.94.055002
124. Brdar V, Picek I, Radovcic B. Radiative neutrino mass with scotogenic scalar triplet. Phys Lett. (2014) B728:198–201. doi: 10.1016/j.physletb.2013.11.045
125. Aoki M, Kanemura S, Yagyu K. Doubly-charged scalar bosons from the doublet. Phys Lett. (2011) B702:355–8. doi: 10.1016/j.physletb.2011.07.017
126. Cai Y, He XG, Ramsey-Musolf M, Tsai LH. RνMDM and lepton flavor violation. J High Energy Phys. (2011) 12:054. doi: 10.1007/JHEP12(2011)054
127. Chen CH, Law SSC. Exotic fermion multiplets as a solution to baryon asymmetry, dark matter and neutrino masses. Phys Rev. (2012) D85:055012. doi: 10.1103/PhysRevD.85.055012
128. Law SSC, McDonald KL. A class of inert N-tuplet models with radiative neutrino mass and dark matter. J High Energy Phys. (2013) 9:92. doi: 10.1007/JHEP09(2013)092
129. Chowdhury TA, Nasri S. Lepton flavor violation in the inert scalar model with higher representations. J High Energy Phys. (2015) 12:40. doi: 10.1007/JHEP12(2015)040
130. Chen CH, Geng CQ, Zhuridov DV. Neutrino masses, leptogenesis and decaying dark matter. J Cosmol Astropart Phys. (2009) 0910:001. doi: 10.1088/1475-7516/2009/10/001
131. Patra S, Sahoo N, Sahu N. Dipolar dark matter in light of the 3.5 keV x-ray line, neutrino mass, and LUX data. Phys Rev. (2015) D91:115013. doi: 10.1103/PhysRevD.91.115013
132. Ferreira PM, Grimus W, Jurciukonis D, Lavoura L. Scotogenic model for co-bimaximal mixing. J High Energy Phys. (2016) 7:10. doi: 10.1007/JHEP07(2016)010
133. Fortes ECFS, Machado ACB, Montaño J, Pleitez V. Lepton masses and mixing in a scotogenic model. (2017) arXiv:1705.09414.
134. Ma E. Dark scalar doublets and neutrino tribimaximal mixing from A4 symmetry. Phys Lett. (2009) B671:366–8. doi: 10.1016/j.physletb.2008.12.038
135. Bhattacharya S, Ma E, Natale A, Rashed A. Radiative scaling neutrino mass with A4 symmetry. Phys Rev. (2013) D87:097301. doi: 10.1103/PhysRevD.87.097301
136. Carcamo Hernandez AE, de Medeiros Varzielas I, Kovalenko SG, Päs H, Schmidt I. Lepton masses and mixings in an A4 multi-Higgs model with a radiative seesaw mechanism. Phys Rev. (2013) D88:076014. doi: 10.1103/PhysRevD.88.076014
137. Campos MD, Cárcamo Hernández AE, Kovalenko S, Schmidt I, Schumacher E. Fermion masses and mixings in an SU(5) grand unified model with an extra flavor symmetry. Phys Rev. (2014) D90:016006. doi: 10.1103/PhysRevD.90.016006
138. Ma E. Neutrino mixing and geometric CP violation with delta(27) symmetry. Phys Lett. (2013) B723:161–3. doi: 10.1016/j.physletb.2013.05.011
139. Ma E, Natale A. Scotogenic Z2 or U(1)D model of neutrino mass with Δ(27) symmetry. Phys Lett. (2014) B734:403–5. doi: 10.1016/j.physletb.2014.05.070
140. Gu PH, Sarkar U. Radiative seesaw in left-right symmetric model. Phys Rev. (2008) D78:073012. doi: 10.1103/PhysRevD.78.073012
141. Adulpravitchai A, Lindner M, Merle A, Mohapatra RN. Radiative transmission of lepton flavor hierarchies. Phys Lett. (2009) B680:476–9. doi: 10.1016/j.physletb.2009.09.042
142. Parida MK. Radiative seesaw in SO(10) with dark matter. Phys Lett. (2011) B704:206–10. doi: 10.1016/j.physletb.2011.09.016
143. Ma E. Unified framework for matter, dark matter, and radiative neutrino mass. Phys Rev. (2013) D88:117702. doi: 10.1103/PhysRevD.88.117702
144. Megrelidze L, Tavartkiladze Z. Soft see-saw: radiative origin of neutrino masses in SUSY theories. Nucl Phys. (2017) B914:553–76. doi: 10.1016/j.nuclphysb.2016.11.019
145. Ma E, Picek I, Radovčić B. New scotogenic model of neutrino mass with U(1)D gauge interaction. Phys Lett. (2013) B726:744–6. doi: 10.1016/j.physletb.2013.09.049
146. Ma E. Supersymmetric model of radiative seesaw majorana neutrino masses. Ann Fond Broglie (2006) 31:285. Available online at: https://arxiv.org/abs/hep-ph/0607142
147. Ma E. SU(5) completion of the dark scalar doublet model of radiative neutrino mass. Phys Lett. (2008) B659:885–7. doi: 10.1016/j.physletb.2007.12.013
148. Khalil S, Lee HS, Ma E. Generalized lepton number and dark left-right gauge model. Phys Rev. (2009) D79:041701. doi: 10.1103/PhysRevD.79.041701
149. Ma E. Variants of the dark left-right gauge model: neutrinos and scotinos. Phys Rev. (2009) D79:117701. doi: 10.1103/PhysRevD.79.117701
150. Budhi RHS, Kashiwase S, Suematsu D. Inflation in a modified radiative seesaw model. Phys Rev. (2014) D90:113013. doi: 10.1103/PhysRevD.90.113013
151. Kashiwase S, Suematsu D. Lepton number asymmetry via inflaton decay in a modified radiative seesaw model. Phys Lett. (2015) B749:603–12. doi: 10.1016/j.physletb.2015.08.062
152. Budhi RHS, Kashiwase S, Suematsu D. Inflation due to a nonminimal coupling of singlet scalars in the radiative seesaw model. Phys Rev. (2016) D93:013022. doi: 10.1103/PhysRevD.93.013022
153. Arhrib A, Bœhm C, Ma E, Yuan TC. Radiative model of neutrino mass with neutrino interacting MeV dark matter. J Cosmol Astropart Phys. (2016) 1604:49. doi: 10.1088/1475-7516/2016/04/049
154. Lu WB, Gu PH. Leptogenesis, radiative neutrino masses and inert Higgs triplet dark matter. J Cosmol Astropart Phys. (2016) 1605:040. doi: 10.1088/1475-7516/2016/05/040
155. Koide Y. Can the zee model explain the observed neutrino data? Phys Rev. (2001) D64:077301. doi: 10.1103/PhysRevD.64.077301
156. He XG. Is the zee model neutrino mass matrix ruled out? Eur Phys J. (2004) C34:371–6. doi: 10.1140/epjc/s2004-01669-8
157. He XG, Majee SK. Implications of recent data on neutrino mixing and lepton flavour violating decays for the zee model. J High Energy Phys. (2012) 3:23. doi: 10.1007/JHEP03(2012)023
158. Babu KS, Julio J. Predictive model of radiative neutrino masses. Phys Rev. (2014) D89:053004. doi: 10.1103/PhysRevD.89.053004
159. Aranda A, Bonilla C, Rojas AD. Neutrino masses generation in a Z4 model. Phys Rev. (2012) D85:036004. doi: 10.1103/PhysRevD.85.036004
160. Leontaris GK, Tamvakis K. The supersymmetric singlet. Phys Lett. (1987) B191:421–6. doi: 10.1016/0370-2693(87)90633-2
161. Haba N, Matsuda M, Tanimoto M. Large neutrino flavor mixings and gauge mediated supersymmetry breaking scenario. Phys Lett. (2000) B478:351–7. doi: 10.1016/S0370-2693(00)00275-6
162. Cheung Km, Kong OCW. Zee neutrino mass model in SUSY framework. Phys Rev. (2000) D61:113012. doi: 10.1103/PhysRevD.61.113012
163. Kanemura S, Shindou T, Sugiyama H. R-parity conserving supersymmetric extension of the zee model. Phys Rev. (2015) D92:115001. doi: 10.1103/PhysRevD.92.115001
164. Tamvakis K, Vergados JD. Neutrino masses and oscillations in an unconventional model of lepton number violation. Phys Lett. (1985) B155:373–80.
165. Fileviez Perez P, Murgui C. Renormalizable SU(5) unification. Phys Rev. (2016) D94:075014. doi: 10.1103/PhysRevD.94.075014
166. Chang WF, Ng JN. Neutrino masses in 5-D orbifold SU(5) unification models without right handed singlets. J High Energy Phys. (2003) 10:036. doi: 10.1088/1126-6708/2003/10/036
167. Chang WF, Chen IT, Liou SC. Neutrino masses via the zee mechanism in 5D split fermions model. Phys Rev. (2011) D83:025017. doi: 10.1103/PhysRevD.83.025017
168. Babu KS, Mohapatra RN. Model for large transition magnetic moment of the νe. Phys Rev Lett. (1989) 63:228. doi: 10.1103/PhysRevLett.63.228
169. Babu KS, Mohapatra RN. Large transition magnetic moment of the neutrino from horizontal symmetry. Phys Rev. (1990) D42:3778–93. doi: 10.1103/PhysRevD.42.3778
170. Koide Y, Ghosal A. Bimaximal neutrino mixing in a Zee type model with badly broken flavor symmetry. Phys Rev. (2001) D63:037301. doi: 10.1103/PhysRevD.63.037301
171. Kitabayashi T, Yasue M. Large solar neutrino mixing and radiative neutrino mechanism. Phys Lett. (2002) B524:308–18. doi: 10.1016/S0370-2693(01)01368-5
172. Adhikary B, Brahmachari B, Ghosal A, Ma E, Parida MK. A4 symmetry and prediction of Ue3 in a modified Altarelli-Feruglio model. Phys Lett. (2006) B638:345–9. doi: 10.1016/j.physletb.2006.05.051
173. Fukuyama T, Sugiyama H, Tsumura K. Phenomenology in the zee model with the A4 symmetry. Phys Rev. (2011) D83:056016. doi: 10.1103/PhysRevD.83.056016
174. Aranda A, Bonilla C, Ramos R, Rojas AD. A renormalizable fermion mass model with the double tetrahedral group. (2010) arXiv:1011.6470.
175. Aranda A, Bonilla C, Ramos R, Rojas AD. Model of flavor with quaternion symmetry. Phys Rev. (2011) D84:016009. doi: 10.1103/PhysRevD.84.016009
176. Okamoto Y, Yasue M. Comment on radiative neutrino mass matrix with a sterile neutrino. Prog Theor Phys. (1999) 101:1119–27. doi: 10.1143/PTP.101.1119
177. Hall LJ, Suzuki M. Explicit R-parity breaking in supersymmetric models. Nucl Phys. (1984) B231:419–44. doi: 10.1016/0550-3213(84)90513-3
178. Nieves JF. Baryon and lepton number nonconserving processes and intermediate mass scales. Nucl Phys. (1981) B189:182–204.
179. Chua CK, He XG, Hwang WYP. Neutrino mass induced radiatively by supersymmetric leptoquarks. Phys Lett. (2000) B479:224–9. doi: 10.1016/S0370-2693(00)00325-7
180. Mahanta U. Neutrino masses and mixing angles from leptoquark interactions. Phys Rev. (2000) D62:073009. doi: 10.1103/PhysRevD.62.073009
181. Aristizabal Sierra D, Hirsch M, Kovalenko SG. Leptoquarks: neutrino masses and accelerator phenomenology. Phys Rev. (2008) D77:055011. doi: 10.1103/PhysRevD.77.055011
182. Helo JC, Hirsch M, Ota T, Pereira dos Santos FA. Double beta decay and neutrino mass models. J High Energy Phys. (2015) 5:92. doi: 10.1007/JHEP05(2015)092
183. Päs H, Schumacher E. Common origin of RK and neutrino masses. Phys Rev. (2015) D92:114025. doi: 10.1103/PhysRevD.92.114025
184. Cheung K, Nomura T, Okada H. Testable radiative neutrino mass model without additional symmetries and explanation for the b → sℓ+ℓ− anomaly. Phys Rev. (2016) D94:115024. doi: 10.1103/PhysRevD.94.115024
185. Doršner I, Fajfer S, Košnik N. Leptoquark mechanism of neutrino masses within the grand unification framework. Eur Phys J. (2017) C77:417. doi: 10.1140/epjc/s10052-017-4987-2
186. Kong OCW. LR scalar mixings and oneloop neutrino masses. J High Energy Phys. (2000) 9:37. doi: 10.1088/1126-6708/2000/09/037
187. Davidson S, Losada M. Neutrino masses in the Rp violating MSSM. J High Energy Phys. (2000) 5:21. doi: 10.1088/1126-6708/2000/05/021
188. Koide Y, Sato J. R-parity violation in a SUSY GUT model and radiative neutrino masses. Phys Rev. (2003) D68:056004. doi: 10.1103/PhysRevD.68.056004
189. Koide Y. Radiative neutrino masses in a SUSY GUT model. Phys Lett. (2003) B574:82–8. doi: 10.1016/j.physletb.2003.09.002
190. Koide Y. Neutrino masses without seesaw mechanism in a SUSY SU(5) model with additional . Phys Lett. (2004) B595:469–75. doi: 10.1016/j.physletb.2004.05.072
191. Longas R, Portillo D, Restrepo D, Zapata O. The inert zee model. J High Energy Phys. (2016) 3:162. doi: 10.1007/JHEP03(2016)162
192. Ma E, Raidal M, Sarkar U. Neutrino masses in supersymmetry: R-parity and leptogenesis. Phys Lett. (1999) B460:359–64. doi: 10.1016/S0370-2693(99)00755-8
193. Suematsu D, Toma T, Yoshida T. Neutrino masses and μ terms in a supersymmetric extra U(1) model. Int J Mod Phys. (2010) A25:4033–53. doi: 10.1142/S0217751X1005024X
194. Ma E. Supersymmetric U(1) gauge realization of the dark scalar doublet model of radiative neutrino mass. Mod Phys Lett. (2008) A23:721–5. doi: 10.1142/S0217732308026753
195. Ma E. Axionic extensions of the supersymmetric standard model. Mod Phys Lett. (2009) A24:1335–42. doi: 10.1142/S0217732309030837
196. Fukuoka H, Kubo J, Suematsu D. Anomaly induced dark matter decay and PAMELA/ATIC experiments. Phys Lett. (2009) B678:401–6. doi: 10.1016/j.physletb.2009.06.048
197. Suematsu D, Toma T. Dark matter in the supersymmetric radiative seesaw model with an anomalous U(1) symmetry. Nucl Phys. (2011) B847:567–89. doi: 10.1016/j.nuclphysb.2011.02.007
198. Fukuoka H, Suematsu D, Toma T. Signals of dark matter in a supersymmetric two dark matter model. J Cosmol Astropart Phys. (2011) 1107:001. doi: 10.1088/1475-7516/2011/07/001
199. Bhattacharya S, Ma E, Wegman D. Supersymmetric left-right model with radiative neutrino mass and multipartite dark matter. Eur Phys J. (2014) C74:2902. doi: 10.1140/epjc/s10052-014-2902-7
200. Kanemura S, Machida N, Shindou T, Yamada T. A UV complete model for radiative seesaw scenarios and electroweak baryogenesis based on the supersymmetric gauge theory. Phys Rev. (2014) D89:013005. doi: 10.1103/PhysRevD.89.013005
201. R Figueiredo AJ. Neutrino masses from SUSY breaking in radiative seesaw models. Eur Phys J. (2015) C75:99. doi: 10.1140/epjc/s10052-014-3244-1
202. Kanemura S, Machida N, Shindou T. Radiative neutrino mass, dark matter and electroweak baryogenesis from the supersymmetric gauge theory with confinement. Phys Lett. (2014) B738:178–86. doi: 10.1016/j.physletb.2014.09.013
203. Hundi RS. μ → eγ in a supersymmetric radiative neutrino mass model. Phys Rev. (2016) D93:015008. doi: 10.1103/PhysRevD.93.015008
204. Fraser S, Ma E, Popov O. Scotogenic inverse seesaw model of neutrino mass. Phys Lett. (2014) B737:280–2. doi: 10.1016/j.physletb.2014.08.069
205. Restrepo D, Rivera A, Sánchez-Peláez M, Zapata O, Tangarife W. Radiative neutrino masses in the singlet-doublet fermion dark matter model with scalar singlets. Phys Rev. (2015) D92:013005. doi: 10.1103/PhysRevD.92.013005
206. Chiang C-W, Okada H, Senaha E. Dark matter, muon g−2, electric dipole moments, and in a one-loop induced neutrino model. Phys Rev. (2017) D96:015002. doi: 10.1103/PhysRevD.96.015002
207. Mohapatra RN. Mechanism for understanding small neutrino mass in superstring theories. Phys Rev Lett. (1986) 56:561–3. doi: 10.1103/PhysRevLett.56.561
208. Mohapatra RN, Valle JWF. Neutrino mass and baryon number nonconservation in superstring models. Phys Rev. (1986) D34:1642. doi: 10.1103/PhysRevD.34.1642
209. Ma E. Transformative A4 mixing of neutrinos with CP violation. Phys Rev. (2015) D92:051301. doi: 10.1103/PhysRevD.92.051301
210. Natale A. A radiative model of quark masses with binary tetrahedral symmetry. Nucl Phys. (2017) B914:201–19. doi: 10.1016/j.nuclphysb.2016.11.006
211. Ma E. Soft A4 → Z3 symmetry breaking and cobimaximal neutrino mixing. Phys Lett. (2016) B755:348–50. doi: 10.1016/j.physletb.2016.02.032
212. Ma E, Sarkar U. Scalar neutrino as asymmetric dark matter: radiative neutrino mass and leptogenesis. Phys Rev. (2012) D85:075015. doi: 10.1016/S0375-9601(96)00888-2
213. Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. B-L violating masses in softly broken supersymmetry. Phys Lett. (1997) B398:311–4. doi: 10.1016/S0370-2693(97)00234-7
214. Cai Y, Clarke JD, Schmidt MA, Volkas RR. Testing radiative neutrino mass models at the LHC. J High Energy Phys. (2015) 2:161. doi: 10.1007/JHEP02(2015)161
215. Popov O, White GA. One Leptoquark to unify them? Neutrino masses and unification in the light of (g−2)μ, and RK anomalies. Nucl Phys. (2017) B923:324–38. doi: 10.1016/j.nuclphysb.2017.08.007
216. Ma E. Derivation of dark matter parity from lepton parity. Phys Rev Lett. (2015) 115:011801. doi: 10.1103/PhysRevLett.115.011801
217. Fraser S, Kownacki C, Ma E, Popov O. Type II radiative seesaw model of neutrino mass with dark matter. Phys Rev. (2016) D93:013021. doi: 10.1103/PhysRevD.93.013021
218. Guo SY, Han ZL, Liao Y. Testing the type II radiative seesaw model: from dark matter detection to LHC signatures. Phys Rev. (2016) D94:115014. doi: 10.1103/PhysRevD.94.115014
219. Dasgupta B, Ma E, Tsumura K. Weakly interacting massive particle dark matter and radiative neutrino mass from Peccei-Quinn symmetry. Phys Rev. (2014) D89:041702. doi: 10.1103/PhysRevD.89.041702
220. Ma E. Syndetic model of fundamental interactions. Phys Lett. (2015) B741:202–4. doi: 10.1016/j.physletb.2014.12.045
221. Ho SY, Toma T, Tsumura K. Systematic U(1)B−L extensions of loop-induced neutrino mass models with dark matter. Phys Rev. (2016) D94:033007. doi: 10.1103/PhysRevD.94.033007
222. Ma E, Pollard N, Popov O, Zakeri M. Gauge B − L model of radiative neutrino mass with multipartite dark matter. Mod Phys Lett. (2016) A31:1650163. doi: 10.1142/S0217732316501637
223. Nomura T, Okada H. Radiative neutrino mass in an alternative U(1)B−L gauge symmetry. (2017) arXiv:1705.08309.
224. Chang WF, Wong CF. A model for neutrino masses and dark matter with the discrete gauge symmetry. Phys Rev. (2012) D85:013018. doi: 10.1103/PhysRevD.85.013018
225. Lindner M, Schmidt D, Watanabe A. Dark matter and U(1)' symmetry for the right-handed neutrinos. Phys Rev. (2014) D89:013007. doi: 10.1103/PhysRevD.89.013007
226. Kownacki C, Ma E. Gauge U(1) dark symmetry and radiative light fermion masses. Phys Lett. (2016) B760:59–62. doi: 10.1016/j.physletb.2016.06.024
227. Adhikari R, Borah D, Ma E. New U(1) gauge model of radiative lepton masses with sterile neutrino and dark matter. Phys Lett. (2016) B755:414–7. doi: 10.1016/j.physletb.2016.02.039
228. Babu KS, Mathur VS. Radiatively induced seesaw mechanism for neutrino masses. Phys Rev. (1988) D38:3550. doi: 10.1103/PhysRevD.38.3550
229. Fileviez Perez P, Murgui C. Lepton flavour violation in left-right theory. Phys Rev. (2017) D95:075010. doi: 10.1103/PhysRevD.95.075010
230. Fileviez Perez P, Murgui C, Ohmer S. Simple left-right theory: lepton number violation at the LHC. Phys Rev. (2016) D94:051701. doi: 10.1103/PhysRevD.94.051701
231. Hue LT, Arbuzov AB, Ngan NTK, Long HN. Probing neutrino and Higgs sectors in SU(2)1 × SU(2)2 × U(1)Y model with lepton-flavor non-universality. Eur Phys J. (2017) C77:346. doi: 10.1140/epjc/s10052-017-4866-x
232. Ma E. Gauged B−3Lτ and radiative neutrino masses. Phys Lett. (1998) B433:74–81. doi: 10.1016/S0370-2693(98)00599-1
234. Dicus DA, He HJ, Ng JN. Neutrino - lepton masses, Zee scalars and muon g-2. Phys Rev Lett. (2001) 87:111803. doi: 10.1103/PhysRevLett.87.111803
235. Sahu N, Sarkar U. Extended zee model for neutrino mass, leptogenesis and sterile neutrino like dark matter. Phys Rev. (2008) D78:115013. doi: 10.1103/PhysRevD.78.115013
236. Foot R, Kobakhidze A, McDonald KL, Volkas RR. Neutrino mass in radiatively-broken scale-invariant models. Phys Rev. (2007) D76:075014. doi: 10.1103/PhysRevD.76.075014
237. Chen CS, Chou CH. Neutrino masses, muon g-2, dark matter, lithium problem, and leptogenesis at TeV-scale. Phys Lett. (2011) B699:68–73. doi: 10.1016/j.physletb.2011.03.050
238. Arbeláez C, Cárcamo Hernández AE, Kovalenko S, Schmidt I. Radiative seesaw-type mechanism of fermion masses and non-trivial quark mixing. Eur Phys J. (2017) C77:422. doi: 10.1140/epjc/s10052-017-4948-9
239. Nomura T, Okada H, Orikasa Y. SU(2)L septet scalar linking to a radiative neutrino model. Phys Rev. (2016) D94:055012. doi: 10.1103/PhysRevD.94.055012
241. Haba N, Tsumura K. ν-two higgs doublet model and its collider phenomenology. J High Energy Phys. (2011) 6:68. doi: 10.1007/JHEP06(2011)068
242. Okada H, Toma T. 3.55 keV X-ray line signal from excited dark matter in radiative neutrino model. Phys Lett. (2014) B737:162–6. doi: 10.1016/j.physletb.2014.08.046
243. Okada H, Orikasa Y. Classically conformal radiative neutrino model with gauged B − L symmetry. Phys Lett. (2016) B760:558–64. doi: 10.1016/j.physletb.2016.07.039
244. Ahriche A, Manning A, McDonald KL, Nasri S. Scale-invariant models with one-loop neutrino mass and dark matter candidates. Phys Rev. (2016) D94:053005. doi: 10.1103/PhysRevD.94.053005
245. Ahriche A, McDonald KL, Nasri S. The scale-invariant scotogenic model. J High Energy Phys. (2016) 6:182. doi: 10.1007/JHEP06(2016)182
246. Kanemura S, Seto O, Shimomura T. Masses of dark matter and neutrino from TeV scale spontaneous U(1)B−L breaking. Phys Rev. (2011) D84:016004. doi: 10.1103/PhysRevD.84.016004
247. Kajiyama Y, Okada H, Toma T. Light dark matter candidate in B-L gauged radiative inverse seesaw. Eur Phys J. (2013) C73:2381. doi: 10.1140/epjc/s10052-013-2381-2
248. Okada H, Toma T. Fermionic dark matter in Radiative Inverse Seesaw Model with U(1)B−L. Phys Rev. (2012) D86:033011. doi: 10.1103/PhysRevD.86.033011
249. Dasgupta A, Hati C, Patra S, Sarkar U. A minimal model of TeV scale WIMPy leptogenesis. (2016) arXiv:1605.01292.
250. Seto O, Shimomura T. Atomki anomaly and dark matter in a radiative seesaw model with gauged B − L symmetry. Phys Rev. (2017) D95:095032. doi: 10.1103/PhysRevD.95.095032
251. Machado ACB, Montano J, Pleite V, Rodriguez MC. Scotogenic model with B − L symmetry and exotic neutrinos. (2017) arXiv:1705.01009.
252. Kashiwase S, Suematsu D. Radiative neutrino mass model with degenerate right-handed neutrinos. Eur Phys J. (2016) C76:117. doi: 10.1140/epjc/s10052-016-3964-5
253. Yu JH. Hidden gauged U(1) model: unifying scotogenic neutrino and flavor dark matter. Phys Rev. (2016) D93:113007. doi: 10.1103/PhysRevD.93.113007
254. Ko P, Nomura T, Okada H. A flavor dependent gauge symmetry, predictive radiative seesaw and LHCb anomalies. Phys Lett. (2017) B772:547–52. doi: 10.1016/j.physletb.2017.07.021
255. Baek S, Okada H, Yagyu K. Flavour dependent gauged radiative neutrino mass model. J High Energy Phys. (2015) 4:49. doi: 10.1007/JHEP04(2015)049
256. Baek S. Dark matter and muon (g−2) in local U(1)Lμ−Lτ-extended Ma Model. Phys Lett. (2016) B756:1–5. doi: 10.1016/j.physletb.2016.02.062
257. Kajiyama Y, Kubo J, Okada H. D(6) family symmetry and cold dark matter at LHC. Phys Rev. (2007) D75:033001. doi: 10.1103/PhysRevD.75.033001
258. Ahn YH, Chen CS. Non-zero Ue3 and TeV-leptogenesis through A4 symmetry breaking. Phys Rev. (2010) D81:105013. doi: 10.1103/PhysRevD.81.105013
259. Ahn YH. Probing lepton flavor violation with nonzero Ue3 and leptogenesis through A4 symmetry breaking. (2010) arXiv:1006.2953.
260. Ahn YH, Okada H. Non-zero θ13 linking to dark matter from non-abelian discrete flavor model in radiative seesaw. Phys Rev. (2012) D85:073010. doi: 10.1103/PhysRevD.85.073010
261. Ma E, Natale A, Rashed A. Scotogenic A4 neutrino model for nonzero θ13 and large δCP. Int J Mod Phys. (2012) A27:1250134. doi: 10.1142/S0217751X12501345
262. Holthausen M, Lindner M, Schmidt MA. Lepton flavor at the electroweak scale: a complete A4 model. Phys Rev. (2013) D87:033006. doi: 10.1103/PhysRevD.87.033006
263. Mukherjee A, Borah D, Das MK. Common origin of non-zero θ13 and dark matter in an S4 flavour symmetric model with inverse seesaw. Phys Rev. (2017) D96:015014. doi: 10.1103/PhysRevD.96.015014
264. Borah D. Light sterile neutrino and dark matter in left-right symmetric models without a Higgs bidoublet. Phys Rev. (2016) D94:075024. doi: 10.1103/PhysRevD.94.075024
265. Hirsch M, Lineros RA, Morisi S, Palacio J, Rojas N, Valle JWF. WIMP dark matter as radiative neutrino mass messenger. J High Energy Phys. (2013) 10:149. doi: 10.1007/JHEP10(2013)149
266. Rocha-Moran P, Vicente A. Lepton flavor violation in the singlet-triplet scotogenic model. J High Energy Phys. (2016) 7:78. doi: 10.1007/JHEP07(2016)078
267. Merle A, Platscher M, Rojas N, Valle JWF, Vicente A. Consistency of WIMP dark matter as radiative neutrino mass messenger. J High Energy Phys. (2016) 7:13. doi: 10.1007/JHEP07(2016)013
268. Okada H, Yagyu K. Radiative generation of lepton masses. Phys Rev. (2014) D89:053008. doi: 10.1103/PhysRevD.89.053008
269. Okada H, Yagyu K. Radiative generation of lepton masses with the U(1)′ gauge symmetry. Phys Rev. (2014) D90:035019. doi: 10.1103/PhysRevD.90.035019
270. Wang W, Han ZL. Radiative linear seesaw model, dark matter, and U(1)B−L. Phys Rev. (2015) D92:095001. doi: 10.1016/j.physletb.2011.02.014
271. Nomura T, Okada H. Loop induced type-II seesaw model and GeV dark matter with U(1)B−L gauge symmetry. Phys Lett. (2017) B774:575–81. doi: 10.1016/j.physletb.2017.10.033
272. Kanemura S, Sugiyama H. Dark matter and a suppression mechanism for neutrino masses in the Higgs triplet model. Phys Rev. (2012) D86:073006. doi: 10.1103/PhysRevD.86.073006
273. Franceschini R, Mohapatra RN. Radiatively induced type II seesaw models and vectorlike 5/3 charge quarks. Phys Rev. (2014) D89:055013. doi: 10.1103/PhysRevD.89.055013
274. Kanemura S, Ota T. Neutrino masses from loop-induced d ≥ 7 operators. Phys Lett. (2011) B694:233–7. doi: 10.1016/j.physletb.2010.09.064
275. Chang D, Keung WY, Pal PB. Spontaneous lepton number breaking at electroweak scale. Phys Rev Lett. (1988) 61:2420–3. doi: 10.1103/PhysRevLett.61.2420
276. Santamaria A. The hyperchargeless triplet majoron model. Phys Rev. (1989) D39:2715. doi: 10.1103/PhysRevD.39.2715
277. Law SSC, McDonald KL. Inverse seesaw and dark matter in models with exotic lepton triplets. Phys Lett. (2012) B713:490–4. doi: 10.1016/j.physletb.2012.06.044
278. Baldes I, Bell NF, Petraki K, Volkas RR. Two radiative inverse seesaw models, dark matter, and baryogenesis. J Cosmol Astropart Phys. (2013) 1307:29. doi: 10.1088/1475-7516/2013/07/029
279. Aranda A, Peinado E. A new radiative neutrino mass generation mechanism with higher dimensional scalar representations and custodial symmetry. Phys Lett. (2016) B754:11–3. doi: 10.1016/j.physletb.2016.01.007
280. Ahriche A, Boucenna SM, Nasri S. Dark radiative inverse seesaw mechanism. Phys Rev. (2016) D93:075036. doi: 10.1103/PhysRevD.93.075036
281. Pilaftsis A. Radiatively induced neutrino masses and large Higgs neutrino couplings in the standard model with Majorana fields. Z Phys. (1992) C55:275–82. doi: 10.1007/BF01482590
282. Grimus W, Neufeld H. Radiative neutrino masses in an SU(2) X U(1) model. Nucl Phys. (1989) B325:18–32. doi: 10.1016/0550-3213(89)90370-2
283. Aristizabal Sierra D, Yaguna CE. On the importance of the 1-loop finite corrections to seesaw neutrino masses. J High Energy Phys. (2011) 8:13. doi: 10.1007/JHEP08(2011)013
284. Grimus W, Lavoura L. One-loop corrections to the seesaw mechanism in the multi-Higgs-doublet standard model. Phys Lett. (2002) B546:86–95. doi: 10.1016/S0370-2693(02)02672-2
285. Dev PSB, Pilaftsis A. Minimal radiative neutrino mass mechanism for inverse seesaw models. Phys Rev. (2012) D86:113001. doi: 10.1103/PhysRevD.86.113001
286. McDonald KL, McKellar BHJ. Evaluating the two loop diagram responsible for neutrino mass in Babu's model. (2003) e-Print: hep-ph/0309270.
287. Angel PW, Cai Y, Rodd NL, Schmidt MA, Volkas RR. Testable two-loop radiative neutrino mass model based on an LLQdcQdc effective operator. J High Energy Phys. (2013) 10:118. doi: 10.1007/JHEP10(2013)118
288. Zee A. Quantum numbers of majorana neutrino masses. Nucl Phys. (1986) B264:99–110. doi: 10.1016/0550-3213(86)90475-X
289. Babu KS. Model of ‘calculable’ majorana neutrino masses. Phys Lett. (1988) B203:132–6. doi: 10.1016/0370-2693(88)91584-5
290. Petcov ST, Toshev ST. Conservation of lepton charges, massive majorana and massless neutrinos. Phys Lett. (1984) B143:175–8. doi: 10.1016/0370-2693(84)90829-3
291. Babu KS, Ma E. Natural hierarchy of radiatively induced majorana neutrino masses. Phys Rev Lett. (1988) 61:674. doi: 10.1103/PhysRevLett.61.674
292. Branco GC, Grimus W, Lavoura L. The seesaw mechanism in the presence of a conserved lepton number. Nucl Phys. (1989) B312:492–508. doi: 10.1016/0550-3213(89)90304-0
293. Lavoura L. New model for the neutrino mass matrix. Phys Rev. (2000) D62:093011. doi: 10.1103/PhysRevD.62.093011
294. Kitabayashi T, Yasue M. Neutrino oscillations induced by two loop radiative mechanism. Phys Lett. (2000) B490:236–41. doi: 10.1016/S0370-2693(00)00988-6
295. Araki T, Geng CQ. μ − τ symmetry in Zee-Babu model. Phys Lett. (2011) B694:113–8. doi: 10.1016/j.physletb.2010.09.046
296. Aoki M, Kanemura S, Shindou T, Yagyu K. An R-parity conserving radiative neutrino mass model without right-handed neutrinos. J High Energy Phys. (2010) 7:84. doi: 10.1007/JHEP07(2010)084
297. Haba N, Shindou T. Tiny neutrino mass from SUSY and lepton number breaking sector. Phys Lett. (2011) B701:229–33. doi: 10.1016/j.physletb.2011.05.050
298. Kohda M, Sugiyama H, Tsumura K. Lepton number violation at the LHC with leptoquark and diquark. Phys Lett. (2013) B718:1436–40. doi: 10.1016/j.physletb.2012.12.048
299. Nomura T, Okada H. An extended colored zee-babu model. Phys Rev. (2016) D94:075021. doi: 10.1103/PhysRevD.94.075021
300. Chang WF, Liou SC, Wong CF, Xu F. Charged lepton flavor violating processes and scalar leptoquark decay branching ratios in the colored Zee-Babu model. J High Energy Phys. (2016) 10:106. doi: 10.1007/JHEP10(2016)106
301. Ma E. Z3 dark matter and two-loop neutrino mass. Phys Lett. (2008) B662:49–52. doi: 10.1016/j.physletb.2008.02.053
302. Ding R, Han ZL, Liao Y, Xie WP. Radiative neutrino mass with ℤ3 dark matter: from relic density to LHC signatures. J High Energy Phys. (2016) 5:30. doi: 10.1007/JHEP05(2016)030
303. Nomura T, Okada H. Generalized Zee–Babu model with 750 GeV diphoton resonance. Phys Lett. (2016) B756:295–302. doi: 10.1016/j.physletb.2016.03.034
304. Okada H, Toma T, Yagyu K. Inert extension of the Zee-Babu model. Phys Rev. (2014) D90:095005. doi: 10.1103/PhysRevD.90.095005
305. Aoki M, Toma T. Impact of semi-annihilation of ℤ3 symmetric dark matter with radiative neutrino masses. J Cosmol Astropart Phys. (2014) 1409:016. doi: 10.1088/1475-7516/2014/09/016
306. Ho S-Y, Toma T, Tsumura K. A radiative neutrino mass model with SIMP dark matter. J High Energy Phys. (2017) 7:101. doi: 10.1007/JHEP07(2017)101
307. Baek S, Okada H, Orikasa Y. A radiative neutrino model linking to a monochromatic gamma-ray line. (2017) arXiv:1703.00685.
308. Wu Dd. The masses of the neutrinos in the unification gauge theories and the neutrino - anti-neutrino oscillations. Phys Rev. (1981) D23:2038. doi: 10.1103/PhysRevD.23.2038
309. Babu KS, Ma E, Pantaleone JT. Model of radiative neutrino masses: mixing and a possible fourth generation. Phys Lett. (1989) B218:233–7. doi: 10.1016/0370-2693(89)91425-1
310. Aparici A, Herrero-García J, Rius N, Santamaria A. Neutrino masses from new generations. J High Energy Phys. (2011) 7:122. doi: 10.1007/JHEP07(2011)122
311. Liao Y, Liu JY, Ning GZ. Radiative neutrino mass in Type III seesaw model. Phys Rev. (2009) D79:073003. doi: 10.1103/PhysRevD.79.073003
312. Babu KS, Julio J. Two-loop neutrino mass generation through leptoquarks. Nucl Phys. (2010) B841:130–56. doi: 10.1016/j.nuclphysb.2010.07.022
313. Cai Y, Gargalionis J, Schmidt MA, Volkas RR. Reconsidering the one leptoquark solution: flavor anomalies and neutrino mass. J High Energy Phys. (2017) 10:047. doi: 10.1007/JHEP10(2017)047
314. Bamba K, Geng CQ, Ho SH. Radiative neutrino mass generation and dark energy. J Cosmol Astropart Phys. (2008) 0809:001. 10.1088/1475-7516/2008/09/001
315. Porto RA, Zee A. Neutrino mixing and the private higgs. Phys Rev. (2009) D79:013003. doi: 10.1103/PhysRevD.79.013003
316. Lindner M, Schmidt D, Schwetz T. Dark matter and neutrino masses from global U(1)B−L symmetry breaking. Phys Lett. (2011) B705:324–30. doi: 10.1016/j.physletb.2011.10.022
317. Chang D, Keung WY. Higgs mediated neutrinoless double beta decay and neutrino mass in a majoron model. Phys Rev. (1989) D39:1386.
318. Guo G, He XG, Li GN. Radiative two loop inverse seesaw and dark matter. J High Energy Phys. (2012) 10:044. doi: 10.1007/JHEP10(2012)044
319. Kajiyama Y, Okada H, Yagyu K. Two loop radiative seesaw model with inert triplet scalar field. Nucl Phys. (2013) B874:198–216. doi: 10.1016/j.nuclphysb.2013.05.020
320. Nomura T, Okada H. Two-loop induced majorana neutrino mass in a radiatively induced quark and lepton mass model. Phys Rev. (2016) D94:093006. doi: 10.1103/PhysRevD.94.093006
321. Aoki M, Kubo J, Takano H. Two-loop radiative seesaw mechanism with multicomponent dark matter explaining the possible γ excess in the Higgs boson decay and at the Fermi LAT. Phys Rev. (2013) D87:116001. doi: 10.1103/PhysRevD.87.116001
322. Aoki M, Kubo J, Takano H. Multicomponent dark matter in radiative seesaw model and monochromatic neutrino flux. Phys Rev. (2014) D90:076011. doi: 10.1103/PhysRevD.90.076011
323. Ma E, Sarkar U. Revelations of the E(6)/U(1)(N) model: two-loop neutrino mass and dark matter. Phys Lett. (2007) B653:288–91. doi: 10.1016/j.physletb.2007.08.019
324. Kajiyama Y, Okada H, Toma T. Multicomponent dark matter particles in a two-loop neutrino model. Phys Rev. (2013) D88:015029. doi: 10.1103/PhysRevD.88.015029
325. Baek S, Okada H, Toma T. Two loop neutrino model and dark matter particles with global B-L symmetry. J Cosmol Astropart Phys. (2014) 1406:027. doi: 10.1088/1475-7516/2014/06/027
326. Ghosh A, Mondal T, Mukhopadhyaya B. Heavy stable charged tracks as signatures of non-thermal dark matter at the LHC : a study in some non-supersymmetric scenarios. (2017) arXiv:1706.06815.
327. Ma E. Radiative quark and lepton masses in a left-right gauge model. Phys Rev Lett. (1989) 63:1042. doi: 10.1103/PhysRevLett.63.1042
328. Nasri S, Moussa S. Model for small neutrino masses at the TeV scale. Mod Phys Lett. (2002) A17:771–8. doi: 10.1142/S0217732302007119
329. Chao W. Neutrino masses and A TeV scale seesaw mechanism. Phys Rev. (2010) D82:016008. doi: 10.1103/PhysRevD.82.016008
330. Ma E, Wudka J. Vector-boson-induced neutrino mass. Phys Lett. (2012) B712:391–5. doi: 10.1016/j.physletb.2012.05.008
331. Nomura T, Okada H. Loop suppressed light fermion masses with U(1)R gauge symmetry. Phys. Rev. (2017) D96:015016. doi: 10.1103/PhysRevD.96.015016
332. Okada H, Orikasa Y. Two-loop neutrino model with exotic leptons. Phys Rev. (2016) D93:013008. doi: 10.1103/PhysRevD.93.013008
333. Witten E. Neutrino masses in the minimal O(10) theory. Phys Lett. (1980) B91:81–4. doi: 10.1016/0370-2693(80)90666-8
334. Arbeláez Rodríguez C, Kolešová H, Malinský M. Witten's mechanism in the flipped SU(5) unification. Phys Rev. (2014) D89:055003. doi: 10.1103/PhysRevD.89.055003
335. Ma E. Radiative inverse seesaw mechanism for nonzero neutrino mass. Phys Rev. (2009) D80:013013.
336. Babu KS, Ma E. Radiative hierarchy of majorana neutrino masses. Phys Lett. (1989) B228:508–12. doi: 10.1016/0370-2693(89)90983-0
337. Babu KS, Julio J. Radiative neutrino mass generation through vector-like quarks. Phys Rev. (2012) D85:073005. doi: 10.1103/PhysRevD.85.073005
338. Kanemura S, Nabeshima T, Sugiyama H. TeV-scale seesaw with loop-induced dirac mass term and dark matter from U(1)B−L gauge symmetry breaking. Phys Rev. (2012) D85:033004. doi: 10.1103/PhysRevD.85.033004
339. Ma E. Radiative origin of all quark and lepton masses through dark matter with flavor symmetry. Phys Rev Lett. (2014) 112:091801. doi: 10.1103/PhysRevLett.112.091801
340. Baek S, Okada H, Toma T. Radiative lepton model and dark matter with global U(1)′ symmetry. Phys Lett. (2014) B732:85–90. doi: 10.1016/j.physletb.2014.03.021
341. Kanemura S, Matsui T, Sugiyama H. Neutrino mass and dark matter from gauged U(1)B−L breaking. Phys Rev. (2014) D90:013001. doi: 10.1103/PhysRevD.90.013001
342. Kashiwase S, Okada H, Orikasa Y, Toma T. Two loop neutrino model with dark matter and leptogenesis. Int J Mod Phys. (2016) A31:1650121. doi: 10.1142/S0217751X16501219
343. Nomura T, Okada H, Orikasa Y. Radiative neutrino mass in alternative left–right model. Eur Phys J. (2017) C77:103. doi: 10.1140/epjc/s10052-017-4657-4
344. Nomura T, Okada H, Orikasa Y. Radiative neutrino model with SU(2)L triplet fields. Phys Rev. (2016) D94:115018. doi: 10.1103/PhysRevD.94.115018
345. Chen CS, Geng CQ, Ng JN. Unconventional neutrino mass generation, neutrinoless double beta decays, and collider phenomenology. Phys Rev. (2007) D75:053004. doi: 10.1103/PhysRevD.75.053004
346. Chen CS, Geng CQ, Ng JN, Wu JMS. Testing radiative neutrino mass generation at the LHC. J High Energy Phys. (2007) 8:22. doi: 10.1088/1126-6708/2007/08/022
347. del Aguila F, Aparici A, Bhattacharya S, Santamaria A, Wudka J. A realistic model of neutrino masses with a large neutrinoless double beta decay rate. J High Energy Phys. (2012) 5:133. doi: 10.1007/JHEP05(2012)133
348. Chen CS, Geng CQ, Huang D, Tsai LH. Many high-charged scalars in LHC searches and Majorana neutrino mass generations. Phys Rev. (2013) D87:077702. doi: 10.1103/PhysRevD.87.077702
349. del Águila F, Aparici A, Bhattacharya S, Santamaria A, Wudka J. Neutrinoless double β decay with small neutrino masses. PoS (2013) Corfu2012:028. Available online at: https://arxiv.org/abs/1305.4900
350. King SF, Merle A, Panizzi L. Effective theory of a doubly charged singlet scalar: complementarity of neutrino physics and the LHC. J High Energy Phys. (2014) 11:124. doi: 10.1007/JHEP11(2014)124
351. Geng CQ, Tsai LH. Study of two-loop neutrino mass generation models. Ann Phys. (2016) 365:210–22. doi: 10.1016/j.aop.2015.11.010
352. Appelquist T, Shrock R. Neutrino masses in theories with dynamical electroweak symmetry breaking. Phys Lett. (2002) B548:204–14. doi: 10.1016/S0370-2693(02)02854-X
353. Appelquist T, Shrock R. Dynamical symmetry breaking of extended gauge symmetries. Phys Rev Lett. (2003) 90:201801. doi: 10.1103/PhysRevLett.90.201801
354. Appelquist T, Piai M, Shrock R. Fermion masses and mixing in extended technicolor models. Phys Rev. (2004) D69:015002. doi: 10.1103/PhysRevD.69.015002
355. Krauss LM, Nasri S, Trodden M. A Model for neutrino masses and dark matter. Phys Rev. (2003) D67:085002. doi: 10.1103/PhysRevD.67.085002
356. Chen CS, McDonald KL, Nasri S. A class of three-loop models with neutrino mass and dark matter. Phys Lett. (2014) B734:388–93. doi: 10.1016/j.physletb.2014.05.082
357. Cheung K, Seto O. Phenomenology of TeV right-handed neutrino and the dark matter model. Phys Rev. (2004) D69:113009. doi: 10.1103/PhysRevD.69.113009
358. Ahriche A, Nasri S. Dark matter and strong electroweak phase transition in a radiative neutrino mass model. J Cosmol Astropart Phys. (2013) 1307:035. doi: 10.1088/1475-7516/2013/07/035
359. Ahriche A, Nasri S, Soualah R. Radiative neutrino mass model at the e−e+ linear collider. Phys Rev. (2014) D89:095010. doi: 10.1103/PhysRevD.89.095010
360. Ahriche A, Chen CS, McDonald KL, Nasri S. Three-loop model of neutrino mass with dark matter. Phys Rev. (2014) D90:015024. doi: 10.1103/PhysRevD.90.015024
361. Ahriche A, McDonald KL, Nasri S. A model of radiative neutrino mass: with or without dark matter. J High Energy Phys. (2014) 10:167. doi: 10.1007/JHEP10(2014)167
362. Ahriche A, McDonald KL, Nasri S, Toma T. A model of neutrino mass and dark matter with an accidental symmetry. Phys Lett. (2015) B746:430–5. doi: 10.1016/j.physletb.2015.05.031
363. Ahriche A, McDonald KL, Nasri S. A radiative model for the weak scale and neutrino mass via dark matter. J High Energy Phys. (2016) 2:38. doi: 10.1007/JHEP02(2016)038
364. Ahriche A, McDonald KL, Nasri S. Scalar sector phenomenology of three-loop radiative neutrino mass models. Phys Rev. (2015) D92:095020. doi: 10.1103/PhysRevD.92.095020
365. Nomura T, Okada H, Okada N. A colored KNT neutrino model. Phys Lett. (2016) B762:409–14. doi: 10.1016/j.physletb.2016.09.038
366. Cheung K, Nomura T, Okada H. Three-loop neutrino mass model with a colored triplet scalar. Phys Rev. (2017) D95:015026. doi: 10.1103/PhysRevD.95.015026
367. Okada H, Orikasa Y. X-ray line in radiative neutrino model with global U(1) symmetry. Phys Rev. (2014) D90:075023. doi: 10.1103/PhysRevD.90.075023
368. Okada H, Yagyu K. Renormalizable model for neutrino mass, dark matter, muon g−2 and 750 GeV diphoton excess. Phys Lett. (2016) B756:337–44. doi: 10.1016/j.physletb.2016.03.040
369. Cheung K, Ishida H, Okada H. Accommodation of the dirac phase in the Krauss-Nasri-Trodden model. (2016) arXiv:1609.06231.
370. Aoki M, Kanemura S, Seto O. Neutrino mass, dark matter and baryon asymmetry via TeV-scale physics without fine-tuning. Phys Rev Lett. (2009) 102:051805. doi: 10.1103/PhysRevLett.102.051805
371. Gu PH. High-scale leptogenesis with three-loop neutrino mass generation and dark matter. J High Energy Phys. (2017) 4:159. doi: 10.1007/JHEP04(2017)159
372. Cheung K, Nomura T, Okada H. A three-loop neutrino model with leptoquark triplet scalars. Phys Lett. (2017) B768:359–64. doi: 10.1016/j.physletb.2017.03.021
373. Culjak P, Kumericki K, Picek I. Scotogenic RνMDM at three-loop level. Phys Lett. (2015) B744:237–43. doi: 10.1016/j.physletb.2015.03.062
374. Okada H, Yagyu K. Three-loop neutrino mass model with doubly charged particles from isodoublets. Phys Rev. (2016) D93:013004. doi: 10.1103/PhysRevD.93.013004
375. Ko P, Nomura T, Okada H, Orikasa Y. Confronting a new three-loop seesaw model with the 750 GeV diphoton excess. Phys Rev. (2016) D94:013009. doi: 10.1103/PhysRevD.94.013009
376. Gustafsson M, No JM, Rivera MA. Predictive model for radiatively induced neutrino masses and mixings with dark matter. Phys Rev Lett. (2013) 110:211802. doi: 10.1103/PhysRevLett.110.211802
377. Geng CQ, Huang D, Tsai LH. Loop-induced neutrino masses: a case study. Phys Rev. (2014) D90:113005. doi: 10.1103/PhysRevD.90.113005
378. Hatanaka H, Nishiwaki K, Okada H, Orikasa Y. A three-loop neutrino model with global U(1) symmetry. Nucl Phys. (2015) B894:268–83. doi: 10.1016/j.nuclphysb.2015.03.006
379. Alcaide J, Das D, Santamaria A. A model of neutrino mass and dark matter with large neutrinoless double beta decay. J High Energy Phys. (2017) 4:49. doi: 10.1007/JHEP04(2017)049
380. Nishiwaki K, Okada H, Orikasa Y. Three loop neutrino model with isolated k±±. Phys Rev. (2015) D92:093013. doi: 10.1103/PhysRevD.92.093013
381. Kanemura S, Nishiwaki K, Okada H, Orikasa Y, Park SC, Watanabe R. LHC 750 GeV diphoton excess in a radiative seesaw model. PTEP (2016) 2016:123B04. doi: 10.1093/ptep/ptw164
382. Jin LG, Tang R, Zhang F. A three-loop radiative neutrino mass model with dark matter. Phys Lett. (2015) B741:163–7. doi: 10.1016/j.physletb.2014.12.034
383. Nomura T, Okada H, Orikasa Y. Radiative seesaw model with degenerate majorana dark matter. Phys Rev. (2016) D93:113008. doi: 10.1103/PhysRevD.93.113008
384. Geng CQ, Huang D. Large ν- oscillations from high-dimensional lepton number violating operator. J High Energy Phys. (2017) 3:103. doi: 10.1007/JHEP03(2017)103
385. Cirelli M, Fornengo N, Strumia A. Minimal dark matter. Nucl Phys. (2006) B753:178–94. doi: 10.1016/j.nuclphysb.2006.07.012
386. Cirelli M, Strumia A. Minimal dark matter: model and results. New J Phys. (2009) 11:105005. doi: 10.1088/1367-2630/11/10/105005
387. Gustafsson M, No JM, Rivera MA. Radiative neutrino mass generation linked to neutrino mixing and 0νββ-decay predictions. Phys Rev. (2014) D90:013012. doi: 10.1103/PhysRevD.90.013012
388. Liu Z, Gu PH. Extending two Higgs doublet models for two-loop neutrino mass generation and one-loop neutrinoless double beta decay. Nucl Phys. (2017) B915:206–23. doi: 10.1016/j.nuclphysb.2016.12.001
390. Wang W, Wang R, Han ZL, Han JZ. The B − L scotogenic models for dirac neutrino masses. (2017) arXiv:1705.00414.
391. Kanemura S, Sakurai K, Sugiyama H. Probing models of dirac neutrino masses via the flavor structure of the mass matrix. Phys Lett. (2016) B758:465–72. doi: 10.1016/j.physletb.2016.05.046
392. Mohapatra RN. A model for dirac neutrino masses and mixings. Phys Lett. (1987) B198:69–72. doi: 10.1016/0370-2693(87)90161-4
393. Mohapatra RN. Left-right symmetry and finite one loop dirac neutrino mass. Phys Lett. (1988) B201:517–24.
394. Balakrishna BS, Mohapatra RN. Radiative fermion masses from new physics at Tev scale. Phys Lett. (1989) B216:349–52.
395. Gu PH, Sarkar U. Radiative neutrino mass, dark matter and leptogenesis. Phys Rev. (2008) D77:105031. doi: 10.1103/PhysRevD.77.105031
396. Borah D, Dasgupta A. Observable lepton number violation with predominantly dirac nature of active neutrinos. J High Energy Phys. (2017) 1:72. doi: 10.1007/JHEP01(2017)072
397. Borah D, Dasgupta A. Naturally light dirac neutrino in left-right symmetric model. J Cosmol Astropart Phys. (2017) 1706:003. doi: 10.1088/1475-7516/2017/06/003
398. Rajpoot S. Model with calculable Dirac neutrino masses. Phys Rev. (1991) D44:225–8. doi: 10.1103/PhysRevD.44.225
399. Kanemura S, Nabeshima T, Sugiyama H. Neutrino masses from loop-induced dirac yukawa couplings. Phys Lett. (2011) B703:66–70. doi: 10.1016/j.physletb.2011.07.047
400. Farzan Y, Ma E. Dirac neutrino mass generation from dark matter. Phys Rev. (2012) D86:033007. doi: 10.1103/PhysRevD.86.033007
401. Kanemura S, Matsui T, Sugiyama H. Loop suppression of dirac neutrino mass in the neutrinophilic two higgs doublet model. Phys Lett. (2013) B727:151–6. doi: 10.1016/j.physletb.2013.09.061
402. Borah D, Dasgupta A. Common origin of neutrino mass, dark matter and dirac leptogenesis. J Cosmol Astropart Phys. (2016) 1612:034. doi: 10.1088/1475-7516/2016/12/034
403. Bonilla C, Ma E, Peinado E, Valle JWF. Two-loop dirac neutrino mass and WIMP dark matter. Phys Lett. (2016) B762:214–8. doi: 10.1016/j.physletb.2016.09.027
404. Kanemura S, Sakurai K, Sugiyama H. Neutrino mass, dark matter and baryon asymmetry without lepton number violation. (2017) arXiv:1705.07040.
405. Pilaftsis A. Anomalous fermion mass generation at three loops. Mod Phys Lett. (2013) A28:13500831. doi: 10.1142/S0217732313500831
406. Gutierrez DA, Ponce WA, Sanchez LA. Study of the SU(3)c × SU(3)L × U(1)X model with the minimal scalar sector. Int J Mod Phys. (2006) A21:2217–35. doi: 10.1142/S0217751X06029442
407. Okamoto Y, Yasue M. Radiatively generated neutrino masses in SU(3)L × U(1)N gauge models. Phys Lett. (1999) B466:267–73. doi: 10.1016/S0370-2693(99)01134-X
408. Kitabayashi T, Yasue M. Nearly bimaximal neutrino mixing in an SU(3)L × U(1)N gauge model with radiative neutrino masses. (2000) e-Print: hep-ph/0006040.
409. Kitabayashi T, Yasue M. Radiatively induced neutrino masses and oscillations in an SU(3)L × U(1)N gauge model. Phys Rev. (2001) D63:095002. doi: 10.1103/PhysRevD.63.095002
410. Kitabayashi T, Yasue M. Two loop radiative neutrino mechanism in an SU(3)L × U(1)N gauge model. Phys Rev. (2001) D63:095006. doi: 10.1103/PhysRevD.63.095006
411. Kitabayashi T. Comment on neutrino masses and oscillations in an SU(3)L × U(1)N model with radiative mechanism. Phys Rev. (2001) D64:057301. doi: 10.1103/PhysRevD.64.057301
412. Kitabayashi T, Yasue M. The interplay between neutrinos and charged leptons in the minimal SU(3)L × U(1)N gauge model. Nucl Phys. (2001) B609:61–82. doi: 10.1016/S0550-3213(01)00276-0
413. Kitabayashi T, Yasue M. S2L permutation symmetry for left-handed μ and τ families and neutrino oscillations in an SU(3)L × U(1)N gauge model. Phys Rev. (2003) D67:015006. doi: 10.1103/PhysRevD.67.015006
414. Chang CHV, Chang WF, Ng JN. Neutrino masses in a 5-D SU(3)W TeV unification model. Phys Lett. (2003) B558:92–102. doi: 10.1016/S0370-2693(03)00219-3
415. Chang WF, Ng JN. Phenomenology of a 5-D orbifold SU(3)W unification model. Phys Rev. (2004) D69:056005. doi: 10.1103/PhysRevD.69.056005
416. Ponce WA, Zapata O. Lepton masses and mixing without Yukawa hierarchies. Phys Rev. (2006) D74:093007. doi: 10.1103/PhysRevD.74.093007
417. Salazar JC, Ponce WA, Gutierrez DA. Phenomenology of the SU(3)c × SU(3)L × U(1)X model with exotic charged leptons. Phys Rev. (2007) D75:075016. doi: 10.1103/PhysRevD.75.075016
418. Dong PV, Long HN. The economical SU(3)c × SU(3)L × U(1)Xmodel. Adv High Energy Phys. (2008) 2008:739492. doi: 10.1155/2008/739492
419. Boucenna SM, Morisi S, Valle JWF. Radiative neutrino mass in 3-3-1 scheme. Phys Rev. (2014) D90:013005. doi: 10.1103/PhysRevD.90.013005
420. Boucenna SM, Fonseca RM, Gonzalez-Canales F, Valle JWF. Small neutrino masses and gauge coupling unification. Phys Rev. (2015) D91:031702. doi: 10.1103/PhysRevD.91.031702
421. Deppisch FF, Hati C, Patra S, Sarkar U, Valle JWF. 331 models and grand unification: from minimal SU(5) to minimal SU(6). Phys Lett. (2016) B762:432–40. doi: 10.1016/j.physletb.2016.10.002
422. Okada H, Okada N, Orikasa Y. Radiative seesaw mechanism in a minimal 3-3-1 model. Phys Rev. (2016) D93:073006. doi: 10.1103/PhysRevD.93.073006
423. Cárcamo Hernández AE, Long HN. A highly predictive A4 flavour 3-3-1 model with radiative inverse seesaw mechanism. (2017) arXiv:1705.05246.
424. Kitabayashi T, Yasue M. Large mixing angle MSW solution in an SU(3)L × U(1)N gauge model with two loop radiative mechanism. Phys Lett. (2001) B508:85–95. doi: 10.1016/S0370-2693(01)00397-5
425. Aizawa I, Ishiguro M, Kitabayashi T, Yasue M. Bilarge neutrino mixing and mu - tau permutation symmetry for two-loop radiative mechanism. Phys Rev. (2004) D70:015011. doi: 10.1103/PhysRevD.70.015011
426. Sanchez LA, Ponce WA, Mira JM. Hierarchical radiative masses in a supersymmetric three-family model without Higgsinos. Eur Phys J. (2005) C42:205–15. doi: 10.1140/epjc/s2005-02286-9
427. Chang D, Long HN. Interesting radiative patterns of neutrino mass in an SU(3)c × SU(3)L × U(1)X model with right-handed neutrinos. Phys Rev. (2006) D73:053006. doi: 10.1103/PhysRevD.73.053006
428. Benavides RH, Ponce WA, Giraldo Y. SU(3)c⊗SU(3)L⊗U(1)X models with four families. Phys Rev. (2010) D82:013004. doi: 10.1103/PhysRevD.82.013004
429. Cárcamo Hernández AE, Kovalenko S, Long HN, Schmidt I. A novel 3-3-1 model for the generation of the SM fermion mass and mixing pattern. (2017) arXiv:1705.09169.
430. Cárcamo Hernández AE. A novel and economical explanation for SM fermion masses and mixings. Eur Phys J. (2016) C76:503. doi: 10.1140/epjc/s10052-016-4351-y
431. Fonseca RM, Hirsch M. Lepton number violation in 331 models. Phys Rev. (2016) D94:115003. doi: 10.1103/PhysRevD.94.115003
432. Antusch S, Biggio C, Fernandez-Martinez E, Gavela MB, Lopez-Pavon J. Unitarity of the leptonic mixing matrix. J High Energy Phys. (2006) 10:084. doi: 10.1088/1126-6708/2006/10/084
433. Abada A, Biggio C, Bonnet F, Gavela MB, Hambye T. Low energy effects of neutrino masses. J High Energy Phys. (2007) 12:061. doi: 10.1088/1126-6708/2007/12/061
434. Bilenky MS, Santamaria A. One loop effective Lagrangian for a standard model with a heavy charged scalar singlet. Nucl Phys. (1994) B420:47–93. doi: 10.1016/0550-3213(94)90375-1
435. Nebot M, Oliver JF, Palao D, Santamaria A. Prospects for the Zee-Babu Model at the CERN LHC and low energy experiments. Phys Rev. (2008) D77:093013. doi: 10.1103/PhysRevD.77.093013
436. Farzan Y. A model for large non-standard interactions of neutrinos leading to the LMA-Dark solution. Phys Lett. (2015) B748:311–5. doi: 10.1016/j.physletb.2015.07.015
437. Farzan Y, Shoemaker IM. Lepton flavor violating non-standard interactions via light mediators. J High Energy Phys. (2016) 7:33. doi: 10.1007/JHEP07(2016)033
438. Davidson S, Pena-Garay C, Rius N, Santamaria A. Present and future bounds on nonstandard neutrino interactions. J High Energy Phys. (2003) 3:11. doi: 10.1088/1126-6708/2003/03/011
439. Ibarra A, Masso E, Redondo J. Systematic approach to gauge-invariant relations between lepton flavor violating processes. Nucl Phys. (2005) B715:523–35. doi: 10.1016/j.nuclphysb.2005.03.017
440. Gavela MB, Hernandez D, Ota T, Winter W. Large gauge invariant non-standard neutrino interactions. Phys Rev. (2009) D79:013007. doi: 10.1103/PhysRevD.79.013007
441. Biggio C, Blennow M, Fernandez-Martinez E. General bounds on non-standard neutrino interactions. J High Energy Phys. (2009) 8:90. doi: 10.1088/1126-6708/2009/08/090
442. Biggio C, Blennow M, Fernandez-Martinez E. Loop bounds on non-standard neutrino interactions. J High Energy Phys. (2009) 3:139. doi: 10.1088/1126-6708/2009/03/139
443. Antusch S, Baumann JP, Fernandez-Martinez E. Non-standard neutrino interactions with matter from physics beyond the standard model. Nucl Phys. (2009) B810:369–88. doi: 10.1016/j.nuclphysb.2008.11.018
444. Ohlsson T. Status of non-standard neutrino interactions. Rept Prog Phys. (2013) 76:044201. doi: 10.1088/0034-4885/76/4/044201
445. Porod W, Staub F, Vicente A. A flavor kit for BSM models. Eur Phys J. (2014) C74:2992. doi: 10.1140/epjc/s10052-014-2992-2
446. Lee BW, Pakvasa S, Shrock RE, Sugawara H. Muon and electron number nonconservation in a v-a six quark model. Phys Rev Lett. (1977) 38:937. doi: 10.1103/PhysRevLett.38.937
447. Lee BW, Shrock RE. Natural suppression of symmetry violation in gauge theories: Muon - Lepton and electron lepton number nonconservation. Phys Rev. (1977) D16:1444. doi: 10.1103/PhysRevD.16.1444
448. Marciano WJ, Sanda AI. Exotic decays of the muon and heavy leptons in gauge theories. Phys Lett. (1977) 67B:303–5.
449. Carpentier M, Davidson S. Constraints on two-lepton, two quark operators. Eur Phys J. (2010) C70:1071–90. doi: 10.1140/epjc/s10052-010-1482-4
450. Pruna GM, Signer A. The μ → eγ decay in a systematic effective field theory approach with dimension 6 operators. J High Energy Phys. (2014) 10:014. doi: 10.1007/JHEP10(2014)014
451. Ghosal A, Koide Y, Fusaoka H. Lepton flavor violating Z decays in the Zee model. Phys Rev. (2001) D64:053012. doi: 10.1103/PhysRevD.64.053012
452. Li B, Liao Y, Ma XD. Charged Lepton flavor-violating transitions in color octet model. Eur Phys J. (2016) C76:615. doi: 10.1140/epjc/s10052-016-4462-5
453. Baldini AM, Bao Y, Baracchini E, Bemporad C, Berg F, Biasotti M, et al. Search for the lepton flavour violating decay μ+ → e+γ with the full dataset of the MEG experiment. Eur Phys J. (2016) C76:434. doi: 10.1140/epjc/s10052-016-4271-x
454. Baldini AM, Cei F, Cerri C, Dussoni S, Galli L, Grassi M, et al. MEG upgrade proposal. (2013) arXiv:1301.7225.
455. Aubert B, Karyotakis Y, Lees JP, Poireau V, Prencipe E, Prudent X, et al. Searches for lepton flavor violation in the decays τ± → e±γ and τ± → μ±γ. Phys Rev Lett. (2010) 104:021802. doi: 10.1103/PhysRevLett.104.021802
456. Aushev T, Bartel W, Bondar A, Brodzicka J, Browder TE, Chang P, et al. Physics at super B factory. (2010) arXiv:1002.5012.
457. Hisano J, Moroi T, Tobe K, Yamaguchi M. Lepton flavor violation via right-handed neutrino Yukawa couplings in supersymmetric standard model. Phys Rev. (1996) D53:2442–59. doi: 10.1103/PhysRevD.53.2442
458. Lavoura L. General formulae for f(1) → f(2)γ. Eur Phys J. (2003) C29:191–5. doi: 10.1140/epjc/s2003-01212-7
459. Schmidt D, Schwetz T, Toma T. Direct detection of leptophilic dark matter in a model with radiative neutrino masses. Phys Rev. (2012) D85:073009. doi: 10.1103/PhysRevD.85.073009
460. Vicente A, Yaguna CE. Probing the scotogenic model with lepton flavor violating processes. J High Energy Phys. (2015) 2:144. doi: 10.1007/JHEP02(2015)144
462. Abada A, Davidson S, Losada M. Neutrino masses and mixings in the MSSM with soft bilinear R(p) violation. Phys Rev. (2002) D65:075010. doi: 10.1103/PhysRevD.65.075010
463. Carvalho DF, Gomez ME, Romao JC. Charged lepton flavor violation in supersymmetry with bilinear R-parity violation. Phys Rev. (2002) D65:093013. doi: 10.1103/PhysRevD.65.093013
464. Blondel A, Bravar A, Pohl M, Bachmann S, Berger N, Kiehn M, et al. Research proposal for an experiment to search for the decay μ → eee. (2013) arXiv:1301.6113.
465. Bellgardt U, Otter G, Eichler R, Felawka L, Niebuhr C, Walter HK, et al. Search for the decay μ+ → e+e+e−. Nucl Phys. (1988) B299:1–6.
466. Hayasaka K, Inami K, Miyazaki Y, Arinstein K, Aulchenko VM, Aushev T, et al. Search for lepton flavor violating τ decays into three leptons with 719 million produced τ+τ− pairs. Phys Lett. (2010) B687:139–43. doi: 10.1016/j.physletb.2010.03.037
467. Abada A, Krauss ME, Porod W, Staub F, Vicente A, Weiland C. Lepton flavor violation in low-scale seesaw models: SUSY and non-SUSY contributions. J High Energy Phys. (2014) 11:48. doi: 10.1007/JHEP11(2014)048
468. Kubo J, Ma E, Suematsu D. Cold dark matter, radiative neutrino mass, μ → eγ, and neutrinoless double beta decay. Phys Lett. (2006) B642:18–23. doi: 10.1016/j.physletb.2006.08.085
469. Aristizabal Sierra D, Kubo J, Restrepo D, Suematsu D, Zapata O. Radiative seesaw: warm dark matter, collider and lepton flavour violating signals. Phys Rev. (2009) D79:013011. doi: 10.1103/PhysRevD.79.013011
470. Suematsu D, Toma T, Yoshida T. Reconciliation of CDM abundance and μ → eγ in a radiative seesaw model. Phys Rev. (2009) D79:093004. doi: 10.1103/PhysRevD.79.093004
471. Adulpravitchai A, Lindner M, Merle A. Confronting flavour symmetries and extended scalar sectors with Lepton flavour violation bounds. Phys Rev. (2009) D80:055031. doi: 10.1103/PhysRevD.80.055031
472. Toma T, Vicente A. Lepton flavor violation in the scotogenic model. J High Energy Phys. (2014) 1:160. doi: 10.1007/JHEP01(2014)160
473. Cai Y, Schmidt MA. Revisiting the RνMDM models. J High Energy Phys. (2016) 5:28. doi: 10.1007/JHEP05(2016)028
474. Dohmen C, Groth K-D, Heer B, Honecker W, Otter G, Steinrücken B, et al. Test of lepton flavor conservation in μ → e conversion on titanium. Phys Lett. (1993) B317:631–6. doi: 10.1016/0370-2693(93)91383-X
475. The PRIME Working Group Collaboration. Search for the μ → e Conversion Process at an Ultimate Sensitivity of the Order of 10−18 with PRISM. LOI to J-PARC 50-GeV PS, LOI-25. Available online at: http://www-ps.kek.jp/jhf-np/LOIlist/pdf/L25.pdf
476. Bertl W, Engfer R, Hermes EA, Kurz G, Kozlowski T, Kuth J, et al. A search for muon to electron conversion in muonic gold. Eur Phys J. (2006) C47:337–46. doi: 10.1140/epjc/s2006-02582-x
477. Pezzullo G. The Mu2e experiment at Fermilab: a search for lepton flavor violation. Nucl Part Phys Proc. (2017) 285–286:3–7. doi: 10.1016/j.nuclphysbps.2017.03.002
478. Natori H. DeeMe experiment - an experimental search for a mu-e conversion reaction at J-PARC MLF. Nucl Phys Proc Suppl. (2014) 248–250:52–7. doi: 10.1016/j.nuclphysbps.2014.02.010
479. Kuno Y, Okada Y. Muon decay and physics beyond the standard model. Rev Mod Phys. (2001) 73:151–202. doi: 10.1103/RevModPhys.73.151
480. Arganda E, Herrero MJ, Teixeira AM. mu-e conversion in nuclei within the CMSSM seesaw: universality versus non-universality. J High Energy Phys. (2007) 10:104. doi: 10.1088/1126-6708/2007/10/104
481. Chiang HC, Oset E, Kosmas TS, Faessler A, Vergados JD. Coherent and incoherent (μ−, e−) conversion in nuclei. Nucl Phys. (1993) A559:526–42.
482. Kosmas TS, Kovalenko S, Schmidt I. Nuclear muon- e- conversion in strange quark sea. Phys Lett. (2001) B511:203. doi: 10.1016/S0370-2693(01)00657-8
483. Albrecht J, Artuso M, Babu K, Bernstein RH, Blum T, Brown DN, et al. Working Group Report: Charged Leptons. In: Proceedings, 2013 Community Summer Study on the Future of U.S. Particle Physics: Snowmass on the Mississippi (CSS2013), July 29-August 6, 2013. Minneapolis, MN (2013). Available online at: http://inspirehep.net/record/1265506/files/arXiv:1311.5278.pdf
484. de Gouvea A, Vogel P. Lepton flavor and number conservation, and physics beyond the standard model. Prog Part Nucl Phys. (2013) 71:75–92. doi: 10.1016/j.ppnp.2013.03.006
485. Crivellin A, Davidson S, Pruna GM, Signer A. Renormalisation-group improved analysis of μ → e processes in a systematic effective-field-theory approach. J High Energy Phys. (2017) 5:117. doi: 10.1007/JHEP05(2017)117
486. de Gouvea A, Lola S, Tobe K. Lepton flavor violation in supersymmetric models with trilinear R-parity violation. Phys Rev. (2001) D63:035004. doi: 10.1103/PhysRevD.63.035004
487. Klasen M, Lamprea DR, Yaguna CE. Lepton flavor violation and scalar dark matter in a radiative model of neutrino masses. (2016) arXiv:1602.05137.
488. Doršner I, Fajfer S, Greljo A, Kamenik JF, Košnik N, Nišandžic I. New physics models facing lepton flavor violating higgs decays at the percent level. J High Energy Phys. (2015) 6:108. doi: 10.1007/JHEP06(2015)108
489. Blankenburg G, Ellis J, Isidori G. Flavour-changing decays of a 125 GeV higgs-like particle. Phys Lett. (2012) B712:386–90. doi: 10.1016/j.physletb.2012.05.007
490. Harnik R, Kopp J, Zupan J. Flavor violating higgs decays. J High Energy Phys. (2013) 3:26. doi: 10.1007/JHEP03(2013)026
491. Herrero-García J, Rius N, Santamaria A. Higgs lepton flavour violation: UV completions and connection to neutrino masses. J High Energy Phys. (2016) 11:84. doi: 10.1007/JHEP11(2016)084
492. Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, Aben R, et al. Search for lepton-flavour-violating decays of the Higgs and Z bosons with the ATLAS detector. Eur Phys J. (2017) C77:70. doi: 10.1140/epjc/s10052-017-4624-0
493. CMS Collaboration. Search for lepton flavour violating decays of the Higgs boson to μτ and eτ in proton-proton collisions at . CMS-PAS-HIG-17-001 (2017).
495. Arganda E, Curiel AM, Herrero MJ, Temes D. Lepton flavor violating Higgs boson decays from massive seesaw neutrinos. Phys Rev. (2005) D71:035011. doi: 10.1103/PhysRevD.71.035011
496. Arganda E, Herrero MJ, Marcano X, Weiland C. Imprints of massive inverse seesaw model neutrinos in lepton flavor violating Higgs boson decays. Phys Rev. (2015) D91:015001. doi: 10.1103/PhysRevD.91.015001
497. Thao NH, Hue LT, Hung HT, Xuan NT. Lepton flavor violating Higgs boson decays in seesaw models: new discussions. Nucl Phys. (2017) B921:159–80. doi: 10.1016/j.nuclphysb.2017.05.014
498. Arganda E, Herrero MJ, Marcano X, Morales R, Szynkman A. Effective lepton flavor violating HâŞiâṢj vertex from right-handed neutrinos within the mass insertion approximation. Phys Rev. (2017) D95:095029. doi: 10.1103/PhysRevD.95.095029
499. Davidson S, Grenier GJ. Lepton flavour violating Higgs and tau to mu gamma. Phys Rev. (2010) D81:095016. doi: 10.1103/PhysRevD.81.095016
500. Aristizabal Sierra D, Vicente A. Explaining the CMS higgs flavor violating decay excess. Phys Rev. (2014) D90:115004. doi: 10.1103/PhysRevD.90.115004
501. Omura Y, Senaha E, Tobe K. Lepton-flavor-violating Higgs decay h → μτ and muon anomalous magnetic moment in a general two Higgs doublet model. J High Energy Phys. (2015) 5:28. doi: 10.1007/JHEP05(2015)028
502. Botella FJ, Branco GC, Nebot M, Rebelo MN. Flavour changing higgs couplings in a class of two higgs doublet models. Eur Phys J. (2016) C76:161. doi: 10.1140/epjc/s10052-016-3993-0
503. Raidal M, van der Schaaf A, Bigi I, Mangano ML, Semertzidis Y, Abel S, et al. Flavour physics of leptons and dipole moments. Eur Phys J. (2008) C57:13–182. doi: 10.1140/epjc/s10052-008-0715-2
504. Patrignani C, Agashe K, Aielli G, Amsler C, Antonelli M, Asner DM, et al. Review of particle physics. Chin Phys. (2016) C40:100001. doi: 10.1088/1674-1137/40/10/100001
505. Lee S, Nomura T, Okada H. Radiatively induced neutrino mass model with flavor dependent gauge symmetry. (2017) arXiv:1702.03733.
506. Lindner M, Platscher M, Queiroz FS. A call for new physics : the muon anomalous magnetic moment and lepton flavor violation. (2016) arXiv:1610.06587.
507. Furry WH. On transition probabilities in double beta-disintegration. Phys Rev. (1939) 56:1184–93. doi: 10.1103/PhysRev.56.1184
508. Albert JB, Auty DJ, Barbeau PS, Beauchamp E, Beck D, Belov V, et al. Search for Majorana neutrinos with the first two years of EXO-200 data. Nature (2014) 510:229–34. doi: 10.1038/nature13432
509. Aad G, Abajyan T, Abbott B, Abdallah J, Abdel Khalek S, Abdinov O, et al. Limit on neutrinoless ββ decay of 136Xe from the first phase of KamLAND-Zen and comparison with the positive claim in 76Ge. Phys Rev Lett. (2013) 110:062502. doi: 10.1103/PhysRevLett.110.062502
510. Asakura K, Gando A, Gando Y, Hachiya T, Hayashida S, Ikeda H, et al. Results from KamLAND-Zen. AIP Conf Proc. (2015) 1666:170003. doi: 10.1063/1.4915593
511. Dell'Oro S, Marcocci S, Viel M, Vissani F. Neutrinoless double beta decay: 2015 review. Adv High Energy Phys. (2016) 2016:2162659. doi: 10.1155/2016/2162659
512. Schechter J, Valle JWF. Neutrinoless double beta decay in SU(2) × U(1) theories. Phys Rev. (1982) D25:2951.
513. Duerr M, Lindner M, Merle A. On the quantitative impact of the schechter-valle theorem. J High Energy Phys. (2011) 6:91. doi: 10.1007/JHEP06(2011)091
514. Rodejohann W. Neutrinoless double beta decay and neutrino physics. J Phys. (2012) G39:124008. doi: 10.1088/0954-3899/39/12/124008
515. Bilenky SM, Giunti C. Neutrinoless double-beta decay: a brief review. Mod Phys Lett. (2012) A27:1230015. doi: 10.1142/S0217732312300157
516. Päs H, Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. Towards a superformula for neutrinoless double beta decay. Phys Lett. (1999) B453:194–98. doi: 10.1016/S0370-2693(99)00330-5
517. Päs H, Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. A Superformula for neutrinoless double beta decay. 2. The short range part. Phys Lett. (2001) B498:35–9. doi: 10.1016/S0370-2693(00)01359-9
518. Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. New leptoquark mechanism of neutrinoless double beta decay. Phys Rev. (1996) D54:R4207–210.
519. Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. New low-energy leptoquark interactions. Phys Lett. (1996) B378:17–22.
520. Mohapatra RN. New contributions to neutrinoless double beta decay in supersymmetric theories. Phys Rev. (1986) D34:3457–61. doi: 10.1103/PhysRevD.34.3457
521. Babu KS, Mohapatra RN. New vector - scalar contributions to neutrinoless double beta decay and constraints on R-parity violation. Phys Rev Lett. (1995) 75:2276–79. doi: 10.1103/PhysRevLett.75.2276
522. Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. Supersymmetry and neutrinoless double beta decay. Phys Rev. (1996) D53:1329–48.
523. Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. New supersymmetric contributions to neutrinoless double beta decay. Phys Lett. (1995) B352:1–7. doi: 10.1016/0370-2693(95)00460-3
524. Choubey S, Duerr M, Mitra M, Rodejohann W. Lepton Number and Lepton Flavor Violation through Color Octet States. J High Energy Phys. (2012) 5:17. doi: 10.1007/JHEP05(2012)017
525. Brahmachari B, Ma E. Neutrinoless double beta decay with negligible neutrino mass. Phys Lett. (2002) B536:259–62. doi: 10.1016/S0370-2693(02)01869-5
526. Gu PH. Significant neutrinoless double beta decay with quasi-Dirac neutrinos. Phys Rev. (2012) D85:093016. doi: 10.1103/PhysRevD.85.093016
527. Quintero N. Constraints on lepton number violating short-range interactions from |ΔL| = 2 processes. Phys Lett. (2017) B764:60–5. doi: 10.1016/j.physletb.2016.10.056
528. Rodejohann W. Neutrino oscillation experiments and limits on lepton number and lepton flavor violating processes. Phys Rev. (2000) D62:013011. doi: 10.1103/PhysRevD.62.013011
529. Berryman JM, de Gouvêa A, Kelly KJ, Kobach A. Lepton-number-violating searches for muon to positron conversion. Phys Rev. (2017) D95:115010. doi: 10.1103/PhysRevD.95.115010
530. Geib T, Merle A. μ−−e+ conversion from short-range operators. Phys Rev. (2017) D95:055009. doi: 10.1103/PhysRevD.95.055009
531. Deppisch FF, Bhupal Dev PS, Pilaftsis A. Neutrinos and collider physics. New J Phys. (2015) 17:075019. doi: 10.1088/1367-2630/17/7/075019
532. Babu KS, Jana S. Probing doubly charged higgs bosons at the LHC through photon initiated processes. Phys Rev. (2017) D95:055020. doi: 10.1103/PhysRevD.95.055020
533. The ATLAS Collaboration. Search for doubly-charged Higgs bosons in same-charge electron pair final states using proton-proton collisions at with the ATLAS detector. ATLAS-CONF-2016-051. (2016).
534. Collaboration C. A search for doubly-charged Higgs boson production in three and four lepton final states at . CMS-PAS-HIG-16-036. (2017).
535. Sugiyama H, Tsumura K, Yokoya H. Discrimination of models including doubly charged scalar bosons by using tau lepton decay distributions. Phys Lett. (2012) B717:229–34. doi: 10.1016/j.physletb.2012.09.044
536. del Águila F, Chala M. LHC bounds on Lepton Number Violation mediated by doubly and singly-charged scalars. J High Energy Phys. (2014) 3:27. doi: 10.1007/JHEP03(2014)027
537. del Aguila F, Chala M, Santamaria A, Wudka J. Discriminating between lepton number violating scalars using events with four and three charged leptons at the LHC. Phys Lett. (2013) B725:310–5. doi: 10.1016/j.physletb.2013.07.014
538. Kanemura S, Yagyu K, Yokoya H. First constraint on the mass of doubly-charged Higgs bosons in the same-sign diboson decay scenario at the LHC. Phys Lett. (2013) B726:316–9. doi: 10.1016/j.physletb.2013.08.054
539. Helo JC, Hirsch M, Päs H, Kovalenko SG. Short-range mechanisms of neutrinoless double beta decay at the LHC. Phys Rev. (2013) D88:073011. doi: 10.1103/PhysRevD.88.073011
540. Peng T, Ramsey-Musolf MJ, Winslow P. TeV lepton number violation: from neutrinoless double-β decay to the LHC. Phys Rev. (2016) D93:093002. doi: 10.1103/PhysRevD.93.093002
541. Gonzales L, Helo JC, Hirsch M, Kovalenko SG. Scalar-mediated double beta decay and LHC. J High Energy Phys. (2016) 12:130. doi: 10.1007/JHEP12(2016)130
542. Buchmuller W, Ruckl R, Wyler D. Leptoquarks in Lepton - Quark collisions. Phys Lett. (1987) B191:442–8. doi: 10.1016/0370-2693(87)90637-X
543. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Search for direct top-squark pair production in final states with two leptons in pp collisions at 8TeV with the ATLAS detector. J High Energy Phys. (2014) 6:124. doi: 10.1007/JHEP06(2014)124
544. CMS Collaboration. Search for direct stop pair production in the dilepton final state at 13 TeV. CMS-PAS-SUS-17-001. (2017).
545. Carrà S. Search for top squark with two leptons in the final state at LHC Run 2 with the ATLAS detector. Nuovo Cim. (2017) C40:26. doi: 10.1393/ncc/i2017-17026-5
546. Cai Y, Schmidt MA. A case study of the sensitivity to LFV operators with precision measurements and the LHC. J High Energy Phys. (2016) 2:176. doi: 10.1007/JHEP02(2016)176
547. Aguilar-Saavedra JA. Identifying top partners at LHC. J High Energy Phys. (2009) 11:030. doi: 10.1088/1126-6708/2009/11/030
548. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Analysis of events with b-jets and a pair of leptons of the same charge in pp collisions at TeV with the ATLAS detector. J High Energy Phys. (2015) 10:150. doi: 10.1007/JHEP10(2015)150
549. Aad G, Abbott B, Abdallah J, Abdel KS, Abdinov O, Aben R, et al. Search for pair and single production of new heavy quarks that decay to a Z boson and a third-generation quark in pp collisions at TeV with the ATLAS detector. J High Energy Phys. (2014) 11:104. doi: 10.1007/JHEP11(2014)104
550. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Search for production of vector-like quark pairs and of four top quarks in the lepton-plus-jets final state in pp collisions at TeV with the ATLAS detector. J High Energy Phys. (2015) 8:105. doi: 10.1007/JHEP08(2015)105
551. Khachatryan V, Besancon M, Couderc F, Dejardin M, Denegri D, Fabbro B, et al. Search for vector-like charge 2/3 T quarks in proton-proton collisions at sqrt(s) = 8 TeV. Phys Rev. (2016) D93:012003. doi: 10.1103/PhysRevD.93.012003
552. Aaboud M, Aad G, Abbott B, Abdinov O, Abeloos B, Abidi SH, et al. Search for pair production of vector-like top quarks in events with one lepton, jets, and missing transverse momentum in TeV pp collisions with the ATLAS detector. J High Energy Phys. (2017) 8:052. doi: 10.1007/JHEP08(2017)052
553. Aaboud M, Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, et al. Search for top squarks in final states with one isolated lepton, jets, and missing transverse momentum in TeV pp collisions with the ATLAS detector. Phys Rev. (2016) D94:052009. doi: 10.1103/PhysRevD.94.052009
554. The ATLAS collaboration. Search for new physics using events with b-jets and a pair of same charge leptons in 3.2 fb−1 of pp collisions at TeV with the ATLAS detector. ATLAS-CONF-2016-032 (2016).
555. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Search for pair production of vector-like T and B quarks in single-lepton final states using boosted jet substructure in proton-proton collisions at TeV. J High Energy Phys. (2017) 11:085. doi: 10.1007/JHEP11(2017)085
556. Chatrchyan S, Besancon M, Couderc F, Dejardin M, Denegri D, Fabbro B, et al. Inclusive search for a vector-like T quark with charge in pp collisions at = 8 TeV. Phys Lett. (2014) B729:149–71. doi: 10.1016/j.physletb.2014.01.006
557. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Search for pair production of a new heavy quark that decays into a W boson and a light quark in pp collisions at TeV with the ATLAS detector. Phys Rev. (2015) D92:112007. doi: 10.1103/PhysRevD.92.112007
558. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Asilar E, Bergauer T, et al. Search for pair-produced vectorlike B quarks in proton-proton collisions at =8 TeV. Phys Rev. (2016) D93:112009. doi: 10.1103/PhysRevD.93.112009
559. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Search for vector-like B quarks in events with one isolated lepton, missing transverse momentum and jets at 8 TeV with the ATLAS detector. Phys Rev. (2015) D91:112011.
560. Altmannshofer W, Bauer M, Carena M. Exotic leptons: higgs, flavor and collider phenomenology. J High Energy Phys. (2014) 1:60. doi: 10.1007/JHEP01(2014)060
561. Falkowski A, Straub DM, Vicente A. Vector-like leptons: higgs decays and collider phenomenology. J High Energy Phys. (2014) 5:92. doi: 10.1007/JHEP05(2014)092
562. Dermisek R, Hall JP, Lunghi E, Shin S. Limits on vectorlike leptons from searches for anomalous production of multi-lepton events. J High Energy Phys. (2014) 12:13. doi: 10.1007/JHEP12(2014)013
563. Kumar N, Martin SP. Vectorlike leptons at the Large Hadron Collider. Phys Rev. (2015) D92:115018. doi: 10.1103/PhysRevD.92.115018
564. Hamada Y, Kawai H, Kawana K, Tsumura K. Models of the LHC diphoton excesses valid up to the Planck scale. Phys Rev. (2016) D94:014007. doi: 10.1103/PhysRevD.94.014007
565. Pati JC, Salam A. Lepton number as the fourth color. Phys Rev. (1974) D10:275–89. doi: 10.1103/PhysRevD.10.275
566. Georgi H, Glashow SL. Unity of all elementary particle forces. Phys Rev Lett. (1974) 32:438–41. doi: 10.1103/PhysRevLett.32.438
567. Aaboud M, Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, et al. Search for scalar leptoquarks in pp collisions at = 13 TeV with the ATLAS experiment. New J Phys. (2016) 18:093016. doi: 10.1088/1367-2630/18/9/093016
568. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Searches for scalar leptoquarks in pp collisions at = 8 TeV with the ATLAS detector. Eur Phys J. (2016) C76:5. doi: 10.1140/epjc/s10052-015-3823-9
569. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, et al. CMS Collaboration. Search for pair-production of first generation scalar leptoquarks in pp collisions at with 2.6 fb−1. CMS-PAS-EXO-16-043 (2016).
570. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, et al. CMS Collaboration. Search for pair-production of second-generation scalar leptoquarks in pp collisions at with the CMS detector. CMS-PAS-EXO-16-007 (2016).
571. CMS Collaboration. Search for the third-generation scalar leptoquarks and heavy right-handed neutrinos in τℓτhjj final states in pp collisions at 13 TeV. CMS-PAS-EXO-16-023 (2016).
572. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Search for heavy long-lived multi-charged particles in pp collisions at TeV using the ATLAS detector. Eur Phys J. (2015) C75:362. doi: 10.1140/epjc/s10052-015-3534-2
573. Khoze VV, Plascencia AD, Sakurai K. Simplified models of dark matter with a long-lived co-annihilation partner. J High Energy Phys. (2017) 6:41. doi: 10.1007/JHEP06(2017)041
574. The ATLAS Collaboration. Search for electroweak production of supersymmetric particles in the two and three lepton final state at TeV with the ATLAS detector. ATLAS-CONF-2017-039 (2017).
575. Ahriche A, McDonald KL, Nasri S, Picek I. A critical analysis of one-loop neutrino mass models with minimal dark matter. Phys Lett. (2016) B757:399–404. doi: 10.1016/j.physletb.2016.04.022
576. Aristizabal Sierra D, Simoes C, Wegman D. Closing in on minimal dark matter and radiative neutrino masses. J High Energy Phys. (2016) 6:108. doi: 10.1007/JHEP06(2016)108
577. Aad G, Abajyan T, Abbott B, Abdallah J, Khalek SA, Abdinov O., et al. Search for charginos nearly mass degenerate with the lightest neutralino based on a disappearing-track signature in pp collisions at TeV with the ATLAS detector. Phys Rev. (2013) D88:112006.
578. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, et al. Search for disappearing tracks in proton-proton collisions at TeV. J High Energy Phys. (2015) 1:96. doi: 10.1007/JHEP01(2015)096
579. The ATLAS collaboration. Search for Long-lived Charginos based on a Disappearing-Track Signature in pp Collisions at TeV with the ATLAS Detector. (2017) Report number: ATLAS-CONF-2017-017.
580. Sakharov AD. Violation of CP invariance, c asymmetry, and baryon asymmetry of the universe. Pisma Zh Eksp Teor Fiz. (1967) 5:32–5. doi: 10.1070/PU1991v034n05ABEH002497
581. Kuzmin VA, Rubakov VA, Shaposhnikov ME. On the anomalous electroweak baryon number nonconservation in the early universe. Phys Lett. (1985) B155:36. doi: 10.1016/0370-2693(85)91028-7
582. Davidson S, Nardi E, Nir Y. Leptogenesis. Phys Rept. (2008) 466:105–77. doi: 10.1016/j.physrep.2008.06.002
583. Ma E. Common origin of neutrino mass, dark matter, and baryogenesis. Mod Phys Lett. (2006) A21:1777–82. doi: 10.1142/S0217732306021141
584. Kashiwase S, Suematsu D. Baryon number asymmetry and dark matter in the neutrino mass model with an inert doublet. Phys Rev. (2012) D86:053001. doi: 10.1103/PhysRevD.86.053001
585. Kashiwase S, Suematsu D. Leptogenesis and dark matter detection in a TeV scale neutrino mass model with inverted mass hierarchy. Eur Phys J. (2013) C73:2484. doi: 10.1140/epjc/s10052-013-2484-9
586. Racker J. Mass bounds for baryogenesis from particle decays and the inert doublet model. J Cosmol Astropart Phys. (2014) 1403:025. doi: 10.1088/1475-7516/2014/03/025
587. Dev PSB, Mohapatra RN. TeV scale model for baryon and lepton number violation and resonant baryogenesis. Phys Rev. (2015) D92:016007. doi: 10.1103/PhysRevD.92.016007
588. Hambye T, Kannike K, Ma E, Raidal M. Emanations of dark matter: muon anomalous magnetic moment, radiative neutrino mass, and novel leptogenesis at the TeV scale. Phys Rev. (2007) D75:095003. doi: 10.1103/PhysRevD.75.095003
589. Babu KS, Ma E. Singlet fermion dark matter and electroweak baryogenesis with radiative neutrino mass. Int J Mod Phys. (2008) A23:1813–19. doi: 10.1142/S0217751X08040299
590. Suematsu D. Leptogenesis in a neutrino mass model coupled with inflaton. Phys Lett. (2016) B760:538–43. doi: 10.1016/j.physletb.2016.07.048
591. Bertolini S, Di Luzio L, Kolešová H, Malinský M. Massive neutrinos and invisible axion minimally connected. Phys Rev. (2015) D91:055014.
592. Aoki M, Kanemura S, Seto O. A model of TeV scale physics for neutrino mass, dark matter and baryon asymmetry and its phenomenology. Phys Rev. (2009) D80:033007. doi: 10.1103/PhysRevD.80.033007
593. Fischler W, Giudice GF, Leigh RG, Paban S. Constraints on the baryogenesis scale from neutrino masses. Phys Lett. (1991) B258:45–8.
594. Campbell BA, Davidson S, Ellis JR, Olive KA. Cosmological baryon asymmetry constraints on extensions of the standard model. Phys Lett. (1991) B256:484–90.
595. Nelson AE, Barr SM. Upper bound on baryogenesis scale from neutrino masses. Phys Lett. (1990) B246:141–3.
596. Harvey JA, Turner MS. Cosmological baryon and lepton number in the presence of electroweak fermion number violation. Phys Rev. (1990) D42:3344–49.
597. Antaramian A, Hall LJ, Rasin A. Hypercharge and the cosmological baryon asymmetry. Phys Rev. (1994) D49:3881–5.
598. Frere JM, Hambye T, Vertongen G. Is leptogenesis falsifiable at LHC? J High Energy Phys. (2009) 1:51. doi: 10.1088/1126-6708/2009/01/051
599. Deppisch FF, Harz J, Hirsch M. Falsifying high-scale leptogenesis at the LHC. Phys Rev Lett. (2014) 112:221601. doi: 10.1103/PhysRevLett.112.221601
600. Deppisch FF, Harz J, Hirsch M, Huang WC, Päs H. Falsifying high-scale baryogenesis with neutrinoless double beta decay and lepton flavor violation. Phys Rev. (2015) D92:036005. doi: 10.1103/PhysRevD.92.036005
601. Boehm C, Farzan Y, Hambye T, Palomares-Ruiz S, Pascoli S. Is it possible to explain neutrino masses with scalar dark matter? Phys Rev. (2008) D77:043516. doi: 10.1103/PhysRevD.77.043516
602. El Aisati C, Garcia-Cely C, Hambye T, Vanderheyden L. Prospects for discovering a neutrino line induced by dark matter annihilation. J Cosmol Astropart Phys. (2017) 1710:021. doi: 10.1088/1475-7516/2017/10/021
603. Ma E, Ohata T, Tsumura K. Majoron as the QCD axion in a radiative seesaw model. Phys Rev. (2017) D96:075039. doi: 10.1103/PhysRevD.96.075039
604. Babu KS, Macesanu C. Two loop neutrino mass generation and its experimental consequences. Phys Rev. (2003) D67:073010. doi: 10.1103/PhysRevD.67.073010
605. Petcov ST. Remarks on the zee model of neutrino mixing (μ → eγ, heavy neutrino → light neutrino gamma, etc.). Phys Lett. (1982) B115:401–6.
606. Bertolini S, Santamaria A. The doublet majoron model and solar neutrino oscillations. Nucl Phys. (1988) B310:714–42.
607. Bertolini S, Santamaria A. The strong CP problem and the solar neutrino puzzle: are they related? Nucl Phys. (1991) B357:222–40.
608. Smirnov AYu, Tao Zj. Neutrinos with Zee mass matrix in vacuum and matter. Nucl Phys. (1994) B426:415–33. doi: 10.1016/0550-3213(94)90318-2
609. Smirnov AYu, Tanimoto M. Is zee model the model of neutrino masses? In: Neutrino '96. Proceedings, 17th International Conference on Neutrino Physics and Astrophysics, June 13-19, 1996 Helsinki (1996). p. 309–14.
610. Frampton PH, Glashow SL. Can the Zee ansatz for neutrino masses be correct? Phys Lett. (1999) B461:95–8. doi: 10.1016/S0370-2693(99)00824-2
611. Jarlskog C, Matsuda M, Skadhauge S, Tanimoto M. Zee mass matrix and bimaximal neutrino mixing. Phys Lett. (1999) B449:240.
612. Kanemura S, Kasai T, Lin GL, Okada Y, Tseng JJ, Yuan CP. Phenomenology of Higgs bosons in the Zee model. Phys Rev. (2001) D64:053007. doi: 10.1103/PhysRevD.64.053007
613. Balaji KRS, Grimus W, Schwetz T. The Solar LMA neutrino oscillation solution in the Zee model. Phys Lett. (2001) B508:301–10. doi: 10.1016/S0370-2693(01)00532-9
614. Koide Y. Prospect of the zee model. Nucl Phys Proc Suppl. (2002) 111:294–6. doi: 10.1016/S0920-5632(02)01726-7
615. Brahmachari B, Choubey S. Viability of bimaximal solution of the Zee mass matrix. Phys Lett. (2002) B531:99–104. doi: 10.1016/S0370-2693(02)01366-7
616. Frampton PH, Oh MC, Yoshikawa T. Zee model confronts SNO data. Phys Rev. (2002) D65:073014. doi: 10.1103/PhysRevD.65.073014
617. Assamagan KA, Deandrea A, Delsart PA. Search for the lepton flavor violating decay A0/H0 → τ±μ∓ at hadron colliders. Phys Rev. (2003) D67:035001. doi: 10.1103/PhysRevD.67.035001
618. Kanemura S, Ota T, Tsumura K. Lepton flavor violation in Higgs boson decays under the rare tau decay results. Phys Rev. (2006) D73:016006. doi: 10.1103/PhysRevD.73.016006
619. Aristizabal Sierra D, Restrepo D. Leptonic charged higgs decays in the zee model. J High Energy Phys. (2006) 8:36. doi: 10.1088/1126-6708/2006/08/036
620. Aristizabal Sierra D, Hirsch M. Experimental tests for the Babu-Zee two-loop model of Majorana neutrino masses. J High Energy Phys. (2006) 12:052. doi: 10.1088/1126-6708/2006/12/052
621. Ohlsson T, Schwetz T, Zhang H. Non-standard neutrino interactions in the Zee-Babu model. Phys Lett. (2009) B681:269–75. doi: 10.1016/j.physletb.2009.10.025
622. Schmidt D, Schwetz T, Zhang H. Status of the Zee–Babu model for neutrino mass and possible tests at a like-sign linear collider. Nucl Phys. (2014) B885:524–41. doi: 10.1016/j.nuclphysb.2014.05.024
623. Aristizabal Sierra D, Dhen M, Fong CS, Vicente A. Dynamical flavor origin of ℤN symmetries. Phys Rev. (2015) D91:096004. doi: 10.1103/PhysRevD.91.096004
624. Deshpande NG, Ma E. Pattern of symmetry breaking with two higgs doublets. Phys Rev. (1978) D18:2574.
625. Lopez Honorez L, Nezri E, Oliver JF, Tytgat MHG. The inert doublet model: an archetype for dark matter. J Cosmol Astropart Phys. (2007) 702:28. doi: 10.1088/1475-7516/2007/02/028
626. Borah D, Gupta A. A new viable region of inert higgs doublet dark matter model with scotogenic extension. (2017) arXiv:1706.05034.
627. Ho SY, Tandean J. Probing scotogenic effects in higgs boson decays. Phys Rev. (2013) D87:095015. doi: 10.1103/PhysRevD.87.095015
628. Ho SY, Tandean J. Probing scotogenic effects in e+e− colliders. Phys Rev. (2014) D89:114025. doi: 10.1103/PhysRevD.89.114025
629. Hessler AG, Ibarra A, Molinaro E, Vogl S. Probing the scotogenic FIMP at the LHC. J High Energy Phys. (2017) 1:100. doi: 10.1007/JHEP01(2017)100
630. Díaz MA, Rojas N, Urrutia-Quiroga S, Valle JWF. Heavy higgs boson production at colliders in the singlet-triplet scotogenic dark matter model. J High Energy Phys. (2017) 8:017. doi: 10.1007/JHEP08(2017)017
631. Molinaro E, Yaguna CE, Zapata O. FIMP realization of the scotogenic model. J Cosmol Astropart Phys. (2014) 1407:15. doi: 10.1088/1475-7516/2014/07/015
632. Faisel G, Ho SY, Tandean J. Exploring X-ray lines as scotogenic signals. Phys Lett. (2014) B738:380–5. doi: 10.1016/j.physletb.2014.09.063
633. Ho SY, Faisel G, Tandean J. Exploring X-ray lines as scotogenic signals. PoS (2016) DSU2015:68.
634. Chowdhury TA, Nasri S. The sommerfeld enhancement in the scotogenic model with large electroweak scalar multiplets. J Cosmol Astropart Phys. (2017) 1701:041. doi: 10.1088/1475-7516/2017/01/041
635. Merle A, Platscher M. Parity problem of the scotogenic neutrino model. Phys Rev. (2015) D92:095002. doi: 10.1103/PhysRevD.92.095002
636. Merle A, Platscher M. Running of radiative neutrino masses: the scotogenic model - revisited. J High Energy Phys. (2015) 11:148. doi: 10.1007/JHEP11(2015)148
637. Lindner M, Platscher M, Yaguna CE, Merle A. Fermionic WIMPs and vacuum stability in the scotogenic model. Phys Rev. (2016) D94:115027. doi: 10.1103/PhysRevD.94.115027
638. Doršner I, Fajfer S, Greljo A, Kamenik JF, Košnik N. Physics of leptoquarks in precision experiments and at particle colliders. Phys Rept. (2016) 641:1–68. doi: 10.1016/j.physrep.2016.06.001
639. Aaij R, Adeva B, Adinolfi M, Affolder A, Ajaltouni Z, Akar S, et al. Test of lepton universality using B+ → K+ℓ+ℓ− decays. Phys Rev Lett. (2014) 113:151601. doi: 10.1103/PhysRevLett.113.151601
640. Lees JP, Poireau V, Tisserand V, Garra Tico J, Grauges E, Palano A, et al. Evidence for an excess of decays. Phys Rev Lett. (2012) 109:101802. doi: 10.1103/PhysRevLett.109.101802
641. Lees JP, Poireau V, Tisserand V, Grauges E, Palano A, Eigen G, et al. Measurement of an excess of decays and implications for charged higgs bosons. Phys Rev. (2013) D88:072012. doi: 10.1103/PhysRevD.88.072012
642. Huschle M, Kuhr T, Heck M, Goldenzweig P, Abdesselam A, Adachi I, et al. Measurement of the branching ratio of relative to decays with hadronic tagging at Belle. Phys Rev. (2015) D92:072014. doi: 10.1103/PhysRevD.92.072014
643. Sato Y, Iijima T, Adamczyk K, Aihara H, Asner DM, Atmacan H, et al. Measurement of the branching ratio of relative to decays with a semileptonic tagging method. Phys Rev. (2016) D94:072007. doi: 10.1103/PhysRevD.94.072007
644. Hirose S, Iijima T, Adachi I, Adamczyk K, Aihara H, Al Said S, et al. Measurement of the τ lepton polarization and R(D*) in the decay . Phys Rev Lett. (2017) 118:211801. doi: 10.1103/PhysRevLett.118.211801
645. Aaij R, Adeva B, Adinolfi M, Affolder A, Ajaltouni Z, Akar S, et al. Measurement of the ratio of branching fractions . Phys Rev Lett. (2015) 115:111803. doi: 10.1103/PhysRevLett.115.111803
646. Barbier R, Berat C, Besancon M, Chemtob M, Deandrea A, Dudas E, et al. R-parity violating supersymmetry. Phys Rept. (2005) 420:1–202. doi: 10.1016/j.physrep.2005.08.006
647. Ibanez LE, Ross GG. Discrete gauge symmetries and the origin of baryon and lepton number conservation in supersymmetric versions of the standard model. Nucl Phys. (1992) B368:3–37. doi: 10.1016/0550-3213(92)90195-H
648. Hirsch M, Valle JWF. Supersymmetric origin of neutrino mass. New J Phys. (2004) 6:76. doi: 10.1088/1367-2630/6/1/076
649. Hirsch M, Diaz MA, Porod W, Romao JC, Valle JWF. Neutrino masses and mixings from supersymmetry with bilinear R parity violation: a Theory for solar and atmospheric neutrino oscillations. Phys Rev. (2000) D62:113008. doi: 10.1103/PhysRevD.62.113008
650. Diaz MA, Hirsch M, Porod W, Romao JC, Valle JWF. Solar neutrino masses and mixing from bilinear R parity broken supersymmetry: analytical versus numerical results. Phys Rev. (2003) D68:013009. doi: 10.1103/PhysRevD.71.059904
651. Grossman Y, Rakshit S. Neutrino masses in R-parity violating supersymmetric models. Phys Rev. (2004) D69:093002. doi: 10.1103/PhysRevD.69.093002
652. de Campos F, Eboli OJP, Magro MB, Porod W, Restrepo D, Das SP, et al. Probing neutralino properties in minimal supergravity with bilinear R-parity violation. Phys Rev. (2012) D86:075001. doi: 10.1103/PhysRevD.86.075001
653. Mukhopadhyaya B, Roy S, Vissani F. Correlation between neutrino oscillations and collider signals of supersymmetry in an R-parity violating model. Phys Lett. (1998) B443:191–5.
654. Choi SY, Chun EJ, Kang SK, Lee JS. Neutrino oscillations and R-parity violating collider signals. Phys Rev. (1999) D60:075002.
655. Romao JC, Diaz MA, Hirsch M, Porod W, Valle JWF. A Supersymmetric solution to the solar and atmospheric neutrino problems. Phys Rev. (2000) D61:071703. doi: 10.1103/PhysRevD.61.071703
656. Porod W, Hirsch M, Romao J, Valle JWF. Testing neutrino mixing at future collider experiments. Phys Rev. (2001) D63:115004. doi: 10.1103/PhysRevD.63.115004
657. Hirsch M, Vicente A, Porod W. Spontaneous R-parity violation: lightest neutralino decays and neutrino mixing angles at future colliders. Phys Rev. (2008) D77:075005. doi: 10.1103/PhysRevD.77.075005
658. Bartl A, Hirsch M, Vicente A, Liebler S, Porod W. LHC phenomenology of the μνSSM. J High Energy Phys. (2009) 5:120. doi: 10.1088/1126-6708/2009/05/120
659. Liebler S, Porod W. On-shell renormalization of neutralino and chargino mass matrices in R-parity violating models - Correlation between LSP decays and neutrino mixing angles revisited. Nucl Phys. (2012) B855:774–800. doi: 10.1016/j.nuclphysb.2011.10.027
660. Deshpande NG, He XG. Consequences of R-parity violating interactions for anomalies in and b → sμ+μ−. Eur Phys J. (2017) C77:134. doi: 10.1140/epjc/s10052-017-4707-y
661. Dreiner HK, Staub F, Vicente A, Porod W. General MSSM signatures at the LHC with and without R-parity. Phys Rev. (2012) D86:035021. doi: 10.1103/PhysRevD.86.035021
662. Bennett GW, Bousquet B, Brown HN, Bunce G, Carey RM, Cushman P, et al. Final report of the muon E821 anomalous magnetic moment measurement at BNL. Phys Rev. (2006) D73:072003. doi: 10.1103/PhysRevD.73.072003
663. Ellis J. TikZ-Feynman: Feynman diagrams with TikZ. Comput Phys Commun. (2017) 210:103–23. doi: 10.1016/j.cpc.2016.08.019
Appendix
On the Relative Contribution of Operators
Oftentimes the effective ΔL = 2 operators are discussed using a cutoff regularization scheme. In the following, however, we outline the relative contribution of the different ΔL = 2 operators to neutrino mass using dimensional regularization with a momentum-independent renormalization scheme such as renormalization. Power counting in the SM effective theory establishes that the dominant contributions to neutrino mass are given by (i) the lowest-dimensional Weinberg-like operator which is induced via matching at the new physics scale Λ and (ii) the contributions induced by mixing via renormalization group running of the operator into the Weinberg operator or other lower-dimensional Weinberg-like operators.
Using naive dimensional analysis we discuss in more detail the relative contribution to neutrino mass from each operator in the SM effective field theory. Note that here we follow the matching and running from low energy scale to high energy scale. Below the electroweak scale effective operators that can contribute to neutrino masses should contain two neutrinos and possibly additional fields. Those additional fields have to be closed off and their contribution to neutrino masses vary: for photons and gluons, the contribution from the tadpole diagram vanishes; for fermions f, the contribution is proportional to a factor m3/16π2Λ3 per fermion loop. Thus, the contribution of operators with additional fields to neutrino mass either vanishes or is generally suppressed. Matching at the electroweak scale may similarly include loops with electroweak gauge bosons or the top quark and lead to a suppression of the respective operator. Additional Higgs fields yield a factor v/Λ each. Above the electroweak scale the operators generally mix. Higher-dimensional operators also mix into lower dimensional ones. For example although the operator mixes into the operator O1 via renormalization group running and thus it is an operator of lower dimension, its contribution to the Wilson coefficient is suppressed by a factor of order and therefore it is of the same order as the operator . At the new physics scale the relative size of the Wilson coefficients is determined by the couplings and the loop level at which they are generated. The Wilson coefficient of the Weinberg-like operators at the new physics scale may be suppressed by a loop factor compared to other operators, but the other operators receive a further loop-factor suppression when matching onto the effective interactions at the electroweak scale or finally onto the neutrino mass term at a lower scale. The contributions of all operators to neutrino mass has at least the same loop-factor suppression as the leading Weinberg-like operator which is induced by matching at the new physics scale. Higher-dimensional Weinberg-like operators will induce the lower-dimensional ones via mixing when running the Wilson coefficients to the low scale, but the contribution of the induced operator is still of the same order as the original higher-dimensional operator. In summary, an order of magnitude estimate of neutrino mass can be obtained from the leading Weinberg-like operator which is induced from matching at the new physics scale keeping in mind that its contribution to lower-dimensional Weinberg-like operators will be of a similar order of magnitude.
Keywords: neutrino masses, lepton flavor violation, lepton number violation, beyond the standard model, effective field theory, model building, LHC, dark matter
Citation: Cai Y, Herrero García J, Schmidt MA, Vicente A and Volkas RR (2017) From the Trees to the Forest: A Review of Radiative Neutrino Mass Models. Front. Phys. 5:63. doi: 10.3389/fphy.2017.00063
Received: 18 July 2017; Accepted: 14 November 2017;
Published: 04 December 2017.
Edited by:
Frank Franz Deppisch, University College London, United KingdomReviewed by:
Mayumi Aoki, Kanazawa University, JapanKoji Tsumura, Kyoto University, Japan
Hiroaki Sugiyama, Toyama Prefectural University, Japan
Copyright © 2017 Cai, Herrero García, Schmidt, Vicente and Volkas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Juan Herrero García, anVhbi5oZXJyZXJvLWdhcmNpYUBjb2VwcC5vcmcuYXU=
Michael A. Schmidt, bWljaGFlbC5zY2htaWR0QHN5ZG5leS5lZHUuYXU=
 Yi Cai
Yi Cai Juan Herrero García
Juan Herrero García Michael A. Schmidt
Michael A. Schmidt Avelino Vicente
Avelino Vicente Raymond R. Volkas
Raymond R. Volkas