- 1Department of Operations Management, Quantitative Methods and Information Systems, Indian Institute of Management, Udaipur, India
- 2Department of Technology, Leadership and Innovation, Purdue Polytechnic Institute, Purdue University, West Lafayette, IN, United States
- 3Faculty of Law, University of Hong Kong, Pokfulam, Hong Kong
This paper analyzes court priority queuing behavior by examining the time lapse between when a case enters a court's docket and when it is ultimately disposed of. Using data from the Supreme courts of the United States, Massachusetts, and Canada we show that each court's docket features a slow decay with a decreasing tail. This demonstrates that, in each of the courts examined, the vast majority of cases are resolved relatively quickly, while there remains a small number of outlier cases that take an extremely long time to resolve. We discuss the implications for this on legal systems, the study of the law, and future research.
Introduction
The patterns with which courts resolve cases is a core aspect of how a judicial system functions, yet one that has remained largely unexplored in the empirical literature. Understanding the underlying distribution of case resolution timing can help us better understand both how the courts function as part of the legal system, while also providing a new dimension of insight into courts, enabling more nuanced comparisons and analyses. This article is the first to model case resolution timing distributions, showing that courts feature a slow decay with a decreasing tail.
We will proceed in four parts, first we will provide an overview of modeling priority queuing behavior, briefly discussing how it has been applied in other substantive fields and what implications priority queues have for courts. We will then describe our data collection and analysis methods followed by a model for court case priority queueing, an empirical demonstration, and finally a brief discussion of the implications these findings have.
Overview
Modeling and measuring the priority queuing behavior of courts contributes to the growing body of legal complex systems research. This body of work attempts to describe and understand the dynamics of the law at the system level, revealing universalities and emergent phenomena that had gone largely unnoticed under the traditional doctrinal focus of legal researchers.
Legal complex systems research has focused on examining legal systems from a wide variety of perspectives. Much work has focused on judicial opinions and the structure of the precedent citation network. For instance, Fowler and colleagues explored opinion centrality and how it relates to an opinion's perceived importance [1, 2]. Building on this work, Whalen et al. examine which backwards citation patterns relate to an opinion's future forward citation centrality [3] and the general trend toward an increase in network-focused legal studies [4].
Although the body of legal complex systems research is relatively new, the trend toward increasingly computational and system-level legal research represents an important movement within legal research [5, 6]. Traditional legal research has tended to focus on doctrinal analysis, and has featured a strong normative component. Although this remains an important approach for legal research to take, there is much to be gained from drawing on developments in other fields.
One key area where complex systems and computational researchers have made substantial progress is in describing and understanding how individual agent-level behaviors can lead to emergent system-level patterns. This is often done using agent-based model simulations. In a well-known example, the Schelling [7] model uses the behavior of individual agents to explain the emergence of racial segregation, even in populations that have low levels of preference for racial homophily. Others have expanded agent based models in attempts to simulate large and complex social systems [8]. However, these agent-level studies need not rely on simulation and can also be empirical in nature, measuring individual behavior and attempting to describe and understand the patterns that underlie it.
Such is the case with research exploring the timing distribution of human behavior. This body of research has demonstrated that the timing of human actions in many domains is not randomly distributed, but rather correlated or bursty [9, 10]. Within this context of studying the timing of human behavior, priority queuing theory has emerged to help describe and understand the processes through which agents choose to execute tasks from a queue. Researchers have used inter-event timing to explore how agents behave in a variety of contexts, including how they respond to emails [9, 11], how they execute tasks in online games [12], and how they prioritize the updating of academic articles [13].
Task queuing by legal actors has yet to be empirically examined. In many ways, such examinations offer similar benefits and potential insights as queuing research in other substantive domains. Modeling queuing behavior helps us understand the underlying dynamics, how those dynamics lead to system-level patterns, and in some cases, can help guide assessment or optimization efforts. However, despite the similarities between legal priority queues and fields that have been studied, the details of how the queuing occurs will differ. Unlike more commonly studied domains such as human communication patterns, or simple assigned task management, queuing in many legal contexts does not rely solely on the task management preferences of a single agent. Rather, these processes are the outcome of the interplay between many different agents and factors. For instance, the case docket queue management of a court implicates the preferences of judges, clerks, and court officials, but perhaps more importantly depends on case complexity, the actions of the parties and their representation, and the number of motions made.
There are diverse factors that can influence case pendency. Especially at the lower court levels, the number of motions made by parties is an important factor in determining how long the court will take to resolve a dispute. Political, economic, or social expediency can also affect pendency time. Concerns about potential harm while a dispute remains unresolved can lead courts to prioritize a pressing dispute over other cases that are less time sensitive. The number and complexity of the underlying legal issues in a dispute can also influence the length of time it takes for a court to dispose of the case. Cases with relatively few simple issues are easier for the court to resolve and remove from its docket. On the other hand, cases with many discrete legal issues, or issues that do not have a clear answer are likely to take the court more time to resolve. Disagreement amongst judges—at least for courts that hear cases as a panel—can also influence the degree of time it takes for the court to dispose of a case. When there are contending viewpoints among judges about how an issue should be resolved, courts may take more time in an attempt to reach consensus [14].
We focus below on measuring and interpreting case queue resolution in three different courts. Modeling court case priority queuing can provide new perspective on courts. Traditional ways of empirically assessing courts include attempting to describe their ideological leanings [15–17], or the quality of their opinions [18]. Assessing courts in these ways allow us to better describe, understand, and compare them. Similarly, measuring court case priority queuing will provide a new dimension of insight into courts, allowing us to better understand the temporal dynamics of how they function.
In addition to its descriptive value, modeling case priority queues has the potential to provide insight into judicial efficiency, a pressing issue in many jurisdictions. For instance, following a landmark ruling in R. v. Jordan (2016)—finding that the constitutional right to trial within a reasonable time requires trials to be completed within 18–30 months depending on their procedural posture—criminal courts in Canada are facing increased pressure to quickly dispose of cases. This pressure has led to multiple cases of the accused being freed after courts have been unable to hear their trials within the newly-imposed time limits. Measuring and modeling case priority queueing can provide insight into court behavior and those cases at the margins that take much longer than the norm.
Materials and Methods
We begin by accessing the docket records from various high courts and explain how “queuing models” provide insights into the priority in human and judicial dynamics.
Data Collection
To answer these questions, we utilized the publically available docket history data from three different courts. Because there is no easily accessible, and machine readable public database of case docket histories, we collected data by downloading official court websites containing docket information including status of cases, both pending and decided. We download cases from the supreme courts of the United States, Canada, and Massachusetts.
We access the information of court cases by searching the court docket number and dates of proceedings of any case (See Table 1 for demonstration). Included in our sample are 24,607 case dockets from the Supreme Court of the United States (2001–2015), 2,739 case dockets from the Supreme Court of Canada (1983–2015), and 2,307 court dockets from the Supreme Court of Massachusetts (1992–2016). As an example, in Table 1 we demonstrate the proceedings and the corresponding dates of the case Dancorp Developments Ltd. v. Metropolitan Trust Company of Canada, et al. in Supreme Court of Canada. This case's leave to appeal was filed with the court on 1996/06/03 and formal judgement was delivered on 1999/01/11. In our study, we estimate the time to decision of the case, i.e., the difference between date of filing the case and date on which it is disposed of.
Modeling and Empirical Analysis Methods
Drawing upon prior studies on bursts in human dynamics, we adopt the queueing theory framework [9, 19–21] to model the updating mechanism in supreme court cases. Similar to queueing systems in human dynamics, a court in judicial system prioritizes the proceedings of the court by assigning new dates based on some protocols. As in the model proposed by Jo et al. [13], in this work we present a microscopic approach in which a Supreme court follows priority of two types: a task with time varying priority and another task with random priority.
At each time step t, a task y(t) increases as a power-law with time, with y(0) = 0. The priority of the power-law increasing priority task increases to a maximum value of 1. Execution of the task is completed once y(t) reaches the value of 1. Following the work by [13], the priority y(t) is given as:
Where, satisfying the condition y(tc) = 1, the scale factor d acts a quantifier of deadline to the task, y0 is interpreted as intrinsic priority of the task draw from the uniform distribution of (0, 1), and the exponent β serves as a controller of speed of priority [13]. If the priority task is executed with probability p, the waiting time distribution P(x) is obtained by:
Where Jo et al. [13]. In the limit of ϵ ≪ 1 the product term of the above equation is approximated as:
Adopting the above approximation and utilizing the waiting time distribution obtained by Jo et al. [13], approximated in the limit x ≪ d we obtain the distribution of time to court decision as:
Where, p is the probability with which a Supreme court case is disposed of with high priority. The above equation can be reformulated as:
In the limit of ϵx ≪ 1 the above equation (Equation 5) is approximated as:
Next, following the work on decreasing priority by Jo et al. [13], we consider a task y(t) which is changing in time with algebraically decreasing priority as
Where γ is the controlling parameter for the decreasing power-law priority. Implementing the above equation in Equation (2) we get the waiting time distribution as:
Using the approximation in Equation (3) and in the limit γ ≫ 1 we obtain the distribution of waiting times as:
As mentioned by Jo et al. [13], using the condition of γ ≫ 1 and ϵx ≪ 1 we get the approximate waiting time distribution as
The above approximated equations (Equations 6, 10) are next used to explain the distribution of time to decision in the three Supreme court cases registered in the US, Canada and Massachusetts. For the range of , the time to decision is dominated by the first term in Equation (6), which is approximated as a power-law increasing distribution function [13]. We observe that the empirical distributions of time to final decision in Supreme courts fit reasonably well with the functional form described in Equation (6).
Results
We next empirically demonstrate the priority queueing model observable in the dockets of the supreme courts of the United States, Canada, and Massachusetts. We plot the time to decision (measured in days) for case disposal in the supreme courts of the US (♢), Canada (+), and Massachusetts (*) as shown in Figure 1. In all the three cases, the data is fitted by the form
Where, a, b, and c are the fitting parameters. The estimated parameters are shown in Table 2.
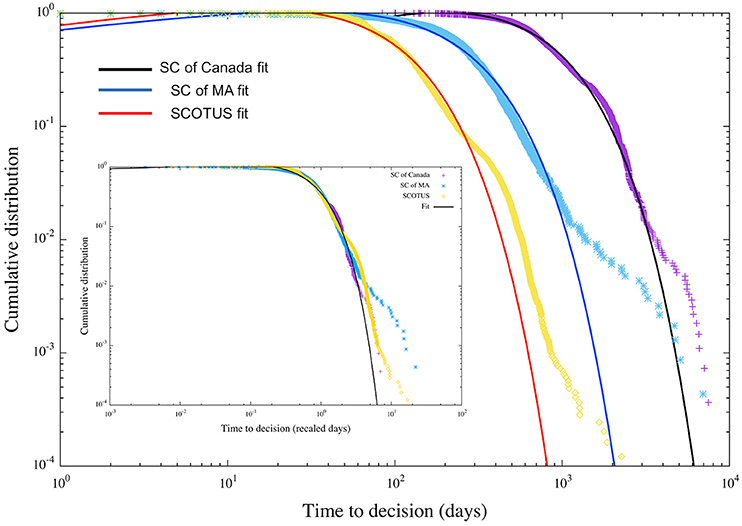
Figure 1. Probability distributions of time to decision for different courts. The distribution is plotted for the time to decision in the SCOTUS, the Supreme court of Canada, and the Supreme Court of Massachusetts. The inset shows the fit of the distribution of the rescaled data. The data are fitted by the functional form P(x) ∝ (xa + b)e−x/c. We present (a, b, c), the parameters of the fit in Table 2.
For each Supreme court, we ignore the extremely large decision times due to uncertainty in fitting. We observe that Canadian Supreme Court takes longest time to decision, while SCOTUS is the fastest to dispose of court cases. This is also reflected in the fitting parameter c, where c ~ 583 (±2.778) for Canadian Supreme Court, c ~ 205.98 (±1.708) for Supreme Court of Massachusetts and, c ~ 80.149 (±0.647) for SCOTUS. As is evident from the plot in Figure 1, c indicates the point where the distribution of decision times makes a transition from slow decay to faster decay. We observe that the fitting parameter a for the three supreme courts is less than 1, and b is negative suggesting that the distribution neither fits to a perfect power-law increasing nor power-law decreasing priority. On the contrary, the distributions are rather a mixture of slow decay and a decreasing tail which fits well with the functional form where, α = 1.001 (±0.031) and β = 203.5 (±8.2) for SCOTUS, and α = 0.898 (±0.045); β = 300 (±9.5) for Supreme Court of Massachusetts, and α = 0.370 (±0.014); β = 957 (±13) for Supreme Court of Canada.
We rescaled the absolute value of decision times for each court decision by average decision time per court < x>, and interestingly we observe the rescaled decision times collapse into a universal curve (See Figure 1 inset). The choice of rescaling is akin to citation distribution in academic institutions and journals [22] and earthquake inter-time distributions [23]. Irrespective of the wide variation in the fitting parameters of the three different courts, the rescaled distribution fits well with the priority model of the form
Where a, b, and c are the fitting parameters of the collapsed data of rescaled decision times (See Table 2 for fitting parameters). We fit the tail of the three rescaled distributions by using the functional form of , where α = 0.169 ± 0.003 and β = 1.052 ± 0.006 are the parameters of the fit. The distribution of the rescaled time to decision for all the three Supreme courts shows a universal phenomenon—mixed priority comprising of a slow decay similar to constant priority along with a faster decay typical of a power-law with exponential cut-off. Our empirical findings also provide evidence of a “performance” metric for the three courts. While the SCOTUS and SC of MA get involved and resolves cases almost immediately, the SC of Canada resolves cases much more slowly. The time to decision of a court case can be comprehended as a queueing process from the point of view of judicial referees, akin to the review process in scientific papers [13]. In this model, as cases are filed in a court, the court assigns an initial priority to every case, depending on the significance and importance of the case. The priority of providing final judgement of a case remains almost constant in time, before falling off rapidly as a court attempts to give a final verdict. As observed in scientific gatekeeping [13], a slow decay priority mixed with bimodal combination of power-law and exponential distributions of judgement timings explains the distribution of disposal times of Supreme court cases (Figure 1).
Discussion
The time to decision of a court case can be understood as a queueing process featuring a mixture of slow decay with a decreasing tail. The functional form of the tail of time to decision is similar to the review process in scientific papers [13]. This sort of highly-skewed distribution means that the vast majority of cases are disposed of within a relatively short period of time, but there remain outlier cases that take extremely long to work their way through a court's docket. Immediately after a case is entered into a court's docket we see a near constant priority, with decisions being reached relatively quickly. Subsequently, in each of the jurisdictions we examine, there is an eventual transition where priority begins to fall off rapidly and cases take much longer to reach completion. Each of the courts we examine share similar functional forms, suggesting that there is a degree of universality in the way that cases work their way through a legal system. That said, our findings are necessarily qualified by the data we were able to analyze. Limitations in freely available docket data constrained us to analyzing three common law courts. Courts in different legal systems—especially civil law systems—or at different levels of the appeals hierarchy may exhibit different priority queueing behavior.
Our findings suggest that, as in many other fields (see 9), the timing of judicial activity is not randomly or normally distributed but rather “bursty” in nature. The “bursty” nature of the judicial activity is reminiscent of Gutenberg-Richter law observed in earthquake size distribution, Galilean stick-slip dynamics [24], and various econophysical systems like financial markets 25. This means that when trying to understand or model judicial timing, turning to a Poisson process, as many may instinctively do, would be inappropriate. The highly-skewed distribution of disposal times means that the majority of cases are disposed of relatively quickly. For example, the United States Supreme Court case of Bashir v. US was disposed of in just over 3 months, with the petition for certiorari filed on February 2, 2005 and judgement issued on May 6, 2005. The Bashir case is notable in that it involved the court vacating and remanding for further consideration in light of another opinion it had recently rendered. Other cases though inhabit the long tail of the distribution and take a very long time to finally dispose of. The Canadian Supreme Court case of Her Majesty the Queen v. Daniel Jolivet provides an example of one of these long-tail-dwelling cases. This case—with the appeal originally filed with the Supreme Court in 1998, and the appeal finally closed in 2014—featured numerous motions to extend time, as well as an eventual re-hearing of the appeal.
Although the three courts we examined follow a similar functional form, their constants a, b, and c vary significantly. These can be used to gain some insight into how the courts differ in their docket timing. For instance, we can see that the higher value for c in the Canadian Supreme Court corresponds to a much later drop off in the function and accordingly a set of cases that take extremely long for the court to dispose of. However, it is important to note that the data gathered on each court does not necessarily follow the same pattern. Different docketing norms at courts may lead to somewhat different results.
These findings provide another new perspective on legal complex systems. This small-but-growing body of work attempts to understand how the law and its operation can be measured, modeled, and understood at the system level. As an increasing number of research projects provide insight into more-and-more aspects of legal systems we begin to gain a fuller picture of how the law operates at the system level. We see universalities, and perhaps more importantly, when a full enough picture is attained will be able to more accurately detect deviations and plan interventions. The priority queuing results here are particularly helpful in providing a metric that can be used to compare courts—and perhaps once more courts have been modeled develop a taxonomy of case priority queuing. These results may also prove useful in attempts to simulate legal systems in the future. Demonstrating a model of case priority queuing—at least at the level of courts with discretionary appeal—will allow researchers to create more accurate simulations.
Future Work
This is the first project to examine priority queuing behavior at courts. It suggests a degree of universality in how courts prioritize dispute resolution, with the vast majority of cases being resolved in a relatively short period of time, and a second set of “hard cases” that take much longer to resolve. There are a number of avenues for future work to pursue that would help further our understanding of these results, and expand our understanding of how legal systems resolve disputes.
Future in depth work at the case level would help provide more context for the patterns observed here. By examining case details and trying to understand what elements of a dispute—whether it be the legal issues implicated, factual patterns, political aspects of the dispute, or other reasons—lead to it being resolved in a particularly timely or slow fashion. In addition to close examination at the case level, these results suggest it would be useful to perform similar analyses for more courts. Our research was limited by available data. However, as more high-quality legal data becomes available it may be possible to expand this analysis comparing courts in different jurisdictions, at different levels of the appeals hierarchy, and at different times in history. Doing so would provide useful insight into the underlying processes that shape legal systems.
Although we observe a degree of universality in the functional form that court priority queuing takes, we note that the courts we examine are all courts of discretionary appeal in common law jurisdictions. Future work should strive to compare these results to lower level courts, and courts in civil law jurisdictions. It is also possible that the method of appointing judges may be an important factor in determining how cases are disposed of. Future work should explore a variety of legal systems to test how truly universal the findings presented here are.
Conclusion
By examining the time to disposal of cases on the dockets of three supreme courts, we show that judicial priority queueing features a mixture of slow decay with a decreasing tail. This suggests a degree of universality in the way judicial systems manage their dockets as the majority of cases are relatively quickly disposed of, while a few extremely-lengthy cases occupy the tail of the power law distribution. This accords with priority queues observed in other substantive domains, and furthers the position that the complex system that is the law can potentially be better understood by modeling emergent phenomena.
Author Contributions
Both RW and SM participated approximately equally in conceiving of the paper. SM was in charge of the majority of data collection/analysis. RW was in charge of interpretation and much of the writing.
Funding
This research was supported by the University of Hong Kong Research Grant 201709159005.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Fowler JH, Johnson TR, Spriggs JF, Jeon S, Wahlbeck PJ. Network analysis and the law: measuring the legal importance of precedents at the U.S. supreme court. Polit Anal. (2007) 15:324–46. doi: 10.1093/pan/mpm011
2. Fowler JH, Jeon S. The authority of Supreme Court precedent. Soc Netw. (2008) 30:16–30. doi: 10.1016/j.socnet.2007.05.001
3. Whalen R, Uzzi B, Mukherjee S. Common Law Evolution and judicial impact in the age of information. Elon Law Rev. (2017) 9:115–70.
4. Whalen R. Legal networks: the promises and challenges of legal network analysis. Michigan State Law Rev. (2016) 2016:539.
5. Lettieri N, Faro S. Computational social science and its potential impact upon law. Eur J Law Technol. (2012) 3:1–17.
6. Ruhl JB, Katz DM, Bommarito MJ. Harnessing legal complexity. Science (2017) 355:1377–8. doi: 10.1126/science.aag3013
7. Schelling TC. Dynamic models of segregation. J Math Sociol. (1971) 1:143–86. doi: 10.1080/0022250X.1971.9989794
8. Deissenberg C, Van Der Hoog S, Dawid H. EURACE: a massively parallel agent-based model of the European economy. Appl Math Comput. (2008) 204:541–52. doi: 10.1016/j.amc.2008.05.116
9. Barabási AL. The origin of bursts and heavy tails in human dynamics. Nature (2005) 435:207–11. doi: 10.1038/nature03459
10. Wu Y, Zhou C, Xiao J, Kurths J, Schellnhuber HJ. Evidence for a bimodal distribution in human communication. Proc Natl Acad Sci USA. (2010) 107:18803–8. doi: 10.1073/pnas.1013140107
11. Malmgren RD, Stouffer DB, Motter AE, Amaral LAN. A Poissonian explanation for heavy tails in e-mail communication. Proc Natl Acad Sci USA. (2008) 105:18153–8. doi: 10.1073/pnas.0800332105
12. Mryglod O, Fuchs B, Szell M, Holovatch Y, Thurner S. Interevent time distributions of human multi-level activity in a virtual world. Phys A Stat Mech Appl. (2015) 419:681–90. doi: 10.1016/j.physa.2014.09.056
13. Jo HH, Pan RK, Kaski K. Time-varying priority queuing models for human dynamics. Phys Rev E (2012) 85:066101. doi: 10.1103/PhysRevE.85.066101
14. Goldman, S. Conflict and consensus in the United States Courts of Appeals Law and Society. Wis. L. Rev. (1968) 1968:461.
15. Epstein L, Andrew MD, Quinn KM, Segal JA. Ideological drift among supreme court justices. Nw Univ Law Rev. (2007) 101:1483–542.
16. Martin AD, Quinn KM, Epstein, L. The median justice on the United States Supreme Court. N C L Rev. (2004) 83:1275.
17. Segal JA, Cover AD. Ideological values and the votes of US Supreme Court Justices. Am Polit Sci Rev. (1989) 83:557–65. doi: 10.2307/1962405
18. Posner RA. Is the ninth circuit too large? A statistical study of judicial quality. J Legal Stud. (2000) 29:711–9. doi: 10.1086/468090
19. Anteneodo C. Exact results for the Barabási queuing model. Phys Rev E (2009) 80:041131. doi: 10.1103/PhysRevE.80.041131
20. Vázquez A. Exact results for the Barabási model of human dynamics. Phys Rev Lett. (2005) 95:248701. doi: 10.1103/PhysRevLett.95.248701
21. Vázquez A. Modeling bursts and heavy tails in human dynamics. Phys Rev E (2006) 73:036127. doi: 10.1103/PhysRevE.73.036127
22. Chatterjee A, Ghosh A, Chakrabarti BK. Universality of citation distributions for academic institutions and journals. PLoS ONE (2016) 11:e0146762. doi: 10.1371/journal.pone.0146762
23. Lippiello E. Scaling behavior of the earthquake intertime distribution: Influence of large shocks and time scales in the Omori law. Phys Rev E Stat Nonlin Soft Matter Phys. (2012) 86:066119. doi: 10.1103/PhysRevE.86.066119
24. Parteli EJR. Nontrivial temporal scaling in a Galilean stick-slip dynamics. Phys Rev E Stat Nonlin Soft Matter Phys. (2005) 71:036137. doi: 10.1103/PhysRevE.71.036137
Keywords: judicial priority queuing, legal complex systems, empirical legal studies, judicial behavior, law as a natural phenomenon
Citation: Mukherjee S and Whalen R (2018) Priority Queuing on the Docket: Universality of Judicial Dispute Resolution Timing. Front. Phys. 6:1. doi: 10.3389/fphy.2018.00001
Received: 31 August 2017; Accepted: 03 January 2018;
Published: 24 January 2018.
Edited by:
Nicola Lettieri, Istituto Nazionale per L'Analisi delle Politiche Pubbliche (INAPP), ItalyReviewed by:
Antonio Stabile, Università Degli Studi di Salerno, ItalyEric Josef Ribeiro Parteli, University of Cologne, Germany
Daniele Vilone, Consiglio Nazionale Delle Ricerche (CNR), Italy
Copyright © 2018 Mukherjee and Whalen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ryan Whalen, d2hhbGVuQGhrdS5oaw==
 Satyam Mukherjee
Satyam Mukherjee Ryan Whalen
Ryan Whalen