- 1Laboratoire de Physique Corpusculaire, Centre National de la Recherche Scientifique/IN2P3 UMR 6533, Aubière, France
- 2Department of Physics, Indian Institute of Technology Bhilai, Chhattisgarh, India
- 3Center of Excellence in Theoretical and Mathematical Sciences, Siksha ‘O’ Anusandhan University, Bhubaneswar, India
- 4Department of Physics, Indian Institute of Technology Kharagpur, Kharagpur, India
In this review, we present several variants of left–right symmetric models in the context of neutrino masses and leptogenesis. In particular, we discuss various low scale seesaw mechanisms like linear seesaw, inverse seesaw, extended seesaw and their implications to lepton number violating process like neutrinoless double beta decay. We also visit an alternative framework of left–right models with the inclusion of vector-like fermions to analyze the aspects of universal seesaw. The symmetry breaking of left–right symmetric model around few TeV scale predicts the existence of massive right-handed gauge bosons WR and ZR which might be detected at the LHC in near future. If such signals are detected at the LHC that can have severe implications for leptogenesis, a mechanism to explain the observed baryon asymmetry of the Universe. We review the implications of TeV scale left–right symmetry breaking for leptogenesis.
1. Introduction
Although the Standard Model (SM) of particle physics is highly successful in explaining the low energy phenomenology of fundamental particles, the reasons to believe it is incomplete are not less. The most glaring of them all is the issue of neutrino mass which has been confirmed by the oscillation experiments. Some more unsolved puzzles like dark matter, dark energy, baryon asymmetry of the universe strongly suggest that SM is only an effective limit of a more fundamental theory of interactions. In addition to the fact that gravity is completely left out in the SM, the strong interaction is not unified with weak and electromagnetic interactions. In fact, even in the electroweak “unification” one still has two coupling constants, g and g′ corresponding to SU(2)L and U(1)Y. Thus, one is tempted to seek for a more complete theory where the couplings gs, g, and g′ unify at some higher energy scale giving a unified description of the fundamental interactions. Given that the ratio mPl/mW is so large, where is the Planck scale, another major issue in the SM is the infamous “hierarchy problem.” The discovery of the Higgs boson with a mass around 125 GeV has the consequence that, if one assumes the Standard Model as an effective theory, then λ ~ (0.1) and μ2 ~ ((100) GeV)2 (including the effects of 2-loop corrections). The problem is that every particle that couples, directly or indirectly, to the Higgs field yields a correction to μ2 resulting in an enormous quantum correction. For instance, let us consider a one-loop correction to μ2 coming from a loop containing a Dirac fermion f with mass mf. If f couples to the Higgs boson via the coupling term , then the correction coming from the one-loop diagram is given by
where ΛUV is the ultraviolet momentum cutoff and the ellipsis are the terms proportional to , growing at most logarithmically with ΛUV. Each of the quarks and leptons in the SM plays the role of f, and if ΛUV is of the order of mPl, then the quantum correction to μ2 is about 30 orders of magnitude larger than the required value of μ2 = 92.9 GeV2. Since all the SM quarks, leptons, and gauge bosons obtain masses from 〈ϕ〉, the entire mass spectrum of the Standard Model is sensitive to ΛUV. Thus, one expects some new physics between mW and mPl addressing this problem. There are also other questions such as why the fermion families have three generations; is there any higher symmetry that dictates different fermion masses even within each generation; in the CKM matrix the weak mixing angles and the CP violating phase are inputs of the theory, instead of being predicted by the SM. Finally, in the cosmic arena, the observed baryon asymmetry of the universe cannot be explained within the SM. Also there are no suitable candidates for dark matter and dark energy in the SM. These also point toward the existence of physics beyond the SM.
In this review, we study several variants of left–right symmetric models which is one of the most popular candidates for physics beyond the standard model. We will review the left–right symmetric models in the context of neutrino masses and leptogenesis. We will study various low scale seesaw mechanisms in the context of left–right symmetric models and their implications to lepton number violating process like neutrinoless double beta decay. We will also discuss an alternative framework of left–right models with the inclusion of vector-like fermions as proposed to analyze various aspects. Interestingly, the breaking of left–right symmetry around few TeV scale predicts the existence of massive right-handed gauge bosons WR and ZR in left–right symmetric models. These heavy gauge bosons might be detected at the LHC in near future. If such signals are detected at the LHC that can have conclusive implications for leptogenesis, a mechanism to explain the observed baryon asymmetry of the Universe. In this review we will also discuss the implications of such a detection of left–right symmetry breaking for leptogenesis in detail. Before closing this paragraph we would like to stress the fact that this review is far from comprehensive and covers only a limited variety of topics from the vast choices of LRSM-related scenarios. For example, a detailed discussion of the relevant collider phenomenology of the right-handed gauge bosons WR and ZR and the Higgs sector is beyond the scope of this review. Some relevant references for the LHC phenomenology of WR and heavy neutrinos are in Keung and Senjanovic [1], Nemevsek et al. [2], Das et al. [3], Chen et al. [4] and Mitra et al. [5] and for Higgs sector some relevant references are in Bambhaniya et al. [6], Dutta et al. [7], Dev et al. [8] and Mitra et al. [9].
The plan for rest of the review is as follows. In section 2 we briefly review the standard seesaw and radiative mechanisms for light neutrino mass generation. In section 3 we first introduce and then review the standard left–right symmetric theories and the implementation of different types of low scale seesaw implementations. In section 4 we review an alternative formulation of left–right symmetric theories which uses a universal seesaw to generate fermion masses. We also discuss the implications of this model for neutrinoless double beta decay in this case for the specific scenario of type II seesaw dominance. In section 5 we give a brief introduction to leptogenesis and review some of the standard leptogenesis scenarios associated with neutrino mass generation. In section 6 we review the situation of leptogenesis in left–right symmetric theories and the implications of a TeV scale left–right symmetry breaking for leptogenesis. Finally, in section 7 we make concluding remarks.
2. Neutrino Masses
The atmospheric, solar and reactor neutrino experiments have established that the neutrinos have small non-zero masses which are predicted to be orders of magnitude smaller than the charged lepton masses. However, in the SM the left handed neutrinos νiL, i = e, μ, τ, transform as (1, 2, −1) under the gauge group SU(3)c×SU(2)L×U(1)Y. Consequently, one cannot write a gauge singlet Majorana mass term for the neutrinos. On the other hand, there are no right handed neutrinos in the SM which would allow a Dirac mass term. The simplest way around this problem is to add singlet right handed neutrinos νiR with the transformation (1, 1, 0) under the SM gauge group. Then one can straightaway write the Yukawa couplings giving Dirac mass to the neutrinos
such that once ϕ acquires a VEV, the neutrinos get Dirac mass mDij = hijυ. Here ψiL stands for the SU(2)L lepton doublet. However, to explain the lightness of the neutrinos one needs to assume a very small Yukawa coupling for neutrinos in comparison to charged leptons and quarks. However, we do not have a theoretical understanding of why the Yukawa coupling should be so small. Moreover, the accidental B−L symmetry of the SM forbids Majorana masses for the neutrinos. One way out is to consider the dimension-5 effective lepton number violating operator [10–13] of the form
where Λ is the scale corresponding to some new extension of the SM violating lepton number. This dimension-5 term can induce small Majorana masses to the neutrinos after the eletroweak symmetry breaking
with . Here, C is the charge conjugation matrix. Consequently, lepton number violating new physics at a high scale Λ would naturally explain the smallness of neutrino masses. In what follows, we discuss some of the popular mechanisms of realizing the same.
2.1. Seesaw Mechanism: Type-I
The type-I seesaw mechanism1 [14–20] is the simplest mechanism of obtaining tiny neutrino masses. In this mechanism, three singlet right handed neutrinos NiR are added to the SM; and one can write a Yukawa term similar to Equation (2) and a Majorana mass term for the right handed neutrinos since they are singlets under the SM gauge group. The relevant Lagrangian is given by
Note that, the Majorana mass term breaks the lepton number explicitly and since the right handed neutrinos are SM gauge singlets, there is no symmetry protecting Mij and it can be very large. Now after the symmetry breaking, combining the Dirac and Majorana mass matrices we can write
where mDαi = hDαiυ. Now assuming that the eigenvalues of mD are much less than those of M one can block diagonalize the mass matrix to obtain the light Majorana neutrinos with masses and heavy neutrinos with mass mN = Mi. Note that if any of the right handed neutrino mass eigenvalues (Mi) vanish then some of the left handed neutrinos will combine with the right handed neutrinos to form Dirac neutrinos. For n generations, if the rank of M is r, then there will be 2r Majorana neutrinos and n − r Dirac neutrinos. The type-I seesaw mechanism not only generates tiny neutrino masses, but also provides the necessary ingredients for explaining the baryon asymmetry of the universe via leptogenesis [21], which we will discuss in length in the next section.
2.2. Seesaw Mechanism: Type-II
In type-II seesaw mechanism [18, 19, 22–28], the effective operator given in Equation (3) is realized by extending the SM to include an SU(2)L triplet Higgs ξ which transforms under the SM gauge group SU(3)c × SU(2)L × U(1)Y as (1, 3, 1). For simplicity we assume that there are no right handed neutrinos in this model and only one triplet scalar is present. The Yukawa couplings of the triplet Higgs with the left handed lepton doublet (νi, li) are given by
Now a non-zero VEV acquired by ξ0 (〈ξ0〉 = u) gives Majorana masses to the neutrinos. Note that u has to be less than a few GeV to not affect the electroweak ρ-parameter. The most general Higgs potential with a doublet and a triplet Higgs has the form
We assume λ4 ≠ 0, which manifests explicit lepton number violation and the mass of the triplet Higgs Mξ ~ λ4 ≫ υ. The mass matrix of the scalars and is given by
which tells us that one combination of these fields remains massless, which becomes the longitudinal mode of the Z boson; while the other combination becomes massive with a mass of the order of triplet Higgs and hence the danger of Z decaying into Majorons 2 is absent in this model. The minimization of the scalar potential yields
giving a seesaw mass to the left handed neutrinos
Note that in the left–right symmetric extension of the SM, which we will discuss in the next subsection, both type-I and type-II seesaw mechanisms are present together. The type-II seesaw mechanism can also provide a very attractive solution to leptogenesis, which we will discuss in the next section.
2.3. Seesaw Mechanism: Type-III
In type-III seesaw mechanism [29, 30] the SM is extended to include SU(2)L triplet fermions to realize the effective operator given in Equation (3)3. The Yukawa interactions in Equation (5) are generalized straightforwardly to SU(2)L triplet fermions Σ with hypercharge Y = 0. The corresponding interaction Lagrangian is given by
where α = 1, 2, 3. In exactly similar manner as in the case of type-I seesaw, one obtains for MΣ ≫ υ, the left handed neutrino mass
2.4. Radiative Models of Neutrino Mass
Small neutrino masses can also be induced via radiative corrections. The advantage of these models is that without introducing a very large scale into the theory the smallness of the neutrino masses can be addressed. In fact, several of these models can explain naturally the smallness of the neutrino masses with only TeV scale new particles. Thus, new physics scale in these models can be as low as TeV, which can be probed in current and next generation colliders.
One realization of this idea is the so-called Zee model [31, 32], where one extends the SM to have two (or more) Higgs doublets ϕ1 and ϕ2, and a scalar η+ which transforms under the SM gauge group SU(3)c × SU(2)L × U(1)Y as (1, 1, 1). The lepton number violating Yukawa couplings are given by
where fij is antisymmetric in the family indices i, j and εab is the totally antisymmetric tensor. Now, the VEV of the SM Higgs doublet allows mixing between the singlet charged scalar and the charged component of the second Higgs doublet, resulting in a neutrino mass induced through the one-loop diagram showed in Figure 1 (left). The antisymmetric couplings of η+ with the leptons make the diagonal terms of the mass matrix vanish, with the non-diagonal entries given by
where i, j = e, μ, τ and A is a numerical constant. In the Zee model, if the second Higgs doublet is replaced by a doubly charged singlet scalar ζ++, then one gets what is called Zee-Babu Model [33, 34]. In this model a Majorana neutrino mass can be obtained through a two loop diagram shown in Figure 1(right). In fact, there are several other radiative models of Majorana neutrino mass such as the Ma model [35] connecting the Majorana neutrino mass to dark matter at one-loop; Krauss-Nasri-Trodden model [36] and Aoki-Kanemura-Sato model [37] giving neutrino mass at the three loop level with a dark matter candidate in the loop; Gustafsson-No-Rivera model [38] involving a three loop diagram with a dark matter candidate and the W boson; and Kanemura–Sugiyama model [39] utilizing an extension of the Higgs triplet model. There are also models for radiative Dirac neutrino masses such as the Nasri-Moussa model [40] utilizing a softly broken symmetry; Gu-Sarkar model [41] with dark matter candidates in the loop; Kanemura-Matsui-Sugiyama model [42] utilizing an extension of the two Higgs doublet model; Bonilla-Ma-Peinado-Valle model where the Dirac neutrino masses are generated at two-loops with dark matter in the loop [43], etc.
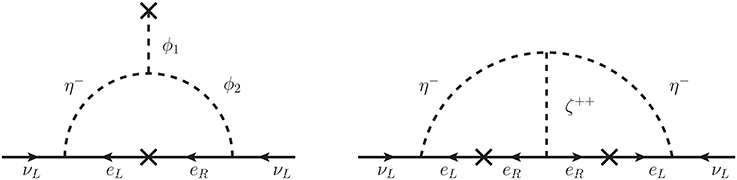
Figure 1. (Left) one-loop diagram diagram generating neutrino mass in Zee model. (Right) two loop diagram generating neutrino mass in Zee-Babu model.
3. Left–Right Symmetric Theories
The SM gauge group SM ≡ SU(3)c × SU(2)L × U(1)Y explains the (V − A) structure of the weak interaction and parity violation, which is reflected by the trivial transformation of all right handed fields under SU(2)L. However, the origin of parity violation is not explained within the SM, and it is natural to seek an explanation for parity violation starting from a parity conserved theory at some higher energy scale. This motivated a left–right symmetric extension of the SM gauge theory, called the Left–Right Symmetric Model (LRSM) [44–49], in which the Standard Model gauge group is extended to
where B − L is the difference between baryon (B) and lepton (L) numbers. The left–right symmetric theory, initially proposed to explain the origin of parity violation in low-energy weak interactions has come a long way answering various other issues like small neutrino mass, dark matter as left by the Standard Model. Originally suggested by Pati-Salam, the model has been studied over and over because of its versatility and many alternative formulations of the model have also been proposed. The model stands on the foundation of a complete symmetry between left and right which means Parity is an explicit symmetry in it until spontaneous symmetry breaking occurs. As evident from the gauge group, the natural inclusion of a right-handed neutrino in it makes the issue of neutrino mass an easy affair to discuss. Three new gauge bosons namely that are the heavier parity counterparts of of the standard model and a Z′ boson analogous to the Z boson also find place in the framework. LRSM breaks down to Standard Model gauge theory at low energy scales, SU(2)L × SU(2)R × U(1)B−L × SU(3)C → SU(2)L × U(1)Y × SU(3)C. It has been noticed that the choices of Higgs and their mass scales in the model offers rich phenomenology which can be verified at the current and planned experiments.
The basic framework and properties of Left–Right Symmetric Models are already discussed at length in various original works [46–48], thus we only intend to study here various seesaw mechanisms for the generation of neutrino mass and its implications to leptogenesis in various Left–Right Symmetric models.
A very brief sketch of the manifest left–right symmetric model is given here. The model is based on the gauge group,
The electric charge Q is difined as,
Here, T3L and T3R are, respectively, the third components of isospin of the gauge groups SU(2)L and SU(2)R, and Y is the hypercharge. The particle spectrum of a generic LRSM can be sketched as,
The spontaneous symmetry breaking of the gauge group which occurs in two steps gives masses to fermions including neutrinos. In the first step the gauge group SU(2)L × SU(2)R × U(1)B−L × SU(3)C breaks down to SU(2)L × U(1)Y × SU(3)C i.e., the SM gauge group. This gauge group then breaks down to U(1)em × SU(3)C. However these symmetry breakings totally depend upon the choices of Higgs that we consider in the framework and their mass scales. Thus, in this review we intend to discuss fermion masses emphasizing on neutrino mass in possible choices of symmetry breakings of LRSM.
3.1. LRSM With Bidoublet (B − L = 0) and Doublets (B − L = −1).
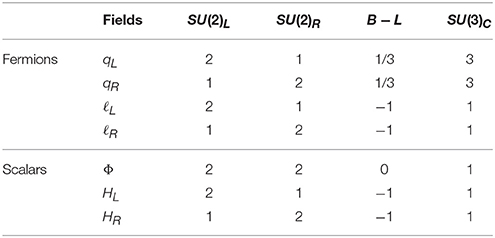
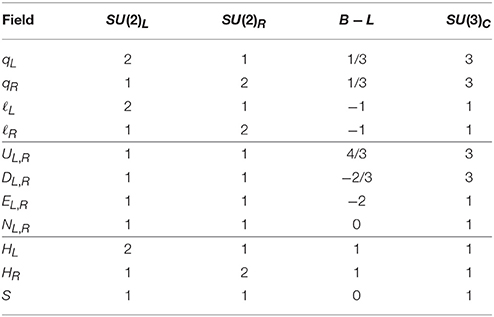
Here we use Higgs bidoublet Φ to implement the symmetry breaking of SM down to low energy theory leading to charged fermion masses. The symmetry breaking of LRSM to SM occurs via RH Higgs doublet HR (B − L = −1). We need the left-handed counterpart HL to ensure left–right invariance. The fermions including usual quarks and leptons along with scalars are presented in Table 1.
The matrix structure of the scalar fields looks as follows,
With usual quarks and leptons the Yukawa Lagrangian reads as,
where and σ2 is the second Pauli matrix. When the scalar bidoublet (Φ) takes non-zero VEV,
it gives masses to quarks and charged leptons in the following manner,
It also yields Dirac mass for light neutrinos as
The only role that the Higgs doublets play here is helping in the spontaneous symmetry breaking of LRSM to SM. It is also important to note that the breaking of SU(2)R by doublet Higgs leads to Dirac neutrinos.
3.2. LRSM With Bidoublet (B − L = 0) and Triplets (B − L = 2).
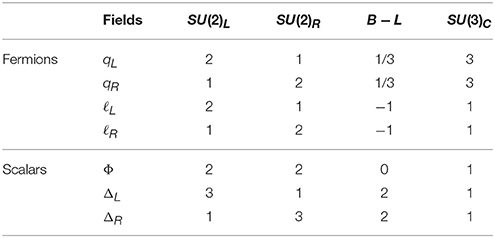
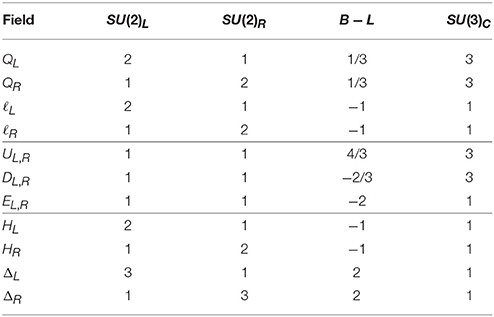
Along with the bidoublet Φ, here we use triplets ΔL, ΔR for the spontaneous symmetry breakings.
The particle content of the model is shown in Table 2.
The Yukawa Lagrangian is given by
The scalar triplets ΔL, ΔR give Majorana masses to light left-handed and heavy right-handed neutrinos. The neutral lepton mass matrix is given by
Here ML = fL〈ΔL〉 = fυL (MR = fR〈ΔR〉 = fυR) denoted as the Majorana mass matrix for left-handed (right-handed) neutrinos and MD = Y3υ1 + Y4υ2 is the Dirac neutrino mass matrix connecting light-heavy neutrinos. The complete diagonalization results type-I+II seesaw formula for light neutrinos as,
3.3. LRSM With Inverse Seesaw
In canonical seesaw mechanisms, the tiny mass of light neutrinos is explained with large value of seesaw scale thereby making it inaccessible to the ongoing collider experiments. On the other hand, the light neutrino masses may arise from low scale seesaw mechanisms like inverse seesaw [50, 51] where the seesaw scale can be probed at upcoming accelerators. The inverse seesaw mechanism in LRSM can be realized with the following particle content;
The fermion sector here comprises of the usual quarks and leptons plus one extra fermion singlet per generation. The scalar sector holds the doublets HL,R with B − L charge −1 and the bidoublet Φ with B − L charge 0. The Yukawa Langrangian for inverse seesaw mechanism is given by,
After spontaneous symmetry breaking the resulting neutral lepton mass matrix reads as follows,
With the mass hierarchhy mD, M ≫ μS, the light neutrino mass formula is given by,
3.4. LRSM With Linear Seesaw
Another interesting low scale seesaw type is linear seesaw mechanism [52, 53] which can be realized with the following particle content in a LRSM.
The scalars take non-zero vev as follows:
Let us write down the relevant Yukawa terms in the Lagrangian that contribute to the fermion masses:
where with j = L, R and . The singlet Majorana field S in Equation (34) is defined as
resulting in the neutral lepton mass matrix
The violation of lepton number by two units arises here through the combination mL and μS. As a result, assuming mL≪mD < M, one gets the light Majorana masses of the active neutrinos to be
The last line in Equation (37) follows from the fact that in left–right symmetric model where Parity and SU(2)R breaking occurs at different scales υL is given by
where μ1, μ2 are the trilinear terms arising in the Higgs potential involving Higgs bidoublet and Higgs doublets, ηP is the parity breaking scale and M′ is the SU(2)R breaking scale. From Equation (37) it is clear that the light neutrino mass is suppressed by the parity breaking scale . The fL and fR are Majorana couplings, k1, k2 being VEV of Higgs bidoublet while υL(υR) is the VEV of LH (RH) scalar doublet. The smallness of νL thus ensures the smallness of the observed sub-eV scale neutrino masses. The SU(2)R × U(1)B−L breaking scale υR can be as low as a few TeV. This is in contrast to the usual left–right symmetric model without D-parity, where the neutrino mass is suppressed by vR and hence cannot be brought to TeV scales easily [54].
In addition we get two heavy pseudo-Dirac states, whose masses are separated by the light neutrino mass, given by
In the above equation, the small masses of active neutrinos can arise through small values of mL/M. As a result of M around TeV and mD in the range of 100 GeV, sizable mixing between the light and heavy states arises, and the Pseudo-Dirac pair with mass M can be probed at colliders4.
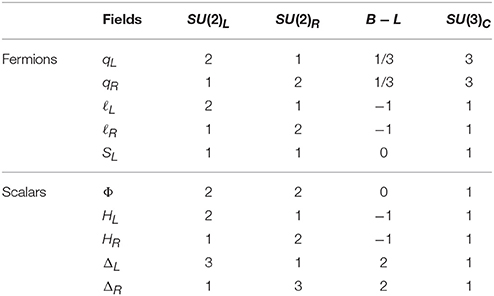
3.5. LRSM With Extended Seesaw
The LRSM here is extended with the addition of a neutral fermion SL per generation to the usual quarks and leptons.5 The scalar sector consists of bidoublet Φ with B − L = 0, triplets ΔL ⊕ ΔR with B − L = 2 and doublets HL ⊕ HR with B − L = −1. We call the model Extended LR model and thus the seesaw mechanism is called extended seesaw. Table 3 shows the complete particle spectrum.
The leptonic Yukawa interaction terms can be written as,
The neutral lepton mass matrix comes out to be;
in the basis after spontaneous symmetry breaking. The individual elements of the matrix hold the following meaning; MD = Y〈Φ〉 measures the light-heavy neutrino mixing and is usually called the Dirac neutrino mass matrix, MN = fυR = f〈ΔR〉 (ML = fυL = f〈ΔL〉) is the Majorana mass term for heavy (light) neutrinos, M = F〈HR〉 is the N − S mixing matrix, stands for the small mass term connecting ν − S and μS is the Majorana mass term for the singlet fermion SL.
Inverse Seesaw:- In Equation (42), following the mass hierarchy M≫MD≫μS and with the assumption that ML, MR, μL → 0 one obtains the inverse seesaw mass formula for light neutrinos [59]
Let us have a look at the model parameters of inverse seesaw framework and see how the light neutrino mass can be parametrized in terms of these.
Testable collider phenomenology can be expected in such a scenario because M lies at a few TeV scale which allows large left–right mixing. For an extension of such a scenario which allows large LNV and LFV one may refer the work [60].
Linear Seesaw:- Alternatively, in Equation (42), the assumption of ML, MR, μS → 0 leads to the linear seesaw mass formula for light neutrinos given by Deppisch et al. [61]
whereas the heavy neutrinos form a pair of pseudo-Dirac states with masses
Type-II Seesaw Dominance:- On the other hand a type-II seesaw dominance can be realized with the assumption that μL, μS → 0 in Equation (42).This allows large left–right mixing and thus leads to an interesting scenario.
A natural type-II seesaw dominance can be realized from the following Yukawa interactions
The gauge singlet mass term does not appear in the above Lagrangian since we have considered this to be zero or negligbly small to suppress the generic inverse seesaw contribution involving μS. We have also assumed the induced VEV for HL to be zero, i.e., 〈HL〉 → 0.
Now the complete 9 × 9 mass matrix for the neutral fermions in flavor basis can be written as
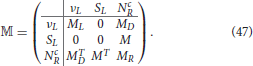
The heaviest right-handed neutrinos can be integrated out following the standard formalism of seesaw mechanism. Using mass hierarchy MR > M > MD ≫ ML one obtains
where the intermediate block diagonalised neutrino states are modified as
The following transformation relates the intermediate block diagonalised neutrino states to the flavor eigenstates.
In the mass matrix M′ the (2, 2) entry is larger than other entries in the limit MR > M > MD ≫ ML. The same procedure can be repeated in Equation (48) and S′ can be integrated out. Now the mass formula for light neutrino is given by
and the physical block diagonalised states are
with the corresponding block diagonalised transformation as
Following this block diagonalization procedure the flavor eigenstates can be related to mass eigenstates through the following transformation
Finally, the physical masses can be obtained by diagonalising the final block diagonalised mass matrices by a 9 × 9 unitary matrix V9 × 9. The block diagonalised neutrino states can be expressed in terms of mass eigenstates as follows,
while the block diagonalised mass matrices for light left-handed neutrinos, heavy right-handed neutrinos and extra sterile neutrinos are
Further these mass matrices can be diagonalised by respective 3 × 3 unitarity matrices as,
The complete block diagonalization results,
where 𝕎 is the block diagonalised mixing matrix and 𝕌 is the unitarity matrix given by,
Thus, the complete 9 × 9 unitary mixing matrix diagonalizing the neutral leptons is as follows
Expressing Masses and Mixing in terms of UPMNS and light neutrino masses:- Usually, the light neutrino mass matrix is diagonalised by the UPMNS mixing matrix in the basis where the charged leptons are already diagonal i.e., . The structure of the Dirac neutrino mass matrix MD which is a complex matrix in general can be considered to be the up-quark type in LRSM. Its origin can be motivated from a high scale Pati-Salam symmetry or SO(10) GUT. If we consider M to be diagonal and degenerate i.e., M = mS diag{1, 1, 1}, then the mass formulas for neutral leptons are given by
After some simplification the active LH neutrinos νL, active RH neutrinos NR and heavy sterile neutrinos SL in the flavor basis are related to their mass basis as
4. Alternative Formulation of Left–Right Symmetric Model: Universal Seesaw
Among the various alternative formulations of left–right symmetric model that have been proposed so far, the model which includes isosinglet vector like fermions looks more upgraded. The advantages of this alternative formulation over the manifest one are the following:
• Due to the presence of vector like fermions and absence of the usual scalar bidoublet in it, the charged fermions get their masses through a seesaw mechanism called the universal seesaw instead of standard Yukawa interaction. Thus, one does not need to finetune the Yukawa couplings. The universal seesaw is named as such since both quarks and leptons get their masses through a common seesaw.
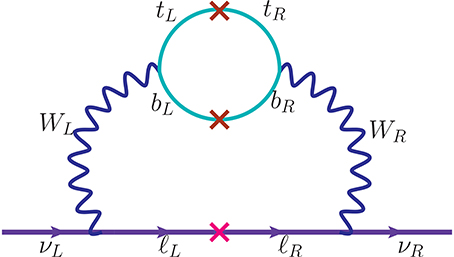
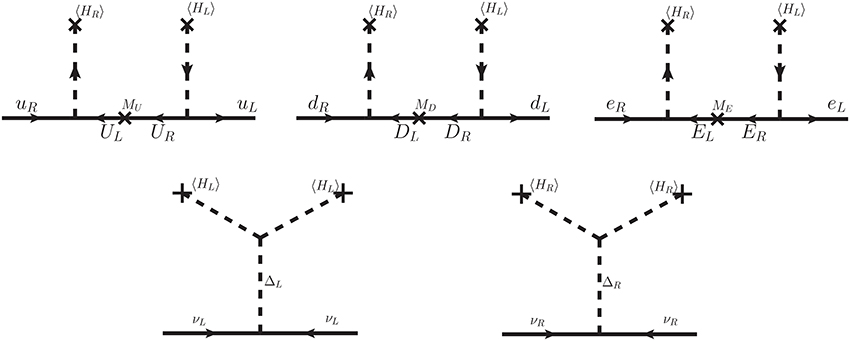
• Due to the absence of scalar bidoublet no tree level Dirac neutrino mass arises. However, the tiny Dirac neutrino mass is generated at two loop level while the right-handed interactions still lie at TeV scale, as shown in Figure 2.
• The same set of symmetries offer the ambiance to address the issue of weak and strong CP-violation.
• The scalar sector of the model is too simple which consists of two isodoublets.
4.1. Left–Right Symmetry With Vector-Like Fermions and Universal Seesaw
The fermion content of this model includes the usual quarks and leptons,
and the additional vector-like quarks and charged leptons [62–70]
To this new setup of left–right symmetric model, we add vector like neutral lepton in the fermion sector and a singlet scalar in the Higgs sector. The purpose behind the inclusion of vector like neutral lepton is to allow seesaw mechanism for light neutrinos leading to Dirac neutrino mass. Similarly, the scalar singlet is introduced to give consistent vacuum stability in the scalar sector. The particle content and the relevant transformations under the LRSM gauge group are shown in Table 4.
We now extend the standard LRSM framework having isosinglet vector-like copies of fermions with additional neutral vector like fermions [71–75]. This kind of a vector-like fermion spectrum is very naturally embedded in gauged flavor groups with left–right symmetry [76] or quark-lepton symmetric models [77].
The relevant Yukawa part of the Lagrangian is given by
where the summation is over X = U, D, E, N and we suppress flavor and color indices on the fields and couplings. denotes , where τ2 is the usual second Pauli matrix. We would like to stress that Parity Symmetry is present in order to distinguish between for instance NR and NL, otherwise extra terms in the Lagrangian Equation (64) would appear with the vector-like fermions Left and Right exchanged.
The LRSM gauge group breaks to the SM gauge group when HR(1, 2, −1) acquires a VEV and the SM gauge group breaks to U(1)EM when HL(2, 1, −1) acquires a VEV. However, parity can break either at TeV scale or at a much higher scale MP. For the latter case the Yukawa couplings can be different for right-type and left-type Yukawa terms () because of the renormalization group running below MP. Consequently, we will distinguish the left and right handed couplings explicitly with the subscripts L and R. We use the VEV normalizations and . The scale of vR has to lie between at around a few TeV (depending on the right-handed gauge coupling) to suit the experimental searches for the heavy right-handed WR boson at colliders and at low energies.
Since the particle spectrum does not contain a bidoublet Higgs, Dirac mass terms for the SM fermions can not be written and the charged fermion mass matrices assume a seesaw structure. Alternatively, a Higgs bidoublet Φ can be introduced along with HL,R.
After symmetry breaking, the mass matrices for the fermions are given by
The mass eigenstates can be found by rotating the mass matrices via left and right orthogonal transformations OL, R (we assume all parameters to be real). For example, the up quark diagonalization yields . Up to leading order in , the resulting up-quark masses are
and the mixing angles parametrizing ,
The other fermion masses and mixings are given analogously. For an order of magnitude estimate one may approximate the phenomenologically interesting regime with the limit in which case the mixing angles approach and . This means that is negligible for all fermions but the top quark and its vector partner [72].
We here neglect the flavor structure of the Yukawa couplings and λSXX which will determine the observed quark and leptonic mixing. The hierarchy of SM fermion masses can be generated by either a hierarchy in the Yukawa couplings or in the masses of the of the vector like fermions.
As described above, the light neutrino masses are of Dirac-type as well, analogously given by
It is natural to assume that MN ≫ vR, as the vector like N is a singlet under the model gauge group. In this case, the scenario predicts naturally light Dirac neutrinos [76].
4.2. Left–Right Symmetry With Vector-Like Fermions and Type-II Seesaw for Neutrino Masses
In Table 5, we present the field content of this model and their transformations under the LRSM gauge group.
We implement a scalar sector consisting of SU(2)L,R doublets and triplets, however the conventional scalar bidoublet is absent. We use the Higgs doublets to implement the left–right and the electroweak symmetry breaking: breaks the left–right symmetry, while breaks the electroweak symmetry once they acquire vacuum expectation values (VEVs),
Note that the present framework requires only doublet Higgs fields for spontaneous symmetry breaking. However, in the absence of a Higgs bidoublet, we use the vector-like new fermions to generate correct charged fermion masses through a universal seesaw mechanism. For the neutrinos we note that in the absence of a scalar bidoublet there is no Dirac mass term for light neutrinos and without scalar triplets no Majorana masses are generated either. To remedy this fact we introduce additional scalar triplets ΔL and ΔR,
which transform as ΔL ≡ [3, 1, 2, 1] and ΔR ≡ [1, 3, 2, 1], respectively. They generate Majorana masses for the light and heavy neutrinos although they are not essential in spontaneous symmetry breaking here. The particle content of the model is shown in Table 5. In the presence of the Higgs triplets, the manifestly Left–Right symmetric scalar potential has the form
where the scalar potential is given by
Assigning non-zero VEV to Higgs doublets HR and HL and triplets ΔR and ΔL,
the scalar potential takes the form,
As non-zero VEV breaks LRSM to SM at high scale and breaks SM down to low energy at electroweak scale, we consider vL ≠ vR. We chose the induced VEVs for scalar triplets much smaller than VEVs of Higgs doublets, i.e., uL, uR ≪ vL, vR.
One can approximately write down the Higgs triplets induced VEVs as follows,
4.2.1. Fermion Masses via Universal Seesaw
As discussed earlier, in this scheme normal Dirac mass terms for the SM fermions are not allowed due to the absence of a bidoublet Higgs. However, in the presence of vector-like copies of quark and charged lepton gauge isosinglets, the charged fermion mass matrices can assume a seesaw structure. The Yukawa interaction Lagrangian in this model is given by
where we suppress the flavor and color indices on the fields and couplings. denotes , where τ2 is the usual second Pauli matrix. Note that there is an ambiguity regarding the breaking of parity, which can either be broken spontaneously with the left–right symmetry at around the TeV scale or at a much higher scale independent of the left–right symmetry breaking. In the latter case, the Yukawa couplings corresponding to the right-type and left-type Yukawa terms can be different because of the renormalization group running below the parity breaking scale, . Thus, while writing the Yukawa terms above we distinguish the left- and right-handed couplings explicitly with the subscripts L and R.
After spontaneous symmetry breaking we can write the mass matrices for the charged fermions as [73]
The corresponding generation of fermion masses is diagrammatically depicted in Figure 3. Note that we are interested in a scenario where the VEVs of the Higgs doublets are much larger than the VEVs of the Higgs triplets i.e., uL ≪ υL, uR ≪ υR. In the context of this work, we do not attempt to explain how the hierarchy between VEVs can be achieved.
Assuming all parameters to be real one can obtain the mass eigenstates by rotating the mass matrices via left and right orthogonal transformations L, R. For example, up to leading order in , the SM and heavy vector partner up-quark masses are
and the mixing angles in L, R are determined as
The other fermion masses and mixing are obtained in an analogous manner. Note that here we have neglected the flavor structure of the Yukawa couplings which will determine the observed quark and charged lepton mixings. The hierarchy of SM fermion masses can be explained by assuming either a hierarchical structure of the Yukawa couplings or a hierarchical structure of the vector-like fermion masses.
4.2.2. Neutrino Masses and Type II Seesaw Dominance
In the model under consideration there is no tree level Dirac mass term for the neutrinos due to the absence of a Higgs bidoublet. The scalar triplets acquire induced VEVs 〈ΔL〉 = uL and 〈ΔR〉 = uR giving the neutral lepton mass matrix in the basis (νL, νR) given by
Thus, the light and heavy neutrino masses are simply mν = fuL ∝ MN = fuR. A Dirac mass term is generated at the two-loop level via the one-loop W boson mixing θW (see the next section) and the exchange of a charged lepton. It is of the order eV for MWR ≈ 5 TeV. This is intriguingly of the order of the observed neutrino masses; as long as the right-handed neutrinos are much heavier than the left-handed neutrinos, the type-II seesaw dominance is preserved and the induced mixing mD/MN is negligible. The mixing between charged gauge bosons is generated through the exchange of bottom and top quarks, and their vector-like partners. This yields a very small mixing of the order for TeV scale WR bosons.
Incorporating three fermion generations leads to the mixing matrices for the left- and right-handed matrices which we take to be equal
where U is the phenomenological PMNS mixing matrix. Thus, the unmeasured mixing matrix for the right-handed neutrinos is fully determined by the left-handed counterpart. The present framework gives a natural realization of type-II seesaw providing a direct relation between light and heavy neutrinos, Mi ∝ mi, i.e., the heavy neutrino masses Mi can be expressed in terms of the light neutrino masses mi as Mi = mi(M3/m3), for a normal and Mi = mi(M2/m2) for a inverse hierarchy of light and heavy neutrino masses.
4.3. Implication to Neutrinoless Double Beta Decay
As discussed earlier, there is no tree level Dirac neutrino mass term connecting light and heavy neutrinos. Consequently, the mixing between light and heavy neutrinos is vanishing at this order. Also, the mixing between the charged gauge bosons is vanishing at the tree level due to the absence of a scalar bidoublet.
The charged current interaction in the mass basis for the leptons is given by
The charged current interaction for leptons leads to 0νββ decay via the exchange of light and heavy neutrinos. There are additional contributions to 0νββ decay due to doubly charged triplet scalar exchange. While the left-handed triplet exchange is suppressed because of its small induced VEV, the right-handed triplet can contribute sizeably to 0νββ decay.
Before numerical estimation, let us point out the mass relations between light and heavy neutrinos under natural type-II seesaw dominance. For a hierarchical pattern of light neutrinos the mass eigenvalues are given as m1 < m2 ≪ m3. The lightest neutrino mass eigenvalue is m1 while the other mass eigenvalues are determined using the oscillation parameters as follows, , . On the other hand, for the inverted hierarchical pattern of the light neutrino masses m3 ≪ m1 ≈ m2 where m3 is the lightest mass eigenvalue while other mass eigenvalues are determined by , . The quasi-degenerate pattern of light neutrinos is . In any case, the heavy neutrino masses are directly proportional to the light neutrino masses.
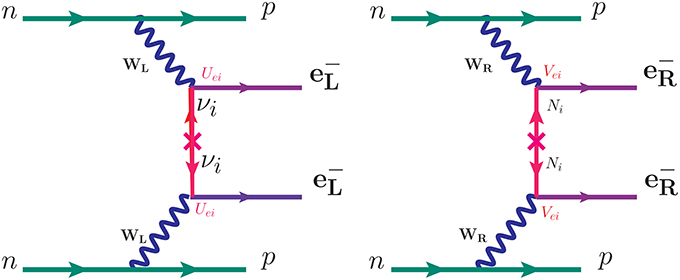
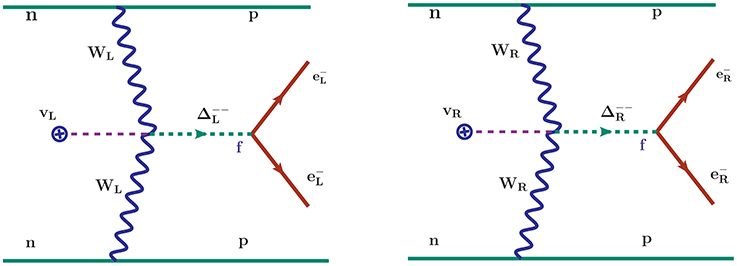
In the present analysis, we discuss 0νββ decay due to exchange of light neutrinos via left-handed currents, right-handed neutrinos via right handed currents as shown in Figure 4. 0νββ decay can also be induced by a right handed doubly charged scalar as shown in Figure 56. The half-life for a given isotope for these contributions is given by
where G01 corresponds to the standard 0νββ phase space factor, the correspond to the nuclear matrix elements for the different exchange processes and ηi are dimensionless parameters determined below.
Light Neutrinos
The lepton number violating dimensionless particle physics parameter derived from 0νββ decay due to the standard mechanism via the exchange of light neutrinos is
Here, me is the electron mass and the effective 0νββ mass is explicitly given by
with the sine and cosine of the oscillation angles θ12 and θ13, c12 = cosθ12, etc. and the unconstrained Majorana phases 0 ≤ α, β < 2π.
Right-Handed Neutrinos
The contribution to 0νββ decay arising from the purely right-handed currents via the exchange of right-handed neutrinos generally results in the lepton number violating dimensionless particle physics parameter
The virtual neutrino momentum |p| is of the order of the nuclear Fermi scale, p ≈ 100 MeV. mp is the proton mass and for the manifest LRSM case we have gL = gR, or else the new contributions are rescaled by the ratio between these two couplings. We in general consider right-handed neutrinos that can be either heavy or light compared to nuclear Fermi scale.
If the mass of the exchanged neutrino is much higher than its momentum, Mi ≫ |p|, the propagator simplifies as
and the effective parameter for right-handed neutrino exchange yields
where in the expression for the individual neutrino masses are replaced by their inverse values. Such a contribution clearly becomes suppressed the smaller the right-handed neutrino masses are.
On the other hand, if the mass of the neutrino is much less than its typical momentum, Mi ≪ |p|, the propagator simplifies in the same way as for the light neutrino exchange,
because both currents are right-handed. As a result, the 0νββ decay contribution leads to the dimensionless parameter
This is proportional to the standard parameter ην but in the case of very light right-handed neutrinos, e.g., Mi ≈ mi, the contribution becomes negligible because of the strong suppression with the heavy right-handed W boson mass.
In general, we consider right-handed neutrinos both lighter and heavier than 100 MeV and use (86) to calculate the contribution. In addition, the relevant nuclear matrix element changes; for Mi ≫ 100 MeV it approaches whereas for Mi ≪ 100 MeV it approaches . For intermediate values, we use a simple smooth interpolation scheme within the regime 10 MeV – 1 GeV, which yields a sufficient accuracy for our purposes.
Right-Handed Triplet Scalar
Finally, the exchange of a doubly charged right-handed triplet scalar shown in Figure 5 (where doubly charged left-handed triplet scalar contributes negligible and thus, neglected from the present discussion) gives
This expression is also proportional to the standard ην because the relevant coupling of the triplet scalar is proportional to the right-handed neutrino mass.
Numerical Estimate
In the following, we numerically estimate the half-life for 0νββ decay of the isotope 136Xe as shown in Figure 6. We use the current values of masses and mixing parameters from neutrino oscillation data reported in the global fits taken from Gonzalez-Garcia et al. [94]. For the 0νββ phase space factors and nuclear matrix elements we use the values given in Table 6. In Figure 6, we show the dependence of the 0νββ decay half-life on the lightest neutrino mass, i.e., m1 for normal and m3 for inverse hierarchical neutrinos. The other model parameters are fixed as
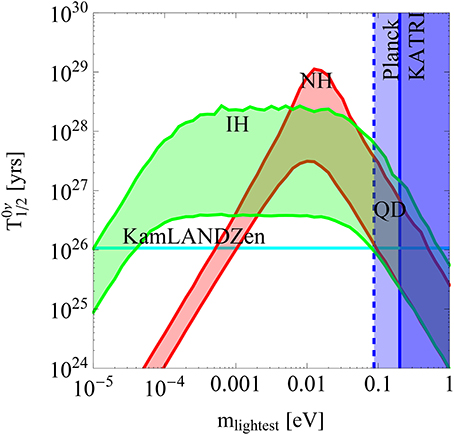
Figure 6. 0νββ decay half-life as a function of the lightest neutrino mass in the case of normal hierarchical (NH) and inverse hierarchical (IH) light neutrinos in red and green bands respectively. We defined mlightest ≃ mi such that m1 is the lightest neutrino mass for NH and m3 for IH pattern. The other parameters are fixed as MWR = 5 TeV, TeV and the heaviest right-handed neutrino mass is 1 TeV. The gauge couplings are assumed universal, gL = gR, and the intermediate values for the nuclear matrix elements are used, , . The bound on the sum of light neutrino masses from the KATRIN and Planck experiments are represented as vertical lines. The bound from KamLAND-Zen experiment is presented in horizontal line for Xenon isotope. The bands arise due to 3σ range of neutrino oscillation parameters and variation in the Majorana phases from 0 − 2π.

Table 6. Phase space factor G01 and ranges of nuclear matrix elements for light and heavy neutrino exchange for the isotopes 76Ge and 136Xe [95].
The lower limit on lightest neutrino mass is derived to be m< ≈ 0.9 meV, 0.01 meV for NH and IH pattern of light neutrino masses respectively by saturating the KamLAND-Zen experimental bound.
As for the experimental constraints, we use the current best limits at 90% C.L., yr and yr from KamLAND-Zen [96] and the GERDA Phase I [97], respectively. Representative for the sensitivity of future 0νββ experiments, we use the expected reach of the planned nEXO experiment, yr [98]. As for the other experimental probes on the neutrino mass scale, we use the future sensitivity of the KATRIN experiment on the effective single β decay mass mβ ≈ 0.2 eV [99] and the current limit on the sum of neutrino masses from cosmological observations, Σimi ≲ 0.7 eV [100].
For a better understanding of the interplay between the left- and right-handed neutrino mass scales, we show in Figure 7 the 0νββ decay half-life as a function of the lightest neutrino mass and the heaviest neutrino mass for a normal (left) and inverse (right) neutrino mass hierarchy. The other model parameters are fixed, with right-handed gauge boson and doubly-charged scalar masses of 5 TeV. The oscillation parameters are at their best fit values and the Majorana phases are always chosen to yield the smallest rate at a given point, i.e., the longest half life. The nuclear matrix employed are at the lower end in Table 6. This altogether yields the longest, i.e., most pessimistic, prediction for the 0νββ decay half-life. The red-shaded area is already excluded with a predicted half life of 1026 yr or faster. As expected, this sets an upper limit on the lightest neutrino mass mlightest ≲ 1 eV, but it also puts stringent constraints on the mass scale of the right-handed neutrinos. For an inverse hierarchy, the range 50MeV ≲ M2 ≲ 5 GeV is excluded whereas in the normal hierarchy case, large M3 can be excluded if there is a strong hierarchy, m1 → 0. This is due the large contribution of the lightest heavy neutrino N1 in such a case.
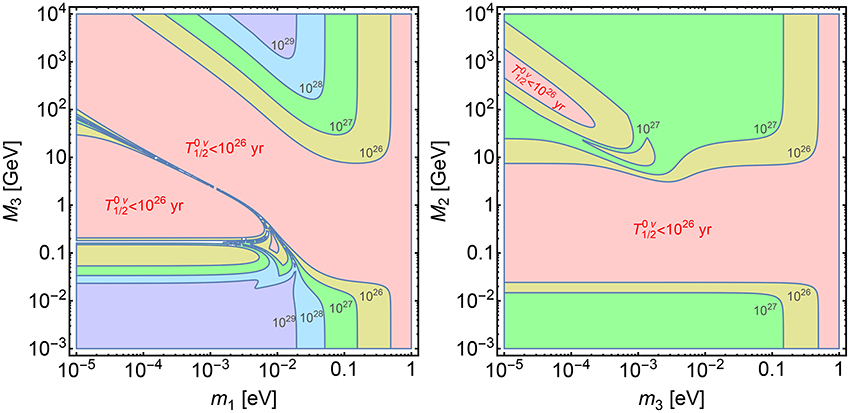
Figure 7. Half-life of 0νββ decay in Xe as a function of the lightest and the heaviest neutrino mass for a normal (left) and inverse (right) neutrino mass hierarchy. The contours denote the half-life in years. Best-fit oscillation data are used and the Majorana phases are chosen to yield the longest half-life. Likewise, the smallest values of the nuclear matrix elements in Table 6 are employed. The other model parameters are chosen as gR = gL and MWR = MΔ = 5 TeV.
5. Leptogenesis
Cosmological observations (studies of the cosmic microwave background radiation, large scale structure data, the primordial abundances of light elements) indicate that our visible universe is dominated by matter and there is very little antimatter. The baryon asymmetry normalized to number density of photons (nγ) can be extracted out of these observations, which gives
The astrophysical observations suggest that at an early epoch before the big-bang nucleosynthesis this asymmetry was generated. Thus, it is natural to seek an explanation for this asymmetry from the fundamental particle interactions within or beyond the SM of particle physics. There are three conditions, often called Sakharov's conditions [101], that must be met in order to generate a baryon asymmetry dynamically:
1. baryon number violation,
2. C and CP violation, and
3. departure from thermal equilibrium.
In principle, the SM has all the ingredients to satisfy all three conditions.
1. In the SM baryon number B and lepton number L are violated due to the triangle anomaly, leading to 12-fermion processes involving nine left handed quarks (three of each generation) and three left handed leptons (one from each generation) obeying the selection rule Δ(B−L) = 0. These processes have a highly suppressed amplitude proportional to e−4π/α (where , with αEM being the fine structure constant and θW being the weak mixing angle) at zero temperature. However, at high temperature this suppression is lifted and these processes can be very fast.
2. The weak interactions in the SM violate C in a maximal way. CP is also violated via the CKM phase δCKM.
3. The electroweak phase transition can result in the departure from thermal equilibrium if it is sufficiently strongly first order.
However, in practice it turns out that only the first Sakharov condition is fulfilled in a satisfactory manner in the SM. The CP violation coming from the CKM phase is suppressed by a factor in the denominator, where TEW ~ 100 GeV is the temperature during the electroweak phase transition. Consequently, the CP violation in the SM is too small to explain the observed baryon asymmetry of the universe. Furthermore, the electroweak phase transition is not first order; but just a smooth crossover.
Thus, to explain the baryon asymmetry of the universe one must go beyond the SM, either by introducing new sources of CP violation and a new kind of out-of-equilibrium situations (such as the out-of-equilibrium decay of some new heavy particles) or modifying the electroweak phase transition itself. One such alternative is leptogenesis. Leptogenesis is a mechanism where a lepton asymmetry is generated before the electroweak phase transition, which then gets converted to baryon asymmetry of the universe in the presence of sphaleron induced anomalous B + L violating processes, which converts any primordial L asymmetry, and hence B − L asymmetry, into a baryon asymmetry. A realization of leptogenesis via the decay of out-of-equilibrium heavy neutrinos transforming as singlets under the SM gauge group was proposed in Fukugita and Yanagida [21]. The Yukawa couplings provide the CP through interference between tree level and one-loop decay diagrams. The departure from thermal equilibrium occurs when the Yukawa interactions are sufficiently slow7. The lepton number violation in this scenario comes from the Majorana masses of the heavy neutrinos. The generated lepton asymmetry then gets partially converted to baryon asymmetry in the presence of sphaleron induced anomalous B + L violating interactions before the electroweak phase transition. In what follows, we will discuss the sphaleron processes and few of the most popular scenarios of leptogenesis in some detail to set the stage before discussing leptogenesis in LRSM scenarios in particular.
5.1. Anomalous B + L Violating Processes and Relating Baryon and Lepton Asymmetries
In the SM both B and L are accidental symmetries and at the tree level these symmetries are not violated. However, the chiral nature of weak interactions gives rise to equal global anomalies for B and L, giving a vanishing B − L anomaly, but a non-vanishing axial current corresponding to B + L, given by t Hooft [102, 103]
where and Bμν are the SU(2)L and U(1)Y field strength tensors and Nf is the number of fermion generations. The corresponding B + L violation can obtained by integrating the divergence of the B + L current, which is related to the change in the topological charges of the gauge field
where Ncs = ±1, ±2,⋯ corresponds to the topological charge of gauge fields, called the Chern-Simons number. In the SM there are three generations of fermions (Nf = 3), leading to ΔB = ΔL = 3Ncs, thus the vacuum to vacuum transition changes B and L by multiples of 3 units. At the lowest order, one has the B + L violating effective operator
which gives rise to 12-fermion sphaleron induced transitions, such as
At zero temperature the transition rate is suppressed by [102, 103]. However, when the temperature is larger than the barrier height, this Boltzmann suppression disappears and B + L violating transitions can occur at a significant rate [104]. In the symmetric phase, when the temperature is grater than the electroweak phase transition temperature, T ≥ TEW, the transition rate per unit volume is [105–108]
where , with αEM being the fine structure constant and θW being the weak mixing angle.
An account of the B − L symmetry getting converted to a baryon asymmetry via an analysis of the chemical potential can be found in Khlebnikov and Shaposhnikov [109], Harvey and Turner [110] and Sarkar [111]. The baryon asymmetry in terms of the B − L number density can be written as
Thus, the primordial B − L asymmetry gets partially converted into a baron asymmetry of the universe after the electroweak phase transition.
5.2. Leptogenesis With Right Handed Neutrinos
In section 2, we have discussed how adding singlet right handed neutrinos NRi to the SM can generate tiny seesaw masses [14–20] for light neutrinos. Beyond the generation of light neutrino masses, the interaction terms
can also provide all the ingredients necessary for realizing leptogenesis. We will work on a basis where the right handed neutrino mass matrix is real and diagonal. Furthermore we assume a hierarchical mass spectrum for the right handed neutrinos M3 > M2 > M1. The Majorana mass term gives rise to lepton number violating decays of the right handed neutrinos
which can generate a lepton asymmetry if there is CP violation and the decay is out of equilibrium [21]. This lepton asymmetry (equivalently B − L asymmetry) then gets converted to baryon asymmetry in presence of anomalous B + L violating processes before the electroweak phase transition.
In the original proposal [21] and few subsequent works [112–116], only the CP violation coming from interference of tree level and one-loop vertex diagrams, shown in Figure 8. was considered. This is somewhat analogous to the CP violation in K-physics coming from the penguin diagram. The CP asymmetry parameter corresponding to the vertex type CP violation is given by
where the loop function fv is defined by
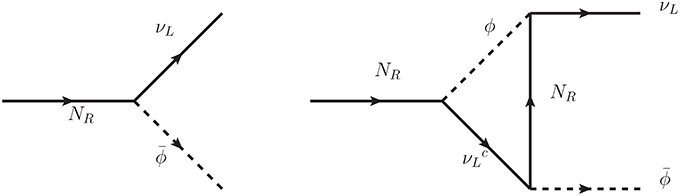
Figure 8. Tree level and one-loop vertex diagrams contributing to the vertex type CP violation in models with right handed neutrinos.
In the limit M1 ≪ M2, M3 the asymmetry simplifies to
It was later pointed out in Flanz et al. [117] and Flanz et al. [118] and confirmed rigorously in Pilaftsis [119], Pilaftsis and Resonant [120], Roulet et al. [121], Buchmuller and Plumacher [122], Flanz and Paschos [123], Hambye et al. [124] and Pilaftsis and Underwood [125], that there is another source of CP violation coming from interference of tree level diagram with one-loop self-energy diagram shown in Figure 9. This CP violation is similar to the CP violation due to the box diagram, entering the mass matrix in mixing in K-physics. If the heavy neutrinos decay in equilibrium, the CP asymmetry coming from the self-energy diagram due to one of the heavy neutrinos may cancel with the asymmetry from the decay of another heavy neutrino to preserve unitarity. However, in out-of-equilibrium decay of heavy neutrinos the number densities of the two heavy neutrinos differ during their decay and consequently, this cancellation is no longer present. This can be understood as the right handed neutrinos oscillating into antineutrinos of different generations, which under the condition Γ[particle → antiparticle] ≠ Γ[antiparticle → particle], can create an asymmetry in right handed neutrinos before they decay. An elementary discussion regarding how the CP violation enters in Majorana mass matrix, which then generates a lepton asymmetry can be found in Sarkar [111] and Langacker et al. [126]. The basic idea is to treat the particles and the antiparticles independently. The CP eigenstates |Ni 〉 and are no longer physical eigenstates, which evolves with time. Consequently, the physical states, which are admixtures of |Ni 〉 and , can decay into both leptons and antileptons, giving rise to a CP violation. The CP asymmetry parameter coming from the interference of tree level and one-loop self-energy diagram is given by
where the loop function fs is defined by
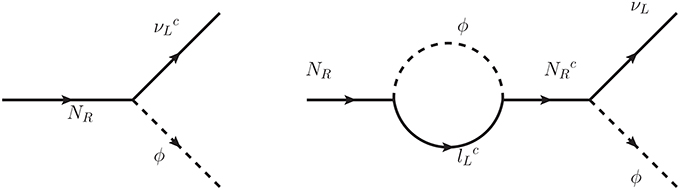
Figure 9. Tree level and one-loop self-energy diagrams contributing to the CP violation in models with right handed neutrinos.
When the mass difference between the right handed neutrinos is very large compared to the width, , the CP asymmetries coming from vertex and self-energy diagrams are comparable. However, when two right handed neutrinos are nearly degenerate, such that their mass difference is comparable to their width, then CP violation contribution coming from the self-energy diagram becomes very large (orders of magnitude larger than the CP asymmetry generated by the vertex type diagram). This is often referred to as the resonance effect.
To ensure that the lightest right handed neutrino decays out-of-equilibrium so that an asymmetry is generated, the out-of-equilibrium condition given by
must be satisfied, where g* correspond to the effective number of relativistic degrees of freedom. This gives a lower bound GeV [127]. Though this gives us a rough estimate, in an actual calculation of the asymmetry one solves the Boltzmann equation, which takes into account both lepton number violating as well as lepton number conserving processes mediated by heavy neutrinos. The Boltzmann equation governing lepton number asymmetry , is given by
where Γψ1 is the decay rate of the physical state |ψ1〉, is the equilibrium number density of ψ1 given by
where s is the entropy density. The first term on the right hand side of Equation (108) corresponds to the CP violating contribution to the asymmetry and is the only term that generates asymmetry when ψ1 decays out-of-equilibrium, while the second term corresponds to inverse decay of ψ1, and the last term corresponds to 2↔2 lepton number violating scattering process such as l + ϕ† ↔ lc + ϕ, with 〈σ|v|〉 being the thermally averaged cross section. The number density of ψ1 is governed by the Boltzmann equation
One often defines a parameter K = Γψ1(T = mψ1)/H(T = mψ1), where the Hubble rate , which gives a measure of the deviation from thermal equilibrium. For K ≪ 1 one can find an approximate solution for Equation (108) given by
The Yukawa couplings are constrained by the required amount of primordial lepton asymmetry required to generate the correct baryon asymmetry of the universe, while the lightest right handed neutrino mass is constrained from the out-of-equilibrium condition. In the resonant leptogenesis scenario, the CP violation is largely enhanced, making the constrains on Yukawa couplings relaxed. Consequently the scale of leptogenesis can be considerably lower, making it possible to realize a TeV scale leptogenesis, which can be put to test at the LHC [128, 129].
5.3. Leptogenesis With Triplet Higgs
In section 2, we have discussed how small neutrino masses can be generated by adding triplet Higgs ξa to the SM [22, 26–28, 130–132]. The interactions of these triplet Higgs that are relevant for leptogenesis are given by
From these interactions we have the decay modes of the triplet Higgs
The CP violation is obtained through the interference between the tree level and one-loop self-energy diagrams shown in Figure 10. There are no one-loop vertex diagrams in this case. One needs at least two ξ's. To see how this works, we will follow the mass-matrix formalism [22], in which the diagonal tree-level mass matrix of ξa is modified in the presence of interactions to
where
with and . From the absorptive part of the one-loop diagram for ξa → ξb we obtain
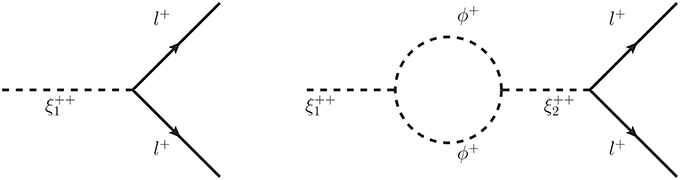
Figure 10. Tree level and one-loop self-energy diagrams contributing to the CP violation in a model with triplet Higgs.
Assuming Γa ≡ Γaa ≪ Ma, the eigenvalues of are given by
where and M1 > M2. The physical states, which evolves with time, can be written as linear combinations of the CP eigenstates as
where , , with
The physical states evolve with time and decay into lepton and antilepton pairs. Assuming , the CP asymmetry is given by Ma [22]
For M1 > M2, when the temperature drops below M1, ψ1 decays away to create a lepton asymmetry. However, this asymmetry is washed out by lepton number violating interactions of ψ2; and the subsequent decay of ψ2 at a temperature below M2 sustains. The generated lepton asymmetry then gets converted to the baryon asymmetry in the presence of the sphaleron induced anomalous B + L violating processes before the electroweak phase transition. The approximate final baryon asymmetry is given by
where K ≡ Γ2(T = M2)/H(T = M2) is the parameter measuring the deviation from thermal equilibrium when, is the Hubble rate, and g* corresponds to the number of relativistic degrees of freedom.
In a more rigorous estimation of the baryon asymmetry, in addition to the decays and the inverse decays of triplet scalars, one needs to incorporate the gauge scatterings (F corresponds to SM fermions and G corresponds to gauge bosons) and ΔL = 2 scattering processes ll ↔ ϕ*ϕ* and into the Boltzmann equation analysis of the asymmetry. Including these washout processes, one finds a lower limit on Mξ, [133]. For a quasi-degenerate spectrum of scalar triplets the resonance effect can enhance the CP asymmetry by a large amount and a successful leptogenesis scenario can be attained for a much smaller value of triplet scalar mass. In Strumia [134] and Aristizabal Sierra et al. [135], an absolute bound of Mξ ≳ 1.6TeV is obtained for a successful resonant leptogenesis scenario with triplet Higgs.
6. Leptogenesis in LRSM
In Left–Right Symmetric Model (LRSM) [17, 19, 44–49] the left–right parity symmetry breaking implies the existence of a heavy right-handed charged gauge boson . In this section, we will discuss the aspect that if is detected at the LHC with a mass of a few TeV then it can have profound implications for leptogenesis. If indeed is detected at the LHC then that will give rise to an excess in the dilepton + dijet channel as reported sometime back by the CMS collaboration. A signal of 2.8 σ level was reported in the mass bin 1.8TeV < Mlljj < 2.1TeV in the di-lepton + di-jet channel at the LHC by the CMS collaboration [136]. One of the popular interpretations of this signal was decay in the framework of LRSM with gL ≠ gR via an embedding of LRSM in SO(10) [137, 138]. Another popular interpretation was for the case gL = gR which utilized the CP phases and non-degenerate mass spectrum of the heavy neutrinos [139]. Around the same time the ATLAS collaboration had also reported a resonance signal decaying into a pair of SM gauge bosons. They found a local excess signal of 3.4σ (2.5σ global) in the WZ channel at around 2TeV [140]. This signal was shown to be explained by a WR in LRSM framework for a coupling gR ~ 0.4 in Brehmer et al. [141]. Some other notable work along this direction can be found in Dobrescu and Liu Bhupal [142], Dev and Mohapatra [143] and Das et al. [144]. However, these interesting signals were either washed out by more accumulated data or reduced significantly below their initial reported levels. Nevertheless such signals have intrigued several studies concerning the impact of a TeV scale on leptogenesis.
As discussed earlier, the Higgs sector in one of the popular versions of LRSM consists of one bidoublet Higgs Φ and two triplet complex scalar fields ΔL,R. The relevant gauge transformations are as follows
Here one breaks the left–right symmetry in a spontaneous manner to reproduce the Standard Model. On the other hand the smallness of the neutrino masses is realized using the seesaw mechanism [14–20].
In another variant of LRSM one has only the doublet Higgs which are employed to break all the relevant symmetries. Here the Higgs sector consists of doublet scalars with the gauge transformations
In addition there is one fermion gauge singlet SR ~ (1, 1, 0, 1). The Higgs doublet HR acquires a VEV to break the left–right symmetry which results in the mixing of S with right-handed neutrinos. This gives rise to a light Majorana neutrino and a heavy pseudo-Dirac neutrino or alternatively a pair of Majorana neutrinos.
Historically, in LRSM, the left–right symmetry was broken at a fairly high scale, . This serves two purposes– firstly, the requirement of gauge coupling unification implies this scale to be high, and secondly, thermal leptogenesis in this scenario gives a comparable bound. To get around this problem one often introduces a parity odd scalar which is then given a large VEV. This is often called D-parity breaking. Consequently, one can have gL ≠ gR even before the left–right symmetry breaking. This in turn allows the possibility of a gauge coupling unification with TeV scale WR. This is true for both triplet and doublet models of LRSM. Embedding the LRSM in an SO(10) GUT framework, the violation of D-parity [54] at a very high scale helps in explaining the CMS TeV scale WR signal for gR ≈ 0.6gL as shown in Deppisch et al. [137, 138].
6.1. Can a TeV-Scale at the LHC Falsify Leptogenesis?
For a TeV scale , all leptogenesis scenarios may be broadly classified into two groups:
• At a very high scale a leptonic asymmetry is generated. It can be either in the context of LRSM with D-parity breaking or through some other interactions (both thermal and non-thermal).
• At the TeV scale a lepton asymmetry is generated with resonant enhancement, when the left–right symmetry breaking phase transition is taking place.
The following discussions hold for the LRSM variants with a Higgs sector consisting of triplet Higgs as well as a Higgs sector with exclusively doublet Higgs. We will often refer to these two broad classes of the LRSM mentioned above to discuss the lepton number violating washout processes and point out how all these possible scenarios of leptogenesis are falsifiable for a WR of TeV scale. In the case where high-scale leptogenesis happens at T > 109 GeV, the low energy B − L breaking gives rise to gauge interactions which depletes all the baryon asymmetry very rapidly before the electroweak phase transition is over. Now, these same lepton number violating gauge interactions will significantly slow down the generation of the lepton asymmetry for resonant leptogenesis at around TeV scale. Consequently, it is not possible to generate the required baryon asymmetry of the universe for TeV scale in this case.
For the case MN3R ≫ MN2R ≫ MN1R = MNR, severe constraints on the mass for a successful scenario of high-scale leptogenesis come from the SU(2)R gauge interactions as pointed out in Ma [145]. To have successful leptogenesis in the case MNR > MWR, the condition that the gauge scattering process goes out-of-equilibrium yields
with mWR/mNR ≳ 0.1. For the scenario where MWR > MNR leptogenesis happens either at T > MWR after the breaking of B − L gauge symmetry or at T≃MNR, the out-of equilibrium condition for the scattering process through NR exchange leads to the constraint
Thus, a WR with mass in the TeV range (in the case of a hierarchical neutrino mass spectrum) rules out the high-scale leptogenesis scenario. In Deppisch et al. [146, 147], neutrinoless double beta decay and the observation of the lepton number violating processes at the colliders were studied in the context of high-scale thermal leptogenesis. In Flanz et al. [117, 118], Pilaftsis [119], Roulet et al. [121], Buchmuller and Plumacher [122], Flanz and Paschos [123], Hambye et al. [124], Pilaftsis and Underwood [125] resonant leptogenesis has been discussed in the context of a considerably low mass WR. In Frere et al. [148] it was pointed out that one requires an absolute lower bound of 18 TeV on the WR mass in order to have successful low-scale leptogenesis with a quasi-degenerate right-handed neutrinos. Recently, it was found that just the correct lepton asymmetry can be obtained by utilizing relatively large Yukawa couplings, for WR mass scale higher than 13.1TeV in Bhupal Dev et al. [149, 150]. Note that in Frere et al. [148] and Bhupal Dev et al. [150], the lepton number violating gauge scattering processes such as NReR → ūRdR, NR ū R → eRdR, NRdR → eRuR and NRNR → eR ē R have been analyzed in detail. However, lepton number violating scattering processes with external WR were ignored because for a heavy WR there is a relative suppression of in comparison to the processes where there is no WR in the external legs. Now, if indeed the mass of WR is around a few TeV, as was suggested by an excess signal reported by the CMS experiment then one has to take the latter processes seriously. In Dhuria et al. [151], it was pointed out that the lepton number violating washout processes ( and ) can be mediated via the doubly charged Higgs in the conventional LRSM. In Bhupal Dev et al. [149] it was shown that in a parity-asymmetric type-I seesaw model with relatively small MNR one obtains a small contribution from this process which is expected for a large MWR/MNR. However, in this scenario some other relevant gauge scattering processes are efficient in washing out the lepton asymmetry. Including these washout processes one obtains a lower bound of 13.1TeV on the WR mass [149]. Here we will mainly discuss and NR mediated lepton number violating scattering processes in a much more general context to establish their importance as washout processes which can falsify the possibility of leptogenesis depending on WR mass [152]. One of the vertices in the mediated process is gauge vertex while the other one is a Yukawa vertex. On the other hand for NR mediated lepton number violating scattering processes both the vertices are gauge vertices. Consequently, these lepton number violating scattering processes are very rapid as compared to the scattering processes involving only Yukawa vertices. It turns out that NR and mediated scattering process does not go out of equilibrium till the electroweak phase transition if the mass of WR is around TeV scale. Consequently, these lepton number violating scattering processes continue to wash out or slow down the generation of lepton asymmetry8. In the scenario of LRSM involving only doublet Higgs in the Higgs sector the doubly charged Higgs is absent. Nevertheless, the NR mediated lepton number violating scattering processes will be present and will wash out the lepton asymmetry in such a scenario.
In LRSM the right handed leptonic charged current interaction is given by
where JRμ = ēR γ μ(1 + γ5)NR. The relevant interactions of the right-handed Higgs triplet are given by
where . The covariant derivative is given by , where and Bμ are gauge fields corresponding to SU(2)R and U(1)B−L gauge groups with the associated gauge couplings given by gR and g′, respectively. When the neutral Higgs field acquires a VEV SU(2)R, the interaction between the gauge boson WR and the doubly charged Higgs is given by Doi [153]
The Yukawa interaction between the lepton doublet and the components of triplet Higgs are given by
where τ's are the Pauli matrices. After the Higgs triplet field acquires a VEV, the relevant Yukawa coupling can be written as where MNR is the Majorana mass of NR.
The relevant Feynman diagrams for the lepton number violating processes induced by these interactions are depicted in Figure 11.
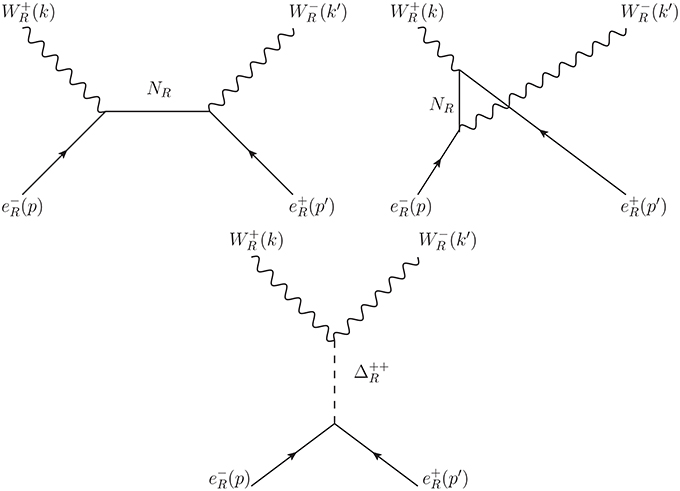
Figure 11. Feynman diagrams for scattering mediated by NR and fields. The Feynman diagrams for can be obtained by appropriately changing the direction of the external legs.
Using the interactions given in Equations (126)–(129), one can estimate the differential scattering cross section for the process to obtain [153]
where
and
where we neglect any mixing between WL and WR. On the right-hand side of Equation (133), the first term corresponds to the Higgs exchange. The last two terms are due to the interference between Higgs and NR exchange. The Mandelstam variables s = (p+k)2, t = (p−p′)2 and u = (p−k′)2 are related by the scattering angle θ as follows
The differential scattering cross section for the process is given by Doi [153]
where
The expressions for can be obtained after interchanging s ↔ t in : = . The Mandelstem variables t = (p − k)2 and u = (p − k′)2 can be written in terms of s = (p + p′)2 and scattering angle θ as follows
6.1.1. Wash Out of Lepton Asymmetry for T > MWR
During the period when the temperature is such that vR > T > MWR, the lepton number violating washout processes are very rapid in the absence any suppression. To have a quantitative estimate of the strength of these scattering processes in depleting the lepton asymmetry one can estimate the parameter defined as
for both the processes during vR > T > MWR, where n corresponds to the number density of relativistic species and is given by . H corresponds to the Hubble rate , where g* ~ 100 corresponds to the relativistic degrees of freedom. The thermally averaged cross section is denoted by 〈σ|υ|〉. To choose a rough estimate of vR, let us compare the situation with the Standard Model, where we have where vL = 246GeV, and MWL ~ 80GeV. Now in case of LRSM breaks the left–right symmetry and MWR = gR υ R. Taking gR ~ gL, we have
Making use of the differential scattering cross sections in Equations (130) and (135), we plot the behavior of K as a function of temperature in Figure 12. The plot corresponds to a temperature range 3MWR > T > MWR and right handed charged gauge boson mass MWR = 3.5TeV.
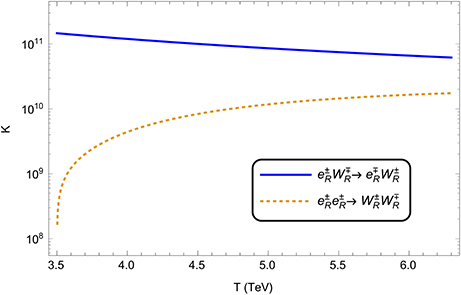
Figure 12. Plot showing the behavior of K as a function of temperature T for the processes and (including both and NR mediated diagrams) for υR > T > MWR. The right handed charged gauge boson mass is taken to be MWR = 3.5TeV.
In Figure 12, the large values of K for both the processes indicates that high wash out efficiency of these scattering processes for T ≳ MWR. For the LRSM variant with its Higgs sector consisting of only doublet Higgs the doubly charged Higgs mediated channels are absent for these processes and the right handed neutrino will mediate these processes, which will washout the lepton asymmetry for T ≳ MWR.
6.1.2. Wash Out of Asymmetry for T < MWR
During the period when the temperature is such that T < MWR, the process is of more importance. Let us now estimate a lower bound on T below T = MWR till which this process stays in equilibrium and continues to deplete lepton asymmetry. The scattering rate can be written as9 For T < MWR the Boltzmann suppression of the scattering rate stems from the number density . Now, the scattering process stays in thermal equilibrium when the condition Γ > H is satisfied.
In Figure 13 we show the temperature until which the scattering process stays in equilibrium as a function of MWR for three values of MΔR and taking MNR ≲ MWR and vrel = 1. We have taken the lowest value of MΔR to be 500 GeV to be consistent with the recent collider limits on the doubly charged Higgs mass [154]. The plot shows that unless MWR is significantly heavier than a few TeV, the process will continue to be in equilibrium till a temperature similar to the electroweak phase transition. Consequently, this process will continue to washout or slow down the generation of lepton asymmetry until the electroweak phase transition. In the LRSM variant with doublet Higgs, the heavy neutrinos will mediated lepton number violating scattering processes will washout or slow down the generation of lepton asymmetry until the electroweak phase transition. Thus, the lower limit on the WR mass for a successful leptogenesis scenario is significantly higher a few TeV. This was also confirmed by explicitly solving the relevant Boltzmann equations in Bhupal Dev et al. [149, 150].
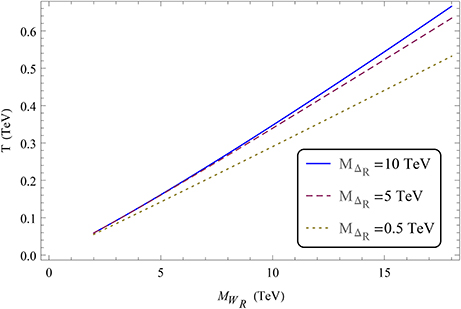
Figure 13. Plot showing the dependance of out of equilibrium temperature (T) on MWR for the process (mediated via and NR fields) for MNR ~ MWR. The three different lines correspond to three different values of MΔR.
7. Concluding Remarks
We have reviewed the standard left–right symmetric theories and the implementation of different types of low scale seesaw mechanisms in the context of neutrino masses. We have also discussed a left–right symmetric model with additional vector-like fermions in order to simultaneously explain the charged fermion and Majorana neutrino masses. In this model the quark and charged lepton masses and mixings are realized via a universal seesaw mechanism while spontaneous symmetry breaking is achieved with two doublet Higgs fields with non-zero B − L charge, we have introduced scalar triplets with small induced VEVs such that they give Majorana masses to light as well as heavy neutrinos. We have also discussed how the Majorana nature of these neutrinos leads to 0νββ decay. Interestingly, the right-handed currents play an important role in discriminating between the mass hierarchy as well as the absolute scale of light neutrinos. To summarize the situation for leptogenesis, in the high-scale leptogenesis scenario (T ≳ MWR), in all the variants of LRSM the lepton number violating processes and are highly efficient in washing out the lepton asymmetry. In the case of resonant leptogenesis scenario at around TeV scale we found that the latter process stays in equilibrium until the electroweak phase transition, making the generation of lepton asymmetry for T < MWR significantly weaker. Thus, if the LHC discovers a TeV scale then one needs to look for some post-electroweak phase transition mechanism to explain the baryon asymmetry of the Universe. To this end the observation of the neutron-antineutron oscillation [155, 156] or (B − L) violating proton decay [157] will play a guiding role in confirming such scenarios. Complementing these results, the low-energy subgroups of the superstring motivated E6 model have also been explored which can also give rise to left–right symmetric gauge structures but with a number of additional exotic particles as compared to the conventional LRSM. Interestingly, one of the low-energy supersymmetric subgroups of E6, also known as the Alternative Left–Right Symmetric Model, gives a model alternative to successfully realize high-scale leptogenesis in the absence of the dangerous gauge washout processes [158]. The vector-like fermions added to the minimal framework of LRSM to realize a universal seesaw can pave new ways to realize baryogenesis as discussed in Deppisch et al. [73].
Author contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank Frank F. Deppisch for many helpful discussions and encouragement. The authors are also thankful to both the reviewers for many valuable suggestions and CH and US are thankful to Mansi Dhuria and Raghavan Rangarajan for several wonderful collaborations which have resulted in some of the interesting findings covered in this review. The work of US is supported partly by the JC Bose National Fellowship grant under DST, India.
Footnotes
1. ^The seesaw mechanisms generically require a new heavy scale (as compared to the electroweak scale) in the theory, inducing a small neutrino mass (millions of times smaller than the charged lepton masses). Hence the name “seesaw.”
2. ^Majorons correspond to Goldstone bosons associated with the spontaneous breaking of a global lepton number symmetry.
3. ^Ma [30] established the nomenclature Types I, II, III, for the three and only three tree-level seesaw mechanisms.
4. ^Most often the linear seesaw is assumed to be realized with M ≫ mD ~ mL ~ 100 GeV, which results in the same expression for the mν. This would result in unobservable heavy fermions and negligible mixing.
5. ^The discussion of extended seesaw mechanism can be found in Gavela et al. [55], Barry et al. [56], Zhang [57] and Dev and Pilaftsis[58].
6. ^A detailed discussion of 0νββ decay within LRSMs can be found e.g., in Mohapatra and Senjanovic [19], Mohapatra and Vergados [78], Hirsch et al. [79], Tello et al. [80], Chakrabortty et al. [81], Patra [75], Awasthi et al. [60], Barry and Rodejohann [82], Bhupal Dev et al. [83], Ge et al. [84], Awasthi et al. [85], Huang and Lopez-Pavon [86], Bhupal Dev et al. [87], Borah and Dasgupta [88], Bambhaniya et al. [89], Gu [90], Borah and Dasgupta [91] and Awasthi et al. [92] and for an early study of the effects of light and heavy Majorana neutrinos in neutrinoless double beta decay see in Halprin et al. [93].
7. ^The out of equilibrium condition can be understood as follows. In thermal equilibrium the expectation value of the baryon number can be written as 〈B〉 = Tr[Be−βH]/Tr[e−βH], where β is the inverse temperature. Since particles and anti particles have opposite baryon number, B is odd under C operation, while it is even under P and T operations. Thus, CPT conservation implies a vanishing total baryon number since B is odd and H is even under CPT, unless there is a non-vanishing chemical potential. Assuming a non-vanishing chemical potential implies that the above equation for the expectation value of the baryon number is no longer valid and the baryon number density departs from the equilibrium distribution. This is achieved when the interaction rate is very slow compared to the expansion rate of the universe.
8. ^In passing we would like to note that the other relevant lepton number violating scattering process is doubly phase space suppressed for a temperature below the WR mass scale. Consequently, we will neglect such a process for leptogenesis occurring at T ≲ MWR.
9. ^We ignore any finite temperature effects to simplify the analysis.
References
1. Keung WY, Senjanovic G. Majorana neutrinos and the production of the right-handed charged gauge boson. Phys Rev Lett. (1983) 50:1427. doi: 10.1103/PhysRevLett.50.1427
2. Nemevsek M, Nesti F, Senjanovic G, Zhang Y. First limits on left-right symmetry scale from LHC data. Phys Rev D (2011) 83:115014. arXiv:1103.1627. doi: 10.1103/PhysRevD.83.115014
3. Das SP, Deppisch FF, Kittel O, Valle JWF. Heavy neutrinos and lepton flavour violation in left-right symmetric models at the LHC. Phys Rev D (2012) 86:055006. 055006, arXiv:1206.0256. doi: 10.1103/PhysRevD.86.055006
4. Chen CY, Dev PSB, Mohapatra RN. Probing heavy-light neutrino mixing in left-right seesaw models at the LHC. Phys Rev D (2013) 88:033014. arXiv:1306.2342. doi: 10.1103/PhysRevD.88.033014
5. Mitra M, Ruiz R, Scott DJ, Spannowsky M. Neutrino jets from high-mass WR gauge bosons in TeV-scale left-right symmetric models. Phys Rev D (2016) 94:095016. arXiv:1607.03504. doi: 10.1103/PhysRevD.94.095016
6. Bambhaniya G, Chakrabortty J, Gluza J, Jelinski T, Szafron R. Search for doubly charged Higgs bosons through vector boson fusion at the LHC and beyond. Phys Rev D (2015) 92:015016. arXiv:1504.03999.
7. Dutta B, Eusebi R, Gao Y, Ghosh T, Kamon T. Exploring the doubly charged Higgs boson of the left-right symmetric model using vector boson fusionlike events at the LHC. Phys Rev D (2014) 90:055015. arXiv:1404.0685. doi: 10.1103/PhysRevD.90.055015
8. Dev PSB, Mohapatra RN, Zhang Y. Probing the higgs sector of the minimal left-right symmetric model at future hadron colliders. JHEP (2016) 05:174. doi: 10.1007/JHEP05(2016174
9. Mitra M, Niyogi S, Spannowsky M. Type-II seesaw model and multilepton signatures at hadron colliders. Phys Rev D (2017) 95:035042. doi: 10.1103/PhysRevD.95.035042
10. Weinberg S. Baryon and lepton nonconserving processes. Phys Rev Lett. (1979) 43:1566–70. doi: 10.1103/PhysRevLett.43.1566
11. Wilczek F, Zee A. Operator analysis of nucleon decay. Phys Rev Lett. (1979) 43:1571–3. doi: 10.1103/PhysRevLett.43.1571
12. Weinberg S. Varieties of baryon and lepton nonconservation. Phys Rev D (1980) 22:1694. doi: 10.1103/PhysRevD.22.1694
13. Weldon HA, Zee A. Operator analysis of new physics. Nucl Phys B (1980) 173:269–90. doi: 10.1016/0550-3213(80)90218-7
15. Gell-Mann M, Ramond P, Slansky R. Complex spinors and unified theories. Conf Proc. (1979) C790927:315–21.
17. Mohapatra RN, Senjanović G. Neutrino mass and spontaneous parity violation. Phys Rev Lett. (1980) 44:912. doi: 10.1103/PhysRevLett.44.912
18. Schechter J, Valle JWF. Neutrino masses in SU(2) x U(1) theories. Phys Rev D (1980) 22:2227. doi: 10.1103/PhysRevD.22.2227
19. Mohapatra RN, Senjanovic G. Neutrino masses and mixings in gauge models with spontaneous parity violation. Phys Rev D (1981) 23:165. doi: 10.1103/PhysRevD.23.165
20. Schechter J, Valle JWF. Neutrino decay and spontaneous violation of lepton number. Phys Rev D (1982) 25:774. doi: 10.1103/PhysRevD.25.774
21. Fukugita M, Yanagida T. Baryogenesis without grand unification. Phys Lett B (1986) 174:45–7. doi: 10.1016/0370-2693(86)91126-3
22. Ma E, Sarkar U. Neutrino masses and leptogenesis with heavy Higgs triplets. Phys Rev Lett. (1998) 80:5716–9. doi: 10.1103/PhysRevLett.80.5716
23. Magg M, Wetterich C. Neutrino mass problem and gauge hierarchy. Phys Lett B (1980) 94:61–4. doi: 10.1016/0370-2693(80)90825-4
24. Cheng TP, Li LF. Neutrino masses, mixings and oscillations in SU(2) x U(1) models of electroweak interactions. Phys Rev D (1980) 22:2860. doi: 10.1103/PhysRevD.22.2860
25. Lazarides G, Shafi Q, Wetterich C. Proton lifetime and fermion masses in an SO(10) model. Nucl Phys B (1981) 181:287–300.
26. Lazarides G, Shafi Q. R symmetry in minimal supersymmetry standard model and beyond with several consequences. Phys Rev D (1998) 58:071702.
27. Grimus W, Pfeiffer R, Schwetz T. A Four neutrino model with a Higgs triplet. Eur Phys J C (2000) 13:125–32. doi: 10.1007/s100520000255
28. Hambye T, Ma E, Sarkar U. Supersymmetric triplet Higgs model of neutrino masses and leptogenesis. Nucl Phys B (2001) 602:23–38. doi: 10.1016/S0550-3213(01)00109-2
29. Foot R, Lew H, He XG, Joshi GC. Seesaw neutrino masses induced by a triplet of leptons. Z Phys C (1989) 44:441.
30. Ma E. Pathways to naturally small neutrino masses. Phys Rev Lett. (1998) 81:1171–4. doi: 10.1103/PhysRevLett.81.1171
31. Zee A. A theory of lepton number violation, neutrino majorana mass, and oscillation. Phys Lett B (1980) 93:389. doi: 10.1016/0370-2693(80)90349-4 [Erratum: Phys. Lett.B95,461(1980)].
32. Wolfenstein L. A theoretical pattern for neutrino oscillations. Nucl Phys B (1980) 175:93–6. doi: 10.1016/0550-3213(80)90004-8
35. Ma E. Verifiable radiative seesaw mechanism of neutrino mass and dark matter. Phys Rev D (2006) 73:077301. arXiv:hep-ph/0601225. doi: 10.1103/PhysRevD.73.077301
36. Krauss LM, Nasri S, Trodden M. A model for neutrino masses and dark matter. Phys Rev D (2003) 67:085002. arXiv:hep-ph/0210389. doi: 10.1103/PhysRevD.67.085002
37. Aoki M, Kanemura S, Seto O. Neutrino mass, dark matter and baryon asymmetry via TeV-scale physics without fine-tuning. Phys Rev Lett. (2009) 102:051805. doi: 10.1103/PhysRevLett.102.051805
38. Gustafsson M, No JM, Rivera MA. Predictive model for radiatively induced neutrino masses and mixings with dark matter. Phys Rev Lett. (2013) 110:211802. arXiv:1212.4806. doi: 10.1103/PhysRevLett.110.211802 [Erratum: Phys. Rev. Lett.112: 259902(2014)].
39. Kanemura S, Sugiyama H. Dark matter and a suppression mechanism for neutrino masses in the Higgs triplet model. Phys Rev D (2012) 86:073006. doi: 10.1103/PhysRevD.86.073006
40. Nasri S, Moussa S. Model for small neutrino masses at the TeV scale. Mod Phys Lett A (2002) 17:771–8. doi: 10.1142/S0217732302007119
41. Gu PH, Sarkar U. Radiative neutrino mass, dark matter and leptogenesis. Phys Rev D (2008) 77:105031. doi: 10.1103/PhysRevD.77.105031
42. Kanemura S, Matsui T, Sugiyama H. Loop suppression of dirac neutrino mass in the neutrinophilic two higgs doublet model. Phys Lett B (2013) 727:151–6. arXiv:1305.4521. doi: 10.1016/j.physletb.2013.09.061
43. Bonilla C, Ma E, Peinado E, Valle JWF. Two-loop Dirac neutrino mass and WIMP dark matter. Phys Lett B (2016) 762:214–8. arXiv:1607.03931.
44. Pati JC, Salam A. Is baryon number conserved? Phys Rev Lett. (1973) 31:661–4. doi: 10.1103/PhysRevLett.31.661
45. Pati JC, Salam A. Unified lepton-hadron symmetry and a gauge theory of the basic interactions. Phys Rev D (1973) 8:1240–51. doi: 10.1103/PhysRevD.8.1240
48. Senjanović G, Mohapatra RN. Exact left-right symmetry and spontaneous violation of parity. Phys Rev D (1975) 12:1502. doi: 10.1103/PhysRevD.12.1502
49. Mohapatra RN, Marshak RE. Local B-L symmetry of electroweak interactions, majorana neutrinos and neutron oscillations. Phys Rev Lett. (1980) 44:1316–9. [Erratum: Phys. Rev. Lett.44: 1643(1980)]. doi: 10.1103/PhysRevLett.44.1316
50. Mohapatra RN. Mechanism for understanding small neutrino mass in superstring theories. Phys Rev Lett. (1986) 56:561–3. doi: 10.1103/PhysRevLett.56.561
51. Mohapatra RN, Valle JWF. Neutrino mass and baryon number nonconservation in superstring models. Phys Rev D (1986) 34:1642.
52. Akhmedov EK, Lindner M, Schnapka E, Valle JWF. Left-right symmetry breaking in NJL approach. Phys Lett B (1996) 368:270–80.
53. Malinsky M, Romao JC, Valle JWF. Novel supersymmetric SO(10) seesaw mechanism. Phys Rev Lett. (2005) 95:161801. doi: 10.1103/PhysRevLett.95.161801
54. Chang D, Mohapatra RN, Parida MK. Decoupling parity and SU(2)-R breaking scales: a new approach to left-right symmetric models. Phys Rev Lett. (1984) 52:1072. doi: 10.1103/PhysRevLett.52.1072
55. Gavela MB, Hambye T, Hernandez D, Hernandez P. Minimal flavour seesaw models. JHEP (2009) 09:038. arXiv:0906.1461.
56. Barry J, Rodejohann W, Zhang H. Light sterile neutrinos: models and phenomenology. JHEP (2011) 07:091. arXiv:1105.3911. doi: 10.1007/JHEP07(2011)091
57. Zhang H. Light sterile neutrino in the minimal extended seesaw. Phys Lett B (2012) 714:262–6. doi: 10.1016/j.physletb.2012.06.074
58. Dev PSB, Pilaftsis A. Minimal radiative neutrino mass mechanism for inverse seesaw models. Phys Rev D (2012) 86:113001. doi: 10.1103/PhysRevD.86.113001
59. Dev PSB, Mohapatra RN. TeV scale inverse seesaw in SO(10) and leptonic non-unitarity effects. Phys Rev D (2010) 81:013001. arXiv:0910.3924. doi: 10.1103/PhysRevD.81.013001
60. Awasthi RL, Parida MK, Patra S. Neutrino masses, dominant neutrinoless double beta decay, and observable lepton flavor violation in left-right models and SO(10) grand unification with low mass WR, ZR bosons. JHEP (2013) 1308:122. doi: 10.1007/JHEP08(2013)122
61. Deppisch FF, Graf L, Kulkarni S, Patra S, Rodejohann W, Sahu N, et al. Reconciling the 2 TeV excesses at the LHC in a linear seesaw left-right model. Phys Rev D (2016) 93:013011. doi: 10.1103/PhysRevD.93.013011
62. Davidson A, Wali KC. Universal seesaw mechanism? Phys Rev Lett. (1987) 59:393. doi: 10.1103/PhysRevLett.59.393
63. Rajpoot S. Seesaw masses for quarks and leptons in an ambidextrous electroweak interaction model. Phys Lett B (1987) 191:122–6. doi: 10.1016/0370-2693(87)91332-3
64. Chang D, Mohapatra RN. Small and calculable dirac neutrino mass. Phys Rev Lett. (1987) 58:1600. doi: 10.1103/PhysRevLett.58.1600
65. Babu KS, He XG. Dirac neutrino masses as two loop radiative corrections. Mod Phys Lett A (1989) 4:61. doi: 10.1142/S0217732389000095
66. Babu KS, Mohapatra RN. CP violation in seesaw models of quark masses. Phys Rev Lett. (1989) 62:1079. doi: 10.1103/PhysRevLett.62.1079
67. Babu KS, Mohapatra RN. A solution to the strong CP problem without an axion. Phys Rev D (1990) 41:1286.
68. Balakrishna BS. Fermion mass hierarchy from radiative corrections. Phys Rev Lett. (1988) 60:1602. doi: 10.1103/PhysRevLett.60.1602
69. Balakrishna BS, Mohapatra RN. Radiative fermion masses from new physics at tev scale. Phys Lett B (1989) 216:349–52. doi: 10.1016/0370-2693(89)91129-5
70. Balakrishna BS, Kagan AL, Mohapatra RN. Quark mixings and mass hierarchy from radiative corrections. Phys Lett B (1988) 205:345–52. doi: 10.1016/0370-2693(88)91676-0
71. Mohapatra RN, Zhang Y. TeV scale universal seesaw, vacuum stability and heavy higgs. JHEP (2014) 06:072. arXiv:1401.6701.
72. Dev PSB, Mohapatra RN, Zhang Y. Quark seesaw, vectorlike fermions and diphoton excess. JHEP (2016) 2:186. doi: 10.1007/JHEP02(2016)186
73. Deppisch FF, Hati C, Patra S, Pritimita P, Sarkar U. Implications of the diphoton excess on left?right models and gauge unification. Phys Lett B (2016) 757:223–30. doi: 10.1016/j.physletb.2016.03.081
74. Gabrielli E, Marzola L, Raidal M. Radiative yukawa couplings in the simplest left-right symmetric model. Phys Rev D (2017) 95:035005. doi: 10.1103/PhysRevD.95.035005
75. Patra S. Neutrinoless double beta decay process in left-right symmetric models without scalar bidoublet. Phys Rev D (2013) 87:015002. arXiv:1212.0612.
76. Guadagnoli D, Mohapatra RN, Sung I. Gauged flavor group with left-right symmetry. JHEP (2011) 04:093. arXiv:1103.4170. doi: 10.1007/JHEP04(2011)093
77. Joshi GC, Volkas RR. Extended weak isospin and fermion masses in a unified model. Phys Rev D (1992) 45:1711–9. doi: 10.1103/PhysRevD.45.1711
78. Mohapatra RN, Vergados JD. A new contribution to neutrinoless double beta decay in gauge models. Phys Rev Lett. (1981) 47:1713–6. doi: 10.1103/PhysRevLett.47.1713
79. Hirsch M, Klapdor-Kleingrothaus HV, Panella O. Double beta decay in left-right symmetric models. Phys Lett B (1996) 374:7–12. doi: 10.1016/0370-2693(96)00185-2
80. Tello V, Nemevsek M, Nesti F, Senjanovic G, Vissani F. Left-right symmetry: from LHC to neutrinoless double beta decay. Phys Rev Lett. (2011) 106:151801. doi: 10.1103/PhysRevLett.106.151801
81. Chakrabortty J, Devi HZ, Goswami S, Patra S. Neutrinoless double-β decay in TeV scale Left-Right symmetric models. JHEP (2012) 08:008. arXiv:hep-ph/9602306.
82. Barry J, Rodejohann W. Lepton number and flavour violation in TeV-scale left-right symmetric theories with large left-right mixing. JHEP (2013) 09:153. doi: 10.1007/JHEP09(2013)153
83. Bhupal Dev PS, Goswami S, Mitra M, Rodejohann W. Constraining neutrino mass from neutrinoless double beta decay. Phys Rev D (2013) 88:091301. arXiv:1305.0056.
84. Ge SF, Lindner M, Patra S. New physics effects on neutrinoless double beta decay from right-handed current. JHEP (2015) 10:077. arXiv:1508.07286.
85. Awasthi RL, Dev PSB, Mitra M. Implications of the diboson excess for neutrinoless double beta decay and lepton flavor violation in TeV scale left right symmetric model. Phys Rev D (2016) 93:011701. doi: 10.1103/PhysRevD.93.011701
86. Huang WC, Lopez-Pavon J. On neutrinoless double beta decay in the minimal left-right symmetric model. Eur Phys J C (2014) 74:2853. doi: 10.1140/epjc/s10052-014-2853-z
87. Bhupal Dev PS, Goswami S, Mitra M. TeV scale left-right symmetry and large mixing effects in neutrinoless double beta decay. Phys Rev D (2015) 91:113004. doi: 10.1103/PhysRevD.91.113004
88. Borah D, Dasgupta A. Neutrinoless double beta decay in Type I+II seesaw models. JHEP (2015) 11:208. doi: 10.1007/JHEP11(2015)208
89. Bambhaniya G, Dev PSB, Goswami S, Mitra M. The scalar triplet contribution to lepton flavour violation and neutrinoless double beta decay in left-right symmetric model. JHEP (2016) 04:046. arXiv:1512.00440. doi: 10.1007/JHEP04(2016)046
90. Gu PH. Neutrinoless double beta decay in the left-right symmetric models for linear seesaw. JHEP (2016) 09:152. doi: 10.1007/JHEP09(2016)152
91. Borah D, Dasgupta A. Charged lepton flavour violcxmation and neutrinoless double beta decay in left-right symmetric models with type I+II seesaw. JHEP (2016) 07:022. arXiv:1606.00378.
92. Awasthi RL, Dasgupta A, Mitra M. Limiting the effective mass and new physics parameters from 0νββ. Phys Rev D (2016) 94:073003. arXiv:1607.03835.
93. Halprin A, Petcov ST, Rosen SP. Effects of light and heavy majorana neutrinos in neutrinoless double beta decay. Phys Lett B (1983) 125:335–8. doi: 10.1016/0370-2693(83)91296-0
94. Gonzalez-Garcia MC, Maltoni M, Salvado J, Schwetz T. Global fit to three neutrino mixing: critical look at present precision. JHEP (2012) 12:123. doi: 10.1007/JHEP12(2012)123
95. Meroni A, Petcov ST, Simkovic F. Multiple CP non-conserving mechanisms of (ββ)0ν-decay and nuclei with largely different nuclear matrix elements. JHEP (2013) 02:025. arXiv:1212.1331.
96. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H, et al. Search for Majorana Neutrinos near the Inverted Mass Hierarchy Region with KamLAND-Zen. Phys Rev Lett. (2016) 117:082503. doi: 10.1103/PhysRevLett.117.082503 [Addendum: Phys. Rev. Lett. 117: 109903 (2016)].
97. Agostini M, Bakalyarov AM, Balata M, Barabanov I, Baudis L, Bauer C, et al. Searching for neutrinoless double beta decay with GERDA. In: 15th International Conference on Topics in Astroparticle and Underground Physics (TAUP 2017) (Sudbury, ON). Available online at: http://inspirehep.net/record/1632043/files/arXiv:1710.07776.pdf
98. Albert J. Status and results from the EXO collaboration. EPJ Web Conf. (2014) 66:08001. doi: 10.1051/epjconf/20146608001
99. Mertens S. Status of the KATRIN Experiment and Prospects to Search for keV-mass Sterile Neutrinos in Tritium β-decay. Phys Procedia. (2015) 61:267–73. doi: 10.1016/j.phpro.2014.12.043
100. Ade PAR, Aghanim N, Arnaud M, Ashdown M, Aumont J, Baccigalupi C, et al. Planck 2015 Results. XIII. Cosmological Parameters (2015). 594:A13. arXiv:1502.01589. doi: 10.1051/0004-6361/201525830
101. Sakharov AD. Violation of CP Invariance, c Asymmetry, and Baryon Asymmetry of the Universe. Pisma Zh Eksp Teor Fiz. (1967) 5:32–5.
102. 't Hooft G. Symmetry breaking through bell-jackiw anomalies. Phys Rev Lett. (1976) 37:8–11. doi: 10.1103/PhysRevLett.37.8
103. 't Hooft G. Computation of the quantum effects due to a four-dimensional pseudoparticle. Phys Rev D (1976) 14:3432–50. [Erratum: Phys. Rev. D18, 2199(1978)]. doi: 10.1103/PhysRevD.14.3432
104. Kuzmin VA, Rubakov VA, Shaposhnikov ME. On the anomalous electroweak baryon number nonconservation in the early universe. Phys Lett B (1985) 155:36.
105. Arnold PB, Son D, Yaffe LG. The Hot baryon violation rate is O (alpha-w**5 T**4). Phys Rev D (1997) 55:6264–73. arXiv:hep-ph/9609481
106. Arnold PB, Son DT, Yaffe LG. Effective dynamics of hot, soft nonAbelian gauge fields. Color conductivity and log(1/alpha) effects. Phys Rev D (1999) 59:105020.
107. Bodeker D. On the effective dynamics of soft nonAbelian gauge fields at finite temperature. Phys Lett B (1998) 426:351–60.
109. Khlebnikov SYu, Shaposhnikov ME. The statistical theory of anomalous fermion number nonconservation. Nucl Phys B (1988) 308:885–912.
110. Harvey JA, Turner MS. Cosmological baryon and lepton number in the presence of electroweak fermion number violation. Phys Rev D (1990) 42:3344–9.
111. Sarkar U. Particle Astroparticle Physics. New York, NY: Taylor & Francis (2008). Available online at: http://www.crcpress.com/product/isbn/9781584889311.
112. Langacker P, Peccei RD, Yanagida T. Invisible axions and light neutrinos: are they connected? Mod Phys Lett A (1986) 1:541. doi: 10.1142/S0217732386000683
113. Luty MA. Baryogenesis via leptogenesis. Phys Rev D (1992) 45:455–65. doi: 10.1103/PhysRevD.45.455
114. Murayama H, Suzuki H, Yanagida T, Yokoyama J. Chaotic inflation and baryogenesis by right-handed sneutrinos. Phys Rev Lett. (1993) 70:1912–5. doi: 10.1103/PhysRevLett.70.1912
115. Acker A, Kikuchi H, Ma E, Sarkar U. CP violation and leptogenesis. Phys Rev D (1993) 48:5006–8. arXiv:hep-ph/9305290.
116. Buchmuller W, Plumacher M. Baryon asymmetry and neutrino mixing. Phys Lett B (1996) 389:73–7. arXiv:hep-ph/9608308. doi: 10.1016/S0370-2693(96)01232-4
117. Flanz M, Paschos EA, Sarkar U. Baryogenesis from a lepton asymmetric universe. Phys Lett B (1995) 345:248–52. arXiv:hep-ph/9411366. [Erratum: Phys. Lett. B382, 447 (1996)]. doi: 10.1016/0370-2693(94)01555-Q
118. Flanz M, Paschos EA, Sarkar U, Weiss J. Baryogenesis through mixing of heavy Majorana neutrinos. Phys Lett B (1996) 389:693–9. arXiv:hep-ph/9607310. doi: 10.1016/S0370-2693(96)80011-6
119. Pilaftsis A. CP violation and baryogenesis due to heavy Majorana neutrinos. Phys Rev D (1997) 56:5431–51. arXiv:hep-ph/9707235. doi: 10.1103/PhysRevD.56.5431
120. Pilaftsis A. Resonant CP violation induced by particle mixing in transition amplitudes. Nucl Phys B (1997) 504:61–107. arXiv:hep-ph/9702393. doi: 10.1016/S0550-3213(97)00469-0
121. Roulet E, Covi L, Vissani F. On the CP asymmetries in Majorana neutrino decays. Phys Lett B (1998) 424:101–5. arXiv:hep-ph/9712468. doi: 10.1016/S0370-2693(98)00135-X
122. Buchmuller W, Plumacher M. CP asymmetry in Majorana neutrino decays. Phys Lett B (1998) 431:354–62. arXiv:hep-ph/9710460. doi: 10.1016/S0370-2693(97)01548-7
123. Flanz M, Paschos EA. Further considerations on the CP asymmetry in heavy Majorana neutrino decays. Phys Rev B (1998) 58:113009. arXiv:hep-ph/9805427. doi: 10.1103/PhysRevD.58.113009
124. Hambye T, March-Russell J, West SM. TeV scale resonant leptogenesis from supersymmetry breaking. JHEP (2004) 07:070. arXiv:hep-ph/0403183. doi: 10.1088/1126-6708/2004/07/070
125. Pilaftsis A, Underwood TEJ. Resonant leptogenesis. Nucl Phys B (2004) 692:303–45. arXiv:hep-ph/0309342. doi: 10.1016/j.nuclphysb.2004.05.029
126. Rangarajan R, Mishra H. Leptogenesis with heavy Majorana neutrinos revisited. Phys Rev D (2000) 61:043509. arXiv:hep-ph/9908417.
127. Davidson S, Ibarra A. A Lower bound on the right-handed neutrino mass from leptogenesis. Phys Lett B (2002) 535:25–32. arXiv:hep-ph/0202239. doi: 10.1016/S0370-2693(02)01735-5
128. Pilaftsis A, Underwood TEJ. Electroweak-scale resonant leptogenesis. Phys Rev D (2005) 72:113001. arXiv:hep-ph/0506107. doi: 10.1103/PhysRevD.72.113001
129. Bhupal Dev PS, Millington P, Pilaftsis A, Teresi D. Flavour covariant transport equations: an application to resonant leptogenesis. Nucl Phys B (2014) 886:569–664. arXiv:1404.1003. doi: 10.1016/j.nuclphysb.2014.06.020
130. Hambye T, Senjanovic G. Consequences of triplet seesaw for leptogenesis. Phys Lett B (2004) 582:73–81. arXiv:hep-ph/0307237. doi: 10.1016/j.physletb.2003.11.061
131. Hallgren T, Konstandin T, Ohlsson T. Triplet leptogenesis in left-right symmetric seesaw models. JCAP (2008) 0801:014. arXiv:0710.2408.
132. Lavignac S, Schmauch B. Flavour always matters in scalar triplet leptogenesis. JHEP (2015) 05:124. arXiv:1503.00629. doi: 10.1007/JHEP05(2015)124
133. Hambye T, Raidal M, Strumia A. Efficiency and maximal CP-asymmetry of scalar triplet leptogenesis. Phys Lett B (2006) 632:667–74. arXiv:hep-ph/0510008. doi: 10.1016/j.physletb.2005.11.007
134. Strumia A. Sommerfeld corrections to type-II and III leptogenesis. Nucl Phys B (2009) 809:308–17. arXiv:0806.1630. doi: 10.1016/j.nuclphysb.2008.10.007
135. Aristizabal Sierra D, Dhen M, Hambye T. Scalar triplet flavored leptogenesis: a systematic approach. JCAP (2014) 1408:003. arXiv:1401.4347. doi: 10.1088/1475-7516/2014/08/003
136. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, et al. Search for heavy neutrinos and W bosons with right-handed couplings in proton-proton collisions at . Eur Phys J C (2014) 74:3149. arXiv:1407.3683. doi: 10.1140/epjc/s10052-014-3149-z
137. Deppisch FF, Gonzalo TE, Patra S, Sahu N, Sarkar U. Signal of right-handed charged gauge bosons at the LHC? Phys Rev D (2014) 90:053014. arXiv:1407.5384. doi: 10.1103/PhysRevD.90.053014
138. Deppisch FF, Gonzalo TE, Patra S, Sahu N, Sarkar U. Double beta decay, lepton flavor violation, and collider signatures of left-right symmetric models with spontaneous D-parity breaking. Phys Rev D (2015) 91:015018. arXiv:1410.6427. doi: 10.1103/PhysRevD.91.015018
139. Gluza J, Jelinski T. Heavy neutrinos and the pp?lljj CMS data. Phys Lett B (2015) 748:125–31. arXiv:1504.05568. doi: 10.1016/j.physletb.2015.06.077
140. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Search for high-mass diboson resonances with boson-tagged jets in proton-proton collisions at TeV with the ATLAS detector. JHEP (2015) 12:055. arXiv:1506.00962. doi: 10.1007/JHEP12(2015)055
141. Brehmer J, Hewett J, Kopp J, Rizzo T, Tattersall J. Symmetry restored in dibosons at the LHC? JHEP (2015) 10:182. arXiv:1507.00013.
142. Dobrescu BA, Liu Z. W' Boson near 2 TeV: Predictions for Run 2 of the LHC. Phys Rev Lett. (2015) 115:211802. arXiv:1506.06736. doi: 10.1103/PhysRevLett.115.211802
143. Bhupal Dev PS, Mohapatra RN. Unified explanation of the eejj, diboson and dijet resonances at the LHC. Phys Rev Lett. (2015) 115:181803. doi: 10.1103/PhysRevLett.115.181803
144. Das A, Nagata N, Okada N. Testing the 2-TeV Resonance with Trileptons. JHEP (2016) 03:049. arXiv:1601.05079. doi: 10.1007/JHEP03(2016)049
145. Ma E, Sarkar S, Sarkar U. Scale of SU(2)(R) symmetry breaking and leptogenesis. Phys Lett B (1999) 458:73–8. arXiv:hep-ph/9812276.
146. Deppisch FF, Harz J, Hirsch M. Falsifying high-scale leptogenesis at the LHC. Phys Rev Lett. (2014) 112:221601. doi: 10.1103/PhysRevLett.112.221601
147. Deppisch FF, Harz J, Hirsch M, Huang WC, Pas H. Falsifying high-scale baryogenesis with neutrinoless double beta decay and lepton flavor violation. Phys Rev D (2015) 92:036005. doi: 10.1103/PhysRevD.92.036005
148. Frere JM, Hambye T, Vertongen G. Is leptogenesis falsifiable at LHC? JHEP (2009) 01:051. arXiv:0806.0841.
149. Bhupal Dev PS, Lee CH, Mohapatra RN. TeV scale lepton number violation and baryogenesis. J Phys Conf Ser. (2015) 631:012007. doi: 10.1088/1742-6596/631/1/012007
150. Bhupal Dev PS, Lee CH, Mohapatra RN. Leptogenesis constraints on the mass of right-handed gauge bosons. Phys Rev D (2014) 90:095012. arXiv:1408.2820.
151. Dhuria M, Hati C, Rangarajan R, Sarkar U. The eejj Excess Signal at the LHC and Constraints on Leptogenesis. JCAP (2015) 1509:035. arXiv:1502.01695. doi: 10.1088/1475-7516/2015/09/035
152. Dhuria M, Hati C, Rangarajan R, Sarkar U. Falsifying leptogenesis for a TeV scale at the LHC. Phys Rev D (2015) 92:031701. arXiv:1503.07198.
153. Doi M. Lepton number violating e- W+ –> e+ W- and e- e- –> W- W- processes in the left-right gauge model. Prog Theor Phys. (1999) 101:639–60. doi: 10.1143/PTP.101.639
154. Olive KA, Agashe K, Amsler C, Antonelli M, Arguin JF, Asner DM, et al. Review of particle physics. Chin Phys C (2014) 38:090001.
155. Mohapatra RN, Marshak RE. Phenomenology of neutron oscillations. Phys Lett B (1980) 94:183–6. doi: 10.1016/0370-2693(80)90853-9 [Erratum: Phys. Lett. B96, 444 (1980)].
156. Phillips DG II, Snow WM, Babu K, Banerjee S, Baxter DV, Berezhiani Z, et al. Neutron-antineutron oscillations: theoretical status and experimental prospects. Phys Rept. (2016) 612:1–45. doi: 10.1016/j.physrep.2015.11.001
157. Pati JC, Salam A, Sarkar U. Delta B = - Delta L, neutron —> e- pi+, e- K+, mu- pi+ and mu- K+ DECAY modes in SU(2)-L X SU(2)-R X SU(4)-C or SO(10). Phys Lett B (1983) 133:330–6.
Keywords: left-right symmetry, neutrino mass, leptogenesis, neutrinoless double beta decay, low scale seesaw
Citation: Hati C, Patra S, Pritimita P and Sarkar U (2018) Neutrino Masses and Leptogenesis in Left–Right Symmetric Models: A Review From a Model Building Perspective. Front. Phys. 6:19. doi: 10.3389/fphy.2018.00019
Received: 17 October 2017; Accepted: 14 February 2018;
Published: 06 March 2018.
Edited by:
Alexander Merle, Max Planck Institute for Physics (MPG), GermanyReviewed by:
Eduardo Peinado, Instituto de Física, Universidad Nacional Autónoma de México, MexicoBhupal Dev, Washington University in St. Louis, United States
Copyright © 2018 Hati, Patra, Pritimita and Sarkar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chandan Hati, Y2hhbmRhbi5oYXRpQGNsZXJtb250LmluMnAzLmZy
 Chandan Hati
Chandan Hati Sudhanwa Patra2
Sudhanwa Patra2