Lepton Number Violation: Seesaw Models and Their Collider Tests

The Majorana nature of neutrinos is strongly motivated from the theoretical and phenomenological point of view. A plethora of neutrino mass models, known collectively as Seesaw models, exist that could generate both a viable neutrino mass spectrum and mixing pattern. They can also lead to rich, new phenomenology, including lepton number non-conservation as well as new particles, that may be observable at collider experiments. It is therefore vital to search for such new phenomena and the mass scale associated with neutrino mass generation at high energy colliders. In this review, we consider a number of representative Seesaw scenarios as phenomenological benchmarks, including the characteristic Type I, II, and III Seesaw mechanisms, their extensions and hybridizations, as well as radiative constructions. We present new and updated predictions for analyses featuring lepton number violation and expected coverage in the theory parameter space at current and future colliders. We emphasize new production and decay channels, their phenomenological relevance and treatment across different facilities in e⁺e⁻, e⁻p, and pp collisions, as well as the available Monte Carlo tools available for studying Seesaw partners in collider environments.

1. Introduction

Neutrino flavor oscillation experiments from astrophysical and terrestrial sources provide overwhelming evidence that neutrinos have small but nonzero masses. Current observations paint a picture consistent with a mixing structure parameterized by the 3 × 3 Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix [1–3] with at least two massive neutrinos. This is contrary to the Standard Model of particle physics (SM) [4], which allows three massless neutrinos and hence no flavor oscillations. Consequently, to accommodate these observations, the SM must [5] be extended to a more complete theory by new degrees of freedom.

One could of course introduce right-handed (RH) neutrino states (ν_R) and construct Dirac mass terms, $m_D\overline{{\nu }_L}{\nu }_R$, in the same fashion as for all the other elementary fermions in the SM. However, in this minimal construction, the new states do not carry any SM gauge charges, and thus these “sterile neutrinos” have the capacity to be Majorana fermions [6]. The most significant consequence of this would be the existence of the RH Majorana mass term $M_R\overline{{({\nu }_R)}^c}{\nu }_R$ and the explicit violation of lepton number (L). In light of this prospect, a grand frontier opens for theoretical model-building with rich and new phenomenology at the collider energy scales, which we will review in this article.

Generically, if we integrate out the new states, presumably much heavier than the electroweak (EW) scale, the new physics may be parameterized at leading order through the dimension-5 lepton number violating operator [7], the so-called “Weinberg operator,”

$\begin{array}{ll}{{L}}_5=\frac{\alpha }{\Lambda } (LH)(LH)\stackrel{\text{EWSB}}{\to }{{L}}_5\ni \frac{\alpha v_0^2}{2\Lambda }\overline{{({\nu }_L)}^c}{\nu }_L,& (1.1)\end{array}$

where L and H are, respectively, the SM left-handed (LH) lepton doublet and Higgs doublet, with vacuum expectation value (vev) v₀ ≈ 246 GeV. After electroweak (EW) symmetry breaking (EWSB), ${{L}}_5$ generates a Majorana mass term for neutrinos. One significance of Equation (1.1) is the fact that its ultraviolet (UV) completions are severely restricted. For example: extending the SM field content minimally, i.e., by only a single SM multiplet, permits only three [5] tree-level completions of Equation (1.1), a set of constructions famously known as the Type I [8–14], Type II [14–18], and Type III [19] Seesaw mechanisms. These minimal mechanisms can be summarized with the following:

Minimal Type I Seesaw [8–14]: In the minimal Type I Seesaw, one hypothesizes the existence of a right-handed (RH) neutrino ν_R, which transforms as a singlet, i.e., (1, 1, 0), under the SM gauge group SU(3)_c⊗SU(2)_L⊗U(1)_Y, that possesses a RH Majorana mass M_νR and interacts with a single generation of SM leptons through a Yukawa coupling y_ν. After mass mixing and assuming M_νR ≫ y_νv₀, the light neutrino mass eigenvalue m_ν is given by $m_{\nu }~y_{\nu }^2{v}_0^2/M_{{\nu }_R}$, If y_ν ≃ 1, to obtain a light neutrino mass of order an eV, M_νR is required to be of order 10¹⁴−10¹⁵ GeV. M_νR can be made much lower though by balancing against a correspondingly lower y_ν.

Minimal Type II Seesaw [14–18]: The minimal Type II Seesaw features the introduction of a Higgs field Δ with mass M_Δ in a triplet representation of SU(2)_L and transforms as (1, 3, 2) under the SM gauge group. In this mechanism, light neutrino masses are given by LH Majorana masses m_ν ≈ Y_νv_Δ, where v_Δ is the vev of the neutral component of the new scalar triplet and Y_ν is the corresponding Yukawa coupling. Due to mixing between the SM Higgs doublet and the new scalar triplet via a dimensionful parameter μ, EWSB leads to a relation $v_{\Delta }~\mu v_0^2/M_{\Delta }^2$. In this case the new scale Λ is replaced by $M_{\Delta }^2/\mu$. With Y_ν ≈ 1 and μ ~ M_Δ, the scale is also 10¹⁴−10¹⁵ GeV. Again, M_Δ can be of TeV scale if Y_ν is small or μ ≪ M_Δ. It is noteworthy that in the Type II Seesaw, no RH neutrinos are needed to explain the observed neutrino masses and mixing.

Minimal Type III Seesaw [19]: The minimal Type III Seesaw is similar to the other two cases in that one introduces the fermionic multiplet Σ_L that is a triplet (adjoint representation) under SU(2)_L and transforms as (1, 3, 0) under the SM gauge group. The resulting mass matrix for neutrinos has the same form as in Type I Seesaw, but in addition features heavy leptons that are electrically charged. The new physics scale Λ in Equation (1.1) is replaced by the mass of the leptons Σ_L, which can also be as low as a TeV if balanced with a small Yukawa coupling.

However, to fully reproduce oscillation data, at least two of the three known neutrinos need nonzero masses. This requires a nontrivial Yukawa coupling matrix for neutrinos if appealing to any of the aforementioned Seesaws mechanisms, and, if invoking the Type I or III Seesaws, extending the SM by at least two generations of multiplets [20], which need not be in the same SM gauge representation. In light of this, one sees that Weinberg's assumption of a high-scale Seesaw [7] is not necessary to generate tiny neutrino masses in connection with lepton (L) number violation. For example: the so-called Inverse [21–24] or Linear [25, 26] variants of the Type I and III Seesaw models, their generic extensions as well as hybridizations, i.e., the combination of two or more Seesaw mechanisms, can naturally lead to mass scales associated with neutrino mass-generation accessible at present-day experiments, and in particular, collider experiments. A qualitative feature of these low-scale Seesaws is that light neutrino masses are proportional to the scale of L violation, as opposed to inversely related as in high-scale Seesaws [27].

The Weinberg operator in Equation (1.1) is the lowest order and simplest parameterization of neutrino mass generation using only the SM particle spectrum and its gauge symmetries. Beyond its tree-level realizations, however, neutrino Majorana masses may alternatively be generated radiatively. Suppression by loop factors may provide a partial explanation for the smallness of neutrino masses and again allow much lower mass scales associated with neutrino mass-generation. The first of such models was proposed at one-loop in Zee [28] and Hall and Suzuki [29], at two-loop order in Cheng and Li [16], Zee [30], and Babu [31], and at three-loop order in Krauss et al. [32]. A key feature of radiative neutrino mass models is the absence of tree-level contributions to neutrino masses either because there the necessary particles, such as SM singlet fermion as in Type I Seesaw, are not present or because relevant couplings are forbidden by additional symmetries. Consequently, it is necessary that the new field multiplets run in the loops that generate neutrino masses.

As observing lepton number violation would imply the existence of Majorana masses for neutrinos [33–35], confirming the existence of this new mass scale would, in addition, verify the presence of a Seesaw mechanism. To this end, there have been on-going efforts in several directions, most notably the neutrinoless double beta (0νββ)-decay experiments, both current [36–39] and upcoming [40–42], as well as proposed general purpose fixed-target facilities [43, 44]. Complementary to this are on-going searches for lepton number violating processes at collider experiments, which focus broadly on rare meson decays [45–47], heavy neutral fermions in Type I-like models [48–52], heavy bosons in Type II-like models [53–55], heavy charged leptons in Type III-like models [56–58], and lepton number violating contact interactions [59, 60]. Furthermore, accurate measurements of the PMNS matrix elements and stringent limits on the neutrino masses themselves provide crucial information and knowledge of lepton flavor mixing that could shed light on the construction of Seesaw models.

In this context, we present a review of searches for lepton number violation at current and future collider experiments. Along with the current bounds from the experiments at LEP, Belle, LHCb and ATLAS/CMS at 8 and 13 TeV, we present studies for the 13 and 14 TeV LHC. Where available, we also include results for a future 100 TeV hadron collider, an ep collider (LHeC), and a future high-energy e⁺e⁻ collider. We consider a number of tree- and loop-level Seesaw models, including, as phenomenological benchmarks, the canonical Type I, II, and III Seesaw mechanisms, their extensions and hybridizations, and radiative Seesaw formulations in pp, ep, and ee collisions. We note that the classification of collider signatures based on the canonical Seesaws is actually highly suitable, as the same underlying extended and hybrid Seesaw mechanism can be molded to produce wildly varying collider predictions.

We do not attempt to cover the full aspects of UV-complete models for each type. This review is only limited to a selective, but representative, presentation of tests of Seesaw models at collider experiments. For complementary reviews, we refer readers to Gluza [61], Barger et al. [62], Mohapatra and Smirnov [63], Rodejohann [64], Chen and Huang [65], Atre et al. [66], Deppisch et al. [67] and references therein.

This review is organized according to the following: In section 2 we first show the PMNS matrix and summarize the mixing and mass-difference parameters from neutrino oscillation data. With those constraints, we also show the allowed mass spectra for the three massive neutrino scheme. Our presentation is agnostic, phenomenological, and categorized according to collider signature, i.e., according to the presence of Majorana neutrinos (Type I) as in section 3, doubly charged scalars (Type II) as in section 4, new heavy charged/neutral leptons (Type III) as in section 5, and new Higgs, diquarks and leptoquarks in section 6. Particular focus is given to state-of-the-art computations, newly available Monte Carlo tools, and new collider signatures that offer expanded coverage of Seesaw parameter spaces at current and future colliders. Finally in section 7 we summarize our main results.

2. Neutrino Mass and Oscillation Parameters

In order to provide a general guidance for model construction and collider searches, we first summarize the neutrino mass and mixing parameters in light of oscillation data. Neutrino mixing can be parameterized by the PMNS matrix [1–3] as

$\begin{array}{l}{U}_{PMNS}=\left(\begin{array}{ccc}1& 0& 0\\ 0& c_{23}& s_{23}\\ 0& -s_{23}& c_{23}\end{array}\right)\left(\begin{array}{ccc}{c}_{13}& 0& e^{-i\delta }{s}_{13}\\ 0& 1& 0\\ -e^{i\delta }{s}_{13}& 0& c_{13}\end{array}\right)\left(\begin{array}{ccc}{c}_{12}& s_{12}& 0\\ -s_{12}& c_{12}& 0\\ 0& 0& 1\end{array}\right)\\ \text{diag}(e^{i{\Phi }_1/2},1,e^{i{\Phi }_2/2})& (2.1)\end{array}$

$\begin{array}{l}=\left(\begin{array}{lll}{c}_{12}{c}_{13}\hfill & c_{13}{s}_{12}\hfill & e^{-\text{i}\delta }{s}_{13}\hfill \\ -c_{12}{s}_{13}{s}_{23}{e}^{\text{i}\delta }-c_{23}{s}_{12}\hfill & c_{12}{c}_{23}-e^{\text{i}\delta }{s}_{12}{s}_{13}{s}_{23}\hfill & c_{13}{s}_{23}\hfill \\ s_{12}{s}_{23}-e^{\text{i}\delta }{c}_{12}{c}_{23}{s}_{13}\hfill & -c_{23}{s}_{12}{s}_{13}{e}^{\text{i}\delta }-c_{12}{s}_{23}\hfill & c_{13}{c}_{23}\hfill \end{array}\right)\\ \times \text{diag}(e^{i{\Phi }_1/2},1,e^{i{\Phi }_2/2}),& (2.2)\end{array}$

where s_ij ≡ sin θ_ij, c_ij ≡cosθ_ij, 0 ≤ θ_ij ≤ π/2, and 0 ≤ δ, Φ_i ≤ 2π, with δ being the Dirac CP phase and Φ_i the Majorana phases. While the PMNS is a well-defined 3 × 3 unitary matrix, throughout this review, we use the term generically to describe the 3 × 3 active-light mixing that may not, in general, be unitary.

The neutrino mixing matrix is very different from the quark-sector Cabbibo-Kobayashi-Maskawa (CKM) matrix, in that most of the PMNS mixing angles are large whereas CKM angles are small-to-negligible. In recent years, several reactor experiments, such as Daya Bay [68], Double Chooz [69], and RENO [70] have reported non-zero measurements of θ₁₃ by searching for the disappearance of anti-electron neutrinos. Among these reactor experiments, Daya Bay gives the most conclusive result with ${sin}^{2}2{\theta }_{13}\approx 0.084$ or ${\theta }_{13}\approx 8.4^{°}$ [71, 72], the smallest entry of the PMNS matrix. More recently, there have been reports on indications of a non-zero Dirac CP phase, with δ ≈ 3π/2 [73–75]. However, it cannot presently be excluded that evidence for such a large Dirac phase may instead be evidence for sterile neutrinos or new neutral currents [76–79].

Neutrino oscillation experiments can help to extract the size of the mass-squared splitting between three neutrino mass eigenstates. The sign of $\Delta m_{31}^2=m_3^2-m_1^2$, however, still remains unknown at this time. It can be either positive, commonly referred as the Normal Hierarchy (NH), or negative and referred to as the Inverted Hierarchy (IH). The terms Normal Ordering (NO) and Inverted Ordering (IO) are also often used in the literature in lieu of NH and IH, respectively. Taking into account the reactor data from the antineutrino disappearance experiments mentioned above together with other disappearance and appearance measurement, the latest global fit of the neutrino masses and mixing parameters from the NuFit collaboration [72], are listed in Table 1 for NH (left) and IH (center). The tightest constraint on the sum of neutrino masses comes from cosmological data. Combining Planck+WMAP+highL+BAO data, this yields at 95% confidence level (CL) [80]

$\begin{array}{ll}{\displaystyle \sum _{i=1}^3{m}_i}<0.230\text{eV}.& (2.3)\end{array}$

TABLE 1

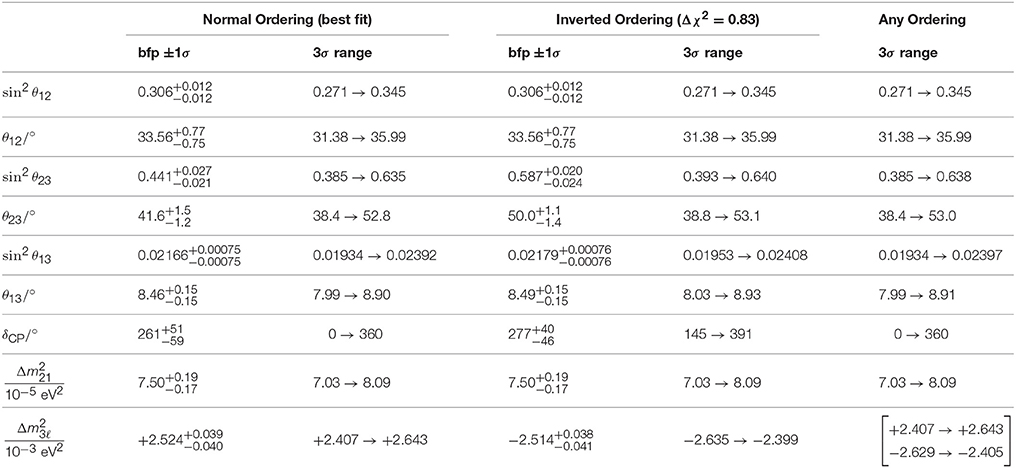
Table 1. Three-neutrino oscillation fit based as obtained by the NuFit collaboration, taken from Esteban et al. [72], where $\Delta m_{3\ell }^2=\Delta m_{31}^2>0$ for NO (or NH) and $\Delta m_{3\ell }^2=\Delta m_{32}^2<0$ for IO (or IH).

Given this and the measured neutrino mass splittings, we show in Figure 1 the three active neutrino mass spectra as a function of the lowest neutrino mass in (a) NH and (b) IH. With the potential sensitivity of the sum of neutrino masses being close to 0.1eV in the near future (5–7 years) [81], upcoming cosmological probes will not be able to settle the issue of the neutrino mass hierarchy. However, the improved measurement ~0.01eV over a longer term (7 − 15 years) [81, 82] would be sensitive to determine the absolute mass scale of a heavier neutrino spectrum. In addition, there are multiple proposed experiments aiming to determine the neutrino mass hierarchy. The Deep Underground Neutrino Experiment (DUNE) will detect neutrino beams from the Long Baseline Neutrino Facility (LBNF), and probes the CP-phase and the mass hierarchy. With a baseline of 1,300 km, DUNE is able to determine the mass hierarchy with at least 5σ significance [83]. The Jiangmen Underground Neutrino Observatory (JUNO) plans to precisely measure the reactor electron antineutrinos and improve the accuracy of $\Delta m_{21}^2$, $\Delta m_{32}^2$ and ${sin}^2{\theta }_{12}$ to 1% level [84]. The Hyper-Kamiokande (Hyper-K) experiment as an update of T2K can measure the precision of δ to be 7° − 21° and reach 3 (5)σ significance of mass hierarchy determination for 5 (10) years exposure [85]. Finally, the Karlsruhe Tritium Neutrino experiment (KATRIN) as a tritium β decay experiment aims to measure the effective electron-neutrino mass with the sensitivity of sub-eV [86].

FIGURE 1

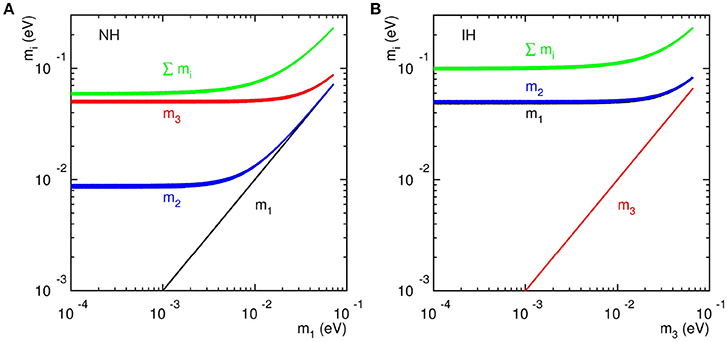
Figure 1. The three active neutrino mass spectra vs. the lowest neutrino mass for (A) NH and (B) IH.

3. The Type I Seesaw and Lepton Number Violation at Colliders

We begin our presentation of collider searches for lepton number violation in the context of Type I Seesaw models. After describing the canonical Type I mechanism [8–12] and its phenomenological decoupling at collider scales in section 3.1.1, we discuss various representative, low-scale models that incorporate the Type I mechanism and its extensions. We then present collider searches for lepton number violation mediated by Majorana neutrinos (N), which is the characteristic feature of Type I-based scenarios, in section 3.2. This is further categorized according to associated phenomena of increasing complexity: N production via massive Abelian gauge bosons is reviewed in section 3.2.4, via massive non-Abelian gauge bosons in section 3.2.5, and via dimension-six operators in section 3.2.6.

3.1. Type I Seesaw Models

3.1.1. The Canonical Type I Seesaw Mechanism

In the canonical Type I Seesaw mechanism one hypothesizes a single RH neutral leptonic state, N_R ~ (1, 1, 0), in addition to the SM matter content. However, reproducing neutrino oscillation data requires more degrees of freedom. Therefore, for our purposes, we assume i = 1, …, 3 LH states and j = 1, …, n RH states. Following the notation of Atre et al. [66] and Han et al. [87], the full theory is

$\begin{array}{ll}{{L}}_{\text{Type} \text{I}}={{L}}_{\text{SM}}+{{L}}_{N \text{Kin}}+{{L}}_N,& (3.1)\end{array}$

where ${{L}}_{\text{SM}}$ is the SM Lagrangian, ${{L}}_{N\text{ Kin}}$ is N_R's kinetic term, and its interactions and mass are

$\begin{array}{ll}{{L}}_N=-\overline{L}{Y}_{\nu }^D\tilde{H}{N}_R-\frac{1}{2}{\overline{(N^c)}}_L{M}_R{N}_R+\text{H}\text{.c}\mathrm{..}& (3.2)\end{array}$

L and H are the SM LH lepton and Higgs doublets, respectively, and $\tilde{H}=i{\sigma }_2{H}^{*}$. Once H settles on the vev $\langle H\rangle =v_0/\sqrt{2}$, neutrinos acquire Dirac masses $m_D=Y_{\nu }^D{v}_0/\sqrt{2}$ and we have

$\begin{array}{l}{{L}}_N\ni -\frac{1}{2}\left({\overline{\nu }}_L{m}_D{N}_R+{\overline{(N^c)}}_L{m}_D^T{({\nu }^c)}_R+{\overline{(N^c)}}_L{M}_R{N}_R\right)\\ +\text{H}\text{.c}\text{.}& (3.3)\end{array}$

After introducing a unitary transformation into m (m′) light (heavy) mass eigenstates,

$\begin{array}{ll}{\left(\begin{array}{c}\nu \\ N^c\end{array}\right)}_L=\mathbb{N}{\left(\begin{array}{c}{\nu }_m\\ N_{m^{\prime }}^c\end{array}\right)}_L,\mathbb{N}=\left(\begin{array}{c}UV\\ XY\end{array}\right),& (3.4)\end{array}$

one obtains the diagonalized mass matrix for neutrinos

$\begin{array}{ll}{\mathbb{N}}^{†}\left(\begin{array}{cc}0& m_D\\ m_D^T& M\end{array}\right){\mathbb{N}}^{\ast }=\left(\begin{array}{cc}{m}_{\nu }& 0\\ 0& M_N\end{array}\right),& (3.5)\end{array}$

with mass eigenvalues m_ν = diag(m₁, m₂, m₃) and $M_N=diag(M_1,\cdots ,M_{m^{\prime }})$. In the limit m_D ≪ M_R, the light (m_ν) and heavy (M_N) neutrino masses are

$\begin{array}{ll}{m}_{\nu }\approx -m_D{M}_R^{-1}{m}_D^T \text{and} M_N\approx M_R.& (3.6)\end{array}$

The mixing elements typically scale like

$\begin{array}{ll}U{U}^{†}\approx I-m_{\nu }{M}_N^{-1},V{V}^{†}\approx m_{\nu }{M}_N^{-1},& (3.7)\end{array}$

with the unitarity condition UU^† + VV^† = I. With another matrix U_ℓ diagonalizing the charged lepton mass matrix, we have the approximate neutrino mass mixing matrix U_PMNS and the matrix V_ℓN, which transits heavy neutrinos to charged leptons, and are given by

$\begin{array}{ll}\begin{array}{l}{U}_{\ell }^{†}U\equiv U_{PMNS},U_{\ell }^{†}V\equiv V_{\ell N}, \text{and}\\ U_{PMNS}{U}_{PMNS}^{†}+V_{\ell N}{V}_{\ell N}^{†}=I.\end{array}& (3.8)\end{array}$

The decomposition of active neutrino states into a general number of massive eigenstates is then given by Atre et al. [66] and Han et al. [87], ${\nu }_{\ell }=\sum _{m=1}^3{U}_{\ell m}{\nu }_m+\sum _{m^{\prime }=1}^n{V}_{\ell m^{\prime }}{N}_{m^{\prime }}^c.$ From this, the SM EW boson couplings to heavy mass eigenstates (in the mixed mass-flavor basis) are

$\begin{array}{ll}\begin{array}{l}{{L}}_{\text{Int}.}=-\frac{g}{\sqrt{2}}{W}_{\mu }^{+}{\displaystyle \sum _{\ell =e}^{\tau }\left({\displaystyle \sum _{m=1}^3 }\overline{{\nu }_m} U_{\ell m}^{*}+{\displaystyle \sum _{m^{\prime }=1}^n\overline{N_{m^{\prime }}^c}} V_{\ell N_{m^{\prime }}}^{*}\right)}{\gamma }^{\mu }{P}_L{\ell }^{-}\\ -\frac{g}{2\cos {\theta }_W}{Z}_{\mu }{\displaystyle \sum _{\ell =e}^{\tau }\left({\displaystyle \sum _{m=1}^3 }\overline{{\nu }_m} U_{\ell m}^{*}+{\displaystyle \sum _{m^{\prime }=1}^n\overline{N_{m^{\prime }}^c}} V_{\ell N_{m^{\prime }}}^{*}\right)}{\gamma }^{\mu }{P}_L{\nu }_{\ell }\\ -\frac{g}{2M_W}h{\displaystyle \sum _{\ell =e}^{\tau }{\displaystyle \sum _{m^{\prime }=1}^n }}{m}_{N_{m^{\prime }}}\overline{N_{m^{\prime }}^c} V_{\ell N_{m^{\prime }}}^{*}{P}_L{\nu }_{\ell }+\text{H}\text{.c}\text{.}\end{array}& (3.9)\end{array}$

There is a particular utility of using this mixed mass-flavor basis in collider searches for heavy neutrinos. Empirically, $\left|V_{\ell N_{m^{\prime }}}\right|\lesssim 10^{-2}$ [88–91], which means pair production of $N_{m^{\prime }}$ via EW processes is suppressed by $|V_{\ell N_{m^{\prime }}}{|}^2\lesssim 10^{-4}$ relative to single production of $N_{m^{\prime }}$. Moreover, in collider processes involving ${\nu }_m-N_{m^{\prime }}$ vertices, one sums over ν_m either because it is an internal particle or an undetected external state. This summation effectively undoes the decomposition of one neutrino interaction state for neutral current vertices, resulting in the basis above. In phenomenological analyses, it is common practice to consider in only the lightest heavy neutrino mass eigenstate, i.e., $N_{m^{\prime }=4}$, to reduce the effective number of independent model parameters. In such cases, the mass eigenstate is denoted simply as N and one reports sensitivity on the associated mixing element, labeled correspondingly as |V_ℓN| or |V_ℓ4|, which are equivalent to $\left|V_{\ell N_{m^{\prime }=4}}\right|.$ Throughout this text, the |V_ℓN| notation is adopted where possible.

From Equation (3.5), an important relation among neutrino masses can be derived. Namely, that

$\begin{array}{ll}{U}_{PMNS}^{\ast }{m}_{\nu }{U}_{PMNS}^{†}+V_{\ell N}^{\ast }{M}_N{V}_{\ell N}^{†}=0.& (3.10)\end{array}$

Here the masses and mixing of the light neutrinos in the first term are measurable from the oscillation experiments, and the second term contains the masses and mixing of the new heavy neutrinos. We now consider a simple case: degenerate heavy neutrinos with mass $M_N=diag(M_1,\cdots ,M_{m^{\prime }})=M_N{𝕀}_{m^{\prime }}$. Using this assumption, we obtain from Equation (3.10),

$\begin{array}{ll}{M}_N{\displaystyle \sum _N{(V_{\ell N}^{\ast })}^2}={(U_{PMNS}^{\ast }{m}_{\nu }{U}_{PMNS}^{†})}_{\ell \ell }.& (3.11)\end{array}$

Using the oscillation data in Table 1 as inputs¹, we display in Figure 2 the normalized mixing of each lepton flavor in this scenario². Interestingly, one can see the characteristic features:

$\begin{array}{ll}{\displaystyle \sum _N|}{V}_{eN}{|}^2\ll {\displaystyle {\sum }_N|V_{\mu N}{|}^2},{\displaystyle {\sum }_N|V_{\tau N}{|}^2} \text{for}\text{NH},& (3.12)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _N|V_{eN}{|}^2}>{\displaystyle {\sum }_N|V_{\mu N}{|}^2},{\displaystyle {\sum }_N|V_{\tau N}{|}^2} \text{for}\text{IH}.& (3.13)\end{array}$

As shown in Figure 3, a corresponding pattern also emerges in the branching fraction³ of the degenerate neutrinos decaying into charged leptons plus a W boson,

$\begin{array}{ll}\begin{array}{l}\text{BR}({\mu }^{\pm }{W}^{\mp }),\text{BR}({\tau }^{\pm }{W}^{\mp })~(20-30)\%\gg \text{BR}(e^{\pm }{W}^{\mp })\\ ~(3-4)\%\text{for}\text{NH},\end{array}& (3.14)\end{array}$

$\begin{array}{ll}\begin{array}{l}\text{BR}(e^{\pm }{W}^{\mp })~27\%>\text{BR}({\mu }^{\pm }{W}^{\mp }),\text{BR}({\tau }^{\pm }{W}^{\mp })\\ ~(10-20)\%\text{for}\text{IH},\end{array}& (3.15)\end{array}$

with $\text{BR}({\ell }^{\pm }{W}^{\mp })=\text{BR}(N_i\to {\ell }^{+}{W}^{-}+{\ell }^{-}{W}^{+})$. These patterns show a rather general feature that ratios of Seesaw partner observables, e.g., cross sections and branching fractions, encode information on light neutrinos, such as their mass hierarchy [93, 94]. Hence, one can distinguish between competing light neutrino mass and mixing patterns with high energy observables.

FIGURE 2

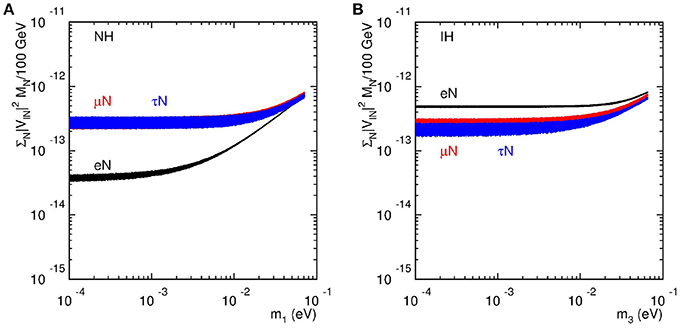
Figure 2. ${\Sigma }_N|V_{\ell N}{|}^2{M}_N/100\mathrm{\text{GeV}}$ vs. the lightest neutrino mass for (A) NH and (B) IH in the case of degenerate heavy neutrinos, assuming vanishing phases.

FIGURE 3

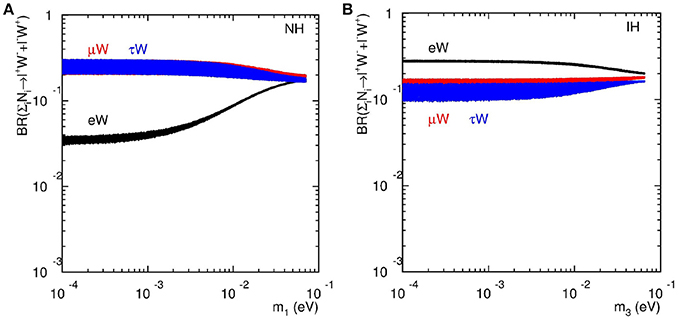
Figure 3. Branching fractions of process $\sum _i{N}_i\to {\ell }^{+}{W}^{-}+{\ell }^{-}{W}^{+}$ vs. the lightest neutrino mass for (A) NH and (B) IH in the degenerate case with M_N = 300 GeV and m_h = 125 GeV, assuming vanishing phases.

More generally, the V_ℓN in Equation (3.10) can be formally solved in terms of an arbitrary orthogonal complex matrix Ω, known as the Casas-Ibarra parametrization [95], using the ansatz

$\begin{array}{ll}{V}_{\ell N}=U_{PMNS} m_{\nu }^{1/2}\Omega M_N^{-1/2},& (3.16)\end{array}$

with the orthogonality condition ΩΩ^T = I. For the simplest incarnation with a unity matrix Ω = I, $|V_{\ell N_{m^{\prime }}}{|}^2$ are proportional to one and only one light neutrino mass, and thus the branching ratio of $N_{m^{\prime }}\to {\ell }^{\pm }{W}^{\mp }$ for each lepton flavor is independent of neutrino mass and universal for both NH and IH [93]. Nevertheless, one can still differentiate between the three heavy neutrinos according to the decay rates to their leading decay channels. As shown in Figure 4 for Ω = I, one sees

$\begin{array}{ll}\begin{array}{l}\text{BR}(e^{\pm }{W}^{\mp })~40\%>\text{BR}({\mu }^{\pm }{W}^{\mp }),\text{BR}({\tau }^{\pm }{W}^{\mp })\\ ~(4-15)\%\text{for}{N}_1,\end{array}& (3.17)\end{array}$

$\begin{array}{ll}\begin{array}{l}\text{BR}(e^{\pm }{W}^{\mp })~20\%\approx \text{BR}({\mu }^{\pm }{W}^{\mp })\approx \text{BR}({\tau }^{\pm }{W}^{\mp })\\ ~(10-30)\%\text{for}{N}_2,\end{array}& (3.18)\end{array}$

$\begin{array}{ll}\begin{array}{l}\text{BR}({\mu }^{\pm }{W}^{\mp }),\text{BR}({\tau }^{\pm }{W}^{\mp })~(15-40)\%\gg \text{BR}(e^{\pm }{W}^{\mp })\\ ~1\%\text{for}{N}_3.\end{array}& (3.19)\end{array}$

A realistic Dirac mass matrix can be quite arbitrary with three complex angles parameterizing the orthogonal matrix Ω. However, this arbitrariness of the Dirac mass matrix is not a universal feature of Seesaw models; the neutrino Yukawa matrix in the Type II Seesaw, for example, is much more constrained.

FIGURE 4

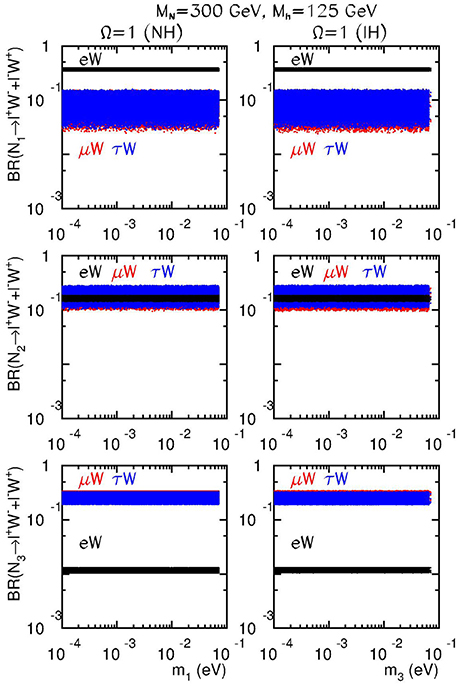
Figure 4. Branching fractions of process $N_i\to {\ell }^{+}{W}^{-}+{\ell }^{-}{W}^{+}$ vs. the lightest neutrino mass for NH and IH in the case Ω = I with M_i = 300 GeV and m_h = 125 GeV, assuming vanishing Majorana phases.

Beyond this, Figure 2 also shows another general feature of minimal, high-scale Seesaw constructions, namely that the active-sterile mixing |V_ℓN| is vanishingly small. For a heavy neutrino mass of M_N ~ 100 GeV, Equation (3.11) implies $|V_{\ell N}{|}^2~10^{-14}-10^{-12}$. This leads to the well-known decoupling of observable lepton number violation in the minimal, high-scale Type I Seesaw scenario at colliders experiments [27, 96, 97]. For low-scale Type I Seesaws, such decoupling of observable lepton number violation also occurs: Due to the allowed arbitrariness of the matrix Ω in Equation (3.16), it is possible to construct Ω and M_N with particular entry patterns or symmetry structures, also known as textures in the literature, such that V_ℓN is nonzero but m_ν vanishes. Light neutrino masses can then be generated as perturbations from these textures. In Moffat et al. [27] it was proved that such delicate (and potentially fine-tuned [98–100]) constructions result in small neutrino masses being proportional to small L-violating parameters, instead of being inversely proportional as in the high-scale case. Subsequently, in low-scale Seesaw scenarios that assume only fermionic gauge singlets, tiny neutrino masses is equivalent to an approximate conservation of lepton number, and leads to the suppression of observable L violation in high energy processes. Hence, any observation of lepton number violation (and Seesaw partners in general) at collider experiments implies a much richer neutrino mass-generation scheme than just the canonical, high-scale Type I Seesaw.

3.1.2. Type I+II Hybrid Seesaw Mechanism

While the discovery of lepton number violation in, say, 0νββ or hadron collisions would imply the Majorana nature of neutrinos [33–35], it would be less clear which mechanism or mechanisms are driving light neutrino masses to their sub-eV values. This is because in the most general case neutrinos possess both LH and RH Majorana masses in addition to Dirac masses. In such hybrid Seesaw models, two or more “canonical” tree- and loop-level mechanisms are combined and, so to speak, may give rise to phenomenology that is greater than the sum of its parts.

A well-studied hybrid model is the Type I+II Seesaw mechanism, wherein the light neutrino mass matrix M_ν, when $M_D{M}_R^{-1}\ll 1$, is given by Chen et al. [101], Akhmedov and Frigerio [102], Akhmedov et al. [103], Chao et al. [104, 105], Gu et al. [106], and Chao et al. [107]

$\begin{array}{ll}{M}_{\nu }^{light}=M_L-M_D{M}_R^{-1}{M}_D^T.& (3.20)\end{array}$

Here, the Dirac and Majorana mass terms, M_D, M_R, have their respective origins according to the Type I model, whereas M_L originates from the Type II mechanism; see section 4 for details. In this scenario, sub-eV neutrino masses can arise not only from parametrically small Type I and II masses but additionally from an incomplete cancellation of the two terms [102–104]. While a significant or even moderate cancellation requires a high-degree of fine tuning and is radiatively instable [107], this situation cannot theoretically be ruled out a priori. For a one-generation mechanism, the relative minus sign in Equation (3.20) is paramount for such a cancellation; however, in a multi-generation scheme, it is not as crucial as M_D is, in general, complex and can even absorb the sign through a phase rotation. Moreover, this fine-tuning scenario is a caveat of the aforementioned decoupling of L-violation in a minimal Type I Seesaw from LHC phenomenology [27, 96, 97]. As we will discuss shortly, regardless of its providence, if such a situation were to be realized in nature, then vibrant and rich collider signatures emerges.

3.1.3. Type I Seesaw in U(1)_X Gauge Extensions of the Standard Model

Another manner in which the decoupling of heavy Majorana neutrinos N from collider experiments can be avoided is through the introduction of new gauge symmetries, under which N is charged. One such example is the well-studied U(1)_X Abelian gauge extension of the SM [108–112], where U(1)_X is a linear combination of U(1)_Y and U(1)_B−L after the spontaneous breaking of electroweak symmetry and B − L (baryon minus lepton number) symmetries. In this class of models, RH neutrinos are introduced to cancel gauge anomalies and realize a Type I Seesaw mechanism.

Generally, such a theory can be described by modifying the SM covariant derivatives by Salvioni et al. [113]

$\begin{array}{ll}{D}_{\mu }\ni i{g}_{1}Y{B}_{\mu } \to D_{\mu }\ni i{g}_{1}Y{B}_{\mu }+i(\tilde{g}Y+g_1^{\prime }{Y}_{BL})B_{\mu }^{\prime },& (3.21)\end{array}$

where B_μ(Y) and $B_{\mu }^{\prime }(Y_{BL})$ are the gauge fields (quantum numbers) of U(1)_Y and U(1)_B−L, respectively. The most economical extension with vanishing mixing between U(1)_Y and U(1)_B−L, i.e., , U(1)_X = U(1)_B−L and $\tilde{g}=0$ in Equation (3.21), introduces three RH neutrinos and a new complex scalar S that are all charged under the new gauge group but remain singlets under the SM symmetries [114–116]. In this extension one can then construct the neutrino Yukawa interactions

$\begin{array}{ll}{{L}}_I^Y=-{\overline{L}}_L{Y}_{\nu }^D\tilde{H}{N}_R-\frac{1}{2}{Y}_{\nu }^M\overline{{(N^c)}_L}{N}_{R}S+\text{H}.\text{c}.& (3.22)\end{array}$

Once the Higgs S acquires the vacuum expectation value $\langle S\rangle =v_S/\sqrt{2}$, B − L is broken, spontaneously generating the RH Majorana mass matrix $M_N=Y_{\nu }^M{v}_S/\sqrt{2}$ from Equation (3.22).

It is interesting to note that the scalar vev provides a dynamical mechanism for the heavy, RH Majorana mass generation, i.e., a Type I Seesaw via a Type II mechanism; see section 4 for more details. The Seesaw formula and the mixing between the SM charged leptons and heavy neutrinos here are exactly the same as those in the canonical Type I Seesaw. The mass of neutral gauge field $B_{\mu }^{\prime }$, $M_{Z^{\prime }}=M_{Z_{B-L}}=2g_{BL}{v}_S$, is generated from S' kinetic term, ${(D_{\mu }S)}^{†}$ $(D^{\mu }S)$ with $D_{\mu }S={\partial }_{\mu }S+i2g_{BL}{B}_{\mu }^{\prime }S$. Note that in the minimal model, $g_{BL}=g_1^{\prime }$. As in other extended scalar scenarios, the quadratic term H^†HS^†S in the scalar potential results in the SM Higgs H and S interaction states mixing into two CP-even mass eigenstates, H₁ and H₂.

3.1.4. Type I+II Hybrid Seesaw in Left-Right Symmetric Model

As discussed in section 3.1.2, it may be the case the light neutrino masses result from the interplay of multiple Seesaw mechanisms. For example: the Type I+II hybrid mechanism with light neutrino masses given by Equation (3.20). It is also worth observing two facts: First, in the absence of Majorana masses, the minimum fermionic field content for a Type I+II Seesaw automatically obeys an accidental global U(1)_B−L symmetry. Second, with three RH neutrinos, all fermions can be sorted into either SU(2)_L doublets (as in the SM) or SU(2)_R doublets, its RH analog. As the hallmark of the Type II model (see section 4) is the spontaneous generation of LH Majorana masses from a scalar SU(2)_L triplet Δ_L, it is conceivable that RH neutrino Majorana masses could also be generated spontaneously, but from a scalar SU(2)_R triplet Δ_R. (This is similar to the spontaneous breaking of U(1)_B−L in section 3.1.3.) This realization of the Type I+II Seesaw is known as the Left-Right Symmetric Model (LRSM) [117–121], and remains one of the best-motivated and well-studied extensions of the SM. For recent, dedicated reviews, see Mohapatra and Smirnov [63], Duka et al. [122], and Senjanović [123].

The high energy symmetries of the LRSM is based on the extended gauge group

$\begin{array}{ll}{{G}}_{\text{LRSM}}=\text{SU}{(3)}_c\otimes \text{SU}{(2)}_L\otimes \text{SU}{(2)}_R\otimes \text{U}{(1)}_{B-L},& (3.23)\end{array}$

or its embeddings, and conjectures that elementary states, in the UV limit, participate in LH and RH chiral currents with equal strength. While the original formulation of model supposes a generalized parity ${{P}}_X={P}$ that enforces an exchange symmetry between fields charged under SU(2)_L and SU(2)_R, it is also possible to achieve this symmetry via a generalized charge conjugation ${{P}}_X={C}$ [124]. For fermionic and scalar multiplets Q_L,R and Φ, the exchange relationships are [124],

$\begin{array}{ll}\begin{array}{l}{P}:\{\begin{array}{c}{Q}_L\leftrightarrow Q_R\\ \Phi \leftrightarrow {\Phi }^{†}\end{array}, \text{and} {C}:\{\begin{array}{c}{Q}_L\leftrightarrow {(Q_R)}^c\\ \Phi \leftrightarrow {\Phi }^T\end{array},\\ \text{where} {\left(Q_R\right)}^c=C{\gamma }^0{Q}_R^{*}.\end{array}& (3.24)\end{array}$

A non-trivial, low-energy consequence of these complementary formulations of the LRSM is the relationship between the LH CKM matrix in the SM, $V_{ij}^{\text{L}}$, and its RH analog, $V_{ij}^{\text{R}}$. For generalized conjugation, one has $\left|V_{ij}^{\text{R}}\right|=\left|V_{ij}^{\text{L}}\right|$, whereas $\left|V_{ij}^{\text{R}}\right|\approx \left|V_{ij}^{\text{L}}\right|+{O}(m_b/m_t)$ for generalized parity [124–128]. Moreover, LR parity also establishes a connection between the Dirac and Majorana masses in the leptonic sector [129, 130]. Under generalized parity, for example, the Dirac $(Y_{1,2}^D)$ and Majorana (Y_L,R) Yukawa matrices must satisfy [130],

$\begin{array}{ll}{Y}_{1,2}^D=Y_{1,2}^{D†} \text{and} Y_L=Y_R.& (3.25)\end{array}$

Such relationships in the LRSM remove the arbitrariness of neutrino Dirac mass matrices, as discussed in section 3.1.1, and permits one to calculate Ω, even for nonzero Δ_L vev [129, 131]. However, the potential cancellation between Type I and II Seesaw masses in Equation 3.20 still remains.

In addition to the canonical formulation of the LRSM are several alternatives. For example: It is possible to instead generate LH and RH Majorana neutrino masses radiatively in the absence of triplet scalars [132, 133]. One can gauge baryon number and lepton number independently, which, for an anomaly-free theory, gives rise to vector-like leptons and a Type III Seesaw mechanism [134, 135] (see section 5), as well as embed the model into an R-parity-violating Supersymmetric framework [136, 137].

Despite the large scalar sector of the LRSM (two complex triplets and one complex bidoublet), and hence a litany of neutral and charged Higgses, the symmetry structure in Equation (3.23) confines the number in independent degrees of freedom to 18 [122, 138]. These consist of three mass scales μ_{1, …, 3}, 14 dimensionless couplings λ_{1, …, 4}, ρ_{1, …, 4}, α_{1, …, 3}, β_{1, …, 3}, and one CP-violating phase, δ₂. For further discussions on the spontaneous breakdown of CP in LR scenarios, see also Senjanović [121], Basecq et al. [139], and Kiers et al. [140]. With explicit CP conservation, the minimization conditions on the scalar potential give rise to the so-called LRSM vev Seesaw relationship [138],

$\begin{array}{ll}{v}_L=\frac{{\beta }_2{k}_1^2+{\beta }_1{k}_1{k}_2+{\beta }_3{k}_2^2}{(2{\rho }_1-{\rho }_3)v_R},& (3.26)\end{array}$

where, v_L,R and k_1,2 are the vevs of Δ_L,R and the Higgs bidoublet Φ, respectively, with $v_L^2\ll k_1^2+k_2^2\approx {(246\text{ GeV})}^2\ll v_R$.

In the LRSM, the bidoublet Φ fulfills the role of the SM Higgs to generate the known Dirac masses of elementary fermions and permits a neutral scalar h_i with mass m_hi ≈ 125 GeV and SM-like couplings. In the absence of egregious fine-tuning, i.e., ρ₃ ≉ 2ρ₁, Equation (3.26) suggests that v_L in the LRSM is inherently small because, in addition to k₁, k₂ ≪ v_R, custodial symmetry is respected (up to hypercharge corrections) when all β_i are identically zero [141]. Consistent application of such naturalness arguments reveals a lower bound on the scalar potential parameters [141],

$\begin{array}{ll}\begin{array}{l}{\rho }_{1,2,4}>\frac{g_R^2}{4}{\left(\frac{m_{\text{FCNH}}}{M_{W_R}}\right)}^2,\\ {\rho }_3>g_R^2{\left(\frac{m_{\text{FCNH}}}{M_{W_R}}\right)}^2+2{\rho }_1~6{\rho }_1,\end{array}& (3.27)\end{array}$

$\begin{array}{ll}\begin{array}{l}{\alpha }_{1,\dots ,3}>g_R^2{\left(\frac{m_{\text{FCNH}}}{M_{W_R}}\right)}^2,\\ {\mu }_{1,2}^2>{\left(m_{\text{FCNH}}\right)}^2, {\mu }_3^2>\frac{1}{2}{\left(m_{\text{FCNH}}\right)}^2,\end{array}& (3.28)\end{array}$

where M_WR and g_R are the mass and coupling of the $W_R^{\pm }$ gauge boson associated with SU(2)_R, and m_FCNH is the mass scale of the LRSM scalar sector participating in flavor-changing neutral transitions. Present searches for neutron EDMs [125, 126, 142, 143] and FCNCs [143–147] require m_FCNH > 10 − 20 TeV at 90% CL. Subsequently, in the absence of FCNC-suppressing mechanisms, ρ_i > 1 for LHC-scale W_R. Thus, discovering LRSM at the LHC may suggest a strongly coupled scalar sector. Conversely, for ρ_i < 1 and m_FCNH ~ 15 (20)TeV, one finds M_WR ≳ 10 (12)TeV, scales that are within the reach of future hadron colliders [141, 148, 149]. For more detailed discussions on the perturbativity and stability of the LRSM scalar section, see Mitra et al. [141], Maiezza et al. [146], Bertolini et al. [150–152], Mohapatra and Zhang [153], and Maiezza and Senjanović [154] and references therein.

After Δ_R acquires a vev and LR symmetry is broken spontaneously, the neutral component of SU(2)_R, i.e., $W_R^3$, and the U(1)_B−L boson, i.e., X_B−L, mix into the massive eigenstate $Z_{\text{LRSM}}^{\prime }$ (sometimes labeled Z_R) and the orthogonal, massless vector boson B. B is recognized as the gauge field associated with weak hypercharge in the SM, the generators of which are built from the remnants of SU(2)_R and U(1)_B−L. The relation between electric charge Q, weak left/right isospin $T_{L/R}^3$, baryon minus lepton number B-L, and weak hypercharge Y is given by

$\begin{array}{ll}Q=T_L^3+T_R^3+\frac{(B-L)}{2}\equiv T_L^3+\frac{Y}{2}, \text{with} Y=2T_R^3+(B-L).& (3.29)\end{array}$

This in turn implies that the remaining components of SU(2)_R, $W_R^1$ and $W_R^2$, combine into the state $W_R^{\pm }$ with electric charge $Q^{W_R}=\pm 1$ and mass $M_{W_R}=g_R{v}_R/\sqrt{2}$. After EWSB, it is possible for the massive W_R and W_L gauge fields to mix, with the mixing angle ξ_LR given by $tan2{\xi }_{\text{LR}}=2k_1{k}_2/(v_R^2-v_L^2)\lesssim 2v_{\text{SM}}^2/v_R^2$. Neutral meson mass splittings [124, 147, 155–158] coupled with improved lattice calculations, e.g., [159, 160], Weak CPV [124, 158, 161], EDMs [124–126, 158], and CP violation in the electron EDM [129], are particularly sensitive to this mixing, implying the competitive bound of M_WR ≳ 3 TeV at 95% CL [147]. This forces W_L − W_R mixing to be, $tan2{\xi }_{\text{LR}}/2\approx {\xi }_{\text{LR}}\lesssim M_W^2/M_{W_R}^2<7-7.5\times 10^{-4}.$ A similar conclusion can be reached on $Z-Z_{LRSM}^{\prime }$ mixing. Subsequently, the light and heavy mass eigenstates of LRSM gauge bosons, $W_1^{\pm },W_2^{\pm },Z_1,Z_2$, where M_V1 < M_V2, are closely aligned with their gauge states. In other words, to a very good approximation, W₁ ≈ W_SM, Z₁ ≈ Z_SM, W₂ ≈ W_R and $Z^{\prime }\approx Z_{LRSM}^{\prime }$ (or sometimes $Z^{\prime }\approx Z_R$). The mass relation between the LR gauge bosons is $M_{Z_R}=\sqrt{2{cos}^2{\theta }_W/cos2{\theta }_W}{M}_{W_R}\approx (1.7)\times M_{W_R}$, and implies that bounds on one mass results in indirect bounds on the second mass; see, for example, Lindner et al. [162].

3.1.5. Heavy Neutrino Effective Field Theory

It is possible that the coupling of TeV-scale Majorana neutrinos to the SM sector is dominated by new states with masses that are hierarchically larger than the heavy neutrino mass or the reach of present-day collider experiments. For example: Scalar SU(2)_R triplets in the Left-Right Symmetric Model may acquire vevs ${O}(10)$ TeV, resulting in new gauge bosons that are kinematically accessible at the LHC but, due to ${O}(10^{-3}-10^{-2})$ triplet Yukawa couplings, give rise to EW-scale RH Majorana neutrino masses. In such a pathological but realistic scenario, the LHC phenomenology appears as a canonical Type I Seesaw mechanism despite originating from a different Seesaw mechanism [163]. While it is generally accepted that such mimicry can occur among Seesaws, few explicit examples exist in the literature and further investigation is encouraged.

For such situations, it is possible to parameterize the effects of super-heavy degrees of freedom using the Heavy Neutrino Effective Field Theory (NEFT) framework [164]. NEFT is an extension of the usual SM Effective Field Theory (SMEFT) [165–168], whereby instead of augmenting the SM Lagrangian with higher dimension operators one starts from the Type I Seesaw Lagrangian in Equation (3.1) and builds operators using that field content. Including all SU(3) ⊗ SU(2)_L ⊗ U(1)_Y-invariant, operators of mass dimension d > 4, the NEFT Lagrangian before EWSB is given by

$\begin{array}{ll}{{L}}_{\text{NEFT}}={{L}}_{\text{Type} \text{I}}+{\displaystyle \sum _{d=5}{\displaystyle \sum _i\frac{{\alpha }_i^{(d)}}{{\Lambda }^{(d-4)}}}}{{O}}_i^{(d)}.& (3.30)\end{array}$

Here, ${{O}}_i^{(d)}$ are dimension d, Lorentz and gauge invariant permutations of Type I fields, and ${\alpha }_i^{(d)}\ll 4\pi$ are the corresponding Wilson coefficients. The list of ${{O}}_i^{(d)}$ are known explicitly for d = 5 [169, 170], 6 [164, 170], and 7 [170–172], and can be built for larger d following [173–175].

After EWSB, fermions should then be decomposed into their mass eigenstates via quark and lepton mixing. For example: among the d = 6, four-fermion contact operations ${{O}}_i^{(6)}$ that contribute to heavy N production in hadron colliders (see Equation 3.33) in the interaction/gauge basis are [164]

$\begin{array}{ll}\begin{array}{l}{{O}}_V^{(6)}=\left(\overline{d}{\gamma }^{\mu }{P}_{R}u\right)\left(\overline{e}{\gamma }_{\mu }{P}_R{N}_R\right) \text{and} \\ {{O}}_{S3}^{(6)}=\left(\overline{Q}{\gamma }^{\mu }{P}_R{N}_R\right)\epsilon \left(\overline{L}{\gamma }_{\mu }{P}_{R}d\right).\end{array}& (3.31)\end{array}$

In terms of light (ν_m) and heavy $(N_{m^{\prime }})$ mass eigenstates and using Equation (3.4), one can generically [66, 87] decompose the heavy neutrino interaction state N_ℓ as $N_{\ell }=\sum _{m=1}^3{X}_{\ell m}{\nu }_m^c+\sum _{m^{\prime }=1}^n{Y}_{\ell N_{m^{\prime }}}{N}_{m^{\prime }},$ with $\left|Y_{\ell N_{m^{\prime }}}\right|$ of order the elements of U_PMNS. Inserting this into the preceding operators gives quantities in terms of leptonic mass eigenstates:

$\begin{array}{ll}\begin{array}{l}{{O}}_V^{(6)}={\displaystyle \sum _{m=1}^3\left(\overline{d}{\gamma }^{\mu }{P}_{R}u\right)}\left(\overline{\ell }{\gamma }_{\mu }{P}_R X_{\ell m} {\nu }_m^c\right)\\ +{\displaystyle \sum _{m^{\prime }=1}\left(\overline{d}{\gamma }^{\mu }{P}_{R}u\right)}\left(\overline{\ell }{\gamma }_{\mu }{P}_R Y_{\ell N_{m^{\prime }}} N_{m^{\prime }}\right), \text{and}\\ {{O}}_{S3}^{(6)}={\displaystyle \sum _{m=1}^3\left(\overline{Q}{\gamma }^{\mu }{P}_R X_{\ell m}{\nu }_m^c\right)}\left(\overline{\ell }{\gamma }_{\mu }{P}_{R}d\right)\\ +{\displaystyle \sum _{m^{\prime }=1}\left(\overline{Q}{\gamma }^{\mu }{P}_R Y_{\ell N_{m^{\prime }}}{N}_{m^{\prime }}\right)}\left(\overline{\ell }{\gamma }_{\mu }{P}_{R}d\right).\end{array}& (3.32)\end{array}$

After EWSB, a similar decomposition for quarks gauge states in terms of CKM matrix elements and mass eigenstates should be applied. For more information on such decompositions, see, e.g., Ruiz [163] and references therein. It should be noted that after integrating out the heavy N field, the marginal operators at d > 5 generated from the Type I Lagrangian are not the same operators generated by integrating the analogous Seesaw partner in the Type II and III scenarios [176, 177].

3.2. Heavy Neutrinos at Colliders

The connection between low-scale Seesaw models and colliders is made no clearer than in searches for heavy neutrinos, both Majorana and (pseudo-)Dirac, in the context of Type I-based scenarios. While extensive, the topic's body of literature is still progressing in several directions. This is particularly true for the development of collider signatures, Monte Carlo tools, and high-order perturbative corrections. Together, these advancements greatly improve sensitivity to neutrinos and their mixing structures at collider experiments.

We now review the various searches for L-violating collider processes facilitated by Majorana neutrinos N. We start with low-mass (section 3.2.1) and high-mass (sections 3.2.2 and 3.2.3) neutrinos in the context of Type I-based hybrid scenarios, before moving onto Abelian (section 3.2.4) and non-Abelian (section 3.2.5) gauge extensions, and finally the semi-model independent NEFT framework (section 3.2.6). Lepton number violating collider processes involving pseudo-Dirac neutrinos are, by construction, suppressed [178–181]. Thus, a discussion of their phenomenology is outside the scope of this review and we refer readers to thorough reviews such as Ibarra et al. [94], Weiland [182], and Antusch et al. [183].

3.2.1. Low-Mass Heavy Neutrinos at pp and ee Colliders

For Majorana neutrinos below the M_W mass scale, lepton number violating processes may manifest in numerous way, including rare decays of mesons, baryons, μ and τ leptons, and even SM electroweak bosons. Specifically, one may discover L violation in three-body meson decays to lighter mesons $M_1^{\pm }\to M_2^{\mp }{\ell }_1^{\pm }{\ell }_2^{\pm }$ [66, 184–199], such as that shown in Figure 5A; four-body meson decays to lighter mesons $M_1^{\pm }\to M_2^{\mp }{M}_3^0{\ell }_1^{\pm }{\ell }_2^{\pm }$ [195, 196, 200–202]; four-body meson decays to leptons $M^{\pm }\to {\ell }_1^{\pm }{\ell }_1^{\pm }{\ell }_2^{\mp }\nu$ [192, 193, 202–204]; five-body meson decays [202]; four-body baryon decays to mesons, $B\to M{\ell }_1^{\pm }{\ell }_2^{\pm }$ [205]; three-body τ decay to mesons, ${\tau }^{\pm }\to {\ell }^{\mp }{M}_1^{\pm }{M}_2^{\pm }$ [195, 206, 207]; four-body τ decays to mesons, ${\tau }^{\pm }\to {\ell }_1^{\pm }{\ell }_1^{\pm }{M}^{\mp }\nu$ [195, 206, 208–210]; four-body W boson decays, $W^{\pm }\to {\ell }_1^{\pm }{\ell }_1^{\pm }{\ell }_2^{\mp }\nu$ [211–215]; Higgs boson decays, $h\to NN\to {\ell }_1^{\pm }{\ell }_2^{\pm }+X$ [216–219]. and even top quark decays, $t\to b{W}^{+*}\to b{\ell }_1^{+}N\to b{\ell }_1^{+}{\ell }_2^{\pm }q\overline{q^{\prime }}$ [7, 211, 220, 221]. The W boson case is notable as azimuthal and polar distributions [87] or exploiting endpoint kinematics [214] can differentiate between L conservation and non-conservation. Of the various collider searches for GeV-scale N, great complementarity is afforded by B-factories. As shown in Figure 5B, an analysis of Belle I [45] and LHCb Run I [46, 47] searches for L-violating final states from meson decays excluded [222] $|V_{\mu N}{|}^2\gtrsim 3\times 10^{-5}$ for M_N = 1 − 5 GeV. Along these same lines, the observability of displaced decays of heavy neutrinos [217, 223–227] and so-called “neutrino-antineutrino oscillations” [228–231] (in analogy to ${B}-\overline{{B}}$ oscillations) and have also been discussed.

FIGURE 5

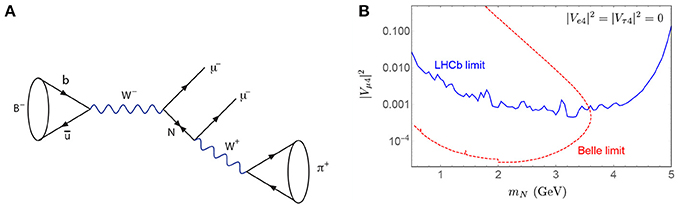
Figure 5. (A) B⁻ meson decay to L-violating final state via heavy Majorana N [47]. (B) LHCb and Belle I limits on $|V_{\mu N}{|}^2$ (labeled $|V_{\mu 4}{|}^2$ in the figure) as a function of N mass after ${L}=3$ fb⁻¹ at 7-8 TeV LHC [222].

Indirectly, the presence of heavy Majorana neutrinos can appear in precision EW measurements as deviations from lepton flavor unitarity and universality, and is ideally suited for e⁺e⁻ colliders [88–91, 183, 232, 233], such as the International Linear Collider (ILC) [234, 235], Circular e⁻e⁺ Collider (CepC) [236], and Future Circular Collider-ee (FCC-ee) [232]. An especially famous example of this is the number of active, light neutrino flavors N_ν, which can be inferred from the Z boson's invisible width ${\Gamma }_{\text{Inv}}^Z$. At lepton colliders, ${\Gamma }_{\text{Inv}}^Z$ can be determined in two different ways: The first is from line-shape measurements of the Z resonance as a function of $\sqrt{s}$, and is measured to be $N_{\nu }^{\text{Line}}=2.9840 \pm 0.0082$ [237]. The second is from searches for invisible Z decays, i.e., , e⁺e⁻ → Zγ, and is found to be $N_{\nu }^{\text{Inv}}=2.92\pm 0.05$ [238]. Provocatively, both measurements deviate from the SM prediction of $N_{\nu }^{\text{SM}}=3$ at the 2σ level. It is unclear if deviations from $N_{\nu }^{\text{SM}}$ are the result of experimental uncertainty or indicate the presence of, for example, RH neutrinos [224, 239]. Nonetheless, a future Z-pole machine can potentially clarify this discrepancy [224]. For investigations into EW constraints on heavy neutrinos, see del Águila et al. [88], Antusch and Fischer [89], de Gouvêa and Kobach [90], and Fernandez-Martinez et al. [91].

3.2.2. High-Mass Heavy Neutrinos at pp Colliders

Collider searches for heavy Majorana neutrinos with masses above M_W have long been of interest to the community [240–243], with exceptionally notable works appearing in the early 1990s [96, 244–247] and late-2000s [66, 97, 248–253]. In the past decade, among the biggest advancements in Seesaw phenomenology is the treatment of collider signatures for such hefty N in Type I-based models. While coupled to concurrent developments in Monte Carlo simulation packages, the progression has been driven by attempts to reconcile conflicting reports of heavy neutrino production cross sections for the LHC. This was at last resolved in Alva et al. [254] and Degrande et al. [255], wherein new, infrared- and collinear- (IRC-)safe definitions for inclusive and semi-inclusive⁴ production channels were introduced. The significance of such collider signatures is that they are well-defined at all orders in α_s, and hence correspond to physical observables. We now summarize this extensive body of literature, emphasizing recent results.

For Majorana neutrinos with M_N > M_W, the most extensively studied [66, 105, 183, 230, 240, 241, 246, 248–253, 256] collider production mechanism is the L-violating, charged current (CC) Drell-Yan (DY) process [240], shown in Figure 6A, and given by

$\begin{array}{ll}{q}_1 {\overline{q}}_2\to W^{\pm *}\to N {\ell }_1^{\pm }, \text{with} N\to {\ell }_2^{\pm }{W}^{\mp }\to {\ell }_2^{\pm }{q}_{1^{\prime }} {\overline{q^{\prime }}}_2.& (3.33)\end{array}$

A comparison of Figure 6A to the meson decay diagram of Figure 5A immediately reveals that Equation (3.33) is the former's high momentum transfer completion. Subsequently, much of the aforementioned kinematical properties related to L-violating meson decays also hold for the CC DY channel [87, 257]. Among the earliest studies are those likewise focusing on neutral current (NC) DY production [241, 242, 245–247], again shown in Figure 6A, and given by

$\begin{array}{ll}q \overline{q}\to Z^{*}\to N \stackrel{(-)}{{\nu }_{\ell }},& (3.34)\end{array}$

as well as the gluon fusion mechanism [242, 245], shown in Figure 6B, and given by

$\begin{array}{ll}g g\to Z^{*}/h^{*}\to N \stackrel{(-)}{{\nu }_{\ell }}.& (3.35)\end{array}$

Interestingly, despite gluon fusion being formally an ${O}({\alpha }_s^2)$ correction to Equation (3.34), it is non-interfering, separately gauge invariant, and the subject of renewed interest [255, 258, 259]. Moreover, in accordance to the Goldstone Equivalence Theorem [260, 261], the ggZ* contribution has been shown [258, 259] to be as large as the ggh* contribution, and therefore should not be neglected. Pair production of N via s-channel scattering [242, 246], e.g., gg → NN, or weak boson scattering [244, 247, 248], e.g., W^±W^∓ → NN, have also been discussed, but are relatively suppressed compared to single production by an additional mixing factor of $|V_{\ell N_{m^{\prime }}}{|}^2\lesssim 10^{-4}$.

FIGURE 6

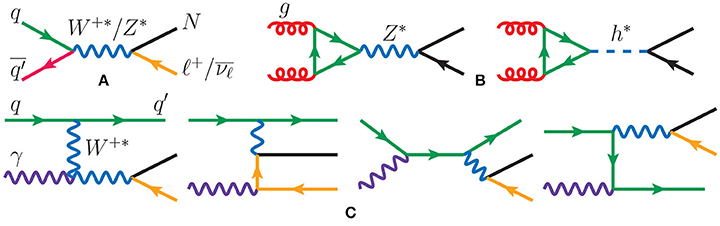
Figure 6. Born diagrams for heavy neutrino (N) production via (A) Drell-Yan, (B) gluon fusion, and (C) electroweak vector boson fusion; from Ruiz et al. [259] and drawn using JaxoDraw [267].

A recent, noteworthy development is the interest in semi-inclusive and exclusive production of heavy neutrinos at hadron colliders, i.e., , N production in association with jets. In particular, several studies have investigated the semi-inclusive, photon-initiated vector boson fusion (VBF) process [247, 254, 255, 262], shown in Figure 6C, and given by

$\begin{array}{ll}q \gamma \to N {\ell }^{\pm } q^{\prime },& (3.36)\end{array}$

and its deeply inelastic, ${O}(\alpha )$ radiative correction [247, 254, 255, 262–266],

$\begin{array}{ll}{q}_1 q_2\stackrel{W\gamma +WZ\to N{\ell }^{\pm }}{\to }N {\ell }^{\pm } {q^{\prime }}_1 {q^{\prime }}_2.& (3.37)\end{array}$

At ${O}({\alpha }^4)$ (here we do not distinguish between α and α_W), the full, gauge invariant set of diagrams, which includes the sub-leading W^±Z → Nℓ^± scattering, is given in Figure 7.

FIGURE 7

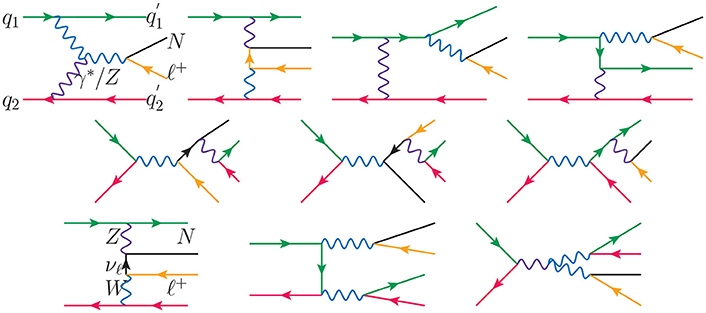
Figure 7. Born diagrams for the ${O}({\alpha }^4)$ heavy neutrino (N) production process $q_1{q}_2\to N{\ell }^{\pm }{q}_1^{\prime }{q}_2^{\prime }$ [254].

Treatment of the VBF channel is somewhat subtle in that it receives contributions from collinear QED radiation off the proton [262], collinear QED radiation off initial-states quarks [254], and QED radiation in the deeply inelastic/high momentum transfer limit [247]. For example: In the top line of diagrams in Figure 7, one sees that in the collinear limit of the $q_2\to {\gamma }^{*}{q}_2^{\prime }$ splitting, the virtual γ* goes on-shell and the splitting factorizes into a photon parton distribution function (PDF), recovering the process in Equation (3.36) [254, 255]. As these sub-channels are different kinematic limits of the same process, care is needed when combining channels so as to not double count regions of phase space. While ingredients to the VBF channel have been known for some time, consistent schemes to combine/match the processes are more recent [254, 255]. Moreover, for inclusive studies, Degrande et al. [255] showed that the use of Equation (3.36) in conjunction with a γ-PDF containing both elastic and inelastic contributions [268] can reproduce the fully matched calculation of Ref. [254] within the ${O}(20\%)$ uncertainty resulting from missing NLO in QED terms. Neglecting the collinear $q_2\to {\gamma }^{*}{q}_2^{\prime }$ splitting accounts for the unphysical cross sections reported in Deppisch et al. [67] and Dev et al. [262]. Presently, recommended PDF sets containing such γ-PDFs include: MMHT QED (no available lhaid) [268, 269], NNPDF 3.1+LUXqed (lhaid=324900) [270], LUXqed17+PDF4LHC15 (lhaid=82200) [271, 272], and CT14 QED Inclusive (lhaid = 13300) [273]. Qualitatively, the MMHT [268] and LUXqed [271, 272] treatments of photon PDFs are the most rigorous. In analogy to the gluon fusion and NC DY, Equation (3.36) (and hence Equation 3.37) is a non-interfering, ${O}(\alpha )$ correction to the CC DY process. Thus, the CC DY and VBF channels can be summed coherently.

In addition to these channels, the semi-inclusive, associated n-jet production mode,

$\begin{array}{ll}pp\to W^{*}+\ge nj+X \to N{\ell }^{\pm }+\ge nj+X, \text{for} n\in \mathbb{N},& (3.38)\end{array}$

has also appeared in the recent literature [255, 262, 274]. As with VBF, much care is needed to correctly model Equation (3.38). As reported in Degrande et al. [255] and Ruiz [275], the production of heavy leptons in association with QCD jets is nuanced due to the presence of additional t-channel propagators that can lead to artificially large cross sections if matrix element poles are not sufficiently regulated. (It is not enough to simply remove the divergences with phase space cuts). After phase space integration, these propagators give rise to logarithmic dependence on the various process scales. Generically Ruiz [275] and Collins et al. [276], the cross section for heavy lepton and jets in Equation (3.38) scales as:

$\begin{array}{ll}\sigma (pp\to N{\ell }^{\pm }+nj+X)~{\displaystyle \sum _{k=1}^n{\alpha }_s^k}(Q^2){\log }^{(2k-1)}\left(\frac{Q^2}{q_T^2}\right),& (3.39)\end{array}$

Here, Q ~ M_N is the scale of the hard scattering process, $q_T=\sqrt{|{\overrightarrow{q}}_T{|}^2}$, and ${\overrightarrow{q}}_T\equiv \sum _k^n{\overrightarrow{p}}_{T,k}^j$, is the (Nℓ)-system's transverse momentum, which recoils against the vector sum of all jet ${\overrightarrow{p}}_T$. It is clear for a fixed M_N that too low jet p_T cuts can lead to too small q_T and cause numerically large (collinear) logarithms such that $log(M_N^2/q_T^2)\gg 1/{\alpha }_s(Q)$, spoiling the perturbative convergence of Equation (3.39). Similarly, for a fixed q_T, arbitrarily large M_N can again spoil perturbative convergence. As noted in Alva et al. [254] and Degrande et al. [255], neglecting this fact has led to conflicting predictions in several studies on heavy neutrino production in pp collisions.

It is possible [255], however, to tune p_T cuts on jets with varying M_N to enforce the validity of Equation (3.39). Within the Collins-Soper-Sterman (CSS) resummation formalism [276], Equation (3.39) is only trustworthy when ${\alpha }_s(Q^2)$ is perturbative and q_T ~ Q, i.e.,

$\begin{array}{ll}\log (Q/{\Lambda }_{\text{QCD}})\gg 1 \text{and} {\alpha }_s(Q){\log }^2(Q^2/q_T^2)\lesssim 1.& (3.40)\end{array}$

Noting that at 1-loop α_s(Q) can be expressed by 1/α_s(Q) ≈ (β₀/2π)log(Q/Λ_QCD), and setting Q = M_N, one can invert the second CSS condition and obtain a consistency relationship [255]:

$\begin{array}{ll}{q}_T=|{\overrightarrow{q}}_T|=\left|{\displaystyle \sum _{k=1}^n{\overrightarrow{p}}_{T,k}^{ j}}\right|\gtrsim M_N\times e^{-(1/2)\sqrt{({\beta }_0/2\pi )\log (M_N/{\Lambda }_{\text{QCD}})}}.& (3.41)\end{array}$

This stipulate a minimum q_T needed for semi-inclusive processes like Equation (3.39) to be valid in perturbation theory. When q_T of the (Nℓ)-system is dominated by a single, hard radiation, Equation (3.41) is consequential: In this approximation, $q_T\approx \left|{\overrightarrow{p}}_{T,1}^j\right|$ and Equation (3.41) suggests a scale-dependent, minimum jet p_T cut to ensure that specifically the semi-inclusive pp → Nℓ + ≥ 1j + X cross section is well-defined in perturbation theory. Numerically, this is sizable: for M_N = 30 (300) [3000] GeV, one requires that $\left|{\overrightarrow{p}}_{T,1}^j\right|\gtrsim 9(65)\left[540\right]$ GeV, or alternatively $\left|{\overrightarrow{p}}_{T,1}^j\right|\gtrsim 0.3(0.22)\left[0.18\right]\times M_N$, and indicates that naïve application of fiducial $p_T^j$ cuts for the LHC do not readily apply for $\sqrt{s}=$ 27-100 TeV scenarios, where one can probe much larger M_N. The perturbative stability of this approach is demonstrated by the (roughly) flat K-factor of K^NLO ≈ 1.2 for the semi-inclusive pp → Nℓ^± + 1j process, shown in the lower panel of Figure 8A. Hence, the artificially large N production cross sections reported in Deppisch et al. [67], Dev et al. [262], and Das et al. [274] can be attributed to a loss of perturbative control over their calculation, not the presence of an enhancement mechanism. Upon the appropriate replacement of M_N, Equation (3.41) holds for other color-singlet processes [255], including mono-jet searches, and is consistent with explicit p_T resummations of high-mass lepton [275] and slepton [277, 278] production.

FIGURE 8

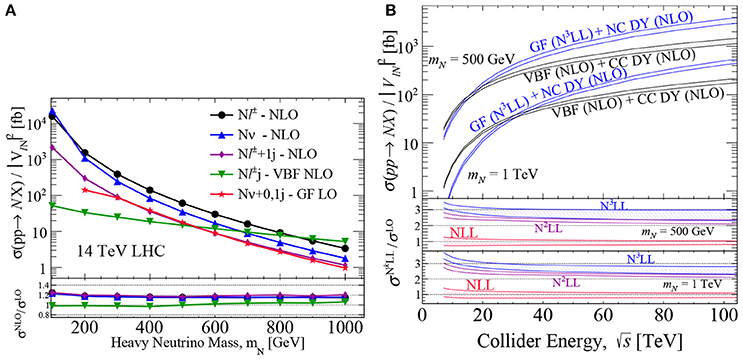
Figure 8. Heavy neutrino (N) hadron collider production cross sections, divided by active-heavy mixing $|V_{\ell N}{|}^2$, for various production modes as a function of (A) N mass at $\sqrt{s}=14$ [255] and (B) collider energy for representative M_N (band thickness corresponds to residual scale uncertainty) [259].

A characteristic of heavy neutrino production cross sections is that the active-sterile mixing, |V_ℓN|, factorizes out of the partonic and hadronic scattering expressions. Exploiting this one can define [248] a “bare” cross section σ₀, given by

$\begin{array}{ll}{\sigma }_0(pp\to N+X) \equiv \sigma (pp\to N+X)/|V_{\ell N}{|}^2.& (3.42)\end{array}$

Assuming resonant production of N, a similar expression can be extracted at the N decay level,

$\begin{array}{ll}\begin{array}{l}{\sigma }_0(pp\to {\ell }_1^{\pm }{\ell }_2^{\pm }+X)\equiv \sigma (pp\to {\ell }_1^{\pm }{\ell }_2^{\pm }+X)/S_{{\ell }_1{\ell }_2},\\ S_{{\ell }_1{\ell }_2}=\frac{\left|V_{{\ell }_{1}N}{|}^2\right|V_{{\ell }_{2}N}{|}^2}{{\displaystyle {\sum }_{\ell =e}^{\tau }|V_{\ell N}{|}^2}}.\end{array}& (3.43)\end{array}$

These definitions, which hold at all orders in α_s [255, 275], allow one to make cross section predictions and comparisons independent of a particular flavor model, including those that largely conserve lepton number, such as the inverse and linear Seesaws. It also allows for a straightforward reinterpretation of limits on collider cross sections as limits on S_ℓ1ℓ2, or |V_ℓN| with additional but generic assumptions. An exception to this factorizablity is the case of nearly degenerate neutrinos with total widths that are comparable to their mass splitting [228, 249, 279, 280].

Figure 8 shows a comparison of the leading, single N hadronic production cross sections, divided by active-heavy mixing $|V_{\ell N}{|}^2$, as a function of (a) heavy neutrino mass M_N at $\sqrt{s}=14$ [255] and (b) collider energy $\sqrt{s}$ up to 100 TeV for M_N = 500, 1000 GeV [259]. The various accuracies reported reflect the maturity of modern Seesaw calculations. Presently, state-of-the-art predictions for single N production modes are automated up to NLO+PS in QCD for the Drell-Yan and VBF channels [255, 281], amongst others, and known up to N³LL(threshold) for the gluon fusion channel [259]. With Monte Carlo packages, predictions are available at LO with multi-leg merging (MLM) [251, 255, 282, 283] as well as up to NLO with parton shower matching and merging [255, 283]. The NLO accurate [284], HeavyNnlo universal FeynRules object (UFO) [285] model file is available from Degrande et al. [255, 283]. Model files built using FeynRules [285–287] construct and evaluate L-violating currents following the Feynman rules convention of Denner et al. [288]. A brief comment is needed regarding choosing MLM+PS or NLO+PS computations: To produce MLM Monte Carlo samples, one must sum semi-inclusive channels with successively higher leg multiplicities in accordance with Equations (3.39)–(3.41) and correct for phase space double-counting. However, such MLM samples are formally LO in ${O}({\alpha }_s)$ because of missing virtual corrections. NLO+PS is formally more accurate, under better perturbative control, and thus is recommended for modeling heavy N at colliders. Such computations are possible with modern, general-purpose event generators, such as Herwig [289], MadGraph5_aMC@NLO [290], and Sherpa [291].

At the 13 and 14 TeV LHC, heavy N production is dominated by charged-current mechanisms for phenomenologically relevant mass scales, i.e., M_N ≲ 700 GeV [254]. At more energetic colliders, however, the growth in the gluon-gluon luminosity increases the gg → Nν cross section faster than the CC DY channel. In particular, at $\sqrt{s}=20-30$ TeV, neutral-current mechanisms surpass charged-current modes for heavy N production with M_N = 500 − 1000 GeV [259]. As seen in the sub-panel of Figure 8A, NLO in QCD contributions only modify inclusive, DY-type cross section normalizations by +20 to +30% and VBF negligibly, indicating that the prescriptions of Degrande et al. [255] are sufficient to ensure perturbative control over a wide-range of scales. One should emphasize that while VBF normalizations do not appreciably change under QCD corrections [292], VBF kinematics do change considerably [255, 293–295]. The numerical impact, however, is observable-dependent and can be large if new kinematic channels are opened at higher orders of α_s. In comparison to this, the sub-panel of Figure 8B shows that QCD corrections to gluon fusion are huge (+150 to +200%), but convergent and consistent with SM Higgs, heavy Higgs, and heavy pseudoscalar production [296–298]; for additional details, see Ruiz et al. [259].

With these computational advancements, considerable collider sensitivity to L-violating processes in the Type I Seesaw has been reached. In Figure 9 is the expected sensitivity to active-sterile neutrino mixing via the combined CC DY+VBF channels and in same-sign μ^±μ^± + X final-state. With ${L}=1$ ab⁻¹ of data for M_N > M_W at $\sqrt{s}=$ 14 (100) TeV, one can exclude at 2σ $S_{\mu \mu }\approx |V_{\mu N}{|}^2\gtrsim 10^{-4}(10^{-5})$ [254]. This is assuming the 2013 Snowmass benchmark detector configuration for $\sqrt{s}=100$ TeV [299]. Sensitivity to the e^±e^± and e^±μ^± channels is comparable, up to detector (in)efficiencies for electrons and muons. As shown in Figure 10, with ${L}\approx 20$ fb⁻¹ at 8 TeV, the ATLAS and CMS experiments have excluded at 95% CLs $|V_{\ell N}{|}^2\gtrsim 10^{-3}-10^{-1}$ for M_N = 100 − 450 GeV [48–52]. For heavier M_N, quarks from the on-shell W boson decay can form a single jet instead of the usual two-jet configuration. In such cases, well-known “fat jet” techniques can be used [300, 301]. Upon discovery of L-violating processes involving heavy neutrinos, among the most pressing quantities to measure are N's chiral couplings to other fields [87, 257], its flavor structure [129, 228, 230, 256], and a potential determination if the signal is actually made of multiple, nearly degenerate N [105, 229].

FIGURE 9

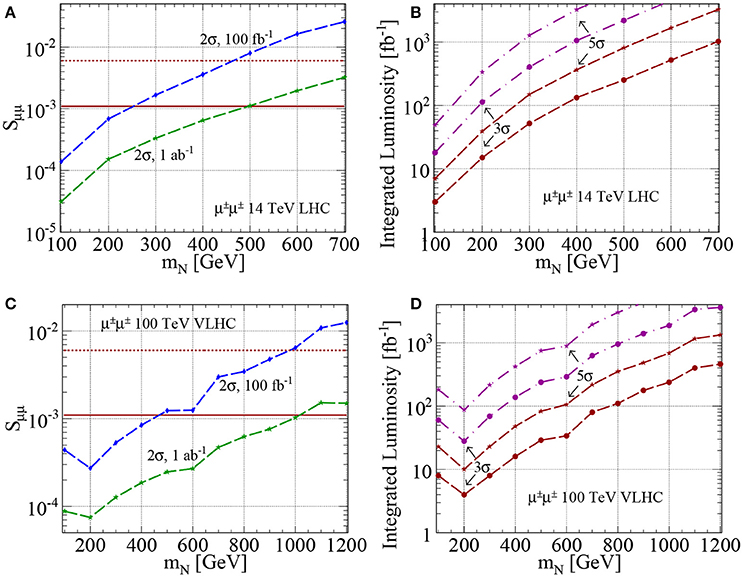
Figure 9. At 14 TeV and as a function of M_N, (A) the 2σ sensitivity to $S_{\ell {\ell }^{{}^{\prime }}}$ for the pp → μ^±μ^± + X process. (B) The required luminosity for a 3 (dash-circle) and 5σ (dash-star) discovery in the same channel (C,D) Same as (A,B) but for 100 TeV [254].

FIGURE 10

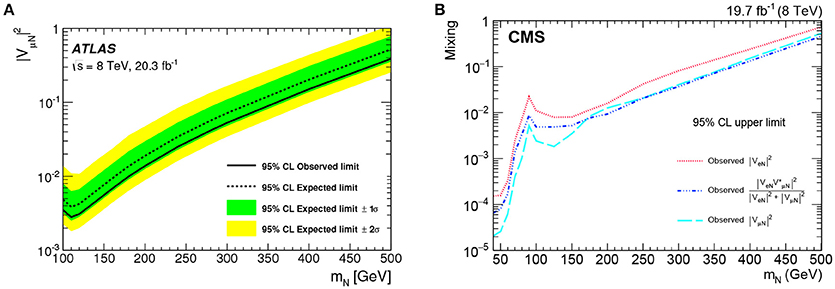
Figure 10. 8 TeV LHC limits on neutrino mixing $|V_{\ell N}{|}^2$ from searches for $pp\to {\ell }_1^{\pm }{\ell }_2^{\pm }+nj$ at (A) ATLAS [52] and (B) CMS [50] with ${L}\approx 20\text{f}{\text{b}}^{-1}$ of data.

3.2.3. High-Mass Heavy Neutrinos at ep Colliders

Complementary to searches for L violation in pp collisions are the prospects for heavy N production at ep deeply inelastic scattering (DIS) colliders [183, 302–309], such as proposed Large Hadron-electron Collider (LHeC) [310], or a μp analog [304]. As shown in Figure 10, DIS production of Majorana neutrinos can occur in multiple ways, including (a) W exchange and (b) Wγ fusion. For treatment of initial-state photons from electron beams, see Frixione et al. [311]. Search strategies for Majorana neutrinos at DIS experiments typically rely on production via the former since eγ → NW associated production can suffer from large phase space suppression, especially at lower beam energies. On the other hand, at higher beam energies, the latter process can provide additional polarization information on N and its decays [183].

At DIS facilities, one usually searches for L violation by requiring that N decays to a charged lepton of opposite sign from the original beam configuration, i.e.,

$\begin{array}{ll}{\ell }_1^{\pm } q_i \to N q_f, \text{with} N\to {\ell }_2^{\mp }{W}^{\pm }\to {\ell }_2^{\mp } q \overline{q^{\prime }},& (3.44)\end{array}$

which is only possible of N is Majorana and is relatively free of SM backgrounds: As in the pp case, the existence of a high-p_T charged lepton without accompanying MET (at the partonic level) greatly reduces SM backgrounds. At the hadronic level, this translates to requiring one charged lepton and three high-p_T jets: two that arise from the decay of N, which scale as $p_T^j~M_N/4$, and the third from the W exchange, which scales as $p_T^j~M_W/2$. However, it was recently noted [312] that tagging this third jet is not necessary to reconstruct and identify the heavy neutrino, and that a more inclusive search may prove more sensitive. Although Equation (3.44) represents the so-called “golden channel,” searches for N → Z/h + ν decays, but which do not manifestly violate lepton number, have also been proposed [308].

While the lower beam energies translate to a lower mass reach for M_N, large luminosity targets and relative cleaner hadronic environment result in a better sensitivity than the LHC to smaller active-sterile mixing for smaller neutrino Majorana masses. In Figure 11, one sees the expected 90% CL active-sterile mixing |θ|² (or $|V_{\ell N}{|}^2$) sensitivity assuming (c) ep configuration with E_e = 150 GeV and (d) μp configuration with E_μ = 2 TeV. For ${L}~{O}(100)$ fb⁻¹, one can probe $|V_{\ell N}{|}^2~10^{-5}-10^{-3}$ for M_N = 250 − 750 GeV [304].

FIGURE 11

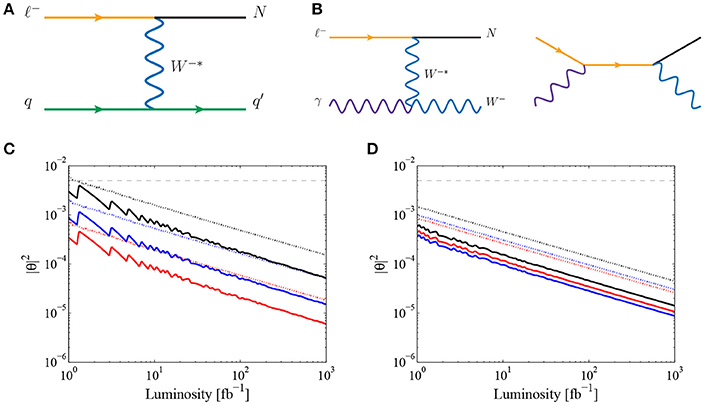
Figure 11. Born diagrams for DIS heavy neutrino (N) production via (A) W-exchange and (B) Wγ fusion. 90% CL active-sterile mixing |θ|² (or $|V_{\ell N}{|}^2$) sensitivity vs. integrated luminosity at DIS experiment assuming (C) ep configuration with E_e = 150 GeV and (D) μp configuration with E_μ = 2 TeV; red (blue) [black] line in (C,D) correspond to M_N = 250 (500) [750] GeV, whereas the solid/dotted lines are the sensitivities with/without cuts [304].

3.2.4. Heavy Neutrinos and U(1)_X Gauge Extensions at Colliders

Due to the small mixing between the heavy neutrinos and the SM leptons in minimal Type I Seesaw scenarios, typically of the order $|V_{\ell N}{|}^2~{O}(m_{\nu }/M_N)$, the predicted rates for collider-scale lepton number violation is prohibitively small. With a new gauge interaction, say, from U(1)_B−L, the gauge boson $Z^{\prime }=Z_{BL}$ can be produced copiously in pp and $p\bar{p}$ collisions via gauge interactions in quark annihilation [113, 313–319] and at Linear Colliders in e⁺e⁻ annihilation [317, 320–322],

$\begin{array}{ll}q\overline{q}\to Z^{\prime }\to NN \text{and} e^{+}{e}^{-}\to Z^{\prime }\to NN.& (3.45)\end{array}$

Z_BL's subsequent decay to a pair of heavy Majorana neutrinos may lead to a large sample of events without involving the suppression from a small active-sterile mixing angles [93, 323–330]. As a function of M_ZBL, Figure 12A shows the NLO+NLL(Thresh.) $pp\to Z_{BL}\to {\ell }^{+}{\ell }^{-}$ production and decay rate for $\sqrt{s}=13$ TeV and representative values of coupling g_BL. As a function of Majorana neutrino mass M_N1, Figure 12B shows the LO pp → Z_BL → NN production and decay rate for $\sqrt{s}=14$ TeV and 100 TeV and representative M_ZBL. As N is Majorana, the mixing-induced decays modes N → ℓ^±W^∓, νZ, νh open for M_N1 > M_W, M_Z, M_h, respectively. Taking these into account, followed by the leptonic and/or hadronic decays of W, Z and h, the detectable signatures include the lepton number violating, same-sign dileptons, NN → ℓ^±ℓ^±W^∓W^∓ → ℓ^±ℓ^± + nj [93, 301]; final states with three charged leptons, ℓ^±ℓ^±ℓ^∓ + nj+MET [325, 330, 331]; and four-charged lepton, ℓ^±ℓ^±ℓ^∓ℓ^∓+MET [324, 332]. Assuming only third generation fermions charged under B − L symmetry, HL-LHC can probe Z′ mass up to 2.2 TeV and heavy neutrino mass in the range of 0.2 − 1.1 TeV as shown in Figure 13 [301].

FIGURE 12

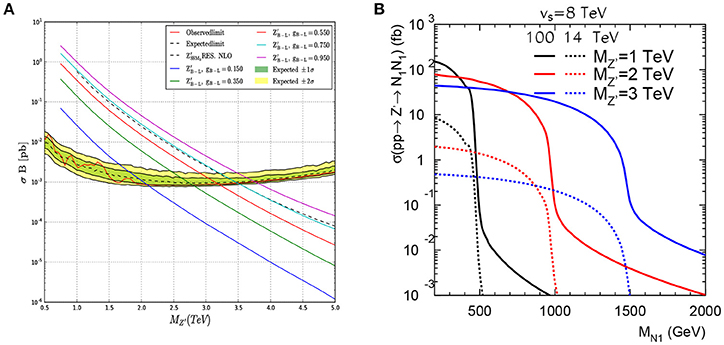
Figure 12. (A) The total cross section of $pp\to Z_{BL}\to {\ell }^{+}{\ell }^{-}$ as a function of for various representative values of g_BL at NLO+NLL(thresh.) for $\sqrt{s}=13$ TeV [343]. (B) The total cross section of pp → Z′ → NN as a function of M_N for $M_{Z^{\prime }}=1,2,3$ TeV, v_S = 8 TeV, with $\sqrt{s}=14$ TeV and 100 TeV.

FIGURE 13

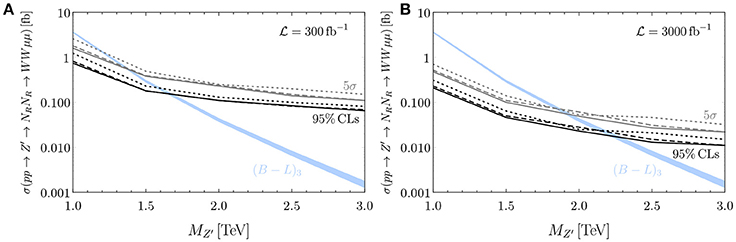
Figure 13. HL-LHC sensitivity for pp → Z′ → NN with $\sqrt{s}=14$ TeV for (A) ${L}=300$ fb⁻¹ and for (B) ${L}=3,000$ fb⁻¹, assuming $M_N=M_{Z^{\prime }}/4$ and $g_1^{\prime }=0.6$ [301].

For super-heavy Z_BL, e.g., M_ZBL ≳ 5 TeV ≫ M_N, one should note that at the 13 TeV LHC, a nontrivial contribution of the total pp → Z_BL → NN cross section comes from the kinematical threshold region, where the (NN) system's invariant mass is near m_NN ~ 2M_N and $Z_{BL}^{*}$ is far off-shell. This implies that the L-violating process pp → NN → ℓ^±ℓ^± + nj can still proceed despite Z_BL being kinematically inaccessible [163]. For more details, see section 3.2.6. Additionally, for such heavy Z_BL that are resonantly produced, the emergent N are highly boosted with Lorentz factors of γ ~ M_ZBL/2M_N. For M_N ≪ M_ZBL, this leads to highly collimated decay products, with separations scaling as ΔR ~ 2/γ ~ 4M_N/M_ZBL, and eventually the formation of lepton jets [225, 333], i.e., collimated clusters of light, charged leptons and electromagnetic radiation, and neutrino jets [141, 301, 312, 334], i.e., collimated clusters of electromagnetic and hadronic activity from decays of high-p_T heavy neutrinos.

Leading Order-accurate Monte Carlo simulations for tree-level processes involving Z′ bosons and heavy neutrinos in U(1)_X theories are possible using the SM+B-L FeynRules UFO model [325, 335, 336]. At NLO+PS accuracy, Monte Carlo simulations can be performed using the Effective LRSM at NLO in QCD UFO model [312, 337], and, for light, long-lived neutrinos and arbitrary Z′ boson couplings, the SM + W' and Z' at NLO in QCD UFO model [338, 339].

In B − L models, heavy neutrino pairs can also be produced through the gluon fusion process mediated by the two H₁ and H₂ [330, 340–342], and given by

$\begin{array}{ll}gg\to H_1,H_2\to NN.& (3.46)\end{array}$

For long-lived heavy neutrinos with M_N ≲ 200 GeV, this process becomes important compared to the channel mediated by Z′. Figure 14A shows that for M_H2 < 500 GeV, M_N < 200 GeV, and $M_{Z^{\prime }}=5$ TeV, the cross section σ(pp → H₂ → NN) can be above 1 fb at the $\sqrt{s}=13$ TeV LHC. For M_N < 60 GeV, decays of the SM-like Higgs H₁ also contributes to neutrino pair production. Summing over the contributions via H₁ and H₂ the total cross section can reach about 700 fb for M_H2 < 150 GeV as shown in Figure 14B.

FIGURE 14

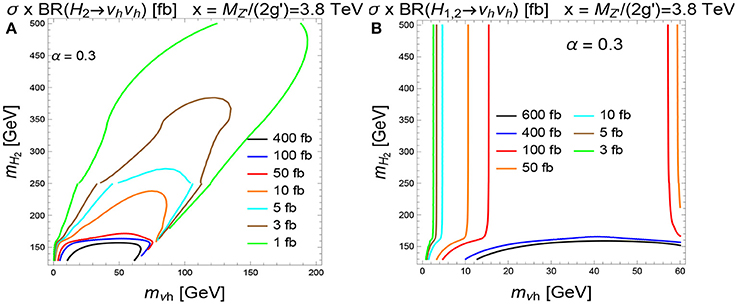
Figure 14. (A) Contour of the cross section for pp → H₂ → NN with $\sqrt{s}=13$ TeV in the plane of M_H2 vs. M_N for $M_{Z^{\prime }}=5$ TeV and $g_1^{\prime }=0.65$; (B) the same but for pp → H₁, H₂ → NN with $\sqrt{s}=13$ TeV and M_N < M_W [330].

Owing to this extensive phenomenology, collider experiments are broadly sensitive to Z′ bosons from U(1)_BL gauge theories. For example: Searches at LEP-II have set the lower bound $M_{Z^{\prime }}/g_{BL}\gtrsim 6$ TeV [314]. For more generic Z′ (including Z_R in LRSM models), comparable limits from combined LEP+EW precision data have been derived in del Águila et al. [345, 346]. Direct searches for a Z′ with SM-like couplings to fermions exclude $M_{Z^{\prime }}<2.9$ TeV at 95% CLs by ATLAS [347] and CMS [348] at $\sqrt{s}=8$ TeV. Z_BL gauge bosons with the benchmark coupling ${g_1}^{\prime }=g_{BL}$ are stringently constrained by searches for dilepton resonances at the LHC, with $M_{Z^{\prime }}\lesssim 2.1-3.75$ TeV excluded at 95% CLs for g_BL = 0.15 − 0.95, as seen in Figure 12A [343]. Searches for Z′ decays to dijets at the LHC have exclude $M_{Z^{\prime }}<1.5-3.5$ TeV for g_BL = 0.07 − 0.27 [349, 350]. Figure 15A shows that ATLAS excludes $M_{Z^{\prime }}<4.5$ TeV at $\sqrt{s}=13$ TeV. Further constraints are given in the plane of coupling strength ${\gamma }^{\prime }=g_{BL}/g_Z$ vs. $M_{Z^{\prime }}$ by ATLAS at $\sqrt{s}=13$ TeV with 36.1 fb⁻¹ [344] as shown in the lower curve of Figure 15B. For $\sqrt{s}=27$ TeV, early projections show that with ${L}=1(3)$ ab⁻¹, $M_{Z^{\prime }}\lesssim 19(20)$ TeV can be probed in the dijet channel [351].

FIGURE 15

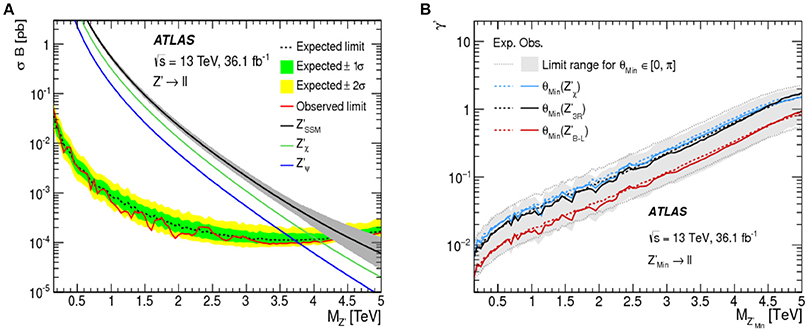
Figure 15. (A) Exclusion limit on pp → Z′ → ℓ⁺ℓ⁻ by ATLAS at $\sqrt{s}=13$ TeV with 36.1 fb⁻¹; (B) 13 TeV upper limit at 95% CL on the coupling strength ${\gamma }^{\prime }=g_{BL}/g_Z$ as a function of $M_{Z^{\prime }}$ [344].

3.2.5. Heavy Neutrinos and the Left-Right Symmetric Model at Colliders

In addition to the broad triplet scalar phenomenology discussed later in section 4.2, the LRSM predicts at low scales massive $W_R^{\pm }$ and Z_R gauge bosons that couple appreciably to SM fields as well as to heavy Majorana neutrinos N. The existence of these exotic states leads to a rich collider phenomenology that we now address, focusing, of course, on lepton number violating final states. The collider phenomenology for Z_R searches is very comparable to that for Z′ gauge bosons in U(1)_X theories [93, 323–330], and thus we refer readers to section 3.2.4 for more generic collider phenomenology.

In the LRSM, for M_N < M_WR or M_N < M_ZR/2, the most remarkable collider processes are the single and pair production of heavy Majorana neutrinos N through resonant charged and neutral SU(2)_R currents,

$\begin{array}{ll}q\overline{q^{\prime }}\to W_R^{\pm }\to N_i {\ell }^{\pm } \text{and} q\overline{q^{\prime }}\to Z_R\to N_i N_j.& (3.47)\end{array}$

As first observed in Keung and Senjanović [240], N_i can decay into L-violating final-states, giving rise to the collider signatures,

$\begin{array}{ll}\begin{array}{l}pp\to W_R^{\pm }\to N_i {\ell }^{\pm }\to {\ell }_1^{\pm } {\ell }_2^{\pm }+nj \text{and}\\ pp\to Z_R\to N_i N_j\to {\ell }_1^{\pm } {\ell }_2^{\pm }+nj.\end{array}& (3.48)\end{array}$

In the minimal/manifest LRSM, the decay of N_i proceeds primarily via off-shell three-body right-handed currents, as shown in Figure 16A, due to mixing suppression to left-handed currents. In a generic LRSM scenario, the naïve mixing suppression of $|V_{\ell N}{|}^2~{O}(m_{\nu }/M_N)$ is not guaranteed due to the interplay between the Types I and II Seesaws, e.g., as in Anamiati et al. [228] and Das et al. [230]. (However, heavy-light neutrino mixing in the LRSM is much less free than in pure Type I scenarios due to constraints on Dirac and RH masses from LR parity; see section 3.1.4 for more details). Subsequently, if |V_ℓN| is not too far from present bounds (see e.g., [91]), then decays of N_i to on-shell EW bosons, as shown in Figure 16B, can occur with rates comparable to decays via off-shell $W_R^{*}$ [87]. The inverse process [352], i.e., N_i production via off-shell EW currents and decay via off-shell RH currents as well as vector boson scattering involving t-channel W_R and Z_R bosons [353] are in theory also possible but insatiably phase space-suppressed. For M_N > M_WR, M_ZR, resonant N production via off-shell SU(2)_R currents is also possible, and is analogous to the production through off-shell, SU(2)_L currents in Equations (3.33)–(3.34). As M_WR, M_ZR are bound to be above a few-to-several TeV, the relevant collider phenomenology is largely the same as when M_N < M_WR, M_ZR [144], and hence will not be individually discussed.

FIGURE 16

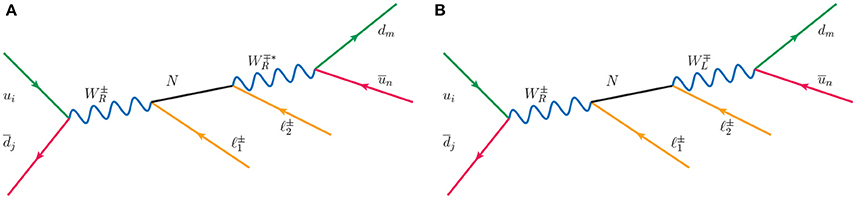
Figure 16. Born-level diagrams depicting resonant W_R, N production and decay to same-sign leptons in LRSM via (A) successive right-handed currents and (B) mixed right- and left-handed currents.

Aside from the mere possibility of L violation, what makes these channels so exceptional, if they exist, are their production rates. Up to symmetry-breaking corrections, the RH gauge coupling is g_R ≈ g_L ≈ 0.65, which is not a small number. In Figure 17, we show for $\sqrt{s}=13$ and 100 TeV the production rate for resonant W_R at various accuracies as a function of mass [141]; rates for Z_R are marginally smaller due to slight coupling suppression. As in other Seesaw scenarios, much recent progress has gone into advancing the precision of integrated and differential predictions for the LRSM: The inclusive production of W_R and Z_R are now known up to NLO+NNLL(Thresh) [141], automated at NLO+NLL(Thresh+k_T) [354, 355], automated at NNLO [356, 357], and differentially has been automated at NLO with parton shower matching for Monte Carlo simulations [312]. For $\sqrt{{\tau }_0}=M_{W_R/Z_R}/\sqrt{s}\gtrsim 0.3$, threshold corrections become as large as (N)NLO corrections, which span roughly +20% to +30%, and have an important impact cross section normalizations [141, 358]. For example: The inclusive W_R cross section at LO (NLO+NNLL) for M_WR = 5 TeV is σ ~ 0.7 (1.7) fb. After ${L}=1\text{a}{\text{b}}^{-1}$ and assuming a combined branching-detection efficiency-selection acceptance of BR$\times \epsilon \times {A}=2\%$, the number of observed events is N ~ 14 (34). For simple Gaussian statistics with a zero background hypothesis, this is the difference between a 6σ “discovery” and 4σ “evidence”. Clearly, the HL-LHC program is much more sensitive to ultra-high-mass resonances than previously argued.

FIGURE 17

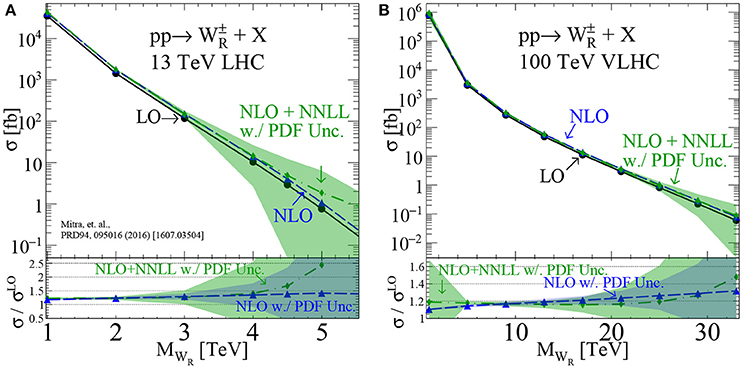
Figure 17. Upper panel: As a function of M_WR, pp → W_R production cross section for $\sqrt{s}=$ (A) 13 and (B) 100 TeV, at LO (solid), NLO (dash), and NLO+NNLL (dash-dot) with 1σ PDF uncertainty (shaded); Lower: NLO (dash) and NLO+NNLL (dash-dot) K-factors and PDF uncertainties [141].

For the collider processes in Equation (3.48), such estimations of branching, acceptance/selection, and background rates resemble actual rates: see, e.g., [87, 141, 240, 352, 353, 359–361]. For M_WR, M_ZR ≫ M_N, one finds generically that BR$(W_R\to {\ell }^{\pm }{N}_i)~1/(1+3N_c)~{O}(10\%)$, BR$(Z_R\to N_i{N}_j)~{O}(10\%)$, and, for the lightest heavy N_i in this limit, BR$(N_1\to {\ell }^{\pm }X)~{O}(100\%)$. Trigger rates for multi-TeV, stable charged leptons (e, μ) at ATLAS and CMS exceed 80–95%, but conversely, the momentum resolution for such energetic muons begins to degrade severely; for additional information, see Aad et al. [52], Collaboration [362], Khachatryan [363, 364] and references therein. As in searches for Majorana neutrinos in the previous Type I-based scenarios, the final-states in Equation (3.48) possess same-sign, high-p_T charged leptons without accompanying MET at the partonic level [240, 248, 359]. For the LRSM, this is particularly distinct since the kinematics of the signal process scale with the TeV-scale W_R and Z_R masses. Accordingly, top quark and EW background processes that can mimic the fiducial collider definition correspondingly must carry multi-TeV system invariant masses, and are inherently more phase space suppressed than the signal processes at the LHC [359]. Consequently, so long as $M_N\lesssim M_{W_R},M_{Z_R}\ll \sqrt{s}$, s-channel production of W_R and Z_R remains the most promising mechanism for discovering L violation in the LRSM at hadron colliders. In Figure 18 we show the discovery potential at 14 TeV LHC of W_R and N in (a) the minimal LRSM as in Figure 16A after ${L}=30\text{f}{\text{b}}^{-1}$ [360] and (b) the agnostic mixing scenario as in Figure 16B [87]. Final-states involving τ leptons are also possible, but inherently suffer from the difficult signal event reconstruction and larger backgrounds due to partonic-level MET induced by τ decays [365].

FIGURE 18

Figure 18. Discovery potential at 14 TeV LHC of W_R and N in (A) the minimal LRSM as in Figure 16A after ${L}=30\text{f}{\text{b}}^{-1}$ [360] and (B) the agnostic mixing scenario as in Figure 16B [87].

Unfortunately, direct searches at the $\sqrt{s}=7/8$ TeV LHC via the DY channels have yielded no evidence for lepton number violating processes mediated by W_R and Z_R gauge bosons from the LRSM [52, 300, 363, 366]. As shown in Figure 19, searches for W_R/Z_R in the e^±e^± + nj and μ^±μ^± + nj final state have excluded, approximately, M_WR/ZR ≲ 1.5 − 2.5 TeV and M_N ≲ 2 TeV. However, sensitivity to the e^±e^± + nj greatly diminishes for M_N ≪ M_WR/ZR.

FIGURE 19

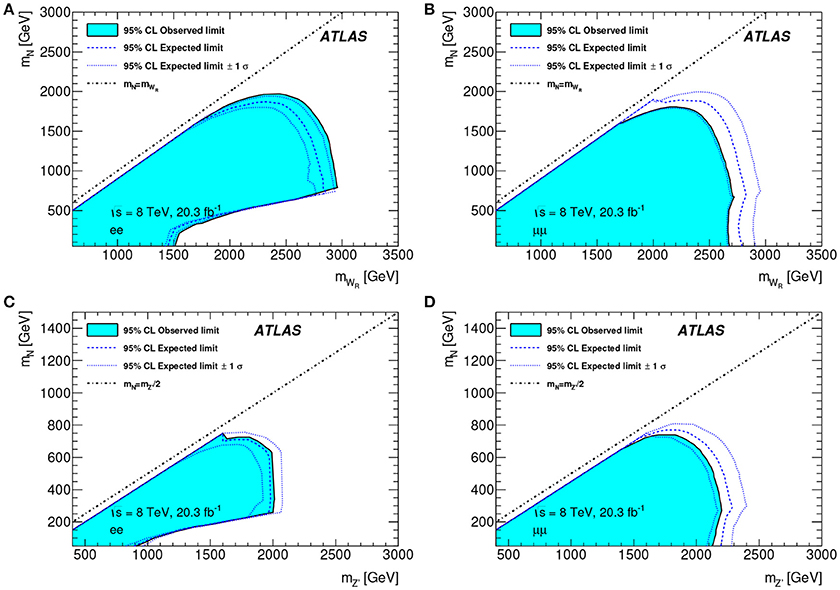
Figure 19. 95% CL exclusion of the (M_V, M_N) parameter space by the ATLAS experiment at $\sqrt{s}=8$ for V = W_R (Top) and V = Z_R (Bottom) production in the (L) e^±e^± + nj and (R) μ^±μ^± + nj final state [52].

Interestingly, for M_N ≪ M_WR, M_ZR, decays of N become highly boosted and its decay products, i.e., ${\ell }_2^{\pm }q\overline{q^{\prime }}$, become highly collimated. In such cases, the isolation criterion for electrons (and some muons) in detector experiments fail, particularly when $\sqrt{r}=M_N/M_{W_R}<0.1$ [52, 87, 141, 359]. Instead of requiring the identification of two well-isolated charged leptons for the processes given in Equation (3.48), one can instead consider the N-decay system as a single, high-p_T neutrino jet [141, 312]. The hadronic-level collider signature is then

$\begin{array}{ll}pp\to W_R\to {\ell }^{\pm } N\to {\ell }^{\pm } j_N,& (3.49)\end{array}$

where the neutrino jet j_N is comprised of three “partons”, $({\ell }_2,q,\overline{q^{\prime }})$, with an invariant mass of m_j ~ M_N. (Neutrino jets are distinct from so-called “lepton jets” [225], which are built from collimated charged leptons and largely absent of hadrons). This alternative topology for M_N ≪ M_WR recovers the lost sensitivity of the same-sign dilepton final state, as seen in Figure 20. Inevitably, for N masses below the EW scale, rare L-violating decay modes also of SM particles open. In particular, for M_N below the top quark mass m_t, one has the rare decay mode, $t\to b{W}_R^{+*}\to b{\ell }_1^{+}N\to b{\ell }_1^{+}{\ell }_2^{\pm }q\overline{q^{\prime }}$ [220]. Such processes, however, can be especially difficult to distinguish from rare SM processes, e.g., t → Wbℓ⁺ℓ⁻ [367], particularly due to the large jet combinatorics.

FIGURE 20

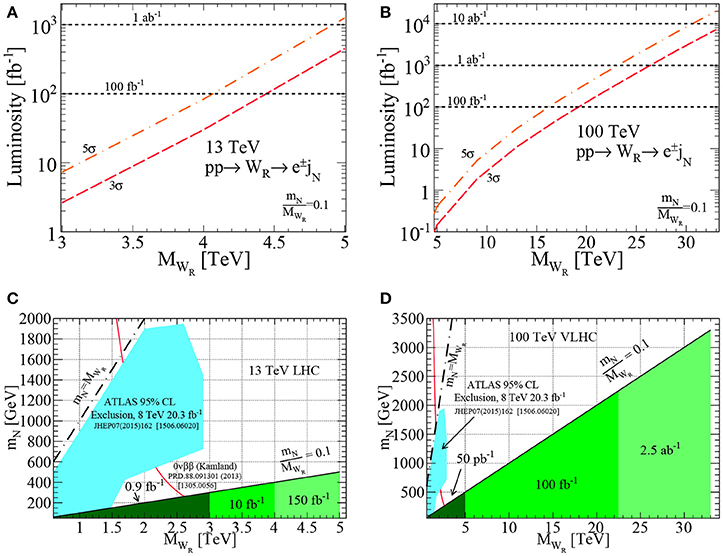
Figure 20. Discovery (A,B) and 95% CL exclusion (C,D) potential of neutrino jet searches, i.e., $pp\to W_R\to e^{\pm }{j}_N$, at (A,C) $\sqrt{s}=$ 13 and (B,D) 100 TeV. Also shown in (C,D), ATLAS experiment's 8 TeV 95% CL [52] and KamLAND-Zen 90% CL [36, 402] exclusion limits. Figure from Mitra et al. [141].

For too small M_N/M_WR ratio, the lifetime for N, which scales as ${\tau }_N~M_{W_R}^4/M_N^5$, can become quite long. In such instances, the decays of N are no longer prompt and searches for pp → W_R → Nℓ map onto searches for Sequential Standard Model W′ bosons [338, 368]. Likewise, searches for L-violating top quark decays become searches for RH currents in t → bℓp_T decays. For intermediate lifetimes, displaced vertex searches become relevant [223, 228, 230, 334, 369].

Another recent avenue of exploration is the reassessment for resonant production of W_R and Z_R in Equation (3.48). In the limit where $M_{W_R}\gtrsim \sqrt{s}$ but $M_N\ll \sqrt{s}$, resonant production of N, and hence a lepton number violating final state, is still possible despite W_R being kinematically inaccessible [163]. In such cases, N is produced near mass threshold with $p_T^N~M_N$ instead of the usual $p_T^N~M_{W_R}/2$. The same-sign leptons discovery channel is then kinematically and topologically identical to Type I Seesaw searches, and hence is actively searched for at the LHC, despite this kinematic regime not being well-studied in the literature. Reinterpretation of observed and expected sensitivities at the 14 and 100 TeV LHC are shown in Figure 21. One sees that with the anticipated cache of LHC data, M_WR ≲ 9 TeV can be excluded for M_N ≲ 1 TeV.

FIGURE 21

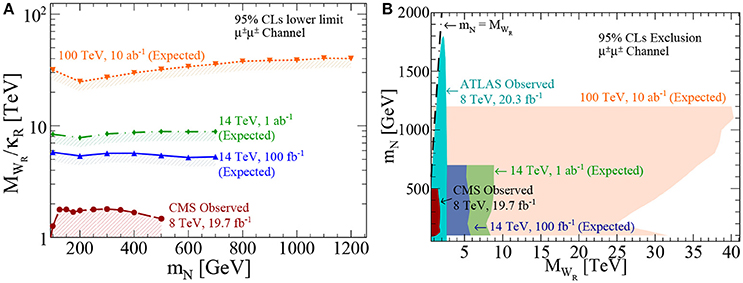
Figure 21. (A) As a function of M_N and for right-left coupling ratio κ_R = g_R/g_L, the observed 8 TeV LHC 95% CLs lower limit on (M_WR/κ_R) (dash-dot), expected 14 TeV sensitivity with ${L}=100$ fb⁻¹ (solid-triangle) and 1 ab⁻¹ (dash-dot-diamond), and expected 100 TeV VLHC sensitivity with 10 ab⁻¹ (dot-star). (B) Observed and expected 95% CL_s sensitivities to the (M_WR, M_N) parameter space for various collider configurations via direct and indirect searches in the μ^±μ^± final state [163].

In addition to the aforementioned DY and VBF channels, there has been recent attention [312, 353, 370, 371] given to the production of LRSM scalar and vector bosons in association with heavy flavor quarks, e.g.,

$\begin{array}{ll}g\stackrel{(-)}{b}\to \stackrel{(-)}{t}{W}_R^{\pm } \text{or} \stackrel{(-)}{t}{H}_R^{\pm } \text{and} gg\to t\overline{t}{Z}_R \text{or} t\overline{t}{H}_R^0.& (3.50)\end{array}$

As in the SM, such processes are critical in measuring the couplings of gauge bosons to quarks as well as determining heavy flavor PDFs. However, also as in the SM, care is needed in calculating the rates of these processes when M_R ≫ m_b, m_t. Here, M_R is generically the mass of the RH scalar or vector boson. As discussed just after Equation (3.38), it has been noted recently in Mattelaer et al. [312] that such associated processes possess logarithmic dependence on the outgoing top quarks' kinematics, i.e., that the inclusive cross section scales as $\sigma ~{\alpha }_s^k{log}^{2k-1}(M_R^2/(m_t^2+p_T^{t2}))$. Subsequently, for M_R ≳ 1 − 2 TeV, these logarithms grow numerically large since ${log}^2(M_R^2/m_t^2)\gtrsim 1/{\alpha }_s$ and can spoil the perturbativity convergence of fixed order predictions. For example, the (N)NLO K-factor of K^(N)NLO ≳ 1.6 − 2.0 claimed in Dev et al. [353] indicate a loss of perturbative control, not an enhancement, and leads to a significant overestimation of their cross sections. As in the case of EW boson production in association with heavy flavors [372, 373], the correct treatment requires either a matching/subtraction scheme with top quark PDFs to remove double counting of phase space configurations [374, 375] or kinematic requirements on the associated top quarks/heavy quark jets, e.g., Equation (3.41) [255].

In all of these various estimates for discovery potential, it is important to also keep in mind what can be learned from observing L violation and LR symmetry at the LHC or a future collider, including ep machines [87, 129, 383]. Primary goals post-discovery include: determination of W_R and Z_R chiral coupling to fermions [87, 383, 129], which can be quantified for quarks and leptons independently [87], determination of the leptonic and quark mixing [129, 130, 228, 230, 384–387], as well as potential CP violation [228, 230, 386–388]. We emphasize that the discovery of TeV-scale LRSM could have profound implications on high-scale baryo- and leptogenesis [10, 389–392] as well as searches for 0νββ [129, 162, 385, 393, 394]. The latter instance is particularly noteworthy as the relationship between $m_{\nu }^{ee}$ and m_ν1 in the LRSM is different because of the new mediating fields [385].

We finish this section by noting our many omissions, in particular: supersymmetric extensions of the LRSM, e.g., Frank and Saif [395], and Demir et al. [396]; embeddings into larger internal symmetry structures, e.g., Goh and Krenke [361] and Appelquist and Shrock [397]; as well as generic extensions with additional vector-like or mirror quarks, e.g., Goh and Krenke [361], and de Almeida et al. [398]. While each of these extensions have their phenomenological uniquenesses, their collider signatures are broadly indistinguishable from the minimal LRSM scenario. With regard to Type I-based Seesaws in extra dimensional frameworks, it is worthwhile to note that it has recently [399–401] been observed that in warped five-dimensional models, a more careful organization of Kaluza-Klein states and basis decomposition results in an inverse Seesaw mechanism as opposed to a canonical Type I-like Seesaw mechanism, as conventionally believed. Again, this leads to greatly suppressed L violation at collider experiments.

3.2.6. Heavy Neutrino Effective Field Theory at Colliders

As discussed in section 3.1.5, the production and decay of Majorana neutrinos in colliders may occur through contact interactions if mediating degrees of freedom are much heavier than the hard scattering process scale. Such scenarios have recently become a popular topic [163, 171, 172, 218, 305, 403–406], in part because of the considerable sensitivity afforded by collider experiments. This is particularly true for L-violating final-states in pp collisions, which naturally have small experimental backgrounds. As shown in Figure 22, for various operators, searches for L-violating process $pp\to N{\ell }_1^{\pm }\to {\ell }_1^{\pm }{\ell }_2^{\pm }+X$ by the ATLAS and CMS experiments have set wide limits on the effective mass scale of Λ > 1 − 5 TeV for M_N = 100 GeV−4.5 TeV [59, 163, 403]. Projections for $\sqrt{s}=14(100)$ TeV after ${L}=1(10)$ ab⁻¹ show that Λ ≲ 9 (40) TeV can be achieved [163]. These search strategies are also applicable for the more general situation where L violation is mediated entirely via SMEFT operators [176, 177] as introduced in section 3.1.5.

FIGURE 22

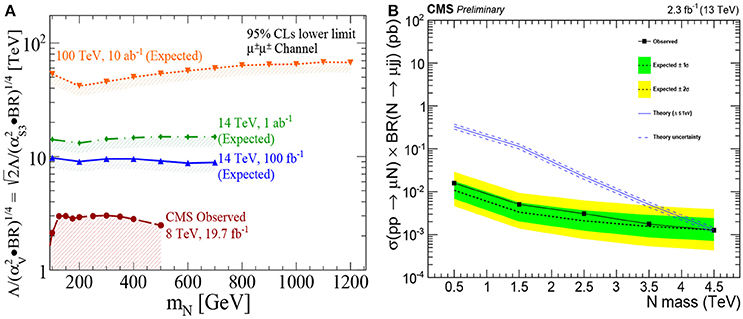
Figure 22. Observed limits and expected sensitivities at current and future hadron collider experiments on NEFT mass scale Λ for (A) low-mass [163] and (B) high-mass [59] Majorana neutrinos N via the L-violating $pp\to {\ell }_1^{\pm }{\ell }_2^{\pm }+X$.

4. The Type II Seesaw and Lepton Number Violation at Colliders

In this section we review lepton number violating collider signatures associated with the Type II Seesaw mechanism [14–18, 407] and its extensions. The Type II model is unique among the original tree-level realizations of the Weinberg operator in that lepton number is spontaneously broken; in the original formulations of the Type I and III Seesaws, lepton number violation is explicit by means of a Majorana mass allowed by gauge invariance. In section 4.1, we summarize the main highlights of the canonical Type II Seesaw and other Type II-based scenarios. We then review in section 4.2 collider searches for lepton number violation mediated by exotically charged scalars (H^±, H^±±), which is the characteristic feature of Type II-based scenarios.

4.1. Type II Seesaw Models

In the Type II mechanism [14–18, 407], tiny neutrino masses arise through the Yukawa interaction,

$\begin{array}{ll}\Delta {{L}}_{II}^m=-\overline{L^c} Y_{\nu } i{\sigma }_2{\Delta }_{L}L+ \text{H}\text{.c}\text{.},& (4.1)\end{array}$

between the SM LH lepton doublet L, its charge conjugate, and an SU(2)_L scalar triplet (adjoint representation) Δ_L with mass M_Δ and Yukawa coupling Y_ν. More precisely, the new scalar transforms as (1, 3, 1) under the full SM gauge symmetry and possesses lepton number L = −2, thereby ensuring that Equation (4.1) conserves lepton number before EWSB. Due to its hypercharge and L assignments, Δ_L does not couple to quarks at tree-level. It does, however, couple to the SM Higgs doublet, particularly through the doublet-triplet mixing operator

$\begin{array}{ll}\Delta {{L}}_{H{\Delta }_L}\ni \mu H^{T}i{\sigma }_2{\Delta }_L^{†}H+ \text{H}\text{.c}\text{.}& (4.2)\end{array}$

The importance of this term is that after minimizing the full Type II scalar potential V_{Type II}, Δ_L acquires a small vev v_Δ that in turn induces a LH Majorana mass for SM neutrinos, given by

$\begin{array}{ll}{M}_{\nu }=\sqrt{2}{Y}_{\nu }{v}_{\Delta } \text{with} v_{\Delta }=\langle {\Delta }_L\rangle =\frac{\mu v_0^2}{\sqrt{2}{M}_{\Delta }^2}.& (4.3)\end{array}$

In the above, $v_0=\sqrt{2}\langle H\rangle$ is the vev of the SM Higgs and $v_0^2+v_{\Delta }^2={(\sqrt{2}{G}_F)}^{-1}\approx {(246\text{ GeV})}^2$. As a result of B − L being spontaneously broken by Δ_L, tiny 0.1eV neutrino masses follow from the combination of three scales: μ, v₀, and M_Δ. In addition, after EWSB, there are seven physical Higgses, including the singly and doubly electrically charged H^± and H^±± with masses $M_{H^{\pm },H^{\pm \pm }}~M_{\Delta }$. As v_Δ contributes to EWSB at tree-level, and hence the EW ρ/T-parameter, v_Δ is constrained by precision EW observables, with present limits placing $v_{\Delta }\lesssim {O}(1$ GeV) [408–416]. The impact of triplet scalars on the naturalness of the SM-like Higgs at 125 GeV has also been studied [412, 417, 418]. The simultaneous sensitivity of M_ν to collider, neutrino mass measurement, and neutrino oscillation experiments is one of the clearest examples of their complementarity and necessity to understanding neutrinos physics.

For SM-like Yukawas $Y_{\nu }~10^{-6}-1$, one finds that v_Δ ~ 0.1eV − 100keV are needed in order to reproduce 0.1 eV neutrino masses. Subsequently, for μ ~ M_Δ, then $M_{\Delta }~\mu ~10^8-10^{14}$ GeV, and for μ ~ v₀, then $M_{\Delta }~10^5-10^8$ GeV. In either case, these scales are too high for present-day experiments. However, as nonzero μ is associated with both lepton number and custodial symmetry non-conservation, one may expect it to be small [121] and natural, in the t'Hooft sense [419]. Imposing technical naturalness can have dramatic impact on LHC phenomenology: for example, if μ ~ 1 MeV (keV), then $M_{\Delta }~10^2-10^5(10^1-10^4)$ GeV, scales well within the LHC's energy budget. Moreover, this also indicates that proposed future hadron collider experiments [148, 149] will be sensitive to MeV-to-GeV values of the scalar-doublet mixing parameter μ, independent of precision Higgs coupling measurements, which are presently at the 10% level [420]. Assuming Higgs coupling deviations of ${O}(\mu /M_h)$, this implies the weak 7/8 TeV LHC limit of $\mu \lesssim {O}$(10 GeV). While not yet competitive with constraints from EW precision data, improvements on Higgs coupling measurements will be greatly improved over the LHC's lifetime.

After decomposition of leptons into their mass eigenstates, the Yukawa interactions of the singly and doubly charged Higgses are

$\begin{array}{ll}{\nu }_L^{T}C{\Gamma }_{+}{H}^{+}{\ell }_L, : {\Gamma }_{+}=\cos {\theta }_{+}\frac{m_{\nu }^{diag}}{v_{\Delta }}{U}_{PMNS}^{†},{\theta }_{+}\approx \frac{\sqrt{2}{v}_{\Delta }}{v_0},& (4.4)\end{array}$

$\begin{array}{ll}{\ell }_L^{T}C{\Gamma }_{++}{H}^{++}{\ell }_L : {\Gamma }_{++}=\frac{M_{\nu }}{\sqrt{2}{v}_{\Delta }}=U_{PMNS}^{*}\frac{m_{\nu }^{diag}}{\sqrt{2}{v}_{\Delta }}{U}_{PMNS}^{†}.& (4.5)\end{array}$

The constrained neutrino mass matrix $M_{\nu }=\sqrt{2}{v}_{\Delta }{\Gamma }_{++}$ and squared Yukawa coupling $Y_{+}^i\equiv \sum _j|{\Gamma }_{+}^{ji}{|}^2{v}_{\Delta }^2$ with vanishing Majorana phases are shown in Figures 23, 24 respectively. The results reveal the following mass and Yukawa patterns:

$\begin{array}{ll}{M}_{\nu }^{22},M_{\nu }^{33}\gg M_{\nu }^{11}; Y_{+}^2,Y_{+}^3\gg Y_{+}^1\text{for}\text{NH};& (4.6)\end{array}$

$\begin{array}{ll}{M}_{\nu }^{11}\gg M_{\nu }^{22},M_{\nu }^{33}; Y_{+}^1\gg Y_{+}^2,Y_{+}^3\text{for}\text{IH}.& (4.7)\end{array}$

FIGURE 23

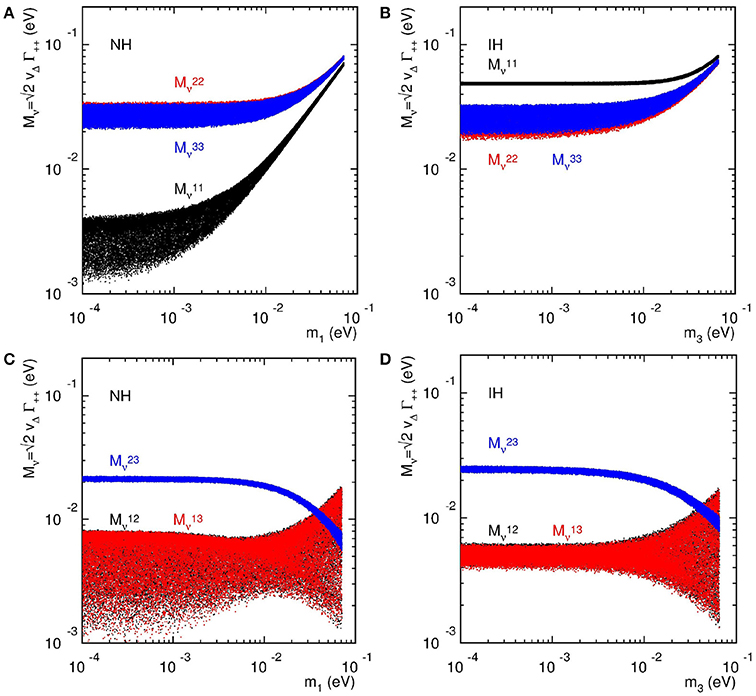
Figure 23. Constraints on the diagonal (A,B) and off-diagonal (C,D) elements of the neutrino mass matrix $M_{\nu }\equiv \sqrt{2}{v}_{\Delta }{\Gamma }_{++}$ vs. the lowest neutrino mass for NH (A,C) and IH (B,D) when Φ₁ = 0 and Φ₂ = 0.

FIGURE 24

Figure 24. Constraints on the squared coupling $Y_{+}^i\equiv \sum _j|{\Gamma }_{+}^{ji}{|}^2{v}_{\Delta }^2$, vs. the lowest neutrino mass for NH (A) and IH (B).

Below $v_{\Delta }\approx 10^{-4}$ GeV, the doubly charged Higgs H^±± decays dominantly to same-sign lepton pairs. For vanishing Majorana phases Φ₁ = Φ₂ = 0, we show in Figures 25, 26 the branching fraction of the decays into same-flavor and different-flavor leptonic final states, respectively. Relations among the branching fractions of the lepton number violating Higgs decays of both the singly- and doubly-charged Higgs in the NH and IH, with vanishing Majorana phases, are summarized in Table 2.

FIGURE 25

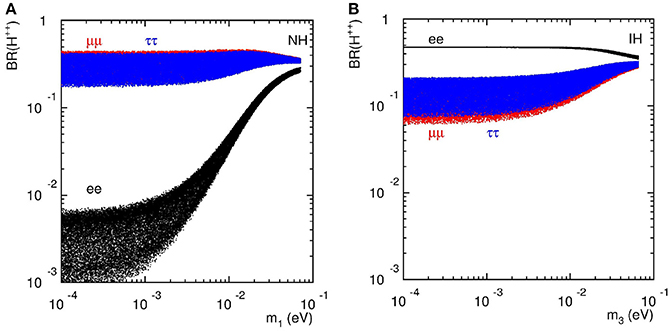
Figure 25. Scatter plots for the H⁺⁺ decay branching fractions to the flavor-diagonal like-sign dileptons vs. the lowest neutrino mass for NH (A) and IH (B) with Φ₁ = Φ₂ = 0.

FIGURE 26

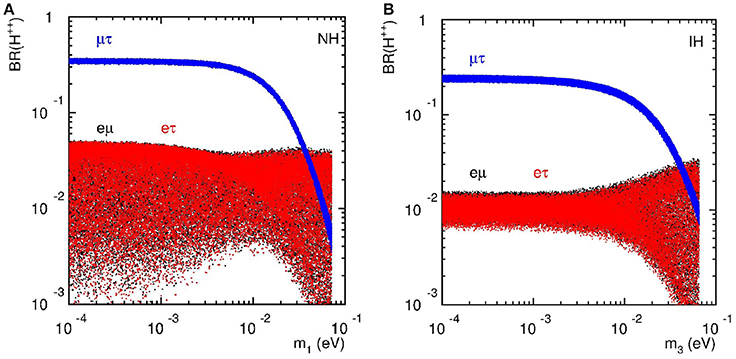
Figure 26. H⁺⁺ decay to the flavor-off-diagonal like-sign dileptons vs. the lowest neutrino mass for NH (A) and IH (B) with Φ₁ = Φ₂ = 0.

TABLE 2

Table 2. Relations among the branching fractions of the lepton number violating Higgs decays for the neutrino mass patterns of NH and IH, with vanishing Majorana phases.

The impact of Majorana phases can be substantial in doubly charged Higgs decays [421, 422]. In the case of the IH, a large cancellation among the relevant channels occurs due to the phase at Φ₁ = π. As a result, in this scenario, the dominant channels swap from H⁺⁺ → e⁺e⁺, μ⁺τ⁺ when Φ₁ ≈ 0 to H⁺⁺ → e⁺μ⁺, e⁺τ⁺ when Φ₁ ≈ π, as shown in Figure 27. Therefore this qualitative change can be made use of to extract the value of the Majorana phase Φ₁. In the NH case, however, the dependence of the decay branching fractions on the phase is rather weak because of the lack of a subtle cancellation [408].

FIGURE 27

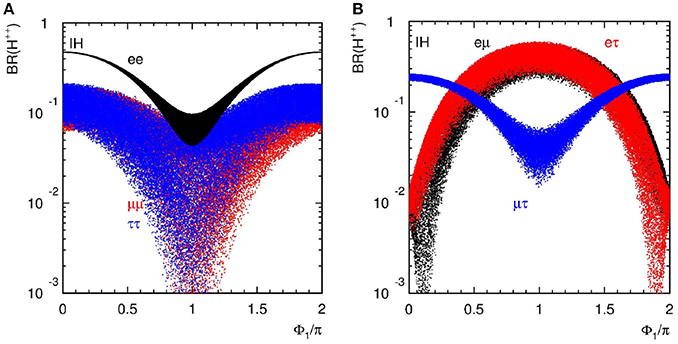
Figure 27. Scatter plots of the same (A) and different (B) flavor leptonic branching fractions for the H⁺⁺ decay vs. the Majorana phase Φ₁ for the IH with m₃ = 0 and Φ₂∈(0, 2π).

The Type II mechanism can be embedded in a number of extended gauge scenarios, for example the LRSM as discussed in section 3.1.4, as well as GUTs, such as (331) theories [423–426] and the extensions of minimal SU(5) [427]. For (331) models, one finds the presence of bileptons [428, 429], i.e., gauge bosons with L = ±2 charges and hence Q = ±2 electric charges. In a realistic extension of the Georgi-Glashow model, a scalar 15-dimensional representation is added [430] and the scalar triplet stays in the 15 representation together with scalar leptoquark Φ ~ (3, 2, 1/6). The SU(5) symmetry thus indicates that the couplings of the leptoquark to matter gain the same Yukawas Y_ν responsible for neutrino mass matrix [431]. Extensions with vector-like leptons in nontrivial SU(2)_L representations are also possible [432]. Unsurprisingly, the phenomenology [423, 425, 433–435] and direct search constraints [433, 434] for L-violating, doubly charged vector bosons are similar to L-violating, doubly charged scalar bosons, which we now discuss.

4.2. Triplet Higgs Scalars at Colliders

4.2.1. Triplet Higgs Scalars and the type II Seesaw at Colliders

If kinematically accessible, the canonical and well-studied [145, 408, 436, 437] triplet scalars production channels at hadron colliders are the neutral and charged current DY processes, given by

$\begin{array}{ll}pp\to {\gamma }^{*}/Z^{*}\to H^{++}{H}^{--},pp\to W^{\pm *}\to H^{\pm \pm }{H}^{\mp },& (4.8)\end{array}$

and shown in Figure 28A. Unlike Type I models, scalars in the Type II Seesaw couple to EW bosons directly via gauge couplings. Subsequently, their production rates are sizable and can be predicted as a function of mass without additional input. In Figure 29 we show the LO pair production cross section of triplet scalars via the (a) neutral and (b) charged current DY process at $\sqrt{s}=14$ and 100 TeV. NLO in QCD corrections to these processes are well-known [438] and span K^NLO = σ^NLO/σ^LO = 1.1 − 1.3 away from boundaries of collider phase space; moreover, due to the color-structure of DY-like processes, inclusive kinematics of very heavy scalar triplets are Born-like and thus naïve normalization of kinematics by K^NLO gives reliable estimates of both NLO- and NLO+PS-accurate results [275, 338]. For $M_{H^{\pm \pm }}=1$ TeV, one finds that the LO pair production rates can reach σ ~ 0.1 (10) fb at $\sqrt{s}=14$ (100) TeV, indicating ${O}(10^2)({O}(10^4))$ of events with the ab⁻¹-scale data sets expected at the respective collider program.

FIGURE 28

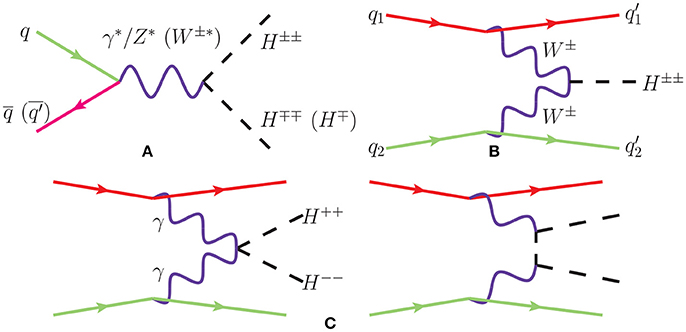
Figure 28. Born-level diagrams depicting Type II triplet scalar production in pp collisions via (A) the DY mechanism, (B) same-sign W^±W^± scattering, and (C) γγ fusion.

FIGURE 29

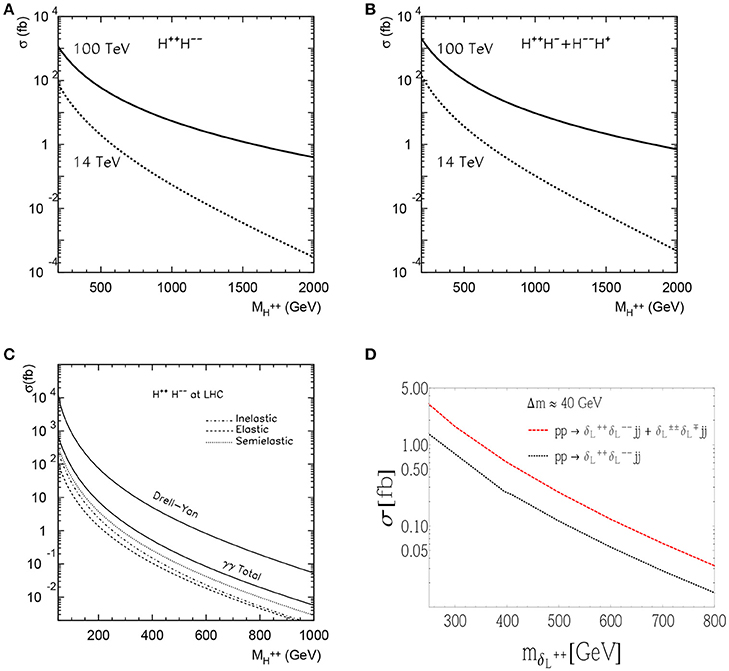
Figure 29. Production cross section for (A) pp → H⁺⁺H⁻⁻ and (B) H^±±H^∓ at $\sqrt{s}=14$ and 100 TeV, as well as for (C) pp → H⁺⁺H⁻⁻jj from γγ fusion [440] and (D) pp → H⁺⁺H⁻⁻jj + H^±±H^∓ from VBF at $\sqrt{s}=14$ TeV [409].

In addition to the DY channels are: single production of charged Higgses via weak boson scatter, as shown in Figure 28B and investigated in Han et al. [410], and Chen et al. [439]; charged Higgs pair production via γγ scattering, as shown in Figure 28C, studied in Dutta et al. [409], Han et al. [440], Drees et al. [441], Bambhaniya et al. [442], and Babu and Jana [443], and computed at $\sqrt{s}=14$ TeV [440] in Figure 29C; as well as pair production through weak boson scattering, as studied in Dutta et al. [409] and Bambhaniya et al. [442] and computed for the 14 TeV LHC [409] in Figure 29D. As in the case of Wγ scattering in heavy N production in section 3, there is renewed interest [442] in the γγ-mechanisms due to the new availability of photon PDFs that include both elastic and (deeply) inelastic contributions, e.g., NNPDF 2.3 and 3.0 QED PDF sets [444, 445]. However, care should be taken in drawing conclusions based on these specific PDF sets due to the (presently) large γ-PDF uncertainty, particularly at large Bjorken-x where this can reach greater than 100% [444]. For example: As shown in Figure 29C, γγ production is unambiguously sub-leading to the DY mechanism and only contributes about 10% despite recent claims to the contrary [443, 446]. The collinear behavior and the factorization scale dependence of the incoming photons must be treated with great care. As more data is collected and γ-PDF methodology further matures, one anticipates these uncertainties to greatly shrink; for further discussions of γ-PDFs, see Alva et al. [254], Degrande et al. [255], Martin and Ryskin [268], Harland-Lang et al. [269], Manohar et al. [271, 272]. For a list of recommended γ-PDFs, see the discussion just above Equation (3.38).

Similar to the γγ channel, production of triplet scalars from gluon fusion is sub-leading with respect to DY due to multiple vanishing contributions [258, 447] and despite an expectedly large QCD correction of K^N3LL = σ^N3LL/σ^LO ~ 2.5 − 3 [259]. If triplet scalar couplings to the SM-like Higgs are not too small and if sufficiently light, then such scalars may appear in pairs as rare decays of the 125 GeV scalar boson [448]. Likewise, if neutral triplet scalars mix appreciably with the SM-like Higgs, then single production via gluon fusion is also possible [448]; one should note that in such cases, the QCD K-factors calculated in Ruiz et al. [259] are applicable.

A noteworthy direction of progress in searches for triplet scalars at colliders are the implementation of exotically charged scalars into FeynRules model files. In particular, lepton number violating scalars are available in the LNV-Scalars [449, 450] model file as well as in a full implementation of LRSM at LO accuracy [451, 452]; the Georgi-Machacek model [453] is also available at NLO in QCD accuracy [293, 454]. These permit simulation of triplet scalar production in inclusive ℓℓ/ℓp/pp collisions using modern, general-purpose event generators, such as Herwig [289], MadGraph5_aMC@NLO [290], and Sherpa[291].

Due to the unknown Yukawa structure in Equation (4.1), the decays of the triplet scalars to SM states are much more ambiguous than their production. Subsequently, branching rates of H^± → ℓ^±ν and $H^{\pm \pm }\to {\ell }_1^{\pm }{\ell }_2^{\pm }$ are often taken as phenomenological parameters in analyses and experimental searches. When taking such a model-agnostic approach, it may be necessary to also consider the lifetimes of scalar triplets: In a pure Type II scenario, for $M_{H^{\pm \pm }}<270$ GeV and sub-MeV values of the triplet vev v_L, the proper decay length of H^±± can exceed 10 μm [410]. As a result, exotically charged triplet scalars may manifest at collider experiments in searches for long-lived, multi-charged particles such as Aad et al. [455, 456], Collaboration [457], and Barrie et al. [458].

For prompt decays of triplet scalars, the discovery potential at hadron colliders is quantified in Figure 30. In particular, following the analysis of Fileviez Pérez et al. [408], Figures 30A,B show event contours in the BR(H⁺⁺ → μ⁺μ⁺) vs. $M_{H^{\pm \pm }}$ plane after ${L}=300(3000)\text{f}{\text{b}}^{-1}$ of data at $\sqrt{s}=14$ TeV and 100 TeV, respectively. At the 2σ level, one finds the sensitivity to doubly charged Higgs is about $M_{H^{\pm \pm }}=0.75(1.1)$ TeV at 14 TeV and $M_{H^{\pm \pm }}=2(3.5)$ TeV at 100 TeV. In Figures 30C,D, one similarly has the signal significance $\sigma =S/\sqrt{S+B}$ after ${L}=1$ and 3ab⁻¹ at the 14 TeV LHC for VBF production of doubly charged Higgs pairs and their decays to e^±μ^± and τ^±τ^± final-states, respectively [409]. Upon the fortuitous discovery of a doubly charged scalar, however, will require also observing other charged scalars to determine its precise weak isospin and hypercharge quantum numbers [145, 449, 459].

FIGURE 30

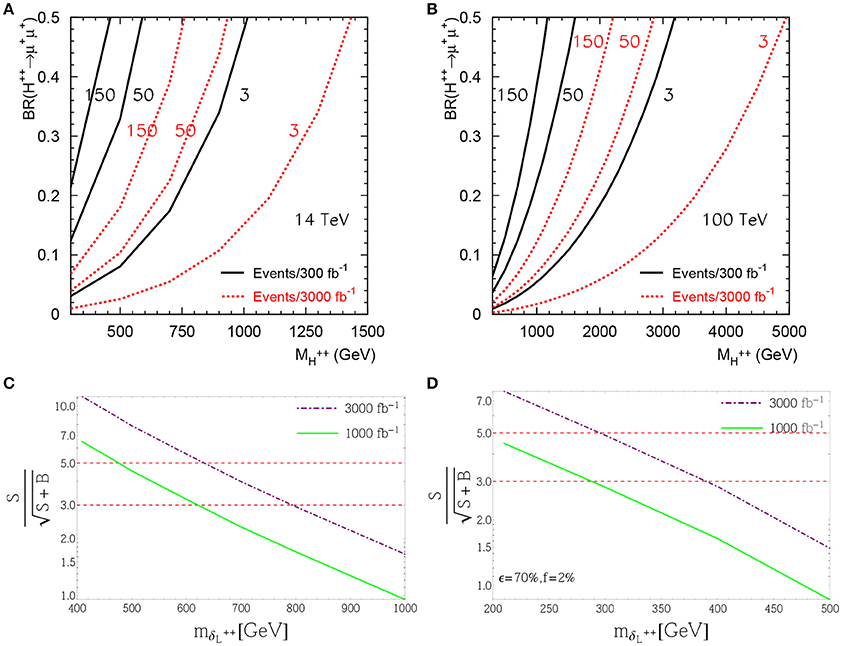
Figure 30. Event contour for H⁺⁺H⁻⁻ → μ⁺μ⁺μ⁻μ⁻ in the BR(H⁺⁺ → μ⁺μ⁺) vs. $M_{H^{++}}$ plane at (A) $\sqrt{s}=$14 TeV and (B) 100 TeV, assuming ${L}=$300 fb⁻¹ and 3,000 fb⁻¹, and based on the analysis of Fileviez Perez et al. [408]. Signal significance for VBF production of doubly charged Higgs pairs and their decays to (C) e^±μ^± and (D) τ^±τ^± final-states, after ${L}=1$ and 3ab⁻¹ at the 14 TeV LHC [409].

In light of such sensitivity at hadron colliders, it is unsurprising then that null results from searches at the 7/8/13 TeV LHC [54, 55, 460, 461] have placed stringent constraints on EW-scale triplet scalar masses, assuming benchmark branching rates. As seen in Figure 31, results from the ATLAS experiment in searches for doubly charged Higgs pairs decaying to leptons, after collecting ${L}=36\text{f}{\text{b}}^{-1}$ of data at 13 TeV, have ruled out $M_{H^{\pm \pm }}>600-900$ GeV at 95% CLs in both the (a) single-flavor and (b) mixed light-lepton final states [460]. Comparable limits have been reached by the CMS experiment [461].

FIGURE 31

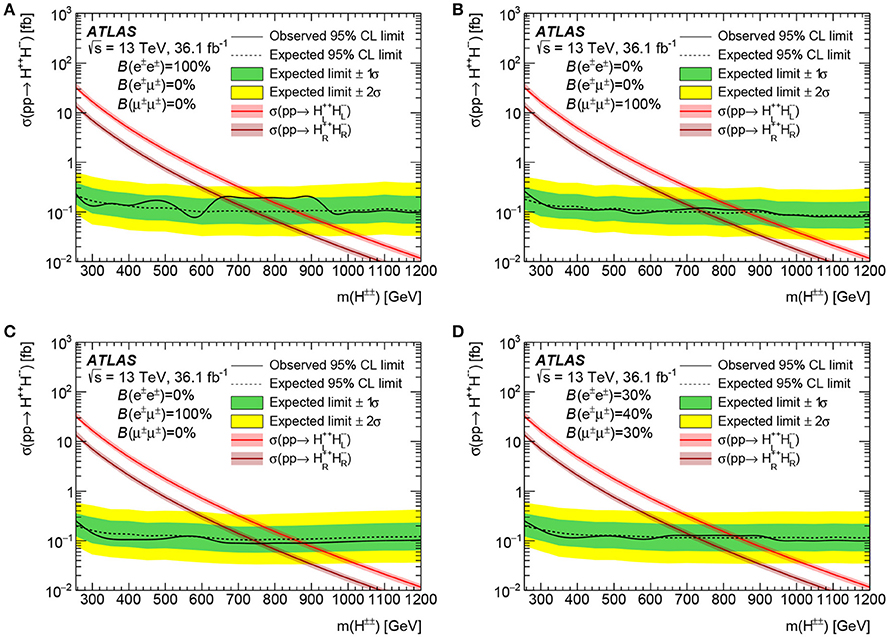
Figure 31. ATLAS 95% CLs exclusion at 13 TeV after ${L}=36\text{f}{\text{b}}^{-1}$ on σ(pp → H⁺⁺H⁻⁻) for various representative branching rates to SM charged leptons in the (A) pure e^±e^±, (B) pure μ^±μ^±, (C) pure e^±μ^±, and (D) mixed final-states [460].

At future e⁻e⁺ colliders, triplet scalars can appear in t-channel exchanges, inducing charged lepton flavor violation (cLFV) and forward-backward asymmetries [462]; in three-body decays of taus that are absent of light-neutrinos in the final state, i.e., τ^± → ℓ^∓H^±±* → ℓ^∓μ^±μ^± [463]; and, of course, in pairs via s-channel gauge currents [464]. In the event of such observations, the nontrivial conversion of an e⁻e⁺ beam into an e⁻e⁻/e⁻μ⁻/μ⁻μ⁻ facility could provide complimentary information on scalar triplet Yukawa couplings by means of the “inverse” 0νββ processes, ${\ell }_i^{-}{\ell }_j^{-}\to W_{L/R}^{-}{W}_{L/R}^{-}$ [465–467].

4.2.2. Triplet Higgs Scalars and the Left-Right Symmetric Model at Colliders

Turning to scalars in the LRSM, as introduced in section 3.1.4, it was recently observed [368, 448] that in a certain class of neutrino mass models, decays of the SM-like Higgs boson h(125 GeV) to heavy neutrino pairs, h → NN, may occur much more readily than previously thought. The significance of this reaction is one's ability to confirm neutrino masses are generated, in part, through EWSB. It would also indicate sensitivity to the scalar sector responsible for generating RH Majorana masses. Interactions between SM particles and N typically proceed through heavy-light neutrino mixing, |V_ℓN|, which, is a numerically small quantity. As h → NN involves two N, the issue is compounded and usually renders the decay rate prohibitively small in a pure Type I scenario. For H ∈ {H⁰, H^±, H^±±} predicted in Type I+II Seesaws, and in particular the LRSM, the situation is more interesting: it may be that h(125 GeV) and the RH neutral scalars mix sufficiently that decays to relatively light (2M_N < 125 GeV) heavy neutrino pairs are possible [368]. This is allowed as H can couple appreciable to N and the mixing between H⁰ and h is much less constrained. Subsequently, the naïve neutrino mixing suppression is avoided by exploiting that h → NN decays can proceed instead through H⁰−h mixing. In a similar vein, it may be possible for h to decay to triplet pairs and subsequently to N or same-sign charged leptons, or for single H⁰ production to proceed directly [448]. Such processes are shown diagrammatically in Figure 32. As a result, the L-violating Higgs decays,

$\begin{array}{ll}h(125\text{GeV})\to N N\to W_R^{\pm *}{W}_R^{\pm *}{\ell }_1^{\mp }{\ell }_2^{\mp } \to {\ell }_1^{\mp } {\ell }_2^{\mp }+nj,& (4.9)\end{array}$

$\begin{array}{ll}h(125\text{GeV})\to H^0 H^0\to 4N\to {\ell }_1^{\pm } {\ell }_2^{\mp } {\ell }_3^{\pm } {\ell }_4^{\mp } + nj,& (4.10)\end{array}$

$\begin{array}{ll}h(125\text{GeV})\to H^{++} H^{--} \to {\ell }_1^{\pm } {\ell }_2^{\pm } {\ell }_3^{\mp } {\ell }_4^{\mp },& (4.11)\end{array}$

are not only possible, but also provide complementary coverage of low-mass N scenarios that are outside the reach of 0νββ experiments and direct searches for W_R at colliders. The sensitivity of such modes are summarized in Figure 33 [368, 448]. The associated production channels,

$\begin{array}{ll}pp\to H^{0,\pm \pm } W_R^{\mp } \text{and} pp\to H^0{Z}_R,& (4.12)\end{array}$

are also possible. However, as in the SM, these channels are s-channel and phase space suppressed, which lead to prohibitively small cross sections in light of present mass limits [145].

FIGURE 32

Figure 32. Feynman diagrams depicting gluon fusion production of Majorana neutrinos via (A) SM Higgs boson (h) and (B) SU(2)_R triplet Higgs (H) through their mixing in pp collisions [368, 448].

FIGURE 33

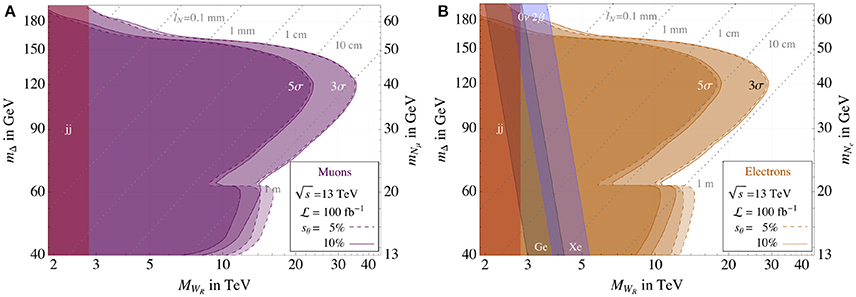
Figure 33. (A,B) 13 TeV LHC sensitivity to the LRSM in the (M_N, M_WR) plane to the processes shown in Figure 32 after ${L}=100\text{f}{\text{b}}^{-1}$ [368, 448].

Lastly, one should note that the search for such Higgs decays is not limited to hadron colliders. As presently designed future lepton colliders are aimed at operating as Higgs factories, searches for such L-violating Higgs decays [468–470] at such facilities represent an attractive discovery prospect. In this context, a relatively understudied topic is the possible manifestation of Seesaw in precision measurements of the known SM-like Higgs boson [216, 368, 471]. Some related studies also exist in the literature such as for generic pheno [440, 440, 449]; for little Higgs [410, 472]; and for decay ratios and mixing patterns of exotically charged Higgs[473, 474].

5. The Type III Seesaw and Lepton Number Violation at Colliders

We now turn to collider searches for lepton number violation in the context of the Type III Seesaw mechanism [19] as well as its embedding in GUTs and other SM extensions. In some sense, the Type III model is the fermionic version of the Type II scenario, namely that Seesaw partner fermions couple to the SM via both weak gauge and Yukawa couplings. Subsequently, much of the Type III collider phenomenology resembles that of Type I-based models. However, quantitatively, the presence of gauge couplings lead to a very different outlook and level of sensitivity. We now summarize the main highlights of the canonical Type III Seesaw (section 5.1.1), Type III-based models (section 5.1.2), and then review their L-violating collider phenomenology (section 5.2). As with the previous Seesaw scenarios, a discussion of cLFV is outside the scope of this review. For recent summaries on cLFV in the Type III Seesaw, see Abada et al. [176, 475], Eboli et al. [476], and Agostinho et al. [477] and references therein.

5.1. Type III Seesaw Models

5.1.1. The Canonical Type III Seesaw Mechanism

In addition to the SM field content, the Type III Seesaw [19] consists of SU(2)_L triplet (adjoint) leptons,

$\begin{array}{ll}\begin{array}{l}{\Sigma }_L={\Sigma }_L^a{\sigma }^a=\left(\begin{array}{cc}{\Sigma }_L^0/\sqrt{2}& {\Sigma }_L^{+}\\ {\Sigma }_L^{-}& -{\Sigma }_L^0/\sqrt{2}\end{array}\right),\\ {\Sigma }_L^{\pm }\equiv \frac{{\Sigma }_L^1\mp i{\Sigma }_L^2}{\sqrt{2}}, {\Sigma }_L^0={\Sigma }_L^3,\end{array}& (5.1)\end{array}$

which transform as (1, 3, 0) under the SM gauge group. Here ${\Sigma }_L^{\pm }$ have U(1)_EM charges Q = ±1, and the σ^a for a = 1, …, 3, are the usual Pauli SU(2) matrices. The RH conjugate fields are related by

$\begin{array}{ll}{\Sigma }_R^c=\left(\begin{array}{cc}{\Sigma }_R^{0c}/\sqrt{2}& {\Sigma }_R^{-c}\\ {\Sigma }^{+c}& -{\Sigma }_R^{0c}/\sqrt{2}\end{array}\right), \text{for} {\psi }_R^c\equiv {({\psi }^c)}_R={({\psi }_L)}^c.& (5.2)\end{array}$

The Type III Lagrangian is given by the sum of the SM Lagrangian, the triplet's kinetic and mass terms,

$\begin{array}{ll}{{L}}_T=\frac{1}{2}\text{Tr}[\overline{{\Sigma }_L}i\cancel{D}{\Sigma }_L]-\left(\frac{M_{\Sigma }}{2}\overline{{\Sigma }_L^0}{\Sigma }_R^{0c}+M_{\Sigma }\overline{{\Sigma }_L^{-}}{\Sigma }_R^{+c}+\text{H}\text{.c}\text{.}\right),& (5.3)\end{array}$

and the triplet's Yukawa coupling to the SM LH lepton (L) and Higgs (H) doublet fields,

$\begin{array}{ll}{{L}}_Y=-Y_{\Sigma }\overline{L} {\Sigma }_R^c i{\sigma }^2{H}^{*}+\text{H}\text{.c}\text{.}& (5.4)\end{array}$

From Equation (5.4), one can deduce the emergence of a Yukawa coupling between the charged SM leptons and the charged triplet leptons. This, in turn, induces a mass mixing among charged leptons that is similar to doublet-singlet and doublet-triplet neutrino mass mixing, and represents one of the more remarkable features of the Type III mechanism. The impact of EW fermion triplets on the SM Higgs, naturalness in the context of the Type III Seesaw has been discussed in Gogoladze et al. [478], He et al. [479], and Gogoladze et al. [480].

After expanding Equations (5.3)–(5.4), the relevant charged lepton and neutrino mass terms are [481]

$\begin{array}{ll}\begin{array}{l}{{L}}_{\text{III}}^m=-\left(\begin{array}{c}\overline{l_R}\overline{{\Psi }_R}\end{array}\right)\left(\begin{array}{cc}{m}_l& 0\\ Y_{\Sigma }{v}_0& M_{\Sigma }\end{array}\right)\left(\begin{array}{c}{l}_L\\ {\Psi }_L\end{array}\right)\\ -\left(\begin{array}{c}\overline{{\nu }_L^c}\overline{{\Sigma }_L^{0c}}\end{array}\right)\left(\begin{array}{cc}0& Y_{\Sigma }^T{v}_0/2\sqrt{2}\\ Y_{\Sigma }{v}_0/2\sqrt{2}& M_{\Sigma }/2\end{array}\right)\left(\begin{array}{c}{\nu }_L\\ {\Sigma }_L^0\end{array}\right)+\text{H}\text{.c}\text{.},\end{array}& (5.5)\end{array}$

with ${\text{Ψ}}_L\equiv {\Sigma }_L^{-}$, ${\text{Ψ}}_R\equiv {\Sigma }_L^{+c}$, and Ψ = Ψ_L+Ψ_R. After introducing unitarity matrices to transit light doublet and heavy triplet lepton fields as below

$\begin{array}{ll}\left(\begin{array}{c}{l}_{L,R}\\ {\Psi }_{L,R}\end{array}\right)=U_{L,R}\left(\begin{array}{c}{l}_{mL,R}\\ {\Psi }_{mL,R}\end{array}\right),\left(\begin{array}{c}{\nu }_L\\ {\Sigma }_L^0\end{array}\right)=U_0\left(\begin{array}{c}{\nu }_{mL}\\ {\Sigma }_{mL}^0\end{array}\right),& (5.6)\end{array}$

$\begin{array}{ll}\begin{array}{l}{U}_L\equiv \left(\begin{array}{cc}{U}_{Lll}& U_{Ll\Psi }\\ U_{L\Psi l}& U_{L\Psi \Psi }\end{array}\right),U_R\equiv \left(\begin{array}{cc}{U}_{Rll}& U_{Rl\Psi }\\ U_{R\Psi l}& U_{R\Psi \Psi }\end{array}\right),\\ U_0\equiv \left(\begin{array}{cc}{U}_{0\nu \nu }& U_{0\nu \Sigma }\\ U_{0\Sigma \nu }& U_{0\Sigma \Sigma }\end{array}\right),\end{array}& (5.7)\end{array}$

one obtains the diagonal mass matrices and mass eigenvalues for neutrinos and charged leptons,

$\begin{array}{ll}\text{diag}({N})=U_0^{†}\left(\begin{array}{cc}0& Y_{\Sigma }^{†}{v}_0/\sqrt{2}\\ Y_{\Sigma }^{\ast }{v}_0/\sqrt{2}& M_{\Sigma }^{\ast }\end{array}\right)U_0^{\ast }=\left(\begin{array}{cc}{m}_{\nu }^{diag}& 0\\ 0& M_N^{diag}\end{array}\right),& (5.8)\end{array}$

$\begin{array}{ll}\text{diag}(ℰ)=U_L^{†}\left(\begin{array}{cc}{m}_l^{†}& Y_{\Sigma }^{†}{v}_0\\ 0& M_{\Sigma }^{†}\end{array}\right)U_R=\left(\begin{array}{cc}{m}_l^{diag}& 0\\ 0& M_E^{diag}\end{array}\right).& (5.9)\end{array}$

The light neutrino mass eigenstates are denoted by ν_j for j = 1, …, 3; whereas the heavy neutral and charged leptons are respectively given by $N_{j^{\prime }}$ and $E_{k^{\prime }}^{\pm }$. In the literature, N and E^± are often denoted as T⁰, T^± or Σ⁰, Σ^±. However, there is no standard convention as to what set of symbols are used to denote gauge and mass eigenstates. Where possible, we follow the convention of Arhrib et al. [482] and generically denote triplet-doublet mixing by Y_T and ε_T. This means that in the mass basis, triplet gauge states are given by

$\begin{array}{ll}\begin{array}{l}{\Psi }^{\pm }=Y_T E^{\pm }+\sqrt{2}{\epsilon }_T {\ell }^{\pm } \text{and} {\Psi }^0=Y_T N+{\epsilon }_T {\nu }_m,\\ \text{with} \left|Y_T\right|~{O}(1) \text{and} \left|{\epsilon }_T\right|~\frac{Y_{\Sigma }{v}_0}{\sqrt{2}{M}_{\Sigma }}\ll 1.\end{array}& (5.10)\end{array}$

The resulting interaction Lagrangian, in the mass eigenbasis then contains [482]

$\begin{array}{ll}\begin{array}{l}{{L}}_{\text{Type} \text{III}}^{\text{Mass} \text{Basis}}\ni -\overline{E_{k^{\prime }}^{-}}\left(e{Y}_T{A}_{\mu }{\gamma }^{\mu }+g\cos {\theta }_W{Y}_T{Z}_{\mu }{\gamma }^{\mu }\right)E_{k^{\prime }}^{-}\\ -g{Y}_T\overline{E_{k^{\prime }}^{-}}{W}_{\mu }^{-}{\gamma }^{\mu }{N}_{j^{\prime }}\\ -\frac{e}{2s_w{c}_w}{Z}_{\mu }\left({\epsilon }_T\overline{N_{j^{\prime }}}{\gamma }^{\mu }{P}_R{\nu }_j+\sqrt{2}{\epsilon }_T\overline{E_{k^{\prime }}^{-}}{\gamma }^{\mu }{P}_R{\ell }_k^{-}\right)\\ -\frac{e}{s_w}{W}_{\mu }^{+}\left({\epsilon }_T\overline{{\nu }_j}{\gamma }^{\mu }{P}_L{E}_{k^{\prime }}^{-}+\frac{1}{\sqrt{2}}{\epsilon }_T\overline{N_{j^{\prime }}}{\gamma }^{\mu }{P}_R{\ell }_k^{-}\right)+\text{H}.\text{c}.\end{array}& (5.11)\end{array}$

From this, one sees a second key feature of the Type III Seesaw, that gauge interactions between heavy lepton pairs proceeds largely through pure vector currents with axial-vector deviations (not shown) suppressed by ${O}({\epsilon }_T^2)$ at the Lagrangian level. This follows from the triplet fermions vector-like nature. Similarly, the mixing-suppressed gauge couplings between heavy and light leptons proceeds through SM-like currents.

Explicitly, the light and heavy neutrino mass eigenvalues are

$\begin{array}{ll}{m}_{\nu }\approx \frac{Y_{\Sigma }^2{v}_0^2}{2M_{\Sigma }},M_N\approx M_{\Sigma },& (5.12)\end{array}$

and for the charged leptons are

$\begin{array}{ll}{m}_l-m_l\frac{Y_{\Sigma }^2{v}_0^2}{2M_{\Sigma }^2}\approx m_l,M_E\approx M_{\Sigma }.& (5.13)\end{array}$

This slight deviation in the light, charged leptons' mass eigenvalues implies a similar variation in the anticipated Higgs coupling to the same charged leptons. At tree-level, the heavy leptons N and E^± are degenerate in mass, a relic of SU(2)_L gauge invariance. However, after EWSB, and for M_Σ ≳ 100 GeV, radiative corrections split this degeneracy by Arhrib et al. [482],

$\begin{array}{ll}\begin{array}{l}\Delta M_T\equiv M_E-M_N=\frac{{\alpha }_W}{2\pi }\frac{M_W^2}{M_{\Sigma }}\left[f\left(\frac{M_{\Sigma }}{M_Z}\right)-f\left(\frac{M_{\Sigma }}{M_W}\right)\right]\\ \approx 160 \text{MeV},\end{array}& (5.14)\end{array}$

$\begin{array}{ll}\begin{array}{l}\text{where} f\left(y\right)=\frac{1}{4y^2}\log y^2-\left(1+\frac{1}{2y^2}\right)\sqrt{4y^2-1}\arctan \\ \sqrt{4y^2-1},\end{array}& (5.15)\end{array}$

and opens the E^± → Nπ^± decay mode. Beyond this are the heavy lepton decays to EW bosons and light leptons that proceed through doublet-triplet lepton mixing. The mixings are governed by the elements in the unitary matrices U_{L, R} and U₀. Expanding U_{L, R} and U₀ up to order $Y_{\Sigma }^2{v}_0^2{M}_{\Sigma }^{-2}$, one gets the following results [475, 483]

$\begin{array}{l}{U}_{Lll}=1-ϵ,U_{Ll\Psi }=Y_{\Sigma }^{†}{M}_{\Sigma }^{-1}{v}_0,U_{L\Psi l}=-M_{\Sigma }^{-1}{Y}_{\Sigma }{v}_0,\\ U_{L\Psi \Psi }=1-{ϵ}^{\prime },\\ U_{Rll}=1,U_{Rl\Psi }=m_l{Y}_{\Sigma }^{†}{M}_{\Sigma }^{-2}{v}_0,U_{R\Psi l}=-M_{\Sigma }^{-2}{Y}_{\Sigma }{m}_l{v}_0,\\ U_{R\Psi \Psi }=1,\\ U_{0\nu \nu }=(1-ϵ/2)U_{PMNS},U_{0\nu \Sigma }=Y_{\Sigma }^{†}{M}_{\Sigma }^{-1}{v}_0/\sqrt{2},U_{0\Sigma \nu }=\\ -M_{\Sigma }^{-1}{Y}_{\Sigma }{U}_{0\nu \nu }{v}_0/\sqrt{2},\\ U_{0\Sigma \Sigma }=1-{ϵ}^{\prime }/2,ϵ=Y_{\Sigma }^{†}{M}_{\Sigma }^{-2}{Y}_{\Sigma }{v}_0^2/2,\\ {ϵ}^{\prime }=M_{\Sigma }^{-1}{Y}_{\Sigma }{Y}_{\Sigma }^{†}{M}_{\Sigma }^{-1}{v}_0^2/2.\end{array}$

To the order of $Y_{\Sigma }{v}_0{M}_{\Sigma }^{-1}$, the mixing between the SM charged leptons and triplet leptons, i.e., $V_{\ell N}=-Y_{\Sigma }^{†}{v}_0{M}_{\Sigma }^{-1}/\sqrt{2}$, follows the same relation as Equation (3.10) in the Type I Seesaw [481] and the couplings in the interactions in Equation (5.11) are all given by V_ℓN [326, 481].

Hence, the partial widths for both the heavy charged lepton and heavy neutrino are proportional to $|V_{\ell N}{|}^2$. For M_E ≈ M_N ≫ M_W, M_Z, M_h, the partial widths behave like [252, 326]

$\begin{array}{ll}\begin{array}{l}\frac{1}{2}\Gamma (N\to {\displaystyle \sum _{\ell }{\ell }^{+}}{W}^{-}+{\ell }^{-}{W}^{+})\approx \Gamma (N\to {\displaystyle \sum _{\nu }\nu }Z+\overline{\nu }Z)\\ \approx \Gamma (N\to {\displaystyle \sum _{\nu }\nu }h+\overline{\nu }h)\\ \approx \frac{1}{2}\Gamma (E^{\pm }\to {\displaystyle \sum _{\nu }\stackrel{(-)}{\nu }}{W}^{\pm })\approx \Gamma (E^{\pm }\to {\displaystyle \sum _{\ell }{\ell }^{\pm }}Z)\\ \approx \Gamma (E^{\pm }\to {\displaystyle \sum _{\ell }{\ell }^{\pm }}h)\\ \approx \frac{G_F}{8\sqrt{2}\pi }{\displaystyle \sum _{\ell }|}{V}_{\ell N}{|}^2{M}_{\Sigma }^3.\end{array}& (5.16)\end{array}$

Thus the heavy lepton branching ratios exhibit asymptotic behavior consistent with the Goldstone Equivalence Theorem [260, 261], and are given by the relations [252, 326, 482, 484],

$\begin{array}{ll}\begin{array}{l}\frac{1}{2}\text{BR}(N\to {\displaystyle \sum _{\ell }{\ell }^{+}}{W}^{-}+{\ell }^{-}{W}^{+})\approx \text{BR}(N\to {\displaystyle \sum _{\nu }\nu }Z+\overline{\nu }Z)\\ \approx \text{BR}(N\to {\displaystyle \sum _{\nu }\nu }h+\overline{\nu }h)\\ \approx \frac{1}{2}\text{BR}(E^{\pm }\to {\displaystyle \sum _{\nu }\stackrel{(-)}{\nu }}{W}^{\pm })\approx \text{BR}(E^{\pm }\to {\displaystyle \sum _{\ell }{\ell }^{\pm }}Z)\\ \approx \text{BR}(E^{\pm }\to {\displaystyle \sum _{\ell }{\ell }^{\pm }}h)\approx \frac{1}{4}. \end{array}& (5.17)\end{array}$

As displayed in Figure 34 by Franceschini et al. [484], as the triplet mass grows, this asymptotic behavior can be seen explicitly in the triplet lepton partial widths.

FIGURE 34

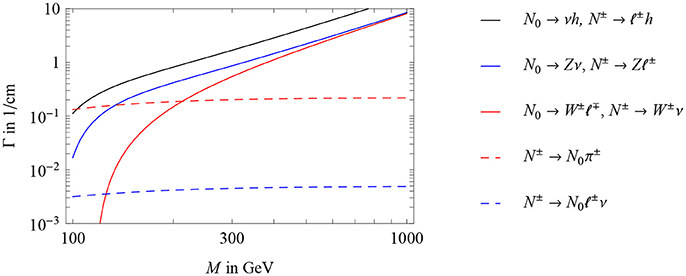
Figure 34. Triplet decay widths as function of the triplet mass and assuming M_hSM = 115GeV [484].

5.1.2. Type I+III Hybrid Seesaw in Grand Unified and Extended Gauge Theory

One plausible possibility to rescue the minimal grand unified theory, i.e., SU(5), is to introduce an adjoint 24_F fermion multiplet in addition to the original 10_F and ${\bar{5}}_F$ fermionic representations [5, 485]. As the 24_F contains both singlet and triplet fermions in this non-supersymmetric SU(5), the SM gauge couplings unify and neutrino masses can generated through a hybridization of the Types I and III Seesaw mechanisms. The Yukawa interactions and Majorana masses in this Type I+III Seesaw read [482]

$\begin{array}{ll}\Delta {{L}}_{\text{I+III}}^Y=Y_{S}LHS+Y_{T}LHT-\frac{M_S}{2}SS-\frac{M_T}{2}TT+\text{H}.\text{c}.,& (5.18)\end{array}$

where S and $T=\left(\frac{T^{-}+T^{+}}{\sqrt{2}},\frac{T^{-}-T^{+}}{i\sqrt{2}},T^0\right)$ are the fermionic singlet and triplet fields, respectively, with masses M_S and M_T. In the limit that M_S, M_T ≫ Y_Sv₀, Y_Tv₀, the light neutrino masses are then given by the sum of the individual Type I and III contributions

$\begin{array}{ll}{m}_{\nu }=-{(Y_S{v}_0/\sqrt{2})}^2{M}_S^{-1}-{(Y_T{v}_0/\sqrt{2})}^2{M}_T^{-1},& (5.19)\end{array}$

The most remarkable prediction of this SU(5) theory is that the unification constraint and the stability of proton require the triplet mass to be small: M_T ≲ 1 TeV [485, 486]. Thus, in SU(5) scenarios, the triplet leptons of this Type I+III Seesaw are within the LHC's kinematic reach and can be tested via L-violating collider signatures [5, 487–491].

Other GUT models that can accommodate the Type III Seesaw and potentially lead to collider-scale L-violation include variations of SO(10) [492] theories. It is also possible to embed the Type III scenario into extended gauge sectors, including Left-Right Symmetric theories [134, 135, 493, 494], which also represents a Type I+II+III hybrid Seesaw hat trick. Additionally, Type III-based hybrid Seesaws can be triggered via fermions in other SU(2)_L×U(1)_Y representations [495–498], The collider phenomenology in many of these cases is very comparable to that of the Type I and II Seesaws, as discussed in sections 3 and 4, or the more traditional Type III scenario, which we now discuss.

5.2. Heavy Charged Leptons and Neutrinos at Colliders

5.2.1. Heavy Charged Leptons and Neutrinos at pp Colliders

Due to the presence of both gauge and Yukawa couplings to SM fields, the collider phenomenology for triplet leptons is exceedingly rich. In hadron collisions, for example, pairs of heavy triplet leptons are produced dominantly via charged and neutral Drell-Yan (DY) currents, given by

$\begin{array}{ll}q{\overline{q}}^{\prime }\to W^{\ast \pm }\to T^{\pm }{T}^0 \text{and} q\overline{q}\to {\gamma }^{\ast }/Z^{\ast }\to T^{+}{T}^{-},& (5.20)\end{array}$

and shown in Figure 35A. For the DY process, the total cross section is now known up to NLO and differentially at NLO+LL in p_T resummation [275]. As function of mass, the Nℓ^± (singlet) as well as T⁺T⁻ and T^±T⁰ (triplet) DY production cross sections at $\sqrt{s}=14$ and 100 TeV are displayed in Figure 36A. While the three rates are naïvely comparable, one should assign a mixing factor of $|V_{\ell N}{|}^2\lesssim 10^{-2}$ to the singlet production since it proceeds through active-sterile neutrino mixing, i.e., Yukawa couplings, whereas triplet lepton pair production proceeds through gauge couplings. Heavy triplet leptons can also be produced singly in the association with light leptons and neutrinos,

$\begin{array}{ll}q{\overline{q}}^{\prime }\to W^{\ast \pm }\to T^{\pm }\nu , T^0{\ell }^{\pm }\text{and}q\overline{q}\to {\gamma }^{\ast }/Z^{\ast }\to T^{\pm }{\ell }^{\mp }.& (5.21)\end{array}$

As single production modes are proportional to the small [88] doublet-triplet mixing, denoted by |V_ℓT|, these processes suffer from the same small signal rates at colliders as does singlet production in Type I-based Seesaws (see section 3.1.1). However, as heavy-light lepton vertices also posses axial-vector contributions, new production channels are present, such as through the gluon fusion mechanism [242, 245, 258, 259], shown in Figure 35B and given by

$\begin{array}{ll}gg\to Z^{\ast }/h^{\ast }\to T^{\pm }{\ell }^{\mp }.& (5.22)\end{array}$

It is noteworthy that the partonic expression for gluon fusion channels gg → Z*/h* → T^±ℓ^∓ is equal to the Type I analog gg → Nν_ℓ [258], and hence its QCD corrections [259], but that heavy triplet pair production through gluon fusion, i.e., $gg\to T\overline{T}$, is zero since their couplings to weak bosons are vector-like, and hence vanish according to Furry's Theorem [242, 245, 447]. For $\sqrt{s}=7-100$ TeV, the N³LL(Threshold) corrections to the Born rates span +160% to +260% [259]. Hence, for singly produced triplet leptons, the gluon fusion mechanism is dominant over the DY channel for $\sqrt{s}\gtrsim 20-25$ TeV, over a wide range of EW- and TeV-scale triplet masses [258, 259]. More exotic production channels also exist, such as the γγ → T⁺T⁻ VBF channel, shown in Figure 35C, as well as permutations involving W and Z. However, their contributions are sub-leading due to coupling and phase space suppression.

FIGURE 35

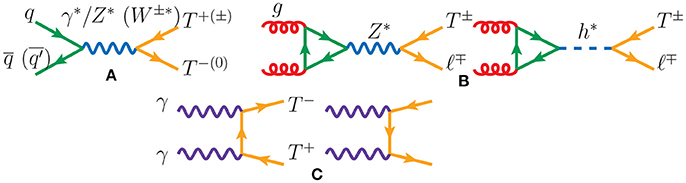
Figure 35. Born level production of Type III lepton pairs via (A) Drell-Yan, (B) gluon fusion, and (C) photon fusion.

FIGURE 36

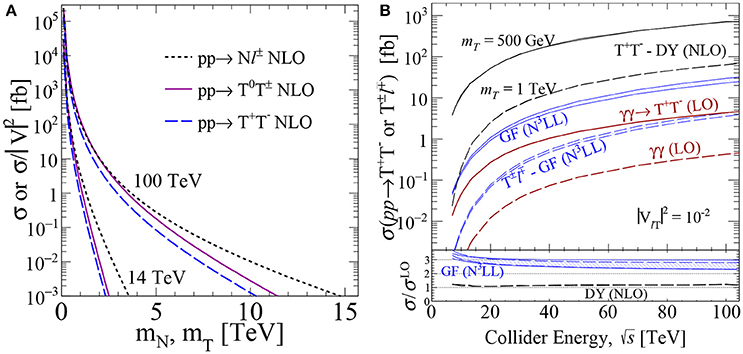
Figure 36. (A) As a function of mass, the Nℓ^± (singlet) as well as T⁺T⁻ and T^±T⁰ (triplet) DY production cross sections at $\sqrt{s}=14$ and 100 TeV. (B) As a function of collider energy $\sqrt{s}$, the T⁺T⁻ and T^±ℓ^∓ (assuming benchmark $|V_{\ell T}{|}^2=10^{-2}$) production cross sections via various production mechanisms.

For representative heavy lepton masses of M_T = 500 GeV and 1 TeV as well as doublet-triplet mixing of $|V_{\ell T}{|}^2=10^{-2}$, we display in Figure 36B the pp → T⁺T⁻ and T^±ℓ^∓ production cross sections via various hadronic production mechanisms as a function of collider energy $\sqrt{s}$. In the figure, the dominance of pair production over single production is unambiguous. Interestingly, considering that the triplet mass splitting is $\Delta M_T~{O}(200)$ MeV as stated above, one should not expect to discover the neutral current single production mode without also observing the charged channel almost simultaneously. Hence, despite sharing much common phenomenology, experimentally differentiating a Type I scenario from a Type III (or I+III) scenario is straightforward.

Leading order-accurate Monte Carlo simulations for tree-level processes involving Type III leptons are possible with the Type III Seesaw FeynRules UFO model [475, 499, 500], as well as a Minimal Lepton Flavor Violation variant MLFV Type III Seesaw [476, 477, 501]. The models can be ported into modern, general-purpose event generators, such at Herwig [289], MadGraph5_aMC@NLO [290], and Sherpa [291].

Hadron collider tests of the Type III Seesaw can be categorized according to the final-state lepton multiplicities, which include: the L-violating, same-sign dilepton and jets final state, ${\ell }_1^{\pm }{\ell }_2^{\pm }+nj$ [252, 326, 481, 482, 484, 485, 499, 502]; the four-lepton final state, ${\ell }_1^{\pm }{\ell }_2^{\pm }{\ell }_3^{\mp }{\ell }_4^{\mp }+nj$ [252, 326, 481, 484, 499]; other charged lepton multiplicities [252, 326, 484, 499, 503]; and also displaced charged lepton vertices [484, 504]. Other “displaced” signatures, include triplet lepton decays to displaced Higgs bosons [505]. Direct searches for Type III Seesaw partners at the $\sqrt{s}=7/8$ TeV [56, 57, 506] and $\sqrt{s}=13$ TeV [58, 507, 508] LHC have yet to show evidence of heavy leptons. As shown in Figure 37A, triplet masses below M_T ≲ 800 GeV have been excluded at 95% CLs [508]. Figure 37B displays the discovery potential of triplet leptons at high-luminosity 100 TeV collider. One can discover triplet lepton as heavy as 4 (6.5) TeV with 300 (3000) fb⁻¹ integrated luminosity. The absence of triplet leptons in multi-lepton final states can also be interpreted as a constrain on doublet-triplet neutrino mixing. In Figures 37C,D, one sees the exclusion contours of doublet-triplet neutrino mixing in |V_μN| − |V_eN| and |V_τN| − |V_eN| spaces after ${L}=4.9$ fb⁻¹ of data at CMS (labels denote heavy neutral lepton mass in GeV) [490].

FIGURE 37

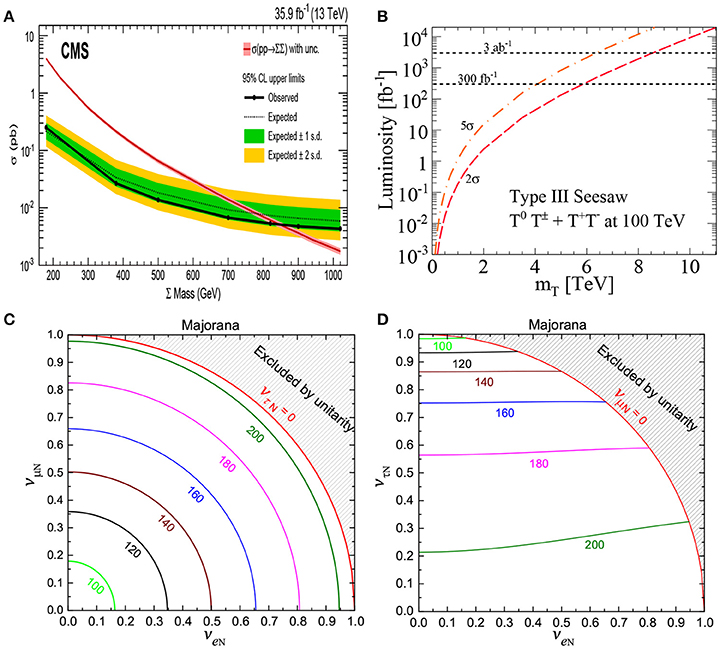
Figure 37. (A) Limits on Type III leptons at $\sqrt{s}=13$ TeV LHC [58, 508]; (B) required luminosity for 2 (5)σ sensitivity (discovery) with fully reconstructible final states [149, 275]. (C,D) Exclusion contours of doublet-triplet neutrino mixing in |V_μN|−|V_eN| and |V_τN|−|V_eN| spaces after ${L}=4.9$ fb⁻¹ of data at CMS (labels denote heavy neutral lepton mass in GeV) [490].

5.2.2. Heavy Charged Leptons and Neutrinos at ee and ep Colliders

The triplet leptons can also be produced at the leptonic colliders like the ILC and the Compact Linear Collider (CLIC) [482, 509], and the electron-hadron collider like LHeC [309]. Besides the similar s-channels as hadron colliders, at e⁺e⁻ colliders, the triplet lepton single and pair productions can also happen in t-channel via the exchange of h, W, or Z boson. Triplet leptons can also lead to anomalous pair production of SM weak bosons [470]. Assuming M_Σ = 500 GeV and V_eN = 0.05, the cross sections of triplet lepton single and pair productions are shown in Figure 38A. For the single production at 1 TeV e⁺e⁻ collider, the triplet lepton with mass up to about 950-980 GeV can be reached with 300 fb⁻¹. To discover the heavy charged lepton through e⁺e⁻ → Σ⁺Σ⁻ production at $\sqrt{s}=2$ TeV, the luminosity as low (high) as 60 (480) fb⁻¹ is needed as shown in Figure 38B.

FIGURE 38

Figure 38. (A) Production cross section of e⁺e⁻ → Σ⁰ν, Σ^±e^∓, Σ⁺Σ⁻ as a function of the center of mass energy for e⁺e⁻ colliders, with M_Σ = 500 GeV and V_eN = 0.05 [509]; (B) Significance of Σ⁺Σ⁻ production vs. integrated luminosity at $\sqrt{s}=2$ TeV [509].

6. Radiative Neutrino Mass Models and Lepton Number Violation at Colliders

A common feature of the Seesaw mechanisms discussed in the previous sessions is that they are all tree-level, UV completion of the dimension-5 Weinberg operator in of Equation (1.1). Though economical and elegant, these models often imply subtle balancing between a Seesaw mass scale at TeV or below and small Yukawa couplings, in the hope for them to be observable in the current and near future experiments. In an altogether different paradigm, it may be the case that small neutrino masses are instead generated radiatively. In radiative neutrino mass models, loop and (heavy) mass factors can contribute to the suppression of light neutrino masses and partly explain their smallness. A key feature of radiative neutrino mass models is that the Weinberg operator is not generated at tree-level: For some models, this may be because the particles required to generate tree-level masses, i.e., SM singlet fermions in Type I, triplet scalars in Type II, or triplet leptons in Type III, do not exist in the theory. For others, it may be the case that the required couplings are forbidden by new symmetries. Whatever the case, it is necessary that the new field multiplets run in the loops to generate neutrino masses.

At one-loop, such models were first proposed in Zee [28] and Hall and Suzuki [29], at two-loop in Cheng and Li [16], Zee [30], and Babu [31], and more recently at three-loop order in Krauss et al. [32]. Besides these early works, a plethora of radiative mass models exist due to the relative ease with which unique loop topologies can be constructed at a given loop order, as well as the feasibility to accommodate loop contributions from various exotic particles, including leptoquarks, vector-like leptons and quarks, electrically charged scalars, and EW multiplets. For a recent, comprehensive review, see Cai et al. [510].

However, the diversity of the exotic particles and interactions in radiative neutrino mass models make it neither feasible nor pragmatic to develop a simple and unique strategy to test these theories at colliders. Although some effort has been made to advance approaches to collider tests of radiative neutrino mass models more systematically [511, 512], it remains largely model-dependent. As a comprehensive summary of the literature for radiative neutrino mass models and their collider study is beyond the scope of this review, in this section, we focus on a small number of representative models with distinctive L-violating collider signatures.

It is worth pointing out that some popular radiative neutrino mass models do not predict clear lepton number violation at collider scales. A prime example are the Scotogenic models [513], a class of one-loop radiative neutrino mass scenario with a discrete Z₂ symmetry. Scotogenic models typically contain three SM singlet fermions N_i with Majorana masses and are odd under the Z₂, whereas SM fields are even. The discrete symmetry forbids the mixing between the SM neutrinos and N_i that one needs to trigger the Type I and III Seesaw mechanisms. As a result, collider strategies to search for lepton number violation mediated by heavy Majorana neutrinos as presented in section 3 are not applicable to the Scotogenic model. Instead, collider tests of Scotogenic models include, for example, searches for the additional EW scalars [514–517] that facilitate lepton number conserving processes. Subsequently, we avoid further discussing radiative models without collider-scale lepton number violation.

Like in the previous sections, we first present in section 6.1 an overview of representative radiative models. Then, in section 6.2, we review collider searches for lepton number violation associated with radiative neutrino mass models.

6.1. Selected Radiative Neutrino Mass Models

6.1.1. The Zee-Babu Model

The first radiative scenario we consider is the well-known Zee-Babu model, a two-loop radiative neutrino mass model proposed independently by Zee [30] and Babu [31]. In the model, the SM field content is extended by including one singly-charged scalar (h^±) and one doubly-charged scalar (k^±±). Both scalars are singlets under SU(3)_c×SU(2)_L, leading to the lepton number violating interaction Lagrangian

$\begin{array}{ll}\Delta {L}=\overline{L}{Y}^{†}{e}_{R}H+\overline{\tilde{L}}fL{h}^{+}+\overline{e_R^c}g{e}_R{k}^{++}+{\mu }_{ZB}{h}^{+}{h}^{+}{k}^{--}+\text{H}.\text{c}.,& (6.1)\end{array}$

where L (H) is the SM LH lepton (Higgs) doublet. The 3 × 3 Yukawa coupling matrices f and g are anti-symmetric and symmetric, respectively. The trilinear coupling μ_ZB contributes to the masses of the charged scalars at the loop level. For large values of $({\mu }_{ZB}/m_{h^{\pm }})$ or $({\mu }_{ZB}/m_{k^{\pm \pm }})$, where $m_{h^{\pm },k^{\pm \pm }}$ are the masses of h^± and k^±±, the scalar potential may have QED-breaking minima. This can be avoided by imposing the condition |μ_ZB|≪4πmin(m_h, m_k).

The combined presence of Y, f, g and μ_ZB collectively break lepton number and lead to the generation of a small Majorana neutrino mass. At lowest order, neutrino masses in the Zee-Babu model arise at two-loop order, as depicted in Figure 39A. The resulting neutrino mass matrix scales as

$\begin{array}{ll}{{M}}_{\nu }\simeq \left(\frac{v^2{\mu }_{ZB}}{96{\pi }^2{M}^2}\right) fY{g}^{†}{Y}^T{f}^T,& (6.2)\end{array}$

FIGURE 39

Figure 39. (A) Feynman diagram for the generation of neutrino masses at two-loop order in the Zee-Babu model. (B) Feynman diagram at three-loop order in the cocktail model [518].

where $M=max(m_{h^{\pm }},m_{k^{\pm \pm }})$ is the heaviest mass in the loop. Since f is antisymmetric, the determinant of the neutrino mass matrix vanishes, $det{{M}}_{\nu }=0$. Therefore the Zee-Babu models yields at least one exactly massless neutrino. An important consequence is that the heaviest neutrino mass is determined by the atmospheric mass difference, which can be estimated as

$\begin{array}{ll}{m}_{\nu }\approx 6.6\times {10}^{-3}{f}^{2}g\left(\frac{m_{\tau }^2}{M}\right)\approx 0.05 \text{eV},& (6.3)\end{array}$

where m_τ ≈ 1.778 GeV is the tau lepton mass. This implies the product f²g can not be arbitrarily small, e.g., for M ~ 100 GeV, one finds g²f ≳ 10⁻⁷. Subsequently, the parameter space of the Zee-Babu model is constrained by both neutrino oscillation data, low-energy experiments such as decays mediated k^±± at tree level, and high-energy searches for direct pair production of k^±±.

The study of h^± is mostly similar to that of the singly-charged scalar in the Zee model [28], although the lepton number violating effects are not experimentally observable due to the missing information carried away by the light (Majorana) neutrino in the decay product. The doubly-charged scalar k^±± can decay to a pair of same-sign leptons, which manifestly violates lepton number by ΔL = ±2, with a partial decay width given by

$\begin{array}{ll}\Gamma (k^{\pm \pm }\to {\ell }_a^{\pm }{\ell }_b^{\pm })=\frac{{\left|g_{ab}\right|}^2}{4\pi (1+{\delta }_{ab})}{m}_k.& (6.4)\end{array}$

If $m_{k^{\pm \pm }}>2m_{h^{\pm }},$ then the k^±± → h^±h^± decay mode opens with a partial decay width of

$\begin{array}{ll}\Gamma (k^{\pm \pm }\to h^{\pm }{h}^{\pm })=\frac{m_{k^{\pm \pm }}}{8\pi }{\left(\frac{{\mu }_{ZB}}{m_{k^{\pm \pm }}}\right)}^2\sqrt{1-\frac{4m_{h^{\pm }}^2}{m_{k^{\pm \pm }}^2}}.& (6.5)\end{array}$

Doubly-charged scalars, appear in many other radiative neutrino mass models, including the three-loop Cocktail Model [518], whose eponymous mass-generating diagram is shown in the right panel of Figure 39. The doubly-charged scalar couples to the SM lepton doublet and a singly-charged scalar in the same manner as in the Zee-Babu model, and thus again is similar to a Type II scenario. Radiative Type II Seesaw model [519] that generates neutrino mass at one-loop order contains an SU(2)_L triplet scalar and thus also has similar LHC phenomenology as the tree-level Type II Seesaw mechanism [520].

6.1.2. The Colored Zee-Babu Model With Leptoquark

In a particularly interesting variant of the Zee-Babu model, proposed in Kohda et al. [521], all particles in the neutrino mass-loop are charged under QCD. As shown in Figure 40, the lepton doublet in the loop of the Zee-Babu model is replaced with down-type quark while the singly- and doubly-charged scalars are replaced with a leptoquark $S_{LQ}^{-\frac{1}{3}}$ and a diquark $S_{DQ}^{-\frac{2}{3}}$. Under the SM gauge group, the leptoquark and diquark quantum numbers are

$\begin{array}{ll}{S}_{LQ}^{-\frac{1}{3}} : (3,1,-\frac{1}{3}) \text{and} S_{DQ}^{-\frac{2}{3}} : (6,1,-\frac{2}{3}).& (6.6)\end{array}$

FIGURE 40

Figure 40. Feynman diagram for the generation of neutrino masses at two-loop order in the colored Zee-Babu model [521].

The decay of the diquark $S_{DQ}^{-\frac{2}{3}}$ is analogous to that of the doubly-charged scalar k^±± in that it can decay to a pair of same-sign down-type quarks or a pair of same-sign leptoquarks, if kinematically allowed.

For the models mentioned above, we will only review the collider study with the characteristics different from the tree-level Seesaws in the following.

6.2. Radiative Neutrino Mass Models at Colliders

6.2.1. Doubly-Charged Scalar at the LHC

As mentioned above, the Zee-Babu model contains two singlet charged scalars, h^± and k^±±. Moreover, due to the presence of the doubly-charged scalar decay mode to two same-sign leptons k^±± → ℓ^±ℓ^± via the coupling μ_ZB, collider searches for L-violating effects in the context of the Zee-Babu model are centered on k^±± and its decays.

Like the triplet Higgs in Type II Seesaw, the doubly-charged scalar k^±± can be pair produced via the Drell-Yan process at the LHC if kinematically accessible and is given by

$\begin{array}{ll}pp\to {\gamma }^{\ast }/Z^{\ast }\to k^{++}{k}^{--}.& (6.7)\end{array}$

This is the same process as shown in Figure 28A. However, an important distinction is that while H^±± in the Type II Seesaw is an SU(2)_L triplet, the k^±± here is a singlet. As this quantum-number assignment leads to different Z boson couplings, and hence different production cross section at colliders, it is a differentiating characteristic of the model. Note the γγ fusion processes, shown in Figure 28, also applies to k⁺⁺k⁻⁻ pair production and leads to the same production cross section.

Since the collider signal for pair produced k^±± is the same as H^±± in the Type II Seesaw, the search for doubly-charged scalar can be easily performed for both cases as shown in Figure 31. Obviously the constraint on the singlet is less stringent due to the absence of weak isospin interactions. With 36.1 fb⁻¹ data at 13 TeV, ATLAS has excluded k^±± mass lower than 656-761 GeV for BR(k^±± → e^±e^±) + BR(k^±± → μ^±μ^±) = 1 at 95% CLs [460].

Low energy LFV experiments, especially μ → eγ, impose very stringent constraints on the parameter space of the Zee-Babu model. The MEG experiment [522, 523] has placed an upper bound on the decay branching ratio BR(μ → eγ) < 4.2 × 10⁻¹³, which can be roughly translated as [524]

$\begin{array}{ll}{\left|f_{13}^{*}{f}_{23}\right|}^2\frac{m_{k^{\pm \pm }}^2}{m_{h^{\pm }}^2}+16{\left|{\displaystyle \sum g_{1i}^{*}}{g}_{i2}\right|}^2<1.2\times {10}^{-6}{\left(\frac{m_k}{\text{TeV}}\right)}^4.& (6.8)\end{array}$

To satisfy LFV constraints, the doubly- and singly-charged scalar masses are pushed well above TeV, with $m_{k^{\pm \pm }}>1.3(1.9)$ TeV and $m_{h^{\pm }}>1.3(2.0)$ TeV for the NH (IH), assuming ${\mu }_{ZB}=min(m_{k^{\pm \pm }},m_{h^{\pm }})$. This can be very easily relaxed, however, by choosing larger μ_ZB and balancing smaller Yukawa couplings to generate the right neutrino mass spectrum.

A recent study has projected the sensitivities of the LHC with large luminosities by scaling the cross section bound by $1/\sqrt{{L}}$ for two benchmark scenarios: one for NH and one for IH [525]. The projected sensitivities are shown in Figure 41 for model parameters consistant with neutrino oscillation data. Note that these benchmarks are chosen to have ${\mu }_{ZB}=5min(m_{k^{\pm \pm }},m_{h^{\pm }})$ such that the constraints from flavor experiments such as μ → eγ are much less stringent at the price of a more fine-tuned the scalar potential. We can see that the NH benchmark is less constrained than the IH one when $m_{k^{\pm \pm }}<2m_{h^{\pm }}$ because k^±± has a smaller branching ratio to leptons.

FIGURE 41

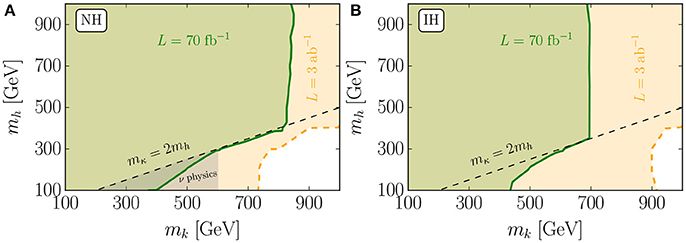
Figure 41. Projection of sensitivities at the LHC in the $m_{k^{\pm \pm }}$-$m_{h^{\pm }}$ plane: (A) the NH benchmark with g_{11, 22} = 0.1, g_{12, 13, 33} = 0.001, f_{12, 13} = 0.01 and f₂₃ = 0.02; (B) the IH benchmark with g_{11, 23} = 0.1, g_{12, 22, 13, 33} = 0.0001, f₁₂ = −f₁₃ = 0.1 and f₂₃ = 0.01. For both benchmarks, the trilinear coupling is chosen to be ${\mu }_{ZB}=5min(m_{k^{\pm \pm }},m_{h^{\pm }})$. The gray shaded region in the left panel is excluded by low energy experiments. The green and orange regions are excluded by future experiments with an integrated luminosity of 70 fb⁻¹ and 3 ab⁻¹ respectively [525].

6.2.2. Leptoquark at the LHC

In the colored Zee-Babu model, L-violating signals can be observed in events with pair produced leptoquarks $S_{LQ}^{-\frac{1}{3}}$ via s-channel diquark $S_{DQ}^{-\frac{2}{3}}$, shown in Figure 42, and given by,

$\begin{array}{ll}pp\to S_{DQ}^{-\frac{2}{3}\ast }\to S_{LQ}^{-\frac{1}{3}}{S}_{LQ}^{-\frac{1}{3}}\to u{\ell }^{-}u{\ell }^{\prime -}.& (6.9)\end{array}$

One benchmark has been briefly studied in Kohda et al. [521]. For leptoquark mass of 1 TeV and diquark mass of 4 TeV, a benchmark consistent with neutrino oscillation data and low energy experiments, the L-violating process in Equation (6.9) can proceed with an LHC cross section of 0.18 fb at $\sqrt{s}=14$ TeV. So far, no dedicated collider study for this model. In general, however, one can recast either ATLAS or CMS search for heavy neutrinos, such as Aad et al. [52] and Khachatryan et al. [363], to derive the limit on the model parameter space.

FIGURE 42

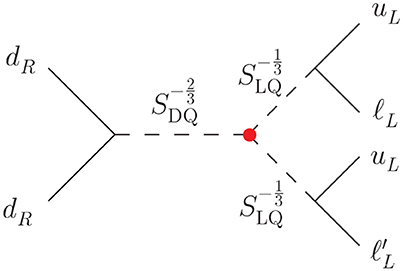
Figure 42. L-violating processes at the LHC in the colored Zee-Babu model [521].

Lepton number violating collider processes, pp → ℓ^±ℓ^± + nj, involving charged scalars, leptoquarks and diquarks have also been studied for the LHC in Peng et al. [394], Helo et al. [526, 527]. Example diagrams are shown in Figure 43. Even though these studies are performed without a concrete neutrino mass model, they possess the most important ingredient of Majorana neutrino mass models: L violation by two units. Therefore radiative neutrino mass models can be constructed from the relevant matter content. Some processes, however, are realized with a SM singlet fermion (for example the left panel of Figure 43), which implies the existence of a tree-level Seesaw. Other processes without SM singlet fermions, SU(2)_L triplet scalars, or triplet fermions, such as the one on the right panel of Figure 43, can be realized in a radiative neutrino mass model. Detailed kinematical analyses for resonant mass reconstruction would help to sort out the underlying dynamics.

FIGURE 43

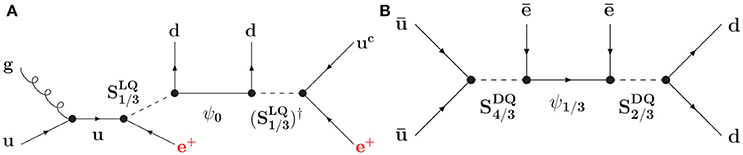
Figure 43. Example diagrams of L violation processes with (A) leptoquark $S_{1/3}^{\text{LQ}}$ and (B) diquarks $S_{4/3,2/3}^{\text{DQ}}$ [526, 527]. The singlet fermion ψ₀ in the left panel leads to Type I Seesaw.

6.2.3. Correlation With Lepton Flavor Violation

In radiative neutrino mass models the breaking of lepton number generally needs the simultaneous presence of multiple couplings. For example, in the Zee-Babu model, Y, f, g and μ_ZB together break lepton number. The observation of pair produced k^±± itself is insufficient to declare L violation. In order to establish L violation in the theory and thus probe the Majorana nature of the neutrinos, the couplings of h^± to SM leptons and to k^±± have to be studied at the same time. For the colored Zee-Babu model, the L violation process shown in Figure 42 involves all couplings except the SM Yukawa necessary to break the lepton number. Note, however, the cross section for this process is proportional to the product of couplings and suppressed by the heavy exotic masses which both contributes to the smallness of the neutrino masses. Thus the cross section for this processes must be kinematically suppressed. For radiative neutrino mass models with dark matter candidates, probing lepton number violation at colliders alone is generally much more difficult as the dark matter candidate appears as missing transverse energy just as neutrinos. Overall, the study of L-violation of radiative neutrino mass models can be performed either with the combination of different processes that test different subsets of the couplings or in a single process that involves all couplings at once whose production cross section is generally suppressed.

On the contrary, radiative neutrino mass models contain LFV couplings and exotic particles that can be tested much easier than L violation stated above. The search strategies for LFV couplings and new particles vary from model to model. It is definitely impossible to cover all and they are also not the focus of this review. Thus we will take a few simple examples to illustrate the searches.

The leading LFV signals can be produced in a radiative neutrino mass model from the QCD pair production of the leptoquark $S_{LQ}^{-\frac{1}{3}}$ with its suitable subsequent decays such as

$\begin{array}{ll}pp \to S_{LQ}^{+\frac{1}{3}}{S}_{LQ}^{-\frac{1}{3}} \to \overline{t}{\ell }^{+}t{\ell }^{\prime -}& (6.10)\end{array}$

where $S_{LQ}^{+\frac{1}{3}}={(S_{LQ}^{-\frac{1}{3}})}^{*}$ and the top quarks decay hadronically. Note that the leptoquark pair can also decay to $\bar{b}{\nu }_{\ell }t{\ell }^{\prime -}$ or $\bar{b}{\nu }_{\ell }b{\bar{\nu }}_{{\ell }^{\prime }}$, where the LFV effects are not easy to disentangle at colliders due to the invisible neutrinos. However, these decay channels can result in final states ℓ⁺ℓ′−X, inclusive flavour off-diagonal charged lepton pair accompanied by missing transverse energy, jets etc., if the quarks decay to appropriate leptons. The same final states have been used to search for stop in SUSY theories and thus the results for stop searches at the LHC can be translated to that of the leptoquark $S_{LQ}^{-\frac{1}{3}}$, $m(S_{LQ}^{-\frac{1}{3}})\gtrsim 600$ GeV [511] based on the ATLAS stop search at $\sqrt{s}=8$ TeV [528] ⁵. No recast of stop search has been performed for 13 TeV run yet. Besides leptoquarks, radiative neutrino mass models also comprise exotic particles such as vector-like quarks, vector-like leptons, charged scalar singlets (both singly- and doubly-charged) and higher-dimensional EW multiplets. For example, disappearing tracks can be used to search for higher-dimensional EW multiplet fermions whose mass splitting between the neutral and the singly-charged component is around 100 MeV. The current LHC searches have set a lower mass limit of 430 GeV at 95% CL for a triplet fermion with a lifetime of about 0.2 ns [534–536]. We refer the readers to the section about collider tests of radiative neutrino mass model in Cai et al. [510] and the references therein for details.

We want to stress, however, that even though L violation in the radiative models is more complicated and challenging to search for in collider experiments, their observation is essential and conclusive to establish the Majorana nature of neutrinos. So once we find signals in either LFV processes or new particles searches, we should search for L violation in specific radiative neutrino mass models that give these LFV processes or contain these new particles, in order to ultimately test the generation of neutrino masses.

7. Summary and Conclusions

Exploring the origin of neutrinos' tiny masses, their large mixing, and their Dirac or Majorana nature are among the most pressing issues in particle physics today. If one or more neutrino Seesaw mechanisms are realized in nature, it would be ultimately important to identify the new scales responsible for generating neutrino masses. Neutrino oscillation experiments, however, may not provide such information, and thus complementary pathways, such as collider experiments, are vital to understanding the nature of neutrinos. Observing lepton number violation at collider experiments would be a conclusive verdict for the existence of neutrino Majorana masses, but also direct evidence of a mass scale qualitatively distinct from those in the SM.

In this context, we have reviewed tests of low-scale neutrino mass models at pp, ep, and ee colliders, focusing particularly on searches for lepton number (L) violation: We begin with summarizing present neutrino oscillation and cosmology data and their impact on the light neutrino mass spectra in section 2. We then consider several representative scenarios as phenomenological benchmarks, including the characteristic Type I Seesaw in section 3, the Type II Seesaw in section 4, the Type III in section 5, radiative constructions in section 6, as well as extensions and hybridizations of these scenarios. We summarize the current status of experimental signatures featuring L violation, and present anticipated coverage in the theory parameter space at current and future colliders. We emphasize new production and decay channels, their phenomenological relevance and treatment across different collider facilities. We also summarize available Monte Carlo tools available for studying Seesaw partners in collider environments.

The Type I Seesaw is characterized by new right-handed, SM gauge singlet neutrinos, known also as “sterile neutrinos,” which mix with left-handed neutrinos via mass diagonalization. As this mixing scales with light neutrino masses and elements of the PMNS matrix, heavy neutrino decays to charged leptons may exhibit some predictable patterns if one adopts some simplifying assumptions for the mixing matrix, as shown for example in Figures 3, 4, that are correlated with neutrino oscillation data. The canonical high-scale Type I model, however, predicts tiny active-sterile mixing, with $|V_{\ell N}{|}^2~m_{\nu }/M_N$, and thus that heavy N decouple from collider experiments. Subsequently, observing lepton number violation in collider experiments, as discussed in section 3.2, implies a much richer neutrino mass-generation scheme than just the canonical, high-scale Type I Seesaw. In exploring the phenomenological parameter space, the 14 TeV LHC (and potential 100 TeV successor) and ${L}=1$ ab⁻¹ integrated luminosity could reach at least 2σ sensitivity for heavy neutrino masses of M_N ≲ 500 GeV (1 TeV) with a mixing $|V_{\ell N}{|}^2\lesssim 10^{-3}$, as seen in Figure 9. If N is charged under another gauge group that also couples to the SM, as in B-L or LR gauge extensions, then the discovery limit may be extended to $M_N~M_{Z^{\prime }},M_{W_R}$, when kinematically accessible; see sections 3.2.4 and 3.2.5.

The Type II Seesaw is characterized by heavy SU(2)_L triplet scalars, which result in new singly- and doubly-charged Higgs bosons. They can be copiously produced in pairs via SM electroweak gauge interactions if kinematically accessible at collider energies, and search for the doubly-charged Higgs bosons via the same-sign dilepton channel H^±± → ℓ^±ℓ^± is an on-going effort at the LHC. Current direct searches at 13 TeV bound triplet scalar masses to be above (roughly) 800 GeV. With anticipated LHC luminosity and energy upgrades, one can expect for the search to go beyond a TeV. Furthermore, if neutrino masses are dominantly from triplet Yukawa couplings, then the patterns of the neutrino mixing and mass relations from the oscillation experiments will correlate with the decays of the triplet Higgs bosons to charged leptons, as seen from the branching fraction predictions in Figures 25, 26 and in Table 2. Since a Higgs triplet naturally exists in certain extensions beyond the SM, such as in Little Higgs theory, the LRSM, and GUT theories, the search for such signals may prove beneficial as discussed in section 4.2.2.

The Type III Seesaw is characterized by heavy SU(2)_L triplet leptons, which result in vector-like, charged and neutral leptons. Such multiplets can be realized in realistic GUT theories in hybridization with heavy singlet neutrinos from a Type I Seesaw. Drell-Yan pair production of heavy charged leptons at hadron colliders is sizable as it is governed by the SM gauge interactions. They can decay to the SM leptons plus EW bosons, leading to same-sign dilepton events. Direct searches for promptly decaying triplet leptons at the LHC set a lower bound on the triplet mass scale of around 800 GeV. A future 100 TeV pp collider can extend the mass reach to at least several TeV, as seen in Figure 37.

Finally, neutrino masses can also be generated radiatively, which provides an attractive explanation for the smallness of neutrino masses with a plausibly low mass scale. Among the large collection of radiative neutrino mass models, the Zee-Babu model contains a doubly-charged SU(2)_L singlet scalar with collider signal akin to the doubly-charged Higgs in the Type II Seesaw. ATLAS has excluded k^±± mass below 660 − 760 GeV assuming the benchmark decay rate $\sum _{{\ell }_i=e,\mu }\text{BR}(k^{\pm \pm }\to {\ell }_1^{\pm }{\ell }_2^{\pm })=1$. The high luminosity LHC is sensitive up to about a TeV for both k^±± and its companion scalar h^± in the Zee-Babu model with constraints from neutrino oscillation data and other low energy experiments. For the colored variant of the Zee-Babu model, a pair of same-sign leptoquark can be produced via an s-channel diquark at the LHC. Their subsequent decay lead to the lepton number violating same-sign dilepton plus jets final state, which still await dedicated studies.

As a final remark, viable low-scale neutrino mass models often generate a rich flavor structure in the charged lepton sector that predict lepton flavor-violating transitions. Such processes are typically much more easily observable than lepton number violating processes, in part due to their larger production and decay rates, and should be searched for in both high- and low-energy experiments.

Author Contributions

The conception and content scope of this review was mainly designed by TH. TL edited the chapter on neutrino masses; TL and RR edited the chapters on the Type I, II, III seesaw models and their collider tests; YC edited the chapter on radiative neutrino mass models. TH drafted the concluding section. TH and RR revised the manuscript critically for important, intellectual content and expressions. Most of the materials compiled in the review came from the early publications from the collective works by the authors.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Michael A. Schmidt for useful discussions. Past and present members of the IPPP are thanked for discussions. The work of TH was supported in part by the U.S. Department of Energy under grant No. DE-FG02- 95ER40896 and in part by the PITT PACC. The work of TL was supported in part by the Australian Research Council Centre of Excellence for Particle Physics at the Tera-scale. The work of RR was funded in part by the UK Science and Technology Facilities Council (STFC), the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreements No 690575 (InvisiblesPlus RISE) and No 674896 (InvisiblesPlus RISE). Support for the open accessibility of this work is provided by the Research Councils UK, external grant number ST/G000905/1.

Republication of the various figures is granted under the terms of the Creative Commons Attribution Licenses, American Physical Society PRD License Nos.: 4234250091794, 4234250774584, 4234260138469, 4234270420615, 4234270625995, 4234270758210, 4234280275772, 4234280455112, 4234291212539, 4234300360477, 4234301170893, 4234310175148, and PRL License No. 4234301302410.

Footnotes

1. ^This is done for simplicity since U_PMNS in Table 1 is unitary whereas here it is not; for more details, see Esteban et al. [72], and Parke and Ross-Lonergan [92].

2. ^$\sum _N{(V_{\ell N}^{*})}^2=\sum _N|V_{\ell N}{|}^2$ only when all phases on the right-hand side of Equation (3.11) vanish [93].

3. ^Where $\mathrm{\text{BR}}(A\to X)\equiv \Gamma (A\to X)/\sum _Y\Gamma (A\to Y)$ for partial width Γ(A → Y).

4. ^A note on terminology: High-p_T hadron collider observables, e.g., fiducial distributions, are inherently inclusive with respect to jets with arbitrarily low p_T. In this sense, we refer to hadronic-level processes with a fixed multiplicity of jets satisfying kinematical requirements (and with an arbitrary number of additional jets that do not) as exclusive, e.g., pp → W^±+3j + X; those with a minimum multiplicity meeting these requirements are labeled semi-inclusive, e.g., pp → W^±+≥3j + X; and those with an arbitrary number of jets are labeled inclusive, e.g., pp → W^± + X. Due to DGLAP-evolution, exclusive, partonic amplitudes convolved with PDFs are semi-inclusive at the hadronic level.

5. ^There are many dedicated leptoquark searches at the LHC [529–533]. However, the leptoquarks searched only couple to one generation of fermions at a time and thus generate no LFV signals.

References

1. Pontecorvo B. Inverse beta processes and nonconservation of lepton charge. Sov Phys JETP (1958) 7:172–3.

Google Scholar

2. Pontecorvo B. Mesonium and anti-mesonium. Sov Phys JETP (1957) 6:429.

Google Scholar

3. Maki Z, Nakagawa M, Sakata S. Remarks on the unified model of elementary particles. Prog Theor Phys. (1962) 28:870–80. doi: 10.1143/PTP.28.870

CrossRef Full Text | Google Scholar

4. Weinberg S. A model of leptons. Phys Rev Lett. (1967) 19:1264–66. doi: 10.1103/PhysRevLett.19.1264

CrossRef Full Text | Google Scholar

5. Ma E. Pathways to naturally small neutrino masses. Phys Rev Lett. (1998) 81:1171–4. doi: 10.1103/PhysRevLett.81.1171

CrossRef Full Text | Google Scholar

6. Majorana E. Teoria simmetrica dellelettrone e del positrone. Nuovo Cim. (1937) 14:171–84. doi: 10.1007/BF02961314

CrossRef Full Text | Google Scholar

7. Weinberg S. Baryon and lepton nonconserving processes. Phys Rev Lett. (1979) 43:1566–70. doi: 10.1103/PhysRevLett.43.1566

CrossRef Full Text | Google Scholar

8. Minkowski P. μ → eγ at a rate of one out of 10⁹ muon decays? Phys Lett. (1977) 67B:421–8. doi: 10.1016/0370-2693(77)90435-X

CrossRef Full Text | Google Scholar

9. Yanagida T. Horizontal Symmetry and masses of neutrinos. Conf Proc. (1979) C7902131:95–9.

Google Scholar

10. Gell-Mann M, Ramond P, Slansky R. Complex spinors and unified theories. Conf Proc. (1979) C790927:315–21.

Google Scholar

11. Glashow SL. The future of elementary particle physics. NATO Sci Ser B (1980) 61:687. doi: 10.1007/978-1-4684-7197-7_15

CrossRef Full Text | Google Scholar

12. Mohapatra RN, Senjanović G. Neutrino mass and spontaneous parity violation. Phys Rev Lett. (1980) 44:912. doi: 10.1103/PhysRevLett.44.912

CrossRef Full Text | Google Scholar

13. Shrock RE. General theory of weak leptonic and semileptonic decays. 1. Leptonic pseudoscalar meson decays, with associated tests for, and bounds on, neutrino masses and lepton mixing. Phys Rev. (1981) D24:1232. doi: 10.1103/PhysRevD.24.1232

CrossRef Full Text | Google Scholar

14. Schechter J, Valle JWF. Neutrino masses in SU(2) ⊗ U(1) theories. Phys Rev. (1980) D22:2227. doi: 10.1103/PhysRevD.22.2227

CrossRef Full Text | Google Scholar

15. Konetschny W, Kummer W. Nonconservation of total lepton number with scalar bosons. Phys Lett. (1977) 70B:433–5. doi: 10.1016/0370-2693(77)90407-5

CrossRef Full Text | Google Scholar

16. Cheng TP, Li LF. Neutrino masses, mixings and oscillations in SU(2) × U(1) models of electroweak interactions. Phys Rev. (1980) D22:2860. doi: 10.1103/PhysRevD.22.2860

CrossRef Full Text | Google Scholar

17. Lazarides G, Shafi Q, Wetterich C. Proton lifetime and fermion masses in an SO(10) model. Nucl Phys. (1981) B181:287–300. doi: 10.1016/0550-3213(81)90354-0

CrossRef Full Text | Google Scholar

18. Mohapatra RN, Senjanović G. Neutrino masses and mixings in gauge models with spontaneous parity violation. Phys Rev. (1981) D23:165. doi: 10.1103/PhysRevD.23.165

CrossRef Full Text | Google Scholar

19. Foot R, Lew H, He XG, Joshi GC. Seesaw neutrino masses induced by a triplet of leptons. Z Phys. (1989) C44:441.

Google Scholar

20. Wyler D, Wolfenstein L. Massless neutrinos in left-right symmetric models. Nucl Phys. (1983) B218:205–14. doi: 10.1016/0550-3213(83)90482-0

CrossRef Full Text | Google Scholar

21. Mohapatra RN. Mechanism for understanding small neutrino mass in superstring theories. Phys Rev Lett. (1986) 56:561–3. doi: 10.1103/PhysRevLett.56.561

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Mohapatra RN, Valle JWF. Neutrino mass and baryon number nonconservation in superstring models. Phys Rev. (1986) D34:1642. doi: 10.1103/PhysRevD.34.1642

CrossRef Full Text | Google Scholar

23. Bernabéu J, Santamaria A, Vidal J, Mendez A, Valle JWF. Lepton flavor nonconservation at high-energies in a superstring inspired standard model. Phys Lett. (1987) B187:303–8. doi: 10.1016/0370-2693(87)91100-2

CrossRef Full Text | Google Scholar

24. Gavela MB, Hambye T, Hernandez D, Hernandez P. Minimal flavour seesaw models. J High Energy Phys. (2009) 9:38. doi: 10.1088/1126-6708/2009/09/038

CrossRef Full Text | Google Scholar

25. Akhmedov EK, Lindner M, Schnapka E, Valle JWF. Left-right symmetry breaking in NJL approach. Phys Lett. (1996) B368:270–80. doi: 10.1016/0370-2693(95)01504-3

CrossRef Full Text | Google Scholar

26. Akhmedov EK, Lindner M, Schnapka E, Valle JWF. Dynamical left-right symmetry breaking. Phys Rev. (1996) D53:2752–2780. doi: 10.1103/PhysRevD.53.2752

CrossRef Full Text | Google Scholar

27. Moffat K, Pascoli S, Weiland C. Equivalence between massless neutrinos and lepton number conservation in fermionic singlet extensions of the Standard Model. (2017) arXiv:1712.07611.

Google Scholar

28. Zee A. A theory of lepton number violation, neutrino majorana mass, and oscillation. Phys Lett. (1980) 93B:389. doi: 10.1016/0370-2693(80)90349-4

CrossRef Full Text | Google Scholar

29. Hall LJ, Suzuki M. Explicit R-parity breaking in supersymmetric models. Nucl Phys. (1984) B231:419–44. doi: 10.1016/0550-3213(84)90513-3

CrossRef Full Text | Google Scholar

30. Zee A. Quantum numbers of majorana neutrino masses. Nucl Phys. (1986) B264:99–110. doi: 10.1016/0550-3213(86)90475-X

CrossRef Full Text | Google Scholar

31. Babu KS. Model of 'calculable' majorana neutrino masses. Phys Lett. (1988) B203:132–6. doi: 10.1016/0370-2693(88)91584-5

CrossRef Full Text | Google Scholar

32. Krauss LM, Nasri S, Trodden M. A model for neutrino masses and dark matter. Phys Rev. (2003) D67:085002. doi: 10.1103/PhysRevD.67.085002

CrossRef Full Text | Google Scholar

33. Schechter J, Valle JWF. Neutrinoless double-β decay in SU(2) × U(1) theories. Phys Rev. (1982) D25:2951.

Google Scholar

34. Hirsch M, Kovalenko S, Schmidt I. Extended black box theorem for lepton number and flavor violating processes. Phys Lett. (2006) B642:106–10. doi: 10.1016/j.physletb.2006.09.012

CrossRef Full Text | Google Scholar

35. Duerr M, Lindner M, Merle A. On the quantitative impact of the schechter-valle theorem. J High Energy Phys. (2011) 6:91. doi: 10.1007/JHEP06(2011)091

CrossRef Full Text | Google Scholar

36. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H. Search for majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen. Phys Rev Lett. (2016) 117:082503. doi: 10.1103/PhysRevLett.117.082503

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Agostini M, Allardt M, Bakalyarov AM, Balata M, Barabanov I, Baudis L, et al. Background free search for neutrinoless double beta decay with GERDA Phase II. (2017) Nature 544:47. doi: 10.1038/nature21717

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Alfonso K, Artusa DR, Avignone FT 3rd, Azzolini O, Balata M, Banks TI, et al. Search for neutrinoless double-beta decay of ¹³⁰Te with CUORE-0. Phys Rev Lett. (2015) 115:102502. doi: 10.1103/PhysRevLett.115.102502

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Albert JB, Auty DJ, Barbeau PS, Beauchamp E, Beck D, Belov V, et al. Search for Majorana neutrinos with the first two years of EXO-200 data. Nature (2014) 510:229–34. doi: 10.1038/nature13432

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Arnaboldi C, Avignone FT, Beeman J, Barucci M, Balata M, Brofferio C, et al. CUORE: a Cryogenic underground observatory for rare events. Nucl Instrum Meth. (2004) A518:775–98. doi: 10.1016/j.nima.2003.07.067

CrossRef Full Text | Google Scholar

41. Arnold R, Augier C, Baker J, Barabash AS, Basharina-Freshville A, Bongrand M, et al. Probing new physics models of neutrinoless double beta decay with superNEMO. Eur Phys J. (2010) C70:927–43. doi: 10.1140/epjc/s10052-010-1481-5

CrossRef Full Text | Google Scholar

42. Alvarez V, Borges FIGM, Cárcel S, Carmona JM, Castel J, Catalá JM, et al. NEXT-100 technical design report (TDR): executive summary. J Instrum. (2012) 7:T06001. doi: 10.1088/1748-0221/7/06/T06001

CrossRef Full Text | Google Scholar

43. Alekhin S, Altmannshofer W, Asaka T, Batell B, Bezrukov F, Bondarenko K, et al. A facility to Search for Hidden Particles at the CERN SPS: the SHiP physics case. Rept Prog Phys. (2016) 79:124201. doi: 10.1088/0034-4885/79/12/124201

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Anelli M, Aoki S, Arduini G, Back JJ, Bagulya A, Baldini W. A facility to Search for Hidden Particles (SHiP) at the CERN SPS. (2015) arXiv:1504.04956.

Google Scholar

45. Liventsev D, Adachi I, Aihara H, Arinstein K, Asner DM, Aulchenko V, et al. Search for heavy neutrinos at Belle. Phys Rev. (2013) D87:071102. doi: 10.1103/PhysRevD.87.071102

CrossRef Full Text | Google Scholar

46. Aaij R, Abellan Beteta C, Adeva B, Adinolfi M, Adrover C, Affolder A, et al. Searches for Majorana neutrinos in B⁻ decays. Phys Rev. (2012) D85:112004. doi: 10.1103/PhysRevD.85.112004

CrossRef Full Text | Google Scholar

47. Aaij R, Adeva B, Adinolfi M, Affolder A, Ajaltouni Z, Albrecht J, et al. Search for Majorana neutrinos in B⁻ → π⁺μ⁻μ⁻ decays. Phys Rev Lett. (2014) 112:131802. doi: 10.1103/PhysRevLett.112.131802

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Sirunyan AM, Tumasyan A, Adam W, Aşilar E, Bergauer T, Brandstetter J. Search for third-generation scalar leptoquarks and heavy right-handed neutrinos in final states with two tau leptons and two jets in proton-proton collisions at $\sqrt{s}=13$ TeV. J High Energy Phys. (2017) 7:121. doi: 10.1007/JHEP07(2017)121

CrossRef Full Text | Google Scholar

49. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Aşilar E, Bergauer T. Search for heavy neutrinos or third-generation leptoquarks in final states with two hadronically decaying τ leptons and two jets in proton-proton collisions at $\sqrt{s}=13$ TeV. J High Energy Phys. (2017) 3:77. doi: 10.1007/JHEP03(2017)077

CrossRef Full Text | Google Scholar

50. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Aşilar E, Bergauer T. Search for heavy Majorana neutrinos in ee+ jets and e μ + jets events in proton-proton collisions at $\sqrt{s}=8$ TeV. J High Energy Phys. (2016) 4:169. doi: 10.1007/JHEP04(2016)169

CrossRef Full Text | Google Scholar

51. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M. Search for heavy Majorana neutrinos in μ^±μ^±+ jets events in proton-proton collisions at $\sqrt{s}$ = 8 TeV. Phys Lett. (2015) B748:144–66. doi: 10.1016/j.physletb.2015.06.070

CrossRef Full Text | Google Scholar

52. Aad G, Abbott B, Abdallah J, Abdel Khalek S, Abdinov O, Aben R, et al. Search for heavy Majorana neutrinos with the ATLAS detector in pp collisions at $\sqrt{s}=8$ TeV. J High Energy Phys. (2015) 7:162. doi: 10.1007/JHEP07(2015)162

CrossRef Full Text | Google Scholar

53. ATLAS Collaboration. Search for doubly-charged Higgs bosons in same-charge electron pair final states using proton-proton collisions at $\sqrt{s}=13\text{TeV}$ with the ATLAS detector. ATLAS-CONF-2016-051 (2016).

54. Aad G, Abbott B, Abdallah J, Abdel Khalek S, Abdinov O, Aben R, et al. Search for anomalous production of prompt same-sign lepton pairs and pair-produced doubly charged Higgs bosons with $\sqrt{s}=8$ TeV pp collisions using the ATLAS detector. J High Energy Phys. (2015) 3:041.

Google Scholar

55. Chatrchyan S, Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T. A search for a doubly-charged Higgs boson in pp collisions at $\sqrt{s}=7$ TeV. Eur Phys J. (2012) C72:2189. doi: 10.1140/epjc/s10052-012-2189-5

CrossRef Full Text | Google Scholar

56. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M. Search for type-III Seesaw heavy leptons in pp collisions at $\sqrt{s}=8$ TeV with the ATLAS Detector. Phys Rev. (2015) D92:032001. doi: 10.1103/PhysRevD.92.032001

CrossRef Full Text | Google Scholar

57. Chatrchyan S, Khachatryan V, Sirunyan AM, Tumasyan A. Search for heavy lepton partners of neutrinos in proton-proton collisions in the context of the type III seesaw mechanism. Phys Lett. (2012) B718:348–68. doi: 10.1016/j.physletb.2012.10.070

CrossRef Full Text | Google Scholar

58. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Search for evidence of the type-III seesaw mechanism in multilepton final states in proton-proton collisions at sqrt[s] = 13 TeV. Phys Rev Lett. (2017) 119:221802. doi: 10.1103/PhysRevLett.119.221802

PubMed Abstract | CrossRef Full Text | Google Scholar

59. CMS Collaboration. Search for heavy composite Majorana neutrinos produced in association with a lepton and decaying into a same-flavour lepton plus two quarks at $\sqrt{s}=13\text{ TeV}$ with the CMS detector. CMS-PAS-EXO-16-026 (2016).

60. CMS Collaboration. Search for a heavy composite Majorana neutrino in the final state with two leptons and two quarks at $\sqrt{s}$ = 13 TeV. Phys. Lett. B (2017) 775:315–37. doi: 10.1016/j.physletb.2017.11.001

CrossRef Full Text

61. Gluza J. On teraelectronvolt Majorana neutrinos. Acta Phys Polon. (2002) B33:1735–46.

Google Scholar

62. Barger V, Marfatia D, Whisnant K. Progress in the physics of massive neutrinos. Int J Mod Phys. (2003) E12:569–647. doi: 10.1142/S0218301303001430

CrossRef Full Text | Google Scholar

63. Mohapatra RN, Smirnov AY. Neutrino mass and new physics. Ann Rev Nucl Part Sci. (2006) 56:569–628. doi: 10.1146/annurev.nucl.56.080805.140534

CrossRef Full Text | Google Scholar

64. Rodejohann W. Neutrino-less double beta decay and particle physics. Int J Mod Phys. (2011) E20:1833–930. doi: 10.1142/S0218301311020186

CrossRef Full Text | Google Scholar

65. Chen MC, Huang J. TeV scale models of neutrino masses and their phenomenology. Mod Phys Lett. (2011) A26:1147–67. doi: 10.1142/S0217732311035985

CrossRef Full Text | Google Scholar

66. Atre A, Han T, Pascoli S, Zhang B. The search for heavy majorana neutrinos. J High Energy Phys. (2009) 5:30. doi: 10.1088/1126-6708/2009/05/030

CrossRef Full Text | Google Scholar

67. Deppisch FF, Bhupal Dev PS, Pilaftsis A. Neutrinos and collider physics. New J Phys. (2015) 17:075019. doi: 10.1088/1367-2630/17/7/075019

CrossRef Full Text | Google Scholar

68. An FP, Bai JZ, Balantekin AB, Band HR, Beavis D, Beriguete W, et al. Observation of electron-antineutrino disappearance at Daya Bay. Phys Rev Lett. (2012) 108:171803. doi: 10.1103/PhysRevLett.108.171803

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Abe Y, Aberle C, Akiri T, dos Anjos JC, Ardellier F, Barbosa AF. Indication of reactor ${\bar{\nu }}_e$ disappearance in the double chooz experiment. Phys Rev Lett. (2012) 108:131801. doi: 10.1103/PhysRevLett.108.131801

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Ahn JK, Chebotaryov S, Choi JH, Choi S, Choi W, Choi Y, et al. Observation of reactor electron antineutrino disappearance in the RENO experiment. Phys Rev Lett. (2012) 108:191802. doi: 10.1103/PhysRevLett.108.191802

PubMed Abstract | CrossRef Full Text | Google Scholar

71. An FP, Balantekin AB, Band HR, Bishai M, Blyth S, Butorov I, et al. New measurement of antineutrino oscillation with the full detector configuration at daya bay. Phys Rev Lett. (2015) 115:111802. doi: 10.1103/PhysRevLett.115.111802

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Esteban I, Gonzalez-Garcia MC, Maltoni M, Martinez-Soler I, Schwetz T. Updated fit to three neutrino mixing: exploring the accelerator-reactor complementarity. J High Energy Phys. (2017) 1:87. doi: 10.1007/JHEP01(2017)087

CrossRef Full Text | Google Scholar

73. Abe K, Adam J, Aihara H, Akiri T, Andreopoulos C, Aoki S, et al. Observation of electron neutrino appearance in a muon neutrino beam. Phys Rev Lett. (2014) 112:061802. doi: 10.1103/PhysRevLett.112.061802

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Adamson P, Ader C, Andrews M, Anfimov N, Anghel I, Arms K, et al. First measurement of electron neutrino appearance in NOvA. Phys Rev Lett. (2016) 116:151806. doi: 10.1103/PhysRevLett.116.151806

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Abe K, Amey J, Andreopoulos C, Antonova M, Aoki S, Ariga A, et al. Combined analysis of neutrino and antineutrino oscillations at T2K. Phys Rev Lett. (2017) 118:151801. doi: 10.1103/PhysRevLett.118.151801

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Forero DV, Huber P. Hints for leptonic CP violation or New Physics? Phys Rev Lett. (2016) 117:031801. doi: 10.1103/PhysRevLett.117.031801

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Ge SF, Smirnov AY. Non-standard interactions and the CP phase measurements in neutrino oscillations at low energies. J High Energy Phys. (2016) 10:138. doi: 10.1007/JHEP10(2016)138

CrossRef Full Text | Google Scholar

78. de Gouvêa A, Kelly KJ. False signals of CP-invariance violation at DUNE. (2016) arXiv:1605.09376.

Google Scholar

79. Miranda OG, Tórtola M, Valle JWF. New ambiguity in probing CP violation in neutrino oscillations. Phys Rev Lett. (2016) 117:061804. doi: 10.1103/PhysRevLett.117.061804

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Ade PAR, Aghanim N, Arnaud M, Ashdown M, Aumont J, Baccigalupi C, et al. Planck 2015 results. XIII. Cosmological parameters. Astron Astrophys. (2016) 594:A13. doi: 10.1051/0004-6361/201525830

CrossRef Full Text | Google Scholar

81. Lesgourgues J, Pastor S. Neutrino cosmology and planck. New J Phys. (2014) 16:65002. doi: 10.1088/1367-2630/16/6/065002

CrossRef Full Text | Google Scholar

82. Hamann J, Hannestad S, Wong YYY. Measuring neutrino masses with a future galaxy survey. J Cosmol Astropart Phys. (2012) 1211:52. doi: 10.1088/1475-7516/2012/11/052

CrossRef Full Text | Google Scholar

83. Acciarri R, Acero MA, Adamowski M, Adams C, Adamson P, Adhikari S. Long-Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE). (2016) arXiv:1601.05471.

Google Scholar

84. An F, An G, An Q, Antonelli V, Baussan E, Beacom J, et al. Neutrino physics with JUNO. J Phys. (2016) G43:030401. doi: 10.1088/0954-3899/43/3/030401

CrossRef Full Text | Google Scholar

85. Abe K, Aihara H, Andreopoulos C, Anghel I, Ariga A, Ariga T, et al. Physics potential of a long-baseline neutrino oscillation experiment using a J-PARC neutrino beam and hyper-kamiokande. PTEP (2015) 2015:053C02. doi: 10.1093/ptep/ptv061

CrossRef Full Text | Google Scholar

86. Osipowicz A, Blumer H, Drexlin G, Eitel K, Meisel G, Plischke P. KATRIN Collaboration. KATRIN: a next generation tritium beta decay experiment with sub-eV sensitivity for the electron neutrino mass. (2001) arXiv:hep-ex/0109033.

Google Scholar

87. Han T, Lewis I, Ruiz R, Si Z-g. Lepton number violation and W′ chiral couplings at the LHC. Phys Rev. (2013) D87:035011. doi: 10.1103/PhysRevD.87.035011

CrossRef Full Text | Google Scholar

88. del Águila F, de Blas J, Pérez-Victoria M. Effects of new leptons in Electroweak Precision Data. Phys Rev. (2008) D78:013010. doi: 10.1103/PhysRevD.78.013010

CrossRef Full Text | Google Scholar

89. Antusch S, Fischer O. Non-unitarity of the leptonic mixing matrix: present bounds and future sensitivities. J High Energy Phys. (2014) 10:094. doi: 10.1007/JHEP10(2014)094

CrossRef Full Text | Google Scholar

90. de Gouvêa A, Kobach A. Global constraints on a heavy neutrino. Phys Rev. (2016) D93:033005. doi: 10.1103/PhysRevD.93.033005

CrossRef Full Text | Google Scholar

91. Fernandez-Martinez E, Hernandez-Garcia J, Lopez-Pavon J. Global constraints on heavy neutrino mixing. J High Energy Phys. (2016) 8:33. doi: 10.1007/JHEP08(2016)033

CrossRef Full Text | Google Scholar

92. Parke S, Ross-Lonergan M. Unitarity and the three flavor neutrino mixing matrix. Phys Rev. (2016) D93:113009. doi: 10.1103/PhysRevD.93.113009

CrossRef Full Text | Google Scholar

93. Fileviez Pérez P, Han T, Li T. Testability of type I seesaw at the CERN LHC: revealing the existence of the B-L symmetry. Phys Rev. (2009) D80:073015. doi: 10.1103/PhysRevD.80.073015

CrossRef Full Text | Google Scholar

94. Ibarra A, Molinaro E, Petcov ST. Low energy signatures of the TeV scale see-saw mechanism. Phys Rev. (2011) D84:013005. doi: 10.1103/PhysRevD.84.013005

CrossRef Full Text | Google Scholar

95. Casas JA, Ibarra A. Oscillating neutrinos and muon → e, gamma. Nucl Phys. (2001) B618:171–204. doi: 10.1016/S0550-3213(01)00475-8

CrossRef Full Text | Google Scholar

96. Pilaftsis A. Radiatively induced neutrino masses and large Higgs neutrino couplings in the standard model with Majorana fields. Z Phys. (1992) C55:275–82. doi: 10.1007/BF01482590

CrossRef Full Text | Google Scholar

97. Kersten J, Smirnov AY. Right-handed neutrinos at CERN LHC and the mechanism of neutrino mass generation. Phys Rev. (2007) D76:073005. doi: 10.1103/PhysRevD.76.073005

CrossRef Full Text | Google Scholar

98. Aristizabal Sierra D, Yaguna CE. On the importance of the 1-loop finite corrections to seesaw neutrino masses. J High Energy Phys. (2011) 8:13. doi: 10.1007/JHEP08(2011)013

CrossRef Full Text | Google Scholar

99. Lopez-Pavon J, Molinaro E, Petcov ST. Radiative corrections to light neutrino masses in low scale type I seesaw scenarios and neutrinoless double beta decay. J High Energy Phys. (2015) 11:30. doi: 10.1007/JHEP11(2015)030

CrossRef Full Text | Google Scholar

100. Fernandez-Martinez E, Hernandez-Garcia J, Lopez-Pavon J, Lucente M. Loop level constraints on Seesaw neutrino mixing. J High Energy Phys. (2015) 10:130. doi: 10.1007/JHEP10(2015)130

CrossRef Full Text | Google Scholar

101. Chen SL, Frigerio M, Ma E. Hybrid seesaw neutrino masses with A(4) family symmetry. Nucl Phys. (2005) B724:423–31. doi: 10.1016/j.nuclphysb.2005.07.012

CrossRef Full Text | Google Scholar

102. Akhmedov EK, Frigerio M. Interplay of type I and type II seesaw contributions to neutrino mass. J High Energy Phys. (2007) 1:43. doi: 10.1088/1126-6708/2007/01/043

CrossRef Full Text | Google Scholar

103. Akhmedov EK, Blennow M, Hallgren T, Konstandin T, Ohlsson T. Stability and leptogenesis in the left-right symmetric seesaw mechanism. J High Energy Phys. (2007) 4:22. doi: 10.1088/1126-6708/2007/04/022

CrossRef Full Text | Google Scholar

104. Chao W, Luo S, Xing Z-z, Zhou S. A compromise between neutrino masses and collider signatures in the type-II seesaw model. Phys Rev. (2008) D77:016001. doi: 10.1103/PhysRevD.77.016001

CrossRef Full Text | Google Scholar

105. Chao W, Si Z-g, Zheng Yj, Zhou S. Testing the realistic seesaw model with two heavy Majorana neutrinos at the CERN large hadron collider. Phys Lett. (2010) B683:26–32. doi: 10.1016/j.physletb.2009.11.059

CrossRef Full Text | Google Scholar

106. Gu PH, Hirsch M, Sarkar U, Valle JWF. Neutrino masses, leptogenesis and dark matter in hybrid seesaw. Phys Rev. (2009) D79:033010. doi: 10.1103/PhysRevD.79.033010

CrossRef Full Text | Google Scholar

107. Chao W, Si ZG, Xing Z-z, Zhou S. Correlative signatures of heavy Majorana neutrinos and doubly-charged Higgs bosons at the Large Hadron Collider. Phys Lett. (2008) B666:451–4. doi: 10.1016/j.physletb.2008.08.003

CrossRef Full Text | Google Scholar

108. Langacker P. Grand unified theories and proton decay. Phys Rept. (1981) 72:185. doi: 10.1016/0370-1573(81)90059-4

CrossRef Full Text | Google Scholar

109. Hewett JL, Rizzo TG. Low-energy phenomenology of superstring inspired E₆ models. Phys Rept. (1989) 183:193. doi: 10.1016/0370-1573(89)90071-9

CrossRef Full Text | Google Scholar

110. Faraggi AE, Nanopoulos DV. A SUPERSTRING Z′ AT O (1-TeV) ? Mod Phys Lett. (1991) A6:61–8. doi: 10.1142/S0217732391002621

CrossRef Full Text | Google Scholar

111. Accomando E, Belyaev A, Fedeli L, King SF, Shepherd-Themistocleous C. Z′ physics with early LHC data. Phys Rev. (2011) D83:075012. doi: 10.1103/PhysRevD.83.075012

CrossRef Full Text | Google Scholar

112. Faraggi AE, Guzzi M. Extra Z′ s and W′ s in heterotic-string derived models. Eur Phys J. (2015) C75:537. doi: 10.1140/epjc/s10052-015-3763-4

CrossRef Full Text | Google Scholar

113. Salvioni E, Villadoro G, Zwirner F. Minimal Z-prime models: present bounds and early LHC reach. J High Energy Phys. (2009) 11:068. doi: 10.1088/1126-6708/2009/11/068

CrossRef Full Text | Google Scholar

114. Carlson ED. Limits on a new U(1) coupling. Nucl Phys. (1987) B286:378–98. doi: 10.1016/0550-3213(87)90446-9

CrossRef Full Text | Google Scholar

115. Buchmüller W, Greub C, Minkowski P. Neutrino masses, neutral vector bosons and the scale of B-L breaking. Phys Lett. (1991) B267:395–9. doi: 10.1016/0370-2693(91)90952-M

CrossRef Full Text | Google Scholar

116. Abbas M, Khalil S. Neutrino masses, mixing and leptogenesis in TeV scale B - L extension of the standard model. J High Energy Phys. (2008) 4:56. doi: 10.1088/1126-6708/2008/04/056

CrossRef Full Text | Google Scholar

117. Pati JC, Salam A. Lepton number as the fourth color. Phys Rev. (1974) D10:275–89. doi: 10.1103/PhysRevD.10.275

CrossRef Full Text | Google Scholar

118. Mohapatra RN, Pati JC. Left-right gauge symmetry and an isoconjugate model of CP violation. Phys Rev. (1975) D11:566–71.

Google Scholar

119. Mohapatra RN, Pati JC. A natural left-right symmetry. Phys Rev. (1975) D11:2558. doi: 10.1103/PhysRevD.11.2558

CrossRef Full Text | Google Scholar

120. Senjanović G, Mohapatra RN. Exact left-right symmetry and spontaneous violation of parity. Phys Rev. (1975) D12:1502. doi: 10.1103/PhysRevD.12.1502

CrossRef Full Text | Google Scholar

121. Senjanović G. Spontaneous breakdown of parity in a class of Gauge theories. Nucl Phys. (1979) B153:334–64. doi: 10.1016/0550-3213(79)90604-7

CrossRef Full Text | Google Scholar

122. Duka P, Gluza J, Zralek M. Quantization and renormalization of the manifest left-right symmetric model of electroweak interactions. Ann Phys. (2000) 280:336–408. doi: 10.1006/aphy.1999.5988

CrossRef Full Text | Google Scholar

123. Senjanović G. Is left right symmetry the key? Mod Phys Lett. (2017) A32:1730004. doi: 10.1142/S021773231730004X

CrossRef Full Text | Google Scholar

124. Maiezza A, Nemevšek M, Nesti F, Senjanović G. Left-right symmetry at LHC. Phys Rev. (2010) D82:055022. doi: 10.1103/PhysRevD.82.055022

CrossRef Full Text | Google Scholar

125. Zhang Y, An H, Ji X, Mohapatra RN. Right-handed quark mixings in minimal left-right symmetric model with general CP violation. Phys Rev. (2007) D76:091301. doi: 10.1103/PhysRevD.76.091301

CrossRef Full Text | Google Scholar

126. Zhang Y, An H, Ji X, Mohapatra RN. General CP violation in minimal left-right symmetric model and constraints on the right-handed scale. Nucl Phys. (2008) B802:247–79. doi: 10.1016/j.nuclphysb.2008.05.019

CrossRef Full Text | Google Scholar

127. Senjanović G, Tello V. Right handed quark mixing in left-right symmetric theory. Phys Rev Lett. (2015) 114:071801. doi: 10.1103/PhysRevLett.114.071801

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Senjanović G, Tello V. Restoration of parity and the right-handed analog of the CKM matrix. Phys Rev. (2016) D94:095023. doi: 10.1103/PhysRevD.94.095023

CrossRef Full Text | Google Scholar

129. Nemevšek M, Senjanović G, Tello V. Connecting dirac and Majorana neutrino mass matrices in the minimal left-right symmetric model. Phys Rev Lett. (2013) 110:151802. doi: 10.1103/PhysRevLett.110.151802

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Senjanović G, Tello V. Probing seesaw with parity restoration. Phys Rev Lett. (2016) 119:201803. doi: 10.1103/PhysRevLett.119.201803

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Akhmedov EK, Rodejohann W. A Yukawa coupling parameterization for type I + II seesaw formula and applications to lepton flavor violation and leptogenesis. J High Energy Phys. (2008) 6:106. doi: 10.1088/1126-6708/2008/06/106

CrossRef Full Text | Google Scholar

132. Fileviez Pérez P, Murgui C. Lepton flavour violation in left-right theory. Phys Rev. (2017) D95:075010. doi: 10.1103/PhysRevD.95.075010

CrossRef Full Text | Google Scholar

133. Fileviez Pérez P, Murgui C, Ohmer S. Simple left-right theory: lepton number violation at the LHC. Phys Rev. (2016) D94:051701. doi: 10.1103/PhysRevD.94.051701

CrossRef Full Text | Google Scholar

134. Fileviez Pérez P. Type III seesaw and left-right symmetry. J High Energy Phys. (2009) 3:142. doi: 10.1088/1126-6708/2009/03/142

CrossRef Full Text | Google Scholar

135. Duerr M, Fileviez Pérez P, Lindner M. Left-right symmetric theory with light sterile neutrinos. Phys Rev. (2013) D88:051701. doi: 10.1103/PhysRevD.88.051701

CrossRef Full Text | Google Scholar

136. Fileviez Pérez P, Spinner S. Spontaneous R-parity breaking and left-right symmetry. Phys Lett. (2009) B673:251–4. doi: 10.1016/j.physletb.2009.02.047

CrossRef Full Text | Google Scholar

137. Everett LL, Fileviez Pérez P, Spinner S. The right side of Tev scale spontaneous R-parity violation. Phys Rev. (2009) D80:055007. doi: 10.1103/PhysRevD.80.055007

CrossRef Full Text | Google Scholar

138. Deshpande NG, Gunion JF, Kayser B, Olness FI. Left-right symmetric electroweak models with triplet Higgs. Phys Rev. (1991) D44:837–58. doi: 10.1103/PhysRevD.44.837

CrossRef Full Text | Google Scholar

139. Basecq J, Liu J, Milutinovic J, Wolfenstein L. Spontaneous CP violation in SU(2)_L×SU(2)_R×U(1)_B−L models. Nucl Phys. (1986) B272:145–57. doi: 10.1016/0550-3213(86)90345-7

CrossRef Full Text | Google Scholar

140. Kiers K, Kolb J, Lee J, Soni A, Wu GH. Ubiquitous CP violation in a top inspired left-right model. Phys Rev. (2002) D66:095002. doi: 10.1103/PhysRevD.66.095002

CrossRef Full Text | Google Scholar

141. Mitra M, Ruiz R, Scott DJ, Spannowsky M. Neutrino Jets from High-Mass W_R Gauge Bosons in TeV-Scale Left-Right Symmetric Models. Phys Rev. (2016) D94:095016. doi: 10.1103/PhysRevD.94.095016

CrossRef Full Text | Google Scholar

142. Xu F, An H, Ji X. Neutron electric dipole moment constraint on scale of minimal left-right symmetric model. J High Energy Phys. (2010) 3:88. doi: 10.1007/JHEP03(2010)088

CrossRef Full Text | Google Scholar

143. Maiezza A, Nemevšek M. Strong P invariance, neutron electric dipole moment, and minimal left-right parity at LHC. Phys Rev. (2014) D90:095002. doi: 10.1103/PhysRevD.90.095002

CrossRef Full Text | Google Scholar

144. Chakrabortty J, Gluza J, Sevillano R, Szafron R. Left-right symmetry at LHC and precise 1-loop low energy data. J High Energy Phys. (2012) 7:38. doi: 10.1007/JHEP07(2012)038

CrossRef Full Text | Google Scholar

145. Bambhaniya G, Chakrabortty J, Gluza J, Kordiaczyska M, Szafron R. Left-right symmetry and the charged higgs bosons at the LHC. J High Energy Phys. (2014) 5:33. doi: 10.1007/JHEP05(2014)033

CrossRef Full Text | Google Scholar

146. Maiezza A, Nemevšek M, Nesti F. Perturbativity and mass scales in the minimal left-right symmetric model. Phys Rev. (2016) D94:035008. doi: 10.1103/PhysRevD.94.035008

CrossRef Full Text | Google Scholar

147. Bertolini S, Maiezza A, Nesti F. Present and Future K and B meson mixing constraints on TeV scale left-right symmetry. Phys Rev. (2014) D89:095028. doi: 10.1103/PhysRevD.89.095028

CrossRef Full Text | Google Scholar

148. Arkani-Hamed N, Han T, Mangano M, Wang LT. Physics opportunities of a 100 TeV proton proton collider. Phys Rept. (2016) 652:1–49. doi: 10.1016/j.physrep.2016.07.004

CrossRef Full Text | Google Scholar

149. Golling T, Hance M, Harris P, Mangano ML, McCullough M, Moortgat F, et al. Physics at a 100 TeV pp collider: beyond the Standard Model phenomena. CERN Yellow Rep (2017) 3:441–634. doi: 10.23731/CYRM-2017-003.441

CrossRef Full Text | Google Scholar

150. Bertolini S, Di Luzio L, Malinský M. Intermediate mass scales in the non-supersymmetric SO(10) grand unification: a reappraisal. Phys Rev. (2009) D80:015013. doi: 10.1103/PhysRevD.80.015013

CrossRef Full Text | Google Scholar

151. Bertolini S, Di Luzio L, Malinský M. On the vacuum of the minimal nonsupersymmetric SO(10) unification. Phys Rev. (2010) D81:035015. doi: 10.1103/PhysRevD.81.035015

CrossRef Full Text | Google Scholar

152. Bertolini S, Di Luzio L, Malinský M. Seesaw scale in the minimal renormalizable SO(10) grand unification. Phys Rev. (2012) D85:095014. doi: 10.1103/PhysRevD.85.095014

CrossRef Full Text | Google Scholar

153. Mohapatra RN, Zhang Y. TeV scale universal seesaw, vacuum stability and heavy higgs. J High Energy Phys. (2014) 6:72. doi: 10.1007/JHEP06(2014)072

CrossRef Full Text | Google Scholar

154. Maiezza A, Senjanović G, Vasquez JC. Higgs sector of the minimal left-right symmetric theory. Phys Rev. (2017) D95:095004. doi: 10.1103/PhysRevD.95.095004

CrossRef Full Text | Google Scholar

155. Beall G, Bander M, Soni A. Constraint on the mass scale of a left-right symmetric electroweak theory from the K_L−K_S mass difference. Phys Rev Lett. (1982) 48:848. doi: 10.1103/PhysRevLett.48.848

CrossRef Full Text | Google Scholar

156. Langacker P, Sankar SU. Bounds on the mass of W_R and the W_L−W_R mixing angle ξ in general SU(2)_L×SU(2)_R×U(1) models. Phys Rev. (1989) D40:1569–85.

Google Scholar

157. Bernard V, Descotes-Genon S, Vale Silva L. Short-distance QCD corrections to $K^0{\overline{K}}^0$ mixing at next-to-leading order in Left-Right models. J High Energy Phys. (2016) 8:128. doi: 10.1007/JHEP08(2016)128

CrossRef Full Text | Google Scholar

158. Buras AJ, Girrbach J. Towards the identification of new physics through quark flavour violating processes. Rept Prog Phys. (2014) 77:086201. doi: 10.1088/0034-4885/77/8/086201

PubMed Abstract | CrossRef Full Text | Google Scholar

159. Mescia F, Virto J. Natural SUSY and Kaon Mixing in view of recent results from Lattice QCD. Phys Rev. (2012) D86:095004. doi: 10.1103/PhysRevD.86.095004

CrossRef Full Text | Google Scholar

160. Garron N, Hudspith RJ, Lytle AT. Neutral kaon mixing beyond the standard model with n_f = 2+1 chiral fermions part 1: bare matrix elements and physical results. J High Energy Phys. (2016) 11:1. doi: 10.1007/JHEP11(2016)001

CrossRef Full Text | Google Scholar

161. Cirigliano V, Dekens W, de Vries J, Mereghetti E. An ϵ′ improvement from right-handed currents. Phys Lett. (2017) B767:1–9. doi: 10.1016/j.physletb.2017.01.037

CrossRef Full Text | Google Scholar

162. Lindner M, Queiroz FS, Rodejohann W. Dilepton bounds on left right symmetry at the LHC run II and neutrinoless double beta decay. Phys Lett. (2016) B762:190–5. doi: 10.1016/j.physletb.2016.08.068

CrossRef Full Text | Google Scholar

163. Ruiz R. Lepton number violation at colliders from kinematically inaccessible gauge bosons. Eur Phys J. (2017) C77:375. doi: 10.1140/epjc/s10052-017-4950-2

CrossRef Full Text | Google Scholar

164. del Águila F, Bar-Shalom S, Soni A, Wudka J. Heavy majorana neutrinos in the effective lagrangian description: application to hadron colliders. Phys Lett. (2009) B670:399–402. doi: 10.1016/j.physletb.2008.11.031

CrossRef Full Text | Google Scholar

165. Burges CJC, Schnitzer HJ. Virtual effects of excited quarks as probes of a possible new hadronic mass scale. Nucl Phys. (1983) B228:464–500. doi: 10.1016/0550-3213(83)90555-2

CrossRef Full Text | Google Scholar

166. Leung CN, Love ST, Rao S. Low-energy manifestations of a new interaction scale: operator analysis. Z Phys. (1986) C31:433. doi: 10.1007/BF01588041

CrossRef Full Text | Google Scholar

167. Buchmüller W, Wyler D. Effective lagrangian analysis of new interactions and flavor conservation. Nucl Phys. (1986) B268:621–53. doi: 10.1016/0550-3213(86)90262-2

CrossRef Full Text | Google Scholar

168. Grzadkowski B, Iskrzynski M, Misiak M, Rosiek J. Dimension-six terms in the standard model lagrangian. J High Energy Phys. (2010) 10:085. doi: 10.1007/JHEP10(2010)085

CrossRef Full Text | Google Scholar

169. Aparici A, Kim K, Santamaria A, Wudka J. Right-handed neutrino magnetic moments. Phys Rev. (2009) D80:013010. doi: 10.1103/PhysRevD.80.013010

CrossRef Full Text | Google Scholar

170. Elgaard-Clausen G, Trott M. On expansions in neutrino effective field theory. J High Energ Phys. (2017) 2017:88. doi: 10.1007/JHEP11(2017)088

CrossRef Full Text | Google Scholar

171. Bhattacharya S, Wudka J. Dimension-seven operators in the standard model with right handed neutrinos. Phys Rev. (2016) D94:055022. doi: 10.1103/PhysRevD.94.055022

CrossRef Full Text | Google Scholar

172. Liao Y, Ma XD. Operators up to dimension seven in standard model effective field theory extended with sterile neutrinos. Phys Rev. (2017) D96:015012. doi: 10.1103/PhysRevD.96.015012

CrossRef Full Text | Google Scholar

173. Henning B, Lu X, Melia T, Murayama H. 2, 84, 30, 993, 560, 15456, 11962, 261485, …: Higher dimension operators in the SM EFT. J High Energy Phys. (2017) 8:16. doi: 10.1007/JHEP08(2017)016

CrossRef Full Text | Google Scholar

174. Kobach A. Baryon number, lepton number, and operator dimension in the standard model. Phys Lett. (2016) B758:455–7. doi: 10.1016/j.physletb.2016.05.050

CrossRef Full Text | Google Scholar

175. Liao Y, Ma X-D. Perturbative power counting, lowest-index operators and their renormalization in standard model effective field theory. Commun Theor Phys. (2018) 69:285. doi: 10.1088/0253-6102/69/3/285

CrossRef Full Text | Google Scholar

176. Abada A, Biggio C, Bonnet F, Gavela MB, Hambye T. Low energy effects of neutrino masses. J High Energy Phys. (2007) 12:61. doi: 10.1088/1126-6708/2007/12/061

CrossRef Full Text | Google Scholar

177. del Águila F, Aparici A, Bhattacharya S, Santamaria A, Wudka J. Effective lagrangian approach to neutrinoless double beta decay and neutrino masses. J High Energy Phys. (2012) 6:146. doi: 10.1007/JHEP06(2012)146

CrossRef Full Text | Google Scholar

178. Wolfenstein L. Different varieties of massive dirac neutrinos. Nucl Phys. (1981) B186:147–52. doi: 10.1016/0550-3213(81)90096-1

CrossRef Full Text | Google Scholar

179. Petcov ST. On pseudodirac neutrinos, neutrino oscillations and neutrinoless double beta decay. Phys Lett. (1982) 110B:245–9. doi: 10.1016/0370-2693(82)91246-1

CrossRef Full Text | Google Scholar

180. Leung CN, Petcov ST. A comment on the coexistence of dirac and Majorana massive neutrinos. Phys Lett. (1983) 125B:461–6. doi: 10.1016/0370-2693(83)91326-6

CrossRef Full Text | Google Scholar

181. Valle JWF, Singer M. Lepton number violation with quasi dirac neutrinos. Phys Rev. (1983) D28:540. doi: 10.1103/PhysRevD.28.540

CrossRef Full Text | Google Scholar

182. Weiland C. Effects of fermionic singlet neutrinos on high- and low-energy observables. Orsay, LPT (2013). Available online at: https://inspirehep.net/record/1265676/files/arXiv:1311.5860.pdf

Google Scholar

183. Antusch S, Cazzato E, Fischer O. Sterile neutrino searches at future e⁻e⁺, pp, and e⁻p colliders. Int J Mod Phys. (2017) A32:1750078. doi: 10.1142/S0217751X17500786

CrossRef Full Text | Google Scholar

184. Littenberg LS, Shrock RE. Upper bounds on lepton number violating meson decays. Phys Rev Lett. (1992) 68:443–6. doi: 10.1103/PhysRevLett.68.443

PubMed Abstract | CrossRef Full Text | Google Scholar

185. Littenberg LS, Shrock R. Implications of improved upper bounds on |ΔL| = 2 processes. Phys Lett. (2000) B491:285–90. doi: 10.1016/S0370-2693(00)01041-8

CrossRef Full Text | Google Scholar

186. Dib C, Gribanov V, Kovalenko S, Schmidt I. K meson neutrinoless double muon decay as a probe of neutrino masses and mixings. Phys Lett. (2000) B493:82–7. doi: 10.1016/S0370-2693(00)01134-5

CrossRef Full Text | Google Scholar

187. Atre A, Barger V, Han T. Upper bounds on lepton-number violating processes. Phys Rev. (2005) D71:113014. doi: 10.1103/PhysRevD.71.113014

CrossRef Full Text | Google Scholar

188. Cvetič G, Dib C, Kang SK, Kim CS. Probing Majorana neutrinos in rare K and D, D_s, B, B_c meson decays. Phys Rev. (2010) D82:053010. doi: 10.1103/PhysRevD.82.053010

CrossRef Full Text | Google Scholar

189. Dib C, Kim CS. Remarks on the lifetime of sterile neutrinos and the effect on detection of rare meson decays M⁺→M′−ℓ⁺ℓ⁺. Phys Rev. (2014) D89:077301. doi: 10.1103/PhysRevD.89.077301

CrossRef Full Text | Google Scholar

190. Cvetič G, Kim CS, Zamora-Sa J. CP violation in lepton number violating semihadronic decays of K, D, D_s, B, B_c. Phys Rev. (2014) D89:093012. doi: 10.1103/PhysRevD.89.093012

CrossRef Full Text | Google Scholar

191. Cvetič G, Kim CS, Kogerler R, Zamora-Saa J. Oscillation of heavy sterile neutrino in decay of B → μeπ. Phys Rev. (2015) D92:013015. doi: 10.1103/PhysRevD.92.013015

CrossRef Full Text | Google Scholar

192. Cvetič G, Dib C, Kim CS, Zamora-Saa J. Probing the Majorana neutrinos and their CP violation in decays of charged scalar mesons π, K, D, D_s, B, B_c. Symmetry (2015) 7:726–73. doi: 10.3390/sym7020726

CrossRef Full Text | Google Scholar

193. Cvetič G, Kim CS. Rare decays of B mesons via on-shell sterile neutrinos. Phys Rev. (2016) D94:053001. doi: 10.1103/PhysRevD.94.053001

CrossRef Full Text | Google Scholar

194. Dib CO, Campos M, Kim CS. CP Violation with Majorana neutrinos in K Meson Decays. J High Energy Phys. (2015) 2:108. doi: 10.1007/JHEP02(2015)108

CrossRef Full Text | Google Scholar

195. Quintero N. Constraints on lepton number violating short-range interactions from |ΔL| = 2 processes. Phys Lett. (2017) B764:60–5. doi: 10.1016/j.physletb.2016.10.056

CrossRef Full Text | Google Scholar

196. Milanes D, Quintero N, Vera CE. Sensitivity to Majorana neutrinos in ΔL = 2 decays of B_c meson at LHCb. Phys Rev. (2016) D93:094026. doi: 10.1103/PhysRevD.93.094026

CrossRef Full Text | Google Scholar

197. Wang Y, Bao SS, Li ZH, Zhu N, Si ZG. Study Majorana neutrino contribution to B-meson semi-leptonic rare decays. Phys Lett. (2014) B736:428–32. doi: 10.1016/j.physletb.2014.08.006

CrossRef Full Text | Google Scholar

198. Dong HR, Feng F, Li HB. Lepton number violation in D meson decay. Chin Phys. (2015) C39:013101. doi: 10.1088/1674-1137/39/1/013101

CrossRef Full Text | Google Scholar

199. Asaka T, Ishida H. Lepton number violation by heavy Majorana neutrino in B decays. Phys Lett. (2016) B763:393–6. doi: 10.1016/j.physletb.2016.10.070

CrossRef Full Text | Google Scholar

200. Castro GL, Quintero N. Bounding resonant Majorana neutrinos from four-body B and D decays. Phys Rev. (2013) D87:077901. doi: 10.1103/PhysRevD.87.077901

CrossRef Full Text | Google Scholar

201. Yuan H, Wang T, Wang GL, Ju WL, Zhang JM. Lepton-number violating four-body decays of heavy mesons. J High Energy Phys. (2013) 8:66. doi: 10.1007/JHEP08(2013)066

CrossRef Full Text | Google Scholar

202. Cvetič G, Kim CS. Sensitivity limits on heavy-light mixing $|U_{\mu N}{|}^2$ from lepton number violating B meson decays. Phys Rev. (2017) D96:35025. doi: 10.1103/PhysRevD.96.035025

CrossRef Full Text | Google Scholar

203. Cvetič G, Dib C, Kim CS. Probing Majorana neutrinos in rare π⁺→e⁺e⁺μ⁻ν decays. J High Energy Phys. (2012) 6:149. doi: 10.1007/JHEP06(2012)149

CrossRef Full Text | Google Scholar

204. Cvetič G, Kim CS, Zamora-Saá J. CP violations in π^± Meson Decay. J Phys. (2014) G41:075004. doi: 10.1088/0954-3899/41/7/075004

CrossRef Full Text | Google Scholar

205. Mejía-Guisao J, Milanés D, Quintero N, Ruiz-Álvarez JD. Exploring GeV-scale Majorana neutrinos in lepton-number-violating ${\Lambda }_b^0$ baryon decays. Phys Rev. (2017) D96:015039. doi: 10.1103/PhysRevD.96.015039

CrossRef Full Text | Google Scholar

206. Kobach A, Dobbs S. Heavy neutrinos and the kinematics of Tau decays. Phys Rev. (2015) D91:053006. doi: 10.1103/PhysRevD.91.053006

CrossRef Full Text | Google Scholar

207. Zamora-Saa J. Resonant CP violation in rare τ^± decays. J High Energy Phys. (2017) 5:110. doi: 10.1007/JHEP05(2017)110

CrossRef Full Text | Google Scholar

208. Yuan H, Jiang Y, Wang Th, Li Q, Wang GL. Testing the nature of neutrinos from four-body τ decays. J Phys. (2017) G44:115002. doi: 10.1088/1361-6471/aa8a1e

CrossRef Full Text | Google Scholar

209. Lopez Castro G, Quintero N. Lepton number violating four-body tau lepton decays. Phys Rev. (2012) D85:076006. doi: 10.1103/PhysRevD.85.076006

CrossRef Full Text | Google Scholar

210. Mandal S, Sinha N. Favoured B_c Decay modes to search for a Majorana neutrino. Phys Rev. (2016) D94:033001. doi: 10.1103/PhysRevD.94.033001

CrossRef Full Text | Google Scholar

211. Bar-Shalom S, Deshpande NG, Eilam G, Jiang J, Soni A. Majorana neutrinos and lepton-number-violating signals in top-quark and W-boson rare decays. Phys Lett. (2006) B643:342–7. doi: 10.1016/j.physletb.2006.10.060

CrossRef Full Text | Google Scholar

212. Dib CO, Kim CS, Wang K. Signatures of Dirac and Majorana sterile neutrinos in trilepton events at the LHC. Phys Rev. (2017) D95:115020. doi: 10.1103/PhysRevD.95.115020

CrossRef Full Text | Google Scholar

213. Dib CO, Kim CS, Wang K. Search for heavy sterile neutrinos in trileptons at the LHC. (2017) Chin Phys. C41:103103. doi: 10.1088/1674-1137/41/10/103103

CrossRef Full Text | Google Scholar

214. Dib CO, Kim CS, Wang K, Zhang J. Distinguishing Dirac/Majorana sterile neutrinos at the LHC. Phys Rev. (2016) D94:013005. doi: 10.1103/PhysRevD.94.013005

CrossRef Full Text | Google Scholar

215. Dib CO, Kim CS. Discovering sterile Neutrinos ligther than M_W at the LHC. Phys Rev. (2015) D92:093009. doi: 10.1103/PhysRevD.92.093009

CrossRef Full Text | Google Scholar

216. Bhupal Dev PS, Franceschini R, Mohapatra RN. Bounds on TeV seesaw models from LHC higgs data. Phys Rev. (2012) D86:093010. doi: 10.1103/PhysRevD.86.093010

CrossRef Full Text | Google Scholar

217. Gago AM, Hernández P, Jones-Pérez J, Losada M, Moreno Briceño A. Probing the type I seesaw mechanism with displaced vertices at the LHC. Eur Phys J. (2015) C75:470. doi: 10.1140/epjc/s10052-015-3693-1

CrossRef Full Text | Google Scholar

218. Caputo A, Hernández P, López-Pavón J, Salvado J. The seesaw portal in testable models of neutrino masses. J High Energy Phys. (2017) 6:112. doi: 10.1007/JHEP06(2017)112

CrossRef Full Text | Google Scholar

219. Das A, Dev PSB, Kim CS. Constraining sterile neutrinos from precision higgs data. Phys Rev. (2017) D95:115013. doi: 10.1103/PhysRevD.95.115013

CrossRef Full Text | Google Scholar

220. Si Z, Wang K. GeV Majorana neutrinos in top-quark decay at the LHC. Phys Rev. (2009) D79:014034. doi: 10.1103/PhysRevD.79.014034

CrossRef Full Text | Google Scholar

221. Quintero N, López Castro G, Delepine D. Lepton number violation in top quark and neutral B meson decays. Phys Rev. (2011) D84:096011. doi: 10.1103/PhysRevD.84.096011

CrossRef Full Text | Google Scholar

222. Shuve B, Peskin ME. Revision of the LHCb limit on majorana neutrinos. Phys Rev. (2016) D94:113007. doi: 10.1103/PhysRevD.94.113007

CrossRef Full Text | Google Scholar

223. Helo JC, Hirsch M, Kovalenko S. Heavy neutrino searches at the LHC with displaced vertices. Phys Rev. (2014) D89:073005. doi: 10.1103/PhysRevD.89.073005

CrossRef Full Text | Google Scholar

224. Blondel A, Graverini E, Serra N, Shaposhnikov M. Search for heavy right handed neutrinos at the FCC-ee. Nucl Part Phys Proc. (2016) 273–275:1883–90. doi: 10.1016/j.nuclphysbps.2015.09.304

CrossRef Full Text | Google Scholar

225. Izaguirre E, Shuve B. Multilepton and Lepton jet probes of sub-weak-scale right-handed neutrinos. Phys Rev. (2015) D91:093010. doi: 10.1103/PhysRevD.91.093010

CrossRef Full Text | Google Scholar

226. Antusch S, Cazzato E, Fischer O. Sterile neutrino searches via displaced vertices at LHCb. Phys Lett. (2017) B774:114–8. doi: 10.1016/j.physletb.2017.09.057

CrossRef Full Text | Google Scholar

227. Antusch S, Cazzato E, Fischer O. Displaced vertex searches for sterile neutrinos at future lepton colliders. J High Energy Phys. (2016) 12:7. doi: 10.1007/JHEP12(2016)007

CrossRef Full Text | Google Scholar

228. Anamiati G, Hirsch M, Nardi E. Quasi-Dirac neutrinos at the LHC. J High Energy Phys. (2016) 10:10. doi: 10.1007/JHEP10(2016)010

CrossRef Full Text | Google Scholar

229. Antusch S, Cazzato E, Fischer O. Heavy neutrino-antineutrino oscillations at colliders. (2017) arXiv:1709.03797.

Google Scholar

230. Das A, Dev PSB, Mohapatra RN. Same sign vs opposite sign dileptons as a probe of low scale seesaw mechanisms. Phys Rev D (2017) 97:015018. doi: 10.1103/PhysRevD.97.015018

CrossRef Full Text | Google Scholar

231. Antusch S, Cazzato E, Drewes M, Fischer O, Garbrecht B, Gueter D. Probing leptogenesis at future colliders. (2017) arXiv:1710.03744.

Google Scholar

232. Bicer M, Duran Yildiz H, Yildiz I, Coignet G, Delmastro M, Alexopoulos T, et al. First look at the physics case of TLEP. J High Energy Phys. (2014) 1:164. doi: 10.1007/JHEP01(2014)164

CrossRef Full Text | Google Scholar

233. Antusch S, Fischer O. Testing sterile neutrino extensions of the Standard Model at future lepton colliders. J High Energy Phys. (2015) 5:53. doi: 10.1007/JHEP05(2015)053

CrossRef Full Text | Google Scholar

234. Baer H, Barklow T, Fujii K, Gao Y, Hoang A, Kanemura S. The international linear collider technical design report - Volume 2: Physics. (2013) arXiv:1306.6352.

Google Scholar

235. Fujii K, Grojean C, Peskin ME, Barklow T, Gao Y, Kanemura S. Physics case for the international linear collider. arXiv:1506.05992.

236. Group CSS. CEPC-SPPC preliminary conceptual design report. 1. Physics and detector. (2015).

Google Scholar

237. Schael S, Barate R, Bruneliere R, Buskulic D, De Bonis I, Decamp D. Precision electroweak measurements on the Z resonance. Phys Rept. (2006) 427:257–454. doi: 10.1016/j.physrep.2005.12.006

CrossRef Full Text | Google Scholar

238. Beringer J, Arguin JF, Barnett RM, Copic K, Dahl O, Groom DE. Review of particle physics (RPP). Phys Rev. (2012) D86:010001. doi: 10.1103/PhysRevD.86.010001

CrossRef Full Text | Google Scholar

239. Jarlskog C. Neutrino counting at the Z peak and right-handed neutrinos. Phys Lett. (1990) B241:579–83. doi: 10.1016/0370-2693(90)91873-A

CrossRef Full Text | Google Scholar

240. Keung WY, Senjanović G. Majorana neutrinos and the production of the right-handed charged gauge boson. Phys Rev Lett. (1983) 50:1427. doi: 10.1103/PhysRevLett.50.1427

CrossRef Full Text | Google Scholar

241. Gronau M, Leung CN, Rosner JL. Extending limits on neutral heavy leptons. Phys Rev. (1984) D29:2539. doi: 10.1103/PhysRevD.29.2539

CrossRef Full Text | Google Scholar

242. Willenbrock SSD, Dicus DA. Production of heavy leptons from gluon fusion. Phys Lett. (1985) 156B:429–33. doi: 10.1016/0370-2693(85)91638-7

CrossRef Full Text | Google Scholar

243. Petcov ST. Possible signature for production of majorana particles in e+ e- and p anti-p collisions. Phys Lett. (1984) 139B:421. doi: 10.1016/0370-2693(84)91844-6

CrossRef Full Text | Google Scholar

244. Dicus DA, Karatas DD, Roy P. Lepton nonconservation at supercollider energies. Phys Rev. (1991) D44:2033–7. doi: 10.1103/PhysRevD.44.2033

CrossRef Full Text | Google Scholar

245. Dicus DA, Roy P. Supercollider signatures and correlations of heavy neutrinos. Phys Rev. (1991) D44:1593–6. doi: 10.1103/PhysRevD.44.1593

CrossRef Full Text | Google Scholar

246. Datta A, Pilaftsis A. Revealing the Majorana nature of heavy neutrinos via a heavy Higgs boson. Phys Lett. (1992) B278:162–6. doi: 10.1016/0370-2693(92)90727-L

CrossRef Full Text | Google Scholar

247. Datta A, Guchait M, Pilaftsis A. Probing lepton number violation via majorana neutrinos at hadron supercolliders. Phys Rev. (1994) D50:3195–203. doi: 10.1103/PhysRevD.50.3195

CrossRef Full Text | Google Scholar

248. Han T, Zhang B. Signatures for Majorana neutrinos at hadron colliders. Phys Rev Lett. (2006) 97:171804. doi: 10.1103/PhysRevLett.97.171804

PubMed Abstract | CrossRef Full Text | Google Scholar

249. Bray S, Lee JS, Pilaftsis A. Resonant CP violation due to heavy neutrinos at the LHC. Nucl Phys. (2007) B786:95–118. doi: 10.1016/j.nuclphysb.2007.07.002

CrossRef Full Text | Google Scholar

250. del Águila F, Aguilar-Saavedra JA, Pittau R. Neutrino physics at large colliders. J Phys Conf Ser. (2006) 53:506–27. doi: 10.1088/1742-6596/53/1/032

CrossRef Full Text | Google Scholar

251. del Águila F, Aguilar-Saavedra JA, Pittau R. Heavy neutrino signals at large hadron colliders. J High Energy Phys. (2007) 10:47. doi: 10.1088/1126-6708/2007/10/047

CrossRef Full Text | Google Scholar

252. del Águila F, Aguilar-Saavedra JA. Distinguishing seesaw models at LHC with multi-lepton signals. Nucl Phys. (2009) B813:22–90. doi: 10.1016/j.nuclphysb.2008.12.029

CrossRef Full Text | Google Scholar

253. del Águila F, Aguilar-Saavedra JA, de Blas J. Trilepton signals: the golden channel for seesaw searches at LHC. Acta Phys Polon. (2009) B40:2901–11.

Google Scholar

254. Alva D, Han T, Ruiz R. Heavy Majorana neutrinos from Wγ fusion at hadron colliders. J High Energy Phys. (2015) 2:72. doi: 10.1007/JHEP02(2015)072

CrossRef Full Text | Google Scholar

255. Degrande C, Mattelaer O, Ruiz R, Turner J. Fully-automated precision predictions for heavy neutrino production mechanisms at hadron colliders. Phys Rev. (2016) D94:053002. doi: 10.1103/PhysRevD.94.053002

CrossRef Full Text | Google Scholar

256. Chen CY, Dev PSB. Multi-lepton collider signatures of heavy dirac and majorana neutrinos. Phys Rev. (2012) D85:093018. doi: 10.1103/PhysRevD.85.093018

CrossRef Full Text | Google Scholar

257. Dev PSB, Kim D, Mohapatra RN. Disambiguating seesaw models using invariant mass variables at hadron colliders. J High Energy Phys. (2016) 1:118. doi: 10.1007/JHEP01(2016)118

CrossRef Full Text | Google Scholar

258. Hessler AG, Ibarra A, Molinaro E, Vogl S. Impact of the Higgs boson on the production of exotic particles at the LHC. Phys Rev. (2015) D91:115004. doi: 10.1103/PhysRevD.91.115004

CrossRef Full Text | Google Scholar

259. Ruiz R, Spannowsky M, Waite P. Heavy neutrinos from gluon fusion. Phys Rev. (2017) D96:055042. doi: 10.1103/PhysRevD.96.055042

CrossRef Full Text | Google Scholar

260. Chanowitz MS, Gaillard MK. The TeV physics of strongly interacting W's and Z's. Nucl Phys. (1985) B261:379–431. doi: 10.1016/0550-3213(85)90580-2

CrossRef Full Text | Google Scholar

261. Lee BW, Quigg C, Thacker HB. The strength of weak interactions at very high-energies and the Higgs Boson mass. Phys Rev Lett. (1977) 38:883–5. doi: 10.1103/PhysRevLett.38.883

CrossRef Full Text | Google Scholar

262. Dev PSB, Pilaftsis A, Yang Uk. New production mechanism for heavy neutrinos at the LHC. Phys Rev Lett. (2014) 112:081801. doi: 10.1103/PhysRevLett.112.081801

CrossRef Full Text | Google Scholar

263. Bambhaniya G, Khan S, Konar P, Mondal T. Constraints on a seesaw model leading to quasidegenerate neutrinos and signatures at the LHC. Phys Rev. (2015) D91:095007. doi: 10.1103/PhysRevD.91.095007

CrossRef Full Text | Google Scholar

264. Ng JN, de la Puente A, Pan BWP. Search for heavy right-handed neutrinos at the LHC and beyond in the same-sign same-flavor leptons final state. J High Energy Phys. (2015) 12:172. doi: 10.1007/JHEP12(2015)172

CrossRef Full Text | Google Scholar

265. Arganda E, Herrero MJ, Marcano X, Weiland C. Exotic μτjj events from heavy ISS neutrinos at the LHC. Phys Lett. (2016) B752:46–50. doi: 10.1016/j.physletb.2015.11.013

CrossRef Full Text | Google Scholar

266. Andrés F, Alfredo G, Kaiwen G, Carlos P, Diego R. Expanding the reach of heavy neutrino searches at the LHC. Phys Lett. (2017) B778:94–100. doi: 10.1016/j.physletb.2018.01.009

CrossRef Full Text | Google Scholar

267. Binosi D, Collins J, Kaufhold C, Theussl L. JaxoDraw: a graphical user interface for drawing Feynman diagrams. Version 2.0 release notes. Comput Phys Commun. (2009) 180:1709–15. doi: 10.1016/j.cpc.2009.02.020

CrossRef Full Text | Google Scholar

268. Martin AD, Ryskin MG. The photon PDF of the proton. Eur Phys J. (2014) C74:3040. doi: 10.1140/epjc/s10052-014-3040-y

CrossRef Full Text | Google Scholar

269. Harland-Lang LA, Khoze VA, Ryskin MG. Photon-initiated processes at high mass. Phys Rev. (2016) D94:074008. doi: 10.1103/PhysRevD.94.074008

CrossRef Full Text | Google Scholar

270. Bertone V, Carrazza S, Hartland NP, Rojo J. Illuminating the photon content of the proton within a global PDF analysis. arXiv:1712.07053.

271. Manohar AV, Nason P, Salam GP, Zanderighi G. The photon content of the proton. J High Energ Phys. (2017) 12:046. doi: 10.1007/JHEP12(2017)046

CrossRef Full Text | Google Scholar

272. Manohar A, Nason P, Salam GP, Zanderighi G. How bright is the proton? A precise determination of the photon parton distribution function. Phys Rev Lett. (2016) 117:242002. doi: 10.1103/PhysRevLett.117.242002

PubMed Abstract | CrossRef Full Text | Google Scholar

273. Schmidt C, Pumplin J, Stump D, Yuan CP. CT14QED parton distribution functions from isolated photon production in deep inelastic scattering. Phys Rev. (2016) D93:114015. doi: 10.1103/PhysRevD.93.114015

CrossRef Full Text | Google Scholar

274. Das A, Bhupal Dev PS, Okada N. Direct bounds on electroweak scale pseudo-Dirac neutrinos from $\sqrt{s}=8$ TeV LHC data. Phys Lett. (2014) B735:364–70. doi: 10.1016/j.physletb.2014.06.058

CrossRef Full Text | Google Scholar

275. Ruiz R. QCD corrections to pair production of type III seesaw leptons at hadron colliders. J High Energy Phys. (2015) 12:165. doi: 10.1007/JHEP12(2015)165

CrossRef Full Text | Google Scholar

276. Collins JC, Soper DE, Sterman GF. Transverse momentum distribution in Drell-Yan pair and W and Z Boson production. Nucl Phys. (1985) B250:199–224. doi: 10.1016/0550-3213(85)90479-1

CrossRef Full Text | Google Scholar

277. Dreiner HK, Grab S, Kramer M, Trenkel MK. Supersymmetric NLO QCD corrections to resonant slepton production and signals at the Tevatron and the CERN LHC. Phys Rev. (2007) D75:035003. doi: 10.1103/PhysRevD.75.035003

CrossRef Full Text | Google Scholar

278. Chen YQ, Han T, Si ZG. QCD corrections to single slepton production at hadron colliders. J High Energy Phys. (2007) 5:68. doi: 10.1088/1126-6708/2007/05/068

CrossRef Full Text | Google Scholar

279. Fuchs E, Thewes S, Weiglein G. Interference effects in BSM processes with a generalised narrow-width approximation. Eur Phys J. (2015) C75:254. doi: 10.1140/epjc/s10052-015-3472-z

CrossRef Full Text | Google Scholar

280. Fuchs E, Weiglein G. Breit-Wigner approximation for propagators of mixed unstable states. J High Energy Phys. (2017) 9:79. doi: 10.1007/JHEP09(2017)079

CrossRef Full Text | Google Scholar

281. Ruiz RE. Hadron Collider Tests of Neutrino Mass-Generating Mechanisms. Pittsburgh: PA (2015). Available online at: https://inspirehep.net/record/1394386/files/arXiv:1509.06375.pdf

282. del Águila F, Aguilar-Saavedra JA, Pittau R. Heavy Neutrino Production at Hadron Colliders. Available online at: http://mlm.home.cern.ch/mlm/alpgen/

283. Degrande C, Mattelaer O, Ruiz R, Turner J. SM + Heavy N at NLO in QCD. Available online at: http://feynrules.irmp.ucl.ac.be/wiki/HeavyN

284. Degrande C. Automatic evaluation of UV and R2 terms for beyond the Standard Model Lagrangians: a proof-of-principle. Comput Phys Commun. (2015) 197:239–62. doi: 10.1016/j.cpc.2015.08.015

CrossRef Full Text | Google Scholar

285. Degrande C, Duhr C, Fuks B, Grellscheid D, Mattelaer O, Reiter T. UFO - the universal FeynRules output. Comput Phys Commun. (2012) 183:1201–14. doi: 10.1016/j.cpc.2012.01.022

CrossRef Full Text | Google Scholar

286. Christensen ND, Duhr C. FeynRules - Feynman rules made easy. Comput Phys Commun. (2009) 180:1614–41. doi: 10.1016/j.cpc.2009.02.018

CrossRef Full Text | Google Scholar

287. Alloul A, Christensen ND, Degrande C, Duhr C, Fuks B. FeynRules 2.0 - A complete toolbox for tree-level phenomenology. Comput Phys Commun. (2014) 185:2250–300. doi: 10.1016/j.cpc.2014.04.012

CrossRef Full Text | Google Scholar

288. Denner A, Eck H, Hahn O, Kublbeck J. Compact Feynman rules for Majorana fermions. Phys Lett. (1992) B291:278–80. doi: 10.1016/0370-2693(92)91045-B

CrossRef Full Text | Google Scholar

289. Bellm J, Gieseke S, Grellscheid D, Plätzer S, Rauch M, Reuschle C, et al. Herwig 7.0/Herwig++ 3.0 release note. Eur Phys J. (2016) C76:196. doi: 10.1140/epjc/s10052-016-4018-8

CrossRef Full Text | Google Scholar

290. Alwall J, Frederix R, Frixione S, Hirschi V, Maltoni F, Mattelaer O, et al. The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. J High Energy Phys. (2014) 7:79. doi: 10.1007/JHEP07(2014)079

CrossRef Full Text | Google Scholar

291. Gleisberg T, Höche S, Krauss F, Schönherr M, Schumann S, Siegert F, et al. Event generation with SHERPA 1.1. J High Energy Phys. (2009) 2:7. doi: 10.1088/1126-6708/2009/02/007

CrossRef Full Text | Google Scholar

292. Han T, Valencia G, Willenbrock S. Structure function approach to vector boson scattering in p p collisions. Phys Rev Lett. (1992) 69:3274–7. doi: 10.1103/PhysRevLett.69.3274

PubMed Abstract | CrossRef Full Text | Google Scholar

293. Degrande C, Hartling K, Logan HE, Peterson AD, Zaro M. Automatic predictions in the Georgi-Machacek model at next-to-leading order accuracy. Phys Rev. (2016) D93:035004. doi: 10.1103/PhysRevD.93.035004

CrossRef Full Text | Google Scholar

294. Cacciari M, Dreyer FA, Karlberg A, Salam GP, Zanderighi G. Fully differential vector-boson-fusion higgs production at next-to-next-to-leading order. Phys Rev Lett. (2015) 115:082002. doi: 10.1103/PhysRevLett.115.082002

PubMed Abstract | CrossRef Full Text | Google Scholar

295. Dreyer FA, Karlberg A. Vector-Boson fusion higgs production at three loops in QCD. Phys Rev Lett. (2016) 117:072001. doi: 10.1103/PhysRevLett.117.072001

PubMed Abstract | CrossRef Full Text | Google Scholar

296. Bonvini M, Forte S, Ridolfi G, Rottoli L. Resummation prescriptions and ambiguities in SCET vs. direct QCD: Higgs production as a case study. J High Energy Phys. (2015) 1:46. doi: 10.1007/JHEP01(2015)046

CrossRef Full Text | Google Scholar

297. Anastasiou C, Duhr C, Dulat F, Furlan E, Gehrmann T, Herzog F, et al. High precision determination of the gluon fusion Higgs boson cross-section at the LHC. J High Energy Phys. (2016) 5:58. doi: 10.1007/JHEP05(2016)058

CrossRef Full Text | Google Scholar

298. Anastasiou C, Duhr C, Dulat F, Herzog F, Mistlberger B. Higgs Boson Gluon-fusion production in QCD at three loops. Phys Rev Lett. (2015) 114:212001. doi: 10.1103/PhysRevLett.114.212001

PubMed Abstract | CrossRef Full Text | Google Scholar

299. Avetisyan A, Campbell JM, Cohen T, Dhingra N, Hirschauer J, Howe K. Methods and results for standard model event generation at $\sqrt{s}$ = 14 TeV, 33 TeV and 100 TeV proton colliders (A snowmass whitepaper). In: Proceedings, 2013 Community Summer Study on the Future of U.S. Particle Physics: Snowmass on the Mississippi (CSS2013): USA, July 29-August 6, 2013. Minneapolis, MN (2013). Available online at: http://lss.fnal.gov/archive/test-fn/0000/fermilab-fn-0965-t.pdf

Google Scholar

300. Aad G, Abbott B, Abdallah J, Ali Abdelalim A, Abdesselam A, Abdinov O. Search for heavy neutrinos and right-handed W bosons in events with two leptons and jets in pp collisions at $\sqrt{s}=7$ TeV with the ATLAS detector. Eur Phys J. (2012) C72:2056. doi: 10.1140/epjc/s10052-012-2056-4

CrossRef Full Text | Google Scholar

301. Cox P, Han C, Yanagida TT. LHC search for right-handed neutrinos in Z′ models. J High Energ Phys. (2018) 1:37. doi: 10.1007/JHEP01(2018)037

CrossRef Full Text | Google Scholar

302. Buchmüller W, Greub C. Electroproduction of Majorana neutrinos. Phys Lett. (1991) B256:465–70. doi: 10.1016/0370-2693(91)91792-T

CrossRef Full Text | Google Scholar

303. Buchmüller W, Greub C. Heavy Majorana neutrinos in electron - positron and electron - proton collisions. Nucl Phys. (1991) B363:345–68. doi: 10.1016/0550-3213(91)80024-G

CrossRef Full Text | Google Scholar

304. Blaksley C, Blennow M, Bonnet F, Coloma P, Fernandez-Martinez E. Heavy neutrinos and lepton number violation in lp colliders. Nucl Phys. (2011) B852:353–65. doi: 10.1016/j.nuclphysb.2011.06.021

CrossRef Full Text | Google Scholar

305. Duarte L, Gonzlez-Sprinberg GA, Sampayo OA. Majorana neutrinos production at LHeC in an effective approach. Phys Rev. (2015) D91:053007. doi: 10.1103/PhysRevD.91.053007

CrossRef Full Text | Google Scholar

306. Banerjee S, Dev PSB, Ibarra A, Mandal T, Mitra M. Prospects of heavy neutrino searches at future lepton colliders. Phys Rev. (2015) D92:075002. doi: 10.1103/PhysRevD.92.075002

CrossRef Full Text | Google Scholar

307. Mondal S, Rai SK. Probing the heavy neutrinos of inverse seesaw model at the LHeC. Phys Rev. (2016) D94:033008. doi: 10.1103/PhysRevD.94.033008

CrossRef Full Text | Google Scholar

308. Ingelman G, Rathsman J. Heavy Majorana neutrinos at e p colliders. Z Phys. (1993) C60:243–54.

Google Scholar

309. Liang H, He XG, Ma WG, Wang SM, Zhang RY. Seesaw type I and III at the LHeC. J High Energy Phys. (2010) 9:23. doi: 10.1007/JHEP09(2010)023

CrossRef Full Text | Google Scholar

310. Abelleira Fernandez JL, Adolphsen C, Akay AN, Aksakal H, Albacete JL, Alekhin S, et al. A large hadron electron collider at CERN: report on the physics and design concepts for machine and detector. J Phys. (2012) G39:075001. doi: 10.1088/0954-3899/39/7/075001

CrossRef Full Text | Google Scholar

311. Frixione S, Mangano ML, Nason P, Ridolfi G. Improving the Weizsacker-Williams approximation in electron - proton collisions. Phys Lett. (1993) B319:339–45. doi: 10.1016/0370-2693(93)90823-Z

CrossRef Full Text | Google Scholar

312. Mattelaer O, Mitra M, Ruiz R. Automated neutrino jet and top jet predictions at next-to-leading-order with parton shower matching in effective left-right symmetric models. (2016) arXiv:1610.08985.

Google Scholar

313. Jenkins EE. Searching for a B−L Gauge Boson in $p\bar{p}$ Collisions. Phys Lett. (1987) B192:219–22. doi: 10.1016/0370-2693(87)91172-5

CrossRef Full Text | Google Scholar

314. Carena M, Daleo A, Dobrescu BA, Tait TMP. Z′ gauge bosons at the Tevatron. Phys Rev. (2004) D70:093009. doi: 10.1103/PhysRevD.70.093009

CrossRef Full Text | Google Scholar

315. Emam W, Khalil S. Higgs and Z-prime phenomenology in B−L extension of the standard model at LHC. Eur Phys J. (2007) C52:625–33. doi: 10.1140/epjc/s10052-007-0411-7

CrossRef Full Text | Google Scholar

316. Langacker P. The physics of heavy Z′ gauge bosons. Rev Mod Phys. (2009) 81:1199–228. doi: 10.1103/RevModPhys.81.1199

CrossRef Full Text | Google Scholar

317. Iso S, Okada N, Orikasa Y. The minimal B-L model naturally realized at TeV scale. Phys Rev. (2009) D80:115007. doi: 10.1103/PhysRevD.80.115007

CrossRef Full Text | Google Scholar

318. Basso L, Belyaev A, Moretti S, Pruna GM, Shepherd-Themistocleous CH. Z′ discovery potential at the LHC in the minimal B−L extension of the Standard Model. Eur Phys J. (2011) C71:1613. doi: 10.1140/epjc/s10052-011-1613-6

CrossRef Full Text | Google Scholar

319. Deppisch FF, Desai N, Valle JWF. Is charged lepton flavor violation a high energy phenomenon? Phys Rev. (2014) D89:051302. doi: 10.1103/PhysRevD.89.051302

CrossRef Full Text | Google Scholar

320. Freitas A. Weakly coupled neutral gauge bosons at future linear colliders. Phys Rev. (2004) D70:015008. doi: 10.1103/PhysRevD.70.015008

CrossRef Full Text | Google Scholar

321. Basso L, Belyaev A, Moretti S, Pruna GM. Probing the Z-prime sector of the minimal B-L model at future Linear Colliders in the e⁺e⁻ → μ⁺μ⁻ process. J High Energy Phys. (2009) 10:6. doi: 10.1088/1126-6708/2009/10/006

CrossRef Full Text | Google Scholar

322. Ramirez-Sánchez F, Gutiérrez-Rodríguez A, Hernández-Ruíz MA. Higgs bosons production and decay at future e⁺e⁻ linear colliders as a probe of the BL model. J Phys. (2016) G43:095003. doi: 10.1088/0954-3899/43/9/095003

CrossRef Full Text | Google Scholar

323. del Águila F, Aguilar-Saavedra JA. Like-sign dilepton signals from a leptophobic Z′ boson. J High Energy Phys. (2007) 11:72. doi: 10.1088/1126-6708/2007/11/072

CrossRef Full Text | Google Scholar

324. Huitu K, Khalil S, Okada H, Rai SK. Signatures for right-handed neutrinos at the Large Hadron Collider. Phys Rev Lett. (2008) 101:181802. doi: 10.1103/PhysRevLett.101.181802

PubMed Abstract | CrossRef Full Text | Google Scholar

325. Basso L, Belyaev A, Moretti S, Shepherd-Themistocleous CH. Phenomenology of the minimal B-L extension of the Standard model: Z' and neutrinos. Phys Rev. (2009) D80:055030. doi: 10.1103/PhysRevD.80.055030

CrossRef Full Text | Google Scholar

326. Aguilar-Saavedra JA. Heavy lepton pair production at LHC: model discrimination with multi-lepton signals. Nucl Phys. (2010) B828:289–316. doi: 10.1016/j.nuclphysb.2009.11.021

CrossRef Full Text | Google Scholar

327. Li T, Chao W. Neutrino masses, dark matter and B-L symmetry at the LHC. Nucl Phys. (2011) B843:396–412. doi: 10.1016/j.nuclphysb.2010.10.004

CrossRef Full Text | Google Scholar

328. Aguilar-Saavedra JA, Joaquim FR. Measuring heavy neutrino couplings at the LHC. Phys Rev. (2012) D86:073005. doi: 10.1103/PhysRevD.86.073005

CrossRef Full Text | Google Scholar

329. Accomando E, Coriano C, Delle Rose L, Fiaschi J, Marzo C, Moretti S. Z. Higgses and heavy neutrinos in U(1) models: from the LHC to the GUT scale. J High Energy Phys. (2016) 7:86. doi: 10.1007/JHEP07(2016)086

CrossRef Full Text | Google Scholar

330. Accomando E, Delle Rose L, Moretti S, Olaiya E, Shepherd-Themistocleous CH. Extra higgs boson and Z′ as portals to signatures of heavy neutrinos at the LHC. (2017).

Google Scholar

331. Kang Z, Ko P, Li J. New avenues to heavy right-handed neutrinos with pair production at hadronic colliders. Phys Rev. (2016) D93:075037. doi: 10.1103/PhysRevD.93.075037

CrossRef Full Text | Google Scholar

332. Abdelalim AA, Hammad A, Khalil S. B-L heavy neutrinos and neutral gauge boson Z at the LHC. Phys Rev. (2014) D90:115015. doi: 10.1103/PhysRevD.90.115015

CrossRef Full Text | Google Scholar

333. Dube S, Gadkari D, Thalapillil AM. Lepton-jets and low-mass sterile neutrinos at hadron colliders. Phys Rev. (2017) D96:055031. doi: 10.1103/PhysRevD.96.055031

CrossRef Full Text | Google Scholar

334. Nemevšek M, Nesti F, Popara G. Keung-Senjanović process at LHC: from LNV to displaced vertices to invisible decays. (2018) arXiv:1801.05813.

Google Scholar

335. Basso L, Belyaev A, Moretti S, Shepherd-Themistocleous CH. SM + B−L. Available online at: http://feynrules.irmp.ucl.ac.be/wiki/B-L-SM

336. Basso L, Moretti S, Pruna GM. Theoretical constraints on the couplings of non-exotic minimal Z′ bosons. J High Energy Phys. (2011) 8:122. doi: 10.1007/JHEP08(2011)122

CrossRef Full Text | Google Scholar

337. Mattelaer O, Mitra M, Ruiz R. Effective Left-Right Symmetric Model at NLO in QCD. Available online at: http://feynrules.irmp.ucl.ac.be/wiki/EffLRSM

338. Fuks B, Ruiz R. A comprehensive framework for studying W′ and Z′ bosons at hadron colliders with automated jet veto resummation. J High Energy Phys. (2017) 5:32. doi: 10.1007/JHEP05(2017)032

CrossRef Full Text | Google Scholar

339. Fuks B, Ruiz R. SM + W′ and Z′ at NLO in QCD. Available online at: http://feynrules.irmp.ucl.ac.be/wiki/WZPrimeAtNLO

340. Basso L, Moretti S, Pruna GM. Phenomenology of the minimal B−L extension of the Standard Model: the Higgs sector. Phys Rev. (2011) D83:055014. doi: 10.1103/PhysRevD.83.055014

CrossRef Full Text | Google Scholar

341. Pruna GM. Phenomenology of the Minimal B−L Model: The Higgs Sector at the Large Hadron Collider Future Linear Colliders. Southampton (2011). Available online at: https://inspirehep.net/record/914976/files/arXiv:1106.4691.pdf

342. Accomando E, Delle Rose L, Moretti S, Olaiya E, Shepherd-Themistocleous CH. Novel SM-like Higgs decay into displaced heavy neutrino pairs in U(1) models. J High Energy Phys. (2017) 4:81. doi: 10.1007/JHEP04(2017)081

CrossRef Full Text | Google Scholar

343. Klasen M, Lyonnet F, Queiroz FS. NLO+NLL collider bounds, Dirac fermion and scalar dark matter in the BL model. Eur Phys J. (2017) C77:348. doi: 10.1140/epjc/s10052-017-4904-8

CrossRef Full Text | Google Scholar

344. Aaboud M, Aad G, Abbott B, Abdinov O, Abeloos B, Haider Abidi S. Search for new high-mass phenomena in the dilepton final state using 36.1 fb⁻¹ of proton-proton collision data at $\sqrt{s}$ = 13 TeV with the ATLAS detector. (2017). doi: 10.1007/JHEP10(2017)182

CrossRef Full Text | Google Scholar

345. del Águila F, de Blas J, Perez-Victoria M. Electroweak limits on general new vector bosons. J High Energy Phys. (2010) 9:33. doi: 10.1007/JHEP09(2010)033

CrossRef Full Text | Google Scholar

346. del Águila F, de Blas J, Langacker P, Perez-Victoria M. Impact of extra particles on indirect Z' limits. Phys Rev. (2011) D84:015015. doi: 10.1103/PhysRevD.84.015015

CrossRef Full Text | Google Scholar

347. Aad G, Abbott B, Abdallah J, Abdel Khalek S, Abdinov O, Aben R. Search for high-mass dilepton resonances in pp collisions $\sqrt{s}=8$ TeV with the ATLAS detector. Phys Rev. (2014) D90:052005. doi: 10.1103/PhysRevD.90.052005

CrossRef Full Text | Google Scholar

348. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M. Search for physics beyond the standard model in dilepton mass spectra in proton-proton collisions at $\sqrt{s}=8$ TeV. J High Energy Phys. (2015) 4:25. doi: 10.1007/JHEP04(2015)025

CrossRef Full Text | Google Scholar

349. Sirunyan AM, Tumasyan A, Adam W, Aşilar E, Bergauer T, Brandstetter J. Search for dijet resonances in proton-proton collisions at $\sqrt{s}$ = 13 TeV and constraints on dark matter and other models. Phys Lett. (2017) B769:520–42. doi: 10.1016/j.physletb.2017.02.012

CrossRef Full Text | Google Scholar

350. Aaboud M, Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B. Search for new phenomena in dijet events using 37 fb⁻¹ of pp collision data collected $\sqrt{s}=$ 13 TeV with the ATLAS detector. Phys Rev. (2017) D96:052004. doi: 10.1103/PhysRevD.96.052004

CrossRef Full Text | Google Scholar

351. Chekanov SV, Childers JT, Frizzell D, Proudfoot J, Wang R. Precision searches in dijets at the HL-LHC and HE-LHC. (2017). arXiv:1710.09484.

Google Scholar

352. Chen CY, Dev PSB, Mohapatra RN. Probing heavy-light neutrino mixing in left-right seesaw models at the LHC. Phys Rev. (2013) D88:033014. doi: 10.1103/PhysRevD.88.033014

CrossRef Full Text | Google Scholar

353. Dev PSB, Mohapatra RN, Zhang Y. Probing the higgs sector of the minimal left-right symmetric model at future hadron colliders. J High Energy Phys. (2016) 5:174. doi: 10.1007/JHEP05(2016)174

CrossRef Full Text | Google Scholar

354. Fuks B, Klasen M, Lamprea DR, Rothering M. Precision predictions for electroweak superpartner production at hadron colliders with Resummino. Eur Phys J. (2013) C73:2480. doi: 10.1140/epjc/s10052-013-2480-0

CrossRef Full Text | Google Scholar

355. Jezo T, Klasen M, Lamprea DR, Lyonnet F, Schienbein I. NLO+NLL limits on W′ and Z′ gauge boson masses in general extensions of the Standard Model. J High Energy Phys. (2014) 12:92. doi: 10.1007/JHEP12(2014)092

CrossRef Full Text | Google Scholar

356. Gavin R, Li Y, Petriello F, Quackenbush S. FEWZ 2.0: a code for hadronic Z production at next-to-next-to-leading order. Comput Phys Commun. (2011) 182:2388–403. doi: 10.1016/j.cpc.2011.06.008

CrossRef Full Text | Google Scholar

357. Gavin R, Li Y, Petriello F, Quackenbush S. W physics at the LHC with FEWZ 2.1. Comput Phys Commun. (2013) 184:208–14. doi: 10.1016/j.cpc.2012.09.005

CrossRef Full Text | Google Scholar

358. Appell D, Sterman GF, Mackenzie PB. Soft Gluons and the Normalization of the Drell-Yan Cross-section. Nucl Phys. (1988) B309:259–81. doi: 10.1016/0550-3213(88)90082-X

CrossRef Full Text | Google Scholar

359. Ferrari A, Collot J, Andrieux ML, Belhorma B, de Saintignon P, Hostachy JY, et al. Sensitivity study for new gauge bosons and right-handed Majorana neutrinos in pp collisions at $\sqrt{s}$ = 14 TeV. Phys Rev. (2000) D62:013001. doi: 10.1103/PhysRevD.62.013001

CrossRef Full Text | Google Scholar

360. Das SP, Deppisch FF, Kittel O, Valle JWF. Heavy neutrinos and lepton flavour violation in left-right symmetric models at the LHC. Phys Rev. (2012) D86:055006. doi: 10.1103/PhysRevD.86.055006

CrossRef Full Text | Google Scholar

361. Goh HS, Krenke CA. Lepton number violating signals of the top partners in the left-right twin higgs model. Phys Rev. (2010) D81:055008. doi: 10.1103/PhysRevD.81.055008

CrossRef Full Text | Google Scholar

362. The ATLAS Collaboration. Search for new resonances decaying to a charged lepton and a neutrino in pp collisions at $\sqrt{s}=13$ TeV with the ATLAS detector. ATLAS-CONF-2016-061 (2016).

363. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M. Search for heavy neutrinos and W bosons with right-handed couplings in proton-proton collisions $\sqrt{s}=8\text{TeV}$. Eur Phys J. (2014) C74:3149. doi: 10.1140/epjc/s10052-014-3149-z

CrossRef Full Text | Google Scholar

364. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Aşilar E, Bergauer T. Search for heavy gauge W' boson in events with an energetic lepton and large missing transverse momentum at $\sqrt{s}=$ 13 TeV. Phys Lett. (2017) B770:278–301. doi: 10.1016/j.physletb.2017.04.043

CrossRef Full Text | Google Scholar

365. Aguilar-Saavedra JA, Deppisch F, Kittel O, Valle JWF. Flavour in heavy neutrino searches at the LHC. Phys Rev. (2012) D85:091301. doi: 10.1103/PhysRevD.85.091301

CrossRef Full Text | Google Scholar

366. Chatrchyan S, Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Aguilo E, et al. Search for heavy neutrinos and W[R] bosons with right-handed couplings in a left-right symmetric model in pp collisions at sqrt(s) = 7 TeV. Phys Rev Lett. (2012) 109:261802. doi: 10.1103/PhysRevLett.109.261802

PubMed Abstract | CrossRef Full Text | Google Scholar

367. Quintero N, Diaz-Cruz JL, Lopéz Castro G. Lepton pair emission in the top quark decay t→bW⁺ℓ⁻ℓ⁺. Phys Rev. (2014) D89:093014. doi: 10.1103/PhysRevD.89.093014

CrossRef Full Text | Google Scholar

368. Maiezza A, Nemevšek M, Nesti F. Lepton number violation in higgs decay at LHC. Phys Rev Lett. (2015) 115:081802. doi: 10.1103/PhysRevLett.115.081802

PubMed Abstract | CrossRef Full Text | Google Scholar

369. Cottin G, Helo JC, Hirsch M. Searches for light sterile neutrinos with multitrack. Phys Rev. D (2018) 97:055025. doi: 10.1103/PhysRevD.97.055025

CrossRef Full Text | Google Scholar

370. Chen CH, Nomura T. Search for δ^±± with new decay patterns at the LHC. Phys Rev. (2015) D91:035023. doi: 10.1103/PhysRevD.91.035023

CrossRef Full Text | Google Scholar

371. Frank M, Hayreter A, Turan I. Production and Decays of W_R bosons at the LHC. Phys Rev. (2011) D83:035001. doi: 10.1103/PhysRevD.83.035001

CrossRef Full Text | Google Scholar

372. Dicus DA, Willenbrock S. Higgs boson production from heavy quark fusion. Phys Rev. (1989) D39:751. doi: 10.1103/PhysRevD.39.751

CrossRef Full Text | Google Scholar

373. Maltoni F, Ridolfi G, Ubiali M. b-initiated processes at the LHC: a reappraisal. J High Energy Phys. (2012) 7:22. doi: 10.1007/JHEP07(2012)022

CrossRef Full Text | Google Scholar

374. Dawson S, Ismail A, Low I. Redux on When is the top quark a parton?. Phys Rev. (2014) D90:014005. doi: 10.1103/PhysRevD.90.014005

CrossRef Full Text | Google Scholar

375. Han T, Sayre J, Westhoff S. Top-quark initiated processes at high-energy hadron colliders. J High Energy Phys. (2015) 4:145. doi: 10.1007/JHEP04(2015)145

CrossRef Full Text | Google Scholar

376. Kaya U, Sahin M, Sultansoy S. Majorana neutrino and W_R at TeV scale ep colliders. (2015) arXiv:1502.04115.

Google Scholar

377. Lindner M, Queiroz FS, Rodejohann W, Yaguna CE. Left-right symmetry and lepton number violation at the large hadron electron collider. J High Energy Phys. (2016) 6:140. doi: 10.1007/JHEP06(2016)140

CrossRef Full Text | Google Scholar

378. Buchmüller W, Greub C. Right-handed currents and heavy neutrinos in high-energy ep and e⁺e⁻ scattering. Nucl Phys. (1992) B381:109–28. doi: 10.1016/0550-3213(92)90642-O

CrossRef Full Text | Google Scholar

379. Mondal S, Rai SK. Reply to Comment on Polarized window for left-right symmetry and a right-handed neutrino at the Large Hadron-Electron Collider. Phys Rev. (2016) D93:118702. doi: 10.1103/PhysRevD.93.118702

CrossRef Full Text | Google Scholar

380. Mondal S, Rai SK. Polarized window for left-right symmetry and a right-handed neutrino at the Large Hadron-Electron Collider. Phys Rev. (2016) D93:011702. doi: 10.1103/PhysRevD.93.011702

CrossRef Full Text | Google Scholar

381. Sarmiento-Alvarado IA, Bouzas AO, Larios F. Analysis of top-quark charged-current coupling at the LHeC. J Phys. (2015) G42:085001. doi: 10.1088/0954-3899/42/8/085001

CrossRef Full Text | Google Scholar

382. Bhupal Dev PS, Lee CH, Mohapatra RN. TeV scale lepton number violation and baryogenesis. J Phys Conf Ser. (2015) 631:012007. doi: 10.1088/1742-6596/631/1/012007

CrossRef Full Text | Google Scholar

383. Gopalakrishna S, Han T, Lewis I, Si Zg, Zhou YF. Chiral couplings of W' and top quark polarization at the LHC. Phys Rev. (2010) D82:115020. doi: 10.1103/PhysRevD.82.115020

CrossRef Full Text | Google Scholar

384. Vasquez JC. Right-handed lepton mixings at the LHC. J High Energy Phys. (2016) 5:176. doi: 10.1007/JHEP05(2016)176

CrossRef Full Text | Google Scholar

385. Tello V, Nemevšek M, Nesti F, Senjanović G, Vissani F. Left-right symmetry: from LHC to neutrinoless double beta decay. Phys Rev Lett. (2011) 106:151801. doi: 10.1103/PhysRevLett.106.151801

PubMed Abstract | CrossRef Full Text | Google Scholar

386. Gluza J, Jeliński T. Heavy neutrinos and the pp → ℓℓjj CMS data. Phys Lett. (2015) B748:125–31. doi: 10.1016/j.physletb.2015.06.077

CrossRef Full Text | Google Scholar

387. Gluza J, Jelinski T, Szafron R. Lepton number violation and ‘Diracness' of massive neutrinos composed of Majorana states. Phys Rev. (2016) D93:113017. doi: 10.1103/PhysRevD.93.113017

CrossRef Full Text | Google Scholar

388. Bajc B, Nemevšek M, Senjanović G. Probing leptonic CP phases in LFV processes. Phys Lett. (2010) B684:231–5. doi: 10.1016/j.physletb.2010.01.025

CrossRef Full Text | Google Scholar

389. Frere JM, Hambye T, Vertongen G. Is leptogenesis falsifiable at LHC? J High Energy Phys. (2009) 1:51. doi: 10.1088/1126-6708/2009/01/051

CrossRef Full Text | Google Scholar

390. Dhuria M, Hati C, Rangarajan R, Sarkar U. Falsifying leptogenesis for a TeV scale $W_R^{\pm }$ at the LHC. Phys Rev. (2015) D92:031701. doi: 10.1103/PhysRevD.92.031701

CrossRef Full Text | Google Scholar

391. Deppisch FF, Harz J, Hirsch M. Falsifying high-scale leptogenesis at the LHC. Phys Rev Lett. (2014) 112:221601. doi: 10.1103/PhysRevLett.112.221601

PubMed Abstract | CrossRef Full Text | Google Scholar

392. Harz J, Huang WC, Ps H. Lepton number violation and the baryon asymmetry of the universe. Int J Mod Phys. (2015) A30:1530045. doi: 10.1142/S0217751X15300458

CrossRef Full Text | Google Scholar

393. Barry J, Rodejohann W. Lepton number and flavour violation in TeV-scale left-right symmetric theories with large left-right mixing. J High Energy Phys. (2013) 9:153. doi: 10.1007/JHEP09(2013)153

CrossRef Full Text | Google Scholar

394. Peng T, Ramsey-Musolf MJ, Winslow P. TeV lepton number violation: from neutrinoless double-β decay to the LHC. Phys Rev. (2016) D93:093002. doi: 10.1103/PhysRevD.93.093002

CrossRef Full Text | Google Scholar

395. Frank M, Saif HN. Signals of left-right supersymmetry in e+ e- collisions. Z Phys. (1996) C69:673–82. doi: 10.1007/s002880050071

CrossRef Full Text | Google Scholar

396. Demir DA, Frank M, Ghosh DK, Huitu K, Rai SK, Turan I. Doubly charged higgsinos at tevatron. Phys Rev. (2009) D79:095006. doi: 10.1103/PhysRevD.79.095006

CrossRef Full Text | Google Scholar

397. Appelquist T, Shrock R. Dynamical symmetry breaking of extended gauge symmetries. Phys Rev Lett. (2003) 90:201801. doi: 10.1103/PhysRevLett.90.201801

PubMed Abstract | CrossRef Full Text | Google Scholar

398. de Almeida FML, Coutinho YA, Martins Simoes JA, Ramalho AJ, Ribeiro Pinto L, Wulck S, et al. Double seesaw mechanism in a left-right symmetric model with TeV neutrinos. Phys Rev. (2010) D81:053005. doi: 10.1103/PhysRevD.81.053005

CrossRef Full Text | Google Scholar

399. Agashe K, Hong S, Vecchi L. Warped seesaw mechanism is physically inverted. Phys Rev. (2016) D94:013001. doi: 10.1103/PhysRevD.94.013001

CrossRef Full Text | Google Scholar

400. Agashe K, Du P, Hong S. LHC signals for singlet neutrinos from a natural warped seesaw (II). Phys Rev D (2017) 97:075032. doi: 10.1103/PhysRevD.97.075033

CrossRef Full Text | Google Scholar

401. Agashe K, Du P, Hong S. LHC signals for singlet neutrinos from a natural warped seesaw (II). Phys Rev D (2017) 97:075033. doi: 10.1103/PhysRevD.97.075033

CrossRef Full Text | Google Scholar

402. Bhupal Dev PS, Goswami S, Mitra M, Rodejohann W. Constraining neutrino mass from neutrinoless double beta decay. Phys Rev. (2013) D88:091301. doi: 10.1103/PhysRevD.88.091301

CrossRef Full Text | Google Scholar

403. Leonardi R, Alunni L, Romeo F, Fan L, Panella O. Hunting for heavy composite Majorana neutrinos at the LHC. Eur Phys J. (2016) C76:593. doi: 10.1140/epjc/s10052-016-4396-y

CrossRef Full Text | Google Scholar

404. Duarte L, Romero I, Peressutti J, Sampayo OA. Effective Majorana neutrino decay. Eur Phys J. (2016) C76:453. doi: 10.1140/epjc/s10052-016-4301-8

CrossRef Full Text | Google Scholar

405. Duarte L, Peressutti J, Sampayo OA. Not-that-heavy Majorana neutrino signals at the LHC. J Phys. (2018) G45:025001. doi: 10.1088/1361-6471/aa99f5

CrossRef Full Text | Google Scholar

406. Duarte L, Peressutti J, Sampayo OA. Majorana neutrino decay in an Effective Approach. Phys Rev. (2015) D92:093002. doi: 10.1103/PhysRevD.92.093002

CrossRef Full Text | Google Scholar

407. Gelmini GB, Roncadelli M. Left-handed neutrino mass scale and spontaneously broken lepton number. Phys Lett. (1981) 99B:411–5. doi: 10.1016/0370-2693(81)90559-1

CrossRef Full Text | Google Scholar

408. Fileviez Pérez P, Han T, Huang Gy, Li T, Wang K. Neutrino masses and the CERN LHC: testing type II seesaw. Phys Rev. (2008) D78:015018. doi: 10.1103/PhysRevD.78.015018

CrossRef Full Text | Google Scholar

409. Dutta B, Eusebi R, Gao Y, Ghosh T, Kamon T. Exploring the doubly charged Higgs boson of the left-right symmetric model using vector boson fusionlike events at the LHC. Phys Rev. (2014) D90:055015. doi: 10.1103/PhysRevD.90.055015

CrossRef Full Text | Google Scholar

410. Han T, Logan HE, Mukhopadhyaya B, Srikanth R. Neutrino masses and lepton-number violation in the littlest Higgs scenario. Phys Rev. (2005) D72:053007. doi: 10.1103/PhysRevD.72.053007

CrossRef Full Text | Google Scholar

411. Melfo A, Nemevšek M, Nesti F, Senjanović G, Zhang Y. Type II seesaw at LHC: the roadmap. Phys Rev. (2012) D85:055018. doi: 10.1103/PhysRevD.85.055018

CrossRef Full Text | Google Scholar

412. Arhrib A, Benbrik R, Chabab M, Moultaka G, Peyranère MC, Rahili L, et al. The higgs potential in the type II seesaw model. Phys Rev. (2011) D84:095005. doi: 10.1103/PhysRevD.84.095005

CrossRef Full Text | Google Scholar

413. Kanemura S, Yagyu K. Radiative corrections to electroweak parameters in the Higgs triplet model and implication with the recent Higgs boson searches. Phys Rev. (2012) D85:115009. doi: 10.1103/PhysRevD.85.115009

CrossRef Full Text | Google Scholar

414. Chen MC, Dawson S, Jackson CB. Higgs triplets, decoupling, and precision measurements. Phys Rev. (2008) D78:093001. doi: 10.1103/PhysRevD.78.093001

CrossRef Full Text | Google Scholar

415. Chen MC, Dawson S, Krupovnickas T. Constraining new models with precision electroweak data. Int J Mod Phys. (2006) A21:4045–70. doi: 10.1142/S0217751X0603388X

CrossRef Full Text | Google Scholar

416. Das D, Santamaria A. Updated scalar sector constraints in the Higgs triplet model. Phys Rev. (2016) D94:015015. doi: 10.1103/PhysRevD.94.015015

CrossRef Full Text | Google Scholar

417. Bhupal Dev PS, Ghosh DK, Okada N, Saha I. 125 GeV higgs boson and the type-II seesaw model. J High Energy Phys. (2013) 3:150. doi: 10.1007/JHEP05(2013)04910.1007/JHEP03(2013)150

CrossRef Full Text | Google Scholar

418. Dev PSB, Vila CM, Rodejohann W. Naturalness in testable type II seesaw scenarios. Nucl Phys. (2017) B921:436–53. doi: 10.1016/j.nuclphysb.2017.06.007

CrossRef Full Text | Google Scholar

419. Hooft G. Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking. NATO Sci Ser B (1980) 59:135–57. doi: 10.1007/978-1-4684-7571-5_9

CrossRef Full Text | Google Scholar

420. Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, Aben R. Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $\sqrt{s}=7$ and 8 TeV. J High Energy Phys. (2016) 8:45. doi: 10.1007/JHEP08(2016)045

CrossRef Full Text | Google Scholar

421. Akeroyd AG, Aoki M, Sugiyama H. Probing majorana phases and neutrino mass spectrum in the higgs triplet model at the CERN LHC. Phys Rev. (2008) D77:075010. doi: 10.1103/PhysRevD.77.075010

CrossRef Full Text | Google Scholar

422. Garayoa J, Schwetz T. Neutrino mass hierarchy and Majorana CP phases within the Higgs triplet model at the LHC. J High Energy Phys. (2008) 3:9. doi: 10.1088/1126-6708/2008/03/009

CrossRef Full Text | Google Scholar

423. Cuypers F, Davidson S. Bileptons: present limits and future prospects. Eur Phys J. (1998) C2:503–28. doi: 10.1007/s100529800705

CrossRef Full Text | Google Scholar

424. Tully MB, Joshi GC. Generating neutrino mass in the 331 model. Phys Rev. (2001) D64:011301. doi: 10.1103/PhysRevD.64.011301

CrossRef Full Text | Google Scholar

425. Fonseca RM, Hirsch M. Lepton number violation in 331 models. Phys Rev. (2016) D94:115003. doi: 10.1103/PhysRevD.94.115003

CrossRef Full Text | Google Scholar

426. Cogollo D, Diniz H, de S Pires CA, Rodrigues da Silva PS. The Seesaw mechanism at TeV scale in the 3-3-1 model with right-handed neutrinos. Eur Phys J. (2008) C58:455–61. doi: 10.1140/epjc/s10052-008-0749-5

CrossRef Full Text | Google Scholar

427. Georgi H, Glashow SL. Unity of all elementary particle forces. Phys Rev Lett. (1974) 32:438–41. doi: 10.1103/PhysRevLett.32.438

CrossRef Full Text | Google Scholar

428. Frampton PH. Chiral dilepton model and the flavor question. Phys Rev Lett. (1992) 69:2889–91. doi: 10.1103/PhysRevLett.69.2889

PubMed Abstract | CrossRef Full Text | Google Scholar

429. Pisano F, Pleitez V. An SU(3) × U(1) model for electroweak interactions. Phys Rev. (1992) D46:410–7. doi: 10.1103/PhysRevD.46.410

CrossRef Full Text | Google Scholar

430. Dorsner I, Fileviez Pérez P. Unification without supersymmetry: neutrino mass, proton decay and light leptoquarks. Nucl Phys. (2005) B723:53–76. doi: 10.1016/j.nuclphysb.2005.06.016

CrossRef Full Text | Google Scholar

431. Fileviez Pérez P, Han T, Li T, Ramsey-Musolf MJ. Leptoquarks and Neutrino Masses at the LHC. Nucl Phys. (2009) B819:139–76. doi: 10.1016/j.nuclphysb.2009.04.009

CrossRef Full Text | Google Scholar

432. Bahrami S, Frank M. Vector leptons in the higgs triplet model. Phys Rev. (2013) D88:095002. doi: 10.1103/PhysRevD.88.095002

CrossRef Full Text | Google Scholar

433. Nepomuceno A, Meirose B, Eccard F. First results on bilepton production based on LHC collision data and predictions for run II. Phys Rev. (2016) D94:055020. doi: 10.1103/PhysRevD.94.055020

CrossRef Full Text | Google Scholar

434. Corcella G, Coriano C, Costantini A, Frampton PH. Bilepton signatures at the LHC. Phys Lett. (2017) B773:544–52. doi: 10.1016/j.physletb.2017.09.015

CrossRef Full Text | Google Scholar

435. Meirose B, Nepomuceno AA. Searching for doubly-charged vector bileptons in the Golden Channel at the LHC. Phys Rev. (2011) D84:055002. doi: 10.1103/PhysRevD.84.055002

CrossRef Full Text | Google Scholar

436. Rizzo TG. Doubly charged higgs bosons and lepton number violating processes. Phys Rev. (1982) D25:1355–64. doi: 10.1103/PhysRevD.25.1355

CrossRef Full Text | Google Scholar

437. Akeroyd AG, Aoki M. Single and pair production of doubly charged Higgs bosons at hadron colliders. Phys Rev. (2005) D72:035011. doi: 10.1103/PhysRevD.72.035011

CrossRef Full Text | Google Scholar

438. Mühlleitner M, Spira M. A note on doubly charged Higgs pair production at hadron colliders. Phys Rev. (2003) D68:117701. doi: 10.1103/PhysRevD.68.117701

CrossRef Full Text | Google Scholar

439. Chen CS, Geng CQ, Zhuridov DV. Same-sign single dilepton productions at the LHC. Phys Lett. (2008) B666:340–3. doi: 10.1016/j.physletb.2008.07.088

CrossRef Full Text | Google Scholar

440. Han T, Mukhopadhyaya B, Si Z, Wang K. Pair production of doubly-charged scalars: neutrino mass constraints and signals at the LHC. Phys Rev. (2007) D76:075013. doi: 10.1103/PhysRevD.76.075013

CrossRef Full Text | Google Scholar

441. Drees M, Godbole RM, Nowakowski M, Rindani SD. gamma gamma processes at high-energy p p colliders. Phys Rev. (1994) D50:2335–8.

Google Scholar

442. Bambhaniya G, Chakrabortty J, Gluza J, Jelinski T, Szafron R. Search for doubly charged Higgs bosons through vector boson fusion at the LHC and beyond. Phys Rev. (2015) D92:015016. doi: 10.1103/PhysRevD.92.015016

CrossRef Full Text | Google Scholar

443. Babu KS, Jana S. Probing doubly charged higgs bosons at the LHC through photon initiated processes. Phys Rev. (2017) D95:055020. doi: 10.1103/PhysRevD.95.055020

CrossRef Full Text | Google Scholar

444. Ball RD, Bertone V, Carrazza S, Del Debbio L, Forte S, Guffanti A, et al. Parton distributions with QED corrections. Nucl Phys. (2013) B877:290–320. doi: 10.1016/j.nuclphysb.2013.10.010

CrossRef Full Text | Google Scholar

445. Ball RD, Bertone V, Carrazza S, Deans CS, Del Debbio L, Forte S, et al. Parton distributions for the LHC Run II. J High Energy Phys. (2015) 4:40. doi: 10.1007/JHEP04(2015)040

CrossRef Full Text | Google Scholar

446. Ghosh K, Jana S, Nandi S. Neutrino mass generation at TeV scale and new physics signatures from charged Higgs at the LHC for photon initiated processes. J High Energ Phys. (2018) 3:180. doi: 10.1007/JHEP03(2018)180

CrossRef Full Text | Google Scholar

447. del Águila F, Ametller L. On the detectability of sleptons at large hadron colliders. Phys Lett. (1991) B261:326–33. doi: 10.1016/0370-2693(91)90336-O

CrossRef Full Text | Google Scholar

448. Nemevšek M, Nesti F, Vasquez JC. Majorana Higgses at colliders. J High Energy Phys. (2017) 4:114. doi: 10.1007/JHEP04(2017)114

CrossRef Full Text | Google Scholar

449. del Águila F, Chala M. LHC bounds on lepton number violation mediated by doubly and singly-charged scalars. J High Energy Phys. (2014) 3:27. doi: 10.1007/JHEP03(2014)027

CrossRef Full Text | Google Scholar

450. del Águila F, Chala M. LNV-Scalars. Available online at: http://cafpe.ugr.es/index.php/pages/other/software

451. Roitgrund A, Eilam G, Bar-Shalom S. Implementation of the left-right symmetric model in FeynRules. Comput Phys Commun. (2016) 203:18–44. doi: 10.1016/j.cpc.2015.12.009

CrossRef Full Text | Google Scholar

452. Roitgrund A, Eilam G, Bar-Shalom S. FeynRules Mod-File for the MLRSM/QMLRSM. Available online at: https://drive.google.com/folderview?id=0BxMAGX_Tlpi9X0RUZW9tS2RaQ0E&usp=sharing

453. Georgi H, Machacek M. Doubly charged higgs bosons. Nucl Phys. (1985) B262:463–77. doi: 10.1016/0550-3213(85)90325-6

CrossRef Full Text | Google Scholar

454. Degrande C, Hartling K, Logan HE, Peterson AD, Zaro M. Georgi-Machacek Model at Next-to-Leading Order Accuracy. Available online at: http://feynrules.irmp.ucl.ac.be/wiki/GeorgiMachacekModel.

455. Aad G, Abajyan T, Abbott B, Abdallah J, Abdel Khalek S, Ali Abdelalim A. Search for long-lived, multi-charged particles in pp collisions $\sqrt{s}$ =7 TeV using the ATLAS detector. Phys Lett. (2013) B722:305–23. doi: 10.1016/j.physletb.2013.04.036

CrossRef Full Text | Google Scholar

456. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M. Search for heavy long-lived multi-charged particles in pp collisions at $\sqrt{s}=8$ TeV using the ATLAS detector. Eur Phys J. (2015) C75:362. doi: 10.1140/epjc/s10052-015-3534-2

CrossRef Full Text | Google Scholar

457. CMS Collaboration. Search for multi-charged heavy stable charged particles. CMS-PAS-EXO-11-090 (2012).

458. Barrie ND, Kobakhidze A, Liang S, Talia M, Wu L. Exotic lepton searches via bound state production at the LHC. Phys Lett. (2018) B781:364–7. doi: 10.1016/j.physletb.2018.03.087

CrossRef Full Text | Google Scholar

459. del Águila F, Chala M, Santamaria A, Wudka J. Discriminating between lepton number violating scalars using events with four and three charged leptons at the LHC. Phys Lett. (2013) B725:310–5. doi: 10.1016/j.physletb.2013.07.014

CrossRef Full Text | Google Scholar

460. Aaboud M, Aad G, Abbott B, Abdinov O, Abeloos B, Abidi SH. Search for doubly charged Higgs boson production in multi-lepton final states with the ATLAS detector using proton-proton collisions $\sqrt{s}=13\text{TeV}$. Eur Phys J. (2018) C78:199. doi: 10.1140/EPJC/S10052-018-5661-Z

CrossRef Full Text | Google Scholar

461. CMS Collaboration. A search for doubly-charged Higgs boson production in three and four lepton final states $\sqrt{s}=13\text{ TeV}$. CMS-PAS-HIG-16-036 (2017).

462. Nomura T, Okada H, Yokoya H. Discriminating leptonic Yukawa interactions with doubly charged scalar at the ILC. Nucl Phys. (2018) B929:193–206. doi: 10.1016/j.nuclphysb.2018.02.011

CrossRef Full Text | Google Scholar

463. Hays C, Mitra M, Spannowsky M, Waite P. Prospects for new physics in τ → lμμ at current and future colliders. J High Energy Phys. (2017) 5:14. doi: 10.1007/JHEP05(2017)014

CrossRef Full Text | Google Scholar

464. Frank M, Hamidian H. Higgs pair production in the left-right symmetric extension of the standard model. Nuovo Cim. (1995) A108:323–34. doi: 10.1007/BF02787059

CrossRef Full Text | Google Scholar

465. Rizzo TG. Inverse neutrinoless double beta decay. Phys Lett. (1982) 116B:23–8. doi: 10.1016/0370-2693(82)90027-2

CrossRef Full Text | Google Scholar

466. Rodejohann W. Inverse neutrino-less double beta decay revisited: neutrinos, higgs triplets and a muon collider. Phys Rev. (2010) D81:114001. doi: 10.1103/PhysRevD.81.114001

CrossRef Full Text | Google Scholar

467. Barry J, Dorame L, Rodejohann W. Linear collider test of a neutrinoless double beta decay mechanism in left-right symmetric theories. Eur Phys J. (2012) C72:2023. doi: 10.1140/epjc/s10052-012-2023-0

CrossRef Full Text | Google Scholar

468. Atwood D, Bar-Shalom S, Soni A. Signature of heavy Majorana neutrinos at a linear collider: enhanced charged Higgs pair production. Phys Rev. (2007) D76:033004. doi: 10.1103/PhysRevD.76.033004

CrossRef Full Text | Google Scholar

469. Ren P, Xing Zz. Lepton-number-violating decays of singly-charged Higgs bosons in the minimal type-(I+II) seesaw model at the TeV scale. Chin Phys. (2010) C34:433–43. doi: 10.1088/1674-1137/34/4/003

CrossRef Full Text | Google Scholar

470. Yue CX, Feng HL, Ma W. Heavy charged leptons from type-III seesaw and pair production of the Higgs boson H at the International Linear e⁺e⁻ Collider. Chin Phys Lett. (2010) 27:011202. doi: 10.1088/0256-307X/27/1/011202

CrossRef Full Text | Google Scholar

471. Banks T, Carpenter LM, Fortin JF. Undetected Higgs decays and neutrino masses in gauge mediated, lepton number violating models. J High Energy Phys. (2008) 9:87. doi: 10.1088/1126-6708/2008/09/087

CrossRef Full Text | Google Scholar

472. Hektor A, Kadastik M, Muntel M, Raidal M, Rebane L. Testing neutrino masses in little Higgs models via discovery of doubly charged Higgs at LHC. Nucl Phys. (2007) B787:198–210. doi: 10.1016/j.nuclphysb.2007.07.014

CrossRef Full Text | Google Scholar

473. Kadastik M, Raidal M, Rebane L. Direct determination of neutrino mass parameters at future colliders. Phys Rev. (2008) D77:115023. doi: 10.1103/PhysRevD.77.115023

CrossRef Full Text | Google Scholar

474. Chun EJ, Lee KY, Park SC. Testing Higgs triplet model and neutrino mass patterns. Phys Lett. (2003) B566:142–51. doi: 10.1016/S0370-2693(03)00770-6

CrossRef Full Text | Google Scholar

475. Abada A, Biggio C, Bonnet F, Gavela MB, Hambye T. mu → e gamma and tau → l gamma decays in the fermion triplet seesaw model. Phys Rev. (2008) D78:033007. doi: 10.1103/PhysRevD.78.033007

CrossRef Full Text | Google Scholar

476. Eboli OJP, Gonzalez-Fraile J, Gonzalez-Garcia MC. Neutrino masses at LHC: minimal lepton flavour violation in type-III see-saw. J High Energy Phys. (2011) 12:009. doi: 10.1007/JHEP12(2011)009

CrossRef Full Text | Google Scholar

477. Agostinho NR, Eboli OJP, Gonzalez-Garcia MC. LHC run I bounds on minimal lepton flavour violation in type-III see-saw: a case study. J High Energ Phys. (2017) 11:118. doi: 10.1007/JHEP11(2017)118

CrossRef Full Text | Google Scholar

478. Gogoladze I, Okada N, Shafi Q. Higgs boson mass bounds in the standard model with type III and type I seesaw. Phys Lett. (2008) B668:121–5. doi: 10.1016/j.physletb.2008.08.023

CrossRef Full Text | Google Scholar

479. He B, Okada N, Shafi Q. 125 GeV Higgs, type III seesaw and gauge Higgs unification. Phys Lett. (2012) B716:197–202. doi: 10.1016/j.physletb.2012.08.012

CrossRef Full Text | Google Scholar

480. Gogoladze I, He B, Shafi Q. New fermions at the LHC and mass of the higgs boson. Phys Lett. (2010) B690:495–500. doi: 10.1016/j.physletb.2010.05.076

CrossRef Full Text | Google Scholar

481. Li T, He XG. Neutrino masses and heavy triplet leptons at the LHC: testability of type III seesaw. Phys Rev. (2009) D80:093003. doi: 10.1103/PhysRevD.80.093003

CrossRef Full Text | Google Scholar

482. Arhrib A, Bajc B, Ghosh DK, Han T, Huang GY, Puljak I, et al. Collider signatures for heavy lepton triplet in type I+III seesaw. Phys Rev. (2010) D82:053004. doi: 10.1103/PhysRevD.82.053004

CrossRef Full Text | Google Scholar

483. He XG, Oh S. Lepton FCNC in type III seesaw model. J High Energy Phys. (2009) 9:27. doi: 10.1088/1126-6708/2009/09/027

CrossRef Full Text | Google Scholar

484. Franceschini R, Hambye T, Strumia A. Type-III see-saw at LHC. Phys Rev. (2008) D78:033002. doi: 10.1103/PhysRevD.78.033002

CrossRef Full Text | Google Scholar

485. Bajc B, Senjanović G. Seesaw at LHC. J High Energy Phys. (2007) 8:14. doi: 10.1088/1126-6708/2007/08/014

CrossRef Full Text | Google Scholar

486. Dorsner I, Fileviez Pérez P. Upper bound on the mass of the type III seesaw triplet in an SU(5) model. J High Energy Phys. (2007) 6:29. doi: 10.1088/1126-6708/2007/06/029

CrossRef Full Text | Google Scholar

487. Bajc B, Nemevšek M, Senjanović G. Probing seesaw at LHC. Phys Rev. (2007) D76:055011.

Google Scholar

488. Fileviez Pérez P. Renormalizable adjoint SU(5). Phys Lett. (2007) B654:189–93. doi: 10.1016/j.physletb.2007.07.075

CrossRef Full Text | Google Scholar

489. Aristizabal Sierra D, Kamenik JF, Nemevšek M. Implications of flavor dynamics for fermion triplet leptogenesis. J High Energy Phys. (2010) 10:36. doi: 10.1007/JHEP10(2010)036

CrossRef Full Text | Google Scholar

490. Aguilar-Saavedra JA, Boavida PM, Joaquim FR. Flavored searches for type-III seesaw mechanism at the LHC. Phys Rev. (2013) D88:113008. doi: 10.1103/PhysRevD.88.113008

CrossRef Full Text | Google Scholar

491. Biggio C, Calibbi L. Phenomenology of SUSY SU(5) with type I+III seesaw. J High Energy Phys. (2010) 10:37. doi: 10.1007/JHEP10(2010)037

CrossRef Full Text | Google Scholar

492. Chakrabortty J, Goswami S, Raychaudhuri A. An SO(10) model with adjoint fermions for double seesaw neutrino masses. Phys Lett. (2011) B698:265–70. doi: 10.1016/j.physletb.2011.03.016

CrossRef Full Text | Google Scholar

493. Gu PH. A left-right symmetric model with SU(2)-triplet fermions. Phys Rev. (2011) D84:097301. doi: 10.1103/PhysRevD.84.097301

CrossRef Full Text | Google Scholar

494. Mohapatra RN. Natural suppression of proton decay in supersymmetric type III seesaw models. Phys Lett. (2009) B679:382–5. doi: 10.1016/j.physletb.2009.07.064

CrossRef Full Text | Google Scholar

495. Delgado A, Garcia Cely C, Han T, Wang Z. Phenomenology of a lepton triplet. Phys Rev. (2011) D84:073007. doi: 10.1103/PhysRevD.84.073007

CrossRef Full Text | Google Scholar

496. Ma T, Zhang B, Cacciapaglia G. Triplet with a doubly-charged lepton at the LHC. Phys Rev. (2014) D89:015020. doi: 10.1103/PhysRevD.89.015020

CrossRef Full Text | Google Scholar

497. Yu Y, Yue CX, Yang S. Signatures of the quintuplet leptons at the LHC. Phys Rev. (2015) D91:093003. doi: 10.1103/PhysRevD.91.093003

CrossRef Full Text | Google Scholar

498. Nomura T, Okada H. Neutrino mass with large SU(2)_L multiplet fields. Phys Rev. (2017) D96:095017. doi: 10.1103/PhysRevD.96.095017

CrossRef Full Text | Google Scholar

499. Biggio C, Bonnet F. Implementation of the type III seesaw model in FeynRules/MadGraph and prospects for discovery with early LHC data. Eur Phys J. (2012) C72:1899. doi: 10.1140/epjc/s10052-012-1899-z

CrossRef Full Text | Google Scholar

500. Biggio C, Bonnet F. Type III Seesaw Model in FeynRules. Available online at: http://feynrules.irmp.ucl.ac.be/wiki/TypeIIISeeSaw

501. Minimal Lepton Flavor Violation Type III Seesaw Model. Available online at: http://feynrules.irmp.ucl.ac.be/wiki/MLFVtIIIseesaw

502. Choubey S, Mitra M. Spontaneous R-parity violating type III seesaw. J High Energy Phys. (2010) 5:21. doi: 10.1007/JHEP05(2010)021

CrossRef Full Text | Google Scholar

503. Bandyopadhyay P, Choi S, Chun EJ, Min K. Probing Higgs bosons via the type III seesaw mechanism at the LHC. Phys Rev. (2012) D85:073013. doi: 10.1103/PhysRevD.85.073013

CrossRef Full Text | Google Scholar

504. He XG, Oh S, Tandean J, Wen CC. Large mixing of light and heavy neutrinos in seesaw models and the LHC. Phys Rev. (2009) D80:073012. doi: 10.1103/PhysRevD.80.073012

CrossRef Full Text | Google Scholar

505. Bandyopadhyay P, Chun EJ. Displaced Higgs production in type III seesaw. J High Energy Phys. (2010) 11:006. doi: 10.1007/JHEP11(2010)006

CrossRef Full Text | Google Scholar

506. Aad G, et al. Search for heavy lepton resonances decaying to a Z boson and a lepton in pp collisions at $\sqrt{s}=8$ TeV with the ATLAS detector. J High Energy Phys. (2015) 9:108. doi: 10.1007/JHEP09(2015)108

CrossRef Full Text | Google Scholar

507. CMS Collaboration. Search for Type-III seesaw heavy fermions with multilepton final states using 2.3/fb of 13 TeV proton-proton collision data. CMS-PAS-EXO-16-002 (2016).

508. CMS Collaboration. Search for evidence of type-III seesaw mechanism in multilepton final states in pp collisions $\sqrt{s}=13\text{ TeV}$. Phys Rev Lett. (2017) 119:221802. doi: 10.1103/PhysRevLett.119.221802

PubMed Abstract | CrossRef Full Text

509. Goswami D, Poulose P. Direct searches of Type III seesaw triplet fermions at high energy e⁺e⁻ collider. Eur Phys J. (2018) C78:1. doi: 10.1140/epjc/s10052-017-5478-1

CrossRef Full Text | Google Scholar

510. Cai Y, Herrero García J, Schmidt MA, Vicente A, Volkas RR. From the trees to the forest: a review of radiative neutrino mass models. Front Phys. (2017) 5:63. doi: 10.3389/fphy.2017.00063

CrossRef Full Text | Google Scholar

511. Cai Y, Clarke JD, Schmidt MA, Volkas RR. Testing radiative neutrino mass models at the LHC. J High Energy Phys. (2015) 2:161. doi: 10.1007/JHEP02(2015)161

CrossRef Full Text | Google Scholar

512. Aristizabal Sierra D, Hirsch M, Kovalenko SG. Leptoquarks: neutrino masses and accelerator phenomenology. Phys Rev. (2008) D77:055011. doi: 10.1103/PhysRevD.77.055011

CrossRef Full Text | Google Scholar

513. Ma E. Verifiable radiative seesaw mechanism of neutrino mass and dark matter. Phys Rev. (2006) D73:077301. doi: 10.1103/PhysRevD.73.077301

CrossRef Full Text | Google Scholar

514. Ho SY, Tandean J. Probing scotogenic effects in higgs boson decays. Phys Rev. (2013) D87:095015. doi: 10.1103/PhysRevD.87.095015

CrossRef Full Text | Google Scholar

515. Ho SY, Tandean J. Probing scotogenic effects in e⁺e⁻ colliders. Phys Rev. (2014) D89:114025. doi: 10.1103/PhysRevD.89.114025

CrossRef Full Text | Google Scholar

516. Hessler AG, Ibarra A, Molinaro E, Vogl S. Probing the scotogenic FIMP at the LHC. J High Energy Phys. (2017) 1:100. doi: 10.1007/JHEP01(2017)100

CrossRef Full Text | Google Scholar

517. Daz MA, Rojas N, Urrutia-Quiroga S, Valle JWF. Heavy higgs boson production at colliders in the singlet-triplet scotogenic dark matter model. J High Energy Phys. (2017) 8:17. doi: 10.1007/JHEP08(2017)017

CrossRef Full Text | Google Scholar

518. Gustafsson M, No JM, Rivera MA. Predictive model for radiatively induced neutrino masses and mixings with dark matter. Phys Rev Lett. (2013) 110:211802. doi: 10.1103/PhysRevLett.110.211802

PubMed Abstract | CrossRef Full Text | Google Scholar

519. Ma E. Derivation of dark matter parity from lepton parity. Phys Rev Lett. (2015) 115:011801. doi: 10.1103/PhysRevLett.115.011801

PubMed Abstract | CrossRef Full Text | Google Scholar

520. Guo SY, Han ZL, Liao Y. Testing the type II radiative seesaw model: from dark matter detection to LHC signatures. Phys Rev. (2016) D94:115014. doi: 10.1103/PhysRevD.94.115014

CrossRef Full Text | Google Scholar

521. Kohda M, Sugiyama H, Tsumura K. Lepton number violation at the LHC with leptoquark and diquark. Phys Lett. (2013) B718:1436–40. doi: 10.1016/j.physletb.2012.12.048

CrossRef Full Text | Google Scholar

522. Adam J, Bai X, Baldini AM, Baracchini E, Bemporad C, Boca G, et al. New constraint on the existence of the μ⁺→e⁺γ decay. Phys Rev Lett. (2013) 110:201801. doi: 10.1103/PhysRevLett.110.201801

PubMed Abstract | CrossRef Full Text | Google Scholar

523. Baldini AM, Bao Y, Baracchini E, Bemporad C, Berg F, Biasotti M. Search for the lepton flavour violating decay μ⁺→e⁺γ with the full dataset of the MEG experiment. Eur Phys J. (2016) C76:434. doi: 10.1140/epjc/s10052-016-4271-x

CrossRef Full Text | Google Scholar

524. Herrero-Garcia J, Nebot M, Rius N, Santamaria A. The ZeeBabu model revisited in the light of new data. Nucl Phys. (2014) B885:542–70. doi: 10.1016/j.nuclphysb.2014.06.001

CrossRef Full Text | Google Scholar

525. Alcaide J, Chala M, Santamaria A. LHC signals of radiatively-induced neutrino masses and implications for the Zee-Babu model. Phys Lett. B779:107–16. doi: 10.1016/j.physletb.2018.02.001

CrossRef Full Text

526. Helo JC, Hirsch M, Ps H, Kovalenko SG. Short-range mechanisms of neutrinoless double beta decay at the LHC. Phys Rev. (2013) D88:073011. doi: 10.1103/PhysRevD.88.073011

CrossRef Full Text | Google Scholar

527. Helo JC, Hirsch M, Kovalenko SG, Pas H. Neutrinoless double beta decay and lepton number violation at the LHC. Phys Rev. (2013) D88:011901. doi: 10.1103/PhysRevD.88.011901

CrossRef Full Text | Google Scholar

528. Aad G, Abajyan T, Abbott B, Abdallah J, Khalek SA, Abdinov O. Search for direct top-squark pair production in final states with two leptons in pp collisions at $\sqrt{s}=$ 8TeV with the ATLAS detector. J High Energy Phys. (2014) 6:124. doi: 10.1007/JHEP06(2014)124

CrossRef Full Text | Google Scholar

529. Aaboud M, Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, et al. Search for scalar leptoquarks in pp collisions at $\sqrt{s}$ = 13 TeV with the ATLAS experiment. New J Phys. (2016) 18:093016. doi: 10.1088/1367-2630/18/9/093016

CrossRef Full Text | Google Scholar

530. Aad G, et al. Searches for scalar leptoquarks in pp collisions at $\sqrt{s}$ = 8 TeV with the ATLAS detector. Eur Phys J. (2016) C76:5. doi: 10.1140/epjc/s10052-015-3823-9

CrossRef Full Text | Google Scholar

531. CMS Collaboration. Search for pair-production of first generation scalar leptoquarks in pp collisions at $\sqrt{s}=13\text{ TeV}$ with 2.6 fb⁻¹. (2016).

532. CMS Collaboration. Search for pair-production of second-generation scalar leptoquarks in pp collisions at $\sqrt{s}=13\text{ TeV}$ with the CMS detector. (2016).

533. Collaboration C. Search for the third-generation scalar leptoquarks and heavy right-handed neutrinos in τ_ℓτ_hjj final states in pp collisions at 13 TeV. (2016).

Google Scholar

534. Collaboration TA. Search for long-lived charginos based on a disappearing-track signature in pp collisions at $\sqrt{s}=13$ TeV with the ATLAS detector. (2017).

Google Scholar

535. Aad G, Abajyan T, Abbott B, Abdallah J, Khalek SA, Abdinov O. Search for charginos nearly mass degenerate with the lightest neutralino based on a disappearing-track signature in pp collisions $\sqrt{s}$ =8 TeV with the ATLAS detector. Phys Rev. (2013) D88:112006. doi: 10.1103/PhysRevD.88.112006

CrossRef Full Text | Google Scholar

536. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M Search for disappearing tracks in proton-proton collisions at $\sqrt{s}=8$ TeV. J High Energy Phys. (2015) 1:96. doi: 10.1007/JHEP01(2015)096

CrossRef Full Text | Google Scholar